Fix typo

Update 04 Normal Mapping.md

.github/workflows/deploy.yml

@@ -1,34 +0,0 @@
-name: deploy
-on:
-  push:
-    branches: ['new-theme']
-jobs:
-  deploy:
-    runs-on: ubuntu-latest
-    steps:
-    - uses: actions/checkout@v4
-    - name: set up python
-      uses: actions/setup-python@v5
-      with:
-        python-version: 3.9
-    - name: install dependencies
-      shell: bash
-      run: |
-        pip install mkdocs==1.4.2 python-markdown-math==0.8
-    - name: build site
-      shell: bash
-      run: mkdocs build --clean
-    - name: deploy
-      shell: bash
-      env:
-        GH_NAME: ${{ secrets.GH_NAME }}
-        GH_EMAIL: ${{ secrets.GH_EMAIL }}
-        API_TOKEN: ${{ secrets.API_TOKEN }}
-      run: |
-        cd site
-        touch .nojekyll
-        git init
-        git add .
-        git -c user.name=$GH_NAME -c user.email=$GH_EMAIL commit -m "Auto Deployment"
-        git push -f -q "https://learnopengl-bot:$API_TOKEN@github.com/LearnOpenGL-CN/learnopengl-cn.github.io" master
-

README.md

@@ -1,17 +1,16 @@
 # LearnOpenGL中文化工程
 
-[![Status badge](https://github.com/LearnOpenGL-CN/LearnOpenGL-CN/actions/workflows/deploy.yml/badge.svg?branch=new-theme)](https://github.com/LearnOpenGL-CN/LearnOpenGL-CN/actions/workflows/deploy.yml)
+[![Build Status](https://travis-ci.org/LearnOpenGL-CN/LearnOpenGL-CN.svg?branch=new-theme)](https://travis-ci.org/LearnOpenGL-CN/LearnOpenGL-CN)
 
-learnopengl.com系列教程的中文翻译，目前正在校对及翻译中。
+**要更新的话请到`new-theme`分支，这个分支可能会停止更新**
 
-**英文原版**：[learnopengl.com](https://learnopengl.com/)
+learnopengl.com系列教程的中文翻译，目前正在翻译中。
 
-**目前状态**：
+**英文原版**：[learnopengl.com](learnopengl.com)
 
-- 原文大部分代码都有改变（使用的新的库），需要从头开始重新校对（Krasjet正在处理中，最重要的配置部分已经更新完毕）
-- 5-2节之后都没有按照新版的格式来排版，而且错误极多，也没有统一译名，需要进行整体的修改（Krasjet正在处理中，可能比较漫长）
-- 从头校对整体修改之后的文章（志愿者希望）
-- PBL 章节和 In Practice 章节下还有几篇教程没有翻译（志愿者希望）
+**当前翻译进度**：![Progress](http://progressed.io/bar/70?title=44/58)
+
+**目前状态**：请认领一下In Practice下的章节
 
 ## 阅读地址
 
@@ -51,20 +50,15 @@ learnopengl.com系列教程的中文翻译，目前正在校对及翻译中。
 05 Advanced Lighting/03 Shadows/02 Point Shadows.md
 ```
 
-**翻译之前请先阅读[样式指南](https://github.com/LearnOpenGL-CN/LearnOpenGL-CN/blob/new-theme/styleguide.md)**
-
 之后请联系我们，将您加入LearnOpenGL-CN组织，然后提交并Push您的翻译。或者您也可以Fork这个工程在本地编辑之后发送Pull Request。
 
-## 样式指南
-
-在文档的写作过程中，请遵守我们的[样式指南](https://github.com/LearnOpenGL-CN/LearnOpenGL-CN/blob/new-theme/styleguide.md)方便之后的校对以及修改工作。
-
 ## 构建
 
-首先请安装Python 3.7+，之后初始化环境：
+首先请安装Python，2和3都可以，之后初始化环境：
 
 ```bash
-$ pip install mkdocs==1.4.2 python-markdown-math==0.8
+$ pip install mkdocs
+$ python setup.py install
 ```
 
 初始化以后，每次构建只需要输入以下指令即可，构建后的文件在`site`文件夹内：
@@ -85,6 +79,10 @@ $ mkdocs serve
 
 如果您发现教程有任何错误的话，欢迎Fork这个工程并发送Pull Request到 `new-theme` 分支。如果您不想修改的话，可以点击页面上方的 `Issues` 按钮提交一个Issue，我们看到后会及时更正。如果是对教程的内容有问题，请先查看原文，如果不是翻译错误的话，请直接在原网站评论区向作者（JoeyDeVries）反馈。
 
+## 样式指南
+
+在文档的写作过程中，请遵守我们的[样式指南](https://github.com/LearnOpenGL-CN/LearnOpenGL-CN/blob/new-theme/styleguide.md)方便之后的校对以及修改工作。
+
 ## 联系方式
 
-QQ群：383745868
+QQ群：383745868

docs/01 Getting started/01 OpenGL.md

@@ -3,15 +3,15 @@
 原文     | [OpenGL](http://learnopengl.com/#!Getting-started/OpenGL)
       ---|---
 作者     | JoeyDeVries
-翻译     | gjy_1992, Krasjet
-校对     | 暂未校对
+翻译     | gjy_1992
+校对     | Geequlim
 
 
 在开始这段旅程之前我们先了解一下OpenGL到底是什么。一般它被认为是一个API(<def>Application Programming Interface</def>, 应用程序编程接口)，包含了一系列可以操作图形、图像的函数。然而，OpenGL本身并不是一个API，它仅仅是一个由[Khronos组织](http://www.khronos.org/)制定并维护的规范(Specification)。
 
 <img alt="OpenGL Logo" src="../../img/01/01/opengl.jpg" class="right" />
 
-OpenGL规范严格规定了每个函数该如何执行，以及它们的输出值。至于内部具体每个函数是如何实现(Implement)的，将由OpenGL库的开发者自行决定（译注：这里开发者是指编写OpenGL库的人）。因为OpenGL规范并没有规定实现的细节，具体的OpenGL库允许使用不同的实现，只要其功能和结果与规范相匹配（亦即，作为用户不会感受到功能上的差异）。
+OpenGL规范严格规定了每个函数该如何执行，以及它们的输出值。至于内部具体每个函数是如何实现(Implement)的，将由OpenGL库的开发者自行决定（注：这里开发者是指编写OpenGL库的人）。因为OpenGL规范并没有规定实现的细节，具体的OpenGL库允许使用不同的实现，只要其功能和结果与规范相匹配（亦即，作为用户不会感受到功能上的差异）。
 
 实际的OpenGL库的开发者通常是显卡的生产商。你购买的显卡所支持的OpenGL版本都为这个系列的显卡专门开发的。当你使用Apple系统的时候，OpenGL库是由Apple自身维护的。在Linux下，有显卡生产商提供的OpenGL库，也有一些爱好者改编的版本。这也意味着任何时候OpenGL库表现的行为与规范规定的不一致时，基本都是库的开发者留下的bug。
 
@@ -23,9 +23,9 @@ OpenGL规范严格规定了每个函数该如何执行，以及它们的输出
 
 ## 核心模式与立即渲染模式
 
-早期的OpenGL使用<def>立即渲染模式</def>（Immediate mode，也就是<def>固定渲染管线</def>），这个模式下绘制图形很方便。OpenGL的大多数功能都被库隐藏起来，开发者很少有控制OpenGL如何进行计算的自由。而开发者迫切希望能有更多的灵活性。随着时间推移，规范越来越灵活，开发者对绘图细节有了更多的掌控。立即渲染模式确实容易使用和理解，但是效率太低。因此从OpenGL3.2开始，规范文档开始废弃立即渲染模式，并鼓励开发者在OpenGL的<def>核心模式</def>(Core-profile)下进行开发，这个分支的规范完全移除了旧的特性。
+早期的OpenGL使用<def>立即渲染模式</def>（Immediate mode，也就是<def>固定渲染管线</def>），这个模式下绘制图形很方便。OpenGL的大多数功能都被库隐藏起来，开发者很少能控制OpenGL如何进行计算的自由。而开发者迫切希望能有更多的灵活性。随着时间推移，规范越来越灵活，开发者对绘图细节有了更多的掌控。立即渲染模式确实容易使用和理解，但是效率太低。因此从OpenGL3.2开始，规范文档开始废弃立即渲染模式，推出<def>核心模式</def>(Core-profile)，这个模式完全移除了旧的特性。
 
-当使用OpenGL的核心模式时，OpenGL迫使我们使用现代的函数。当我们试图使用一个已废弃的函数时，OpenGL会抛出一个错误并终止绘图。现代函数的优势是更高的灵活性和效率，然而也更难于学习。立即渲染模式从OpenGL**实际**运作中抽象掉了很多细节，因此它在易于学习的同时，也很难让人去把握OpenGL具体是如何运作的。现代函数要求使用者真正理解OpenGL和图形编程，它有一些难度，然而提供了更多的灵活性，更高的效率，更重要的是可以更深入的理解图形编程。
+当使用OpenGL的核心模式时，OpenGL迫使我们使用现代的函数。当我们试图使用一个已废弃的函数时，OpenGL会抛出一个错误并终止绘图。现代函数的优势是更高的灵活性和效率，然而也更难于学习。立即渲染模式从OpenGL**实际**运作中抽象掉了很多细节，因而它易于学习的同时，也很难去把握OpenGL具体是如何运作的。现代函数要求使用者真正理解OpenGL和图形编程，它有一些难度，然而提供了更多的灵活性，更高的效率，更重要的是可以更深入的理解图形编程。
 
 这也是为什么我们的教程面向OpenGL3.3的核心模式。虽然上手更困难，但这份努力是值得的。
 
@@ -46,7 +46,7 @@ OpenGL的一大特性就是对扩展(Extension)的支持，当一个显卡公司
 ```c++
 if(GL_ARB_extension_name)
 {
-    // 使用硬件支持的全新的现代特性
+    // 使用一些新的特性
 }
 else
 {
@@ -62,7 +62,7 @@ OpenGL自身是一个巨大的状态机(State Machine)：一系列的变量描
 
 假设当我们想告诉OpenGL去画线段而不是三角形的时候，我们通过改变一些上下文变量来改变OpenGL状态，从而告诉OpenGL如何去绘图。一旦我们改变了OpenGL的状态为绘制线段，下一个绘制命令就会画出线段而不是三角形。
 
-当使用OpenGL的时候，我们会遇到一些<def>状态设置</def>函数(State-changing Function)，这类函数将会改变上下文。以及<def>状态使用</def>函数(State-using Function)，这类函数会根据当前OpenGL的状态执行一些操作。只要你记住OpenGL本质上是个大状态机，就能更容易理解它的大部分特性。
+当使用OpenGL的时候，我们会遇到一些<def>状态设置</def>函数(State-changing Function)，这类函数将会改变上下文。以及<def>状态应用</def>函数(State-using Function)，这类函数会根据当前OpenGL的状态执行一些操作。只要你记住OpenGL本质上是个大状态机，就能更容易理解它的大部分特性。
 
 ## 对象
 
@@ -72,30 +72,33 @@ OpenGL库是用C语言写的，同时也支持多种语言的派生，但其内
 
 ```c++
 struct object_name {
-    float  option1;
-    int    option2;
-    char[] name;
+    GLfloat  option1;
+    GLuint   option2;
+    GLchar[] name;
 };
 ```
 
-!!! note "译注"
-
-	在更新前的教程中一直使用的都是OpenGL的基本类型，但由于作者觉得在本教程系列中并没有一个必须使用它们的原因，所有的类型都改为了自带类型。但是请仍然记住，使用OpenGL的类型的好处是保证了在各平台中每一种类型的大小都是统一的。你也可以使用其它的定宽类型(Fixed-width Type)来实现这一点。
+!!! important
+	
+	**基元类型(Primitive Type)**
+	
+	使用OpenGL时，建议使用OpenGL定义的基元类型。比如使用`float`时我们加上前缀`GL`（因此写作`GLfloat`）。`int`、`uint`、`char`、`bool`等等也类似。OpenGL定义的这些GL基元类型的内存布局是与平台无关的，而int等基元类型在不同操作系统上可能有不同的内存布局。使用GL基元类型可以保证你的程序在不同的平台上工作一致。
 
 当我们使用一个对象时，通常看起来像如下一样（把OpenGL上下文看作一个大的结构体）：
 
 ```c++
 // OpenGL的状态
-struct OpenGL_Context {
-  	...
-  	object* object_Window_Target;
-  	...  	
+struct OpenGL_Context 
+{
+    ...
+    object* object_Window_Target;
+    ...  	
 };
 ```
 
 ```c++
 // 创建对象
-unsigned int objectId = 0;
+GLuint objectId = 0;
 glGenObject(1, &objectId);
 // 绑定对象至上下文
 glBindObject(GL_WINDOW_TARGET, objectId);

docs/01 Getting started/02 Creating a window.md

@@ -3,52 +3,50 @@
 原文     | [Creating a window](http://learnopengl.com/#!Getting-started/Creating-a-window)
       ---|---
 作者     | JoeyDeVries
-翻译     | gjy_1992, Krasjet
-校对     | 暂未校对
+翻译     | gjy_1992
+校对     | Geequlim
 
-!!! note "译注"
+在我们画出出色的效果之前，首先要做的就是创建一个OpenGL上下文(Context)和一个用于显示的窗口。然而，这些操作在每个系统上都是不一样的，OpenGL有目的地从这些操作抽象(Abstract)出去。这意味着我们不得不自己处理创建窗口，定义OpenGL上下文以及处理用户输入。
 
-	注意，由于作者对教程做出了更新，之前本节使用的是GLEW库，但现在改为了使用GLAD库，关于GLEW配置的部分现在已经被修改，但我仍决定将这部分教程保留起来，放到一个历史存档中，如果有需要的话可以到[这里](../legacy.md)来查看。
-
-在我们画出出色的效果之前，首先要做的就是创建一个OpenGL上下文(Context)和一个用于显示的窗口。然而，这些操作在每个系统上都是不一样的，OpenGL有意将这些操作抽象(Abstract)出去。这意味着我们不得不自己处理创建窗口，定义OpenGL上下文以及处理用户输入。
-
-幸运的是，有一些库已经提供了我们所需的功能，其中一部分是特别针对OpenGL的。这些库节省了我们书写操作系统相关代码的时间，提供给我们一个窗口和一个OpenGL上下文用来渲染。最流行的几个库有GLUT，SDL，SFML和GLFW。在教程里我们将使用**GLFW**。你可以随意选用其他类似的库，大多数库的配置方法和GLFW差不多。
+幸运的是，有一些库已经提供了我们所需的功能，其中一部分是特别针对OpenGL的。这些库节省了我们书写操作系统相关代码的时间，提供给我们一个窗口和上下文用来渲染。最流行的几个库有GLUT，SDL，SFML和GLFW。在教程里我们将使用**GLFW**。
 
 ## GLFW
 
-GLFW是一个专门针对OpenGL的C语言库，它提供了一些渲染物体所需的最低限度的接口。它允许用户创建OpenGL上下文、定义窗口参数以及处理用户输入，对我们来说这就够了。
+GLFW是一个专门针对OpenGL的C语言库，它提供了一些渲染物体所需的最低限度的接口。它允许用户创建OpenGL上下文，定义窗口参数以及处理用户输入，这正是我们需要的。
 
-本节和下一节的目标是把GLFW环境配好能且能够跑起来，并保证它正确创建了OpenGL上下文并显示出一个简单的窗口来让我们随意使用。这篇教程会一步步教你如何获取、编译、链接GLFW库。我们使用的是Microsoft Visual Studio 2019 IDE（操作过程在更新的Visual Studio都是相同的）。如果你用的不是Visual Studio（或者用的是它的旧版本）请不要担心，大多数IDE上的操作都是类似的。
+<img alt="GLFW Logo" src="../../img/01/02/glfw.png" class="right" />
+
+本节和下一节的目标是建立GLFW环境，并保证它恰当地创建OpenGL上下文并显示窗口。这篇教程会一步步从获取、编译、链接GLFW库讲起。我们使用的是Microsoft Visual Studio 2012 IDE（操作过程在新版的Visual Studio都是相同的）。如果你用的不是Visual Studio（或者用的是它的旧版本）请不要担心，大多数IDE上的操作都是类似的。
 
 ## 构建GLFW
 
-GLFW可以从它官方网站的[下载页](http://www.glfw.org/download.html)上获取。GLFW已提供为Visual Studio（2012到2019都有）预编译好的二进制版本和相应的头文件，但是为了完整性我们将从编译源代码开始。所以我们需要下载**源代码包**。
+GLFW可以从它官方网站的[下载页](http://www.glfw.org/download.html)上获取。GLFW已经有针对Visual Studio 2012/2013的预编译的二进制版本和相应的头文件，但是为了完整性我们将从编译源代码开始。所以我们需要下载**源代码包**。
 
 
 !!! Attention
 
-	本教程中，我们将采用64位构建所有的库。因此如果您使用的是预编译的二进制文件，请确保你下载的是64位的二进制文件。
+	当你下载二进制版本时，请下载32位的版本而不是64位的除非你清楚你在做什么。大部分读者反映64位版本会出现很多奇怪的问题。
 
 下载源码包之后，将其解压并打开。我们只需要里面的这些内容：
 
 - 编译生成的库
 - **include**文件夹
 
-从源代码编译库可以保证生成的库完全适合你的操作系统和CPU的，而预编译的二进制文件则并非总是提供（有时候，即便提供了预编译的二进制文件，也可能不适用于您的系统）。开放源代码所产生问题在于：并不是每个人都用相同的IDE或者构建系统来搞开发，因而提供的项目/解决方案文件可能和一些人的IDE不兼容。所以人们必须使用给定的.c/.cpp和.h/.hpp文件来自己建立项目/解决方案，这是一项很枯燥的工作。但因此也诞生了一个叫做CMake的工具。
+从源代码编译库可以保证生成的库是兼容你的操作系统和CPU的，而预编译的二进制文件可能会出现兼容问题（甚至有时候没提供支持你系统的文件）。提供源代码所产生的一个问题在于不是每个人都用相同的IDE开发程序，因而提供的工程文件可能和一些人的IDE不兼容。所以人们只能从.cpp和.h文件来自己建立工程，这是一项笨重的工作。因此诞生了一个叫做CMake的工具。
 
 ### CMake
 
-CMake是一个工程文件生成工具。用户可以使用预定义好的CMake脚本，根据自己的选择（像是Visual Studio, Code::Blocks, Eclipse）生成不同IDE的工程文件。这允许我们从GLFW源码创建一个Visual Studio 2019工程文件，之后进行编译。首先，我们需要从[这里](http://www.cmake.org/cmake/resources/software.html)下载安装CMake。
+CMake是一个工程文件生成工具。用户可以使用预定义好的CMake脚本，根据自己的选择（像是Visual Studio, Code::Blocks, Eclipse）生成不同IDE的工程文件。这允许我们从GLFW源码里创建一个Visual Studio 2012工程文件，之后进行编译。首先，我们需要从[这里](http://www.cmake.org/cmake/resources/software.html)下载安装CMake。我选择的是Win32安装程序。
 
-当CMake安装成功后，你可以选择从命令行或者GUI启动CMake，由于我们不想让事情变得太过复杂，我们选择用GUI。CMake需要一个源代码目录和一个存放编译结果的目标文件目录。源代码目录我们选择GLFW的源代码的根目录，然后我们新建一个 *build* 文件夹，选中作为目标目录。
+当CMake安装成功后，你可以选择从命令行或者GUI启动CMake，由于我不想让事情变得太过复杂，我们选择用GUI。CMake需要一个源代码目录和一个存放编译结果的目标文件目录。源代码目录我们选择GLFW的源代码的根目录，然后我们新建一个 *build* 文件夹，选中作为目标目录。
 
 ![](../img/01/02/cmake.png)
 
-在设置完源代码目录和目标目录之后，点击**Configure(设置)**按钮，让CMake读取设置和源代码。我们接下来需要选择工程的生成器，由于我们使用的是Visual Studio 2019，我们选择 **Visual Studio 16** 选项（因为Visual Studio 2019的内部版本号是16）。CMake会显示可选的编译选项用来配置最终生成的库。这里我们使用默认设置，并再次点击**Configure(设置)**按钮保存设置。保存之后，点击**Generate(生成)**按钮，生成的工程文件会在你的**build**文件夹中。
+之后，点击**Configure(设置)**按钮，让CMake读取设置和源代码。接下来，我们选择工程的生成器为**Visual Studio 11**（因为Visual Studio 2012的内部版本号是11.0）。CMake会显示可选的编译选项，这里我们使用默认设置，再次点击**Configure(设置)**按钮保存设置。保存之后，点击**Generate(生成)**按钮，生成的工程文件会在你的**build**文件夹中。
 
 ### 编译
 
-在**build**文件夹里可以找到**GLFW.sln**文件，用Visual Studio 2019打开。因为CMake已经配置好了项目，并按照默认配置将其编译为64位的库，所以我们直接点击**Build Solution(生成解决方案)**按钮，然后在**build/src/Debug**文件夹内就会出现我们编译出的库文件**glfw3.lib**。
+在**build**文件夹里可以找到**GLFW.sln**文件，用Visual Studio 2012打开。因为CMake已经配置好了项目，所以我们直接点击**Build Solution(生成解决方案)**按钮，然后编译的库**glfw3.lib**（注意我们用的是第3版）就会出现在**src/Debug**文件夹内。
 
 库生成完毕之后，我们需要让IDE知道库和头文件的位置。有两种方法：
 
@@ -59,11 +57,7 @@ CMake是一个工程文件生成工具。用户可以使用预定义好的CMake
 
 ## 我们的第一个工程
 
-首先，打开Visual Studio，创建一个新的项目。如果VS提供了多个选项，选择Visual C++，然后选择**Empty Project(空项目)**（别忘了给你的项目起一个合适的名字）。由于我们将在64位模式中执行所有操作，而新项目默认是32位的，因此我们需要将Debug旁边顶部的下拉列表从x86更改为x64：
-
-![](../img/01/02/x64.png)
-
-现在我们终于有一个空的工作空间了，开始创建我们第一个OpenGL程序吧！
+首先，打开Visual Studio，创建一个新的项目。如果VS提供了多个选项，选择Visual C++，然后选择**Empty Project(空项目)**（别忘了给你的项目起一个合适的名字）。现在我们终于有一个空的工作空间了，开始创建我们第一个OpenGL程序吧。
 
 ## 链接
 
@@ -87,7 +81,7 @@ CMake是一个工程文件生成工具。用户可以使用预定义好的CMake
 
 ### Windows上的OpenGL库
 
-如果你是Windows平台，**opengl32.lib**已经包含在Microsoft SDK里了，它在Visual Studio安装的时候就默认安装了。由于这篇教程用的是VS编译器，并且是在Windows操作系统上，我们只需将**opengl32.lib**添加进连接器设置里就行了。值得注意的是，OpenGL库64位版本的文件名仍然是**opengl32.lib**（和32位版本一样），虽然很奇怪但确实如此。
+如果你是Windows平台，**opengl32.lib**已经包含在Microsoft SDK里了，它在Visual Studio安装的时候就默认安装了。由于这篇教程用的是VS编译器，并且是在Windows操作系统上，我们只需将**opengl32.lib**添加进连接器设置里就行了。
 
 ### Linux上的OpenGL库
 
@@ -99,15 +93,11 @@ CMake是一个工程文件生成工具。用户可以使用预定义好的CMake
 #include <GLFW\glfw3.h>
 ```
 
-!!! Important
-
-	对于用GCC编译的Linux用户建议使用这个命令行选项`-lglfw3 -lGL -lX11 -lpthread -lXrandr -lXi -ldl`。没有正确链接相应的库会产生 *undefined reference* (未定义的引用) 这个错误。
-
 GLFW的安装与配置就到此为止。
 
-## GLAD
+## GLEW
 
-到这里还没有结束，我们仍然还有一件事要做。因为OpenGL只是一个标准/规范，具体的实现是由驱动开发商针对特定显卡实现的。由于OpenGL驱动版本众多，它大多数函数的位置都无法在编译时确定下来，需要在运行时查询。所以任务就落在了开发者身上，开发者需要在运行时获取函数地址并将其保存在一个函数指针中供以后使用。取得地址的方法[因平台而异](https://www.khronos.org/opengl/wiki/Load_OpenGL_Functions)，在Windows上会是类似这样：
+到这里，我们仍然有一件事要做。因为OpenGL只是一个标准/规范，具体的实现是由驱动开发商针对特定显卡实现的。由于OpenGL驱动版本众多，它大多数函数的位置都无法在编译时确定下来，需要在运行时查询。任务就落在了开发者身上，开发者需要在运行时获取函数地址并将其保存在一个函数指针中供以后使用。取得地址的方法因平台而异，在Windows上会是类似这样：
 
 ```c++
 // 定义函数原型
@@ -119,29 +109,40 @@ GLuint buffer;
 glGenBuffers(1, &buffer);
 ```
 
-你可以看到代码非常复杂，而且很繁琐，我们需要对每个可能使用的函数都要重复这个过程。幸运的是，有些库能简化此过程，其中**GLAD**是目前最新，也是最流行的库。
+你可以看到代码非常复杂，而且很繁琐，我们需要对每个可能使用的函数都要重复这个过程。幸运的是，有些库能简化此过程，其中**GLEW**是目前最新，也是最流行的库。
 
-### 配置GLAD
+### 编译和链接GLEW
 
-GLAD是一个[开源](https://github.com/Dav1dde/glad)的库，它能解决我们上面提到的那个繁琐的问题。GLAD的配置与大多数的开源库有些许的不同，GLAD使用了一个[在线服务](http://glad.dav1d.de/)。在这里我们能够告诉GLAD需要定义的OpenGL版本，并且根据这个版本加载所有相关的OpenGL函数。
+GLEW是OpenGL Extension Wrangler Library的缩写，它能解决我们上面提到的那个繁琐的问题。因为GLEW也是一个库，我们同样需要构建并将其链接进工程。GLEW可以从[这里](http://glew.sourceforge.net/index.html)下载，你同样可以选择下载二进制版本，如果你的目标平台列在上面的话，或者下载源码编译，步骤和编译GLFW时差不多。记住，如果不确定的话，选择32位的二进制版本。
 
-打开GLAD的[在线服务](http://glad.dav1d.de/)，将语言(Language)设置为**C/C++**，在API选项中，选择**3.3**以上的OpenGL(gl)版本（我们的教程中将使用3.3版本，但更新的版本也能用）。之后将模式(Profile)设置为**Core**，并且保证选中了**生成加载器**(Generate a loader)选项。现在可以先（暂时）忽略扩展(Extensions)中的内容。都选择完之后，点击**生成**(Generate)按钮来生成库文件。
+我们使用GLEW的**静态**版本**glew32s.lib**（注意这里的“s”），将库文件添加到你的库目录，将**include**内容添加到你的include目录。接下来，在VS的链接器选项里加上**glew32s.lib**。注意GLFW3（默认）也是编译成了一个静态库。
 
-GLAD现在应该提供给你了一个zip压缩文件，包含两个头文件目录，和一个**glad.c**文件。将两个头文件目录（**glad**和**KHR**）复制到你的**Include**文件夹中（或者增加一个额外的项目指向这些目录），并添加**glad.c**文件到你的工程中。
 
-经过前面的这些步骤之后，你就应该可以将以下的指令加到你的文件顶部了：
+!!! Important
+
+	**静态**(Static)链接是指编译时就将库代码里的内容整合进你的二进制文件。优点就是你不需要管理额外的文件了，只需要发布你单独的一个二进制文件就行了。缺点就是你的可执行文件会变得更大，另外当库有升级版本时，你必须重新进行编译整个程序。
+	
+	**动态**(Dynamic)链接是指一个库通过`.dll`或`.so`的方式存在，它的代码与你的二进制文件的代码是分离的。优点是使你的二进制文件大小变小并且更容易升级，缺点是你最终发布程序时必须带上这些DLL。
+
+如果你希望静态链接GLEW，必须在包含GLEW头文件之前定义预处理器宏`GLEW_STATIC`：
 
 ```c++
-#include <glad/glad.h> 
+#define GLEW_STATIC
+#include <GL/glew.h>
 ```
 
-点击编译按钮应该不会给你提示任何的错误，到这里我们就已经准备好继续学习[下一节](03 Hello Window.md)去真正使用GLFW和GLAD来设置OpenGL上下文并创建一个窗口了。记得确保你的头文件和库文件的目录设置正确，以及链接器里引用的库文件名正确。如果仍然遇到错误，可以先看一下评论有没有人遇到类似的问题，请参考额外资源中的例子或者在下面的评论区提问。
+如果你希望动态链接，那么你可以省略这个宏。但是记住使用动态链接的话你需要拷贝一份.DLL文件到你的应用程序目录。
+
+!!! Important
+
+	对于用GCC编译的Linux用户建议使用这个命令行选项`-lGLEW -lglfw3 -lGL -lX11 -lpthread -lXrandr -lXi`。没有正确链接相应的库会产生 *undefined reference*(未定义的引用) 这个错误。
+
+我们现在成功编译了GLFW和GLEW库，我们已经准备好将进入[下一节](03 Hello Window.md)去真正使用GLFW和GLEW来设置OpenGL上下文并创建窗口。记得确保你的头文件和库文件的目录设置正确，以及链接器里引用的库文件名正确。如果仍然遇到错误，可以先看一下评论有没有人遇到类似的问题，请参考额外资源中的例子或者在下面的评论区提问。
 
 ## 附加资源
 
-- [GLFW: Window Guide](http://www.glfw.org/docs/latest/window_guide.html)：GLFW官方的配置GLFW窗口的指南。
-- [Building applications](http://www.opengl-tutorial.org/miscellaneous/building-your-own-c-application/)：提供了很多编译或链接相关的信息和一大列错误及对应的解决方案。
-- [GLFW with Code::Blocks](http://wiki.codeblocks.org/index.php?title=Using_GLFW_with_Code::Blocks)：使用Code::Blocks IDE编译GLFW。
-- [Running CMake](http://www.cmake.org/runningcmake/)：简要的介绍如何在Windows和Linux上使用CMake。
-- [Writing a build system under Linux](http://learnopengl.com/demo/autotools_tutorial.txt)：Wouter Verholst写的一个autotools的教程，讲的是如何在Linux上编写构建系统，尤其是针对这些教程。
-- [Polytonic/Glitter](https://github.com/Polytonic/Glitter)：一个简单的样板项目，它已经提前配置了所有相关的库；如果你想要很方便地搞到一个LearnOpenGL教程的范例工程，这也是很不错的。
+- [Building applications](http://www.opengl-tutorial.org/miscellaneous/building-your-own-c-application/): 提供了很多编译或链接相关的信息和一大列错误及对应的解决方案。
+- [GLFW with Code::Blocks](http://wiki.codeblocks.org/index.php?title=Using_GLFW_with_Code::Blocks):使用Code::Blocks IDE编译GLFW。
+- [Running CMake](http://www.cmake.org/runningcmake/): 简要的介绍如何在Windows和Linux上使用CMake。
+- [Writing a build system under Linux](http://learnopengl.com/demo/autotools_tutorial.txt): Wouter Verholst写的一个autotools的教程，讲的是如何在Linux上编写构建系统，尤其是针对这些教程。
+- [Polytonic/Glitter](https://github.com/Polytonic/Glitter): 一个简单的样板项目，它已经提前配置了所有相关的库；如果你想要很方便地搞到一个LearnOpenGL教程的范例工程，这也是很不错的。

docs/01 Getting started/03 Hello Window.md

@@ -3,19 +3,22 @@
 原文     | [Hello Window](http://learnopengl.com/#!Getting-started/Hello-Window)
       ---|---
 作者     | JoeyDeVries
-翻译     | Geequlim, Krasjet
-校对     | 暂未校对
+翻译     | Geequlim
+校对     | Geequlim
 
-让我们试试能不能让GLFW正常工作。首先，新建一个`.cpp`文件，然后把下面的代码粘贴到该文件的最前面。
+让我们试试能不能让GLFW正常工作。首先，新建一个`.cpp`文件，然后把下面的代码粘贴到该文件的最前面。注意，之所以定义`GLEW_STATIC`宏，是因为我们使用的是GLEW静态的链接库。
 
 ```c++
-#include <glad/glad.h>
+// GLEW
+#define GLEW_STATIC
+#include <GL/glew.h>
+// GLFW
 #include <GLFW/glfw3.h>
 ```
 
 !!! Attention
 
-	请确认是在包含GLFW的头文件之前包含了GLAD的头文件。GLAD的头文件包含了正确的OpenGL头文件（例如`GL/gl.h`），所以需要在其它依赖于OpenGL的头文件之前包含GLAD。
+	请确认在包含GLFW的头文件之前包含了GLEW的头文件。在包含glew.h头文件时会引入许多OpenGL必要的头文件（例如`GL/gl.h`），所以你需要在包含其它依赖于OpenGL的头文件之前先包含GLEW。
 
 接下来我们创建<fun>main</fun>函数，在这个函数中我们将会实例化GLFW窗口：
 
@@ -26,15 +29,15 @@ int main()
     glfwWindowHint(GLFW_CONTEXT_VERSION_MAJOR, 3);
     glfwWindowHint(GLFW_CONTEXT_VERSION_MINOR, 3);
     glfwWindowHint(GLFW_OPENGL_PROFILE, GLFW_OPENGL_CORE_PROFILE);
-    //glfwWindowHint(GLFW_OPENGL_FORWARD_COMPAT, GL_TRUE);
-  
+    glfwWindowHint(GLFW_RESIZABLE, GL_FALSE);
+
     return 0;
 }
 ```
 
-首先，我们在main函数中调用<fun>glfwInit</fun>函数来初始化GLFW，然后我们可以使用<fun>glfwWindowHint</fun>函数来配置GLFW。<fun>glfwWindowHint</fun>函数的第一个参数代表选项的名称，我们可以从很多以`GLFW_`开头的枚举值中选择；第二个参数接受一个整型，用来设置这个选项的值。该函数的所有的选项以及对应的值都可以在 [GLFW's window handling](http://www.glfw.org/docs/latest/window.html#window_hints) 这篇文档中找到。如果你现在编译你的cpp文件会得到大量的 *undefined reference* (未定义的引用)错误，也就是说你并未顺利地链接GLFW库。
+首先，我们在main函数中调用<fun>glfwInit</fun>函数来初始化GLFW，然后我们可以使用<fun>glfwWindowHint</fun>函数来配置GLFW。<fun>glfwWindowHint</fun>函数的第一个参数代表选项的名称，我们可以从很多以`GLFW_`开头的枚举值中选择；第二个参数接受一个整形，用来设置这个选项的值。该函数的所有的选项以及对应的值都可以在 [GLFW's window handling](http://www.glfw.org/docs/latest/window.html#window_hints) 这篇文档中找到。如果你现在编译你的cpp文件会得到大量的 *undefined reference* (未定义的引用)错误，也就是说你并未顺利地链接GLFW库。
 
-由于本站的教程都是基于OpenGL 3.3版本展开讨论的，所以我们需要告诉GLFW我们要使用的OpenGL版本是3.3，这样GLFW会在创建OpenGL上下文时做出适当的调整。这也可以确保用户在没有适当的OpenGL版本支持的情况下无法运行。我们将主版本号(Major)和次版本号(Minor)都设为3。我们同样明确告诉GLFW我们使用的是核心模式(Core-profile)。明确告诉GLFW我们需要使用核心模式意味着我们只能使用OpenGL功能的一个子集（没有我们已不再需要的向后兼容特性）。如果使用的是Mac OS X系统，你还需要加下面这行代码到你的初始化代码中这些配置才能起作用（将上面的代码解除注释）：
+由于本站的教程都是基于OpenGL 3.3版本展开讨论的，所以我们需要告诉GLFW我们要使用的OpenGL版本是3.3，这样GLFW会在创建OpenGL上下文时做出适当的调整。这也可以确保用户在没有适当的OpenGL版本支持的情况下无法运行。我们将主版本号(Major)和次版本号(Minor)都设为3。我们同样明确告诉GLFW我们使用的是核心模式(Core-profile)，并且不允许用户调整窗口的大小。在明确告诉GLFW使用核心模式的情况下，使用旧版函数将会导致**invalid operation**(无效操作)的错误，而这不正是一个很好的提醒吗？在我们不小心用了旧函数时报错，就能避免使用一些被废弃的用法了。如果使用的是Mac OS X系统，你还需要加下面这行代码到你的初始化代码中这些配置才能起作用：
 
 ```c++
 glfwWindowHint(GLFW_OPENGL_FORWARD_COMPAT, GL_TRUE);
@@ -47,8 +50,8 @@ glfwWindowHint(GLFW_OPENGL_FORWARD_COMPAT, GL_TRUE);
 接下来我们创建一个窗口对象，这个窗口对象存放了所有和窗口相关的数据，而且会被GLFW的其他函数频繁地用到。
 
 ```c++
-GLFWwindow* window = glfwCreateWindow(800, 600, "LearnOpenGL", NULL, NULL);
-if (window == NULL)
+GLFWwindow* window = glfwCreateWindow(800, 600, "LearnOpenGL", nullptr, nullptr);
+if (window == nullptr)
 {
     std::cout << "Failed to create GLFW window" << std::endl;
     glfwTerminate();
@@ -57,32 +60,35 @@ if (window == NULL)
 glfwMakeContextCurrent(window);
 ```
 
-<fun>glfwCreateWindow</fun>函数需要窗口的宽和高作为它的前两个参数。第三个参数表示这个窗口的名称（标题），这里我们使用`"LearnOpenGL"`，当然你也可以使用你喜欢的名称。最后两个参数我们暂时忽略。这个函数将会返回一个<fun>GLFWwindow</fun>对象，我们会在其它的GLFW操作中使用到。创建完窗口我们就可以通知GLFW将我们窗口的上下文设置为当前线程的主上下文了。
+<fun>glfwCreateWindow</fun>函数需要窗口的宽和高作为它的前两个参数；第三个参数表示这个窗口的名称（标题），这里我们使用`"LearnOpenGL"`，当然你也可以使用你喜欢的名称；最后两个参数我们暂时忽略，先设置为空指针就行。它的返回值<fun>GLFWwindow</fun>对象的指针会在其他的GLFW操作中使用到。创建完窗口我们就可以通知GLFW将我们窗口的上下文设置为当前线程的主上下文了。
 
-## GLAD
+## GLEW
 
-在之前的教程中已经提到过，GLAD是用来管理OpenGL的函数指针的，所以在调用任何OpenGL的函数之前我们需要初始化GLAD。
+在之前的教程中已经提到过，GLEW是用来管理OpenGL的函数指针的，所以在调用任何OpenGL的函数之前我们需要初始化GLEW。
 
 ```c++
-if (!gladLoadGLLoader((GLADloadproc)glfwGetProcAddress))
+glewExperimental = GL_TRUE;
+if (glewInit() != GLEW_OK)
 {
-    std::cout << "Failed to initialize GLAD" << std::endl;
+    std::cout << "Failed to initialize GLEW" << std::endl;
     return -1;
 }
 ```
 
-我们给GLAD传入了用来加载系统相关的OpenGL函数指针地址的函数。GLFW给我们的是`glfwGetProcAddress`，它根据我们编译的系统定义了正确的函数。
+请注意，我们在初始化GLEW之前设置<var>glewExperimental</var>变量的值为`GL_TRUE`，这样做能让GLEW在管理OpenGL的函数指针时更多地使用现代化的技术，如果把它设置为`GL_FALSE`的话可能会在使用OpenGL的核心模式时出现一些问题。
 
+## 视口(Viewport)
 
-## 视口
-
-在我们开始渲染之前还有一件重要的事情要做，我们必须告诉OpenGL渲染窗口的尺寸大小，即视口(Viewport)，这样OpenGL才只能知道怎样根据窗口大小显示数据和坐标。我们可以通过调用<fun>glViewport</fun>函数来设置视口的**尺寸**(Dimension)：
+在我们开始渲染之前还有一件重要的事情要做，我们必须告诉OpenGL渲染窗口的尺寸大小，这样OpenGL才只能知道怎样相对于窗口大小显示数据和坐标。我们可以通过调用<fun>glViewport</fun>函数来设置窗口的**维度**(Dimension)：
 
 ```c++
-glViewport(0, 0, 800, 600);
+int width, height;
+glfwGetFramebufferSize(window, &width, &height);
+  
+glViewport(0, 0, width, height);
 ```
 
-<fun>glViewport</fun>函数前两个参数控制窗口左下角的位置。第三个和第四个参数控制渲染窗口的宽度和高度（像素）。
+<fun>glViewport</fun>函数前两个参数控制窗口左下角的位置。第三个和第四个参数控制渲染窗口的宽度和高度（像素），这里我们是直接从GLFW中获取的。我们从GLFW中获取视口的维度而不设置为800*600是为了让它在高DPI的屏幕上（比如说Apple的视网膜显示屏）也能[正常工作](http://www.glfw.org/docs/latest/window.html#window_size)。
 
 我们实际上也可以将视口的维度设置为比GLFW的维度小，这样子之后所有的OpenGL渲染将会在一个更小的窗口中显示，这样子的话我们也可以将一些其它元素显示在OpenGL视口之外。
 
@@ -90,46 +96,21 @@ glViewport(0, 0, 800, 600);
 
 	OpenGL幕后使用<fun>glViewport</fun>中定义的位置和宽高进行2D坐标的转换，将OpenGL中的位置坐标转换为你的屏幕坐标。例如，OpenGL中的坐标(-0.5, 0.5)有可能（最终）被映射为屏幕中的坐标(200,450)。注意，处理过的OpenGL坐标范围只为-1到1，因此我们事实上将(-1到1)范围内的坐标映射到(0, 800)和(0, 600)。
 
-然而，当用户改变窗口的大小的时候，视口也应该被调整。我们可以对窗口注册一个回调函数(Callback Function)，它会在每次窗口大小被调整的时候被调用。这个回调函数的原型如下：
-
-```c++
-void framebuffer_size_callback(GLFWwindow* window, int width, int height);
-```
-
-这个帧缓冲大小函数需要一个<fun>GLFWwindow</fun>作为它的第一个参数，以及两个整数表示窗口的新维度。每当窗口改变大小，GLFW会调用这个函数并填充相应的参数供你处理。
-
-```c++
-void framebuffer_size_callback(GLFWwindow* window, int width, int height)
-{
-    glViewport(0, 0, width, height);
-}
-```
-
-我们还需要注册这个函数，告诉GLFW我们希望每当窗口调整大小的时候调用这个函数：
-
-```c++
-glfwSetFramebufferSizeCallback(window, framebuffer_size_callback);
-```
-
-当窗口被第一次显示的时候<fun>framebuffer_size_callback</fun>也会被调用。对于视网膜(Retina)显示屏，<var>width</var>和<var>height</var>都会明显比原输入值更高一点。
-
-我们还可以将我们的函数注册到其它很多的回调函数中。比如说，我们可以创建一个回调函数来处理手柄输入变化，处理错误消息等。我们会在创建窗口之后，渲染循环初始化之前注册这些回调函数。
-
 # 准备好你的引擎
 
-我们可不希望只绘制一个图像之后我们的应用程序就立即退出并关闭窗口。我们希望程序在我们主动关闭它之前不断绘制图像并能够接受用户输入。因此，我们需要在程序中添加一个while循环，我们可以把它称之为<def>渲染循环</def>(Render Loop)，它能在我们让GLFW退出前一直保持运行。下面几行的代码就实现了一个简单的渲染循环：
+我们可不希望只绘制一个图像之后我们的应用程序就立即退出并关闭窗口。我们希望程序在我们明确地关闭它之前不断绘制图像并能够接受用户输入。因此，我们需要在程序中添加一个while循环，我们可以把它称之为<def>游戏循环</def>(Game Loop)，它能在我们让GLFW退出前一直保持运行。下面几行的代码就实现了一个简单的游戏循环：
 
 ```c++
 while(!glfwWindowShouldClose(window))
 {
+    glfwPollEvents();
     glfwSwapBuffers(window);
-    glfwPollEvents();    
 }
 ```
 
-- <fun>glfwWindowShouldClose</fun>函数在我们每次循环的开始前检查一次GLFW是否被要求退出，如果是的话，该函数返回`true`，渲染循环将停止运行，之后我们就可以关闭应用程序。
-- <fun>glfwPollEvents</fun>函数检查有没有触发什么事件（比如键盘输入、鼠标移动等）、更新窗口状态，并调用对应的回调函数（可以通过回调方法手动设置）。
-- <fun>glfwSwapBuffers</fun>函数会交换颜色缓冲（它是一个储存着GLFW窗口每一个像素颜色值的大缓冲），它在这一迭代中被用来绘制，并且将会作为输出显示在屏幕上。
+- <fun>glfwWindowShouldClose</fun>函数在我们每次循环的开始前检查一次GLFW是否被要求退出，如果是的话该函数返回`true`然后游戏循环便结束了，之后为我们就可以关闭应用程序了。
+- <fun>glfwPollEvents</fun>函数检查有没有触发什么事件（比如键盘输入、鼠标移动等），然后调用对应的回调函数（可以通过回调方法手动设置）。我们一般在游戏循环的开始调用事件处理函数。
+- <fun>glfwSwapBuffers</fun>函数会交换颜色缓冲（它是一个储存着GLFW窗口每一个像素颜色的大缓冲），它在这一迭代中被用来绘制，并且将会作为输出显示在屏幕上。
 
 !!! Important
 
@@ -139,7 +120,7 @@ while(!glfwWindowShouldClose(window))
 
 ## 最后一件事
 
-当渲染循环结束后我们需要正确释放/删除之前的分配的所有资源。我们可以在<fun>main</fun>函数的最后调用<fun>glfwTerminate</fun>函数来完成。
+当游戏循环结束后我们需要正确释放/删除之前的分配的所有资源。我们可以在<fun>main</fun>函数的最后调用<fun>glfwTerminate</fun>函数来释放GLFW分配的内存。
 
 ```c++
 glfwTerminate();
@@ -150,54 +131,57 @@ return 0;
 
 ![](../img/01/03/hellowindow.png)
 
-如果你看见了一个非常无聊的黑色窗口，那么就对了！如果你没得到正确的结果，或者你不知道怎么把所有东西放到一起，请到[这里](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/1.1.hello_window/hello_window.cpp)参考源代码。
+如果你看见了一个非常无聊的黑色窗口，那么就对了！如果你没得到正确的结果，或者你不知道怎么把所有东西放到一起，请到[这里](http://learnopengl.com/code_viewer.php?code=getting-started/hellowindow)参考源代码。
 
 如果程序编译有问题，请先检查连接器选项是否正确，IDE中是否导入了正确的目录（前面教程解释过）。并且请确认你的代码是否正确，直接对照上面提供的源代码就行了。如果还是有问题，欢迎评论，我或者其他人可能会帮助你的。
 
 ## 输入
 
-我们同样也希望能够在GLFW中实现一些输入控制，这可以通过使用GLFW的几个输入函数来完成。我们将会使用GLFW的<fun>glfwGetKey</fun>函数，它需要一个窗口以及一个按键作为输入。这个函数将会返回这个按键是否正在被按下。我们将创建一个<fun>processInput</fun>函数来让所有的输入代码保持整洁。
+我们同样也希望能够在GLFW中实现一些键盘控制，这可以通过使用GLFW的回调函数(Callback Function)来完成。<def>回调函数</def>事实上是一个函数指针，当我们设置好后，GLWF会在合适的时候调用它。**按键回调**(KeyCallback)是众多回调函数中的一种。当我们设置了按键回调之后，GLFW会在用户有键盘交互时调用它。该回调函数的原型如下所示：
 
 ```c++
-void processInput(GLFWwindow *window)
-{
-    if(glfwGetKey(window, GLFW_KEY_ESCAPE) == GLFW_PRESS)
-        glfwSetWindowShouldClose(window, true);
-}
+void key_callback(GLFWwindow* window, int key, int scancode, int action, int mode);
 ```
 
-这里我们检查用户是否按下了返回键(Esc)（如果没有按下，<fun>glfwGetKey</fun>将会返回<var>GLFW_RELEASE</var>。如果用户的确按下了返回键，我们将通过使用<fun>glfwSetwindowShouldClose</fun>把`WindowShouldClose`属性设置为 `true`来关闭GLFW。下一次while循环的条件检测将会失败，程序将关闭。
+按键回调函数接受一个<fun>GLFWwindow</fun>指针作为它的第一个参数；第二个整形参数用来表示按下的按键；`action`参数表示这个按键是被按下还是释放；最后一个整形参数表示是否有Ctrl、Shift、Alt、Super等按钮的操作。GLFW会在合适的时候调用它，并为各个参数传入适当的值。
 
-我们接下来在渲染循环的每一个迭代中调用<fun>processInput</fun>：
 
 ```c++
-while (!glfwWindowShouldClose(window))
+void key_callback(GLFWwindow* window, int key, int scancode, int action, int mode)
 {
-    processInput(window);
-
-    glfwSwapBuffers(window);
-    glfwPollEvents();
-}
+    // 当用户按下ESC键,我们设置window窗口的WindowShouldClose属性为true
+    // 关闭应用程序
+    if(key == GLFW_KEY_ESCAPE && action == GLFW_PRESS)
+    	glfwSetWindowShouldClose(window, GL_TRUE);
+}    
 ```
 
-这就给我们一个非常简单的方式来检测特定的键是否被按下，并在每一帧做出处理。
+在我们（新创建的）<fun>key_callback</fun>函数中，我们检测了键盘是否按下了Escape键。如果键的确按下了(不释放)，我们使用<fun>glfwSetwindowShouldClose</fun>函数设定`WindowShouldClose`属性为`true`从而关闭GLFW。main函数的`while`循环下一次的检测将为失败，程序就关闭了。
+
+最后一件事就是通过GLFW注册我们的函数至合适的回调，代码是这样的:
+
+```c++
+glfwSetKeyCallback(window, key_callback);  
+```
+
+除了按键回调函数之外，我们还能我们自己的函数注册其它的回调。例如，我们可以注册一个回调函数来处理窗口尺寸变化、处理一些错误信息等。我们可以在创建窗口之后，开始游戏循环之前注册各种回调函数。
+
 
 ## 渲染
 
-我们要把所有的渲染(Rendering)操作放到渲染循环中，因为我们想让这些渲染指令在每次渲染循环迭代的时候都能被执行。代码将会是这样的：
+我们要把所有的渲染(Rendering)操作放到游戏循环中，因为我们想让这些渲染指令在每次游戏循环迭代的时候都能被执行。代码将会是这样的：
 
 ```c++
-// 渲染循环
+// 程序循环
 while(!glfwWindowShouldClose(window))
 {
-    // 输入
-    processInput(window);
+    // 检查事件
+    glfwPollEvents();
 
     // 渲染指令
     ...
 
-    // 检查并调用事件，交换缓冲
-    glfwPollEvents();
+    // 交换缓冲
     glfwSwapBuffers(window);
 }
 ```
@@ -213,10 +197,10 @@ glClear(GL_COLOR_BUFFER_BIT);
 
 !!! Important
 
-	你应该能够回忆起来我们在 *OpenGL* 这节教程的内容，<fun>glClearColor</fun>函数是一个**状态设置**函数，而<fun>glClear</fun>函数则是一个**状态使用**的函数，它使用了当前的状态来获取应该清除为的颜色。
+	你应该能够回忆起来我们在 *OpenGL* 这节教程的内容，<fun>glClearColor</fun>函数是一个状态设置函数，而<fun>glClear</fun>函数则是一个状态应用的函数。
 
 ![](../img/01/03/hellowindow2.png)
 
-这个程序的完整源代码可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/1.2.hello_window_clear/hello_window_clear.cpp)找到。
+这个程序的完整源代码可以在[这里](http://learnopengl.com/code_viewer.php?code=getting-started/hellowindow2)找到。
 
-好了，现在我们已经做好开始在渲染循环中添加许多渲染调用的准备了，但这是[下一节](04 Hello Triangle.md)教程了，这一节的内容已经太多了。
+好了，现在我们已经做好开始在游戏循环中添加许多渲染调用的准备了，但这是[下一节](04 Hello Triangle.md)教程了，这一节的内容已经太多了。

docs/01 Getting started/04 Hello Triangle.md

@@ -3,18 +3,9 @@
 原文     | [Hello Triangle](http://www.learnopengl.com/#!Getting-started/Hello-Triangle)
       ---|---
 作者     | JoeyDeVries
-翻译     | [Django](http://bullteacher.com/), Krasjet, Geequlim
-校对     | Kang Lin <kl222@126.com>, [AoZhang](https://github.com/SuperAoao)
+翻译     | [Django](http://bullteacher.com/)
+校对     | Geequlim
 
-!!! note "译注"
-
-	在学习此节之前，建议将这三个单词先记下来：
-	
-	- 顶点数组对象：Vertex Array Object，VAO
-	- 顶点缓冲对象：Vertex Buffer Object，VBO
-	- 元素缓冲对象：Element Buffer Object，EBO 或 索引缓冲对象 Index Buffer Object，IBO
-	
-	当指代这三个东西的时候，可能使用的是全称，也可能用的是英文缩写，翻译的时候和原文保持的一致。由于没有英文那样的分词间隔，中文全称的部分可能不太容易注意。但请记住，缩写和中文全称指代的是一个东西。
 
 在OpenGL中，任何事物都在3D空间中，而屏幕和窗口却是2D像素数组，这导致OpenGL的大部分工作都是关于把3D坐标转变为适应你屏幕的2D像素。3D坐标转为2D坐标的处理过程是由OpenGL的<def>图形渲染管线</def>（Graphics Pipeline，大多译为管线，实际上指的是一堆原始图形数据途经一个输送管道，期间经过各种变化处理最终出现在屏幕的过程）管理的。图形渲染管线可以被划分为两个主要部分：第一部分把你的3D坐标转换为2D坐标，第二部分是把2D坐标转变为实际的有颜色的像素。这个教程里，我们会简单地讨论一下图形渲染管线，以及如何利用它创建一些漂亮的像素。
 
@@ -24,7 +15,7 @@
 
 图形渲染管线接受一组3D坐标，然后把它们转变为你屏幕上的有色2D像素输出。图形渲染管线可以被划分为几个阶段，每个阶段将会把前一个阶段的输出作为输入。所有这些阶段都是高度专门化的（它们都有一个特定的函数），并且很容易并行执行。正是由于它们具有并行执行的特性，当今大多数显卡都有成千上万的小处理核心，它们在GPU上为每一个（渲染管线）阶段运行各自的小程序，从而在图形渲染管线中快速处理你的数据。这些小程序叫做<def>着色器</def>(Shader)。
 
-有些着色器可以由开发者配置，因为允许用自己写的着色器来代替默认的，所以能够更细致地控制图形渲染管线中的特定部分了。因为它们运行在GPU上，所以节省了宝贵的CPU时间。OpenGL着色器是用<def>OpenGL着色器语言</def>(OpenGL Shading Language, <def>GLSL</def>)写成的，在下一节中我们再花更多时间研究它。
+有些着色器允许开发者自己配置，这就允许我们用自己写的着色器来替换默认的。这样我们就可以更细致地控制图形渲染管线中的特定部分了，而且因为它们运行在GPU上，所以它们可以给我们节约宝贵的CPU时间。OpenGL着色器是用<def>OpenGL着色器语言</def>(OpenGL Shading Language, <def>GLSL</def>)写成的，在下一节中我们再花更多时间研究它。
 
 下面，你会看到一个图形渲染管线的每个阶段的抽象展示。要注意蓝色部分代表的是我们可以注入自定义的着色器的部分。
 
@@ -32,7 +23,7 @@
 
 如你所见，图形渲染管线包含很多部分，每个部分都将在转换顶点数据到最终像素这一过程中处理各自特定的阶段。我们会概括性地解释一下渲染管线的每个部分，让你对图形渲染管线的工作方式有个大概了解。
 
-首先，我们以数组的形式传递3个3D坐标作为图形渲染管线的输入，用来表示一个三角形，这个数组叫做顶点数据(Vertex Data)；顶点数据是一系列顶点的集合。一个<def>顶点</def>(Vertex)是一个3D坐标的数据的集合。而这样一个顶点的数据是用<def>顶点属性</def>(Vertex Attribute)表示的，它可以包含任何我们想用的数据，但是简单起见，我们还是假定每个顶点只由一个3D位置(译注1)和一些颜色值组成的吧。
+首先，我们以数组的形式传递3个3D坐标作为图形渲染管线的输入，用来表示一个三角形，这个数组叫做顶点数据(Vertex Data)；顶点数据是一系列顶点的集合。一个<def>顶点</def>(Vertex)是一个3D坐标的数据的集合。而顶点数据是用<def>顶点属性</def>(Vertex Attribute)表示的，它可以包含任何我们想用的数据，但是简单起见，我们还是假定每个顶点只由一个3D位置(译注1)和一些颜色值组成的吧。
 
 !!! note "译注1"
 
@@ -44,11 +35,11 @@
 
 图形渲染管线的第一个部分是<def>顶点着色器</def>(Vertex Shader)，它把一个单独的顶点作为输入。顶点着色器主要的目的是把3D坐标转为另一种3D坐标（后面会解释），同时顶点着色器允许我们对顶点属性进行一些基本处理。
 
-顶点着色器阶段的输出可以选择性地传递给<def>几何着色器</def>(Geometry Shader)。几何着色器将一组顶点作为输入，这些顶点形成图元，并且能够通过发出新的顶点来形成新的(或其他)图元来生成其他形状。在这个例子中，它从给定的形状中生成第二个三角形。
+<def>图元装配</def>(Primitive Assembly)阶段将顶点着色器输出的所有顶点作为输入（如果是<var>GL_POINTS</var>，那么就是一个顶点），并所有的点装配成指定图元的形状；本节例子中是一个三角形。
 
-<def>图元装配</def>(Primitive Assembly)阶段将顶点着色器（或几何着色器）输出的所有顶点作为输入（如果是<var>GL_POINTS</var>，那么就是一个顶点），并将所有的点装配成指定图元的形状；本节例子中是两个三角形。
+图元装配阶段的输出会传递给<def>几何着色器</def>(Geometry Shader)。几何着色器把图元形式的一系列顶点的集合作为输入，它可以通过产生新顶点构造出新的（或是其它的）图元来生成其他形状。例子中，它生成了另一个三角形。
 
-图元装配阶段的输出会被传入<def>光栅化阶段</def>(Rasterization Stage)，这里它会把图元映射为最终屏幕上相应的像素，生成供片段着色器(Fragment Shader)使用的片段(Fragment)。在片段着色器运行之前会执行<def>裁切</def>(Clipping)。裁切会丢弃超出你的视图以外的所有像素，用来提升执行效率。
+几何着色器的输出会被传入<def>光栅化阶段</def>(Rasterization Stage)，这里它会把图元映射为最终屏幕上相应的像素，生成供片段着色器(Fragment Shader)使用的片段(Fragment)。在片段着色器运行之前会执行<def>裁切</def>(Clipping)。裁切会丢弃超出你的视图以外的所有像素，用来提升执行效率。
 
 !!! Important
 
@@ -64,19 +55,19 @@
 
 ## 顶点输入
 
-开始绘制图形之前，我们需要先给OpenGL输入一些顶点数据。OpenGL是一个3D图形库，所以在OpenGL中我们指定的所有坐标都是3D坐标（x、y和z）。OpenGL不是简单地把**所有的**3D坐标变换为屏幕上的2D像素；OpenGL仅当3D坐标在3个轴（x、y和z）上-1.0到1.0的范围内时才处理它。所有在这个范围内的坐标叫做<def>标准化设备坐标</def>(Normalized Device Coordinates)，此范围内的坐标最终显示在屏幕上（在这个范围以外的坐标则不会显示）。
+开始绘制图形之前，我们必须先给OpenGL输入一些顶点数据。OpenGL是一个3D图形库，所以我们在OpenGL中指定的所有坐标都是3D坐标（x、y和z）。OpenGL不是简单地把**所有的**3D坐标变换为屏幕上的2D像素；OpenGL仅当3D坐标在3个轴（x、y和z）上都为-1.0到1.0的范围内时才处理它。所有在所谓的<def>标准化设备坐标</def>(Normalized Device Coordinates)范围内的坐标才会最终呈现在屏幕上（在这个范围以外的坐标都不会显示）。
 
-由于我们希望渲染一个三角形，我们一共要指定三个顶点，每个顶点都有一个3D位置。我们会将它们以标准化设备坐标的形式（OpenGL的可见区域）定义为一个`float`数组。
+由于我们希望渲染一个三角形，我们一共要指定三个顶点，每个顶点都有一个3D位置。我们会将它们以标准化设备坐标的形式（OpenGL的可见区域）定义为一个`GLfloat`数组。
 
 ```c++
-float vertices[] = {
+GLfloat vertices[] = {
     -0.5f, -0.5f, 0.0f,
      0.5f, -0.5f, 0.0f,
      0.0f,  0.5f, 0.0f
 };
 ```
 
-由于OpenGL是在3D空间中工作的，而我们渲染的是一个2D三角形，我们将它顶点的z坐标设置为0.0。这样子的话三角形每一点的*深度*(Depth，译注2)都是一样的，从而使它看上去像是2D的。
+由于OpenGL是在3D空间中工作的，而我们渲染的是一个2D三角形，我们将它顶点的z坐标设置为0.0。这样子的话三角形每一点的**深度**(Depth，译注2)都是一样的，从而使它看上去像是2D的。
 
 !!! note "译注2"
 
@@ -86,22 +77,23 @@ float vertices[] = {
 
 	**标准化设备坐标(Normalized Device Coordinates, NDC)**
 
+	一旦你的顶点坐标已经在顶点着色器中处理过，它们就应该是**标准化设备坐标**了，标准化设备坐标是一个x、y和z值在-1.0到1.0的一小段空间。任何落在范围外的坐标都会被丢弃/裁剪，不会显示在你的屏幕上。下面你会看到我们定义的在标准化设备坐标中的三角形(忽略z轴)：
 
-一旦你的顶点坐标已经在顶点着色器中处理过，它们就应该是**标准化设备坐标**了，标准化设备坐标是一个x、y和z值在-1.0到1.0的一小段空间。任何落在范围外的坐标都会被丢弃/裁剪，不会显示在你的屏幕上。下面你会看到我们定义的在标准化设备坐标中的三角形(忽略z轴)：
-![NDC](../img/01/04/ndc.png "NDC")
+	<img alt="NDC" src="../../img/01/04/ndc.png" class="noborder" />
 
-与通常的屏幕坐标不同，y轴正方向为向上，(0, 0)坐标是这个图像的中心，而不是左上角。最终你希望所有(变换过的)坐标都在这个坐标空间中，否则它们就不可见了。
+	与通常的屏幕坐标不同，y轴正方向为向上，(0, 0)坐标是这个图像的中心，而不是左上角。最终你希望所有(变换过的)坐标都在这个坐标空间中，否则它们就不可见了。
+
+	你的标准化设备坐标接着会变换为<def>屏幕空间坐标</def>(Screen-space Coordinates)，这是使用你通过<fun>glViewport</fun>函数提供的数据，进行<def>视口变换</def>(Viewport Transform)完成的。所得的屏幕空间坐标又会被变换为片段输入到片段着色器中。
 
-通过使用由<fun>glViewport</fun>函数提供的数据，进行<def>视口变换</def>(Viewport Transform)，<def>标准化设备坐标</def>(Normalized Device Coordinates)会变换为<def>屏幕空间坐标</def>(Screen-space Coordinates)。所得的屏幕空间坐标又会被变换为片段输入到片段着色器中。
 定义这样的顶点数据以后，我们会把它作为输入发送给图形渲染管线的第一个处理阶段：顶点着色器。它会在GPU上创建内存用于储存我们的顶点数据，还要配置OpenGL如何解释这些内存，并且指定其如何发送给显卡。顶点着色器接着会处理我们在内存中指定数量的顶点。
 
-我们通过<def>顶点缓冲对象</def>(Vertex Buffer Objects, VBO)管理这个内存，它会在GPU内存（通常被称为显存）中储存大量顶点。使用这些缓冲对象的好处是我们可以一次性的发送一大批数据到显卡上，而不是每个顶点发送一次。从CPU把数据发送到显卡相对较慢，所以只要可能我们都要尝试尽量一次性发送尽可能多的数据。当数据发送至显卡的内存中后，顶点着色器几乎能立即访问顶点，这是个非常快的过程。
+我们通过<def>顶点缓冲对象</def>(Vertex Buffer Objects, VBO)管理这个内存，它会在GPU内存(通常被称为显存)中储存大量顶点。使用这些缓冲对象的好处是我们可以一次性的发送一大批数据到显卡上，而不是每个顶点发送一次。从CPU把数据发送到显卡相对较慢，所以只要可能我们都要尝试尽量一次性发送尽可能多的数据。当数据发送至显卡的内存中后，顶点着色器几乎能立即访问顶点，这是个非常快的过程。
 
-顶点缓冲对象是我们在[OpenGL](01 OpenGL.md)教程中第一个出现的OpenGL对象。就像OpenGL中的其它对象一样，这个缓冲有一个独一无二的ID，所以我们可以使用<fun>glGenBuffers</fun>函数生成一个带有缓冲ID的VBO对象：
+顶点缓冲对象是我们在[OpenGL](01 OpenGL.md)教程中第一个出现的OpenGL对象。就像OpenGL中的其它对象一样，这个缓冲有一个独一无二的ID，所以我们可以使用<fun>glGenBuffers</fun>函数和一个缓冲ID生成一个VBO对象：
 
 ```c++
-unsigned int VBO;
-glGenBuffers(1, &VBO);
+GLuint VBO;
+glGenBuffers(1, &VBO);  
 ```
 
 OpenGL有很多缓冲对象类型，顶点缓冲对象的缓冲类型是<var>GL_ARRAY_BUFFER</var>。OpenGL允许我们同时绑定多个缓冲，只要它们是不同的缓冲类型。我们可以使用<fun>glBindBuffer</fun>函数把新创建的缓冲绑定到<var>GL_ARRAY_BUFFER</var>目标上：
@@ -126,7 +118,7 @@ glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
 
 三角形的位置数据不会改变，每次渲染调用时都保持原样，所以它的使用类型最好是<var>GL_STATIC_DRAW</var>。如果，比如说一个缓冲中的数据将频繁被改变，那么使用的类型就是<var>GL_DYNAMIC_DRAW</var>或<var>GL_STREAM_DRAW</var>，这样就能确保显卡把数据放在能够高速写入的内存部分。
 
-现在我们已经把顶点数据储存在显卡的内存中，用<var>VBO</var>这个顶点缓冲对象管理。下面我们会创建一个顶点着色器和片段着色器来真正处理这些数据。现在我们开始着手创建它们吧。
+现在我们已经把顶点数据储存在显卡的内存中，用<var>VBO</var>这个顶点缓冲对象管理。下面我们会创建一个顶点和片段着色器来真正处理这些数据。现在我们开始着手创建它们吧。
 
 ## 顶点着色器
 
@@ -136,46 +128,37 @@ glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;
+  
+layout (location = 0) in vec3 position;
 
 void main()
 {
-    gl_Position = vec4(aPos.x, aPos.y, aPos.z, 1.0);
+    gl_Position = vec4(position.x, position.y, position.z, 1.0);
 }
 ```
 
 可以看到，GLSL看起来很像C语言。每个着色器都起始于一个版本声明。OpenGL 3.3以及和更高版本中，GLSL版本号和OpenGL的版本是匹配的（比如说GLSL 420版本对应于OpenGL 4.2）。我们同样明确表示我们会使用核心模式。
 
-下一步，使用`in`关键字，在顶点着色器中声明所有的输入顶点属性(Input Vertex Attribute)。现在我们只关心位置(Position)数据，所以我们只需要一个顶点属性。GLSL有一个向量数据类型，它包含1到4个`float`分量，包含的数量可以从它的后缀数字看出来。由于每个顶点都有一个3D坐标，我们就创建一个`vec3`输入变量<var>aPos</var>。我们同样也通过`layout (location = 0)`设定了输入变量的位置值(Location)你后面会看到为什么我们会需要这个位置值。
+下一步，使用`in`关键字，在顶点着色器中声明所有的输入顶点属性(Input Vertex Attribute)。现在我们只关心位置(Position)数据，所以我们只需要一个顶点属性。GLSL有一个向量数据类型，它包含1到4个`float`分量，包含的数量可以从它的后缀数字看出来。由于每个顶点都有一个3D坐标，我们就创建一个`vec3`输入变量<var>position</var>。我们同样也通过`layout (location = 0)`设定了输入变量的位置值(Location)你后面会看到为什么我们会需要这个位置值。
 
 !!! Important
 
 	**向量(Vector)**
 
-	在图形编程中我们经常会使用向量这个数学概念，因为它简明地表达了任意空间中的位置和方向，并且它有非常有用的数学属性。在GLSL中一个向量有最多4个分量，每个分量值都代表空间中的一个坐标，它们可以通过`vec.x`、`vec.y`、`vec.z`和`vec.w`来获取。注意`vec.w`分量不是用作表达空间中的位置的（我们处理的是3D不是4D），而是用在所谓透视除法(Perspective Division)上。我们会在后面的教程中更详细地讨论向量。
+	在图形编程中我们经常会使用向量这个数学概念，因为它简明地表达了任意空间中的位置和方向，并且它有非常有用的数学属性。在GLSL中一个向量有最多4个分量，每个分量值都代表空间中的一个坐标，它们可以通过`vec.x`、`vec.y`、`vec.z`和`vec.w`来获取。注意`vec.w`分量不是用作表达空间中的位置的（我们处理的是3D不是4D），而是用在所谓透视划分(Perspective Division)上。我们会在后面的教程中更详细地讨论向量。
 
 为了设置顶点着色器的输出，我们必须把位置数据赋值给预定义的<var>gl_Position</var>变量，它在幕后是`vec4`类型的。在<fun>main</fun>函数的最后，我们将<var>gl_Position</var>设置的值会成为该顶点着色器的输出。由于我们的输入是一个3分量的向量，我们必须把它转换为4分量的。我们可以把`vec3`的数据作为`vec4`构造器的参数，同时把`w`分量设置为`1.0f`（我们会在后面解释为什么）来完成这一任务。
 
 当前这个顶点着色器可能是我们能想到的最简单的顶点着色器了，因为我们对输入数据什么都没有处理就把它传到着色器的输出了。在真实的程序里输入数据通常都不是标准化设备坐标，所以我们首先必须先把它们转换至OpenGL的可视区域内。
 
 ## 编译着色器
-现在，我们暂时将顶点着色器的源代码硬编码在代码文件顶部的C风格字符串中：
+
+我们已经写了一个顶点着色器源码（储存在一个C的字符串中），但是为了能够让OpenGL使用它，我们必须在运行时动态编译它的源码。
+
+我们首先要做的是创建一个着色器对象，注意还是用ID来引用的。所以我们储存这个顶点着色器为`GLuint`，然后用<fun>glCreateShader</fun>创建这个着色器：
 
 ```c++
-const char *vertexShaderSource = "#version 330 core\n"
-    "layout (location = 0) in vec3 aPos;\n"
-    "void main()\n"
-    "{\n"
-    "   gl_Position = vec4(aPos.x, aPos.y, aPos.z, 1.0);\n"
-    "}\0";
-```
-
-为了能够让OpenGL使用它，我们必须在运行时动态编译它的源代码。
-
-我们首先要做的是创建一个着色器对象，注意还是用ID来引用的。所以我们储存这个顶点着色器为`unsigned int`，然后用<fun>glCreateShader</fun>创建这个着色器：
-
-```c++
-unsigned int vertexShader;
+GLuint vertexShader;
 vertexShader = glCreateShader(GL_VERTEX_SHADER);
 ```
 
@@ -194,23 +177,23 @@ glCompileShader(vertexShader);
 
 	你可能会希望检测在调用<fun>glCompileShader</fun>后编译是否成功了，如果没成功的话，你还会希望知道错误是什么，这样你才能修复它们。检测编译时错误可以通过以下代码来实现：
 	
-	    int  success;
-    	char infoLog[512];
-    	glGetShaderiv(vertexShader, GL_COMPILE_STATUS, &success);
+		GLint success;
+		GLchar infoLog[512];
+		glGetShaderiv(vertexShader, GL_COMPILE_STATUS, &success);
 
 	首先我们定义一个整型变量来表示是否成功编译，还定义了一个储存错误消息（如果有的话）的容器。然后我们用<fun>glGetShaderiv</fun>检查是否编译成功。如果编译失败，我们会用<fun>glGetShaderInfoLog</fun>获取错误消息，然后打印它。
 
 		if(!success)
 		{
-		    glGetShaderInfoLog(vertexShader, 512, NULL, infoLog);
-		    std::cout << "ERROR::SHADER::VERTEX::COMPILATION_FAILED\n" << infoLog << std::endl;
+	    	glGetShaderInfoLog(vertexShader, 512, NULL, infoLog);
+	    	std::cout << "ERROR::SHADER::VERTEX::COMPILATION_FAILED\n" << infoLog << std::endl;
 		}
 
 如果编译的时候没有检测到任何错误，顶点着色器就被编译成功了。
 
 ## 片段着色器
 
-片段着色器(Fragment Shader)是第二个也是最后一个我们打算创建的用于渲染三角形的着色器。片段着色器所做的是计算像素最后的颜色输出。为了让事情更简单，我们的片段着色器将会一直输出橘黄色。
+片段着色器(Fragment Shader)是第二个也是最后一个我们打算创建的用于渲染三角形的着色器。片段着色器全是关于计算你的像素最后的颜色输出。为了让事情更简单，我们的片段着色器将会一直输出橘黄色。
 
 !!! Important
 
@@ -218,37 +201,38 @@ glCompileShader(vertexShader);
 
 ```c++
 #version 330 core
-out vec4 FragColor;
+
+out vec4 color;
 
 void main()
 {
-    FragColor = vec4(1.0f, 0.5f, 0.2f, 1.0f);
-} 
+    color = vec4(1.0f, 0.5f, 0.2f, 1.0f);
+}
 ```
 
-片段着色器只需要一个输出变量，这个变量是一个4分量向量，它表示的是最终的输出颜色，我们应该自己将其计算出来。声明输出变量可以使用`out`关键字，这里我们命名为<var>FragColor</var>。下面，我们将一个Alpha值为1.0(1.0代表完全不透明)的橘黄色的`vec4`赋值给颜色输出。
+片段着色器只需要一个输出变量，这个变量是一个4分量向量，它表示的是最终的输出颜色，我们应该自己将其计算出来。我们可以用`out`关键字声明输出变量，这里我们命名为<var>color</var>。下面，我们将一个alpha值为1.0(1.0代表完全不透明)的橘黄色的`vec4`赋值给颜色输出。
 
 编译片段着色器的过程与顶点着色器类似，只不过我们使用<var>GL_FRAGMENT_SHADER</var>常量作为着色器类型：
 
 ```c++
-unsigned int fragmentShader;
+GLuint fragmentShader;
 fragmentShader = glCreateShader(GL_FRAGMENT_SHADER);
-glShaderSource(fragmentShader, 1, &fragmentShaderSource, NULL);
+glShaderSource(fragmentShader, 1, &fragmentShaderSource, null);
 glCompileShader(fragmentShader);
 ```
 
-两个着色器现在都编译了，剩下的事情是把两个着色器对象链接到一个用来渲染的<def>着色器程序</def>(Shader Program)中。
+两个着色器现在都编译了，剩下的事情是把两个着色器对象链接到一个用来渲染的着色器程序(Shader Program)中。
 
 ### 着色器程序
 
-着色器程序对象(Shader Program Object)是多个着色器合并之后并最终链接完成的版本。如果要使用刚才编译的着色器我们必须把它们<def>链接</def>(Link)为一个着色器程序对象，然后在渲染对象的时候激活这个着色器程序。已激活着色器程序的着色器将在我们发送渲染调用的时候被使用。
+着色器程序对象(Shader Program Object)是多个着色器合并之后并最终链接完成的版本。如果要使用刚才编译的着色器我们必须把它们<def>链接</def>为一个着色器程序对象，然后在渲染对象的时候激活这个着色器程序。已激活着色器程序的着色器将在我们发送渲染调用的时候被使用。
 
 当链接着色器至一个程序的时候，它会把每个着色器的输出链接到下个着色器的输入。当输出和输入不匹配的时候，你会得到一个连接错误。
 
 创建一个程序对象很简单：
 
 ```c++
-unsigned int shaderProgram;
+GLuint shaderProgram;
 shaderProgram = glCreateProgram();
 ```
 
@@ -268,8 +252,8 @@ glLinkProgram(shaderProgram);
 
 		glGetProgramiv(shaderProgram, GL_LINK_STATUS, &success);
 		if(!success) {
-		    glGetProgramInfoLog(shaderProgram, 512, NULL, infoLog);
-		    ...
+	    	glGetProgramInfoLog(shaderProgram, 512, NULL, infoLog);
+	  	  ...
 		}
 
 得到的结果就是一个程序对象，我们可以调用<fun>glUseProgram</fun>函数，用刚创建的程序对象作为它的参数，以激活这个程序对象：
@@ -297,15 +281,15 @@ glDeleteShader(fragmentShader);
 
 ![](../img/01/04/vertex_attribute_pointer.png)
 
-- 位置数据被储存为32位（4字节）浮点值。
+- 位置数据被储存为32-bit（4字节）浮点值。
 - 每个位置包含3个这样的值。
-- 在这3个值之间没有空隙（或其他值）。这几个值在数组中<def>紧密排列</def>(Tightly Packed)。
+- 在这3个值之间没有空隙（或其他值）。这几个值在数组中<def>紧密排列</def>。
 - 数据中第一个值在缓冲开始的位置。
 
 有了这些信息我们就可以使用<fun>glVertexAttribPointer</fun>函数告诉OpenGL该如何解析顶点数据（应用到逐个顶点属性上）了：
 
 ```c++
-glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), (void*)0);
+glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(GLfloat), (GLvoid*)0);
 glEnableVertexAttribArray(0);
 ```
 
@@ -315,12 +299,12 @@ glEnableVertexAttribArray(0);
 - 第二个参数指定顶点属性的大小。顶点属性是一个`vec3`，它由3个值组成，所以大小是3。
 - 第三个参数指定数据的类型，这里是<var>GL_FLOAT</var>(GLSL中`vec*`都是由浮点数值组成的)。
 - 下个参数定义我们是否希望数据被标准化(Normalize)。如果我们设置为<var>GL_TRUE</var>，所有数据都会被映射到0（对于有符号型signed数据是-1）到1之间。我们把它设置为<var>GL_FALSE</var>。
-- 第五个参数叫做<def>步长</def>(Stride)，它告诉我们在连续的顶点属性组之间的间隔。由于下个组位置数据在3个`float`之后，我们把步长设置为`3 * sizeof(float)`。要注意的是由于我们知道这个数组是紧密排列的（在两个顶点属性之间没有空隙）我们也可以设置为0来让OpenGL决定具体步长是多少（只有当数值是紧密排列时才可用）。一旦我们有更多的顶点属性，我们就必须更小心地定义每个顶点属性之间的间隔，我们在后面会看到更多的例子（译注: 这个参数的意思简单说就是从这个属性第二次出现的地方到整个数组0位置之间有多少字节）。
-- 最后一个参数的类型是`void*`，所以需要我们进行这个奇怪的强制类型转换。它表示位置数据在缓冲中起始位置的<def>偏移量</def>(Offset)。由于位置数据在数组的开头，所以这里是0。我们会在后面详细解释这个参数。
+- 第五个参数叫做<def>步长</def>(Stride)，它告诉我们在连续的顶点属性组之间的间隔。由于下个组位置数据在3个`GLfloat`之后，我们把步长设置为`3 * sizeof(GLfloat)`。要注意的是由于我们知道这个数组是紧密排列的（在两个顶点属性之间没有空隙）我们也可以设置为0来让OpenGL决定具体步长是多少（只有当数值是紧密排列时才可用）。一旦我们有更多的顶点属性，我们就必须更小心地定义每个顶点属性之间的间隔，我们在后面会看到更多的例子(译注: 这个参数的意思简单说就是从这个属性第二次出现的地方到整个数组0位置之间有多少字节)。
+- 最后一个参数的类型是`GLvoid*`，所以需要我们进行这个奇怪的强制类型转换。它表示位置数据在缓冲中起始位置的<def>偏移量</def>(Offset)。由于位置数据在数组的开头，所以这里是0。我们会在后面详细解释这个参数。
 
 !!! Important
 
-	每个顶点属性从一个VBO管理的内存中获得它的数据，而具体是从哪个VBO（程序中可以有多个VBO）获取则是通过在调用<fun>glVertexAttribPointer</fun>时绑定到<var>GL_ARRAY_BUFFER</var>的VBO决定的。由于在调用<fun>glVertexAttribPointer</fun>之前绑定的是先前定义的<var>VBO</var>对象，顶点属性`0`现在会链接到它的顶点数据。
+	每个顶点属性从一个VBO管理的内存中获得它的数据，而具体是从哪个VBO（程序中可以有多个VBO）获取则是通过在调用<fun>glVetexAttribPointer</fun>时绑定到<var>GL_ARRAY_BUFFER</var>的VBO决定的。由于在调用<fun>glVetexAttribPointer</fun>之前绑定的是先前定义的<var>VBO</var>对象，顶点属性`0`现在会链接到它的顶点数据。
 
 现在我们已经定义了OpenGL该如何解释顶点数据，我们现在应该使用<fun>glEnableVertexAttribArray</fun>，以顶点属性位置值作为参数，启用顶点属性；顶点属性默认是禁用的。自此，所有东西都已经设置好了：我们使用一个顶点缓冲对象将顶点数据初始化至缓冲中，建立了一个顶点和一个片段着色器，并告诉了OpenGL如何把顶点数据链接到顶点着色器的顶点属性上。在OpenGL中绘制一个物体，代码会像是这样：
 
@@ -329,7 +313,7 @@ glEnableVertexAttribArray(0);
 glBindBuffer(GL_ARRAY_BUFFER, VBO);
 glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
 // 1. 设置顶点属性指针
-glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), (void*)0);
+glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(GLfloat), (GLvoid*)0);
 glEnableVertexAttribArray(0);
 // 2. 当我们渲染一个物体时要使用着色器程序
 glUseProgram(shaderProgram);
@@ -351,15 +335,15 @@ someOpenGLFunctionThatDrawsOurTriangle();
 
 - <fun>glEnableVertexAttribArray</fun>和<fun>glDisableVertexAttribArray</fun>的调用。
 - 通过<fun>glVertexAttribPointer</fun>设置的顶点属性配置。
-- 通过<fun>glVertexAttribPointer</fun>调用与顶点属性关联的顶点缓冲对象。
+- 通过`glVertexAttribPointer`调用进行的顶点缓冲对象与顶点属性链接。
 
 ![](../img/01/04/vertex_array_objects.png)
 
 创建一个VAO和创建一个VBO很类似：
 
 ```c++
-unsigned int VAO;
-glGenVertexArrays(1, &VAO);
+GLuint VAO;
+glGenVertexArrays(1, &VAO);  
 ```
 
 要想使用VAO，要做的只是使用<fun>glBindVertexArray</fun>绑定VAO。从绑定之后起，我们应该绑定和配置对应的VBO和属性指针，之后解绑VAO供之后使用。当我们打算绘制一个物体的时候，我们只要在绘制物体前简单地把VAO绑定到希望使用的设定上就行了。这段代码应该看起来像这样：
@@ -368,22 +352,29 @@ glGenVertexArrays(1, &VAO);
 // ..:: 初始化代码（只运行一次 (除非你的物体频繁改变)） :: ..
 // 1. 绑定VAO
 glBindVertexArray(VAO);
-// 2. 把顶点数组复制到缓冲中供OpenGL使用
-glBindBuffer(GL_ARRAY_BUFFER, VBO);
-glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
-// 3. 设置顶点属性指针
-glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), (void*)0);
-glEnableVertexAttribArray(0);
+    // 2. 把顶点数组复制到缓冲中供OpenGL使用
+    glBindBuffer(GL_ARRAY_BUFFER, VBO);
+    glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
+    // 3. 设置顶点属性指针
+    glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(GLfloat), (GLvoid*)0);
+    glEnableVertexAttribArray(0);
+//4. 解绑VAO
+glBindVertexArray(0);
  
 [...]
  
-// ..:: 绘制代码（渲染循环中） :: ..
-// 4. 绘制物体
+// ..:: 绘制代（游戏循环中） :: ..
+// 5. 绘制物体
 glUseProgram(shaderProgram);
 glBindVertexArray(VAO);
 someOpenGLFunctionThatDrawsOurTriangle();
+glBindVertexArray(0);
 ```
 
+!!! Attention
+
+	通常情况下当我们配置好OpenGL对象以后要解绑它们，这样我们才不会在其它地方错误地配置它们。
+
 就这么多了！前面做的一切都是等待这一刻，一个储存了我们顶点属性配置和应使用的VBO的顶点数组对象。一般当你打算绘制多个物体时，你首先要生成/配置所有的VAO（和必须的VBO及属性指针)，然后储存它们供后面使用。当我们打算绘制物体的时候就拿出相应的VAO，绑定它，绘制完物体后，再解绑VAO。
 
 ### 我们一直期待的三角形
@@ -394,24 +385,25 @@ someOpenGLFunctionThatDrawsOurTriangle();
 glUseProgram(shaderProgram);
 glBindVertexArray(VAO);
 glDrawArrays(GL_TRIANGLES, 0, 3);
+glBindVertexArray(0);  
 ```
 
-<fun>glDrawArrays</fun>函数第一个参数是我们打算绘制的OpenGL图元的类型。由于我们在一开始时说过，我们希望绘制的是一个三角形，这里传递<var>GL_TRIANGLES</var>给它。第二个参数指定了顶点数组的起始索引，我们这里填`0`。最后一个参数指定我们打算绘制多少个顶点，这里是`3`（我们只从我们的数据中渲染一个三角形，它只有3个顶点长）。
+<fun>glDrawArrays</fun>函数第一个参数是我们打算绘制的OpenGL图元的类型。由于我们在一开始时说过，我们希望绘制的是一个三角形，这里传递<var>GL_TRIANGLES</var>给它。第二个参数指定了顶点数组的起始索引，我们这里填`0`。最后一个参数指定我们打算绘制多少个顶点，这里是3（我们只从我们的数据中渲染一个三角形，它只有3个顶点长）。
 
 现在尝试编译代码，如果弹出了任何错误，回头检查你的代码。如果你编译通过了，你应该看到下面的结果：
 
 ![](../img/01/04/hellotriangle.png)
 
-完整的程序源码可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/2.1.hello_triangle/hello_triangle.cpp)找到。
+完整的程序源码可以在[这里](http://learnopengl.com/code_viewer.php?code=getting-started/hellotriangle)找到。
 
 如果你的输出和这个看起来不一样，你可能做错了什么。去查看一下源码，检查你是否遗漏了什么东西，或者你也可以在评论区提问。
 
-## 元素缓冲对象
+## 索引缓冲对象
 
-在渲染顶点这一话题上我们还有最后一个需要讨论的东西——元素缓冲对象(Element Buffer Object，EBO)，也叫索引缓冲对象(Index Buffer Object，IBO)。要解释元素缓冲对象的工作方式最好还是举个例子：假设我们不再绘制一个三角形而是绘制一个矩形。我们可以绘制两个三角形来组成一个矩形（OpenGL主要处理三角形）。这会生成下面的顶点的集合：
+在渲染顶点这一话题上我们还有最有一个需要讨论的东西——索引缓冲对象(Element Buffer Object，EBO，也叫Index Buffer Object，IBO)。要解释索引缓冲对象的工作方式最好还是举个例子：假设我们不再绘制一个三角形而是绘制一个矩形。我们可以绘制两个三角形来组成一个矩形（OpenGL主要处理三角形）。这会生成下面的顶点的集合：
 
 ```c++
-float vertices[] = {
+GLfloat vertices[] = {
     // 第一个三角形
     0.5f, 0.5f, 0.0f,   // 右上角
     0.5f, -0.5f, 0.0f,  // 右下角
@@ -425,30 +417,26 @@ float vertices[] = {
 
 可以看到，有几个顶点叠加了。我们指定了`右下角`和`左上角`两次！一个矩形只有4个而不是6个顶点，这样就产生50%的额外开销。当我们有包括上千个三角形的模型之后这个问题会更糟糕，这会产生一大堆浪费。更好的解决方案是只储存不同的顶点，并设定绘制这些顶点的顺序。这样子我们只要储存4个顶点就能绘制矩形了，之后只要指定绘制的顺序就行了。如果OpenGL提供这个功能就好了，对吧？
 
-值得庆幸的是，元素缓冲区对象的工作方式正是如此。 EBO是一个缓冲区，就像一个顶点缓冲区对象一样，它存储 OpenGL 用来决定要绘制哪些顶点的索引。这种所谓的<def>索引绘制</def>(Indexed Drawing)正是我们问题的解决方案。首先，我们先要定义（不重复的）顶点，和绘制出矩形所需的索引：
+很幸运，索引缓冲对象的工作方式正是这样的。和顶点缓冲对象一样，EBO也是一个缓冲，它专门储存索引，OpenGL调用这些顶点的索引来决定该绘制哪个顶点。所谓的<def>索引绘制</def>(Indexed Drawing)正是我们问题的解决方案。首先，我们先要定义（独一无二的）顶点，和绘制出矩形所需的索引：
 
 ```c++
-float vertices[] = {
+GLfloat vertices[] = {
     0.5f, 0.5f, 0.0f,   // 右上角
     0.5f, -0.5f, 0.0f,  // 右下角
     -0.5f, -0.5f, 0.0f, // 左下角
     -0.5f, 0.5f, 0.0f   // 左上角
 };
  
-unsigned int indices[] = {
-    // 注意索引从0开始! 
-    // 此例的索引(0,1,2,3)就是顶点数组vertices的下标，
-    // 这样可以由下标代表顶点组合成矩形
-
+GLuint indices[] = { // 注意索引从0开始! 
     0, 1, 3, // 第一个三角形
     1, 2, 3  // 第二个三角形
 };
 ```
 
-你可以看到，当使用索引的时候，我们只定义了4个顶点，而不是6个。下一步我们需要创建元素缓冲对象：
+你可以看到，当时用索引的时候，我们只定义了4个顶点，而不是6个。下一步我们需要创建索引缓冲对象：
 
 ```c++
-unsigned int EBO;
+GLuint EBO;
 glGenBuffers(1, &EBO);
 ```
 
@@ -456,10 +444,10 @@ glGenBuffers(1, &EBO);
 
 ```c++
 glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, EBO);
-glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(indices), indices, GL_STATIC_DRAW);
+glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(indices), indices, GL_STATIC_DRAW); 
 ```
 
-注意：我们传递了<var>GL_ELEMENT_ARRAY_BUFFER</var>当作缓冲目标。最后一件要做的事是用<fun>glDrawElements</fun>来替换<fun>glDrawArrays</fun>函数，表示我们要从索引缓冲区渲染三角形。使用<fun>glDrawElements</fun>时，我们会使用当前绑定的索引缓冲对象中的索引进行绘制：
+要注意的是，我们传递了<var>GL_ELEMENT_ARRAY_BUFFER</var>当作缓冲目标。最后一件要做的事是用<fun>glDrawElements</fun>来替换<fun>glDrawArrays</fun>函数，来指明我们从索引缓冲渲染。使用<fun>glDrawElements</fun>时，我们会使用当前绑定的索引缓冲对象中的索引进行绘制：
 
 ```c++
 glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, EBO);
@@ -468,7 +456,7 @@ glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_INT, 0);
 
 第一个参数指定了我们绘制的模式，这个和<fun>glDrawArrays</fun>的一样。第二个参数是我们打算绘制顶点的个数，这里填6，也就是说我们一共需要绘制6个顶点。第三个参数是索引的类型，这里是<var>GL_UNSIGNED_INT</var>。最后一个参数里我们可以指定EBO中的偏移量（或者传递一个索引数组，但是这是当你不在使用索引缓冲对象的时候），但是我们会在这里填写0。
 
-<fun>glDrawElements</fun>函数从当前绑定到<var>GL_ELEMENT_ARRAY_BUFFER</var>目标的EBO中获取其索引。这意味着我们每次想要使用索引渲染对象时都必须绑定相应的EBO，这又有点麻烦。碰巧顶点数组对象也跟踪元素缓冲区对象绑定。在绑定VAO时，绑定的最后一个元素缓冲区对象存储为VAO的元素缓冲区对象。然后，绑定到VAO也会自动绑定该EBO。
+<fun>glDrawElements</fun>函数从当前绑定到<var>GL_ELEMENT_ARRAY_BUFFER</var>目标的EBO中获取索引。这意味着我们必须在每次要用索引渲染一个物体时绑定相应的EBO，这还是有点麻烦。不过顶点数组对象同样可以保存索引缓冲对象的绑定状态。VAO绑定时正在绑定的索引缓冲对象会被保存为VAO的元素缓冲对象。绑定VAO的同时也会自动绑定EBO。
 
 ![](../img/01/04/vertex_array_objects_ebo.png)
 
@@ -482,22 +470,25 @@ glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_INT, 0);
 // ..:: 初始化代码 :: ..
 // 1. 绑定顶点数组对象
 glBindVertexArray(VAO);
-// 2. 把我们的顶点数组复制到一个顶点缓冲中，供OpenGL使用
-glBindBuffer(GL_ARRAY_BUFFER, VBO);
-glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
-// 3. 复制我们的索引数组到一个索引缓冲中，供OpenGL使用
-glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, EBO);
-glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(indices), indices, GL_STATIC_DRAW);
-// 4. 设定顶点属性指针
-glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), (void*)0);
-glEnableVertexAttribArray(0);
+    // 2. 把我们的顶点数组复制到一个顶点缓冲中，供OpenGL使用
+    glBindBuffer(GL_ARRAY_BUFFER, VBO);
+    glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
+    // 3. 复制我们的索引数组到一个索引缓冲中，供OpenGL使用
+    glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, EBO);
+    glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(indices), indices, GL_STATIC_DRAW);
+    // 3. 设定顶点属性指针
+    glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(GLfloat), (GLvoid*)0);
+    glEnableVertexAttribArray(0);
+// 4. 解绑VAO（不是EBO！）
+glBindVertexArray(0);
  
 [...]
  
-// ..:: 绘制代码（渲染循环中） :: ..
+// ..:: 绘制代码（游戏循环中） :: ..
+ 
 glUseProgram(shaderProgram);
 glBindVertexArray(VAO);
-glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_INT, 0);
+glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_INT, 0)
 glBindVertexArray(0);
 ```
 
@@ -511,21 +502,20 @@ glBindVertexArray(0);
 
 	要想用线框模式绘制你的三角形，你可以通过`glPolygonMode(GL_FRONT_AND_BACK, GL_LINE)`函数配置OpenGL如何绘制图元。第一个参数表示我们打算将其应用到所有的三角形的正面和背面，第二个参数告诉我们用线来绘制。之后的绘制调用会一直以线框模式绘制三角形，直到我们用`glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)`将其设置回默认模式。
 
-如果你遇到任何错误，回头检查代码，看看是否遗漏了什么。同时，你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/2.2.hello_triangle_indexed/hello_triangle_indexed.cpp)找到全部源码，你也可以在评论区自由提问。
+如果你遇到任何错误，回头检查代码，看看是否遗漏了什么。同时，你可以在[这里](http://learnopengl.com/code_viewer.php?code=getting-started/hellotriangle2)找到全部源码，你也可以在评论区自由提问。
 
 如果你像我这样成功绘制出了这个三角形或矩形，那么恭喜你，你成功地通过了现代OpenGL最难部分之一：绘制你自己的第一个三角形。这部分很难，因为在可以绘制第一个三角形之前你需要了解很多知识。幸运的是我们现在已经越过了这个障碍，接下来的教程会比较容易理解一些。
 
 ## 附加资源
 
 - [antongerdelan.net/hellotriangle](http://antongerdelan.net/opengl/hellotriangle.html)：Anton Gerdelan的渲染第一个三角形教程。
-- [open.gl/drawing](https://open.gl/drawing)：Alexander Overvoorde的渲染第一个三角形教程。
-- [antongerdelan.net/vertexbuffers](http://antongerdelan.net/opengl/vertexbuffers.html)：顶点缓冲对象的一些深入探讨。
-- [调试](https://learnopengl.com/#!In-Practice/Debugging)：这个教程中涉及到了很多步骤，如果你在哪卡住了，阅读一点调试的教程是非常值得的（只需要阅读到调试输出部分）。
+- [open.gl/drawing](https://open.gl/drawing): Alexander Overvoorde的渲染第一个三角形教程。
+- [antongerdelan.net/vertexbuffers](http://antongerdelan.net/opengl/vertexbuffers.html): 顶点缓冲对象的一些深入探讨。
 
 # 练习
 
 为了更好的掌握上述概念，我准备了一些练习。建议在继续下一节的学习之前先做完这些练习，确保你对这些知识有比较好的理解。
 
-1. 添加更多顶点到数据中，使用<fun>glDrawArrays</fun>，尝试绘制两个彼此相连的三角形：[参考解答](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/2.3.hello_triangle_exercise1/hello_triangle_exercise1.cpp)
-2. 创建相同的两个三角形，但对它们的数据使用不同的VAO和VBO：[参考解答](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/2.4.hello_triangle_exercise2/hello_triangle_exercise2.cpp)
-3. 创建两个着色器程序，第二个程序使用一个不同的片段着色器，输出黄色；再次绘制这两个三角形，让其中一个输出为黄色：[参考解答](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/2.5.hello_triangle_exercise3/hello_triangle_exercise3.cpp)
+1. 添加更多顶点到数据中，使用<fun>glDrawArrays</fun>，尝试绘制两个彼此相连的三角形：[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/hello-triangle-exercise1)
+2. 创建相同的两个三角形，但对它们的数据使用不同的VAO和VBO：[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/hello-triangle-exercise2)
+3. 创建两个着色器程序，第二个程序使用与第一个不同的片段着色器，输出黄色；再次绘制这两个三角形，其中一个输出为黄色：[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/hello-triangle-exercise3)

docs/01 Getting started/05 Shaders.md

@@ -3,8 +3,8 @@
 原文     | [Shaders](http://learnopengl.com/#!Getting-started/Shaders)
       ---|---
 作者     | JoeyDeVries
-翻译     | [Django](http://bullteacher.com/), Krasjet, Geequlim
-校对     | 暂未校对
+翻译     | [Django](http://bullteacher.com/)
+校对     | Geequlim
 
 在[Hello Triangle](04 Hello Triangle.md)教程中提到，着色器(Shader)是运行在GPU上的小程序。这些小程序为图形渲染管线的某个特定部分而运行。从基本意义上来说，着色器只是一种把输入转化为输出的程序。着色器也是一种非常独立的程序，因为它们之间不能相互通信；它们之间唯一的沟通只有通过输入和输出。
 
@@ -20,6 +20,7 @@
 
 ```c++
 #version version_number
+
 in type in_variable_name;
 in type in_variable_name;
 
@@ -27,7 +28,7 @@ out type out_variable_name;
 
 uniform type uniform_name;
 
-void main()
+int main()
 {
   // 处理输入并进行一些图形操作
   ...
@@ -39,7 +40,7 @@ void main()
 当我们特别谈论到顶点着色器的时候，每个输入变量也叫<def>顶点属性</def>(Vertex Attribute)。我们能声明的顶点属性是有上限的，它一般由硬件来决定。OpenGL确保至少有16个包含4分量的顶点属性可用，但是有些硬件或许允许更多的顶点属性，你可以查询<var>GL_MAX_VERTEX_ATTRIBS</var>来获取具体的上限：
 
 ```c++
-int nrAttributes;
+GLint nrAttributes;
 glGetIntegerv(GL_MAX_VERTEX_ATTRIBS, &nrAttributes);
 std::cout << "Maximum nr of vertex attributes supported: " << nrAttributes << std::endl;
 ```
@@ -52,7 +53,7 @@ std::cout << "Maximum nr of vertex attributes supported: " << nrAttributes << st
 
 ### 向量
 
-GLSL中的向量是一个可以包含有2、3或者4个分量的容器，分量的类型可以是前面默认基础类型的任意一个。它们可以是下面的形式（`n`代表分量的数量）：
+GLSL中的向量是一个可以包含有1、2、3或者4个分量的容器，分量的类型可以是前面默认基础类型的任意一个。它们可以是下面的形式（`n`代表分量的数量）：
 
   类型|含义
    ---|---
@@ -78,12 +79,12 @@ vec4 otherVec = someVec.xxxx + anotherVec.yxzy;
 你可以使用上面4个字母任意组合来创建一个和原来向量一样长的（同类型）新向量，只要原来向量有那些分量即可；然而，你不允许在一个`vec2`向量中去获取`.z`元素。我们也可以把一个向量作为一个参数传给不同的向量构造函数，以减少需求参数的数量：
 
 ```c++
-vec2 vect = vec2(0.5, 0.7);
-vec4 result = vec4(vect, 0.0, 0.0);
-vec4 otherResult = vec4(result.xyz, 1.0);
+vec2 vect = vec2(0.5f, 0.7f);
+vec4 result = vec4(vect, 0.0f, 0.0f);
+vec4 otherResult = vec4(result.xyz, 1.0f);
 ```
 
-向量是一种灵活的数据类型，我们可以把它用在各种输入和输出上。学完教程你会看到很多新颖的管理向量的例子。
+向量是一种灵活的数据类型，我们可以把用在各种输入和输出上。学完教程你会看到很多新颖的管理向量的例子。
 
 ## 输入与输出
 
@@ -103,27 +104,27 @@ vec4 otherResult = vec4(result.xyz, 1.0);
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos; // 位置变量的属性位置值为0
+layout (location = 0) in vec3 position; // position变量的属性位置值为0
 
 out vec4 vertexColor; // 为片段着色器指定一个颜色输出
 
 void main()
 {
-    gl_Position = vec4(aPos, 1.0); // 注意我们如何把一个vec3作为vec4的构造器的参数
-    vertexColor = vec4(0.5, 0.0, 0.0, 1.0); // 把输出变量设置为暗红色
+    gl_Position = vec4(position, 1.0); // 注意我们如何把一个vec3作为vec4的构造器的参数
+    vertexColor = vec4(0.5f, 0.0f, 0.0f, 1.0f); // 把输出变量设置为暗红色
 }
 ```
 **片段着色器**
 
 ```c++
 #version 330 core
-out vec4 FragColor;
-  
 in vec4 vertexColor; // 从顶点着色器传来的输入变量（名称相同、类型相同）
 
+out vec4 color; // 片段着色器输出的变量名可以任意命名，类型必须是vec4
+
 void main()
 {
-    FragColor = vertexColor;
+    color = vertexColor;
 }
 ```
 
@@ -135,20 +136,20 @@ void main()
 
 ## Uniform
 
-<def>Uniform</def>是另一种从我们的应用程序在 CPU 上传递数据到 GPU 上的着色器的方式，但uniform和顶点属性有些不同。首先，uniform是<def>全局的</def>(Global)。全局意味着uniform变量必须在每个着色器程序对象中都是独一无二的，而且它可以被着色器程序的任意着色器在任意阶段访问。第二，无论你把uniform值设置成什么，uniform会一直保存它们的数据，直到它们被重置或更新。
+<def>Uniform</def>是一种从CPU中的应用向GPU中的着色器发送数据的方式，但uniform和顶点属性有些不同。首先，uniform是<def>全局的</def>(Global)。全局意味着uniform变量必须在每个着色器程序对象中都是独一无二的，而且它可以被着色器程序的任意着色器在任意阶段访问。第二，无论你把uniform值设置成什么，uniform会一直保存它们的数据，直到它们被重置或更新。
 
-要在 GLSL 中声明 uniform，我们只需在着色器中使用 `uniform` 关键字，并带上类型和名称。从那时起，我们就可以在着色器中使用新声明的 uniform。我们来看看这次是否能通过uniform设置三角形的颜色：
+我们可以在一个着色器中添加`uniform`关键字至类型和变量名前来声明一个GLSL的uniform。从此处开始我们就可以在着色器中使用新声明的uniform了。我们来看看这次是否能通过uniform设置三角形的颜色：
 
 ```c++
 #version 330 core
-out vec4 FragColor;
-  
+out vec4 color;
+
 uniform vec4 ourColor; // 在OpenGL程序代码中设定这个变量
 
 void main()
 {
-    FragColor = ourColor;
-}
+    color = ourColor;
+}  
 ```
 
 我们在片段着色器中声明了一个uniform `vec4`的<var>ourColor</var>，并把片段着色器的输出颜色设置为uniform值的内容。因为uniform是全局变量，我们可以在任何着色器中定义它们，而无需通过顶点着色器作为中介。顶点着色器中不需要这个uniform，所以我们不用在那里定义它。
@@ -160,16 +161,16 @@ void main()
 这个uniform现在还是空的；我们还没有给它添加任何数据，所以下面我们就做这件事。我们首先需要找到着色器中uniform属性的索引/位置值。当我们得到uniform的索引/位置值后，我们就可以更新它的值了。这次我们不去给像素传递单独一个颜色，而是让它随着时间改变颜色：
 
 ```c++
-float timeValue = glfwGetTime();
-float greenValue = (sin(timeValue) / 2.0f) + 0.5f;
-int vertexColorLocation = glGetUniformLocation(shaderProgram, "ourColor");
+GLfloat timeValue = glfwGetTime();
+GLfloat greenValue = (sin(timeValue) / 2) + 0.5;
+GLint vertexColorLocation = glGetUniformLocation(shaderProgram, "ourColor");
 glUseProgram(shaderProgram);
 glUniform4f(vertexColorLocation, 0.0f, greenValue, 0.0f, 1.0f);
 ```
 
 首先我们通过<fun>glfwGetTime()</fun>获取运行的秒数。然后我们使用<fun>sin</fun>函数让颜色在0.0到1.0之间改变，最后将结果储存到<var>greenValue</var>里。
 
-接着，我们用<fun>glGetUniformLocation</fun>查询uniform <var>ourColor</var>的位置值。我们为查询函数提供着色器程序和uniform的名字（这是我们希望获得的位置值的来源）。如果<fun>glGetUniformLocation</fun>返回`-1`就代表没有找到这个位置值。最后，我们可以通过<fun>glUniform4f</fun>函数设置uniform值。注意，查询uniform地址不要求你之前使用过着色器程序，但是更新一个uniform之前你**必须**先使用程序（调用<fun>glUseProgram</fun>)，因为它是在当前激活的着色器程序中设置uniform的。
+接着，我们用<fun>glGetUniformLocation</fun>查询uniform `ourColor`的位置值。我们为查询函数提供着色器程序和uniform的名字（这是我们希望获得的位置值的来源）。如果<fun>glGetUniformLocation</fun>返回`-1`就代表没有找到这个位置值。最后，我们可以通过<fun>glUniform4f</fun>函数设置uniform值。注意，查询uniform地址不要求你之前使用过着色器程序，但是更新一个unform之前你**必须**先使用程序（调用<fun>glUseProgram</fun>)，因为它是在当前激活的着色器程序中设置unform的。
 
 !!! Important
 
@@ -190,30 +191,27 @@ glUniform4f(vertexColorLocation, 0.0f, greenValue, 0.0f, 1.0f);
 ```c++
 while(!glfwWindowShouldClose(window))
 {
-    // 输入
-    processInput(window);
+    // 检测并调用事件
+    glfwPollEvents();
 
     // 渲染
-    // 清除颜色缓冲
+    // 清空颜色缓冲
     glClearColor(0.2f, 0.3f, 0.3f, 1.0f);
     glClear(GL_COLOR_BUFFER_BIT);
 
     // 记得激活着色器
     glUseProgram(shaderProgram);
-  
+
     // 更新uniform颜色
-    float timeValue = glfwGetTime();
-    float greenValue = sin(timeValue) / 2.0f + 0.5f;
-    int vertexColorLocation = glGetUniformLocation(shaderProgram, "ourColor");
+    GLfloat timeValue = glfwGetTime();
+    GLfloat greenValue = (sin(timeValue) / 2) + 0.5;
+    GLint vertexColorLocation = glGetUniformLocation(shaderProgram, "ourColor");
     glUniform4f(vertexColorLocation, 0.0f, greenValue, 0.0f, 1.0f);
 
     // 绘制三角形
     glBindVertexArray(VAO);
     glDrawArrays(GL_TRIANGLES, 0, 3);
-  
-    // 交换缓冲并查询IO事件
-    glfwSwapBuffers(window);
-    glfwPollEvents();
+    glBindVertexArray(0);
 }
 ```
 
@@ -221,7 +219,7 @@ while(!glfwWindowShouldClose(window))
 
 <video src="../../img/01/05/shaders.mp4" controls="controls"/></video>
 
-如果你在哪儿卡住了，可以到[这里](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/3.1.shaders_uniform/shaders_uniform.cpp)查看源码。
+如果你在哪儿卡住了，可以到[这里](http://www.learnopengl.com/code_viewer.php?code=getting-started/shaders-uniform)查看源码。
 
 可以看到，uniform对于设置一个在渲染迭代中会改变的属性是一个非常有用的工具，它也是一个在程序和着色器间数据交互的很好工具，但假如我们打算为每个顶点设置一个颜色的时候该怎么办？这种情况下，我们就不得不声明和顶点数目一样多的uniform了。在这一问题上更好的解决方案是在顶点属性中包含更多的数据，这是我们接下来要做的事情。
 
@@ -230,7 +228,7 @@ while(!glfwWindowShouldClose(window))
 在前面的教程中，我们了解了如何填充VBO、配置顶点属性指针以及如何把它们都储存到一个VAO里。这次，我们同样打算把颜色数据加进顶点数据中。我们将把颜色数据添加为3个float值至<var>vertices</var>数组。我们将把三角形的三个角分别指定为红色、绿色和蓝色：
 
 ```c++
-float vertices[] = {
+GLfloat vertices[] = {
     // 位置              // 颜色
      0.5f, -0.5f, 0.0f,  1.0f, 0.0f, 0.0f,   // 右下
     -0.5f, -0.5f, 0.0f,  0.0f, 1.0f, 0.0f,   // 左下
@@ -238,19 +236,19 @@ float vertices[] = {
 };
 ```
 
-由于现在有更多的数据要发送到顶点着色器，我们有必要去调整一下顶点着色器，使它能够接收颜色值作为一个顶点属性输入。需要注意的是我们用`layout`标识符来把<var>aColor</var>属性的位置值设置为1：
+由于现在有更多的数据要发送到顶点着色器，我们有必要去调整一下顶点着色器，使它能够接收颜色值作为一个顶点属性输入。需要注意的是我们用`layout`标识符来把<var>color</var>属性的位置值设置为1：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;   // 位置变量的属性位置值为 0 
-layout (location = 1) in vec3 aColor; // 颜色变量的属性位置值为 1
-  
+layout (location = 0) in vec3 position; // 位置变量的属性位置值为 0 
+layout (location = 1) in vec3 color;	// 颜色变量的属性位置值为 1
+
 out vec3 ourColor; // 向片段着色器输出一个颜色
 
 void main()
 {
-    gl_Position = vec4(aPos, 1.0);
-    ourColor = aColor; // 将ourColor设置为我们从顶点数据那里得到的输入颜色
+    gl_Position = vec4(position, 1.0);
+    ourColor = color; // 将ourColor设置为我们从顶点数据那里得到的输入颜色
 }
 ```
 
@@ -258,12 +256,12 @@ void main()
 
 ```c++
 #version 330 core
-out vec4 FragColor;  
 in vec3 ourColor;
+out vec4 color;
   
 void main()
 {
-    FragColor = vec4(ourColor, 1.0);
+    color = vec4(ourColor, 1.0f);
 }
 ```
 
@@ -275,23 +273,23 @@ void main()
 
 ```c++
 // 位置属性
-glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(float), (void*)0);
+glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(GLfloat), (GLvoid*)0);
 glEnableVertexAttribArray(0);
 // 颜色属性
-glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(float), (void*)(3* sizeof(float)));
+glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(GLfloat), (GLvoid*)(3* sizeof(GLfloat)));
 glEnableVertexAttribArray(1);
 ```
 
 <fun>glVertexAttribPointer</fun>函数的前几个参数比较明了。这次我们配置属性位置值为1的顶点属性。颜色值有3个float那么大，我们不去标准化这些值。
 
 由于我们现在有了两个顶点属性，我们不得不重新计算**步长**值。为获得数据队列中下一个属性值（比如位置向量的下个`x`分量）我们必须向右移动6个float，其中3个是位置值，另外3个是颜色值。这使我们的步长值为6乘以float的字节数（=24字节）。  
-同样，这次我们必须指定一个偏移量。对于每个顶点来说，位置顶点属性在前，所以它的偏移量是0。颜色属性紧随位置数据之后，所以偏移量就是`3 * sizeof(float)`，用字节来计算就是12字节。
+同样，这次我们必须指定一个偏移量。对于每个顶点来说，位置顶点属性在前，所以它的偏移量是0。颜色属性紧随位置数据之后，所以偏移量就是`3 * sizeof(GLfloat)`，用字节来计算就是12字节。
 
 运行程序你应该会看到如下结果：
 
 ![](../img/01/05/shaders3.png)
 
-如果你在哪卡住了，可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/3.2.shaders_interpolation/shaders_interpolation.cpp)查看源码。
+如果你在哪卡住了，可以在[这里](http://learnopengl.com/code_viewer.php?code=getting-started/shaders-interpolated)查看源码。
 
 这个图片可能不是你所期望的那种，因为我们只提供了3个颜色，而不是我们现在看到的大调色板。这是在片段着色器中进行的所谓<def>片段插值</def>(Fragment Interpolation)的结果。当渲染一个三角形时，光栅化(Rasterization)阶段通常会造成比原指定顶点更多的片段。光栅会根据每个片段在三角形形状上所处相对位置决定这些片段的位置。  
 基于这些位置，它会<def>插值</def>(Interpolate)所有片段着色器的输入变量。比如说，我们有一个线段，上面的端点是绿色的，下面的端点是蓝色的。如果一个片段着色器在线段的70%的位置运行，它的颜色输入属性就会是一个绿色和蓝色的线性结合；更精确地说就是30%蓝 + 70%绿。
@@ -308,30 +306,24 @@ glEnableVertexAttribArray(1);
 #ifndef SHADER_H
 #define SHADER_H
 
-#include <glad/glad.h>; // 包含glad来获取所有的必须OpenGL头文件
-  
 #include <string>
 #include <fstream>
 #include <sstream>
 #include <iostream>
-  
+
+#include <GL/glew.h>; // 包含glew来获取所有的必须OpenGL头文件
 
 class Shader
 {
 public:
-    // 程序ID
-    unsigned int ID;
-  
-    // 构造器读取并构建着色器
-    Shader(const char* vertexPath, const char* fragmentPath);
-    // 使用/激活程序
-    void use();
-    // uniform工具函数
-    void setBool(const std::string &name, bool value) const;  
-    void setInt(const std::string &name, int value) const;   
-    void setFloat(const std::string &name, float value) const;
+  	// 程序ID
+  	GLuint Program;
+  	// 构造器读取并构建着色器
+  	Shader(const GLchar* vertexPath, const GLchar* fragmentPath);
+  	// 使用程序
+  	void Use();
 };
-  
+
 #endif
 ```
 
@@ -339,14 +331,14 @@ public:
 
 	在上面，我们在头文件顶部使用了几个<def>预处理指令</def>(Preprocessor Directives)。这些预处理指令会告知你的编译器只在它没被包含过的情况下才包含和编译这个头文件，即使多个文件都包含了这个着色器头文件。它是用来防止链接冲突的。
 
-着色器类储存了着色器程序的ID。它的构造器需要顶点和片段着色器源代码的文件路径，这样我们就可以把源码的文本文件储存在硬盘上了。除此之外，为了让我们的生活更轻松一点，还加入了一些工具函数：<fun>use</fun>用来激活着色器程序，所有的<fun>set...</fun>函数能够查询一个unform的位置值并设置它的值。
+着色器类储存了着色器程序的ID。它的构造器需要顶点和片段着色器源代码的文件路径，这样我们就可以把源码的文本文件储存在硬盘上了。我们还添加了一个<fun>Use</fun>函数，它其实不那么重要，但是能够显示这个自造类如何让我们的生活变得轻松（虽然只有一点）。
 
 ## 从文件读取
 
 我们使用C++文件流读取着色器内容，储存到几个`string`对象里：
 
 ```c++
-Shader(const char* vertexPath, const char* fragmentPath)
+Shader(const GLchar* vertexPath, const GLchar* fragmentPath)
 {
     // 1. 从文件路径中获取顶点/片段着色器
     std::string vertexCode;
@@ -354,30 +346,30 @@ Shader(const char* vertexPath, const char* fragmentPath)
     std::ifstream vShaderFile;
     std::ifstream fShaderFile;
     // 保证ifstream对象可以抛出异常：
-    vShaderFile.exceptions (std::ifstream::failbit | std::ifstream::badbit);
-    fShaderFile.exceptions (std::ifstream::failbit | std::ifstream::badbit);
+    vShaderFile.exceptions(std::ifstream::badbit);
+    fShaderFile.exceptions(std::ifstream::badbit);
     try 
     {
         // 打开文件
         vShaderFile.open(vertexPath);
         fShaderFile.open(fragmentPath);
         std::stringstream vShaderStream, fShaderStream;
-        // 读取文件的缓冲内容到数据流中
+        // 读取文件的缓冲内容到流中
         vShaderStream << vShaderFile.rdbuf();
         fShaderStream << fShaderFile.rdbuf();		
-        // 关闭文件处理器
+        // 关闭文件
         vShaderFile.close();
         fShaderFile.close();
-        // 转换数据流到string
-        vertexCode   = vShaderStream.str();
+        // 转换流至GLchar数组
+        vertexCode = vShaderStream.str();
         fragmentCode = fShaderStream.str();		
     }
     catch(std::ifstream::failure e)
     {
         std::cout << "ERROR::SHADER::FILE_NOT_SUCCESFULLY_READ" << std::endl;
     }
-    const char* vShaderCode = vertexCode.c_str();
-    const char* fShaderCode = fragmentCode.c_str();
+    const GLchar* vShaderCode = vertexCode.c_str();
+    const GLchar* fShaderCode = fragmentCode.c_str();
     [...]
 ```
 
@@ -385,10 +377,10 @@ Shader(const char* vertexPath, const char* fragmentPath)
 
 ```c++
 // 2. 编译着色器
-unsigned int vertex, fragment;
-int success;
-char infoLog[512];
-   
+GLuint vertex, fragment;
+GLint success;
+GLchar infoLog[512];
+
 // 顶点着色器
 vertex = glCreateShader(GL_VERTEX_SHADER);
 glShaderSource(vertex, 1, &vShaderCode, NULL);
@@ -405,15 +397,15 @@ if(!success)
 [...]
   
 // 着色器程序
-ID = glCreateProgram();
-glAttachShader(ID, vertex);
-glAttachShader(ID, fragment);
-glLinkProgram(ID);
+this->Program = glCreateProgram();
+glAttachShader(this->Program, vertex);
+glAttachShader(this->Program, fragment);
+glLinkProgram(this->Program);
 // 打印连接错误（如果有的话）
-glGetProgramiv(ID, GL_LINK_STATUS, &success);
+glGetProgramiv(this->Program, GL_LINK_STATUS, &success);
 if(!success)
 {
-    glGetProgramInfoLog(ID, 512, NULL, infoLog);
+    glGetProgramInfoLog(this->Program, 512, NULL, infoLog);
     std::cout << "ERROR::SHADER::PROGRAM::LINKING_FAILED\n" << infoLog << std::endl;
 }
   
@@ -422,51 +414,34 @@ glDeleteShader(vertex);
 glDeleteShader(fragment);
 ```
 
-<fun>use</fun>函数非常简单：
+最后我们也会实现<fun>Use</fun>函数：
 
 ```c++
-void use() 
-{ 
-    glUseProgram(ID);
-}
-```
-
-uniform的setter函数也很类似：
-
-```c++
-void setBool(const std::string &name, bool value) const
+void Use()
 {
-    glUniform1i(glGetUniformLocation(ID, name.c_str()), (int)value); 
+    glUseProgram(this->Program);
 }
-void setInt(const std::string &name, int value) const
-{ 
-    glUniform1i(glGetUniformLocation(ID, name.c_str()), value); 
-}
-void setFloat(const std::string &name, float value) const
-{ 
-    glUniform1f(glGetUniformLocation(ID, name.c_str()), value); 
-} 
 ```
 
-现在我们就写完了一个完整的[着色器类](https://learnopengl.com/code_viewer_gh.php?code=includes/learnopengl/shader_s.h)。使用这个着色器类很简单；只要创建一个着色器对象，从那一点开始我们就可以开始使用了：
+现在我们就写完了一个完整的着色器类。使用这个着色器类很简单；只要创建一个着色器对象，从那一点开始我们就可以开始使用了：
 
 ```c++
-Shader ourShader("path/to/shaders/shader.vs", "path/to/shaders/shader.fs");
+Shader ourShader("path/to/shaders/shader.vs", "path/to/shaders/shader.frag");
 ...
 while(...)
 {
-    ourShader.use();
-    ourShader.setFloat("someUniform", 1.0f);
+    ourShader.Use();
+    glUniform1f(glGetUniformLocation(ourShader.Program, "someUniform"), 1.0f);
     DrawStuff();
 }
 ```
 
-我们把顶点和片段着色器储存为两个叫做`shader.vs`和`shader.fs`的文件。你可以使用自己喜欢的名字命名着色器文件；我自己觉得用`.vs`和`.fs`作为扩展名很直观。
+我们把顶点和片段着色器储存为两个叫做`shader.vs`和`shader.frag`的文件。你可以使用自己喜欢的名字命名着色器文件；我自己觉得用`.vs`和`.frag`作为扩展名很直观。
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/3.3.shaders_class/shaders_class.cpp)找到使用[新着色器类](https://learnopengl.com/code_viewer_gh.php?code=includes/learnopengl/shader_s.h)的源代码。注意你可以点击源码中的着色器文件路径来查看每一个着色器的源代码。
+源码：[使用新着色器类的程序](http://learnopengl.com/code_viewer.php?code=getting-started/shaders-using-object)，[着色器类](http://learnopengl.com/code_viewer.php?type=header&code=shader)，[顶点着色器](http://learnopengl.com/code_viewer.php?type=vertex&code=getting-started/basic)，和[片段着色器](http://learnopengl.com/code_viewer.php?type=fragment&code=getting-started/basic)。
 
 # 练习
 
-1. 修改顶点着色器让三角形上下颠倒：[参考解答](https://learnopengl.com/code_viewer.php?code=getting-started/shaders-exercise1)
-2. 使用uniform定义一个水平偏移量，在顶点着色器中使用这个偏移量把三角形移动到屏幕右侧：[参考解答](https://learnopengl.com/code_viewer.php?code=getting-started/shaders-exercise2)
-3. 使用`out`关键字把顶点位置输出到片段着色器，并将片段的颜色设置为与顶点位置相等（来看看连顶点位置值都在三角形中被插值的结果）。做完这些后，尝试回答下面的问题：为什么在三角形的左下角是黑的?：[参考解答](https://learnopengl.com/code_viewer.php?code=getting-started/shaders-exercise3)
+1. 修改顶点着色器让三角形上下颠倒：[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/shaders-exercise1)
+2. 使用uniform定义一个水平偏移量，在顶点着色器中使用这个偏移量把三角形移动到屏幕右侧：[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/shaders-exercise2)
+3. 使用`out`关键字把顶点位置输出到片段着色器，并将片段的颜色设置为与顶点位置相等（来看看连顶点位置值都在三角形中被插值的结果）。做完这些后，尝试回答下面的问题：为什么在三角形的左下角是黑的?：[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/shaders-exercise3)

docs/01 Getting started/06 Textures.md

@@ -3,12 +3,8 @@
 原文     | [Textures](http://learnopengl.com/#!Getting-started/Textures)
       ---|---
 作者     | JoeyDeVries
-翻译     | [Django](http://bullteacher.com/), Krasjet, Geequlim, [BLumia](https://github.com/blumia/)
-校对     | AoZhang
-
-!!! note "译注"
-
-	注意，由于作者对教程做出了更新，之前本节使用的是SOIL库，但现在改为了使用`stb_image.h`库，关于SOIL配置的部分现在已经被修改，但我仍决定将这部分教程保留起来，放到一个历史存档中，如果有需要的话可以到[这里](../legacy.md)来查看。
+翻译     | [Django](http://bullteacher.com/)
+校对     | Geequlim, [BLumia](https://github.com/blumia/)
 
 我们已经了解到，我们可以为每个顶点添加颜色来增加图形的细节，从而创建出有趣的图像。但是，如果想让图形看起来更真实，我们就必须有足够多的顶点，从而指定足够多的颜色。这将会产生很多额外开销，因为每个模型都会需求更多的顶点，每个顶点又需求一个颜色属性。
 
@@ -24,19 +20,19 @@
 
 为了能够把纹理映射(Map)到三角形上，我们需要指定三角形的每个顶点各自对应纹理的哪个部分。这样每个顶点就会关联着一个<def>纹理坐标</def>(Texture Coordinate)，用来标明该从纹理图像的哪个部分采样（译注：采集片段颜色）。之后在图形的其它片段上进行片段插值(Fragment Interpolation)。
 
-纹理坐标在x和y轴上，范围为0到1之间（注意我们使用的是2D纹理图像）。使用纹理坐标获取纹理颜色叫做<def>采样</def>(Sampling)。纹理坐标起始于(0, 0)，也就是纹理图片的左下角，终止于(1, 1)，即纹理图片的右上角。下面的图片展示了我们是如何把纹理坐标映射到三角形上的。
+纹理坐标在x和y轴上，范围为0到1之间（注意我们使用的是2D纹理图像）。使用纹理坐标获取纹理颜色叫做<def>采样</def>(Sampling)。纹理坐标起始于(0, 0)，也就是纹理图片的左下角，终始于(1, 1)，即纹理图片的右上角。下面的图片展示了我们是如何把纹理坐标映射到三角形上的。
 
 ![](../img/01/06/tex_coords.png)
 
-我们为三角形指定了3个纹理坐标点。如上图所示，我们希望三角形的左下角对应纹理的左下角，因此我们把三角形左下角顶点的纹理坐标设置为(0, 0)；同理右下方的顶点设置为(1, 0)；三角形的上顶点对应于图片的上中位置所以我们把它的纹理坐标设置为(0.5, 1.0)。我们只要给顶点着色器传递这三个纹理坐标就行了，接下来它们会被传到片段着色器中，它会为每个片段进行纹理坐标的插值。
+我们为三角形指定了3个纹理坐标点。如上图所示，我们希望三角形的左下角对应纹理的左下角，因此我们把三角形左下角顶点的纹理坐标设置为(0, 0)；三角形的上顶点对应于图片的上中位置所以我们把它的纹理坐标设置为(0.5, 1.0)；同理右下方的顶点设置为(1, 0)。我们只要给顶点着色器传递这三个纹理坐标就行了，接下来它们会被传片段着色器中，它会为每个片段进行纹理坐标的插值。
 
 纹理坐标看起来就像这样：
 
 ```c++
-float texCoords[] = {
+GLfloat texCoords[] = {
     0.0f, 0.0f, // 左下角
     1.0f, 0.0f, // 右下角
-    0.5f, 1.0f  // 上中
+    0.5f, 1.0f // 上中
 };
 ```
 
@@ -46,7 +42,7 @@ float texCoords[] = {
 
 纹理坐标的范围通常是从(0, 0)到(1, 1)，那如果我们把纹理坐标设置在范围之外会发生什么？OpenGL默认的行为是重复这个纹理图像（我们基本上忽略浮点纹理坐标的整数部分），但OpenGL提供了更多的选择：
 
-环绕方式              | 描述
+环绕方式(Wrapping)              | 描述
                             ---|---
 <var>GL_REPEAT</var>           | 对纹理的默认行为。重复纹理图像。
 <var>GL_MIRRORED_REPEAT</var>  | 和<var>GL_REPEAT</var>一样，但每次重复图片是镜像放置的。
@@ -64,7 +60,7 @@ glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_MIRRORED_REPEAT);
 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_MIRRORED_REPEAT);
 ```
 
-第一个参数指定了纹理目标；我们使用的是2D纹理，因此纹理目标是<var>GL_TEXTURE_2D</var>。第二个参数需要我们指定设置的选项与应用的纹理轴。我们打算配置的是`WRAP`选项，并且指定`S`和`T`轴。最后一个参数需要我们传递一个环绕方式(Wrapping)，在这个例子中OpenGL会给当前激活的纹理设定纹理环绕方式为<var>GL_MIRRORED_REPEAT</var>。
+第一个参数指定了纹理目标；我们使用的是2D纹理，因此纹理目标是<var>GL_TEXTURE_2D</var>。第二个参数需要我们指定设置的选项与应用的纹理轴。我们打算配置的是`WRAP`选项，并且指定`S`和`T`轴。最后一个参数需要我们传递一个环绕方式，在这个例子中OpenGL会给当前激活的纹理设定纹理环绕方式为<var>GL_MIRRORED_REPEAT</var>。
 
 如果我们选择<var>GL_CLAMP_TO_BORDER</var>选项，我们还需要指定一个边缘的颜色。这需要使用<fun>glTexParameter</fun>函数的`fv`后缀形式，用<var>GL_TEXTURE_BORDER_COLOR</var>作为它的选项，并且传递一个float数组作为边缘的颜色值：
 
@@ -110,7 +106,7 @@ OpenGL使用一种叫做<def>多级渐远纹理</def>(Mipmap)的概念来解决
 
 ![](../img/01/06/mipmaps.png)
 
-手工为每个纹理图像创建一系列多级渐远纹理很麻烦，幸好OpenGL有一个<fun>glGenerateMipmap</fun>函数，在创建完一个纹理后调用它OpenGL就会承担接下来的所有工作了。后面的教程中你会看到该如何使用它。
+手工为每个纹理图像创建一系列多级渐远纹理很麻烦，幸好OpenGL有一个<fun>glGenerateMipmaps</fun>函数，在创建完一个纹理后调用它OpenGL就会承担接下来的所有工作了。后面的教程中你会看到该如何使用它。
 
 在渲染中切换多级渐远纹理级别(Level)时，OpenGL在两个不同级别的多级渐远纹理层之间会产生不真实的生硬边界。就像普通的纹理过滤一样，切换多级渐远纹理级别时你也可以在两个不同多级渐远纹理级别之间使用<var>NEAREST</var>和<var>LINEAR</var>过滤。为了指定不同多级渐远纹理级别之间的过滤方式，你可以使用下面四个选项中的一个代替原有的过滤方式：
 
@@ -135,38 +131,31 @@ glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
 
 使用纹理之前要做的第一件事是把它们加载到我们的应用中。纹理图像可能被储存为各种各样的格式，每种都有自己的数据结构和排列，所以我们如何才能把这些图像加载到应用中呢？一个解决方案是选一个需要的文件格式，比如`.PNG`，然后自己写一个图像加载器，把图像转化为字节序列。写自己的图像加载器虽然不难，但仍然挺麻烦的，而且如果要支持更多文件格式呢？你就不得不为每种你希望支持的格式写加载器了。
 
-另一个解决方案也许是一种更好的选择，使用一个支持多种流行格式的图像加载库来为我们解决这个问题。比如说我们要用的`stb_image.h`库。
+另一个解决方案也许是一种更好的选择，使用一个支持多种流行格式的图像加载库来为我们解决这个问题。比如说我们要用的SOIL库。
 
-## stb_image.h
+## SOIL
 
-`stb_image.h`是[Sean Barrett](https://github.com/nothings)的一个非常流行的单头文件图像加载库，它能够加载大部分流行的文件格式，并且能够很简单得整合到你的工程之中。`stb_image.h`可以在[这里](https://github.com/nothings/stb/blob/master/stb_image.h)下载。下载这一个头文件，将它以`stb_image.h`的名字加入你的工程，并另创建一个新的C++文件，输入以下代码：
+SOIL是简易OpenGL图像库(Simple OpenGL Image Library)的缩写，它支持大多数流行的图像格式，使用起来也很简单，你可以从他们的[主页](http://www.lonesock.net/soil.html)下载。像其它库一样，你必须自己生成**.lib**。你可以使用**/projects**文件夹内的任意一个解决方案(Solution)文件（不用担心他们的Visual Studio版本太老，你可以把它们转变为新的版本，这一般是没问题的。译注：用VS2010的时候，你要用VC8而不是VC9的解决方案，想必更高版本的情况亦是如此）来生成你自己的**.lib**文件。你还要添加**src**文件夹里面的文件到你的**includes**文件夹；对了，不要忘记添加**SOIL.lib**到你的链接器选项，并在你代码文件的开头加上`#include <SOIL.h>`。
+
+下面的教程中，我们会使用一张[木箱](../img/01/06/container.jpg)的图片。要使用SOIL加载图片，我们需要使用它的<fun>SOIL_load_image</fun>函数：
 
 ```c++
-#define STB_IMAGE_IMPLEMENTATION
-#include "stb_image.h"
+int width, height;
+unsigned char* image = SOIL_load_image("container.jpg", &width, &height, 0, SOIL_LOAD_RGB);
 ```
 
-通过定义<var>STB_IMAGE_IMPLEMENTATION</var>，预处理器会修改头文件，让其只包含相关的函数定义源码，等于是将这个头文件变为一个 `.cpp` 文件了。现在只需要在你的程序中包含`stb_image.h`并编译就可以了。
-
-下面的教程中，我们会使用一张[木箱](../img/01/06/container.jpg)的图片。要使用`stb_image.h`加载图片，我们需要使用它的<fun>stbi_load</fun>函数：
-
-```c++
-int width, height, nrChannels;
-unsigned char *data = stbi_load("container.jpg", &width, &height, &nrChannels, 0);
-```
-
-这个函数首先接受一个图像文件的位置作为输入。接下来它需要三个`int`作为它的第二、第三和第四个参数，`stb_image.h`将会用图像的**宽度**、**高度**和**颜色通道的个数**填充这三个变量。我们之后生成纹理的时候会用到的图像的宽度和高度的。
+函数首先需要输入图片文件的路径。然后需要两个`int`指针作为第二个和第三个参数，SOIL会分别返回图片的**宽度**和**高度**到其中。后面我们在生成纹理的时候会用图像的宽度和高度。第四个参数指定图片的**通道**(Channel)数量，但是这里我们只需留为`0`。最后一个参数告诉SOIL如何来加载图片：我们只关注图片的`RGB`值。结果会储存为一个很大的char/byte数组。
 
 ## 生成纹理
 
 和之前生成的OpenGL对象一样，纹理也是使用ID引用的。让我们来创建一个：
 
 ```c++
-unsigned int texture;
+GLuint texture;
 glGenTextures(1, &texture);
 ```
 
-<fun>glGenTextures</fun>函数首先需要输入生成纹理的数量，然后把它们储存在第二个参数的`unsigned int`数组中（我们的例子中只是单独的一个`unsigned int`），就像其他对象一样，我们需要绑定它，让之后任何的纹理指令都可以配置当前绑定的纹理：
+<fun>glGenTextures</fun>函数首先需要输入生成纹理的数量，然后把它们储存在第二个参数的`GLuint`数组中（我们的例子中只是一个单独的`GLuint`），就像其他对象一样，我们需要绑定它，让之后任何的纹理指令都可以配置当前绑定的纹理：
 
 ```c++
 glBindTexture(GL_TEXTURE_2D, texture);
@@ -175,7 +164,7 @@ glBindTexture(GL_TEXTURE_2D, texture);
 现在纹理已经绑定了，我们可以使用前面载入的图片数据生成一个纹理了。纹理可以通过<fun>glTexImage2D</fun>来生成：
 
 ```c++
-glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data);
+glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, image);
 glGenerateMipmap(GL_TEXTURE_2D);
 ```
 
@@ -185,42 +174,34 @@ glGenerateMipmap(GL_TEXTURE_2D);
 - 第二个参数为纹理指定多级渐远纹理的级别，如果你希望单独手动设置每个多级渐远纹理的级别的话。这里我们填0，也就是基本级别。
 - 第三个参数告诉OpenGL我们希望把纹理储存为何种格式。我们的图像只有`RGB`值，因此我们也把纹理储存为`RGB`值。
 - 第四个和第五个参数设置最终的纹理的宽度和高度。我们之前加载图像的时候储存了它们，所以我们使用对应的变量。
-- 下个参数应该总是被设为`0`（历史遗留的问题）。
+- 下个参数应该总是被设为`0`（历史遗留问题）。
 - 第七第八个参数定义了源图的格式和数据类型。我们使用RGB值加载这个图像，并把它们储存为`char`(byte)数组，我们将会传入对应值。
 - 最后一个参数是真正的图像数据。
 
 当调用<fun>glTexImage2D</fun>时，当前绑定的纹理对象就会被附加上纹理图像。然而，目前只有基本级别(Base-level)的纹理图像被加载了，如果要使用多级渐远纹理，我们必须手动设置所有不同的图像（不断递增第二个参数）。或者，直接在生成纹理之后调用<fun>glGenerateMipmap</fun>。这会为当前绑定的纹理自动生成所有需要的多级渐远纹理。
 
-生成了纹理和相应的多级渐远纹理后，释放图像的内存是一个很好的习惯。
+生成了纹理和相应的多级渐远纹理后，释放图像的内存并解绑纹理对象是一个很好的习惯。
 
 ```c++
-stbi_image_free(data);
+SOIL_free_image_data(image);
+glBindTexture(GL_TEXTURE_2D, 0);
 ```
 
 生成一个纹理的过程应该看起来像这样：
 
 ```c++
-unsigned int texture;
+GLuint texture;
 glGenTextures(1, &texture);
 glBindTexture(GL_TEXTURE_2D, texture);
 // 为当前绑定的纹理对象设置环绕、过滤方式
-glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);	
-glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
-glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
-glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
+...
 // 加载并生成纹理
-int width, height, nrChannels;
-unsigned char *data = stbi_load("container.jpg", &width, &height, &nrChannels, 0);
-if (data)
-{
-    glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data);
-    glGenerateMipmap(GL_TEXTURE_2D);
-}
-else
-{
-    std::cout << "Failed to load texture" << std::endl;
-}
-stbi_image_free(data);
+int width, height;
+unsigned char* image = SOIL_load_image("container.jpg", &width, &height, 0, SOIL_LOAD_RGB);
+glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, image);
+glGenerateMipmap(GL_TEXTURE_2D);
+SOIL_free_image_data(image);
+glBindTexture(GL_TEXTURE_2D, 0); 
 ```
 
 ## 应用纹理
@@ -228,7 +209,7 @@ stbi_image_free(data);
 后面的这部分我们会使用<fun>glDrawElements</fun>绘制[「你好，三角形」](04 Hello Triangle.md)教程最后一部分的矩形。我们需要告知OpenGL如何采样纹理，所以我们必须使用纹理坐标更新顶点数据：
 
 ```c++
-float vertices[] = {
+GLfloat vertices[] = {
 //     ---- 位置 ----       ---- 颜色 ----     - 纹理坐标 -
      0.5f,  0.5f, 0.0f,   1.0f, 0.0f, 0.0f,   1.0f, 1.0f,   // 右上
      0.5f, -0.5f, 0.0f,   0.0f, 1.0f, 0.0f,   1.0f, 0.0f,   // 右下
@@ -242,46 +223,46 @@ float vertices[] = {
 ![](../img/01/06/vertex_attribute_pointer_interleaved_textures.png)
 
 ```c++
-glVertexAttribPointer(2, 2, GL_FLOAT, GL_FALSE, 8 * sizeof(float), (void*)(6 * sizeof(float)));
+glVertexAttribPointer(2, 2, GL_FLOAT,GL_FALSE, 8 * sizeof(GLfloat), (GLvoid*)(6 * sizeof(GLfloat)));
 glEnableVertexAttribArray(2);
 ```
 
-注意，我们同样需要调整前面两个顶点属性的步长参数为`8 * sizeof(float)`。
+注意，我们同样需要调整前面两个顶点属性的步长参数为`8 * sizeof(GLfloat)`。
 
 接着我们需要调整顶点着色器使其能够接受顶点坐标为一个顶点属性，并把坐标传给片段着色器：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;
-layout (location = 1) in vec3 aColor;
-layout (location = 2) in vec2 aTexCoord;
+layout (location = 0) in vec3 position;
+layout (location = 1) in vec3 color;
+layout (location = 2) in vec2 texCoord;
 
 out vec3 ourColor;
 out vec2 TexCoord;
 
 void main()
 {
-    gl_Position = vec4(aPos, 1.0);
-    ourColor = aColor;
-    TexCoord = aTexCoord;
+    gl_Position = vec4(position, 1.0f);
+    ourColor = color;
+    TexCoord = texCoord;
 }
 ```
-片段着色器应该接下来会把输出变量`TexCoord`作为输入变量。
+片段着色器应该把输出变量`TexCoord`作为输入变量。
 
 片段着色器也应该能访问纹理对象，但是我们怎样能把纹理对象传给片段着色器呢？GLSL有一个供纹理对象使用的内建数据类型，叫做<def>采样器</def>(Sampler)，它以纹理类型作为后缀，比如`sampler1D`、`sampler3D`，或在我们的例子中的`sampler2D`。我们可以简单声明一个`uniform sampler2D`把一个纹理添加到片段着色器中，稍后我们会把纹理赋值给这个uniform。
 
 ```c++
 #version 330 core
-out vec4 FragColor;
-  
 in vec3 ourColor;
 in vec2 TexCoord;
 
+out vec4 color;
+
 uniform sampler2D ourTexture;
 
 void main()
 {
-    FragColor = texture(ourTexture, TexCoord);
+    color = texture(ourTexture, TexCoord);
 }
 ```
 
@@ -293,22 +274,19 @@ void main()
 glBindTexture(GL_TEXTURE_2D, texture);
 glBindVertexArray(VAO);
 glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_INT, 0);
+glBindVertexArray(0);
 ```
 
 如果你跟着这个教程正确地做完了，你会看到下面的图像：
 
 ![](../img/01/06/textures2.png)
 
-如果你的矩形是全黑或全白的你可能在哪儿做错了什么。检查你的着色器日志，并尝试对比一下[源码](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/4.1.textures/textures.cpp)。
-
-!!! attention
-
-	如果你的纹理代码不能正常工作或者显示是全黑，请继续阅读，并一直跟进我们的代码到最后的例子，它是应该能够工作的。在一些驱动中，必须要对每个采样器uniform都附加上纹理单元才可以，这个会在下面介绍。
+如果你的矩形是全黑或全白的你可能在哪儿做错了什么。检查你的着色器日志，并尝试对比一下[源码](http://learnopengl.com/code_viewer.php?code=getting-started/textures)。
 
 我们还可以把得到的纹理颜色与顶点颜色混合，来获得更有趣的效果。我们只需把纹理颜色与顶点颜色在片段着色器中相乘来混合二者的颜色：
 
 ```c++
-FragColor = texture(ourTexture, TexCoord) * vec4(ourColor, 1.0);
+color = texture(ourTexture, TexCoord) * vec4(ourColor, 1.0f);
 ```
 
 最终的效果应该是顶点颜色和纹理颜色的混合色：
@@ -324,7 +302,7 @@ FragColor = texture(ourTexture, TexCoord) * vec4(ourColor, 1.0);
 纹理单元的主要目的是让我们在着色器中可以使用多于一个的纹理。通过把纹理单元赋值给采样器，我们可以一次绑定多个纹理，只要我们首先激活对应的纹理单元。就像<fun>glBindTexture</fun>一样，我们可以使用<fun>glActiveTexture</fun>激活纹理单元，传入我们需要使用的纹理单元：
 
 ```c++
-glActiveTexture(GL_TEXTURE0); // 在绑定纹理之前先激活纹理单元
+glActiveTexture(GL_TEXTURE0); //在绑定纹理之前先激活纹理单元
 glBindTexture(GL_TEXTURE_2D, texture);
 ```
 
@@ -333,83 +311,67 @@ glBindTexture(GL_TEXTURE_2D, texture);
 !!! Important
 
 	OpenGL至少保证有16个纹理单元供你使用，也就是说你可以激活从<var>GL_TEXTURE0</var>到<var>GL_TEXTRUE15</var>。它们都是按顺序定义的，所以我们也可以通过<var>GL_TEXTURE0 + 8</var>的方式获得<var>GL_TEXTURE8</var>，这在当我们需要循环一些纹理单元的时候会很有用。
-
+        
 我们仍然需要编辑片段着色器来接收另一个采样器。这应该相对来说非常直接了：
 
 ```c++
 #version 330 core
 ...
 
-uniform sampler2D texture1;
-uniform sampler2D texture2;
+uniform sampler2D ourTexture1;
+uniform sampler2D ourTexture2;
 
 void main()
 {
-    FragColor = mix(texture(texture1, TexCoord), texture(texture2, TexCoord), 0.2);
+    color = mix(texture(ourTexture1, TexCoord), texture(ourTexture2, TexCoord), 0.2);
 }
 ```
 
-最终输出颜色现在是两个纹理的结合。GLSL内建的<fun>mix</fun>函数需要接受两个值作为参数，并对它们根据第三个参数进行线性插值。如果第三个值是`0.0`，它会返回第一个输入；如果是`1.0`，会返回第二个输入值。`0.2`会返回`80%`的第一个输入颜色和`20%`的第二个输入颜色，即返回两个纹理的混合色。
+最终输出颜色现在是两个纹理的结合。GLSL内建的<fun>mix</fun>函数需要接受两个值作为参数，并对它们根据第三个参数进行线性插值。。如果第三个值是`0.0`，它会返回第一个输入；如果是`1.0`，会返回第二个输入值。`0.2`会返回`80%`的第一个输入颜色和`20%`的第二个输入颜色，即返回两个纹理的混合色。
 
-我们现在需要载入并创建另一个纹理；你应该对这些步骤很熟悉了。记得创建另一个纹理对象，载入图片，使用<fun>glTexImage2D</fun>生成最终纹理。对于第二个纹理我们使用一张[你学习OpenGL时的面部表情](../img/01/06/awesomeface.png)图片：
-
-```c++
-unsigned char *data = stbi_load("awesomeface.png", &width, &height, &nrChannels, 0);
-if (data)
-{
-    glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGBA, GL_UNSIGNED_BYTE, data);
-    glGenerateMipmap(GL_TEXTURE_2D);
-}
-```
-
-注意，我们现在要读取一张包含alpha（透明度）通道的`.png`图片，这意味着我们现在需要使用<var>GL_RGBA</var>参数，指定该图片数据包含了alpha通道；否则OpenGL将无法正确解析图片数据。
+我们现在需要载入并创建另一个纹理；你应该对这些步骤很熟悉了。记得创建另一个纹理对象，载入图片，使用<fun>glTexImage2D</fun>生成最终纹理。对于第二个纹理我们使用一张[你学习OpenGL时的面部表情](../img/01/06/awesomeface.png)图片。
 
 为了使用第二个纹理（以及第一个），我们必须改变一点渲染流程，先绑定两个纹理到对应的纹理单元，然后定义哪个uniform采样器对应哪个纹理单元：
 
 ```c++
 glActiveTexture(GL_TEXTURE0);
 glBindTexture(GL_TEXTURE_2D, texture1);
+glUniform1i(glGetUniformLocation(ourShader.Program, "ourTexture1"), 0);
 glActiveTexture(GL_TEXTURE1);
 glBindTexture(GL_TEXTURE_2D, texture2);
+glUniform1i(glGetUniformLocation(ourShader.Program, "ourTexture2"), 1);
 
 glBindVertexArray(VAO);
 glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_INT, 0);
+glBindVertexArray(0);
 ```
 
-我们还要通过使用<fun>glUniform1i</fun>设置每个采样器的方式告诉OpenGL每个着色器采样器属于哪个纹理单元。我们只需要设置一次即可，所以这个会放在渲染循环的前面：
-
-```c++
-ourShader.use(); // 不要忘记在设置uniform变量之前激活着色器程序！
-glUniform1i(glGetUniformLocation(ourShader.ID, "texture1"), 0); // 手动设置
-ourShader.setInt("texture2", 1); // 或者使用着色器类设置
-  
-while(...) 
-{
-    [...]
-}
-```
-
-通过使用<fun>glUniform1i</fun>设置采样器，我们保证了每个uniform采样器对应着正确的纹理单元。你应该能得到下面的结果：
+注意，我们使用<fun>glUniform1i</fun>设置uniform采样器的位置值，或者说纹理单元。通过<fun>glUniform1i</fun>的设置，我们保证每个uniform采样器对应着正确的纹理单元。你应该能得到下面的结果：
 
 ![](../img/01/06/textures_combined.png)
 
-你可能注意到纹理上下颠倒了！这是因为OpenGL要求y轴`0.0`坐标是在图片的底部的，但是图片的y轴`0.0`坐标通常在顶部。很幸运，`stb_image.h`能够在图像加载时帮助我们翻转y轴，只需要在加载任何图像前加入以下语句即可：
+你可能注意到纹理上下颠倒了！这是因为OpenGL要求y轴`0.0`坐标是在图片的底部的，但是图片的y轴`0.0`坐标通常在顶部。一些图片加载器比如[DevIL](http://openil.sourceforge.net/tuts/tut_10/index.htm)在加载的时候有选项重置y原点，但是SOIL没有。SOIL却有一个叫做<fun>SOIL_load_OGL_texture</fun>函数可以使用一个叫做<var>SOIL_FLAG_INVERT_Y</var>的标记加载**并**生成纹理，这可以解决我们的问题。不过这个函数用了一些在现代OpenGL中失效的特性，所以现在我们仍需坚持使用<fun>SOIL_load_image</fun>，自己做纹理的生成。
 
-```c++
-stbi_set_flip_vertically_on_load(true);
-```
+所以修复我们的小问题，有两个选择：
 
-在让`stb_image.h`在加载图片时翻转y轴之后你就应该能够获得下面的结果了：
+1. 我们可以改变顶点数据的纹理坐标，翻转`y`值（用1减去y坐标）。
+2. 我们可以编辑顶点着色器来自动翻转`y`坐标，替换`TexCoord`的值为`TexCoord = vec2(texCoord.x, 1.0f - texCoord.y);`。
+
+!!! Attention
+
+	上面提供的解决方案仅仅通过一些黑科技让图片翻转。它们在大多数情况下都能正常工作，然而实际上这种方案的效果取决于你的实现和纹理，所以最好的解决方案是调整你的图片加载器，或者以一种y原点符合OpenGL需求的方式编辑你的纹理图像。
+        
+如果你编辑了顶点数据，在顶点着色器中翻转了纵坐标，你会得到下面的结果：
 
 ![](../img/01/06/textures_combined2.png)
 
-如果你看到了一个开心的箱子，你就做对了。你可以对比一下[源代码](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/4.2.textures_combined/textures_combined.cpp)。
+如果你看到了一个开心的箱子，你就做对了。你可以对比一下[源代码](http://learnopengl.com/code_viewer.php?code=getting-started/textures_combined)，以及[顶点](http://learnopengl.com/code_viewer.php?type=vertex&code=getting-started/texture)和[片段](http://learnopengl.com/code_viewer.php?type=fragment&code=getting-started/texture)着色器。
 
 ## 练习
 
 为了更熟练地使用纹理，建议在继续之后的学习之前做完这些练习：
 
-- 修改片段着色器，**仅**让笑脸图案朝另一个方向看，[参考解答](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/4.3.textures_exercise1/textures_exercise1.cpp)
-- 尝试用不同的纹理环绕方式，设定一个从`0.0f`到`2.0f`范围内的（而不是原来的`0.0f`到`1.0f`）纹理坐标。试试看能不能在箱子的角落放置4个笑脸：[参考解答](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/4.4.textures_exercise2/textures_exercise2.cpp)，[结果](../img/01/06/textures_exercise2.png)。记得一定要试试其它的环绕方式。
-- 尝试在矩形上只显示纹理图像的中间一部分，修改纹理坐标，达到能看见单个的像素的效果。尝试使用<var>GL_NEAREST</var>的纹理过滤方式让像素显示得更清晰：[参考解答](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/4.5.textures_exercise3/textures_exercise3.cpp)
-- 使用一个uniform变量作为<fun>mix</fun>函数的第三个参数来改变两个纹理可见度，使用上和下键来改变箱子或笑脸的可见度：[参考解答](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/4.6.textures_exercise4/textures_exercise4.cpp)。
+- 修改片段着色器，**仅**让笑脸图案朝另一个方向看，[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/textures-exercise1)
+- 尝试用不同的纹理环绕方式，设定一个从`0.0f`到`2.0f`范围内的（而不是原来的`0.0f`到`1.0f`）纹理坐标。试试看能不能在箱子的角落放置4个笑脸：[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/textures-exercise2)，[结果](http://learnopengl.com/img/getting-started/textures_exercise2.png)。记得一定要试试其他的环绕方式。
+- 尝试在矩形上只显示纹理图像的中间一部分，修改纹理坐标，达到能看见单个的像素的效果。尝试使用<var>GL_NEAREST</var>的纹理过滤方式让像素显示得更清晰：[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/textures-exercise3)
+- 使用一个uniform变量作为<fun>mix</fun>函数的第三个参数来改变两个纹理可见度，使用上和下键来改变箱子或笑脸的可见度：[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/textures-exercise4)，[片段着色器](http://learnopengl.com/code_viewer.php?code=getting-started/textures-exercise4_fragment)。

docs/01 Getting started/07 Transformations.md

@@ -3,8 +3,8 @@
 原文     | [Transformations](http://learnopengl.com/#!Getting-started/Transformations)
       ---|---
 作者     | JoeyDeVries
-翻译     | Django, Krasjet, [BLumia](https://github.com/blumia/)
-校对     | 暂未校对
+翻译     | Django
+校对     | Meow J, [BLumia](https://github.com/blumia/)
 
 尽管我们现在已经知道了如何创建一个物体、着色、加入纹理，给它们一些细节的表现，但因为它们都还是静态的物体，仍是不够有趣。我们可以尝试着在每一帧改变物体的顶点并且重配置缓冲区从而使它们移动，但这太繁琐了，而且会消耗很多的处理时间。我们现在有一个更好的解决方案，使用（多个）<def>矩阵</def>(Matrix)对象可以更好的<def>变换</def>(Transform)一个物体。当然，这并不是说我们会去讨论武术和数字虚拟世界（译注：Matrix同样也是电影「黑客帝国」的英文名，电影中人类生活在数字虚拟世界，主角会武术）。
 
@@ -40,10 +40,6 @@ $$
 
 其中的+可以是+，-，·或÷，其中·是乘号。注意－和÷运算时不能颠倒（标量-/÷向量），因为颠倒的运算是没有定义的。
 
-!!! note "译注"
-
-	注意，数学上是没有向量与标量相加这个运算的，但是很多线性代数的库都对它有支持（比如说我们用的GLM）。如果你使用过numpy的话，可以把它理解为[Broadcasting](https://numpy.org/doc/1.18/user/basics.broadcasting.html)。
-
 ## 向量取反
 
 对一个向量取反(Negate)会将其方向逆转。一个指向东北的向量取反后就指向西南方向了。我们在一个向量的每个分量前加负号就可以实现取反了（或者说用-1数乘该向量）:
@@ -182,10 +178,6 @@ $$
 \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} - \color{green}3 = \begin{bmatrix} 1 - \color{green}3 & 2 - \color{green}3 \\ 3 - \color{green}3 & 4 - \color{green}3 \end{bmatrix} = \begin{bmatrix} -2 & -1 \\ 0 & 1 \end{bmatrix}
 $$
 
-!!! note "译注"
-
-	注意，数学上是没有矩阵与标量相加减的运算的，但是很多线性代数的库都对它有支持（比如说我们用的GLM）。如果你使用过numpy的话，可以把它理解为[Broadcasting](https://numpy.org/doc/1.18/user/basics.broadcasting.html)。
-
 矩阵与矩阵之间的加减就是两个矩阵对应元素的加减运算，所以总体的规则和与标量运算是差不多的，只不过在相同索引下的元素才能进行运算。这也就是说加法和减法只对同维度的矩阵才是有定义的。一个3×2矩阵和一个2×3矩阵（或一个3×3矩阵与4×4矩阵）是不能进行加减的。我们看看两个2×2矩阵是怎样相加的：
 
 $$
@@ -198,7 +190,6 @@ $$
 \begin{bmatrix} \color{red}4 & \color{red}2 \\ \color{green}1 & \color{green}6 \end{bmatrix} - \begin{bmatrix} \color{red}2 & \color{red}4 \\ \color{green}0 & \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}4 - \color{red}2 & \color{red}2  - \color{red}4 \\ \color{green}1 - \color{green}0 & \color{green}6 - \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}2 & -\color{red}2 \\ \color{green}1 & \color{green}5 \end{bmatrix}
 $$
 
-
 ## 矩阵的数乘
 
 和矩阵与标量的加减一样，矩阵与标量之间的乘法也是矩阵的每一个元素分别乘以该标量。下面的例子展示了乘法的过程：
@@ -239,7 +230,7 @@ $$
 我们用一个更大的例子来结束对矩阵相乘的讨论。试着使用颜色来寻找规律。作为一个有用的练习，你可以试着自己解答一下这个乘法问题，再将你的结果和图中的这个进行对比（如果用笔计算，你很快就能掌握它们）。
 
 $$
-\begin{bmatrix} \color{red}4 & \color{red}2 & \color{red}0 \\ \color{green}0 & \color{green}8 & \color{green}1 \\ \color{blue}0 & \color{blue}1 & \color{blue}0 \end{bmatrix} \cdot \begin{bmatrix} \color{red}4 & \color{green}2 & \color{blue}1 \\ \color{red}2 & \color{green}0 & \color{blue}4 \\ \color{red}9 & \color{green}4 & \color{blue}2 \end{bmatrix} = \begin{bmatrix} \color{red}4 \cdot \color{red}4 + \color{red}2 \cdot \color{red}2 + \color{red}0 \cdot \color{red}9 & \color{red}4 \cdot \color{green}2 + \color{red}2 \cdot \color{green}0 + \color{red}0 \cdot \color{green}4 & \color{red}4 \cdot \color{blue}1 + \color{red}2 \cdot \color{blue}4 + \color{red}0 \cdot \color{blue}2 \\ \color{green}0 \cdot \color{red}4 + \color{green}8 \cdot \color{red}2 + \color{green}1 \cdot \color{red}9 & \color{green}0 \cdot \color{green}2 + \color{green}8 \cdot \color{green}0 + \color{green}1 \cdot \color{green}4 & \color{green}0 \cdot \color{blue}1 + \color{green}8 \cdot \color{blue}4 + \color{green}1 \cdot \color{blue}2 \\ \color{blue}0 \cdot \color{red}4 + \color{blue}1 \cdot \color{red}2 + \color{blue}0 \cdot \color{red}9 & \color{blue}0 \cdot \color{green}2 + \color{blue}1 \cdot \color{green}0 + \color{blue}0 \cdot \color{green}4 & \color{blue}0 \cdot \color{blue}1 + \color{blue}1 \cdot \color{blue}4 + \color{blue}0 \cdot \color{blue}2 \end{bmatrix}
+\begin{bmatrix} \color{red}4 & \color{red}2 & \color{red}0 \\ \color{green}0 & \color{green}8 & \color{green}1 \\ \color{blue}0 & \color{blue}1 & \color{blue}0 \end{bmatrix} \cdot \begin{bmatrix} \color{red}4 & \color{green}2 & \color{blue}1 \\ \color{red}2 & \color{green}0 & \color{blue}4 \\ \color{red}9 & \color{green}4 & \color{blue}2 \end{bmatrix} = \begin{bmatrix} \color{red}4 \cdot \color{red}4 + \color{red}2 \cdot \color{red}2 + \color{red}0 \cdot \color{red}9 & \color{red}4 \cdot \color{green}2 + \color{red}2 \cdot \color{green}0 + \color{red}0 \cdot \color{green}4 & \color{red}4 \cdot \color{blue}1 + \color{red}2 \cdot \color{blue}4 + \color{red}0 \cdot \color{blue}2 \\ \color{green}0 \cdot \color{red}4 + \color{green}8 \cdot \color{red}2 + \color{green}1 \cdot \color{red}9 & \color{green}0 \cdot \color{green}2 + \color{green}8 \cdot \color{green}0 + \color{green}1 \cdot \color{green}4 & \color{green}0 \cdot \color{blue}1 + \color{green}8 \cdot \color{blue}4 + \color{green}1 \cdot \color{blue}2 \\ \color{blue}0 \cdot \color{red}4 + \color{blue}1 \cdot \color{red}2 + \color{blue}0 \cdot \color{red}9 & \color{blue}0 \cdot \color{green}2 + \color{blue}1 \cdot \color{green}0 + \color{blue}0 \cdot \color{green}4 & \color{blue}0 \cdot \color{blue}1 + \color{blue}1 \cdot \color{blue}4 + \color{blue}0 \cdot \color{blue}2 \end{bmatrix} 
  \\ = \begin{bmatrix} 20 & 8 & 12 \\ 25 & 4 & 34 \\ 2 & 0 & 4 \end{bmatrix}
 $$
 
@@ -275,7 +266,7 @@ $$
 
 ![](../img/01/07/vectors_scale.png)
 
-记住，OpenGL通常是在3D空间进行操作的，对于2D的情况我们可以把z轴缩放1倍，这样z轴的值就不变了。我们刚刚的缩放操作是<def>不均匀</def>(Non-uniform)缩放，因为每个轴的缩放因子(Scaling Factor)都不一样。如果每个轴的缩放因子都一样那么就叫<def>均匀缩放</def>(Uniform Scale)。
+记住，OpenGL通常是在3D空间进行操作的，对于2D的情况我们可以把z轴缩放1倍，这样z轴的值就不变了。我们刚刚的缩放操作是<def>不均匀(Non-uniform)<def>缩放，因为每个轴的缩放因子(Scaling Factor)都不一样。如果每个轴的缩放因子都一样那么就叫<def>均匀缩放</def>(Uniform Scale)。
 
 我们下面会构造一个变换矩阵来为我们提供缩放功能。我们从单位矩阵了解到，每个对角线元素会分别与向量的对应元素相乘。如果我们把1变为3会怎样？这样子的话，我们就把向量的每个元素乘以3了，这事实上就把向量缩放3倍。如果我们把缩放变量表示为\((\color{red}{S_1}, \color{green}{S_2}, \color{blue}{S_3})\)我们可以为任意向量\((x,y,z)\)定义一个缩放矩阵：
 
@@ -302,7 +293,7 @@ $$
 	**齐次坐标(Homogeneous Coordinates)**
 
 	向量的w分量也叫<def>齐次坐标</def>。想要从齐次向量得到3D向量，我们可以把x、y和z坐标分别除以w坐标。我们通常不会注意这个问题，因为w分量通常是1.0。使用齐次坐标有几点好处：它允许我们在3D向量上进行位移（如果没有w分量我们是不能位移向量的），而且下一章我们会用w值创建3D视觉效果。
-
+	
 	如果一个向量的齐次坐标是0，这个坐标就是<def>方向向量</def>(Direction Vector)，因为w坐标是0，这个向量就不能位移（译注：这也就是我们说的不能位移一个方向）。
 
 有了位移矩阵我们就可以在3个方向(x、y、z)上移动物体，它是我们的变换工具箱中非常有用的一个变换矩阵。
@@ -316,10 +307,10 @@ $$
 !!! Important
 
 	大多数旋转函数需要用弧度制的角，但幸运的是角度制的角也可以很容易地转化为弧度制的：
-
+	
 	- 弧度转角度：`角度 = 弧度 * (180.0f / PI)`
 	- 角度转弧度：`弧度 = 角度 * (PI / 180.0f)`
-
+	
 	`PI`约等于3.14159265359。
 
 转半圈会旋转360/2 = 180度，向右旋转1/5圈表示向右旋转360/5 = 72度。下图中展示的2D向量\(\color{red}{\bar{v}}\)是由\(\color{green}{\bar{k}}\)向右旋转72度所得的：
@@ -350,19 +341,13 @@ $$
 \begin{bmatrix} \color{red}{\cos \theta} & - \color{red}{\sin \theta} & \color{red}0 & \color{red}0 \\ \color{green}{\sin \theta} & \color{green}{\cos \theta} & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{\cos \theta} \cdot x - \color{red}{\sin \theta} \cdot y  \\ \color{green}{\sin \theta} \cdot x + \color{green}{\cos \theta} \cdot y \\ z \\ 1 \end{pmatrix}
 $$
 
-利用旋转矩阵我们可以把任意位置向量沿一个单位旋转轴进行旋转。也可以将多个矩阵复合，比如先沿着x轴旋转再沿着y轴旋转。但是这会很快导致一个问题——<def>万向节死锁</def>（Gimbal Lock，可以看看[这个视频](https://www.youtube.com/watch?v=zc8b2Jo7mno)[（优酷）](http://v.youku.com/v_show/id_XNzkyOTIyMTI=.html)来了解）。在这里我们不会讨论它的细节，但是对于3D空间中的旋转，一个更好的模型是沿着任意的一个轴，比如单位向量$(0.662, 0.2, 0.7222)$旋转，而不是对一系列旋转矩阵进行复合。这样的一个（超级麻烦的）矩阵是存在的，见下面这个公式，其中\((\color{red}{R_x}, \color{green}{R_y}, \color{blue}{R_z})\)代表任意旋转轴：
+利用旋转矩阵我们可以把我们的位置向量沿一个单位轴进行旋转。也可以把多个矩阵结合起来，比如先沿着x轴旋转再沿着y轴旋转。但是这会很快导致一个问题——<def>万向节死锁</def>（Gimbal Lock，可以看看[这个视频](https://www.youtube.com/watch?v=zc8b2Jo7mno)[（优酷）](http://v.youku.com/v_show/id_XNzkyOTIyMTI=.html)来了解）。我们不会讨论它的细节，但是一个更好的解决方案是沿着任意轴比如(0.662, 0.2, 0.7222)（注意这是个单位向量）旋转，而不是使用一系列旋转矩阵的组合。这样一个（超级麻烦的）矩阵是存在的，见下面这个公式，\((\color{red}{R_x}, \color{green}{R_y}, \color{blue}{R_z})\)代表任意旋转轴：
 
 $$
 \begin{bmatrix} \cos \theta + \color{red}{R_x}^2(1 - \cos \theta) & \color{red}{R_x}\color{green}{R_y}(1 - \cos \theta) - \color{blue}{R_z} \sin \theta & \color{red}{R_x}\color{blue}{R_z}(1 - \cos \theta) + \color{green}{R_y} \sin \theta & 0 \\ \color{green}{R_y}\color{red}{R_x} (1 - \cos \theta) + \color{blue}{R_z} \sin \theta & \cos \theta + \color{green}{R_y}^2(1 - \cos \theta) & \color{green}{R_y}\color{blue}{R_z}(1 - \cos \theta) - \color{red}{R_x} \sin \theta & 0 \\ \color{blue}{R_z}\color{red}{R_x}(1 - \cos \theta) - \color{green}{R_y} \sin \theta & \color{blue}{R_z}\color{green}{R_y}(1 - \cos \theta) + \color{red}{R_x} \sin \theta & \cos \theta + \color{blue}{R_z}^2(1 - \cos \theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
 $$
 
-在数学上讨论如何生成这样的矩阵仍然超出了本节内容。但是记住，即使这样一个矩阵也不能完全解决万向节死锁问题（尽管会极大地避免）。避免万向节死锁的真正解决方案是使用<def>四元数</def>(Quaternion)，它不仅更安全，而且计算会更有效率。四元数可能会在后面的教程中讨论。
-
-!!! note "译注"
-
-	对四元数的理解会用到非常多的数学知识。如果你想了解四元数与3D旋转之间的关系，可以来阅读我的[教程](https://krasjet.github.io/quaternion/)。如果你对万向节死锁的概念仍不是那么清楚，可以来阅读我教程的[Bonus章节](https://krasjet.github.io/quaternion/bonus_gimbal_lock.pdf)。
-
-	现在3Blue1Brown也已经开始了一个四元数的视频系列，他采用球极平面投影(Stereographic Projection)的方式将四元数投影到3D空间，同样有助于理解四元数的概念（仍在更新中）：[https://www.youtube.com/watch?v=d4EgbgTm0Bg](https://www.youtube.com/watch?v=d4EgbgTm0Bg)
+在数学上讨论如何生成这样的矩阵仍然超出了本节内容。但是记住，即使这样一个矩阵也不能完全解决万向节死锁问题（尽管会极大地避免）。避免万向节死锁的真正解决方案是使用<def>四元数</def>(Quaternion)，它不仅安全，而且计算更加友好。有关四元数会在后面的教程中讨论。
 
 ## 矩阵的组合
 
@@ -390,11 +375,7 @@ $$
 
 <img alt="GLM Logo" src="../../img/01/07/glm.png" class="right" />
 
-GLM是Open**GL** **M**athematics的缩写，它是一个**只有头文件的**库，也就是说我们只需包含对应的头文件就行了，不用链接和编译。GLM可以在它们的[网站](https://glm.g-truc.net/0.9.8/index.html)上下载。把头文件的根目录复制到你的**includes**文件夹，然后你就可以使用这个库了。
-
-!!! attention
-
-	GLM库从0.9.9版本起，默认会将矩阵类型初始化为一个零矩阵（所有元素均为0），而不是单位矩阵（对角元素为1，其它元素为0）。如果你使用的是0.9.9或0.9.9以上的版本，你需要将所有的矩阵初始化改为 `glm::mat4 mat = glm::mat4(1.0f)`。如果你想与本教程的代码保持一致，请使用低于0.9.9版本的GLM，或者改用上述代码初始化所有的矩阵。
+GLM是Open**GL** **M**athematics的缩写，它是一个**只有头文件的**库，也就是说我们只需包含对应的头文件就行了，不用链接和编译。GLM可以在它们的[网站](http://glm.g-truc.net/0.9.5/index.html)上下载。把头文件的根目录复制到你的**includes**文件夹，然后你就可以使用这个库了。
 
 我们需要的GLM的大多数功能都可以从下面这3个头文件中找到：
 
@@ -408,44 +389,47 @@ GLM是Open**GL** **M**athematics的缩写，它是一个**只有头文件的**
 
 ```c++
 glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
-// 译注：下面就是矩阵初始化的一个例子，如果使用的是0.9.9及以上版本
-// 下面这行代码就需要改为:
-// glm::mat4 trans = glm::mat4(1.0f)
-// 之后将不再进行提示
 glm::mat4 trans;
 trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
 vec = trans * vec;
 std::cout << vec.x << vec.y << vec.z << std::endl;
 ```
 
-我们先用GLM内建的向量类定义一个叫做`vec`的向量。接下来定义一个`mat4`类型的`trans`，默认是一个4×4单位矩阵。下一步是创建一个变换矩阵，我们是把单位矩阵和一个位移向量传递给`glm::translate`函数来完成这个工作的（然后用给定的矩阵乘以位移矩阵就能获得最后需要的矩阵）。
+我们先用GLM内建的向量类定义一个叫做`vec`的向量。接下来定义一个`mat4`类型的`trans`，默认是一个4×4单位矩阵。下一步是创建一个变换矩阵，我们是把单位矩阵和一个位移向量传递给`glm::translate`函数来完成这个工作的（然后用给定的矩阵乘以位移矩阵就能获得最后需要的矩阵）。  
 之后我们把向量乘以位移矩阵并且输出最后的结果。如果你仍记得位移矩阵是如何工作的话，得到的向量应该是(1 + 1, 0 + 1, 0 + 0)，也就是(2, 1, 0)。这个代码片段将会输出`210`，所以这个位移矩阵是正确的。
 
 我们来做些更有意思的事情，让我们来旋转和缩放之前教程中的那个箱子。首先我们把箱子逆时针旋转90度。然后缩放0.5倍，使它变成原来的一半大。我们先来创建变换矩阵：
 
 ```c++
 glm::mat4 trans;
-trans = glm::rotate(trans, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0));
-trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));
+trans = glm::rotate(trans, 90.0f, glm::vec3(0.0, 0.0, 1.0));
+trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));  
 ```
 
-首先，我们把箱子在每个轴都缩放到0.5倍，然后沿z轴旋转90度。GLM希望它的角度是弧度制的(Radian)，所以我们使用`glm::radians`将角度转化为弧度。注意有纹理的那面矩形是在XY平面上的，所以我们需要把它绕着z轴旋转。因为我们把这个矩阵传递给了GLM的每个函数，GLM会自动将矩阵相乘，返回的结果是一个包括了多个变换的变换矩阵。
+首先，我们把箱子在每个轴都缩放到0.5倍，然后沿z轴旋转90度。注意有纹理的那面矩形是在XY平面上的，所以我们需要把它绕着z轴旋转。因为我们把这个矩阵传递给了GLM的每个函数，GLM会自动将矩阵相乘，返回的结果是一个包括了多个变换的变换矩阵。
+
+!!! Attention
+
+	有些GLM版本接收的是弧度而不是角度，这种情况下你可以用`glm::radians(90.0f)`将角度转换为弧度。
 
 下一个大问题是：如何把矩阵传递给着色器？我们在前面简单提到过GLSL里也有一个`mat4`类型。所以我们将修改顶点着色器让其接收一个`mat4`的uniform变量，然后再用矩阵uniform乘以位置向量：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;
-layout (location = 1) in vec2 aTexCoord;
+layout (location = 0) in vec3 position;
+layout (location = 1) in vec3 color;
+layout (location = 2) in vec2 texCoord;
 
+out vec3 ourColor;
 out vec2 TexCoord;
-
+  
 uniform mat4 transform;
 
 void main()
 {
-    gl_Position = transform * vec4(aPos, 1.0f);
-    TexCoord = vec2(aTexCoord.x, 1.0 - aTexCoord.y);
+    gl_Position = transform * vec4(position, 1.0f);
+    ourColor = color;
+    TexCoord = vec2(texCoord.x, 1.0 - texCoord.y);
 }
 ```
 
@@ -456,11 +440,11 @@ void main()
 在把位置向量传给<var>gl_Position</var>之前，我们先添加一个uniform，并且将其与变换矩阵相乘。我们的箱子现在应该是原来的二分之一大小并（向左）旋转了90度。当然，我们仍需要把变换矩阵传递给着色器：
 
 ```c++
-unsigned int transformLoc = glGetUniformLocation(ourShader.ID, "transform");
+GLuint transformLoc = glGetUniformLocation(ourShader.Program, "transform");
 glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));
 ```
 
-我们首先查询uniform变量的地址，然后用有`Matrix4fv`后缀的<fun>glUniform</fun>函数把矩阵数据发送给着色器。第一个参数你现在应该很熟悉了，它是uniform的位置值。第二个参数告诉OpenGL我们将要发送多少个矩阵，这里是1。第三个参数询问我们是否希望对我们的矩阵进行转置(Transpose)，也就是说交换我们矩阵的行和列。OpenGL开发者通常使用一种内部矩阵布局，叫做<def>列主序</def>(Column-major Ordering)布局。GLM的默认布局就是列主序，所以并不需要转置矩阵，我们填`GL_FALSE`。最后一个参数是真正的矩阵数据，但是GLM并不是把它们的矩阵储存为OpenGL所希望接受的那种，因此我们要先用GLM的自带的函数<fun>value_ptr</fun>来变换这些数据。
+我们首先查询uniform变量的地址，然后用有`Matrix4fv`后缀的<fun>glUniform</fun>函数把矩阵数据发送给着色器。第一个参数你现在应该很熟悉了，它是uniform的位置值。第二个参数告诉OpenGL我们将要发送多少个矩阵，这里是1。第三个参数询问我们我们是否希望对我们的矩阵进行置换(Transpose)，也就是说交换我们矩阵的行和列。OpenGL开发者通常使用一种内部矩阵布局，叫做<def>列主序</def>(Column-major Ordering)布局。GLM的默认布局就是列主序，所以并不需要置换矩阵，我们填`GL_FALSE`。最后一个参数是真正的矩阵数据，但是GLM并不是把它们的矩阵储存为OpenGL所希望接受的那种，因此我们要先用GLM的自带的函数<fun>value_ptr</fun>来变换这些数据。
 
 我们创建了一个变换矩阵，在顶点着色器中声明了一个uniform，并把矩阵发送给了着色器，着色器会变换我们的顶点坐标。最后的结果应该看起来像这样：
 
@@ -471,7 +455,7 @@ glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));
 ```c++
 glm::mat4 trans;
 trans = glm::translate(trans, glm::vec3(0.5f, -0.5f, 0.0f));
-trans = glm::rotate(trans, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));
+trans = glm::rotate(trans,(GLfloat)glfwGetTime() * 50.0f, glm::vec3(0.0f, 0.0f, 1.0f));
 ```
 
 要记住的是前面的例子中我们可以在任何地方声明变换矩阵，但是现在我们必须在每一次迭代中创建它，从而保证我们能够不断更新旋转角度。这也就意味着我们不得不在每次游戏循环的迭代中重新创建变换矩阵。通常在渲染场景的时候，我们也会有多个需要在每次渲染迭代中都用新值重新创建的变换矩阵
@@ -482,17 +466,13 @@ trans = glm::rotate(trans, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));
 
 <video src="../../img/01/07/transformations.mp4" controls="controls"></video>
 
-这就是我们刚刚做到的！一个位移过的箱子，它会一直转，一个变换矩阵就做到了！现在你可以明白为什么矩阵在图形领域是一个如此重要的工具了。我们可以定义无限数量的变换，而把它们组合为仅仅一个矩阵，如果愿意的话我们还可以重复使用它。在着色器中使用矩阵可以省去重新定义顶点数据的功夫，它也能够节省处理时间，因为我们没有一直重新发送我们的数据（这是个非常慢的过程）。
+这就是我们刚刚做到的！一个位移过的箱子，它会一直转，一个变换矩阵就做到了！现在你可以明白为什么矩阵在图形领域是一个如此重要的工具了。我们可以定义一个无限数量的变换，把它们组合为仅仅一个矩阵，如果愿意的话我们还可以重复使用它。在着色器中使用矩阵可以省去重新定义顶点数据的功夫，它也能够节省处理时间，因为我们没有一直重新发送我们的数据（这是个非常慢的过程）。
 
-如果你没有得到正确的结果，或者你有哪儿不清楚的地方。可以看[源码](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/5.1.transformations/transformations.cpp)。
+如果你没有得到正确的结果，或者你有哪儿不清楚的地方。可以看[源码](http://learnopengl.com/code_viewer.php?code=getting-started/transformations)和[顶点](http://learnopengl.com/code_viewer.php?code=getting-started/transformations&type=vertex)、[片段](http://learnopengl.com/code_viewer.php?code=getting-started/transformations&type=fragment)着色器。
 
 下一节中，我们会讨论怎样使用矩阵为顶点定义不同的坐标空间。这将是我们进入实时3D图像的第一步！
 
-## 拓展阅读
-
-- [线性代数的本质](https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab)：Grant Sanderson制作的非常棒的视频教程系列，它讨论了变换和线性代数内在的数学本质（[中文字幕版本](http://space.bilibili.com/88461692#!/channel/detail?cid=9450)）。
-
 ## 练习
 
-- 使用应用在箱子上的最后一个变换，尝试将其改变为先旋转，后位移。看看发生了什么，试着想想为什么会发生这样的事情：[参考解答](https://learnopengl.com/code_viewer.php?code=getting-started/transformations-exercise1)
-- 尝试再次调用<fun>glDrawElements</fun>画出第二个箱子，**只**使用变换将其摆放在不同的位置。让这个箱子被摆放在窗口的左上角，并且会不断的缩放（而不是旋转）。（`sin`函数在这里会很有用，不过注意使用`sin`函数时应用负值会导致物体被翻转）：[参考解答](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/5.2.transformations_exercise2/transformations_exercise2.cpp)
+- 使用应用在箱子上的最后一个变换，尝试将其改变为先旋转，后位移。看看发生了什么，试着想想为什么会发生这样的事情：[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/transformations-exercise1)
+- 尝试再次调用<fun>glDrawElements</fun>画出第二个箱子，**只**使用变换将其摆放在不同的位置。让这个箱子被摆放在窗口的左上角，并且会不断的缩放（而不是旋转）。`sin`函数在这里会很有用，不过注意使用`sin`函数时应用负值会导致物体被翻转：[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/transformations-exercise2)

docs/01 Getting started/08 Coordinate Systems.md

@@ -3,12 +3,12 @@
 原文     | [Coordinate Systems](http://learnopengl.com/#!Getting-started/Coordinate-Systems)
       ---|---
 作者     | JoeyDeVries
-翻译     | linkoln, Geequlim, Krasjet, [BLumia](https://github.com/blumia/)
-校对     | AoZhang
+翻译     | linkoln
+校对     | Geequlim, Meow J, [BLumia](https://github.com/blumia/)
 
-在上一个教程中，我们学习了如何有效地利用矩阵的变换来对所有顶点进行变换。OpenGL希望在每次顶点着色器运行后，我们可见的所有顶点都为标准化设备坐标(Normalized Device Coordinate, NDC)。也就是说，每个顶点的**x**，**y**，**z**坐标都应该在**-1.0**到**1.0**之间，超出这个坐标范围的顶点都将不可见。我们通常会自己设定一个坐标的范围，之后再在顶点着色器中将这些坐标变换为标准化设备坐标。然后将这些标准化设备坐标传入光栅器(Rasterizer)，将它们变换为屏幕上的二维坐标或像素。
+在上一个教程中，我们学习了如何有效地利用矩阵变换来对所有顶点进行转换。OpenGL希望在所有顶点着色器运行后，所有我们可见的顶点都变为标准化设备坐标(Normalized Device Coordinate, NDC)。也就是说，每个顶点的x，y，z坐标都应该在-1.0到1.0之间，超出这个坐标范围的顶点都将不可见。我们通常会自己设定一个坐标的范围，之后再在顶点着色器中将这些坐标转换为标准化设备坐标。然后将这些标准化设备坐标传入光栅器(Rasterizer)，再将他们转换为屏幕上的二维坐标或像素。
 
-将坐标变换为标准化设备坐标，接着再转化为屏幕坐标的过程通常是分步进行的，也就是类似于流水线那样子。在流水线中，物体的顶点在最终转化为屏幕坐标之前还会被变换到多个坐标系统(Coordinate System)。将物体的坐标变换到几个**过渡**坐标系(Intermediate Coordinate System)的优点在于，在这些特定的坐标系统中，一些操作或运算更加方便和容易，这一点很快就会变得很明显。对我们来说比较重要的总共有5个不同的坐标系统：
+将坐标转换为标准化设备坐标，接着再转化为屏幕坐标的过程通常是分步，也就是类似于流水线那样子，实现的，在流水线里面我们在将对象转换到屏幕空间之前会先将其转换到多个坐标系统(Coordinate System)。将对象的坐标转换到几个过渡坐标系(Intermediate Coordinate System)的优点在于，在这些特定的坐标系统中进行一些操作或运算更加方便和容易，这一点很快将会变得很明显。对我们来说比较重要的总共有5个不同的坐标系统：
 
  - 局部空间(Local Space，或者称为物体空间(Object Space))
  - 世界空间(World Space)
@@ -16,191 +16,195 @@
  - 裁剪空间(Clip Space)
  - 屏幕空间(Screen Space)
  
-这就是一个顶点在最终被转化为片段之前需要经历的所有不同状态。
+这些就是我们将所有顶点转换为片段之前，顶点需要处于的不同的状态。
 
-你现在可能会对什么是坐标空间，什么是坐标系统感到非常困惑，所以我们将用一种更加通俗的方式来解释它们。下面，我们将显示一个整体的图片，之后我们会讲解每个空间的具体功能。
+你现在可能对什么是空间或坐标系到底是什么感到困惑，所以接下来我们将会通过展示完整的图片来解释每一个坐标系实际做了什么。
 
 ## 概述
 
-为了将坐标从一个坐标系变换到另一个坐标系，我们需要用到几个变换矩阵，最重要的几个分别是<def>模型</def>(Model)、<def>观察</def>(View)、<def>投影</def>(Projection)三个矩阵。我们的顶点坐标起始于<def>局部空间</def>(Local Space)，在这里它称为<def>局部坐标</def>(Local Coordinate)，它在之后会变为<def>世界坐标</def>(World Coordinate)，<def>观察坐标</def>(View Coordinate)，<def>裁剪坐标</def>(Clip Coordinate)，并最后以<def>屏幕坐标</def>(Screen Coordinate)的形式结束。下面的这张图展示了整个流程以及各个变换过程做了什么：
+为了将坐标从一个坐标系转换到另一个坐标系，我们需要用到几个转换矩阵，最重要的几个分别是**模型(Model)**、**视图(View)**、**投影(Projection)**三个矩阵。首先，顶点坐标开始于**局部空间(Local Space)**，称为**局部坐标(Local Coordinate)**，然后经过**世界坐标(World Coordinate)**，**观察坐标(View Coordinate)**，**裁剪坐标(Clip Coordinate)**，并最后以**屏幕坐标(Screen Coordinate)**结束。下面的图示显示了整个流程及各个转换过程做了什么：
 
-![coordinate_systems](../img/01/08/coordinate_systems.png)
+![coordinate_systems](http://learnopengl.com/img/getting-started/coordinate_systems.png)
 
 
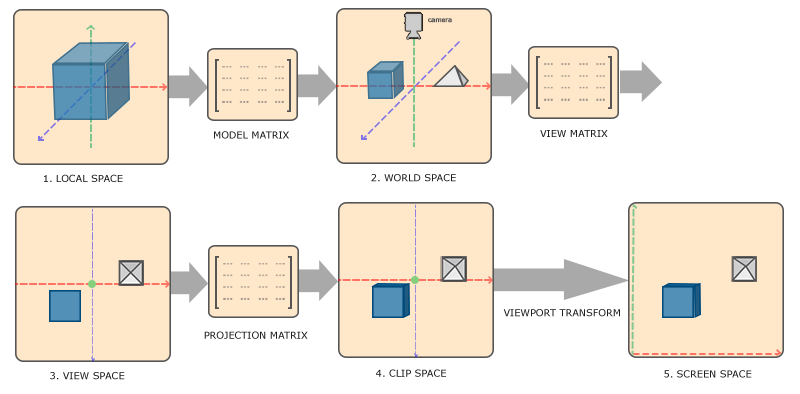
- 1. 局部坐标是对象相对于局部原点的坐标，也是物体起始的坐标。
- 2. 下一步是将局部坐标变换为世界空间坐标，世界空间坐标是处于一个更大的空间范围的。这些坐标相对于世界的全局原点，它们会和其它物体一起相对于世界的原点进行摆放。
- 3. 接下来我们将世界坐标变换为观察空间坐标，使得每个坐标都是从摄像机或者说观察者的角度进行观察的。
- 4. 坐标到达观察空间之后，我们需要将其投影到裁剪坐标。裁剪坐标会被处理至-1.0到1.0的范围内，并判断哪些顶点将会出现在屏幕上。
- 5. 最后，我们将裁剪坐标变换为屏幕坐标，我们将使用一个叫做<def>视口变换</def>(Viewport Transform)的过程。视口变换将位于-1.0到1.0范围的坐标变换到由<fun>glViewport</fun>函数所定义的坐标范围内。最后变换出来的坐标将会送到光栅器，将其转化为片段。
+ 1. 局部坐标是对象相对于局部原点的坐标；也是对象开始的坐标。
+ 2. 将局部坐标转换为世界坐标，世界坐标是作为一个更大空间范围的坐标系统。这些坐标是相对于世界的原点的。
+ 3. 接下来我们将世界坐标转换为观察坐标，观察坐标是指以摄像机或观察者的角度观察的坐标。
+ 4. 在将坐标处理到观察空间之后，我们需要将其投影到裁剪坐标。裁剪坐标是处理-1.0到1.0范围内并判断哪些顶点将会出现在屏幕上。
+ 5. 最后，我们需要将裁剪坐标转换为屏幕坐标，我们将这一过程成为**视口变换(Viewport Transform)**。视口变换将位于-1.0到1.0范围的坐标转换到由`glViewport`函数所定义的坐标范围内。最后转换的坐标将会送到光栅器，由光栅器将其转化为片段。
 
-你可能已经大致了解了每个坐标空间的作用。我们之所以将顶点变换到各个不同的空间的原因是有些操作在特定的坐标系统中才有意义且更方便。例如，当需要对物体进行修改的时候，在局部空间中来操作会更说得通；如果要对一个物体做出一个相对于其它物体位置的操作时，在世界坐标系中来做这个才更说得通，等等。如果我们愿意，我们也可以定义一个直接从局部空间变换到裁剪空间的变换矩阵，但那样会失去很多灵活性。
 
-接下来我们将要更仔细地讨论各个坐标系统。
+你可能了解了每个单独的坐标空间的作用。我们之所以将顶点转换到各个不同的空间的原因是有些操作在特定的坐标系统中才有意义且更方便。例如，当修改对象时，如果在局部空间中则是有意义的；当对对象做相对于其它对象的位置的操作时，在世界坐标系中则是有意义的；等等这些。如果我们愿意，本可以定义一个直接从局部空间到裁剪空间的转换矩阵，但那样会失去灵活性。接下来我们将要更仔细地讨论各个坐标系。
 
 ## 局部空间
 
-局部空间是指物体所在的坐标空间，即对象最开始所在的地方。想象你在一个建模软件（比如说Blender）中创建了一个立方体。你创建的立方体的原点有可能位于(0, 0, 0)，即便它有可能最后在程序中处于完全不同的位置。甚至有可能你创建的所有模型都以(0, 0, 0)为初始位置（译注：然而它们会最终出现在世界的不同位置）。所以，你的模型的所有顶点都是在**局部**空间中：它们相对于你的物体来说都是局部的。
+局部空间(Local Space)是指对象所在的坐标空间，例如，对象最开始所在的地方。想象你在一个模型建造软件(比如说Blender)中创建了一个立方体。你创建的立方体的原点有可能位于(0，0，0)，即使有可能在最后的应用中位于完全不同的另外一个位置。甚至有可能你创建的所有模型都以(0，0，0)为初始位置，然而他们会在世界的不同位置。则你的模型的所有顶点都是在**局部**空间：他们相对于你的对象来说都是局部的。
+
+我们一直使用的那个箱子的坐标范围为-0.5到0.5，设定(0, 0)为它的原点。这些都是局部坐标。
 
-我们一直使用的那个箱子的顶点是被设定在-0.5到0.5的坐标范围中，(0, 0)是它的原点。这些都是局部坐标。
 
 ## 世界空间
 
-如果我们将我们所有的物体导入到程序当中，它们有可能会全挤在世界的原点(0, 0, 0)上，这并不是我们想要的结果。我们想为每一个物体定义一个位置，从而能在更大的世界当中放置它们。世界空间中的坐标正如其名：是指顶点相对于（游戏）世界的坐标。如果你希望将物体分散在世界上摆放（特别是非常真实的那样），这就是你希望物体变换到的空间。物体的坐标将会从局部变换到世界空间；该变换是由<def>模型</def>矩阵(Model Matrix)实现的。
+如果我们想将我们所有的对象导入到程序当中，它们有可能会全挤在世界的原点上(0，0，0)，然而这并不是我们想要的结果。我们想为每一个对象定义一个位置，从而使对象位于更大的世界当中。世界空间(World Space)中的坐标就如它们听起来那样：是指顶点相对于(游戏)世界的坐标。物体变换到的最终空间就是世界坐标系，并且你会想让这些物体分散开来摆放(从而显得更真实)。对象的坐标将会从局部坐标转换到世界坐标；该转换是由**模型矩阵(Model Matrix)**实现的。
 
-模型矩阵是一种变换矩阵，它能通过对物体进行位移、缩放、旋转来将它置于它本应该在的位置或朝向。你可以将它想像为变换一个房子，你需要先将它缩小（它在局部空间中太大了），并将其位移至郊区的一个小镇，然后在y轴上往左旋转一点以搭配附近的房子。你也可以把上一节将箱子到处摆放在场景中用的那个矩阵大致看作一个模型矩阵；我们将箱子的局部坐标变换到场景/世界中的不同位置。
+模型矩阵是一种转换矩阵，它能通过对对象进行平移、缩放、旋转来将它置于它本应该在的位置或方向。你可以想象一下，我们需要转换一栋房子，通过将它缩小(因为它在局部坐标系中显得太大了)，将它往郊区的方向平移，然后沿着y轴往坐标旋转。经过这样的变换之后，它将恰好能够与邻居的房子重合。你能够想到上一节讲到的利用模型矩阵将各个箱子放置到这个屏幕上；我们能够将箱子中的局部坐标转换为观察坐标或世界坐标。
 
 ## 观察空间
 
-观察空间经常被人们称之OpenGL的<def>摄像机</def>(Camera)（所以有时也称为<def>摄像机空间</def>(Camera Space)或<def>视觉空间</def>(Eye Space)）。观察空间是将世界空间坐标转化为用户视野前方的坐标而产生的结果。因此观察空间就是从摄像机的视角所观察到的空间。而这通常是由一系列的位移和旋转的组合来完成，平移/旋转场景从而使得特定的对象被变换到摄像机的前方。这些组合在一起的变换通常存储在一个<def>观察矩阵</def>(View Matrix)里，它被用来将世界坐标变换到观察空间。在下一节中我们将深入讨论如何创建一个这样的观察矩阵来模拟一个摄像机。
+观察空间(View Space)经常被人们称之OpenGL的**摄像机(Camera)**(所以有时也称为摄像机空间(Camera Space)或视觉空间(Eye Space))。观察空间就是将对象的世界空间的坐标转换为观察者视野前面的坐标。因此观察空间就是从摄像机的角度观察到的空间。而这通常是由一系列的平移和旋转的组合来平移和旋转场景从而使得特定的对象被转换到摄像机前面。这些组合在一起的转换通常存储在一个**观察矩阵(View Matrix)**里，用来将世界坐标转换到观察空间。在下一个教程我们将广泛讨论如何创建一个这样的观察矩阵来模拟一个摄像机。
 
 ## 裁剪空间
 
-在一个顶点着色器运行的最后，OpenGL期望所有的坐标都能落在一个特定的范围内，且任何在这个范围之外的点都应该被<def>裁剪掉</def>(Clipped)。被裁剪掉的坐标就会被忽略，所以剩下的坐标就将变为屏幕上可见的片段。这也就是<def>裁剪空间</def>(Clip Space)名字的由来。
+在一个顶点着色器运行的最后，OpenGL期望所有的坐标都能落在一个给定的范围内，且任何在这个范围之外的点都应该被裁剪掉(Clipped)。被裁剪掉的坐标就被忽略了，所以剩下的坐标就将变为屏幕上可见的片段。这也就是**裁剪空间(Clip Space)**名字的由来。
 
-因为将所有可见的坐标都指定在-1.0到1.0的范围内不是很直观，所以我们会指定自己的坐标集(Coordinate Set)并将它变换回标准化设备坐标系，就像OpenGL期望的那样。
+因为将所有可见的坐标都放置在-1.0到1.0的范围内不是很直观，所以我们会指定自己的坐标集(Coordinate Set)并将它转换回标准化设备坐标系，就像OpenGL期望它做的那样。
 
-为了将顶点坐标从观察变换到裁剪空间，我们需要定义一个<def>投影矩阵</def>(Projection Matrix)，它指定了一个范围的坐标，比如在每个维度上的-1000到1000。投影矩阵接着会将在这个指定的范围内的坐标变换为标准化设备坐标的范围(-1.0, 1.0)。所有在范围外的坐标不会被映射到在-1.0到1.0的范围之间，所以会被裁剪掉。在上面这个投影矩阵所指定的范围内，坐标(1250, 500, 750)将是不可见的，这是由于它的x坐标超出了范围，它被转化为一个大于1.0的标准化设备坐标，所以被裁剪掉了。
+为了将顶点坐标从观察空间转换到裁剪空间，我们需要定义一个**投影矩阵(Projection Matrix)**，它指定了坐标的范围，例如，每个维度都是从-1000到1000。投影矩阵接着会将在它指定的范围内的坐标转换到标准化设备坐标系中(-1.0，1.0)。所有在在范围(-1.0,1.0)外的坐标都不会被绘制出来并且会被裁剪。在投影矩阵所指定的范围内，坐标(1250，500，750)将是不可见的，这是由于它的x坐标超出了范围，随后被转化为在标准化设备坐标中坐标值大于1.0的值并且被裁剪掉。
 
-!!! important
+!!! Important
 
-    如果只是图元(Primitive)，例如三角形，的一部分超出了<def>裁剪体积</def>(Clipping Volume)，则OpenGL会重新构建这个三角形为一个或多个三角形让其能够适合这个裁剪范围。
+    如果只是片段的一部分例如三角形，超出了裁剪体积(Clipping Volume)，则OpenGL会重新构建三角形以使一个或多个三角形能适应在裁剪范围内。
 
-由投影矩阵创建的**观察箱**(Viewing Box)被称为<def>平截头体</def>(Frustum)，每个出现在平截头体范围内的坐标都会最终出现在用户的屏幕上。将特定范围内的坐标转化到标准化设备坐标系的过程（而且它很容易被映射到2D观察空间坐标）被称之为<def>投影</def>(Projection)，因为使用投影矩阵能将3D坐标<def>投影</def>(Project)到很容易映射到2D的标准化设备坐标系中。
+由投影矩阵创建的**观察区域(Viewing Box)**被称为**平截头体(Frustum)**，且每个出现在平截头体范围内的坐标都会最终出现在用户的屏幕上。将一定范围内的坐标转化到标准化设备坐标系的过程(而且它很容易被映射到2D观察空间坐标)被称之为**投影(Projection)**，因为使用投影矩阵能将3维坐标**投影(Project)**到很容易映射的2D标准化设备坐标系中。
 
-一旦所有顶点被变换到裁剪空间，最终的操作——<def>透视除法</def>(Perspective Division)将会执行，在这个过程中我们将位置向量的x，y，z分量分别除以向量的齐次w分量；透视除法是将4D裁剪空间坐标变换为3D标准化设备坐标的过程。这一步会在每一个顶点着色器运行的最后被自动执行。
+一旦所有顶点被转换到裁剪空间，最终的操作——**透视划分(Perspective Division)**将会执行，在这个过程中我们将位置向量的x，y，z分量分别除以向量的齐次w分量；透视划分是将4维裁剪空间坐标转换为3维标准化设备坐标。这一步会在每一个顶点着色器运行的最后被自动执行。
 
-在这一阶段之后，最终的坐标将会被映射到屏幕空间中（使用<fun>glViewport</fun>中的设定），并被变换成片段。
+在这一阶段之后，坐标经过转换的结果将会被映射到屏幕空间(由`glViewport`设置)且被转换成片段。
 
-将观察坐标变换为裁剪坐标的投影矩阵可以为两种不同的形式，每种形式都定义了不同的平截头体。我们可以选择创建一个<def>正射</def>投影矩阵(Orthographic Projection Matrix)或一个<def>透视</def>投影矩阵(Perspective Projection Matrix)。
+投影矩阵将观察坐标转换为裁剪坐标的过程采用两种不同的方式，每种方式分别定义自己的平截头体。我们可以创建一个正射投影矩阵(Orthographic Projection Matrix)或一个透视投影矩阵(Perspective Projection Matrix)。
 
 ### 正射投影
 
-正射投影矩阵定义了一个类似立方体的平截头箱，它定义了一个裁剪空间，在这空间之外的顶点都会被裁剪掉。创建一个正射投影矩阵需要指定可见平截头体的宽、高和长度。在使用正射投影矩阵变换至裁剪空间之后处于这个平截头体内的所有坐标将不会被裁剪掉。它的平截头体看起来像一个容器：
+正射投影(Orthographic Projection)矩阵定义了一个类似立方体的平截头体，指定了一个裁剪空间，每一个在这空间外面的顶点都会被裁剪。创建一个正射投影矩阵需要指定可见平截头体的宽、高和长度。所有在使用正射投影矩阵转换到裁剪空间后如果还处于这个平截头体里面的坐标就不会被裁剪。它的平截头体看起来像一个容器：
 
-![orthographic projection frustum](../img/01/08/orthographic_frustum.png)
+![orthographic projection frustum](http://learnopengl.com/img/getting-started/orthographic_frustum.png)
 
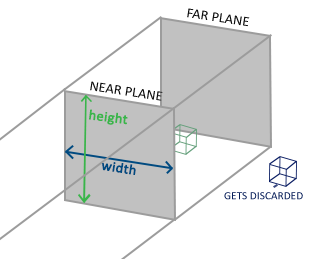
-上面的平截头体定义了可见的坐标，它由宽、高、<def>近</def>(Near)平面和<def>远</def>(Far)平面所指定。任何出现在近平面之前或远平面之后的坐标都会被裁剪掉。正射平截头体直接将平截头体内部的所有坐标映射为标准化设备坐标，因为每个向量的w分量都没有进行改变；如果w分量等于1.0，透视除法则不会改变这个坐标。
+上面的平截头体定义了由宽、高、**近**平面和**远**平面决定的可视的坐标系。任何出现在近平面前面或远平面后面的坐标都会被裁剪掉。正视平截头体直接将平截头体内部的顶点映射到标准化设备坐标系中，因为每个向量的w分量都是不变的；如果w分量等于1.0，则透视划分不会改变坐标的值。
 
-要创建一个正射投影矩阵，我们可以使用GLM的内置函数`glm::ortho`：
+为了创建一个正射投影矩阵，我们利用GLM的构建函数`glm::ortho`：
 
 ```c++
 glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f);
 ```
 
-前两个参数指定了平截头体的左右坐标，第三和第四参数指定了平截头体的底部和顶部。通过这四个参数我们定义了近平面和远平面的大小，然后第五和第六个参数则定义了近平面和远平面的距离。这个投影矩阵会将处于这些x，y，z值范围内的坐标变换为标准化设备坐标。
+前两个参数指定了平截头体的左右坐标，第三和第四参数指定了平截头体的底部和上部。通过这四个参数我们定义了近平面和远平面的大小，然后第五和第六个参数则定义了近平面和远平面的距离。这个指定的投影矩阵将处于这些x，y，z范围之间的坐标转换到标准化设备坐标系中。
 
-正射投影矩阵直接将坐标映射到2D平面中，即你的屏幕，但实际上一个直接的投影矩阵会产生不真实的结果，因为这个投影没有将<def>透视</def>(Perspective)考虑进去。所以我们需要<def>透视投影</def>矩阵来解决这个问题。
+正射投影矩阵直接将坐标映射到屏幕的二维平面内，但实际上一个直接的投影矩阵将会产生不真实的结果，因为这个投影没有将**透视(Perspective)**考虑进去。所以我们需要**透视投影**矩阵来解决这个问题。
 
-### 透视投影
+#### 透视投影
 
-如果你曾经体验过**实际生活**给你带来的景象，你就会注意到离你越远的东西看起来更小。这个奇怪的效果称之为<def>透视</def>(Perspective)。透视的效果在我们看一条无限长的高速公路或铁路时尤其明显，正如下面图片显示的那样：
+如果你曾经体验过**实际生活**给你带来的景象，你就会注意到离你越远的东西看起来更小。这个神奇的效果我们称之为透视(Perspective)。透视的效果在我们看一条无限长的高速公路或铁路时尤其明显，正如下面图片显示的那样:
 
-![perspective](../img/01/08/perspective.png)
+![perspective](http://learnopengl.com/img/getting-started/perspective.png)
 
-正如你看到的那样，由于透视，这两条线在很远的地方看起来会相交。这正是透视投影想要模仿的效果，它是使用<def>透视投影矩阵</def>来完成的。这个投影矩阵将给定的平截头体范围映射到裁剪空间，除此之外还修改了每个顶点坐标的w值，从而使得离观察者越远的顶点坐标w分量越大。被变换到裁剪空间的坐标都会在-w到w的范围之间（任何大于这个范围的坐标都会被裁剪掉）。OpenGL要求所有可见的坐标都落在-1.0到1.0范围内，作为顶点着色器最后的输出，因此，一旦坐标在裁剪空间内之后，透视除法就会被应用到裁剪空间坐标上：
+正如你看到的那样，由于透视的原因，平行线似乎在很远的地方看起来会相交。这正是透视投影(Perspective Projection)想要模仿的效果，它是使用透视投影矩阵来完成的。这个投影矩阵不仅将给定的平截头体范围映射到裁剪空间，同样还修改了每个顶点坐标的w值，从而使得离观察者越远的顶点坐标w分量越大。被转换到裁剪空间的坐标都会在-w到w的范围之间(任何大于这个范围的对象都会被裁剪掉)。OpenGL要求所有可见的坐标都落在-1.0到1.0范围内从而作为最后的顶点着色器输出，因此一旦坐标在裁剪空间内，透视划分就会被应用到裁剪空间坐标：
 
 $$
 out = \begin{pmatrix} x /w \\ y / w \\ z / w \end{pmatrix}
 $$
 
-顶点坐标的每个分量都会除以它的w分量，距离观察者越远顶点坐标就会越小。这是w分量重要的另一个原因，它能够帮助我们进行透视投影。最后的结果坐标就是处于标准化设备空间中的。如果你对正射投影矩阵和透视投影矩阵是如何计算的很感兴趣（且不会对数学感到恐惧的话）我推荐这篇由Songho写的[文章](http://www.songho.ca/opengl/gl_projectionmatrix.html)。
+每个顶点坐标的分量都会除以它的w分量，得到一个距离观察者的较小的顶点坐标。这是也是另一个w分量很重要的原因，因为它能够帮助我们进行透射投影。最后的结果坐标就是处于标准化设备空间内的。如果你对研究正射投影矩阵和透视投影矩阵是如何计算的很感兴趣(且不会对数学感到恐惧的话)我推荐[这篇由Songho写的文章](http://www.songho.ca/opengl/gl_projectionmatrix.html)。
 
 在GLM中可以这样创建一个透视投影矩阵：
 
 ```c++
-glm::mat4 proj = glm::perspective(glm::radians(45.0f), (float)width/(float)height, 0.1f, 100.0f);
+glm::mat4 proj = glm::perspective(45.0f, (float)width/(float)height, 0.1f, 100.0f);
 ```
 
-同样，`glm::perspective`所做的其实就是创建了一个定义了可视空间的大**平截头体**，任何在这个平截头体以外的东西最后都不会出现在裁剪空间体积内，并且将会受到裁剪。一个透视平截头体可以被看作一个不均匀形状的箱子，在这个箱子内部的每个坐标都会被映射到裁剪空间上的一个点。下面是一张透视平截头体的图片：
+`glm::perspective`所做的其实就是再次创建了一个定义了可视空间的大的**平截头体**，任何在这个平截头体的对象最后都不会出现在裁剪空间体积内，并且将会受到裁剪。一个透视平截头体可以被可视化为一个不均匀形状的盒子，在这个盒子内部的每个坐标都会被映射到裁剪空间的点。一张透视平截头体的照片如下所示：
 
-![ perspective_frustum](../img/01/08/perspective_frustum.png)
+![ perspective_frustum](http://learnopengl.com/img/getting-started/perspective_frustum.png)
 
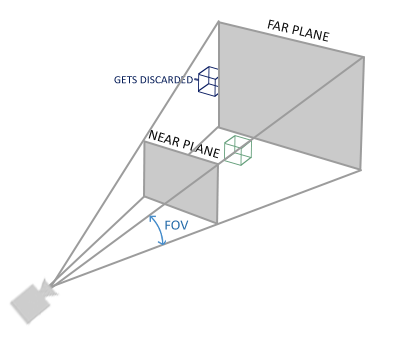
-它的第一个参数定义了<def>fov</def>的值，它表示的是<def>视野</def>(Field of View)，并且设置了观察空间的大小。如果想要一个真实的观察效果，它的值通常设置为45.0f，但想要一个毁灭战士(DOOM,经典的系列第一人称射击游戏)风格的结果你可以将其设置一个更大的值。第二个参数设置了宽高比，由视口的宽除以高所得。第三和第四个参数设置了平截头体的**近**和**远**平面。我们通常设置近距离为0.1f，而远距离设为100.0f。所有在近平面和远平面内且处于平截头体内的顶点都会被渲染。
+它的第一个参数定义了**fov**的值，它表示的是**视野(Field of View)**，并且设置了观察空间的大小。对于一个真实的观察效果，它的值经常设置为45.0，但想要看到更多结果你可以设置一个更大的值。第二个参数设置了宽高比，由视口的高除以宽。第三和第四个参数设置了平截头体的近和远平面。我们经常设置近距离为0.1而远距离设为100.0。所有在近平面和远平面的顶点且处于平截头体内的顶点都会被渲染。
 
-!!! important
+!!! Important
 
-	当你把透视矩阵的 *near* 值设置太大时（如10.0f），OpenGL会将靠近摄像机的坐标（在0.0f和10.0f之间）都裁剪掉，这会导致一个你在游戏中很熟悉的视觉效果：在太过靠近一个物体的时候你的视线会直接穿过去。
+	当你把透视矩阵的*near*值设置太大时(如10.0)，OpenGL会将靠近摄像机的坐标都裁剪掉(在0.0和10.0之间)，这会导致一个你很熟悉的视觉效果：在太过靠近一个物体的时候视线会直接穿过去。
 
-当使用正射投影时，每一个顶点坐标都会直接映射到裁剪空间中而不经过任何精细的透视除法（它仍然会进行透视除法，只是w分量没有被改变（它保持为1），因此没有起作用）。因为正射投影没有使用透视，远处的物体不会显得更小，所以产生奇怪的视觉效果。由于这个原因，正射投影主要用于二维渲染以及一些建筑或工程的程序，在这些场景中我们更希望顶点不会被透视所干扰。某些如 *Blender* 等进行三维建模的软件有时在建模时也会使用正射投影，因为它在各个维度下都更准确地描绘了每个物体。下面你能够看到在Blender里面使用两种投影方式的对比：
+当使用正射投影时，每一个顶点坐标都会直接映射到裁剪空间中而不经过任何精细的透视划分(它仍然有进行透视划分，只是w分量没有被操作(它保持为1)因此没有起作用)。因为正射投影没有使用透视，远处的对象不会显得小以产生神奇的视觉输出。由于这个原因，正射投影主要用于二维渲染以及一些建筑或工程的应用，或者是那些我们不需要使用投影来转换顶点的情况下。某些如Blender的进行三维建模的软件有时在建模时会使用正射投影，因为它在各个维度下都更准确地描绘了每个物体。下面你能够看到在Blender里面使用两种投影方式的对比：
 
-![perspective_orthographic](../img/01/08/perspective_orthographic.png)
+![perspective_orthographic](http://learnopengl.com/img/getting-started/perspective_orthographic.png)
 
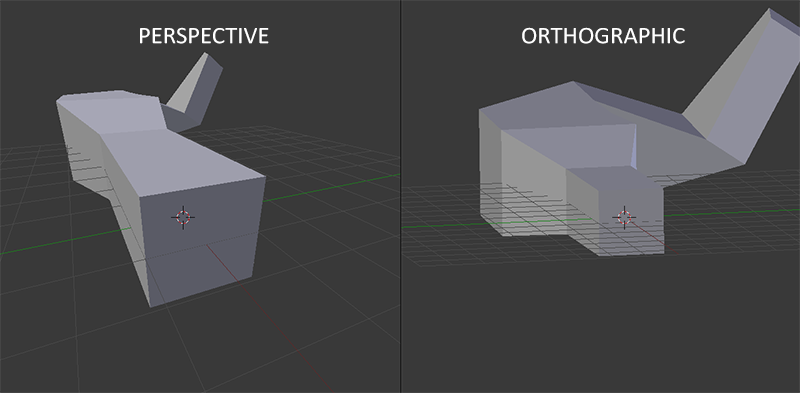
-你可以看到，使用透视投影的话，远处的顶点看起来比较小，而在正射投影中每个顶点距离观察者的距离都是一样的。
+你可以看到使用透视投影的话，远处的顶点看起来比较小，而在正射投影中每个顶点距离观察者的距离都是一样的。
 
-## 把它们都组合到一起
+### 把它们都组合到一起
 
-我们为上述的每一个步骤都创建了一个变换矩阵：模型矩阵、观察矩阵和投影矩阵。一个顶点坐标将会根据以下过程被变换到裁剪坐标：
+我们为上述的每一个步骤都创建了一个转换矩阵：模型矩阵、观察矩阵和投影矩阵。一个顶点的坐标将会根据以下过程被转换到裁剪坐标：
 
 $$
 V_{clip} = M_{projection} \cdot M_{view} \cdot M_{model} \cdot V_{local}
 $$
 
-注意矩阵运算的顺序是相反的（记住我们需要从右往左阅读矩阵的乘法）。最后的顶点应该被赋值到顶点着色器中的<var>gl_Position</var>，OpenGL将会自动进行透视除法和裁剪。
+注意每个矩阵被运算的顺序是相反的(记住我们需要从右往左乘上每个矩阵)。最后的顶点应该被赋予顶点着色器中的`gl_Position`且OpenGL将会自动进行透视划分和裁剪。
 
-!!! important
+!!! Important
 
 	**然后呢？**
 
-	顶点着色器的输出要求所有的顶点都在裁剪空间内，这正是我们刚才使用变换矩阵所做的。OpenGL然后对**裁剪坐标**执行**透视除法**从而将它们变换到**标准化设备坐标**。OpenGL会使用<fun>glViewPort</fun>内部的参数来将标准化设备坐标映射到**屏幕坐标**，每个坐标都关联了一个屏幕上的点（在我们的例子中是一个800x600的屏幕）。这个过程称为视口变换。
+	顶点着色器的输出需要所有的顶点都在裁剪空间内，而这是我们的转换矩阵所做的。OpenGL然后在裁剪空间中执行透视划分从而将它们转换到标准化设备坐标。OpenGL会使用`glViewPort`内部的参数来将标准化设备坐标映射到屏幕坐标，每个坐标都关联了一个屏幕上的点(在我们的例子中屏幕是800 *600)。这个过程称为视口转换。
 
-这一章的主题可能会比较难理解，如果你仍然不确定每个空间的作用的话，你也不必太担心。接下来你会看到我们是怎样运用这些坐标空间的，而且之后也会有足够多的例子。
+这一章的主题可能会比较难理解，如果你仍然不确定每个空间的作用的话，你也不必太担心。接下来你会看到我们是怎样好好运用这些坐标空间的并且会有足够的展示例子在接下来的教程中。
 
 # 进入3D
 
-既然我们知道了如何将3D坐标变换为2D坐标，我们可以开始使用真正的3D物体，而不是枯燥的2D平面了。
+既然我们知道了如何将三维坐标转换为二维坐标，我们可以开始将我们的对象展示为三维对象而不是目前我们所展示的缺胳膊少腿的二维平面。
 
-在开始进行3D绘图时，我们首先创建一个模型矩阵。这个模型矩阵包含了位移、缩放与旋转操作，它们会被应用到所有物体的顶点上，以**变换**它们到全局的世界空间。让我们变换一下我们的平面，将其绕着x轴旋转，使它看起来像放在地上一样。这个模型矩阵看起来是这样的：
+在开始进行三维画图时，我们首先创建一个模型矩阵。这个模型矩阵包含了平移、缩放与旋转，我们将会运用它来将对象的顶点转换到全局世界空间。让我们平移一下我们的平面，通过将其绕着x轴旋转使它看起来像放在地上一样。这个模型矩阵看起来是这样的：
 
 ```c++
 glm::mat4 model;
-model = glm::rotate(model, glm::radians(-55.0f), glm::vec3(1.0f, 0.0f, 0.0f));
+model = glm::rotate(model, -55.0f, glm::vec3(1.0f, 0.0f, 0.0f));
 ```
 
-通过将顶点坐标乘以这个模型矩阵，我们将该顶点坐标变换到世界坐标。我们的平面看起来就是在地板上，代表全局世界里的平面。
+通过将顶点坐标乘以这个模型矩阵我们将该顶点坐标转换到世界坐标。我们的平面看起来就是在地板上的因此可以代表真实世界的平面。
 
-接下来我们需要创建一个观察矩阵。我们想要在场景里面稍微往后移动，以使得物体变成可见的（当在世界空间时，我们位于原点(0,0,0)）。要想在场景里面移动，先仔细想一想下面这个句子：
+接下来我们需要创建一个观察矩阵。我们想要在场景里面稍微往后移动以使得对象变成可见的(当在世界空间时，我们位于原点(0,0,0))。要想在场景里面移动，思考下面的问题：
 
-- 将摄像机向后移动，和将整个场景向前移动是一样的。
+- 将摄像机往后移动跟将整个场景往前移是一样的。
  
-这正是观察矩阵所做的，我们以相反于摄像机移动的方向移动整个场景。因为我们想要往后移动，并且OpenGL是一个右手坐标系(Right-handed System)，所以我们需要沿着z轴的正方向移动。我们会通过将场景沿着z轴负方向平移来实现。它会给我们一种我们在往后移动的感觉。
+这就是观察空间所做的，我们以相反于移动摄像机的方向移动整个场景。因为我们想要往后移动，并且OpenGL是一个右手坐标系(Right-handed System)所以我们沿着z轴的负方向移动。我们会通过将场景沿着z轴正方向平移来实现这个。它会给我们一种我们在往后移动的感觉。
 
-!!! important
+!!! Important
 
 	**右手坐标系(Right-handed System)**
 
-	按照惯例，OpenGL是一个右手坐标系。简单来说，就是正x轴在你的右手边，正y轴朝上，而正z轴是朝向后方的。想象你的屏幕处于三个轴的中心，则正z轴穿过你的屏幕朝向你。坐标系画起来如下：
+	按照约定，OpenGL是一个右手坐标系。最基本的就是说正x轴在你的右手边，正y轴往上而正z轴是往后的。想象你的屏幕处于三个轴的中心且正z轴穿过你的屏幕朝向你。坐标系画起来如下：
 
-	![coordinate_systems_right_handed](../img/01/08/coordinate_systems_right_handed.png)
+	![coordinate_systems_right_handed](http://learnopengl.com/img/getting-started/coordinate_systems_right_handed.png)
 
 	为了理解为什么被称为右手坐标系，按如下的步骤做：
 
-	- 沿着正y轴方向伸出你的右臂，手指着上方。
-	- 大拇指指向右方。
-	- 食指指向上方。
-	- 中指向下弯曲90度。 
+	- 张开你的右手使正y轴沿着你的手往上。
+	- 使你的大拇指往右。
+	- 使你的食指往上。
+	- 向下90度弯曲你的中指。 
 
-	如果你的动作正确，那么你的大拇指指向正x轴方向，食指指向正y轴方向，中指指向正z轴方向。如果你用左臂来做这些动作，你会发现z轴的方向是相反的。这个叫做左手坐标系，它被DirectX广泛地使用。注意在标准化设备坐标系中OpenGL实际上使用的是左手坐标系（投影矩阵交换了左右手）。
+	如果你都正确地做了，那么你的大拇指朝着正x轴方向，食指朝着正y轴方向，中指朝着正z轴方向。如果你用左手来做这些动作，你会发现z轴的方向是相反的。这就是有名的左手坐标系，它被DirectX广泛地使用。注意在标准化设备坐标系中OpenGL使用的是左手坐标系(投影矩阵改变了惯用手的习惯)。
 
-在下一个教程中我们将会详细讨论如何在场景中移动。就目前来说，观察矩阵是这样的：
+在下一个教程中我们将会详细讨论如何在场景中移动。目前的观察矩阵是这样的：
 
 ```c++
 glm::mat4 view;
-// 注意，我们将矩阵向我们要进行移动场景的反方向移动。
-view = glm::translate(view, glm::vec3(0.0f, 0.0f, -3.0f));
+// 注意，我们将矩阵向我们要进行移动场景的反向移动。
+view = glm::translate(view, glm::vec3(0.0f, 0.0f, -3.0f)); 
 ```
 
-最后我们需要做的是定义一个投影矩阵。我们希望在场景中使用透视投影，所以像这样声明一个投影矩阵：
+最后我们需要做的是定义一个投影矩阵。我们想要在我们的场景中使用透视投影所以我们声明的投影矩阵是像这样的：
 
 ```c++
 glm::mat4 projection;
-projection = glm::perspective(glm::radians(45.0f), screenWidth / screenHeight, 0.1f, 100.0f);
+projection = glm::perspective(45.0f, screenWidth / screenHeight, 0.1f, 100.0f);
 ```
 
-既然我们已经创建了变换矩阵，我们应该将它们传入着色器。首先，让我们在顶点着色器中声明一个uniform变换矩阵然后将它乘以顶点坐标：
+!!! Attention
+
+	再重复一遍，在glm指定角度的时候要注意。这里我们将参数fov设置为45度，但有些GLM的实现是将fov当成弧度，在这种情况你需要使用`glm::radians(45.0)`来设置。
+
+既然我们创建了转换矩阵，我们应该将它们传入着色器。首先，让我们在顶点着色器中声明一个单位转换矩阵然后将它乘以顶点坐标：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;
+layout (location = 0) in vec3 position;
 ...
 uniform mat4 model;
 uniform mat4 view;
@@ -208,67 +212,67 @@ uniform mat4 projection;
 
 void main()
 {
-    // 注意乘法要从右向左读
-    gl_Position = projection * view * model * vec4(aPos, 1.0);
+    // 注意从右向左读
+    gl_Position = projection * view * model * vec4(position, 1.0f);
     ...
 }
 ```
 
-我们还应该将矩阵传入着色器（这通常在每次的渲染迭代中进行，因为变换矩阵会经常变动）：
+我们应该将矩阵传入着色器(这通常在每次渲染的时候即转换矩阵将要改变的时候完成)：
 
 ```c++
-int modelLoc = glGetUniformLocation(ourShader.ID, "model");
+GLint modelLoc = glGetUniformLocation(ourShader.Program, "model");
 glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
 ... // 观察矩阵和投影矩阵与之类似
 ```
 
-我们的顶点坐标已经使用模型、观察和投影矩阵进行变换了，最终的物体应该会：
+现在我们的顶点坐标通过模型、观察和投影矩阵来转换，最后的对象应该是：
 
- - 稍微向后倾斜至地板方向。
- - 离我们有一些距离。
- - 有透视效果（顶点越远，变得越小）。
+ - 往后向地板倾斜。
+ - 离我们有点距离。
+ - 由透视展示(顶点越远，变得越小)。
 
 让我们检查一下结果是否满足这些要求：
 
-![coordinate_systems_result](../img/01/08/coordinate_systems_result.png)
+![coordinate_systems_result](http://learnopengl.com/img/getting-started/coordinate_systems_result.png)
 
-它看起来就像是一个3D的平面，静止在一个虚构的地板上。如果你得到的不是相同的结果，请检查下完整的[源代码](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/6.1.coordinate_systems/coordinate_systems.cpp)。
+它看起来就像是一个三维的平面，是静止在一些虚构的地板上的。如果你不是得到相同的结果，请检查下完整的[源代码](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems) 以及[顶点](http://learnopengl.com/code_viewer.php?code=getting-started/transform&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=getting-started/transform&type=fragment)着色器。
 
-## 更加 3D
+## 更多的3D
 
-到目前为止，我们一直都在使用一个2D平面，而且甚至是在3D空间里！所以，让我们大胆地拓展我们的2D平面为一个3D立方体。要想渲染一个立方体，我们一共需要36个顶点（6个面 x 每个面有2个三角形组成 x 每个三角形有3个顶点），这36个顶点的位置你可以从[这里](https://learnopengl.com/code_viewer.php?code=getting-started/cube_vertices)获取。
+到目前为止，我们在二维平面甚至在三维空间中画图，所以让我们采取大胆的方式来将我们的二维平面扩展为三维立方体。要渲染一个立方体，我们一共需要36个顶点(6个面 x 每个面有2个三角形组成 x 每个三角形有3个顶点)，这36个顶点的位置你可以[从这里获取](http://learnopengl.com/code_viewer.php?code=getting-started/cube_vertices)。注意，这一次我们省略了颜色值，因为这次我们只在乎顶点的位置和，我们使用纹理贴图。
 
-为了有趣一点，我们将让立方体随着时间旋转：
+为了好玩，我们将让立方体随着时间旋转：
 
 ```c++
-model = glm::rotate(model, (float)glfwGetTime() * glm::radians(50.0f), glm::vec3(0.5f, 1.0f, 0.0f));
+model = glm::rotate(model, (GLfloat)glfwGetTime() * 50.0f, glm::vec3(0.5f, 1.0f, 0.0f));
 ```
 
-然后我们使用<fun>glDrawArrays</fun>来绘制立方体，但这一次总共有36个顶点。
+然后我们使用`glDrawArrays`来画立方体，这一次总共有36个顶点。
 
 ```c++
 glDrawArrays(GL_TRIANGLES, 0, 36);
 ```
 
-如果一切顺利的话你应该能得到下面这样的效果：
+如果一切顺利的话绘制效果将与下面的类似：
 
-<video src="../../img/01/08/coordinate_system_no_depth.mp4" controls="controls"></video>
+<video src="http://learnopengl.com/video/getting-started/coordinate_system_no_depth.mp4" controls="controls"></video>
 
-这的确有点像是一个立方体，但又有种说不出的奇怪。立方体的某些本应被遮挡住的面被绘制在了这个立方体其他面之上。之所以这样是因为OpenGL是一个三角形一个三角形地来绘制你的立方体的，所以即便之前那里有东西它也会覆盖之前的像素。因为这个原因，有些三角形会被绘制在其它三角形上面，虽然它们本不应该是被覆盖的。
+这有点像一个立方体，但又有种说不出的奇怪。立方体的某些本应被遮挡住的面被绘制在了这个立方体的其他面的上面。之所以这样是因为OpenGL是通过画一个一个三角形来画你的立方体的，所以它将会覆盖之前已经画在那里的像素。因为这个原因，有些三角形会画在其它三角形上面，虽然它们本不应该是被覆盖的。
 
-幸运的是，OpenGL存储深度信息在一个叫做<def>Z缓冲</def>(Z-buffer)的缓冲中，它允许OpenGL决定何时覆盖一个像素而何时不覆盖。通过使用Z缓冲，我们可以配置OpenGL来进行深度测试。
+幸运的是，OpenGL存储深度信息在z缓冲区(Z-buffer)里面，它允许OpenGL决定何时覆盖一个像素何时不覆盖。通过使用z缓冲区我们可以设置OpenGL来进行深度测试。
 
-### Z缓冲
+### Z缓冲区
 
-OpenGL存储它的所有深度信息于一个Z缓冲(Z-buffer)中，也被称为<def>深度缓冲</def>(Depth Buffer)。GLFW会自动为你生成这样一个缓冲（就像它也有一个颜色缓冲来存储输出图像的颜色）。深度值存储在每个片段里面（作为片段的**z**值），当片段想要输出它的颜色时，OpenGL会将它的深度值和z缓冲进行比较，如果当前的片段在其它片段之后，它将会被丢弃，否则将会覆盖。这个过程称为<def>深度测试</def>(Depth Testing)，它是由OpenGL自动完成的。
+OpenGL存储它的所有深度信息于Z缓冲区(Z-buffer)中，也被称为深度缓冲区(Depth Buffer)。GLFW会自动为你生成这样一个缓冲区 (就如它有一个颜色缓冲区来存储输出图像的颜色)。深度存储在每个片段里面(作为片段的z值)当片段像输出它的颜色时，OpenGL会将它的深度值和z缓冲进行比较然后如果当前的片段在其它片段之后它将会被丢弃，然后重写。这个过程称为**深度测试(Depth Testing)**并且它是由OpenGL自动完成的。
 
-然而，如果我们想要确定OpenGL真的执行了深度测试，首先我们要告诉OpenGL我们想要启用深度测试；它默认是关闭的。我们可以通过<fun>glEnable</fun>函数来开启深度测试。<fun>glEnable</fun>和<fun>glDisable</fun>函数允许我们启用或禁用某个OpenGL功能。这个功能会一直保持启用/禁用状态，直到另一个调用来禁用/启用它。现在我们想启用深度测试，需要开启<var>GL_DEPTH_TEST</var>：
+然而，如果我们想要确定OpenGL是否真的执行深度测试，首先我们要告诉OpenGL我们想要开启深度测试；而这通常是默认关闭的。我们通过`glEnable`函数来开启深度测试。`glEnable`和`glDisable`函数允许我们开启或关闭某一个OpenGL的功能。该功能会一直是开启或关闭的状态直到另一个调用来关闭或开启它。现在我们想开启深度测试就需要开启`GL_DEPTH_TEST`：
 
 ```c++
 glEnable(GL_DEPTH_TEST);
 ```
 
-因为我们使用了深度测试，我们也想要在每次渲染迭代之前清除深度缓冲（否则前一帧的深度信息仍然保存在缓冲中）。就像清除颜色缓冲一样，我们可以通过在<fun>glClear</fun>函数中指定<var>DEPTH_BUFFER_BIT</var>位来清除深度缓冲：
+既然我们使用了深度测试我们也想要在每次重复渲染之前清除深度缓冲区(否则前一个片段的深度信息仍然保存在缓冲区中)。就像清除颜色缓冲区一样，我们可以通过在`glclear`函数中指定`DEPTH_BUFFER_BIT`位来清除深度缓冲区：
 
 ```c++
 glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
@@ -276,15 +280,15 @@ glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
 
 我们来重新运行下程序看看OpenGL是否执行了深度测试：
 
-<video src="../../img/01/08/coordinate_system_depth.mp4" controls="controls"></video>
+<video src="http://learnopengl.com/video/getting-started/coordinate_system_depth.mp4" controls="controls"></video>
 
-就是这样！一个开启了深度测试，各个面都是纹理，并且还在旋转的立方体！如果你的程序有问题可以到[这里](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/6.2.coordinate_systems_depth/coordinate_systems_depth.cpp)下载源码进行比对。
+就是这样！一个开启了深度测试，各个面都是纹理，并且还在旋转的立方体！如果你的程序有问题可以到[这里](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems_with_depth)下载源码进行比对。
 
-### 更多的立方体！
+### 更多的立方体
 
-现在我们想在屏幕上显示10个立方体。每个立方体看起来都是一样的，区别在于它们在世界的位置及旋转角度不同。立方体的图形布局已经定义好了，所以当渲染更多物体的时候我们不需要改变我们的缓冲数组和属性数组，我们唯一需要做的只是改变每个对象的模型矩阵来将立方体变换到世界坐标系中。
+现在我们想在屏幕上显示10个立方体。每个立方体看起来都是一样的，区别在于它们在世界的位置及旋转角度不同。立方体的图形布局已经定义好了，所以当渲染更多物体的时候我们不需要改变我们的缓冲数组和属性数组，我们唯一需要做的只是改变每个对象的模型矩阵来将立方体转换到世界坐标系中。
 
-首先，让我们为每个立方体定义一个位移向量来指定它在世界空间的位置。我们将在一个`glm::vec3`数组中定义10个立方体位置：
+首先，让我们为每个立方体定义一个转换向量来指定它在世界空间的位置。我们将要在`glm::vec3`数组中定义10个立方体位置向量。
 
 ```c++
 glm::vec3 cubePositions[] = {
@@ -301,31 +305,32 @@ glm::vec3 cubePositions[] = {
 };
 ```
 
-现在，在游戏循环中，我们调用<fun>glDrawArrays</fun> 10次，但这次在我们渲染之前每次传入一个不同的模型矩阵到顶点着色器中。我们将会在游戏循环中创建一个小的循环用不同的模型矩阵渲染我们的物体10次。注意我们也对每个箱子加了一点旋转：
+现在，在循环中，我们调用`glDrawArrays`10次，在我们开始渲染之前每次传入一个不同的模型矩阵到顶点着色器中。我们将会创建一个小的循环来通过一个不同的模型矩阵重复渲染我们的对象10次。注意我们也传入了一个旋转参数到每个箱子中：
 
 ```c++
 glBindVertexArray(VAO);
-for(unsigned int i = 0; i < 10; i++)
+for(GLuint i = 0; i < 10; i++)
 {
   glm::mat4 model;
   model = glm::translate(model, cubePositions[i]);
-  float angle = 20.0f * i; 
-  model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));
-  ourShader.setMat4("model", model);
+  GLfloat angle = 20.0f * i; 
+  model = glm::rotate(model, angle, glm::vec3(1.0f, 0.3f, 0.5f));
+  glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
 
   glDrawArrays(GL_TRIANGLES, 0, 36);
 }
+glBindVertexArray(0);
 ```
 
-这段代码将会在每次新立方体绘制出来的时候更新模型矩阵，如此总共重复10次。然后我们应该就能看到一个拥有10个正在奇葩地旋转着的立方体的世界。
+这个代码将会每次都更新模型矩阵然后画出新的立方体，如此总共重复10次。然后我们应该就能看到一个拥有10个正在奇葩旋转着的立方体的世界。
 
-![coordinate_systems_multiple_objects](../img/01/08/coordinate_systems_multiple_objects.png)
+![coordinate_systems_multiple_objects](http://learnopengl.com/img/getting-started/coordinate_systems_multiple_objects.png)
 
-完美！看起来我们的箱子已经找到志同道合的小伙伴了。如果你在这里卡住了，你可以对照一下[源代码](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/6.3.coordinate_systems_multiple/coordinate_systems_multiple.cpp) 。
+完美！这就像我们的箱子找到了志同道合的小伙伴一样。如果你在这里卡住了，你可以对照一下[代码](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems_multiple_objects) 以及[顶点着色器](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems&type=vertex)和[片段着色器](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems&type=fragment) 。
 
 ## 练习
 
-- 对GLM的`projection`函数中的`FoV`和`aspect-ratio`参数进行实验。看能否搞懂它们是如何影响透视平截头体的。
-- 将观察矩阵在各个方向上进行位移，来看看场景是如何改变的。注意把观察矩阵当成摄像机对象。
-- 使用模型矩阵只让是3倍数的箱子旋转（以及第1个箱子），而让剩下的箱子保持静止。[参考解答](https://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems-exercise3)。
+- 对GLM的投影函数中的`FoV`和`aspect-ratio`参数进行试验。看能否搞懂它们是如何影响透视平截头体的。
+- 将观察矩阵在各个方向上进行平移，来看看场景是如何改变的。注意把观察矩阵当成摄像机对象。
+- 只使用模型矩阵每次只让3个箱子旋转(包括第1个)而让剩下的箱子保持静止。[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems-exercise3)。
 

docs/01 Getting started/09 Camera.md

@@ -1,36 +1,36 @@
-# 摄像机
+# 摄像机(Camera)
 
 原文     | [Camera](http://learnopengl.com/#!Getting-started/Camera)
       ---|---
 作者     | JoeyDeVries
-翻译     | [Django](http://bullteacher.com/), Krasjet, Geequlim, [BLumia](https://github.com/blumia/)
-校对     | 暂未校对
+翻译     | [Django](http://bullteacher.com/)
+校对     | Geequlim, [BLumia](https://github.com/blumia/)
 
-前面的教程中我们讨论了观察矩阵以及如何使用观察矩阵移动场景（我们向后移动了一点）。OpenGL本身没有**摄像机**(Camera)的概念，但我们可以通过把场景中的所有物体往相反方向移动的方式来模拟出摄像机，产生一种**我们**在移动的感觉，而不是场景在移动。
+前面的教程中我们讨论了观察矩阵以及如何使用观察矩阵移动场景。OpenGL本身没有摄像机的概念，但我们可以通过把场景中的所有物体往相反方向移动的方式来模拟出摄像机，这样感觉就像我们在移动，而不是场景在移动。
 
-本节我们将会讨论如何在OpenGL中配置一个摄像机，并且将会讨论FPS风格的摄像机，让你能够在3D场景中自由移动。我们也会讨论键盘和鼠标输入，最终完成一个自定义的摄像机类。
+本节我们将会讨论如何在OpenGL中模拟一个摄像机，将会讨论FPS风格的可自由在3D场景中移动的摄像机。我们也会讨论键盘和鼠标输入，最终完成一个自定义的摄像机类。
 
 ## 摄像机/观察空间
 
-当我们讨论摄像机/观察空间(Camera/View Space)的时候，是在讨论以摄像机的视角作为场景原点时场景中所有的顶点坐标：观察矩阵把所有的世界坐标变换为相对于摄像机位置与方向的观察坐标。要定义一个摄像机，我们需要它在世界空间中的位置、观察的方向、一个指向它右侧的向量以及一个指向它上方的向量。细心的读者可能已经注意到我们实际上创建了一个三个单位轴相互垂直的、以摄像机的位置为原点的坐标系。
+当我们讨论摄像机/观察空间(Camera/View Space)的时候，是我们在讨论以摄像机的透视图作为场景原点时场景中所有可见顶点坐标。观察矩阵把所有的世界坐标变换到观察坐标，这些新坐标是相对于摄像机的位置和方向的。定义一个摄像机，我们需要一个摄像机在世界空间中的位置、观察的方向、一个指向它的右测的向量以及一个指向它上方的向量。细心的读者可能已经注意到我们实际上创建了一个三个单位轴相互垂直的、以摄像机的位置为原点的坐标系。
 
-![](../img/01/09/camera_axes.png)
+![](http://learnopengl.com/img/getting-started/camera_axes.png)
 
 ### 1. 摄像机位置
 
-获取摄像机位置很简单。摄像机位置简单来说就是世界空间中一个指向摄像机位置的向量。我们把摄像机位置设置为上一节中的那个相同的位置：
+获取摄像机位置很简单。摄像机位置简单来说就是世界空间中代表摄像机位置的向量。我们把摄像机位置设置为前面教程中的那个相同的位置：
 
 ```c++
 glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f);
 ```
 
-!!! important
+!!! Important
 
-	不要忘记正z轴是从屏幕指向你的，如果我们希望摄像机向后移动，我们就沿着z轴的正方向移动。
+	不要忘记正z轴是从屏幕指向你的，如果我们希望摄像机向后移动，我们就往z轴正方向移动。
 
 ### 2. 摄像机方向
 
-下一个需要的向量是摄像机的方向，这里指的是摄像机指向哪个方向。现在我们让摄像机指向场景原点：(0, 0, 0)。还记得如果将两个矢量相减，我们就能得到这两个矢量的差吗？用场景原点向量减去摄像机位置向量的结果就是摄像机的指向向量。由于我们知道摄像机指向z轴负方向，但我们希望方向向量(Direction Vector)指向摄像机的z轴正方向。如果我们交换相减的顺序，我们就会获得一个指向摄像机正z轴方向的向量：
+下一个需要的向量是摄像机的方向，比如它指向哪个方向。现在我们让摄像机指向场景原点：(0, 0, 0)。用摄像机位置向量减去场景原点向量的结果就是摄像机指向向量。由于我们知道摄像机指向z轴负方向，我们希望方向向量指向摄像机的z轴正方向。如果我们改变相减的顺序，我们就会获得一个指向摄像机正z轴方向的向量(译注：注意看前面的那个图，所说的「方向向量/Direction Vector」是指向z的正方向的，而不是摄像机所注视的那个方向)：
 
 ```c++
 glm::vec3 cameraTarget = glm::vec3(0.0f, 0.0f, 0.0f);
@@ -39,38 +39,38 @@ glm::vec3 cameraDirection = glm::normalize(cameraPos - cameraTarget);
 
 !!! Attention
 
-	**方向**向量(Direction Vector)并不是最好的名字，因为它实际上指向从它到目标向量的相反方向（译注：注意看前面的那个图，蓝色的方向向量大概指向z轴的正方向，与摄像机实际指向的方向是正好相反的）。
+	方向向量(Direction Vector)并不是最好的名字，因为它正好指向从它到目标向量的相反方向。
 
 ### 3. 右轴
 
-我们需要的另一个向量是一个**右向量**(Right Vector)，它代表摄像机空间的x轴的正方向。为获取右向量我们需要先使用一个小技巧：先定义一个**上向量**(Up Vector)。接下来把上向量和第二步得到的方向向量进行叉乘。两个向量叉乘的结果会同时垂直于两向量，因此我们会得到指向x轴正方向的那个向量（如果我们交换两个向量叉乘的顺序就会得到相反的指向x轴负方向的向量）：
+我们需要的另一个向量是一个**右向量(Right Vector)**，它代表摄像机空间的x轴的正方向。为获取右向量我们需要先使用一个小技巧：定义一个**上向量(Up Vector)**。我们把上向量和第二步得到的摄像机方向向量进行叉乘。两个向量叉乘的结果就是同时垂直于两向量的向量，因此我们会得到指向x轴正方向的那个向量(如果我们交换两个向量的顺序就会得到相反的指向x轴负方向的向量)：
 
 ```c++
 glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f); 
 glm::vec3 cameraRight = glm::normalize(glm::cross(up, cameraDirection));
 ```
 
-### 4. 上轴
+#### 4. 上轴
 
-现在我们已经有了x轴向量和z轴向量，获取一个指向摄像机的正y轴向量就相对简单了：我们把右向量和方向向量进行叉乘：
+现在我们已经有了x轴向量和z轴向量，获取摄像机的正y轴相对简单；我们把右向量和方向向量(Direction Vector)进行叉乘：
 
 ```c++
 glm::vec3 cameraUp = glm::cross(cameraDirection, cameraRight);
 ```
 
-在叉乘和一些小技巧的帮助下，我们创建了所有构成观察/摄像机空间的向量。对于想学到更多数学原理的读者，提示一下，在线性代数中这个处理叫做[格拉姆—施密特正交化](http://en.wikipedia.org/wiki/Gram%E2%80%93Schmidt_process)(Gram-Schmidt Process)。使用这些摄像机向量我们就可以创建一个<def>LookAt</def>矩阵了，它在创建摄像机的时候非常有用。
+在叉乘和一些小技巧的帮助下，我们创建了所有观察/摄像机空间的向量。对于想学到更多数学原理的读者，提示一下，在线性代数中这个处理叫做[Gram-Schmidt(葛兰—施密特)正交](http://en.wikipedia.org/wiki/Gram%E2%80%93Schmidt_process)。使用这些摄像机向量我们就可以创建一个**LookAt**矩阵了，它在创建摄像机的时候非常有用。
 
 ## Look At
 
-使用矩阵的好处之一是如果你使用3个相互垂直（或非线性）的轴定义了一个坐标空间，你可以用这3个轴外加一个平移向量来创建一个矩阵，并且你可以用这个矩阵乘以任何向量来将其变换到那个坐标空间。这正是**LookAt**矩阵所做的，现在我们有了3个相互垂直的轴和一个定义摄像机空间的位置坐标，我们可以创建我们自己的LookAt矩阵了：
+使用矩阵的好处之一是如果你定义了一个坐标空间，里面有3个相互垂直的轴，你可以用这三个轴外加一个平移向量来创建一个矩阵，你可以用这个矩阵乘以任何向量来变换到那个坐标空间。这正是LookAt矩阵所做的，现在我们有了3个相互垂直的轴和一个定义摄像机空间的位置坐标，我们可以创建我们自己的LookAt矩阵了：
 
 $$
 LookAt = \begin{bmatrix} \color{red}{R_x} & \color{red}{R_y} & \color{red}{R_z} & 0 \\ \color{green}{U_x} & \color{green}{U_y} & \color{green}{U_z} & 0 \\ \color{blue}{D_x} & \color{blue}{D_y} & \color{blue}{D_z} & 0 \\ 0 & 0 & 0  & 1 \end{bmatrix} * \begin{bmatrix} 1 & 0 & 0 & -\color{purple}{P_x} \\ 0 & 1 & 0 & -\color{purple}{P_y} \\ 0 & 0 & 1 & -\color{purple}{P_z} \\ 0 & 0 & 0  & 1 \end{bmatrix}
 $$
 
-其中\(\color{red}R\)是右向量，\(\color{green}U\)是上向量，\(\color{blue}D\)是方向向量\(\color{purple}P\)是摄像机位置向量。注意，位置向量是相反的，因为我们最终希望把世界平移到与我们自身移动的相反方向。把这个LookAt矩阵作为观察矩阵可以很高效地把所有世界坐标变换到刚刚定义的观察空间。LookAt矩阵就像它的名字表达的那样：它会创建一个看着(Look at)给定目标的观察矩阵。
+\(\color{red}R\)是右向量，\(\color{green}U\)是上向量，\(\color{blue}D\)是方向向量\(\color{purple}P\)是摄像机位置向量。注意，位置向量是相反的，因为我们最终希望把世界平移到与我们自身移动的相反方向。使用这个LookAt矩阵坐标观察矩阵可以很高效地把所有世界坐标变换为观察坐标LookAt矩阵就像它的名字表达的那样：它会创建一个观察矩阵looks at(看着)一个给定目标。
 
-幸运的是，GLM已经提供了这些支持。我们要做的只是定义一个摄像机位置，一个目标位置和一个表示世界空间中的上向量的向量（我们计算右向量使用的那个上向量）。接着GLM就会创建一个LookAt矩阵，我们可以把它当作我们的观察矩阵：
+幸运的是，GLM已经提供了这些支持。我们要做的只是定义一个摄像机位置，一个目标位置和一个表示上向量的世界空间中的向量(我们使用上向量计算右向量)。接着GLM就会创建一个LookAt矩阵，我们可以把它当作我们的观察矩阵：
 
 ```c++
 glm::mat4 view;
@@ -79,30 +79,30 @@ view = glm::lookAt(glm::vec3(0.0f, 0.0f, 3.0f),
   		   glm::vec3(0.0f, 1.0f, 0.0f));
 ```
 
-<fun>glm::LookAt</fun>函数需要一个位置、目标和上向量。它会创建一个和在上一节使用的一样的观察矩阵。
+`glm::LookAt`函数需要一个位置、目标和上向量。它可以创建一个和前面所说的同样的观察矩阵。
 
-在讨论用户输入之前，我们先来做些有意思的事，把我们的摄像机在场景中旋转。我们会将摄像机的注视点保持在(0, 0, 0)。
+在开始做用户输入之前，我们来做些有意思的事，把我们的摄像机在场景中旋转。我们的注视点保持在(0, 0, 0)。
 
-我们需要用到一点三角学的知识来在每一帧创建一个x和z坐标，它会代表圆上的一点，我们将会使用它作为摄像机的位置。通过重新计算x和y坐标，我们会遍历圆上的所有点，这样摄像机就会绕着场景旋转了。我们预先定义这个圆的半径<var>radius</var>，在每次渲染迭代中使用GLFW的<fun>glfwGetTime</fun>函数重新创建观察矩阵，来扩大这个圆。
+我们在每一帧都创建x和z坐标，这要使用一点三角学知识。x和z表示一个在一个圆圈上的一点，我们会使用它作为摄像机的位置。通过重复计算x和y坐标，遍历所有圆圈上的点，这样摄像机就会绕着场景旋转了。我们预先定义这个圆圈的半径，使用`glfwGetTime`函数不断增加它的值，在每次渲染迭代创建一个新的观察矩阵。
 
 ```c++
-float radius = 10.0f;
-float camX = sin(glfwGetTime()) * radius;
-float camZ = cos(glfwGetTime()) * radius;
+GLfloat radius = 10.0f;
+GLfloat camX = sin(glfwGetTime()) * radius;
+GLfloat camZ = cos(glfwGetTime()) * radius;
 glm::mat4 view;
-view = glm::lookAt(glm::vec3(camX, 0.0, camZ), glm::vec3(0.0, 0.0, 0.0), glm::vec3(0.0, 1.0, 0.0)); 
+view = glm::lookAt(glm::vec3(camX, 0.0, camZ), glm::vec3(0.0, 0.0, 0.0), glm::vec3(0.0, 1.0, 0.0));  
 ```
 
-如果你运行代码，应该会得到下面的结果：
+如果你运行代码你会得到下面的东西：
 
-<video src="../../img/01/09/camera_circle.mp4" controls="controls">
+<video src="http://learnopengl.com/video/getting-started/camera_circle.mp4" controls="controls">
 </video>
 
-通过这一小段代码，摄像机现在会随着时间流逝围绕场景转动了。自己试试改变半径和位置/方向参数，看看**LookAt**矩阵是如何工作的。同时，如果你在哪卡住的话，这里有[源码](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/7.1.camera_circle/camera_circle.cpp)。
+这一小段代码中，摄像机围绕场景转动。自己试试改变半径和位置/方向参数，看看LookAt矩阵是如何工作的。同时，这里有[源码](http://learnopengl.com/code_viewer.php?code=getting-started/camera_circle)、[顶点](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems&type=fragment)着色器。
 
 # 自由移动
 
-让摄像机绕着场景转的确很有趣，但是让我们自己移动摄像机会更有趣！首先我们必须设置一个摄像机系统，所以在我们的程序前面定义一些摄像机变量很有用：
+让摄像机绕着场景转很有趣，但是让我们自己移动摄像机更有趣！首先我们必须设置一个摄像机系统，在我们的程序前面定义一些摄像机变量很有用：
 
 ```c++
 glm::vec3 cameraPos   = glm::vec3(0.0f, 0.0f,  3.0f);
@@ -110,67 +110,123 @@ glm::vec3 cameraFront = glm::vec3(0.0f, 0.0f, -1.0f);
 glm::vec3 cameraUp    = glm::vec3(0.0f, 1.0f,  0.0f);
 ```
 
-`LookAt`函数现在成了：
+LookAt函数现在成了：
 
 ```c++
 view = glm::lookAt(cameraPos, cameraPos + cameraFront, cameraUp);
 ```
 
-我们首先将摄像机位置设置为之前定义的<var>cameraPos</var>。方向是当前的位置加上我们刚刚定义的方向向量。这样能保证无论我们怎么移动，摄像机都会注视着目标方向。让我们摆弄一下这些向量，在按下某些按钮时更新<var>cameraPos</var>向量。
+我们首先设置之前定义的`cameraPos`为摄像机位置。方向(Direction)是当前的位置加上我们刚刚定义的方向向量。这样能保证无论我们怎么移动，摄像机都会注视目标。我们在按下某个按钮时更新`cameraPos`向量。
 
-我们已经为GLFW的键盘输入定义过一个<fun>processInput</fun>函数了，我们来新添加几个需要检查的按键命令：
+我们已经为GLFW的键盘输入定义了一个`key_callback`函数，我们来添加几个新按键命令：
 
 ```c++
-void processInput(GLFWwindow *window)
+void key_callback(GLFWwindow* window, int key, int scancode, int action, int mode)
 {
     ...
-    float cameraSpeed = 0.05f; // adjust accordingly
-    if (glfwGetKey(window, GLFW_KEY_W) == GLFW_PRESS)
+    GLfloat cameraSpeed = 0.05f;
+    if(key == GLFW_KEY_W)
         cameraPos += cameraSpeed * cameraFront;
-    if (glfwGetKey(window, GLFW_KEY_S) == GLFW_PRESS)
+    if(key == GLFW_KEY_S)
         cameraPos -= cameraSpeed * cameraFront;
-    if (glfwGetKey(window, GLFW_KEY_A) == GLFW_PRESS)
+    if(key == GLFW_KEY_A)
         cameraPos -= glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
-    if (glfwGetKey(window, GLFW_KEY_D) == GLFW_PRESS)
-        cameraPos += glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
+    if(key == GLFW_KEY_D)
+        cameraPos += glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;  
 }
 ```
 
-当我们按下**WASD**键的任意一个，摄像机的位置都会相应更新。如果我们希望向前或向后移动，我们就把位置向量加上或减去方向向量。如果我们希望向左右移动，我们使用叉乘来创建一个**右向量**(Right Vector)，并沿着它相应移动就可以了。这样就创建了使用摄像机时熟悉的<def>横移</def>(Strafe)效果。
+当我们按下WASD键，摄像机的位置都会相应更新。如果我们希望向前或向后移动，我们就把位置向量加上或减去方向向量。如果我们希望向旁边移动，我们做一个叉乘来创建一个右向量，沿着它移动就可以了。这样就创建了类似使用摄像机横向、前后移动的效果。
 
-!!! important
+!!! Important
 
-	注意，我们对**右向量**进行了标准化。如果我们没对这个向量进行标准化，最后的叉乘结果会根据<var>cameraFront</var>变量返回大小不同的向量。如果我们不对向量进行标准化，我们就得根据摄像机的朝向不同加速或减速移动了，但如果进行了标准化移动就是匀速的。
+	注意，我们对右向量进行了标准化。如果我们没对这个向量进行标准化，最后的叉乘结果会根据`cameraFront`变量的大小返回不同的大小。如果我们不对向量进行标准化，我们就得根据摄像机的方位加速或减速移动了，但假如进行了标准化移动就是匀速的。
 
-现在你就应该能够移动摄像机了，虽然移动速度和系统有关，你可能会需要调整一下<var>cameraSpeed</var>。
+如果你用这段代码更新`key_callback`函数，你就可以在场景中自由的前后左右移动了。
+
+<video src="http://learnopengl.com/video/getting-started/camera_inside.mp4" controls="controls">
+</video>
+
+你可能会注意到这个摄像机系统不能同时朝两个方向移动，当你按下一个按键时，它会先顿一下才开始移动。这是因为大多数事件输入系统一次只能处理一个键盘输入，它们的函数只有当我们激活了一个按键时才被调用。大多数GUI系统都是这样的，它对摄像机来说用并不合理。我们可以用一些小技巧解决这个问题。
+
+这个技巧是只在回调函数中跟踪哪个键被按下/释放。在游戏循环中我们读取这些值，检查那个按键被激活了，然后做出相应反应。我们只储存哪个键被按下/释放的状态信息，在游戏循环中对状态做出反应，我们来创建一个布尔数组代表按下/释放的键：
+
+```c++
+bool keys[1024];
+```
+
+然后我们必须在`key_callback`函数中设置按下/释放键为`true`或`false`：
+
+```c++
+if(action == GLFW_PRESS)
+    keys[key] = true;
+else if(action == GLFW_RELEASE)
+    keys[key] = false;
+```
+
+我们创建一个新的叫做`do_movement`的函数，用它根据按下的按键来更新摄像机的值：
+
+```c++
+void do_movement()
+{
+  // 摄像机控制
+  GLfloat cameraSpeed = 0.01f;
+  if(keys[GLFW_KEY_W])
+  	cameraPos += cameraSpeed * cameraFront;
+  if(keys[GLFW_KEY_S])
+  	cameraPos -= cameraSpeed * cameraFront;
+  if(keys[GLFW_KEY_A])
+  	cameraPos -= glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
+  if(keys[GLFW_KEY_D])
+  	cameraPos += glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
+}
+```
+
+之前的代码移动到了`do_movement`函数中。由于所有GLFW的按键枚举都是整数，我们可以把它们当数组索引使用。
+
+最后，我们需要在游戏循环中添加新函数的调用：
+
+```c++
+while(!glfwWindowShouldClose(window))
+{
+  // 检测并调用事件
+  glfwPollEvents();
+  do_movement();  
+  
+  // 渲染
+  ...
+}
+```
+
+至此，你可以同时向多个方向移动了，并且当你按下按钮也会立刻运动了。如遇困难查看[源码](http://learnopengl.com/code_viewer.php?code=getting-started/camera_keyboard)。
 
 ## 移动速度
 
-目前我们的移动速度是个常量。理论上没什么问题，但是实际情况下根据处理器的能力不同，有些人可能会比其他人每秒绘制更多帧，也就是以更高的频率调用<fun>processInput</fun>函数。结果就是，根据配置的不同，有些人可能移动很快，而有些人会移动很慢。当你发布你的程序的时候，你必须确保它在所有硬件上移动速度都一样。
+目前我们的移动速度是个常量。看起来不错，但是实际情况下根据处理器的能力不同，有的人在同一段时间内会比其他人绘制更多帧。也就是调用了更多次`do_movement`函数。每个人的运动速度就都不同了。当你要发布的你应用的时候，你必须确保在所有硬件上移动速度都一样。
 
-图形程序和游戏通常会跟踪一个<def>时间差</def>(Deltatime)变量，它储存了渲染上一帧所用的时间。我们把所有速度都去乘以<var>deltaTime</var>值。结果就是，如果我们的<var>deltaTime</var>很大，就意味着上一帧的渲染花费了更多时间，所以这一帧的速度需要变得更高来平衡渲染所花去的时间。使用这种方法时，无论你的电脑快还是慢，摄像机的速度都会相应平衡，这样每个用户的体验就都一样了。
+图形和游戏应用通常有回跟踪一个`deltaTime`变量，它储存渲染上一帧所用的时间。我们把所有速度都去乘以`deltaTime`值。当我们的`deltaTime`变大时意味着上一帧渲染花了更多时间，所以这一帧使用这个更大的`deltaTime`的值乘以速度，会获得更高的速度，这样就与上一帧平衡了。使用这种方法时，无论你的机器快还是慢，摄像机的速度都会保持一致，这样每个用户的体验就都一样了。
 
-我们跟踪两个全局变量来计算出<var>deltaTime</var>值：
+我们要用两个全局变量来计算出`deltaTime`值：
 
 ```c++
-float deltaTime = 0.0f;	// 当前帧与上一帧的时间差
-float lastFrame = 0.0f; // 上一帧的时间
+GLfloat deltaTime = 0.0f;	// 当前帧遇上一帧的时间差
+GLfloat lastFrame = 0.0f;  	// 上一帧的时间
 ```
 
-在每一帧中我们计算出新的<var>deltaTime</var>以备后用。
+在每一帧中我们计算出新的`deltaTime`以备后用
 
 ```c++
-float currentFrame = glfwGetTime();
+GLfloat currentFrame = glfwGetTime();
 deltaTime = currentFrame - lastFrame;
-lastFrame = currentFrame;
+lastFrame = currentFrame;  
 ```
 
-现在我们有了<var>deltaTime</var>，在计算速度的时候可以将其考虑进去了：
+现在我们有了`deltaTime`在计算速度的使用可以使用了：
 
 ```c++
-void processInput(GLFWwindow *window)
+void Do_Movement()
 {
-  float cameraSpeed = 2.5f * deltaTime;
+  GLfloat cameraSpeed = 5.0f * deltaTime;
   ...
 }
 ```
@@ -178,121 +234,126 @@ void processInput(GLFWwindow *window)
 与前面的部分结合在一起，我们有了一个更流畅点的摄像机系统：
 
 
-<video src="../../img/01/09/camera_smooth.mp4" controls="controls">
+<video src="http://learnopengl.com/video/getting-started/camera_smooth.mp4" controls="controls">
 </video>
 
-现在我们有了一个在任何系统上移动速度都一样的摄像机。同样，如果你卡住了，查看一下[源码](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/7.2.camera_keyboard_dt/camera_keyboard_dt.cpp)。我们可以看到任何移动都会影响返回的<var>deltaTime</var>值。
+现在我们有了一个在任何系统上移动速度都一样的摄像机。这里是源码。我们可以看到任何移动都会影响返回的`deltaTime`值。
 
 
 # 视角移动
 
-只用键盘移动没什么意思。特别是我们还不能转向，移动很受限制。是时候加入鼠标了！
+只用键盘移动没什么意思。特别是我们还不能转向。是时候使用鼠标了！
 
-为了能够改变视角，我们需要根据鼠标的输入改变<var>cameraFront</var>向量。然而，根据鼠标移动改变方向向量有点复杂，需要一些三角学知识。如果你对三角学知之甚少，别担心，你可以跳过这一部分，直接复制粘贴我们的代码；当你想了解更多的时候再回来看。
+为了能够改变方向，我们必须根据鼠标的输入改变`cameraFront`向量。然而，根据鼠标旋转改变方向向量有点复杂，需要更多的三角学知识。如果你对三角学知之甚少，别担心，你可以跳过这一部分，直接复制粘贴我们的代码；当你想了解更多的时候再回来看。
 
 ## 欧拉角
 
-欧拉角(Euler Angle)是可以表示3D空间中任何旋转的3个值，由莱昂哈德·欧拉(Leonhard Euler)在18世纪提出。一共有3种欧拉角：俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll)，下面的图片展示了它们的含义：
+欧拉角(Euler Angle)是表示3D空间中可以表示任何旋转的三个值，由莱昂哈德·欧拉在18世纪提出。有三种欧拉角：俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll)，下面的图片展示了它们的含义：
 
-![](../img/01/09/camera_pitch_yaw_roll.png)
+![](http://www.learnopengl.com/img/getting-started/camera_pitch_yaw_roll.png)
 
-<def>俯仰角</def>是描述我们如何往上或往下看的角，可以在第一张图中看到。第二张图展示了<def>偏航角</def>，偏航角表示我们往左和往右看的程度。<def>滚转角</def>代表我们如何**翻滚**摄像机，通常在太空飞船的摄像机中使用。每个欧拉角都有一个值来表示，把三个角结合起来我们就能够计算3D空间中任何的旋转向量了。
+**俯仰角**是描述我们如何往上和往下看的角，它在第一张图中表示。第二张图显示了**偏航角**，偏航角表示我们往左和往右看的大小。**滚转角**代表我们如何翻滚摄像机。每个欧拉角都有一个值来表示，把三个角结合起来我们就能够计算3D空间中任何的旋转了。
 
-对于我们的摄像机系统来说，我们只关心俯仰角和偏航角，所以我们不会讨论滚转角。给定一个俯仰角和偏航角，我们可以把它们转换为一个代表新的方向向量的3D向量。俯仰角和偏航角转换为方向向量的处理需要一些三角学知识，我们先从最基本的情况开始：
+对于我们的摄像机系统来说，我们只关心俯仰角和偏航角，所以我们不会讨论滚转角。用一个给定的俯仰角和偏航角，我们可以把它们转换为一个代表新的方向向量的3D向量。俯仰角和偏航角转换为方向向量的处理需要一些三角学知识，我们以最基本的情况开始：
 
-![](../img/01/09/camera_triangle.png)
+![](http://www.learnopengl.com/img/getting-started/camera_triangle.png)
 
-如果我们把斜边边长定义为1，我们就能知道邻边的长度是\(\cos \ \color{red}x/\color{purple}h = \cos \ \color{red}x/\color{purple}1 = \cos\ \color{red}x\)，它的对边是\(\sin \ \color{green}y/\color{purple}h = \sin \ \color{green}y/\color{purple}1 = \sin\ \color{green}y\)。这样我们获得了能够得到x和y方向长度的通用公式，它们取决于所给的角度。我们使用它来计算方向向量的分量：
+如果我们把斜边边长定义为1，我们就能知道邻边的长度是\(\cos \ \color{red}x/\color{purple}h = \cos \ \color{red}x/\color{purple}1 = \cos\ \color{red}x\)，它的对边是\(\sin \ \color{green}y/\color{purple}h = \sin \ \color{green}y/\color{purple}1 = \sin\ \color{green}y\)。这样我们获得了能够得到x和y方向的长度的公式，它们取决于所给的角度。我们使用它来计算方向向量的元素：
 
-![](../img/01/09/camera_pitch.png)
+![](http://www.learnopengl.com/img/getting-started/camera_pitch.png)
 
-这个三角形看起来和前面的三角形很像，所以如果我们想象自己在xz平面上，看向y轴，我们可以基于第一个三角形计算来计算它的长度/y方向的强度(Strength)（我们往上或往下看多少）。从图中我们可以看到对于一个给定俯仰角的y值等于\(\sin\ \theta\)：
+这个三角形看起来和前面的三角形很像，所以如果我们想象自己在xz平面上，正望向y轴，我们可以基于第一个三角形计算长度/y方向的强度(我们往上或往下看多少)。从图中我们可以看到一个给定俯仰角的y值等于sinθ:
 
 ```c++
 direction.y = sin(glm::radians(pitch)); // 注意我们先把角度转为弧度
 ```
 
-这里我们只更新了y值，仔细观察x和z分量也被影响了。从三角形中我们可以看到它们的值等于：
+这里我们只更新了y值，仔细观察x和z元素也被影响了。从三角形中我们可以看到它们的值等于：
 
 ```c++
 direction.x = cos(glm::radians(pitch));
 direction.z = cos(glm::radians(pitch));
 ```
 
-看看我们是否能够为偏航角找到需要的分量：
+看看我们是否能够为偏航角找到需要的元素：
 
-![](../img/01/09/camera_yaw.png)
+![](http://www.learnopengl.com/img/getting-started/camera_yaw.png)
 
-就像俯仰角的三角形一样，我们可以看到x分量取决于`cos(yaw)`的值，z值同样取决于偏航角的正弦值。把这个加到前面的值中，会得到基于俯仰角和偏航角的方向向量：
+就像俯仰角一样我们可以看到x元素取决于cos(偏航角)的值，z值同样取决于偏航角的正弦值。把这个加到前面的值中，会得到基于俯仰角和偏航角的方向向量：
+
+!!! note "译注"
+
+    这里的球坐标与笛卡尔坐标的转换把x和z弄反了，如果你去看最后的源码，会发现作者在摄像机源码那里写了`yaw = yaw – 90`，实际上在这里x就应该是`sin(glm::radians(yaw))`，z也是同样处理，当然也可以认为是这个诡异的坐标系，但是在这里使用球坐标转笛卡尔坐标有个大问题，就是在初始渲染时，无法指定摄像机的初始朝向，还要花一些功夫自己实现这个；此外这只能实现像第一人称游戏一样的简易摄像机，类似Maya、Unity3D编辑器窗口的那种摄像机还是最好自己设置摄像机的位置、上、右、前轴，在旋转时用四元数对这四个变量进行调整，才能获得更好的效果，而不是仅仅调整摄像机前轴。
 
 ```c++
-direction.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw)); // 译注：direction代表摄像机的前轴(Front)，这个前轴是和本文第一幅图片的第二个摄像机的方向向量是相反的
+direction.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw));//译注：direction代表摄像机的“前”轴，但此前轴是和本文第一幅图片的第二个摄像机的direction是相反的
 direction.y = sin(glm::radians(pitch));
 direction.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));
 ```
 
-这样我们就有了一个可以把俯仰角和偏航角转化为用来自由旋转视角的摄像机的3维方向向量了。你可能会奇怪：我们怎么得到俯仰角和偏航角？
+这样我们就有了一个可以把俯仰角和偏航角转化为用来自由旋转的摄像机的3个维度的方向向量了。你可能会奇怪：我们怎么得到俯仰角和偏航角？
 
 ## 鼠标输入
 
-偏航角和俯仰角是通过鼠标（或手柄）移动获得的，水平的移动影响偏航角，竖直的移动影响俯仰角。它的原理就是，储存上一帧鼠标的位置，在当前帧中我们当前计算鼠标位置与上一帧的位置相差多少。如果水平/竖直差别越大那么俯仰角或偏航角就改变越大，也就是摄像机需要移动更多的距离。
+偏航角和俯仰角是从鼠标移动获得的，鼠标水平移动影响偏航角，鼠标垂直移动影响俯仰角。它的思想是储存上一帧鼠标的位置，在当前帧中我们当前计算鼠标位置和上一帧的位置相差多少。如果差别越大那么俯仰角或偏航角就改变越大。
+
+首先我们要告诉GLFW，应该隐藏光标，并**捕捉(Capture)**它。捕捉鼠标意味着当应用集中焦点到鼠标上的时候光标就应该留在窗口中(除非应用拾取焦点或退出)。我们可以进行简单的配置:
 
-首先我们要告诉GLFW，它应该隐藏光标，并<def>捕捉</def>(Capture)它。捕捉光标表示的是，如果焦点在你的程序上（译注：即表示你正在操作这个程序，Windows中拥有焦点的程序标题栏通常是有颜色的那个，而失去焦点的程序标题栏则是灰色的），光标应该停留在窗口中（除非程序失去焦点或者退出）。我们可以用一个简单地配置调用来完成：
 
 ```c++
 glfwSetInputMode(window, GLFW_CURSOR, GLFW_CURSOR_DISABLED);
 ```
 
-在调用这个函数之后，无论我们怎么去移动鼠标，光标都不会显示了，它也不会离开窗口。对于FPS摄像机系统来说非常完美。
+这个函数调用后，无论我们怎么去移动鼠标，它都不会显示了，也不会离开窗口。对于FPS摄像机系统来说很好：
 
-为了计算俯仰角和偏航角，我们需要让GLFW监听鼠标移动事件。（和键盘输入相似）我们会用一个回调函数来完成，函数的原型如下：
+为计算俯仰角和偏航角我们需要告诉GLFW监听鼠标移动事件。我们用下面的原型创建一个回调函数来做这件事(和键盘输入差不多)：
 
 ```c++
 void mouse_callback(GLFWwindow* window, double xpos, double ypos);
 ```
 
-这里的<var>xpos</var>和<var>ypos</var>代表当前鼠标的位置。当我们用GLFW注册了回调函数之后，鼠标一移动<fun>mouse_callback</fun>函数就会被调用：
+这里的`xpos`和`ypos`代表当前鼠标的位置。我们注册了GLFW的回调函数，鼠标一移动`mouse_callback`函数就被调用：
 
 ```c++
 glfwSetCursorPosCallback(window, mouse_callback);
 ```
 
-在处理FPS风格摄像机的鼠标输入的时候，我们必须在最终获取方向向量之前做下面这几步：
+在处理FPS风格的摄像机鼠标输入的时候，我们必须在获取最终的方向向量之前做下面这几步：
 
-1. 计算鼠标距上一帧的偏移量。
-2. 把偏移量添加到摄像机的俯仰角和偏航角中。
+1. 计算鼠标和上一帧的偏移量。
+2. 把偏移量添加到摄像机和俯仰角和偏航角中。
 3. 对偏航角和俯仰角进行最大和最小值的限制。
 4. 计算方向向量。
 
-第一步是计算鼠标自上一帧的偏移量。我们必须先在程序中储存上一帧的鼠标位置，我们把它的初始值设置为屏幕的中心（屏幕的尺寸是800x600）：
+第一步计算鼠标自上一帧的偏移量。我们必须先储存上一帧的鼠标位置，我们把它的初始值设置为屏幕的中心(屏幕的尺寸是800乘600)：
 
 ```c++
-float lastX = 400, lastY = 300;
+GLfloat lastX = 400, lastY = 300;
 ```
 
-然后在鼠标的回调函数中我们计算当前帧和上一帧鼠标位置的偏移量：
+然后在回调函数中我们计算当前帧和上一帧鼠标位置的偏移量：
 
 ```c++
-float xoffset = xpos - lastX;
-float yoffset = lastY - ypos; // 注意这里是相反的，因为y坐标是从底部往顶部依次增大的
+GLfloat xoffset = xpos - lastX;
+GLfloat yoffset = lastY - ypos; // 注意这里是相反的，因为y坐标的范围是从下往上的
 lastX = xpos;
 lastY = ypos;
 
-float sensitivity = 0.05f;
+GLfloat sensitivity = 0.05f;
 xoffset *= sensitivity;
 yoffset *= sensitivity;
 ```
 
-注意我们把偏移量乘以了<var>sensitivity</var>（灵敏度）值。如果我们忽略这个值，鼠标移动就会太大了；你可以自己实验一下，找到适合自己的灵敏度值。
+注意我们把偏移量乘以了`sensitivity`值。如果我们移除它，鼠标移动就会太大了；你可以自己调整`sensitivity`的值。
 
-接下来我们把偏移量加到全局变量<var>pitch</var>和<var>yaw</var>上：
+下面我们把偏移量加到全局变量`pitch`和`yaw`上：
 
 ```c++
 yaw   += xoffset;
-pitch += yoffset;
+pitch += yoffset;  
 ```
 
-第三步，我们需要给摄像机添加一些限制，这样摄像机就不会发生奇怪的移动了（这样也会避免一些奇怪的问题）。对于俯仰角，要让用户不能看向高于89度的地方（在90度时视角会发生逆转，所以我们把89度作为极限），同样也不允许小于-89度。这样能够保证用户只能看到天空或脚下，但是不能超越这个限制。我们可以在值超过限制的时候将其改为极限值来实现：
+第三步我们给摄像机添加一些限制，这样摄像机就不会发生奇怪的移动了。对于俯仰角，要让用户不能看向高于89度(90度时视角会逆转，所以我们把89度作为极限)的地方，同样也不允许小于-89度。这样能够保证用户只能看到天空或脚下但是不能更进一步超越过去。限制可以这样做：
 
 ```c++
 if(pitch > 89.0f)
@@ -301,9 +362,9 @@ if(pitch < -89.0f)
   pitch = -89.0f;
 ```
 
-注意我们没有给偏航角设置限制，这是因为我们不希望限制用户的水平旋转。当然，给偏航角设置限制也很容易，如果你愿意可以自己实现。
+注意我们没有给偏航角设置限制是因为我们不希望限制用户的水平旋转。然而，给偏航角设置限制也很容易，只要你愿意。
 
-第四也是最后一步，就是通过俯仰角和偏航角来计算以得到真正的方向向量：
+第四也是最后一步，就是通过俯仰角和偏航角来计算以得到前面提到的实际方向向量：
 
 ```c++
 glm::vec3 front;
@@ -313,16 +374,16 @@ front.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));
 cameraFront = glm::normalize(front);
 ```
 
-计算出来的方向向量就会包含根据鼠标移动计算出来的所有旋转了。由于<var>cameraFront</var>向量已经包含在GLM的<fun>lookAt</fun>函数中，我们这就没什么问题了。
+这回计算出方向向量，根据鼠标点的移动它包含所有的旋转。由于`cameraFront`向量已经包含在`glm::lookAt`函数中，我们直接去设置。
 
-如果你现在运行代码，你会发现在窗口第一次获取焦点的时候摄像机会突然跳一下。这个问题产生的原因是，在你的鼠标移动进窗口的那一刻，鼠标回调函数就会被调用，这时候的<var>xpos</var>和<var>ypos</var>会等于鼠标刚刚进入屏幕的那个位置。这通常是一个距离屏幕中心很远的地方，因而产生一个很大的偏移量，所以就会跳了。我们可以简单的使用一个`bool`变量检验我们是否是第一次获取鼠标输入，如果是，那么我们先把鼠标的初始位置更新为<var>xpos</var>和<var>ypos</var>值，这样就能解决这个问题；接下来的鼠标移动就会使用刚进入的鼠标位置坐标来计算偏移量了：
+如果你现在运行代码，你会发现当程序运行第一次捕捉到鼠标的时候摄像机会突然跳一下。原因是当你的鼠标进入窗口鼠标回调函数会使用这时的`xpos`和`ypos`。这通常是一个距离屏幕中心很远的地方，因而产生一个很大的偏移量，所以就会跳了。我们可以简单的使用一个布尔变量检验我们是否是第一次获取鼠标输入，如果是，那么我们先把鼠标的位置更新为`xpos`和`ypos`，这样就能解决这个问题；最后的鼠标移动会使用进入以后鼠标的位置坐标来计算它的偏移量：
 
 ```c++
-if(firstMouse) // 这个bool变量初始时是设定为true的
+if(firstMouse) // 这个bool变量一开始是设定为true的
 {
-    lastX = xpos;
-    lastY = ypos;
-    firstMouse = false;
+  lastX = xpos;
+  lastY = ypos;
+  firstMouse = false;
 }
 ```
 
@@ -338,12 +399,12 @@ void mouse_callback(GLFWwindow* window, double xpos, double ypos)
         firstMouse = false;
     }
   
-    float xoffset = xpos - lastX;
-    float yoffset = lastY - ypos; 
+    GLfloat xoffset = xpos - lastX;
+    GLfloat yoffset = lastY - ypos; 
     lastX = xpos;
     lastY = ypos;
 
-    float sensitivity = 0.05;
+    GLfloat sensitivity = 0.05;
     xoffset *= sensitivity;
     yoffset *= sensitivity;
 
@@ -360,66 +421,67 @@ void mouse_callback(GLFWwindow* window, double xpos, double ypos)
     front.y = sin(glm::radians(pitch));
     front.z = sin(glm::radians(yaw)) * cos(glm::radians(pitch));
     cameraFront = glm::normalize(front);
-}
+}  
 ```
 
-现在我们就可以自由地在3D场景中移动了！
+现在我们可以自由的在3D场景中移动了！如果你遇到困难，[这是](http://www.learnopengl.com/code_viewer.php?code=getting-started/camera_mouse)源码。
 
 ## 缩放
 
-作为我们摄像机系统的一个附加内容，我们还会来实现一个缩放(Zoom)接口。在之前的教程中我们说**视野**(Field of View)或**fov**定义了我们可以看到场景中多大的范围。当视野变小时，场景投影出来的空间就会减小，产生放大(Zoom In)了的感觉。我们会使用鼠标的滚轮来放大。与鼠标移动、键盘输入一样，我们需要一个鼠标滚轮的回调函数：
+我们还要往摄像机系统里加点东西，实现一个缩放接口。前面教程中我们说视野(Field of View或fov)定义了我们可以看到场景中多大的范围。当视野变小时可视区域就会减小，产生放大了的感觉。我们用鼠标滚轮来放大。和鼠标移动、键盘输入一样我们需要一个鼠标滚轮的回调函数：
 
 ```c++
 void scroll_callback(GLFWwindow* window, double xoffset, double yoffset)
 {
-  if(fov >= 1.0f && fov <= 45.0f)
-  	fov -= yoffset;
-  if(fov <= 1.0f)
-  	fov = 1.0f;
-  if(fov >= 45.0f)
-  	fov = 45.0f;
+  if(aspect >= 1.0f && aspect <= 45.0f)
+  	aspect -= yoffset;
+  if(aspect <= 1.0f)
+  	aspect = 1.0f;
+  if(aspect >= 45.0f)
+  	aspect = 45.0f;
 }
 ```
 
-当滚动鼠标滚轮的时候，<var>yoffset</var>值代表我们竖直滚动的大小。当<fun>scroll_callback</fun>函数被调用后，我们改变全局变量<var>fov</var>变量的内容。因为`45.0f`是默认的视野值，我们将会把缩放级别(Zoom Level)限制在`1.0f`到`45.0f`。
+`yoffset`值代表我们滚动的大小。当`scroll_callback`函数调用后，我们改变全局`aspect`变量的内容。因为`45.0f`是默认的`fov`，我们将会把缩放级别限制在`1.0f`到`45.0f`。
 
-我们现在在每一帧都必须把透视投影矩阵上传到GPU，但现在使用<var>fov</var>变量作为它的视野：
+我们现在在每一帧都必须把透视投影矩阵上传到GPU，但这一次使`aspect`变量作为它的fov：
 
 ```c++
-projection = glm::perspective(glm::radians(fov), 800.0f / 600.0f, 0.1f, 100.0f);
+projection = glm::perspective(aspect, (GLfloat)WIDTH/(GLfloat)HEIGHT, 0.1f, 100.0f);
 ```
 
-最后不要忘记注册鼠标滚轮的回调函数：
+最后不要忘记注册滚动回调函数：
 
 ```c++
 glfwSetScrollCallback(window, scroll_callback);
 ```
 
-现在，我们就实现了一个简单的摄像机系统了，它能够让我们在3D环境中自由移动。
+现在我们实现了一个简单的摄像机系统，它能够让我们在3D环境中自由移动。
 
-<video src="../../img/01/09/camera_mouse.mp4" controls="controls">
+<video src="http://learnopengl.com/video/getting-started/camera_mouse.mp4" controls="controls">
 </video>
 
-你可以去自由地实验，如果遇到困难，可以对比[源代码](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/7.3.camera_mouse_zoom/camera_mouse_zoom.cpp)。
+自由的去实验，如果遇到困难对比[源代码](http://learnopengl.com/code_viewer.php?code=getting-started/camera_zoom)。
 
 !!! Important
 
-	注意，使用欧拉角的摄像机系统并不完美。根据你的视角限制或者是配置，你仍然可能引入[万向节死锁](http://en.wikipedia.org/wiki/Gimbal_lock)问题。最好的摄像机系统是使用四元数(Quaternions)的，但我们将会把这个留到后面讨论。（译注：[这里](https://github.com/cybercser/OpenGL_3_3_Tutorial_Translation/blob/master/Tutorial%2017%20Rotations.md)可以查看四元数摄像机的实现）
+	注意，使用欧拉角作为摄像机系统并不完美。你仍然可能遇到[万向节死锁](http://en.wikipedia.org/wiki/Gimbal_lock)。最好的摄像机系统是使用四元数的，后面会有讨论。
 
 # 摄像机类
 
-接下来的教程中，我们将会一直使用一个摄像机来浏览场景，从各个角度观察结果。然而，由于一个摄像机会占用每篇教程很大的篇幅，我们将会从细节抽象出来，创建我们自己的摄像机对象，它会完成大多数的工作，而且还会提供一些附加的功能。与着色器教程不同，我们不会带你一步一步创建摄像机类，我们只会提供你一份（有完整注释的）代码，如果你想知道它的内部构造的话可以自己去阅读。
+接下来的教程我们会使用一个摄像机来浏览场景，从各个角度观察结果。然而由于一个摄像机会占教程的很大的篇幅，我们会从细节抽象出创建一个自己的摄像机对象。与着色器教程不同我们不会带你一步一步创建摄像机类，如果你想知道怎么工作的的话，只会给你提供一个(有完整注释的)源码。
 
-和着色器对象一样，我们把摄像机类写在一个单独的头文件中。你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=includes/learnopengl/camera.h)找到它，你现在应该能够理解所有的代码了。我们建议您至少看一看这个类，看看如何创建一个自己的摄像机类。
+像着色器对象一样，我们把摄像机类写在一个单独的头文件中。你可以在[这里](http://learnopengl.com/code_viewer.php?type=header&code=camera)找到它。你应该能够理解所有的代码。我们建议您至少看一看这个类，看看如何创建一个自己的摄像机类。
 
 !!! Attention
 
-	我们介绍的摄像机系统是一个FPS风格的摄像机，它能够满足大多数情况需要，而且与欧拉角兼容，但是在创建不同的摄像机系统，比如飞行模拟摄像机，时就要当心。每个摄像机系统都有自己的优点和不足，所以确保对它们进行了详细研究。比如，这个FPS摄像机不允许俯仰角大于90度，而且我们使用了一个固定的上向量(0, 1, 0)，这在需要考虑滚转角的时候就不能用了。
+	我们介绍的欧拉角FPS风格摄像机系统能够满足大多数情况需要，但是在创建不同的摄像机系统，比如飞行模拟就要当心。每个摄像机系统都有自己的有点和不足，所以确保对它们进行了详细研究。比如，这个FPS摄像机不允许俯仰角大于90度，由于使用了固定的上向量(0, 1, 0)，我们就不能用滚转角。
+
+使用新的摄像机对象的更新后的版本源码可以[在这里找到](http://learnopengl.com/code_viewer.php?code=getting-started/camera_with_class)。(译注：总而言之这个摄像机实现并不十分完美，你可以看看最终的源码。建议先看[这篇文章](https://github.com/cybercser/OpenGL_3_3_Tutorial_Translation/blob/master/Tutorial%2017%20Rotations.md)，对旋转有更深的理解后，你就能做出更好的摄像机类，不过本文有些内容比如如何防止按键停顿和glfw鼠标事件实现摄像机的注意事项比较重要，其它的就要做一定的取舍了)
 
-使用新摄像机对象，更新后版本的源码可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/1.getting_started/7.4.camera_class/camera_class.cpp)找到。
 
 ## 练习
 
-- 看看你是否能够修改摄像机类，使得其能够变成一个**真正的**FPS摄像机（也就是说不能够随意飞行）；你只能够呆在xz平面上：[参考解答](https://learnopengl.com/code_viewer.php?code=getting-started/camera-exercise1)
+- 看看你是否能够变换摄像机类从而使得其能够变- 成一个**真正的**FPS摄像机(也就是说不能够随意飞行)；你只能够呆在xz平面上: [参考解答](http://www.learnopengl.com/code_viewer.php?code=getting-started/camera-exercise1)
 
-- 试着创建你自己的LookAt函数，其中你需要手动创建一个我们在一开始讨论的观察矩阵。用你的函数实现来替换GLM的LookAt函数，看看它是否还能一样地工作：[参考解答](https://learnopengl.com/code_viewer.php?code=getting-started/camera-exercise2)
+- 试着创建你自己的LookAt函数，使你能够手动创建一个我们在一开始讨论的观察矩阵。用你的函数实现来替换glm的LookAt函数，看看它是否还能一样的工作：[参考解答](http://www.learnopengl.com/code_viewer.php?code=getting-started/camera-exercise2)

docs/01 Getting started/10 Review.md

@@ -1,10 +1,10 @@
 # 复习
 
-原文     | [Review](https://learnopengl.com/#!Getting-started/Review)
+原文     | [Review](http://learnopengl.com/#!Getting-started/Review)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | Geequlim，[orbitgw](https://github.com/orbitgw/)
+翻译     | Meow J
+校对     | Geequlim
 
 恭喜您完成了本章的学习，至此为止你应该能够创建一个窗口，创建并且编译着色器，通过缓冲对象或者uniform发送顶点数据，绘制物体，使用纹理，理解向量和矩阵，并且可以综合上述知识创建一个3D场景并可以通过摄像机来移动。
 
@@ -12,29 +12,29 @@
 
 ## 词汇表
 
-- **OpenGL**： 一个定义了函数布局和输出的图形API的正式规范。
-- **GLAD**： 一个扩展加载库，用来为我们加载并设定所有OpenGL函数指针，从而让我们能够使用所有（现代）OpenGL函数。
-- **视口(Viewport)**： 我们需要渲染的窗口。
-- **图形管线(Graphics Pipeline)**： 一个顶点在呈现为像素之前经过的全部过程。
-- **着色器(Shader)**： 一个运行在显卡上的小型程序。很多阶段的图形管道都可以使用自定义的着色器来代替原有的功能。
-- **标准化设备坐标(Normalized Device Coordinates, NDC)**： 顶点在通过在剪裁坐标系中剪裁与透视除法后最终呈现在的坐标系。所有位置在NDC下-1.0到1.0的顶点将不会被丢弃并且可见。
-- **顶点缓冲对象(Vertex Buffer Object)**： 一个调用显存并存储所有顶点数据供显卡使用的缓冲对象。
-- **顶点数组对象(Vertex Array Object)**： 存储缓冲区和顶点属性状态。
-- **元素缓冲对象(Element Buffer Object，EBO)，也叫索引缓冲对象(Index Buffer Object，IBO)**： 一个存储元素索引供索引化绘制使用的缓冲对象。
-- **Uniform**： 一个特殊类型的GLSL变量。它是全局的（在一个着色器程序中每一个着色器都能够访问uniform变量），并且只需要被设定一次。
-- **纹理(Texture)**： 一种包裹着物体的特殊类型图像，给物体精细的视觉效果。
-- **纹理环绕(Texture Wrapping)**： 定义了一种当纹理顶点超出范围(0, 1)时指定OpenGL如何采样纹理的模式。
-- **纹理过滤(Texture Filtering)**： 定义了一种当有多种纹素选择时指定OpenGL如何采样纹理的模式。这通常在纹理被放大情况下发生。
-- **多级渐远纹理(Mipmaps)**： 被存储的材质的一些缩小版本，根据距观察者的距离会使用材质的合适大小。
-- **stb_image.h**： 图像加载库。
-- **纹理单元(Texture Units)**： 通过绑定纹理到不同纹理单元从而允许多个纹理在同一对象上渲染。
-- **向量(Vector)**： 一个定义了在空间中方向和/或位置的数学实体。
-- **矩阵(Matrix)**： 一个矩形阵列的数学表达式。
-- **GLM**： 一个为OpenGL打造的数学库。
-- **局部空间(Local Space)**： 一个物体的初始空间。所有的坐标都是相对于物体的原点的。
-- **世界空间(World Space)**： 所有的坐标都相对于全局原点。
-- **观察空间(View Space)**： 所有的坐标都是从摄像机的视角观察的。
-- **裁剪空间(Clip Space)**： 所有的坐标都是从摄像机视角观察的，但是该空间应用了投影。这个空间应该是一个顶点坐标最终的空间，作为顶点着色器的输出。OpenGL负责处理剩下的事情（裁剪/透视除法）。
-- **屏幕空间(Screen Space)**： 所有的坐标都由屏幕视角来观察。坐标的范围是从0到屏幕的宽/高。
-- **LookAt矩阵**： 一种特殊类型的观察矩阵，它创建了一个坐标系，其中所有坐标都根据从一个位置正在观察目标的用户旋转或者平移。
-- **欧拉角(Euler Angles)**： 被定义为偏航角(Yaw)，俯仰角(Pitch)，和滚转角(Roll)从而允许我们通过这三个值构造任何3D方向。
+- **OpenGL**: 一个定义了函数布局和输出的图形API的正式规范。
+- **GLEW**: 一个拓展加载库，用来为我们加载并设定所有OpenGL函数指针从而让我们能够使用所有（现代）OpenGL函数。
+- **视口(Viewport)**: 我们需要渲染的窗口。
+- **图形管线(Graphics Pipeline)**: 一个顶点在呈现为像素之前通过的过程。
+- **着色器(Shader)**: 一个运行在显卡上的小型程序。很多阶段的图形管道都可以使用自定义的着色器来代替原来的功能。
+- **标准化设备坐标(Normalized Device Coordinates)**: 顶点在通过在剪裁坐标系中剪裁与透视划分后最终呈现在的坐标系。所有位置在NDC下-1.0到1.0的顶点将不会被丢弃并且可见。
+- **顶点缓冲对象(Vertex Buffer Object)**: 一个调用显存并存储所有顶点数据供显卡使用的缓冲对象。
+- **顶点数组对象(Vertex Array Object)**: 存储缓冲区和顶点属性状态。
+- **索引缓冲对象(Element Buffer Object)**: 一个存储索引供索引化绘制使用的缓冲对象。
+- **Uniform**: 一个特殊类型的GLSL变量。它是全局的(在一个着色器程序中每一个着色器都能够访问uniform变量)并且只能被设定一次。
+- **纹理(Texture)**: 一种缠绕物体的特殊类型图片，给物体精细的视觉效果。
+- **纹理缠绕(Texture Wrapping)**: 定义了一种当纹理顶点超出范围(0, 1)时指定OpenGL如何采样纹理的模式。
+- **纹理过滤(Texture Filtering)**: 定义了一种当有多种纹素选择时指定OpenGL如何采样纹理的模式。这通常在纹理被放大情况下发生。
+- **多级渐远纹理(Mipmaps)**: 被存储的材质一些的缩小版本，根据距观察者的距离会使用材质的合适大小。
+- **SOIL**: 图像加载库。
+- **纹理单元(Texture Units)**: 通过绑定纹理到不同纹理单元从而允许多个纹理在同一对象上渲染。
+- **向量(Vector)**: 一个定义了在空间中方向和/或位置数学实体。
+- **矩阵(Matrix)**: 一个矩形阵列的数学表达式。
+- **GLM**: 一个为OpenGL打造的数学库。
+- **局部空间(Local Space)**: 一个对象的初始空间。所有的坐标都是相对于对象的原点的。
+- **世界空间(World Space)**: 所有的坐标都相对于全局原点。
+- **观察空间(View Space)**: 所有的坐标都是从摄像机的视角观察的。
+- **裁剪空间(Clip Space)**: 所有的坐标都是从摄像机视角观察的，但是该空间应用了投影。这个空间应该是一个顶点坐标最终的空间，作为顶点着色器的输出。OpenGL负责处理剩下的事情（裁剪/透视划分）。
+- **屏幕空间(Screen Space)**: 所有的坐标都由屏幕视角来观察。坐标的范围是从0到屏幕的宽/高。
+- **LookAt矩阵**: 一种特殊类型的观察矩阵，它创建了一个坐标系，其中所有坐标都根据从一个位置正在观察目标的用户旋转或者平移。
+- **欧拉角(Euler Angles)**: 被定义为偏航角(yaw)，俯仰角(pitch)，和滚动角(roll)从而允许我们通过这三个值构造任何3D方向。

docs/02 Lighting/01 Colors.md

@@ -3,28 +3,25 @@
 原文     | [Colors](http://learnopengl.com/#!Lighting/Colors)
       ---|---
 作者     | JoeyDeVries
-翻译     | [Geequlim](http://geequlim.com/), Krasjet
-校对     | [AoZhang](https://github.com/SuperAoao)
+翻译     | [Geequlim](http://geequlim.com/)
+校对     | [Geequlim](http://geequlim.com/)
 
-在前面的教程中我们已经简要提到过该如何在OpenGL中使用颜色(Color)，但是我们至今所接触到的都是很浅层的知识。本节我们将会更深入地讨论什么是颜色，并且还会为接下来的光照(Lighting)教程创建一个场景。
+在前面的教程中我们已经简要提到过该如何在OpenGL中使用颜色(Color)，但是我们至今所接触到的都是很浅层的知识。本节我们将会更广泛地讨论颜色，并且还会为接下来的光照(Lighting)教程创建一个场景。
 
-现实世界中有无数种颜色，每一个物体都有它们自己的颜色。我们需要使用（有限的）数值来模拟真实世界中（无限）的颜色，所以并不是所有现实世界中的颜色都可以用数值来表示的。然而我们仍能通过数值来表现出非常多的颜色，甚至你可能都不会注意到与现实的颜色有任何的差异。颜色可以数字化的由红色(Red)、绿色(Green)和蓝色(Blue)三个分量组成，它们通常被缩写为RGB。仅仅用这三个值就可以组合出任意一种颜色。例如，要获取一个**珊瑚红(Coral)**色的话，我们可以定义这样的一个颜色向量：
+
+现实世界中有无数种颜色，每一个物体都有它们自己的颜色。我们要做的工作是使用(有限的)数字来模拟真实世界中(无限)的颜色，因此并不是所有的现实世界中的颜色都可以用数字来表示。然而我们依然可以用数字来代表许多种颜色，并且你甚至可能根本感觉不到他们与真实颜色之间的差异。颜色可以数字化的由红色(Red)、绿色(Green)和蓝色(Blue)三个分量组成，它们通常被缩写为RGB。这三个不同的分量组合在一起几乎可以表示存在的任何一种颜色。例如,要获取一个**珊瑚红(Coral)**颜色我们可以这样定义一个颜色向量:
 
 ```c++
 glm::vec3 coral(1.0f, 0.5f, 0.31f);
 ```
 
-我们在现实生活中看到某一物体的颜色并不是这个物体真正拥有的颜色，而是它所<def>反射的</def>(Reflected)颜色。换句话说，那些不能被物体所吸收(Absorb)的颜色（被拒绝的颜色）就是我们能够感知到的物体的颜色。例如，太阳光能被看见的白光其实是由许多不同的颜色组合而成的（如下图所示）。如果我们将白光照在一个蓝色的玩具上，这个蓝色的玩具会吸收白光中除了蓝色以外的所有子颜色，不被吸收的蓝色光被反射到我们的眼中，让这个玩具看起来是蓝色的。下图显示的是一个珊瑚红的玩具，它以不同强度反射了多个颜色。
+我们在现实生活中看到某一物体的颜色并不是这个物体的真实颜色，而是它所反射(Reflected)的颜色。换句话说，那些不能被物体吸收(Absorb)的颜色(被反射的颜色)就是我们能够感知到的物体的颜色。例如,太阳光被认为是由许多不同的颜色组合成的白色光(如下图所示)。如果我们将白光照在一个蓝色的玩具上，这个蓝色的玩具会吸收白光中除了蓝色以外的所有颜色，不被吸收的蓝色光被反射到我们的眼中，使我们看到了一个蓝色的玩具。下图显示的是一个珊瑚红的玩具，它以不同强度的方式反射了几种不同的颜色。
 
-![](../img/02/01/light_reflection.png)
+![](http://learnopengl.com/img/lighting/light_reflection.png)
 
-你可以看到，白色的阳光实际上是所有可见颜色的集合，物体吸收了其中的大部分颜色。它仅反射了代表物体颜色的部分，被反射颜色的组合就是我们所感知到的颜色（此例中为珊瑚红）。
+正如你所见，白色的阳光是一种所有可见颜色的集合，上面的物体吸收了其中的大部分颜色，它仅反射了那些代表这个物体颜色的部分，这些被反射颜色的组合就是我们感知到的颜色(此例中为珊瑚红)。
 
-!!! important
-
-    从技术上来说，情况会更复杂一些，但我们将在PBR章节中进一步探讨。
-
-这些颜色反射的定律被直接地运用在图形领域。当我们在OpenGL中创建一个光源时，我们希望给光源一个颜色。在上一段中我们有一个白色的太阳，所以我们也将光源设置为白色。当我们把光源的颜色与物体的颜色值相乘，所得到的就是这个物体所反射的颜色（也就是我们所感知到的颜色）。让我们再次审视我们的玩具（这一次它还是珊瑚红），看看如何在图形学中计算出它的反射颜色。我们将这两个颜色向量作分量相乘，结果就是最终的颜色向量了：
+这些颜色反射的规律被直接地运用在图形领域。我们在OpenGL中创建一个光源时都会为它定义一个颜色。在前面的段落中所提到光源的颜色都是白色的，那我们就继续来创建一个白色的光源吧。当我们把光源的颜色与物体的颜色相乘，所得到的就是这个物体所反射该光源的颜色(也就是我们感知到的颜色)。让我们再次审视我们的玩具(这一次它还是珊瑚红)并看看如何计算出他的反射颜色。我们通过检索结果颜色的每一个分量来看一下光源色和物体颜色的反射运算：
 
 ```c++
 glm::vec3 lightColor(1.0f, 1.0f, 1.0f);
@@ -32,7 +29,7 @@ glm::vec3 toyColor(1.0f, 0.5f, 0.31f);
 glm::vec3 result = lightColor * toyColor; // = (1.0f, 0.5f, 0.31f);
 ```
 
-我们可以看到玩具的颜色**吸收**了白色光源中很大一部分的颜色，但它根据自身的颜色值对红、绿、蓝三个分量都做出了一定的反射。这也表现了现实中颜色的工作原理。由此，我们可以定义物体的颜色为**物体从一个光源反射各个颜色分量的大小**。现在，如果我们使用绿色的光源又会发生什么呢？
+我们可以看到玩具在进行反射时**吸收**了白色光源颜色中的大部分颜色，但它对红、绿、蓝三个分量都有一定的反射，反射量是由物体本身的颜色所决定的。这也代表着现实中的光线原理。由此，我们可以定义物体的颜色为**这个物体从一个光源反射各个颜色分量的多少**。现在，如果我们使用一束绿色的光又会发生什么呢？
 
 ```c++
 glm::vec3 lightColor(0.0f, 1.0f, 0.0f);
@@ -40,7 +37,7 @@ glm::vec3 toyColor(1.0f, 0.5f, 0.31f);
 glm::vec3 result = lightColor * toyColor; // = (0.0f, 0.5f, 0.0f);
 ```
 
-可以看到，并没有红色和蓝色的光让我们的玩具来吸收或反射。这个玩具吸收了光线中一半的绿色值，但仍然也反射了一半的绿色值。玩具现在看上去是深绿色(Dark-greenish)的。我们可以看到，如果我们用绿色光源来照射玩具，那么只有绿色分量能被反射和感知到，红色和蓝色都不能被我们所感知到。这样做的结果是，一个珊瑚红的玩具突然变成了深绿色物体。现在我们来看另一个例子，使用深橄榄绿色(Dark olive-green)的光源：
+可以看到，我们的玩具没有红色和蓝色的光让它来吸收或反射，这个玩具也吸收了光线中一半的绿色，当然它仍然反射了光的一半绿色。它现在看上去是深绿色(Dark-greenish)的。我们可以看到，如果我们用一束绿色的光线照来照射玩具，那么只有绿色能被反射和感知到，没有红色和蓝色能被反射和感知。这样做的结果是，一个珊瑚红的玩具突然变成了深绿色物体。现在我们来看另一个例子，使用深橄榄绿色(Dark olive-green)的光线：
 
 ```c++
 glm::vec3 lightColor(0.33f, 0.42f, 0.18f);
@@ -48,23 +45,23 @@ glm::vec3 toyColor(1.0f, 0.5f, 0.31f);
 glm::vec3 result = lightColor * toyColor; // = (0.33f, 0.21f, 0.06f);
 ```
 
-可以看到，我们可以使用不同的光源颜色来让物体显现出意想不到的颜色。有创意地利用颜色其实并不难。
+如你所见，我们可以通过物体对不同颜色光的反射来的得到意想不到的不到的颜色，从此创作颜色已经变得非常简单。
 
-这些颜色的理论已经足够了，下面我们来构造一个实验用的场景吧。
+目前有了这些颜色相关的理论已经足够了，接下来我们将创建一个场景用来做更多的实验。
 
 # 创建一个光照场景
 
-在接下来的教程中，我们将会广泛地使用颜色来模拟现实世界中的光照效果，创造出一些有趣的视觉效果。由于我们现在将会使用光源了，我们希望将它们显示为可见的物体，并在场景中至少加入一个物体来测试模拟光照的效果。
+在接下来的教程中，我们将通过模拟真实世界中广泛存在的光照和颜色现象来创建有趣的视觉效果。现在我们将在场景中创建一个看得到的物体来代表光源，并且在场景中至少添加一个物体来模拟光照。
 
-首先我们需要一个物体来作为被投光(Cast the light)的对象，我们将使用前面教程中的那个著名的立方体箱子。我们还需要一个物体来代表光源在3D场景中的位置。简单起见，我们依然使用一个立方体来代表光源（我们已拥有立方体的[顶点数据](https://learnopengl.com/code_viewer.php?code=getting-started/cube_vertices)是吧？）。
+首先我们需要一个物体来投光(Cast the light)，我们将无耻地使用前面教程中的立方体箱子。我们还需要一个物体来代表光源，它代表光源在这个3D空间中的确切位置。简单起见，我们依然使用一个立方体来代表光源(我们已拥有立方体的[顶点数据](http://www.learnopengl.com/code_viewer.php?code=getting-started/cube_vertices)是吧？)。
 
-填一个顶点缓冲对象(VBO)，设定一下顶点属性指针和其它一些乱七八糟的东西现在对你来说应该很容易了，所以我们就不再赘述那些步骤了。如果你仍然觉得这很困难，我建议你复习[之前的教程](../01 Getting started/04 Hello Triangle.md)，并且在继续学习之前先把练习过一遍。
+当然，填一个顶点缓冲对象(VBO)，设定一下顶点属性指针和其他一些乱七八糟的东西现在对你来说应该很容易了，所以我们就不再赘述那些步骤了。如果你仍然觉得这很困难，我建议你复习[之前的教程](../01 Getting started/04 Hello Triangle.md)，并且在继续学习之前先把练习过一遍。
 
-我们首先需要一个顶点着色器来绘制箱子。与之前的顶点着色器相比，容器的顶点位置是保持不变的（虽然这一次我们不需要纹理坐标了），因此顶点着色器中没有新的代码。我们将会使用之前教程顶点着色器的精简版：
+所以，我们首先需要一个顶点着色器来绘制箱子。与上一个教程的顶点着色器相比，容器的顶点位置保持不变(虽然这一次我们不需要纹理坐标)，因此顶点着色器中没有新的代码。我们将会使用上一篇教程顶点着色器的精简版：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;
+layout (location = 0) in vec3 position;
 
 uniform mat4 model;
 uniform mat4 view;
@@ -72,66 +69,68 @@ uniform mat4 projection;
 
 void main()
 {
-    gl_Position = projection * view * model * vec4(aPos, 1.0);
+    gl_Position = projection * view * model * vec4(position, 1.0f);
 }
 ```
 
-记得更新你的顶点数据和属性指针使其与新的顶点着色器保持一致（当然你可以继续留着纹理数据和属性指针。在这一节中我们将不会用到它们，但有一个全新的开始也不是什么坏主意）。
+请确认更新你的顶点数据和属性对应的指针与新的顶点着色器一致(当然你可以继续保留纹理数据并保持属性对应的指针有效。在这一节中我们不使用纹理，但如果你想要一个全新的开始那也不是什么坏主意)。
 
-因为我们还要创建一个表示灯（光源）的立方体，所以我们还要为这个灯创建一个专门的VAO。当然我们也可以让这个灯和其它物体使用同一个VAO，简单地对它的<var>model</var>（模型）矩阵做一些变换就好了，然而接下来的教程中我们会频繁地对顶点数据和属性指针做出修改，我们并不想让这些修改影响到灯（我们只关心灯的顶点位置），因此我们有必要为灯创建一个新的VAO。
+因为我们还要创建一个表示灯(光源)的立方体，所以我们还要为这个灯创建一个特殊的VAO。当然我们也可以让这个灯和其他物体使用同一个VAO然后对他的`model`(模型)矩阵做一些变换，然而接下来的教程中我们会频繁地对顶点数据做一些改变并且需要改变属性对应指针设置，我们并不想因此影响到灯(我们只在乎灯的位置)，因此我们有必要为灯创建一个新的VAO。
 
 ```c++
-unsigned int lightVAO;
+GLuint lightVAO;
 glGenVertexArrays(1, &lightVAO);
 glBindVertexArray(lightVAO);
-// 只需要绑定VBO不用再次设置VBO的数据，因为箱子的VBO数据中已经包含了正确的立方体顶点数据
+// 只需要绑定VBO不用再次设置VBO的数据，因为容器(物体)的VBO数据中已经包含了正确的立方体顶点数据
 glBindBuffer(GL_ARRAY_BUFFER, VBO);
-// 设置灯立方体的顶点属性（对我们的灯来说仅仅只有位置数据）
-glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), (void*)0);
+// 设置灯立方体的顶点属性指针(仅设置灯的顶点数据)
+glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(GLfloat), (GLvoid*)0);
 glEnableVertexAttribArray(0);
+glBindVertexArray(0);
 ```
 
-这段代码对你来说应该非常直观。现在我们已经创建了表示灯和被照物体箱子，我们只需要再定义一个片段着色器就行了：
+这段代码对你来说应该非常直观。既然我们已经创建了表示灯和被照物体的立方体，我们只需要再定义一个东西就行了了，那就是片段着色器
 
 ```c++
 #version 330 core
-out vec4 FragColor;
-  
+out vec4 color;
+
 uniform vec3 objectColor;
 uniform vec3 lightColor;
 
 void main()
 {
-    FragColor = vec4(lightColor * objectColor, 1.0);
+    color = vec4(lightColor * objectColor, 1.0f);
 }
 ```
 
-这个片段着色器从uniform变量中接受物体的颜色和光源的颜色。正如本节一开始所讨论的那样，我们将光源的颜色和物体（反射的）颜色相乘。这个着色器理解起来应该很容易。我们把物体的颜色设置为之前提到的珊瑚红色，并把光源设置为白色。
+这个片段着色器接受两个分别表示物体颜色和光源颜色的uniform变量。正如本篇教程一开始所讨论的一样，我们将光源的颜色与物体(能反射)的颜色相乘。这个着色器应该很容易理解。接下来让我们把物体的颜色设置为上一节中所提到的珊瑚红并把光源设置为白色：
 
 ```c++
-// 在此之前不要忘记首先 use 对应的着色器程序（来设定uniform）
-lightingShader.use();
-lightingShader.setVec3("objectColor", 1.0f, 0.5f, 0.31f);
-lightingShader.setVec3("lightColor",  1.0f, 1.0f, 1.0f);
+// 在此之前不要忘记首先'使用'对应的着色器程序(来设定uniform)
+GLint objectColorLoc = glGetUniformLocation(lightingShader.Program, "objectColor");
+GLint lightColorLoc  = glGetUniformLocation(lightingShader.Program, "lightColor");
+glUniform3f(objectColorLoc, 1.0f, 0.5f, 0.31f);// 我们所熟悉的珊瑚红
+glUniform3f(lightColorLoc,  1.0f, 1.0f, 1.0f); // 依旧把光源设置为白色
 ```
 
-要注意的是，当我们修改顶点或者片段着色器后，灯的位置或颜色也会随之改变，这并不是我们想要的效果。我们不希望灯的颜色在接下来的教程中因光照计算的结果而受到影响，而是希望它能够与其它的计算分离。我们希望灯一直保持明亮，不受其它颜色变化的影响（这样它才更像是一个真实的光源）。
+要注意的是，当我们修改顶点或者片段着色器后，灯的位置或颜色也会随之改变，这并不是我们想要的效果。我们不希望灯对象的颜色在接下来的教程中因光照计算的结果而受到影响，而希望它能够独立。希望表示灯不受其他光照的影响而一直保持明亮(这样它才更像是一个真实的光源)。
 
-为了实现这个目标，我们需要为灯的绘制创建另外的一套着色器，从而能保证它能够在其它光照着色器发生改变的时候不受影响。顶点着色器与我们当前的顶点着色器是一样的，所以你可以直接把现在的顶点着色器用在灯上。灯的片段着色器给灯定义了一个不变的常量白色，保证了灯的颜色一直是亮的：
+为了实现这个目的，我们需要为灯创建另外的一套着色器程序，从而能保证它能够在其他光照着色器变化的时候保持不变。顶点着色器和我们当前的顶点着色器是一样的，所以你可以直接把灯的顶点着色器复制过来。片段着色器保证了灯的颜色一直是亮的，我们通过给灯定义一个常量的白色来实现：
 
 ```c++
 #version 330 core
-out vec4 FragColor;
+out vec4 color;
 
 void main()
 {
-    FragColor = vec4(1.0); // 将向量的四个分量全部设置为1.0
+    color = vec4(1.0f); //设置四维向量的所有元素为 1.0f
 }
 ```
 
-当我们想要绘制我们的物体的时候，我们需要使用刚刚定义的光照着色器来绘制箱子（或者可能是其它的物体）。当我们想要绘制灯的时候，我们会使用灯的着色器。在之后的教程里我们会逐步更新这个光照着色器，从而能够慢慢地实现更真实的效果。
+当我们想要绘制我们的物体的时候，我们需要使用刚刚定义的光照着色器绘制箱子(或者可能是其它的一些物体)，让我们想要绘制灯的时候，我们会使用灯的着色器。在之后的教程里我们会逐步升级这个光照着色器从而能够缓慢的实现更真实的效果。
 
-使用这个灯立方体的主要目的是为了让我们知道光源在场景中的具体位置。我们通常在场景中定义一个光源的位置，但这只是一个位置，它并没有视觉意义。为了显示真正的灯，我们将表示光源的立方体绘制在与光源相同的位置。我们将使用我们为它新建的片段着色器来绘制它，让它一直处于白色的状态，不受场景中的光照影响。
+使用这个灯立方体的主要目的是为了让我们知道光源在场景中的具体位置。我们通常在场景中定义一个光源的位置，但这只是一个位置，它并没有视觉意义。为了显示真正的灯，我们将表示光源的灯立方体绘制在与光源同样的位置。我们将使用我们为它新建的片段着色器让它保持它一直处于白色状态，不受场景中的光照影响。
 
 我们声明一个全局`vec3`变量来表示光源在场景的世界空间坐标中的位置：
 
@@ -139,7 +138,7 @@ void main()
 glm::vec3 lightPos(1.2f, 1.0f, 2.0f);
 ```
 
-然后我们把灯位移到这里，然后将它缩小一点，让它不那么明显：
+然后我们把灯平移到这儿，当然我们需要对它进行缩放，让它不那么明显：
 
 ```c++
 model = glm::mat4();
@@ -150,20 +149,21 @@ model = glm::scale(model, glm::vec3(0.2f));
 绘制灯立方体的代码应该与下面的类似：
 
 ```c++
-lampShader.use();
+lampShader.Use();
 // 设置模型、视图和投影矩阵uniform
 ...
 // 绘制灯立方体对象
 glBindVertexArray(lightVAO);
 glDrawArrays(GL_TRIANGLES, 0, 36);
+glBindVertexArray(0);
 ```
 
 请把上述的所有代码片段放在你程序中合适的位置，这样我们就能有一个干净的光照实验场地了。如果一切顺利，运行效果将会如下图所示：
 
-![](../img/02/01/colors_scene.png)
+![](http://learnopengl.com/img/lighting/colors_scene.png)
 
-没什么好看的是吗？但我保证在接下来的教程中它会变得更加有趣。
+没什么好看的是吗？但我保证在接下来的教程中它会给你有趣的视觉效果。
 
-如果你觉得将上面的代码片段整合到一起非常困难，可以来[这里](https://learnopengl.com/code_viewer_gh.php?code=src/2.lighting/1.colors/colors.cpp)看一下源代码，并仔细研究我的代码和注释。
+如果你在把上述代码片段放到一起编译遇到困难，可以去认真地看看我的[源代码](http://learnopengl.com/code_viewer.php?code=lighting/colors_scene)。你好最自己实现一遍这些操作。
 
-我们现在已经对颜色有一定的了解了，并且已经创建了一个简单的场景供我们之后绘制动感的光照，我们可以进入[下一节](02 Basic Lighting.md)进行学习，真正的魔法即将开始！
+现在我们有了一些关于颜色的知识，并且创建了一个基本的场景能够绘制一些漂亮的光线。你现在可以阅读[下一节](02 Basic Lighting.md)，真正的魔法即将开始！

docs/02 Lighting/02 Basic Lighting.md

@@ -1,104 +1,102 @@
-# 基础光照
+# 光照基础
 
 原文     | [Basic Lighting](http://learnopengl.com/#!Lighting/Basic-Lighting)
       ---|---
 作者     | JoeyDeVries
-翻译     | [Django](http://bullteacher.com/), Krasjet, Geequlim, [BLumia](https://github.com/blumia/)
-校对     | [AoZhang](https://github.com/SuperAoao)
+翻译     | [Django](http://bullteacher.com/)
+校对     | Geequlim, [BLumia](https://github.com/blumia/)
 
-现实世界的光照是极其复杂的，而且会受到诸多因素的影响，这是我们有限的计算能力所无法模拟的。因此OpenGL的光照使用的是简化的模型，对现实的情况进行近似，这样处理起来会更容易一些，而且看起来也差不多一样。这些光照模型都是基于我们对光的物理特性的理解。其中一个模型被称为<def>风氏光照模型</def>(Phong Lighting Model)。风氏光照模型的主要结构由3个分量组成：环境(Ambient)、漫反射(Diffuse)和镜面(Specular)光照。下面这张图展示了这些光照分量看起来的样子：
+现实世界的光照是极其复杂的，而且会受到诸多因素的影响，这是以目前我们所拥有的处理能力无法模拟的。因此OpenGL的光照仅仅使用了简化的模型并基于对现实的估计来进行模拟，这样处理起来会更容易一些，而且看起来也差不多一样。这些光照模型都是基于我们对光的物理特性的理解。其中一个模型被称为冯氏光照模型(Phong Lighting Model)。冯氏光照模型的主要结构由3个元素组成：环境(Ambient)、漫反射(Diffuse)和镜面(Specular)光照。这些光照元素看起来像下面这样：
 
-![](../img/02/02/basic_lighting_phong.png)
+![](http://learnopengl.com/img/lighting/basic_lighting_phong.png)
 
-- <def>环境光照</def>(Ambient Lighting)：即使在黑暗的情况下，世界上通常也仍然有一些光亮（月亮、远处的光），所以物体几乎永远不会是完全黑暗的。为了模拟这个，我们会使用一个环境光照常量，它永远会给物体一些颜色。
-- <def>漫反射光照</def>(Diffuse Lighting)：模拟光源对物体的方向性影响(Directional Impact)。它是风氏光照模型中视觉上最显著的分量。物体的某一部分越是正对着光源，它就会越亮。
-- <def>镜面光照</def>(Specular Lighting)：模拟有光泽物体上面出现的亮点。镜面光照的颜色相比于物体的颜色会更倾向于光的颜色。
+- 环境光照(Ambient Lighting)：即使在黑暗的情况下，世界上也仍然有一些光亮(月亮、一个来自远处的光)，所以物体永远不会是完全黑暗的。我们使用环境光照来模拟这种情况，也就是无论如何永远都给物体一些颜色。
+- 漫反射光照(Diffuse Lighting)：模拟一个发光物对物体的方向性影响(Directional Impact)。它是冯氏光照模型最显著的组成部分。面向光源的一面比其他面会更亮。
+- 镜面光照(Specular Lighting)：模拟有光泽物体上面出现的亮点。镜面光照的颜色，相比于物体的颜色更倾向于光的颜色。
 
-为了创建有趣的视觉场景，我们希望模拟至少这三种光照分量。我们将以最简单的一个开始：**环境光照**。
+为了创建有趣的视觉场景，我们希望模拟至少这三种光照元素。我们将以最简单的一个开始：**环境光照**。
 
 # 环境光照
 
-光通常都不是来自于同一个光源，而是来自于我们周围分散的很多光源，即使它们可能并不是那么显而易见。光的一个属性是，它可以向很多方向发散并反弹，从而能够到达不是非常直接临近的点。所以，光能够在其它的表面上**反射**，对一个物体产生间接的影响。考虑到这种情况的算法叫做<def>全局照明</def>(Global Illumination)算法，但是这种算法既开销高昂又极其复杂。
+光通常都不是来自于同一光源，而是来自散落于我们周围的很多光源，即使它们可能并不是那么显而易见。光的一个属性是，它可以向很多方向发散和反弹，所以光最后到达的地点可能并不是它所临近的直射方向；光能够像这样**反射(Reflect)**到其他表面，一个物体的光照可能受到来自一个非直射的光源影响。考虑到这种情况的算法叫做**全局照明(Global Illumination)**算法，但是这种算法既开销高昂又极其复杂。
 
-由于我们现在对那种又复杂又开销高昂的算法不是很感兴趣，所以我们将会先使用一个简化的全局照明模型，即<def>环境光照</def>。正如你在上一节所学到的，我们使用一个很小的常量（光照）颜色，添加到物体片段的最终颜色中，这样子的话即便场景中没有直接的光源也能看起来存在有一些发散的光。
+因为我们不是复杂和昂贵算法的死忠粉丝，所以我们将会使用一种简化的全局照明模型，叫做环境光照(Ambient Lighting)。如你在前面章节所见，我们使用一个(数值)很小的常量(光)颜色添加进物体**片段**(Fragment，指当前讨论的光线在物体上的照射点)的最终颜色里，这看起来就像即使没有直射光源也始终存在着一些发散的光。
 
-把环境光照添加到场景里非常简单。我们用光的颜色乘以一个很小的常量环境因子，再乘以物体的颜色，然后将最终结果作为片段的颜色：
+把环境光照添加到场景里非常简单。我们用光的颜色乘以一个(数值)很小常量环境因子，再乘以物体的颜色，然后使用它作为片段的颜色：
 
 ```c++
 void main()
 {
-    float ambientStrength = 0.1;
+    float ambientStrength = 0.1f;
     vec3 ambient = ambientStrength * lightColor;
-
     vec3 result = ambient * objectColor;
-    FragColor = vec4(result, 1.0);
+    color = vec4(result, 1.0f);
 }
 ```
 
-如果你现在运行你的程序，你会注意到风氏光照的第一个阶段已经应用到你的物体上了。这个物体非常暗，但由于应用了环境光照（注意光源立方体没受影响是因为我们对它使用了另一个着色器），也不是完全黑的。它看起来应该像这样：
+如果你现在运行你的程序，你会注意到冯氏光照的第一个阶段已经应用到你的物体上了。这个物体非常暗，但不是完全的黑暗，因为我们应用了环境光照(注意发光立方体没被环境光照影响是因为我们对它使用了另一个着色器)。它看起来应该像这样：
 
-![](../img/02/02/ambient_lighting.png)
+![](http://learnopengl.com/img/lighting/ambient_lighting.png)
 
 # 漫反射光照
 
-环境光照本身不能提供最有趣的结果，但是漫反射光照就能开始对物体产生显著的视觉影响了。漫反射光照使物体上与光线方向越接近的片段能从光源处获得更多的亮度。为了能够更好的理解漫反射光照，请看下图：
+环境光本身不提供最明显的光照效果，但是漫反射光照(Diffuse Lighting)会对物体产生显著的视觉影响。漫反射光使物体上与光线排布越近的片段越能从光源处获得更多的亮度。为了更好的理解漫反射光照，请看下图：
 
-![](../img/02/02/diffuse_light.png)
+![](http://learnopengl.com/img/lighting/diffuse_light.png)
 
-图左上方有一个光源，它所发出的光线落在物体的一个片段上。我们需要测量这个光线是以什么角度接触到这个片段的。如果光线垂直于物体表面，这束光对物体的影响会最大化（译注：更亮）。为了测量光线和片段的角度，我们使用一个叫做<def>法向量</def>(Normal Vector)的东西，它是垂直于片段表面的一个向量（这里以黄色箭头表示），我们在后面再讲这个东西。这两个向量之间的角度很容易就能够通过点乘计算出来。
+图左上方有一个光源，它所发出的光线落在物体的一个片段上。我们需要测量这个光线与它所接触片段之间的角度。如果光线垂直于物体表面，这束光对物体的影响会最大化(译注：更亮)。为了测量光线和片段的角度，我们使用一个叫做法向量(Normal Vector)的东西，它是垂直于片段表面的一种向量(这里以黄色箭头表示)，我们在后面再讲这个东西。两个向量之间的角度就能够根据点乘计算出来。
 
-你可能记得在[变换](../01 Getting started/07 Transformations.md)那一节教程里，我们知道两个单位向量的夹角越小，它们点乘的结果越倾向于1。当两个向量的夹角为90度的时候，点乘会变为0。这同样适用于\(\theta\)，\(\theta\)越大，光对片段颜色的影响就应该越小。
+你可能记得在[变换](../01 Getting started/07 Transformations.md)那一节教程里，我们知道两个单位向量的角度越小，它们点乘的结果越倾向于1。当两个向量的角度是90度的时候，点乘会变为0。这同样适用于θ，θ越大，光对片段颜色的影响越小。
 
 !!! Important
 
-    注意，为了（只）得到两个向量夹角的余弦值，我们使用的是单位向量（长度为1的向量），所以我们需要确保所有的向量都是标准化的，否则点乘返回的就不仅仅是余弦值了（见[变换](../01 Getting started/07 Transformations.md)）。
+    注意，我们使用的是单位向量(Unit Vector，长度是1的向量)取得两个向量夹角的余弦值，所以我们需要确保所有的向量都被标准化，否则点乘返回的值就不仅仅是余弦值了(如果你不明白，可以复习[变换](../01 Getting started/07 Transformations.md)那一节的点乘部分)。
 
-点乘返回一个标量，我们可以用它计算光线对片段颜色的影响。不同片段朝向光源的方向的不同，这些片段被照亮的情况也不同。
+点乘返回一个标量，我们可以用它计算光线对片段颜色的影响，基于不同片段所朝向光源的方向的不同，这些片段被照亮的情况也不同。
 
-所以，计算漫反射光照需要什么？
+所以，我们需要些什么来计算漫反射光照？
 
 - 法向量：一个垂直于顶点表面的向量。
-- 定向的光线：作为光源的位置与片段的位置之间向量差的方向向量。为了计算这个光线，我们需要光的位置向量和片段的位置向量。
+- 定向的光线：作为光的位置和片段的位置之间的向量差的方向向量。为了计算这个光线，我们需要光的位置向量和片段的位置向量。
 
 ## 法向量
 
-法向量是一个垂直于顶点表面的（单位）向量。由于顶点本身并没有表面（它只是空间中一个独立的点），我们利用它周围的顶点来计算出这个顶点的表面。我们能够使用一个小技巧，使用叉乘对立方体所有的顶点计算法向量，但是由于3D立方体不是一个复杂的形状，所以我们可以简单地把法线数据手工添加到顶点数据中。更新后的顶点数据数组可以在[这里](https://learnopengl.com/code_viewer.php?code=lighting/basic_lighting_vertex_data)找到。试着去想象一下，这些法向量真的是垂直于立方体各个平面的表面的（一个立方体由6个平面组成）。
+法向量(Normal Vector)是垂直于顶点表面的(单位)向量。由于顶点自身并没有表面(它只是空间中一个独立的点)，我们利用顶点周围的顶点计算出这个顶点的表面。我们能够使用叉乘这个技巧为立方体所有的顶点计算出法线，但是由于3D立方体不是一个复杂的形状，所以我们可以简单的把法线数据手工添加到顶点数据中。更新的顶点数据数组可以在[这里](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting_vertex_data)找到。试着去想象一下，这些法向量真的是垂直于立方体的各个面的表面的(一个立方体由6个面组成)。
 
-由于我们向顶点数组添加了额外的数据，所以我们应该更新光照的顶点着色器：
+因为我们向顶点数组添加了额外的数据，所以我们应该更新光照的顶点着色器：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;
-layout (location = 1) in vec3 aNormal;
+layout (location = 0) in vec3 position;
+layout (location = 1) in vec3 normal;
 ...
 ```
 
-现在我们已经向每个顶点添加了一个法向量并更新了顶点着色器，我们还要更新顶点属性指针。注意，灯使用同样的顶点数组作为它的顶点数据，然而灯的着色器并没有使用新添加的法向量。我们不需要更新灯的着色器或者是属性的配置，但是我们必须至少修改一下顶点属性指针来适应新的顶点数组的大小：
+现在我们已经向每个顶点添加了一个法向量，已经更新了顶点着色器，我们还要更新顶点属性指针(Vertex Attibute Pointer)。注意，发光物使用同样的顶点数组作为它的顶点数据，然而发光物的着色器没有使用新添加的法向量。我们不会更新发光物的着色器或者属性配置，但是我们必须至少修改一下顶点属性指针来适应新的顶点数组的大小：
 
 ```c++
-glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(float), (void*)0);
+glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(GLfloat), (GLvoid * )0);
 glEnableVertexAttribArray(0);
 ```
 
-我们只想使用每个顶点的前三个float，并且忽略后三个float，所以我们只需要把**步长**参数改成`float`大小的6倍就行了。
+我们只想使用每个顶点的前三个浮点数，并且我们忽略后三个浮点数，所以我们只需要把**步长**参数改成`GLfloat`尺寸的6倍就行了。
 
 !!! Important
 
-	虽然对灯的着色器使用不能完全利用的顶点数据看起来不是那么高效，但这些顶点数据已经从箱子对象载入后开始就储存在GPU的内存里了，所以我们并不需要储存新数据到GPU内存中。这实际上比给灯专门分配一个新的VBO更高效了。
+    发光物着色器顶点数据的不完全使用看起来有点低效，但是这些顶点数据已经从立方体对象载入到GPU的内存里了，所以GPU内存不是必须再储存新数据。相对于重新给发光物分配VBO，实际上却是更高效了。
 
-所有光照的计算都是在片段着色器里进行，所以我们需要将法向量由顶点着色器传递到片段着色器。我们这么做：
+所有光照的计算需要在片段着色器里进行，所以我们需要把法向量由顶点着色器传递到片段着色器。我们这么做：
 
 ```c++
 out vec3 Normal;
-
 void main()
 {
-    gl_Position = projection * view * model * vec4(aPos, 1.0);
-    Normal = aNormal;
+    gl_Position = projection * view * model * vec4(position, 1.0f);
+    Normal = normal;
 }
 ```
 
-接下来，在片段着色器中定义相应的输入变量：
+剩下要做的事情是，在片段着色器中定义相应的输入值：
 
 ```c++
 in vec3 Normal;
@@ -106,29 +104,30 @@ in vec3 Normal;
 
 ## 计算漫反射光照
 
-我们现在对每个顶点都有了法向量，但是我们仍然需要光源的位置向量和片段的位置向量。由于光源的位置是一个静态变量，我们可以简单地在片段着色器中把它声明为uniform：
+每个顶点现在都有了法向量，但是我们仍然需要光的位置向量和片段的位置向量。由于光的位置是一个静态变量，我们可以简单的在片段着色器中把它声明为uniform：
 
 ```c++
 uniform vec3 lightPos;
 ```
 
-然后在渲染循环中（渲染循环的外面也可以，因为它不会改变）更新uniform。我们使用在前面声明的<def>lightPos</def>向量作为光源位置：
+然后再游戏循环中(外面也可以，因为它不会变)更新uniform。我们使用在前面教程中声明的`lightPos`向量作为光源位置：
 
 ```c++
-lightingShader.setVec3("lightPos", lightPos);
+GLint lightPosLoc = glGetUniformLocation(lightingShader.Program, "lightPos");
+glUniform3f(lightPosLoc, lightPos.x, lightPos.y, lightPos.z);
 ```
 
-最后，我们还需要片段的位置。我们会在世界空间中进行所有的光照计算，因此我们需要一个在世界空间中的顶点位置。我们可以通过把顶点位置属性乘以模型矩阵（不是观察和投影矩阵）来把它变换到世界空间坐标。这个在顶点着色器中很容易完成，所以我们声明一个输出变量，并计算它的世界空间坐标：
+最后，我们还需要片段的位置(Position)。我们会在世界空间中进行所有的光照计算，因此我们需要一个在世界空间中的顶点位置。我们可以通过把顶点位置属性乘以模型矩阵(Model Matrix,只用模型矩阵不需要用观察和投影矩阵)来把它变换到世界空间坐标。这个在顶点着色器中很容易完成，所以让我们就声明一个输出(out)变量，然后计算它的世界空间坐标：
 
 ```c++
-out vec3 FragPos;  
+out vec3 FragPos;
 out vec3 Normal;
-  
+
 void main()
 {
-    gl_Position = projection * view * model * vec4(aPos, 1.0);
-    FragPos = vec3(model * vec4(aPos, 1.0));
-    Normal = aNormal;
+    gl_Position = projection * view * model * vec4(position, 1.0f);
+    FragPos = vec3(model * vec4(position, 1.0f));
+    Normal = normal;
 }
 ```
 
@@ -138,9 +137,9 @@ void main()
 in vec3 FragPos;
 ```
 
-这个in类型变量将被插入三角形的3维世界位置向量值，形成FragPos向量，即每个片段的世界位置。现在，所有需要的变量都设置好了，我们可以在片段着色器中添加光照计算了。
+现在，所有需要的变量都设置好了，我们可以在片段着色器中开始光照的计算了。
 
-我们需要做的第一件事是计算光源和片段位置之间的方向向量。前面提到，光的方向向量是光源位置向量与片段位置向量之间的向量差。你可能记得在[变换](../01 Getting started/07 Transformations.md)教程中，我们能够简单地通过让两个向量相减的方式计算向量差。我们同样希望确保所有相关向量最后都转换为单位向量，所以我们把法线和最终的方向向量都进行标准化：
+我们需要做的第一件事是计算光源和片段位置之间的方向向量。前面提到，光的方向向量是光的位置向量与片段的位置向量之间的向量差。你可能记得，在变换教程中，我们简单的通过两个向量相减的方式计算向量差。我们同样希望确保所有相关向量最后都转换为单位向量，所以我们把法线和方向向量这个结果都进行标准化：
 
 ```c++
 vec3 norm = normalize(Normal);
@@ -149,138 +148,137 @@ vec3 lightDir = normalize(lightPos - FragPos);
 
 !!! Important
 
-	当计算光照时我们通常不关心一个向量的模长或它的位置，我们只关心它们的方向。所以，几乎所有的计算都使用单位向量完成，因为这简化了大部分的计算（比如点乘）。所以当进行光照计算时，确保你总是对相关向量进行标准化，来保证它们是真正地单位向量。忘记对向量进行标准化是一个十分常见的错误。
+	当计算光照时我们通常不关心一个向量的“量”或它的位置，我们只关心它们的方向。所有的计算都使用单位向量完成，因为这会简化了大多数计算(比如点乘)。所以当进行光照计算时，确保你总是对相关向量进行标准化，这样它们才会保证自身为单位向量。忘记对向量进行标准化是一个十分常见的错误。
 
-下一步，我们对<var>norm</var>和<var>lightDir</var>向量进行点乘，计算光源对当前片段实际的漫反射影响。结果值再乘以光的颜色，得到漫反射分量。两个向量之间的角度越大，漫反射分量就会越小：
+下一步，我们对`norm`和`lightDir`向量进行点乘，来计算光对当前片段的实际的散射影响。结果值再乘以光的颜色，得到散射因子。两个向量之间的角度越大，散射因子就会越小：
 
 ```c++
 float diff = max(dot(norm, lightDir), 0.0);
 vec3 diffuse = diff * lightColor;
 ```
 
-如果两个向量之间的角度大于90度，点乘的结果就会变成负数，这样会导致漫反射分量变为负数。为此，我们使用<fun>max</fun>函数返回两个参数之间较大的参数，从而保证漫反射分量不会变成负数。负数颜色的光照是没有定义的，所以最好避免它，除非你是那种古怪的艺术家。
+如果两个向量之间的角度大于90度，点乘的结果就会变成负数，这样会导致散射因子变为负数。为此，我们使用`max`函数返回两个参数之间较大的参数，从而保证散射因子不会变成负数。负数的颜色是没有实际定义的，所以最好避免它，除非你是那种古怪的艺术家。
 
-现在我们有了环境光分量和漫反射分量，我们把它们相加，然后把结果乘以物体的颜色，来获得片段最后的输出颜色。
+既然我们有了一个环境光照颜色和一个散射光颜色，我们把它们相加，然后把结果乘以物体的颜色，来获得片段最后的输出颜色。
 
 ```c++
 vec3 result = (ambient + diffuse) * objectColor;
-FragColor = vec4(result, 1.0);
+color = vec4(result, 1.0f);
 ```
 
 如果你的应用(和着色器)编译成功了，你可能看到类似的输出：
 
-![](../img/02/02/basic_lighting_diffuse.png)
+![](http://learnopengl.com/img/lighting/basic_lighting_diffuse.png)
 
-你可以看到使用了漫反射光照，立方体看起来就真的像个立方体了。尝试在你的脑中想象一下法向量，并在立方体周围移动，注意观察法向量和光的方向向量之间的夹角越大，片段就会越暗。
+你可以看到使用了散射光照，立方体看起来就真的像个立方体了。尝试在你的脑中想象，通过移动正方体，法向量和光的方向向量之间的夹角增大，片段变得更暗。
 
-如果你在哪卡住了，可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/2.lighting/2.1.basic_lighting_diffuse/basic_lighting_diffuse.cpp)对比一下完整的源代码。
+如果你遇到很多困难，可以对比[完整的源代码](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting_diffuse)以及[片段着色器](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting_diffuse&type=fragment)代码。
 
 ## 最后一件事
 
-现在我们已经把法向量从顶点着色器传到了片段着色器。可是，目前片段着色器里的计算都是在世界空间坐标中进行的。所以，我们是不是应该把法向量也转换为世界空间坐标？基本正确，但是这不是简单地把它乘以一个模型矩阵就能搞定的。
+现在我们已经把法向量从顶点着色器传到了片段着色器。可是，目前片段着色器里，我们都是在世界空间坐标中进行计算的，所以，我们不是应该把法向量转换为世界空间坐标吗？基本正确，但是这不是简单地把它乘以一个模型矩阵就能搞定的。
 
-首先，法向量只是一个方向向量，不能表达空间中的特定位置。同时，法向量没有齐次坐标（顶点位置中的w分量）。这意味着，位移不应该影响到法向量。因此，如果我们打算把法向量乘以一个模型矩阵，我们就要从矩阵中移除位移部分，只选用模型矩阵左上角3×3的矩阵（注意，我们也可以把法向量的w分量设置为0，再乘以4×4矩阵；这同样可以移除位移）。对于法向量，我们只希望对它实施缩放和旋转变换。
+首先，法向量只是一个方向向量，不能表达空间中的特定位置。同时，法向量没有齐次坐标(顶点位置中的w分量)。这意味着，平移不应该影响到法向量。因此，如果我们打算把法向量乘以一个模型矩阵，我们就要把模型矩阵左上角的3×3矩阵从模型矩阵中移除(译注：所谓移除就是设置为0)，它是模型矩阵的平移部分(注意，我们也可以把法向量的w分量设置为0，再乘以4×4矩阵；同样可以移除平移)。对于法向量，我们只能对它应用缩放(Scale)和旋转(Rotation)变换。
 
-其次，如果模型矩阵执行了不等比缩放，顶点的改变会导致法向量不再垂直于表面了。因此，我们不能用这样的模型矩阵来变换法向量。下面的图展示了应用了不等比缩放的模型矩阵对法向量的影响：
+其次，如果模型矩阵执行了不等比缩放，法向量就不再垂直于表面了，顶点就会以这种方式被改变了。因此，我们不能用这样的模型矩阵去乘以法向量。下面的图展示了应用了不等比缩放的矩阵对法向量的影响：
 
-![](../img/02/02/basic_lighting_normal_transformation.png)
+![](http://learnopengl.com/img/lighting/basic_lighting_normal_transformation.png)
 
-每当我们应用一个不等比缩放时（注意：等比缩放不会破坏法线，因为法线的方向没被改变，仅仅改变了法线的长度，而这很容易通过标准化来修复），法向量就不会再垂直于对应的表面了，这样光照就会被破坏。
+无论何时当我们提交一个不等比缩放(注意：等比缩放不会破坏法线，因为法线的方向没被改变，而法线的长度很容易通过标准化进行修复)，法向量就不会再垂直于它们的表面了，这样光照会被扭曲。
 
-修复这个行为的诀窍是使用一个为法向量专门定制的模型矩阵。这个矩阵称之为<def>法线矩阵</def>(Normal Matrix)，它使用了一些线性代数的操作来移除对法向量错误缩放的影响。如果你想知道这个矩阵是如何计算出来的，建议去阅读这个[文章](http://www.lighthouse3d.com/tutorials/glsl-tutorial/the-normal-matrix/)。
+修复这个行为的诀窍是使用另一个为法向量专门定制的模型矩阵。这个矩阵称之为正规矩阵(Normal Matrix)，它是进行了一点线性代数操作移除了对法向量的错误缩放效果。如果你想知道这个矩阵是如何计算出来的，我建议看[这个文章](http://www.lighthouse3d.com/tutorials/glsl-tutorial/the-normal-matrix/)。
 
-法线矩阵被定义为「模型矩阵左上角3x3部分的逆矩阵的转置矩阵」。真是拗口，如果你不明白这是什么意思，别担心，我们还没有讨论逆矩阵(Inverse Matrix)和转置矩阵(Transpose Matrix)。注意，大部分的资源都会将法线矩阵定义为应用到模型-观察矩阵(Model-view Matrix)上的操作，但是由于我们只在世界空间中进行操作（不是在观察空间），我们只使用模型矩阵。
+正规矩阵被定义为“模型矩阵左上角的逆矩阵的转置矩阵”。真拗口，如果你不明白这是什么意思，别担心；我们还没有讨论逆矩阵(Inverse Matrix)和转置矩阵(Transpose Matrix)。注意，定义正规矩阵的大多资源就像应用到模型观察矩阵(Model-view Matrix)上的操作一样，但是由于我们只在世界空间工作(而不是在观察空间)，我们只使用模型矩阵。
 
-在顶点着色器中，我们可以使用<fun>inverse</fun>和<fun>transpose</fun>函数自己生成这个法线矩阵，这两个函数对所有类型矩阵都有效。注意我们还要把被处理过的矩阵强制转换为3×3矩阵，来保证它失去了位移属性以及能够乘以`vec3`的法向量。
+在顶点着色器中，我们可以使用`inverse`和`transpose`函数自己生成正规矩阵，`inverse`和`transpose`函数对所有类型矩阵都有效。注意，我们也要把这个被处理过的矩阵强制转换为3×3矩阵，这是为了保证它失去了平移属性，之后它才能乘以法向量。
 
 ```c++
-Normal = mat3(transpose(inverse(model))) * aNormal;
+Normal = mat3(transpose(inverse(model))) * normal;
 ```
 
+在环境光照部分，光照表现没问题，这是因为我们没有对物体本身执行任何缩放操作，因而不是非得使用正规矩阵不可，用模型矩阵乘以法线也没错。可是，如果你进行了不等比缩放，使用正规矩阵去乘以法向量就是必不可少的了。
+
 !!! Attention
 
-    矩阵求逆是一项对于着色器开销很大的运算，因为它必须在场景中的每一个顶点上进行，所以应该尽可能地避免在着色器中进行求逆运算。以学习为目的的话这样做还好，但是对于一个高效的应用来说，你最好先在CPU上计算出法线矩阵，再通过uniform把它传递给着色器（就像模型矩阵一样）。
-
-在漫反射光照部分，光照表现并没有问题，这是因为我们没有对物体进行任何缩放操作，所以我们并不真的需要使用一个法线矩阵，而是仅以模型矩阵乘以法线就可以。但是如果你会进行不等比缩放，使用法线矩阵去乘以法向量就是必须的了。
+    对于着色器来说，逆矩阵也是一种开销比较大的操作，因此，无论何时，在着色器中只要可能就应该尽量避免逆操作，因为它们必须为你场景中的每个顶点进行这样的处理。以学习的目的这样做很好，但是对于一个对于效率有要求的应用来说，在绘制之前，你最好用CPU计算出正规矩阵，然后通过uniform把值传递给着色器(和模型矩阵一样)。
 
 # 镜面光照
 
-如果你还没被这些光照计算搞得精疲力尽，我们就再把镜面高光(Specular Highlight)加进来，这样风氏光照才算完整。
+如果你还没被这些光照计算搞得精疲力尽，我们就再把镜面高光(Specular Highlight)加进来，这样冯氏光照才算完整。
 
-和漫反射光照一样，镜面光照也决定于光的方向向量和物体的法向量，但是它也决定于观察方向，例如玩家是从什么方向看向这个片段的。镜面光照决定于表面的反射特性。如果我们把物体表面设想为一面镜子，那么镜面光照最强的地方就是我们看到表面上反射光的地方。你可以在下图中看到效果：
+和环境光照一样，镜面光照(Specular Lighting)同样依据光的方向向量和物体的法向量，但是这次它也会依据观察方向，例如玩家是从什么方向看着这个片段的。镜面光照根据光的反射特性。如果我们想象物体表面像一面镜子一样，那么，无论我们从哪里去看那个表面所反射的光，镜面光照都会达到最大化。你可以从下面的图片看到效果：
 
-![](../img/02/02/basic_lighting_specular_theory.png)
+![](http://learnopengl.com/img/lighting/basic_lighting_specular_theory.png)
 
-我们通过根据法向量翻折入射光的方向来计算反射向量。然后我们计算反射向量与观察方向的角度差，它们之间夹角越小，镜面光的作用就越大。由此产生的效果就是，我们看向在入射光在表面的反射方向时，会看到一点高光。
+我们通过反射法向量周围光的方向计算反射向量。然后我们计算反射向量和视线方向的角度，如果之间的角度越小，那么镜面光的作用就会越大。它的作用效果就是，当我们去看光被物体所反射的那个方向的时候，我们会看到一个高光。
 
-观察向量是我们计算镜面光照时需要的一个额外变量，我们可以使用观察者的世界空间位置和片段的位置来计算它。之后我们计算出镜面光照强度，用它乘以光源的颜色，并将它与环境光照和漫反射光照部分加和。
+观察向量是镜面光照的一个附加变量，我们可以使用观察者世界空间位置(Viewer’s World Space Position)和片段的位置来计算。之后，我们计算镜面光亮度，用它乘以光的颜色，在用它加上作为之前计算的光照颜色。
 
 !!! Important
 
-    我们选择在世界空间进行光照计算，但是大多数人趋向于更偏向在观察空间进行光照计算。在观察空间计算的优势是，观察者的位置总是在(0, 0, 0)，所以你已经零成本地拿到了观察者的位置。然而，若以学习为目的，我认为在世界空间中计算光照更符合直觉。如果你仍然希望在观察空间计算光照的话，你需要将所有相关的向量也用观察矩阵进行变换（不要忘记也修改法线矩阵）。
+    我们选择在世界空间(World Space)进行光照计算，但是大多数人趋向于在观察空间(View Space)进行光照计算。在观察空间计算的好处是，观察者的位置总是(0, 0, 0)，所以这样你直接就获得了观察者位置。可是，我发现出于学习的目的，在世界空间计算光照更符合直觉。如果你仍然希望在视野空间计算光照的话，那就使用观察矩阵应用到所有相关的需要变换的向量(不要忘记，也要改变正规矩阵)。
 
-要得到观察者的世界空间坐标，我们直接使用摄像机的位置向量即可（它当然就是那个观察者）。那么让我们把另一个uniform添加到片段着色器中，并把摄像机的位置向量传给着色器：
+为了得到观察者的世界空间坐标，我们简单地使用摄像机对象的位置坐标代替(它就是观察者)。所以我们把另一个uniform添加到片段着色器，把相应的摄像机位置坐标传给片段着色器：
 
 ```c++
 uniform vec3 viewPos;
+
+GLint viewPosLoc = glGetUniformLocation(lightingShader.Program, "viewPos");
+glUniform3f(viewPosLoc, camera.Position.x, camera.Position.y, camera.Position.z);
 ```
 
+现在我们已经获得所有需要的变量，可以计算高光亮度了。首先，我们定义一个镜面强度(Specular Intensity)变量`specularStrength`，给镜面高光一个中等亮度颜色，这样就不会产生过度的影响了。
+
 ```c++
-lightingShader.setVec3("viewPos", camera.Position);
+float specularStrength = 0.5f;
 ```
 
-现在我们已经获得所有需要的变量，可以计算高光强度了。首先，我们定义一个镜面强度(Specular Intensity)变量，给镜面高光一个中等亮度颜色，让它不要产生过度的影响。
-
-```c++
-float specularStrength = 0.5;
-```
-
-如果我们把它设置为1.0f，我们会得到一个非常亮的镜面光分量，这对于一个珊瑚色的立方体来说有点太多了。[下一节教程](03 Materials.md)中我们会讨论如何合理设置这些光照强度，以及它们是如何影响物体的。下一步，我们计算视线方向向量，和对应的沿着法线轴的反射向量：
+如果我们把它设置为1.0f，我们会得到一个对于珊瑚色立方体来说过度明亮的镜面亮度因子。下一节教程，我们会讨论所有这些光照亮度的合理设置，以及它们是如何影响物体的。下一步，我们计算视线方向坐标，和沿法线轴的对应的反射坐标：
 
 ```
 vec3 viewDir = normalize(viewPos - FragPos);
 vec3 reflectDir = reflect(-lightDir, norm);
 ```
 
-需要注意的是我们对`lightDir`向量进行了取反。`reflect`函数要求第一个向量是**从**光源指向片段位置的向量，但是`lightDir`当前正好相反，是从片段**指向**光源（由先前我们计算`lightDir`向量时，减法的顺序决定）。为了保证我们得到正确的`reflect`向量，我们通过对`lightDir`向量取反来获得相反的方向。第二个参数要求是一个法向量，所以我们提供的是已标准化的`norm`向量。
+需要注意的是我们使用了`lightDir`向量的相反数。`reflect`函数要求的第一个是从光源指向片段位置的向量，但是`lightDir`当前是从片段指向光源的向量(由先前我们计算`lightDir`向量时，(减数和被减数)减法的顺序决定)。为了保证我们得到正确的`reflect`坐标，我们通过`lightDir`向量的相反数获得它的方向的反向。第二个参数要求是一个法向量，所以我们提供的是已标准化的`norm`向量。
 
-剩下要做的是计算镜面分量。下面的代码完成了这件事：
+剩下要做的是计算镜面亮度分量。下面的代码完成了这件事：
 
 ```c++
 float spec = pow(max(dot(viewDir, reflectDir), 0.0), 32);
 vec3 specular = specularStrength * spec * lightColor;
 ```
 
-我们先计算视线方向与反射方向的点乘（并确保它不是负值），然后取它的32次幂。这个32是高光的<def>反光度</def>(Shininess)。一个物体的反光度越高，反射光的能力越强，散射得越少，高光点就会越小。在下面的图片里，你会看到不同反光度的视觉效果影响：
+我们先计算视线方向与反射方向的点乘(确保它不是负值)，然后得到它的32次幂。这个32是高光的**发光值(Shininess)**。一个物体的发光值越高，反射光的能力越强，散射得越少，高光点越小。在下面的图片里，你会看到不同发光值对视觉(效果)的影响：
 
-![](../img/02/02/basic_lighting_specular_shininess.png)
+![](http://learnopengl.com/img/lighting/basic_lighting_specular_shininess.png)
 
-我们不希望镜面成分过于显眼，所以我们把指数保持为32。剩下的最后一件事情是把它加到环境光分量和漫反射分量里，再用结果乘以物体的颜色：
+我们不希望镜面成分过于显眼，所以我们把指数设置为32。剩下的最后一件事情是把它添加到环境光颜色和散射光颜色里，然后再乘以物体颜色：
 
 ```c++
 vec3 result = (ambient + diffuse + specular) * objectColor;
-FragColor = vec4(result, 1.0);
+color = vec4(result, 1.0f);
 ```
 
-我们现在为风氏光照计算了全部的光照分量。根据你的视角，你可以看到类似下面的画面：
+我们现在为冯氏光照计算了全部的光照元素。根据你的观察点，你可以看到类似下面的画面：
 
-![](../img/02/02/basic_lighting_specular.png)
+![](http://learnopengl.com/img/lighting/basic_lighting_specular.png)
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/2.lighting/2.2.basic_lighting_specular/basic_lighting_specular.cpp)找到完整源码。
+你可以[在这里找到完整源码](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting_specular)，在这里有[顶点](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting&type=fragment)着色器。
 
 !!! Important
 
-    在光照着色器的早期，开发者曾经在顶点着色器中实现风氏光照模型。在顶点着色器中做光照的优势是，相比片段来说，顶点要少得多，因此会更高效，所以（开销大的）光照计算频率会更低。然而，顶点着色器中的最终颜色值是仅仅只是那个顶点的颜色值，片段的颜色值是由插值光照颜色所得来的。结果就是这种光照看起来不会非常真实，除非使用了大量顶点。
+    早期的光照着色器，开发者在顶点着色器中实现冯氏光照。在顶点着色器中做这件事的优势是，相比片段来说，顶点要少得多，因此会更高效，所以(开销大的)光照计算频率会更低。然而，顶点着色器中的颜色值是只是顶点的颜色值，片段的颜色值是它与周围的颜色值的插值。结果就是这种光照看起来不会非常真实，除非使用了大量顶点。
 
-    ![](../img/02/02/basic_lighting_gouruad.png)
+    ![](http://learnopengl.com/img/lighting/basic_lighting_gouruad.png)
 
-    在顶点着色器中实现的风氏光照模型叫做<def>Gouraud着色</def>(Gouraud Shading)，而不是<def>风氏着色</def>(Phong Shading)。记住，由于插值，这种光照看起来有点逊色。风氏着色能产生更平滑的光照效果。
+    在顶点着色器中实现的冯氏光照模型叫做Gouraud着色，而不是冯氏着色。记住由于插值，这种光照连起来有点逊色。冯氏着色能产生更平滑的光照效果。
 
-现在你应该能够看到着色器的强大之处了。只用很少的信息，着色器就能计算出光照如何影响到所有物体的片段颜色。[下一节](03 Materials.md)中，我们会更深入的研究光照模型，看看我们还能做些什么。
+现在你可以看到着色器的强大之处了。只用很少的信息，着色器就能计算出光照，影响到为我们所有物体的片段颜色。[下一节](03 Materials.md)中，我们会更深入的研究光照模型，看看我们还能做些什么。
 
 ## 练习
 
-- 目前，我们的光源是静止的，你可以尝试使用<fun>sin</fun>或<fun>cos</fun>函数让光源在场景中来回移动。观察光照随时间的改变能让你更容易理解风氏光照模型。[参考解答](https://learnopengl.com/code_viewer.php?code=lighting/basic_lighting-exercise1)。
-- 尝试使用不同的环境光、漫反射和镜面强度，观察它们怎么是影响光照效果的。同样，尝试实验一下镜面光照的反光度因子。尝试理解为什么某一个值能够有着特定视觉输出。
-- 在观察空间（而不是世界空间）中计算风氏光照：[参考解答](https://learnopengl.com/code_viewer.php?code=lighting/basic_lighting-exercise2)。
-- 尝试实现一个Gouraud着色（而不是风氏着色）。如果你做对了话，立方体的光照应该会[看起来有些奇怪](../img/02/02/basic_lighting_exercise3.png)，尝试推理为什么它会看起来这么奇怪：[参考解答](https://learnopengl.com/code_viewer.php?code=lighting/basic_lighting-exercise3)。
+- 目前，我们的光源时静止的，你可以尝试使用`sin`和`cos`函数让光源在场景中来回移动，此时再观察光照效果能让你更容易理解冯氏光照模型。[参考解答](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting-exercise1)。
+- 尝试使用不同的环境光、散射镜面强度，观察光照效果。改变镜面光照的`shininess`因子试试。
+- 在观察空间(而不是世界空间)中计算冯氏光照：[参考解答](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting-exercise2)。
+- 尝试实现一个Gouraud光照来模拟冯氏光照，[参考解答](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting-exercise3)。

docs/02 Lighting/03 Materials.md

@@ -3,169 +3,176 @@
 原文     | [Materials](http://learnopengl.com/#!Lighting/Materials)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | [AoZhang](https://github.com/SuperAoao)
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com)
 
-在现实世界里，每个物体会对光产生不同的反应。比如，钢制物体看起来通常会比陶土花瓶更闪闪发光，一个木头箱子也不会与一个钢制箱子反射同样程度的光。有些物体反射光的时候不会有太多的散射(Scatter)，因而产生较小的高光点，而有些物体则会散射很多，产生一个有着更大半径的高光点。如果我们想要在OpenGL中模拟多种类型的物体，我们必须针对每种表面定义不同的<def>材质</def>(Material)属性。
+在真实世界里，每个物体会对光产生不同的反应。钢看起来比陶瓷花瓶更闪闪发光，一个木头箱子不会像钢箱子一样对光产生很强的反射。每个物体对镜面高光也有不同的反应。有些物体不会散射(Scatter)很多光却会反射(Reflect)很多光，结果看起来就有一个较小的高光点(Highlight)，有些物体散射了很多，它们就会产生一个半径更大的高光。如果我们想要在OpenGL中模拟多种类型的物体，我们必须为每个物体分别定义材质(Material)属性。
 
-在上一节中，我们定义了一个物体和光的颜色，并结合环境光与镜面强度分量，来决定物体的视觉输出。当描述一个表面时，我们可以分别为三个光照分量定义一个材质颜色(Material Color)：环境光照(Ambient Lighting)、漫反射光照(Diffuse Lighting)和镜面光照(Specular Lighting)。通过为每个分量指定一个颜色，我们就能够对表面的颜色输出有细粒度的控制了。现在，我们再添加一个反光度(Shininess)分量，结合上述的三个颜色，我们就有了全部所需的材质属性了：
+在前面的教程中，我们指定一个物体和一个光的颜色来定义物体的图像输出，并使之结合环境(Ambient)和镜面强度(Specular Intensity)元素。当描述物体的时候，我们可以使用3种光照元素：环境光照(Ambient Lighting)、漫反射光照(Diffuse Lighting)、镜面光照(Specular Lighting)定义一个材质颜色。通过为每个元素指定一个颜色，我们已经对物体的颜色输出有了精密的控制。现在把一个镜面高光元素添加到这三个颜色里，这是我们需要的所有材质属性：
 
 ```c++
-
 #version 330 core
-struct Material {
+struct Material
+{
     vec3 ambient;
     vec3 diffuse;
     vec3 specular;
     float shininess;
-}; 
-  
+};
 uniform Material material;
 ```
 
-在片段着色器中，我们创建一个结构体(Struct)来储存物体的材质属性。我们也可以把它们储存为独立的uniform值，但是作为一个结构体来储存会更有条理一些。我们首先定义结构体的布局(Layout)，然后简单地以刚创建的结构体作为类型声明一个uniform变量。
+在片段着色器中，我们创建一个结构体(Struct)，来储存物体的材质属性。我们也可以把它们储存为独立的uniform值，但是作为一个结构体来储存可以更有条理。我们首先定义结构体的布局，然后简单声明一个uniform变量，以新创建的结构体作为它的类型。
 
-如你所见，我们为风氏光照模型的每个分量都定义一个颜色向量。<var>ambient</var>材质向量定义了在环境光照下这个表面反射的是什么颜色，通常与表面的颜色相同。<var>diffuse</var>材质向量定义了在漫反射光照下表面的颜色。漫反射颜色（和环境光照一样）也被设置为我们期望的物体颜色。<var>specular</var>材质向量设置的是表面上镜面高光的颜色（或者甚至可能反映一个特定表面的颜色）。最后，<var>shininess</var>影响镜面高光的散射/半径。
+就像你所看到的，我们为每个冯氏光照模型的元素都定义一个颜色向量。`ambient`材质向量定义了在环境光照下这个物体反射的是什么颜色；通常这是和物体颜色相同的颜色。`diffuse`材质向量定义了在漫反射光照下物体的颜色。漫反射颜色被设置为(和环境光照一样)我们需要的物体颜色。`specular`材质向量设置的是物体受到的镜面光照的影响的颜色(或者可能是反射一个物体特定的镜面高光颜色)。最后，`shininess`影响镜面高光的散射/半径。
 
-有这4个元素定义一个物体的材质，我们能够模拟很多现实世界中的材质。[devernay.free.fr](http://devernay.free.fr/cours/opengl/materials.html)中的一个表格展示了一系列材质属性，它们模拟了现实世界中的真实材质。下图展示了几组现实世界的材质参数值对我们的立方体的影响：
+这四个元素定义了一个物体的材质，通过它们我们能够模拟很多真实世界的材质。这里有一个列表[devernay.free.fr](http://devernay.free.fr/cours/opengl/materials.html)展示了几种材质属性，这些材质属性模拟外部世界的真实材质。下面的图片展示了几种真实世界材质对我们的立方体的影响：
 
-![](../img/02/03/materials_real_world.png)
+![](http://www.learnopengl.com/img/lighting/materials_real_world.png)
 
-可以看到，通过正确地指定一个物体的材质属性，我们对这个物体的感知也就不同了。效果非常明显，但是要想获得更真实的效果，我们需要以更复杂的形状替换这个立方体。在[模型加载](../03 Model Loading/01 Assimp.md)章节中，我们会讨论更复杂的形状。
+如你所见，正确地指定一个物体的材质属性，似乎就是改变我们物体的相关属性的比例。效果显然很引人注目，但是对于大多数真实效果，我们最终需要更加复杂的形状，而不单单是一个立方体。在[后面的教程](../03 Model Loading/01 Assimp.md)中，我们会讨论更复杂的形状。
 
-搞清楚一个物体正确的材质设定是个困难的工程，这主要需要实验和丰富的经验。用了不合适的材质而毁了物体的视觉质量是件经常发生的事。
+为一个物体赋予一款正确的材质是非常困难的，这需要大量实验和丰富的经验，所以由于错误的设置材质而毁了物体的画面质量是件经常发生的事。
 
-让我们试着在着色器中实现这样的一个材质系统。
+让我们试试在着色器中实现这样的一个材质系统。
 
 
 # 设置材质
 
-我们在片段着色器中创建了一个材质结构体的uniform，所以下面我们希望修改一下光照的计算来遵从新的材质属性。由于所有材质变量都储存在一个结构体中，我们可以从uniform变量<var>material</var>中访问它们：
+我们在片段着色器中创建了一个uniform材质结构体，所以下面我们希望改变光照计算来顺应新的材质属性。由于所有材质元素都储存在结构体中，我们可以从uniform变量`material`取得它们：
 
 ```c++
 void main()
-{    
+{
     // 环境光
     vec3 ambient = lightColor * material.ambient;
-  	
-    // 漫反射 
+
+    // 漫反射光
     vec3 norm = normalize(Normal);
     vec3 lightDir = normalize(lightPos - FragPos);
     float diff = max(dot(norm, lightDir), 0.0);
     vec3 diffuse = lightColor * (diff * material.diffuse);
-    
-    // 镜面光
+
+    // 镜面高光
     vec3 viewDir = normalize(viewPos - FragPos);
     vec3 reflectDir = reflect(-lightDir, norm);  
     float spec = pow(max(dot(viewDir, reflectDir), 0.0), material.shininess);
     vec3 specular = lightColor * (spec * material.specular);  
-        
+
     vec3 result = ambient + diffuse + specular;
-    FragColor = vec4(result, 1.0);
+    color = vec4(result, 1.0f);
 }
 ```
 
-可以看到，我们现在在需要的地方访问了材质结构体中的所有属性，并且这次是根据材质的颜色来计算最终的输出颜色的。物体的每个材质属性都乘上了它们各自对应的光照分量。
+你可以看到，我们现在获得所有材质结构体的属性，无论在哪儿我们都需要它们，这次通过材质颜色的帮助，计算结果输出的颜色。物体的每个材质属性都乘以它们对应的光照元素。
 
-我们现在可以通过设置适当的uniform来设置应用中物体的材质了。GLSL中一个结构体在设置uniform时并无任何区别，结构体只是充当uniform变量们的一个命名空间。所以如果想填充这个结构体的话，我们必须设置每个单独的uniform，但要以结构体名为前缀：
+通过设置适当的uniform，我们可以在应用中设置物体的材质。当设置uniform时，GLSL中的一个结构体并不会被认为有什么特别之处。一个结构体值扮演uniform变量的封装体，所以如果我们希望填充这个结构体，我们就仍然必须设置结构体中的各个元素的uniform值，但是这次带有结构体名字作为前缀：
 
 ```c++
-lightingShader.setVec3("material.ambient",  1.0f, 0.5f, 0.31f);
-lightingShader.setVec3("material.diffuse",  1.0f, 0.5f, 0.31f);
-lightingShader.setVec3("material.specular", 0.5f, 0.5f, 0.5f);
-lightingShader.setFloat("material.shininess", 32.0f);
+GLint matAmbientLoc = glGetUniformLocation(lightingShader.Program, "material.ambient");
+GLint matDiffuseLoc = glGetUniformLocation(lightingShader.Program, "material.diffuse");
+GLint matSpecularLoc = glGetUniformLocation(lightingShader.Program, "material.specular");
+GLint matShineLoc = glGetUniformLocation(lightingShader.Program, "material.shininess");
+
+glUniform3f(matAmbientLoc, 1.0f, 0.5f, 0.31f);
+glUniform3f(matDiffuseLoc, 1.0f, 0.5f, 0.31f);
+glUniform3f(matSpecularLoc, 0.5f, 0.5f, 0.5f);
+glUniform1f(matShineLoc, 32.0f);
 ```
 
-我们将环境光和漫反射分量设置成我们想要让物体所拥有的颜色，而将镜面分量设置为一个中等亮度的颜色，我们不希望镜面分量过于强烈。我们仍将反光度保持为32。
+我们将`ambient`和`diffuse`元素设置成我们想要让物体所呈现的颜色，设置物体的`specular`元素为中等亮度颜色；我们不希望`specular`元素对这个指定物体产生过于强烈的影响。我们同样设置`shininess`为32。我们现在可以简单的在应用中影响物体的材质。
 
-现在我们能够轻松地在应用中影响物体的材质了。运行程序，你会得到像这样的结果：
+运行程序，会得到下面这样的结果：
 
-![](../img/02/03/materials_with_material.png)
+![](http://www.learnopengl.com/img/lighting/materials_with_material.png)
 
-不过看起来真的不太对劲？
+看起来很奇怪不是吗？
 
 
 ## 光的属性
 
-这个物体太亮了。物体过亮的原因是环境光、漫反射和镜面光这三个颜色对任何一个光源都全力反射。光源对环境光、漫反射和镜面光分量也分别具有不同的强度。前面的章节中，我们通过使用一个强度值改变环境光和镜面光强度的方式解决了这个问题。我们想做类似的事情，但是这次是要为每个光照分量分别指定一个强度向量。如果我们假设<var>lightColor</var>是`vec3(1.0)`，代码会看起来像这样：
+这个物体太亮了。物体过亮的原因是环境、漫反射和镜面三个颜色任何一个光源都会去全力反射。光源对环境、漫反射和镜面元素同时具有不同的强度。前面的教程，我们通过使用一个强度值改变环境和镜面强度的方式解决了这个问题。我们想做一个相同的系统，但是这次为每个光照元素指定了强度向量。如果我们想象`lightColor`是`vec3(1.0)`，代码看起来像是这样：
 
 ```c++
-vec3 ambient  = vec3(1.0) * material.ambient;
-vec3 diffuse  = vec3(1.0) * (diff * material.diffuse);
-vec3 specular = vec3(1.0) * (spec * material.specular);
+vec3 ambient = vec3(1.0f) * material.ambient;
+vec3 diffuse = vec3(1.0f) * (diff * material.diffuse);
+vec3 specular = vec3(1.0f) * (spec * material.specular);
 ```
 
-所以物体的每个材质属性对每一个光照分量都返回了最大的强度。对单个光源来说，这些`vec3(1.0)`值同样可以对每种光源分别改变，而这通常就是我们想要的。现在，物体的环境光分量完全地影响了立方体的颜色，可是环境光分量实际上不应该对最终的颜色有这么大的影响，所以我们会将光源的环境光强度设置为一个小一点的值，从而限制环境光颜色：
+所以物体的每个材质属性返回了每个光照元素的全强度。这些vec3(1.0)值可以各自独立的影响各个光源，这通常就是我们想要的。现在物体的`ambient`元素完全地展示了立方体的颜色，可是环境元素不应该对最终颜色有这么大的影响，所以我们要设置光的`ambient`亮度为一个小一点的值，从而限制环境色：
 
 ```c++
-vec3 ambient = vec3(0.1) * material.ambient;
+vec3 result = vec3(0.1f) * material.ambient;
 ```
 
-我们可以用同样的方式影响光源的漫反射和镜面光强度。这和我们在[上一节](02 Basic Lighting.md)中所做的极为相似，你可以认为我们已经创建了一些光照属性来影响各个光照分量。我们希望为光照属性创建类似材质结构体的东西：
+我们可以用同样的方式影响光源`diffuse`和`specular`的强度。这和我们[前面教程](http://learnopengl-cn.readthedocs.org/zh/latest/02%20Lighting/02%20Basic%20Lighting/)所做的极为相似；你可以说我们已经创建了一些光的属性来各自独立地影响每个光照元素。我们希望为光的属性创建一些与材质结构体相似的东西：
 
 ```c++
-struct Light {
+struct Light
+{
     vec3 position;
-  
     vec3 ambient;
     vec3 diffuse;
     vec3 specular;
 };
-
 uniform Light light;
 ```
 
-一个光源对它的<var>ambient</var>、<var>diffuse</var>和<var>specular</var>光照分量有着不同的强度。环境光照通常被设置为一个比较低的强度，因为我们不希望环境光颜色太过主导。光源的漫反射分量通常被设置为我们希望光所具有的那个颜色，通常是一个比较明亮的白色。镜面光分量通常会保持为`vec3(1.0)`，以最大强度发光。注意我们也将光源的位置向量加入了结构体。
+一个光源的`ambient`、`diffuse`和`specular`光都有不同的亮度。环境光通常设置为一个比较低的亮度，因为我们不希望环境色太过显眼。光源的`diffuse`元素通常设置为我们希望光所具有的颜色；经常是一个明亮的白色。`specular`元素通常被设置为`vec3(1.0f)`类型的全强度发光。要记住的是我们同样把光的位置添加到结构体中。
 
-和材质uniform一样，我们需要更新片段着色器：
+就像材质uniform一样，需要更新片段着色器：
 
 ```c++
-vec3 ambient  = light.ambient * material.ambient;
-vec3 diffuse  = light.diffuse * (diff * material.diffuse);
+vec3 ambient = light.ambient * material.ambient;
+vec3 diffuse = light.diffuse * (diff * material.diffuse);
 vec3 specular = light.specular * (spec * material.specular);
 ```
 
-我们接下来在应用中设置光照强度：
+然后我们要在应用里设置光的亮度：
 
 ```c++
-lightingShader.setVec3("light.ambient",  0.2f, 0.2f, 0.2f);
-lightingShader.setVec3("light.diffuse",  0.5f, 0.5f, 0.5f); // 将光照调暗了一些以搭配场景
-lightingShader.setVec3("light.specular", 1.0f, 1.0f, 1.0f); 
+GLint lightAmbientLoc = glGetUniformLocation(lightingShader.Program, "light.ambient");
+GLint lightDiffuseLoc = glGetUniformLocation(lightingShader.Program, "light.diffuse");
+GLint lightSpecularLoc = glGetUniformLocation(lightingShader.Program, "light.specular");
+
+glUniform3f(lightAmbientLoc, 0.2f, 0.2f, 0.2f);
+glUniform3f(lightDiffuseLoc, 0.5f, 0.5f, 0.5f);// 让我们把这个光调暗一点，这样会看起来更自然
+glUniform3f(lightSpecularLoc, 1.0f, 1.0f, 1.0f);
 ```
 
-现在我们已经调整了光照对物体材质的影响，我们得到了一个与上一节很相似的视觉效果。但这次我们有了对光照和物体材质的完全掌控：
+现在，我们调整了光是如何影响物体所有的材质的，我们得到一个更像前面教程的视觉输出。这次我们完全控制了物体光照和材质：
 
-![](../img/02/03/materials_light.png)
+![](http://www.learnopengl.com/img/lighting/materials_light.png)
+
+现在改变物体的外观相对简单了些。我们做点更有趣的事！
 
-改变物体的视觉效果现在变得相对容易了。让我们做点更有趣的事！
 
 ## 不同的光源颜色
 
-到目前为止，我们都只对光源设置了从白到灰到黑范围内的颜色，这样只会改变物体各个分量的强度，而不是它的真正颜色。由于现在能够非常容易地访问光照的属性了，我们可以随着时间改变它们的颜色，从而获得一些非常有意思的效果。由于所有的东西都在片段着色器中配置好了，修改光源的颜色非常简单，并立刻创造一些很有趣的效果：
+目前为止，我们使用光源的颜色仅仅去改变物体各个元素的强度(通过选用从白到灰到黑范围内的颜色)，并没有影响物体的真实颜色(只是强度)。由于现在能够非常容易地访问光的属性了，我们可以随着时间改变它们的颜色来获得一些有很意思的效果。由于所有东西都已经在片段着色器做好了，改变光的颜色很简单，我们可以立即创建出一些有趣的效果：
 
-<video src="../../img/02/03/materials.mp4" controls="controls">
+<video src="http://www.learnopengl.com/video/lighting/materials.mp4" controls="controls">
 </video>
 
-你可以看到，不同的光照颜色能够极大地影响物体的最终颜色输出。由于光照颜色能够直接影响物体能够反射的颜色（回想[颜色](01 Colors.md)这一节），这对视觉输出有着显著的影响。
+如你所见，不同光的颜色极大地影响了物体的颜色输出。由于光的颜色直接影响物体反射的颜色(你可能想起在颜色教程中有讨论过)，它对视觉输出有显著的影响。
 
-我们可以利用<fun>sin</fun>和<fun>glfwGetTime</fun>函数改变光源的环境光和漫反射颜色，从而很容易地让光源的颜色随着时间变化：
+利用`sin`和`glfwGetTime`改变光的环境和漫反射颜色，我们可以随着时间流逝简单的改变光源颜色：
 
 ```c++
-glm::vec3 lightColor;
-lightColor.x = sin(glfwGetTime() * 2.0f);
+glm::vec3 lightColor; lightColor.x = sin(glfwGetTime() * 2.0f);
 lightColor.y = sin(glfwGetTime() * 0.7f);
 lightColor.z = sin(glfwGetTime() * 1.3f);
-  
-glm::vec3 diffuseColor = lightColor   * glm::vec3(0.5f); // 降低影响
-glm::vec3 ambientColor = diffuseColor * glm::vec3(0.2f); // 很低的影响
-  
-lightingShader.setVec3("light.ambient", ambientColor);
-lightingShader.setVec3("light.diffuse", diffuseColor);
+
+glm::vec3 diffuseColor = lightColor * glm::vec3(0.5f);
+glm::vec3 ambientColor = diffuseColor * glm::vec3(0.2f);
+
+glUniform3f(lightAmbientLoc, ambientColor.x, ambientColor.y, ambientColor.z);
+glUniform3f(lightDiffuseLoc, diffuseColor.x, diffuseColor.y, diffuseColor.z);
 ```
 
-尝试并实验一些光照和材质值，看看它们是怎样影响视觉输出的。你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/2.lighting/3.1.materials/materials.cpp)找到应用的源码。
+尝试和实验使用这些光照和材质值，看看它们怎样影响图像输出的。你可以从这里找到[程序的源码](http://learnopengl.com/code_viewer.php?code=lighting/materials)，[片段着色器](http://learnopengl.com/code_viewer.php?code=lighting/materials&type=fragment)的源码。
 
 ## 练习
 
-- 你能做到这件事吗，改变光照颜色导致改变光源立方体的颜色？
-- 你能像教程一开始那样，通过定义相应的材质来模拟现实世界的物体吗？注意[材质表格](http://devernay.free.fr/cours/opengl/materials.html)中的环境光值与漫反射值不一样，它们没有考虑光照的强度。要想正确地设置它们的值，你需要将所有的光照强度都设置为`vec3(1.0)`，这样才能得到一致的输出：[参考解答](https://learnopengl.com/code_viewer_gh.php?code=src/2.lighting/3.2.materials_exercise1/materials_exercise1.cpp)：青色塑料(Cyan Plastic)容器。
+- 你能像我们教程一开始那样根据一些材质的属性来模拟一个真实世界的物体吗？
+注意[材质表](http://devernay.free.fr/cours/opengl/materials.html)中的环境光颜色与漫反射光的颜色可能不一样，因为他们并没有把光照强度考虑进去来模拟，你需要将光照颜色的强度改为`vec(1.0f)`来输出正确的结果：[参考解答](http://learnopengl.com/code_viewer.php?code=lighting/materials-exercise1)，我做了一个青色(Cyan)的塑料箱子

docs/02 Lighting/04 Lighting maps.md

@@ -3,160 +3,156 @@
 原文     | [Lighting maps](http://learnopengl.com/#!Lighting/Lighting-maps)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | [AoZhang](https://github.com/SuperAoao)
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com), [BLumia](https://github.com/blumia/)
 
-在[上一节](03 Materials.md)中，我们讨论了让每个物体都拥有自己独特的材质从而对光照做出不同的反应的方法。这样子能够很容易在一个光照的场景中给每个物体一个独特的外观，但是这仍不能对一个物体的视觉输出提供足够多的灵活性。
+前面的教程，我们讨论了让不同的物体拥有各自不同的材质并对光照做出不同的反应的方法。在一个光照场景中，让每个物体拥有和其他物体不同的外观很棒，但是这仍然不能对一个物体的图像输出提供足够多的灵活性。
 
-在上一节中，我们将整个物体的材质定义为一个整体，但现实世界中的物体通常并不只包含有一种材质，而是由多种材质所组成。想想一辆汽车：它的外壳非常有光泽，车窗会部分反射周围的环境，轮胎不会那么有光泽，所以它没有镜面高光，轮毂非常闪亮（如果你洗车了的话）。汽车同样会有漫反射和环境光颜色，它们在整个物体上也不会是一样的，汽车有着许多种不同的环境光/漫反射颜色。总之，这样的物体在不同的部件上都有不同的材质属性。
+前面的教程中我们将一个物体自身作为一个整体为其定义了一个材质，但是现实世界的物体通常不会只有这么一种材质，而是由多种材质组成。想象一辆车：它的外表质地光亮，车窗会部分反射环境，它的轮胎没有specular高光，轮彀却非常闪亮（在洗过之后）。汽车同样有diffuse和ambient颜色，它们在整个车上都不相同；一辆车显示了多种不同的ambient/diffuse颜色。总之，这样一个物体每个部分都有多种材质属性。
 
-所以，上一节中的那个材质系统是肯定不够的，它只是一个最简单的模型，所以我们需要拓展之前的系统，引入**漫反射**和**镜面光**贴图(Map)。这允许我们对物体的漫反射分量（以及间接地对环境光分量，它们几乎总是一样的）和镜面光分量有着更精确的控制。
+所以，前面的材质系统对于除了最简单的模型以外都是不够的，所以我们需要扩展前面的系统，我们要介绍diffuse和specular贴图。它们允许你对一个物体的diffuse（而对于简洁的ambient成分来说，它们几乎总是是一样的）和specular成分能够有更精确的影响。
 
 # 漫反射贴图
 
-我们希望通过某种方式对物体的每个片段单独设置漫反射颜色。有能够让我们根据片段在物体上的位置来获取颜色值的系统吗？
+我们希望通过某种方式对每个原始像素独立设置diffuse颜色。有可以让我们基于物体原始像素的位置来获取颜色值的系统吗？
 
-这可能听起来很熟悉，而且事实上这个系统我们已经使用很长时间了。这听起来很像在[之前](../01 Getting started/06 Textures.md)教程中详细讨论过的**纹理**，而这基本就是这样：一个纹理。我们仅仅是对同样的原理使用了不同的名字：其实都是使用一张覆盖物体的图像，让我们能够逐片段索引其独立的颜色值。在光照场景中，它通常叫做一个<def>漫反射贴图</def>(Diffuse Map)（在PBR之前3D艺术家通常都这么叫它），它是一个表现了物体所有的漫反射颜色的纹理图像。
+这可能听起来极其相似，坦白来讲我们使用这样的系统已经有一段时间了。听起来很像在一个[之前的教程](../01 Getting started/06 Textures.md)中谈论的**纹理**，它基本就是一个纹理。我们其实是使用同一个潜在原则下的不同名称：使用一张图片覆盖住物体，以便我们为每个原始像素索引独立颜色值。在光照场景中，通过纹理来呈现一个物体的diffuse颜色，这个做法被称做**漫反射贴图(Diffuse texture)**(因为3D建模师就是这么称呼这个做法的)。
 
-为了演示漫反射贴图，我们将会使用[下面的图片](../img/02/04/container2.png)，它是一个有钢边框的木箱：
+为了演示漫反射贴图，我们将会使用[下面的图片](http://learnopengl.com/img/textures/container2.png)，它是一个有一圈钢边的木箱：
 
-![](../img/02/04/container2.png)
+![](http://www.learnopengl.com/img/textures/container2.png)
 
-在着色器中使用漫反射贴图的方法和纹理教程中是完全一样的。但这次我们会将纹理储存为<fun>Material</fun>结构体中的一个`sampler2D`。我们将之前定义的`vec3`漫反射颜色向量替换为漫反射贴图。
+在着色器中使用漫反射贴图和纹理教程介绍的一样。这次我们把纹理以sampler2D类型储存在Material结构体中。我们使用diffuse贴图替代早期定义的vec3类型的diffuse颜色。
 
 !!! Attention
-
-	注意`sampler2D`是所谓的<def>不透明类型</def>(Opaque Type)，也就是说我们不能将它实例化，只能通过uniform来定义它。如果我们使用除uniform以外的方法（比如函数的参数）实例化这个结构体，GLSL会抛出一些奇怪的错误。这同样也适用于任何封装了不透明类型的结构体。
-
-我们也移除了环境光材质颜色向量，因为环境光颜色在几乎所有情况下都等于漫反射颜色，所以我们不需要将它们分开储存：
+    
+    要记住的是sampler2D也叫做模糊类型，这意味着我们不能以某种类型对它实例化，只能用uniform定义它们。如果我们用结构体而不是uniform实例化（就像函数的参数那样），GLSL会抛出奇怪的错误；这同样也适用于其他模糊类型。
+我们也要移除amibient材质颜色向量，因为ambient颜色绝大多数情况等于diffuse颜色，所以不需要分别去储存它：
 
 ```c++
-struct Material {
+struct Material
+{
     sampler2D diffuse;
-    vec3      specular;
-    float     shininess;
-}; 
+    vec3 specular;
+    float shininess;
+};
 ...
 in vec2 TexCoords;
 ```
-
 !!! Important
 
-	如果你非常固执，仍想将环境光颜色设置为一个（漫反射值之外）不同的值，你也可以保留这个环境光的`vec3`，但整个物体仍只能拥有一个环境光颜色。如果想要对不同片段有不同的环境光值，你需要对环境光值单独使用另外一个纹理。
-
-注意我们将在片段着色器中再次需要纹理坐标，所以我们声明一个额外的输入变量。接下来我们只需要从纹理中采样片段的漫反射颜色值即可：
+    如果你非把ambient颜色设置为不同的值不可（不同于diffuse值），你可以继续保留ambient的vec3，但是整个物体的ambient颜色会继续保持不变。为了使每个原始像素得到不同ambient值，你需要对ambient值单独使用另一个纹理。
 
+注意，在片段着色器中我们将会再次需要纹理坐标，所以我们声明一个额外输入变量。然后我们简单地从纹理采样，来获得原始像素的diffuse颜色值：
+    
 ```c++
 vec3 diffuse = light.diffuse * diff * vec3(texture(material.diffuse, TexCoords));
 ```
 
-不要忘记将环境光的材质颜色设置为漫反射材质颜色同样的值。
+同样，不要忘记把ambient材质的颜色设置为diffuse材质的颜色：
 
 ```c++
 vec3 ambient = light.ambient * vec3(texture(material.diffuse, TexCoords));
 ```
 
-这就是使用漫反射贴图的全部步骤了。你可以看到，这并不是什么新的东西，但这能够极大地提高视觉品质。为了让它正常工作，我们还需要使用纹理坐标更新顶点数据，将它们作为顶点属性传递到片段着色器，加载材质并绑定材质到合适的纹理单元。
+这就是diffuse贴图的全部内容了。就像你看到的，这不是什么新的东西，但是它却极大提升了视觉品质。为了让它工作，我们需要用到纹理坐标更新顶点数据，把它们作为顶点属性传递到片段着色器，把纹理加载并绑定到合适的纹理单元。
 
-更新后的顶点数据可以在[这里](https://learnopengl.com/code_viewer.php?code=lighting/vertex_data_textures)找到。顶点数据现在包含了顶点位置、法向量和立方体顶点处的纹理坐标。让我们更新顶点着色器来以顶点属性的形式接受纹理坐标，并将它们传递到片段着色器中：
+更新的顶点数据可以从[这里](http://learnopengl.com/code_viewer.php?code=lighting/vertex_data_textures)找到。顶点数据现在包括了顶点位置，法线向量和纹理坐标，每个立方体的顶点都有这些属性。让我们更新顶点着色器来接受纹理坐标作为顶点属性，然后发送到片段着色器：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;
-layout (location = 1) in vec3 aNormal;
-layout (location = 2) in vec2 aTexCoords;
+layout (location = 0) in vec3 position;
+layout (location = 1) in vec3 normal;
+layout (location = 2) in vec2 texCoords;
 ...
 out vec2 TexCoords;
 
 void main()
 {
     ...
-    TexCoords = aTexCoords;
+    TexCoords = texCoords;
 }
 ```
 
-记得去更新两个VAO的顶点属性指针来匹配新的顶点数据，并加载箱子图像为一个纹理。在绘制箱子之前，我们希望将要用的纹理单元赋值到<var>material.diffuse</var>这个uniform采样器，并绑定箱子的纹理到这个纹理单元：
+要保证更新的顶点属性指针，不仅是VAO匹配新的顶点数据，也要把箱子图片加载为纹理。在绘制箱子之前，我们希望首选纹理单元被赋为material.diffuse这个uniform采样器，并绑定箱子的纹理到这个纹理单元：
 
 ```c++
-lightingShader.setInt("material.diffuse", 0);
+glUniform1i(glGetUniformLocation(lightingShader.Program, "material.diffuse"), 0);
 ...
 glActiveTexture(GL_TEXTURE0);
 glBindTexture(GL_TEXTURE_2D, diffuseMap);
 ```
 
-使用了漫反射贴图之后，细节再一次得到惊人的提升，这次箱子有了光照开始闪闪发光（字面意思也是）了。你的箱子看起来可能像这样：
+现在，使用一个diffuse贴图，我们在细节上再次获得惊人的提升，这次添加到箱子上的光照开始闪光了（名符其实）。你的箱子现在可能看起来像这样：
 
-![](../img/02/04/materials_diffuse_map.png)
+![](http://www.learnopengl.com/img/lighting/materials_diffuse_map.png)
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/2.lighting/4.1.lighting_maps_diffuse_map/lighting_maps_diffuse.cpp)找到程序的全部代码。
+你可以在这里得到应用的[全部代码](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps_diffuse)。
 
 
-# 镜面光贴图
+# 镜面贴图
 
-你可能会注意到，镜面高光看起来有些奇怪，因为我们的物体大部分都是木头，我们知道木头不应该有这么强的镜面高光的。我们可以将物体的镜面光材质设置为`vec3(0.0)`来解决这个问题，但这也意味着箱子钢制的边框将不再能够显示镜面高光了，我们知道钢铁**应该**是有一些镜面高光的。所以，我们想要让物体的某些部分以不同的强度显示镜面高光。这个问题看起来和漫反射贴图非常相似。是巧合吗？我想不是。
+你可能注意到，specular高光看起来不怎么样，由于我们的物体是个箱子，大部分是木头，我们知道木头是不应该有镜面高光的。我们通过把物体设置specular材质设置为vec3(0.0f)来修正它。但是这样意味着铁边会不再显示镜面高光，我们知道钢铁是会显示一些镜面高光的。我们会想要控制物体部分地显示镜面高光，它带有修改了的亮度。这个问题看起来和diffuse贴图的讨论一样。这是巧合吗？我想不是。
 
-我们同样可以使用一个专门用于镜面高光的纹理贴图。这也就意味着我们需要生成一个黑白的（如果你想得话也可以是彩色的）纹理，来定义物体每部分的镜面光强度。下面是一个[镜面光贴图](../img/02/04/container2_specular.png)(Specular Map)的例子：
+我们同样用一个纹理贴图，来获得镜面高光。这意味着我们需要生成一个黑白（或者你喜欢的颜色）纹理来定义specular亮度，把它应用到物体的每个部分。下面是一个[镜面贴图(Specular Map)](http://learnopengl.com/img/textures/container2_specular.png)的例子：
 
-![](../img/02/04/container2_specular.png)
+![](http://www.learnopengl.com/img/textures/container2_specular.png)
 
-镜面高光的强度可以通过图像每个像素的亮度来获取。镜面光贴图上的每个像素都可以由一个颜色向量来表示，比如说黑色代表颜色向量`vec3(0.0)`，灰色代表颜色向量`vec3(0.5)`。在片段着色器中，我们接下来会取样对应的颜色值并将它乘以光源的镜面强度。一个像素越「白」，乘积就会越大，物体的镜面光分量就会越亮。
+一个specular高光的亮度可以通过图片中每个纹理的亮度来获得。specular贴图的每个像素可以显示为一个颜色向量，比如：在那里黑色代表颜色向量vec3(0.0f)，灰色是vec3(0.5f)。在片段着色器中，我们采样相应的颜色值，把它乘以光的specular亮度。像素越“白”，乘积的结果越大，物体的specualr部分越亮。
 
-由于箱子大部分都由木头所组成，而且木头材质应该没有镜面高光，所以漫反射纹理的整个木头部分全部都转换成了黑色。箱子钢制边框的镜面光强度是有细微变化的，钢铁本身会比较容易受到镜面高光的影响，而裂缝则不会。
+由于箱子几乎是由木头组成，木头作为一个材质不会有镜面高光，整个木头部分的diffuse纹理被用黑色覆盖：黑色部分不会包含任何specular高光。箱子的铁边有一个修改的specular亮度，它自身更容易受到镜面高光影响，木纹部分则不会。
 
-!!! important
+从技术上来讲，木头也有镜面高光，尽管这个闪亮值很小（更多的光被散射），影响很小，但是为了学习目的，我们可以假装木头不会有任何specular光反射。
 
-	从实际角度来说，木头其实也有镜面高光，尽管它的反光度(Shininess)很小（更多的光被散射），影响也比较小，但是为了教学目的，我们可以假设木头不会对镜面光有任何反应。
-
-使用**Photoshop**或**Gimp**之类的工具，将漫反射纹理转换为镜面光纹理还是比较容易的，只需要剪切掉一些部分，将图像转换为黑白的，并增加亮度/对比度就好了。
+使用Photoshop或Gimp之类的工具，通过将图片进行裁剪，将某部分调整成黑白图样，并调整亮度/对比度的做法，可以非常容易将一个diffuse纹理贴图处理为specular贴图。
 
 
-## 采样镜面光贴图
+## 镜面贴图采样
 
-镜面光贴图和其它的纹理非常类似，所以代码也和漫反射贴图的代码很类似。记得要保证正确地加载图像并生成一个纹理对象。由于我们正在同一个片段着色器中使用另一个纹理采样器，我们必须要对镜面光贴图使用一个不同的纹理单元（见[纹理](../01 Getting started/06 Textures.md)），所以我们在渲染之前先把它绑定到合适的纹理单元上：
+一个specular贴图和其他纹理一样，所以代码和diffuse贴图的代码也相似。确保合理的加载了图片，生成一个纹理对象。由于我们在同样的片段着色器中使用另一个纹理采样器，我们必须为specular贴图使用一个不同的纹理单元(参见[纹理](../01 Getting started/06 Textures.md))，所以在渲染前让我们把它绑定到合适的纹理单元
 
 ```c++
-lightingShader.setInt("material.specular", 1);
+glUniform1i(glGetUniformLocation(lightingShader.Program, "material.specular"), 1);
 ...
 glActiveTexture(GL_TEXTURE1);
 glBindTexture(GL_TEXTURE_2D, specularMap);
 ```
 
-接下来更新片段着色器的材质属性，让其接受一个`sampler2D`而不是`vec3`作为镜面光分量：
+然后更新片段着色器材质属性，接受一个sampler2D作为这个specular部分的类型，而不是vec3：
 
 ```c++
-struct Material {
+struct Material
+{
     sampler2D diffuse;
     sampler2D specular;
-    float     shininess;
+    float shininess;
 };
 ```
 
-最后我们希望采样镜面光贴图，来获取片段所对应的镜面光强度：
+最后我们希望采样这个specular贴图，来获取原始像素相应的specular亮度：
 
 ```c++
-vec3 ambient  = light.ambient  * vec3(texture(material.diffuse, TexCoords));
-vec3 diffuse  = light.diffuse  * diff * vec3(texture(material.diffuse, TexCoords));  
+vec3 ambient = light.ambient * vec3(texture(material.diffuse, TexCoords));
+vec3 diffuse = light.diffuse * diff * vec3(texture(material.diffuse, TexCoords));
 vec3 specular = light.specular * spec * vec3(texture(material.specular, TexCoords));
-FragColor = vec4(ambient + diffuse + specular, 1.0);
+color = vec4(ambient + diffuse + specular, 1.0f);
 ```
 
-通过使用镜面光贴图我们可以可以对物体设置大量的细节，比如物体的哪些部分需要有**闪闪发光**的属性，我们甚至可以设置它们对应的强度。镜面光贴图能够在漫反射贴图之上给予我们更高一层的控制。
+通过使用一个specular贴图我们可以定义极为精细的细节，物体的这个部分会获得闪亮的属性，我们可以设置它们相应的亮度。specular贴图给我们一个附加的高于diffuse贴图的控制权限。
 
-!!! important
+如果你不想成为主流，你可以在specular贴图里使用颜色，不单单为每个原始像素设置specular亮度，同时也设置specular高光的颜色。从真实角度来说，specular的颜色基本是由光源自身决定的，所以它不会生成真实的图像（这就是为什么图片通常是黑色和白色的：我们只关心亮度）。
 
-	如果你想另辟蹊径，你也可以在镜面光贴图中使用真正的颜色，不仅设置每个片段的镜面光强度，还设置了镜面高光的颜色。从现实角度来说，镜面高光的颜色大部分（甚至全部）都是由光源本身所决定的，所以这样并不能生成非常真实的视觉效果（这也是为什么图像通常是黑白的，我们只关心强度）。
+如果你现在运行应用，你可以清晰地看到箱子的材质现在非常类似真实的铁边的木头箱子了：
 
-如果你现在运行程序的话，你可以清楚地看到箱子的材质现在和真实的钢制边框箱子非常类似了：
+![](http://www.learnopengl.com/img/lighting/materials_specular_map.png)
 
-![](../img/02/04/materials_specular_map.png)
+你可以在这里找到[全部源码](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps_specular)。也对比一下你的[顶点着色器](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps&type=vertex)和[片段着色器](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps&type=fragment)。
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/2.lighting/4.2.lighting_maps_specular_map/lighting_maps_specular.cpp)找到程序的全部源码。
-
-通过使用漫反射和镜面光贴图，我们可以给相对简单的物体添加大量的细节。我们甚至可以使用<def>法线/凹凸贴图</def>(Normal/Bump Map)或者<def>反射贴图</def>(Reflection Map)给物体添加更多的细节，但这些将会留到之后的教程中。把你的箱子给你的朋友或者家人看看，并且坚信我们的箱子有一天会比现在更加漂亮！
+使用diffuse和specular贴图，我们可以给相关但简单物体添加一个极为明显的细节。我们可以使用其他纹理贴图，比如法线/bump贴图或者反射贴图，给物体添加更多的细节。但是这些在后面教程才会涉及。把你的箱子给你所有的朋友和家人看，有一天你会很满足，我们的箱子会比现在更漂亮！
 
 ## 练习
 
-- 调整光源的环境光、漫反射和镜面光向量，看看它们如何影响箱子的视觉输出。
-- 尝试在片段着色器中反转镜面光贴图的颜色值，让木头显示镜面高光而钢制边缘不反光（由于钢制边缘中有一些裂缝，边缘仍会显示一些镜面高光，虽然强度会小很多）：[参考解答](https://learnopengl.com/code_viewer.php?code=lighting/lighting_maps-exercise2)
-- 使用漫反射贴图创建一个彩色而不是黑白的镜面光贴图，看看结果看起来并不是那么真实了。如果你不会生成的话，可以使用这张[彩色的镜面光贴图](../img/02/04/lighting_maps_specular_color.png)：[最终效果](../img/02/04/lighting_maps_exercise3.png)
-- 添加一个叫做<def>放射光贴图</def>(Emission Map)的东西，它是一个储存了每个片段的发光值(Emission Value)的贴图。发光值是一个包含（假设）光源的物体发光(Emit)时可能显现的颜色，这样的话物体就能够忽略光照条件进行发光(Glow)。游戏中某个物体在发光的时候，你通常看到的就是放射光贴图（比如 [机器人的眼](../img/02/04/shaders_enemy.jpg)，或是[箱子上的灯带](../img/02/04/emissive.png)）。将[这个](../img/02/04/matrix.jpg)纹理（作者为 creativesam）作为放射光贴图添加到箱子上，产生这些字母都在发光的效果：[参考解答](https://learnopengl.com/code_viewer_gh.php?code=src/2.lighting/4.4.lighting_maps_exercise4/lighting_maps_exercise4.cpp)，[最终效果](../img/02/04/lighting_maps_exercise4.png)
+- 调整光源的ambient，diffuse和specular向量值，看看它们如何影响实际输出的箱子外观。
+- 尝试在片段着色器中反转镜面贴图(Specular Map)的颜色值，然后木头就会变得反光而边框不会反光了（由于贴图中钢边依然有一些残余颜色，所以钢边依然会有一些高光，不过反光明显小了很多）。[参考解答](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps-exercise2)
+- 使用漫反射纹理(Diffuse Texture)原本的颜色而不是黑白色来创建镜面贴图，并观察，你会发现结果显得并不那么真实了。如果你不会处理图片，你可以使用这个[带颜色的镜面贴图](http://learnopengl.com/img/lighting/lighting_maps_specular_color.png)。[最终效果](learnopengl.com/img/lighting/lighting_maps_exercise3.png)
+- 添加一个叫做**放射光贴图(Emission Map)**的东西，即记录每个片段发光值(Emission Value)大小的贴图，发光值是(模拟)物体自身**发光(Emit)**时可能产生的颜色。这样的话物体就可以忽略环境光自身发光。通常在你看到游戏里某个东西(比如 [机器人的眼](http://www.witchbeam.com.au/unityboard/shaders_enemy.jpg),或是[箱子上的小灯](http://www.tomdalling.com/images/posts/modern-opengl-08/emissive.png))在发光时，使用的就是放射光贴图。使用[这个](http://learnopengl.com/img/textures/matrix.jpg)贴图(作者为 creativesam)作为放射光贴图并使用在箱子上，你就会看到箱子上有会发光的字了。[参考解答](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps-exercise4),[片段着色器](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps-exercise4_fragment), [最终效果](http://learnopengl.com/img/lighting/lighting_maps_exercise4.png)

docs/02 Lighting/05 Light casters.md

@@ -3,30 +3,30 @@
 原文     | [Light casters](http://www.learnopengl.com/#!Lighting/Light-casters)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | [AoZhang](https://github.com/SuperAoao)
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com), [BLumia](https://github.com/BLumia)
 
-我们目前使用的光照都来自于空间中的一个点。它能给我们不错的效果，但现实世界中，我们有很多种类的光照，每种的表现都不同。将光**投射**(Cast)到物体的光源叫做<def>投光物</def>(Light Caster)。在这一节中，我们将会讨论几种不同类型的投光物。学会模拟不同种类的光源是又一个能够进一步丰富场景的工具。
+我们目前使用的所有光照都来自于一个单独的光源，这是空间中的一个点。它的效果不错，但是在真实世界，我们有多种类型的光，它们每个表现都不同。一个光源把光投射到物体上，叫做投光。这个教程里我们讨论几种不同的投光类型。学习模拟不同的光源是你未来丰富你的场景的另一个工具。
 
-我们首先将会讨论定向光(Directional Light)，接下来是点光源(Point Light)，它是我们之前学习的光源的拓展，最后我们将会讨论聚光(Spotlight)。在[下一节](06 Multiple lights.md)中我们将讨论如何将这些不同种类的光照类型整合到一个场景之中。
+我们首先讨论定向光(directional light)，接着是作为之前学到知识的扩展的点光(point light)，最后我们讨论聚光(Spotlight)。下面的教程我们会把这几种不同的光类型整合到一个场景中。
 
-# 平行光
+# 定向光
 
-当一个光源处于很远的地方时，来自光源的每条光线就会近似于互相平行。不论物体和/或者观察者的位置，看起来好像所有的光都来自于同一个方向。当我们使用一个假设光源处于**无限**远处的模型时，它就被称为<def>定向光</def>，因为它的所有光线都有着相同的方向，它与光源的位置是没有关系的。
+当一个光源很远的时候，来自光源的每条光线接近于平行。这看起来就像所有的光线来自于同一个方向，无论物体和观察者在哪儿。当一个光源被设置为无限远时，它被称为定向光(Directional Light)，因为所有的光线都有着同一个方向；它会独立于光源的位置。
 
-定向光非常好的一个例子就是太阳。太阳距离我们并不是无限远，但它已经远到在光照计算中可以把它视为无限远了。所以来自太阳的所有光线将被模拟为平行光线，我们可以在下图看到：
+我们知道的定向光源的一个好例子是，太阳。太阳和我们不是无限远，但它也足够远了，在计算光照的时候，我们感觉它就像无限远。在下面的图片里，来自于太阳的所有的光线都被定义为平行光：
 
-![](../img/02/05/light_casters_directional.png)
+![](http://www.learnopengl.com/img/lighting/light_casters_directional.png)
 
-因为所有的光线都是平行的，所以物体与光源的相对位置是不重要的，因为对场景中每一个物体光的方向都是一致的。由于光的位置向量保持一致，场景中每个物体的光照计算将会是类似的。
+因为所有的光线都是平行的，对于场景中的每个物体光的方向都保持一致，物体和光源的位置保持怎样的关系都无所谓。由于光的方向向量保持一致，光照计算会和场景中的其他物体相似。
 
-我们可以定义一个光线方向向量而不是位置向量来模拟一个定向光。着色器的计算基本保持不变，但这次我们将直接使用光的<var>direction</var>向量而不是通过<var>position</var>来计算<var>lightDir</var>向量。
+我们可以通过定义一个光的方向向量，来模拟这样一个定向光，而不是使用光的位置向量。着色器计算保持大致相同的要求，这次我们直接使用光的方向向量来代替用`lightDir`向量和`position`向量的计算：
 
 ```c++
-struct Light {
-    // vec3 position; // 使用定向光就不再需要了
+struct Light
+{
+    // vec3 position; // 现在不在需要光源位置了，因为它是无限远的
     vec3 direction;
-  
     vec3 ambient;
     vec3 diffuse;
     vec3 specular;
@@ -34,90 +34,93 @@ struct Light {
 ...
 void main()
 {
-  vec3 lightDir = normalize(-light.direction);
-  ...
+    vec3 lightDir = normalize(-light.direction);
+    ...
 }
 ```
 
-注意我们首先对<var>light.direction</var>向量取反。我们目前使用的光照计算需求一个从片段**至**光源的光线方向，但人们更习惯定义定向光为一个**从**光源出发的全局方向。所以我们需要对全局光照方向向量取反来改变它的方向，它现在是一个指向光源的方向向量了。而且，记得对向量进行标准化，假设输入向量为一个单位向量是很不明智的。
+注意，我们首先对`light.direction`向量取反。目前我们使用的光照计算需要光的方向作为一个来自片段朝向的光源的方向，但是人们通常更习惯定义一个定向光作为一个全局方向，它从光源发出。所以我们必须对全局光的方向向量取反来改变它的方向；它现在是一个方向向量指向光源。同时，确保对向量进行标准化处理，因为假定输入的向量就是一个单位向量是不明智的。
 
-最终的<var>lightDir</var>向量将和以前一样用在漫反射和镜面光计算中。
+作为结果的`lightDir`向量被使用在`diffuse`和`specular`计算之前。
 
-为了清楚地展示定向光对多个物体具有相同的影响，我们将会再次使用[坐标系统](../01 Getting started/08 Coordinate Systems.md)章节最后的那个箱子派对的场景。如果你错过了派对，我们先定义了十个不同的[箱子位置](https://learnopengl.com/code_viewer.php?code=lighting/light_casters_container_positions)，并对每个箱子都生成了一个不同的模型矩阵，每个模型矩阵都包含了对应的局部-世界坐标变换：
+为了清晰地强调一个定向光对所有物体都有同样的影响，我们再次访问[坐标系教程](../01 Getting started/08 Coordinate Systems.md)结尾部分的箱子场景。例子里我们先定义10个不同的箱子位置，为每个箱子生成不同的模型矩阵，每个模型矩阵包含相应的本地到世界变换：
 
 ```c++
-for(unsigned int i = 0; i < 10; i++)
+for(GLuint i = 0; i < 10; i++)
 {
-    glm::mat4 model;
+    model = glm::mat4();
     model = glm::translate(model, cubePositions[i]);
-    float angle = 20.0f * i;
-    model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));
-    lightingShader.setMat4("model", model);
-
+    GLfloat angle = 20.0f * i;
+    model = glm::rotate(model, angle, glm::vec3(1.0f, 0.3f, 0.5f));
+    glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
     glDrawArrays(GL_TRIANGLES, 0, 36);
 }
 ```
 
-同时，不要忘记定义光源的方向（注意我们将方向定义为**从**光源出发的方向，你可以很容易看到光的方向朝下）。
+同时，不要忘记定义光源的方向（注意，我们把方向定义为：从光源处发出的方向；在下面，你可以快速看到光的方向的指向）：
 
 ```c++
-lightingShader.setVec3("light.direction", -0.2f, -1.0f, -0.3f);
+GLint lightDirPos = glGetUniformLocation(lightingShader.Program, "light.direction");
+glUniform3f(lightDirPos, -0.2f, -1.0f, -0.3f);
 ```
 
 !!! Important
+    
+    我们已经把光的位置和方向向量传递为vec3，但是有些人去想更喜欢把所有的向量设置为vec4.当定义位置向量为vec4的时候，把w元素设置为1.0非常重要，这样平移和投影才会合理的被应用。然而，当定义一个方向向量为vec4时，我们并不想让平移发挥作用（因为它们除了代表方向，其他什么也不是）所以我们把w元素设置为0.0。
 
-	我们一直将光的位置和位置向量定义为`vec3`，但一些人会喜欢将所有的向量都定义为`vec4`。当我们将位置向量定义为一个`vec4`时，很重要的一点是要将w分量设置为1.0，这样变换和投影才能正确应用。然而，当我们定义一个方向向量为`vec4`的时候，我们不想让位移有任何的效果（因为它仅仅代表的是方向），所以我们将w分量设置为0.0。
+    方向向量被表示为：vec4(0.2f, 1.0f, 0.3f, 0.0f)。这可以作为简单检查光的类型的方法：你可以检查w元素是否等于1.0，查看我们现在所拥有的光的位置向量，w是否等于0.0，我们有一个光的方向向量，所以根据那个调整计算方法：
+    
+    ```c++
+    if(lightVector.w == 0.0) // 请留意浮点数错误
+        // 执行定向光照计算
+    
+    else if(lightVector.w == 1.0)
+        // 像上一个教程一样执行顶点光照计算
+    ```
+    
+    有趣的事实：这就是旧OpenGL（固定函数式）决定一个光源是一个定向光还是位置光源，更具这个修改它的光照。
+    
+如果你现在编译应用，飞跃场景，它看起来像有一个太阳一样的光源，把光抛到物体身上。你可以看到`diffuse`和`specular`元素都对该光源进行反射了，就像天空上有一个光源吗？看起来就像这样：
 
-	方向向量就会像这样来表示：`vec4(0.2f, 1.0f, 0.3f, 0.0f)`。这也可以作为一个快速检测光照类型的工具：你可以检测w分量是否等于1.0，来检测它是否是光的位置向量；w分量等于0.0，则它是光的方向向量，这样就能根据这个来调整光照计算了：
+![](http://www.learnopengl.com/img/lighting/light_casters_directional_light.png)
 
-		if(lightVector.w == 0.0) // 注意浮点数据类型的误差
-		  // 执行定向光照计算
-		else if(lightVector.w == 1.0)
-		  // 根据光源的位置做光照计算（与上一节一样）
-
-	你知道吗：这正是旧OpenGL（固定函数式）决定光源是定向光还是位置光源(Positional Light Source)的方法，并根据它来调整光照。
-
-如果你现在编译程序，在场景中自由移动，你就可以看到好像有一个太阳一样的光源对所有的物体投光。你能注意到漫反射和镜面光分量的反应都好像在天空中有一个光源的感觉吗？它会看起来像这样：
-
-![](../img/02/05/light_casters_directional_light.png)
-
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/2.lighting/5.1.light_casters_directional/light_casters_directional.cpp)找到程序的所有代码。
+你可以在这里获得[应用的所有代码](http://learnopengl.com/code_viewer.php?code=lighting/light_casters_directional)，这里是[顶点](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=lighting/light_casters_directional&type=fragment)着色器代码。
 
 # 点光源
 
-定向光对于照亮整个场景的全局光源是非常棒的，但除了定向光之外我们也需要一些分散在场景中的<def>点光源</def>(Point Light)。点光源是处于世界中某一个位置的光源，它会朝着所有方向发光，但光线会随着距离逐渐衰减。想象作为投光物的灯泡和火把，它们都是点光源。
+定向光作为全局光可以照亮整个场景，这非常棒，但是另一方面除了定向光，我们通常也需要几个点光源(Point Light)，在场景里发亮。点光是一个在时间里有位置的光源，它向所有方向发光，光线随距离增加逐渐变暗。想象灯泡和火炬作为投光物，它们可以扮演点光的角色。
 
-![](../img/02/05/light_casters_point.png)
+![](http://www.learnopengl.com/img/lighting/light_casters_point.png)
 
-在之前的教程中，我们一直都在使用一个（简化的）点光源。我们在给定位置有一个光源，它会从它的光源位置开始朝着所有方向散射光线。然而，我们定义的光源模拟的是永远不会衰减的光线，这看起来像是光源亮度非常的强。在大部分的3D模拟中，我们都希望模拟的光源仅照亮光源附近的区域而不是整个场景。
+之前的教程我们已经使用了（最简单的）点光。我们指定了一个光源以及其所在的位置，它从这个位置向所有方向发散光线。然而，我们定义的光源所模拟光线的强度却不会因为距离变远而衰减，这使得看起来像是光源亮度极强。在大多数3D仿真场景中，我们更希望去模拟一个仅仅能照亮靠近光源点附近场景的光源，而不是照亮整个场景的光源。
 
-如果你将10个箱子加入到上一节光照场景中，你会注意到在最后面的箱子和在灯面前的箱子都以相同的强度被照亮，并没有定义一个公式来将光随距离衰减。我们希望在后排的箱子与前排的箱子相比仅仅是被轻微地照亮。
+如果你把10个箱子添加到之前教程的光照场景中，你会注意到黑暗中的每个箱子都会有同样的亮度，就像箱子在光照的前面；没有公式定义光的距离衰减。我们想让黑暗中与光源比较近的箱子被轻微地照亮。
 
 ## 衰减
 
-随着光线传播距离的增长逐渐削减光的强度通常叫做<def>衰减</def>(Attenuation)。随距离减少光强度的一种方式是使用一个线性方程。这样的方程能够随着距离的增长线性地减少光的强度，从而让远处的物体更暗。然而，这样的线性方程通常会看起来比较假。在现实世界中，灯在近处通常会非常亮，但随着距离的增加光源的亮度一开始会下降非常快，但在远处时剩余的光强度就会下降的非常缓慢了。所以，我们需要一个不同的公式来减少光的强度。
+随着光线穿越距离的变远使得亮度也相应地减少的现象，通常称之为**衰减(Attenuation)**。一种随着距离减少亮度的方式是使用线性等式。这样的一个随着距离减少亮度的线性方程，可以使远处的物体更暗。然而，这样的线性方程效果会有点假。在真实世界，通常光在近处时非常亮，但是一个光源的亮度，开始的时候减少的非常快，之后随着距离的增加，减少的速度会慢下来。我们需要一种不同的方程来减少光的亮度。
 
-幸运的是一些聪明的人已经帮我们解决了这个问题。下面这个公式根据片段距光源的距离计算了衰减值，之后我们会将它乘以光的强度向量：
+幸运的是一些聪明人已经早就把它想到了。下面的方程把一个片段的光的亮度除以一个已经计算出来的衰减值，这个值根据光源的远近得到：
 
 $$
 \begin{equation} F_{att} = \frac{1.0}{K_c + K_l * d + K_q * d^2} \end{equation}
 $$
 
-在这里\(d\)代表了片段距光源的距离。接下来为了计算衰减值，我们定义3个（可配置的）项：<def>常数</def>项\(K_c\)、<def>一次</def>项\(K_l\)和<def>二次</def>项\(K_q\)。
+在这里\(d\)代表片段到光源的距离。为了计算衰减值，我们定义3个（可配置）项：**常数**项\(K_c\)，**一次**项\(K_l\)和**二次**项\(K_q\)。
 
-- 常数项通常保持为1.0，它的主要作用是保证分母永远不会比1小，否则的话在某些距离上它反而会增加强度，这肯定不是我们想要的效果。
-- 一次项会与距离值相乘，以线性的方式减少强度。
-- 二次项会与距离的平方相乘，让光源以二次递减的方式减少强度。二次项在距离比较小的时候影响会比一次项小很多，但当距离值比较大的时候它就会比一次项更大了。
+- 常数项通常是1.0，它的作用是保证分母永远不会比1小，因为它可以利用一定的距离增加亮度，这个结果不会影响到我们所寻找的。
+- 一次项用于与距离值相乘，这会以线性的方式减少亮度。
+- 二次项用于与距离的平方相乘，为光源设置一个亮度的二次递减。二次项在距离比较近的时候相比一次项会比一次项更小，但是当距离更远的时候比一次项更大。
 
-由于二次项的存在，光线会在大部分时候以线性的方式衰退，直到距离变得足够大，让二次项超过一次项，光的强度会以更快的速度下降。这样的结果就是，光在近距离时亮度很高，但随着距离变远亮度迅速降低，最后会以更慢的速度减少亮度。下面这张图显示了在100的距离内衰减的效果：
+由于二次项的光会以线性方式减少，指导距离足够大的时候，就会超过一次项，之后，光的亮度会减少的更快。最后的效果就是光在近距离时，非常量，但是距离变远亮度迅速降低，最后亮度降低速度再次变慢。下面的图展示了在100以内的范围，这样的衰减效果。
 
-![](../img/02/05/attenuation.png)
+![](http://www.learnopengl.com/img/lighting/attenuation.png)
 
-你可以看到光在近距离的时候有着最高的强度，但随着距离增长，它的强度明显减弱，并缓慢地在距离大约100的时候强度接近0。这正是我们想要的。
+你可以看到当距离很近的时候光有最强的亮度，但是随着距离增大，亮度明显减弱，大约接近100的时候，就会慢下来。这就是我们想要的。
 
 ### 选择正确的值
 
-但是，该对这三个项设置什么值呢？正确地设定它们的值取决于很多因素：环境、希望光覆盖的距离、光的类型等。在大多数情况下，这都是经验的问题，以及适量的调整。下面这个表格显示了模拟一个（大概）真实的，覆盖特定半径（距离）的光源时，这些项可能取的一些值。第一列指定的是在给定的三项时光所能覆盖的距离。这些值是大多数光源很好的起始点，它们由[Ogre3D的Wiki](http://www.ogre3d.org/tikiwiki/tiki-index.php?page=-Point+Light+Attenuation)所提供：
+但是，我们把这三个项设置为什么值呢？正确的值的设置由很多因素决定：环境、你希望光所覆盖的距离范围、光的类型等。大多数场合，这是经验的问题，也要适度调整。下面的表格展示一些各项的值，它们模拟现实（某种类型的）光源，覆盖特定的半径（距离）。第一栏定义一个光的距离，它覆盖所给定的项。这些值是大多数光的良好开始，它是来自Ogre3D的维基的礼物：
 
 距离|常数项|一次项|二次项
 -------|------|-----|------
@@ -134,185 +137,186 @@ $$
 600|1.0|0.007|0.0002
 3250|1.0|0.0014|0.000007
 
-你可以看到，常数项\(K_c\)在所有的情况下都是1.0。一次项\(K_l\)为了覆盖更远的距离通常都很小，二次项\(K_q\)甚至更小。尝试对这些值进行实验，看看它们在你的实现中有什么效果。在我们的环境中，32到100的距离对大多数的光源都足够了。
+就像你所看到的，常数项\(K_c\)一直都是1.0。一次项\(K_l\)为了覆盖更远的距离通常很小，二次项\(K_q\)就更小了。尝试用这些值进行实验，看看它们在你的实现中各自的效果。我们的环境中，32到100的距离对大多数光通常就足够了。
 
 ### 实现衰减
 
-为了实现衰减，在片段着色器中我们还需要三个额外的值：也就是公式中的常数项、一次项和二次项。它们最好储存在之前定义的<fun>Light</fun>结构体中。注意我们使用上一节中计算<var>lightDir</var>的方法，而不是上面**定向光**部分的。
+为了实现衰减，在着色器中我们会需要三个额外数值：也就是公式的常量、一次项和二次项。最好把它们储存在之前定义的Light结构体中。要注意的是我们计算`lightDir`，就是在前面的教程中我们所做的，不是像之前的定向光的那部分。
 
 ```c++
-struct Light {
-    vec3 position;  
-  
+struct Light
+{
+    vec3 position;
     vec3 ambient;
     vec3 diffuse;
     vec3 specular;
-	
     float constant;
     float linear;
     float quadratic;
 };
 ```
 
-然后我们将在OpenGL中设置这些项：我们希望光源能够覆盖50的距离，所以我们会使用表格中对应的常数项、一次项和二次项：
+然后，我们在OpenGL中设置这些项：我们希望光覆盖50的距离，所以我们会使用上面的表格中合适的常数项、一次项和二次项：
 
 ```c++
-lightingShader.setFloat("light.constant",  1.0f);
-lightingShader.setFloat("light.linear",    0.09f);
-lightingShader.setFloat("light.quadratic", 0.032f);
+glUniform1f(glGetUniformLocation(lightingShader.Program, "light.constant"), 1.0f);
+glUniform1f(glGetUniformLocation(lightingShader.Program, "light.linear"), 0.09);
+glUniform1f(glGetUniformLocation(lightingShader.Program, "light.quadratic"), 0.032);
 ```
 
-在片段着色器中实现衰减还是比较直接的：我们根据公式计算衰减值，之后再分别乘以环境光、漫反射和镜面光分量。
+在片段着色器中实现衰减很直接：我们根据公式简单的计算衰减值，在乘以`ambient`、`diffuse`和`specular`元素。
 
-我们仍需要公式中距光源的距离，还记得我们是怎么计算一个向量的长度的吗？我们可以通过获取片段和光源之间的向量差，并获取结果向量的长度作为距离项。我们可以使用GLSL内建的<fun>length</fun>函数来完成这一点：
+我们需要将光源的距离提供给公式；还记得我们是怎样计算向量的长度吗？我们可以通过获取片段和光源之间的不同向量把向量的长度结果作为距离项。我们可以使用GLSL的内建`length`函数做这件事：
 
 ```c++
-float distance    = length(light.position - FragPos);
-float attenuation = 1.0 / (light.constant + light.linear * distance + 
-    		    light.quadratic * (distance * distance));
+float distance = length(light.position - FragPos);
+float attenuation = 1.0f / (light.constant + light.linear*distance +light.quadratic*(distance*distance));
 ```
 
-接下来，我们将包含这个衰减值到光照计算中，将它分别乘以环境光、漫反射和镜面光颜色。
+然后，我们在光照计算中，通过把衰减值乘以`ambient`、`diffuse`和`specular`颜色，包含这个衰减值。
 
 !!! Important
 
-	我们可以将环境光分量保持不变，让环境光照不会随着距离减少，但是如果我们使用多于一个的光源，所有的环境光分量将会开始叠加，所以在这种情况下我们也希望衰减环境光照。简单实验一下，看看什么才能在你的环境中效果最好。
+    我们可以可以把`ambient`元素留着不变，这样`amient`光照就不会随着距离减少，但是如果我们使用多余1个的光源，所有的`ambient`元素会开始叠加，因此这种情况，我们希望`ambient`光照也衰减。简单的调试出对于你的环境来说最好的效果。
 
 ```c++
-ambient  *= attenuation; 
-diffuse  *= attenuation;
+ambient *= attenuation;
+diffuse *= attenuation;
 specular *= attenuation;
 ```
 
-如果你运行程序的话，你会获得这样的结果：
+如果你运行应用后获得这样的效果：
 
-![](../img/02/05/light_casters_point_light.png)
+![](http://learnopengl.com/img/lighting/light_casters_point_light.png)
 
-你可以看到，只有前排的箱子被照亮的，距离最近的箱子是最亮的。后排的箱子一点都没有照亮，因为它们离光源实在是太远了。你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/2.lighting/5.2.light_casters_point/light_casters_point.cpp)找到程序的代码。
+你可以看到现在只有最近处的箱子的前面被照得最亮。后面的箱子一点都没被照亮，因为它们距离光源太远了。你可以在这里找到[应用源码](http://learnopengl.com/code_viewer.php?code=lighting/light_casters_point)和[片段着色器](http://learnopengl.com/code_viewer.php?code=lighting/light_casters_point&type=fragment)的代码。
 
-点光源就是一个能够配置位置和衰减的光源。它是我们光照工具箱中的又一个光照类型。
+定点光就是一个可配的置位置和衰减值应用到光照计算中。还有另一种类型光可用于我们照明库当中。
 
-# 聚光
 
-我们要讨论的最后一种类型的光是<def>聚光</def>(Spotlight)。聚光是位于环境中某个位置的光源，它只朝一个特定方向而不是所有方向照射光线。这样的结果就是只有在聚光方向的特定半径内的物体才会被照亮，其它的物体都会保持黑暗。聚光很好的例子就是路灯或手电筒。
+## 聚光
 
-OpenGL中聚光是用一个世界空间位置、一个方向和一个<def>切光</def>角(Cutoff Angle)来表示的，切光角指定了聚光的半径（译注：是圆锥的半径不是距光源距离那个半径）。对于每个片段，我们会计算片段是否位于聚光的切光方向之间（也就是在锥形内），如果是的话，我们就会相应地照亮片段。下面这张图会让你明白聚光是如何工作的：
+我们要讨论的最后一种类型光是聚光(Spotlight)。聚光是一种位于环境中某处的光源，它不是向所有方向照射，而是只朝某个方向照射。结果是只有一个聚光照射方向的确定半径内的物体才会被照亮，其他的都保持黑暗。聚光的好例子是路灯或手电筒。
 
-![](../img/02/05/light_casters_spotlight_angles.png)
+OpenGL中的聚光用世界空间位置，一个方向和一个指定了聚光半径的切光角来表示。我们计算的每个片段，如果片段在聚光的切光方向之间（就是在圆锥体内），我们就会把片段照亮。下面的图可以让你明白聚光是如何工作的：
 
-- `LightDir`：从片段指向光源的向量。
-- `SpotDir`：聚光所指向的方向。
-- `Phi`\(\phi\)：指定了聚光半径的切光角。落在这个角度之外的物体都不会被这个聚光所照亮。
-- `Theta`\(\theta\)：<var>LightDir</var>向量和<var>SpotDir</var>向量之间的夹角。在聚光内部的话\(\theta\)值应该比\(\phi\)值小。
+![](http://www.learnopengl.com/img/lighting/light_casters_spotlight_angles.png)
 
-所以我们要做的就是计算<var>LightDir</var>向量和<var>SpotDir</var>向量之间的点积（还记得它会返回两个单位向量夹角的余弦值吗？），并将它与切光角\(\phi\)值对比。你现在应该了解聚光究竟是什么了，下面我们将以手电筒的形式创建一个聚光。
+* `LightDir`：从片段指向光源的向量。
+* `SpotDir`：聚光所指向的方向。
+* `Phi`\(\phi\)：定义聚光半径的切光角。每个落在这个角度之外的，聚光都不会照亮。
+* `Theta`\(\theta\)：`LightDir`向量和`SpotDir`向量之间的角度。\(\theta\)值应该比\(\Phi\)值小，这样才会在聚光内。
+
+所以我们大致要做的是，计算`LightDir`向量和`SpotDir`向量的点乘（返回两个单位向量的点乘，还记得吗？），然后在和切光角\(\phi\)对比。现在你应该明白聚光是我们下面将创建的手电筒的范例。
 
 ## 手电筒
 
-手电筒(Flashlight)是一个位于观察者位置的聚光，通常它都会瞄准玩家视角的正前方。基本上说，手电筒就是普通的聚光，但它的位置和方向会随着玩家的位置和朝向不断更新。
+手电筒(Flashlight)是一个坐落在观察者位置的聚光，通常瞄准玩家透视图的前面。基本上说，一个手电筒是一个普通的聚光，但是根据玩家的位置和方向持续的更新它的位置和方向。
 
-所以，在片段着色器中我们需要的值有聚光的位置向量（来计算光的方向向量）、聚光的方向向量和一个切光角。我们可以将它们储存在<fun>Light</fun>结构体中：
+所以我们需要为片段着色器提供的值，是聚光的位置向量（来计算光的方向坐标），聚光的方向向量和切光角。我们可以把这些值储存在`Light`结构体中：
 
 ```c++
-struct Light {
-    vec3  position;
-    vec3  direction;
+struct Light
+{
+    vec3 position;
+    vec3 direction;
     float cutOff;
     ...
 };
 ```
 
-接下来我们将合适的值传到着色器中：
+下面我们把这些适当的值传给着色器：
 
 ```c++
-lightingShader.setVec3("light.position",  camera.Position);
-lightingShader.setVec3("light.direction", camera.Front);
-lightingShader.setFloat("light.cutOff",   glm::cos(glm::radians(12.5f)));
+glUniform3f(lightPosLoc, camera.Position.x, camera.Position.y, camera.Position.z);
+glUniform3f(lightSpotdirLoc, camera.Front.x, camera.Front.y, camera.Front.z);
+glUniform1f(lightSpotCutOffLoc, glm::cos(glm::radians(12.5f)));
 ```
 
-你可以看到，我们并没有给切光角设置一个角度值，反而是用角度值计算了一个余弦值，将余弦结果传递到片段着色器中。这样做的原因是在片段着色器中，我们会计算`LightDir`和`SpotDir`向量的点积，这个点积返回的将是一个余弦值而不是角度值，所以我们不能直接使用角度值和余弦值进行比较。为了获取角度值我们需要计算点积结果的反余弦，这是一个开销很大的计算。所以为了节约一点性能开销，我们将会计算切光角对应的余弦值，并将它的结果传入片段着色器中。由于这两个角度现在都由余弦角来表示了，我们可以直接对它们进行比较而不用进行任何开销高昂的计算。
+你可以看到，我们为切光角设置一个角度，但是我们根据一个角度计算了余弦值，把这个余弦结果传给了片段着色器。这么做的原因是在片段着色器中，我们计算`LightDir`和`SpotDir`向量的点乘，而点乘返回一个余弦值，不是一个角度，所以我们不能直接把一个角度和余弦值对比。为了获得这个角度，我们必须计算点乘结果的反余弦，这个操作开销是很大的。所以为了节约一些性能，我们先计算给定切光角的余弦值，然后把结果传递给片段着色器。由于每个角度都被表示为余弦了，我们可以直接对比它们，而不用进行任何开销高昂的操作。
 
-接下来就是计算\(\theta\)值，并将它和切光角\(\phi\)对比，来决定是否在聚光的内部：
+现在剩下要做的是计算\(\theta\)值，用它和\(\phi\)值对比，以决定我们是否在或不在聚光的内部：
 
 ```c++
 float theta = dot(lightDir, normalize(-light.direction));
-    
-if(theta > light.cutOff) 
-{       
-  // 执行光照计算
+if(theta > light.cutOff)
+{
+    // 执行光照计算
 }
-else  // 否则，使用环境光，让场景在聚光之外时不至于完全黑暗
-  color = vec4(light.ambient * vec3(texture(material.diffuse, TexCoords)), 1.0);
+else // 否则使用环境光，使得场景不至于完全黑暗
+color = vec4(light.ambient*vec3(texture(material.diffuse,TexCoords)), 1.0f);
 ```
 
-我们首先计算了<var>lightDir</var>和取反的<var>direction</var>向量（取反的是因为我们想让向量指向光源而不是从光源出发）之间的点积。记住要对所有的相关向量标准化。
+我们首先计算`lightDir`和取反的`direction`向量的点乘（它是取反过的因为我们想要向量指向光源，而不是从光源作为指向出发点。译注：前面的`specular`教程中作者却用了相反的表示方法，这里读者可以选择喜欢的表达方式）。确保对所有相关向量进行了标准化处理。
 
 !!! Important
 
-	你可能奇怪为什么在if条件中使用的是 > 符号而不是 < 符号。<var>theta</var>不应该比光的切光角更小才是在聚光内部吗？这并没有错，但不要忘记角度值现在都由余弦值来表示的。一个0度的角度表示的是1.0的余弦值，而一个90度的角度表示的是0.0的余弦值，你可以在下图中看到：
+    你可能奇怪为什么if条件中使用>符号而不是<符号。为了在聚光以内，`theta`不是应该比光的切光值更小吗？这没错，但是不要忘了，角度值是以余弦值来表示的，一个0度的角表示为1.0的余弦值，当一个角是90度的时候被表示为0.0的余弦值，你可以在这里看到：
 
-    ![](../img/02/05/light_casters_cos.png)
+    ![](http://www.learnopengl.com/img/lighting/light_casters_cos.png)
 
-	你现在可以看到，余弦值越接近1.0，它的角度就越小。这也就解释了为什么<var>theta</var>要比切光值更大了。切光值目前设置为12.5的余弦，约等于0.9978，所以在0.9979到1.0内的<var>theta</var>值才能保证片段在聚光内，从而被照亮。
+    现在你可以看到，余弦越是接近1.0，角度就越小。这就解释了为什么θ需要比切光值更大了。切光值当前被设置为12.5的余弦，它等于0.9978，所以θ的余弦值在0.9979和1.0之间，片段会在聚光内，被照亮。
 
-运行程序，你将会看到一个聚光，它仅会照亮聚光圆锥内的片段。看起来像是这样的：
+运行应用，在聚光内的片段才会被照亮。这看起来像这样：
 
-![](../img/02/05/light_casters_spotlight_hard.png)
+![](http://www.learnopengl.com/img/lighting/light_casters_spotlight_hard.png)
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/2.lighting/5.3.light_casters_spot/light_casters_spot.cpp)获得全部源码。
+你可以在这里获得[全部源码](http://learnopengl.com/code_viewer.php?code=lighting/light_casters_spotlight_hard)和[片段着色器的源码](http://learnopengl.com/code_viewer.php?code=lighting/light_casters_spotlight_hard&type=fragment)。
 
-但这仍看起来有些假，主要是因为聚光有一圈硬边。当一个片段遇到聚光圆锥的边缘时，它会完全变暗，没有一点平滑的过渡。一个真实的聚光将会在边缘处逐渐减少亮度。
+它看起来仍然有点假，原因是聚光有了一个硬边。片段着色器一旦到达了聚光的圆锥边缘，它就立刻黑了下来，却没有任何平滑减弱的过度。一个真实的聚光的光会在它的边界处平滑减弱的。
 
 ## 平滑/软化边缘
 
-为了创建一种看起来边缘平滑的聚光，我们需要模拟聚光有一个<def>内</def>圆锥(Inner Cone)和一个<def>外</def>圆锥(Outer Cone)。我们可以将内圆锥设置为上一部分中的那个圆锥，但我们也需要一个外圆锥，来让光从内圆锥逐渐减暗，直到外圆锥的边界。
+为创建聚光的平滑边，我们希望去模拟的聚光有一个内圆锥和外圆锥。我们可以把内圆锥设置为前面部分定义的圆锥，我们希望外圆锥从内边到外边逐步的变暗。
 
-为了创建一个外圆锥，我们只需要再定义一个余弦值来代表聚光方向向量和外圆锥向量（等于它的半径）的夹角。然后，如果一个片段处于内外圆锥之间，将会给它计算出一个0.0到1.0之间的强度值。如果片段在内圆锥之内，它的强度就是1.0，如果在外圆锥之外强度值就是0.0。
+为创建外圆锥，我们简单定义另一个余弦值，它代表聚光的方向向量和外圆锥的向量（等于它的半径）的角度。然后，如果片段在内圆锥和外圆锥之间，就会给它计算出一个0.0到1.0之间的亮度。如果片段在内圆锥以内这个亮度就等于1.0，如果在外面就是0.0。
 
-我们可以用下面这个公式来计算这个值：
+我们可以使用下面的公式计算这样的值：
 
 $$
 \begin{equation} I = \frac{\theta - \gamma}{\epsilon} \end{equation}
 $$
 
-这里\(\epsilon\)(Epsilon)是内（\(\phi\)）和外圆锥（\(\gamma\)）之间的余弦值差（\(\epsilon =  \phi - \gamma\)）。最终的\(I\)值就是在当前片段聚光的强度。
+这里\(\epsilon\)是内部（\(\phi\)）和外部圆锥（\(\gamma\)）（\epsilon =  \phi - \gamma）的差。结果\(I\)的值是聚光在当前片段的亮度。
 
-很难去表现这个公式是怎么工作的，所以我们用一些实例值来看看：
+很难用图画描述出这个公式是怎样工作的，所以我们尝试使用一个例子：
 
-\(\theta\)|\(\theta\)（角度）|\(\phi\)（内光切）|\(\phi\)（角度）|\(\gamma\)（外光切）|\(\gamma\)（角度）|\(\epsilon\)|\(I\)
+
+\(\theta\)|\(\theta\)（角度）|\(\phi\)（内切）|\(\phi\)（角度）|\(\gamma\)（外切）|\(\gamma\)（角度）|\(\epsilon\)|\(I\)
 --|---|---|---|---|---|---|---
 0.87|30|0.91|25|0.82|35|0.91 - 0.82 = 0.09|0.87 - 0.82 / 0.09 = 0.56
 0.9|26|0.91|25|0.82|35|0.91 - 0.82 = 0.09|0.9 - 0.82 / 0.09 = 0.89
 0.97|14|0.91|25|0.82|35|0.91 - 0.82 = 0.09|0.97 - 0.82 / 0.09 = 1.67
+0.97|14|0.91|25|0.82|35|0.91 - 0.82 = 0.09|0.97 - 0.82 / 0.09 = 1.67
 0.83|34|0.91|25|0.82|35|0.91 - 0.82 = 0.09|0.83 - 0.82 / 0.09 = 0.11
 0.64|50|0.91|25|0.82|35|0.91 - 0.82 = 0.09|0.64 - 0.82 / 0.09 = -2.0
-0.966|15|0.9978|12.5|0.953|17.5|0.9978 - 0.953 = 0.0448|0.966 - 0.953 / 0.0448 = 0.29
+0.966|15|0.9978|12.5|0.953|17.5|0.966 - 0.953 = 0.0448|0.966 - 0.953 / 0.0448 = 0.29
 
-你可以看到，我们基本是在内外余弦值之间根据\(\theta\)插值。如果你仍不明白发生了什么，不必担心，只需要记住这个公式就好了，在你更聪明的时候再回来看看。
+就像你看到的那样我们基本是根据θ在外余弦和内余弦之间插值。如果你仍然不明白怎么继续，不要担心。你可以简单的使用这个公式计算，当你更加老道和明白的时候再来看。
 
-我们现在有了一个在聚光外是负的，在内圆锥内大于1.0的，在边缘处于两者之间的强度值了。如果我们正确地约束(Clamp)这个值，在片段着色器中就不再需要`if-else`了，我们能够使用计算出来的强度值直接乘以光照分量：
+由于我们现在有了一个亮度值，当在聚光外的时候是个负的，当在内部圆锥以内大于1。如果我们适当地把这个值固定，我们在片段着色器中就再不需要if-else了，我们可以简单地用计算出的亮度值乘以光的元素：
 
 ```c++
-float theta     = dot(lightDir, normalize(-light.direction));
-float epsilon   = light.cutOff - light.outerCutOff;
-float intensity = clamp((theta - light.outerCutOff) / epsilon, 0.0, 1.0);    
+float theta = dot(lightDir, normalize(-light.direction));
+float epsilon = light.cutOff - light.outerCutOff;
+float intensity = clamp((theta - light.outerCutOff) / epsilon,0.0, 1.0);
 ...
-// 将不对环境光做出影响，让它总是能有一点光
-diffuse  *= intensity;
-specular *= intensity;
+// We’ll leave ambient unaffected so we always have a little
+light.diffuse* = intensity;
+specular* = intensity;
 ...
 ```
 
-注意我们使用了<fun>clamp</fun>函数，它把第一个参数约束(Clamp)在了0.0到1.0之间。这保证强度值不会在[0, 1]区间之外。
+注意，我们使用了`clamp`函数，它把第一个参数固定在0.0和1.0之间。这保证了亮度值不会超出[0, 1]以外。
 
-确定你将<var>outerCutOff</var>值添加到了<fun>Light</fun>结构体之中，并在程序中设置它的uniform值。下面的图片中，我们使用的内切光角是12.5，外切光角是17.5：
+确定你把`outerCutOff`值添加到了`Light`结构体，并在应用中设置了它的uniform值。对于下面的图片，内部切光角`12.5f`，外部切光角是`17.5f`：
 
-![](../img/02/05/light_casters_spotlight.png)
+![](http://www.learnopengl.com/img/lighting/light_casters_spotlight.png)
 
-啊，这样看起来就好多了。稍微对内外切光角实验一下，尝试创建一个更能符合你需求的聚光。你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/2.lighting/5.4.light_casters_spot_soft/light_casters_spot_soft.cpp)找到程序的源码。
+看起来好多了。仔细看看内部和外部切光角，尝试创建一个符合你求的聚光。可以在这里找到应用源码，以及片段的源代码。
 
-这样的手电筒/聚光类型的灯光非常适合恐怖游戏，结合定向光和点光源，环境就会开始被照亮了。在[下一节](06 Multiple lights.md)的教程中，我们将会结合我们至今讨论的所有光照和技巧。
+这样的一个手电筒/聚光类型的灯光非常适合恐怖游戏，结合定向和点光，环境会真的开始被照亮了。[下一节](06 Multiple lights.md)中，我们会结合所有我们目前讨论了的光和技巧。
 
 ## 练习
 
-- 尝试实验一下上面的所有光照类型和它们的片段着色器。试着对一些向量进行取反，并使用 < 来代替 >。试着解释不同视觉效果产生的原因。
+- 试着修改上面的各种不同种类的光源及其片段着色器。试着将部分矢量进行反向并尝试使用 < 来代替 > 。试着解释这些修改导致不同显示效果的原因。

docs/02 Lighting/06 Multiple lights.md

@@ -3,48 +3,48 @@
 原文     | [Multiple lights](http://learnopengl.com/#!Lighting/Multiple-lights)
       ---|---
 作者     | JoeyDeVries
-翻译     | [Geequlim](http://geequlim.com), Krasjet
-校对     | [AoZhang](https://github.com/SuperAoao)
+翻译     | [Geequlim](http://geequlim.com)
+校对     | [Geequlim](http://geequlim.com)
 
-我们在前面的教程中已经学习了许多关于OpenGL中光照的知识，其中包括风氏着色(Phong Shading)、材质(Material)、光照贴图(Lighting Map)以及不同种类的投光物(Light Caster)。在这一节中，我们将结合之前学过的所有知识，创建一个包含六个光源的完全照明场景。我们将模拟一个类似太阳的定向光(Directional Light)光源，四个分散在场景中的点光源(Point Light)，以及一个手电筒(Flashlight)。
+我们在前面的教程中已经学习了许多关于OpenGL 光照的知识，其中包括冯氏照明模型（Phong shading）、光照材质（Materials）、光照图（Lighting maps）以及各种投光物（Light casters）。本教程将结合上述所学的知识，创建一个包含六个光源的场景。我们将模拟一个类似阳光的平行光（Directional light）和4个定点光（Point lights）以及一个手电筒(Flashlight).
 
-为了在场景中使用多个光源，我们希望将光照计算封装到GLSL<def>函数</def>中。这样做的原因是，每一种光源都需要一种不同的计算方法，而一旦我们想对多个光源进行光照计算时，代码很快就会变得非常复杂。如果我们只在<fun>main</fun>函数中进行所有的这些计算，代码很快就会变得难以理解。
+要在场景中使用多光源我们需要封装一些GLSL函数用来计算光照。如果我们对每个光源都去写一遍光照计算的代码，这将是一件令人恶心的事情，并且这些放在main函数中的代码将难以理解，所以我们将一些操作封装为函数。
 
-GLSL中的函数和C函数很相似，它有一个函数名、一个返回值类型，如果函数不是在main函数之前声明的，我们还必须在代码文件顶部声明一个原型。我们对每个光照类型都创建一个不同的函数：定向光、点光源和聚光。
+GLSL中的函数与C语言的非常相似，它需要一个函数名、一个返回值类型。并且在调用前必须提前声明。接下来我们将为下面的每一种光照来写一个函数。
 
-当我们在场景中使用多个光源时，通常使用以下方法：我们需要有一个单独的颜色向量代表片段的输出颜色。对于每一个光源，它对片段的贡献颜色将会加到片段的输出颜色向量上。所以场景中的每个光源都会计算它们各自对片段的影响，并结合为一个最终的输出颜色。大体的结构会像是这样：
+当我们在场景中使用多个光源时一般使用以下途径：创建一个代表输出颜色的向量。每一个光源都对输出颜色贡献一些颜色。因此，场景中的每个光源将进行独立运算，并且运算结果都对最终的输出颜色有一定影响。下面是使用这种方式进行多光源运算的一般结构：
 
 ```c++
-out vec4 FragColor;
-  
+out vec4 color;
+
 void main()
 {
-  // 定义一个输出颜色值
+  // 定义输出颜色
   vec3 output;
-  // 将定向光的贡献加到输出中
+  // 将平行光的运算结果颜色添加到输出颜色
   output += someFunctionToCalculateDirectionalLight();
-  // 对所有的点光源也做相同的事情
+  // 同样，将定点光的运算结果颜色添加到输出颜色
   for(int i = 0; i < nr_of_point_lights; i++)
   	output += someFunctionToCalculatePointLight();
-  // 也加上其它的光源（比如聚光）
+  // 添加其他光源的计算结果颜色（如投射光）
   output += someFunctionToCalculateSpotLight();
-  
-  FragColor = vec4(output, 1.0);
-}
+
+  color = vec4(output, 1.0);
+}  
 ```
 
-实际的代码对每一种实现都可能不同，但大体的结构都是差不多的。我们定义了几个函数，用来计算每个光源的影响，并将最终的结果颜色加到输出颜色向量上。例如，如果两个光源都很靠近一个片段，那么它们所结合的贡献将会形成一个比单个光源照亮时更加明亮的片段。
+即使对每一种光源的运算实现不同，但此算法的结构一般是与上述出入不大的。我们将定义几个用于计算各个光源的函数，并将这些函数的结算结果（返回颜色）添加到输出颜色向量中。例如，靠近被照射物体的光源计算结果将返回比远离背照射物体的光源更明亮的颜色。
 
-## 定向光
+## 平行光
 
-我们需要在片段着色器中定义一个函数来计算定向光对相应片段的贡献：它接受一些参数并计算一个定向光照颜色。
+我们要在片段着色器中定义一个函数用来计算平行光(Directional light)在对应的照射点上的光照颜色，这个函数需要几个参数并返回一个计算平行光照结果的颜色。
 
-首先，我们需要定义一个定向光源最少所需要的变量。我们可以将这些变量储存在一个叫做<fun>DirLight</fun>的结构体中，并将它定义为一个uniform。需要的变量在[上一节](05 Light casters.md)中都介绍过：
+首先我们需要设置一系列用于表示平行光的变量，正如上一节中所讲过的，我们可以将这些变量定义在一个叫做**DirLight**的结构体中，并定义一个这个结构体类型的uniform变量。
 
 ```c++
 struct DirLight {
     vec3 direction;
-  
+
     vec3 ambient;
     vec3 diffuse;
     vec3 specular;
@@ -52,85 +52,84 @@ struct DirLight {
 uniform DirLight dirLight;
 ```
 
-接下来我们可以将<var>dirLight</var>传入一个有着以下原型的函数。
+之后我们可以将`dirLight`这个uniform变量作为下面这个函数原型的参数。
 
 ```c++
-vec3 CalcDirLight(DirLight light, vec3 normal, vec3 viewDir);
+vec3 CalcDirLight(DirLight light, vec3 normal, vec3 viewDir);  
 ```
 
 !!! Important
 
-	和C/C++一样，如果我们想调用一个函数（这里是在<fun>main</fun>函数中调用），这个函数需要在调用者的行数之前被定义过。在这个例子中我们更喜欢在<fun>main</fun>函数以下定义函数，所以上面要求就不满足了。所以，我们需要在<fun>main</fun>函数之上定义函数的原型，这和C语言中是一样的。
-
-你可以看到，这个函数需要一个<fun>DirLight</fun>结构体和其它两个向量来进行计算。如果你认真完成了上一节的话，这个函数的内容应该理解起来很容易：
+        和C/C++一样，我们调用一个函数的前提是这个函数在调用前已经被声明过（此例中我们是在main函数中调用）。通常情况下我们都将函数定义在main函数之后，为了能在main函数中调用这些函数，我们就必须在main函数之前声明这些函数的原型，这就和我们写C语言是一样的。
+        
+你已经知道，这个函数需要一个`DirLight`和两个其他的向量作为参数来计算光照。如果你看过之前的教程的话，你会觉得下面的函数定义得一点也不意外：
 
 ```c++
 vec3 CalcDirLight(DirLight light, vec3 normal, vec3 viewDir)
 {
     vec3 lightDir = normalize(-light.direction);
-    // 漫反射着色
+    // 计算漫反射强度
     float diff = max(dot(normal, lightDir), 0.0);
-    // 镜面光着色
+    // 计算镜面反射强度
     vec3 reflectDir = reflect(-lightDir, normal);
     float spec = pow(max(dot(viewDir, reflectDir), 0.0), material.shininess);
-    // 合并结果
+    // 合并各个光照分量
     vec3 ambient  = light.ambient  * vec3(texture(material.diffuse, TexCoords));
     vec3 diffuse  = light.diffuse  * diff * vec3(texture(material.diffuse, TexCoords));
     vec3 specular = light.specular * spec * vec3(texture(material.specular, TexCoords));
     return (ambient + diffuse + specular);
-}
+}  
 ```
 
-我们基本上只是从上一节中复制了代码，并使用函数参数的两个向量来计算定向光的贡献向量。最终环境光、漫反射和镜面光的贡献将会合并为单个颜色向量返回。
+我们从之前的教程中复制了代码，并用两个向量来作为函数参数来计算出平行光的光照颜色向量，该结果是一个由该平行光的环境反射、漫反射和镜面反射的各个分量组成的一个向量。
 
 ## 点光源
 
-和定向光一样，我们也希望定义一个用于计算点光源对相应片段贡献，以及衰减，的函数。同样，我们定义一个包含了点光源所需所有变量的结构体：
+和计算平行光一样，我们同样需要定义一个函数用于计算点光源(Point Light)。同样的，我们定义一个包含点光源所需属性的结构体：
 
 ```c++
 struct PointLight {
     vec3 position;
-    
+
     float constant;
     float linear;
-    float quadratic;
+    float quadratic;  
 
     vec3 ambient;
     vec3 diffuse;
     vec3 specular;
 };  
-#define NR_POINT_LIGHTS 4
+#define NR_POINT_LIGHTS 4  
 uniform PointLight pointLights[NR_POINT_LIGHTS];
 ```
 
-你可以看到，我们在GLSL中使用了预处理指令来定义了我们场景中点光源的数量。接着我们使用了这个<var>NR_POINT_LIGHTS</var>常量来创建了一个<fun>PointLight</fun>结构体的数组。GLSL中的数组和C数组一样，可以使用一对方括号来创建。现在我们有四个待填充数据的<fun>PointLight</fun>结构体。
+如你所见，我们在GLSL中使用预处理器指令来定义点光源的数目。之后我们使用这个`NR_POINT_LIGHTS`常量来创建一个`PointLight`结构体的数组。和C语言一样，GLSL也是用一对中括号来创建数组的。现在我们有了4个`PointLight`结构体对象了。
 
 !!! Important
 
-	我们也可以定义**一个**大的结构体（而不是为每种类型的光源定义不同的结构体），包含**所有**不同种光照类型所需的变量，并将这个结构体用到所有的函数中，只需要忽略用不到的变量就行了。然而，我个人觉得当前的方法会更直观一点，不仅能够节省一些代码，而且由于不是所有光照类型都需要所有的变量，这样也能节省一些内存。
-
-点光源函数的原型如下：
+    我们同样可以简单粗暴地定义一个大号的结构体（而不是为每一种类型的光源定义一个结构体），它包含所有类型光源所需要属性变量。并且将这个结构体应用与所有的光照计算函数，在各个光照结算时忽略不需要的属性变量。然而，就我个人来说更喜欢分开定义，这样可以省下一些内存，因为定义一个大号的光源结构体在计算过程中会有用不到的变量。
 
 ```c++
-vec3 CalcPointLight(PointLight light, vec3 normal, vec3 fragPos, vec3 viewDir);
+vec3 CalcPointLight(PointLight light, vec3 normal, vec3 fragPos, vec3 viewDir);  
 ```
 
-这个函数从参数中获取所需的所有数据，并返回一个代表该点光源对片段的颜色贡献的`vec3`。我们再一次聪明地从之前的教程中复制粘贴代码，完成了下面这样的函数：
+这个函数将所有用得到的数据作为它的参数并使用一个`vec3`作为它的返回值类表示一个顶点光的结算结果。我们再一次聪明地从之前的教程中复制代码来把它定义成下面的样子：
 
 ```c++
+// 计算定点光在确定位置的光照颜色
 vec3 CalcPointLight(PointLight light, vec3 normal, vec3 fragPos, vec3 viewDir)
 {
     vec3 lightDir = normalize(light.position - fragPos);
-    // 漫反射着色
+    // 计算漫反射强度
     float diff = max(dot(normal, lightDir), 0.0);
-    // 镜面光着色
+    // 计算镜面反射
     vec3 reflectDir = reflect(-lightDir, normal);
     float spec = pow(max(dot(viewDir, reflectDir), 0.0), material.shininess);
-    // 衰减
+    // 计算衰减
     float distance    = length(light.position - fragPos);
-    float attenuation = 1.0 / (light.constant + light.linear * distance + 
-  			     light.quadratic * (distance * distance));    
-    // 合并结果
+    float attenuation = 1.0f / (light.constant + light.linear * distance +
+  			     light.quadratic * (distance * distance));
+    // 将各个分量合并
     vec3 ambient  = light.ambient  * vec3(texture(material.diffuse, TexCoords));
     vec3 diffuse  = light.diffuse  * diff * vec3(texture(material.diffuse, TexCoords));
     vec3 specular = light.specular * spec * vec3(texture(material.specular, TexCoords));
@@ -141,48 +140,44 @@ vec3 CalcPointLight(PointLight light, vec3 normal, vec3 fragPos, vec3 viewDir)
 }
 ```
 
-将这些功能抽象到这样一个函数中的优点是，我们能够不用重复的代码而很容易地计算多个点光源的光照了。在<fun>main</fun>函数中，我们只需要创建一个循环，遍历整个点光源数组，对每个点光源调用<fun>CalcPointLight</fun>就可以了。
+有了这个函数我们就可以在main函数中调用它来代替写很多个计算点光源的代码了。通过循环调用此函数就能实现同样的效果，当然代码更简洁。
 
-## 合并结果
+## 把它们放到一起
 
-现在我们已经定义了一个计算定向光的函数和一个计算点光源的函数了，我们可以将它们合并放到<fun>main</fun>函数中。
+我们现在定义了用于计算平行光和点光源的函数，现在我们把这些代码放到一起，写入文开始的一般结构中：
 
 ```c++
 void main()
 {
-    // 属性
+    // 一些属性
     vec3 norm = normalize(Normal);
     vec3 viewDir = normalize(viewPos - FragPos);
 
-    // 第一阶段：定向光照
+    // 第一步，计算平行光照
     vec3 result = CalcDirLight(dirLight, norm, viewDir);
-    // 第二阶段：点光源
+    // 第二步，计算顶点光照
     for(int i = 0; i < NR_POINT_LIGHTS; i++)
-        result += CalcPointLight(pointLights[i], norm, FragPos, viewDir);    
-    // 第三阶段：聚光
-    //result += CalcSpotLight(spotLight, norm, FragPos, viewDir);    
-    
-    FragColor = vec4(result, 1.0);
+        result += CalcPointLight(pointLights[i], norm, FragPos, viewDir);
+    // 第三部，计算 Spot light
+    //result += CalcSpotLight(spotLight, norm, FragPos, viewDir);
+
+    color = vec4(result, 1.0);
 }
 ```
 
-每个光源类型都将它们的贡献加到了最终的输出颜色上，直到所有的光源都处理完了。最终的颜色包含了场景中所有光源的颜色影响所合并的结果。如果你想的话，你也可以实现一个聚光，并将它的效果加到输出颜色中。我们会将<fun>CalcSpotLight</fun>函数留给读者作为练习。
+每一个光源的运算结果都添加到了输出颜色上，输出颜色包含了此场景中的所有光源的影响。如果你想实现手电筒的光照效果，同样的把计算结果添加到输出颜色上。我在这里就把`CalcSpotLight`的实现留作个读者们的练习吧。
 
-!!! Important
+设置平行光结构体的uniform值和之前所讲过的方式没什么两样，但是你可能想知道如何设置场景中`PointLight`结构体的uniforms变量数组。我们之前并未讨论过如何做这件事。
 
-	在这种方法中有很多重复的计算在光类型函数上(例如计算反射向量，漫反射和高光项，以及对材料纹理进行采样)，所以这里有优化的空间。
-
-设置定向光结构体的uniform应该非常熟悉了，但是你可能会在想我们该如何设置点光源的uniform值，因为点光源的uniform现在是一个<fun>PointLight</fun>的数组了。这并不是我们以前讨论过的话题。
-
-很幸运的是，这并不是很复杂，设置一个结构体数组的uniform和设置一个结构体的uniform是很相似的，但是这一次在访问uniform位置的时候，我们需要定义对应的数组下标值：
+庆幸的是，这并不是什么难题。设置uniform变量数组和设置单个uniform变量值是相似的，只需要用一个合适的下标就能够检索到数组中我们想要的uniform变量了。
 
 ```c++
-lightingShader.setFloat("pointLights[0].constant", 1.0f);
+glUniform1f(glGetUniformLocation(lightingShader.Program, "pointLights[0].constant"), 1.0f);
 ```
 
-在这里我们索引了<var>pointLights</var>数组中的第一个<fun>PointLight</fun>，并获取了<var>constant</var>变量的位置。但这也意味着不幸的是我们必须对这四个点光源手动设置uniform值，这让点光源本身就产生了28个uniform调用，非常冗长。你也可以尝试将这些抽象出去一点，定义一个点光源类，让它来为你设置uniform值，但最后你仍然要用这种方式设置所有光源的uniform值。
+这样我们检索到`pointLights`数组中的第一个`PointLight`结构体元素，同时也可以获取到该结构体中的各个属性变量。不幸的是这一位置我们还需要手动对这个四个光源的每一个属性都进行设置，这样手动设置这28个uniform变量是相当乏味的工作。你可以尝试去定义个光源类来为你设置这些uniform属性来减少你的工作，但这依旧不能改变去设置每个uniform属性的事实。
 
-别忘了，我们还需要为每个点光源定义一个位置向量，所以我们让它们在场景中分散一点。我们会定义另一个`glm::vec3`数组来包含点光源的位置：
+别忘了，我们还需要为每个光源设置它们的位置。这里，我们定义一个`glm::vec3`类的数组来包含这些点光源的坐标：
 
 ```c++
 glm::vec3 pointLightPositions[] = {
@@ -190,27 +185,24 @@ glm::vec3 pointLightPositions[] = {
 	glm::vec3( 2.3f, -3.3f, -4.0f),
 	glm::vec3(-4.0f,  2.0f, -12.0f),
 	glm::vec3( 0.0f,  0.0f, -3.0f)
-};
+};  
 ```
 
-接下来我们从<var>pointLights</var>数组中索引对应的<fun>PointLight</fun>，将它的<var>position</var>值设置为刚刚定义的位置值数组中的其中一个。同时我们还要保证现在绘制的是四个灯立方体而不是仅仅一个。只要对每个灯物体创建一个不同的模型矩阵就可以了，和我们之前对箱子的处理类似。
+同时我们还需要根据这些光源的位置在场景中绘制4个表示光源的立方体，这样的工作我们在之前的教程中已经做过了。
 
-如果你还使用了手电筒的话，所有光源组合的效果将看起来和下图差不多：
+如果你在还是用了手电筒的话，将所有的光源结合起来看上去应该和下图差不多：
 
-![](../img/02/06/multiple_lights_combined.png)
+![](http://learnopengl.com/img/lighting/multiple_lights_combined.png)
 
-你可以看到，很显然天空中有一个全局照明（像一个太阳），我们有四个光源分散在场景中，以及玩家视角的手电筒。看起来是不是非常不错？
+你可以在此处获取本教程的[源代码](http://learnopengl.com/code_viewer.php?code=lighting/multiple_lights)，同时可以查看[顶点着色器](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps&type=vertex)和[片段着色器](http://learnopengl.com/code_viewer.php?code=lighting/multiple_lights&type=fragment)的代码。
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/2.lighting/6.multiple_lights/multiple_lights.cpp)找到最终程序的源代码。
+上面的图片的光源都是使用默认的属性的效果，如果你尝试对光源属性做出各种修改尝试的话，会出现很多有意思的画面。很多艺术家和场景编辑器都提供大量的按钮或方式来修改光照以使用各种环境。使用最简单的光照属性的改变我们就足已创建有趣的视觉效果：
 
-上面图片中的所有光源都是使用上一节中所使用的默认属性，但如果你愿意实验这些数值的话，你能够得到很多有意思的结果。艺术家和关卡设计师通常都在编辑器中不断的调整这些光照参数，保证光照与环境相匹配。在我们刚刚创建的简单光照环境中，你可以简单地调整一下光源的属性，创建很多有意思的视觉效果：
+![](http://learnopengl.com/img/lighting/multiple_lights_atmospheres.png)
 
-![](../img/02/06/multiple_lights_atmospheres.png)
-
-我们也改变了清屏的颜色来更好地反应光照。你可以看到，只需要简单地调整一些光照参数，你就能创建完全不同的氛围。
-
-相信你现在已经对OpenGL的光照有很好的理解了。有了目前所学的这些知识，我们已经可以创建出丰富有趣的环境和氛围了。尝试实验一下不同的值，创建出你自己的氛围吧。
+相信你现在已经对OpenGL的光照有很好的理解了。有了这些知识我们便可以创建丰富有趣的环境和氛围了。快试试改变所有的属性的值来创建你的光照环境吧！
 
 ## 练习
 
-- 你能通过调节光照属性变量，（大概地）重现最后一张图片上不同的氛围吗？[参考解答](https://learnopengl.com/code_viewer.php?code=lighting/multiple_lights-exercise2)
+* 创建一个表示手电筒光的结构体Spotlight并实现CalcSpotLight(...)函数：[解决方案](http://learnopengl.com/code_viewer.php?code=lighting/multiple_lights-exercise1)
+* 你能通过调节不同的光照属性来重新创建一个不同的氛围吗？[解决方案](http://learnopengl.com/code_viewer.php?code=lighting/multiple_lights-exercise2)

docs/02 Lighting/07 Review.md

@@ -3,34 +3,40 @@
 原文     | [Review](http://learnopengl.com/#!Lighting/Review)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | [Geequlim](http://geequlim.com), Krasjet, [orbitgw](https://github.com/orbitgw/), [AoZhang](https://github.com/SuperAoao)
+翻译     | Meow J
+校对     | [Geequlim](http://geequlim.com)
 
-恭喜您已经学习到了这个地方！辛苦啦！不知道你有没有注意到，总的来说我们在学习光照教程的时候关于OpenGL本身并没有什么新东西，除了像访问uniform数组这样细枝末节的知识。目前为止的所有教程都是关于使用一些技巧或者公式来操作着色器，达到真实的光照效果。这再一次向你展示了着色器的威力。着色器是非常灵活的，你也亲眼见证了我们仅仅使用一些3D向量和可配置的变量就能够创造出惊人的图像这一点。
+恭喜您已经学习到了这个地方！辛苦啦！不知道你有没有注意到，总的来说我们在学习光照教程的时候学习的并不是OpenGL本身，当然我们仍然学习了一些细枝末节的知识(像访问uniform数组)。
 
-在前面的几个教程中，你学习了颜色、风氏光照模型（包括环境光照、漫反射光照和镜面光照）、物体的材质、可配置的光照属性、漫反射和镜面光贴图、不同种类的光，并且学习了怎样将所有所学知识融会贯通，结合到一个完全照明的场景中。记得去实验一下不同的光照、材质颜色、光照属性，并且试着利用你无穷的创造力创建自己的环境。
+到现在的所有教程都是关于用一些技巧和公式来操作着色器从而达到真实的光照效果。这同样向你展示了着色器的威力。
 
-在[下一节](../03 Model Loading/01 Assimp.md)当中，我们在我们的场景当中加入更高级的几何形状，这些形状将会在我们之前讨论过的光照模型中非常好看。
+着色器是非常灵活的，你也亲眼见证了我们仅仅使用一些3D向量和可配置的变量就能够创造出惊人的图形这一点。
+
+在你学过的最后几个教程中，你学习了有关颜色，冯氏光照模型(包括环境，漫反射，镜面反射光照)，对象材质，可配置的光照属性，漫反射和镜面反射贴图，不同种类的光，并且学习了怎样将所有所学知识融会贯通。
+
+记得去实验一下不同的光照，材质颜色，光照属性，并且试着利用你无穷的创造力创建自己的环境。
+
+在[下一个教程](../03 Model Loading/01 Assimp.md)当中，我们将加入更高级的形状到我们的场景中，这些形状将会在我们之前讨论过的光照模型中非常好看。
 
 ## 词汇表
 
-- **颜色向量(Color Vector)**：一个通过红绿蓝(RGB)分量的组合描绘大部分真实颜色的向量。一个物体的颜色实际上是该物体所不能吸收的反射颜色分量。
-- **风氏光照模型(Phong Lighting Model)**：一个通过计算环境光，漫反射，和镜面光分量的值来近似真实光照的模型。
-- **环境光照(Ambient Lighting)**：通过给每个没有被光照的物体很小的亮度，使其不是完全黑暗的，从而对全局光照进行近似。
-- **漫反射着色(Diffuse Shading)**：一个顶点/片段与光线方向越接近，光照会越强。使用了法向量来计算角度。
+- **颜色向量(Color Vector)**：一个通过红绿蓝(RGB)分量的组合描绘大部分真实颜色的向量. 一个对象的颜色实际上是该对象不能吸收的反射颜色分量。
+- **冯氏光照模型(Phong Lighting Model)**：一个通过计算环境，漫反射，和镜面反射分量的值来估计真实光照的模型。
+- **环境光照(Ambient Lighting)**：通过给每个没有被光照的物体很小的亮度，使其不是完全黑暗的，从而对全局光照的估计。
+- **漫反射着色法(Diffuse Shading)**：光照随着更多的顶点/片段排列在光源上变强. 该方法使用了法向量来计算角度。
 - **法向量(Normal Vector)**：一个垂直于平面的单位向量。
-- **法线矩阵(Normal Matrix)**：一个3x3矩阵，或者说是没有平移的模型（或者模型-观察）矩阵。它也被以某种方式修改（逆转置），从而在应用非统一缩放时，保持法向量朝向正确的方向。否则法向量会在使用非统一缩放时被扭曲。
+- **正规矩阵(Normal Matrix)**：一个3x3矩阵, 或者说是没有平移的模型(或者模型观察)矩阵.它也被以某种方式修改(逆转置)从而当应用非统一缩放时保持法向量朝向正确的方向. 否则法向量会在使用非统一缩放时失真。
 - **镜面光照(Specular Lighting)**：当观察者视线靠近光源在表面的反射线时会显示的镜面高光。镜面光照是由观察者的方向，光源的方向和设定高光分散量的反光度值三个量共同决定的。
-- **风氏着色(Phong Shading)**：风氏光照模型应用在片段着色器。
-- **Gouraud着色(Gouraud shading)**：风氏光照模型应用在顶点着色器上。在使用很少数量的顶点时会产生明显的瑕疵。会得到效率提升但是损失了视觉质量。
-- **GLSL结构体(GLSL struct)**：一个类似于C的结构体，用作着色器变量的容器。大部分时间用来管理输入/输出/uniform。
-- **材质(Material)**：一个物体反射的环境光，漫反射，镜面光颜色。这些东西设定了物体所拥有的颜色。
-- **光照属性(Light(properties))**：一个光的环境光，漫反射，镜面光的强度。可以使用任何颜色值，对每一个风氏分量(Phong Component)定义光源发出的颜色/强度。
+- **冯氏着色法(Phong Shading)**：冯氏光照模型应用在片段着色器。
+- **高氏着色法(Gouraud shading)**：冯氏光照模型应用在顶点着色器上. 在使用很少树木的顶点时会产生明显的瑕疵. 会得到效率提升但是损失了视觉质量。
+- **GLSL结构体(GLSL struct)**：一个类似于C的结构体，用作着色器变量的容器. 大部分时间用来管理输入/输出/uniform。
+- **材质(Material)**：一个物体反射的环境，漫反射，镜面反射光照. 这些东西设定了物体的颜色。
+- **光照(性质)(Light(properties))**：一个光的环境，漫反射，镜面反射的强度. 可以应用任何颜色值并对每一个冯氏分量(Phong Component)都定义一个光源闪烁的颜色/强度。
 - **漫反射贴图(Diffuse Map)**：一个设定了每个片段中漫反射颜色的纹理图片。
-- **镜面光贴图(Specular Map)**：一个设定了每一个片段的镜面光强度/颜色的纹理贴图。仅在物体的特定区域显示镜面高光。
-- **定向光(Directional Light)**：只有方向的光源。它被建模为无限距离，这使得它的所有光线看起来都是平行的，因此它的方向矢量在整个场景中保持不变。
-- **点光源(Point Light)**：一个在场景中有位置的，光线逐渐衰减的光源。
-- **衰减(Attenuation)**：光随着距离减少强度减小的过程，通常使用在点光源和聚光下。
-- **聚光(Spotlight)**：一个被定义为在某一个方向上的锥形的光源。
+- **镜面贴图(Specular Map)**：一个设定了每一个片段的镜面强度/颜色的纹理贴图. 仅在物体的特定区域允许镜面高光。
+- **平行光(Directional Light)**：只有一个方向的光源. 它被建模为不管距离有多长所有光束都是平行而且其方向向量在整个场景中保持不变。
+- **点光源(Point Light)**：一个场景中光线逐渐淡出的光源。
+- **衰减(Attenuation)**：光减少强度的过程，通常使用在点光源和聚光下。
+- **聚光(Spotlight)**：一个被定义为在某一个方向上锥形的光源。
 - **手电筒(Flashlight)**：一个摆放在观察者视角的聚光。
-- **GLSL Uniform数组(GLSL Uniform Array)**：一个uniform值数组。它的工作原理和C语言数组大致一样，只是不能动态分配内存。
+- **GLSL uniform数组(GLSL Uniform Array)**：一个数组的uniform值. 就像C语言数组一样工作，只是不能被动态调用。

docs/03 Model Loading/01 Assimp.md

@@ -3,67 +3,68 @@
 原文     | [Assimp](http://learnopengl.com/#!Model-Loading/Assimp)
       ---|---
 作者     | JoeyDeVries
-翻译     | Cocoonshu, Krasjet, [Geequlim](http://geequlim.com)
-校对     | 暂未校对
+翻译     | Cocoonshu
+校对     | [Geequlim](http://geequlim.com)
 
-到目前为止的所有场景中，我们一直都在滥用我们的箱子朋友，但时间久了甚至是我们最好的朋友也会感到无聊。在日常的图形程序中，通常都会使用非常复杂且好玩的模型，它们比静态的箱子要好看多了。然而，和箱子对象不同，我们不太能够对像是房子、汽车或者人形角色这样的复杂形状手工定义所有的顶点、法线和纹理坐标。我们想要的是将这些模型(Model)**导入**(Import)到程序当中。模型通常都由3D艺术家在[Blender](http://www.blender.org/)、[3DS Max](http://www.autodesk.nl/products/3ds-max/overview)或者[Maya](http://www.autodesk.com/products/autodesk-maya/overview)这样的工具中精心制作。
 
-这些所谓的<def>3D建模工具</def>(3D Modeling Tool)可以让艺术家创建复杂的形状，并使用一种叫做<def>UV映射</def>(uv-mapping)的手段来应用贴图。这些工具将会在导出到模型文件的时候自动生成所有的顶点坐标、顶点法线以及纹理坐标。这样子艺术家们即使不了解图形技术细节的情况下，也能拥有一套强大的工具来构建高品质的模型了。所有的技术细节都隐藏在了导出的模型文件中。但是，作为图形开发者，我们就**必须**要了解这些技术细节了。
+到目前为止，我们已经在所有的场景中大面积滥用了我们的容器盒小盆友，但就是容器盒是我们的好朋友，时间久了我们也会喜新厌旧。一些图形应用里经常会使用很多复杂且好玩儿的模型，它们看起来比静态的容器盒可爱多了。但是，我们无法像定义容器盒一样手动地去指定房子、货车或人形角色这些复杂模型的顶点、法线和纹理坐标。我们需要做的也是应该要做的，是把这些模型导入到应用程序中，而设计制作这些3D模型的工作应该交给像[Blender](http://www.blender.org/)、[3DS Max](http://www.autodesk.nl/products/3ds-max/overview)或者[Maya](http://www.autodesk.com/products/autodesk-maya/overview)这样的工具软件。
 
-所以，我们的工作就是解析这些导出的模型文件以及提取所有有用的信息，将它们储存为OpenGL能够理解的格式。一个很常见的问题是，模型的文件格式有很多种，每一种都会以它们自己的方式来导出模型数据。像是[Wavefront的.obj](http://en.wikipedia.org/wiki/Wavefront_.obj_file)这样的模型格式，只包含了模型数据以及材质信息，像是模型颜色和漫反射/镜面光贴图。而以XML为基础的[Collada文件格式](http://en.wikipedia.org/wiki/COLLADA)则非常的丰富，包含模型、光照、多种材质、动画数据、摄像机、完整的场景信息等等。Wavefront的.obj格式通常被认为是一个易于解析的模型格式。建议至少去Wavefront的wiki页面上看看文件格式的信息是如何封装的。这应该能让你认识到模型文件的基本结构。
+那些3D建模工具，可以让美工们构建一些复杂的形状，并将贴图应用到形状上去，即纹理映射。然后，在导出模型文件时，建模工具会自己生成所有的顶点坐标、顶点法线和纹理坐标。这样，美工们可以不用了解大量的图像技术细节，就能有大量的工具集去随心地构建高品质的模型。所有的技术细节内容都隐藏在里导出的模型文件里。而我们，这些图形开发者，就必须得去关注这些技术细节了。
 
-总而言之，不同种类的文件格式有很多，它们之间通常并没有一个通用的结构。所以如果我们想从这些文件格式中导入模型的话，我们必须要去自己对每一种需要导入的文件格式写一个导入器。很幸运的是，正好有一个库专门处理这个问题。
+因此，我们的工作就是去解析这些导出的模型文件，并将其中的模型数据存储为OpenGL能够使用的数据。一个常见的问题是，导出的模型文件通常有几十种格式，不同的工具会根据不同的文件协议把模型数据导出到不同格式的模型文件中。有的模型文件格式只包含模型的静态形状数据和颜色、漫反射贴图、高光贴图这些基本的材质信息，比如Wavefront的.obj文件。而有的模型文件则采用XML来记录数据，且包含了丰富的模型、光照、各种材质、动画、摄像机信息和完整的场景信息等，比如Collada文件格式。Wavefront的obj格式是为了考虑到通用性而设计的一种便于解析的模型格式。建议去Wavefront的Wiki上看看obj文件格式是如何封装的。这会给你形成一个对模型文件格式的一个基本概念和印象。
 
 ## 模型加载库
 
-一个非常流行的模型导入库是[Assimp](http://assimp.org/)，它是**Open Asset Import Library**（开放的资产导入库）的缩写。Assimp能够导入很多种不同的模型文件格式（并也能够导出部分的格式），它会将所有的模型数据加载至Assimp的通用数据结构中。当Assimp加载完模型之后，我们就能够从Assimp的数据结构中提取我们所需的所有数据了。由于Assimp的数据结构保持不变，不论导入的是什么种类的文件格式，它都能够将我们从这些不同的文件格式中抽象出来，用同一种方式访问我们需要的数据。
+现在市面上有一个很流行的模型加载库，叫做Assimp，全称为Open Asset Import Library。Assimp可以导入几十种不同格式的模型文件（同样也可以导出部分模型格式）。只要Assimp加载完了模型文件，我们就可以从Assimp上获取所有我们需要的模型数据。Assimp把不同的模型文件都转换为一个统一的数据结构，所有无论我们导入何种格式的模型文件，都可以用同一个方式去访问我们需要的模型数据。
 
-当使用Assimp导入一个模型的时候，它通常会将整个模型加载进一个**场景**(Scene)对象，它会包含导入的模型/场景中的所有数据。Assimp会将场景载入为一系列的节点(Node)，每个节点包含了场景对象中所储存数据的索引，每个节点都可以有任意数量的子节点。Assimp数据结构的（简化）模型如下：
+当导入一个模型文件时，即Assimp加载一整个包含所有模型和场景数据的模型文件到一个scene对象时，Assimp会为这个模型文件中的所有场景节点、模型节点都生成一个具有对应关系的数据结构，且将这些场景中的各种元素与模型数据对应起来。下图展示了一个简化的Assimp生成的模型文件数据结构：
 
-![](../img/03/01/assimp_structure.png)
 
-- 和材质和网格(Mesh)一样，所有的场景/模型数据都包含在<u>Scene</u>对象中。<u>Scene</u>对象也包含了场景根节点的引用。
-- 场景的<u>Root node</u>（根节点）可能包含子节点（和其它的节点一样），它会有一系列指向场景对象中<var>mMeshes</var>数组中储存的网格数据的索引。<u>Scene</u>下的<var>mMeshes</var>数组储存了真正的<u>Mesh</u>对象，节点中的<var>mMeshes</var>数组保存的只是场景中网格数组的索引。
-- 一个<u>Mesh</u>对象本身包含了渲染所需要的所有相关数据，像是顶点位置、法向量、纹理坐标、面(Face)和物体的材质。
-- 一个网格包含了多个面。<u>Face</u>代表的是物体的渲染图元(Primitive)（三角形、方形、点）。一个面包含了组成图元的顶点的索引。由于顶点和索引是分开的，使用一个索引缓冲来渲染是非常简单的（见[你好，三角形](../01 Getting started/04 Hello Triangle.md)）。
-- 最后，一个网格也包含了一个<u>Material</u>对象，它包含了一些函数能让我们获取物体的材质属性，比如说颜色和纹理贴图（比如漫反射和镜面光贴图）。
+![](http://learnopengl.com/img/model_loading/assimp_structure.png)
 
-所以，我们需要做的第一件事是将一个物体加载到<u>Scene</u>对象中，遍历节点，获取对应的<u>Mesh</u>对象（我们需要递归搜索每个节点的子节点），并处理每个<u>Mesh</u>对象来获取顶点数据、索引以及它的材质属性。最终的结果是一系列的网格数据，我们会将它们包含在一个`Model`对象中。
+
+ - 所有的模型、场景数据都包含在scene对象中，如所有的材质和Mesh。同样，场景的根节点引用也包含在这个scene对象中
+ - 场景的根节点可能也会包含很多子节点和一个指向保存模型点云数据mMeshes[]的索引集合。根节点上的mMeshes[]里保存了实际了Mesh对象，而每个子节点上的mMesshes[]都只是指向根节点中的mMeshes[]的一个引用(译者注：C/C++称为指针，Java/C#称为引用)
+ - 一个Mesh对象本身包含渲染所需的所有相关数据，比如顶点位置、法线向量、纹理坐标、面片及物体的材质
+ - 一个Mesh会包含多个面片。一个Face（面片）表示渲染中的一个最基本的形状单位，即图元（基本图元有点、线、三角面片、矩形面片）。一个面片记录了一个图元的顶点索引，通过这个索引，可以在mMeshes[]中寻找到对应的顶点位置数据。顶点数据和索引分开存放，可以便于我们使用缓存（VBO、NBO、TBO、IBO）来高速渲染物体。（详见[Hello Triangle](http://www.learnopengl.com/#!Getting-started/Hello-Triangle)）
+ - 一个Mesh还会包含一个Material（材质）对象用于指定物体的一些材质属性。如颜色、纹理贴图（漫反射贴图、高光贴图等）
+
+所以我们要做的第一件事，就是加载一个模型文件为scene对象，然后获取每个节点对应的Mesh对象（我们需要递归搜索每个节点的子节点来获取所有的节点），并处理每个Mesh对象对应的顶点数据、索引以及它的材质属性。最终我们得到一个只包含我们需要的数据的Mesh集合。
 
 !!! Important
 
-	**网格**
+    **网格(Mesh)**
+    
+    用建模工具构建物体时，美工通常不会直接使用单个形状来构建一个完整的模型。一般来说，一个模型会由几个子模型/形状组合拼接而成。而模型中的那些子模型/形状就是我们所说的一个网格。例如一个人形模型，美工通常会把头、四肢、衣服、武器这些组件都分别构建出来，然后在把所有的组件拼合在一起，形成最终的完整模型。一个网格（包含顶点、索引和材质属性）是我们在OpenGL中绘制物体的最小单位。一个模型通常有多个网格组成。
 
-	当使用建模工具对物体建模的时候，艺术家通常不会用单个形状创建出整个模型。通常每个模型都由几个子模型/形状组合而成。组合模型的每个单独的形状就叫做一个<def>网格</def>(Mesh)。比如说有一个人形的角色：艺术家通常会将头部、四肢、衣服、武器建模为分开的组件，并将这些网格组合而成的结果表现为最终的模型。一个网格是我们在OpenGL中绘制物体所需的最小单位（顶点数据、索引和材质属性）。一个模型（通常）会包括多个网格。
-
-在[下一节](02 Mesh.md)中，我们将创建我们自己的<fun>Model</fun>和<fun>Mesh</fun>类来加载并使用刚刚介绍的结构储存导入后的模型。如果我们想要绘制一个模型，我们不需要将整个模型渲染为一个整体，只需要渲染组成模型的每个独立的网格就可以了。然而，在我们开始导入模型之前，我们首先需要将Assimp包含到我们的工程当中。
+下一节教程中，我们将用上述描述的数据结构来创建我们自己的Model类和Mesh类，用于加载和保存那些导入的模型。如果我们想要绘制一个模型，我们不会去渲染整个模型，而是去渲染这个模型所包含的所有独立的Mesh。不管怎样，我们开始导入模型之前，我们需要先把Assimp导入到我们的工程中。
 
 ## 构建Assimp
 
-你可以在Assimp的[GitHub页面](https://github.com/assimp/assimp/blob/master/Build.md)中选择相应的版本。本文使用的Assimp最高版本为3.1.1。我们建议你自己编译Assimp库，因为它们的预编译库并不一定能适用于所有系统。如果你忘记如何使用CMake自己编译一个库的话，可以复习[创建窗口](../01 Getting started/02 Creating a window.md)小节。
+你可以在[Assimp的下载页面](http://assimp.sourceforge.net/main_downloads.html)选择一个想要的版本去下载Assimp库。到目前为止，Assimp可用的最新版本是3.1.1。我们建议你自己编译Assimp库，因为Assimp官方的已编译库不能很好地覆盖在所有平台上运行。如果你忘记怎样使用CMake编译一个库，请详见[Creating a window(创建一个窗口)](http://www.learnopengl.com/#!Getting-started/Creating-a-window)教程。
 
-构建Assimp时可能会出现一些问题，所以我会将它们的解决方案列在这里，便于大家排除错误：
+这里我们列出一些编译Assimp时可能遇到的问题，以便大家参考和排除:
 
-- CMake在读取配置列表时，不断报出DirectX库丢失的错误。报错如下：
+ - CMake在读取配置列表时，报出与DirectX库丢失相关的一些错误。报错如下：
  
 ```
-Could not locate DirectX
+Could not locate DirecX
 CMake Error at cmake-modules/FindPkgMacros.cmake:110 (message):
-Required library DirectX not found! Install the library (including dev packages) 
-and try again. If the library is already installed, set the missing variables 
-manually in cmake.
+Required library DirectX not found! Install the library (including dev packages) and try again. If the library is already installed, set the missing variables manually in cmake.
 ```
 
-如果你之前没安装过的话，那么这个问题的解决方案是安装DirectX SDK。你可以从[这里](http://www.microsoft.com/en-us/download/details.aspx?id=6812)下载SDK。
+这个问题的解决方案：如果你之前没有安装过DirectX SDK，那么请安装。下载地址：[DirectX SDK](http://www.microsoft.com/en-us/download/details.aspx?id=6812)
+ - 安装DirectX SDK时，可以遇到一个错误码为<b>S1023</b>的错误。遇到这个问题，请在安装DirectX SDK前，先安装C++ Redistributable package(s)。
+  问题解释：[已知问题：DirectX SDK (June 2010) 安装及S1023错误](https://blogs.msdn.microsoft.com/chuckw/2011/12/09/known-issue-directx-sdk-june-2010-setup-and-the-s1023-error/)
+ - 一旦配置完成，你就可以生成解决方案文件了，打开解决方案文件并编译Assimp库（编译为Debug版本还是Release版本，根据你的需要和心情来定吧）
+ - 使用默认配置构建的Assimp是一个动态库，所以我们需要把编译出来的assimp.dll文件拷贝到我们自己程序的可执行文件的同一目录里
+ - 编译出来的Assimp的LIB文件和DLL文件可以在code/Debug或者code/Release里找到
+ - 把编译好的LIB文件和DLL文件拷贝到工程的相应目录下，并链接到你的解决方案中。同时还好记得把Assimp的头文件也拷贝到工程里去（Assimp的头文件可以在include目录里找到）
 
-- 安装DirectX SDK时，可能遇到一个错误码为`s1023`的错误。这种情况下，请在安装SDK之前先卸载C++ Redistributable package(s)。
+如果你还遇到了其他问题，可以在下面给出的链接里获取帮助。
 
-一旦配置完成，你就可以生成解决方案文件了，打开解决方案文件并编译Assimp库（可以编译为Debug版本也可以编译为Release版本，只要能工作就行）。因为所有的LearnOpenGL代码都是64位项目，所以请确保在64位下编译这个库。
+!!! Important
 
-使用默认配置构建的Assimp是一个动态库(Dynamic Library)，所以所生成的**assimp.dll**文件（文件名可能带有后缀）需要随我们的程序可执行文件一并包含，你可以简单地将DLL复制到我们程序可执行文件的同一目录中。
+    如果你想要让Assimp使用多线程支持来提高性能，你可以使用<b>Boost</b>库来编译 Assimp。在[Boost安装页面](http://assimp.sourceforge.net/lib_html/install.html)，你能找到关于Boost的完整安装介绍。
 
-Assimp编译之后，生成的库和DLL文件位于**code/Debug**或者**code/Release**文件夹中。接着把编译好的LIB文件和DLL文件拷贝到工程的相应目录下，然后在解决方案中链接它们。并且记得把Assimp的头文件也复制到你的**include**目录中（头文件可以在下载的Assimp文件中的**include**目录里找到）。
-
-如果你仍遇到了未报告的错误，欢迎在评论区中寻求帮助。
-
-现在，你应该已经编译完Assimp库并将它链接到你的程序中了。下一步：[导入](02 Mesh.md)漂亮的3D物体！
+现在，你应该已经能够编译Assimp库，并链接Assimp到你的工程里去了。下一步：[导入完美的3D物件！](02 Mesh.md)

docs/03 Model Loading/02 Mesh.md

@@ -3,140 +3,155 @@
 原文     | [Mesh](http://learnopengl.com/#!Model-Loading/Mesh)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | [AoZhang](https://github.com/SuperAoao)
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com)
 
-通过使用Assimp，我们可以加载不同的模型到程序中，但是载入后它们都被储存为Assimp的数据结构。我们最终仍要将这些数据转换为OpenGL能够理解的格式，这样才能渲染这个物体。我们从上一节中学到，网格(Mesh)代表的是单个的可绘制实体，我们现在先来定义一个我们自己的网格类。
+使用Assimp可以把多种不同格式的模型加载到程序中，但是一旦载入，它们就都被储存为Assimp自己的数据结构。我们最终的目的是把这些数据转变为OpenGL可读的数据，才能用OpenGL来渲染物体。我们从前面的教程了解到，一个网格(Mesh)代表一个可绘制实体，现在我们就定义一个自己的网格类。
 
-首先我们来回顾一下我们目前学到的知识，想想一个网格最少需要什么数据。一个网格应该至少需要一系列的顶点，每个顶点包含一个位置向量、一个法向量和一个纹理坐标向量。一个网格还应该包含用于索引绘制的索引以及纹理形式的材质数据（漫反射/镜面光贴图）。
+先来复习一点目前学到知识，考虑一个网格最少需要哪些数据。一个网格应该至少需要一组顶点，每个顶点包含一个位置向量，一个法线向量，一个纹理坐标向量。一个网格也应该包含一个索引绘制用的索引，以纹理（diffuse/specular map）形式表现的材质数据。
+
+为了在OpenGL中定义一个顶点，现在我们设置有最少需求一个网格类:
 
-既然我们有了一个网格类的最低需求，我们可以在OpenGL中定义一个顶点了：
 
 ```c++
-struct Vertex {
+struct Vertex
+{
     glm::vec3 Position;
     glm::vec3 Normal;
     glm::vec2 TexCoords;
 };
 ```
 
-我们将所有需要的向量储存到一个叫做<fun>Vertex</fun>的结构体中，我们可以用它来索引每个顶点属性。除了<fun>Vertex</fun>结构体之外，我们还需要将纹理数据整理到一个<fun>Texture</fun>结构体中。
+我们把每个需要的向量储存到一个叫做`Vertex`的结构体中，它被用来索引每个顶点属性。另外除了`Vertex`结构体外，我们也希望组织纹理数据，所以我们定义一个`Texture`结构体：
+
 
 ```c++
-struct Texture {
-    unsigned int id;
-    string type;
+struct Texture
+{
+    GLuint id;
+    String type;
 };
 ```
 
-我们储存了纹理的id以及它的类型，比如是漫反射贴图或者是镜面光贴图。
+我们储存纹理的id和它的类型，比如`diffuse`纹理或者`specular`纹理。
+
+知道了顶点和纹理的实际表达，我们可以开始定义网格类的结构：
 
-知道了顶点和纹理的实现，我们可以开始定义网格类的结构了：
 
 ```c++
-class Mesh {
-    public:
-        /*  网格数据  */
-        vector<Vertex> vertices;
-        vector<unsigned int> indices;
-        vector<Texture> textures;
-        /*  函数  */
-        Mesh(vector<Vertex> vertices, vector<unsigned int> indices, vector<Texture> textures);
-        void Draw(Shader &shader);
-    private:
-        /*  渲染数据  */
-        unsigned int VAO, VBO, EBO;
-        /*  函数  */
-        void setupMesh();
-};  
+class Mesh
+{
+Public:
+    vector<Vertex> vertices;
+    vector<GLuint> indices;
+    vector<Texture> textures;
+    Mesh(vector<Vertex> vertices, vector<GLuint> indices, vector<Texture> texture);
+    Void Draw(Shader shader);
+ 
+private:
+    GLuint VAO, VBO, EBO;
+    void setupMesh();
+}
 ```
 
-你可以看到这个类并不复杂。在构造函数中，我们将所有必须的数据赋予了网格，我们在<fun>setupMesh</fun>函数中初始化缓冲，并最终使用<fun>Draw</fun>函数来绘制网格。注意我们将一个着色器传入了<fun>Draw</fun>函数中，将着色器传入网格类中可以让我们在绘制之前设置一些uniform（像是链接采样器到纹理单元）。
+如你所见这个类一点都不复杂，构造方法里我们初始化网格所有必须数据。在`setupMesh`函数里初始化缓冲。最后通过`Draw`函数绘制网格。注意，我们把`shader`传递给`Draw`函数。通过把`shader`传递给Mesh，在绘制之前我们设置几个uniform（就像链接采样器到纹理单元）。
+
+构造函数的内容非常直接。我们简单设置类的公有变量，使用的是构造函数相应的参数。我们在构造函数中也调用`setupMesh`函数：
 
-构造函数的内容非常易于理解。我们只需要使用构造函数的参数设置类的公有变量就可以了。我们在构造函数中还调用了<fun>setupMesh</fun>函数：
 
 ```c++
-Mesh(vector<Vertex> vertices, vector<unsigned int> indices, vector<Texture> textures)
+Mesh(vector<Vertex> vertices, vector<GLuint> indices, vector<Texture> textures)
 {
     this->vertices = vertices;
     this->indices = indices;
     this->textures = textures;
-
-    setupMesh();
+ 
+    this->setupMesh();
 }
 ```
 
-这里没什么可说的。我们接下来讨论<fun>setupMesh</fun>函数。
+这里没什么特别的，现在让我们研究一下`setupMesh`函数。
+
  
 ## 初始化
 
-多亏了构造函数，我们现在有一大列的网格数据可以用于渲染。在此之前我们还必须配置正确的缓冲，并通过顶点属性指针定义顶点着色器的布局。现在你应该对这些概念都很熟悉了，但我们这次会稍微有一点变动:使用结构体中的顶点数据：
+现在我们有一大列的网格数据可用于渲染，这要感谢构造函数。我们确实需要设置合适的缓冲，通过顶点属性指针（vertex attribute pointers）定义顶点着色器layout。现在你应该对这些概念很熟悉，但是我们我们通过介绍了结构体中使用顶点数据，所以稍微有点不一样：
+
 
 ```c++
 void setupMesh()
 {
-    glGenVertexArrays(1, &VAO);
-    glGenBuffers(1, &VBO);
-    glGenBuffers(1, &EBO);
+    glGenVertexArrays(1, &this->VAO);
+    glGenBuffers(1, &this->VBO);
+    glGenBuffers(1, &this->EBO);
   
-    glBindVertexArray(VAO);
-    glBindBuffer(GL_ARRAY_BUFFER, VBO);
-
-    glBufferData(GL_ARRAY_BUFFER, vertices.size() * sizeof(Vertex), &vertices[0], GL_STATIC_DRAW);  
-
-    glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, EBO);
-    glBufferData(GL_ELEMENT_ARRAY_BUFFER, indices.size() * sizeof(unsigned int), 
-                 &indices[0], GL_STATIC_DRAW);
-
-    // 顶点位置
-    glEnableVertexAttribArray(0);	
-    glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, sizeof(Vertex), (void*)0);
-    // 顶点法线
-    glEnableVertexAttribArray(1);	
-    glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, sizeof(Vertex), (void*)offsetof(Vertex, Normal));
-    // 顶点纹理坐标
-    glEnableVertexAttribArray(2);	
-    glVertexAttribPointer(2, 2, GL_FLOAT, GL_FALSE, sizeof(Vertex), (void*)offsetof(Vertex, TexCoords));
-
+    glBindVertexArray(this->VAO);
+    glBindBuffer(GL_ARRAY_BUFFER, this->VBO);
+ 
+    glBufferData(GL_ARRAY_BUFFER, this->vertices.size() * sizeof(Vertex), 
+                 &this->vertices[0], GL_STATIC_DRAW);  
+ 
+    glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, this->EBO);
+    glBufferData(GL_ELEMENT_ARRAY_BUFFER, this->indices.size() * sizeof(GLuint), 
+                 &this->indices[0], GL_STATIC_DRAW);
+ 
+    // 设置顶点坐标指针
+    glEnableVertexAttribArray(0); 
+    glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, sizeof(Vertex), 
+                         (GLvoid*)0);
+    // 设置法线指针
+    glEnableVertexAttribArray(1); 
+    glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, sizeof(Vertex), 
+                         (GLvoid*)offsetof(Vertex, Normal));
+    // 设置顶点的纹理坐标
+    glEnableVertexAttribArray(2); 
+    glVertexAttribPointer(2, 2, GL_FLOAT, GL_FALSE, sizeof(Vertex), 
+                         (GLvoid*)offsetof(Vertex, TexCoords));
+ 
     glBindVertexArray(0);
-}  
+}
 ```
 
-代码应该和你所想得没什么不同，但有了<fun>Vertex</fun>结构体的帮助，我们使用了一些小技巧。
+如你所想代码没什么特别不同的地方，在`Vertex`结构体的帮助下有了一些小把戏。
+
+C++的结构体有一个重要的属性，那就是在内存中它们是连续的。如果我们用结构体表示一列数据，这个结构体只包含结构体的连续的变量，它就会直接转变为一个`float`（实际上是byte）数组，我们就能用于一个数组缓冲（array buffer）中了。比如，如果我们填充一个`Vertex`结构体，它在内存中的排布等于：
 
-C++结构体有一个很棒的特性，它们的内存布局是连续的(Sequential)。也就是说，如果我们将结构体作为一个数据数组使用，那么它将会以顺序排列结构体的变量，这将会直接转换为我们在数组缓冲中所需要的float（实际上是字节）数组。比如说，如果我们有一个填充后的<fun>Vertex</fun>结构体，那么它的内存布局将会等于：
 
 ```c++
 Vertex vertex;
-vertex.Position  = glm::vec3(0.2f, 0.4f, 0.6f);
-vertex.Normal    = glm::vec3(0.0f, 1.0f, 0.0f);
+vertex.Position = glm::vec3(0.2f, 0.4f, 0.6f);
+vertex.Normal = glm::vec3(0.0f, 1.0f, 0.0f);
 vertex.TexCoords = glm::vec2(1.0f, 0.0f);
 // = [0.2f, 0.4f, 0.6f, 0.0f, 1.0f, 0.0f, 1.0f, 0.0f];
 ```
 
-由于有了这个有用的特性，我们能够直接传入一大列的<fun>Vertex</fun>结构体的指针作为缓冲的数据，它们将会完美地转换为<fun>glBufferData</fun>所能用的参数：
+感谢这个有用的特性，我们能直接把一个作为缓冲数据的一大列`Vertex`结构体的指针传递过去，它们会翻译成`glBufferData`能用的参数：
+
 
 ```c++
-glBufferData(GL_ARRAY_BUFFER, vertices.size() * sizeof(Vertex), &vertices[0], GL_STATIC_DRAW);
+glBufferData(GL_ARRAY_BUFFER, this->vertices.size() * sizeof(Vertex), 
+             &this->vertices[0], GL_STATIC_DRAW);
 ```
 
-自然`sizeof`运算也可以用在结构体上来计算它的字节大小。这个应该是32字节的（8个float * 每个4字节）。
+自然地，`sizeof`函数也可以使用于结构体来计算字节类型的大小。它应该是32字节（8float * 4）。
+
+一个预处理指令叫做`offsetof(s,m)`把结构体作为它的第一个参数，第二个参数是这个结构体名字的变量。这是结构体另外的一个重要用途。函数返回这个变量从结构体开始的字节偏移量（offset）。这对于定义`glVertexAttribPointer`函数偏移量参数效果很好：
 
-结构体的另外一个很好的用途是它的预处理指令`offsetof(s, m)`，它的第一个参数是一个结构体，第二个参数是这个结构体中变量的名字。这个宏会返回那个变量距结构体头部的字节偏移量(Byte Offset)。这正好可以用在定义<fun>glVertexAttribPointer</fun>函数中的偏移参数：
 
 ```c++
-glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, sizeof(Vertex), (void*)offsetof(Vertex, Normal)); 
+glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, sizeof(Vertex), 
+                     (GLvoid*)offsetof(Vertex, Normal));
 ```
+偏移量现在使用`offsetof`函数定义了，在这个例子里，设置法线向量的字节偏移量等于法线向量在结构体的字节偏移量，它是`3float`，也就是12字节（一个float占4字节）。注意，我们同样设置步长参数等于`Vertex`结构体的大小。
 
-偏移量现在是使用<fun>offsetof</fun>来定义了，在这里它会将法向量的字节偏移量设置为结构体中法向量的偏移量，也就是3个float，即12字节。注意，我们同样将步长参数设置为了<fun>Vertex</fun>结构体的大小。
-
-使用这样的一个结构体不仅能够提供可读性更高的代码，也允许我们很容易地拓展这个结构。如果我们希望添加另一个顶点属性，我们只需要将它添加到结构体中就可以了。由于它的灵活性，渲染的代码不会被破坏。
+使用一个像这样的结构体，不仅能提供可读性更高的代码同时也是我们可以轻松的扩展结构体。如果我们想要增加另一个顶点属性，我们把它可以简单的添加到结构体中，由于它的可扩展性，渲染代码不会被破坏。
 
 ## 渲染
 
-我们需要为<fun>Mesh</fun>类定义最后一个函数，它的<fun>Draw</fun>函数。在真正渲染这个网格之前，我们需要在调用<fun>glDrawElements</fun>函数之前先绑定相应的纹理。然而，这实际上有些困难，我们一开始并不知道这个网格（如果有的话）有多少纹理、纹理是什么类型的。所以我们该如何在着色器中设置纹理单元和采样器呢？
+我们需要为`Mesh`类定义的最后一个函数，是它的Draw函数。在真正渲染前我们希望绑定合适的纹理，然后调用`glDrawElements`。可因为我们从一开始不知道这个网格有多少纹理以及它们应该是什么类型的，所以这件事变得很困难。所以我们该怎样在着色器中设置纹理单元和采样器呢？
+
+解决这个问题，我们需要假设一个特定的名称惯例：每个`diffuse`纹理被命名为`texture_diffuseN`,每个`specular`纹理应该被命名为`texture_specularN`。N是一个从1到纹理才抢其允许使用的最大值之间的数。可以说，在一个网格中我们有3个`diffuse`纹理和2个`specular`纹理，它们的纹理采样器应该这样被调用：
 
-为了解决这个问题，我们需要设定一个命名标准：每个漫反射纹理被命名为`texture_diffuseN`，每个镜面光纹理应该被命名为`texture_specularN`，其中`N`的范围是1到纹理采样器最大允许的数字。比如说我们对某一个网格有3个漫反射纹理，2个镜面光纹理，它们的纹理采样器应该之后会被调用：
 
 ```c++
 uniform sampler2D texture_diffuse1;
@@ -146,48 +161,48 @@ uniform sampler2D texture_specular1;
 uniform sampler2D texture_specular2;
 ```
 
-根据这个标准，我们可以在着色器中定义任意需要数量的纹理采样器，如果一个网格真的包含了（这么多）纹理，我们也能知道它们的名字是什么。根据这个标准，我们也能在一个网格中处理任意数量的纹理，开发者也可以自由选择需要使用的数量，他只需要定义正确的采样器就可以了（虽然定义少的话会有点浪费绑定和uniform调用）。
+使用这样的惯例，我们能定义我们在着色器中需要的纹理采样器的数量。如果一个网格真的有（这么多）纹理，我们就知道它们的名字应该是什么。这个惯例也使我们能够处理一个网格上的任何数量的纹理，通过定义合适的采样器开发者可以自由使用希望使用的数量（虽然定义少的话就会有点浪费绑定和uniform调用了）。
 
-!!! Important
+像这样的问题有很多不同的解决方案，如果你不喜欢这个方案，你可以自己创造一个你自己的方案。
+最后的绘制代码：
 
-	像这样的问题有很多种不同的解决方案。如果你不喜欢这个解决方案，你可以自己想一个你自己的解决办法。
-
-最终的渲染代码是这样的：
 
 ```c++
 void Draw(Shader shader) 
 {
-    unsigned int diffuseNr = 1;
-    unsigned int specularNr = 1;
-    for(unsigned int i = 0; i < textures.size(); i++)
+    GLuint diffuseNr = 1;
+    GLuint specularNr = 1;
+    for(GLuint i = 0; i < this->textures.size(); i++)
     {
-        glActiveTexture(GL_TEXTURE0 + i); // 在绑定之前激活相应的纹理单元
-        // 获取纹理序号（diffuse_textureN 中的 N）
+        glActiveTexture(GL_TEXTURE0 + i); // 在绑定纹理前需要激活适当的纹理单元
+        // 检索纹理序列号 (N in diffuse_textureN)
+        stringstream ss;
         string number;
-        string name = textures[i].type;
+        string name = this->textures[i].type;
         if(name == "texture_diffuse")
-            number = std::to_string(diffuseNr++);
+            ss << diffuseNr++; // 将GLuin输入到string stream
         else if(name == "texture_specular")
-            number = std::to_string(specularNr++);
-
-        shader.setInt(("material." + name + number).c_str(), i);
-        glBindTexture(GL_TEXTURE_2D, textures[i].id);
+            ss << specularNr++; // 将GLuin输入到string stream
+        number = ss.str(); 
+ 
+        glUniform1f(glGetUniformLocation(shader.Program, ("material." + name + number).c_str()), i);
+        glBindTexture(GL_TEXTURE_2D, this->textures[i].id);
     }
     glActiveTexture(GL_TEXTURE0);
-
-    // 绘制网格
-    glBindVertexArray(VAO);
-    glDrawElements(GL_TRIANGLES, indices.size(), GL_UNSIGNED_INT, 0);
+ 
+    // 绘制Mesh
+    glBindVertexArray(this->VAO);
+    glDrawElements(GL_TRIANGLES, this->indices.size(), GL_UNSIGNED_INT, 0);
     glBindVertexArray(0);
 }
 ```
 
-我们首先计算了每个纹理类型的N-分量，并将其拼接到纹理类型字符串上，来获取对应的uniform名称。接下来我们查找对应的采样器，将它的位置值设置为当前激活的纹理单元，并绑定纹理。这也是我们在<fun>Draw</fun>函数中需要着色器的原因。我们也将`"material."`添加到了最终的uniform名称中，因为我们希望将纹理储存在一个材质结构体中（这在每个实现中可能都不同）。
+这不是最漂亮的代码，但是这主要归咎于C++转换类型时的丑陋，比如`int`转`string`时。我们首先计算N-元素每个纹理类型，把它链接到纹理类型字符串来获取合适的uniform名。然后查找合适的采样器位置，给它位置值对应当前激活纹理单元，绑定纹理。这也是我们需要在`Draw`方法是用`shader`的原因。我们添加`material.`到作为结果的uniform名，因为我们通常把纹理储存进材质结构体（对于每个实现也许会有不同）。
 
 !!! Important
 
-	注意我们在将漫反射计数器和镜面光计数器插入`stringstream`时，对它们进行了递增。在C++中，这个递增操作：`variable++`将会返回变量本身，**之后**再递增，而`++variable`则是**先**递增，再返回值。在我们的例子中是首先将原本的计数器值插入`stringstream`，之后再递增它，供下一次循环使用。
+    注意，当我们把`diffuse`和`specular`传递到字符串流（`stringstream`）的时候，计数器会增加，在C++自增叫做：变量++，它会先返回自身然后加1，而++变量，先加1再返回自身，我们的例子里，我们先传递原来的计数器值到字符串流，然后再加1，下一轮生效。
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=includes/learnopengl/mesh.h)找到<fun>Mesh</fun>类的完整源代码
+你可以从这里得到[Mesh类的源码](http://learnopengl.com/code_viewer.php?code=mesh&type=header)。
 
-我们刚定义的<fun>Mesh</fun>类是我们之前讨论的很多话题的抽象结果。在[下一节](03 Model.md)中，我们将创建一个模型，作为多个网格对象的容器，并真正地实现Assimp的加载接口。
+Mesh类是对我们前面的教程里讨论的很多话题的的简洁的抽象在下面的教程里，我们会创建一个模型，它用作乘放多个网格物体的容器，真正的实现Assimp的加载接口。

docs/03 Model Loading/03 Model.md

@@ -3,52 +3,53 @@
 原文     | [Model](http://learnopengl.com/#!Model-Loading/Model)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | [AoZhang](https://github.com/SuperAoao)
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com)
 
-现在是时候接触Assimp并创建实际的加载和转换代码了。这个教程的目标是创建另一个类来完整地表示一个模型，或者说是包含多个网格，多个纹理的模型。一个包含木制阳台、塔楼、甚至游泳池的房子可能仍会被加载为一个模型。我们会使用Assimp来加载模型，并将它转换(Translate)至多个在[上一节](02 Mesh.md)中创建的<var>Mesh</var>对象。
+现在是时候着手启用Assimp，并开始创建实际的加载和转换代码了。本教程的目标是创建另一个类，这个类可以表达模型(Model)的全部。更确切的说，一个模型包含多个网格(Mesh)，一个网格可能带有多个对象。一个别墅，包含一个木制阳台，一个尖顶或许也有一个游泳池，它仍然被加载为一个单一模型。我们通过Assimp加载模型，把它们转变为多个`Mesh`对象，这些对象是是上一节教程里创建的。
 
-
-事不宜迟，我会先把<fun>Model</fun>类的结构给你：
+闲话少说，我把Model类的结构呈现给你：
 
 ```c++
 class Model 
 {
     public:
-        /*  函数   */
-        Model(char *path)
+        /*  成员函数   */
+        Model(GLchar* path)
         {
-            loadModel(path);
+            this->loadModel(path);
         }
-        void Draw(Shader shader);	
+        void Draw(Shader shader); 
     private:
         /*  模型数据  */
         vector<Mesh> meshes;
         string directory;
-        /*  函数   */
+        
+        /*  私有成员函数   */
         void loadModel(string path);
-        void processNode(aiNode *node, const aiScene *scene);
-        Mesh processMesh(aiMesh *mesh, const aiScene *scene);
-        vector<Texture> loadMaterialTextures(aiMaterial *mat, aiTextureType type, 
-                                             string typeName);
+        void processNode(aiNode* node, const aiScene* scene);
+        Mesh processMesh(aiMesh* mesh, const aiScene* scene);
+        vector<Texture> loadMaterialTextures(aiMaterial* mat, aiTextureType type, string typeName);
 };
 ```
 
-<fun>Model</fun>类包含了一个<fun>Mesh</fun>对象的vector（译注：这里指的是C++中的vector模板类，之后遇到均不译），构造函数需要我们给它一个文件路径。在构造函数中，它会直接通过<fun>loadModel</fun>来加载文件。私有函数将会处理Assimp导入过程中的一部分，我们很快就会介绍它们。我们还将储存文件路径的目录，在之后加载纹理的时候还会用到它。
+`Model`类包含一个`Mesh`对象的向量，我们需要在构造函数中给出文件的位置。之后，在构造其中，它通过`loadModel`函数加载文件。私有方法都被设计为处理一部分的Assimp导入的常规动作，我们会简单讲讲它们。同样，我们储存文件路径的目录，这样稍后加载纹理的时候会用到。
+
+函数`Draw`没有什么特别之处，基本上是循环每个网格，调用各自的Draw函数。
 
-<fun>Draw</fun>函数没有什么特别之处，基本上就是遍历了所有网格，并调用它们各自的<fun>Draw</fun>函数。
 
 ```c++
-void Draw(Shader &shader)
+void Draw(Shader shader)
 {
-    for(unsigned int i = 0; i < meshes.size(); i++)
-        meshes[i].Draw(shader);
+    for(GLuint i = 0; i < this->meshes.size(); i++)
+        this->meshes[i].Draw(shader);
 }
 ```
 
 ## 导入3D模型到OpenGL
 
-要想导入一个模型，并将它转换到我们自己的数据结构中的话，首先我们需要包含Assimp对应的头文件：
+为了导入一个模型，并把它转换为我们自己的数据结构，第一件需要做的事是包含合适的Assimp头文件，这样编译器就不会对我们抱怨了。
+
 
 ```c++
 #include <assimp/Importer.hpp>
@@ -56,111 +57,117 @@ void Draw(Shader &shader)
 #include <assimp/postprocess.h>
 ```
 
-首先需要调用的函数是<fun>loadModel</fun>，它会从构造函数中直接调用。在<fun>loadModel</fun>中，我们使用Assimp来加载模型至Assimp的一个叫做<u>scene</u>的数据结构中。你可能还记得在模型加载章节的[第一节](01 Assimp.md)教程中，这是Assimp数据接口的根对象。一旦我们有了这个场景对象，我们就能访问到加载后的模型中所有所需的数据了。
+我们将要调用的第一个函数是`loadModel`,它被构造函数直接调用。在`loadModel`函数里面，我们使用Assimp加载模型到Assimp中被称为scene对象的数据结构。你可能还记得模型加载系列的第一个教程中，这是Assimp的数据结构的根对象。一旦我们有了场景对象，我们就能从已加载模型中获取所有所需数据了。
+
+Assimp最大优点是，它简约的抽象了所加载所有不同格式文件的技术细节，用一行可以做到这一切：
 
-Assimp很棒的一点在于，它抽象掉了加载不同文件格式的所有技术细节，只需要一行代码就能完成所有的工作：
 
 ```c++
 Assimp::Importer importer;
-const aiScene *scene = importer.ReadFile(path, aiProcess_Triangulate | aiProcess_FlipUVs);
+const aiScene* scene = importer.ReadFile(path, aiProcess_Triangulate | aiProcess_FlipUVs);
 ```
 
-我们首先声明了Assimp命名空间内的一个<fun>Importer</fun>，之后调用了它的<var>ReadFile</var>函数。这个函数需要一个文件路径，它的第二个参数是一些<def>后期处理</def>(Post-processing)的选项。除了加载文件之外，Assimp允许我们设定一些选项来强制它对导入的数据做一些额外的计算或操作。通过设定<var>aiProcess_Triangulate</var>，我们告诉Assimp，如果模型不是（全部）由三角形组成，它需要将模型所有的图元形状变换为三角形。<var>aiProcess_FlipUVs</var>将在处理的时候翻转y轴的纹理坐标（你可能还记得我们在[纹理](../01 Getting started/06 Textures.md)教程中说过，在OpenGL中大部分的图像的y轴都是反的，所以这个后期处理选项将会修复这个）。其它一些比较有用的选项有：
+我们先来声明一个`Importer`对象，它的名字空间是`Assimp`，然后调用它的`ReadFile`函数。这个函数需要一个文件路径，第二个参数是后处理（post-processing）选项。除了可以简单加载文件外，Assimp允许我们定义几个选项来强制Assimp去对导入数据做一些额外的计算或操作。通过设置`aiProcess_Triangulate`，我们告诉Assimp如果模型不是（全部）由三角形组成，应该转换所有的模型的原始几何形状为三角形。`aiProcess_FlipUVs`基于y轴翻转纹理坐标，在处理的时候是必须的（你可能记得，我们在纹理教程中，我们说过在OpenGL大多数图像会被沿着y轴反转，所以这个小小的后处理选项会为我们修正这个）。一少部分其他有用的选项如下：
 
-- <var>aiProcess_GenNormals</var>：如果模型不包含法向量的话，就为每个顶点创建法线。
-- <var>aiProcess_SplitLargeMeshes</var>：将比较大的网格分割成更小的子网格，如果你的渲染有最大顶点数限制，只能渲染较小的网格，那么它会非常有用。
-- <var>aiProcess_OptimizeMeshes</var>：和上个选项相反，它会将多个小网格拼接为一个大的网格，减少绘制调用从而进行优化。
+* `aiProcess_GenNormals` : 如果模型没有包含法线向量，就为每个顶点创建法线。
+* `aiProcess_SplitLargeMeshes` : 把大的网格成几个小的的下级网格，当你渲染有一个最大数量顶点的限制时或者只能处理小块网格时很有用。
+* `aiProcess_OptimizeMeshes` : 和上个选项相反，它把几个网格结合为一个更大的网格。以减少绘制函数调用的次数的方式来优化。
 
-Assimp提供了很多有用的后期处理指令，你可以在[这里](http://assimp.sourceforge.net/lib_html/postprocess_8h.html)找到全部的指令。实际上使用Assimp加载模型是非常容易的（你也可以看到）。困难的是之后使用返回的场景对象将加载的数据转换到一个<fun>Mesh</fun>对象的数组。
+Assimp提供了后处理说明，你可以从这里找到所有内容。事实上通过Assimp加载一个模型超级简单。困难的是使用返回的场景对象把加载的数据变换到一个Mesh对象的数组。
+
+完整的`loadModel`函数在这里列出：
 
-完整的<fun>loadModel</fun>函数将会是这样的：
 
 ```c++
 void loadModel(string path)
 {
     Assimp::Importer import;
-    const aiScene *scene = import.ReadFile(path, aiProcess_Triangulate | aiProcess_FlipUVs);	
-
-    if(!scene || scene->mFlags & AI_SCENE_FLAGS_INCOMPLETE || !scene->mRootNode) 
+    const aiScene* scene = import.ReadFile(path, aiProcess_Triangulate | aiProcess_FlipUVs); 
+ 
+    if(!scene || scene->mFlags == AI_SCENE_FLAGS_INCOMPLETE || !scene->mRootNode) 
     {
         cout << "ERROR::ASSIMP::" << import.GetErrorString() << endl;
         return;
     }
-    directory = path.substr(0, path.find_last_of('/'));
-
-    processNode(scene->mRootNode, scene);
+    this->directory = path.substr(0, path.find_last_of('/'));
+ 
+    this->processNode(scene->mRootNode, scene);
 }
 ```
 
-在我们加载了模型之后，我们会检查场景和其根节点不为null，并且检查了它的一个标记(Flag)，来查看返回的数据是不是不完整的。如果遇到了任何错误，我们都会通过导入器的<fun>GetErrorString</fun>函数来报告错误并返回。我们也获取了文件路径的目录路径。
+在我们加载了模型之后，我们检验是否场景和场景的根节点为空，查看这些标记中的一个来看看返回的数据是否完整。如果发生了任何一个错误，我们通过导入器（impoter）的`GetErrorString`函数返回错误报告。我们同样重新获取文件的目录路径。
 
-如果什么错误都没有发生，我们希望处理场景中的所有节点，所以我们将第一个节点（根节点）传入了递归的<fun>processNode</fun>函数。因为每个节点（可能）包含有多个子节点，我们希望首先处理参数中的节点，再继续处理该节点所有的子节点，以此类推。这正符合一个递归结构，所以我们将定义一个递归函数。递归函数在做一些处理之后，使用不同的参数<def>递归</def>调用这个函数自身，直到某个条件被满足停止递归。在我们的例子中<def>退出条件</def>(Exit Condition)是所有的节点都被处理完毕。
+如果没什么错误发生，我们希望处理所有的场景节点，所以我们传递第一个节点（根节点）到递归函数`processNode`。因为每个节点（可能）包含多个子节点，我们希望先处理父节点再处理子节点，以此类推。这符合递归结构，所以我们定义一个递归函数。递归函数就是一个做一些什么处理之后，用不同的参数调用它自身的函数，此种循环不会停止，直到一个特定条件发生。在我们的例子里，特定条件是所有的节点都被处理。
+
+也许你记得，Assimp的结构，每个节点包含一个网格集合的索引，每个索引指向一个在场景对象中特定的网格位置。我们希望获取这些网格索引，获取每个网格，处理每个网格，然后对其他的节点的子节点做同样的处理。`processNode`函数的内容如下：
 
-你可能还记得Assimp的结构中，每个节点包含了一系列的网格索引，每个索引指向场景对象中的那个特定网格。我们接下来就想去获取这些网格索引，获取每个网格，处理每个网格，接着对每个节点的子节点重复这一过程。<fun>processNode</fun>函数的内容如下：
 
 ```c++
-void processNode(aiNode *node, const aiScene *scene)
+void processNode(aiNode* node, const aiScene* scene)
 {
-    // 处理节点所有的网格（如果有的话）
-    for(unsigned int i = 0; i < node->mNumMeshes; i++)
+    // 添加当前节点中的所有Mesh
+    for(GLuint i = 0; i < node->mNumMeshes; i++)
     {
-        aiMesh *mesh = scene->mMeshes[node->mMeshes[i]]; 
-        meshes.push_back(processMesh(mesh, scene));			
+        aiMesh* mesh = scene->mMeshes[node->mMeshes[i]]; 
+        this->meshes.push_back(this->processMesh(mesh, scene)); 
     }
-    // 接下来对它的子节点重复这一过程
-    for(unsigned int i = 0; i < node->mNumChildren; i++)
+    // 递归处理该节点的子孙节点
+    for(GLuint i = 0; i < node->mNumChildren; i++)
     {
-        processNode(node->mChildren[i], scene);
+        this->processNode(node->mChildren[i], scene);
     }
 }
 ```
 
-我们首先检查每个节点的网格索引，并索引场景的<var>mMeshes</var>数组来获取对应的网格。返回的网格将会传递到<fun>processMesh</fun>函数中，它会返回一个<fun>Mesh</fun>对象，我们可以将它存储在<var>meshes</var>列表/vector。
+我们首先利用场景的`mMeshes`数组来检查每个节点的网格索引以获取相应的网格。被返回的网格被传递给`processMesh`函数，它返回一个网格对象，我们可以把它储存在`meshes`的list或vector（STL里的两种实现链表的数据结构）中。
 
-所有网格都被处理之后，我们会遍历节点的所有子节点，并对它们调用相同的<fun>processMesh</fun>函数。当一个节点不再有任何子节点之后，这个函数将会停止执行。
+一旦所有的网格都被处理，我们遍历所有子节点，同样调用processNode函数。一旦一个节点不再拥有任何子节点，函数就会停止执行。
 
 !!! Important
 
-	认真的读者可能会发现，我们可以基本上忘掉处理任何的节点，只需要遍历场景对象的所有网格，就不需要为了索引做这一堆复杂的东西了。我们仍这么做的原因是，使用节点的最初想法是将网格之间定义一个父子关系。通过这样递归地遍历这层关系，我们就能将某个网格定义为另一个网格的父网格了。  
-	这个系统的一个使用案例是，当你想位移一个汽车的网格时，你可以保证它的所有子网格（比如引擎网格、方向盘网格、轮胎网格）都会随着一起位移。这样的系统能够用父子关系很容易地创建出来。
+    认真的读者会注意到，我们可能基本忘记处理任何的节点，简单循环出场景所有的网格，而不是用索引做这件复杂的事。我们这么做的原因是，使用这种节点的原始的想法是，在网格之间定义一个父-子关系。通过递归遍历这些关系，我们可以真正定义特定的网格作为其他网格的父（节点）。
+    
+    关于这个系统的一个有用的例子是，当你想要平移一个汽车网格需要确保把它的子（节点）比如，引擎网格，方向盘网格和轮胎网格都进行平移；使用父-子关系这样的系统很容易被创建出来。
+    
+    现在我们没用这种系统，但是无论何时你想要对你的网格数据进行额外的控制，这通常是一种坚持被推荐的做法。这些模型毕竟是那些定义了这些节点风格的关系的艺术家所创建的。
 
-	然而，现在我们并没有使用这样一种系统，但如果你想对你的网格数据有更多的控制，通常都是建议使用这一种方法的。这种类节点的关系毕竟是由创建了这个模型的艺术家所定义。
-
-下一步就是将Assimp的数据解析到上一节中创建的<fun>Mesh</fun>类中。
+下一步是用上个教程创建的`Mesh`类开始真正处理Assimp的数据。
 
 ### 从Assimp到网格
 
-将一个`aiMesh`对象转化为我们自己的网格对象不是那么困难。我们要做的只是访问网格的相关属性并将它们储存到我们自己的对象中。<fun>processMesh</fun>函数的大体结构如下：
+把一个`aiMesh`对象转换为一个我们自己定义的网格对象并不难。我们所要做的全部是获取每个网格相关的属性并把这些属性储存到我们自己的对象。通常`processMesh`函数的结构会是这样：
+
 
 ```c++
-Mesh processMesh(aiMesh *mesh, const aiScene *scene)
+Mesh processMesh(aiMesh* mesh, const aiScene* scene)
 {
     vector<Vertex> vertices;
-    vector<unsigned int> indices;
+    vector<GLuint> indices;
     vector<Texture> textures;
-
-    for(unsigned int i = 0; i < mesh->mNumVertices; i++)
+ 
+    for(GLuint i = 0; i < mesh->mNumVertices; i++)
     {
         Vertex vertex;
-        // 处理顶点位置、法线和纹理坐标
+        // 处理顶点坐标、法线和纹理坐标
         ...
         vertices.push_back(vertex);
     }
-    // 处理索引
+    // 处理顶点索引
     ...
     // 处理材质
     if(mesh->mMaterialIndex >= 0)
     {
         ...
     }
-
+ 
     return Mesh(vertices, indices, textures);
 }
 ```
 
-处理网格的过程主要有三部分：获取所有的顶点数据，获取它们的网格索引，并获取相关的材质数据。处理后的数据将会储存在三个vector当中，我们会利用它们构建一个<fun>Mesh</fun>对象，并返回它到函数的调用者那里。
+处理一个网格基本由三部分组成：获取所有顶点数据，获取网格的索引，获取相关材质数据。处理过的数据被储存在3个向量其中之一里面，一个Mesh被以这些数据创建，返回到函数的调用者。
+
+获取顶点数据很简单：我们定义一个`Vertex`结构体，在每次遍历后我们把这个结构体添加到`Vertices`数组。我们为存在于网格中的众多顶点循环（通过`mesh->mNumVertices`获取）。在遍历的过程中，我们希望用所有相关数据填充这个结构体。每个顶点位置会像这样被处理：
 
-获取顶点数据非常简单，我们定义了一个<fun>Vertex</fun>结构体，我们将在每个迭代之后将它加到<var>vertices</var>数组中。我们会遍历网格中的所有顶点（使用`mesh->mNumVertices`来获取）。在每个迭代中，我们希望使用所有的相关数据填充这个结构体。顶点的位置是这样处理的：
 
 ```c++
 glm::vec3 vector; 
@@ -170,13 +177,14 @@ vector.z = mesh->mVertices[i].z;
 vertex.Position = vector;
 ```
 
-注意我们为了传输Assimp的数据，我们定义了一个`vec3`的临时变量。使用这样一个临时变量的原因是Assimp对向量、矩阵、字符串等都有自己的一套数据类型，它们并不能完美地转换到GLM的数据类型中。
+注意，为了传输Assimp的数据，我们定义一个`vec3`的宿主，我们需要它是因为Assimp维持它自己的数据类型，这些类型用于向量、材质、字符串等。这些数据类型转换到glm的数据类型时通常效果不佳。
 
 !!! Important
 
-	Assimp将它的顶点位置数组叫做<var>mVertices</var>，这其实并不是那么直观。
+    Assimp调用他们的顶点位置数组`mVertices`真有点违反直觉。
+
+对应法线的步骤毫无疑问是这样的：
 
-处理法线的步骤也是差不多的：
 
 ```c++
 vector.x = mesh->mNormals[i].x;
@@ -185,10 +193,11 @@ vector.z = mesh->mNormals[i].z;
 vertex.Normal = vector;
 ```
 
-纹理坐标的处理也大体相似，但Assimp允许一个模型在一个顶点上有最多8个不同的纹理坐标，我们不会用到那么多，我们只关心第一组纹理坐标。我们同样也想检查网格是否真的包含了纹理坐标（可能并不会一直如此）
+纹理坐标也基本一样，但是Assimp允许一个模型的每个顶点有8个不同的纹理坐标，我们可能用不到，所以我们只关系第一组纹理坐标。我们也希望检查网格是否真的包含纹理坐标（可能并不总是如此）:
+
 
 ```c++
-if(mesh->mTextureCoords[0]) // 网格是否有纹理坐标？
+if(mesh->mTextureCoords[0]) // Does the mesh contain texture coordinates?
 {
     glm::vec2 vec;
     vec.x = mesh->mTextureCoords[0][i].x; 
@@ -199,54 +208,58 @@ else
     vertex.TexCoords = glm::vec2(0.0f, 0.0f);
 ```
 
-<var>vertex</var>结构体现在已经填充好了需要的顶点属性，我们会在迭代的最后将它压入<var>vertices</var>这个vector的尾部。这个过程会对每个网格的顶点都重复一遍。
+`Vertex`结构体现在完全被所需的顶点属性填充了，我们能把它添加到`vertices`向量的尾部。要对每个网格的顶点做相同的处理。
 
-### 索引
+### 顶点
+
+Assimp的接口定义每个网格有一个以面（faces）为单位的数组，每个面代表一个单独的图元，在我们的例子中（由于`aiProcess_Triangulate`选项）总是三角形，一个面包含索引，这些索引定义我们需要绘制的顶点以在那样的顺序提供给每个图元，所以如果我们遍历所有面，把所有面的索引储存到`indices`向量，我们需要这么做：
 
-Assimp的接口定义了每个网格都有一个面(Face)数组，每个面代表了一个图元，在我们的例子中（由于使用了<var>aiProcess_Triangulate</var>选项）它总是三角形。一个面包含了多个索引，它们定义了在每个图元中，我们应该绘制哪个顶点，并以什么顺序绘制，所以如果我们遍历了所有的面，并储存了面的索引到<var>indices</var>这个vector中就可以了。
 
 ```c++
-for(unsigned int i = 0; i < mesh->mNumFaces; i++)
+for(GLuint i = 0; i < mesh->mNumFaces; i++)
 {
     aiFace face = mesh->mFaces[i];
-    for(unsigned int j = 0; j < face.mNumIndices; j++)
+    for(GLuint j = 0; j < face.mNumIndices; j++)
         indices.push_back(face.mIndices[j]);
 }
 ```
 
-所有的外部循环都结束了，我们现在有了一系列的顶点和索引数据，它们可以用来通过<fun>glDrawElements</fun>函数来绘制网格。然而，为了结束这个话题，并且对网格提供一些细节，我们还需要处理网格的材质。
+所有外部循环结束后，我们现在有了一个完整点的顶点和索引数据来绘制网格，这要调用`glDrawElements`函数。可是，为了结束这个讨论，并向网格提供一些细节，我们同样希望处理网格的材质。
+
+ 
 
 ### 材质
 
-和节点一样，一个网格只包含了一个指向材质对象的索引。如果想要获取网格真正的材质，我们还需要索引场景的<var>mMaterials</var>数组。网格材质索引位于它的<var>mMaterialIndex</var>属性中，我们同样可以用它来检测一个网格是否包含有材质：
+如同节点，一个网格只有一个指向材质对象的索引，获取网格实际的材质，我们需要索引场景的`mMaterials`数组。网格的材质索引被设置在`mMaterialIndex`属性中，通过这个属性我们同样能够检验一个网格是否包含一个材质：
 
 ```c++
 if(mesh->mMaterialIndex >= 0)
 {
-    aiMaterial *material = scene->mMaterials[mesh->mMaterialIndex];
-    vector<Texture> diffuseMaps = loadMaterialTextures(material, 
+    aiMaterial* material = scene->mMaterials[mesh->mMaterialIndex];
+    vector<Texture> diffuseMaps = this->loadMaterialTextures(material, 
                                         aiTextureType_DIFFUSE, "texture_diffuse");
     textures.insert(textures.end(), diffuseMaps.begin(), diffuseMaps.end());
-    vector<Texture> specularMaps = loadMaterialTextures(material, 
+    vector<Texture> specularMaps = this->loadMaterialTextures(material, 
                                         aiTextureType_SPECULAR, "texture_specular");
     textures.insert(textures.end(), specularMaps.begin(), specularMaps.end());
 }
 ```
 
-我们首先从场景的<var>mMaterials</var>数组中获取`aiMaterial`对象。接下来我们希望加载网格的漫反射和/或镜面光贴图。一个材质对象的内部对每种纹理类型都存储了一个纹理位置数组。不同的纹理类型都以`aiTextureType_`为前缀。我们使用一个叫做<fun>loadMaterialTextures</fun>的工具函数来从材质中获取纹理。这个函数将会返回一个<fun>Texture</fun>结构体的vector，我们将在模型的<var>textures</var> vector的尾部之后存储它。
+我么先从场景的`mMaterials`数组获取`aimaterial`对象，然后，我们希望加载网格的diffuse或/和specular纹理。一个材质储存了一个数组，这个数组为每个纹理类型提供纹理位置。不同的纹理类型都以`aiTextureType_`为前缀。我们使用一个帮助函数：`loadMaterialTextures`来从材质获取纹理。这个函数返回一个`Texture`结构体的向量，我们在之后储存在模型的`textures`坐标的后面。
+
+`loadMaterialTextures`函数遍历所有给定纹理类型的纹理位置，获取纹理的文件位置，然后加载生成纹理，把信息储存到`Vertex`结构体。看起来像这样：
 
-<fun>loadMaterialTextures</fun>函数遍历了给定纹理类型的所有纹理位置，获取了纹理的文件位置，并加载并和生成了纹理，将信息储存在了一个<fun>Vertex</fun>结构体中。它看起来会像这样：
 
 ```c++
-vector<Texture> loadMaterialTextures(aiMaterial *mat, aiTextureType type, string typeName)
+vector<Texture> loadMaterialTextures(aiMaterial* mat, aiTextureType type, string typeName)
 {
     vector<Texture> textures;
-    for(unsigned int i = 0; i < mat->GetTextureCount(type); i++)
+    for(GLuint i = 0; i < mat->GetTextureCount(type); i++)
     {
         aiString str;
         mat->GetTexture(type, i, &str);
         Texture texture;
-        texture.id = TextureFromFile(str.C_Str(), directory);
+        texture.id = TextureFromFile(str.C_Str(), this->directory);
         texture.type = typeName;
         texture.path = str;
         textures.push_back(texture);
@@ -255,50 +268,53 @@ vector<Texture> loadMaterialTextures(aiMaterial *mat, aiTextureType type, string
 }
 ```
 
-我们首先通过<fun>GetTextureCount</fun>函数检查储存在材质中纹理的数量，这个函数需要一个纹理类型。我们会使用<fun>GetTexture</fun>获取每个纹理的文件位置，它会将结果储存在一个`aiString`中。我们接下来使用另外一个叫做<fun>TextureFromFile</fun>的工具函数，它将会（用`stb_image.h`）加载一个纹理并返回该纹理的ID。如果你不确定这样的代码是如何写出来的话，可以查看最后的完整代码。
+我们先通过`GetTextureCount`函数检验材质中储存的纹理，以期得到我们希望得到的纹理类型。然后我们通过`GetTexture`函数获取每个纹理的文件位置，这个位置以`aiString`类型储存。然后我们使用另一个帮助函数，它被命名为：`TextureFromFile`加载一个纹理（使用SOIL），返回纹理的ID。你可以查看列在最后的完整的代码，如果你不知道这个函数应该怎样写出来的话。
 
 !!! Important
 
-	注意，我们假设了模型文件中纹理文件的路径是相对于模型文件的本地(Local)路径，比如说与模型文件处于同一目录下。我们可以将纹理位置字符串拼接到之前（在<fun>loadModel</fun>中）获取的目录字符串上，来获取完整的纹理路径（这也是为什么<fun>GetTexture</fun>函数也需要一个目录字符串）。
+    注意，我们假设纹理文件与模型是在相同的目录里。我们可以简单的链接纹理位置字符串和之前获取的目录字符串（在`loadModel`函数中得到的）来获得完整的纹理路径（这就是为什么`GetTexture`函数同样需要目录字符串）。
+    
+    有些在互联网上找到的模型使用绝对路径，它们的纹理位置就不会在每台机器上都有效了。例子里，你可能希望手工编辑这个文件来使用本地路径为纹理所使用（如果可能的话）。
 
-	在网络上找到的某些模型会对纹理位置使用绝对(Absolute)路径，这就不能在每台机器上都工作了。在这种情况下，你可能会需要手动修改这个文件，来让它对纹理使用本地路径（如果可能的话）。
-
-这就是使用Assimp导入模型的全部了。
+这就是使用Assimp来导入一个模型的全部了。你可以在这里找到[Model类的代码](http://learnopengl.com/code_viewer.php?code=model_loading/model_unoptimized)。
 
 # 重大优化
 
-这还没有完全结束，因为我们还想做出一个重大的（但不是完全必须的）优化。大多数场景都会在多个网格中重用部分纹理。还是想想一个房子，它的墙壁有着花岗岩的纹理。这个纹理也可以被应用到地板、天花板、楼梯、桌子，甚至是附近的一口井上。加载纹理并不是一个低开销的操作，在我们当前的实现中，即便同样的纹理已经被加载过很多遍了，对每个网格仍会加载并生成一个新的纹理。这很快就会变成模型加载实现的性能瓶颈。
+我们现在还没做完。因为我们还想做一个重大的优化（但是不是必须的）。大多数场景重用若干纹理，把它们应用到网格；还是思考那个别墅，它有个花岗岩的纹理作为墙面。这个纹理也可能应用到地板、天花板，楼梯，或者一张桌子、一个附近的小物件。加载纹理需要不少操作，当前的实现中一个新的纹理被加载和生成，来为每个网格使用，即使同样的纹理之前已经被加载了好几次。这会很快转变为你的模型加载实现的瓶颈。
+
+所以我们打算添加一个小小的微调，把模型的代码改成，储存所有的已加载纹理到全局。无论在哪儿我们都要先检查这个纹理是否已经被加载过了。如果加载过了，我们就直接使用这个纹理并跳过整个加载流程来节省处理能力。为了对比纹理我们同样需要储存它们的路径：
 
-所以我们会对模型的代码进行微调，将所有加载过的纹理全局储存，每当我们想加载一个纹理的时候，首先去检查它有没有被加载过。如果有的话，我们会直接使用那个纹理，并跳过整个加载流程，来为我们省下很多处理能力。为了能够比较纹理，我们还需要储存它们的路径：
 
 ```c++
 struct Texture {
-    unsigned int id;
+    GLuint id;
     string type;
-    aiString path;  // 我们储存纹理的路径用于与其它纹理进行比较
+    aiString path;  // We store the path of the texture to compare with other textures
 };
 ```
 
-接下来我们将所有加载过的纹理储存在另一个vector中，在模型类的顶部声明为一个私有变量：
+然后我们把所有加载过的纹理储存到另一个向量中，它是作为一个私有变量声明在模型类的顶部：
+
 
 ```c++
 vector<Texture> textures_loaded;
 ```
 
-之后，在<fun>loadMaterialTextures</fun>函数中，我们希望将纹理的路径与储存在<var>textures_loaded</var>这个vector中的所有纹理进行比较，看看当前纹理的路径是否与其中的一个相同。如果是的话，则跳过纹理加载/生成的部分，直接使用定位到的纹理结构体为网格的纹理。更新后的函数如下：
+然后，在`loadMaterialTextures`函数中，我们希望把纹理路径和所有`texture_loaded`向量对比，看看是否当前纹理路径和其中任何一个是否相同，如果是，我们跳过纹理加载/生成部分，简单的使用已加载纹理结构体作为网格纹理。这个函数如下所示：
+
 
 ```c++
-vector<Texture> loadMaterialTextures(aiMaterial *mat, aiTextureType type, string typeName)
+vector<Texture> loadMaterialTextures(aiMaterial* mat, aiTextureType type, string typeName)
 {
     vector<Texture> textures;
-    for(unsigned int i = 0; i < mat->GetTextureCount(type); i++)
+    for(GLuint i = 0; i < mat->GetTextureCount(type); i++)
     {
         aiString str;
         mat->GetTexture(type, i, &str);
-        bool skip = false;
-        for(unsigned int j = 0; j < textures_loaded.size(); j++)
+        GLboolean skip = false;
+        for(GLuint j = 0; j < textures_loaded.size(); j++)
         {
-            if(std::strcmp(textures_loaded[j].path.data(), str.C_Str()) == 0)
+            if(textures_loaded[j].path == str)
             {
                 textures.push_back(textures_loaded[j]);
                 skip = true; 
@@ -306,47 +322,47 @@ vector<Texture> loadMaterialTextures(aiMaterial *mat, aiTextureType type, string
             }
         }
         if(!skip)
-        {   // 如果纹理还没有被加载，则加载它
+        {   // 如果纹理没有被加载过，加载之
             Texture texture;
-            texture.id = TextureFromFile(str.C_Str(), directory);
+            texture.id = TextureFromFile(str.C_Str(), this->directory);
             texture.type = typeName;
-            texture.path = str.C_Str();
+            texture.path = str;
             textures.push_back(texture);
-            textures_loaded.push_back(texture); // 添加到已加载的纹理中
+            this->textures_loaded.push_back(texture);  // 添加到纹理列表 textures
         }
     }
     return textures;
 }
 ```
 
-所以现在我们不仅有了个灵活的模型加载系统，我们也获得了一个加载对象很快的优化版本。
+所以现在我们不仅有了一个通用模型加载系统，同时我们也得到了一个能使加载对象更快的优化版本。
 
 !!! Attention
 
-	有些版本的Assimp在使用调试版本或者使用IDE的调试模式下加载模型会非常缓慢，所以在你遇到缓慢的加载速度时，可以试试使用发布版本。
+    有些版本的Assimp当使用调试版或/和使用你的IDE的调试模式时，模型加载模型实在慢，所以确保在当你加载得很慢的时候用发布版再测试。
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=includes/learnopengl/model.h)找到优化后<fun>Model</fun>类的完整源代码。
+你可以从这里获得优化的[Model类的完整源代码](http://learnopengl.com/code_viewer.php?code=model&type=header)。
 
 # 和箱子模型告别
 
-所以，让我们导入一个由真正的艺术家所创造的模型，替代我这个天才的作品（你要承认，这些箱子可能是你看过的最漂亮的立方体了），测试一下我们的实现吧。由于我不想让我占太多的功劳，我会偶尔让别的艺术家也加入我们，这次我们将会加载由Berk Gedik设计的[吉他生存背包](https://sketchfab.com/3d-models/survival-guitar-backpack-low-poly-799f8c4511f84fab8c3f12887f7e6b36)(Survival Guitar Backpack)。我稍微修改了材质和路径，这样便可与我们的模型加载代码兼容。这个模型被输出为一个.obj文件以及一个.mtl文件，.mtl文件包含了模型的漫反射、镜面光和法线贴图（这个会在后面学习到），你可以在[这里](../data/backpack.zip)下载到稍微修改之后的模型，注意，我们不会用到它的一些额外的纹理类型，并且所有的纹理和模型文件应该位于同一个目录下，以供加载纹理。
+现在给我们导入一个天才艺术家创建的模型看看效果，不是我这个天才做的（你不得不承认，这个箱子也许是你见过的最漂亮的立体图形）。因为我不想过于自夸，所以我会时不时的给其他艺术家进入这个行列的机会，这次我们会加载Crytek原版的孤岛危机游戏中的纳米铠甲。这个模型被输出为obj和mtl文件，mtl包含模型的diffuse和specular以及法线贴图（后面会讲）。你可以下载这个模型，注意，所有的纹理和模型文件都应该放在同一个目录，以便载入纹理。
 
 !!! Important
+    
+    你从这个站点下载的版本是修改过的版本，每个纹理文件路径已经修改改为本地相对目录，原来的资源是绝对目录。
 
-	你从本网站中下载到的版本是修改过的版本，每个纹理的路径都被修改为了一个本地的相对路径，而不是原资源的绝对路径。
+现在在代码中，声明一个Model对象，把它模型的文件位置传递给它。模型应该自动加载（如果没有错误的话）在游戏循环中使用它的Draw函数绘制这个对象。没有更多的缓冲配置，属性指针和渲染命令，仅仅简单的一行。如果你创建几个简单的着色器，像素着色器只输出对象的diffuse纹理颜色，结果看上去会有点像这样：
 
-现在在代码中，声明一个<fun>Model</fun>对象，将模型的文件位置传入。接下来模型应该会自动加载并（如果没有错误的话）在渲染循环中使用它的<fun>Draw</fun>函数来绘制物体，这样就可以了。不再需要缓冲分配、属性指针和渲染指令，只需要一行代码就可以了。接下来如果你创建一系列着色器，其中片段着色器仅仅输出物体的漫反射纹理颜色，最终的结果看上去会是这样的：
+![](http://www.learnopengl.com/img/model_loading/model_diffuse.png)
 
-![](../img/03/03/model_diffuse.png)
+你可以从这里找到带有[顶点](http://learnopengl.com/code_viewer.php?code=model_loading/model&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=model_loading/model&type=fragment)着色器的[完整的源码](http://learnopengl.com/code_viewer.php?code=model_loading/model_diffuse)。
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/3.model_loading/1.model_loading/model_loading.cpp)找到完整的源码。注意我们通过stb_image.h来垂直翻转纹理，如果你在我们加载模型之前没有这样做会导致纹理看起来完全混乱。
+我们也可以变得更加有创造力，引入两个点光源到我们之前从光照教程学过的渲染等式，结合高光贴图获得惊艳效果：
 
-我们可以变得更有创造力一点，根据我们之前在[光照](../02 Lighting/05 Light casters.md)教程中学过的知识，引入两个点光源到渲染方程中，结合镜面光贴图，我们能得到很惊人的效果。
+![](http://www.learnopengl.com/img/model_loading/model_lighting.png)
 
-![](../img/03/03/model_lighting.png)
+虽然我不得不承认这个相比之前用过的容器也太炫了。使用Assimp，你可以载入无数在互联网上找到的模型。只有很少的资源网站提供多种格式的免费3D模型给你下载。一定注意，有些模型仍然不能很好的载入，纹理路径无效或者这种格式Assimp不能读。
 
-甚至我都必须要承认这个可能是比一直使用的箱子要好看多了。使用Assimp，你能够加载互联网上的无数模型。有很多资源网站都提供了多种格式的免费3D模型供你下载。但还是要注意，有些模型会不能正常地载入，纹理的路径会出现问题，或者Assimp并不支持它的格式。
+## 练习
 
-## 延伸阅读
-
-- [如何将Wavefront(.obj)模型纹理加载到OpenGL](https://www.youtube.com/watch?v=4DQquG_o-Ac):由Matthew Early制作的如何在Blender中设置3D模型的视频教程，让它们可以直接在当前的模型加载器下正确工作(因为我们选择的纹理设置并不总能做到开箱即用)。
+你可以使用两个点光源重建上个场景吗？[方案](http://learnopengl.com/code_viewer.php?code=model_loading/model-exercise1)，[着色器](http://learnopengl.com/code_viewer.php?code=model_loading/model-exercise1-shaders)。

docs/04 Advanced OpenGL/01 Depth testing.md

@@ -3,198 +3,197 @@
 原文     | [Depth testing](http://learnopengl.com/#!Advanced-OpenGL/Depth-testing)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | 暂未校对
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com)
 
-在[坐标系统](../01 Getting started/08 Coordinate Systems.md)小节中，我们渲染了一个3D箱子，并且运用了<def>深度缓冲</def>(Depth Buffer)来防止被阻挡的面渲染到其它面的前面。在这一节中，我们将会更加深入地讨论这些储存在深度缓冲（或z缓冲(z-buffer)）中的<def>深度值</def>(Depth Value)，以及它们是如何确定一个片段是处于其它片段后方的。
+在[坐标系的教程](../01 Getting started/08 Coordinate Systems.md)中我们呈现了一个3D容器,使用**深度缓冲(Depth Buffer)**,以防止被其他面遮挡的面渲染到前面。在本教程中我们将细致地讨论被深度缓冲(或z-buffer)所存储的**深度值**以及它是如何确定一个片段是否被其他片段遮挡。
 
-深度缓冲就像<def>颜色缓冲</def>(Color Buffer)（储存所有的片段颜色：视觉输出）一样，在每个片段中储存了信息，并且（通常）和颜色缓冲有着一样的宽度和高度。深度缓冲是由窗口系统自动创建的，它会以16、24或32位float的形式储存它的深度值。在大部分的系统中，深度缓冲的精度都是24位的。
+**深度缓冲**就像**颜色缓冲(Color Buffer)**(存储所有的片段颜色:视觉输出)那样存储每个片段的信息，(通常) 和颜色缓冲区有相同的宽度和高度。深度缓冲由窗口系统自动创建并将其深度值存储为 16、 24 或 32 位浮点数。在大多数系统中深度缓冲区为24位。
 
-当深度测试(Depth Testing)被启用的时候，OpenGL会将一个片段的深度值与深度缓冲的内容进行对比。OpenGL会执行一个深度测试，如果这个测试通过了的话，深度缓冲将会更新为新的深度值。如果深度测试失败了，片段将会被丢弃。
+当深度测试启用的时候， OpenGL 测试深度缓冲区内的深度值。OpenGL 执行深度测试的时候，如果此测试通过，深度缓冲内的值将被设为新的深度值。如果深度测试失败，则丢弃该片段。
 
-深度缓冲是在片段着色器运行之后（以及模板测试(Stencil Testing)运行之后，我们将在[下一节](02 Stencil testing.md)中讨论）在屏幕空间中运行的。屏幕空间坐标与通过OpenGL的<fun>glViewport</fun>所定义的视口密切相关，并且可以直接使用GLSL内建变量<var>gl_FragCoord</var>从片段着色器中直接访问。<var>gl_FragCoord</var>的x和y分量代表了片段的屏幕空间坐标（其中(0, 0)位于左下角）。<var>gl_FragCoord</var>中也包含了一个z分量，它包含了片段真正的深度值。z值就是需要与深度缓冲内容所对比的那个值。
+深度测试在片段着色器运行之后(并且模板测试运行之后，我们将在[接下来](http://www.learnopengl.com/#!Advanced-OpenGL/Stencil-testing)的教程中讨论)在屏幕空间中执行的。屏幕空间坐标直接有关的视区，由OpenGL的`glViewport`函数给定，并且可以通过GLSL的片段着色器中内置的 `gl_FragCoord`变量访问。`gl_FragCoord` 的 X 和 y 表示该片段的屏幕空间坐标 ((0，0) 在左下角)。`gl_FragCoord` 还包含一个 z 坐标，它包含了片段的实际深度值。此 z 坐标值是与深度缓冲区的内容进行比较的值。
 
 !!! Important
 
-	现在大部分的GPU都提供一个叫做提前深度测试(Early Depth Testing)的硬件特性。提前深度测试允许深度测试在片段着色器之前运行。只要我们清楚一个片段永远不会是可见的（它在其他物体之后），我们就能提前丢弃这个片段。
+    现在大多数 GPU 都支持一种称为提前深度测试(Early depth testing)的硬件功能。提前深度测试允许深度测试在片段着色器之前运行。明确一个片段永远不会可见的 (它是其它物体的后面) 我们可以更早地放弃该片段。
 
-	片段着色器通常开销都是很大的，所以我们应该尽可能避免运行它们。当使用提前深度测试时，片段着色器的一个限制是你不能写入片段的深度值。如果一个片段着色器对它的深度值进行了写入，提前深度测试是不可能的。OpenGL不能提前知道深度值。
+    片段着色器通常是相当费时的所以我们应该尽量避免运行它们。对片段着色器提前深度测试一个限制是，你不应该写入片段的深度值。如果片段着色器将写入其深度值，提前深度测试是不可能的，OpenGL不能事先知道深度值。
 
-深度测试默认是禁用的，所以如果要启用深度测试的话，我们需要用<var>GL_DEPTH_TEST</var>选项来启用它：
+深度测试默认是关闭的，要启用深度测试的话，我们需要用`GL_DEPTH_TEST`选项来打开它：
 
 ```c++
 glEnable(GL_DEPTH_TEST);
 ```
 
-当它启用的时候，如果一个片段通过了深度测试的话，OpenGL会在深度缓冲中储存该片段的z值；如果没有通过深度缓冲，则会丢弃该片段。如果你启用了深度缓冲，你还应该在每个渲染迭代之前使用<var>GL_DEPTH_BUFFER_BIT</var>来清除深度缓冲，否则你会仍在使用上一次渲染迭代中的写入的深度值：
+一旦启用深度测试，如果片段通过深度测试，OpenGL自动在深度缓冲区存储片段的 z 值，如果深度测试失败，那么相应地丢弃该片段。如果启用深度测试，那么在每个渲染之前还应使用`GL_DEPTH_BUFFER_BIT`清除深度缓冲区，否则深度缓冲区将保留上一次进行深度测试时所写的深度值
 
 ```c++
 glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
 ```
 
-可以想象，在某些情况下你会需要对所有片段都执行深度测试并丢弃相应的片段，但**不**希望更新深度缓冲。基本上来说，你在使用一个<def>只读的</def>(Read-only)深度缓冲。OpenGL允许我们禁用深度缓冲的写入，只需要设置它的深度掩码(Depth Mask)设置为`GL_FALSE`就可以了：
+在某些情况下我们需要进行深度测试并相应地丢弃片段，但我们不希望更新深度缓冲区，基本上，可以使用一个只读的深度缓冲区；OpenGL允许我们通过将其深度掩码设置为`GL_FALSE`禁用深度缓冲区写入:
 
 ```c++
 glDepthMask(GL_FALSE);
 ```
 
-注意这只在深度测试被启用的时候才有效果。
+注意这只在深度测试被启用的时候有效。
 
 ## 深度测试函数
 
-OpenGL允许我们修改深度测试中使用的比较运算符。这允许我们来控制OpenGL什么时候该通过或丢弃一个片段，什么时候去更新深度缓冲。我们可以调用<fun>glDepthFunc</fun>函数来设置比较运算符（或者说深度函数(Depth Function)）：
+OpenGL 允许我们修改它深度测试使用的比较运算符(comparison operators)。这样我们能够控制OpenGL通过或丢弃碎片和如何更新深度缓冲区。我们可以通过调用`glDepthFunc`来设置比较运算符 (或叫做深度函数(depth function)):
 
 ```c++
 glDepthFunc(GL_LESS);
 ```
 
-这个函数接受下面表格中的比较运算符：
+该函数接受在下表中列出的几个比较运算符:
 
-函数|描述
+运算符|描述
  ----------|------------------
- GL_ALWAYS | 永远通过深度测试
- GL_NEVER  | 永远不通过深度测试
- GL_LESS   | 在片段深度值小于缓冲的深度值时通过测试
- GL_EQUAL  | 在片段深度值等于缓冲区的深度值时通过测试
- GL_LEQUAL | 在片段深度值小于等于缓冲区的深度值时通过测试
- GL_GREATER | 在片段深度值大于缓冲区的深度值时通过测试
- GL_NOTEQUAL| 在片段深度值不等于缓冲区的深度值时通过测试
- GL_GEQUAL | 在片段深度值大于等于缓冲区的深度值时通过测试
+ GL_ALWAYS |永远通过测试
+ GL_NEVER  |永远不通过测试
+ GL_LESS   |在片段深度值小于缓冲区的深度时通过测试
+ GL_EQUAL  |在片段深度值等于缓冲区的深度时通过测试
+ GL_LEQUAL |在片段深度值小于等于缓冲区的深度时通过测试
+ GL_GREATER |在片段深度值大于缓冲区的深度时通过测试
+ GL_NOTEQUAL|在片段深度值不等于缓冲区的深度时通过测试
+ GL_GEQUAL |在片段深度值大于等于缓冲区的深度时通过测试
 
-默认情况下使用的深度函数是<var>GL_LESS</var>，它将会丢弃深度值大于等于当前深度缓冲值的所有片段。
+默认情况下使用`GL_LESS`，这将丢弃深度值高于或等于当前深度缓冲区的值的片段。
 
-让我们看看改变深度函数会对视觉输出有什么影响。我们将使用一个新的代码配置，它会显示一个没有光照的基本场景，里面有两个有纹理的立方体，放置在一个有纹理的地板上。你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/1.1.depth_testing/depth_testing.cpp)找到源代码。
+让我们看看改变深度函数对输出的影响。我们将使用新鲜的代码安装程序显示一个没有灯光的有纹理地板上的两个有纹理的立方体。你可以在这里找到源代码和其着色器代码。
 
-在源代码中，我们将深度函数改为<var>GL_ALWAYS</var>：
+代码中我们将深度函数设为`GL_ALWAYS`:
 
 ```c++
-glEnable(GL_DEPTH_TEST);
 glDepthFunc(GL_ALWAYS);
 ```
 
-这将会模拟我们没有启用深度测试时所得到的结果。深度测试将会永远通过，所以最后绘制的片段将会总是会渲染在之前绘制片段的上面，即使之前绘制的片段本就应该渲染在最前面。因为我们是最后渲染地板的，它会覆盖所有的箱子片段：
+这和我们没有启用深度测试得到了相同的行为。深度测试只是简单地通过，所以这样最后绘制的片段就会呈现在之前绘制的片段前面，即使他们应该在前面。由于我们最后绘制地板平面，那么平面的片段会覆盖每个容器的片段:
 
-![](../img/04/01/depth_testing_func_always.png)
+![](http://learnopengl.com/img/advanced/depth_testing_func_always.png)
 
-将它重新设置为<var>GL_LESS</var>，这会将场景还原为原有的样子：
+重新设置到`GL_LESS`给了我们曾经的场景：
 
-![](../img/04/01/depth_testing_func_less.png)
+![](http://learnopengl.com/img/advanced/depth_testing_func_less.png)
 
 ## 深度值精度
 
-深度缓冲包含了一个介于0.0和1.0之间的深度值，它将会与观察者视角所看见的场景中所有物体的z值进行比较。观察空间的z值可能是投影平截头体的**近平面**(Near)和**远平面**(Far)之间的任何值。我们需要一种方式来将这些观察空间的z值变换到[0, 1]范围之间，其中的一种方式就是将它们线性变换到[0, 1]范围之间。下面这个（线性）方程将z值变换到了0.0到1.0之间的深度值：
+在深度缓冲区中包含深度值介于`0.0`和`1.0`之间，从观察者看到其内容与场景中的所有对象的 z 值进行了比较。这些视图空间中的 z 值可以在投影平头截体的近平面和远平面之间的任何值。我们因此需要一些方法来转换这些视图空间 z 值到 [0，1] 的范围内，方法之一就是线性将它们转换为 [0，1] 范围内。下面的 (线性) 方程把 z 值转换为 0.0 和 1.0 之间的值 :
 
 $$
 \begin{equation} F_{depth} = \frac{z - near}{far - near} \end{equation}
 $$
 
-这里的\(near\)和\(far\)值是我们之前提供给投影矩阵设置可视平截头体的（见[坐标系统](../01 Getting started/08 Coordinate Systems.md)）那个 *near* 和 *far* 值。这个方程需要平截头体中的一个z值，并将它变换到了[0, 1]的范围中。z值和对应的深度值之间的关系可以在下图中看到：
+这里far和near是我们用来提供到投影矩阵设置可见视图截锥的远近值 (见[坐标系](../01 Getting started/08 Coordinate Systems.md))。方程带内锥截体的深度值 z，并将其转换到 [0，1] 范围。在下面的图给出 z 值和其相应的深度值的关系:
 
-![](../img/04/01/depth_linear_graph.png)
+![](http://learnopengl.com/img/advanced/depth_linear_graph.png)
 
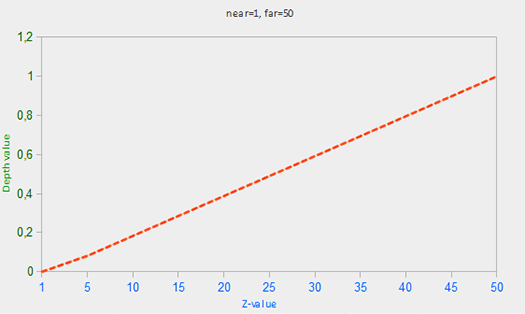
 !!! Important
 
-	注意所有的方程都会将非常近的物体的深度值设置为接近0.0的值，而当物体非常接近远平面的时候，它的深度值会非常接近1.0。
+    注意在物体接近近平面的时候，方程给出的深度值接近0.0，物体接近远平面时，方程给出的深度接近1.0。
 
-然而，在实践中是几乎永远不会使用这样的<def>线性深度缓冲</def>(Linear Depth Buffer)的。要想有正确的投影性质，需要使用一个非线性的深度方程，它是与 1/z 成正比的。它做的就是在z值很小的时候提供非常高的精度，而在z值很远的时候提供更少的精度。花时间想想这个：我们真的需要对1000单位远的深度值和只有1单位远的充满细节的物体使用相同的精度吗？线性方程并不会考虑这一点。
+然而，在实践中是几乎从来不使用这样的线性深度缓冲区。正确的投影特性的非线性深度方程是和1/z成正比的 。这样基本上做的是在z很近是的高精度和 z 很远的时候的低精度。用几秒钟想一想: 我们真的需要让1000单位远的物体和只有1单位远的物体的深度值有相同的精度吗?线性方程没有考虑这一点。
 
-由于非线性方程与 1/z 成正比，在1.0和2.0之间的z值将会变换至1.0到0.5之间的深度值，这就是一个float提供给我们的一半精度了，这在z值很小的情况下提供了非常大的精度。在50.0和100.0之间的z值将会只占2%的float精度，这正是我们所需要的。这样的一个考虑了远近距离的方程是这样的：
+由于非线性函数是和 1/z 成正比，例如1.0 和 2.0 之间的 z 值，将变为 1.0 到 0.5之间， 这样在z非常小的时候给了我们很高的精度。50.0 和 100.0 之间的 Z 值将只占 2%的浮点数的精度，这正是我们想要的。这类方程，也需要近和远距离考虑，下面给出:
 
 $$
 \begin{equation} F_{depth} = \frac{1/z - 1/near}{1/far - 1/near} \end{equation}
 $$
 
-如果你不知道这个方程是怎么回事也不用担心。重要的是要记住深度缓冲中的值在屏幕空间中不是线性的（在透视矩阵应用之前在观察空间中是线性的）。深度缓冲中0.5的值并不代表着物体的z值是位于平截头体的中间了，这个顶点的z值实际上非常接近近平面！你可以在下图中看到z值和最终的深度缓冲值之间的非线性关系：
+如果你不知道这个方程到底怎么回事也不必担心。要记住的重要一点是在深度缓冲区的值不是线性的屏幕空间 (它们在视图空间投影矩阵应用之前是线性)。值为 0.5 在深度缓冲区并不意味着该对象的 z 值是投影平头截体的中间;顶点的 z 值是实际上相当接近近平面!你可以看到 z 值和产生深度缓冲区的值在下列图中的非线性关系:
 
-![](../img/04/01/depth_non_linear_graph.png)
+![](http://learnopengl.com/img/advanced/depth_non_linear_graph.png)
 
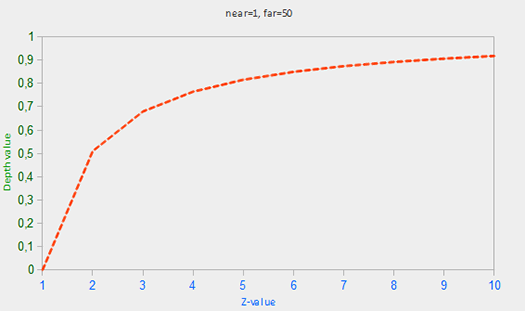
-可以看到，深度值很大一部分是由很小的z值所决定的，这给了近处的物体很大的深度精度。这个（从观察者的视角）变换z值的方程是嵌入在投影矩阵中的，所以当我们想将一个顶点坐标从观察空间至裁剪空间的时候这个非线性方程就被应用了。如果你想深度了解投影矩阵究竟做了什么，我建议阅读[这篇文章](http://www.songho.ca/opengl/gl_projectionmatrix.html)。
+正如你所看到，一个附近的物体的小的 z 值因此给了我们很高的深度精度。变换 (从观察者的角度) 的 z 值的方程式被嵌入在投影矩阵，所以当我们变换顶点坐标从视图到裁剪，然后到非线性方程应用了的屏幕空间中。如果你好奇的投影矩阵究竟做了什么我建议阅读[这个文章](http://www.songho.ca/opengl/gl_projectionmatrix.html)。
 
-如果我们想要可视化深度缓冲的话，非线性方程的效果很快就会变得很清楚。
+接下来我们看看这个非线性的深度值。
 
-## 深度缓冲的可视化
+## 深度缓冲区的可视化
 
-我们知道片段着色器中，内建<var>gl_FragCoord</var>向量的z值包含了那个特定片段的深度值。如果我们将这个深度值输出为颜色，我们可以显示场景中所有片段的深度值。我们可以根据片段的深度值返回一个颜色向量来完成这一工作：
+我们知道在片段渲染器的内置`gl_FragCoord`向量的 z 值包含那个片段的深度值。如果我们要吧深度值作为颜色输出，那么我们可以在场景中显示的所有片段的深度值。我们可以返回基于片段的深度值的颜色向量:
 
 ```c++
 void main()
 {
-    FragColor = vec4(vec3(gl_FragCoord.z), 1.0);
-}
+    color = vec4(vec3(gl_FragCoord.z), 1.0f);
+}  
 ```
 
-如果你再次运行程序的话，你可能会注意到所有东西都是白色的，看起来就想我们所有的深度值都是最大的1.0。所以为什么没有靠近0.0（即变暗）的深度值呢？
+如果再次运行同一程序你可能会发现一切都是白的，它看起来像我们的深度值都是最大值 1.0。那么为什么没有深度值接近 0.0而发暗?
 
-你可能还记得在上一部分中说到，屏幕空间中的深度值是非线性的，即它在z值很小的时候有很高的精度，而z值很大的时候有较低的精度。片段的深度值会随着距离迅速增加，所以几乎所有的顶点的深度值都是接近于1.0的。如果我们小心地靠近物体，你可能会最终注意到颜色会渐渐变暗，显示它们的z值在逐渐变小：
+你可能还记得从上一节中的屏幕空间的深度值是非线性如他们在z很小的时候有很高的精度，，较大的 z 值有较低的精度。该片段的深度值会迅速增加，所以几乎所有顶点的深度值接近 1.0。如果我们小心的靠近物体，你最终可能会看到的色彩越来越暗，意味着它们的 z 值越来越小:
 
-![](../img/04/01/depth_testing_visible_depth.png)
+![](http://www.learnopengl.com/img/advanced/depth_testing_visible_depth.png)
 
-这很清楚地展示了深度值的非线性性质。近处的物体比起远处的物体对深度值有着更大的影响。只需要移动几厘米就能让颜色从暗完全变白。
+这清楚地表明深度值的非线性特性。近的物体相对远的物体对的深度值比对象较大的影响。只移动几英寸就能让暗色完全变亮。
 
-然而，我们也可以让片段非线性的深度值变换为线性的。要实现这个，我们需要仅仅反转深度值的投影变换。这也就意味着我们需要首先将深度值从[0, 1]范围重新变换到[-1, 1]范围的标准化设备坐标（裁剪空间）。接下来我们需要像投影矩阵那样反转这个非线性方程（方程2），并将这个反转的方程应用到最终的深度值上。最终的结果就是一个线性的深度值了。听起来是可行的，对吧？
+但是我们可以让深度值变换回线性。要实现这一目标我们需要让点应用投影变换逆的逆变换，成为单独的深度值的过程。这意味着我们必须首先重新变换范围 [0，1] 中的深度值为单位化的设备坐标(normalized device coordinates)范围内 [-1，1] (裁剪空间(clip space))。然后，我们想要反转非线性方程 (等式2) 就像在投影矩阵做的那样并将此反转方程应用于所得到的深度值。然后，结果是一个线性的深度值。听起来能行对吗?
 
-首先我们将深度值变换为NDC，不是非常困难：
+首先，我们需要并不太难的 NDC 深度值转换:
 
 ```c++
-float ndc = depth * 2.0 - 1.0;
+float z = depth * 2.0 - 1.0;
 ```
 
-接下来使用获取到的NDC值，应用逆变换来获取线性的深度值：
+然后把我们所得到的 z 值应用逆转换来检索的线性深度值:
 
 ```c++
-float linearDepth = (2.0 * near * far) / (far + near - ndc * (far - near));
+float linearDepth = (2.0 * near) / (far + near - z * (far - near));
 ```
 
-这个方程是用投影矩阵推导得出的，它使用了方程2来非线性化深度值，返回一个<var>near</var>与<var>far</var>之间的深度值。这篇注重数学的[文章](http://www.songho.ca/opengl/gl_projectionmatrix.html)为感兴趣的读者详细解释了投影矩阵，它也展示了这些方程是怎么来的。
+注意此方程不是方程 2 的精确的逆方程。这个方程从投影矩阵中导出，可以从新使用等式2将他转换为非线性深度值。这个方程也会考虑使用[0，1] 而不是 [near，far]范围内的 z 值 。[math-heavy](http://www.songho.ca/opengl/gl_projectionmatrix.html)为感兴趣的读者阐述了大量详细的投影矩阵的知识;它还表明了方程是从哪里来的。
 
-将屏幕空间中非线性的深度值变换至线性深度值的完整片段着色器如下：
+这不是从投影矩阵推导出的准确公式;这个方程是除以far的结果。深度值的范围一直到far，这作为一个介于 0.0 和 1.0 之间的颜色值并不合适。除以far的值把深度值映射到介于 0.0 和 1.0，更适合用于演示目的。
+
+这个能够将屏幕空间的非线性深度值转变为线性深度值的完整的片段着色器如下所示：
 
 ```c++
 #version 330 core
-out vec4 FragColor;
 
-float near = 0.1; 
-float far  = 100.0; 
-  
-float LinearizeDepth(float depth) 
+out vec4 color;
+
+float LinearizeDepth(float depth)
 {
-    float z = depth * 2.0 - 1.0; // 转换为 NDC
-    return (2.0 * near * far) / (far + near - z * (far - near));	
+    float near = 0.1;
+    float far = 100.0;
+    float z = depth * 2.0 - 1.0; // Back to NDC
+    return (2.0 * near) / (far + near - z * (far - near));
 }
 
 void main()
-{             
-    float depth = LinearizeDepth(gl_FragCoord.z) / far; // 为了演示除以 far
-    FragColor = vec4(vec3(depth), 1.0);
+{
+    float depth = LinearizeDepth(gl_FragCoord.z);
+    color = vec4(vec3(depth), 1.0f);
 }
 ```
 
-由于线性化的深度值处于<var>near</var>与<var>far</var>之间，它的大部分值都会大于1.0并显示为完全的白色。通过在<fun>main</fun>函数中将线性深度值除以<var>far</var>，我们近似地将线性深度值转化到[0, 1]的范围之间。这样子我们就能逐渐看到一个片段越接近投影平截头体的远平面，它就会变得越亮，更适用于展示目的。
+如果现在运行该应用程序，我们得到在距离实际上线性的深度值。尝试移动现场周围看到深度值线性变化
 
-如果我们现在运行程序，我们就能看见深度值随着距离增大是线性的了。尝试在场景中移动，看看深度值是怎样以线性变化的。
+![](http://www.learnopengl.com/img/advanced/depth_testing_visible_linear.png)。
 
-![](../img/04/01/depth_testing_visible_linear.png)
-
-颜色大部分都是黑色，因为深度值的范围是0.1的**近**平面到100的**远**平面，它离我们还是非常远的。结果就是，我们相对靠近近平面，所以会得到更低的（更暗的）深度值。
+颜色主要是黑色的因为深度值线性范围从 0.1 的近平面到 100 的远平面，那里离我们很远。其结果是，我们相对靠近近平面，从而得到较低 (较暗) 的深度值。
 
 ## 深度冲突
 
-一个很常见的视觉错误会在两个平面或者三角形非常紧密地平行排列在一起时会发生，深度缓冲没有足够的精度来决定两个形状哪个在前面。结果就是这两个形状不断地在切换前后顺序，这会导致很奇怪的花纹。这个现象叫做<def>深度冲突</def>(Z-fighting)，因为它看起来像是这两个形状在争夺(Fight)谁该处于顶端。
+两个平面或三角形如此紧密相互平行深度缓冲区不具有足够的精度以至于无法得到哪一个靠前。结果是，这两个形状不断似乎切换顺序导致怪异出问题。这被称为**深度冲突(Z-fighting)**，因为它看上去像形状争夺顶靠前的位置。
 
-在我们一直使用的场景中，有几个地方的深度冲突还是非常明显的。箱子被放置在地板的同一高度上，这也就意味着箱子的底面和地板是共面的(Coplanar)。这两个面的深度值都是一样的，所以深度测试没有办法决定应该显示哪一个。
+我们到目前为止一直在使用的场景中有几个地方深度冲突很显眼。容器被置于确切高度地板被安置这意味着容器的底平面与地板平面共面。两个平面的深度值是相同的，因此深度测试也没有办法找出哪个是正确。
 
-如果你将摄像机移动到其中一个箱子的内部，你就能清楚地看到这个效果的，箱子的底部不断地在箱子底面与地板之间切换，形成一个锯齿的花纹：
+如果您移动摄像机到容器的里面，那么这个影响清晰可，容器的底部不断切换容器的平面和地板的平面:
 
-![](../img/04/01/depth_testing_z_fighting.png)
+![](http://www.learnopengl.com/img/advanced/depth_testing_z_fighting.png)
 
-深度冲突是深度缓冲的一个常见问题，当物体在远处时效果会更明显（因为深度缓冲在z值比较大的时候有着更小的精度）。深度冲突不能够被完全避免，但一般会有一些技巧有助于在你的场景中减轻或者完全避免深度冲突、
+深度冲突是深度缓冲区的普遍问题，当对象的距离越远一般越强(因为深度缓冲区在z值非常大的时候没有很高的精度)。深度冲突还无法完全避免，但有一般的几个技巧，将有助于减轻或完全防止深度冲突在你的场景中的出现：
 
 ### 防止深度冲突
 
-第一个也是最重要的技巧是**永远不要把多个物体摆得太靠近，以至于它们的一些三角形会重叠**。通过在两个物体之间设置一个用户无法注意到的偏移值，你可以完全避免这两个物体之间的深度冲突。在箱子和地板的例子中，我们可以将箱子沿着正y轴稍微移动一点。箱子位置的这点微小改变将不太可能被注意到，但它能够完全减少深度冲突的发生。然而，这需要对每个物体都手动调整，并且需要进行彻底的测试来保证场景中没有物体会产生深度冲突。
+第一个也是最重要的技巧是让物体之间不要离得太近，以至于他们的三角形重叠。通过在物体之间制造一点用户无法察觉到的偏移，可以完全解决深度冲突。在容器和平面的条件下，我们可以把容器像+y方向上略微移动。这微小的改变可能完全不被注意但是可以有效地减少或者完全解决深度冲突。然而这需要人工的干预每个物体，并进行彻底地测试，以确保这个场景的物体之间没有深度冲突。
 
-第二个技巧是**尽可能将近平面设置远一些**。在前面我们提到了精度在靠近**近**平面时是非常高的，所以如果我们将**近**平面远离观察者，我们将会对整个平截头体有着更大的精度。然而，将近平面设置太远将会导致近处的物体被裁剪掉，所以这通常需要实验和微调来决定最适合你的场景的**近**平面距离。
+另一个技巧是尽可能把近平面设置得远一些。前面我们讨论过越靠近近平面的位置精度越高。所以我们移动近平面远离观察者，我们可以在椎体内很有效的提高精度。然而把近平面移动的太远会导致近处的物体被裁剪掉。所以不断调整测试近平面的值，为你的场景找出最好的近平面的距离。
 
-另外一个很好的技巧是牺牲一些性能，**使用更高精度的深度缓冲**。大部分深度缓冲的精度都是24位的，但现在大部分的显卡都支持32位的深度缓冲，这将会极大地提高精度。所以，牺牲掉一些性能，你就能获得更高精度的深度测试，减少深度冲突。
+另外一个技巧是放弃一些性能来得到更高的深度值的精度。大多数的深度缓冲区都是24位。但现在显卡支持32位深度值，这让深度缓冲区的精度提高了一大节。所以牺牲一些性能你会得到更精确的深度测试，减少深度冲突。
 
-我们上面讨论的三个技术是最普遍也是很容易实现的抗深度冲突技术了。还有一些更复杂的技术，但它们依然不能完全消除深度冲突。深度冲突是一个常见的问题，但如果你组合使用了上面列举出来的技术，你可能不会再需要处理深度冲突了。
+我们已经讨论过的 3 个技术是最常见和容易实现消除深度冲突的技术。还有一些其他技术需要更多的工作，仍然不会完全消除深度冲突。深度冲突是一个常见的问题，但如果你将列举的技术适当结合你可能不会真的需要处理深度冲突。

docs/04 Advanced OpenGL/02 Stencil testing.md

@@ -3,203 +3,201 @@
 原文     | [Stencil testing](http://learnopengl.com/#!Advanced-OpenGL/Stencil-testing)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | 暂未校对
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com)
 
-当片段着色器处理完一个片段之后，<def>模板测试</def>(Stencil Test)会开始执行，和深度测试一样，它也可能会丢弃片段。接下来，被保留的片段会进入深度测试，它可能会丢弃更多的片段。模板测试是根据又一个缓冲来进行的，它叫做<def>模板缓冲</def>(Stencil Buffer)，我们可以在渲染的时候更新它来获得一些很有意思的效果。
+当片段着色器处理完片段之后，**模板测试(Stencil Test)** 就开始执行了，和深度测试一样，它能丢弃一些片段。仍然保留下来的片段进入深度测试阶段，深度测试可能丢弃更多。模板测试基于另一个缓冲，这个缓冲叫做**模板缓冲(Stencil Buffer)**，我们被允许在渲染时更新它来获取有意思的效果。
 
-一个模板缓冲中，（通常）每个<def>模板值</def>(Stencil Value)是8位的。所以每个像素/片段一共能有256种不同的模板值。我们可以将这些模板值设置为我们想要的值，然后当某一个片段有某一个模板值的时候，我们就可以选择丢弃或是保留这个片段了。
+模板缓冲中的**模板值(Stencil Value)**通常是8位的，因此每个片段/像素共有256种不同的模板值（译注：8位就是1字节大小，因此和char的容量一样是256个不同值）。这样我们就能将这些模板值设置为我们链接的，然后在模板测试时根据这个模板值，我们就可以决定丢弃或保留它了。
 
 !!! Important
 
-	每个窗口库都需要为你配置一个模板缓冲。GLFW自动做了这件事，所以我们不需要告诉GLFW来创建一个，但其它的窗口库可能不会默认给你创建一个模板库，所以记得要查看库的文档。
+    每个窗口库都需要为你设置模板缓冲。GLFW自动做了这件事，所以你不必告诉GLFW去创建它，但是其他库可能没默认创建模板库，所以一定要查看你使用的库的文档。
 
-模板缓冲的一个简单的例子如下：
+下面是一个模板缓冲的简单例子：
 
-![](../img/04/02/stencil_buffer.png)
+![image description](http://learnopengl.com/img/advanced/stencil_buffer.png)
 
-模板缓冲首先会被清除为0，之后在模板缓冲中使用1填充了一个空心矩形。场景中的片段将会只在片段的模板值为1的时候会被渲染（其它的都被丢弃了）。
+模板缓冲先清空模板缓冲设置所有片段的模板值为0，然后开启矩形片段用1填充。场景中的模板值为1的那些片段才会被渲染（其他的都被丢弃）。
 
-模板缓冲操作允许我们在渲染片段时将模板缓冲设定为一个特定的值。通过在渲染时修改模板缓冲的内容，我们**写入**了模板缓冲。在同一个（或者接下来的）帧中，我们可以**读取**这些值，来决定丢弃还是保留某个片段。使用模板缓冲的时候你可以尽情发挥，但大体的步骤如下：
+无论我们在渲染哪里的片段，模板缓冲操作都允许我们把模板缓冲设置为一个特定值。改变模板缓冲的内容实际上就是对模板缓冲进行写入。在同一次（或接下来的）渲染迭代我们可以读取这些值来决定丢弃还是保留这些片段。当使用模板缓冲的时候，你可以随心所欲，但是需要遵守下面的原则：
 
-- 启用模板缓冲的写入。
-- 渲染物体，更新模板缓冲的内容。
-- 禁用模板缓冲的写入。
-- 渲染（其它）物体，这次根据模板缓冲的内容丢弃特定的片段。
+* 开启模板缓冲写入。
+* 渲染物体，更新模板缓冲。
+* 关闭模板缓冲写入。
+* 渲染（其他）物体，这次基于模板缓冲内容丢弃特定片段。
 
-所以，通过使用模板缓冲，我们可以根据场景中已绘制的其它物体的片段，来决定是否丢弃特定的片段。
+使用模板缓冲我们可以基于场景中已经绘制的片段，来决定是否丢弃特定的片段。
 
-你可以启用<var>GL_STENCIL_TEST</var>来启用模板测试。在这一行代码之后，所有的渲染调用都会以某种方式影响着模板缓冲。
+你可以开启`GL_STENCIL_TEST`来开启模板测试。接着所有渲染函数调用都会以这样或那样的方式影响到模板缓冲。
 
 ```c++
 glEnable(GL_STENCIL_TEST);
 ```
-
-注意，和颜色和深度缓冲一样，你也需要在每次迭代之前清除模板缓冲。
+要注意的是，像颜色和深度缓冲一样，在每次循环，你也得清空模板缓冲。
 
 ```c++
 glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT | GL_STENCIL_BUFFER_BIT);
 ```
 
-和深度测试的<fun>glDepthMask</fun>函数一样，模板缓冲也有一个类似的函数。<fun>glStencilMask</fun>允许我们设置一个位掩码(Bitmask)，它会与将要写入缓冲的模板值进行与(AND)运算。默认情况下设置的位掩码所有位都为1，不影响输出，但如果我们将它设置为`0x00`，写入缓冲的所有模板值最后都会变成0.这与深度测试中的<fun>glDepthMask(GL_FALSE)</fun>是等价的。
+同时，和深度测试的`glDepthMask`函数一样，模板缓冲也有一个相似函数。`glStencilMask`允许我们给模板值设置一个**位遮罩(Bitmask)**，它与模板值进行按位与(AND)运算决定缓冲是否可写。默认设置的位遮罩都是1，这样就不会影响输出，但是如果我们设置为0x00，所有写入深度缓冲最后都是0。这和深度缓冲的`glDepthMask(GL_FALSE)`很类似：
 
 ```c++
-glStencilMask(0xFF); // 每一位写入模板缓冲时都保持原样
-glStencilMask(0x00); // 每一位在写入模板缓冲时都会变成0（禁用写入）
+
+// 0xFF == 0b11111111
+//此时，模板值与它进行按位与运算结果是模板值，模板缓冲可写
+glStencilMask(0xFF); 
+
+// 0x00 == 0b00000000 == 0
+//此时，模板值与它进行按位与运算结果是0，模板缓冲不可写
+glStencilMask(0x00); 
 ```
 
-大部分情况下你都只会使用`0x00`或者`0xFF`作为模板掩码(Stencil Mask)，但是知道有选项可以设置自定义的位掩码总是好的。
+大多数情况你的模板遮罩（stencil mask）写为0x00或0xFF就行，但是最好知道有一个选项可以自定义位遮罩。
 
 ## 模板函数
 
-和深度测试一样，我们对模板缓冲应该通过还是失败，以及它应该如何影响模板缓冲，也是有一定控制的。一共有两个函数能够用来配置模板测试：<fun>glStencilFunc</fun>和<fun>glStencilOp</fun>。
+和深度测试一样，我们也有几个不同控制权，决定何时模板测试通过或失败以及它怎样影响模板缓冲。一共有两种函数可供我们使用去配置模板测试：`glStencilFunc`和`glStencilOp`。
 
-<fun>glStencilFunc(GLenum func, GLint ref, GLuint mask)</fun>一共包含三个参数：
+`void glStencilFunc(GLenum func, GLint ref, GLuint mask)`函数有三个参数：
 
-- `func`：设置模板测试函数(Stencil Test Function)。这个测试函数将会应用到已储存的模板值上和<fun>glStencilFunc</fun>函数的`ref`值上。可用的选项有：<var>GL_NEVER</var>、<var>GL_LESS</var>、<var>GL_LEQUAL</var>、<var>GL_GREATER</var>、<var>GL_GEQUAL</var>、<var>GL_EQUAL</var>、<var>GL_NOTEQUAL</var>和<var>GL_ALWAYS</var>。它们的语义和深度缓冲的函数类似。
-- `ref`：设置了模板测试的参考值(Reference Value)。模板缓冲的内容将会与这个值进行比较。
-- `mask`：设置一个掩码，它将会与参考值和储存的模板值在测试比较它们之前进行与(AND)运算。初始情况下所有位都为1。
+* **func**：设置模板测试操作。这个测试操作应用到已经储存的模板值和`glStencilFunc`的`ref`值上，可用的选项是：`GL_NEVER`、`GL_LEQUAL`、`GL_GREATER`、`GL_GEQUAL`、`GL_EQUAL`、`GL_NOTEQUAL`、`GL_ALWAYS`。它们的语义和深度缓冲的相似。
+* **ref**：指定模板测试的引用值。模板缓冲的内容会与这个值对比。
+* **mask**：指定一个遮罩，在模板测试对比引用值和储存的模板值前，对它们进行按位与（and）操作，初始设置为1。
 
-在一开始的那个简单的模板例子中，函数被设置为：
+在上面简单模板的例子里，方程应该设置为：
 
-```c++
+```c
 glStencilFunc(GL_EQUAL, 1, 0xFF)
 ```
 
-这会告诉OpenGL，只要一个片段的模板值等于(`GL_EQUAL`)参考值1，片段将会通过测试并被绘制，否则会被丢弃。
+它会告诉OpenGL，无论何时，一个片段模板值等于(`GL_EQUAL`)引用值`1`，片段就能通过测试被绘制了，否则就会被丢弃。
 
-但是<fun>glStencilFunc</fun>仅仅描述了OpenGL应该对模板缓冲内容做什么，而不是我们应该如何更新缓冲。这就需要<fun>glStencilOp</fun>这个函数了。
+但是`glStencilFunc`只描述了OpenGL对模板缓冲做什么，而不是描述我们如何更新缓冲。这就需要`glStencilOp`登场了。
 
-<fun>glStencilOp(GLenum sfail, GLenum dpfail, GLenum dppass)</fun>一共包含三个选项，我们能够设定每个选项应该采取的行为：
+`void glStencilOp(GLenum sfail, GLenum dpfail, GLenum dppass)`函数包含三个选项，我们可以指定每个选项的动作：
 
-- `sfail`：模板测试失败时采取的行为。
-- `dpfail`：模板测试通过，但深度测试失败时采取的行为。
-- `dppass`：模板测试和深度测试都通过时采取的行为。
+* **sfail**：  如果模板测试失败将采取的动作。
+* **dpfail**： 如果模板测试通过，但是深度测试失败时采取的动作。
+* **dppass**： 如果深度测试和模板测试都通过，将采取的动作。
 
-每个选项都可以选用以下的其中一种行为：
+每个选项都可以使用下列任何一个动作。
 
-行为 | 描述
+操作 | 描述
   ---|---
-GL_KEEP     | 保持当前储存的模板值
-GL_ZERO	    | 将模板值设置为0
-GL_REPLACE  | 将模板值设置为<fun>glStencilFunc</fun>函数设置的`ref`值
-GL_INCR	    | 如果模板值小于最大值则将模板值加1
-GL_INCR_WRAP| 与<var>GL_INCR</var>一样，但如果模板值超过了最大值则归零
-GL_DECR	    | 如果模板值大于最小值则将模板值减1
-GL_DECR_WRAP| 与<var>GL_DECR</var>一样，但如果模板值小于0则将其设置为最大值
-GL_INVERT   | 按位翻转当前的模板缓冲值
+GL_KEEP     | 保持现有的模板值
+GL_ZERO	    | 将模板值置为0
+GL_REPLACE  | 将模板值设置为用`glStencilFunc`函数设置的**ref**值
+GL_INCR	    | 如果模板值不是最大值就将模板值+1
+GL_INCR_WRAP| 与`GL_INCR`一样将模板值+1，如果模板值已经是最大值则设为0
+GL_DECR	    | 如果模板值不是最小值就将模板值-1
+GL_DECR_WRAP| 与`GL_DECR`一样将模板值-1，如果模板值已经是最小值则设为最大值
+GL_INVERT   | Bitwise inverts the current stencil buffer value.
 
-默认情况下<fun>glStencilOp</fun>是设置为`(GL_KEEP, GL_KEEP, GL_KEEP)`的，所以不论任何测试的结果是如何，模板缓冲都会保留它的值。默认的行为不会更新模板缓冲，所以如果你想写入模板缓冲的话，你需要至少对其中一个选项设置不同的值。
+`glStencilOp`函数默认设置为 (GL_KEEP, GL_KEEP, GL_KEEP) ，所以任何测试的任何结果，模板缓冲都会保留它的值。默认行为不会更新模板缓冲，所以如果你想写入模板缓冲的话，你必须像任意选项指定至少一个不同的动作。
 
-所以，通过使用<fun>glStencilFunc</fun>和<fun>glStencilOp</fun>，我们可以精确地指定更新模板缓冲的时机与行为了，我们也可以指定什么时候该让模板缓冲通过，即什么时候片段需要被丢弃。
+使用`glStencilFunc`和`glStencilOp`，我们就可以指定在什么时候以及我们打算怎么样去更新模板缓冲了，我们也可以指定何时让测试通过或不通过。什么时候片段会被抛弃。
 
 # 物体轮廓
 
-仅仅看了前面的部分你还是不太可能能够完全理解模板测试的工作原理，所以我们将会展示一个使用模板测试就可以完成的有用特性，它叫做<def>物体轮廓</def>(Object Outlining)。
+看了前面的部分你未必能理解模板测试是如何工作的，所以我们会展示一个用模板测试实现的一个特别的和有用的功能，叫做**物体轮廓(Object Outlining)**。
 
-![](../img/04/02/stencil_object_outlining.png)
+![](http://learnopengl.com/img/advanced/stencil_object_outlining.png)
 
-物体轮廓所能做的事情正如它名字所描述的那样。我们将会为每个（或者一个）物体在它的周围创建一个很小的有色边框。当你想要在策略游戏中选中一个单位进行操作的，想要告诉玩家选中的是哪个单位的时候，这个效果就非常有用了。为物体创建轮廓的步骤如下：
+物体轮廓就像它的名字所描述的那样，它能够给每个（或一个）物体创建一个有颜色的边。在策略游戏中当你打算选择一个单位的时候它特别有用。给物体加上轮廓的步骤如下：
 
-1. 启用模板写入。
-2. 在绘制（需要添加轮廓的）物体之前，将模板函数设置为<var>GL_ALWAYS</var>，每当物体的片段被渲染时，将模板缓冲更新为1。
-3. 渲染物体。
-4. 禁用模板写入以及深度测试。
-5. 将每个物体缩放一点点。
-6. 使用一个不同的片段着色器，输出一个单独的（边框）颜色。
-7. 再次绘制物体，但只在它们片段的模板值不等于1时才绘制。
-8. 再次启用模板写入和深度测试。
+1. 在绘制物体前，把模板方程设置为`GL_ALWAYS`，用1更新物体将被渲染的片段。
+2. 渲染物体，写入模板缓冲。
+3. 关闭模板写入和深度测试。
+4. 每个物体放大一点点。
+5. 使用一个不同的片段着色器用来输出一个纯颜色。
+6. 再次绘制物体，但只是当它们的片段的模板值不为1时才进行。
+7. 开启模板写入和深度测试。
 
-这个过程将每个物体的片段的模板缓冲设置为1，当我们想要绘制边框的时候，我们主要绘制放大版本的物体中模板测试通过的部分，也就是物体的边框的位置。我们主要使用模板缓冲丢弃了放大版本中属于原物体片段的部分。
+这个过程将每个物体的片段模板缓冲设置为1，当我们绘制边框的时候，我们基本上绘制的是放大版本的物体的通过测试的地方，放大的版本绘制后物体就会有一个边。我们基本会使用模板缓冲丢弃所有的不是原来物体的片段的放大的版本内容。
 
-所以我们首先来创建一个很简单的片段着色器，它会输出一个边框颜色。我们简单地给它设置一个硬编码的颜色值，将这个着色器命名为<var>shaderSingleColor</var>：
+我们先来创建一个非常基本的片段着色器，它输出一个边框颜色。我们简单地设置一个固定的颜色值，把这个着色器命名为shaderSingleColor：
 
 ```c++
 void main()
 {
-    FragColor = vec4(0.04, 0.28, 0.26, 1.0);
+    outColor = vec4(0.04, 0.28, 0.26, 1.0);
 }
 ```
 
-我们只想给那两个箱子加上边框，所以我们让地板不参与这个过程。我们希望首先绘制地板，再绘制两个箱子（并写入模板缓冲），之后绘制放大的箱子（并丢弃覆盖了之前绘制的箱子片段的那些片段）。
+我们只打算给两个箱子加上边框，所以我们不会对地面做什么。这样我们要先绘制地面，然后再绘制两个箱子（同时写入模板缓冲），接着我们绘制放大的箱子（同时丢弃前面已经绘制的箱子的那部分片段）。
 
-我们首先启用模板测试：
-
-```c++
-glEnable(GL_STENCIL_TEST);
-```
-
-并设置在每一帧中模板测试通过或失败时，需要执行的操作：
+我们先开启模板测试，设置模板、深度测试通过或失败时才采取动作：
 
 ```c++
+glEnable(GL_DEPTH_TEST);
 glStencilOp(GL_KEEP, GL_KEEP, GL_REPLACE);
 ```
 
-如果其中的一个测试失败了，我们什么都不做，我们仅仅保留当前储存在模板缓冲中的值。如果模板测试和深度测试都通过了，那么我们希望将储存的模板值设置为参考值，参考值能够通过<fun>glStencilFunc</fun>来设置，我们之后会设置为1。
+如果任何测试失败我们都什么也不做，我们简单地保持深度缓冲中当前所储存着的值。如果模板测试和深度测试都成功了，我们就将储存着的模板值替换为`1`，我们要用`glStencilFunc`来做这件事。
 
-我们将模板缓冲清除为0，对箱子中所有绘制的片段，将模板值更新为1：
+我们清空模板缓冲为0，为箱子的所有绘制的片段的模板缓冲更新为1：
 
 ```c++
-glStencilOp(GL_KEEP, GL_KEEP, GL_REPLACE);
-glStencilFunc(GL_ALWAYS, 1, 0xFF); // 所有的片段都应该更新模板缓冲
-glStencilMask(0xFF); // 启用模板缓冲写入
-normalShader.use();
+glStencilFunc(GL_ALWAYS, 1, 0xFF); //所有片段都要写入模板缓冲
+glStencilMask(0xFF); // 设置模板缓冲为可写状态
+normalShader.Use();
 DrawTwoContainers();
 ```
 
-通过使用<var>GL_REPLACE</var>模板测试函数，我们保证了箱子的每个片段都会将模板缓冲的模板值更新为1。因为片段永远会通过模板测试，在绘制片段的地方，模板缓冲会被更新为参考值。
+使用`GL_ALWAYS`模板测试函数，我们确保箱子的每个片段用模板值1更新模板缓冲。因为片段总会通过模板测试，在我们绘制它们的地方，模板缓冲用引用值更新。
 
-现在模板缓冲在箱子被绘制的地方都更新为1了，我们将要绘制放大的箱子，但这次要禁用模板缓冲的写入：
+现在箱子绘制之处，模板缓冲更新为1了，我们将要绘制放大的箱子，但是这次关闭模板缓冲的写入：
 
 ```c++
 glStencilFunc(GL_NOTEQUAL, 1, 0xFF);
-glStencilMask(0x00); // 禁止模板缓冲的写入
+glStencilMask(0x00); // 禁止修改模板缓冲
 glDisable(GL_DEPTH_TEST);
-shaderSingleColor.use(); 
+shaderSingleColor.Use();
 DrawTwoScaledUpContainers();
 ```
 
-我们将模板函数设置为<var>GL_NOTEQUAL</var>，它会保证我们只绘制箱子上模板值不为1的部分，即只绘制箱子在之前绘制的箱子之外的部分。注意我们也禁用了深度测试，让放大的箱子，即边框，不会被地板所覆盖。
+我们把模板方程设置为`GL_NOTEQUAL`，它保证我们只箱子上不等于1的部分，这样只绘制前面绘制的箱子外围的那部分。注意，我们也要关闭深度测试，这样放大的的箱子也就是边框才不会被地面覆盖。
 
-记得要在完成之后重新启用深度缓冲。
+做完之后还要保证再次开启深度缓冲。
 
-场景中物体轮廓的完整步骤会看起来像这样：
+场景中的物体边框的绘制方法最后看起来像这样：
 
 ```c++
 glEnable(GL_DEPTH_TEST);
 glStencilOp(GL_KEEP, GL_KEEP, GL_REPLACE);  
-  
-glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT | GL_STENCIL_BUFFER_BIT); 
 
-glStencilMask(0x00); // 记得保证我们在绘制地板的时候不会更新模板缓冲
-normalShader.use();
+glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT | GL_STENCIL_BUFFER_BIT);
+
+glStencilMask(0x00); // 绘制地板时确保关闭模板缓冲的写入
+normalShader.Use();
 DrawFloor()  
-  
-glStencilFunc(GL_ALWAYS, 1, 0xFF); 
-glStencilMask(0xFF); 
+
+glStencilFunc(GL_ALWAYS, 1, 0xFF);
+glStencilMask(0xFF);
 DrawTwoContainers();
-  
+
 glStencilFunc(GL_NOTEQUAL, 1, 0xFF);
-glStencilMask(0x00); 
+glStencilMask(0x00);
 glDisable(GL_DEPTH_TEST);
-shaderSingleColor.use(); 
+shaderSingleColor.Use();
 DrawTwoScaledUpContainers();
 glStencilMask(0xFF);
-glEnable(GL_DEPTH_TEST);  
+glEnable(GL_DEPTH_TEST);
 ```
 
-只要你理解了模板缓冲背后的大体思路，这个代码片段就不是那么难理解了。如果还是不能理解的话，尝试再次仔细阅读之前的部分，并尝试通过上面使用的范例，完全理解每个函数的功能。
+理解这段代码后面的模板测试的思路并不难以理解。如果还不明白尝试再仔细阅读上面的部分，尝试理解每个函数的作用，现在你已经看到了它的使用方法的例子。
 
-在[深度测试](01 Depth testing.md)小节的场景中，这个轮廓算法的结果看起来会像是这样的：
+这个边框的算法的结果在深度测试教程的那个场景中，看起来像这样：
 
-![](../img/04/02/stencil_scene_outlined.png)
+![](http://learnopengl.com/img/advanced/stencil_scene_outlined.png)
 
-可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/2.stencil_testing/stencil_testing.cpp)查看源代码，看看物体轮廓算法的完整代码。
+在这里[查看源码](http://learnopengl.com/code_viewer.php?code=advanced/stencil_testing)和[着色器](http://learnopengl.com/code_viewer.php?code=advanced/depth_testing_func_shaders)，看看完整的物体边框算法是怎样的。
 
 !!! Important
 
-	你可以看到这两个箱子的边框重合了，这通常都是我们想要的结果（想想策略游戏中，我们希望选择10个单位，合并边框通常是我们想需要的结果）。如果你想让每个物体都有一个完整的边框，你需要对每个物体都清空模板缓冲，并有创意地利用深度缓冲。
+	你可以看到两个箱子边框重合通常正是我们希望得到的（想想策略游戏中，我们打算选择10个单位；我们通常会希望把边界合并）。如果你想要让每个物体都有自己的边界那么你需要为每个物体清空模板缓冲，创造性地使用深度缓冲。
 
-你看到的物体轮廓算法在需要显示选中物体的游戏（想想策略游戏）中非常常见。这样的算法能够在一个模型类中轻松实现。你可以在模型类中设置一个boolean标记，来设置需不需要绘制边框。如果你有创造力的话，你也可以使用后期处理滤镜(Filter)，像是高斯模糊(Gaussian Blur)，让边框看起来更自然。
+你目前看到的物体边框算法在一些游戏中显示备选物体（想象策略游戏）非常常用，这样的算法可以在一个模型类中轻易实现。你可以简单地在模型类设置一个布尔类型的标识来决定是否绘制边框。如果你想要更多的创造性，你可以使用后处理（post-processing）过滤比如高斯模糊来使边框看起来更自然。
 
-除了物体轮廓之外，模板测试还有很多用途，比如在一个后视镜中绘制纹理，让它能够绘制到镜子形状中，或者使用一个叫做阴影体积(Shadow Volume)的模板缓冲技术渲染实时阴影。模板缓冲为我们已经很丰富的OpenGL工具箱又提供了一个很好的工具。
+除了物体边框以外，模板测试还有很多其他的应用目的，比如在后视镜中绘制纹理，这样它会很好的适合镜子的形状，比如使用一种叫做shadow volumes的模板缓冲技术渲染实时阴影。模板缓冲在我们的已扩展的OpenGL工具箱中给我们提供了另一种好用工具。

docs/04 Advanced OpenGL/03 Blending.md

@@ -3,51 +3,57 @@
 原文     | [Blending](http://learnopengl.com/#!Advanced-OpenGL/Blending)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet, [Django](http://bullteacher.com/)
-校对     | 暂无校对
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com)
 
-OpenGL中，<def>混合</def>(Blending)通常是实现物体<def>透明度</def>(Transparency)的一种技术。透明就是说一个物体（或者其中的一部分）不是纯色(Solid Color)的，它的颜色是物体本身的颜色和它背后其它物体的颜色的不同强度结合。一个有色玻璃窗是一个透明的物体，玻璃有它自己的颜色，但它最终的颜色还包含了玻璃之后所有物体的颜色。这也是混合这一名字的出处，我们<def>混合</def>(Blend)（不同物体的）多种颜色为一种颜色。所以透明度能让我们看穿物体。
 
-![](../img/04/03/blending_transparency.png)
+在OpenGL中，物体透明技术通常被叫做**混合(Blending)**。透明是物体（或物体的一部分）非纯色而是混合色，这种颜色来自于不同浓度的自身颜色和它后面的物体颜色。一个有色玻璃窗就是一种透明物体，玻璃有自身的颜色，但是最终的颜色包含了所有玻璃后面的颜色。这也正是混合这名称的出处，因为我们将多种（来自于不同物体）颜色混合为一个颜色，透明使得我们可以看穿物体。
 
-透明的物体可以是完全透明的（让所有的颜色穿过），或者是半透明的（它让颜色通过，同时也会显示自身的颜色）。一个物体的透明度是通过它颜色的<def>alpha</def>值来决定的。Alpha颜色值是颜色向量的第四个分量，你可能已经看到过它很多遍了。在这个教程之前我们都将这个第四个分量设置为1.0，让这个物体的透明度为0.0，而当alpha值为0.0时物体将会是完全透明的。当alpha值为0.5时，物体的颜色有50%是来自物体自身的颜色，50%来自背后物体的颜色。
+![](http://learnopengl.com/img/advanced/blending_transparency.png)
 
-我们目前一直使用的纹理有三个颜色分量：红、绿、蓝。但一些材质会有一个内嵌的alpha通道，对每个纹素(Texel)都包含了一个<def>alpha</def>值。这个alpha值精确地告诉我们纹理各个部分的透明度。比如说，下面这个[窗户纹理](../img/04/03/blending_transparent_window.png)中的玻璃部分的alpha值为0.25（它在一般情况下是完全的红色，但由于它有75%的透明度，能让很大一部分的网站背景颜色穿过，让它看起来不那么红了），角落的alpha值是0.0。
+透明物体可以是完全透明（它使颜色完全穿透）或者半透明的（它使颜色穿透的同时也显示自身颜色）。一个物体的透明度，被定义为它的颜色的alpha值。alpha颜色值是一个颜色向量的第四个元素，你可能已经看到很多了。在这个教程前，我们一直把这个元素设置为1.0，这样物体的透明度就是0.0，同样的，当alpha值是0.0时就表示物体是完全透明的，alpha值为0.5时表示物体的颜色由50%的自身的颜色和50%的后面的颜色组成。
 
-![](../img/04/03/blending_transparent_window.png)
+我们之前所使用的纹理都是由3个颜色元素组成的：红、绿、蓝，但是有些纹理同样有一个内嵌的aloha通道，它为每个纹理像素(Texel)包含着一个alpha值。这个alpha值告诉我们纹理的哪个部分有透明度，以及这个透明度有多少。例如，下面的窗子纹理的玻璃部分的alpha值为0.25(它的颜色是完全红色，但是由于它有75的透明度，它会很大程度上反映出网站的背景色，看起来就不那么红了)，角落部分alpha是0.0。
 
-我们很快就会将这个窗户纹理添加到场景中，但是首先我们需要讨论一个更简单的技术，来实现只有完全透明和完全不透明的纹理的透明度。
+![](http://learnopengl.com/img/advanced/blending_transparent_window.png)
 
-## 丢弃片段
+我们很快就会把这个窗子纹理加到场景中，但是首先，我们将讨论一点简单的技术来实现纹理的半透明，也就是完全透明和完全不透明。
 
-有些图片并不需要半透明，只需要根据纹理颜色值，显示一部分，或者不显示一部分，没有中间情况。比如说草，如果想不太费劲地创建草这种东西，你需要将一个草的纹理贴在一个2D四边形(Quad)上，然后将这个四边形放到场景中。然而，草的形状和2D四边形的形状并不完全相同，所以你只想显示草纹理的某些部分，而忽略剩下的部分。
+## 忽略片段
 
-下面[这个](../img/04/03/grass.png)纹理正是这样的，它要么是完全不透明的（alpha值为1.0），要么是完全透明的（alpha值为0.0），没有中间情况。你可以看到，只要不是草的部分，这个图片显示的都是网站的背景颜色而不是它本身的颜色。
+有些图像并不关心半透明度，但也想基于纹理的颜色值显示一部分。例如，创建像草这种物体你不需要花费很大力气，通常把一个草的纹理贴到2D四边形上，然后把这个四边形放置到你的场景中。可是，草并不是像2D四边形这样的形状，而只需要显示草纹理的一部分而忽略其他部分。
 
-![](../img/04/03/grass.png)
+下面的纹理正是这样的纹理，它既有完全不透明的部分（alpha值为1.0）也有完全透明的部分（alpha值为0.0），而没有半透明的部分。你可以看到没有草的部分，图片显示了网站的背景色，而不是它自身的那部分颜色。
 
-所以当添加像草这样的植被到场景中时，我们不希望看到草的方形图像，而是只显示草的部分，并能看透图像其余的部分。我们想要<def>丢弃</def>(Discard)显示纹理中透明部分的片段，不将这些片段存储到颜色缓冲中
+![](http://learnopengl.com/img/textures/grass.png)
 
-在此之前，我们还要学习如何加载一个透明的纹理。要想加载有alpha值的纹理，我们并不需要改很多东西，`stb_image`在纹理有alpha通道的时候会自动加载，但我们仍要在纹理生成过程中告诉OpenGL，我们的纹理现在使用alpha通道了：
+所以，当向场景中添加像这样的纹理时，我们不希望看到一个方块图像，而是只显示实际的纹理像素，剩下的部分可以被看穿。我们要忽略(丢弃)纹理透明部分的像素，不必将这些片段储存到颜色缓冲中。在此之前，我们还要学一下如何加载一个带有透明像素的纹理。
+
+加载带有alpha值的纹理我们需要告诉SOIL，去加载RGBA元素图像，而不再是RGB元素的。SOIL能以RGBA的方式加载大多数没有alpha值的纹理，它会将这些像素的alpha值设为了1.0。
 
 ```c++
-glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, width, height, 0, GL_RGBA, GL_UNSIGNED_BYTE, data);
+unsigned char * image = SOIL_load_image(path, &width, &height, 0, SOIL_LOAD_RGBA);
 ```
 
-同样，保证你在片段着色器中获取了纹理的全部4个颜色分量，而不仅仅是RGB分量：
+不要忘记还要改变OpenGL生成的纹理：
 
+```c++
+glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, width, height, 0, GL_RGBA, GL_UNSIGNED_BYTE, image);
+```
+
+保证你在片段着色器中获取了纹理的所有4个颜色元素，而不仅仅是RGB元素：
 
 ```c++
 void main()
 {
-    // FragColor = vec4(vec3(texture(texture1, TexCoords)), 1.0);
-    FragColor = texture(texture1, TexCoords);
+    // color = vec4(vec3(texture(texture1, TexCoords)), 1.0);
+    color = texture(texture1, TexCoords);
 }
 ```
 
-既然我们已经知道该如何加载透明的纹理了，是时候将它带入实战了，我们将会在[深度测试](01 Depth testing.md)小节的场景中加入几棵草。
+现在我们知道了如何加载透明纹理，是时候试试在深度测试教程里那个场景中添加几根草了。
 
-我们会创建一个vector，向里面添加几个`glm::vec3`变量来代表草的位置：
+我们创建一个`std::vector`，并向里面添加几个`glm::vec3`变量，来表示草的位置：
 
 ```c++
 vector<glm::vec3> vegetation;
@@ -58,222 +64,224 @@ vegetation.push_back(glm::vec3(-0.3f,  0.0f, -2.3f));
 vegetation.push_back(glm::vec3( 0.5f,  0.0f, -0.6f));
 ```
 
-每个草都被渲染到了一个四边形上，贴上草的纹理。这并不能完美地表示3D的草，但这比加载复杂的模型要快多了。使用一些小技巧，比如在同一个位置加入一些旋转后的草四边形，你仍然能获得比较好的结果的。
+一个单独的四边形被贴上草的纹理，这并不能完美的表现出真实的草，但是比起加载复杂的模型还是要高效很多，利用一些小技巧，比如在同一个地方添加多个不同朝向的草，还是能获得比较好的效果的。
 
-因为草的纹理是添加到四边形对象上的，我们还需要创建另外一个VAO，填充VBO，设置正确的顶点属性指针。接下来，在绘制完地板和两个立方体后，我们将会绘制草：
+由于草纹理被添加到四边形物体上，我们需要再次创建另一个VAO，向里面填充VBO，以及设置合理的顶点属性指针。在我们绘制完地面和两个立方体后，我们就来绘制草叶：
 
 ```c++
 glBindVertexArray(vegetationVAO);
 glBindTexture(GL_TEXTURE_2D, grassTexture);  
-for(unsigned int i = 0; i < vegetation.size(); i++) 
+for(GLuint i = 0; i < vegetation.size(); i++)
 {
-    model = glm::mat4(1.0f);
-    model = glm::translate(model, vegetation[i]);				
-    shader.setMat4("model", model);
+    model = glm::mat4();
+    model = glm::translate(model, vegetation[i]);
+    glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
     glDrawArrays(GL_TRIANGLES, 0, 6);
-}
+}  
+glBindVertexArray(0);
 ```
 
 运行程序你将看到：
+![](http://learnopengl.com/img/advanced/blending_no_discard.png)
 
-![](../img/04/03/blending_no_discard.png)
-
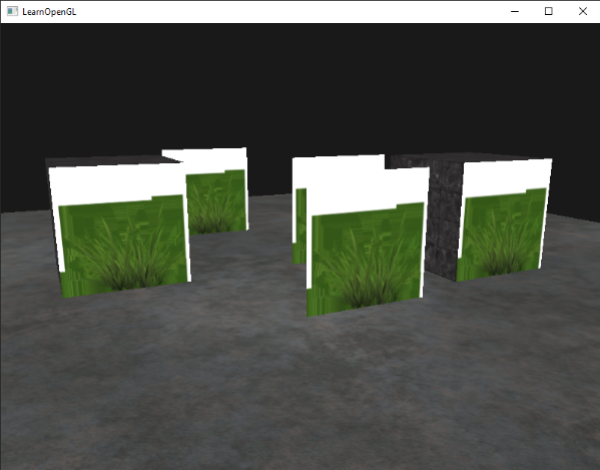
-出现这种情况是因为OpenGL默认是不知道怎么处理alpha值的，更不知道什么时候应该丢弃片段。我们需要自己手动来弄。幸运的是，有了着色器，这还是非常容易的。GLSL给了我们`discard`命令，一旦被调用，它就会保证片段不会被进一步处理，所以就不会进入颜色缓冲。有了这个指令，我们就能够在片段着色器中检测一个片段的alpha值是否低于某个阈值，如果是的话，则丢弃这个片段，就好像它不存在一样：
+出现这种情况是因为OpenGL默认是不知道如何处理alpha值的，不知道何时忽略(丢弃)它们。我们不得不手动做这件事。幸运的是这很简单，感谢着色器，GLSL为我们提供了discard命令，它保证了片段不会被进一步处理，这样就不会进入颜色缓冲。有了这个命令我们就可以在片段着色器中检查一个片段是否有在一定的阈限下的alpha值，如果有，那么丢弃这个片段，就好像它不存在一样：
 
 ```c++
 #version 330 core
-out vec4 FragColor;
-
 in vec2 TexCoords;
 
+out vec4 color;
+
 uniform sampler2D texture1;
 
 void main()
-{             
+{
     vec4 texColor = texture(texture1, TexCoords);
     if(texColor.a < 0.1)
         discard;
-    FragColor = texColor;
+    color = texColor;
 }
 ```
 
-这里，我们检测被采样的纹理颜色的alpha值是否低于0.1的阈值，如果是的话，则丢弃这个片段。片段着色器保证了它只会渲染不是（几乎）完全透明的片段。现在它看起来就正常了：
+在这儿我们检查被采样纹理颜色包含着一个低于0.1这个阈限的alpha值，如果有，就丢弃这个片段。这个片段着色器能够保证我们只渲染哪些不是完全透明的片段。现在我们来看看效果：
 
-![](../img/04/03/blending_discard.png)
+![](http://learnopengl.com/img/advanced/blending_discard.png)
 
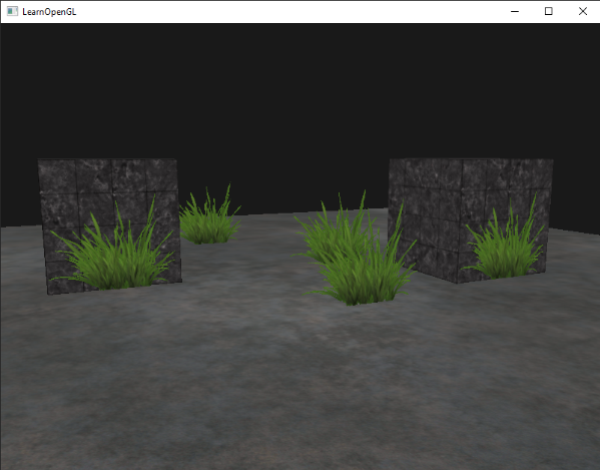
 !!! Important
 
-	注意，当采样纹理的边缘的时候，OpenGL会对边缘的值和纹理下一个重复的值进行插值（因为我们将它的环绕方式设置为了<var>GL_REPEAT</var>。这通常是没问题的，但是由于我们使用了透明值，纹理图像的顶部将会与底部边缘的纯色值进行插值。这样的结果是一个半透明的有色边框，你可能会看见它环绕着你的纹理四边形。要想避免这个，每当你alpha纹理的时候，请将纹理的环绕方式设置为<var>GL_CLAMP_TO_EDGE</var>：
+    需要注意的是，当采样纹理边缘的时候，OpenGL在边界值和下一个重复的纹理的值之间进行插值（因为我们把它的放置方式设置成了GL_REPEAT）。这样就行了，但是由于我们使用的是透明值，纹理图片的上部获得了它的透明值是与底边的纯色值进行插值的。结果就是一个有点半透明的边，你可以从我们的纹理四边形的四周看到。为了防止它的出现，当你使用alpha纹理的时候要把纹理环绕方式设置为`GL_CLAMP_TO_EDGE`：
 
-		glTexParameteri( GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
-		glTexParameteri( GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
+    `glTexParameteri( GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);`
+
+    `glTexParameteri( GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);`
+
+你可以[在这里得到源码](http://learnopengl.com/code_viewer.php?code=advanced/blending_discard)。
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/3.1.blending_discard/blending_discard.cpp)找到源码。
 
 ## 混合
 
-虽然直接丢弃片段很好，但它不能让我们渲染半透明的图像。我们要么渲染一个片段，要么完全丢弃它。要想渲染有多个透明度级别的图像，我们需要启用<def>混合</def>(Blending)。和OpenGL大多数的功能一样，我们可以启用<var>GL_BLEND</var>来启用混合：
+上述丢弃片段的方式，不能使我们获得渲染半透明图像，我们要么渲染出像素，要么完全地丢弃它。为了渲染出不同的透明度级别，我们需要开启**混合**(Blending)。像大多数OpenGL的功能一样，我们可以开启`GL_BLEND`来启用**混合(Blending)**功能：
 
 ```c++
 glEnable(GL_BLEND);
 ```
 
-启用了混合之后，我们需要告诉OpenGL它该**如何**混合。
+开启混合后，我们还需要告诉OpenGL它该如何混合。
 
-OpenGL中的混合是通过下面这个方程来实现的：
+OpenGL以下面的方程进行混合：
 
 $$
 \begin{equation}\bar{C}_{result} = \bar{\color{green}C}_{source} * \color{green}F_{source} + \bar{\color{red}C}_{destination} * \color{red}F_{destination}\end{equation}
 $$
 
-- \(\bar{\color{green}C}_{source}\)：源颜色向量。这是源自纹理的颜色向量。
-- \(\bar{\color{red}C}_{destination}\)：目标颜色向量。这是当前储存在颜色缓冲中的颜色向量。
-- \(\color{green}F_{source}\)：源因子值。指定了alpha值对源颜色的影响。
-- \(\color{red}F_{destination}\)：目标因子值。指定了alpha值对目标颜色的影响。
+* \(\bar{\color{green}C}_{source}\)：源颜色向量。这是来自纹理的本来的颜色向量。
+* \(\bar{\color{red}C}_{destination}\)：目标颜色向量。这是储存在颜色缓冲中当前位置的颜色向量。
+* \(\color{green}F_{source}\)：源因子。设置了对源颜色的alpha值影响。
+* \(\color{red}F_{destination}\)：目标因子。设置了对目标颜色的alpha影响。
 
-片段着色器运行完成后，并且所有的测试都通过之后，这个<def>混合方程</def>(Blend Equation)才会应用到片段颜色输出与当前颜色缓冲中的值（当前片段之前储存的之前片段的颜色）上。源颜色和目标颜色将会由OpenGL自动设定，但源因子和目标因子的值可以由我们来决定。我们先来看一个简单的例子：
+片段着色器运行完成并且所有的测试都通过以后，混合方程才能自由执行片段的颜色输出，当前它在颜色缓冲中（前面片段的颜色在当前片段之前储存）。源和目标颜色会自动被OpenGL设置，而源和目标因子可以让我们自由设置。我们来看一个简单的例子：
 
-![](../img/04/03/blending_equation.png)
+![](http://learnopengl.com/img/advanced/blending_equation.png)
 
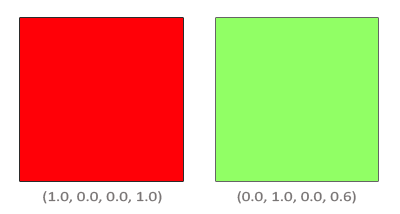
-我们有两个方形，我们希望将这个半透明的绿色方形绘制在红色方形之上。红色的方形将会是目标颜色（所以它应该先在颜色缓冲中），我们将要在这个红色方形之上绘制这个绿色方形。
+我们有两个方块，我们希望在红色方块上绘制绿色方块。红色方块会成为目标颜色（它会先进入颜色缓冲），我们将在红色方块上绘制绿色方块。
 
-问题来了：我们将因子值设置为什么？嘛，我们至少想让绿色方形乘以它的alpha值，所以我们想要将\(F_{src}\)设置为源颜色向量的alpha值，也就是0.6。接下来就应该清楚了，目标方形的贡献应该为剩下的alpha值。如果绿色方形对最终颜色贡献了60%，那么红色方块应该对最终颜色贡献了40%，即`1.0 - 0.6`。所以我们将\(F_{destination}\)设置为1减去源颜色向量的alpha值。这个方程变成了：
+那么问题来了：我们怎样来设置因子呢？我们起码要把绿色方块乘以它的alpha值，所以我们打算把\(F_{src}\)设置为源颜色向量的alpha值：0.6。接着，让目标方块的浓度等于剩下的alpha值。如果最终的颜色中绿色方块的浓度为60%，我们就把红色的浓度设为40%（1.0 – 0.6）。所以我们把\(F_{destination}\)设置为1减去源颜色向量的alpha值。方程将变成：
 
 $$
 \begin{equation}\bar{C}_{result} = \begin{pmatrix} \color{red}{0.0} \\ \color{green}{1.0} \\ \color{blue}{0.0} \\ \color{purple}{0.6} \end{pmatrix} * \color{green}{0.6} + \begin{pmatrix} \color{red}{1.0} \\ \color{green}{0.0} \\ \color{blue}{0.0} \\ \color{purple}{1.0} \end{pmatrix} * \color{red}{(1 - 0.6)} \end{equation}
 $$
 
-结果就是重叠方形的片段包含了一个60%绿色，40%红色的一种脏兮兮的颜色：
+最终方块结合部分包含了60%的绿色和40%的红色，得到一种脏兮兮的颜色：
 
-![](../img/04/03/blending_equation_mixed.png)
+![](http://learnopengl.com/img/advanced/blending_equation_mixed.png)
 
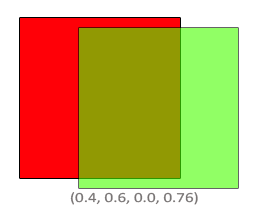
-最终的颜色将会被储存到颜色缓冲中，替代之前的颜色。
+最后的颜色被储存到颜色缓冲中，取代先前的颜色。
 
-这样子很不错，但我们该如何让OpenGL使用这样的因子呢？正好有一个专门的函数，叫做<fun>glBlendFunc</fun>。
+这个方案不错，但我们怎样告诉OpenGL来使用这样的因子呢？恰好有一个叫做`glBlendFunc`的函数。
+
+`void glBlendFunc(GLenum sfactor, GLenum dfactor)`接收两个参数，来设置源（source）和目标（destination）因子。OpenGL为我们定义了很多选项，我们把最常用的列在下面。注意，颜色常数向量\(\bar{\color{blue}C}_{constant}\)可以用`glBlendColor`函数分开来设置。
 
-<fun>glBlendFunc(GLenum sfactor, GLenum dfactor)</fun>函数接受两个参数，来设置<def>源</def>和<def>目标因子</def>。OpenGL为我们定义了很多个选项，我们将在下面列出大部分最常用的选项。注意常数颜色向量\(\bar{\color{blue}C}_{constant}\)可以通过<fun>glBlendColor</fun>函数来另外设置。
 
 选项 |	值
 ---|---
-`GL_ZERO`  |	因子等于\(0\)
-`GL_ONE`	 |  因子等于\(1\)
-`GL_SRC_COLOR` |	因子等于源颜色向量\(\bar{\color{green}C}_{source}\)
-`GL_ONE_MINUS_SRC_COLOR` | 因子等于\(1 - \bar{\color{green}C}_{source}\)
-`GL_DST_COLOR` |	 因子等于目标颜色向量\(\bar{\color{red}C}_{destination}\)
-`GL_ONE_MINUS_DST_COLOR` | 因子等于\(1 - \bar{\color{red}C}_{destination}\)
-`GL_SRC_ALPHA` |	因子等于\(\bar{\color{green}C}_{source}\)的\(alpha\)分量
-`GL_ONE_MINUS_SRC_ALPHA` | 因子等于\(1 -\) \(\bar{\color{green}C}_{source}\)的\(alpha\)分量
-`GL_DST_ALPHA` |	因子等于\(\bar{\color{red}C}_{destination}\)的\(alpha\)分量
-`GL_ONE_MINUS_DST_ALPHA` | 因子等于\(1 -\) \(\bar{\color{red}C}_{destination}\)的\(alpha\)分量
-`GL_CONSTANT_COLOR`	   | 因子等于常数颜色向量\(\bar{\color{blue}C}_{constant}\)
-`GL_ONE_MINUS_CONSTANT_COLOR` |	因子等于\(1 - \bar{\color{blue}C}_{constant}\)
-`GL_CONSTANT_ALPHA`	   | 因子等于\(\bar{\color{blue}C}_{constant}\)的\(alpha\)分量
-`GL_ONE_MINUS_CONSTANT_ALPHA` |	因子等于\(1 -\) \(\bar{\color{blue}C}_{constant}\)的\(alpha\)分量
+GL_ZERO  |	\(0\)
+GL_ONE	 |  \(1\)
+GL_SRC_COLOR |	源颜色向量\(\bar{\color{green}C}_{source}\)
+GL_ONE_MINUS_SRC_COLOR | \(1 - \bar{\color{green}C}_{source}\)
+GL_DST_COLOR |	 目标颜色向量\(\bar{\color{red}C}_{destination}\)
+GL_ONE_MINUS_DST_COLOR | \(1 - \bar{\color{red}C}_{destination}\)
+GL_SRC_ALPHA |	\(\bar{\color{green}C}_{source}\)的\(alpha\)值
+GL_ONE_MINUS_SRC_ALPHA | \(1 -\) \(\bar{\color{green}C}_{source}\)的\(alpha\)值
+GL_DST_ALPHA |	\(\bar{\color{red}C}_{destination}\)的\(alpha\)值
+GL_ONE_MINUS_DST_ALPHA | \(1 -\) \(\bar{\color{red}C}_{destination}\)的\(alpha\)值
+GL_CONSTANT_COLOR	   | 常颜色向量\(\bar{\color{blue}C}_{constant}\)
+GL_ONE_MINUS_CONSTANT_COLOR |	\(1 - \bar{\color{blue}C}_{constant}\)
+GL_CONSTANT_ALPHA	   | \(\bar{\color{blue}C}_{constant}\)的\(alpha\)值
+GL_ONE_MINUS_CONSTANT_ALPHA |	\(1 -\) \(\bar{\color{blue}C}_{constant}\)的\(alpha\)值
 
-为了获得之前两个方形的混合结果，我们需要使用源颜色向量的\(alpha\)作为源因子，使用\(1 - alpha\)作为目标因子。这将会产生以下的<fun>glBlendFunc</fun>：
+为从两个方块获得混合结果，我们打算把源颜色的\(alpha\)给源因子，\(1 - alpha\)给目标因子。调整到`glBlendFunc`之后就像这样：
 
 ```c++
 glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
 ```
 
-也可以使用<fun>glBlendFuncSeparate</fun>为RGB和alpha通道分别设置不同的选项：
+也可以为RGB和alpha通道各自设置不同的选项，使用`glBlendFuncSeperate`：
 
 ```c++
-glBlendFuncSeparate(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA, GL_ONE, GL_ZERO);
+glBlendFuncSeperate(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA,GL_ONE, GL_ZERO);
 ```
 
-这个函数和我们之前设置的那样设置了RGB分量，但这样只能让最终的alpha分量被源颜色向量的alpha值所影响到。
+这个方程就像我们之前设置的那样，设置了RGB元素，但是只让最终的alpha元素被源alpha值影响到。
 
-OpenGL甚至给了我们更多的灵活性，允许我们改变方程中源和目标部分的运算符。当前源和目标是相加的，但如果愿意的话，我们也可以让它们相减。<fun>glBlendEquation(GLenum mode)</fun>允许我们设置运算符，它提供了三个选项：
+OpenGL给了我们更多的自由，我们可以改变方程源和目标部分的操作符。现在，源和目标元素已经相加了。如果我们愿意的话，我们还可以把它们相减。
 
-- GL_FUNC_ADD：默认选项，将两个分量相加：\(\bar{C}_{result} = \color{green}{Src} + \color{red}{Dst}\)。
-- GL_FUNC_SUBTRACT：将两个分量相减： \(\bar{C}_{result} = \color{green}{Src} - \color{red}{Dst}\)。
-- GL_FUNC_REVERSE_SUBTRACT：将两个分量相减，但顺序相反：\(\bar{C}_{result} = \color{red}{Dst} - \color{green}{Src}\)。
-- GL_MIN：取两个分量中的最小值：\(\bar{C}_{result} = {min}(\color{red}{Dst}, \color{green}{Src})\)。
-- GL_MAX：取两个分量中的最大值：\(\bar{C}_{result} = {max}(\color{red}{Dst}, \color{green}{Src})\)。
+`void glBlendEquation(GLenum mode)`允许我们设置这个操作，有3种可行的选项：
 
-通常我们都可以省略调用<fun>glBlendEquation</fun>，因为<var>GL_FUNC_ADD</var>对大部分的操作来说都是我们希望的混合方程，但如果你真的想打破主流，其它的方程也可能符合你的要求。
+* GL_FUNC_ADD：默认的，彼此元素相加：\(\bar{C}_{result} = \color{green}{Src} + \color{red}{Dst}\)
+* GL_FUNC_SUBTRACT：彼此元素相减： \(\bar{C}_{result} = \color{green}{Src} - \color{red}{Dst}\)
+* GL_FUNC_REVERSE_SUBTRACT：彼此元素相减，但顺序相反：\(\bar{C}_{result} = \color{red}{Dst} - \color{green}{Src}\).
+
+通常我们可以简单地省略`glBlendEquation`因为GL_FUNC_ADD在大多数时候就是我们想要的，但是如果你如果你真想尝试努力打破主流常规，其他的方程或许符合你的要求。
 
 ## 渲染半透明纹理
 
-既然我们已经知道OpenGL是如何处理混合的了，是时候将我们的知识运用到实战中了，我们将会在场景中添加几个半透明的窗户。我们将使用本节开始的那个场景，但是这次不再是渲染草的纹理了，我们现在将使用本节开始时的那个[透明的窗户](../img/04/03/blending_transparent_window.png)纹理。
+现在我们知道OpenGL如何处理混合，是时候把我们的知识运用起来了，我们来添加几个半透明窗子。我们会使用本教程开始时用的那个场景，但是不再渲染草纹理，取而代之的是来自教程开始处半透明窗子纹理。
 
-首先，在初始化时我们启用混合，并设定相应的混合函数：
+首先，初始化时我们需要开启混合，设置合适和混合方程：
 
 ```c++
 glEnable(GL_BLEND);
 glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
 ```
 
-由于启用了混合，我们就不需要丢弃片段了，所以我们把片段着色器还原：
+由于我们开启了混合，就不需要丢弃片段了，所以我们把片段着色器设置为原来的那个版本：
 
 ```c++
 #version 330 core
-out vec4 FragColor;
-
 in vec2 TexCoords;
 
+out vec4 color;
+
 uniform sampler2D texture1;
 
 void main()
-{             
-    FragColor = texture(texture1, TexCoords);
+{
+    color = texture(texture1, TexCoords);
 }
 ```
 
-现在（每当OpenGL渲染了一个片段时）它都会将当前片段的颜色和当前颜色缓冲中的片段颜色根据alpha值来进行混合。由于窗户纹理的玻璃部分是半透明的，我们应该能通窗户中看到背后的场景了。
+这一次（无论OpenGL什么时候去渲染一个片段），它都根据alpha值，把当前片段的颜色和颜色缓冲中的颜色进行混合。因为窗子的玻璃部分的纹理是半透明的，我们应该可以透过玻璃看到整个场景。
 
-![](../img/04/03/blending_incorrect_order.png)
+![](http://learnopengl.com/img/advanced/blending_incorrect_order.png)
 
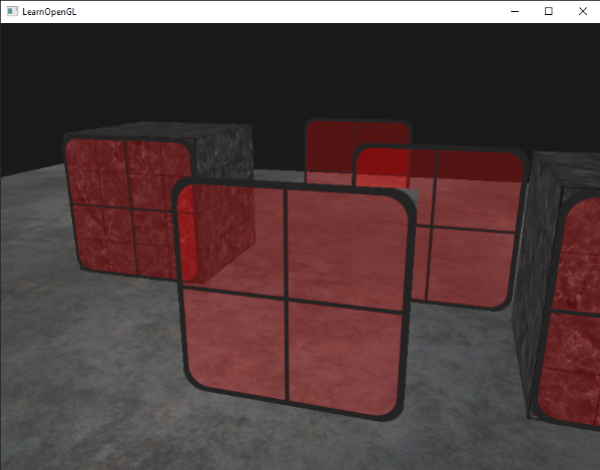
-如果你仔细看的话，你可能会注意到有些不对劲。最前面窗户的透明部分遮蔽了背后的窗户？这为什么会发生呢？
+如果你仔细看看，就会注意到有些不对劲。前面的窗子透明部分阻塞了后面的。为什么会这样？
 
-发生这一现象的原因是，深度测试和混合一起使用的话会产生一些麻烦。当写入深度缓冲时，深度缓冲不会检查片段是否是透明的，所以透明的部分会和其它值一样写入到深度缓冲中。结果就是窗户的整个四边形不论透明度都会进行深度测试。即使透明的部分应该显示背后的窗户，深度测试仍然丢弃了它们。
+原因是深度测试在与混合的一同工作时出现了点状况。当写入深度缓冲的时候，深度测试不关心片段是否有透明度，所以透明部分被写入深度缓冲，就和其他值没什么区别。结果是整个四边形的窗子被检查时都忽视了透明度。即便透明部分应该显示出后面的窗子，深度缓冲还是丢弃了它们。
 
-所以我们不能随意地决定如何渲染窗户，让深度缓冲解决所有的问题了。这也是混合变得有些麻烦的部分。要想保证窗户中能够显示它们背后的窗户，我们需要首先绘制背后的这部分窗户。这也就是说在绘制的时候，我们必须先手动将窗户按照最远到最近来排序，再按照顺序渲染。
+所以我们不能简简单单地去渲染窗子，我们期待着深度缓冲为我们解决这所有问题；这也正是混合之处代码不怎么好看的原因。为保证前面窗子显示了它后面的窗子，我们必须首先绘制后面的窗子。这意味着我们必须手工调整窗子的顺序，从远到近地逐个渲染。
 
 !!! Important
 
-	注意，对于草这种全透明的物体，我们可以选择丢弃透明的片段而不是混合它们，这样就解决了这些头疼的问题（没有深度问题）。
+    对于全透明物体，比如草叶，我们选择简单的丢弃透明像素而不是混合，这样就减少了令我们头疼的问题（没有深度测试问题）。
 
-## 不要打乱顺序
+## 别打乱顺序
 
-要想让混合在多个物体上工作，我们需要最先绘制最远的物体，最后绘制最近的物体。普通不需要混合的物体仍然可以使用深度缓冲正常绘制，所以它们不需要排序。但我们仍要保证它们在绘制（排序的）透明物体之前已经绘制完毕了。当绘制一个有不透明和透明物体的场景的时候，大体的原则如下：
+要让混合在多物体上有效，我们必须先绘制最远的物体，最后绘制最近的物体。普通的无混合物体仍然可以使用深度缓冲正常绘制，所以不必给它们排序。我们一定要保证它们在透明物体前绘制好。当无透明度物体和透明物体一起绘制的时候，通常要遵循以下原则：
 
-1. 先绘制所有不透明的物体。
-2. 对所有透明的物体排序。
-3. 按顺序绘制所有透明的物体。
-
-排序透明物体的一种方法是，从观察者视角获取物体的距离。这可以通过计算摄像机位置向量和物体的位置向量之间的距离所获得。接下来我们把距离和它对应的位置向量存储到一个STL库的<fun>map</fun>数据结构中。<fun>map</fun>会自动根据键值(Key)对它的值排序，所以只要我们添加了所有的位置，并以它的距离作为键，它们就会自动根据距离值排序了。
+先绘制所有不透明物体。
+为所有透明物体排序。
+按顺序绘制透明物体。
+一种排序透明物体的方式是，获取一个物体到观察者透视图的距离。这可以通过获取摄像机的位置向量和物体的位置向量来得到。接着我们就可以把它和相应的位置向量一起储存到一个map数据结构（STL库）中。map会自动基于它的键排序它的值，所以当我们把它们的距离作为键添加到所有位置中后，它们就自动按照距离值排序了：
 
 ```c++
 std::map<float, glm::vec3> sorted;
-for (unsigned int i = 0; i < windows.size(); i++)
+for (GLuint i = 0; i < windows.size(); i++) // windows contains all window positions
 {
-    float distance = glm::length(camera.Position - windows[i]);
+    GLfloat distance = glm::length(camera.Position - windows[i]);
     sorted[distance] = windows[i];
 }
 ```
 
-结果就是一个排序后的容器对象，它根据<var>distance</var>键值从低到高储存了每个窗户的位置。
+最后产生了一个容器对象，基于它们距离从低到高储存了每个窗子的位置。
 
-之后，这次在渲染的时候，我们将以逆序（从远到近）从map中获取值，之后以正确的顺序绘制对应的窗户：
+随后当渲染的时候，我们逆序获取到每个map的值（从远到近），然后以正确的绘制相应的窗子：
 
 ```c++
-for(std::map<float,glm::vec3>::reverse_iterator it = sorted.rbegin(); it != sorted.rend(); ++it) 
+for(std::map<float,glm::vec3>::reverse_iterator it = sorted.rbegin(); it != sorted.rend(); ++it)
 {
     model = glm::mat4();
-    model = glm::translate(model, it->second);				
-    shader.setMat4("model", model);
+    model = glm::translate(model, it->second);
+    glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
     glDrawArrays(GL_TRIANGLES, 0, 6);
 }
 ```
 
-我们使用了<fun>map</fun>的一个反向迭代器(Reverse Iterator)，反向遍历其中的条目，并将每个窗户四边形位移到对应的窗户位置上。这是排序透明物体的一个比较简单的实现，它能够修复之前的问题，现在场景看起来是这样的：
+我们从map得来一个逆序的迭代器，迭代出每个逆序的条目，然后把每个窗子的四边形平移到相应的位置。这个相对简单的方法对透明物体进行了排序，修正了前面的问题，现在场景看起来像这样：
 
-![](../img/04/03/blending_sorted.png)
+![](http://learnopengl.com/img/advanced/blending_sorted.png)
 
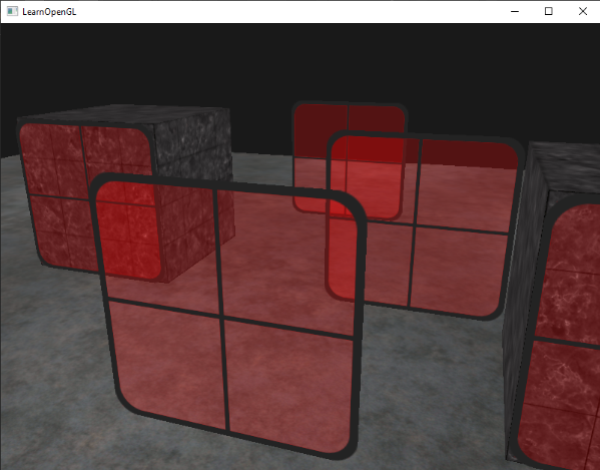
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/3.2.blending_sort/blending_sorted.cpp)找到带有排序的完整源代码。
+你可以[从这里得到完整的带有排序的源码](http://learnopengl.com/code_viewer.php?code=advanced/blending_sorted)。
 
-虽然按照距离排序物体这种方法对我们这个场景能够正常工作，但它并没有考虑旋转、缩放或者其它的变换，奇怪形状的物体需要一个不同的计量，而不是仅仅一个位置向量。
+虽然这个按照它们的距离对物体进行排序的方法在这个特定的场景中能够良好工作，但它不能进行旋转、缩放或者进行其他的变换，奇怪形状的物体需要一种不同的方式，而不能简单的使用位置向量。
 
-在场景中排序物体是一个很困难的技术，很大程度上由你场景的类型所决定，更别说它额外需要消耗的处理能力了。完整渲染一个包含不透明和透明物体的场景并不是那么容易。更高级的技术还有<def>次序无关透明度</def>(Order Independent Transparency, OIT)，但这超出本教程的范围了。现在，你还是必须要普通地混合你的物体，但如果你很小心，并且知道目前方法的限制的话，你仍然能够获得一个比较不错的混合实现。
+在场景中排序物体是个有难度的技术，它很大程度上取决于你场景的类型，更不必说会耗费额外的处理能力了。完美地渲染带有透明和不透明的物体的场景并不那么容易。有更高级的技术例如次序无关透明度（order independent transparency），但是这超出了本教程的范围。现在你不得不采用普通的混合你的物体，但是如果你小心谨慎，并知道这个局限，你仍可以得到颇为合适的混合实现。

docs/04 Advanced OpenGL/04 Face culling.md

@@ -3,86 +3,89 @@
 原文     | [Face culling](http://learnopengl.com/#!Advanced-OpenGL/Face-culling)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | 暂未校对
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com)
 
-尝试在脑子中想象一个3D立方体，数数你从任意方向最多能同时看到几个面。如果你的想象力不是过于丰富了，你应该能得出最大的面数是3。你可以从任意位置和任意方向看向这个球体，但你永远不能看到3个以上的面。所以我们为什么要浪费时间绘制我们不能看见的那3个面呢？如果我们能够以某种方式丢弃这几个看不见的面，我们能省下超过50%的片段着色器执行数！
+尝试在头脑中想象一下有一个3D立方体，你从任何一个方向去看它，最多可以同时看到多少个面。如果你的想象力不是过于丰富，你最终最多能数出来的面是3个。你可以从一个立方体的任意位置和方向上去看它，但是你永远不能看到多于3个面。所以我们为何还要去绘制那三个不会显示出来的3个面呢。如果我们可以以某种方式丢弃它们，我们会提高片段着色器超过50%的性能！
 
 !!! Important
 
-	我说的是**超过**50%而不是50%，因为从特定角度来看的话只能看见2个甚至是1个面。在这种情况下，我们就能省下超过50%了。
+        我们所说的是超过50%而不是50%，因为从一个角度只有2个或1个面能够被看到。这种情况下我们就能够提高50%以上性能了。
 
-这是一个很好的主意，但我们仍有一个问题需要解决：我们如何知道一个物体的某一个面不能从观察者视角看到呢？  
-如果我们想象任何一个闭合形状，它的每一个面都有两侧，每一侧要么**面向**用户，要么背对用户。如果我们能够只绘制**面向**观察者的面呢？
 
-这正是<def>面剔除</def>(Face Culling)所做的。OpenGL能够检查所有<def>面向</def>(Front Facing)观察者的面，并渲染它们，而丢弃那些<def>背向</def>(Back Facing)的面，节省我们很多的片段着色器调用（它们的开销很大！）。但我们仍要告诉OpenGL哪些面是正向面(Front Face)，哪些面是背向面(Back Face)。OpenGL使用了一个很聪明的技巧，分析顶点数据的<def>环绕顺序</def>(Winding Order)。
+这的确是个好主意，但是有个问题需要解决：我们如何知道某个面在观察者的视野中不会出现呢？如果我们去想象任何封闭的几何平面，它们都有两面，一面面向用户，另一面背对用户。假如我们只渲染面向观察者的面会怎样？
 
-## 环绕顺序
+这正是**面剔除**(Face culling)所要做的。OpenGL允许检查所有正面朝向（Front facing）观察者的面，并渲染它们，而丢弃所有背面朝向（Back facing）的面，这样就节约了我们很多片段着色器的命令（它们很昂贵！）。我们必须告诉OpenGL我们使用的哪个面是正面，哪个面是反面。OpenGL使用一种聪明的手段解决这个问题——分析顶点数据的连接顺序（Winding order）。
 
-当我们定义一组三角形顶点时，我们会以特定的环绕顺序来定义它们，可能是<def>顺时针</def>(Clockwise)的，也可能是<def>逆时针</def>(Counter-clockwise)的。每个三角形由3个顶点所组成，我们会从三角形中间来看，为这3个顶点设定一个环绕顺序。
 
-![](../img/04/04/faceculling_windingorder.png)
+## 顶点连接顺序
 
-可以看到，我们首先定义了顶点1，之后我们可以选择定义顶点2或者顶点3，这个选择将定义了这个三角形的环绕顺序。下面的代码展示了这点：
+当我们定义一系列的三角顶点时，我们会把它们定义为一个特定的连接顺序(Winding Order)，它们可能是**顺时针**的或**逆时针**的。每个三角形由3个顶点组成，我们从三角形的中间去看，从而把这三个顶点指定一个连接顺序。
+
+![](http://learnopengl.com/img/advanced/faceculling_windingorder.png)
+
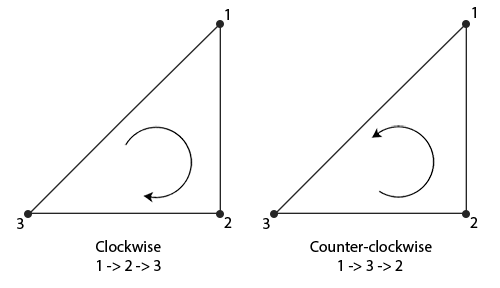
+正如你所看到的那样，我们先定义了顶点1，接着我们定义顶点2或3，这个不同的选择决定了这个三角形的连接顺序。下面的代码展示出这点：
 
 ```c++
-float vertices[] = {
-    // 顺时针
-    vertices[0], // 顶点1
-    vertices[1], // 顶点2
-    vertices[2], // 顶点3
+GLfloat vertices[] = {
+    //顺时针
+    vertices[0], // vertex 1
+    vertices[1], // vertex 2
+    vertices[2], // vertex 3
     // 逆时针
-    vertices[0], // 顶点1
-    vertices[2], // 顶点3
-    vertices[1]  // 顶点2  
+    vertices[0], // vertex 1
+    vertices[2], // vertex 3
+    vertices[1] // vertex 2
 };
 ```
 
-每组组成三角形图元的三个顶点就包含了一个环绕顺序。OpenGL在渲染图元的时候将使用这个信息来决定一个三角形是一个<def>正向</def>三角形还是<def>背向</def>三角形。默认情况下，逆时针顶点所定义的三角形将会被处理为正向三角形。
+每三个顶点都形成了一个包含着连接顺序的基本三角形。OpenGL使用这个信息在渲染你的基本图形的时候决定这个三角形是三角形的正面还是三角形的背面。默认情况下，**逆时针**的顶点连接顺序被定义为三角形的**正面**。
 
-当你定义顶点顺序的时候，你应该想象对应的三角形是面向你的，所以你定义的三角形从正面看去应该是逆时针的。这样定义顶点很棒的一点是，实际的环绕顺序是在光栅化阶段进行的，也就是顶点着色器运行之后。这些顶点就是从**观察者视角**所见的了。
+当定义你的顶点顺序时，你如果定义能够看到的一个三角形，那它一定是正面朝向的，所以你定义的三角形应该是逆时针的，就像你直接面向这个三角形。把所有的顶点指定成这样是件炫酷的事，实际的顶点连接顺序是在**光栅化**阶段（Rasterization stage）计算的，所以当顶点着色器已经运行后。顶点就能够在观察者的观察点被看到。
 
-观察者所面向的所有三角形顶点就是我们所指定的正确环绕顺序了，而立方体另一面的三角形顶点则是以相反的环绕顺序所渲染的。这样的结果就是，我们所面向的三角形将会是正向三角形，而背面的三角形则是背向三角形。下面这张图显示了这个效果：
+我们指定了它们以后，观察者面对的所有的三角形的顶点的连接顺序都是正确的，但是现在渲染的立方体另一面的三角形的顶点的连接顺序被反转。最终，我们所面对的三角形被视为正面朝向的三角形，后部的三角形被视为背面朝向的三角形。下图展示了这个效果：
+
+![](http://learnopengl.com/img/advanced/faceculling_frontback.png)
+
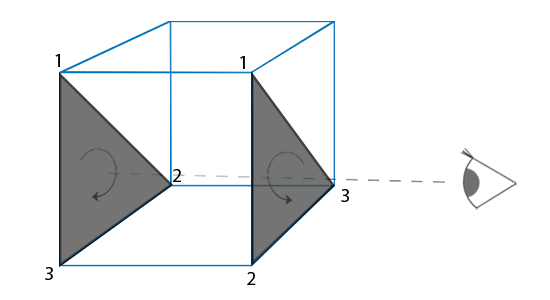
+在顶点数据中，我们定义的是两个逆时针顺序的三角形。然而，从观察者的方面看，后面的三角形是顺时针的，如果我们仍以1、2、3的顺序以观察者当面的视野看的话。即使我们以逆时针顺序定义后面的三角形，它现在还是变为顺时针。它正是我们打算剔除（丢弃）的不可见的面！
 
-![](../img/04/04/faceculling_frontback.png)
 
-在顶点数据中，我们将两个三角形都以逆时针顺序定义（正面的三角形是1、2、3，背面的三角形也是1、2、3（如果我们从正面看这个三角形的话））。然而，如果从观察者当前视角使用1、2、3的顺序来绘制的话，从观察者的方向来看，背面的三角形将会是以顺时针顺序渲染的。虽然背面的三角形是以逆时针定义的，它现在是以顺时针顺序渲染的了。这正是我们想要<def>剔除</def>（Cull，丢弃）的不可见面了！
 
 ## 面剔除
 
-在本节的开头我们就说过，OpenGL能够丢弃那些渲染为背向三角形的三角形图元。既然已经知道如何设置顶点的环绕顺序了，我们就可以使用OpenGL的<def>面剔除</def>选项了，它默认是禁用状态的。
+在教程的开头，我们说过OpenGL可以丢弃背面朝向的三角形。现在我们知道了如何设置顶点的连接顺序，我们可以开始使用OpenGL默认关闭的面剔除选项了。
 
-在之前教程中使用的立方体顶点数据并不是按照逆时针环绕顺序定义的，所以我更新了顶点数据，来反映逆时针的环绕顺序，你可以从[这里](https://learnopengl.com/code_viewer.php?code=advanced/faceculling_vertexdata)复制它们。尝试想象这些顶点，确认在每个三角形中它们都是以逆时针定义的，这是一个很好的习惯。
+记住我们上一节所使用的立方体的定点数据不是以逆时针顺序定义的。所以我更新了顶点数据，好去反应为一个逆时针链接顺序，你可以[从这里复制它](http://learnopengl.com/code_viewer.php?code=advanced/faceculling_vertexdata)。把所有三角的顶点都定义为逆时针是一个很好的习惯。
 
-要想启用面剔除，我们只需要启用OpenGL的<var>GL_CULL_FACE</var>选项：
+开启OpenGL的`GL_CULL_FACE`选项就能开启面剔除功能：
 
 ```c++
 glEnable(GL_CULL_FACE);
 ```
 
-从这一句代码之后，所有背向面都将被丢弃（尝试飞进立方体内部，看看所有的内面是不是都被丢弃了）。目前我们在渲染片段的时候能够节省50%以上的性能，但注意这只对像立方体这样的封闭形状有效。当我们想要绘制[上一节](03 Blending.md)中的草时，我们必须要再次禁用面剔除，因为它们的正向面和背向面都应该是可见的。
+从这儿以后，所有的不是正面朝向的面都会被丢弃（尝试飞入立方体看看，里面什么面都看不见了）。目前，在渲染片段上我们节约了超过50%的性能，但记住这只对像立方体这样的封闭形状有效。当我们绘制上个教程中那个草的时候，我们必须关闭面剔除，这是因为它的前、后面都必须是可见的。
 
-OpenGL允许我们改变需要剔除的面的类型。如果我们只想剔除正向面而不是背向面会怎么样？我们可以调用<fun>glCullFace</fun>来定义这一行为：
+OpenGL允许我们改变剔除面的类型。要是我们剔除正面而不是背面会怎样？我们可以调用`glCullFace`来做这件事：
 
 ```c++
-glCullFace(GL_FRONT);
+glCullFace(GL_BACK);
 ```
 
-<fun>glCullFace</fun>函数有三个可用的选项：
+`glCullFace`函数有三个可用的选项：
 
-- `GL_BACK`：只剔除背向面。
-- `GL_FRONT`：只剔除正向面。
-- `GL_FRONT_AND_BACK`：剔除正向面和背向面。
+* GL_BACK：只剔除背面。
+* GL_FRONT：只剔除正面。
+* GL_FRONT_AND_BACK：剔除背面和正面。
 
-<fun>glCullFace</fun>的初始值是<var>GL_BACK</var>。除了需要剔除的面之外，我们也可以通过调用<fun>glFrontFace</fun>，告诉OpenGL我们希望将顺时针的面（而不是逆时针的面）定义为正向面：
+`glCullFace`的初始值是`GL_BACK`。另外，我们还可以告诉OpenGL使用顺时针而不是逆时针来表示正面，这通过glFrontFace来设置：
 
 ```c++
 glFrontFace(GL_CCW);
 ```
 
-默认值是<var>GL_CCW</var>，它代表的是逆时针的环绕顺序，另一个选项是<var>GL_CW</var>，它（显然）代表的是顺时针顺序。
+默认值是`GL_CCW`，它代表逆时针，`GL_CW`代表顺时针顺序。
 
-我们可以来做一个实验，告诉OpenGL现在顺时针顺序代表的是正向面：
+我们可以做个小实验，告诉OpenGL现在顺时针代表正面：
 
 ```c++
 glEnable(GL_CULL_FACE);
@@ -90,19 +93,19 @@ glCullFace(GL_BACK);
 glFrontFace(GL_CW);
 ```
 
-这样的结果是只有背向面被渲染了：
+最后的结果只有背面被渲染了：
 
-![](../img/04/04/faceculling_reverse.png)
+![](http://learnopengl.com/img/advanced/faceculling_reverse.png)
 
-注意你可以仍使用默认的逆时针环绕顺序，但剔除正向面，来达到相同的效果：
+要注意，你可以使用默认逆时针顺序剔除正面，来创建相同的效果：
 
-```c++
+```c
 glEnable(GL_CULL_FACE);
 glCullFace(GL_FRONT);
 ```
 
-可以看到，面剔除是一个提高OpenGL程序性能的很棒的工具。但你需要记住哪些物体能够从面剔除中获益，而哪些物体不应该被剔除。
+正如你所看到的那样，面剔除是OpenGL提高效率的一个强大工具，它使应用节省运算。你必须跟踪下来哪个物体可以使用面剔除，哪些不能。
 
 ## 练习
 
-- 你能够重新定义顶点数据，将每个三角形设置为顺时针顺序，并将顺时针的三角形设置为正向面，仍将场景渲染出来吗？：[参考解答](https://learnopengl.com/code_viewer.php?code=advanced/faceculling-exercise1)
+你可以自己重新定义一个顺时针的顶点顺序，然后用顺时针作为正面把它渲染出来吗：[解决方案](http://learnopengl.com/code_viewer.php?code=advanced/faceculling-exercise1)。

docs/04 Advanced OpenGL/05 Framebuffers.md

@@ -3,168 +3,163 @@
 原文     | [Framebuffers](http://learnopengl.com/#!Advanced-OpenGL/Framebuffers)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | [AoZhang](https://github.com/SuperAoao)
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com)
 
-到目前为止，我们已经使用了很多屏幕缓冲了：用于写入颜色值的颜色缓冲、用于写入深度信息的深度缓冲和允许我们根据一些条件丢弃特定片段的模板缓冲。这些缓冲结合起来叫做<def>帧缓冲</def>(Framebuffer)，它被储存在GPU内存中的某处。OpenGL允许我们定义我们自己的帧缓冲，也就是说我们能够定义我们自己的颜色缓冲，甚至是深度缓冲和模板缓冲。
+到目前为止，我们使用了几种不同类型的屏幕缓冲：用于写入颜色值的颜色缓冲，用于写入深度信息的深度缓冲，以及允许我们基于一些条件丢弃指定片段的模板缓冲。把这几种缓冲结合起来叫做帧缓冲(Framebuffer)，它被储存于内存中。OpenGL给了我们自己定义帧缓冲的自由，我们可以选择性的定义自己的颜色缓冲、深度和模板缓冲。
 
-我们目前所做的所有操作都是在<def>默认帧缓冲</def>的渲染缓冲上进行的。默认的帧缓冲是在你创建窗口的时候生成和配置的（GLFW帮我们做了这些）。通过创建我们自己的帧缓冲，我们可以获得额外的渲染目标(target)。
+我们目前所做的渲染操作都是是在默认的帧缓冲之上进行的。当你创建了你的窗口的时候默认帧缓冲就被创建和配置好了（GLFW为我们做了这件事）。通过创建我们自己的帧缓冲我们能够获得一种额外的渲染方式。
 
-你可能不能很快理解帧缓冲的应用，但渲染你的场景到不同的帧缓冲能够让我们在场景中加入类似镜子的东西，或者做出很酷的后期处理效果。首先我们会讨论它是如何工作的，之后我们将来实现这些炫酷的后期处理效果。
+你也许不能立刻理解应用程序的帧缓冲的含义，通过帧缓冲可以将你的场景渲染到一个不同的帧缓冲中，可以使我们能够在场景中创建镜子这样的效果，或者做出一些炫酷的特效。首先我们会讨论它们是如何工作的，然后我们将利用帧缓冲来实现一些炫酷的效果。
 
 ## 创建一个帧缓冲
 
-和OpenGL中的其它对象一样，我们会使用一个叫做<fun>glGenFramebuffers</fun>的函数来创建一个帧缓冲对象(Framebuffer Object, FBO)：
+就像OpenGL中其他对象一样，我们可以使用一个叫做`glGenFramebuffers`的函数来创建一个帧缓冲对象（简称FBO）：
 
 ```c++
-unsigned int fbo;
+GLuint fbo;
 glGenFramebuffers(1, &fbo);
 ```
 
-这种创建和使用对象的方式我们已经见过很多次了，所以它的使用函数也和其它的对象类似。首先我们创建一个帧缓冲对象，将它绑定为激活的(Active)帧缓冲，做一些操作，之后解绑帧缓冲。我们使用<fun>glBindFramebuffer</fun>来绑定帧缓冲。
+这种对象的创建和使用的方式我们已经见过不少了，因此它们的使用方式也和之前我们见过的其他对象的使用方式相似。首先我们要创建一个帧缓冲对象，把它绑定到当前帧缓冲，做一些操作，然后解绑帧缓冲。我们使用`glBindFramebuffer`来绑定帧缓冲：
 
 ```c++
 glBindFramebuffer(GL_FRAMEBUFFER, fbo);
 ```
 
-在绑定到<var>GL_FRAMEBUFFER</var>目标之后，所有的**读取**和**写入**帧缓冲的操作将会影响当前绑定的帧缓冲。我们也可以使用<var>GL_READ_FRAMEBUFFER</var>或<var>GL_DRAW_FRAMEBUFFER</var>，将一个帧缓冲分别绑定到读取目标或写入目标。绑定到<var>GL_READ_FRAMEBUFFER</var>的帧缓冲将会使用在所有像是<fun>glReadPixels</fun>的读取操作中，而绑定到<var>GL_DRAW_FRAMEBUFFER</var>的帧缓冲将会被用作渲染、清除等写入操作的目标。大部分情况你都不需要区分它们，通常都会使用<var>GL_FRAMEBUFFER</var>，绑定到两个上。
+绑定到`GL_FRAMEBUFFER`目标后，接下来所有的读、写帧缓冲的操作都会影响到当前绑定的帧缓冲。也可以把帧缓冲分开绑定到读或写目标上，分别使用`GL_READ_FRAMEBUFFER`或`GL_DRAW_FRAMEBUFFER`来做这件事。如果绑定到了`GL_READ_FRAMEBUFFER`，就能执行所有读取操作，像`glReadPixels`这样的函数使用了；绑定到`GL_DRAW_FRAMEBUFFER`上，就允许进行渲染、清空和其他的写入操作。大多数时候你不必分开用，通常把两个都绑定到`GL_FRAMEBUFFER`上就行。
 
-不幸的是，我们现在还不能使用我们的帧缓冲，因为它还不<def>完整</def>(Complete)，一个完整的帧缓冲需要满足以下的条件：
+很遗憾，现在我们还不能使用自己的帧缓冲，因为还没做完呢。建构一个完整的帧缓冲必须满足以下条件：
 
-- 附加至少一个缓冲（颜色、深度或模板缓冲）。
-- 至少有一个颜色附件(Attachment)。
-- 所有的附件都必须是完整的（保留了内存）。
-- 每个缓冲都应该有相同的样本数(sample)。
+* 我们必须往里面加入至少一个附件（颜色、深度、模板缓冲）。
+* 其中至少有一个是颜色附件。
+* 所有的附件都应该是已经完全做好的（已经存储在内存之中）。
+* 每个缓冲都应该有同样数目的样本。
 
-如果你不知道什么是样本，不要担心，我们将在[之后的](11 Anti Aliasing.md)教程中讲到。
+如果你不知道什么是样本也不用担心，我们会在后面的教程中讲到。
 
-从上面的条件中可以知道，我们需要为帧缓冲创建一些附件，并将附件附加到帧缓冲上。在完成所有的条件之后，我们可以以<var>GL_FRAMEBUFFER</var>为参数调用<fun>glCheckFramebufferStatus</fun>，检查帧缓冲是否完整。它将会检测当前绑定的帧缓冲，并返回规范中[这些](https://www.khronos.org/registry/OpenGL-Refpages/gl4/html/glCheckFramebufferStatus.xhtml)值的其中之一。如果它返回的是<var>GL_FRAMEBUFFER_COMPLETE</var>，帧缓冲就是完整的了。
+从上面的需求中你可以看到，我们需要为帧缓冲创建一些附件(Attachment)，还需要把这些附件附加到帧缓冲上。当我们做完所有上面提到的条件的时候我们就可以用  `glCheckFramebufferStatus` 带上 `GL_FRAMEBUFFER` 这个参数来检查是否真的成功做到了。然后检查当前绑定的帧缓冲，返回了这些规范中的哪个值。如果返回的是 `GL_FRAMEBUFFER_COMPLETE`就对了：
 
 ```c++
 if(glCheckFramebufferStatus(GL_FRAMEBUFFER) == GL_FRAMEBUFFER_COMPLETE)
-  // 执行胜利的舞蹈
+  // Execute victory dance
 ```
 
-之后所有的渲染操作将会渲染到当前绑定帧缓冲的附件中。由于我们的帧缓冲不是默认帧缓冲，渲染指令将不会对窗口的视觉输出有任何影响。出于这个原因，渲染到一个不同的帧缓冲被叫做<def>离屏渲染</def>(Off-screen Rendering)。要保证所有的渲染操作在主窗口中有视觉效果，我们需要再次激活默认帧缓冲，将它绑定到`0`。
+后续所有渲染操作将渲染到当前绑定的帧缓冲的附加缓冲中，由于我们的帧缓冲不是默认的帧缓冲，渲染命令对窗口的视频输出不会产生任何影响。出于这个原因，它被称为离屏渲染（off-screen rendering），就是渲染到一个另外的缓冲中。为了让所有的渲染操作对主窗口产生影响我们必须通过绑定为0来使默认帧缓冲被激活：
 
 ```c++
 glBindFramebuffer(GL_FRAMEBUFFER, 0);
 ```
 
-在完成所有的帧缓冲操作之后，不要忘记删除这个帧缓冲对象：
+当我们做完所有帧缓冲操作，不要忘记删除帧缓冲对象：
 
 ```c++
 glDeleteFramebuffers(1, &fbo);
 ```
 
-在完整性检查执行之前，我们需要给帧缓冲附加一个附件。<def>附件</def>是一个内存位置，它能够作为帧缓冲的一个缓冲，可以将它想象为一个图像。当创建一个附件的时候我们有两个选项：纹理或渲染缓冲对象(Renderbuffer Object)。
+现在在执行完成检测前，我们需要把一个或更多的附件附加到帧缓冲上。一个附件就是一个内存地址，这个内存地址里面包含一个为帧缓冲准备的缓冲，它可以是个图像。当创建一个附件的时候我们有两种方式可以采用：纹理或渲染缓冲（renderbuffer）对象。
 
 ### 纹理附件
 
-当把一个纹理附加到帧缓冲的时候，所有的渲染指令将会写入到这个纹理中，就像它是一个普通的颜色/深度或模板缓冲一样。使用纹理的优点是，所有渲染操作的结果将会被储存在一个纹理图像中，我们之后可以在着色器中很方便地使用它。
+当把一个纹理附加到帧缓冲上的时候，所有渲染命令会写入到纹理上，就像它是一个普通的颜色/深度或者模板缓冲一样。使用纹理的好处是，所有渲染操作的结果都会被储存为一个纹理图像，这样我们就可以简单的在着色器中使用了。
 
-为帧缓冲创建一个纹理和创建一个普通的纹理差不多：
+创建一个帧缓冲的纹理和创建普通纹理差不多：
 
 ```c++
-unsigned int texture;
+GLuint texture;
 glGenTextures(1, &texture);
 glBindTexture(GL_TEXTURE_2D, texture);
-  
+
 glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, 800, 600, 0, GL_RGB, GL_UNSIGNED_BYTE, NULL);
 
 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
 ```
 
-主要的区别就是，我们将维度设置为了屏幕大小（尽管这不是必须的），并且我们给纹理的`data`参数传递了`NULL`。对于这个纹理，我们仅仅分配了内存而没有填充它。填充这个纹理将会在我们渲染到帧缓冲之后来进行。同样注意我们并不关心环绕方式或多级渐远纹理，我们在大多数情况下都不会需要它们。
+这里主要的区别是我们把纹理的维度设置为屏幕大小（尽管不是必须的），我们还传递NULL作为纹理的data参数。对于这个纹理，我们只分配内存，而不去填充它。纹理填充会在渲染到帧缓冲的时候去做。同样，要注意，我们不用关心环绕方式或者Mipmap，因为在大多数时候都不会需要它们的。
 
-!!! important
+如果你打算把整个屏幕渲染到一个或大或小的纹理上，你需要用新的纹理的尺寸作为参数再次调用`glViewport`（要在渲染到你的帧缓冲之前做好），否则只有一小部分纹理或屏幕能够绘制到纹理上。
 
-	如果你想将你的屏幕渲染到一个更小或更大的纹理上，你需要（在渲染到你的帧缓冲之前）再次调用<fun>glViewport</fun>，使用纹理的新维度作为参数，否则只有一小部分的纹理或屏幕会被渲染到这个纹理上。
-
-现在我们已经创建好一个纹理了，要做的最后一件事就是将它附加到帧缓冲上了：
+现在我们已经创建了一个纹理，最后一件要做的事情是把它附加到帧缓冲上：
 
 ```c++
-glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, texture, 0);
+glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0,GL_TEXTURE_2D, texture, 0);
 ```
 
-<fun>glFrameBufferTexture2D</fun>有以下的参数：
+`glFramebufferTexture2D`函数需要传入下列参数：
 
-- `target`：帧缓冲的目标（绘制、读取或者两者皆有）
-- `attachment`：我们想要附加的附件类型。当前我们正在附加一个颜色附件。注意最后的`0`意味着我们可以附加多个颜色附件。我们将在之后的教程中提到。
-- `textarget`：你希望附加的纹理类型
-- `texture`：要附加的纹理本身
-- `level`：多级渐远纹理的级别。我们将它保留为0。
+* target：我们所创建的帧缓冲类型的目标（绘制、读取或两者都有）。
+* attachment：我们所附加的附件的类型。现在我们附加的是一个颜色附件。需要注意，最后的那个0是暗示我们可以附加1个以上颜色的附件。我们会在后面的教程中谈到。
+* textarget：你希望附加的纹理类型。
+* texture：附加的实际纹理。
+* level：Mipmap level。我们设置为0。
 
-除了颜色附件之外，我们还可以附加一个深度和模板缓冲纹理到帧缓冲对象中。要附加深度缓冲的话，我们将附件类型设置为<var>GL_DEPTH_ATTACHMENT</var>。注意纹理的<def>格式</def>(Format)和<def>内部格式</def>(Internalformat)类型将变为<var>GL_DEPTH_COMPONENT</var>，来反映深度缓冲的储存格式。要附加模板缓冲的话，你要将第二个参数设置为<var>GL_STENCIL_ATTACHMENT</var>，并将纹理的格式设定为<var>GL_STENCIL_INDEX</var>。
+除颜色附件以外，我们还可以附加一个深度和一个模板纹理到帧缓冲对象上。为了附加一个深度缓冲，我们可以知道那个`GL_DEPTH_ATTACHMENT`作为附件类型。记住，这时纹理格式和内部格式类型（internalformat）就成了 `GL_DEPTH_COMPONENT`去反应深度缓冲的存储格式。附加一个模板缓冲，你要使用 `GL_STENCIL_ATTACHMENT`作为第二个参数，把纹理格式指定为 `GL_STENCIL_INDEX`。
 
-也可以将深度缓冲和模板缓冲附加为一个单独的纹理。纹理的每32位数值将包含24位的深度信息和8位的模板信息。要将深度和模板缓冲附加为一个纹理的话，我们使用<var>GL_DEPTH_STENCIL_ATTACHMENT</var>类型，并配置纹理的格式，让它包含合并的深度和模板值。将一个深度和模板缓冲附加为一个纹理到帧缓冲的例子可以在下面找到：
+也可以同时附加一个深度缓冲和一个模板缓冲为一个单独的纹理。这样纹理的每32位数值就包含了24位的深度信息和8位的模板信息。为了把一个深度和模板缓冲附加到一个单独纹理上，我们使用`GL_DEPTH_STENCIL_ATTACHMENT`类型配置纹理格式以包含深度值和模板值的结合物。下面是一个附加了深度和模板缓冲为单一纹理的例子：
 
 ```c++
-glTexImage2D(
-  GL_TEXTURE_2D, 0, GL_DEPTH24_STENCIL8, 800, 600, 0, 
-  GL_DEPTH_STENCIL, GL_UNSIGNED_INT_24_8, NULL
-);
+glTexImage2D( GL_TEXTURE_2D, 0, GL_DEPTH24_STENCIL8, 800, 600, 0, GL_DEPTH_STENCIL, GL_UNSIGNED_INT_24_8, NULL );
 
 glFramebufferTexture2D(GL_FRAMEBUFFER, GL_DEPTH_STENCIL_ATTACHMENT, GL_TEXTURE_2D, texture, 0);
 ```
 
-### 渲染缓冲对象附件
+### 缓冲对象附件
 
-<def>渲染缓冲对象</def>(Renderbuffer Object)是在纹理之后引入到OpenGL中，作为一个可用的帧缓冲附件类型的，所以在过去纹理是唯一可用的附件。和纹理图像一样，渲染缓冲对象是一个真正的缓冲，即一系列的字节、整数、像素等。渲染缓冲对象附加的好处是，它会将数据储存为OpenGL原生的渲染格式，它是为离屏渲染到帧缓冲优化过的。
+在介绍了帧缓冲的可行附件类型——纹理后，OpenGL引进了渲染缓冲对象(Renderbuffer objects)，所以在过去那些美好时光里纹理是附件的唯一可用的类型。和纹理图像一样，渲染缓冲对象也是一个缓冲，它可以是一堆字节、整数、像素或者其他东西。渲染缓冲对象的一大优点是，它以OpenGL原生渲染格式储存它的数据，因此在离屏渲染到帧缓冲的时候，这些数据就相当于被优化过的了。
 
-渲染缓冲对象直接将所有的渲染数据储存到它的缓冲中，不会做任何针对纹理格式的转换，让它变为一个更快的可写储存介质。然而，渲染缓冲对象通常都是只写的，所以你不能读取它们（比如使用纹理访问）。当然你仍然还是能够使用<fun>glReadPixels</fun>来读取它，这会从当前绑定的帧缓冲，而不是附件本身，中返回特定区域的像素。
+渲染缓冲对象将所有渲染数据直接储存到它们的缓冲里，而不会进行针对特定纹理格式的任何转换，这样它们就成了一种快速可写的存储介质了。然而，渲染缓冲对象通常是只写的，不能修改它们（就像获取纹理，不能写入纹理一样）。可以用`glReadPixels`函数去读取，函数返回一个当前绑定的帧缓冲的特定像素区域，而不是直接返回附件本身。
 
-因为它的数据已经是原生的格式了，当写入或者复制它的数据到其它缓冲中时是非常快的。所以，交换缓冲这样的操作在使用渲染缓冲对象时会非常快。我们在每个渲染迭代最后使用的<fun>glfwSwapBuffers</fun>，也可以通过渲染缓冲对象实现：只需要写入一个渲染缓冲图像，并在最后交换到另外一个渲染缓冲就可以了。渲染缓冲对象对这种操作非常完美。
+因为它们的数据已经是原生格式了，在写入或把它们的数据简单地到其他缓冲的时候非常快。当使用渲染缓冲对象时，像切换缓冲这种操作变得异常高速。我们在每个渲染迭代末尾使用的那个`glfwSwapBuffers`函数，同样以渲染缓冲对象实现：我们简单地写入到一个渲染缓冲图像，最后交换到另一个里。渲染缓冲对象对于这种操作来说很完美。
 
-创建一个渲染缓冲对象的代码和帧缓冲的代码很类似：
+创建一个渲染缓冲对象和创建帧缓冲代码差不多：
 
 ```c++
-unsigned int rbo;
+GLuint rbo;
 glGenRenderbuffers(1, &rbo);
 ```
 
-类似，我们需要绑定这个渲染缓冲对象，让之后所有的渲染缓冲操作影响当前的<var>rbo</var>：
+相似地，我们打算把渲染缓冲对象绑定，这样所有后续渲染缓冲操作都会影响到当前的渲染缓冲对象：
 
 ```c++
 glBindRenderbuffer(GL_RENDERBUFFER, rbo);
 ```
 
-由于渲染缓冲对象通常都是只写的，它们会经常用于深度和模板附件，因为大部分时间我们都不需要从深度和模板缓冲中读取值，只关心深度和模板测试。我们**需要**深度和模板值用于测试，但不需要对它们进行**采样**，所以渲染缓冲对象非常适合它们。当我们不需要从这些缓冲中采样的时候，通常都会选择渲染缓冲对象，因为它会更优化一点。
+由于渲染缓冲对象通常是只写的，它们经常作为深度和模板附件来使用，由于大多数时候，我们不需要从深度和模板缓冲中读取数据，但仍关心深度和模板测试。我们就需要有深度和模板值提供给测试，但不需要对这些值进行采样（sample），所以深度缓冲对象是完全符合的。当我们不去从这些缓冲中采样的时候，渲染缓冲对象通常很合适，因为它们等于是被优化过的。
 
-创建一个深度和模板渲染缓冲对象可以通过调用<fun>glRenderbufferStorage</fun>函数来完成：
+调用`glRenderbufferStorage`函数可以创建一个深度和模板渲染缓冲对象：
 
-```c++
+```c
 glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH24_STENCIL8, 800, 600);
 ```
 
-创建一个渲染缓冲对象和纹理对象类似，不同的是这个对象是专门被设计作为帧缓冲附件使用的，而不是纹理那样的通用数据缓冲(General Purpose Data Buffer)。这里我们选择<var>GL_DEPTH24_STENCIL8</var>作为内部格式，它封装了24位的深度和8位的模板缓冲。
+创建一个渲染缓冲对象与创建纹理对象相似，不同之处在于这个对象是专门被设计用于图像的，而不是通用目的的数据缓冲，比如纹理。这里我们选择`GL_DEPTH24_STENCIL8`作为内部格式，它同时代表24位的深度和8位的模板缓冲。
 
-最后一件事就是附加这个渲染缓冲对象：
+最后一件还要做的事情是把帧缓冲对象附加上：
 
-```c++
+```c
 glFramebufferRenderbuffer(GL_FRAMEBUFFER, GL_DEPTH_STENCIL_ATTACHMENT, GL_RENDERBUFFER, rbo);
 ```
 
-渲染缓冲对象能为你的帧缓冲对象提供一些优化，但知道什么时候使用渲染缓冲对象，什么时候使用纹理是很重要的。通常的规则是，如果你不需要从一个缓冲中采样数据，那么对这个缓冲使用渲染缓冲对象会是明智的选择。如果你需要从缓冲中采样颜色或深度值等数据，那么你应该选择纹理附件。性能方面它不会产生非常大的影响的。
+在帧缓冲项目中，渲染缓冲对象可以提供一些优化，但更重要的是知道何时使用渲染缓冲对象，何时使用纹理。通常的规则是，如果你永远都不需要从特定的缓冲中进行采样，渲染缓冲对象对特定缓冲是更明智的选择。如果哪天需要从比如颜色或深度值这样的特定缓冲采样数据的话，你最好还是使用纹理附件。从执行效率角度考虑，它不会对效率有太大影响。
 
-## 渲染到纹理
+### 渲染到纹理
 
-既然我们已经知道帧缓冲（大概）是怎么工作的了，是时候实践它们了。我们将会将场景渲染到一个附加到帧缓冲对象上的颜色纹理中，之后将在一个横跨整个屏幕的四边形上绘制这个纹理。这样视觉输出和没使用帧缓冲时是完全一样的，但这次是打印到了一个四边形上。这为什么很有用呢？我们会在下一部分中知道原因。
+现在我们知道了（一些）帧缓冲如何工作的，是时候把它们用起来了。我们会把场景渲染到一个颜色纹理上，这个纹理附加到一个我们创建的帧缓冲上，然后把纹理绘制到一个简单的四边形上，这个四边形铺满整个屏幕。输出的图像看似和没用帧缓冲一样，但是这次，它其实是直接打印到了一个单独的四边形上面。为什么这很有用呢？下一部分我们会看到原因。
 
-首先要创建一个帧缓冲对象，并绑定它，这些都很直观：
+第一件要做的事情是创建一个帧缓冲对象，并绑定它，这比较明了：
 
 ```c++
-unsigned int framebuffer;
+GLuint framebuffer;
 glGenFramebuffers(1, &framebuffer);
 glBindFramebuffer(GL_FRAMEBUFFER, framebuffer);
 ```
 
-接下来我们需要创建一个纹理图像，我们将它作为一个颜色附件附加到帧缓冲上。我们将纹理的维度设置为窗口的宽度和高度，并且不初始化它的数据：
+下一步我们创建一个纹理图像，这是我们将要附加到帧缓冲的颜色附件。我们把纹理的尺寸设置为窗口的宽度和高度，并保持数据未初始化：
 
 ```c++
-// 生成纹理
-unsigned int texColorBuffer;
+// Generate texture
+GLuint texColorBuffer;
 glGenTextures(1, &texColorBuffer);
 glBindTexture(GL_TEXTURE_2D, texColorBuffer);
 glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, 800, 600, 0, GL_RGB, GL_UNSIGNED_BYTE, NULL);
@@ -172,200 +167,196 @@ glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR );
 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
 glBindTexture(GL_TEXTURE_2D, 0);
 
-// 将它附加到当前绑定的帧缓冲对象
-glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, texColorBuffer, 0);  
+// Attach it to currently bound framebuffer object
+glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, texColorBuffer, 0);
 ```
 
-我们还希望OpenGL能够进行深度测试（如果你需要的话还有模板测试），所以我们还需要添加一个深度（和模板）附件到帧缓冲中。由于我们只希望采样颜色缓冲，而不是其它的缓冲，我们可以为它们创建一个渲染缓冲对象。还记得当我们不需要采样缓冲的时候，渲染缓冲对象是更好的选择吗？
+我们同样打算要让OpenGL确定可以进行深度测试（模板测试，如果你用的话）所以我们必须还要确保向帧缓冲中添加一个深度（和模板）附件。由于我们只采样颜色缓冲，并不采样其他缓冲，我们可以创建一个渲染缓冲对象来达到这个目的。记住，当你不打算从指定缓冲采样的的时候，它们是一个不错的选择。
 
-创建一个渲染缓冲对象不是非常复杂。我们需要记住的唯一事情是，我们将它创建为一个深度**和**模板附件渲染缓冲对象。我们将它的**内部**格式设置为<var>GL_DEPTH24_STENCIL8</var>，对我们来说这个精度已经足够了。
+创建一个渲染缓冲对象不太难。唯一一件要记住的事情是，我们正在创建的是一个渲染缓冲对象的深度和模板附件。我们把它的内部给事设置为`GL_DEPTH24_STENCIL8`，对于我们的目的来说这个精确度已经足够了。
 
 ```c++
-unsigned int rbo;
+GLuint rbo;
 glGenRenderbuffers(1, &rbo);
-glBindRenderbuffer(GL_RENDERBUFFER, rbo); 
+glBindRenderbuffer(GL_RENDERBUFFER, rbo);
 glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH24_STENCIL8, 800, 600);  
 glBindRenderbuffer(GL_RENDERBUFFER, 0);
 ```
 
-当我们为渲染缓冲对象分配了足够的内存之后，我们可以解绑这个渲染缓冲。
+我们为渲染缓冲对象分配了足够的内存空间以后，我们可以解绑渲染缓冲。
 
-接下来，作为完成帧缓冲之前的最后一步，我们将渲染缓冲对象附加到帧缓冲的深度**和**模板附件上：
+接着，在做好帧缓冲之前，还有最后一步，我们把渲染缓冲对象附加到帧缓冲的深度和模板附件上：
 
 ```c++
 glFramebufferRenderbuffer(GL_FRAMEBUFFER, GL_DEPTH_STENCIL_ATTACHMENT, GL_RENDERBUFFER, rbo);
 ```
 
-最后，我们希望检查帧缓冲是否是完整的，如果不是，我们将打印错误信息。
+然后我们要检查帧缓冲是否真的做好了，如果没有，我们就打印一个错误消息。
 
 ```c++
 if(glCheckFramebufferStatus(GL_FRAMEBUFFER) != GL_FRAMEBUFFER_COMPLETE)
-	std::cout << "ERROR::FRAMEBUFFER:: Framebuffer is not complete!" << std::endl;
+ cout << "ERROR::FRAMEBUFFER:: Framebuffer is not complete!" << endl;
 glBindFramebuffer(GL_FRAMEBUFFER, 0);
 ```
 
-记得要解绑帧缓冲，保证我们不会不小心渲染到错误的帧缓冲上。
+还要保证解绑帧缓冲，这样我们才不会意外渲染到错误的帧缓冲上。
 
-现在这个帧缓冲就完整了，我们只需要绑定这个帧缓冲对象，让渲染到帧缓冲的缓冲中而不是默认的帧缓冲中。之后的渲染指令将会影响当前绑定的帧缓冲。所有的深度和模板操作都会从当前绑定的帧缓冲的深度和模板附件中（如果有的话）读取。如果你忽略了深度缓冲，那么所有的深度测试操作将不再工作，因为当前绑定的帧缓冲中不存在深度缓冲。
+现在帧缓冲做好了，我们要做的全部就是渲染到帧缓冲上，而不是绑定到帧缓冲对象的默认缓冲。余下所有命令会影响到当前绑定的帧缓冲上。所有深度和模板操作同样会从当前绑定的帧缓冲的深度和模板附件中读取，当然，得是在它们可用的情况下。如果你遗漏了比如深度缓冲，所有深度测试就不会工作，因为当前绑定的帧缓冲里没有深度缓冲。
 
-所以，要想绘制场景到一个纹理上，我们需要采取以下的步骤：
+所以，为把场景绘制到一个单独的纹理，我们必须以下面步骤来做：
 
-1. 将新的帧缓冲绑定为激活的帧缓冲，和往常一样渲染场景
-2. 绑定默认的帧缓冲
-3. 绘制一个横跨整个屏幕的四边形，将帧缓冲的颜色缓冲作为它的纹理。
+1. 使用新的绑定为激活帧缓冲的帧缓冲，像往常那样渲染场景。
+2. 绑定到默认帧缓冲。
+3. 绘制一个四边形，让它平铺到整个屏幕上，用新的帧缓冲的颜色缓冲作为他的纹理。
 
-我们将会绘制[深度测试](01 Depth testing.md)小节中的场景，但这次使用的是旧的[箱子](../img/04/05/container.jpg)纹理。
+我们使用在深度测试教程中同一个场景进行绘制，但是这次使用老气横秋的[箱子纹理](http://learnopengl.com/img/textures/container.jpg)。
 
-为了绘制这个四边形，我们将会新创建一套简单的着色器。我们将不会包含任何花哨的矩阵变换，因为我们提供的是标准化设备坐标的[顶点坐标](https://learnopengl.com/code_viewer.php?code=advanced/framebuffers_quad_vertices)，所以我们可以直接将它们设定为顶点着色器的输出。顶点着色器是这样的：
+为了绘制四边形我们将会创建新的着色器。我们不打算引入任何花哨的变换矩阵，因为我们只提供已经是标准化设备坐标的[顶点坐标](http://learnopengl.com/code_viewer.php?code=advanced/framebuffers_quad_vertices)，所以我们可以直接把它们作为顶点着色器的输出。顶点着色器看起来像这样：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec2 aPos;
-layout (location = 1) in vec2 aTexCoords;
+layout (location = 0) in vec2 position;
+layout (location = 1) in vec2 texCoords;
 
 out vec2 TexCoords;
 
 void main()
 {
-    gl_Position = vec4(aPos.x, aPos.y, 0.0, 1.0); 
-    TexCoords = aTexCoords;
+    gl_Position = vec4(position.x, position.y, 0.0f, 1.0f);
+    TexCoords = texCoords;
 }
 ```
 
-并没有太复杂的东西。片段着色器会更加基础，我们做的唯一一件事就是从纹理中采样：
+没有花哨的地方。片段着色器更简洁，因为我们做的唯一一件事是从纹理采样：
 
 ```c++
 #version 330 core
-out vec4 FragColor;
-  
 in vec2 TexCoords;
+out vec4 color;
 
 uniform sampler2D screenTexture;
 
 void main()
-{ 
-    FragColor = texture(screenTexture, TexCoords);
+{
+    color = texture(screenTexture, TexCoords);
 }
 ```
 
-接着就靠你来为屏幕四边形创建并配置一个VAO了。帧缓冲的一个渲染迭代将会有以下的结构：
+接着需要你为屏幕上的四边形创建和配置一个VAO。渲染迭代中帧缓冲处理会有下面的结构：
 
 ```c++
-// 第一处理阶段(Pass)
+// First pass
 glBindFramebuffer(GL_FRAMEBUFFER, framebuffer);
 glClearColor(0.1f, 0.1f, 0.1f, 1.0f);
-glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // 我们现在不使用模板缓冲
+glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // We're not using stencil buffer now
 glEnable(GL_DEPTH_TEST);
-DrawScene();	
-  
-// 第二处理阶段
-glBindFramebuffer(GL_FRAMEBUFFER, 0); // 返回默认
-glClearColor(1.0f, 1.0f, 1.0f, 1.0f); 
+DrawScene();
+
+// Second pass
+glBindFramebuffer(GL_FRAMEBUFFER, 0); // back to default
+glClearColor(1.0f, 1.0f, 1.0f, 1.0f);
 glClear(GL_COLOR_BUFFER_BIT);
-  
-screenShader.use();  
+
+screenShader.Use();  
 glBindVertexArray(quadVAO);
 glDisable(GL_DEPTH_TEST);
 glBindTexture(GL_TEXTURE_2D, textureColorbuffer);
-glDrawArrays(GL_TRIANGLES, 0, 6);  
+glDrawArrays(GL_TRIANGLES, 0, 6);
+glBindVertexArray(0);
 ```
 
-要注意一些事情。第一，由于我们使用的每个帧缓冲都有它自己一套缓冲，我们希望设置合适的位，调用<fun>glClear</fun>，清除这些缓冲。第二，当绘制四边形时，我们将禁用深度测试，因为我们是在绘制一个简单的四边形，并不需要关系深度测试。在绘制普通场景的时候我们将会重新启用深度测试。
+只有很少的事情要说明。第一，由于我们用的每个帧缓冲都有自己的一系列缓冲，我们打算使用`glClear`设置的合适的位（bits）来清空这些缓冲。第二，当渲染四边形的时候，我们关闭深度测试，因为我们不关系深度测试，我们绘制的是一个简单的四边形；当我们绘制普通场景时我们必须再次开启深度测试。
 
-有很多步骤都可能会出错，所以如果你没有得到输出的话，尝试调试程序，并重新阅读本节的相关部分。如果所有的东西都能够正常工作，你将会得到下面这样的视觉输出：
+这里的确有很多地方会做错，所以如果你没有获得任何输出，尝试排查任何可能出现错误的地方，再次阅读教程中相关章节。如果每件事都做对了就一定能成功，你将会得到这样的输出：
 
-![](../img/04/05/framebuffers_screen_texture.png)
+![](http://learnopengl.com/img/advanced/framebuffers_screen_texture.png)
 
-左边展示的是视觉输出，它和[深度测试](01 Depth testing.md)中是完全一样的，但这次是渲染在一个简单的四边形上。如果我们使用线框模式渲染场景，就会变得很明显，我们在默认的帧缓冲中只绘制了一个简单的四边形。
+左侧展示了和深度测试教程中一样的输出结果，但是这次却是渲染到一个简单的四边形上的。如果我们以线框方式显示的话，那么显然，我们只是绘制了一个默认帧缓冲中单调的四边形。
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/5.1.framebuffers/framebuffers.cpp)找到程序的源代码。
+你可以[从这里得到应用的源码](http://learnopengl.com/code_viewer.php?code=advanced/framebuffers_screen_texture)。
+
+然而这有什么好处呢？好处就是我们现在可以自由的获取已经渲染场景中的任何像素，然后把它当作一个纹理图像了，我们可以在片段着色器中创建一些有意思的效果。所有这些有意思的效果统称为后处理特效。
 
-所以这个有什么用处呢？因为我们能够以一个纹理图像的方式访问已渲染场景中的每个像素，我们可以在片段着色器中创建出非常有趣的效果。这些有趣效果统称为<def>后期处理</def>(Post-processing)效果。
 
 # 后期处理
 
-既然整个场景都被渲染到了一个纹理上，我们可以简单地通过修改纹理数据创建出一些非常有意思的效果。在这一部分中，我们将会向你展示一些流行的后期处理效果，并告诉你改如何使用创造力创建你自己的效果。
-
-让我们先从最简单的后期处理效果开始。
+现在，整个场景渲染到了一个单独的纹理上，我们可以创建一些有趣的效果，只要简单操纵纹理数据就能做到。这部分，我们会向你展示一些流行的后期处理(Post-processing)特效，以及怎样添加一些创造性去创建出你自己的特效。
 
 ### 反相
 
-我们现在能够访问渲染输出的每个颜色，所以在（译注：屏幕的）片段着色器中返回这些颜色的反相(Inversion)并不是很难。我们将会从屏幕纹理中取颜色值，然后用1.0减去它，对它进行反相：
+我们已经取得了渲染输出的每个颜色，所以在片段着色器里返回这些颜色的反色(Inversion)并不难。我们得到屏幕纹理的颜色，然后用1.0减去它：
 
 ```c++
 void main()
 {
-    FragColor = vec4(vec3(1.0 - texture(screenTexture, TexCoords)), 1.0);
+    color = vec4(vec3(1.0 - texture(screenTexture, TexCoords)), 1.0);
 }
 ```
 
-尽管反相是一个相对简单的后期处理效果，它已经能创造一些奇怪的效果了：
+虽然反相是一种相对简单的后处理特效，但是已经很有趣了：
 
-![](../img/04/05/framebuffers_inverse.png)
+![image description](http://learnopengl.com/img/advanced/framebuffers_grayscale.png)
 
-在片段着色器中仅仅使用一行代码，就能让整个场景的颜色都反相了。很酷吧？
+整个场景现在的颜色都反转了，只需在着色器中写一行代码就能做到，酷吧？
 
 ### 灰度
 
-另外一个很有趣的效果是，移除场景中除了黑白灰以外所有的颜色，让整个图像灰度化(Grayscale)。很简单的实现方式是，取所有的颜色分量，将它们平均化：
+另一个有意思的效果是移除所有除了黑白灰以外的颜色作用，是整个图像成为黑白的。实现它的简单的方式是获得所有颜色元素，然后将它们平均化：
 
 ```c++
 void main()
 {
-    FragColor = texture(screenTexture, TexCoords);
-    float average = (FragColor.r + FragColor.g + FragColor.b) / 3.0;
-    FragColor = vec4(average, average, average, 1.0);
+    color = texture(screenTexture, TexCoords);
+    float average = (color.r + color.g + color.b) / 3.0;
+    color = vec4(average, average, average, 1.0);
 }
 ```
-
-这已经能创造很好的结果了，但人眼会对绿色更加敏感一些，而对蓝色不那么敏感，所以为了获取物理上更精确的效果，我们需要使用加权的(Weighted)通道：
+这已经创造出很赞的效果了，但是人眼趋向于对绿色更敏感，对蓝色感知比较弱，所以为了获得更精确的符合人体物理的结果，我们需要使用加权通道：
 
 ```c++
 void main()
 {
-    FragColor = texture(screenTexture, TexCoords);
-    float average = 0.2126 * FragColor.r + 0.7152 * FragColor.g + 0.0722 * FragColor.b;
-    FragColor = vec4(average, average, average, 1.0);
+    color = texture(screenTexture, TexCoords);
+    float average = 0.2126 * color.r + 0.7152 * color.g + 0.0722 * color.b;
+    color = vec4(average, average, average, 1.0);
 }
 ```
 
-![](../img/04/05/framebuffers_grayscale.png)
+![](http://learnopengl.com/img/advanced/framebuffers_grayscale.png)
 
-你可能不会立刻发现有什么差别，但在更复杂的场景中，这样的加权灰度效果会更真实一点。
+## Kernel effects
 
-## 核效果
+在单独纹理图像上进行后处理的另一个好处是我们可以从纹理的其他部分进行采样。比如我们可以从当前纹理值的周围采样多个纹理值。创造性地把它们结合起来就能创造出有趣的效果了。
 
-在一个纹理图像上做后期处理的另外一个好处是，我们可以从纹理的其它地方采样颜色值。比如说我们可以在当前纹理坐标的周围取一小块区域，对当前纹理值周围的多个纹理值进行采样。我们可以结合它们创建出很有意思的效果。
-
-<def>核</def>(Kernel)（或卷积矩阵(Convolution Matrix)）是一个类矩阵的数值数组，它的中心为当前的像素，它会用它的核值乘以周围的像素值，并将结果相加变成一个值。所以，基本上我们是在对当前像素周围的纹理坐标添加一个小的偏移量，并根据核将结果合并。下面是核的一个例子：
+kernel是一个长得有点像一个小矩阵的数值数组，它中间的值中心可以映射到一个像素上，这个像素和这个像素周围的值再乘以kernel，最后再把结果相加就能得到一个值。所以，我们基本上就是给当前纹理坐标加上一个它四周的偏移量，然后基于kernel把它们结合起来。下面是一个kernel的例子：
 
 $$
 \begin{bmatrix}2 & 2 & 2 \\ 2 & -15 & 2 \\ 2 & 2 & 2 \end{bmatrix}
 $$
 
-这个核取了8个周围像素值，将它们乘以2，而把当前的像素乘以-15。这个核的例子将周围的像素乘上了一个权重，并将当前像素乘以一个比较大的负权重来平衡结果。
+这个kernel表示一个像素周围八个像素乘以2，它自己乘以-15。这个例子基本上就是把周围像素乘上2，中间像素去乘以一个比较大的负数来进行平衡。
 
 !!! Important
 
-	你在网上找到的大部分核将所有的权重加起来之后都应该会等于1，如果它们加起来不等于1，这就意味着最终的纹理颜色将会比原纹理值更亮或者更暗了。
+    你在网上能找到的kernel的例子大多数都是所有值加起来等于1，如果加起来不等于1就意味着这个纹理值比原来更大或者更小了。
 
-核是后期处理一个非常有用的工具，它们使用和实验起来都很简单，网上也能找到很多例子。我们需要稍微修改一下片段着色器，让它能够支持核。我们假设使用的核都是3x3核（实际上大部分核都是）：
+kernel对于后处理来说非常管用，因为用起来简单。网上能找到有很多实例，为了能用上kernel我们还得改改片段着色器。这里假设每个kernel都是3×3（实际上大多数都是3×3）：
 
 ```c++
-const float offset = 1.0 / 300.0;  
+const float offset = 1.0 / 300;  
 
 void main()
 {
     vec2 offsets[9] = vec2[](
-        vec2(-offset,  offset), // 左上
-        vec2( 0.0f,    offset), // 正上
-        vec2( offset,  offset), // 右上
-        vec2(-offset,  0.0f),   // 左
-        vec2( 0.0f,    0.0f),   // 中
-        vec2( offset,  0.0f),   // 右
-        vec2(-offset, -offset), // 左下
-        vec2( 0.0f,   -offset), // 正下
-        vec2( offset, -offset)  // 右下
+        vec2(-offset, offset),  // top-left
+        vec2(0.0f,    offset),  // top-center
+        vec2(offset,  offset),  // top-right
+        vec2(-offset, 0.0f),    // center-left
+        vec2(0.0f,    0.0f),    // center-center
+        vec2(offset,  0.0f),    // center-right
+        vec2(-offset, -offset), // bottom-left
+        vec2(0.0f,    -offset), // bottom-center
+        vec2(offset,  -offset)  // bottom-right
     );
 
     float kernel[9] = float[](
@@ -373,37 +364,37 @@ void main()
         -1,  9, -1,
         -1, -1, -1
     );
-    
+
     vec3 sampleTex[9];
     for(int i = 0; i < 9; i++)
     {
         sampleTex[i] = vec3(texture(screenTexture, TexCoords.st + offsets[i]));
     }
-    vec3 col = vec3(0.0);
+    vec3 col;
     for(int i = 0; i < 9; i++)
         col += sampleTex[i] * kernel[i];
-    
-    FragColor = vec4(col, 1.0);
+
+    color = vec4(col, 1.0);
 }
 ```
 
-在片段着色器中，我们首先为周围的纹理坐标创建了一个9个`vec2`偏移量的数组。偏移量是一个常量，你可以按照你的喜好自定义它。之后我们定义一个核，在这个例子中是一个<def>锐化</def>(Sharpen)核，它会采样周围的所有像素，锐化每个颜色值。最后，在采样时我们将每个偏移量加到当前纹理坐标上，获取需要采样的纹理，之后将这些纹理值乘以加权的核值，并将它们加到一起。
+在片段着色器中我们先为每个四周的纹理坐标创建一个9个vec2偏移量的数组。偏移量是一个简单的常数，你可以设置为自己喜欢的。接着我们定义kernel，这里应该是一个锐化kernel，它通过一种有趣的方式从所有周边的像素采样，对每个颜色值进行锐化。最后，在采样的时候我们把每个偏移量加到当前纹理坐标上，然后用加在一起的kernel的值乘以这些纹理值。
 
-这个锐化核看起来是这样的：
+这个锐化的kernel看起来像这样：
 
-![](../img/04/05/framebuffers_sharpen.png)
+![](http://learnopengl.com/img/advanced/framebuffers_sharpen.png)
 
-这能创建一些很有趣的效果，比如说你的玩家打了麻醉剂所感受到的效果。
+这里创建的有趣的效果就好像你的玩家吞了某种麻醉剂产生的幻觉一样。
 
 ### 模糊
 
-创建<def>模糊</def>(Blur)效果的核是这样的：
+创建模糊(Blur)效果的kernel定义如下：
 
 $$
-\begin{bmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{bmatrix} / 16
+\(\begin{bmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{bmatrix} / 16\)
 $$
 
-由于所有值的和是16，所以直接返回合并的采样颜色将产生非常亮的颜色，所以我们需要将核的每个值都除以16。最终的核数组将会是：
+由于所有数值加起来的总和为16,简单返回结合起来的采样颜色是非常亮的,所以我们必须将kernel的每个值除以16.最终的kernel数组会是这样的:
 
 ```c++
 float kernel[9] = float[](
@@ -413,33 +404,29 @@ float kernel[9] = float[](
 );
 ```
 
-通过在片段着色器中改变核的<fun>float</fun>数组，我们完全改变了后期处理效果。它现在看起来是这样子的：
+通过在像素着色器中改变kernel的float数组,我们就完全改变了之后的后处理效果.现在看起来会像是这样:
 
-![](../img/04/05/framebuffers_blur.png)
+![](http://learnopengl.com/img/advanced/framebuffers_blur.png)
 
-这样的模糊效果创造了很多的可能性。我们可以随着时间修改模糊的量，创造出玩家醉酒时的效果，或者在主角没带眼镜的时候增加模糊。模糊也能够让我们来平滑颜色值，我们将在之后教程中使用到。
+这样的模糊效果具有创建许多有趣效果的潜力.例如,我们可以随着时间的变化改变模糊量,创建出类似于某人喝醉酒的效果,或者,当我们的主角摘掉眼镜的时候增加模糊.模糊也能为我们在后面的教程中提供都颜色值进行平滑处理的能力.
 
-你可以看到，只要我们有了这个核的实现，创建炫酷的后期处理特效是非常容易的事。我们再来看最后一个很流行的效果来结束本节的讨论。
+你可以看到我们一旦拥有了这个kernel的实现以后,创建一个后处理特效就不再是一件难事.最后,我们再来讨论一个流行的特效,以结束本节内容.
 
-### 边缘检测
+### 边检测
 
-下面的<def>边缘检测</def>(Edge-detection)核和锐化核非常相似：
+下面的边检测(Edge-detection)kernel与锐化kernel类似:
 
 $$
 \begin{bmatrix} 1 & 1 & 1 \\ 1 & -8 & 1 \\ 1 & 1 & 1 \end{bmatrix}
 $$
 
-这个核高亮了所有的边缘，而暗化了其它部分，在我们只关心图像的边角的时候是非常有用的。
+这个kernel将所有的边提高亮度,而对其他部分进行暗化处理,当我们值关心一副图像的边缘的时候,它非常有用.
 
-![](../img/04/05/framebuffers_edge_detection.png)
+![](http://learnopengl.com/img/advanced/framebuffers_edge_detection.png)
 
-你可能不会奇怪，像是Photoshop这样的图像修改工具/滤镜使用的也是这样的核。因为显卡处理片段的时候有着极强的并行处理能力，我们可以很轻松地在实时的情况下逐像素对图像进行处理。所以图像编辑工具在图像处理的时候会更倾向于使用显卡。
-
-!!! note "译注"
-
-	注意，核在对屏幕纹理的边缘进行采样的时候，由于还会对中心像素周围的8个像素进行采样，其实会取到纹理之外的像素。由于环绕方式默认是<var>GL_REPEAT</var>，所以在没有设置的情况下取到的是屏幕另一边的像素，而另一边的像素本不应该对中心像素产生影响，这就可能会在屏幕边缘产生很奇怪的条纹。为了消除这一问题，我们可以将屏幕纹理的环绕方式都设置为<var>GL_CLAMP_TO_EDGE</var>。这样子在取到纹理外的像素时，就能够重复边缘的像素来更精确地估计最终的值了。
+在一些像Photoshop这样的软件中使用这些kernel作为图像操作工具/过滤器一点都不奇怪.因为掀开可以具有很强的平行处理能力，我们以实时进行针对每个像素的图像操作便相对容易，图像编辑工具因而更经常使用显卡来进行图像处理。
 
 ## 练习
 
-- 你能使用framebuffers创建一个后视镜吗?为此，你必须绘制两次场景:一次将相机旋转180度，另一次将相机正常旋转。试着在屏幕顶部创建一个小的四边形来应用镜像纹理，就像[这样](https://learnopengl.com/img/advanced/framebuffers_mirror.png);[解决方案](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/5.2.framebuffers_exercise1/framebuffers_exercise1.cpp)。
-- 摆弄内核值并创建您自己感兴趣的后处理效果。尝试在互联网上搜索其他有趣的内核。
+* 你可以使用帧缓冲来创建一个后视镜吗?做到它,你必须绘制场景两次:一次正常绘制,另一次摄像机旋转180度后绘制.尝试在你的显示器顶端创建一个小四边形,在上面应用后视镜的镜面纹理:[解决方案](http://learnopengl.com/code_viewer.php?code=advanced/framebuffers-exercise1),[视觉效果](http://learnopengl.com/img/advanced/framebuffers_mirror.png)
+* 自己随意调整一下kernel值,创建出你自己后处理特效.尝试在网上搜索其他有趣的kernel.

docs/04 Advanced OpenGL/06 Cubemaps.md

@@ -3,62 +3,65 @@
 原文     | [Cubemaps](http://learnopengl.com/#!Advanced-OpenGL/Cubemaps)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | 暂未校对
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com)
 
-我们已经使用2D纹理很长时间了，但除此之外仍有更多的纹理类型等着我们探索。在本节中，我们将讨论的是将多个纹理组合起来映射到一张纹理上的一种纹理类型：<def>立方体贴图</def>(Cube Map)。
+我们之前一直使用的是2D纹理，还有更多的纹理类型我们没有探索过，本教程中我们讨论的纹理类型是将多个纹理组合起来映射到一个单一纹理，它就是**立方体贴图(Cube Map)**。
 
-简单来说，立方体贴图就是一个包含了6个2D纹理的纹理，每个2D纹理都组成了立方体的一个面：一个有纹理的立方体。你可能会奇怪，这样一个立方体有什么用途呢？为什么要把6张纹理合并到一张纹理中，而不是直接使用6个单独的纹理呢？立方体贴图有一个非常有用的特性，它可以通过一个方向向量来进行索引/采样。假设我们有一个1x1x1的单位立方体，方向向量的原点位于它的中心。使用一个橘黄色的方向向量来从立方体贴图上采样一个纹理值会像是这样：
+基本上说立方体贴图它包含6个2D纹理，这每个2D纹理是一个立方体（cube）的一个面，也就是说它是一个有贴图的立方体。你可能会奇怪这样的立方体有什么用？为什么费事地把6个独立纹理结合为一个单独的纹理，只使用6个各自独立的不行吗？这是因为立方体贴图有自己特有的属性，可以使用方向向量对它们索引和采样。想象一下，我们有一个1×1×1的单位立方体，有个以原点为起点的方向向量在它的中心。
 
-![](../img/04/06/cubemaps_sampling.png)
+从立方体贴图上使用橘黄色向量采样一个纹理值看起来和下图有点像：
+
+![](http://learnopengl.com/img/advanced/cubemaps_sampling.png)
 
 !!! Important
 
-	方向向量的大小并不重要，只要提供了方向，OpenGL就会获取方向向量（最终）所击中的纹素，并返回对应的采样纹理值。
+        方向向量的大小无关紧要。一旦提供了方向，OpenGL就会获取方向向量触碰到立方体表面上的相应的纹理像素（texel），这样就返回了正确的纹理采样值。
 
-如果我们假设将这样的立方体贴图应用到一个立方体上，采样立方体贴图所使用的方向向量将和立方体（插值的）顶点位置非常相像。这样子，只要立方体的中心位于原点，我们就能使用立方体的实际位置向量来对立方体贴图进行采样了。接下来，我们可以将所有顶点的纹理坐标当做是立方体的顶点位置。最终得到的结果就是可以访问立方体贴图上正确<def>面</def>(Face)纹理的一个纹理坐标。
 
-## 创建立方体贴图
+方向向量触碰到立方体表面的一点也就是立方体贴图的纹理位置，这意味着只要立方体的中心位于原点上，我们就可以使用立方体的位置向量来对立方体贴图进行采样。然后我们就可以获取所有顶点的纹理坐标，就和立方体上的顶点位置一样。所获得的结果是一个纹理坐标，通过这个纹理坐标就能获取到立方体贴图上正确的纹理。
 
-立方体贴图是和其它纹理一样的，所以如果想创建一个立方体贴图的话，我们需要生成一个纹理，并将其绑定到纹理目标上，之后再做其它的纹理操作。这次要绑定到<var>GL_TEXTURE_CUBE_MAP</var>：
+## 创建一个立方体贴图
+
+立方体贴图和其他纹理一样，所以要创建一个立方体贴图，在进行任何纹理操作之前，需要生成一个纹理，激活相应纹理单元然后绑定到合适的纹理目标上。这次要绑定到 `GL_TEXTURE_CUBE_MAP`纹理类型：
 
 ```c++
-unsigned int textureID;
+GLuint textureID;
 glGenTextures(1, &textureID);
 glBindTexture(GL_TEXTURE_CUBE_MAP, textureID);
 ```
 
-因为立方体贴图包含有6个纹理，每个面一个，我们需要调用<fun>glTexImage2D</fun>函数6次，参数和之前教程中很类似。但这一次我们将纹理目标(**target**)参数设置为立方体贴图的一个特定的面，告诉OpenGL我们在对立方体贴图的哪一个面创建纹理。这就意味着我们需要对立方体贴图的每一个面都调用一次<fun>glTexImage2D</fun>。
+由于立方体贴图包含6个纹理，立方体的每个面一个纹理，我们必须调用`glTexImage2D`函数6次，函数的参数和前面教程讲的相似。然而这次我们必须把纹理目标（target）参数设置为立方体贴图特定的面，这是告诉OpenGL我们创建的纹理是对应立方体哪个面的。因此我们便需要为立方体贴图的每个面调用一次 `glTexImage2D`。
 
-由于我们有6个面，OpenGL给我们提供了6个特殊的纹理目标，专门对应立方体贴图的一个面。
+由于立方体贴图有6个面，OpenGL就提供了6个不同的纹理目标，来应对立方体贴图的各个面。
 
-纹理目标	   | 方位
-        ---|---
-`GL_TEXTURE_CUBE_MAP_POSITIVE_X` |	右
-`GL_TEXTURE_CUBE_MAP_NEGATIVE_X` |	左
-`GL_TEXTURE_CUBE_MAP_POSITIVE_Y` |	上
-`GL_TEXTURE_CUBE_MAP_NEGATIVE_Y` |	下
-`GL_TEXTURE_CUBE_MAP_POSITIVE_Z` |	后
-`GL_TEXTURE_CUBE_MAP_NEGATIVE_Z` |	前
+纹理目标（Texture target）	   | 方位
+                            ---|---
+GL_TEXTURE_CUBE_MAP_POSITIVE_X |	右
+GL_TEXTURE_CUBE_MAP_NEGATIVE_X |	左
+GL_TEXTURE_CUBE_MAP_POSITIVE_Y |	上
+GL_TEXTURE_CUBE_MAP_NEGATIVE_Y |	下
+GL_TEXTURE_CUBE_MAP_POSITIVE_Z |	后
+GL_TEXTURE_CUBE_MAP_NEGATIVE_Z |	前
 
-和OpenGL的很多枚举(Enum)一样，它们背后的<fun>int</fun>值是线性递增的，所以如果我们有一个纹理位置的数组或者vector，我们就可以从<var>GL_TEXTURE_CUBE_MAP_POSITIVE_X</var>开始遍历它们，在每个迭代中对枚举值加1，遍历了整个纹理目标：
+和很多OpenGL其他枚举一样，对应的int值都是连续增加的，所以我们有一个纹理位置的数组或vector，就能以 `GL_TEXTURE_CUBE_MAP_POSITIVE_X`为起始来对它们进行遍历，每次迭代枚举值加 `1`，这样循环所有的纹理目标效率较高：
 
 ```c++
-int width, height, nrChannels;
-unsigned char *data;  
-for(unsigned int i = 0; i < textures_faces.size(); i++)
+int width,height;
+unsigned char* image;  
+for(GLuint i = 0; i < textures_faces.size(); i++)
 {
-    data = stbi_load(textures_faces[i].c_str(), &width, &height, &nrChannels, 0);
+    image = SOIL_load_image(textures_faces[i], &width, &height, 0, SOIL_LOAD_RGB);
     glTexImage2D(
-        GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 
-        0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data
+        GL_TEXTURE_CUBE_MAP_POSITIVE_X + i,
+        0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, image
     );
 }
 ```
 
-这里我们有一个叫做<var>textures_faces</var>的<fun>vector</fun>，它包含了立方体贴图所需的所有纹理路径，并以表中的顺序排列。这将为当前绑定的立方体贴图中的每个面生成一个纹理。
+这儿我们有个vector叫`textures_faces`，它包含立方体贴图所各个纹理的文件路径，并且以上表所列的顺序排列。它将为每个当前绑定的cubemp的每个面生成一个纹理。
 
-因为立方体贴图和其它纹理没什么不同，我们也需要设定它的环绕和过滤方式：
+由于立方体贴图和其他纹理没什么不同，我们也要定义它的环绕方式和过滤方式：
 
 ```c++
 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
@@ -68,109 +71,105 @@ glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
 ```
 
-不要被<var>GL_TEXTURE_WRAP_R</var>吓到，它仅仅是为纹理的**R**坐标设置了环绕方式，它对应的是纹理的第三个维度（和位置的**z**一样）。我们将环绕方式设置为<var>GL_CLAMP_TO_EDGE</var>，这是因为正好处于两个面之间的纹理坐标可能不能击中一个面（由于一些硬件限制），所以通过使用<var>GL_CLAMP_TO_EDGE</var>，OpenGL将在我们对两个面之间采样的时候，永远返回它们的边界值。
+别被 `GL_TEXTURE_WRAP_R`吓到，它只是简单的设置了纹理的R坐标，R坐标对应于纹理的第三个维度（就像位置的z一样）。我们把放置方式设置为 `GL_CLAMP_TO_EDGE` ，由于纹理坐标在两个面之间，所以可能并不能触及哪个面（由于硬件限制），因此使用 `GL_CLAMP_TO_EDGE` 后OpenGL会返回它们的边界的值，尽管我们可能在两个两个面中间进行的采样。
 
-在绘制使用立方体贴图的物体之前，我们要先激活对应的纹理单元，并绑定立方体贴图，这和普通的2D纹理没什么区别。
+在绘制物体之前，将使用立方体贴图，而在渲染前我们要激活相应的纹理单元并绑定到立方体贴图上，这和普通的2D纹理没什么区别。
 
-在片段着色器中，我们使用了一个不同类型的采样器，`samplerCube`，我们将使用<fun>texture</fun>函数使用它进行采样，但这次我们将使用一个`vec3`的方向向量而不是`vec2`。使用立方体贴图的片段着色器会像是这样的：
+在片段着色器中，我们也必须使用一个不同的采样器——**samplerCube**，用它来从`texture`函数中采样，但是这次使用的是一个`vec3`方向向量，取代`vec2`。下面是一个片段着色器使用了立方体贴图的例子：
 
 ```c++
-in vec3 textureDir; // 代表3D纹理坐标的方向向量
-uniform samplerCube cubemap; // 立方体贴图的纹理采样器
+in vec3 textureDir; // 用一个三维方向向量来表示立方体贴图纹理的坐标
+
+uniform samplerCube cubemap;  // 立方体贴图纹理采样器
 
 void main()
-{             
-    FragColor = texture(cubemap, textureDir);
+{
+    color = texture(cubemap, textureDir);
 }
 ```
 
-看起来很棒，但为什么要用它呢？恰巧有一些很有意思的技术，使用立方体贴图来实现的话会简单多了。其中一个技术就是创建一个<def>天空盒</def>(Skybox)。
+看起来不错，但是何必这么做呢？因为恰巧使用立方体贴图可以简单的实现很多有意思的技术。其中之一便是著名的**天空盒(Skybox)**。
+
+
 
 # 天空盒
 
-天空盒是一个包含了整个场景的（大）立方体，它包含周围环境的6个图像，让玩家以为他处在一个比实际大得多的环境当中。游戏中使用天空盒的例子有群山、白云或星空。下面这张截图中展示的是星空的天空盒，它来自于『上古卷轴3』：
+天空盒(Skybox)是一个包裹整个场景的立方体，它由6个图像构成一个环绕的环境，给玩家一种他所在的场景比实际的要大得多的幻觉。比如有些在视频游戏中使用的天空盒的图像是群山、白云或者满天繁星。比如下面的夜空繁星的图像就来自《上古卷轴》：
 
-![](../img/04/06/cubemaps_morrowind.jpg)
+![](http://learnopengl.com/img/advanced/cubemaps_morrowind.jpg)
 
-你可能现在已经猜到了，立方体贴图能完美满足天空盒的需求：我们有一个6面的立方体，每个面都需要一个纹理。在上面的图片中，他们使用了夜空的几张图片，让玩家产生其位于广袤宇宙中的错觉，但实际上他只是在一个小小的盒子当中。
+你现在可能已经猜到立方体贴图完全满足天空盒的要求：我们有一个立方体，它有6个面，每个面需要一个贴图。上图中使用了几个夜空的图片给予玩家一种置身广袤宇宙的感觉，可实际上，他还是在一个小盒子之中。
 
-你可以在网上找到很多像这样的天空盒资源。比如说这个[网站](http://www.custommapmakers.org/skyboxes.php)就提供了很多天空盒。天空盒图像通常有以下的形式：
+网上有很多这样的天空盒的资源。[这个网站](http://www.custommapmakers.org/skyboxes.php)就提供了很多。这些天空盒图像通常有下面的样式：
 
-![](../img/04/06/cubemaps_skybox.png)
+![](http://learnopengl.com/img/advanced/cubemaps_skybox.png)
 
-如果你将这六个面折成一个立方体，你就会得到一个完全贴图的立方体，模拟一个巨大的场景。一些资源可能会提供了这样格式的天空盒，你必须手动提取六个面的图像，但在大部分情况下它们都是6张单独的纹理图像。
+如果你把这6个面折叠到一个立方体中，你机会获得模拟了一个巨大的风景的立方体。有些资源所提供的天空盒比如这个例子6个图是连在一起的，你必须手工它们切割出来，不过大多数情况它们都是6个单独的纹理图像。
 
-之后我们将在场景中使用这个（高质量的）天空盒，它可以在[这里](../data/skybox.rar)下载到。
+这个细致（高精度）的天空盒就是我们将在场景中使用的那个，你可以[在这里下载](http://learnopengl.com/img/textures/skybox.rar)。
 
 ## 加载天空盒
 
-因为天空盒本身就是一个立方体贴图，加载天空盒和之前加载立方体贴图时并没有什么不同。为了加载天空盒，我们将使用下面的函数，它接受一个包含6个纹理路径的<fun>vector</fun>：
+由于天空盒实际上就是一个立方体贴图，加载天空盒和之前我们加载立方体贴图的没什么大的不同。为了加载天空盒我们将使用下面的函数，它接收一个包含6个纹理文件路径的vector：
 
 ```c++
-unsigned int loadCubemap(vector<std::string> faces)
+GLuint loadCubemap(vector<const GLchar*> faces)
 {
-    unsigned int textureID;
+    GLuint textureID;
     glGenTextures(1, &textureID);
-    glBindTexture(GL_TEXTURE_CUBE_MAP, textureID);
+    glActiveTexture(GL_TEXTURE0);
 
-    int width, height, nrChannels;
-    for (unsigned int i = 0; i < faces.size(); i++)
+    int width,height;
+    unsigned char* image;
+
+    glBindTexture(GL_TEXTURE_CUBE_MAP, textureID);
+    for(GLuint i = 0; i < faces.size(); i++)
     {
-        unsigned char *data = stbi_load(faces[i].c_str(), &width, &height, &nrChannels, 0);
-        if (data)
-        {
-            glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 
-                         0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data
-            );
-            stbi_image_free(data);
-        }
-        else
-        {
-            std::cout << "Cubemap texture failed to load at path: " << faces[i] << std::endl;
-            stbi_image_free(data);
-        }
+        image = SOIL_load_image(faces[i], &width, &height, 0, SOIL_LOAD_RGB);
+        glTexImage2D(
+            GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0,
+            GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, image
+        );
     }
-    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
     glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
+    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
     glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
     glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
     glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
+    glBindTexture(GL_TEXTURE_CUBE_MAP, 0);
 
     return textureID;
 }
 ```
 
-函数本身应该很熟悉了。它基本就是上一部分中立方体贴图的代码，只不过合并到了一个便于管理的函数中。
+这个函数没什么特别之处。这就是我们前面已经见过的立方体贴图代码，只不过放进了一个可管理的函数中。
 
-之后，在调用这个函数之前，我们需要将合适的纹理路径按照立方体贴图枚举指定的顺序加载到一个vector中。
+然后，在我们调用这个函数之前，我们将把合适的纹理路径加载到一个vector之中，顺序还是按照立方体贴图枚举的特定顺序：
 
 ```c++
-vector<std::string> faces
-{
-    "right.jpg",
-    "left.jpg",
-    "top.jpg",
-    "bottom.jpg",
-    "front.jpg",
-    "back.jpg"
-};
-unsigned int cubemapTexture = loadCubemap(faces);
+vector<const GLchar*> faces;
+faces.push_back("right.jpg");
+faces.push_back("left.jpg");
+faces.push_back("top.jpg");
+faces.push_back("bottom.jpg");
+faces.push_back("back.jpg");
+faces.push_back("front.jpg");
+GLuint cubemapTexture = loadCubemap(faces);
 ```
 
-现在我们就将这个天空盒加载为一个立方体贴图了，它的id是<var>cubemapTexture</var>。我们可以将它绑定到一个立方体中，替换掉用了很长时间的难看的纯色背景。
+现在我们已经用`cubemapTexture`作为id把天空盒加载为立方体贴图。我们现在可以把它绑定到一个立方体来替换不完美的`clear color`，在前面的所有教程中这个东西做背景已经很久了。
+
+
 
 ## 显示天空盒
 
-由于天空盒是绘制在一个立方体上的，和其它物体一样，我们需要另一个VAO、VBO以及新的一组顶点。你可以在[这里](https://learnopengl.com/code_viewer.php?code=advanced/cubemaps_skybox_data)找到它的顶点数据。
+因为天空盒绘制在了一个立方体上，我们还需要另一个VAO、VBO以及一组全新的顶点，和任何其他物体一样。你可以[从这里获得顶点数据](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps_skybox_data)。
 
-用于贴图3D立方体的立方体贴图可以使用立方体的位置作为纹理坐标来采样。当立方体处于原点(0, 0, 0)时，它的每一个位置向量都是从原点出发的方向向量。这个方向向量正是获取立方体上特定位置的纹理值所需要的。正是因为这个，我们只需要提供位置向量而不用纹理坐标了。
-
-要渲染天空盒的话，我们需要一组新的着色器，它们都不是很复杂。因为我们只有一个顶点属性，顶点着色器非常简单：
+立方体贴图用于给3D立方体帖上纹理，可以用立方体的位置作为纹理坐标进行采样。当一个立方体的中心位于原点(0，0，0)的时候，它的每一个位置向量也就是以原点为起点的方向向量。这个方向向量就是我们要得到的立方体某个位置的相应纹理值。出于这个理由，我们只需要提供位置向量，而无需纹理坐标。为了渲染天空盒，我们需要一组新着色器，它们不会太复杂。因为我们只有一个顶点属性，顶点着色器非常简单：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;
-
+layout (location = 0) in vec3 position;
 out vec3 TexCoords;
 
 uniform mat4 projection;
@@ -178,121 +177,117 @@ uniform mat4 view;
 
 void main()
 {
-    TexCoords = aPos;
-    gl_Position = projection * view * vec4(aPos, 1.0);
+    gl_Position =   projection * view * vec4(position, 1.0);  
+    TexCoords = position;
 }
 ```
 
-注意，顶点着色器中很有意思的部分是，我们将输入的位置向量作为输出给片段着色器的纹理坐标。片段着色器会将它作为输入来采样`samplerCube`：
+注意，顶点着色器有意思的地方在于我们把输入的位置向量作为输出给片段着色器的纹理坐标。片段着色器就会把它们作为输入去采样samplerCube：
 
 ```c++
 #version 330 core
-out vec4 FragColor;
-
 in vec3 TexCoords;
+out vec4 color;
 
 uniform samplerCube skybox;
 
 void main()
-{    
-    FragColor = texture(skybox, TexCoords);
+{
+    color = texture(skybox, TexCoords);
 }
 ```
 
-片段着色器非常直观。我们将顶点属性的位置向量作为纹理的方向向量，并使用它从立方体贴图中采样纹理值。
-
-有了立方体贴图纹理，渲染天空盒现在就非常简单了，我们只需要绑定立方体贴图纹理，<var>skybox</var>采样器就会自动填充上天空盒立方体贴图了。绘制天空盒时，我们需要将它变为场景中的第一个渲染的物体，并且禁用深度写入。这样子天空盒就会永远被绘制在其它物体的背后了。
+片段着色器比较明了，我们把顶点属性中的位置向量作为纹理的方向向量，使用它们从立方体贴图采样纹理值。渲染天空盒现在很简单，我们有了一个立方体贴图纹理，我们简单绑定立方体贴图纹理，天空盒就自动地用天空盒的立方体贴图填充了。为了绘制天空盒，我们将把它作为场景中第一个绘制的物体并且关闭深度写入。这样天空盒才能成为所有其他物体的背景来绘制出来。
 
 ```c++
+
 glDepthMask(GL_FALSE);
-skyboxShader.use();
-// ... 设置观察和投影矩阵
+skyboxShader.Use();
+// ... Set view and projection matrix
 glBindVertexArray(skyboxVAO);
 glBindTexture(GL_TEXTURE_CUBE_MAP, cubemapTexture);
 glDrawArrays(GL_TRIANGLES, 0, 36);
+glBindVertexArray(0);
 glDepthMask(GL_TRUE);
-// ... 绘制剩下的场景
+// ... Draw rest of the scene
 ```
 
-如果你运行一下的话你就会发现出现了一些问题。我们希望天空盒是以玩家为中心的，这样不论玩家移动了多远，天空盒都不会变近，让玩家产生周围环境非常大的印象。然而，当前的观察矩阵会旋转、缩放和位移来变换天空盒的所有位置，所以当玩家移动的时候，立方体贴图也会移动！我们希望移除观察矩阵中的位移部分，让移动不会影响天空盒的位置向量。
-
-你可能还记得在[基础光照](../02 Lighting/02 Basic Lighting.md)小节中，我们通过取4x4矩阵左上角的3x3矩阵来移除变换矩阵的位移部分。我们可以将观察矩阵转换为3x3矩阵（移除位移），再将其转换回4x4矩阵，来达到类似的效果。
+如果你运行程序就会陷入困境，我们希望天空盒以玩家为中心，这样无论玩家移动了多远，天空盒都不会变近，这样就产生一种四周的环境真的非常大的印象。当前的视图矩阵对所有天空盒的位置进行了转转缩放和平移变换，所以玩家移动，立方体贴图也会跟着移动！我们打算移除视图矩阵的平移部分，这样移动就影响不到天空盒的位置向量了。在基础光照教程里我们提到过我们可以只用4X4矩阵的3×3部分去除平移。我们可以简单地将矩阵转为33矩阵再转回来，就能达到目标
 
 ```c++
 glm::mat4 view = glm::mat4(glm::mat3(camera.GetViewMatrix()));
 ```
 
-这将移除任何的位移，但保留旋转变换，让玩家仍然能够环顾场景。
+这会移除所有平移，但保留所有旋转，因此用户仍然能够向四面八方看。由于有了天空盒，场景即可变得巨大了。如果你添加些物体然后自由在其中游荡一会儿你会发现场景的真实度有了极大提升。最后的效果看起来像这样：
 
-有了天空盒，最终的效果就是一个看起来巨大的场景了。如果你在箱子周围转一转，你就能立刻感受到距离感，极大地提升了场景的真实度。最终的结果看起来是这样的：
+![](http://learnopengl.com/img/advanced/cubemaps_skybox_result.png)
 
-![](../img/04/06/cubemaps_skybox_result.png)
+[这里有全部源码](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps_skybox)，你可以对比一下你写的。
 
-试一试不同的天空盒，看看它们是怎样对场景的观感产生巨大影响的。
+尝试用不同的天空盒实验，看看它们对场景有多大影响。
 
 ## 优化
 
-目前我们是首先渲染天空盒，之后再渲染场景中的其它物体。这样子能够工作，但不是非常高效。如果我们先渲染天空盒，我们就会对屏幕上的每一个像素运行一遍片段着色器，即便只有一小部分的天空盒最终是可见的。可以使用<def>提前深度测试</def>(Early Depth Testing)轻松丢弃掉的片段能够节省我们很多宝贵的带宽。
+现在我们在渲染场景中的其他物体之前渲染了天空盒。这么做没错，但是不怎么高效。如果我们先渲染了天空盒，那么我们就是在为每一个屏幕上的像素运行片段着色器，即使天空盒只有部分在显示着；fragment可以使用前置深度测试（early depth testing）简单地被丢弃，这样就节省了我们宝贵的带宽。
 
-所以，我们将会最后渲染天空盒，以获得轻微的性能提升。这样子的话，深度缓冲就会填充满所有物体的深度值了，我们只需要在提前深度测试通过的地方渲染天空盒的片段就可以了，很大程度上减少了片段着色器的调用。问题是，天空盒很可能会渲染在所有其他对象之上，因为它只是一个1x1x1的立方体（译注：意味着距离摄像机的距离也只有1），会通过大部分的深度测试。不用深度测试来进行渲染不是解决方案，因为天空盒将会复写场景中的其它物体。我们需要欺骗深度缓冲，让它认为天空盒有着最大的深度值1.0，只要它前面有一个物体，深度测试就会失败。
+所以最后渲染天空盒就能够给我们带来轻微的性能提升。采用这种方式，深度缓冲被全部物体的深度值完全填充，所以我们只需要渲染通过前置深度测试的那部分天空的片段就行了，而且能显著减少片段着色器的调用。问题是天空盒是个1×1×1的立方体，极有可能会渲染失败，因为极有可能通不过深度测试。简单地不用深度测试渲染它也不是解决方案，这是因为天空盒会在之后覆盖所有的场景中其他物体。我们需要耍个花招让深度缓冲相信天空盒的深度缓冲有着最大深度值1.0，如此只要有个物体存在深度测试就会失败，看似物体就在它前面了。
 
-在[坐标系统](../01 Getting started/08 Coordinate Systems.md)小节中我们说过，**透视除法**是在顶点着色器运行之后执行的，将<var>gl_Position</var>的`xyz`坐标除以w分量。我们又从[深度测试](01 Depth testing.md)小节中知道，相除结果的z分量等于顶点的深度值。使用这些信息，我们可以将输出位置的z分量等于它的w分量，让z分量永远等于1.0，这样子的话，当透视除法执行之后，z分量会变为`w / w = 1.0`。
+在坐标系教程中我们说过，透视除法（perspective division）是在顶点着色器运行之后执行的，把`gl_Position`的xyz坐标除以w元素。我们从深度测试教程了解到除法结果的z元素等于顶点的深度值。利用这个信息，我们可以把输出位置的z元素设置为它的w元素，这样就会导致z元素等于1.0了，因为，当透视除法应用后，它的z元素转换为w/w = 1.0：
 
 ```c++
 void main()
 {
-    TexCoords = aPos;
-    vec4 pos = projection * view * vec4(aPos, 1.0);
+    vec4 pos = projection * view * vec4(position, 1.0);
     gl_Position = pos.xyww;
+    TexCoords = position;
 }
 ```
 
-最终的**标准化设备坐标**将永远会有一个等于1.0的z值：最大的深度值。结果就是天空盒只会在没有可见物体的地方渲染了（只有这样才能通过深度测试，其它所有的东西都在天空盒前面）。
+最终，标准化设备坐标就总会有个与1.0相等的z值了，1.0就是深度值的最大值。只有在没有任何物体可见的情况下天空盒才会被渲染（只有通过深度测试才渲染，否则假如有任何物体存在，就不会被渲染，只去渲染物体）。
 
-我们还要改变一下深度函数，将它从默认的<var>GL_LESS</var>改为<var>GL_LEQUAL</var>。深度缓冲将会填充上天空盒的1.0值，所以我们需要保证天空盒在值小于或等于深度缓冲而不是小于时通过深度测试。
+我们必须改变一下深度方程，把它设置为`GL_LEQUAL`，原来默认的是`GL_LESS`。深度缓冲会为天空盒用1.0这个值填充深度缓冲，所以我们需要保证天空盒是使用小于等于深度缓冲来通过深度测试的，而不是小于。
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/6.1.cubemaps_skybox/cubemaps_skybox.cpp)找到优化后的源代码。
+你可以在这里找到优化过的版本的[源码](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps_skybox_optimized)。
 
 # 环境映射
 
-我们现在将整个环境映射到了一个纹理对象上了，能利用这个信息的不仅仅只有天空盒。通过使用环境的立方体贴图，我们可以给物体反射和折射的属性。这样使用环境立方体贴图的技术叫做<def>环境映射</def>(Environment Mapping)，其中最流行的两个是<def>反射</def>(Reflection)和<def>折射</def>(Refraction)。
+我们现在有了一个把整个环境映射到为一个单独纹理的对象，我们利用这个信息能做的不仅是天空盒。使用带有场景环境的立方体贴图，我们还可以让物体有一个反射或折射属性。像这样使用了环境立方体贴图的技术叫做**环境贴图技术**，其中最重要的两个是**反射(reflection)**和**折射(refraction)**。
 
 ## 反射
 
-反射这个属性表现为物体（或物体的一部分）<def>反射</def>它周围环境，即根据观察者的视角，物体的颜色或多或少等于它的环境。镜子就是一个反射性物体：它会根据观察者的视角反射它周围的环境。
+凡是是一个物体（或物体的某部分）反射(Reflect)他周围的环境的属性，比如物体的颜色多少有些等于它周围的环境，这要基于观察者的角度。例如一个镜子是一个反射物体：它会基于观察者的角度泛着它周围的环境。
 
-反射的原理并不难。下面这张图展示了我们如何计算反射向量，并如何使用这个向量来从立方体贴图中采样：
+反射的基本思路不难。下图展示了我们如何计算反射向量，然后使用这个向量去从一个立方体贴图中采样：
 
-![](../img/04/06/cubemaps_reflection_theory.png)
+![](http://learnopengl.com/img/advanced/cubemaps_reflection_theory.png)
 
-我们根据观察方向向量\(\color{gray}{\bar{I}}\)和物体的法向量\(\color{red}{\bar{N}}\)，来计算反射向量\(\color{green}{\bar{R}}\)。我们可以使用GLSL内建的<fun>reflect</fun>函数来计算这个反射向量。最终的\(\color{green}{\bar{R}}\)向量将会作为索引/采样立方体贴图的方向向量，返回环境的颜色值。最终的结果是物体看起来反射了天空盒。
+我们基于观察方向向量I和物体的法线向量N计算出反射向量R。我们可以使用GLSL的内建函数reflect来计算这个反射向量。最后向量R作为一个方向向量对立方体贴图进行索引/采样，返回一个环境的颜色值。最后的效果看起来就像物体反射了天空盒。
 
-因为我们已经在场景中配置好天空盒了，创建反射效果并不会很难。我们将会改变箱子的片段着色器，让箱子有反射性：
+因为我们在场景中已经设置了一个天空盒，创建反射就不难了。我们改变一下箱子使用的那个片段着色器，给箱子一个反射属性：
 
 ```c++
 #version 330 core
-out vec4 FragColor;
-
 in vec3 Normal;
 in vec3 Position;
+out vec4 color;
 
 uniform vec3 cameraPos;
 uniform samplerCube skybox;
 
 void main()
-{             
+{
     vec3 I = normalize(Position - cameraPos);
     vec3 R = reflect(I, normalize(Normal));
-    FragColor = vec4(texture(skybox, R).rgb, 1.0);
+    color = texture(skybox, R);
 }
 ```
 
-我们先计算了观察/摄像机方向向量`I`，并使用它来计算反射向量`R`，之后我们将使用`R`来从天空盒立方体贴图中采样。注意，我们现在又有了片段的插值<var>Normal</var>和<var>Position</var>变量，所以我们需要更新一下顶点着色器。
+我们先来计算观察/摄像机方向向量I，然后使用它来计算反射向量R，接着我们用R从天空盒立方体贴图采样。要注意的是，我们有了片段的插值Normal和Position变量，所以我们需要修正顶点着色器适应它。
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;
-layout (location = 1) in vec3 aNormal;
+layout (location = 0) in vec3 position;
+layout (location = 1) in vec3 normal;
 
 out vec3 Normal;
 out vec3 Position;
@@ -303,90 +298,97 @@ uniform mat4 projection;
 
 void main()
 {
-    Normal = mat3(transpose(inverse(model))) * aNormal;
-    Position = vec3(model * vec4(aPos, 1.0));
-    gl_Position = projection * view * model * vec4(aPos, 1.0);
+    gl_Position = projection * view * model * vec4(position, 1.0f);
+    Normal = mat3(transpose(inverse(model))) * normal;
+    Position = vec3(model * vec4(position, 1.0f));
 }
 ```
 
-我们现在使用了一个法向量，所以我们将再次使用法线矩阵(Normal Matrix)来变换它们。<var>Position</var>输出向量是一个世界空间的位置向量。顶点着色器的这个<var>Position</var>输出将用来在片段着色器内计算观察方向向量。
+我们用了法线向量，所以我们打算使用一个**法线矩阵(normal matrix)**变换它们。`Position`输出的向量是一个世界空间位置向量。顶点着色器输出的`Position`用来在片段着色器计算观察方向向量。
 
-因为我们使用了法线，你还需要更新一下[顶点数据](https://learnopengl.com/code_viewer.php?code=lighting/basic_lighting_vertex_data)，并更新属性指针。还要记得去设置<var>cameraPos</var>这个uniform。
+因为我们使用法线，你还得更新顶点数据，更新属性指针。还要确保设置`cameraPos`的uniform。
 
-接下来，我们在渲染箱子之前先绑定立方体贴图纹理：
+然后在渲染箱子前我们还得绑定立方体贴图纹理：
 
 ```c++
 glBindVertexArray(cubeVAO);
-glBindTexture(GL_TEXTURE_CUBE_MAP, skyboxTexture);  		
+glBindTexture(GL_TEXTURE_CUBE_MAP, skyboxTexture);
 glDrawArrays(GL_TRIANGLES, 0, 36);
+glBindVertexArray(0);
 ```
 
-编译并运行代码，你将会得到一个像是镜子一样的箱子。周围的天空盒被完美地反射在箱子上。
+编译运行你的代码，你等得到一个镜子一样的箱子。箱子完美地反射了周围的天空盒：
 
-![](../img/04/06/cubemaps_reflection.png)
+![](http://learnopengl.com/img/advanced/cubemaps_reflection.png)
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/6.2.cubemaps_environment_mapping/cubemaps_environment_mapping.cpp)找到完整的源代码。
+你可以[从这里找到全部源代码](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps_reflection)。
 
-当反射应用到一整个物体上（像是箱子）时，这个物体看起来就像是钢或者铬这样的高反射性材质。如果我们加载[模型加载](../03 Model Loading/03 Model.md)小节中的背包模型，我们会得到一种整个套装都是使用铬做成的效果：
+当反射应用于整个物体之上的时候，物体看上去就像有一个像钢和铬这种高反射材质。如果我们加载[模型教程](../03 Model Loading/03 Model.md)中的纳米铠甲模型，我们就会获得一个铬金属制铠甲：
 
-![](../img/04/06/cubemaps_reflection_backpack.png)
+![](http://learnopengl.com/img/advanced/cubemaps_reflection_nanosuit.png)
 
-这看起来非常棒，但在现实中大部分的模型都不具有完全反射性。我们可以引入<def>反射贴图</def>(Reflection Map)，来给模型更多的细节。与漫反射和镜面光贴图一样，反射贴图也是可以采样的纹理图像，它决定这片段的反射性。通过使用反射贴图，我们可以知道模型的哪些部分该以什么强度显示反射。在本节的练习中，将由你来为我们之前创建的模型加载器中引入反射贴图，显著提升背包模型的细节。
+看起来挺惊艳，但是现实中大多数模型都不是完全反射的。我们可以引进反射贴图（reflection map）来使模型有另一层细节。和diffuse、specular贴图一样，我们可以从反射贴图上采样来决定fragment的反射率。使用反射贴图我们还可以决定模型的哪个部分有反射能力，以及强度是多少。本节的练习中，要由你来在我们早期创建的模型加载器引入反射贴图，这回极大的提升纳米服模型的细节。
 
 ## 折射
 
-环境映射的另一种形式是<def>折射</def>，它和反射很相似。折射是光线由于传播介质的改变而产生的方向变化。在常见的类水表面上所产生的现象就是折射，光线不是直直地传播，而是弯曲了一点。将你的半只胳膊伸进水里，观察出来的就是这种效果。
+环境映射的另一个形式叫做折射(Refraction)，它和反射差不多。折射是光线通过特定材质对光线方向的改变。我们通常看到像水一样的表面，光线并不是直接通过的，而是让光线弯曲了一点。它看起来像你把半只手伸进水里的效果。
 
-折射是通过[斯涅尔定律](https://en.wikipedia.org/wiki/Snell%27s_law)(Snell's Law)来描述的，使用环境贴图的话看起来像是这样：
+折射遵守[斯涅尔定律](http://en.wikipedia.org/wiki/Snell%27s_law)，使用环境贴图看起来就像这样：
 
-![](../img/04/06/cubemaps_refraction_theory.png)
+![](http://learnopengl.com/img/advanced/cubemaps_refraction_theory.png)
 
-同样，我们有一个观察向量\(\color{gray}{\bar{I}}\)，一个法向量\(\color{red}{\bar{N}}\)，而这次是折射向量\(\color{green}{\bar{R}}\)。可以看到，观察向量的方向轻微弯曲了。弯折后的向量\(\color{green}{\bar{R}}\)将会用来从立方体贴图中采样。
+我们有个观察向量I，一个法线向量N，这次折射向量是R。就像你所看到的那样，观察向量的方向有轻微弯曲。弯曲的向量R随后用来从立方体贴图上采样。
 
-折射可以使用GLSL的内建<fun>refract</fun>函数来轻松实现，它需要一个法向量、一个观察方向和两个材质之间的<def>折射率</def>(Refractive Index)。
+折射可以通过GLSL的内建函数refract来实现，除此之外还需要一个法线向量，一个观察方向和一个两种材质之间的折射指数。
 
-折射率决定了材质中光线弯曲的程度，每个材质都有自己的折射率。一些最常见的折射率可以在下表中找到：
+折射指数决定了一个材质上光线扭曲的数量，每个材质都有自己的折射指数。下表是常见的折射指数：
 
-材质  |	折射率
+材质  |	折射指数
 ---|---
 空气 |	1.00
 水	 | 1.33
 冰	 | 1.309
 玻璃 |	1.52
-钻石 |	2.42
+宝石 |	2.42
 
-我们使用这些折射率来计算光传播的两种材质间的比值。在我们的例子中，光线/视线从**空气**进入**玻璃**（如果我们假设箱子是玻璃制的），所以比值为\(\frac{1.00}{1.52} = 0.658\)。
+我们使用这些折射指数来计算光线通过两个材质的比率。在我们的例子中，光线/视线从空气进入玻璃（如果我们假设箱子是玻璃做的）所以比率是1.001.52 = 0.658。
 
-我们已经绑定了立方体贴图，提供了顶点数据和法线，并设置了摄像机位置的uniform。唯一要修改的就是片段着色器：
+我们已经绑定了立方体贴图，提供了定点数据，设置了摄像机位置的uniform。现在只需要改变片段着色器：
 
 ```c++
 void main()
-{             
+{
     float ratio = 1.00 / 1.52;
     vec3 I = normalize(Position - cameraPos);
     vec3 R = refract(I, normalize(Normal), ratio);
-    FragColor = vec4(texture(skybox, R).rgb, 1.0);
+    color = texture(skybox, R);
 }
 ```
 
-通过改变折射率，你可以创建完全不同的视觉效果。编译程序并运行，但结果并不是很有趣，因为我们只使用了一个简单的箱子，它不太能显示折射的效果，现在看起来只是有点像一个放大镜。对背包使用相同的着色器却能够展现出了我们期待的效果：一个类玻璃的物体。
+通过改变折射指数你可以创建出完全不同的视觉效果。编译运行应用，结果也不是太有趣，因为我们只是用了一个普通箱子，这不能显示出折射的效果，看起来像个放大镜。使用同一个着色器，纳米服模型却可以展示出我们期待的效果：玻璃制物体。
 
-![](../img/04/06/cubemaps_refraction_backpack.png)
+![](http://learnopengl.com/img/advanced/cubemaps_refraction.png)
 
-你可以想象出有了光照、反射、折射和顶点移动的正确组合，你可以创建出非常漂亮的水。注意，如果要想获得物理上精确的结果，我们还需要在光线离开物体的时候再次折射，现在我们使用的只是单面折射(Single-side Refraction)，但它对大部分场合都是没问题的。
+你可以向想象一下，如果将光线、反射、折射和顶点的移动合理的结合起来就能创造出漂亮的水的图像。一定要注意，出于物理精确的考虑当光线离开物体的时候还要再次进行折射；现在我们简单的使用了单边（一次）折射，大多数目的都可以得到满足。
 
 ## 动态环境贴图
 
-现在我们使用的都是静态图像的组合来作为天空盒，看起来很不错，但它没有在场景中包括可移动的物体。我们一直都没有注意到这一点，因为我们只使用了一个物体。如果我们有一个镜子一样的物体，周围还有多个物体，镜子中可见的只有天空盒，看起来就像它是场景中唯一一个物体一样。
+现在，我们已经使用了静态图像组合的天空盒，看起来不错，但是没有考虑到物体可能移动的实际场景。我们到现在还没注意到这点，是因为我们目前还只使用了一个物体。如果我们有个镜子一样的物体，它周围有多个物体，只有天空盒在镜子中可见，和场景中只有这一个物体一样。
+
+使用帧缓冲可以为提到的物体的所有6个不同角度创建一个场景的纹理，把它们每次渲染迭代储存为一个立方体贴图。之后我们可以使用这个（动态生成的）立方体贴图来创建真实的反射和折射表面，这样就能包含所有其他物体了。这种方法叫做动态环境映射(Dynamic Environment Mapping),因为我们动态地创建了一个物体的以其四周为参考的立方体贴图，并把它用作环境贴图。
+
+它看起效果很好，但是有一个劣势：使用环境贴图我们必须为每个物体渲染场景6次，这需要非常大的开销。现代应用尝试尽量使用天空盒子，凡可能预编译立方体贴图就创建少量动态环境贴图。动态环境映射是个非常棒的技术，要想在不降低执行效率的情况下实现它就需要很多巧妙的技巧。
 
-通过使用帧缓冲，我们能够为物体的6个不同角度创建出场景的纹理，并在每个渲染迭代中将它们储存到一个立方体贴图中。之后我们就可以使用这个（动态生成的）立方体贴图来创建出更真实的，包含其它物体的，反射和折射表面了。这就叫做<def>动态环境映射</def>(Dynamic Environment Mapping)，因为我们动态创建了物体周围的立方体贴图，并将其用作环境贴图。
 
-虽然它看起来很棒，但它有一个很大的缺点：我们需要为使用环境贴图的物体渲染场景6次，这是对程序是非常大的性能开销。现代的程序通常会尽可能使用天空盒，并在可能的时候使用预编译的立方体贴图，只要它们能产生一点动态环境贴图的效果。虽然动态环境贴图是一个很棒的技术，但是要想在不降低性能的情况下让它工作还是需要非常多的技巧的。
 
 ## 练习
 
-- 尝试在我们之前在[模型加载](../03 Model Loading/01 Assimp.md)小节中创建的模型加载器中引入反射贴图。你可以在[这里](../data/nanosuit_reflection.zip)找到升级后有反射贴图的背包模型。仍有几点要注意的：
-	- Assimp在大多数格式中都不太喜欢反射贴图，所以我们需要欺骗一下它，将反射贴图储存为**漫反射贴图**。你可以在加载材质的时候将反射贴图的纹理类型设置为<var>aiTextureType_AMBIENT</var>。
-	- 我偷懒直接使用镜面光纹理图像来创建了反射贴图，所以反射贴图在模型的某些地方不能准确地映射:)。
-	- 由于模型加载器本身就已经在着色器中占用了3个纹理单元了，你需要将天空盒绑定到第4个纹理单元上，因为我们要从同一个着色器中对天空盒采样。
-- 如果你都做对了，它会看起来像[这样](../img/04/06/cubemaps_reflection_map.png)。
+- 尝试在模型加载中引进反射贴图，你将再次得到很大视觉效果的提升。这其中有几点需要注意：
+	- Assimp并不支持反射贴图，我们可以使用环境贴图的方式将反射贴图从`aiTextureType_AMBIENT`类型中来加载反射贴图的材质。
+	- 我匆忙地使用反射贴图来作为镜面反射的贴图，而反射贴图并没有很好的映射在模型上:)。
+	- 由于加载模型已经占用了3个纹理单元，因此你要绑定天空盒到第4个纹理单元上，这样才能在同一个着色器内从天空盒纹理中取样。
+- 你可以在此获取解决方案的[源代码](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1)，这其中还包括升级过的[Model](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1-model)和[Mesh](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1-mesh)类，还有用来绘制反射贴图的[顶点着色器](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1-vertex)和[片段着色器](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1-fragment)。
+
+如果你一切都做对了，那你应该看到和下图类似的效果：
+
+![](http://learnopengl.com/img/advanced/cubemaps_reflection_map.png)

docs/04 Advanced OpenGL/07 Advanced Data.md

@@ -3,102 +3,104 @@
 原文     | [Advanced Data](http://learnopengl.com/#!Advanced-OpenGL/Advanced-Data)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | 暂未校对
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com)
 
-我们在OpenGL中大量使用缓冲来储存数据已经有很长时间了。这一节中，我们将讨论一些其他的操作缓冲的方法。
 
-OpenGL中的缓冲只是一个管理特定内存块的对象，没有其它更多的功能了。在我们将它绑定到一个<def>缓冲目标</def>(Buffer Target)时，我们才赋予了其意义。当我们绑定一个缓冲到<var>GL_ARRAY_BUFFER</var>时，它就是一个顶点数组缓冲，但我们也可以很容易地将其绑定到<var>GL_ELEMENT_ARRAY_BUFFER</var>。OpenGL内部会为每个目标储存一个缓冲，并且会根据目标的不同，以不同的方式处理缓冲。
+我们在OpenGL中大量使用缓冲来储存数据已经有一会儿了。有一些有趣的方式来操纵缓冲，也有一些有趣的方式通过纹理来向着色器传递大量数据。本教程中，我们会讨论一些更加有意思的缓冲函数，以及如何使用纹理对象来储存大量数据（教程中纹理部分还没写）。
 
-到目前为止，我们一直是调用<fun>glBufferData</fun>函数来填充缓冲对象所管理的内存，这个函数会分配一块GPU内存，并将数据添加到这块内存中。如果我们将它的`data`参数设置为`NULL`，那么这个函数将只会分配内存，但不进行填充。这在我们需要**预留**(Reserve)特定大小的内存，之后回到这个缓冲一点一点填充的时候会很有用。
+OpenGL中缓冲只是一块儿内存区域的对象，除此没有更多点的了。当把缓冲绑定到一个特定缓冲对象的时候，我们就给缓冲赋予了一个特殊的意义。当我们绑定到`GL_ARRAY_BUFFER`的时候，这个缓冲就是一个顶点数组缓冲，我们也可以简单地绑定到`GL_ELEMENT_ARRAY_BUFFER`。OpenGL内部为每个目标（target）储存一个缓冲，并基于目标来处理不同的缓冲。
 
-除了使用一次函数调用填充整个缓冲之外，我们也可以使用<fun>glBufferSubData</fun>，填充缓冲的特定区域。这个函数需要一个缓冲目标、一个偏移量、数据的大小和数据本身作为它的参数。这个函数不同的地方在于，我们可以提供一个偏移量，指定从**何处**开始填充这个缓冲。这能够让我们插入或者更新缓冲内存的某一部分。要注意的是，缓冲需要有足够的已分配内存，所以对一个缓冲调用<fun>glBufferSubData</fun>之前必须要先调用<fun>glBufferData</fun>。
+到目前为止，我们使用`glBufferData`函数填充缓冲对象管理的内存，这个函数分配了一块内存空间，然后把数据存入其中。如果我们向它的`data`这个参数传递的是NULL，那么OpenGL只会帮我们分配内存，而不会填充它。如果我们先打算开辟一些内存，稍后回到这个缓冲一点一点的填充数据，有些时候会很有用。
+
+我们还可以调用`glBufferSubData`函数填充特定区域的缓冲，而不是一次填充整个缓冲。这个函数需要一个缓冲目标（target），一个偏移量（offset），数据的大小以及数据本身作为参数。这个函数新的功能是我们可以给它一个偏移量（offset）来指定我们打算填充缓冲的位置与起始位置之间的偏移量。这样我们就可以插入/更新指定区域的缓冲内存空间了。一定要确保修改的缓冲要有足够的内存分配，所以在调用`glBufferSubData`之前，调用`glBufferData`是必须的。
 
 ```c++
 glBufferSubData(GL_ARRAY_BUFFER, 24, sizeof(data), &data); // 范围： [24, 24 + sizeof(data)]
 ```
 
-将数据导入缓冲的另外一种方法是，请求缓冲内存的指针，直接将数据复制到缓冲当中。通过调用<fun>glMapBuffer</fun>函数，OpenGL会返回当前绑定缓冲的内存指针，供我们操作：
+把数据传进缓冲另一个方式是向缓冲内存请求一个指针，你自己直接把数据复制到缓冲中。调用`glMapBuffer`函数OpenGL会返回一个当前绑定缓冲的内存的地址，供我们操作：
 
 ```c++
 float data[] = {
   0.5f, 1.0f, -0.35f
   ...
 };
+
 glBindBuffer(GL_ARRAY_BUFFER, buffer);
-// 获取指针
-void *ptr = glMapBuffer(GL_ARRAY_BUFFER, GL_WRITE_ONLY);
-// 复制数据到内存
+// 获取当前绑定缓存buffer的内存地址
+void* ptr = glMapBuffer(GL_ARRAY_BUFFER, GL_WRITE_ONLY);
+// 向缓冲中写入数据
 memcpy(ptr, data, sizeof(data));
-// 记得告诉OpenGL我们不再需要这个指针了
+// 完成够别忘了告诉OpenGL我们不再需要它了
 glUnmapBuffer(GL_ARRAY_BUFFER);
 ```
 
-当我们使用<fun>glUnmapBuffer</fun>函数，告诉OpenGL我们已经完成指针操作之后，OpenGL就会知道你已经完成了。在解除映射(Unmapping)之后，指针将会不再可用，并且如果OpenGL能够成功将您的数据映射到缓冲中，这个函数将会返回<var>GL_TRUE</var>。
+调用`glUnmapBuffer`函数可以告诉OpenGL我们已经用完指针了，OpenGL会知道你已经做完了。通过解映射（unmapping），指针会不再可用，如果OpenGL可以把你的数据映射到缓冲上，就会返回`GL_TRUE`。
 
-如果要直接映射数据到缓冲，而不事先将其存储到临时内存中，<fun>glMapBuffer</fun>这个函数会很有用。比如说，你可以从文件中读取数据，并直接将它们复制到缓冲内存中。
+把数据直接映射到缓冲上使用`glMapBuffer`很有用，因为不用把它储存在临时内存里。你可以从文件读取数据然后直接复制到缓冲的内存里。
 
-## 分批顶点属性
+## 分批处理顶点属性
 
-通过使用<fun>glVertexAttribPointer</fun>，我们能够指定顶点数组缓冲内容的属性布局。在顶点数组缓冲中，我们对属性进行了<def>交错</def>(Interleave)处理，也就是说，我们将每一个顶点的位置、法线和/或纹理坐标紧密放置在一起。既然我们现在已经对缓冲有了更多的了解，我们可以采取另一种方式。
+使用`glVertexAttribPointer`函数可以指定缓冲内容的顶点数组的属性的布局(Layout)。我们已经知道，通过使用顶点属性指针我们可以交叉(Interleave)属性，也就是说我们可以把每个顶点的位置、法线、纹理坐标放在彼此挨着的地方。现在我们了解了更多的缓冲的内容，可以采取另一种方式了。
 
-我们可以做的是，将每一种属性类型的向量数据打包(Batch)为一个大的区块，而不是对它们进行交错储存。与交错布局123123123123不同，我们将采用分批(Batched)的方式111122223333。
+我们可以做的是把每种类型的属性的所有向量数据批量保存在一个布局，而不是交叉布局。与交叉布局123123123123不同，我们采取批量方式111122223333。
 
-当从文件中加载顶点数据的时候，你通常获取到的是一个位置数组、一个法线数组和/或一个纹理坐标数组。我们需要花点力气才能将这些数组转化为一个大的交错数据数组。使用分批的方式会是更简单的解决方案，我们可以很容易使用<fun>glBufferSubData</fun>函数实现：
+当从文件加载顶点数据时你通常获取一个位置数组，一个法线数组和一个纹理坐标数组。需要花点力气才能把它们结合为交叉数据。使用`glBufferSubData`可以简单的实现分批处理方式：
 
 ```c++
-float positions[] = { ... };
-float normals[] = { ... };
-float tex[] = { ... };
+GLfloat positions[] = { ... };
+GLfloat normals[] = { ... };
+GLfloat tex[] = { ... };
 // 填充缓冲
 glBufferSubData(GL_ARRAY_BUFFER, 0, sizeof(positions), &positions);
 glBufferSubData(GL_ARRAY_BUFFER, sizeof(positions), sizeof(normals), &normals);
 glBufferSubData(GL_ARRAY_BUFFER, sizeof(positions) + sizeof(normals), sizeof(tex), &tex);
 ```
 
-这样子我们就能直接将属性数组作为一个整体传递给缓冲，而不需要事先处理它们了。我们仍可以将它们合并为一个大的数组，再使用<fun>glBufferData</fun>来填充缓冲，但对于这种工作，使用<fun>glBufferSubData</fun>会更合适一点。
+这样我们可以把属性数组当作一个整体直接传输给缓冲，不需要再处理它们了。我们还可以把它们结合为一个更大的数组然后使用`glBufferData`立即直接填充它，不过对于这项任务使用`glBufferSubData`是更好的选择。
 
-我们还需要更新顶点属性指针来反映这些改变：
+我们还要更新顶点属性指针来反应这些改变：
 
 ```c++
-glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), 0);  
-glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), (void*)(sizeof(positions)));  
+glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(GLfloat), 0);  
+glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(GLfloat), (GLvoid*)(sizeof(positions)));  
 glVertexAttribPointer(
-  2, 2, GL_FLOAT, GL_FALSE, 2 * sizeof(float), (void*)(sizeof(positions) + sizeof(normals)));
+  2, 2, GL_FLOAT, GL_FALSE, 2 * sizeof(GLfloat), (GLvoid*)(sizeof(positions) + sizeof(normals)));
 ```
 
-注意`stride`参数等于顶点属性的大小，因为下一个顶点属性向量能在3个（或2个）分量之后找到。
+注意，`stride`参数等于顶点属性的大小，由于同类型的属性是连续储存的，所以下一个顶点属性向量可以在它的后面3（或2）的元素那儿找到。
 
-这给了我们设置顶点属性的另一种方法。使用哪种方法都是可行的，它只是设置顶点属性的一种更整洁的方式。但是，推荐使用交错方法，因为这样一来，每个顶点着色器运行时所需要的顶点属性在内存中会更加紧密对齐。
+这是我们有了另一种设置和指定顶点属性的方式。使用哪个方式对OpenGL来说也不会有立竿见影的效果，这只是一种采用更加组织化的方式去设置顶点属性。选用哪种方式取决于你的偏好和应用类型。
 
 ## 复制缓冲
 
-当你的缓冲已经填充好数据之后，你可能会想与其它的缓冲共享其中的数据，或者想要将缓冲的内容复制到另一个缓冲当中。<fun>glCopyBufferSubData</fun>能够让我们相对容易地从一个缓冲中复制数据到另一个缓冲中。这个函数的原型如下：
+当你的缓冲被数据填充以后，你可能打算让其他缓冲能分享这些数据或者打算把缓冲的内容复制到另一个缓冲里。`glCopyBufferSubData`函数让我们能够相对容易地把一个缓冲的数据复制到另一个缓冲里。函数的原型是：
 
 ```c++
-void glCopyBufferSubData(GLenum readtarget, GLenum writetarget, GLintptr readoffset,
-                         GLintptr writeoffset, GLsizeiptr size);
+void glCopyBufferSubData(GLenum readtarget, GLenum writetarget, GLintptr readoffset, GLintptr writeoffset, GLsizeiptr size);
 ```
 
-`readtarget`和`writetarget`参数需要填入复制源和复制目标的缓冲目标。比如说，我们可以将<var>VERTEX_ARRAY_BUFFER</var>缓冲复制到<var>VERTEX_ELEMENT_ARRAY_BUFFER</var>缓冲，分别将这些缓冲目标设置为读和写的目标。当前绑定到这些缓冲目标的缓冲将会被影响到。
+`readtarget`和`writetarget`参数是复制的来源和目的的缓冲目标。例如我们可以从一个`VERTEX_ARRAY_BUFFER`复制到一个`VERTEX_ELEMENT_ARRAY_BUFFER`，各自指定源和目的的缓冲目标。当前绑定到这些缓冲目标上的缓冲会被影响到。
 
-但如果我们想读写数据的两个不同缓冲都为顶点数组缓冲该怎么办呢？我们不能同时将两个缓冲绑定到同一个缓冲目标上。正是出于这个原因，OpenGL提供给我们另外两个缓冲目标，叫做<var>GL_COPY_READ_BUFFER</var>和<var>GL_COPY_WRITE_BUFFER</var>。我们接下来就可以将需要的缓冲绑定到这两个缓冲目标上，并将这两个目标作为`readtarget`和`writetarget`参数。
+但如果我们打算读写的两个缓冲都是顶点数组缓冲(`GL_VERTEX_ARRAY_BUFFER`)怎么办？我们不能用通一个缓冲作为操作的读取和写入目标次。出于这个理由，OpenGL给了我们另外两个缓冲目标叫做：`GL_COPY_READ_BUFFER`和`GL_COPY_WRITE_BUFFER`。这样我们就可以把我们选择的缓冲，用上面二者作为`readtarget`和`writetarget`的参数绑定到新的缓冲目标上了。
 
-接下来<fun>glCopyBufferSubData</fun>会从`readtarget`中读取`size`大小的数据，并将其写入`writetarget`缓冲的`writeoffset`偏移量处。下面这个例子展示了如何复制两个顶点数组缓冲：
+接着`glCopyBufferSubData`函数会从readoffset处读取的size大小的数据，写入到writetarget缓冲的writeoffset位置。下面是一个复制两个顶点数组缓冲的例子：
 
 ```c++
+GLfloat vertexData[] = { ... };
 glBindBuffer(GL_COPY_READ_BUFFER, vbo1);
 glBindBuffer(GL_COPY_WRITE_BUFFER, vbo2);
 glCopyBufferSubData(GL_COPY_READ_BUFFER, GL_COPY_WRITE_BUFFER, 0, 0, sizeof(vertexData));
 ```
 
-我们也可以只将`writetarget`缓冲绑定为新的缓冲目标类型之一：
+我们也可以把`writetarget`缓冲绑定为新缓冲目标类型其中之一：
 
 ```c++
-float vertexData[] = { ... };
+GLfloat vertexData[] = { ... };
 glBindBuffer(GL_ARRAY_BUFFER, vbo1);
 glBindBuffer(GL_COPY_WRITE_BUFFER, vbo2);
 glCopyBufferSubData(GL_ARRAY_BUFFER, GL_COPY_WRITE_BUFFER, 0, 0, sizeof(vertexData));
 ```
 
-有了这些关于如何操作缓冲的额外知识，我们已经能够以更有意思的方式使用它们了。当你越深入OpenGL时，这些新的缓冲方法将会变得更加有用。在[下一节](08 Advanced GLSL.md)中，在我们讨论<def>Uniform缓冲对象</def>(Uniform Buffer Object)时，我们将会充分利用<fun>glBufferSubData</fun>。
+有了这些额外的关于如何操纵缓冲的知识，我们已经可以以更有趣的方式来使用它们了。当你对OpenGL更熟悉，这些新缓冲方法就变得更有用。下个教程中我们会讨论unform缓冲对象，彼时我们会充分利用`glBufferSubData`。

docs/04 Advanced OpenGL/08 Advanced GLSL.md

@@ -3,172 +3,177 @@
 原文     | [Advanced GLSL](http://learnopengl.com/#!Advanced-OpenGL/Advanced-GLSL)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | AoZhang
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com)
 
-这一小节并不会向你展示非常先进非常酷的新特性，也不会对场景的视觉质量有显著的提高。但是，这一节会或多或少涉及GLSL的一些有趣的地方以及一些很棒的技巧，它们可能在今后会帮助到你。简单来说，它们就是在组合使用OpenGL和GLSL创建程序时的一些**最好要知道的东西**，和一些**会让你生活更加轻松的特性**。
 
-我们将会讨论一些有趣的<def>内建变量</def>(Built-in Variable)，管理着色器输入和输出的新方式以及一个叫做<def>Uniform缓冲对象</def>(Uniform Buffer Object)的有用工具。
+这章不会向你展示什么新的功能，也不会对你的场景的视觉效果有较大提升。本文多多少少地深入探讨了一些GLSL有趣的知识，它们可能在将来能帮助你。基本来说有些不可不知的内容和功能在你去使用GLSL创建OpenGL应用的时候能让你的生活更轻松。
+
+我们会讨论一些内建变量(Built-in Variable)、组织着色器输入和输出的新方式以及一个叫做uniform缓冲对象(Uniform Buffer Object)的非常有用的工具。
 
 # GLSL的内建变量
 
-着色器都是最简化的，如果需要当前着色器以外地方的数据的话，我们必须要将数据传进来。我们已经学会使用顶点属性、uniform和采样器来完成这一任务了。然而，除此之外，GLSL还定义了另外几个以`gl_`为前缀的变量，它们能提供给我们更多的方式来读取/写入数据。我们已经在前面教程中接触过其中的两个了：顶点着色器的输出向量<var>gl_Position</var>，和片段着色器的<var>gl_FragCoord</var>。
+着色器是很小的，如果我们需要从当前着色器以外的别的资源里的数据，那么我们就不得不传给它。我们学过了使用顶点属性、uniform和采样器可以实现这个目标。GLSL有几个以**gl\_**为前缀的变量，使我们有一个额外的手段来获取和写入数据。其中两个我们已经打过交道了：`gl_Position`和`gl_FragCoord`，前一个是顶点着色器的输出向量，后一个是片段着色器的变量。
 
-我们将会讨论几个有趣的GLSL内建输入和输出变量，并会解释它们能够怎样帮助你。注意，我们将不会讨论GLSL中存在的所有内建变量，如果你想知道所有的内建变量的话，请查看OpenGL的[wiki](https://www.khronos.org/opengl/wiki/Built-in_Variable_(GLSL))。
+我们会讨论几个有趣的GLSL内建变量，并向你解释为什么它们对我们来说很有好处。注意，我们不会讨论到GLSL中所有的内建变量，因此如果你想看到所有的内建变量还是最好去查看[OpenGL的wiki](http://www.opengl.org/wiki/Built-in_Variable_(GLSL)。
 
 ## 顶点着色器变量
 
-我们已经见过<var>gl_Position</var>了，它是顶点着色器的裁剪空间输出位置向量。如果你想在屏幕上显示任何东西，在顶点着色器中设置<var>gl_Position</var>是必须的步骤。这已经是它的全部功能了。
+我们已经了解`gl_Position`是顶点着色器裁切空间输出的位置向量。如果你想让屏幕上渲染出东西`gl_Position`必须使用。否则我们什么都看不到。
 
 ### gl_PointSize
 
-我们能够选用的其中一个图元是<var>GL_POINTS</var>，如果使用它的话，每一个顶点都是一个图元，都会被渲染为一个点。我们可以通过OpenGL的<fun>glPointSize</fun>函数来设置渲染出来的点的大小，但我们也可以在顶点着色器中修改这个值。
+我们可以使用的另一个可用于渲染的基本图形(primitive)是**GL\_POINTS**，使用它每个顶点作为一个基本图形，被渲染为一个点(point)。可以使用`glPointSize`函数来设置这个点的大小，但我们还可以在顶点着色器里修改点的大小。
 
-GLSL定义了一个叫做<var>gl_PointSize</var>输出变量，它是一个<fun>float</fun>变量，你可以使用它来设置点的宽高（像素）。在顶点着色器中修改点的大小的话，你就能对每个顶点设置不同的值了。
+GLSL有另一个输出变量叫做`gl_PointSize`，他是一个`float`变量，你可以以像素的方式设置点的高度和宽度。它在着色器中描述每个顶点做为点被绘制出来的大小。
 
-在顶点着色器中修改点大小的功能默认是禁用的，如果你需要启用它的话，你需要启用OpenGL的<var>GL_PROGRAM_POINT_SIZE</var>：
+在着色器中影响点的大小默认是关闭的，但是如果你打算开启它，你需要开启OpenGL的`GL_PROGRAM_POINT_SIZE`：
 
 ```c++
 glEnable(GL_PROGRAM_POINT_SIZE);
 ```
 
-一个简单的例子就是将点的大小设置为裁剪空间位置的z值，也就是顶点距观察者的距离。点的大小会随着观察者距顶点距离变远而增大。
+把点的大小设置为裁切空间的z值，这样点的大小就等于顶点距离观察者的距离，这是一种影响点的大小的方式。当顶点距离观察者更远的时候，它就会变得更大。
 
 ```c++
 void main()
 {
-    gl_Position = projection * view * model * vec4(aPos, 1.0);    
-    gl_PointSize = gl_Position.z;    
+    gl_Position = projection * view * model * vec4(position, 1.0f);
+    gl_PointSize = gl_Position.z;
 }
 ```
 
-结果就是，当我们远离这些点的时候，它们会变得更大：
+结果是我们绘制的点距离我们越远就越大：
 
-![](../img/04/08/advanced_glsl_pointsize.png)
+![](http://learnopengl.com/img/advanced/advanced_glsl_pointsize.png)
 
-你可以想到，对每个顶点使用不同的点大小，会在粒子生成之类的技术中很有意思。
+想象一下，每个顶点表示出来的点的大小的不同，如果用在像粒子生成之类的技术里会挺有意思的。
 
 ### gl_VertexID
 
-<var>gl_Position</var>和<var>gl_PointSize</var>都是**输出变量**，因为它们的值是作为顶点着色器的输出被读取的。我们可以对它们进行写入，来改变结果。顶点着色器还为我们提供了一个有趣的**输入变量**，我们只能对它进行读取，它叫做<var>gl_VertexID</var>。
+`gl_Position`和`gl_PointSize`都是输出变量，因为它们的值是作为顶点着色器的输出被读取的；我们可以向它们写入数据来影响结果。顶点着色器为我们提供了一个有趣的输入变量，我们只能从它那里读取，这个变量叫做`gl_VertexID`。
 
-整型变量<var>gl_VertexID</var>储存了正在绘制顶点的当前ID。当（使用<fun>glDrawElements</fun>）进行索引渲染的时候，这个变量会存储正在绘制顶点的当前索引。当（使用<fun>glDrawArrays</fun>）不使用索引进行绘制的时候，这个变量会储存从渲染调用开始的已处理顶点数量。
+`gl_VertexID`是个整型变量，它储存着我们绘制的当前顶点的ID。当进行索引渲染（indexed rendering，使用`glDrawElements`渲染）时，这个变量保存着当前绘制的顶点的索引。当用的不是索引绘制（`glDrawArrays`）时，这个变量保存的是从渲染开始起直到当前处理的这个顶点的（当前顶点）编号。
 
-## 片段着色器变量
+尽管目前看似没用，但是我们最好知道我们能获取这样的信息。
 
-在片段着色器中，我们也能访问到一些有趣的变量。GLSL提供给我们两个有趣的输入变量：<var>gl_FragCoord</var>和<var>gl_FrontFacing</var>。
+## 片段着色器的变量
+
+在片段着色器中也有一些有趣的变量。GLSL给我们提供了两个有意思的输入变量，它们是`gl_FragCoord`和`gl_FrontFacing`。
 
 ### gl_FragCoord
 
-在讨论深度测试的时候，我们已经见过<var>gl_FragCoord</var>很多次了，因为<var>gl_FragCoord</var>的z分量等于对应片段的深度值。然而，我们也能使用它的x和y分量来实现一些有趣的效果。
+在讨论深度测试的时候，我们已经看过`gl_FragCoord`好几次了，因为`gl_FragCoord`向量的z元素和特定的fragment的深度值相等。然而，我们也可以使用这个向量的x和y元素来实现一些有趣的效果。
 
-<var>gl_FragCoord</var>的x和y分量是片段的窗口空间(Window-space)坐标，其原点为窗口的左下角。我们已经使用<fun>glViewport</fun>设定了一个800x600的窗口了，所以片段窗口空间坐标的x分量将在0到800之间，y分量在0到600之间。
+`gl_FragCoord`的x和y元素是当前片段的窗口空间坐标（window-space coordinate）。它们的起始处是窗口的左下角。如果我们的窗口是800×600的，那么一个片段的窗口空间坐标x的范围就在0到800之间，y在0到600之间。
+
+我们可以使用片段着色器基于片段的窗口坐标计算出一个不同的颜色。`gl_FragCoord`变量的一个常用的方式是与一个不同的片段计算出来的视频输出进行对比，通常在技术演示中常见。比如我们可以把屏幕分为两个部分，窗口的左侧渲染一个输出，窗口的右边渲染另一个输出。下面是一个基于片段的窗口坐标的位置的不同输出不同的颜色的片段着色器：
 
-通过利用片段着色器，我们可以根据片段的窗口坐标，计算出不同的颜色。<var>gl_FragCoord</var>的一个常见用处是用于对比不同片段计算的视觉输出效果，这在技术演示中可以经常看到。比如说，我们能够将屏幕分成两部分，在窗口的左侧渲染一种输出，在窗口的右侧渲染另一种输出。下面这个例子片段着色器会根据窗口坐标输出不同的颜色：
 
 ```c++
 void main()
-{             
+{
     if(gl_FragCoord.x < 400)
-        FragColor = vec4(1.0, 0.0, 0.0, 1.0);
+        color = vec4(1.0f, 0.0f, 0.0f, 1.0f);
     else
-        FragColor = vec4(0.0, 1.0, 0.0, 1.0);        
+        color = vec4(0.0f, 1.0f, 0.0f, 1.0f);
 }
 ```
 
-因为窗口的宽度是800。当一个像素的x坐标小于400时，它一定在窗口的左侧，所以我们给它一个不同的颜色。
+因为窗口的宽是800，当一个像素的x坐标小于400，那么它一定在窗口的左边，这样我们就让物体有个不同的颜色。
 
-![](../img/04/08/advanced_glsl_fragcoord.png)
+![](http://learnopengl.com/img/advanced/advanced_glsl_frontfacing.png)
 
-我们现在会计算出两个完全不同的片段着色器结果，并将它们显示在窗口的两侧。举例来说，你可以将它用于测试不同的光照技巧。
+我们现在可以计算出两个完全不同的片段着色器结果，每个显示在窗口的一端。这对于测试不同的光照技术很有好处。
 
 ### gl_FrontFacing
 
-片段着色器另外一个很有意思的输入变量是<var>gl_FrontFacing</var>。在[面剔除](04 Face culling.md)教程中，我们提到OpenGL能够根据顶点的环绕顺序来决定一个面是正向还是背向面。如果我们不（启用<var>GL_FACE_CULL</var>来）使用面剔除，那么<var>gl_FrontFacing</var>将会告诉我们当前片段是属于正向面的一部分还是背向面的一部分。举例来说，我们能够对正向面计算出不同的颜色。
+片段着色器另一个有意思的输入变量是`gl_FrontFacing`变量。在面剔除教程中，我们提到过OpenGL可以根据顶点绘制顺序弄清楚一个面是正面还是背面。如果我们不适用面剔除，那么`gl_FrontFacing`变量能告诉我们当前片段是某个正面的一部分还是背面的一部分。然后我们可以决定做一些事情，比如为正面计算出不同的颜色。
 
-<var>gl_FrontFacing</var>变量是一个<fun>bool</fun>，如果当前片段是正向面的一部分那么就是`true`，否则就是`false`。比如说，我们可以这样子创建一个立方体，在内部和外部使用不同的纹理：
+`gl_FrontFacing`变量是一个布尔值，如果当前片段是正面的一部分那么就是true，否则就是false。这样我们可以创建一个立方体，里面和外面使用不同的纹理：
 
 ```c++
 #version 330 core
-out vec4 FragColor;
-  
+out vec4 color;
 in vec2 TexCoords;
 
 uniform sampler2D frontTexture;
 uniform sampler2D backTexture;
 
 void main()
-{             
+{
     if(gl_FrontFacing)
-        FragColor = texture(frontTexture, TexCoords);
+        color = texture(frontTexture, TexCoords);
     else
-        FragColor = texture(backTexture, TexCoords);
+        color = texture(backTexture, TexCoords);
 }
 ```
 
-如果我们往箱子里面看，就能看到使用的是不同的纹理。
+如果我们从箱子的一角往里看，就能看到里面用的是另一个纹理。
 
-![](../img/04/08/advanced_glsl_frontfacing.png)
+![](http://learnopengl.com/img/advanced/advanced_glsl_frontfacing.png)
 
-注意，如果你开启了面剔除，你就看不到箱子内部的面了，所以现在再使用<var>gl_FrontFacing</var>就没有意义了。
+注意，如果你开启了面剔除，你就看不到箱子里面有任何东西了，所以此时使用`gl_FrontFacing`毫无意义。
 
 ### gl_FragDepth
 
-输入变量<var>gl_FragCoord</var>能让我们读取当前片段的窗口空间坐标，并获取它的深度值，但是它是一个<def>只读</def>(Read-only)变量。我们不能修改片段的窗口空间坐标，但实际上修改片段的深度值还是可能的。GLSL提供给我们一个叫做<var>gl_FragDepth</var>的输出变量，我们可以使用它来在着色器内设置片段的深度值。
+输入变量`gl_FragCoord`让我们可以读得当前片段的窗口空间坐标和深度值，但是它是只读的。我们不能影响到这个片段的窗口屏幕坐标，但是可以设置这个像素的深度值。GLSL给我们提供了一个叫做`gl_FragDepth`的变量，我们可以用它在着色器中遂舍之像素的深度值。
 
-要想设置深度值，我们直接写入一个0.0到1.0之间的<fun>float</fun>值到输出变量就可以了：
+为了在着色器中设置深度值，我们简单的写一个0.0到1.0之间的float数，赋值给这个输出变量：
 
 ```c++
-gl_FragDepth = 0.0; // 这个片段现在的深度值为 0.0
+gl_FragDepth = 0.0f; //现在片段的深度值被设为0
 ```
 
-如果着色器没有写入值到<var>gl_FragDepth</var>，它会自动取用`gl_FragCoord.z`的值。
+如果着色器中没有像`gl_FragDepth`变量写入，它就会自动采用`gl_FragCoord.z`的值。
 
-然而，由我们自己设置深度值有一个很大的缺点，只要我们在片段着色器中对<var>gl_FragDepth</var>进行写入，OpenGL就会（像[深度测试](01 Depth testing.md)小节中讨论的那样）禁用所有的<def>提前深度测试</def>(Early Depth Testing)。它被禁用的原因是，OpenGL无法在片段着色器运行**之前**得知片段将拥有的深度值，因为片段着色器可能会完全修改这个深度值。
+我们自己设置深度值有一个显著缺点，因为只要我们在片段着色器中对`gl_FragDepth`写入什么，OpenGL就会关闭所有的前置深度测试。它被关闭的原因是，在我们运行片段着色器之前OpenGL搞不清像素的深度值，因为片段着色器可能会完全改变这个深度值。
 
-在写入<var>gl_FragDepth</var>时，你就需要考虑到它所带来的性能影响。然而，从OpenGL 4.2起，我们仍可以对两者进行一定的调和，在片段着色器的顶部使用<def>深度条件</def>(Depth Condition)重新声明<var>gl_FragDepth</var>变量：
+因此，你需要考虑到`gl_FragDepth`写入所带来的性能的下降。然而从OpenGL4.2起，我们仍然可以对二者进行一定的调和，这需要在片段着色器的顶部使用深度条件（depth condition）来重新声明`gl_FragDepth`：
 
 ```c++
 layout (depth_<condition>) out float gl_FragDepth;
 ```
 
-`condition`可以为下面的值：
+condition可以使用下面的值：
 
- 条件       | 描述
+Condition	| 描述
          ---|---
-`any`	    | 默认值。提前深度测试是禁用的，你会损失很多性能
-`greater`   | 你只能让深度值比`gl_FragCoord.z`更大
-`less`	    | 你只能让深度值比`gl_FragCoord.z`更小
-`unchanged`	| 如果你要写入`gl_FragDepth`，你将只能写入`gl_FragCoord.z`的值
+any	        | 默认值. 前置深度测试是关闭的，你失去了很多性能表现
+greater	    |深度值只能比gl_FragCoord.z大
+less	    |深度值只能设置得比gl_FragCoord.z小
+unchanged	|如果写入gl_FragDepth, 你就会写gl_FragCoord.z
 
-通过将深度条件设置为`greater`或者`less`，OpenGL就能假设你只会写入比当前片段深度值更大或者更小的值了。这样子的话，当深度值比片段的深度值要小的时候，OpenGL仍是能够进行提前深度测试的。
+如果把深度条件定义为greater或less，OpenGL会假定你只写入比当前的像素深度值的深度值大或小的。
 
-下面这个例子中，我们对片段的深度值进行了递增，但仍然也保留了一些提前深度测试：
-
-```c++
-#version 420 core // 注意GLSL的版本！
-out vec4 FragColor;
-layout (depth_greater) out float gl_FragDepth;
-
-void main()
-{             
-    FragColor = vec4(1.0);
-    gl_FragDepth = gl_FragCoord.z + 0.1;
-}  
-```
-
-注意这个特性只在OpenGL 4.2版本或以上才提供。
-
-# 接口块
-
-到目前为止，每当我们希望从顶点着色器向片段着色器发送数据时，我们都声明了几个对应的输入/输出变量。将它们一个一个声明是着色器间发送数据最简单的方式了，但当程序变得更大时，你希望发送的可能就不只是几个变量了，它还可能包括数组和结构体。
-
-为了帮助我们管理这些变量，GLSL为我们提供了一个叫做<def>接口块</def>(Interface Block)的东西，来方便我们组合这些变量。接口块的声明和<fun>struct</fun>的声明有点相像，不同的是，现在根据它是一个输入还是输出块(Block)，使用<fun>in</fun>或<fun>out</fun>关键字来定义的。
+下面是一个在片段着色器里增加深度值的例子，不过仍可开启前置深度测试：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;
-layout (location = 1) in vec2 aTexCoords;
+layout (depth_greater) out float gl_FragDepth;
+out vec4 color;
+
+void main()
+{
+    color = vec4(1.0f);
+    gl_FragDepth = gl_FragCoord.z + 0.1f;
+}
+```
+
+一定要记住这个功能只在OpenGL4.2以上版本才有。
+
+
+
+# 接口块
+
+到目前位置，每次我们打算从顶点向片段着色器发送数据，我们都会声明一个相互匹配的输出/输入变量。从一个着色器向另一个着色器发送数据，一次将它们声明好是最简单的方式，但是随着应用变得越来越大，你也许会打算发送的不仅仅是变量，最好还可以包括数组和结构体。
+
+为了帮助我们组织这些变量，GLSL为我们提供了一些叫做接口块(Interface Blocks)的东西，好让我们能够组织这些变量。声明接口块和声明struct有点像，不同之处是它现在基于块（block），使用in和out关键字来声明，最后它将成为一个输入或输出块（block）。
+
+```c++
+#version 330 core
+layout (location = 0) in vec3 position;
+layout (location = 1) in vec2 texCoords;
 
 uniform mat4 model;
 uniform mat4 view;
@@ -181,18 +186,18 @@ out VS_OUT
 
 void main()
 {
-    gl_Position = projection * view * model * vec4(aPos, 1.0);    
-    vs_out.TexCoords = aTexCoords;
-}  
+    gl_Position = projection * view * model * vec4(position, 1.0f);
+    vs_out.TexCoords = texCoords;
+}
 ```
 
-这次我们声明了一个叫做<var>vs_out</var>的接口块，它打包了我们希望发送到下一个着色器中的所有输出变量。这只是一个很简单的例子，但你可以想象一下，它能够帮助你管理着色器的输入和输出。当我们希望将着色器的输入或输出打包为数组时，它也会非常有用，我们将在[下一节](09 Geometry Shader.md)讨论几何着色器(Geometry Shader)时见到。
+这次我们声明一个叫做vs_out的接口块，它把我们需要发送给下个阶段着色器的所有输出变量组合起来。虽然这是一个微不足道的例子，但是你可以想象一下，它的确能够帮助我们组织着色器的输入和输出。当我们希望把着色器的输入和输出组织成数组的时候它就变得很有用，我们会在下节几何着色器(geometry)中见到。
 
-之后，我们还需要在下一个着色器，即片段着色器，中定义一个输入接口块。<def>块名</def>(Block Name)应该是和着色器中一样的（<fun>VS_OUT</fun>），但<var>实例名</var>(Instance Name)（顶点着色器中用的是<var>vs_out</var>）可以是随意的，但要避免使用误导性的名称，比如对实际上包含输入变量的接口块命名为<var>vs_out</var>。
+然后，我们还需要在下一个着色器——片段着色器中声明一个输入interface block。块名（block name）应该是一样的，但是实例名可以是任意的。
 
 ```c++
 #version 330 core
-out vec4 FragColor;
+out vec4 color;
 
 in VS_OUT
 {
@@ -202,24 +207,24 @@ in VS_OUT
 uniform sampler2D texture;
 
 void main()
-{             
-    FragColor = texture(texture, fs_in.TexCoords);   
+{
+    color = texture(texture, fs_in.TexCoords);
 }
 ```
 
-只要两个接口块的名字一样，它们对应的输入和输出将会匹配起来。这是帮助你管理代码的又一个有用特性，它在几何着色器这样穿插特定着色器阶段的场景下会很有用。
+如果两个interface block名一致，它们对应的输入和输出就会匹配起来。这是另一个可以帮助我们组织代码的有用功能，特别是在跨着色阶段的情况，比如几何着色器。
 
 # Uniform缓冲对象
 
-我们已经使用OpenGL很长时间了，学会了一些很酷的技巧，但也遇到了一些很麻烦的地方。比如说，当使用多于一个的着色器时，尽管大部分的uniform变量都是相同的，我们还是需要不断地设置它们，所以为什么要这么麻烦地重复设置它们呢？
+我们使用OpenGL很长时间了，也学到了一些很酷的技巧，但是产生了一些烦恼。比如说，当时用一个以上的着色器的时候，我们必须一次次设置uniform变量，尽管对于每个着色器来说它们都是一样的，所以为什么还麻烦地多次设置它们呢？
 
-OpenGL为我们提供了一个叫做<def>Uniform缓冲对象</def>(Uniform Buffer Object)的工具，它允许我们定义一系列在多个着色器程序中相同的**全局**Uniform变量。当使用Uniform缓冲对象的时候，我们只需要设置相关的uniform**一次**。当然，我们仍需要手动设置每个着色器中不同的uniform。并且创建和配置Uniform缓冲对象会有一点繁琐。
+OpenGL为我们提供了一个叫做uniform缓冲对象(Uniform Buffer Object)的工具，使我们能够声明一系列的全局uniform变量， 它们会在几个着色器程序中保持一致。当时用uniform缓冲的对象时相关的uniform只能设置一次。我们仍需为每个着色器手工设置唯一的uniform。创建和配置一个uniform缓冲对象需要费点功夫。
 
-因为Uniform缓冲对象仍是一个缓冲，我们可以使用<fun>glGenBuffers</fun>来创建它，将它绑定到<var>GL_UNIFORM_BUFFER</var>缓冲目标，并将所有相关的uniform数据存入缓冲。在Uniform缓冲对象中储存数据是有一些规则的，我们将会在之后讨论它。首先，我们将使用一个简单的顶点着色器，将<var>projection</var>和<var>view</var>矩阵存储到所谓的<def>Uniform块</def>(Uniform Block)中：
+因为uniform缓冲对象是一个缓冲，因此我们可以使用`glGenBuffers`创建一个，然后绑定到`GL_UNIFORM_BUFFER`缓冲目标上，然后把所有相关uniform数据存入缓冲。有一些原则，像uniform缓冲对象如何储存数据，我们会在稍后讨论。首先我们我们在一个简单的顶点着色器中，用uniform块(uniform block)储存投影和视图矩阵：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;
+layout (location = 0) in vec3 position;
 
 layout (std140) uniform Matrices
 {
@@ -231,143 +236,146 @@ uniform mat4 model;
 
 void main()
 {
-    gl_Position = projection * view * model * vec4(aPos, 1.0);
+    gl_Position = projection * view * model * vec4(position, 1.0);
 }
 ```
 
-在我们大多数的例子中，我们都会在每个渲染迭代中，对每个着色器设置<var>projection</var>和<var>view</var> Uniform矩阵。这是利用Uniform缓冲对象的一个非常完美的例子，因为现在我们只需要存储这些矩阵一次就可以了。
+前面，大多数例子里我们在每次渲染迭代，都为projection和view矩阵设置uniform。这个例子里使用了uniform缓冲对象，这非常有用，因为这些矩阵我们设置一次就行了。
+
+在这里我们声明了一个叫做Matrices的uniform块，它储存两个4×4矩阵。在uniform块中的变量可以直接获取，而不用使用block名作为前缀。接着我们在缓冲中储存这些矩阵的值，每个声明了这个uniform块的着色器都能够获取矩阵。
+
+现在你可能会奇怪layout(std140)是什么意思。它的意思是说当前定义的uniform块为它的内容使用特定的内存布局，这个声明实际上是设置uniform块布局(uniform block layout)。
 
-这里，我们声明了一个叫做<var>Matrices</var>的Uniform块，它储存了两个4x4矩阵。Uniform块中的变量可以直接访问，不需要加块名作为前缀。接下来，我们在OpenGL代码中将这些矩阵值存入缓冲中，每个声明了这个Uniform块的着色器都能够访问这些矩阵。
 
-你现在可能会在想`layout (std140)`这个语句是什么意思。它的意思是说，当前定义的Uniform块对它的内容使用一个特定的内存布局。这个语句设置了<def>Uniform块布局</def>(Uniform Block Layout)。
 
 ## Uniform块布局
 
-Uniform块的内容是储存在一个缓冲对象中的，它实际上只是一块预留内存。因为这块内存并不会保存它具体保存的是什么类型的数据，我们还需要告诉OpenGL内存的哪一部分对应着着色器中的哪一个uniform变量。
+一个uniform块的内容被储存到一个缓冲对象中，实际上就是在一块内存中。因为这块内存也不清楚它保存着什么类型的数据，我们就必须告诉OpenGL哪一块内存对应着色器中哪一个uniform变量。
 
-假设着色器中有以下的这个Uniform块：
+假想下面的uniform块在一个着色器中：
 
 ```c++
 layout (std140) uniform ExampleBlock
 {
     float value;
-    vec3  vector;
-    mat4  matrix;
+    vec3 vector;
+    mat4 matrix;
     float values[3];
-    bool  boolean;
-    int   integer;
+    bool boolean;
+    int integer;
 };
 ```
 
-我们需要知道的是每个变量的大小（字节）和（从块起始位置的）偏移量，来让我们能够按顺序将它们放进缓冲中。每个元素的大小都是在OpenGL中有清楚地声明的，而且直接对应C++数据类型，其中向量和矩阵都是大的float数组。OpenGL没有声明的是这些变量间的<def>间距</def>(Spacing)。这允许硬件能够在它认为合适的位置放置变量。比如说，一些硬件可能会将一个<fun>vec3</fun>放置在<fun>float</fun>边上。不是所有的硬件都能这样处理，可能会在附加这个<fun>float</fun>之前，先将<fun>vec3</fun>填充(Pad)为一个4个float的数组。这个特性本身很棒，但是会对我们造成麻烦。
+我们所希望知道的是每个变量的大小（以字节为单位）和偏移量（从block的起始处），所以我们可以以各自的顺序把它们放进一个缓冲里。每个元素的大小在OpenGL中都很清楚，直接与C++数据类型呼应，向量和矩阵是一个float序列（数组）。OpenGL没有澄清的是变量之间的间距。这让硬件能以它认为合适的位置方式变量。比如有些硬件可以在float旁边放置一个vec3。不是所有硬件都能这样做，在vec3旁边附加一个float之前，给vec3加一个边距使之成为4个（空间连续的）float数组。功能很好，但对于我们来说用起来不方便。
 
-默认情况下，GLSL会使用一个叫做<def>共享</def>(Shared)布局的Uniform内存布局，共享是因为一旦硬件定义了偏移量，它们在多个程序中是**共享**并一致的。使用共享布局时，GLSL是可以为了优化而对uniform变量的位置进行变动的，只要变量的顺序保持不变。因为我们无法知道每个uniform变量的偏移量，我们也就不知道如何准确地填充我们的Uniform缓冲了。我们能够使用像是<fun>glGetUniformIndices</fun>这样的函数来查询这个信息，但这超出本节的范围了。
+GLSL 默认使用的uniform内存布局叫做共享布局(shared layout)，叫共享是因为一旦偏移量被硬件定义，它们就会持续地被多个程序所共享。使用共享布局，GLSL可以为了优化而重新放置uniform变量，只要变量的顺序保持完整。因为我们不知道每个uniform变量的偏移量是多少，所以我们也就不知道如何精确地填充uniform缓冲。我们可以使用像`glGetUniformIndices`这样的函数来查询这个信息，但是这超出了本节教程的范围。
 
-虽然共享布局给了我们很多节省空间的优化，但是我们需要查询每个uniform变量的偏移量，这会产生非常多的工作量。通常的做法是，不使用共享布局，而是使用<def>std140</def>布局。std140布局声明了每个变量的偏移量都是由一系列规则所决定的，这**显式地**声明了每个变量类型的内存布局。由于这是显式提及的，我们可以手动计算出每个变量的偏移量。
+由于共享布局给我们做了一些空间优化。通常在实践中并不适用分享布局，而是使用std140布局。std140通过一系列的规则的规范声明了它们各自的偏移量，std140布局为每个变量类型显式地声明了内存的布局。由于被显式的提及，我们就可以手工算出每个变量的偏移量。
 
-每个变量都有一个<def>基准对齐量</def>(Base Alignment)，它等于一个变量在Uniform块中所占据的空间（包括填充量(Padding)），这个基准对齐量是使用std140布局的规则计算出来的。接下来，对每个变量，我们再计算它的<def>对齐偏移量</def>(Aligned Offset)，它是一个变量从块起始位置的字节偏移量。一个变量的对齐字节偏移量**必须**等于基准对齐量的倍数。
+每个变量都有一个基线对齐(base alignment)，它等于在一个uniform块中这个变量所占的空间（包含边距），这个基线对齐是使用std140布局原则计算出来的。然后，我们为每个变量计算出它的对齐偏移(aligned offset)，这是一个变量从块（block）开始处的字节偏移量。变量对齐的字节偏移一定等于它的基线对齐的倍数。
 
-布局规则的原文可以在OpenGL的Uniform缓冲规范[这里](http://www.opengl.org/registry/specs/ARB/uniform_buffer_object.txt)找到，但我们将会在下面列出最常见的规则。GLSL中的每个变量，比如说<fun>int</fun>、<fun>float</fun>和<fun>bool</fun>，都被定义为4字节量。每4个字节将会用一个`N`来表示。
+准确的布局规则可以[在OpenGL的uniform缓冲规范](http://www.opengl.org/registry/specs/ARB/uniform_buffer_object.txt)中得到，但我们会列出最常见的规范。GLSL中每个变量类型比如int、float和bool被定义为4字节，每4字节被表示为N。
 
-类型	    | 布局规则
+类型	    | 布局规范
          ---|---
-标量，比如<fun>int</fun>和<fun>bool</fun> |	每个标量的基准对齐量为N。
-向量      |	2N或者4N。这意味着<fun>vec3</fun>的基准对齐量为4N。
-标量或向量的数组	| 每个元素的基准对齐量与<fun>vec4</fun>的相同。
-矩阵  | 储存为列向量的数组，每个向量的基准对齐量与<fun>vec4</fun>的相同。
-结构体 | 等于所有元素根据规则计算后的大小，但会填充到<fun>vec4</fun>大小的倍数。
+像int和bool这样的标量 |	每个标量的基线为N
+向量      |	每个向量的基线是2N或4N大小。这意味着vec3的基线为4N
+标量与向量数组	| 每个元素的基线与vec4的相同
+矩阵  | 被看做是存储着大量向量的数组，每个元素的基数与vec4相同
+结构体 | 根据以上规则计算其各个元素，并且间距必须是vec4基线的倍数
 
-和OpenGL大多数的规范一样，使用例子就能更容易地理解。我们会使用之前引入的那个叫做<var>ExampleBlock</var>的Uniform块，并使用std140布局计算出每个成员的对齐偏移量：
+像OpenGL大多数规范一样，举个例子就很容易理解。再次利用之前介绍的uniform块`ExampleBlock`，我们用std140布局，计算它的每个成员的aligned offset（对齐偏移）：
 
 ```c++
 layout (std140) uniform ExampleBlock
 {
-                     // 基准对齐量       // 对齐偏移量
-    float value;     // 4               // 0 
-    vec3 vector;     // 16              // 16  (必须是16的倍数，所以 4->16)
-    mat4 matrix;     // 16              // 32  (列 0)
-                     // 16              // 48  (列 1)
-                     // 16              // 64  (列 2)
-                     // 16              // 80  (列 3)
-    float values[3]; // 16              // 96  (values[0])
-                     // 16              // 112 (values[1])
-                     // 16              // 128 (values[2])
-    bool boolean;    // 4               // 144
-    int integer;     // 4               // 148
-}; 
+                     // base alignment ----------  // aligned offset
+    float value;     // 4                          // 0
+    vec3 vector;     // 16                         // 16 (必须是16的倍数，因此 4->16)
+    mat4 matrix;     // 16                         // 32  (第 0 行)
+                     // 16                         // 48  (第 1 行)
+                     // 16                         // 64  (第 2 行)
+                     // 16                         // 80  (第 3 行)
+    float values[3]; // 16 (数组中的标量与vec4相同)//96 (values[0])
+                     // 16                        // 112 (values[1])
+                     // 16                        // 128 (values[2])
+    bool boolean;    // 4                         // 144
+    int integer;     // 4                         // 148
+};
 ```
 
-作为练习，尝试去自己计算一下偏移量，并和表格进行对比。使用计算后的偏移量值，根据std140布局的规则，我们就能使用像是<fun>glBufferSubData</fun>的函数将变量数据按照偏移量填充进缓冲中了。虽然std140布局不是最高效的布局，但它保证了内存布局在每个声明了这个Uniform块的程序中是一致的。
+尝试自己计算出偏移量，把它们和表格对比，你可以把这件事当作一个练习。使用计算出来的偏移量，根据std140布局规则，我们可以用`glBufferSubData`这样的函数，使用变量数据填充缓冲。虽然不是很高效，但std140布局可以保证在每个程序中声明的这个uniform块的布局保持一致。
 
-通过在Uniform块定义之前添加`layout (std140)`语句，我们告诉OpenGL这个Uniform块使用的是std140布局。除此之外还可以选择两个布局，但它们都需要我们在填充缓冲之前先查询每个偏移量。我们已经见过`shared`布局了，剩下的一个布局是`packed`。当使用紧凑(Packed)布局时，是不能保证这个布局在每个程序中保持不变的（即非共享），因为它允许编译器去将uniform变量从Uniform块中优化掉，这在每个着色器中都可能是不同的。
+在定义uniform块前面添加layout (std140)声明，我们就能告诉OpenGL这个uniform块使用了std140布局。另外还有两种其他的布局可以选择，它们需要我们在填充缓冲之前查询每个偏移量。我们已经了解了分享布局（shared layout）和其他的布局都将被封装（packed）。当使用封装（packed）布局的时候，不能保证布局在别的程序中能够保持一致，因为它允许编译器从uniform块中优化出去uniform变量，这在每个着色器中都可能不同。
 
-## 使用Uniform缓冲
+## 使用uniform缓冲
 
-我们已经讨论了如何在着色器中定义Uniform块，并设定它们的内存布局了，但我们还没有讨论该如何使用它们。
+我们讨论了uniform块在着色器中的定义和如何定义它们的内存布局，但是我们还没有讨论如何使用它们。
 
-首先，我们需要调用<fun>glGenBuffers</fun>，创建一个Uniform缓冲对象。一旦我们有了一个缓冲对象，我们需要将它绑定到<var>GL_UNIFORM_BUFFER</var>目标，并调用<fun>glBufferData</fun>，分配足够的内存。
+首先我们需要创建一个uniform缓冲对象，这要使用`glGenBuffers`来完成。当我们拥有了一个缓冲对象，我们就把它绑定到`GL_UNIFORM_BUFFER`目标上，调用`glBufferData`来给它分配足够的空间。
 
 ```c++
-unsigned int uboExampleBlock;
+GLuint uboExampleBlock;
 glGenBuffers(1, &uboExampleBlock);
 glBindBuffer(GL_UNIFORM_BUFFER, uboExampleBlock);
-glBufferData(GL_UNIFORM_BUFFER, 152, NULL, GL_STATIC_DRAW); // 分配152字节的内存
+glBufferData(GL_UNIFORM_BUFFER, 150, NULL, GL_STATIC_DRAW); // 分配150个字节的内存空间
 glBindBuffer(GL_UNIFORM_BUFFER, 0);
 ```
 
-现在，每当我们需要对缓冲更新或者插入数据，我们都会绑定到<var>uboExampleBlock</var>，并使用<fun>glBufferSubData</fun>来更新它的内存。我们只需要更新这个Uniform缓冲一次，所有使用这个缓冲的着色器就都使用的是更新后的数据了。但是，如何才能让OpenGL知道哪个Uniform缓冲对应的是哪个Uniform块呢？
+现在任何时候当我们打算往缓冲中更新或插入数据，我们就绑定到`uboExampleBlock`上，并使用`glBufferSubData`来更新它的内存。我们只需要更新这个uniform缓冲一次，所有的使用这个缓冲着色器就都会使用它更新的数据了。但是，OpenGL是如何知道哪个uniform缓冲对应哪个uniform块呢？
 
-在OpenGL上下文中，定义了一些<def>绑定点</def>(Binding Point)，我们可以将一个Uniform缓冲链接至它。在创建Uniform缓冲之后，我们将它绑定到其中一个绑定点上，并将着色器中的Uniform块绑定到相同的绑定点，把它们连接到一起。下面的这个图示展示了这个：
+在OpenGL环境（context）中，定义了若干绑定点（binding points），在哪儿我们可以把一个uniform缓冲链接上去。当我们创建了一个uniform缓冲，我们把它链接到一个这个绑定点上，我们也把着色器中uniform块链接到同一个绑定点上，这样就把它们链接到一起了。下面的图标表示了这点：
 
-![](../img/04/08/advanced_glsl_binding_points.png)
+![](http://learnopengl.com/img/advanced/advanced_glsl_binding_points.png)
 
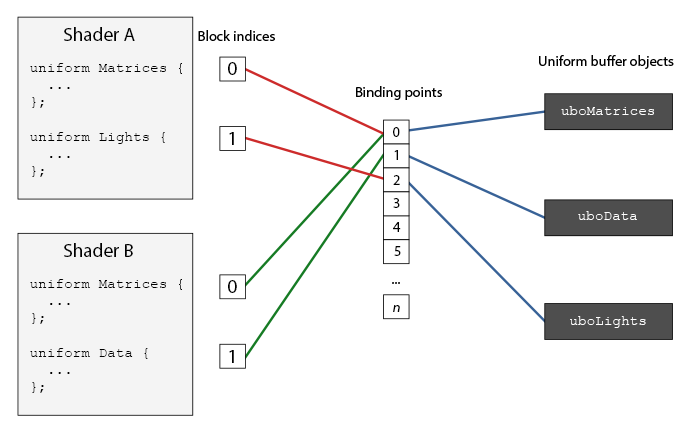
-你可以看到，我们可以绑定多个Uniform缓冲到不同的绑定点上。因为着色器A和着色器B都有一个链接到绑定点0的Uniform块，它们的Uniform块将会共享相同的uniform数据，<var>uboMatrices</var>，前提条件是两个着色器都定义了相同的<var>Matrices</var> Uniform块。
+你可以看到，我们可以将多个uniform缓冲绑定到不同绑定点上。因为着色器A和着色器B都有一个链接到同一个绑定点0的uniform块，它们的uniform块分享同样的uniform数据—`uboMatrices`有一个前提条件是两个着色器必须都定义了Matrices这个uniform块。
 
-为了将Uniform块绑定到一个特定的绑定点中，我们需要调用<fun>glUniformBlockBinding</fun>函数，它的第一个参数是一个程序对象，之后是一个Uniform块索引和链接到的绑定点。<def>Uniform块索引</def>(Uniform Block Index)是着色器中已定义Uniform块的位置值索引。这可以通过调用<fun>glGetUniformBlockIndex</fun>来获取，它接受一个程序对象和Uniform块的名称。我们可以用以下方式将图示中的<var>Lights</var> Uniform块链接到绑定点2：
+我们调用`glUniformBlockBinding`函数来把uniform块设置到一个特定的绑定点上。函数的第一个参数是一个程序对象，接着是一个uniform块索引（uniform block index）和打算链接的绑定点。uniform块索引是一个着色器中定义的uniform块的索引位置，可以调用`glGetUniformBlockIndex`来获取这个值，这个函数接收一个程序对象和uniform块的名字。我们可以从图表设置Lights这个uniform块链接到绑定点2：
 
 ```c++
-unsigned int lights_index = glGetUniformBlockIndex(shaderA.ID, "Lights");   
-glUniformBlockBinding(shaderA.ID, lights_index, 2);
+GLuint lights_index = glGetUniformBlockIndex(shaderA.Program, "Lights");
+glUniformBlockBinding(shaderA.Program, lights_index, 2);
 ```
 
-注意我们需要对**每个**着色器重复这一步骤。
+注意，我们必须在每个着色器中重复做这件事。
 
-!!! important
+从OpenGL4.2起，也可以在着色器中通过添加另一个布局标识符来储存一个uniform块的绑定点，就不用我们调用`glGetUniformBlockIndex`和`glUniformBlockBinding`了。下面的代表显式设置了Lights这个uniform块的绑定点：
 
-	从OpenGL 4.2版本起，你也可以添加一个布局标识符，显式地将Uniform块的绑定点储存在着色器中，这样就不用再调用<fun>glGetUniformBlockIndex</fun>和<fun>glUniformBlockBinding</fun>了。下面的代码显式地设置了<var>Lights</var> Uniform块的绑定点。
-
-		layout(std140, binding = 2) uniform Lights { ... };
-
-接下来，我们还需要绑定Uniform缓冲对象到相同的绑定点上，这可以使用<fun>glBindBufferBase</fun>或<fun>glBindBufferRange</fun>来完成。
 
 ```c++
-glBindBufferBase(GL_UNIFORM_BUFFER, 2, uboExampleBlock); 
-// 或
-glBindBufferRange(GL_UNIFORM_BUFFER, 2, uboExampleBlock, 0, 152);
+layout(std140, binding = 2) uniform Lights { ... };
 ```
 
-<fun>glBindbufferBase</fun>需要一个目标，一个绑定点索引和一个Uniform缓冲对象作为它的参数。这个函数将<var>uboExampleBlock</var>链接到绑定点2上，自此，绑定点的两端都链接上了。你也可以使用<fun>glBindBufferRange</fun>函数，它需要一个附加的偏移量和大小参数，这样子你可以绑定Uniform缓冲的特定一部分到绑定点中。通过使用<fun>glBindBufferRange</fun>函数，你可以让多个不同的Uniform块绑定到同一个Uniform缓冲对象上。
+然后我们还需要把uniform缓冲对象绑定到同样的绑定点上，这个可以使用`glBindBufferBase`或`glBindBufferRange`来完成。
 
-现在，所有的东西都配置完毕了，我们可以开始向Uniform缓冲中添加数据了。只要我们需要，就可以使用<fun>glBufferSubData</fun>函数，用一个字节数组添加所有的数据，或者更新缓冲的一部分。要想更新uniform变量<var>boolean</var>，我们可以用以下方式更新Uniform缓冲对象：
+```c++
+glBindBufferBase(GL_UNIFORM_BUFFER, 2, uboExampleBlock);
+// 或者
+glBindBufferRange(GL_UNIFORM_BUFFER, 2, uboExampleBlock, 0, 150);
+```
+
+函数`glBindBufferBase`接收一个目标、一个绑定点索引和一个uniform缓冲对象作为它的参数。这个函数把`uboExampleBlock`链接到绑定点2上面，自此绑定点所链接的两端都链接在一起了。你还可以使用`glBindBufferRange`函数，这个函数还需要一个偏移量和大小作为参数，这样你就可以只把一定范围的uniform缓冲绑定到一个绑定点上了。使用`glBindBufferRage`函数，你能够将多个不同的uniform块链接到同一个uniform缓冲对象上。
+
+现在所有事情都做好了，我们可以开始向uniform缓冲添加数据了。我们可以使用`glBufferSubData`将所有数据添加为一个单独的字节数组或者更新缓冲的部分内容，只要我们愿意。为了更新uniform变量boolean，我们可以这样更新uniform缓冲对象：
 
 ```c++
 glBindBuffer(GL_UNIFORM_BUFFER, uboExampleBlock);
-int b = true; // GLSL中的bool是4字节的，所以我们将它存为一个integer
-glBufferSubData(GL_UNIFORM_BUFFER, 144, 4, &b); 
+GLint b = true; // GLSL中的布尔值是4个字节，因此我们将它创建为一个4字节的整数
+glBufferSubData(GL_UNIFORM_BUFFER, 142, 4, &b);
 glBindBuffer(GL_UNIFORM_BUFFER, 0);
 ```
 
-同样的步骤也能应用到Uniform块中其它的uniform变量上，但需要使用不同的范围参数。
+同样的处理也能够应用到uniform块中其他uniform变量上。
 
 ## 一个简单的例子
 
-所以，我们来展示一个真正使用Uniform缓冲对象的例子。如果我们回头看看之前所有的代码例子，我们不断地在使用3个矩阵：投影、观察和模型矩阵。在所有的这些矩阵中，只有模型矩阵会频繁变动。如果我们有多个着色器使用了这同一组矩阵，那么使用Uniform缓冲对象可能会更好。
+我们来师范一个真实的使用uniform缓冲对象的例子。如果我们回头看看前面所有演示的代码，我们一直使用了3个矩阵：投影、视图和模型矩阵。所有这些矩阵中，只有模型矩阵是频繁变化的。如果我们有多个着色器使用了这些矩阵，我们可能最好还是使用uniform缓冲对象。
 
-我们会将投影和模型矩阵存储到一个叫做<var>Matrices</var>的Uniform块中。我们不会将模型矩阵存在这里，因为模型矩阵在不同的着色器中会不断改变，所以使用Uniform缓冲对象并不会带来什么好处。
+我们将把投影和视图矩阵储存到一个uniform块中，它被取名为Matrices。我们不打算储存模型矩阵，因为模型矩阵会频繁在着色器间更改，所以使用uniform缓冲对象真的不会带来什么好处。
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;
+layout (location = 0) in vec3 position;
 
 layout (std140) uniform Matrices
 {
@@ -378,79 +386,81 @@ uniform mat4 model;
 
 void main()
 {
-    gl_Position = projection * view * model * vec4(aPos, 1.0);
+    gl_Position = projection * view * model * vec4(position, 1.0);
 }
 ```
 
-这里没什么特别的，除了我们现在使用的是一个std140布局的Uniform块。我们将在例子程序中，显示4个立方体，每个立方体都是使用不同的着色器程序渲染的。这4个着色器程序将使用相同的顶点着色器，但使用的是不同的片段着色器，每个着色器会输出不同的颜色。
+这儿没什么特别的，除了我们现在使用了一个带有std140布局的uniform块。我们在例程中将显示4个立方体，每个立方体都使用一个不同的着色器程序。4个着色器程序使用同样的顶点着色器，但是它们将使用各自的片段着色器，每个片段着色器输出一个单色。
 
-首先，我们将顶点着色器的Uniform块设置为绑定点0。注意我们需要对每个着色器都设置一遍。
+首先，我们把顶点着色器的uniform块设置为绑定点0。注意，我们必须为每个着色器做这件事。
 
 ```c++
-unsigned int uniformBlockIndexRed    = glGetUniformBlockIndex(shaderRed.ID, "Matrices");
-unsigned int uniformBlockIndexGreen  = glGetUniformBlockIndex(shaderGreen.ID, "Matrices");
-unsigned int uniformBlockIndexBlue   = glGetUniformBlockIndex(shaderBlue.ID, "Matrices");
-unsigned int uniformBlockIndexYellow = glGetUniformBlockIndex(shaderYellow.ID, "Matrices");  
-  
-glUniformBlockBinding(shaderRed.ID,    uniformBlockIndexRed, 0);
-glUniformBlockBinding(shaderGreen.ID,  uniformBlockIndexGreen, 0);
-glUniformBlockBinding(shaderBlue.ID,   uniformBlockIndexBlue, 0);
-glUniformBlockBinding(shaderYellow.ID, uniformBlockIndexYellow, 0);
+GLuint uniformBlockIndexRed = glGetUniformBlockIndex(shaderRed.Program, "Matrices");
+GLuint uniformBlockIndexGreen = glGetUniformBlockIndex(shaderGreen.Program, "Matrices");
+GLuint uniformBlockIndexBlue = glGetUniformBlockIndex(shaderBlue.Program, "Matrices");
+GLuint uniformBlockIndexYellow = glGetUniformBlockIndex(shaderYellow.Program, "Matrices");  
+
+glUniformBlockBinding(shaderRed.Program, uniformBlockIndexRed, 0);
+glUniformBlockBinding(shaderGreen.Program, uniformBlockIndexGreen, 0);
+glUniformBlockBinding(shaderBlue.Program, uniformBlockIndexBlue, 0);
+glUniformBlockBinding(shaderYellow.Program, uniformBlockIndexYellow, 0);
 ```
 
-接下来，我们创建Uniform缓冲对象本身，并将其绑定到绑定点0：
+然后，我们创建真正的uniform缓冲对象，并把缓冲绑定到绑定点0：
 
 ```c++
-unsigned int uboMatrices
+GLuint uboMatrices
 glGenBuffers(1, &uboMatrices);
-  
+
 glBindBuffer(GL_UNIFORM_BUFFER, uboMatrices);
 glBufferData(GL_UNIFORM_BUFFER, 2 * sizeof(glm::mat4), NULL, GL_STATIC_DRAW);
 glBindBuffer(GL_UNIFORM_BUFFER, 0);
-  
+
 glBindBufferRange(GL_UNIFORM_BUFFER, 0, uboMatrices, 0, 2 * sizeof(glm::mat4));
 ```
 
-首先我们为缓冲分配了足够的内存，它等于<fun>glm::mat4</fun>大小的两倍。GLM矩阵类型的大小直接对应于GLSL中的<fun>mat4</fun>。接下来，我们将缓冲中的特定范围（在这里是整个缓冲）链接到绑定点0。
+我们先为缓冲分配足够的内存，它等于glm::mat4的2倍。GLM的矩阵类型的大小直接对应于GLSL的mat4。然后我们把一个特定范围的缓冲链接到绑定点0，这个例子中应该是整个缓冲。
 
-剩余的就是填充这个缓冲了。如果我们将投影矩阵的**视野**(Field of View)值保持不变（所以摄像机就没有缩放了），我们只需要将其在程序中定义一次——这也意味着我们只需要将它插入到缓冲中一次。因为我们已经为缓冲对象分配了足够的内存，我们可以使用<fun>glBufferSubData</fun>在进入渲染循环之前存储投影矩阵：
+现在所有要做的事只剩下填充缓冲了。如果我们把视野（ field of view）值保持为恒定的投影矩阵（这样就不会有摄像机缩放），我们只要在程序中定义它一次就行了，这也意味着我们只需向缓冲中把它插入一次。因为我们已经在缓冲对象中分配了足够的内存，我们可以在我们进入游戏循环之前使用`glBufferSubData`来储存投影矩阵：
 
 ```c++
-glm::mat4 projection = glm::perspective(glm::radians(45.0f), (float)width/(float)height, 0.1f, 100.0f);
+glm::mat4 projection = glm::perspective(45.0f, (float)width/(float)height, 0.1f, 100.0f);
 glBindBuffer(GL_UNIFORM_BUFFER, uboMatrices);
 glBufferSubData(GL_UNIFORM_BUFFER, 0, sizeof(glm::mat4), glm::value_ptr(projection));
 glBindBuffer(GL_UNIFORM_BUFFER, 0);
 ```
 
-这里我们将投影矩阵储存在Uniform缓冲的前半部分。在每次渲染迭代中绘制物体之前，我们会将观察矩阵更新到缓冲的后半部分：
+这里我们用投影矩阵储存了uniform缓冲的前半部分。在我们在每次渲染迭代绘制物体前，我们用视图矩阵更新缓冲的第二个部分：
 
 ```c++
-glm::mat4 view = camera.GetViewMatrix();	       
+glm::mat4 view = camera.GetViewMatrix();
 glBindBuffer(GL_UNIFORM_BUFFER, uboMatrices);
-glBufferSubData(GL_UNIFORM_BUFFER, sizeof(glm::mat4), sizeof(glm::mat4), glm::value_ptr(view));
+glBufferSubData(
+  GL_UNIFORM_BUFFER, sizeof(glm::mat4), sizeof(glm::mat4), glm::value_ptr(view));
 glBindBuffer(GL_UNIFORM_BUFFER, 0);
 ```
 
-Uniform缓冲对象的部分就结束了。每个包含了<var>Matrices</var>这个Uniform块的顶点着色器将会包含储存在<var>uboMatrices</var>中的数据。所以，如果我们现在要用4个不同的着色器绘制4个立方体，它们的投影和观察矩阵都会是一样的。
+这就是uniform缓冲对象。每个包含着`Matrices`这个uniform块的顶点着色器都将对应`uboMatrices`所储存的数据。所以如果我们现在使用4个不同的着色器绘制4个立方体，它们的投影和视图矩阵都是一样的：
 
 ```c++
 glBindVertexArray(cubeVAO);
-shaderRed.use();
+shaderRed.Use();
 glm::mat4 model;
-model = glm::translate(model, glm::vec3(-0.75f, 0.75f, 0.0f));	// 移动到左上角
-shaderRed.setMat4("model", model);
-glDrawArrays(GL_TRIANGLES, 0, 36);        
+model = glm::translate(model, glm::vec3(-0.75f, 0.75f, 0.0f)); // 移动到左上方
+glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
+glDrawArrays(GL_TRIANGLES, 0, 36);
 // ... 绘制绿色立方体
 // ... 绘制蓝色立方体
-// ... 绘制黄色立方体 
+// ... 绘制黄色立方体
+glBindVertexArray(0);
 ```
 
-唯一需要设置的uniform只剩<var>model</var> uniform了。在像这样的场景中使用Uniform缓冲对象会让我们在每个着色器中都剩下一些uniform调用。最终的结果会是这样的：
+我们只需要在去设置一个`model`的uniform即可。在一个像这样的场景中使用uniform缓冲对象在每个着色器中可以减少uniform的调用。最后效果看起来像这样：
 
-![](../img/04/08/advanced_glsl_uniform_buffer_objects.png)
+![](http://learnopengl.com/img/advanced/advanced_glsl_uniform_buffer_objects.png)
 
-因为修改了模型矩阵，每个立方体都移动到了窗口的一边，并且由于使用了不同的片段着色器，它们的颜色也不同。这只是一个很简单的情景，我们可能会需要使用Uniform缓冲对象，但任何大型的渲染程序都可能同时激活有上百个着色器程序，这时候Uniform缓冲对象的优势就会很大地体现出来了。
+通过改变模型矩阵，每个立方体都移动到窗口的一边，由于片段着色器不同，物体的颜色也不同。这是一个相对简单的场景，我们可以使用uniform缓冲对象，但是任何大型渲染程序有成百上千的活动着色程序，彼时uniform缓冲对象就会闪闪发光了。
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/8.advanced_glsl_ubo/advanced_glsl_ubo.cpp)找到uniform例子程序的完整源代码。
+你可以[在这里获得例程的完整源码](http://www.learnopengl.com/code_viewer.php?code=advanced/advanced_glsl_uniform_buffer_objects)。
 
-Uniform缓冲对象比起独立的uniform有很多好处。第一，一次设置很多uniform会比一个一个设置多个uniform要快很多。第二，比起在多个着色器中修改同样的uniform，在Uniform缓冲中修改一次会更容易一些。最后一个好处可能不会立即显现，如果使用Uniform缓冲对象的话，你可以在着色器中使用更多的uniform。OpenGL限制了它能够处理的uniform数量，这可以通过<var>GL_MAX_VERTEX_UNIFORM_COMPONENTS</var>来查询。当使用Uniform缓冲对象时，最大的数量会更高。所以，当你达到了uniform的最大数量时（比如再做骨骼动画(Skeletal Animation)的时候），你总是可以选择使用Uniform缓冲对象。
+uniform缓冲对象比单独的uniform有很多好处。第一，一次设置多个uniform比一次设置一个速度快。第二，如果你打算改变一个横跨多个着色器的uniform，在uniform缓冲中只需更改一次。最后一个好处可能不是很明显，使用uniform缓冲对象你可以在着色器中使用更多的uniform。OpenGL有一个对可使用uniform数据的数量的限制，可以用`GL_MAX_VERTEX_UNIFORM_COMPONENTS`来获取。当使用uniform缓冲对象中，这个限制的阈限会更高。所以无论何时，你达到了uniform的最大使用数量（比如做骨骼动画的时候），你可以使用uniform缓冲对象。

docs/04 Advanced OpenGL/09 Geometry Shader.md

@@ -3,166 +3,171 @@
 原文     | [Geometry Shader](http://learnopengl.com/#!Advanced-OpenGL/Geometry-Shader)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | 暂未校对
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com)
 
-在顶点和片段着色器之间有一个可选的<def>几何着色器</def>(Geometry Shader)，几何着色器的输入是一个图元（如点或三角形）的一组顶点。几何着色器可以在顶点发送到下一着色器阶段之前对它们随意变换。然而，几何着色器最有趣的地方在于，它能够将（这一组）顶点变换为完全不同的图元，并且还能生成比原来更多的顶点。
+在顶点和片段着色器之间有一个可选的着色器，叫做几何着色器(Geometry Shader)。几何着色器以一个或多个表示为一个单独基本图形（primitive）的顶点作为输入，比如可以是一个点或者三角形。几何着色器在将这些顶点发送到下一个着色阶段之前，可以将这些顶点转变为它认为合适的内容。几何着色器有意思的地方在于它可以把（一个或多个）顶点转变为完全不同的基本图形（primitive），从而生成比原来多得多的顶点。
 
-废话不多说，我们直接先看一个几何着色器的例子：
+我们直接用一个例子深入了解一下：
 
 ```c++
 #version 330 core
 layout (points) in;
 layout (line_strip, max_vertices = 2) out;
 
-void main() {    
-    gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0); 
+void main() {
+    gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
     EmitVertex();
 
-    gl_Position = gl_in[0].gl_Position + vec4( 0.1, 0.0, 0.0, 0.0);
+    gl_Position = gl_in[0].gl_Position + vec4(0.1, 0.0, 0.0, 0.0);
     EmitVertex();
-    
+
     EndPrimitive();
 }
 ```
 
-在几何着色器的顶部，我们需要声明从顶点着色器输入的图元类型。这需要在<fun>in</fun>关键字前声明一个布局修饰符(Layout Qualifier)。这个输入布局修饰符可以从顶点着色器接收下列任何一个图元值：
+每个几何着色器开始位置我们需要声明输入的基本图形(primitive)类型，这个输入是我们从顶点着色器中接收到的。我们在in关键字前面声明一个layout标识符。这个输入layout修饰符可以从一个顶点着色器接收以下基本图形值：
 
-- `points`：绘制<var>GL_POINTS</var>图元时（1）。
-- `lines`：绘制<var>GL_LINES</var>或<var>GL_LINE_STRIP</var>时（2）
-- `lines_adjacency`：<var>GL_LINES_ADJACENCY</var>或<var>GL_LINE_STRIP_ADJACENCY</var>（4）
-- `triangles`：<var>GL_TRIANGLES</var>、<var>GL_TRIANGLE_STRIP</var>或<var>GL_TRIANGLE_FAN</var>（3）
-- `triangles_adjacency`：<var>GL_TRIANGLES_ADJACENCY</var>或<var>GL_TRIANGLE_STRIP_ADJACENCY</var>（6）
 
-以上是能提供给<fun>glDrawArrays</fun>渲染函数的几乎所有图元了。如果我们想要将顶点绘制为<var>GL_TRIANGLES</var>，我们就要将输入修饰符设置为`triangles`。括号内的数字表示的是一个图元所包含的最小顶点数。
+ 基本图形|描述
+---|---
+points |绘制GL_POINTS基本图形的时候（1）
+lines  |当绘制GL_LINES或GL_LINE_STRIP（2）时
+lines_adjacency | GL_LINES_ADJACENCY或GL_LINE_STRIP_ADJACENCY（4）
+triangles |GL_TRIANGLES, GL_TRIANGLE_STRIP或GL_TRIANGLE_FAN（3）
+triangles_adjacency |GL_TRIANGLES_ADJACENCY或GL_TRIANGLE_STRIP_ADJACENCY（6）
 
-接下来，我们还需要指定几何着色器输出的图元类型，这需要在<fun>out</fun>关键字前面加一个布局修饰符。和输入布局修饰符一样，输出布局修饰符也可以接受几个图元值：
+这是我们能够给渲染函数的几乎所有的基本图形。如果我们选择以GL_TRIANGLES绘制顶点，我们要把输入修饰符设置为triangles。括号里的数字代表一个基本图形所能包含的最少的顶点数。
 
-- `points`
-- `line_strip`
-- `triangle_strip`
+当我们需要指定一个几何着色器所输出的基本图形类型时，我们就在out关键字前面加一个layout修饰符。和输入layout标识符一样，输出的layout标识符也可以接受以下基本图形值：
 
-有了这3个输出修饰符，我们就可以使用输入图元创建几乎任意的形状了。要生成一个三角形的话，我们将输出定义为`triangle_strip`，并输出3个顶点。
+* points
+* line_strip
+* triangle_strip
 
-几何着色器同时希望我们设置一个它最大能够输出的顶点数量（如果你超过了这个值，OpenGL将不会绘制**多出的**顶点），这个也可以在<fun>out</fun>关键字的布局修饰符中设置。在这个例子中，我们将输出一个`line_strip`，并将最大顶点数设置为2个。
+使用这3个输出修饰符我们可以从输入的基本图形创建任何我们想要的形状。为了生成一个三角形，我们定义一个triangle_strip作为输出，然后输出3个顶点。
 
-!!! important
+几何着色器同时希望我们设置一个它能输出的顶点数量的最大值（如果你超出了这个数值，OpenGL就会忽略剩下的顶点），我们可以在out关键字的layout标识符上做这件事。在这个特殊的情况中，我们将使用最大值为2个顶点，来输出一个line_strip。
 
-    如果你不知道什么是线条(Line Strip)：线条连接了一组点，形成一条连续的线，它最少要由两个点来组成。在渲染函数中每多加一个点，就会在这个点与前一个点之间形成一条新的线。在下面这张图中，我们有5个顶点：
+这种情况，你会奇怪什么是线条：一个线条是把多个点链接起来表示出一个连续的线，它最少有两个点来组成。每个后一个点在前一个新渲染的点后面渲染，你可以看看下面的图，其中包含5个顶点：
 
-    ![](../img/04/09/geometry_shader_line_strip.png)
+![](http://learnopengl.com/img/advanced/geometry_shader_line_strip.png)
 
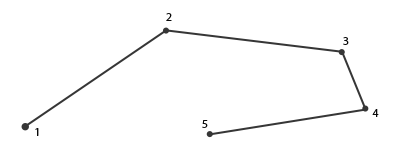
-为了生成更有意义的结果，我们需要某种方式来获取前一着色器阶段的输出。GLSL提供给我们一个名为<fun>gl_in</fun>的<def>内建</def>(Built-in)变量，在内部看起来（可能）是这样的：
+上面的着色器，我们只能输出一个线段，因为顶点的最大值设置为2。
+
+为生成更有意义的结果，我们需要某种方式从前一个着色阶段获得输出。GLSL为我们提供了一个内建变量，它叫做`gl_in`，它的内部看起来可能像这样：
 
 ```c++
 in gl_Vertex
 {
-    vec4  gl_Position;
+    vec4 gl_Position;
     float gl_PointSize;
     float gl_ClipDistance[];
 } gl_in[];
+
 ```
 
-这里，它被声明为一个<def>接口块</def>（Interface Block，我们在[上一节](08 Advanced GLSL.md)已经讨论过），它包含了几个很有意思的变量，其中最有趣的一个是<var>gl_Position</var>，它是和顶点着色器输出非常相似的一个向量。
+这里它被声明为一个接口块(interface block，前面的教程已经讨论过)，它包含几个有意思的变量，其中最有意思的是`gl_Position`，它包含着和我们设置的顶点着色器的输出相似的向量。
 
-要注意的是，它被声明为一个数组，因为大多数的渲染图元包含多于1个的顶点，而几何着色器的输入是一个图元的**所有**顶点。
+要注意的是，它被声明为一个数组，因为大多数渲染基本图形由一个以上顶点组成，几何着色器接收一个基本图形的所有顶点作为它的输入。
 
-有了之前顶点着色器阶段的顶点数据，我们就可以使用2个几何着色器函数，<fun>EmitVertex</fun>和<fun>EndPrimitive</fun>，来生成新的数据了。几何着色器希望你能够生成并输出至少一个定义为输出的图元。在我们的例子中，我们需要至少生成一个线条图元。
+使用从前一个顶点着色阶段的顶点数据，我们就可以开始生成新的数据了，这是通过2个几何着色器函数`EmitVertex`和`EndPrimitive`来完成的。几何着色器需要你去生成/输出至少一个你定义为输出的基本图形。在我们的例子里我们打算至少生成一个线条（line strip）基本图形。
 
 ```c++
 void main() {
-    gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0); 
+    gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
     EmitVertex();
 
-    gl_Position = gl_in[0].gl_Position + vec4( 0.1, 0.0, 0.0, 0.0);
+    gl_Position = gl_in[0].gl_Position + vec4(0.1, 0.0, 0.0, 0.0);
     EmitVertex();
-    
+
     EndPrimitive();
 }
 ```
 
-每次我们调用<fun>EmitVertex</fun>时，<var>gl_Position</var>中的向量会被添加到图元中来。当<fun>EndPrimitive</fun>被调用时，所有发射出的(Emitted)顶点都会合成为指定的输出渲染图元。在一个或多个<fun>EmitVertex</fun>调用之后重复调用<fun>EndPrimitive</fun>能够生成多个图元。在这个例子中，我们发射了两个顶点，它们从原始顶点位置平移了一段距离，之后调用了<fun>EndPrimitive</fun>，将这两个顶点合成为一个包含两个顶点的线条。
+每次我们调用`EmitVertex`，当前设置到`gl_Position`的向量就会被添加到基本图形上。无论何时调用`EndPrimitive`，所有为这个基本图形发射出去的顶点都将结合为一个特定的输出渲染基本图形。一个或多个`EmitVertex`函数调用后，重复调用`EndPrimitive`就能生成多个基本图形。这个特殊的例子里，发射了两个顶点，它们被从顶点原来的位置平移了一段距离，然后调用`EndPrimitive`将这两个顶点结合为一个单独的有两个顶点的线条。
 
-现在你（大概）了解了几何着色器的工作方式，你可能已经猜出这个几何着色器是做什么的了。它接受一个点图元作为输入，以这个点为中心，创建一条水平的线图元。如果我们渲染它，看起来会是这样的：
+现在你了解了几何着色器的工作方式，你就可能猜出这个几何着色器做了什么。这个几何着色器接收一个基本图形——点，作为它的输入，使用输入点作为它的中心，创建了一个水平线基本图形。如果我们渲染它，结果就会像这样：
 
-![](../img/04/09/geometry_shader_lines.png)
+![](http://learnopengl.com/img/advanced/geometry_shader_lines.png)
 
-目前还并没有什么令人惊叹的效果，但考虑到这个输出是通过调用下面的渲染函数来生成的，它还是很有意思的：
+并不是非常引人注目，但是考虑到它的输出是使用下面的渲染命令生成的就很有意思了：
 
 ```c++
 glDrawArrays(GL_POINTS, 0, 4);
 ```
 
-虽然这是一个比较简单的例子，它的确向你展示了如何能够使用几何着色器来（动态地）生成新的形状。在之后我们会利用几何着色器创建出更有意思的效果，但现在我们仍将从创建一个简单的几何着色器开始。
+这是个相对简单的例子，它向你展示了我们如何使用几何着色器来动态地在运行时生成新的形状。本章的后面，我们会讨论一些可以使用几何着色器获得有趣的效果，但是现在我们将以创建一个简单的几何着色器开始。
 
 ## 使用几何着色器
 
-为了展示几何着色器的用法，我们将会渲染一个非常简单的场景，我们只会在标准化设备坐标的z平面上绘制四个点。这些点的坐标是：
+为了展示几何着色器的使用，我们将渲染一个简单的场景，在场景中我们只绘制4个点，这4个点在标准化设备坐标的z平面上。这些点的坐标是：
 
 ```c++
-float points[] = {
-	-0.5f,  0.5f, // 左上
-	 0.5f,  0.5f, // 右上
-	 0.5f, -0.5f, // 右下
-	-0.5f, -0.5f  // 左下
+GLfloat points[] = {
+ -0.5f,  0.5f, // 左上方
+ 0.5f,  0.5f,  // 右上方
+ 0.5f, -0.5f,  // 右下方
+ -0.5f, -0.5f  // 左下方
 };
 ```
 
-顶点着色器只需要在z平面绘制点就可以了，所以我们将使用一个最基本顶点着色器：
+顶点着色器只在z平面绘制点，所以我们只需要一个基本顶点着色器：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec2 aPos;
+layout (location = 0) in vec2 position;
 
 void main()
 {
-    gl_Position = vec4(aPos.x, aPos.y, 0.0, 1.0); 
+    gl_Position = vec4(position.x, position.y, 0.0f, 1.0f);
 }
 ```
 
-直接在片段着色器中硬编码，将所有的点都输出为绿色：
+我们会简单地为所有点输出绿色，我们直接在片段着色器里进行硬编码：
 
 ```c++
 #version 330 core
-out vec4 FragColor;
+out vec4 color;
 
 void main()
 {
-    FragColor = vec4(0.0, 1.0, 0.0, 1.0);   
+    color = vec4(0.0f, 1.0f, 0.0f, 1.0f);
 }
 ```
 
-为点的顶点数据生成一个VAO和一个VBO，然后使用<fun>glDrawArrays</fun>进行绘制：
+为点的顶点生成一个VAO和VBO，然后使用`glDrawArrays`进行绘制：
 
 ```c++
-shader.use();
+shader.Use();
 glBindVertexArray(VAO);
 glDrawArrays(GL_POINTS, 0, 4);
+glBindVertexArray(0);
 ```
 
-结果是在黑暗的场景中有四个（很难看见的）绿点：
+效果是黑色场景中有四个绿点（虽然很难看到）：
 
-![](../img/04/09/geometry_shader_points.png)
+![](http://learnopengl.com/img/advanced/geometry_shader_points.png)
 
-但我们之前不是学过这些吗？是的，但是现在我们将会添加一个几何着色器，为场景添加活力。
+但我们不是已经学到了所有内容了吗？对，现在我们将通过为场景添加一个几何着色器来为这个小场景增加点活力。
 
-出于学习目的，我们将会创建一个<def>传递</def>(Pass-through)几何着色器，它会接收一个点图元，并直接将它**传递**(Pass)到下一个着色器：
+出于学习的目的我们将创建一个叫pass-through的几何着色器，它用一个point基本图形作为它的输入，并把它无修改地传（pass）到下一个着色器。
 
 ```c++
 #version 330 core
 layout (points) in;
 layout (points, max_vertices = 1) out;
 
-void main() {    
-    gl_Position = gl_in[0].gl_Position; 
+void main() {
+    gl_Position = gl_in[0].gl_Position;
     EmitVertex();
     EndPrimitive();
 }
 ```
 
-现在这个几何着色器应该很容易理解了，它只是将它接收到的顶点位置不作修改直接发射出去，并生成一个点图元。
+现在这个几何着色器应该很容易理解了。它简单地将它接收到的输入的无修改的顶点位置发射出去，然后生成一个point基本图形。
 
-和顶点与片段着色器一样，几何着色器也需要编译和链接，但这次在创建着色器时我们将会使用<var>GL_GEOMETRY_SHADER</var>作为着色器类型：
+一个几何着色器需要像顶点和片段着色器一样被编译和链接，但是这次我们将使用`GL_GEOMETRY_SHADER`作为着色器的类型来创建这个着色器：
 
 ```c++
 geometryShader = glCreateShader(GL_GEOMETRY_SHADER);
@@ -173,27 +178,28 @@ glAttachShader(program, geometryShader);
 glLinkProgram(program);
 ```
 
-着色器编译的代码和顶点与片段着色器代码都是一样的。记得要检查编译和链接错误！
+编译着色器的代码和顶点、片段着色器的基本一样。要记得检查编译和链接错误！
 
-如果你现在编译并运行程序，会看到和下面类似的结果：
+如果你现在编译和运行，就会看到和下面相似的结果：
 
-![](../img/04/09/geometry_shader_points.png)
+![](http://learnopengl.com/img/advanced/geometry_shader_points.png)
+
+它和没用几何着色器一样！我承认有点无聊，但是事实上，我们仍能绘制证明几何着色器工作了的点，所以现在是时候来做点更有意思的事了！
 
-这和没使用几何着色器时是完全一样的！我承认这是有点无聊，但既然我们仍然能够绘制这些点，所以几何着色器是正常工作的，现在是时候做点更有趣的东西了！
 
 ## 造几个房子
 
-绘制点和线并没有那么有趣，所以我们会使用一点创造力，利用几何着色器在每个点的位置上绘制一个房子。要实现这个，我们可以将几何着色器的输出设置为<def>triangle_strip</def>，并绘制三个三角形：其中两个组成一个正方形，另一个用作房顶。
+绘制点和线没什么意思，所以我们将在每个点上使用几何着色器绘制一个房子。我们可以通过把几何着色器的输出设置为`triangle_strip`来达到这个目的，总共要绘制3个三角形：两个用来组成方形和另表示一个屋顶。
 
-OpenGL中，三角形带(Triangle Strip)是绘制三角形更高效的方式，它使用顶点更少。在第一个三角形绘制完之后，每个后续顶点将会在上一个三角形边上生成另一个三角形：每3个临近的顶点将会形成一个三角形。如果我们一共有6个构成三角形带的顶点，那么我们会得到这些三角形：(1, 2, 3)、(2, 3, 4)、(3, 4, 5)和(4, 5, 6)，共形成4个三角形。一个三角形带至少需要3个顶点，并会生成N-2个三角形。使用6个顶点，我们创建了6-2 = 4个三角形。下面这幅图展示了这点：
+在OpenGL中三角形带(triangle strip)绘制起来更高效，因为它所使用的顶点更少。第一个三角形绘制完以后，每个后续的顶点会生成一个毗连前一个三角形的新三角形：每3个毗连的顶点都能构成一个三角形。如果我们有6个顶点，它们以三角形带的方式组合起来，那么我们会得到这些三角形：（1, 2, 3）、（2, 3, 4）、（3, 4, 5）、（4,5,6）因此总共可以表示出4个三角形。一个三角形带至少要用3个顶点才行，它能生曾N-2个三角形；6个顶点我们就能创建6-2=4个三角形。下面的图片表达了这点：
 
-![](../img/04/09/geometry_shader_triangle_strip.png)
+![](http://learnopengl.com/img/advanced/geometry_shader_triangle_strip.png)
 
-通过使用三角形带作为几何着色器的输出，我们可以很容易创建出需要的房子形状，只需要以正确的顺序生成3个相连的三角形就行了。下面这幅图展示了顶点绘制的顺序，蓝点代表的是输入点：
+使用一个三角形带作为一个几何着色器的输出，我们可以轻松创建房子的形状，只要以正确的顺序来生成3个毗连的三角形。下面的图像显示，我们需要以何种顺序来绘制点，才能获得我们需要的三角形，图上的蓝点代表输入点：
 
-![](../img/04/09/geometry_shader_house.png)
+![](http://learnopengl.com/img/advanced/geometry_shader_house.png)
 
-变为几何着色器是这样的：
+上图的内容转变为几何着色器：
 
 ```c++
 #version 330 core
@@ -201,35 +207,36 @@ layout (points) in;
 layout (triangle_strip, max_vertices = 5) out;
 
 void build_house(vec4 position)
-{    
-    gl_Position = position + vec4(-0.2, -0.2, 0.0, 0.0);    // 1:左下
-    EmitVertex();   
-    gl_Position = position + vec4( 0.2, -0.2, 0.0, 0.0);    // 2:右下
+{
+    gl_Position = position + vec4(-0.2f, -0.2f, 0.0f, 0.0f);// 1:左下角
     EmitVertex();
-    gl_Position = position + vec4(-0.2,  0.2, 0.0, 0.0);    // 3:左上
+    gl_Position = position + vec4( 0.2f, -0.2f, 0.0f, 0.0f);// 2:右下角
     EmitVertex();
-    gl_Position = position + vec4( 0.2,  0.2, 0.0, 0.0);    // 4:右上
+    gl_Position = position + vec4(-0.2f,  0.2f, 0.0f, 0.0f);// 3:左上
     EmitVertex();
-    gl_Position = position + vec4( 0.0,  0.4, 0.0, 0.0);    // 5:顶部
+    gl_Position = position + vec4( 0.2f,  0.2f, 0.0f, 0.0f);// 4:右上
+    EmitVertex();
+    gl_Position = position + vec4( 0.0f,  0.4f, 0.0f, 0.0f);// 5:屋顶
     EmitVertex();
     EndPrimitive();
 }
 
-void main() {    
+void main()
+{
     build_house(gl_in[0].gl_Position);
 }
 ```
 
-这个几何着色器生成了5个顶点，每个顶点都是原始点的位置加上一个偏移量，来组成一个大的三角形带。最终的图元会被光栅化，然后片段着色器会处理整个三角形带，最终在每个绘制的点处生成一个绿色房子：
+这个几何着色器生成5个顶点，每个顶点是点（point）的位置加上一个偏移量，来组成一个大三角形带。接着最后的基本图形被像素化，片段着色器处理整三角形带，结果是为我们绘制的每个点生成一个绿房子：
 
-![](../img/04/09/geometry_shader_houses.png)
+![](http://learnopengl.com/img/advanced/geometry_shader_houses.png)
 
-你可以看到，每个房子实际上是由3个三角形组成的——全部都是使用空间中一点来绘制的。这些绿房子看起来是有点无聊，所以我们会再给每个房子分配一个不同的颜色。为了实现这个，我们需要在顶点着色器中添加一个额外的顶点属性，表示颜色信息，将它传递至几何着色器，并再次发送到片段着色器中。
+可以看到，每个房子实则是由3个三角形组成，都是仅仅使用空间中一点来绘制的。绿房子看起来还是不够漂亮，所以我们再给每个房子加一个不同的颜色。我们将在顶点着色器中为每个顶点增加一个额外的代表颜色信息的顶点属性。
 
-下面是更新后的顶点数据：
+下面是更新了的顶点数据：
 
 ```c++
-float points[] = {
+GLfloat points[] = {
     -0.5f,  0.5f, 1.0f, 0.0f, 0.0f, // 左上
      0.5f,  0.5f, 0.0f, 1.0f, 0.0f, // 右上
      0.5f, -0.5f, 0.0f, 0.0f, 1.0f, // 右下
@@ -237,12 +244,12 @@ float points[] = {
 };
 ```
 
-然后我们更新顶点着色器，使用一个接口块将颜色属性发送到几何着色器中：
+然后我们更新顶点着色器，使用一个接口块来项几何着色器发送颜色属性：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec2 aPos;
-layout (location = 1) in vec3 aColor;
+layout (location = 0) in vec2 position;
+layout (location = 1) in vec3 color;
 
 out VS_OUT {
     vec3 color;
@@ -250,12 +257,12 @@ out VS_OUT {
 
 void main()
 {
-    gl_Position = vec4(aPos.x, aPos.y, 0.0, 1.0); 
-    vs_out.color = aColor;
+    gl_Position = vec4(position.x, position.y, 0.0f, 1.0f);
+    vs_out.color = color;
 }
 ```
 
-接下来我们还需要在几何着色器中声明相同的接口块（使用一个不同的接口名）：
+接着我们还需要在几何着色器中声明同样的接口块(使用一个不同的接口名)：
 
 ```c++
 in VS_OUT {
@@ -263,80 +270,82 @@ in VS_OUT {
 } gs_in[];
 ```
 
-因为几何着色器是作用于输入的一组顶点的，从顶点着色器发来输入数据总是会以数组的形式表示出来，即便我们现在只有一个顶点。
+因为几何着色器把多个顶点作为它的输入，从顶点着色器来的输入数据总是被以数组的形式表示出来，即使现在我们只有一个顶点。
 
 !!! Important
 
-	我们并不是必须要用接口块来向几何着色器传递数据。我们也可以这样写：
+        我们不是必须使用接口块来把数据发送到几何着色器中。我们还可以这么写：
 
-		in vec3 vColor[];
+        in vec3 vColor[];
 
-	如果顶点着色器发送的颜色向量是`out vec3 vColor`，那这么写就没问题。然而，接口块在几何着色器这样的着色器中会更容易处理一点。实际上，几何着色器的输入能够变得非常大，将它们合并为一个大的接口块数组会更符合逻辑一点。
+        如果顶点着色器发送的颜色向量是out vec3 vColor那么接口块就会在比如几何着色器这样的着色器中更轻松地完成工作。事实上，几何着色器的输入可以非常大，把它们组成一个大的接口块数组会更有意义。
 
-接下来我们还需要为下个片段着色器阶段声明一个输出颜色向量：
+
+然后我们还要为下一个像素着色阶段声明一个输出颜色向量：
 
 ```c++
 out vec3 fColor;
 ```
 
-因为片段着色器只需要一个（插值的）颜色，发送多个颜色并没有什么意义。所以，<var>fColor</var>向量就不是一个数组，而是一个单独的向量。当发射一个顶点的时候，每个顶点将会使用最后在<var>fColor</var>中储存的值，来用于片段着色器的运行。对我们的房子来说，我们只需要在第一个顶点发射之前，使用顶点着色器中的颜色填充<var>fColor</var>一次就可以了。
+因为片段着色器只需要一个（已进行了插值的）颜色，传送多个颜色没有意义。fColor向量这样就不是一个数组，而是一个单一的向量。当发射一个顶点时，为了它的片段着色器运行，每个顶点都会储存最后在fColor中储存的值。对于这些房子来说，我们可以在第一个顶点被发射，对整个房子上色前，只使用来自顶点着色器的颜色填充fColor一次：
 
 ```c++
-fColor = gs_in[0].color; // gs_in[0] 因为只有一个输入顶点
-gl_Position = position + vec4(-0.2, -0.2, 0.0, 0.0);    // 1:左下  
-EmitVertex();   
-gl_Position = position + vec4( 0.2, -0.2, 0.0, 0.0);    // 2:右下
+fColor = gs_in[0].color; //只有一个输出颜色，所以直接设置为gs_in[0]
+gl_Position = position + vec4(-0.2f, -0.2f, 0.0f, 0.0f);    // 1:左下
 EmitVertex();
-gl_Position = position + vec4(-0.2,  0.2, 0.0, 0.0);    // 3:左上
+gl_Position = position + vec4( 0.2f, -0.2f, 0.0f, 0.0f);    // 2:右下
 EmitVertex();
-gl_Position = position + vec4( 0.2,  0.2, 0.0, 0.0);    // 4:右上
+gl_Position = position + vec4(-0.2f,  0.2f, 0.0f, 0.0f);    // 3:左上
 EmitVertex();
-gl_Position = position + vec4( 0.0,  0.4, 0.0, 0.0);    // 5:顶部
+gl_Position = position + vec4( 0.2f,  0.2f, 0.0f, 0.0f);    // 4:右上
 EmitVertex();
-EndPrimitive();  
+gl_Position = position + vec4( 0.0f,  0.4f, 0.0f, 0.0f);    // 5:屋顶
+EmitVertex();
+EndPrimitive();
 ```
 
-所有发射出的顶点都将嵌有最后储存在<var>fColor</var>中的值，即顶点的颜色属性值。所有的房子都会有它们自己的颜色了：
+所有发射出去的顶点都把最后储存在fColor中的值嵌入到他们的数据中，和我们在他们的属性中定义的顶点颜色相同。所有的分房子便都有了自己的颜色：
 
-![](../img/04/09/geometry_shader_houses_colored.png)
+![](http://learnopengl.com/img/advanced/geometry_shader_houses_colored.png)
 
-仅仅是为了有趣，我们也可以假装这是冬天，将最后一个顶点的颜色设置为白色，给屋顶落上一些雪。
+为了好玩儿，我们还可以假装这是在冬天，给最后一个顶点一个自己的白色，就像在屋顶上落了一些雪。
 
 ```c++
-fColor = gs_in[0].color; 
-gl_Position = position + vec4(-0.2, -0.2, 0.0, 0.0);    // 1:左下 
-EmitVertex();   
-gl_Position = position + vec4( 0.2, -0.2, 0.0, 0.0);    // 2:右下
+fColor = gs_in[0].color;
+gl_Position = position + vec4(-0.2f, -0.2f, 0.0f, 0.0f); 
 EmitVertex();
-gl_Position = position + vec4(-0.2,  0.2, 0.0, 0.0);    // 3:左上
+gl_Position = position + vec4( 0.2f, -0.2f, 0.0f, 0.0f);
 EmitVertex();
-gl_Position = position + vec4( 0.2,  0.2, 0.0, 0.0);    // 4:右上
+gl_Position = position + vec4(-0.2f,  0.2f, 0.0f, 0.0f); 
 EmitVertex();
-gl_Position = position + vec4( 0.0,  0.4, 0.0, 0.0);    // 5:顶部
-fColor = vec3(1.0, 1.0, 1.0);
+gl_Position = position + vec4( 0.2f,  0.2f, 0.0f, 0.0f);  
 EmitVertex();
-EndPrimitive();  
+gl_Position = position + vec4( 0.0f,  0.4f, 0.0f, 0.0f); 
+fColor = vec3(1.0f, 1.0f, 1.0f);
+EmitVertex();
+EndPrimitive();
+
 ```
 
-最终结果看起来是这样的：
+结果就像这样：
 
-![](../img/04/09/geometry_shader_houses_snow.png)
+![](http://learnopengl.com/img/advanced/geometry_shader_houses_snow.png)
 
-你可以将你的代码与[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/9.1.geometry_shader_houses/geometry_shader_houses.cpp)的OpenGL代码进行比对。
+你可以对比一下你的[源码](http://learnopengl.com/code_viewer.php?code=advanced/geometry_shader_houses)和[着色器](http://learnopengl.com/code_viewer.php?code=advanced/geometry_shader_houses_shaders)。
 
-你可以看到，有了几何着色器，你甚至可以将最简单的图元变得十分有创意。因为这些形状是在GPU的超快硬件中动态生成的，这会比在顶点缓冲中手动定义图形要高效很多。因此，几何缓冲对简单而且经常重复的形状来说是一个很好的优化工具，比如体素(Voxel)世界中的方块和室外草地的每一根草。
+你可以看到，使用几何着色器，你可以使用最简单的基本图形就能获得漂亮的新玩意。因为这些形状是在你的GPU超快硬件上动态生成的，这要比使用顶点缓冲自己定义这些形状更为高效。几何缓冲在简单的经常被重复的形状比如体素（voxel）的世界和室外的草地上，是一种非常强大的优化工具。
 
 # 爆破物体
 
-尽管绘制房子非常有趣，但我们不会经常这么做。这也是为什么我们接下来要继续深入，来爆破(Explode)物体！虽然这也是一个不怎么常用的东西，但是它能向你展示几何着色器的强大之处。
+绘制房子的确很有趣，但我们不会经常这么用。这就是为什么现在我们将撬起物体缺口，形成爆炸式物体的原因！虽然这个我们也不会经常用到，但是它能向你展示一些几何着色器的强大之处。
 
-当我们说**爆破**一个物体时，我们并不是指要将宝贵的顶点集给炸掉，我们是要将每个三角形沿着法向量的方向移动一小段时间。效果就是，整个物体看起来像是沿着每个三角形的法线向量**爆炸**一样。爆炸三角形的效果在纳米装模型上看起来像是这样的：
+当我们说对一个物体进行爆破(Explode)的时候并不是说我们将要把之前的那堆顶点炸掉，但是我们打算把每个三角形沿着它们的法线向量移动一小段距离。效果是整个物体上的三角形看起来就像沿着它们的法线向量爆炸了一样。纳米服上的三角形的爆炸式效果看起来是这样的：
 
-![](../img/04/09/geometry_shader_explosion_backpack.png)
+![](http://learnopengl.com/img/advanced/geometry_shader_explosion.png)
 
-这样的几何着色器效果的一个好处就是，无论物体有多复杂，它都能够应用上去。
+这样一个几何着色器效果的一大好处是，它可以用到任何物体上，无论它们多复杂。
 
-因为我们想要沿着三角形的法向量位移每个顶点，我们首先需要计算这个法向量。我们所要做的是计算垂直于三角形表面的向量，仅使用我们能够访问的3个顶点。你可能还记得在[变换](../01 Getting started/07 Transformations.md)小节中，我们使用<def>叉乘</def>来获取垂直于其它两个向量的一个向量。如果我们能够获取两个平行于三角形表面的向量<var>a</var>和<var>b</var>，我们就能够对这两个向量进行叉乘来获取法向量了。下面这个几何着色器函数做的正是这个，来使用3个输入顶点坐标来获取法向量：
+因为我们打算沿着三角形的法线向量移动三角形的每个顶点，我们需要先计算它的法线向量。我们要做的是计算出一个向量，它垂直于三角形的表面，使用这三个我们已经的到的顶点就能做到。你可能记得变换教程中，我们可以使用叉乘获取一个垂直于两个其他向量的向量。如果我们有两个向量a和b，它们平行于三角形的表面，我们就可以对这两个向量进行叉乘得到法线向量了。下面的几何着色器函数做的正是这件事，它使用3个输入顶点坐标获取法线向量：
 
 ```c++
 vec3 GetNormal()
@@ -347,22 +356,22 @@ vec3 GetNormal()
 }
 ```
 
-这里我们使用减法获取了两个平行于三角形表面的向量<var>a</var>和<var>b</var>。因为两个向量相减能够得到这两个向量之间的差值，并且三个点都位于三角平面上，对任意两个向量相减都能够得到一个平行于平面的向量。注意，如果我们交换了<fun>cross</fun>函数中<var>a</var>和<var>b</var>的位置，我们会得到一个指向相反方向的法向量——这里的顺序很重要！
+这里我们使用减法获取了两个向量a和b，它们平行于三角形的表面。两个向量相减得到一个两个向量的差值，由于所有3个点都在三角形平面上，任何向量相减都会得到一个平行于平面的向量。一定要注意，如果我们调换了a和b的叉乘顺序，我们得到的法线向量就会使反的，顺序很重要！
 
-既然知道了如何计算法向量了，我们就能够创建一个<fun>explode</fun>函数了，它使用法向量和顶点位置向量作为参数。这个函数会返回一个新的向量，它是位置向量沿着法线向量进行位移之后的结果：
+知道了如何计算法线向量，我们就能创建一个explode函数，函数返回的是一个新向量，它把位置向量沿着法线向量方向平移：
 
 ```c++
 vec4 explode(vec4 position, vec3 normal)
 {
-    float magnitude = 2.0;
-    vec3 direction = normal * ((sin(time) + 1.0) / 2.0) * magnitude; 
-    return position + vec4(direction, 0.0);
+    float magnitude = 2.0f;
+    vec3 direction = normal * ((sin(time) + 1.0f) / 2.0f) * magnitude;
+    return position + vec4(direction, 0.0f);
 }
 ```
 
-函数本身应该不是非常复杂。<fun>sin</fun>函数接收一个<var>time</var>参数，它根据时间返回一个-1.0到1.0之间的值。因为我们不想让物体**向内爆炸**(Implode)，我们将sin值变换到了[0, 1]的范围内。最终的结果会乘以<var>normal</var>向量，并且最终的<var>direction</var>向量会被加到位置向量上。
+函数本身并不复杂，sin（正弦）函数把一个time变量作为它的参数，它根据时间来返回一个-1.0到1.0之间的值。因为我们不想让物体坍缩，所以我们把sin返回的值做成0到1的范围。最后的值去乘以法线向量，direction向量被添加到位置向量上。
 
-当使用我们的[模型加载器](../03 Model Loading/01 Assimp.md)绘制一个模型时，<def>爆破</def>(Explode)效果的完整几何着色器是这样的：
+爆炸效果的完整的几何着色器是这样的，它使用我们的模型加载器，绘制出一个模型：
 
 ```c++
 #version 330 core
@@ -373,7 +382,7 @@ in VS_OUT {
     vec2 texCoords;
 } gs_in[];
 
-out vec2 TexCoords; 
+out vec2 TexCoords;
 
 uniform float time;
 
@@ -381,7 +390,7 @@ vec4 explode(vec4 position, vec3 normal) { ... }
 
 vec3 GetNormal() { ... }
 
-void main() {    
+void main() {
     vec3 normal = GetNormal();
 
     gl_Position = explode(gl_in[0].gl_Position, normal);
@@ -397,52 +406,53 @@ void main() {
 }
 ```
 
-注意我们在发射顶点之前输出了对应的纹理坐标。
+注意我们同样在发射一个顶点前输出了合适的纹理坐标。
 
-而且别忘了在OpenGL代码中设置<var>time</var>变量：
+也不要忘记在OpenGL代码中设置time变量：
 
 ```c++
-shader.setFloat("time", glfwGetTime());
-```
+glUniform1f(glGetUniformLocation(shader.Program, "time"), glfwGetTime());
+ ```
 
-最终的效果是，3D模型看起来随着时间不断在爆破它的顶点，在这之后又回到正常状态。虽然这并不是非常有用，它的确向你展示了几何着色器更高级的用法。你可以将你的代码和[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/9.2.geometry_shader_exploding/geometry_shader_exploding.cpp)完整的源码进行比较。
+最后的结果是一个随着时间持续不断地爆炸的3D模型（不断爆炸不断回到正常状态）。尽管没什么大用处，它却向你展示出很多几何着色器的高级用法。你可以用[完整的源码](http://learnopengl.com/code_viewer.php?code=advanced/geometry_shader_explode)和[着色器](http://learnopengl.com/code_viewer.php?code=advanced/geometry_shader_explode_shaders)对比一下你自己的。
 
-# 法向量可视化
+# 显示法向量
 
-在这一部分中，我们将使用几何着色器来实现一个真正有用的例子：显示任意物体的法向量。当编写光照着色器时，你可能会最终会得到一些奇怪的视觉输出，但又很难确定导致问题的原因。光照错误很常见的原因就是法向量错误，这可能是由于不正确加载顶点数据、错误地将它们定义为顶点属性或在着色器中不正确地管理所导致的。我们想要的是使用某种方式来检测提供的法向量是正确的。检测法向量是否正确的一个很好的方式就是对它们进行可视化，几何着色器正是实现这一目的非常有用的工具。
+在这部分我们将使用几何着色器写一个例子，非常有用：显示一个法线向量。当编写光照着色器的时候，你最终会遇到奇怪的视频输出问题，你很难决定是什么导致了这个问题。通常导致光照错误的是，不正确的加载顶点数据，以及给它们指定了不合理的顶点属性，又或是在着色器中不合理的管理，导致产生了不正确的法线向量。我们所希望的是有某种方式可以检测出法线向量是否正确。把法线向量显示出来正是这样一种方法，恰好几何着色器能够完美地达成这个目的。
 
-思路是这样的：我们首先不使用几何着色器正常绘制场景。然后再次绘制场景，但这次只显示通过几何着色器生成法向量。几何着色器接收一个三角形图元，并沿着法向量生成三条线——每个顶点一个法向量。伪代码看起来会像是这样：
+思路是这样的：我们先不用几何着色器，正常绘制场景，然后我们再次绘制一遍场景，但这次只显示我们通过几何着色器生成的法线向量。几何着色器把一个三角形基本图形作为输入类型，用它们生成3条和法线向量同向的线段，每个顶点一条。伪代码应该是这样的：
 
 ```c++
-shader.use();
+shader.Use();
 DrawScene();
-normalDisplayShader.use();
+normalDisplayShader.Use();
 DrawScene();
 ```
 
-这次在几何着色器中，我们会使用模型提供的顶点法线，而不是自己生成，为了适配（观察和模型矩阵的）缩放和旋转，我们在将法线变换到观察空间坐标之前，先使用法线矩阵变换一次（几何着色器接受的位置向量是观察空间坐标，所以我们应该将法向量变换到相同的空间中）。这可以在顶点着色器中完成：
+这次我们会创建一个使用模型提供的顶点法线，而不是自己去生成。为了适应缩放和旋转我们会在把它变换到裁切空间坐标前，使用法线矩阵来法线（几何着色器用他的位置向量做为裁切空间坐标，所以我们还要把法线向量变换到同一个空间）。这些都能在顶点着色器中完成：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;
-layout (location = 1) in vec3 aNormal;
+layout (location = 0) in vec3 position;
+layout (location = 1) in vec3 normal;
 
 out VS_OUT {
     vec3 normal;
 } vs_out;
 
+uniform mat4 projection;
 uniform mat4 view;
 uniform mat4 model;
 
 void main()
 {
-    gl_Position = view * model * vec4(aPos, 1.0); 
+    gl_Position = projection * view * model * vec4(position, 1.0f);
     mat3 normalMatrix = mat3(transpose(inverse(view * model)));
-    vs_out.normal = normalize(vec3(vec4(normalMatrix * aNormal, 0.0)));
+    vs_out.normal = normalize(vec3(projection * vec4(normalMatrix * normal, 1.0)));
 }
 ```
 
-变换后的观察空间法向量会以接口块的形式传递到下个着色器阶段。接下来，几何着色器会接收每一个顶点（包括一个位置向量和一个法向量），并在每个位置向量处绘制一个法线向量：
+经过变换的裁切空间法线向量接着通过一个接口块被传递到下个着色阶段。几何着色器接收每个顶点（带有位置和法线向量），从每个位置向量绘制出一个法线向量：
 
 ```c++
 #version 330 core
@@ -453,46 +463,43 @@ in VS_OUT {
     vec3 normal;
 } gs_in[];
 
-const float MAGNITUDE = 0.4;
-  
-uniform mat4 projection;
+const float MAGNITUDE = 0.4f;
 
 void GenerateLine(int index)
 {
-    gl_Position = projection * gl_in[index].gl_Position;
+    gl_Position = gl_in[index].gl_Position;
     EmitVertex();
-    gl_Position = projection * (gl_in[index].gl_Position + 
-                                vec4(gs_in[index].normal, 0.0) * MAGNITUDE);
+    gl_Position = gl_in[index].gl_Position + vec4(gs_in[index].normal, 0.0f) * MAGNITUDE;
     EmitVertex();
     EndPrimitive();
 }
 
 void main()
 {
-    GenerateLine(0); // 第一个顶点法线
-    GenerateLine(1); // 第二个顶点法线
-    GenerateLine(2); // 第三个顶点法线
+    GenerateLine(0); // First vertex normal
+    GenerateLine(1); // Second vertex normal
+    GenerateLine(2); // Third vertex normal
 }
 ```
 
-像这样的几何着色器应该很容易理解了。注意我们将法向量乘以了一个<var>MAGNITUDE</var>向量，来限制显示出的法向量大小（否则它们就有点大了）。
+到现在为止，像这样的几何着色器的内容就不言自明了。需要注意的是我们我们把法线向量乘以一个MAGNITUDE向量来限制显示出的法线向量的大小（否则它们就太大了）。
 
-因为法线的可视化通常都是用于调试目的，我们可以使用片段着色器，将它们显示为单色的线（如果你愿意也可以是非常好看的线）：
+由于把法线显示出来通常用于调试的目的，我们可以在片段着色器的帮助下把它们显示为单色的线（如果你愿意也可以更炫一点）。
 
 ```c++
 #version 330 core
-out vec4 FragColor;
+out vec4 color;
 
 void main()
 {
-    FragColor = vec4(1.0, 1.0, 0.0, 1.0);
+    color = vec4(1.0f, 1.0f, 0.0f, 1.0f);
 }
 ```
 
-现在，首先使用普通着色器渲染模型，再使用特别的**法线可视化**着色器渲染，你将看到这样的效果：
+现在先使用普通着色器来渲染你的模型，然后使用特制的法线可视着色器，你会看到这样的效果：
 
-![](../img/04/09/geometry_shader_normals_backpack.png)
+![](http://learnopengl.com/img/advanced/geometry_shader_normals.png)
 
-除了让我们的背包变得毛茸茸之外，它还能让我们很好地判断模型的法向量是否准确。你可以想象到，这样的几何着色器也经常用于给物体添加<def>毛发</def>(Fur)。
+除了我们的纳米服现在看起来有点像一个带着隔热手套的全身多毛的家伙外，它给了我们一种非常有效的检查一个模型的法线向量是否有错误的方式。你可以想象下这样的几何着色器也经常能被用在给物体添加毛发上。
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/9.3.geometry_shader_normals/normal_visualization.cpp)找到源码。
+你可以从这里找到[源码](http://learnopengl.com/code_viewer.php?code=advanced/geometry_shader_normals)和可显示法线的[着色器](http://learnopengl.com/code_viewer.php?code=advanced/geometry_shader_normals_shaders)。

docs/04 Advanced OpenGL/10 Instancing.md

@@ -3,71 +3,70 @@
 原文     | [Instancing](http://learnopengl.com/#!Advanced-OpenGL/Instancing)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | 暂未校对
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com)
 
-假设你有一个绘制了很多模型的场景，而大部分的模型包含的是同一组顶点数据，只不过进行的是不同的世界空间变换。想象一个充满草的场景：每根草都是一个包含几个三角形的小模型。你可能会需要绘制很多根草，最终在每帧中你可能会需要渲染上千或者上万根草。因为每一根草仅仅是由几个三角形构成，渲染几乎是瞬间完成的，但上千个渲染函数调用却会极大地影响性能。
+假如你有一个有许多模型的场景，而这些模型的顶点数据都一样，只是进行了不同的世界空间的变换。想象一下，有一个场景中充满了草叶：每根草都是几个三角形组成的。你可能需要绘制很多的草叶，最终一次渲染循环中就肯能有成千上万个草需要绘制了。因为每个草叶只是由几个三角形组成，绘制一个几乎是即刻完成，但是数量巨大以后，执行起来就很慢了。
 
-如果我们需要渲染大量物体时，代码看起来会像这样：
+如果我们渲染这样多的物体的时候，也许代码会写成这样：
 
 ```c++
-for(unsigned int i = 0; i < amount_of_models_to_draw; i++)
+for(GLuint i = 0; i < amount_of_models_to_draw; i++)
 {
-    DoSomePreparations(); // 绑定VAO，绑定纹理，设置uniform等
+    DoSomePreparations(); //在这里绑定VAO、绑定纹理、设置uniform变量等
     glDrawArrays(GL_TRIANGLES, 0, amount_of_vertices);
 }
 ```
 
-如果像这样绘制模型的大量<def>实例</def>(Instance)，你很快就会因为绘制调用过多而达到性能瓶颈。与绘制顶点本身相比，使用<fun>glDrawArrays</fun>或<fun>glDrawElements</fun>函数告诉GPU去绘制你的顶点数据会消耗更多的性能，因为OpenGL在绘制顶点数据之前需要做很多准备工作（比如告诉GPU该从哪个缓冲读取数据，从哪寻找顶点属性，而且这些都是在相对缓慢的CPU到GPU总线(CPU to GPU Bus)上进行的）。所以，即便渲染顶点非常快，命令GPU去渲染却未必。
 
-如果我们能够将数据一次性发送给GPU，然后使用一个绘制函数让OpenGL利用这些数据绘制多个物体，就会更方便了。这就是<def>实例化</def>(Instancing)。
+像这样绘制出你模型的其他实例，多次绘制之后，很快将达到一个瓶颈，这是因为你`glDrawArrays`或`glDrawElements`这样的函数(Draw call)过多。这样渲染顶点数据，会明显降低执行效率，这是因为OpenGL在它可以绘制你的顶点数据之前必须做一些准备工作(比如告诉GPU从哪个缓冲读取数据，以及在哪里找到顶点属性，所有这些都会使CPU到GPU的总线变慢)。所以即使渲染顶点超快，而多次给你的GPU下达这样的渲染命令却未必。
 
-实例化这项技术能够让我们使用一个渲染调用来绘制多个物体，来节省每次绘制物体时CPU -> GPU的通信，它只需要一次即可。如果想使用实例化渲染，我们只需要将<fun>glDrawArrays</fun>和<fun>glDrawElements</fun>的渲染调用分别改为<fun>glDrawArraysInstanced</fun>和<fun>glDrawElementsInstanced</fun>就可以了。这些渲染函数的**实例化**版本需要一个额外的参数，叫做<def>实例数量</def>(Instance Count)，它能够设置我们需要渲染的实例个数。这样我们只需要将必须的数据发送到GPU一次，然后使用一次函数调用告诉GPU它应该如何绘制这些实例。GPU将会直接渲染这些实例，而不用不断地与CPU进行通信。
+如果我们能够将数据一次发送给GPU，就会更方便，然后告诉OpenGL使用一个绘制函数，将这些数据绘制为多个物体。这就是我们将要展开讨论的**实例化(Instancing)**。
 
-这个函数本身并没有什么用。渲染同一个物体一千次对我们并没有什么用处，每个物体都是完全相同的，而且还在同一个位置。我们只能看见一个物体！出于这个原因，GLSL在顶点着色器中嵌入了另一个内建变量，<var>gl_InstanceID</var>。
+实例化是一种只调用一次渲染函数却能绘制出很多物体的技术，它节省渲染物体时从CPU到GPU的通信时间，而且只需做一次即可。要使用实例化渲染，我们必须将`glDrawArrays`和`glDrawElements`各自改为`glDrawArraysInstanced`和`glDrawElementsInstanced`。这些用于实例化的函数版本需要设置一个额外的参数，叫做**实例数量(Instance Count)**，它设置我们打算渲染实例的数量。这样我们就只需要把所有需要的数据发送给GPU一次就行了，然后告诉GPU它该如何使用一个函数来绘制所有这些实例。
 
-在使用实例化渲染调用时，<var>gl_InstanceID</var>会从0开始，在每个实例被渲染时递增1。比如说，我们正在渲染第43个实例，那么顶点着色器中它的<var>gl_InstanceID</var>将会是42。因为每个实例都有唯一的ID，我们可以建立一个数组，将ID与位置值对应起来，将每个实例放置在世界的不同位置。
+就其本身而言，这个函数用处不大。渲染同一个物体一千次对我们来说没用，因为每个渲染出的物体不仅相同而且还在同一个位置；我们只能看到一个物体！出于这个原因GLSL在着色器中嵌入了另一个内建变量，叫做**`gl_InstanceID`**。
 
-为了体验一下实例化绘制，我们将会在标准化设备坐标系中使用一个渲染调用，绘制100个2D四边形。我们会索引一个包含100个偏移向量的uniform数组，将偏移值加到每个实例化的四边形上。最终的结果是一个排列整齐的四边形网格：
+在通过实例化绘制时，`gl_InstanceID`的初值是0，它在每个实例渲染时都会增加1。如果我们渲染43个实例，那么在顶点着色器`gl_InstanceID`的值最后就是42。每个实例都拥有唯一的值意味着我们可以索引到一个位置数组，并将每个实例摆放在世界空间的不同的位置上。
 
-![](../img/04/10/instancing_quads.png)
+我们调用一个实例化渲染函数，在标准化设备坐标中绘制一百个2D四边形来看看实例化绘制的效果是怎样的。通过对一个储存着100个偏移量向量的索引，我们为每个实例四边形添加一个偏移量。最后，窗口被排列精美的四边形网格填满：
 
-每个四边形由2个三角形所组成，一共有6个顶点。每个顶点包含一个2D的标准化设备坐标位置向量和一个颜色向量。
-下面就是这个例子使用的顶点数据，为了大量填充屏幕，每个三角形都很小：
+![](http://learnopengl.com/img/advanced/instancing_quads.png)
+
+每个四边形是2个三角形所组成的，因此总共有6个顶点。每个顶点包含一个2D标准设备坐标位置向量和一个颜色向量。下面是例子中所使用的顶点数据，每个三角形为了适应屏幕都很小：
 
 ```c++
-float quadVertices[] = {
-    // 位置          // 颜色
+GLfloat quadVertices[] = {
+    //  ---位置---   ------颜色-------
     -0.05f,  0.05f,  1.0f, 0.0f, 0.0f,
      0.05f, -0.05f,  0.0f, 1.0f, 0.0f,
     -0.05f, -0.05f,  0.0f, 0.0f, 1.0f,
 
     -0.05f,  0.05f,  1.0f, 0.0f, 0.0f,
-     0.05f, -0.05f,  0.0f, 1.0f, 0.0f,   
-     0.05f,  0.05f,  0.0f, 1.0f, 1.0f		    		
-};  
+     0.05f, -0.05f,  0.0f, 1.0f, 0.0f,
+     0.05f,  0.05f,  0.0f, 1.0f, 1.0f
+};
 ```
 
-片段着色器会从顶点着色器接受颜色向量，并将其设置为它的颜色输出，来实现四边形的颜色：
+片段着色器接收从顶点着色器发送来的颜色向量，设置为它的颜色输出，从而为四边形上色：
 
 ```c++
 #version 330 core
-out vec4 FragColor;
-  
 in vec3 fColor;
+out vec4 color;
 
 void main()
 {
-    FragColor = vec4(fColor, 1.0);
+    color = vec4(fColor, 1.0f);
 }
 ```
 
-到现在都没有什么新内容，但从顶点着色器开始就变得很有趣了：
+到目前为止没有什么新内容，但顶点着色器开始变得有意思了：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec2 aPos;
-layout (location = 1) in vec3 aColor;
+layout (location = 0) in vec2 position;
+layout (location = 1) in vec3 color;
 
 out vec3 fColor;
 
@@ -76,204 +75,205 @@ uniform vec2 offsets[100];
 void main()
 {
     vec2 offset = offsets[gl_InstanceID];
-    gl_Position = vec4(aPos + offset, 0.0, 1.0);
-    fColor = aColor;
+    gl_Position = vec4(position + offset, 0.0f, 1.0f);
+    fColor = color;
 }
 ```
 
-这里我们定义了一个叫做<var>offsets</var>的数组，它包含100个偏移向量。在顶点着色器中，我们会使用<var>gl_InstanceID</var>来索引<var>offsets</var>数组，获取每个实例的偏移向量。如果我们要实例化绘制100个四边形，仅使用这个顶点着色器我们就能得到100个位于不同位置的四边形。
+这里我们定义了一个uniform数组，叫`offsets`，它包含100个偏移量向量。在顶点着色器里，我们接收一个对应着当前实例的偏移量，这是通过使用 `gl_InstanceID`来索引offsets得到的。如果我们使用实例化绘制100个四边形，使用这个顶点着色器，我们就能得到100位于不同位置的四边形。
 
-当前，我们仍要设置这些偏移位置，我们会在进入渲染循环之前使用一个嵌套for循环计算：
+我们一定要设置偏移位置，在游戏循环之前我们用一个嵌套for循环计算出它来：
 
 ```c++
 glm::vec2 translations[100];
 int index = 0;
-float offset = 0.1f;
-for(int y = -10; y < 10; y += 2)
+GLfloat offset = 0.1f;
+for(GLint y = -10; y < 10; y += 2)
 {
-    for(int x = -10; x < 10; x += 2)
+    for(GLint x = -10; x < 10; x += 2)
     {
         glm::vec2 translation;
-        translation.x = (float)x / 10.0f + offset;
-        translation.y = (float)y / 10.0f + offset;
+        translation.x = (GLfloat)x / 10.0f + offset;
+        translation.y = (GLfloat)y / 10.0f + offset;
         translations[index++] = translation;
     }
 }
 ```
 
-这里，我们创建100个位移向量，表示10x10网格上的所有位置。除了生成<var>translations</var>数组之外，我们还需要将数据转移到顶点着色器的uniform数组中：
+这里我们创建100个平移向量，它包含着10×10格子所有位置。除了生成`translations`数组外，我们还需要把这些位移数据发送到顶点着色器的uniform数组：
 
 ```c++
-shader.use();
-for(unsigned int i = 0; i < 100; i++)
+shader.Use();
+for(GLuint i = 0; i < 100; i++)
 {
-    shader.setVec2(("offsets[" + std::to_string(i) + "]"), translations[i]);
+    stringstream ss;
+    string index;
+    ss << i;
+    index = ss.str();
+    GLint location = glGetUniformLocation(shader.Program, ("offsets[" + index + "]").c_str())
+    glUniform2f(location, translations[i].x, translations[i].y);
 }
 ```
 
-在这一段代码中，我们将for循环的计数器<var>i</var>转换为一个<fun>string</fun>，我们可以用它来动态创建位置值的字符串，用于uniform位置值的索引。接下来，我们会对<var>offsets</var> uniform数组中的每一项设置对应的位移向量。
+这一小段代码中，我们将for循环计数器i变为string，接着就能动态创建一个为请求的uniform的`location`创建一个`location`字符串。将offsets数组中的每个条目，我们都设置为相应的平移向量。
 
-现在所有的准备工作都做完了，我们可以开始渲染四边形了。对于实例化渲染，我们使用<fun>glDrawArraysInstanced</fun>或<fun>glDrawElementsInstanced</fun>。因为我们使用的不是索引缓冲，我们会调用<fun>glDrawArrays</fun>版本的函数：
+现在所有的准备工作都结束了，我们可以开始渲染四边形了。用实例化渲染来绘制四边形，我们需要调用`glDrawArraysInstanced`或`glDrawElementsInstanced`，由于我们使用的不是索引绘制缓冲，所以我们用的是`glDrawArrays`对应的那个版本`glDrawArraysInstanced`：
 
 ```c++
 glBindVertexArray(quadVAO);
-glDrawArraysInstanced(GL_TRIANGLES, 0, 6, 100);
+glDrawArraysInstanced(GL_TRIANGLES, 0, 6, 100);  
+glBindVertexArray(0);
 ```
 
-<fun>glDrawArraysInstanced</fun>的参数和<fun>glDrawArrays</fun>完全一样，除了最后多了个参数用来设置需要绘制的实例数量。因为我们想要在10x10网格中显示100个四边形，我们将它设置为100。运行代码之后，你应该能得到熟悉的100个五彩的四边形。
+`glDrawArraysInstanced`的参数和`glDrawArrays`一样，除了最后一个参数设置了我们打算绘制实例的数量。我们想展示100个四边形，它们以10×10网格形式展现，所以这儿就是100.运行代码，你会得到100个相似的有色四边形。
 
 ## 实例化数组
 
-虽然之前的实现在目前的情况下能够正常工作，但是如果我们要渲染远超过100个实例的时候（这其实非常普遍），我们最终会超过最大能够发送至着色器的uniform数据大小[上限](https://www.khronos.org/opengl/wiki/GLSL_Uniform#Implementation_limits)。它的一个代替方案是<def>实例化数组</def>(Instanced Array)，它被定义为一个顶点属性（能够让我们储存更多的数据），仅在顶点着色器渲染一个新的实例时才会更新。
+在这种特定条件下，前面的实现很好，但是当我们有100个实例的时候（这很正常），最终我们将碰到uniform数据数量的上线。为避免这个问题另一个可替代方案是实例化数组(Instanced Array)，它使用顶点属性来定义，这样就允许我们使用更多的数据了，当顶点着色器渲染一个新实例时它才会被更新。
 
-使用顶点属性时，顶点着色器的每次运行都会让GLSL获取新一组适用于当前顶点的属性。而当我们将顶点属性定义为一个实例化数组时，顶点着色器就只需要对每个实例，而不是每个顶点，更新顶点属性的内容了。这允许我们对逐顶点的数据使用普通的顶点属性，而对逐实例的数据使用实例化数组。
+使用顶点属性，每次运行顶点着色器都将让GLSL获取到下个顶点属性集合，它们属于当前顶点。当把顶点属性定义为实例数组时，顶点着色器只更新每个实例的顶点属性的内容而不是顶点的内容。这使我们在每个顶点数据上使用标准顶点属性，用实例数组来储存唯一的实例数据。
 
-为了给你一个实例化数组的例子，我们将使用之前的例子，并将偏移量uniform数组设置为一个实例化数组。我们需要在顶点着色器中再添加一个顶点属性：
+为了展示一个实例化数组的例子，我们将采用前面的例子，把偏移uniform表示为一个实例数组。我们不得不增加另一个顶点属性，来更新顶点着色器。
 
 ```c++
 #version 330 core
-layout (location = 0) in vec2 aPos;
-layout (location = 1) in vec3 aColor;
-layout (location = 2) in vec2 aOffset;
+layout (location = 0) in vec2 position;
+layout (location = 1) in vec3 color;
+layout (location = 2) in vec2 offset;
 
 out vec3 fColor;
 
 void main()
 {
-    gl_Position = vec4(aPos + aOffset, 0.0, 1.0);
-    fColor = aColor;
+    gl_Position = vec4(position + offset, 0.0f, 1.0f);
+    fColor = color;
 }
 ```
 
-我们不再使用<var>gl_InstanceID</var>，现在不需要索引一个uniform数组就能够直接使用<var>offset</var>属性了。
+我们不再使用`gl_InstanceID`，可以直接用`offset`属性，不用先在一个大uniform数组里进行索引。
 
-因为实例化数组和<var>position</var>与<var>color</var>变量一样，都是顶点属性，我们还需要将它的内容存在顶点缓冲对象中，并且配置它的属性指针。我们首先将（上一部分的）<var>translations</var>数组存到一个新的缓冲对象中：
+因为一个实例化数组实际上就是一个和位置和颜色一样的顶点属性，我们还需要把它的内容储存为一个顶点缓冲对象里，并把它配置为一个属性指针。我们首先将平移变换数组贮存到一个新的缓冲对象上：
 
 ```c++
-unsigned int instanceVBO;
+GLuint instanceVBO;
 glGenBuffers(1, &instanceVBO);
 glBindBuffer(GL_ARRAY_BUFFER, instanceVBO);
 glBufferData(GL_ARRAY_BUFFER, sizeof(glm::vec2) * 100, &translations[0], GL_STATIC_DRAW);
 glBindBuffer(GL_ARRAY_BUFFER, 0);
 ```
 
-之后我们还需要设置它的顶点属性指针，并启用顶点属性：
+之后我们还需要设置它的顶点属性指针，并开启顶点属性：
 
 ```c++
 glEnableVertexAttribArray(2);
 glBindBuffer(GL_ARRAY_BUFFER, instanceVBO);
-glVertexAttribPointer(2, 2, GL_FLOAT, GL_FALSE, 2 * sizeof(float), (void*)0);
-glBindBuffer(GL_ARRAY_BUFFER, 0);	
+glVertexAttribPointer(2, 2, GL_FLOAT, GL_FALSE, 2 * sizeof(GLfloat), (GLvoid*)0);
+glBindBuffer(GL_ARRAY_BUFFER, 0);
 glVertexAttribDivisor(2, 1);
 ```
 
-这段代码很有意思的地方在于最后一行，我们调用了<fun>glVertexAttribDivisor</fun>。这个函数告诉了OpenGL该**什么时候**更新顶点属性的内容至新一组数据。它的第一个参数是需要的顶点属性，第二个参数是<def>属性除数</def>(Attribute Divisor)。默认情况下，属性除数是0，告诉OpenGL我们需要在顶点着色器的每次迭代时更新顶点属性。将它设置为1时，我们告诉OpenGL我们希望在渲染一个新实例的时候更新顶点属性。而设置为2时，我们希望每2个实例更新一次属性，以此类推。我们将属性除数设置为1，是在告诉OpenGL，处于位置值2的顶点属性是一个实例化数组。
+代码中有意思的地方是，最后一行，我们调用了 **`glVertexAttribDivisor`**。这个函数告诉OpenGL什么时候去更新顶点属性的内容到下个元素。它的第一个参数是提到的顶点属性，第二个参数是属性除数（attribute divisor）。默认属性除数是0，告诉OpenGL在顶点着色器的每次迭代更新顶点属性的内容。把这个属性设置为1，我们就是告诉OpenGL我们打算在开始渲染一个新的实例的时候更新顶点属性的内容。设置为2代表我们每2个实例更新内容，依此类推。把属性除数设置为1，我们可以高效地告诉OpenGL，location是2的顶点属性是一个实例数组（instanced array）。
 
-如果我们现在使用<fun>glDrawArraysInstanced</fun>，再次渲染四边形，会得到以下输出：
+如果我们现在再次使用`glDrawArraysInstanced`渲染四边形，我们会得到下面的输出：
 
-![](../img/04/10/instancing_quads.png)
+![](http://learnopengl.com/img/advanced/instancing_quads.png)
 
-这和之前的例子是完全一样的，但这次是使用实例化数组实现的，这让我们能够传递更多的数据到顶点着色器（只要内存允许）来用于实例化绘制。
+和前面的一样，但这次是使用实例数组实现的，它使我们为绘制实例向顶点着色器传递更多的数据（内存允许我们存多少就能存多少）。
 
-为了更有趣一点，我们也可以使用<var>gl_InstanceID</var>，从右上到左下逐渐缩小四边形：
+你还可以使`用gl_InstanceID`从右上向左下缩小每个四边形。
 
 ```c++
 void main()
 {
-    vec2 pos = aPos * (gl_InstanceID / 100.0);
-    gl_Position = vec4(pos + aOffset, 0.0, 1.0);
-    fColor = aColor;
+    vec2 pos = position * (gl_InstanceID / 100.0f);
+    gl_Position = vec4(pos + offset, 0.0f, 1.0f);
+    fColor = color;
 }
 ```
 
-结果就是，第一个四边形的实例会非常小，随着绘制实例的增加，<var>gl_InstanceID</var>会越来越接近100，四边形也就越来越接近原始大小。像这样将实例化数组与<var>gl_InstanceID</var>结合使用是完全可行的。
+结果是第一个实例的四边形被绘制的非常小，随着绘制实例的增加，`gl_InstanceID`越来越接近100，这样更多的四边形会更接近它们原来的大小。这是一种很好的将`gl_InstanceID`与实例数组结合使用的法则：
 
-![](../img/04/10/instancing_quads_arrays.png)
+![](http://learnopengl.com/img/advanced/instancing_quads_arrays.png)
 
-如果你还是不确定实例化渲染是如何工作的，或者想看看所有代码是如何组合起来的，你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/10.1.instancing_quads/instancing_quads.cpp)找到程序的源代码。
+如果你仍然不确定实例渲染如何工作，或者想看看上面的代码是如何组合起来的，你可以在[这里找到应用的源码](http://learnopengl.com/code_viewer.php?code=advanced/instancing_quads)。
 
-虽然很有趣，但是这些例子并不是实例化的好例子。是的，它们的确让你知道实例化是怎么工作的，但是我们还没接触到它最有用的一点：绘制巨大数量的相似物体。出于这个原因，我们将会在下一部分进入太空探险，见识实例化渲染真正的威力。
+这些例子不是实例的好例子，不过挺有意思的。它们可以让你对实例的工作方式有一个概括的理解，但是当绘制拥有极大数量的相同物体的时候，它极其有用，现在我们还没有展示呢。出于这个原因，我们将在接下来的部分进入太空来看看实例渲染的威力。
 
 # 小行星带
 
-想象这样一个场景，在宇宙中有一个大的行星，它位于小行星带的中央。这样的小行星带可能包含成千上万的岩块，在很不错的显卡上也很难完成这样的渲染。实例化渲染正是适用于这样的场景，因为所有的小行星都可以使用一个模型来表示。每个小行星可以再使用不同的变换矩阵来进行少许的变化。
+想象一下，在一个场景中有一个很大的行星，行星周围有一圈小行星带。这样一个小行星大可能包含成千上万的石块，对于大多数显卡来说几乎是难以完成的渲染任务。这个场景对于实例渲染来说却不再话下，由于所有小行星可以使用一个模型来表示。每个小行星使用一个变换矩阵就是一个经过少量变化的独一无二的小行星了。
 
-为了展示实例化渲染的作用，我们首先会**不使用**实例化渲染，来渲染小行星绕着行星飞行的场景。这个场景将会包含一个大的行星模型，它可以在[这里](../data/planet.rar)下载，以及很多环绕着行星的小行星。小行星的岩石模型可以在[这里](../data/rock.rar)下载。
+为了展示实例渲染的影响，我们先不使用实例渲染，来渲染一个小行星围绕行星飞行的场景。这个场景的大天体可以[从这里下载](http://learnopengl.com/data/models/planet.rar)，此外要把小行星放在合适的位置上。小行星可以[从这里下载](http://learnopengl.com/data/models/rock.rar)。
 
-在代码例子中，我们将使用在[模型加载](../03 Model Loading/01 Assimp.md)小节中定义的模型加载器来加载模型。
-
-为了得到想要的效果，我们将会为每个小行星生成一个变换矩阵，用作它们的模型矩阵。变换矩阵首先将小行星位移到小行星带中的某处，我们还会加一个小的随机偏移值到这个偏移量上，让这个圆环看起来更自然一点。接下来，我们应用一个随机的缩放，并且以一个旋转向量为轴进行一个随机的旋转。最终的变换矩阵不仅能将小行星变换到行星的周围，而且会让它看起来更自然，与其它小行星不同。最终的结果是一个布满小行星的圆环，其中每一个小行星都与众不同。
+为了得到我们理想中的效果，我们将为每个小行星生成一个变换矩阵，作为它们的模型矩阵。变换矩阵先将小行星平移到行星带上，我们还要添加一个随机位移值来作为偏移量，这样才能使行星带更自然。接着我们应用一个随机缩放，以及一个随机旋转向量。最后，变换矩阵就会将小行星变换到行星的周围，同时使它们更自然，每个行星都有别于其他的。
 
 ```c++
-unsigned int amount = 1000;
-glm::mat4 *modelMatrices;
+GLuint amount = 1000;
+glm::mat4* modelMatrices;
 modelMatrices = new glm::mat4[amount];
-srand(glfwGetTime()); // 初始化随机种子	
-float radius = 50.0;
-float offset = 2.5f;
-for(unsigned int i = 0; i < amount; i++)
+srand(glfwGetTime()); // initialize random seed
+GLfloat radius = 50.0;
+GLfloat offset = 2.5f;
+for(GLuint i = 0; i < amount; i++)
 {
     glm::mat4 model;
-    // 1. 位移：分布在半径为 'radius' 的圆形上，偏移的范围是 [-offset, offset]
-    float angle = (float)i / (float)amount * 360.0f;
-    float displacement = (rand() % (int)(2 * offset * 100)) / 100.0f - offset;
-    float x = sin(angle) * radius + displacement;
-    displacement = (rand() % (int)(2 * offset * 100)) / 100.0f - offset;
-    float y = displacement * 0.4f; // 让行星带的高度比x和z的宽度要小
-    displacement = (rand() % (int)(2 * offset * 100)) / 100.0f - offset;
-    float z = cos(angle) * radius + displacement;
+    // 1. Translation: displace along circle with 'radius' in range [-offset, offset]
+    GLfloat angle = (GLfloat)i / (GLfloat)amount * 360.0f;
+    GLfloat displacement = (rand() % (GLint)(2 * offset * 100)) / 100.0f - offset;
+    GLfloat x = sin(angle) * radius + displacement;
+    displacement = (rand() % (GLint)(2 * offset * 100)) / 100.0f - offset;
+    GLfloat y = displacement * 0.4f; // y value has smaller displacement
+    displacement = (rand() % (GLint)(2 * offset * 100)) / 100.0f - offset;
+    GLfloat z = cos(angle) * radius + displacement;
     model = glm::translate(model, glm::vec3(x, y, z));
-
-    // 2. 缩放：在 0.05 和 0.25f 之间缩放
-    float scale = (rand() % 20) / 100.0f + 0.05;
+    // 2. Scale: Scale between 0.05 and 0.25f
+    GLfloat scale = (rand() % 20) / 100.0f + 0.05;
     model = glm::scale(model, glm::vec3(scale));
-
-    // 3. 旋转：绕着一个（半）随机选择的旋转轴向量进行随机的旋转
-    float rotAngle = (rand() % 360);
+    // 3. Rotation: add random rotation around a (semi)randomly picked rotation axis vector
+    GLfloat rotAngle = (rand() % 360);
     model = glm::rotate(model, rotAngle, glm::vec3(0.4f, 0.6f, 0.8f));
-
-    // 4. 添加到矩阵的数组中
+    // 4. Now add to list of matrices
     modelMatrices[i] = model;
-}  
+}
 ```
 
-这段代码看起来可能有点吓人，但我们只是将小行星的`x`和`z`位置变换到了一个半径为<var>radius</var>的圆形上，并且在半径的基础上偏移了<var>-offset</var>到<var>offset</var>。我们让`y`偏移的影响更小一点，让小行星带更扁平一点。接下来，我们应用了缩放和旋转变换，并将最终的变换矩阵储存在<var>modelMatrices</var>中，这个数组的大小是<var>amount</var>。这里，我们一共生成1000个模型矩阵，每个小行星一个。
+这段代码看起来还是有点吓人，但我们基本上是沿着一个半径为radius的圆圈变换小行星的x和y的值，让每个小行星在-offset和offset之间随机生成一个位置。我们让y变化的更小，这让这个环带就会成为扁平的。接着我们缩放和旋转变换，把结果储存到一个modelMatrices矩阵里，它的大小是amount。这里我们生成1000个模型矩阵，每个小行星一个。
 
-在加载完行星和岩石模型，并编译完着色器之后，渲染的代码看起来是这样的：
+加载完天体和小行星模型后，编译着色器，渲染代码是这样的：
 
 ```c++
 // 绘制行星
-shader.use();
+shader.Use();
 glm::mat4 model;
-model = glm::translate(model, glm::vec3(0.0f, -3.0f, 0.0f));
+model = glm::translate(model, glm::vec3(0.0f, -5.0f, 0.0f));
 model = glm::scale(model, glm::vec3(4.0f, 4.0f, 4.0f));
-shader.setMat4("model", model);
+glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
 planet.Draw(shader);
-  
-// 绘制小行星
-for(unsigned int i = 0; i < amount; i++)
+
+// 绘制石头
+for(GLuint i = 0; i < amount; i++)
 {
-    shader.setMat4("model", modelMatrices[i]);
+    glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(modelMatrices[i]));
     rock.Draw(shader);
-}  
+}
 ```
 
-我们首先绘制了行星的模型，并对它进行位移和缩放，以适应场景，接下来，我们绘制<var>amount</var>数量的岩石模型。在绘制每个岩石之前，我们首先需要在着色器内设置对应的模型变换矩阵。
+我们先绘制天体模型，要把它平移和缩放一点以适应场景，接着，我们绘制amount数量的小行星，它们按照我们所计算的结果进行变换。在我们绘制每个小行星之前，我们还得先在着色器中设置相应的模型变换矩阵。
 
-最终的结果是一个看起来像是太空的场景，环绕着行星的是看起来很自然的小行星带：
+结果是一个太空样子的场景，我们可以看到有一个自然的小行星带：
 
-![](../img/04/10/instancing_asteroids.png)
+![](http://learnopengl.com/img/advanced/instancing_asteroids.png)
 
-这个场景每帧包含1001次渲染调用，其中1000个是岩石模型。你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/10.2.asteroids/asteroids.cpp)找到源代码。
+这个场景包含1001次渲染函数调用，每帧渲染1000个小行星模型。你可以在这里找到[场景的源码](http://learnopengl.com/code_viewer.php?code=advanced/instancing_asteroids_normal)，以及[顶点](http://learnopengl.com/code_viewer.php?code=advanced/instancing&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced/instancing&type=fragment)着色器。
 
-当我们开始增加这个数字的时候，你很快就会发现场景不再能够流畅运行了，帧数也下降很厉害。当我们将<var>amount</var>设置为2000的时候，场景就已经慢到移动都很困难的程度了。
+当我们开始增加数量的时候，很快就会注意到帧数的下降，而且下降的厉害。当我们设置为2000的时候，场景慢得已经难以移动了。
 
-现在，我们来尝试使用实例化渲染来渲染相同的场景。我们首先对顶点着色器进行一点修改：
+我们再次使用实例渲染来渲染同样的场景。我们先得对顶点着色器进行一点修改：
 
 ```c++
 #version 330 core
-layout (location = 0) in vec3 aPos;
-layout (location = 2) in vec2 aTexCoords;
+layout (location = 0) in vec3 position;
+layout (location = 2) in vec2 texCoords;
 layout (location = 3) in mat4 instanceMatrix;
 
 out vec2 TexCoords;
@@ -283,36 +283,35 @@ uniform mat4 view;
 
 void main()
 {
-    gl_Position = projection * view * instanceMatrix * vec4(aPos, 1.0); 
-    TexCoords = aTexCoords;
+    gl_Position = projection * view * instanceMatrix * vec4(position, 1.0f);
+    TexCoords = texCoords;
 }
 ```
 
-我们不再使用模型uniform变量，改为一个<fun>mat4</fun>的顶点属性，让我们能够存储一个实例化数组的变换矩阵。然而，当我们顶点属性的类型大于<fun>vec4</fun>时，就要多进行一步处理了。顶点属性最大允许的数据大小等于一个<fun>vec4</fun>。因为一个<fun>mat4</fun>本质上是4个<fun>vec4</fun>，我们需要为这个矩阵预留4个顶点属性。因为我们将它的位置值设置为3，矩阵每一列的顶点属性位置值就是3、4、5和6。
+我们不再使用模型uniform变量，取而代之的是把一个mat4的顶点属性，送一我们可以将变换矩阵储存为一个实例数组（instanced array）。然而，当我们声明一个数据类型为顶点属性的时候，它比一个vec4更大，是有些不同的。顶点属性被允许的最大数据量和vec4相等。因为一个mat4大致和4个vec4相等，我们为特定的矩阵必须保留4个顶点属性。因为我们将它的位置赋值为3个列的矩阵，顶点属性的位置就会是3、4、5和6。
 
-接下来，我们需要为这4个顶点属性设置属性指针，并将它们设置为实例化数组：
+然后我们必须为这4个顶点属性设置属性指针，并将其配置为实例数组：
 
 ```c++
-// 顶点缓冲对象
-unsigned int buffer;
-glGenBuffers(1, &buffer);
-glBindBuffer(GL_ARRAY_BUFFER, buffer);
-glBufferData(GL_ARRAY_BUFFER, amount * sizeof(glm::mat4), &modelMatrices[0], GL_STATIC_DRAW);
-  
-for(unsigned int i = 0; i < rock.meshes.size(); i++)
+for(GLuint i = 0; i < rock.meshes.size(); i++)
 {
-    unsigned int VAO = rock.meshes[i].VAO;
+    GLuint VAO = rock.meshes[i].VAO;
+    // Vertex Buffer Object
+    GLuint buffer;
     glBindVertexArray(VAO);
-    // 顶点属性
+    glGenBuffers(1, &buffer);
+    glBindBuffer(GL_ARRAY_BUFFER, buffer);
+    glBufferData(GL_ARRAY_BUFFER, amount * sizeof(glm::mat4), &modelMatrices[0], GL_STATIC_DRAW);
+    // Vertex Attributes
     GLsizei vec4Size = sizeof(glm::vec4);
-    glEnableVertexAttribArray(3); 
-    glVertexAttribPointer(3, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (void*)0);
-    glEnableVertexAttribArray(4); 
-    glVertexAttribPointer(4, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (void*)(1 * vec4Size));
-    glEnableVertexAttribArray(5); 
-    glVertexAttribPointer(5, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (void*)(2 * vec4Size));
-    glEnableVertexAttribArray(6); 
-    glVertexAttribPointer(6, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (void*)(3 * vec4Size));
+    glEnableVertexAttribArray(3);
+    glVertexAttribPointer(3, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (GLvoid*)0);
+    glEnableVertexAttribArray(4);
+    glVertexAttribPointer(4, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (GLvoid*)(vec4Size));
+    glEnableVertexAttribArray(5);
+    glVertexAttribPointer(5, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (GLvoid*)(2 * vec4Size));
+    glEnableVertexAttribArray(6);
+    glVertexAttribPointer(6, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (GLvoid*)(3 * vec4Size));
 
     glVertexAttribDivisor(3, 1);
     glVertexAttribDivisor(4, 1);
@@ -320,33 +319,34 @@ for(unsigned int i = 0; i < rock.meshes.size(); i++)
     glVertexAttribDivisor(6, 1);
 
     glBindVertexArray(0);
-}  
-```
-
-注意这里我们将<fun>Mesh</fun>的<var>VAO</var>从私有变量改为了公有变量，让我们能够访问它的顶点数组对象。这并不是最好的解决方案，只是为了配合本小节的一个简单的改动。除此之外代码就应该很清楚了。我们告诉了OpenGL应该如何解释每个缓冲顶点属性的缓冲，并且告诉它这些顶点属性是实例化数组。
-
-接下来，我们再次使用网格的<var>VAO</var>，这一次使用<fun>glDrawElementsInstanced</fun>进行绘制：
-
-```c++
-// 绘制小行星
-instanceShader.use();
-for(unsigned int i = 0; i < rock.meshes.size(); i++)
-{
-    glBindVertexArray(rock.meshes[i].VAO);
-    glDrawElementsInstanced(
-        GL_TRIANGLES, rock.meshes[i].indices.size(), GL_UNSIGNED_INT, 0, amount
-    );
 }
 ```
 
-这里，我们绘制与之前相同数量<var>amount</var>的小行星，但是使用的是实例渲染。结果应该是非常相似的，但如果你开始增加<var>amount</var>变量，你就能看见实例化渲染的效果了。没有实例化渲染的时候，我们只能流畅渲染1000到1500个小行星。而使用了实例化渲染之后，我们可以将这个值设置为100000，每个岩石模型有576个顶点，每帧加起来大概要绘制5700万个顶点，但性能却没有受到任何影响！
+要注意的是我们将Mesh的VAO变量声明为一个public（公有）变量，而不是一个private（私有）变量，所以我们可以获取它的顶点数组对象。这不是最干净的方案，但这能较好的适应本教程。若没有这点hack，代码就干净了。我们声明了OpenGL该如何为每个矩阵的顶点属性的缓冲进行解释，每个顶点属性都是一个实例数组。
 
-![](../img/04/10/instancing_asteroids_quantity.png)
+下一步我们再次获得网格的VAO，这次使用`glDrawElementsInstanced`进行绘制：
 
-上面这幅图渲染了10万个小行星，半径为`150.0f`，偏移量等于`25.0f`。你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/10.3.asteroids_instanced/asteroids_instanced.cpp)找到实例化渲染的代码。
+```c++
+// Draw meteorites
+instanceShader.Use();
+for(GLuint i = 0; i < rock.meshes.size(); i++)
+{
+    glBindVertexArray(rock.meshes[i].VAO);
+    glDrawElementsInstanced(
+        GL_TRIANGLES, rock.meshes[i].vertices.size(), GL_UNSIGNED_INT, 0, amount
+    );
+    glBindVertexArray(0);
+}
+```
+
+这里我们绘制和前面的例子里一样数量（amount）的小行星，只不过是使用的实例渲染。结果是相似的，但你会看在开始增加数量以后效果的不同。不实例渲染，我们可以流畅渲染1000到1500个小行星。而使用了实例渲染，我们可以设置为100000，每个模型由576个顶点，这几乎有5千7百万个顶点，而且帧率没有丝毫下降！
+
+![](http://learnopengl.com/img/advanced/instancing_asteroids_quantity.png)
+
+上图渲染了十万小行星，半径为150.0f，偏移等于25.0f。你可以在这里找到这个演示实例渲染的[源码](http://learnopengl.com/code_viewer.php?code=advanced/instancing_asteroids_instanced)。
 
 !!! Important
 
-	在某些机器上，10万个小行星可能会太多了，所以尝试修改这个值，直到达到一个你能接受的帧率。
+        有些机器渲染十万可能会有点吃力，所以尝试修改这个数量知道你能获得可以接受的帧率。
 
-可以看到，在合适的环境下，实例化渲染能够大大增加显卡的渲染能力。正是出于这个原因，实例化渲染通常会用于渲染草、植被、粒子，以及上面这样的场景，基本上只要场景中有很多重复的形状，都能够使用实例化渲染来提高性能。
+就像你所看到的，在合适的条件下，实例渲染对于你的显卡来说和普通渲染有很大不同。处于这个理由，实例渲染通常用来渲染草、草丛、粒子以及像这样的场景，基本上来讲只要场景中有很多重复物体，使用实例渲染都会获得好处。

docs/04 Advanced OpenGL/11 Anti Aliasing.md

@@ -3,105 +3,102 @@
 原文     | [Anti Aliasing](http://learnopengl.com/#!Advanced-OpenGL/Anti-Aliasing)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet, [Django](http://bullteacher.com/)
-校对     | 暂未校对
+翻译     | [Django](http://bullteacher.com/)
+校对     | [Geequlim](http://geequlim.com)
 
-在学习渲染的旅途中，你可能会时不时遇到模型边缘有锯齿的情况。这些<def>锯齿边缘</def>(Jagged Edges)的产生和光栅器将顶点数据转化为片段的方式有关。在下面的例子中，你可以看到，我们只是绘制了一个简单的立方体，你就能注意到它存在锯齿边缘了：
+在你的渲染大冒险中，你可能会遇到模型边缘有锯齿的问题。**锯齿边(Jagged Edge)**出现的原因是由顶点数据像素化之后成为片段的方式所引起的。下面是一个简单的立方体，它体现了锯齿边的效果：
 
-![](../img/04/11/anti_aliasing_aliasing.png)
+![](http://learnopengl.com/img/advanced/anti_aliasing_aliasing.png)
 
-可能不是非常明显，但如果你离近仔细观察立方体的边缘，你就应该能够看到锯齿状的图案。如果放大的话，你会看到下面的图案：
+也许不是立即可见的，如果你更近的看看立方体的边，你就会发现锯齿了。如果我们放大就会看到下面的情境：
 
-![](../img/04/11/anti_aliasing_zoomed.png)
+![](http://learnopengl.com/img/advanced/anti_aliasing_zoomed.png)
 
-这很明显不是我们想要在最终程序中所实现的效果。你能够清楚看见形成边缘的像素。这种现象被称之为<def>走样</def>(Aliasing)。有很多种抗锯齿（Anti-aliasing，也被称为反走样）的技术能够帮助我们缓解这种现象，从而产生更**平滑**的边缘。
+这当然不是我们在最终版本的应用里想要的效果。这个效果，很明显能看到边是由像素所构成的，这种现象叫做**走样(Aliasing)**。有很多技术能够减少走样，产生更平滑的边缘，这些技术叫做**抗锯齿技术**(Anti-aliasing，也被称为反走样技术)。
 
-最开始我们有一种叫做<def>超采样抗锯齿</def>(Super Sample Anti-aliasing, SSAA)的技术，它会使用比正常分辨率更高的分辨率（即超采样）来渲染场景，当图像输出在帧缓冲中更新时，分辨率会被下采样(Downsample)至正常的分辨率。这些**额外的**分辨率会被用来防止锯齿边缘的产生。虽然它确实能够解决走样的问题，但是由于这样比平时要绘制更多的片段，它也会带来很大的性能开销。所以这项技术只拥有了短暂的辉煌。
+首先，我们有一个叫做**超级采样抗锯齿技术(Super Sample Anti-aliasing, SSAA)**，它暂时使用一个更高的解析度（以超级采样方式）来渲染场景，当视频输出在帧缓冲中被更新时，解析度便降回原来的普通解析度。这个额外的解析度被用来防止锯齿边。虽然它确实为我们提供了一种解决走样问题的方案，但却由于必须绘制比平时更多的片段而降低了性能。所以这个技术只流行了一段时间。
 
-然而，在这项技术的基础上也诞生了更为现代的技术，叫做<def>多重采样抗锯齿</def>(Multisample Anti-aliasing, MSAA)。它借鉴了SSAA背后的理念，但却以更加高效的方式实现了抗锯齿。我们在这一节中会深度讨论OpenGL中内建的MSAA技术。
+这个技术的基础上诞生了更为现代的技术，叫做**多采样抗锯齿(Multisample Anti-aliasing)**或叫MSAA，虽然它借用了SSAA的理念，但却以更加高效的方式实现了它。这节教程我们会展开讨论这个MSAA技术，它是OpenGL内建的。
 
 ## 多重采样
 
-为了理解什么是多重采样(Multisampling)，以及它是如何解决锯齿问题的，我们有必要更加深入地了解OpenGL光栅器的工作方式。
+为了理解什么是多重采样(Multisampling)，以及它是如何解决锯齿问题的，我们先要更深入了解一个OpenGL光栅化的工作方式。
 
-光栅器是位于最终处理过的顶点之后到片段着色器之前所经过的所有的算法与过程的总和。光栅器会将一个图元的所有顶点作为输入，并将它转换为一系列的片段。顶点坐标理论上可以取任意值，但片段不行，因为它们受限于你窗口的分辨率。顶点坐标与片段之间几乎永远也不会有一对一的映射，所以光栅器必须以某种方式来决定每个顶点最终所在的片段/屏幕坐标。
+光栅化是你的最终的经处理的顶点和片段着色器之间的所有算法和处理的集合。光栅化将属于一个基本图形的所有顶点转化为一系列片段。顶点坐标理论上可以含有任何坐标，但片段却不是这样，这是因为它们与你的窗口的解析度有关。几乎永远都不会有顶点坐标和片段的一对一映射，所以光栅化必须以某种方式决定每个特定顶点最终结束于哪个片段/屏幕坐标上。
 
-![](../img/04/11/anti_aliasing_rasterization.png)
+![](http://learnopengl.com/img/advanced/anti_aliasing_rasterization.png)
 
-这里我们可以看到一个屏幕像素的网格，每个像素的中心包含有一个<def>采样点</def>(Sample Point)，它会被用来决定这个三角形是否遮盖了某个像素。图中红色的采样点被三角形所遮盖，在每一个遮住的像素处都会生成一个片段。虽然三角形边缘的一些部分也遮住了某些屏幕像素，但是这些像素的采样点并没有被三角形**内部**所遮盖，所以它们不会受到片段着色器的影响。
+这里我们看到一个屏幕像素网格，每个像素中心包含一个采样点（sample point），它被用来决定一个像素是否被三角形所覆盖。红色的采样点如果被三角形覆盖，那么就会为这个被覆盖像（屏幕）素生成一个片段。即使三角形覆盖了部分屏幕像素，但是采样点没被覆盖，这个像素仍然不会受到任何片段着色器影响到。
 
-你现在可能已经清楚走样的原因了。完整渲染后的三角形在屏幕上会是这样的：
+你可能已经明白走样的原因来自何处了。三角形渲染后的版本最后在你的屏幕上是这样的：
 
-![](../img/04/11/anti_aliasing_rasterization_filled.png)
+![](http://learnopengl.com/img/advanced/anti_aliasing_rasterization_filled.png)
 
-由于屏幕像素总量的限制，有些边缘的像素能够被渲染出来，而有些则不会。结果就是我们使用了不光滑的边缘来渲染图元，导致之前讨论到的锯齿边缘。
+由于屏幕像素总量的限制，有些边上的像素能被渲染出来，而有些则不会。结果就是我们渲染出的基本图形的非光滑边缘产生了上图的锯齿边。
 
-多重采样所做的正是将单一的采样点变为多个采样点（这也是它名称的由来）。我们不再使用像素中心的单一采样点，取而代之的是以特定图案排列的4个子采样点(Subsample)。我们将用这些子采样点来决定像素的遮盖度。
+多采样所做的正是不再使用单一采样点来决定三角形的覆盖范围，而是采用多个采样点。我们不再使用每个像素中心的采样点，取而代之的是4个子样本（subsample），用它们来决定像素的覆盖率。这意味着颜色缓冲的大小也由于每个像素的子样本的增加而增加了。
 
-![](../img/04/11/anti_aliasing_sample_points.png)
+![](http://learnopengl.com/img/advanced/anti_aliasing_sample_points.png)
 
-上图的左侧展示了正常情况下判定三角形是否遮盖的方式。在例子中的这个像素上不会运行片段着色器（所以它会保持空白）。因为它的采样点并未被三角形所覆盖。上图的右侧展示的是实施多重采样之后的版本，每个像素包含有4个采样点。这里，只有两个采样点遮盖住了三角形。
+左侧的图显示了我们普通决定一个三角形的覆盖范围的方式。这个像素并不会运行一个片段着色器（这就仍保持空白），因为它的采样点没有被三角形所覆盖。右边的图展示了多采样的版本，每个像素包含4个采样点。这里我们可以看到只有2个采样点被三角形覆盖。
 
 !!! Important
 
-    采样点的数量可以是任意的，更多的采样点能带来更精确的遮盖率。
+    采样点的数量是任意的，更多的采样点能带来更精确的覆盖率。
 
-从这里开始多重采样就变得有趣起来了。我们知道三角形只遮盖了2个子采样点，所以下一步是决定这个像素的颜色。你的猜想可能是，我们对每个被遮盖住的子采样点运行一次片段着色器，最后将每个像素所有子采样点的颜色平均一下。在这个例子中，我们需要在两个子采样点上对被插值的顶点数据运行两次片段着色器，并将结果的颜色储存在这些采样点中。（幸运的是）这并**不是**它工作的方式，因为这本质上说还是需要运行更多次的片段着色器，会显著地降低性能。
+多采样开始变得有趣了。2个子样本被三角覆盖，下一步是决定这个像素的颜色。我们原来猜测，我们会为每个被覆盖的子样本运行片段着色器，然后对每个像素的子样本的颜色进行平均化。例子的那种情况，我们在插值的顶点数据的每个子样本上运行片段着色器，然后将这些采样点的最终颜色储存起来。幸好，它不是这么运作的，因为这等于说我们必须运行更多的片段着色器，会明显降低性能。
 
-MSAA真正的工作方式是，无论三角形遮盖了多少个子采样点，（每个图元中）每个像素只运行**一次**片段着色器。片段着色器使用插值到像素**中心**的顶点数据，然后，MSAA使用更大的深度/模板缓冲区来确定子采样点的覆盖率。被覆盖的子采样点数量将决定了像素颜色对帧缓冲的影响程度。因为上图的4个采样点中只有2个被遮盖住了，所以三角形的颜色会有一半与帧缓冲区的颜色（在这里是无色）进行混合，最终形成一种淡蓝色。
+MSAA的真正工作方式是，每个像素只运行一次片段着色器，无论多少子样本被三角形所覆盖。片段着色器运行着插值到像素中心的顶点数据，最后颜色被储存近每个被覆盖的子样本中，每个像素的所有颜色接着将平均化，每个像素最终有了一个唯一颜色。在前面的图片中4个样本中只有2个被覆盖，像素的颜色将以三角形的颜色进行平均化，颜色同时也被储存到其他2个采样点，最后生成的是一种浅蓝色。
 
-这样子做之后，颜色缓冲中所有的图元边缘将会产生一种更平滑的图形。让我们来看看前面三角形的多重采样会是什么样子：
+结果是，颜色缓冲中所有基本图形的边都生成了更加平滑的样式。让我们看看当再次决定前面的三角形覆盖范围时多样本看起来是这样的：
 
-![](../img/04/11/anti_aliasing_rasterization_samples.png)
+![](http://learnopengl.com/img/advanced/anti_aliasing_rasterization_samples.png)
 
-这里，每个像素包含4个子采样点（不相关的采样点都没有标注），蓝色的采样点被三角形所遮盖，而灰色的则没有。对于三角形的内部的像素，片段着色器只会运行一次，颜色输出会被存储到全部的4个子样本中。而在三角形的边缘，并不是所有的子采样点都被遮盖，所以片段着色器的结果将只会储存到部分的子样本中。根据被遮盖的子样本的数量，最终的像素颜色将由三角形的颜色与其它子样本中所储存的颜色来决定。
+这里每个像素包含着4个子样本（不相关的已被隐藏）蓝色的子样本是被三角形覆盖了的，灰色的没有被覆盖。三角形内部区域中的所有像素都会运行一次片段着色器，它输出的颜色被储存到所有4个子样本中。三角形的边缘并不是所有的子样本都会被覆盖，所以片段着色器的结果仅储存在部分子样本中。根据被覆盖子样本的数量，最终的像素颜色由三角形颜色和其他子样本所储存的颜色所决定。
 
-简单来说，一个像素中如果有更多的采样点被三角形遮盖，那么这个像素的颜色就会更接近于三角形的颜色。如果我们给上面的三角形填充颜色，就能得到以下的效果：
+大致上来说，如果更多的采样点被覆盖，那么像素的颜色就会更接近于三角形。如果我们用早期使用的三角形的颜色填充像素，我们会获得这样的结果：
 
-![](../img/04/11/anti_aliasing_rasterization_samples_filled.png)
+![](http://learnopengl.com/img/advanced/anti_aliasing_rasterization_samples_filled.png)
 
-三角形的不平滑边缘被稍浅的颜色所包围后，从远处观察时就会显得更加平滑了。
+对于每个像素来说，被三角形覆盖的子样本越少，像素受到三角形的颜色的影响也越少。现在三角形的硬边被比实际颜色浅一些的颜色所包围，因此观察者从远处看上去就比较平滑了。
 
-深度值和模板值会按各个子采样点存储，并且当多个三角形重叠单个像素时，即使我们只运行一次片段着色器，颜色值也依然会按子采样点存储。对深度测试来说，在运行深度测试之前，每个顶点的深度值会被插值到各个子样本中。而对模板测试来说，我们会为每个子样本存储模板值，这意味着缓冲区的大小会根据每个像素的子采样点数量而相应增加。
-
-我们到目前为止讨论的都是多重采样抗锯齿的背后原理，光栅器背后的实际逻辑比目前讨论的要复杂，但你现在应该已经可以理解多重采样抗锯齿的大体概念和逻辑了。
-
-(译者注： 如果看到这里还是对原理似懂非懂，可以简单看看知乎上[@文刀秋二](https://www.zhihu.com/people/edliu/answers)对抗锯齿技术的[精彩介绍](https://www.zhihu.com/question/20236638/answer/14438218))
+不仅颜色值被多采样影响，深度和模板测试也同样使用了多采样点。比如深度测试，顶点的深度值在运行深度测试前被插值到每个子样本中，对于模板测试，我们为每个子样本储存模板值，而不是每个像素。这意味着深度和模板缓冲的大小随着像素子样本的增加也增加了。
 
+到目前为止我们所讨论的不过是多采样发走样工作的方式。光栅化背后实际的逻辑要比我们讨论的复杂，但你现在可以理解多采样抗锯齿背后的概念和逻辑了。
 
 ## OpenGL中的MSAA
 
-如果我们想要在OpenGL中使用MSAA，我们必须要使用一个能在每个像素中存储大于1个颜色值的颜色缓冲（因为多重采样需要我们为每个采样点都储存一个颜色）。所以，我们需要一个新的缓冲类型，来存储特定数量的多重采样样本，它叫做<def>多重采样缓冲</def>(Multisample Buffer)。
+如果我们打算在OpenGL中使用MSAA，那么我们必须使用一个可以为每个像素储存一个以上的颜色值的颜色缓冲(因为多采样需要我们为每个采样点储存一个颜色)。我们这就需要一个新的缓冲类型，它可以储存要求数量的多重采样样本，它叫做**多样本缓冲(Multisample Buffer)**。
 
-大多数的窗口系统都应该提供了一个多重采样缓冲，用以代替默认的颜色缓冲。GLFW同样给了我们这个功能，我们所要做的只是**提示**(Hint) GLFW，我们希望使用一个包含N个样本的多重采样缓冲。这可以在创建窗口之前调用<fun>glfwWindowHint</fun>来完成。
+多数窗口系统可以为我们提供一个多样本缓冲，以代替默认的颜色缓冲。GLFW同样给了我们这个功能，我们所要作的就是提示GLFW，我们希望使用一个带有N个样本的多样本缓冲，而不是普通的颜色缓冲，这要在创建窗口前调用`glfwWindowHint`来完成：
 
 ```c++
 glfwWindowHint(GLFW_SAMPLES, 4);
 ```
 
-现在再调用<fun>glfwCreateWindow</fun>创建渲染窗口时，每个屏幕坐标就会使用一个包含4个子采样点的颜色缓冲了。GLFW会自动创建一个每像素4个子采样点的深度和样本缓冲。这也意味着所有缓冲的大小都增长了4倍。
+当我们现在调用`glfwCreateWindow`，用于渲染的窗口就被创建了，这次每个屏幕坐标使用一个包含4个子样本的颜色缓冲。这意味着所有缓冲的大小都增长4倍。
 
-现在我们已经向GLFW请求了多重采样缓冲，我们还需要调用<fun>glEnable</fun>并启用<var>GL_MULTISAMPLE</var>，来启用多重采样。在大多数OpenGL的驱动上，多重采样都是默认启用的，所以这个调用可能会有点多余，但显式地调用一下会更保险一点。这样子不论是什么OpenGL的实现都能够正常启用多重采样了。
+现在我们请求GLFW提供了多样本缓冲，我们还要调用`glEnable`来开启多采样，参数是 `GL_MULTISAMPLE`。大多数OpenGL驱动，多采样默认是开启的，所以这个调用有点多余，但通常记得开启它是个好主意。这样所有OpenGL实现的多采样都开启了。
 
 ```c++
 glEnable(GL_MULTISAMPLE);
 ```
 
-因为多重采样的算法都在OpenGL驱动的光栅器中实现了，我们不需要再多做什么。如果现在再来渲染本节一开始的那个绿色的立方体，我们应该能看到更平滑的边缘：
+当默认帧缓冲有了多采样缓冲附件的时候，我们所要做的全部就是调用 `glEnable`开启多采样。因为实际的多采样算法在OpenGL驱动光栅化里已经实现了，所以我们无需再做什么了。如果我们现在来渲染教程开头的那个绿色立方体，我们会看到边缘变得平滑了：
 
-![](../img/04/11/anti_aliasing_multisampled.png)
+![](http://learnopengl.com/img/advanced/anti_aliasing_multisampled.png)
 
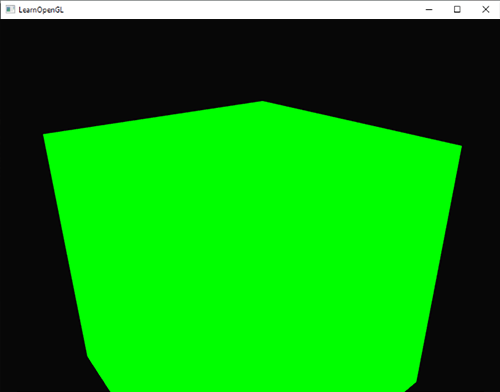
-这个箱子看起来的确要平滑多了，如果在场景中有其它的物体，它们也会看起来平滑很多。你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/11.1.anti_aliasing_msaa/anti_aliasing_msaa.cpp)找到这个简单例子的源代码。
+这个箱子看起来平滑多了，在场景中绘制任何物体都可以利用这个技术。可以[从这里找到](http://learnopengl.com/code_viewer.php?code=advanced/anti_aliasing_multisampling)这个简单的例子。
 
 ## 离屏MSAA
 
-由于GLFW负责了创建多重采样缓冲，启用MSAA非常简单。然而，如果我们想要使用我们自己的帧缓冲来进行离屏渲染，那么我们就必须要自己动手生成多重采样缓冲了。现在，我们**确实**需要自己创建多重采样缓冲区。
+因为GLFW负责创建多采样缓冲，开启MSAA非常简单。如果我们打算使用我们自己的帧缓冲，来进行离屏渲染，那么我们就必须自己生成多采样缓冲了；现在我们需要自己负责创建多采样缓冲。
 
-有两种方式可以创建多重采样缓冲，将其作为帧缓冲的附件：纹理附件和渲染缓冲附件，这和在[帧缓冲](05 Framebuffers.md)教程中所讨论的普通附件很相似。
+有两种方式可以创建多采样缓冲，并使其成为帧缓冲的附件：纹理附件和渲染缓冲附件，和[帧缓冲教程](05 Framebuffers.md)里讨论过的普通的附件很相似。
 
-### 多重采样纹理附件
+### 多采样纹理附件
 
-为了创建一个支持储存多个采样点的纹理，我们使用<fun>glTexImage2DMultisample</fun>来替代<fun>glTexImage2D</fun>，它的纹理目标是<var>GL_TEXTURE_2D_MULTISAPLE</var>。
+为了创建一个支持储存多采样点的纹理，我们使用 `glTexImage2DMultisample`来替代 `glTexImage2D`，它的纹理目标是**`GL_TEXTURE_2D_MULTISAMPLE`**：
 
 ```c++
 glBindTexture(GL_TEXTURE_2D_MULTISAMPLE, tex);
@@ -109,33 +106,33 @@ glTexImage2DMultisample(GL_TEXTURE_2D_MULTISAMPLE, samples, GL_RGB, width, heigh
 glBindTexture(GL_TEXTURE_2D_MULTISAMPLE, 0);
 ```
 
-它的第二个参数设置的是纹理所拥有的样本个数。如果最后一个参数为<var>GL_TRUE</var>，图像将会对每个纹素使用相同的样本位置以及相同数量的子采样点个数。
+第二个参数现在设置了我们打算让纹理拥有的样本数。如果最后一个参数等于 **`GL_TRUE`**，图像上的每一个纹理像素（texel）将会使用相同的样本位置，以及同样的子样本数量。
 
-我们使用<fun>glFramebufferTexture2D</fun>将多重采样纹理附加到帧缓冲上，但这里纹理类型使用的是<var>GL_TEXTURE_2D_MULTISAMPLE</var>。
+为将多采样纹理附加到帧缓冲上，我们使用`glFramebufferTexture2D`，不过这次纹理类型是**`GL_TEXTURE_2D_MULTISAMPLE`**：
 
 ```c++
 glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D_MULTISAMPLE, tex, 0);
 ```
 
-当前绑定的帧缓冲现在就有了一个纹理图像形式的多重采样颜色缓冲。
+当前绑定的帧缓冲现在有了一个纹理图像形式的多采样颜色缓冲。
 
-### 多重采样渲染缓冲对象
+### 多采样渲染缓冲对象
 
-和纹理类似，创建一个多重采样渲染缓冲对象并不难。我们所要做的只是在指定（当前绑定的）渲染缓冲的内存存储时，将<fun>glRenderbufferStorage</fun>的调用改为<fun>glRenderbufferStorageMultisample</fun>就可以了。
+和纹理一样，创建一个多采样渲染缓冲对象(Multisampled Renderbuffer Objects)不难。而且还很简单，因为我们所要做的全部就是当我们指定渲染缓冲的内存的时候将`glRenderbuffeStorage`改为`glRenderbufferStorageMuiltisample`：
 
 ```c++
 glRenderbufferStorageMultisample(GL_RENDERBUFFER, 4, GL_DEPTH24_STENCIL8, width, height);
 ```
 
-函数中，渲染缓冲对象后的参数我们将设定为样本的数量，在当前的例子中是4。
+有一样东西在这里有变化，就是缓冲目标后面那个额外的参数，我们将其设置为样本数量，当前的例子中应该是4.
 
-### 渲染到多重采样帧缓冲
+### 渲染到多采样帧缓冲
 
-渲染到多重采样帧缓冲对象的过程非常简单。只要我们在帧缓冲绑定时绘制任何东西，光栅器就会负责所有的多重采样运算。我们最终会得到一个多重采样颜色缓冲以及/或深度和模板缓冲。因为多重采样缓冲有一点特别，我们不能直接将它们的缓冲图像用于其他运算，比如在着色器中对它们进行采样。
+渲染到多采样帧缓冲对象是自动的。当我们绘制任何东西时，帧缓冲对象就绑定了，光栅化会对负责所有多采样操作。我们接着得到了一个多采样颜色缓冲，以及深度和模板缓冲。因为多采样缓冲有点特别，我们不能为其他操作直接使用它们的缓冲图像，比如在着色器中进行采样。
 
-一个多重采样的图像包含比普通图像更多的信息，我们所要做的是缩小或者<def>还原</def>(Resolve)图像。多重采样帧缓冲的还原通常是通过<fun>glBlitFramebuffer</fun>来完成，它能够将一个帧缓冲中的某个区域复制到另一个帧缓冲中，并且将多重采样缓冲还原。
+一个多采样图像包含了比普通图像更多的信息，所以我们需要做的是压缩或还原图像。还原一个多采样帧缓冲，通常用`glBlitFramebuffer`来完成，它从一个帧缓冲中复制一个区域粘贴另一个里面，同时也将任何多采样缓冲还原。
 
-<fun>glBlitFramebuffer</fun>会将一个用4个屏幕空间坐标所定义的<def>源</def>区域复制到一个同样用4个屏幕空间坐标所定义的<def>目标</def>区域中。你可能记得在[帧缓冲](05 Framebuffers.md)教程中，当我们绑定到<var>GL_FRAMEBUFFER</var>时，我们是同时绑定了读取和绘制的帧缓冲目标。我们也可以将帧缓冲分开绑定至<var>GL_READ_FRAMEBUFFER</var>与<var>GL_DRAW_FRAMEBUFFER</var>。<fun>glBlitFramebuffer</fun>函数会根据这两个目标，决定哪个是源帧缓冲，哪个是目标帧缓冲。接下来，我们可以将图像<def>位块传送</def>(Blit)到默认的帧缓冲中，将多重采样的帧缓冲传送到屏幕上。
+`glBlitFramebuffer`把一个4屏幕坐标源区域传递到一个也是4空间坐标的目标区域。你可能还记得帧缓冲教程中，如果我们绑定到`GL_FRAMEBUFFER`，我们实际上就同时绑定到了读和写的帧缓冲目标。我们还可以通过`GL_READ_FRAMEBUFFER`和`GL_DRAW_FRAMEBUFFER`绑定到各自的目标上。`glBlitFramebuffer`函数从这两个目标读取，并决定哪一个是源哪一个是目标帧缓冲。接着我们就可以通过把图像位块传送(Blitting)到默认帧缓冲里，将多采样帧缓冲输出传递到实际的屏幕了：
 
 ```c++
 glBindFramebuffer(GL_READ_FRAMEBUFFER, multisampledFBO);
@@ -143,65 +140,67 @@ glBindFramebuffer(GL_DRAW_FRAMEBUFFER, 0);
 glBlitFramebuffer(0, 0, width, height, 0, 0, width, height, GL_COLOR_BUFFER_BIT, GL_NEAREST);
 ```
 
-如果现在再来渲染这个程序，我们会得到与之前完全一样的结果：一个使用MSAA显示出来的橄榄绿色的立方体，而且锯齿边缘明显减少了：
+如果我们渲染应用，我们将得到和没用帧缓冲一样的结果：一个绿色立方体，它使用MSAA显示出来，但边缘锯齿明显少了：
 
-![](../img/04/11/anti_aliasing_multisampled.png)
+![](http://learnopengl.com/img/advanced/anti_aliasing_multisampled.png)
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/4.advanced_opengl/11.2.anti_aliasing_offscreen/anti_aliasing_offscreen.cpp)找到源代码。
+你可以[在这里找到源代码](http://learnopengl.com/code_viewer.php?code=advanced/anti_aliasing_framebuffers)。
 
-但如果我们想要使用多重采样帧缓冲的纹理输出来做像是后期处理这样的事情呢？我们不能直接在片段着色器中使用多重采样的纹理。但我们能做的是将多重采样缓冲位块传送到一个没有使用多重采样纹理附件的FBO中。然后用这个普通的颜色附件来做后期处理，从而达到我们的目的。然而，这也意味着我们需要生成一个新的FBO，作为中介帧缓冲对象，将多重采样缓冲还原为一个能在着色器中使用的普通2D纹理。这个过程的伪代码是这样的：
+但是如果我们打算使用一个多采样帧缓冲的纹理结果来做这件事，就像后处理一样会怎样？我们不能在片段着色器中直接使用多采样纹理。我们可以做的事情是把多缓冲位块传送(Blit)到另一个带有非多采样纹理附件的FBO中。之后我们使用这个普通的颜色附件纹理进行后处理，通过多采样来对一个图像渲染进行后处理效率很高。这意味着我们必须生成一个新的FBO，它仅作为一个将多采样缓冲还原为一个我们可以在片段着色器中使用的普通2D纹理中介。伪代码是这样的：
 
 ```c++
-unsigned int msFBO = CreateFBOWithMultiSampledAttachments();
-// 使用普通的纹理颜色附件创建一个新的FBO
+GLuint msFBO = CreateFBOWithMultiSampledAttachments();
+// Then create another FBO with a normal texture color attachment
 ...
 glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, screenTexture, 0);
 ...
 while(!glfwWindowShouldClose(window))
 {
     ...
-    
+
     glBindFramebuffer(msFBO);
     ClearFrameBuffer();
     DrawScene();
-    // 将多重采样缓冲还原到中介FBO上
+    // Now resolve multisampled buffer(s) into intermediate FBO
     glBindFramebuffer(GL_READ_FRAMEBUFFER, msFBO);
     glBindFramebuffer(GL_DRAW_FRAMEBUFFER, intermediateFBO);
     glBlitFramebuffer(0, 0, width, height, 0, 0, width, height, GL_COLOR_BUFFER_BIT, GL_NEAREST);
-    // 现在场景是一个2D纹理缓冲，可以将这个图像用来后期处理
+    // Now scene is stored as 2D texture image, so use that image for post-processing
     glBindFramebuffer(GL_FRAMEBUFFER, 0);
     ClearFramebuffer();
     glBindTexture(GL_TEXTURE_2D, screenTexture);
     DrawPostProcessingQuad();  
-  
-    ... 
+
+    ...
 }
 ```
 
-如果现在再实现[帧缓冲](05 Framebuffers.md)教程中的后期处理效果，我们就能够在一个几乎没有锯齿的场景纹理上进行后期处理了。如果让图像灰度化，看起来将会是这样：
+如果我们实现帧缓冲教程中讲的后处理代码，我们就能创造出没有锯齿边的所有效果很酷的后处理特效。使用模糊kernel过滤器，看起来会像这样：
 
-![](../img/04/11/anti_aliasing_post_processing_grayscale.png)
+![](http://learnopengl.com/img/advanced/anti_aliasing_post_processing.png)
+
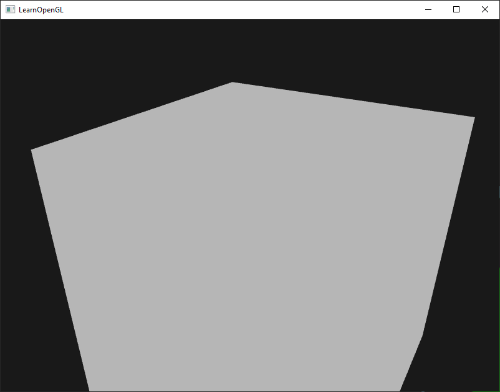
+你可以[在这里找到所有MSAA版本的后处理源码](http://learnopengl.com/code_viewer.php?code=advanced/anti_aliasing_post_processing)。
 
 !!! Important
 
-    因为屏幕纹理又变回了一个只有单一采样点的普通纹理，像是**边缘检测**这样的后期处理滤镜会重新导致锯齿。为了补偿这一问题，你可以之后对纹理进行模糊处理，或者想出你自己的抗锯齿算法。
+    因为屏幕纹理重新变回了只有一个采样点的普通纹理，有些后处理过滤器，比如边检测（edge-detection）将会再次导致锯齿边问题。为了修正此问题，之后你应该对纹理进行模糊处理，或者创建你自己的抗锯齿算法。
 
-你可以看到，如果将多重采样与离屏渲染结合起来，我们需要自己负责一些额外的细节。但所有的这些细节都是值得额外的努力的，因为多重采样能够显著提升场景的视觉质量。当然，要注意，如果使用的采样点非常多，启用多重采样会显著降低程序的性能。在本节写作时，通常采用的是4采样点的MSAA。
+当我们希望将多采样和离屏渲染结合起来时，我们需要自己负责一些细节。所有细节都是值得付出这些额外努力的，因为多采样可以明显提升场景视频输出的质量。要注意，开启多采样会明显降低性能，样本越多越明显。本文写作时，MSAA4样本很常用。
 
 ## 自定义抗锯齿算法
 
-将一个多重采样的纹理图像不进行还原直接传入着色器也是可行的。GLSL提供了这样的选项，让我们能够对纹理图像的每个子样本进行采样，所以我们可以创建我们自己的抗锯齿算法。在大型的图形应用中通常都会这么做。
+可以直接把一个多采样纹理图像传递到着色器中，以取代必须先还原的方式。GLSL给我们一个选项来为每个子样本进行纹理图像采样，所以我们可以创建自己的抗锯齿算法，在比较大的图形应用中，通常这么做。
 
-要想获取每个子样本的颜色值，你需要将纹理uniform采样器设置为<fun>sampler2DMS</fun>，而不是平常使用的<fun>sampler2D</fun>：
+为获取每个子样本的颜色值，你必须将纹理uniform采样器定义为sampler2DMS，而不是使用sampler2D：
 
 ```c++
 uniform sampler2DMS screenTextureMS;
 ```
 
-使用<fun>texelFetch</fun>函数就能够获取每个子样本的颜色值了：
+使用texelFetch函数，就可以获取每个样本的颜色值了：
 
 ```c++
-vec4 colorSample = texelFetch(screenTextureMS, TexCoords, 3);  // 第4个子样本
+vec4 colorSample = texelFetch(screenTextureMS, TexCoords, 3);  // 4th subsample
 ```
 
-我们不会深入探究自定义抗锯齿技术的细节，这里仅仅是给你一点启发。
+我们不会深究自定义抗锯齿技术的创建细节，但是会给你自己去实现它提供一些提示。

docs/05 Advanced Lighting/01 Advanced Lighting.md

@@ -3,70 +3,73 @@
 原文     | [Advanced Lighting](http://learnopengl.com/#!Advanced-Lighting/Advanced-Lighting)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | 暂未校对
+翻译     | [Django](http://bullteacher.com/)
+校对     | gjy_1992
 
-
-在[光照](../02 Lighting/02 Basic Lighting.md)小节中，我们简单地介绍了风氏光照模型，它让我们的场景有了一定的真实感。虽然风氏模型看起来已经很不错了，但是使用它的时候仍然存在一些细节问题，我们将在这一节里讨论它们。
+在光照教程中，我们简单的介绍了Phong光照模型，它给我们的场景带来的基本的现实感。Phong模型看起来还不错，但本章我们把重点放在一些细微差别上。
 
 ## Blinn-Phong
 
-风氏光照不仅对真实光照有很好的近似，而且性能也很高。但是它的镜面反射会在一些情况下出现问题，特别是物体反光度很低时，会导致大片（粗糙的）高光区域。下面这张图展示了当反光度为1.0时地板会出现的效果：
+Phong光照很棒，而且性能较高，但是它的镜面反射在某些条件下会失效，特别是当发光值属性低的时候，对应一个非常大的粗糙的镜面区域。下面的图片展示了，当我们使用镜面的发光值为1.0时，一个带纹理地板的效果：
 
-![](../img/05/01/advanced_lighting_phong_limit.png)
+![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_phong_limit.png)
 
-可以看到，在镜面高光区域的边缘出现了一道很明显的断层。出现这个问题的原因是观察向量和反射向量间的夹角不能大于90度。如果点积的结果为负数，镜面光分量会变为0.0。你可能会觉得，当光线与视线夹角大于90度时你应该不会接收到任何光才对，所以这不是什么问题。
+你可以看到，镜面区域边缘迅速减弱并截止。出现这个问题的原因是在视线向量和反射向量的角度不允许大于90度。如果大于90度的话，点乘的结果就会是负数，镜面的贡献成分就会变成0。你可能会想，这不是一个问题，因为大于90度时我们不应看到任何光，对吧？
 
-然而，这种想法仅仅只适用于漫反射分量。当考虑漫反射光的时候，如果法线和光源夹角大于90度，光源会处于被照表面的下方，这个时候光照的漫反射分量的确是为0.0。但是，在考虑镜面高光时，我们测量的角度并不是光源与法线的夹角，而是视线与反射光线向量的夹角。看一下下面这两张图：
+错了，这只适用于漫散射部分，当法线和光源之间的角度大于90度时意味着光源在被照亮表面的下方，这样光的散射成分就会是0.0。然而，对于镜面光照，我们不会测量光源和法线之间的角度，而是测量视线和反射方向向量之间的。看看下面的两幅图：
 
-![](../img/05/01/advanced_lighting_over_90.png)
+![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_over_90.png)
 
-现在问题就应该很明显了。左图中是我们熟悉的风氏光照中的反射向量，其中$\theta$角小于90度。而右图中，视线与反射方向之间的夹角明显大于90度，这种情况下镜面光分量会变为0.0。这在大多数情况下都不是什么问题，因为观察方向离反射方向都非常远。然而，当物体的反光度非常小时，它产生的镜面高光半径足以让这些相反方向的光线对亮度产生足够大的影响。在这种情况下就不能忽略它们对镜面光分量的贡献了。
+现在看来问题就很明显了。左侧图片显示Phong反射的θ小于90度的情况。我们可以看到右侧图片视线和反射之间的角θ大于90度，这样镜面反射成分将会被消除。通常这也不是问题，因为视线方向距离反射方向很远，但如果我们使用一个数值较低的发光值参数的话，镜面半径就会足够大，以至于能够贡献一些镜面反射的成份了。在例子中，我们在角度大于90度时消除了这个贡献（如第一个图片所示）。
 
-1977年，James F. Blinn在风氏着色模型上加以拓展，引入了<def>Blinn-Phong</def>着色模型。Blinn-Phong模型与风氏模型非常相似，但是它对镜面光模型的处理上有一些不同，让我们能够解决之前提到的问题。Blinn-Phong模型不再依赖于反射向量，而是采用了所谓的<def>半程向量</def>(Halfway Vector)，即光线与视线夹角一半方向上的一个单位向量。当半程向量与法线向量越接近时，镜面光分量就越大。
+1977年James F. Blinn引入了Blinn-Phong着色，它扩展了我们目前所使用的Phong着色。Blinn-Phong模型很大程度上和Phong是相似的，不过它稍微改进了Phong模型，使之能够克服我们所讨论到的问题。它放弃使用反射向量，而是基于我们现在所说的一个叫做半程向量（halfway vector）的向量，这是个单位向量，它在视线方向和光线方向的中间。半程向量和表面法线向量越接近，镜面反射成份就越大。
 
-![](../img/05/01/advanced_lighting_halfway_vector.png)
+![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_halfway_vector.png)
 
-当视线正好与（现在不需要的）反射向量对齐时，半程向量就会与法线完美契合。所以当观察者视线越接近于原本反射光线的方向时，镜面高光就会越强。
+当视线方向恰好与反射向量对称时，半程向量就与法线向量重合。这样观察者距离原来的反射方向越近，镜面反射的高光就会越强。
 
-现在，不论观察者向哪个方向看，半程向量与表面法线之间的夹角都不会超过90度（除非光源在表面以下）。它产生的效果会与风氏光照有些许不同，但是大部分情况下看起来会更自然一点，特别是低高光的区域。Blinn-Phong着色模型正是早期固定渲染管线时代时OpenGL所采用的光照模型。
+这里，你可以看到无论观察者往哪里看，半程向量和表面法线之间的夹角永远都不会超过90度（当然除了光源远远低于表面的情况）。这样会产生和Phong反射稍稍不同的结果，但这时看起来会更加可信，特别是发光值参数比较低的时候。Blinn-Phong着色模型也正是早期OpenGL固定函数输送管道（fixed function pipeline）所使用的着色模型。
 
-获取半程向量的方法很简单，只需要将光线的方向向量和观察向量加到一起，并将结果正规化(Normalize)就可以了：
+得到半程向量很容易，我们将光的方向向量和视线向量相加，然后将结果归一化（normalize）；
 
 $$
-\bar{H} = \frac{\bar{L} + \bar{V}}{||\bar{L} + \bar{V}||}
+\(\bar{H} = \frac{\bar{L} + \bar{V}}{||\bar{L} + \bar{V}||}\)
 $$
 
 翻译成GLSL代码如下：
 
 ```c++
-vec3 lightDir   = normalize(lightPos - FragPos);
-vec3 viewDir    = normalize(viewPos - FragPos);
+vec3 lightDir = normalize(lightPos - FragPos);
+vec3 viewDir = normalize(viewPos - FragPos);
 vec3 halfwayDir = normalize(lightDir + viewDir);
 ```
 
-接下来，镜面光分量的实际计算只不过是对表面法线和半程向量进行一次约束点乘(Clamped Dot Product)，让点乘结果不为负，从而获取它们之间夹角的余弦值，之后我们对这个值取反光度次方：
+实际的镜面反射的计算，就成为计算表面法线和半程向量的点乘，并对其结果进行约束（大于或等于0），然后获取它们之间角度的余弦，再添加上发光值参数：
 
 ```c++
 float spec = pow(max(dot(normal, halfwayDir), 0.0), shininess);
 vec3 specular = lightColor * spec;
 ```
 
-除此之外Blinn-Phong模型就没什么好说的了，Blinn-Phong与风氏模型唯一的区别就是，Blinn-Phong测量的是法线与半程向量之间的夹角，而风氏模型测量的是观察方向与反射向量间的夹角。
+除了我们刚刚讨论的，Blinn-Phong没有更多的内容了。Blinn-Phong和Phong的镜面反射唯一不同之处在于，现在我们要测量法线和半程向量之间的角度，而半程向量是视线方向和反射向量之间的夹角。
 
-在引入半程向量之后，我们现在应该就不会再看到风氏光照中高光断层的情况了。下面两个图片展示的是两种方法在镜面光分量为0.5时的对比：
+!!! Important
+    
+    Blinn-Phong着色的一个附加好处是，它比Phong着色性能更高，因为我们不必计算更加复杂的反射向量了。
 
-![](../img/05/01/advanced_lighting_comparrison.png)
+引入了半程向量来计算镜面反射后，我们再也不会遇到Phong着色的骤然截止问题了。下图展示了两种不同方式下发光值指数为0.5时镜面区域的不同效果：
 
-除此之外，风氏模型与Blinn-Phong模型也有一些细微的差别：半程向量与表面法线的夹角通常会小于观察与反射向量的夹角。所以，如果你想获得和风氏着色类似的效果，就必须在使用Blinn-Phong模型时将镜面反光度设置更高一点。通常我们会选择风氏着色时反光度分量的2到4倍。
+![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_comparrison.png)
 
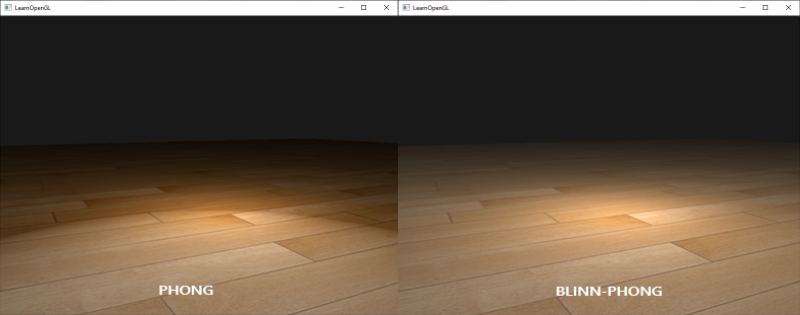
-下面是风氏着色反光度为8.0，Blinn-Phong着色反光度为32.0时的一个对比：
+Phong和Blinn-Phong着色之间另一个细微差别是，半程向量和表面法线之间的角度经常会比视线和反射向量之间的夹角更小。结果就是，为了获得和Phong着色相似的效果，必须把发光值参数设置的大一点。通常的经验是将其设置为Phong着色的发光值参数的2至4倍。
 
-![](../img/05/01/advanced_lighting_comparrison2.png)
+下图是Phong指数为8.0和Blinn-Phong指数为32的时候，两种specular反射模型的对比：
 
-你可以看到，Blinn-Phong的镜面光分量会比风氏模型更锐利一些。为了得到与风氏模型类似的结果，你可能会需要不断进行一些微调，但Blinn-Phong模型通常会产出更真实的结果。
+![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_comparrison2.png)
 
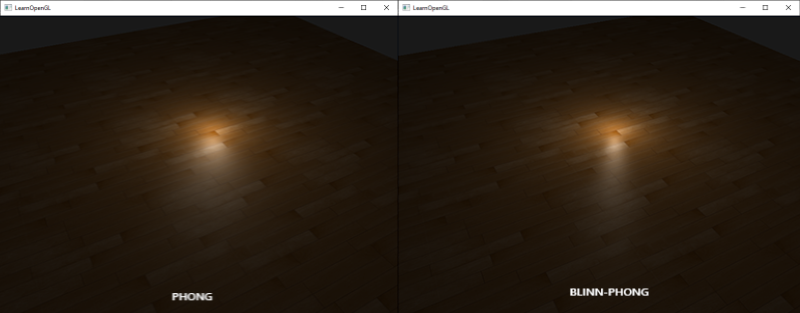
-这里，我们使用了一个简单的片段着色器，让我们能够在风氏反射与Blinn-Phong反射间进行切换：
+你可以看到Blinn-Phong的镜面反射成分要比Phong锐利一些。这通常需要使用一点小技巧才能获得之前你所看到的Phong着色的效果，但Blinn-Phong着色的效果比默认的Phong着色通常更加真实一些。
+
+这里我们用到了一个简单像素着色器，它可以在普通Phong反射和Blinn-Phong反射之间进行切换：
 
 ```c++
 void main()
@@ -85,4 +88,5 @@ void main()
     }
 ``` 
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/5.advanced_lighting/1.advanced_lighting/advanced_lighting.cpp)找到这个Demo的源代码。你可以按下`B`键来切换风氏光照与Blinn-Phong光照。
+你可以在这里找到这个简单的[demo的源码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/blinn_phong)以及[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/blinn_phong&type=vertex)和[片段](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/blinn_phong&type=fragment)着色器。按下b键，这个demo就会从Phong切换到Blinn-Phong光照，反之亦然。
+

docs/05 Advanced Lighting/02 Gamma Correction.md

@@ -6,10 +6,6 @@
 翻译     | [Django](http://bullteacher.com/)
 校对     | 暂无
 
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
 当我们计算出场景中所有像素的最终颜色以后，我们就必须把它们显示在监视器上。过去，大多数监视器是阴极射线管显示器（CRT）。这些监视器有一个物理特性就是两倍的输入电压产生的不是两倍的亮度。输入电压产生约为输入电压的2.2次幂的亮度，这叫做监视器Gamma。
 
 !!! note "译注"
@@ -18,23 +14,23 @@
 
 人类所感知的亮度恰好和CRT所显示出来相似的指数关系非常匹配。为了更好的理解所有含义，请看下面的图片：
 
-![](../img/05/02/gamma_correction_brightness.png)
+![](http://learnopengl.com/img/advanced-lighting/gamma_correction_brightness.png)
 
-第一行是人眼所感知到的正常的灰阶，亮度要增加一倍（比如从0.1到0.2）你才会感觉比原来变亮了一倍（译注：我们在看颜色值从0到1（从黑到白）的过程中，亮度要增加一倍，我们才会感受到明显的颜色变化（变亮一倍）。打个比方：颜色值从0.1到0.2，我们会感受到一倍的颜色变化，而从0.4到0.8我们才能感受到相同程度（变亮一倍）的颜色变化。如果还是不理解，可以参考知乎的[答案](https://www.zhihu.com/question/27467127/answer/37602200)）。然而，当我们谈论光的物理亮度，比如光源发射光子的数量的时候，底部（第二行）的灰阶显示出的才是物理世界真实的亮度。如底部的灰阶显示，亮度加倍时返回的也是真实的物理亮度（译注：这里亮度是指光子数量和正相关的亮度，即物理亮度，前面讨论的是人的感知亮度；物理亮度和感知亮度的区别在于，物理亮度基于光子数量，感知亮度基于人的感觉，比如第二个灰阶里亮度0.1的光子数量是0.2的二分之一），但是由于这与我们的眼睛感知亮度不完全一致（对比较暗的颜色变化更敏感），所以它看起来有差异。
+第一行是人眼所感知到的正常的灰阶，亮度要增加一倍（比如从0.1到0.2）你才会感觉比原来变亮了一倍（译注：这里的意思是说比如一个东西的亮度0.3，让人感觉它比原来变亮一倍，那么现在这个亮度应该成为0.6，而不是0.4，也就是说人眼感知到的亮度的变化并非线性均匀分布的。问题的关键在于这样的一倍相当于一个亮度级，例如假设0.1、0.2、0.4、0.8是我们定义的四个亮度级别，在0.1和0.2之间人眼只能识别出0.15这个中间级，而虽然0.4到0.8之间的差距更大，这个区间人眼也只能识别出一个颜色）。然而，当我们谈论光的物理亮度，比如光源发射光子的数量的时候，底部（第二行）的灰阶显示出的才是物理世界真实的亮度。如底部的灰阶显示，亮度加倍时返回的也是真实的物理亮度（译注：这里亮度是指光子数量和正相关的亮度，即物理亮度，前面讨论的是人的感知亮度；物理亮度和感知亮度的区别在于，物理亮度基于光子数量，感知亮度基于人的感觉，比如第二个灰阶里亮度0.1的光子数量是0.2的二分之一），但是由于这与我们的眼睛感知亮度不完全一致（对比较暗的颜色变化更敏感），所以它看起来有差异。
 
 因为人眼看到颜色的亮度更倾向于顶部的灰阶，监视器使用的也是一种指数关系（电压的2.2次幂），所以物理亮度通过监视器能够被映射到顶部的非线性亮度；因此看起来效果不错（译注：CRT亮度是是电压的2.2次幂而人眼相当于2次幂，因此CRT这个缺陷正好能满足人的需要）。
 
 监视器的这个非线性映射的确可以让亮度在我们眼中看起来更好，但当渲染图像时，会产生一个问题：我们在应用中配置的亮度和颜色是基于监视器所看到的，这样所有的配置实际上是非线性的亮度/颜色配置。请看下图：
 
-![](../img/05/02/gamma_correction_gamma_curves.png)
+![](http://learnopengl.com/img/advanced-lighting/gamma_correction_gamma_curves.png)
 
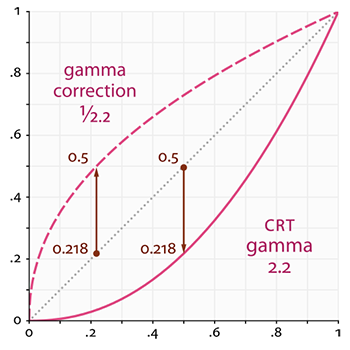
 点线代表线性颜色/亮度值（译注：这表示的是理想状态，Gamma为1），实线代表监视器显示的颜色。如果我们把一个点线线性的颜色翻一倍，结果就是这个值的两倍。比如，光的颜色向量\(\bar{L} = (0.5, 0.0, 0.0)\)代表的是暗红色。如果我们在线性空间中把它翻倍，就会变成\((1.0, 0.0, 0.0)\)，就像你在图中看到的那样。然而，由于我们定义的颜色仍然需要输出的监视器上，监视器上显示的实际颜色就会是\((0.218, 0.0, 0.0)\)。在这儿问题就出现了：当我们将理想中直线上的那个暗红色翻一倍时，在监视器上实际上亮度翻了4.5倍以上！
 
-直到现在，我们还一直假设我们所有的工作都是在线性空间中进行的（译注：Gamma为1），但最终还是要把所有的颜色输出到监视器上，所以我们配置的所有颜色和光照变量从物理角度来看都是不正确的，在我们的监视器上很少能够正确地显示。出于这个原因，我们（以及艺术家）通常将光照值设置得比本来更亮一些（由于监视器会将其亮度显示的更暗一些），如果不是这样，在线性空间里计算出来的光照就会不正确。同时，还要记住，监视器所显示出来的图像和线性图像的最小亮度是相同的，它们最大的亮度也是相同的；只是中间亮度部分会被压暗。
+直到现在，我们还一直假设我们所有的工作都是在线性空间中进行的（译注：Gamma为1），但最终还是要把所哟的颜色输出到监视器上，所以我们配置的所有颜色和光照变量从物理角度来看都是不正确的，在我们的监视器上很少能够正确地显示。出于这个原因，我们（以及艺术家）通常将光照值设置得比本来更亮一些（由于监视器会将其亮度显示的更暗一些），如果不是这样，在线性空间里计算出来的光照就会不正确。同时，还要记住，监视器所显示出来的图像和线性图像的最小亮度是相同的，它们最大的亮度也是相同的；只是中间亮度部分会被压暗。
 
 因为所有中间亮度都是线性空间计算出来的（译注：计算的时候假设Gamma为1）监视器显以后，实际上都会不正确。当使用更高级的光照算法时，这个问题会变得越来越明显，你可以看看下图：
 
-![](../img/05/02/gamma_correction_example.png)
+![](http://learnopengl.com/img/advanced-lighting/gamma_correction_example.png)
 
 ## Gamma校正
 
@@ -58,7 +54,7 @@ Gamma校正(Gamma Correction)的思路是在最终的颜色输出上应用监视
 glEnable(GL_FRAMEBUFFER_SRGB);
 ```
 
-自此，你渲染的图像就被进行gamma校正处理，你不需要做任何事情硬件就帮你处理了。有时候，你应该记得这个建议：gamma校正将把线性颜色空间转变为非线性空间，所以在最后一步进行gamma校正是极其重要的。如果你在最后输出之前就进行gamma校正，所有的后续操作都是在操作不正确的颜色值。例如，如果你使用多个帧缓冲，你可能打算让两个帧缓冲之间传递的中间结果仍然保持线性空间颜色，只是给发送给监视器的最后的那个帧缓冲应用gamma校正。
+自此，你渲染的图像就被进行gamma校正处理，你不需要做任何事情硬件就帮你处理了。有时候，你应该记得这个建议：gamma校正将把线性颜色空间转变为非线性空间，所以在最后一步进行gamma校正是极其重要的。如果你在最后输出之前就进行gamma校正，所有的后续操作都是在操作不正确的颜色值。例如，如果你使用多个怎还冲，你可能打算让两个帧缓冲之间传递的中间结果仍然保持线性空间颜色，只是给发送给监视器的最后的那个帧缓冲应用gamma校正。
 
 第二个方法稍微复杂点，但同时也是我们对gamma操作有完全的控制权。我们在每个相关像素着色器运行的最后应用gamma校正，所以在发送到帧缓冲前，颜色就被校正了。
 
@@ -85,7 +81,7 @@ void main()
 
 结果就是纹理编辑者，所创建的所有纹理都是在sRGB空间中的纹理，所以如果我们在渲染应用中使用这些纹理，我们必须考虑到这点。在我们应用gamma校正之前，这不是个问题，因为纹理在sRGB空间创建和展示，同样我们还是在sRGB空间中使用，从而不必gamma校正纹理显示也没问题。然而，现在我们是把所有东西都放在线性空间中展示的，纹理颜色就会变坏，如下图展示的那样：
 
-![](../img/05/02/gamma_correction_srgbtextures.png)
+![](http://learnopengl.com/img/advanced-lighting/gamma_correction_srgbtextures.png)
 
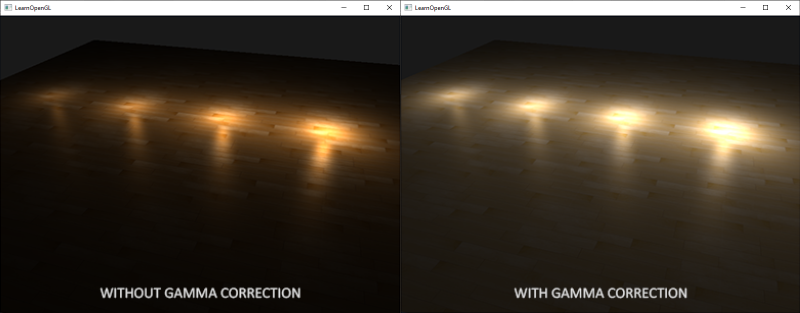
 纹理图像实在太亮了，发生这种情况是因为，它们实际上进行了两次gamma校正！想一想，当我们基于监视器上看到的情况创建一个图像，我们就已经对颜色值进行了gamma校正，所以再次显示在监视器上就没错。由于我们在渲染中又进行了一次gamma校正，图片就实在太亮了。
 
@@ -129,7 +125,7 @@ float attenuation = 1.0 / distance;
 
 双曲线比使用二次函数变体在不用gamma校正的时候看起来更真实，不过但我们开启gamma校正以后线性衰减看起来太弱了，符合物理的二次函数突然出现了更好的效果。下图显示了其中的不同：
 
-![](../img/05/02/gamma_correction_attenuation.png)
+![](http://learnopengl.com/img/advanced-lighting/gamma_correction_attenuation.png)
 
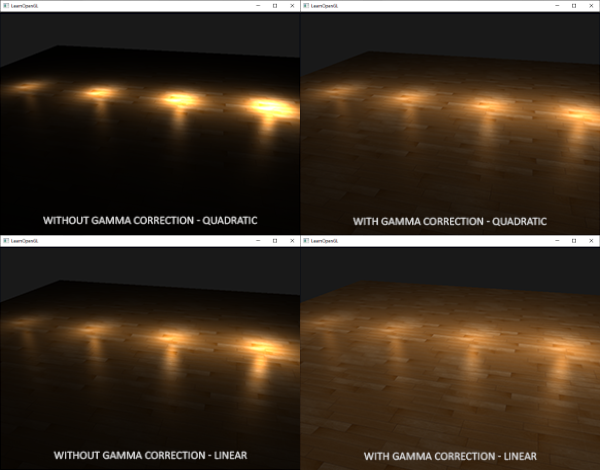
 这种差异产生的原因是，光的衰减方程改变了亮度值，而且屏幕上显示出来的也不是线性空间，在监视器上效果最好的衰减方程，并不是符合物理的。想想平方衰减方程，如果我们使用这个方程，而且不进行gamma校正，显示在监视器上的衰减方程实际上将变成\((1.0 / distance^2)^{2.2}\)。若不进行gamma校正，将产生更强烈的衰减。这也解释了为什么双曲线不用gamma校正时看起来更真实，因为它实际变成了\((1.0 / distance)^{2.2} = 1.0 / distance^{2.2}\)。这和物理公式是很相似的。
 

docs/05 Advanced Lighting/03 Shadows/01 Shadow Mapping.md

@@ -6,13 +6,11 @@
 翻译     | [Django](http://bullteacher.com/)
 校对     | gjy_1992
 
-!!! note
 
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
 
 阴影是光线被阻挡的结果；当一个光源的光线由于其他物体的阻挡不能够达到一个物体的表面的时候，那么这个物体就在阴影中了。阴影能够使场景看起来真实得多，并且可以让观察者获得物体之间的空间位置关系。场景和物体的深度感因此能够得到极大提升，下图展示了有阴影和没有阴影的情况下的不同：
 
-![](../../img/05/03/01/shadow_mapping_with_without.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_with_without.png)
 
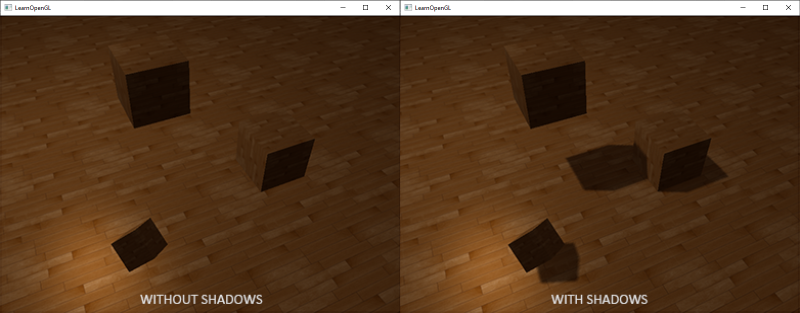
 你可以看到，有阴影的时候你能更容易地区分出物体之间的位置关系，例如，当使用阴影的时候浮在地板上的立方体的事实更加清晰。
 
@@ -24,25 +22,25 @@
 
 阴影映射(Shadow Mapping)背后的思路非常简单：我们以光的位置为视角进行渲染，我们能看到的东西都将被点亮，看不见的一定是在阴影之中了。假设有一个地板，在光源和它之间有一个大盒子。由于光源处向光线方向看去，可以看到这个盒子，但看不到地板的一部分，这部分就应该在阴影中了。
 
-![](../../img/05/03/01/shadow_mapping_theory.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_theory.png)
 
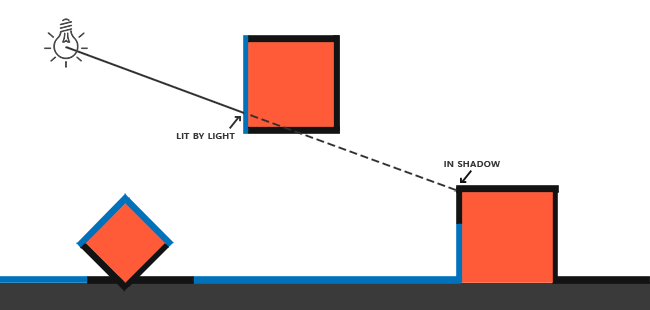
-这里的所有蓝线代表光源可以看到的fragment。黑线代表被遮挡的fragment：它们应该渲染为带阴影的。如果我们绘制一条从光源出发，到达最右边盒子上的一个片段上的线段或射线，那么射线将先击中悬浮的盒子，随后才会到达最右侧的盒子。结果就是悬浮的盒子被照亮，而最右侧的盒子将处于阴影之中。
+这里的所有蓝线代表光源可以看到的fragment。黑线代表被遮挡的fragment：它们应该渲染为带阴影的。如果我们绘制一条从光源出发，到达最右边盒子上的一个片元上的线段或射线，那么射线将先击中悬浮的盒子，随后才会到达最右侧的盒子。结果就是悬浮的盒子被照亮，而最右侧的盒子将处于阴影之中。
 
 我们希望得到射线第一次击中的那个物体，然后用这个最近点和射线上其他点进行对比。然后我们将测试一下看看射线上的其他点是否比最近点更远，如果是的话，这个点就在阴影中。对从光源发出的射线上的成千上万个点进行遍历是个极端消耗性能的举措，实时渲染上基本不可取。我们可以采取相似举措，不用投射出光的射线。我们所使用的是非常熟悉的东西：深度缓冲。
 
-你可能记得在[深度测试](http://learnopengl.com/#!Advanced-OpenGL/Depth-testing)教程中，在深度缓冲里的一个值是摄像机视角下，对应于一个片段的一个0到1之间的深度值。如果我们从光源的透视图来渲染场景，并把深度值的结果储存到纹理中会怎样？通过这种方式，我们就能对光源的透视图所见的最近的深度值进行采样。最终，深度值就会显示从光源的透视图下见到的第一个片段了。我们管储存在纹理中的所有这些深度值，叫做深度贴图（depth map）或阴影贴图。
+你可能记得在[深度测试](http://learnopengl.com/#!Advanced-OpenGL/Depth-testing)教程中，在深度缓冲里的一个值是摄像机视角下，对应于一个片元的一个0到1之间的深度值。如果我们从光源的透视图来渲染场景，并把深度值的结果储存到纹理中会怎样？通过这种方式，我们就能对光源的透视图所见的最近的深度值进行采样。最终，深度值就会显示从光源的透视图下见到的第一个片元了。我们管储存在纹理中的所有这些深度值，叫做深度贴图（depth map）或阴影贴图。
 
-![](../../img/05/03/01/shadow_mapping_theory_spaces.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_theory_spaces.png)
 
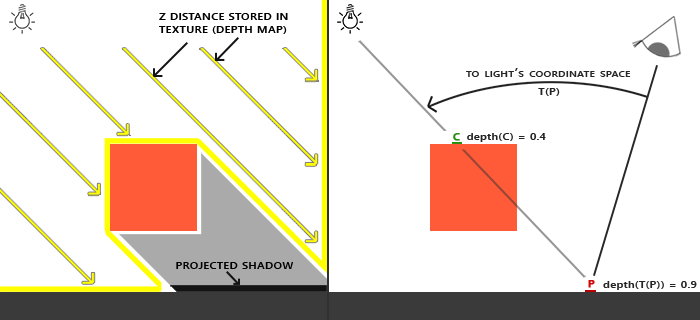
-左侧的图片展示了一个定向光源（所有光线都是平行的）在立方体下的表面投射的阴影。通过储存到深度贴图中的深度值，我们就能找到最近点，用以决定片段是否在阴影中。我们使用一个来自光源的视图和投影矩阵来渲染场景就能创建一个深度贴图。这个投影和视图矩阵结合在一起成为一个\(T\)变换，它可以将任何三维位置转变到光源的可见坐标空间。
+左侧的图片展示了一个定向光源（所有光线都是平行的）在立方体下的表面投射的阴影。通过储存到深度贴图中的深度值，我们就能找到最近点，用以决定片元是否在阴影中。我们使用一个来自光源的视图和投影矩阵来渲染场景就能创建一个深度贴图。这个投影和视图矩阵结合在一起成为一个\(T\)变换，它可以将任何三维位置转变到光源的可见坐标空间。
 
 !!! Important
 
     定向光并没有位置，因为它被规定为无穷远。然而，为了实现阴影贴图，我们得从一个光的透视图渲染场景，这样就得在光的方向的某一点上渲染场景。
 
-在右边的图中我们显示出同样的平行光和观察者。我们渲染一个点\(\bar{\color{red}{P}}\)处的片段，需要决定它是否在阴影中。我们先得使用\(T\)把\(\bar{\color{red}{P}}\)变换到光源的坐标空间里。既然点\(\bar{\color{red}{P}}\)是从光的透视图中看到的，它的z坐标就对应于它的深度，例子中这个值是0.9。使用点\(\bar{\color{red}{P}}\)在光源的坐标空间的坐标，我们可以索引深度贴图，来获得从光的视角中最近的可见深度，结果是点\(\bar{\color{green}{C}}\)，最近的深度是0.4。因为索引深度贴图的结果是一个小于点\(\bar{\color{red}{P}}\)的深度，我们可以断定\(\bar{\color{red}{P}}\)被挡住了，它在阴影中了。
+在右边的图中我们显示出同样的平行光和观察者。我们渲染一个点\(\bar{\color{red}{P}}\)处的片元，需要决定它是否在阴影中。我们先得使用\(T\)把\(\bar{\color{red}{P}}\)变换到光源的坐标空间里。既然点\(\bar{\color{red}{P}}\)是从光的透视图中看到的，它的z坐标就对应于它的深度，例子中这个值是0.9。使用点\(\bar{\color{red}{P}}\)在光源的坐标空间的坐标，我们可以索引深度贴图，来获得从光的视角中最近的可见深度，结果是点\(\bar{\color{green}{C}}\)，最近的深度是0.4。因为索引深度贴图的结果是一个小于点\(\bar{\color{red}{P}}\)的深度，我们可以断定\(\bar{\color{red}{P}}\)被挡住了，它在阴影中了。
 
-阴影映射由两个步骤组成：首先，我们渲染深度贴图，然后我们像往常一样渲染场景，使用生成的深度贴图来计算片段是否在阴影之中。听起来有点复杂，但随着我们一步一步地讲解这个技术，就能理解了。
+深度映射由两个步骤组成：首先，我们渲染深度贴图，然后我们像往常一样渲染场景，使用生成的深度贴图来计算片元是否在阴影之中。听起来有点复杂，但随着我们一步一步地讲解这个技术，就能理解了。
 
 ## 深度贴图
 
@@ -71,7 +69,7 @@ glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
 ```
 
-生成深度贴图不太复杂。因为我们只关心深度值，我们要把纹理格式指定为GL_DEPTH_COMPONENT。我们还要把纹理的高宽设置为1024：这是深度贴图的分辨率。
+生成深度贴图不太复杂。因为我们只关心深度值，我们要把纹理格式指定为GL_DEPTH_COMPONENT。我们还要把纹理的高宽设置为1024：这是深度贴图的解析度。
 
 把我们把生成的深度纹理作为帧缓冲的深度缓冲：
 
@@ -83,7 +81,7 @@ glReadBuffer(GL_NONE);
 glBindFramebuffer(GL_FRAMEBUFFER, 0);
 ```
 
-我们需要的只是在从光的透视图下渲染场景的时候深度信息，所以颜色缓冲没有用。然而，不包含颜色缓冲的帧缓冲对象是不完整的，所以我们需要显式告诉OpenGL我们不适用任何颜色数据进行渲染。我们通过将调用glDrawBuffer和glReadBuffer把读和绘制缓冲设置为GL_NONE来做这件事。
+我们需要的只是在从光的透视图下渲染场景的时候深度信息，所以颜色缓冲没有用。然而帧缓冲对象不是完全不包含颜色缓冲的，所以我们需要显式告诉OpenGL我们不适用任何颜色数据进行渲染。我们通过将调用glDrawBuffer和glReadBuffer把读和绘制缓冲设置为GL_NONE来做这件事。
 
 合理配置将深度值渲染到纹理的帧缓冲后，我们就可以开始第一步了：生成深度贴图。两个步骤的完整的渲染阶段，看起来有点像这样：
 
@@ -91,9 +89,9 @@ glBindFramebuffer(GL_FRAMEBUFFER, 0);
 // 1. 首选渲染深度贴图
 glViewport(0, 0, SHADOW_WIDTH, SHADOW_HEIGHT);
 glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
-glClear(GL_DEPTH_BUFFER_BIT);
-ConfigureShaderAndMatrices();
-RenderScene();
+    glClear(GL_DEPTH_BUFFER_BIT);
+    ConfigureShaderAndMatrices();
+    RenderScene();
 glBindFramebuffer(GL_FRAMEBUFFER, 0);
 // 2. 像往常一样渲染场景，但这次使用深度贴图
 glViewport(0, 0, SCR_WIDTH, SCR_HEIGHT);
@@ -103,7 +101,7 @@ glBindTexture(GL_TEXTURE_2D, depthMap);
 RenderScene();
 ```
 
-这段代码隐去了一些细节，但它表达了阴影映射的基本思路。这里一定要记得调用glViewport。因为阴影贴图经常和我们原来渲染的场景（通常是窗口分辨率）有着不同的分辨率，我们需要改变视口（viewport）的参数以适应阴影贴图的尺寸。如果我们忘了更新视口参数，最后的深度贴图要么太小要么就不完整。
+这段代码隐去了一些细节，但它表达了阴影映射的基本思路。这里一定要记得调用glViewport。因为阴影贴图经常和我们原来渲染的场景（通常是窗口解析度）有着不同的解析度，我们需要改变视口（viewport）的参数以适应阴影贴图的尺寸。如果我们忘了更新视口参数，最后的深度贴图要么太小要么就不完整。
 
 ### 光源空间的变换
 
@@ -116,12 +114,12 @@ GLfloat near_plane = 1.0f, far_plane = 7.5f;
 glm::mat4 lightProjection = glm::ortho(-10.0f, 10.0f, -10.0f, 10.0f, near_plane, far_plane);
 ```
 
-这里有个本节教程的demo场景中使用的正交投影矩阵的例子。因为投影矩阵间接决定可视区域的范围，以及哪些东西不会被裁切，你需要保证投影视锥（frustum）的大小，以包含打算在深度贴图中包含的物体。当物体和片段不在深度贴图中时，它们就不会产生阴影。
+这里有个本节教程的demo场景中使用的正交投影矩阵的例子。因为投影矩阵间接决定可视区域的范围，以及哪些东西不会被裁切，你需要保证投影视锥（frustum）的大小，以包含打算在深度贴图中包含的物体。当物体和片元不在深度贴图中时，它们就不会产生阴影。
 
 为了创建一个视图矩阵来变换每个物体，把它们变换到从光源视角可见的空间中，我们将使用glm::lookAt函数；这次从光源的位置看向场景中央。
 
 ```c++
-glm::mat4 lightView = glm::lookAt(glm::vec3(-2.0f, 4.0f, -1.0f), glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(0.0f, 1.0f, 0.0f));
+glm::mat4 lightView = glm::lookAt(glm::vec(-2.0f, 4.0f, -1.0f), glm::vec3(0.0f), glm::vec3(1.0));
 ```
 
 二者相结合为我们提供了一个光空间的变换矩阵，它将每个世界空间坐标变换到光源处所见到的那个空间；这正是我们渲染深度贴图所需要的。
@@ -130,7 +128,7 @@ glm::mat4 lightView = glm::lookAt(glm::vec3(-2.0f, 4.0f, -1.0f), glm::vec3(0.0f,
 glm::mat4 lightSpaceMatrix = lightProjection * lightView;
 ```
 
-这个lightSpaceMatrix正是前面我们称为\(T\)的那个变换矩阵。有了lightSpaceMatrix只要给shader提供光空间的投影和视图矩阵，我们就能像往常那样渲染场景了。然而，我们只关心深度值，并非所有片段计算都在我们的着色器中进行。为了提升性能，我们将使用一个与之不同但更为简单的着色器来渲染出深度贴图。
+这个lightSpaceMatrix正是前面我们称为\(T\)的那个变换矩阵。有了lightSpaceMatrix只要给shader提供光空间的投影和视图矩阵，我们就能像往常那样渲染场景了。然而，我们只关心深度值，并非所有片元计算都在我们的着色器中进行。为了提升性能，我们将使用一个与之不同但更为简单的着色器来渲染出深度贴图。
 
 ### 渲染至深度贴图
 
@@ -151,7 +149,7 @@ void main()
 
 这个顶点着色器将一个单独模型的一个顶点，使用lightSpaceMatrix变换到光空间中。
 
-由于我们没有颜色缓冲，最后的片段不需要任何处理，所以我们可以简单地使用一个空片段着色器：
+由于我们没有颜色缓冲，最后的片元不需要任何处理，所以我们可以简单地使用一个空像素着色器：
 
 ```c++
 #version 330 core
@@ -162,7 +160,7 @@ void main()
 }
 ```
 
-这个空片段着色器什么也不干，运行完后，深度缓冲会被更新。我们可以取消那行的注释，来显式设置深度，但是这个（指注释掉那行之后）是更有效率的，因为底层无论如何都会默认去设置深度缓冲。
+这个空像素着色器什么也不干，运行完后，深度缓冲会被更新。我们可以取消那行的注释，来显式设置深度，但是这个（指注释掉那行之后）是更有效率的，因为底层无论如何都会默认去设置深度缓冲。
 
 渲染深度缓冲现在成了：
 
@@ -172,18 +170,18 @@ glUniformMatrix4fv(lightSpaceMatrixLocation, 1, GL_FALSE, glm::value_ptr(lightSp
  
 glViewport(0, 0, SHADOW_WIDTH, SHADOW_HEIGHT);
 glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
-glClear(GL_DEPTH_BUFFER_BIT);
-RenderScene(simpleDepthShader);
+    glClear(GL_DEPTH_BUFFER_BIT);
+    RenderScene(simpleDepthShader);
 glBindFramebuffer(GL_FRAMEBUFFER, 0);
 ```
 
 这里的RenderScene函数的参数是一个着色器程序（shader program），它调用所有相关的绘制函数，并在需要的地方设置相应的模型矩阵。
 
-最后，在光的透视图视角下，很完美地用每个可见片段的最近深度填充了深度缓冲。通过将这个纹理投射到一个2D四边形上（和我们在帧缓冲一节做的后处理过程类似），就能在屏幕上显示出来，我们会获得这样的东西：
+最后，在光的透视图视角下，很完美地用每个可见片元的最近深度填充了深度缓冲。通过将这个纹理投射到一个2D四边形上（和我们在帧缓冲一节做的后处理过程类似），就能在屏幕上显示出来，我们会获得这样的东西：
 
-![](../../img/05/03/01/shadow_mapping_depth_map.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_depth_map.png)
 
-将深度贴图渲染到四边形上的片段着色器：
+将深度贴图渲染到四边形上的像素着色器：
 
 ```c++
 #version 330 core
@@ -201,11 +199,11 @@ void main()
 
 要注意的是当用透视投影矩阵取代正交投影矩阵来显示深度时，有一些轻微的改动，因为使用透视投影时，深度是非线性的。本节教程的最后，我们会讨论这些不同之处。
 
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/5.advanced_lighting/3.1.1.shadow_mapping_depth/shadow_mapping_depth.cpp)获得把场景渲染成深度贴图的源码。
+你可以在[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/shadow_mapping_depth_map)获得把场景渲染成深度贴图的源码。
 
 ## 渲染阴影
 
-正确地生成深度贴图以后我们就可以开始生成阴影了。这段代码在片段着色器中执行，用来检验一个片段是否在阴影之中，不过我们在顶点着色器中进行光空间的变换：
+正确地生成深度贴图以后我们就可以开始生成阴影了。这段代码在像素着色器中执行，用来检验一个片元是否在阴影之中，不过我们在顶点着色器中进行光空间的变换：
 
 ```c++
 #version 330 core
@@ -237,9 +235,9 @@ void main()
 }
 ``` 
 
-这儿的新的地方是FragPosLightSpace这个输出向量。我们用同一个lightSpaceMatrix，把世界空间顶点位置转换为光空间。顶点着色器传递一个普通的经变换的世界空间顶点位置vs_out.FragPos和一个光空间的vs_out.FragPosLightSpace给片段着色器。
+这儿的新的地方是FragPosLightSpace这个输出向量。我们用同一个lightSpaceMatrix，把世界空间顶点位置转换为光空间。顶点着色器传递一个普通的经变换的世界空间顶点位置vs_out.FragPos和一个光空间的vs_out.FragPosLightSpace给像素着色器。
 
-片段着色器使用Blinn-Phong光照模型渲染场景。我们接着计算出一个shadow值，当fragment在阴影中时是1.0，在阴影外是0.0。然后，diffuse和specular颜色会乘以这个阴影元素。由于阴影不会是全黑的（由于散射），我们把ambient分量从乘法中剔除。
+像素着色器使用Blinn-Phong光照模型渲染场景。我们接着计算出一个shadow值，当fragment在阴影中时是1.0，在阴影外是0.0。然后，diffuse和specular颜色会乘以这个阴影元素。由于阴影不会是全黑的（由于散射），我们把ambient分量从乘法中剔除。
 
 ```c++
 #version 330 core
@@ -289,9 +287,9 @@ void main()
 }
 ```
 
-片段着色器大部分是从高级光照教程中复制过来，只不过加上了个阴影计算。我们声明一个shadowCalculation函数，用它计算阴影。片段着色器的最后，我们我们把diffuse和specular乘以(1-阴影元素)，这表示这个片段有多大成分不在阴影中。这个片段着色器还需要两个额外输入，一个是光空间的片段位置和第一个渲染阶段得到的深度贴图。
+像素着色器大部分是从高级光照教程中复制过来，只不过加上了个阴影计算。我们声明一个shadowCalculation函数，用它计算阴影。像素着色器的最后，我们我们把diffuse和specular乘以(1-阴影元素)，这表示这个片元有多大成分不在阴影中。这个像素着色器还需要两个额外输入，一个是光空间的片元位置和第一个渲染阶段得到的深度贴图。
 
-首先要检查一个片段是否在阴影中，把光空间片段位置转换为裁切空间的标准化设备坐标。当我们在顶点着色器输出一个裁切空间顶点位置到gl_Position时，OpenGL自动进行一个透视除法，将裁切空间坐标的范围-w到w转为-1到1，这要将x、y、z元素除以向量的w元素来实现。由于裁切空间的FragPosLightSpace并不会通过gl_Position传到片段着色器里，我们必须自己做透视除法：
+首先要检查一个片元是否在阴影中，把光空间片元位置转换为裁切空间的标准化设备坐标。当我们在顶点着色器输出一个裁切空间顶点位置到gl_Position时，OpenGL自动进行一个透视除法，将裁切空间坐标的范围-w到w转为-1到1，这要将x、y、z元素除以向量的w元素来实现。由于裁切空间的FragPosLightSpace并不会通过gl_Position传到像素着色器里，我们必须自己做透视除法：
 
 ```c++
 float ShadowCalculation(vec4 fragPosLightSpace)
@@ -302,13 +300,13 @@ float ShadowCalculation(vec4 fragPosLightSpace)
 }
 ```
 
-返回了片段在光空间的-1到1的范围。
+返回了片元在光空间的-1到1的范围。
 
 !!! Important
 
     当使用正交投影矩阵，顶点w元素仍保持不变，所以这一步实际上毫无意义。可是，当使用透视投影的时候就是必须的了，所以为了保证在两种投影矩阵下都有效就得留着这行。
 
-因为来自深度贴图的深度在0到1的范围，我们也打算使用projCoords从深度贴图中去采样，所以我们将NDC坐标变换为0到1的范围。
+因为来自深度贴图的深度在0到1的范围，我们也打算使用projCoords从深度贴图中去采样，所以我们将NDC坐标变换为0到1的范围：
 （译者注：这里的意思是，上面的projCoords的xyz分量都是[-1,1]（下面会指出这对于远平面之类的点才成立），而为了和深度贴图的深度相比较，z分量需要变换到[0,1]；为了作为从深度贴图中采样的坐标，xy分量也需要变换到[0,1]。所以整个projCoords向量都需要变换到[0,1]范围。）
 
 ```c++
@@ -321,13 +319,13 @@ projCoords = projCoords * 0.5 + 0.5;
 float closestDepth = texture(shadowMap, projCoords.xy).r;
 ```
 
-为了得到片段的当前深度，我们简单获取投影向量的z坐标，它等于来自光的透视视角的片段的深度。
+为了得到片元的当前深度，我们简单获取投影向量的z坐标，它等于来自光的透视视角的片元的深度。
 
 ```c++
 float currentDepth = projCoords.z;
 ```
 
-实际的对比就是简单检查currentDepth是否高于closetDepth，如果是，那么片段就在阴影中。
+实际的对比就是简单检查currentDepth是否高于closetDepth，如果是，那么片元就在阴影中。
 
 ```c++
 float shadow = currentDepth > closestDepth  ? 1.0 : 0.0;
@@ -344,9 +342,9 @@ float ShadowCalculation(vec4 fragPosLightSpace)
     projCoords = projCoords * 0.5 + 0.5;
     // 取得最近点的深度(使用[0,1]范围下的fragPosLight当坐标)
     float closestDepth = texture(shadowMap, projCoords.xy).r; 
-    // 取得当前片段在光源视角下的深度
+    // 取得当前片元在光源视角下的深度
     float currentDepth = projCoords.z;
-    // 检查当前片段是否在阴影中
+    // 检查当前片元是否在阴影中
     float shadow = currentDepth > closestDepth  ? 1.0 : 0.0;
  
     return shadow;
@@ -355,9 +353,9 @@ float ShadowCalculation(vec4 fragPosLightSpace)
 
 激活这个着色器，绑定合适的纹理，激活第二个渲染阶段默认的投影以及视图矩阵，结果如下图所示：
 
-![](../../img/05/03/01/shadow_mapping_shadows.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_shadows.png)
 
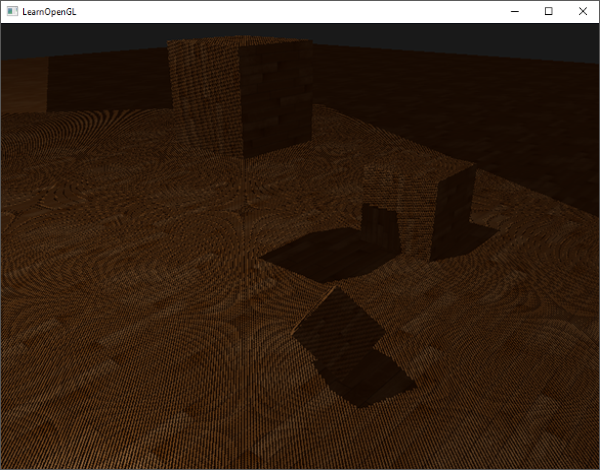
-如果你做对了，你会看到地板和上有立方体的阴影。你可以从这里找到demo程序的[源码](https://learnopengl.com/code_viewer_gh.php?code=src/5.advanced_lighting/3.1.2.shadow_mapping_base/shadow_mapping_base.cpp)。
+如果你做对了，你会看到地板和上有立方体的阴影。你可以从这里找到demo程序的[源码](http://learnopengl.com/code_viewer.php?code=advanced-lighting/shadow_mapping_shadows)。
 
 ## 改进阴影贴图
 
@@ -367,19 +365,19 @@ float ShadowCalculation(vec4 fragPosLightSpace)
 
 前面的图片中明显有不对的地方。放大看会发现明显的线条样式：
 
-![](../../img/05/03/01/shadow_mapping_acne.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_acne.png)
 
 我们可以看到地板四边形渲染出很大一块交替黑线。这种阴影贴图的不真实感叫做**阴影失真(Shadow Acne)**，下图解释了成因：
 
-![](../../img/05/03/01/shadow_mapping_acne_diagram.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_acne_diagram.png)
 
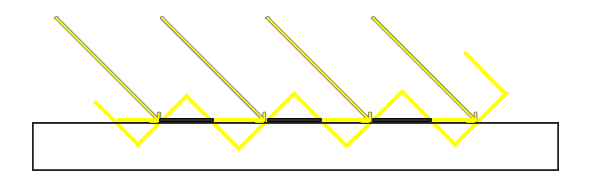
-因为阴影贴图受限于分辨率，在距离光源比较远的情况下，多个片段可能从深度贴图的同一个值中去采样。图片每个斜坡代表深度贴图一个单独的纹理像素。你可以看到，多个片段从同一个深度值进行采样。
+因为阴影贴图受限于解析度，在距离光源比较远的情况下，多个片元可能从深度贴图的同一个值中去采样。图片每个斜坡代表深度贴图一个单独的纹理像素。你可以看到，多个片元从同一个深度值进行采样。
 
-虽然很多时候没问题，但是当光源以一个角度朝向表面的时候就会出问题，这种情况下深度贴图也是从一个角度下进行渲染的。多个片段就会从同一个斜坡的深度纹理像素中采样，有些在地板上面，有些在地板下面；这样我们所得到的阴影就有了差异。因为这个，有些片段被认为是在阴影之中，有些不在，由此产生了图片中的条纹样式。
+虽然很多时候没问题，但是当光源以一个角度朝向表面的时候就会出问题，这种情况下深度贴图也是从一个角度下进行渲染的。多个片元就会从同一个斜坡的深度纹理像素中采样，有些在地板上面，有些在地板下面；这样我们所得到的阴影就有了差异。因为这个，有些片元被认为是在阴影之中，有些不在，由此产生了图片中的条纹样式。
 
-我们可以用一个叫做**阴影偏移**（shadow bias）的技巧来解决这个问题，我们简单的对表面的深度（或深度贴图）应用一个偏移量，这样片段就不会被错误地认为在表面之下了。
+我们可以用一个叫做**阴影偏移**（shadow bias）的技巧来解决这个问题，我们简单的对表面的深度（或深度贴图）应用一个偏移量，这样片元就不会被错误地认为在表面之下了。
 
-![](../../img/05/03/01/shadow_mapping_acne_bias.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_acne_bias.png)
 
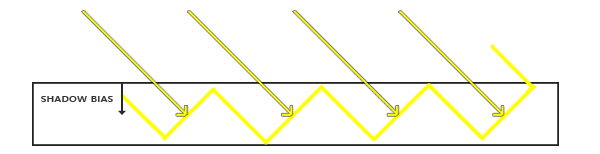
 使用了偏移量后，所有采样点都获得了比表面深度更小的深度值，这样整个表面就正确地被照亮，没有任何阴影。我们可以这样实现这个偏移：
 
@@ -396,7 +394,7 @@ float bias = max(0.05 * (1.0 - dot(normal, lightDir)), 0.005);
 
 这里我们有一个偏移量的最大值0.05，和一个最小值0.005，它们是基于表面法线和光照方向的。这样像地板这样的表面几乎与光源垂直，得到的偏移就很小，而比如立方体的侧面这种表面得到的偏移就更大。下图展示了同一个场景，但使用了阴影偏移，效果的确更好：
 
-![](../../img/05/03/01/shadow_mapping_with_bias.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_with_bias.png)
 
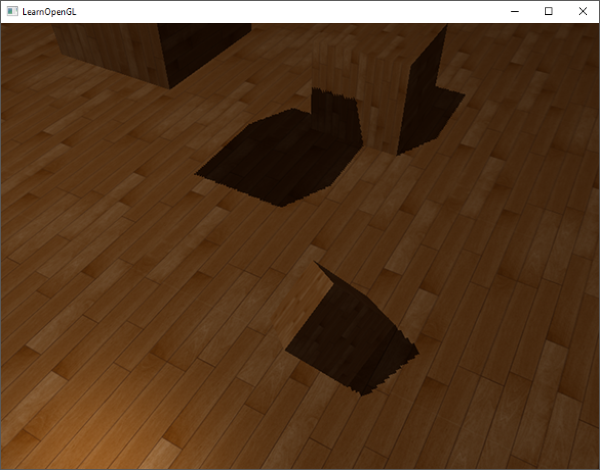
 选用正确的偏移数值，在不同的场景中需要一些像这样的轻微调校，但大多情况下，实际上就是增加偏移量直到所有失真都被移除的问题。
 
@@ -404,13 +402,13 @@ float bias = max(0.05 * (1.0 - dot(normal, lightDir)), 0.005);
 
 使用阴影偏移的一个缺点是你对物体的实际深度应用了平移。偏移有可能足够大，以至于可以看出阴影相对实际物体位置的偏移，你可以从下图看到这个现象（这是一个夸张的偏移值）：
 
-![](../../img/05/03/01/shadow_mapping_peter_panning.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_peter_panning.png)
 
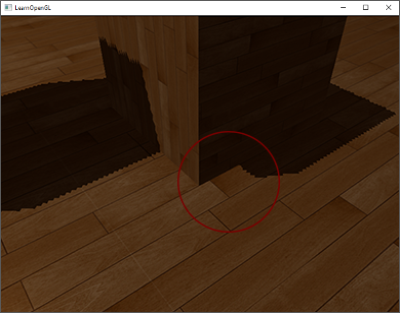
 这个阴影失真叫做悬浮(Peter Panning)，因为物体看起来轻轻悬浮在表面之上（译注Peter Pan就是童话彼得潘，而panning有平移、悬浮之意，而且彼得潘是个会飞的男孩…）。我们可以使用一个叫技巧解决大部分的Peter panning问题：当渲染深度贴图时候使用正面剔除（front face culling）你也许记得在面剔除教程中OpenGL默认是背面剔除。我们要告诉OpenGL我们要剔除正面。
 
 因为我们只需要深度贴图的深度值，对于实体物体无论我们用它们的正面还是背面都没问题。使用背面深度不会有错误，因为阴影在物体内部有错误我们也看不见。
 
-![](../../img/05/03/01/shadow_mapping_culling.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_culling.png)
 
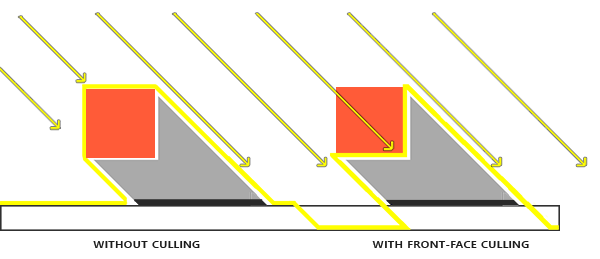
 为了修复peter游移，我们要进行正面剔除，先必须开启GL_CULL_FACE：
 
@@ -420,7 +418,7 @@ RenderSceneToDepthMap();
 glCullFace(GL_BACK); // 不要忘记设回原先的culling face
 ```
 
-这十分有效地解决了peter panning的问题，但只对内部不会对外开口的实体物体有效。我们的场景中，在立方体上工作的很好，但在地板上无效，因为正面剔除完全移除了地板。地面是一个单独的平面，不会被完全剔除。如果有人打算使用这个技巧解决peter panning必须考虑到只有剔除物体的正面才有意义。
+这十分有效地解决了peter panning的问题，但只针对实体物体，内部不会对外开口。我们的场景中，在立方体上工作的很好，但在地板上无效，因为正面剔除完全移除了地板。地面是一个单独的平面，不会被完全剔除。如果有人打算使用这个技巧解决peter panning必须考虑到只有剔除物体的正面才有意义。
 
 另一个要考虑到的地方是接近阴影的物体仍然会出现不正确的效果。必须考虑到何时使用正面剔除对物体才有意义。不过使用普通的偏移值通常就能避免peter panning。
 
@@ -428,7 +426,7 @@ glCullFace(GL_BACK); // 不要忘记设回原先的culling face
 
 无论你喜不喜欢还有一个视觉差异，就是光的视锥不可见的区域一律被认为是处于阴影中，不管它真的处于阴影之中。出现这个状况是因为超出光的视锥的投影坐标比1.0大，这样采样的深度纹理就会超出他默认的0到1的范围。根据纹理环绕方式，我们将会得到不正确的深度结果，它不是基于真实的来自光源的深度值。
 
-![](../../img/05/03/01/shadow_mapping_outside_frustum.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_outside_frustum.png)
 
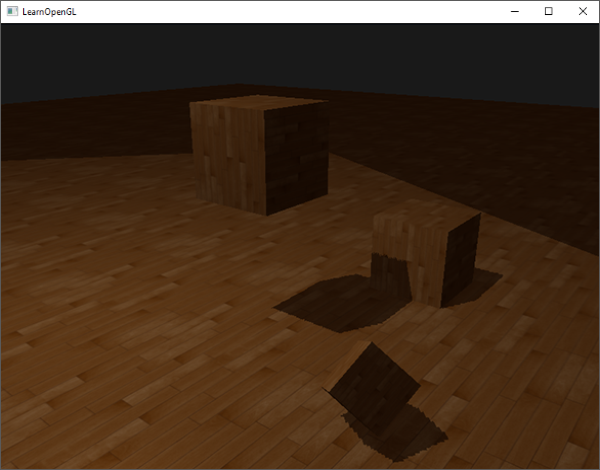
 你可以在图中看到，光照有一个区域，超出该区域就成为了阴影；这个区域实际上代表着深度贴图的大小，这个贴图投影到了地板上。发生这种情况的原因是我们之前将深度贴图的环绕方式设置成了GL_REPEAT。
 
@@ -443,13 +441,13 @@ glTexParameterfv(GL_TEXTURE_2D, GL_TEXTURE_BORDER_COLOR, borderColor);
 
 现在如果我们采样深度贴图0到1坐标范围以外的区域，纹理函数总会返回一个1.0的深度值，阴影值为0.0。结果看起来会更真实：
 
-![](../../img/05/03/01/shadow_mapping_clamp_edge.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_clamp_edge.png)
 
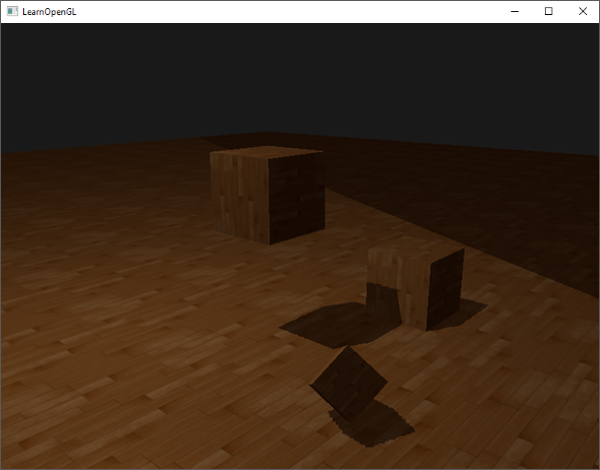
 仍有一部分是黑暗区域。那里的坐标超出了光的正交视锥的远平面。你可以看到这片黑色区域总是出现在光源视锥的极远处。
 
 当一个点比光的远平面还要远时，它的投影坐标的z坐标大于1.0。这种情况下，GL_CLAMP_TO_BORDER环绕方式不起作用，因为我们把坐标的z元素和深度贴图的值进行了对比；它总是为大于1.0的z返回true。
 
-解决这个问题也很简单，只要投影向量的z坐标大于1.0，我们就把shadow的值强制设为0.0：
+解决这个问题也很简单，我们简单的强制把shadow的值设为0.0，不管投影向量的z坐标是否大于1.0：
 
 ```c++
 float ShadowCalculation(vec4 fragPosLightSpace)
@@ -464,19 +462,19 @@ float ShadowCalculation(vec4 fragPosLightSpace)
 
 检查远平面，并将深度贴图限制为一个手工指定的边界颜色，就能解决深度贴图采样超出的问题，我们最终会得到下面我们所追求的效果：
 
-![](../../img/05/03/01/shadow_mapping_over_sampling_fixed.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_over_sampling_fixed.png)
 
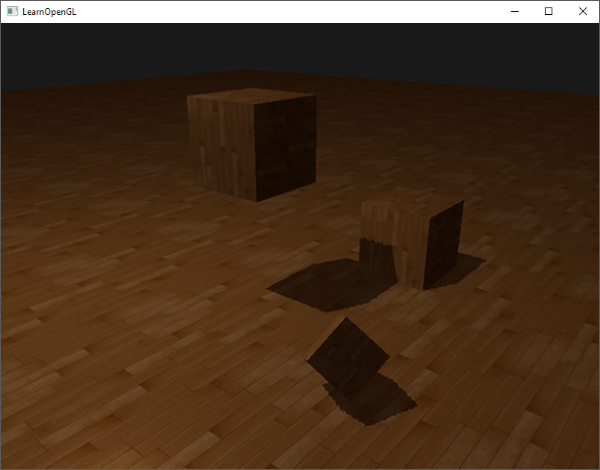
 这些结果意味着，只有在深度贴图范围以内的被投影的fragment坐标才有阴影，所以任何超出范围的都将会没有阴影。由于在游戏中通常这只发生在远处，就会比我们之前的那个明显的黑色区域效果更真实。
 
 ## PCF
 
-阴影现在已经附着到场景中了，不过这仍不是我们想要的。如果你放大看阴影，阴影映射对分辨率的依赖很快变得很明显。
+阴影现在已经附着到场景中了，不过这仍不是我们想要的。如果你放大看阴影，阴影映射对解析度的依赖很快变得很明显。
 
-![](../../img/05/03/01/shadow_mapping_zoom.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_zoom.png)
 
-因为深度贴图有一个固定的分辨率，多个片段对应于一个纹理像素。结果就是多个片段会从深度贴图的同一个深度值进行采样，这几个片段便得到的是同一个阴影，这就会产生锯齿边。
+因为深度贴图有一个固定的解析度，多个片元对应于一个纹理像素。结果就是多个片元会从深度贴图的同一个深度值进行采样，这几个片元便得到的是同一个阴影，这就会产生锯齿边。
 
-你可以通过增加深度贴图的分辨率的方式来降低锯齿块，也可以尝试尽可能的让光的视锥接近场景。
+你可以通过增加深度贴图解析度的方式来降低锯齿块，也可以尝试尽可能的让光的视锥接近场景。
 
 另一个（并不完整的）解决方案叫做PCF（percentage-closer filtering），这是一种多个不同过滤方式的组合，它产生柔和阴影，使它们出现更少的锯齿块和硬边。核心思想是从深度贴图中多次采样，每一次采样的纹理坐标都稍有不同。每个独立的样本可能在也可能不再阴影中。所有的次生结果接着结合在一起，进行平均化，我们就得到了柔和阴影。
 
@@ -500,9 +498,9 @@ shadow /= 9.0;
 
 使用更多的样本，更改texelSize变量，你就可以增加阴影的柔和程度。下面你可以看到应用了PCF的阴影：
 
-![](../../img/05/03/01/shadow_mapping_soft_shadows.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_soft_shadows.png)
 
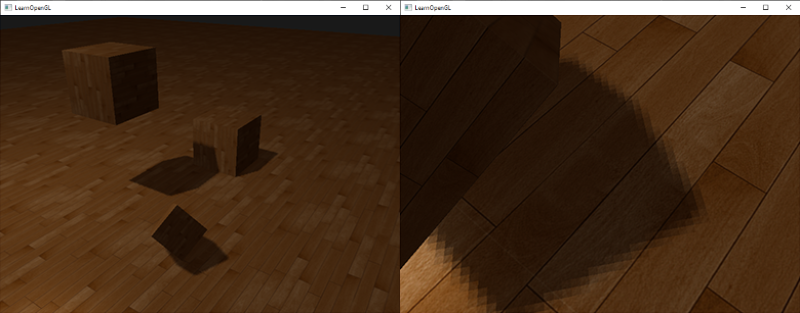
-从稍微远一点的距离看去，阴影效果好多了，也不那么生硬了。如果你放大，仍会看到阴影贴图分辨率的不真实感，但通常对于大多数应用来说效果已经很好了。
+从稍微远一点的距离看去，阴影效果好多了，也不那么生硬了。如果你放大，仍会看到阴影贴图解析度的不真实感，但通常对于大多数应用来说效果已经很好了。
 
 你可以从[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/shadow_mapping)找到这个例子的全部源码和第二个阶段的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/shadow_mapping&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/shadow_mapping&type=fragment)着色器。
 
@@ -513,11 +511,11 @@ shadow /= 9.0;
 
 在渲染深度贴图的时候，正交(Orthographic)和投影(Projection)矩阵之间有所不同。正交投影矩阵并不会将场景用透视图进行变形，所有视线/光线都是平行的，这使它对于定向光来说是个很好的投影矩阵。然而透视投影矩阵，会将所有顶点根据透视关系进行变形，结果因此而不同。下图展示了两种投影方式所产生的不同阴影区域：
 
-![](../../img/05/03/01/shadow_mapping_projection.png)
+![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_projection.png)
 
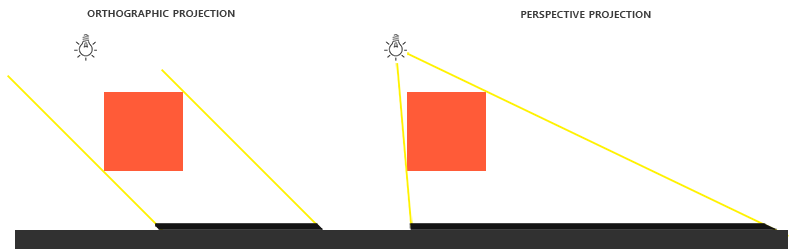
 透视投影对于光源来说更合理，不像定向光，它是有自己的位置的。透视投影因此更经常用在点光源和聚光灯上，而正交投影经常用在定向光上。
 
-另一个细微差别是，透视投影矩阵，将深度缓冲视觉化经常会得到一个几乎全白的结果。发生这个是因为透视投影下，深度变成了非线性的深度值，它的大多数可辨范围都位于近平面附近。为了可以像使用正交投影一样合适地观察深度值，你必须先将非线性深度值转变为线性的，如我们在深度测试教程中已经讨论过的那样。
+另一个细微差别是，透视投影矩阵，将深度缓冲视觉化经常会得到一个几乎全白的结果。发生这个是因为透视投影下，深度变成了非线性的深度值，它的大多数可辨范围接近于近平面。为了可以像使用正交投影一样合适的观察到深度值，你必须先讲过非线性深度值转变为线性的，我们在深度测试教程中已经讨论过。
 
 ```c++
 #version 330 core
@@ -549,4 +547,4 @@ void main()
 - [Tutorial 16 : Shadow mapping](http://www.opengl-tutorial.org/intermediate-tutorials/tutorial-16-shadow-mapping/)：提供的类似的阴影映射教程，里面有一些额外的解释。
 - [Shadow Mapping – Part 1：ogldev](http://ogldev.atspace.co.uk/www/tutorial23/tutorial23.html)：提供的另一个阴影映射教程。
 - [How Shadow Mapping Works](https://www.youtube.com/watch?v=EsccgeUpdsM)：的一个第三方YouTube视频教程，里面解释了阴影映射及其实现。
-- [Common Techniques to Improve Shadow Depth Maps](https://msdn.microsoft.com/en-us/library/windows/desktop/ee416324%28v=vs.85%29.aspx)：微软的一篇好文章，其中理出了很多提升阴影贴图质量的技术。
+- [Common Techniques to Improve Shadow Depth Maps](https://msdn.microsoft.com/en-us/library/windows/desktop/ee416324%28v=vs.85%29.aspx)：微软的一篇好文章，其中理出了很多提升阴影贴图质量的技术。

docs/05 Advanced Lighting/03 Shadows/02 Point Shadows.md

@@ -6,10 +6,6 @@
 翻译     | [Django](http://bullteacher.com/)
 校对     | 暂无
 
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
 上个教程我们学到了如何使用阴影映射技术创建动态阴影。效果不错，但它只适合定向光，因为阴影只是在单一定向光源下生成的。所以它也叫定向阴影映射，深度（阴影）贴图生成自定向光的视角。
 
 !!! Important
@@ -23,7 +19,7 @@
 
 对于深度贴图，我们需要从一个点光源的所有渲染场景，普通2D深度贴图不能工作；如果我们使用立方体贴图会怎样？因为立方体贴图可以储存6个面的环境数据，它可以将整个场景渲染到立方体贴图的每个面上，把它们当作点光源四周的深度值来采样。
 
-![](../../img/05/03/02/point_shadows_diagram.png)
+![](http://learnopengl.com/img/advanced-lighting/point_shadows_diagram.png)
 
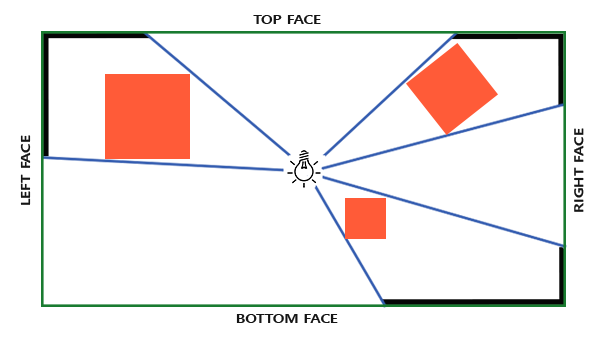
 生成后的深度立方体贴图被传递到光照像素着色器，它会用一个方向向量来采样立方体贴图，从而得到当前的fragment的深度（从光的透视图）。大部分复杂的事情已经在阴影映射教程中讨论过了。算法只是在深度立方体贴图生成上稍微复杂一点。
 
@@ -88,9 +84,9 @@ glBindFramebuffer(GL_FRAMEBUFFER, 0);
 // 1. first render to depth cubemap
 glViewport(0, 0, SHADOW_WIDTH, SHADOW_HEIGHT);
 glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
-glClear(GL_DEPTH_BUFFER_BIT);
-ConfigureShaderAndMatrices();
-RenderScene();
+    glClear(GL_DEPTH_BUFFER_BIT);
+    ConfigureShaderAndMatrices();
+    RenderScene();
 glBindFramebuffer(GL_FRAMEBUFFER, 0);
 // 2. then render scene as normal with shadow mapping (using depth cubemap)
 glViewport(0, 0, SCR_WIDTH, SCR_HEIGHT);
@@ -112,7 +108,7 @@ RenderScene();
 GLfloat aspect = (GLfloat)SHADOW_WIDTH/(GLfloat)SHADOW_HEIGHT;
 GLfloat near = 1.0f;
 GLfloat far = 25.0f;
-glm::mat4 shadowProj = glm::perspective(glm::radians(90.0f), aspect, near, far);
+glm::mat4 shadowProj = glm::perspective(90.0f, aspect, near, far);
 ```
 
 非常重要的一点是，这里glm::perspective的视野参数，设置为90度。90度我们才能保证视野足够大到可以合适地填满立方体贴图的一个面，立方体贴图的所有面都能与其他面在边缘对齐。
@@ -122,17 +118,17 @@ glm::mat4 shadowProj = glm::perspective(glm::radians(90.0f), aspect, near, far);
 ```c++
 std::vector<glm::mat4> shadowTransforms;
 shadowTransforms.push_back(shadowProj * 
-                 glm::lookAt(lightPos, lightPos + glm::vec3(1.0,0.0,0.0), glm::vec3(0.0,-1.0,0.0)));
+                 glm::lookAt(lightPos, lightPos + glm::vec3(1.0,0.0,0.0), glm::vec3(0.0,-1.0,0.0));
 shadowTransforms.push_back(shadowProj * 
-                 glm::lookAt(lightPos, lightPos + glm::vec3(-1.0,0.0,0.0), glm::vec3(0.0,-1.0,0.0)));
+                 glm::lookAt(lightPos, lightPos + glm::vec3(-1.0,0.0,0.0), glm::vec3(0.0,-1.0,0.0));
 shadowTransforms.push_back(shadowProj * 
-                 glm::lookAt(lightPos, lightPos + glm::vec3(0.0,1.0,0.0), glm::vec3(0.0,0.0,1.0)));
+                 glm::lookAt(lightPos, lightPos + glm::vec3(0.0,1.0,0.0), glm::vec3(0.0,0.0,1.0));
 shadowTransforms.push_back(shadowProj * 
-                 glm::lookAt(lightPos, lightPos + glm::vec3(0.0,-1.0,0.0), glm::vec3(0.0,0.0,-1.0)));
+                 glm::lookAt(lightPos, lightPos + glm::vec3(0.0,-1.0,0.0), glm::vec3(0.0,0.0,-1.0));
 shadowTransforms.push_back(shadowProj * 
-                 glm::lookAt(lightPos, lightPos + glm::vec3(0.0,0.0,1.0), glm::vec3(0.0,-1.0,0.0)));
+                 glm::lookAt(lightPos, lightPos + glm::vec3(0.0,0.0,1.0), glm::vec3(0.0,-1.0,0.0));
 shadowTransforms.push_back(shadowProj * 
-                 glm::lookAt(lightPos, lightPos + glm::vec3(0.0,0.0,-1.0), glm::vec3(0.0,-1.0,0.0)));
+                 glm::lookAt(lightPos, lightPos + glm::vec3(0.0,0.0,-1.0), glm::vec3(0.0,-1.0,0.0));
 ```
 
 这里我们创建了6个视图矩阵，把它们乘以投影矩阵，来得到6个不同的光空间变换矩阵。glm::lookAt的target参数是它注视的立方体贴图的面的一个方向。
@@ -193,10 +189,10 @@ void main()
 ```c++
 #version 330 core
 in vec4 FragPos;
-
+ 
 uniform vec3 lightPos;
 uniform float far_plane;
-
+ 
 void main()
 {
     // get distance between fragment and light source
@@ -205,8 +201,8 @@ void main()
     // map to [0;1] range by dividing by far_plane
     lightDistance = lightDistance / far_plane;
     
-    // write this as modified depth
-    gl_FragDepth = lightDistance;
+    // Write this as modified depth
+    gl_FragDepth = gl_FragCoord.z;
 }
 ``` 
 
@@ -317,7 +313,7 @@ void main()
 
 在ShadowCalculation函数中有很多不同之处，现在是从立方体贴图中进行采样，不再使用2D纹理了。我们来一步一步的讨论一下的它的内容。
 
-我们需要做的第一件事是获取立方体贴图的深度。你可能已经从教程的立方体贴图部分想到，我们已经将深度储存为fragment和光位置之间的距离了；我们这里采用相似的处理方式：
+我们需要做的第一件事是获取立方体贴图的森都。你可能已经从教程的立方体贴图部分想到，我们已经将深度储存为fragment和光位置之间的距离了；我们这里采用相似的处理方式：
 
 ```c++
 float ShadowCalculation(vec3 fragPos)
@@ -327,9 +323,9 @@ float ShadowCalculation(vec3 fragPos)
 }
 ```
 
-在这里，我们得到了fragment的位置与光的位置之间的差向量，使用这个向量作为一个方向向量去对立方体贴图进行采样。方向向量不需要是单位向量，所以无需对它进行标准化。最后的closestDepth是光源和它最接近的可见fragment之间的标准化的深度值。
+在这里，我们得到了fragment的位置与光的位置之间的不同的向量，使用这个向量作为一个方向向量去对立方体贴图进行采样。方向向量不需要是单位向量，所以无需对它进行标准化。最后的closestDepth是光源和它最接近的可见fragment之间的标准化的深度值。
 
-closestDepth值现在在0到1的范围内了，所以我们先将其转换回0到far_plane的范围，这需要把他乘以far_plane：
+closestDepth值现在在0到1的范围内了，所以我们先将其转换会0到far_plane的范围，这需要把他乘以far_plane：
 
 ```c++
 closestDepth *= far_plane;
@@ -373,7 +369,7 @@ float ShadowCalculation(vec3 fragPos)
 
 有了这些着色器，我们已经能得到非常好的阴影效果了，这次从一个点光源所有周围方向上都有阴影。有一个位于场景中心的点光源，看起来会像这样：
 
-![](../../img/05/03/02/point_shadows.png)
+![](http://learnopengl.com/img/advanced-lighting/point_shadows.png)
 
 你可以从这里找到这个[demo的源码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/point_shadows)、[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/point_shadows&type=vertex)和[片段](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/point_shadows&type=fragment)着色器。
 
@@ -389,7 +385,7 @@ FragColor = vec4(vec3(closestDepth / far_plane), 1.0);
 
 结果是一个灰度场景，每个颜色代表着场景的线性深度值：
 
-![](../../img/05/03/02/point_shadows_depth_cubemap.png)
+![](http://learnopengl.com/img/advanced-lighting/point_shadows_depth_cubemap.png)
 
 你可能也注意到了带阴影部分在墙外。如果看起来和这个差不多，你就知道深度立方体贴图生成的没错。否则你可能做错了什么，也许是closestDepth仍然还在0到far_plane的范围。
 
@@ -424,11 +420,11 @@ shadow /= (samples * samples * samples);
 
 现在阴影看起来更加柔和平滑了，由此得到更加真实的效果：
 
-![](../../img/05/03/02/point_shadows_soft.png)
+![](http://learnopengl.com/img/advanced-lighting/point_shadows_soft.png)
 
 然而，samples设置为4.0，每个fragment我们会得到总共64个样本，这太多了！
 
-大多数这些采样都是多余的，与其在原始方向向量附近处采样，不如在采样方向向量的垂直方向进行采样更有意义。可是，没有（简单的）方式能够指出哪一个子方向是多余的，这就难了。有个技巧可以使用，用一个偏移量方向数组，它们差不多都是分开的，每一个指向完全不同的方向，剔除彼此接近的那些子方向。下面就是一个有着20个偏移方向的数组：
+大多数这些样本都是多余的，它们在原始方向向量近处采样，不如在采样方向向量的垂直方向进行采样更有意义。可是，没有（简单的）方式能够指出哪一个子方向是多余的，这就难了。有个技巧可以使用，用一个偏移量方向数组，它们差不多都是分开的，每一个指向完全不同的方向，剔除彼此接近的那些子方向。下面就是一个有着20个偏移方向的数组：
 
 ```c++
 vec3 sampleOffsetDirections[20] = vec3[]
@@ -469,7 +465,7 @@ float diskRadius = (1.0 + (viewDistance / far_plane)) / 25.0;
 
 PCF算法的结果如果没有变得更好，也是非常不错的，这是柔和的阴影效果：
 
-![](../../img/05/03/02/point_shadows_soft_better.png)
+![](http://learnopengl.com/img/advanced-lighting/point_shadows_soft_better.png)
 
 当然了，我们添加到每个样本的bias（偏移）高度依赖于上下文，总是要根据场景进行微调的。试试这些值，看看怎样影响了场景。
 这里是最终版本的顶点和像素着色器。
@@ -480,4 +476,4 @@ PCF算法的结果如果没有变得更好，也是非常不错的，这是柔
 
 - [Shadow Mapping for point light sources in OpenGL](http://www.sunandblackcat.com/tipFullView.php?l=eng&topicid=36)：sunandblackcat的万向阴影映射教程。
 - [Multipass Shadow Mapping With Point Lights](http://ogldev.atspace.co.uk/www/tutorial43/tutorial43.html)：ogldev的万向阴影映射教程。
-- [Omni-directional Shadows](http://www.cg.tuwien.ac.at/~husky/RTR/OmnidirShadows-whyCaps.pdf)：Peter Houska的关于万向阴影映射的一组很好的ppt。
+- [Omni-directional Shadows](http://www.cg.tuwien.ac.at/~husky/RTR/OmnidirShadows-whyCaps.pdf)：Peter Houska的关于万向阴影映射的一组很好的ppt。

docs/05 Advanced Lighting/04 Normal Mapping.md

@@ -4,27 +4,23 @@
       ---|---
 作者     | JoeyDeVries
 翻译     | [Django](http://bullteacher.com/)
-校对     | [KenLee](https://hellokenlee.github.io/)
-
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
+校对     | 暂无
 
 我们的场景中已经充满了多边形物体，其中每个都可能由成百上千平坦的三角形组成。我们以向三角形上附加纹理的方式来增加额外细节，提升真实感，隐藏多边形几何体是由无数三角形组成的事实。纹理确有助益，然而当你近看它们时，这个事实便隐藏不住了。现实中的物体表面并非是平坦的，而是表现出无数（凹凸不平的）细节。
 
 例如，砖块的表面。砖块的表面非常粗糙，显然不是完全平坦的：它包含着接缝处水泥凹痕，以及非常多的细小的空洞。如果我们在一个有光的场景中看这样一个砖块的表面，问题就出来了。下图中我们可以看到砖块纹理应用到了平坦的表面，并被一个点光源照亮。
 
-![](../img/05/04/normal_mapping_flat.png)
+![](http://learnopengl.com/img/advanced-lighting/normal_mapping_flat.png)
 
 光照并没有呈现出任何裂痕和孔洞，完全忽略了砖块之间凹进去的线条；表面看起来完全就是平的。我们可以使用specular贴图根据深度或其他细节阻止部分表面被照的更亮，以此部分地解决问题，但这并不是一个好方案。我们需要的是某种可以告知光照系统给所有有关物体表面类似深度这样的细节的方式。
 
 如果我们以光的视角来看这个问题：是什么使表面被视为完全平坦的表面来照亮？答案会是表面的法线向量。以光照算法的视角考虑的话，只有一件事决定物体的形状，这就是垂直于它的法线向量。砖块表面只有一个法线向量，表面完全根据这个法线向量被以一致的方式照亮。如果每个fragment都是用自己的不同的法线会怎样？这样我们就可以根据表面细微的细节对法线向量进行改变；这样就会获得一种表面看起来要复杂得多的幻觉：
 
-![](../img/05/04/normal_mapping_surfaces.png)
+![](http://learnopengl.com/img/advanced-lighting/normal_mapping_surfaces.png)
 
 每个fragment使用了自己的法线，我们就可以让光照相信一个表面由很多微小的（垂直于法线向量的）平面所组成，物体表面的细节将会得到极大提升。这种每个fragment使用各自的法线，替代一个面上所有fragment使用同一个法线的技术叫做法线贴图（normal mapping）或凹凸贴图（bump mapping）。应用到砖墙上，效果像这样：
 
-![](../img/05/04/normal_mapping_compare.png)
+![](http://learnopengl.com/img/advanced-lighting/normal_mapping_compare.png)
 
 你可以看到细节获得了极大提升，开销却不大。因为我们只需要改变每个fragment的法线向量，并不需要改变所有光照公式。现在我们是为每个fragment传递一个法线，不再使用插值表面法线。这样光照使表面拥有了自己的细节。
 
@@ -32,20 +28,21 @@
 
 为使法线贴图工作，我们需要为每个fragment提供一个法线。像diffuse贴图和specular贴图一样，我们可以使用一个2D纹理来储存法线数据。2D纹理不仅可以储存颜色和光照数据，还可以储存法线向量。这样我们可以从2D纹理中采样得到特定纹理的法线向量。
 
-由于法线向量是个几何工具，而纹理通常只用于储存颜色信息，用纹理储存法线向量不是非常直接。如果你想一想，就会知道纹理中的颜色向量用r、g、b元素代表一个3D向量。类似的我们也可以将法线向量的x、y、z元素储存到纹理中，代替颜色的r、g、b元素。法线向量的范围在-1到1之间，所以我们先要将其映射到0到1的范围：
+由于法线向量是个几何工具，而纹理通常只用于储存颜色信息，用纹理储存法线向量不是非常直
+。如果你想一想，就会知道纹理中的颜色向量用r、g、b元素代表一个3D向量。类似的我们也可以将法线向量的x、y、z元素储存到纹理中，代替颜色的r、g、b元素。法线向量的范围在-1到1之间，所以我们先要将其映射到0到1的范围：
 
 
 ```c++
-vec3 rgb_normal = normal * 0.5 + 0.5; // 从 [-1,1] 转换至 [0,1]
+vec3 rgb_normal = normal * 0.5 - 0.5; // transforms from [-1,1] to [0,1]  
 ```
 
 将法线向量变换为像这样的RGB颜色元素，我们就能把根据表面的形状的fragment的法线保存在2D纹理中。教程开头展示的那个砖块的例子的法线贴图如下所示：
 
-![](../img/05/04/normal_mapping_normal_map.png)
+![](http://learnopengl.com/img/advanced-lighting/normal_mapping_normal_map.png)
 
 这会是一种偏蓝色调的纹理（你在网上找到的几乎所有法线贴图都是这样的）。这是因为所有法线的指向都偏向z轴（0, 0, 1）这是一种偏蓝的颜色。法线向量从z轴方向也向其他方向轻微偏移，颜色也就发生了轻微变化，这样看起来便有了一种深度。例如，你可以看到在每个砖块的顶部，颜色倾向于偏绿，这是因为砖块的顶部的法线偏向于指向正y轴方向（0, 1, 0），这样它就是绿色的了。
 
-在一个简单的朝向正z轴的平面上，我们可以用[这个diffuse纹理](https://learnopengl.com/img/textures/brickwall.jpg)和[这个法线贴图](https://learnopengl.com/img/textures/brickwall_normal.jpg)来渲染前面部分的图片。要注意的是这个链接里的法线贴图和上面展示的那个不一样。原因是OpenGL读取的纹理的y（或V）坐标和纹理通常被创建的方式相反。链接里的法线贴图的y（或绿色）元素是相反的（你可以看到绿色现在在下边）；如果你没考虑这个，光照就不正确了（译注：如果你现在不再使用SOIL了，那就不要用链接里的那个法线贴图，这个问题是SOIL载入纹理上下颠倒所致，它也会把法线在y方向上颠倒）。加载纹理，把它们绑定到合适的纹理单元，然后使用下面的改变了的像素着色器来渲染一个平面：
+在一个简单的朝向正z轴的平面上，我们可以用这个diffuse纹理和这个法线贴图来渲染前面部分的图片。要注意的是这个链接里的法线贴图和上面展示的那个不一样。原因是OpenGL读取的纹理的y（或V）坐标和纹理通常被创建的方式相反。链接里的法线贴图的y（或绿色）元素是相反的（你可以看到绿色现在在下边）；如果你没考虑这个，光照就不正确了（译注：如果你现在不再使用SOIL了，那就不要用链接里的那个法线贴图，这个问题是SOIL载入纹理上下颠倒所致，它也会把法线在y方向上颠倒）。加载纹理，把它们绑定到合适的纹理单元，然后使用下面的改变了的像素着色器来渲染一个平面：
 
 ```c++
 uniform sampler2D normalMap;  
@@ -66,16 +63,17 @@ void main()
 
 通过慢慢随着时间慢慢移动光源，你就能明白法线贴图是什么意思了。运行这个例子你就能得到本教程开始的那个效果：
 
-![](../img/05/04/normal_mapping_correct.png)
+![](http://learnopengl.com/img/advanced-lighting/normal_mapping_correct.png)
 
+你可以在这里找到这个简单demo的源代码及其顶点和像素着色器。
 
 然而有个问题限制了刚才讲的那种法线贴图的使用。我们使用的那个法线贴图里面的所有法线向量都是指向正z方向的。上面的例子能用，是因为那个平面的表面法线也是指向正z方向的。可是，如果我们在表面法线指向正y方向的平面上使用同一个法线贴图会发生什么？
 
-![](../img/05/04/normal_mapping_ground.png)
+![](http://learnopengl.com/img/advanced-lighting/normal_mapping_ground.png)
 
 光照看起来完全不对！发生这种情况是平面的表面法线现在指向了y，而采样得到的法线仍然指向的是z。结果就是光照仍然认为表面法线和之前朝向正z方向时一样；这样光照就不对了。下面的图片展示了这个表面上采样的法线的近似情况：
 
-![](../img/05/04/normal_mapping_ground_normals.png)
+![](http://learnopengl.com/img/advanced-lighting/normal_mapping_ground_normals.png)
 
 你可以看到所有法线都指向z方向，它们本该朝着表面法线指向y方向的。一个可行方案是为每个表面制作一个单独的法线贴图。如果是一个立方体的话我们就需要6个法线贴图，但是如果模型上有无数的朝向不同方向的表面，这就不可行了（译注：实际上对于复杂模型可以把朝向各个方向的法线储存在同一张贴图上，你可能看到过不只是蓝色的法线贴图，不过用那样的法线贴图有个问题是你必须记住模型的起始朝向，如果模型运动了还要记录模型的变换，这是非常不方便的；此外就像作者所说的，如果把一个diffuse纹理应用在同一个物体的不同表面上，就像立方体那样的，就需要做6个法线贴图，这也不可取）。
 
@@ -83,7 +81,7 @@ void main()
 
 ## 切线空间
 
-法线贴图中的法线向量定义在切线空间中，在切线空间中，法线永远指着正z方向。切线空间是位于三角形表面之上的空间：法线相对于单个三角形的局部坐标系。它就像法线贴图向量的局部空间；它们都被定义为指向正z方向，无论最终变换到什么方向。使用一个特定的矩阵我们就能将本地/切线空间中的法线向量转成世界或视图空间下，使它们转向到最终的贴图表面的方向。
+法线贴图中的法线向量在切线空间中，法线永远指着正z方向。切线空间是位于三角形表面之上的空间：法线相对于单个三角形的本地参考框架。它就像法线贴图向量的本地空间；它们都被定义为指向正z方向，无论最终变换到什么方向。使用一个特定的矩阵我们就能将本地/切线空寂中的法线向量转成世界或视图坐标，使它们转向到最终的贴图表面的方向。
 
 我们可以说，上个部分那个朝向正y的法线贴图错误的贴到了表面上。法线贴图被定义在切线空间中，所以一种解决问题的方式是计算出一种矩阵，把法线从切线空间变换到一个不同的空间，这样它们就能和表面法线方向对齐了：法线向量都会指向正y方向。切线空间的一大好处是我们可以为任何类型的表面计算出一个这样的矩阵，由此我们可以把切线空间的z方向和表面的法线方向对齐。
 
@@ -91,13 +89,13 @@ void main()
 
 已知上向量是表面的法线向量。右和前向量是切线(Tagent)和副切线(Bitangent)向量。下面的图片展示了一个表面的三个向量：
 
-![](../img/05/04/normal_mapping_tbn_vectors.png)
+![](http://learnopengl.com/img/advanced-lighting/normal_mapping_tbn_vectors.png)
 
 计算出切线和副切线并不像法线向量那么容易。从图中可以看到法线贴图的切线和副切线与纹理坐标的两个方向对齐。我们就是用到这个特性计算每个表面的切线和副切线的。需要用到一些数学才能得到它们；请看下图：
 
-![](../img/05/04/normal_mapping_surface_edges.png)
+![](http://learnopengl.com/img/advanced-lighting/normal_mapping_surface_edges.png)
 
-注意上图中边\(E_2\)与纹理坐标的差\(\Delta U_2\)、\(\Delta V_2\)构成一个三角形。\(\Delta U_2\)与切线向量\(T\)方向相同，而\(\Delta V_2\)与副切线向量\(B\)方向相同。这也就是说，所以我们可以将三角形的边\(E_1\)与\(E_2\)写成切线向量\(\T\)和副切线向量\(B\)的线性组合：
+上图中我们可以看到三角形的边\(E_2\)分别在切线上\(T\)和副切线上\(B\)上的纹理坐标\(\Delta U_2\)和\(\Delta V_2\)。这样我们可以把边\(E_1\)和\(E_2\)用切线向量\(T\)和副切线向量\(B\)的线性组合表示出来（译注：注意\(T\)和\(B\)都是单位长度，在\(TB\)平面中所有点的\(T\)、\(B\)坐标都在0到1之间，因此可以进行这样的组合）：
 
 $$
 E_1 = \Delta U_1T + \Delta V_1B
@@ -106,7 +104,6 @@ $$
 $$
 E_2 = \Delta U_2T + \Delta V_2B
 $$
-
 我们也可以写成这样：
 
 $$
@@ -117,7 +114,7 @@ $$
 (E_{2x}, E_{2y}, E_{2z}) = \Delta U_2(T_x, T_y, T_z) + \Delta V_2(B_x, B_y, B_z)
 $$
 
-\(E\)是两个向量位置的差，\(\Delta U\)和\(\Delta V\)是纹理坐标的差。然后我们得到两个未知数（切线\(T\)和副切线\(B\)）和两个等式。你可能想起你的代数课了，这是让我们去解\(T\)和\(B\)。
+\(E\)是两个向量位置的差，\(\Delta U\)和\(\Delta V\)是纹理坐标的差。然后我们得到两个未知数（切线*T*和副切线*B*）和两个等式。你可能想起你的代数课了，这是让我们去解\(T\)和\(B\)。
 
 上面的方程允许我们把它们写成另一种格式：矩阵乘法
 
@@ -131,7 +128,7 @@ $$
 \begin{bmatrix} \Delta U_1 & \Delta V_1 \\ \Delta U_2 & \Delta V_2 \end{bmatrix}^{-1} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix} = \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix}
 $$
 
-这样我们就可以解出\(T\)和\(B\)了。这需要我们计算出delta纹理坐标矩阵的逆矩阵。我不打算讲解计算逆矩阵的细节，但大致是把它变化为，1除以矩阵的行列式，再乘以它的伴随矩阵(Adjugate Matrix)。
+这样我们就可以解出\(T\)和\(B\)了。这需要我们计算出delta纹理坐标矩阵的逆矩阵。我不打算讲解计算逆矩阵的细节，但大致是把它变化为，1除以矩阵的行列式，再乘以它的共轭矩阵。
 
 $$
 \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix}  = \frac{1}{\Delta U_1 \Delta V_2 - \Delta U_2 \Delta V_1} \begin{bmatrix} \Delta V_2 & -\Delta V_1 \\ -\Delta U_2 & \Delta U_1 \end{bmatrix} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix}
@@ -186,16 +183,16 @@ bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y);
 bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z);
 bitangent1 = glm::normalize(bitangent1);  
   
-[...] // 对平面的第二个三角形采用类似步骤计算切线和副切线
+[...] // similar procedure for calculating tangent/bitangent for plane's second triangle
 ```
 
-我们预先计算出等式的分数部分`f`，然后把它和每个向量的元素进行相应矩阵乘法。如果你把代码和最终的等式对比你会发现，这就是直接套用。最后我们还要进行标准化，来确保切线/副切线向量最后是单位向量。
+我们预先计算出等式的分数部分f，然后把它和每个向量的元素进行相应矩阵乘法。如果你把代码和最终的等式对比你会发现，这就是直接套用。最后我们还要进行标准化，来确保切线/副切线向量最后是单位向量。
 
 因为一个三角形永远是平坦的形状，我们只需为每个三角形计算一个切线/副切线，它们对于每个三角形上的顶点都是一样的。要注意的是大多数实现通常三角形和三角形之间都会共享顶点。这种情况下开发者通常将每个顶点的法线和切线/副切线等顶点属性平均化，以获得更加柔和的效果。我们的平面的三角形之间分享了一些顶点，但是因为两个三角形相互并行，因此并不需要将结果平均化，但无论何时只要你遇到这种情况记住它就是件好事。
 
 最后的切线和副切线向量的值应该是(1, 0, 0)和(0, 1, 0)，它们和法线(0, 0, 1)组成相互垂直的TBN矩阵。在平面上显示出来TBN应该是这样的：
 
-![](../img/05/04/normal_mapping_tbn_shown.png)
+![](http://learnopengl.com/img/advanced-lighting/normal_mapping_tbn_shown.png)
 
 每个顶点定义了切线和副切线向量，我们就可以开始实现正确的法线贴图了。
 
@@ -226,19 +223,14 @@ void main()
 }
 ```
 
-我们先将所有TBN向量变换到我们所操作的坐标系中，现在是世界空间，我们可以乘以model矩阵。然后我们创建实际的TBN矩阵，直接把相应的向量应用到mat3构造器就行。注意，如果我们希望更精确的话就不要将TBN向量乘以model矩阵，而是使用法线矩阵，因为我们只关心向量的方向，不关心平移和缩放。
+我们先将所有TBN向量变换到我们所操作的坐标系中，现在是世界空间，我们可以乘以model矩阵。然后我们创建实际的TBN矩阵，直接把相应的向量应用到mat3构造器就行。注意，如果我们希望更精确的话就不要将TBN向量乘以model矩阵，而是使用法线矩阵，但我们只关心向量的方向，不会平移也和缩放这个变换。
 
-!!! Important
+从技术上讲，顶点着色器中无需副切线。所有的这三个TBN向量都是相互垂直的所以我们可以在顶点着色器中用T和N向量的叉乘，自己计算出副切线：vec3 B = cross(T, N);
+现在我们有了TBN矩阵，如果来使用它呢？基本有两种方式可以使用，我们会把这两种方式都说明一下：
 
-	从技术上讲，顶点着色器中无需副切线。所有的这三个TBN向量都是相互垂直的所以我们可以在顶点着色器中用T和N向量的叉乘，自己计算出副切线：vec3 B = cross(T, N);
-	
-现在我们有了TBN矩阵，如果来使用它呢？通常来说有两种方式使用它，我们会把这两种方式都说明一下：
-
-1. 我们直接使用TBN矩阵，这个矩阵可以把切线坐标空间的向量转换到世界坐标空间。因此我们把它传给片段着色器中，把通过采样得到的法线坐标左乘上TBN矩阵，转换到世界坐标空间中，这样所有法线和其他光照变量就在同一个坐标系中了。
-2. 我们也可以使用TBN矩阵的逆矩阵，这个矩阵可以把世界坐标空间的向量转换到切线坐标空间。因此我们使用这个矩阵左乘其他光照变量，把他们转换到切线空间，这样法线和其他光照变量再一次在一个坐标系中了。
-
-
-**我们来看看第一种情况。**我们从法线贴图采样得来的法线向量，是在切线空间表示的，尽管其他光照向量都是在世界空间表示的。把TBN传给像素着色器，我们就能将采样得来的切线空间的法线乘以这个TBN矩阵，将法线向量变换到和其他光照向量一样的参考空间中。这种方式随后所有光照计算都可以简单的理解。
+我们可以用TBN矩阵把所有向量从切线空间转到世界空间，传给像素着色器，然后把采样得到的法线用TBN矩阵从切线空间变换到世界空间；法线就处于和其他光照变量一样的空间中了。
+我们用TBN的逆矩阵把所有世界空间的向量转换到切线空间，使用这个矩阵将除法线以外的所有相关光照变量转换到切线空间中；这样法线也能和其他光照变量处于同一空间之中。
+我们来看看第一种情况。我们从法线贴图重采样得来的法线向量，是以切线空间表达的，尽管其他光照向量是以世界空间表达的。把TBN传给像素着色器，我们就能将采样得来的切线空间的法线乘以这个TBN矩阵，将法线向量变换到和其他光照向量一样的参考空间中。这种方式随后所有光照计算都可以简单的理解。
 
 把TBN矩阵发给像素着色器很简单：
 
@@ -277,13 +269,13 @@ normal = normalize(fs_in.TBN * normal);
 
 因为最后的normal现在在世界空间中了，就不用改变其他像素着色器的代码了，因为光照代码就是假设法线向量在世界空间中。
 
-**我们同样看看第二种情况。**我们用TBN矩阵的逆矩阵将所有相关的世界空间向量转变到采样所得法线向量的空间：切线空间。TBN的建构还是一样，但我们在将其发送给像素着色器之前先要求逆矩阵：
+我们同样看看第二种情况，我们用TBN矩阵的逆矩阵将所有相关的世界空间向量转变到采样所得法线向量的空间：切线空间。TBN的建构还是一样，但我们在将其发送给像素着色器之前先要求逆矩阵：
 
 ```c++
 vs_out.TBN = transpose(mat3(T, B, N));
 ```
 
-注意，这里我们使用transpose函数，而不是inverse函数。正交矩阵（每个轴既是单位向量同时相互垂直）的一大属性是一个正交矩阵的置换矩阵与它的逆矩阵相等。这个属性很重要因为逆矩阵的求得比求置换开销大；结果却是一样的。
+注意，这里我们使用transpose函数，而不是inverse函数。正交矩阵（每个轴既是单位向量同时相互垂直）的一大属性是一个正交矩阵的置换矩阵与它的逆矩阵相等。这个属性和重要因为逆矩阵的求得比求置换开销大；结果却是一样的。
 
 在像素着色器中我们不用对法线向量变换，但我们要把其他相关向量转换到切线空间，它们是lightDir和viewDir。这样每个向量还是在同一个空间（切线空间）中了。
 
@@ -337,13 +329,13 @@ void main()
 ```c++
 glm::mat4 model;
 model = glm::rotate(model, (GLfloat)glfwGetTime() * -10, glm::normalize(glm::vec3(1.0, 0.0, 1.0)));
-glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
+glUniformMatrix4fv(modelLoc 1, GL_FALSE, glm::value_ptr(model));
 RenderQuad();
 ```
 
 看起来是正确的法线贴图：
 
-![](../img/05/04/normal_mapping_correct_tangent.png)
+![](http://learnopengl.com/img/advanced-lighting/normal_mapping_correct_tangent.png)
 
 你可以在这里找到[源代码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/normal_mapping)、[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/normal_mapping&type=vertex)和[像素](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/normal_mapping&type=fragment)着色器。
 
@@ -372,7 +364,9 @@ vertex.Tangent = vector;
 然后，你还必须更新模型加载器，用以从带纹理模型中加载法线贴图。wavefront的模型格式（.obj）导出的法线贴图有点不一样，Assimp的aiTextureType_NORMAL并不会加载它的法线贴图，而aiTextureType_HEIGHT却能，所以我们经常这样加载它们：
 
 ```c++
-vector normalMaps = loadMaterialTextures(material, aiTextureType_HEIGHT, "texture_normal");
+vector<Texture> specularMaps = this->loadMaterialTextures(
+    material, aiTextureType_HEIGHT, "texture_normal"
+);
 ```
  
 
@@ -380,13 +374,13 @@ vector normalMaps = loadMaterialTextures(material, aiTextureType_HEIGHT, "textur
 
 运行程序，用新的模型加载器，加载一个有specular和法线贴图的模型，看起来会像这样：
 
-![](../img/05/04/normal_mapping_complex_compare.png)
+![](http://learnopengl.com/img/advanced-lighting/normal_mapping_complex_compare.png)
 
 你可以看到在没有太多点的额外开销的情况下法线贴图难以置信地提升了物体的细节。
 
 使用法线贴图也是一种提升你的场景的表现的重要方式。在使用法线贴图之前你不得不使用相当多的顶点才能表现出一个更精细的网格，但使用了法线贴图我们可以使用更少的顶点表现出同样丰富的细节。下图来自Paolo Cignoni，图中对比了两种方式：
 
-![](../img/05/04/normal_mapping_comparison.png)
+![](http://learnopengl.com/img/advanced-lighting/normal_mapping_comparison.png)
 
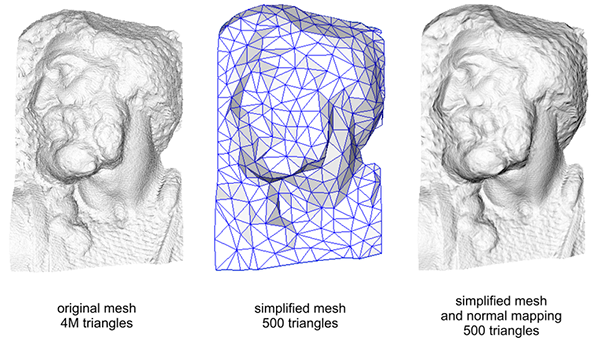
 高精度网格和使用法线贴图的低精度网格几乎区分不出来。所以法线贴图不仅看起来漂亮，它也是一个将高精度多边形转换为低精度多边形而不失细节的重要工具。
 
@@ -400,7 +394,7 @@ vector normalMaps = loadMaterialTextures(material, aiTextureType_HEIGHT, "textur
 
 ```c++
 vec3 T = normalize(vec3(model * vec4(tangent, 0.0)));
-vec3 N = normalize(vec3(model * vec4(normal, 0.0)));
+vec3 N = normalize(vec3(model * vec4(tangent, 0.0)));
 // re-orthogonalize T with respect to N
 T = normalize(T - dot(T, N) * N);
 // then retrieve perpendicular vector B with the cross product of T and N

docs/05 Advanced Lighting/05 Parallax Mapping.md

@@ -6,37 +6,33 @@
 翻译     | [Django](http://bullteacher.com/)
 校对     | 暂无
 
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
 视差贴图(Parallax Mapping)技术和法线贴图差不多，但它有着不同的原则。和法线贴图一样视差贴图能够极大提升表面细节，使之具有深度感。它也是利用了视错觉，然而对深度有着更好的表达，与法线贴图一起用能够产生难以置信的效果。视差贴图和光照无关，我在这里是作为法线贴图的技术延续来讨论它的。需要注意的是在开始学习视差贴图之前强烈建议先对法线贴图，特别是切线空间有较好的理解。
 
-视差贴图属于位移贴图(Displacement Mapping)技术的一种，它对根据储存在纹理中的几何信息对顶点进行位移或偏移。一种实现的方式是比如有1000个顶点，根据纹理中的数据对平面特定区域的顶点的高度进行位移。这样的每个纹理像素包含了高度值纹理叫做高度贴图。一张简单的砖块表面的高度贴图如下所示：
+视差贴图属于位移贴图(Displacement Mapping)技术的一种，它对根据储存在纹理中的几何信息对顶点进行位移或偏移。一种实现的方式是比如有1000个顶点，更具纹理中的数据对平面特定区域的顶点的高度进行位移。这样的每个纹理像素包含了高度值纹理叫做高度贴图。一张简单的砖块表面的告诉贴图如下所示：
 
-![](../img/05/05/parallax_mapping_height_map.png)
+![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_height_map.png)
 
 整个平面上的每个顶点都根据从高度贴图采样出来的高度值进行位移，根据材质的几何属性平坦的平面变换成凹凸不平的表面。例如一个平坦的平面利用上面的高度贴图进行置换能得到以下结果：
 
-![](../img/05/05/parallax_mapping_plane_heightmap.png)
+![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_plane_heightmap.png)
 
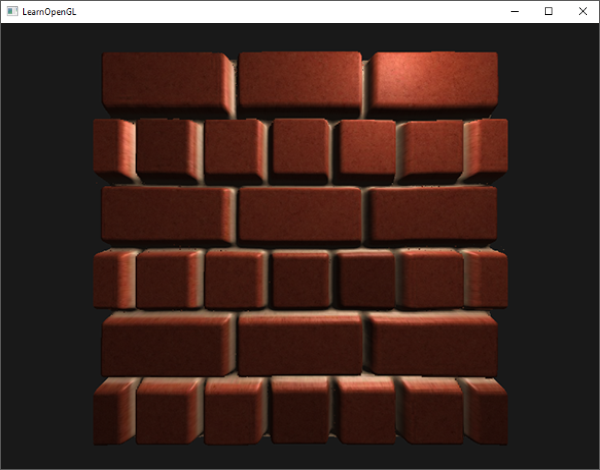
 置换顶点有一个问题就是平面必须由很多顶点组成才能获得具有真实感的效果，否则看起来效果并不会很好。一个平坦的表面上有1000个顶点计算量太大了。我们能否不用这么多的顶点就能取得相似的效果呢？事实上，上面的表面就是用6个顶点渲染出来的（两个三角形）。上面的那个表面使用视差贴图技术渲染，位移贴图技术不需要额外的顶点数据来表达深度，它像法线贴图一样采用一种聪明的手段欺骗用户的眼睛。
 
 视差贴图背后的思想是修改纹理坐标使一个fragment的表面看起来比实际的更高或者更低，所有这些都根据观察方向和高度贴图。为了理解它如何工作，看看下面砖块表面的图片：
 
-![](../img/05/05/parallax_mapping_plane_height.png)
+[](http://learnopengl.com/img/advanced-lighting/parallax_mapping_plane_height.png)
 
 这里粗糙的红线代表高度贴图中的数值的立体表达，向量\(\color{orange}{\bar{V}}\)代表观察方向。如果平面进行实际位移，观察者会在点\(\color{blue}B\)看到表面。然而我们的平面没有实际上进行位移，观察方向将在点\(\color{green}A\)与平面接触。视差贴图的目的是，在\(\color{green}A\)位置上的fragment不再使用点\(\color{green}A\)的纹理坐标而是使用点\(\color{blue}B\)的。随后我们用点\(\color{blue}B\)的纹理坐标采样，观察者就像看到了点\(\color{blue}B\)一样。
 
 这个技巧就是描述如何从点\(\color{green}A\)得到点\(\color{blue}B\)的纹理坐标。视差贴图尝试通过对从fragment到观察者的方向向量\(\color{orange}{\bar{V}}\)进行缩放的方式解决这个问题，缩放的大小是\(\color{green}A\)处fragment的高度。所以我们将\(\color{orange}{\bar{V}}\)的长度缩放为高度贴图在点\(\color{green}A\)处\(\color{green}{H(A)}\)采样得来的值。下图展示了经缩放得到的向量\(\color{brown}{\bar{P}}\)：
 
-![](../img/05/05/parallax_mapping_scaled_height.png)
+![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_scaled_height.png)
 
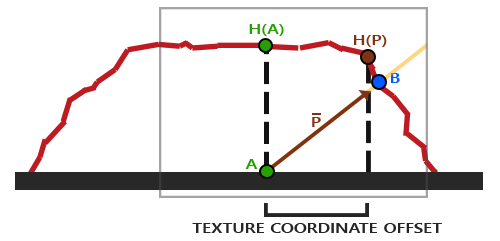
 我们随后选出\(\color{brown}{\bar{P}}\)以及这个向量与平面对齐的坐标作为纹理坐标的偏移量。这能工作是因为向量\(\color{brown}{\bar{P}}\)是使用从高度贴图得到的高度值计算出来的，所以一个fragment的高度越高位移的量越大。
 
 这个技巧在大多数时候都没问题，但点\(\color{blue}B\)是粗略估算得到的。当表面的高度变化很快的时候，看起来就不会真实，因为向量\(\color{brown}{\bar{P}}\)最终不会和\(\color{blue}B\)接近，就像下图这样：
 
-![](../img/05/05/parallax_mapping_incorrect_p.png)
+![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_incorrect_p.png)
 
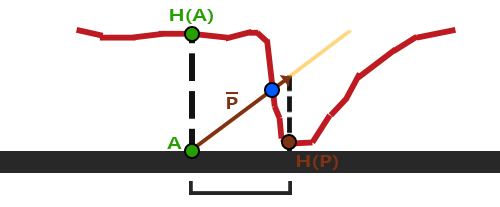
 视差贴图的另一个问题是，当表面被任意旋转以后很难指出从\(\color{brown}{\bar{P}}\)获取哪一个坐标。我们在视差贴图中使用了另一个坐标空间，这个空间\(\color{brown}{\bar{P}}\)向量的x和y元素总是与纹理表面对齐。如果你看了法线贴图教程，你也许猜到了，我们实现它的方法，是的，我们还是在切线空间中实现视差贴图。
 
@@ -46,11 +42,11 @@
 
 ## 视差贴图
 
-我们将使用一个简单的2D平面，在把它发送给GPU之前我们先计算它的切线和副切线向量；和法线贴图教程做的差不多。我们将向平面贴diffuse纹理、法线贴图以及一个位移贴图，你可以点击链接下载。这个例子中我们将视差贴图和法线贴图连用。因为视差贴图生成表面位移了的幻觉，当光照不匹配时这种幻觉就被破坏了。法线贴图通常根据高度贴图生成，法线贴图和高度贴图一起用能保证光照能和位移相匹配。
+我们将使用一个简单的2D平面，在把它发送给GPU之前我们先计算它的切线和副切线向量；和法线贴图教程做的差不多。我们将向平面贴diffuse纹理、法线贴图以及一个位移贴图，你可以点击链接下载。这个例子中我们将视差贴图和法线贴图连用。因为视差贴图生成表面位移了的幻觉，当光照不匹配时这种幻觉就被破坏了。法线贴图通常根据高度贴图生成，法线贴图和高度贴图一起用能保证光照能和位移想匹配。
 
 你可能已经注意到，上面链接上的那个位移贴图和教程一开始的那个高度贴图相比是颜色是相反的。这是因为使用反色高度贴图（也叫深度贴图）去模拟深度比模拟高度更容易。下图反映了这个轻微的改变：
 
-![](../img/05/05/parallax_mapping_depth.png)
+![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_depth.png)
 
 我们再次获得\(\color{green}A\)和\(\color{blue}B\)，但是这次我们用向量\(\color{orange}{\bar{V}}\)减去点\(\color{green}A\)的纹理坐标得到\(\color{brown}{\bar{P}}\)。我们通过在着色器中用1.0减去采样得到的高度贴图中的值来取得深度值，而不再是高度值，或者简单地在图片编辑软件中把这个纹理进行反色操作，就像我们对连接中的那个深度贴图所做的一样。
 
@@ -135,7 +131,7 @@ void main()
 }
 ```
 
-我们定义了一个叫做ParallaxMapping的函数，它把fragment的纹理坐标和切线空间中的fragment到观察者的方向向量为输入。这个函数返回经位移的纹理坐标。然后我们使用这些经位移的纹理坐标进行diffuse和法线贴图的采样。最后fragment的diffuse颜色和法线向量就正确的对应于表面的经位移的位置上了。
+我们定义了一个叫做ParallaxMapping的函数，它把fragment的纹理坐标作和切线空间中的fragment到观察者的方向向量为输入。这个函数返回经位移的纹理坐标。然后我们使用这些经位移的纹理坐标进行diffuse和法线贴图的采样。最后fragment的diffuse颜色和法线向量就正确的对应于表面的经位移的位置上了。
 
 我们来看看ParallaxMapping函数的内部：
 
@@ -143,20 +139,20 @@ void main()
 vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir)
 { 
     float height =  texture(depthMap, texCoords).r;    
-    vec2 p = viewDir.xy / viewDir.z * (height * height_scale);
+    vec3 p = viewDir.xy / viewDir.z * (height * height_scale);
     return texCoords - p;    
 }
 ```
 
-这个相对简单的函数是我们所讨论过的内容的直接表述。我们用本来的纹理坐标texCoords从高度贴图中来采样，得到当前fragment的高度\(\color{green}{H(A)}\)。然后计算出\(\color{brown}{\bar{P}}\)，x和y元素在切线空间中，viewDir向量除以它的z元素，用fragment的高度对它进行缩放。我们同时引入额一个height_scale的uniform，来进行一些额外的控制，因为视差效果如果没有一个缩放参数通常会过于强烈。然后我们用\(\color{brown}{\bar{P}}\)减去纹理坐标来获得最终的经过位移纹理坐标。
+这个相对简单的函数是我们所讨论过的内容的直接表述。我们用本来的纹理坐标texCoords从高度贴图中来采样出当前fragment高度\(\color{green}{H(A)}\)。然后计算出\(\color{brown}{\bar{P}}\)，x和y元素在切线空间中，viewDir向量除以它的z元素，用fragment的高度对它进行缩放。我们同时引入额一个height_scale的uniform，来进行一些额外的控制，因为视差效果如果没有一个缩放参数通常会过于强烈。然后我们用\(\color{brown}{\bar{P}}\)减去纹理坐标来获得最终的经过位移纹理坐标。
 
-有一个地方需要注意，就是viewDir.xy除以viewDir.z那里。因为viewDir向量是经过了标准化的，viewDir.z会在0.0到1.0之间的某处。当viewDir大致平行于表面时，它的z元素接近于0.0，除法会返回比viewDir垂直于表面的时候更大的\(\color{brown}{\bar{P}}\)向量。所以，从本质上，相比正朝向表面，当带有角度地看向平面时，我们会更大程度地缩放\(\color{brown}{\bar{P}}\)的大小，从而增加纹理坐标的偏移；这样做在视角上会获得更大的真实度。
+有一个地方需要注意，就是viewDir.xy除以viewDir.z那里。因为viewDir向量是经过了标准化的，viewDir.z会在0.0到1.0之间的某处。当viewDir大致平行于表面时，它的z元素接近于0.0，除法会返回比viewDir垂直于表面的时候更大的\(\color{brown}{\bar{P}}\)向量。所以基本上我们增加了\(\color{brown}{\bar{P}}\)的大小，当以一个角度朝向一个表面相比朝向顶部时它对纹理坐标会进行更大程度的缩放；这回在角上获得更大的真实度。
 
-有些人更喜欢不在等式中使用viewDir.z，因为普通的视差贴图会在角度上产生不尽如人意的结果；这个技术叫做有偏移量限制的视差贴图（Parallax Mapping with Offset Limiting）。选择哪一个技术是个人偏好问题，但我倾向于普通的视差贴图。
+有些人更喜欢在等式中不使用viewDir.z，因为普通的视差贴图会在角上产生不想要的结果；这个技术叫做有偏移量限制的视差贴图（Parallax Mapping with Offset Limiting）。选择哪一个技术是个人偏好问题，但我倾向于普通的视差贴图。
 
-最后的纹理坐标随后被用来进行采样（diffuse和法线）贴图，下图所展示的位移效果中height_scale等于0.1：
+最后的纹理坐标随后被用来进行采样（diffuse和法线）贴图，下图所展示的位移效果中height_scale等于1：
 
-![](../img/05/05/parallax_mapping.png)
+![](http://learnopengl.com/img/advanced-lighting/parallax_mapping.png)
 
 这里你会看到只用法线贴图和与视差贴图相结合的法线贴图的不同之处。因为视差贴图尝试模拟深度，它实际上能够根据你观察它们的方向使砖块叠加到其他砖块上。
 
@@ -170,23 +166,21 @@ if(texCoords.x > 1.0 || texCoords.y > 1.0 || texCoords.x < 0.0 || texCoords.y <
 
 丢弃了超出默认范围的纹理坐标的所有fragment，视差贴图的表面边缘给出了正确的结果。注意，这个技巧不能在所有类型的表面上都能工作，但是应用于平面上它还是能够是平面看起来真的进行位移了：
 
-![](../img/05/05/parallax_mapping_edge_fix.png)
+![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_edge_fix.png)
 
 你可以在这里找到[源代码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping)，以及[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping&type=vertex)和[像素](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping&type=fragment)着色器。
 
 看起来不错，运行起来也很快，因为我们只要给视差贴图提供一个额外的纹理样本就能工作。当从一个角度看过去的时候，会有一些问题产生（和法线贴图相似），陡峭的地方会产生不正确的结果，从下图你可以看到：
 
-![](../img/05/05/parallax_mapping_issues.png)
+![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_issues.png)
 
 问题的原因是这只是一个大致近似的视差映射。还有一些技巧让我们在陡峭的高度上能够获得几乎完美的结果，即使当以一定角度观看的时候。例如，我们不再使用单一样本，取而代之使用多样本来找到最近点\(\color{blue}B\)会得到怎样的结果？
 
 ## 陡峭视差映射
 
-陡峭视差映射(Steep Parallax Mapping)是视差映射的扩展，原则是一样的，但不是使用一个样本而是多个样本来确定向量\(\color{brown}{\bar{P}}\)到\(\color{blue}B\)。即使在陡峭的高度变化的情况下，它也能得到更好的结果，原因在于该技术通过增加采样的数量提高了精确性。
+陡峭视差映射(Steep Parallax Mapping)是视差映射的扩展，原则是一样的，但不是使用一个样本而是多个样本来确定向量\(\color{brown}{\bar{P}}\)到\(\color{blue}B\)。它能得到更好的结果，它将总深度范围分布到同一个深度/高度的多个层中。从每个层中我们沿着\(\color{brown}{\bar{P}}\)方向移动采样纹理坐标，直到我们找到了一个采样得到的低于当前层的深度值的深度值。看看下面的图片：
 
-陡峭视差映射的基本思想是将总深度范围划分为同一个深度/高度的多个层。从每个层中我们沿着\(\color{brown}{\bar{P}}\)方向移动采样纹理坐标，直到我们找到一个采样低于当前层的深度值。看看下面的图片：
-
-![](../img/05/05/parallax_mapping_steep_parallax_mapping_diagram.png)
+![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_steep_parallax_mapping_diagram.png)
 
 我们从上到下遍历深度层，我们把每个深度层和储存在深度贴图中的它的深度值进行对比。如果这个层的深度值小于深度贴图的值，就意味着这一层的\(\color{brown}{\bar{P}}\)向量部分在表面之下。我们继续这个处理过程直到有一层的深度高于储存在深度贴图中的值：这个点就在（经过位移的）表面下方。
 
@@ -205,7 +199,7 @@ vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir)
     float currentLayerDepth = 0.0;
     // the amount to shift the texture coordinates per layer (from vector P)
     vec2 P = viewDir.xy * height_scale; 
-    vec2 deltaTexCoords = P / numLayers;
+    float deltaTexCoords = P / numLayers;
   
     [...]     
 }
@@ -230,7 +224,7 @@ while(currentLayerDepth < currentDepthMapValue)
     currentLayerDepth += layerDepth;  
 }
  
-return currentTexCoords;
+return texCoords - currentTexCoords;
 
 ```
 
@@ -238,7 +232,7 @@ return currentTexCoords;
 
 有10个样本砖墙从一个角度看上去就已经很好了，但是当有一个强前面展示的木制表面一样陡峭的表面时，陡峭的视差映射的威力就显示出来了：
 
-![](../img/05/05/parallax_mapping_steep_parallax_mapping.png)
+![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_steep_parallax_mapping.png)
 
 我们可以通过对视差贴图的一个属性的利用，对算法进行一点提升。当垂直看一个表面的时候纹理时位移比以一定角度看时的小。我们可以在垂直看时使用更少的样本，以一定角度看时增加样本数量：
 
@@ -254,7 +248,7 @@ float numLayers = mix(maxLayers, minLayers, abs(dot(vec3(0.0, 0.0, 1.0), viewDir
 
 陡峭视差贴图同样有自己的问题。因为这个技术是基于有限的样本数量的，我们会遇到锯齿效果以及图层之间有明显的断层：
 
-![](../img/05/05/parallax_mapping_steep_artifact.png)
+![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_steep_artifact.png)
 
 我们可以通过增加样本的方式减少这个问题，但是很快就会花费很多性能。有些旨在修复这个问题的方法：不适用低于表面的第一个位置，而是在两个接近的深度层进行插值找出更匹配\(\color{blue}B\)的。
 
@@ -266,7 +260,7 @@ float numLayers = mix(maxLayers, minLayers, abs(dot(vec3(0.0, 0.0, 1.0), viewDir
 
 视差遮蔽映射(Parallax Occlusion Mapping)和陡峭视差映射的原则相同，但不是用触碰的第一个深度层的纹理坐标，而是在触碰之前和之后，在深度层之间进行线性插值。我们根据表面的高度距离啷个深度层的深度层值的距离来确定线性插值的大小。看看下面的图片就能了解它是如何工作的：
 
-![](../img/05/05/parallax_mapping_parallax_occlusion_mapping_diagram.png)
+[](http://learnopengl.com/img/advanced-lighting/parallax_mapping_parallax_occlusion_mapping_diagram.png)
 
 你可以看到大部分和陡峭视差映射一样，不一样的地方是有个额外的步骤，两个深度层的纹理坐标围绕着交叉点的线性插值。这也是近似的，但是比陡峭视差映射更精确。
 
@@ -293,15 +287,15 @@ return finalTexCoords;
 
 视差遮蔽映射的效果非常好，尽管有一些可以看到的轻微的不真实和锯齿的问题，这仍是一个好交易，因为除非是放得非常大或者观察角度特别陡，否则也看不到。
 
-![](../img/05/05/parallax_mapping_parallax_occlusion_mapping.png)
+![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_parallax_occlusion_mapping.png)
 
 你可以在这里找到[源代码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping)，及其[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping&type=vertex)和[像素](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping_occlusion&type=fragment)着色器。
 
-视差贴图是提升场景细节非常好的技术，但是使用的时候还是要考虑到它会带来一点不自然。大多数时候视差贴图用在地面和墙壁表面，这种情况下查明表面的轮廓并不容易，同时观察角度往往趋向于垂直于表面。这样视差贴图的不自然也就很难能被注意到了，对于提升物体的细节可以起到难以置信的效果。
+视差贴图是提升场景细节非常好的技术，但是使用的时候还是要考虑到它会带来一点不自然。大多数时候视差贴图用在地面和墙壁表面，这种情况下查明表面的轮廓并不容易，同时观察角度往往趋向于垂直于表面。这样视差贴图的不自然也就很难能被注意到了，对于提升物体的细节可以祈祷难以置信的效果。
 
  
 
 ## 附加资源
 
 - [Parallax Occlusion Mapping in GLSL](http://sunandblackcat.com/tipFullView.php?topicid=28)：sunandblackcat.com上的视差贴图教程。
-- [How Parallax Displacement Mapping Works](https://www.youtube.com/watch?v=xvOT62L-fQI)：TheBennyBox的关于视差贴图原理的视频教程。
+- [How Parallax Displacement Mapping Works](https://www.youtube.com/watch?v=xvOT62L-fQI)：TheBennyBox的关于视差贴图原理的视频教程。

docs/05 Advanced Lighting/06 HDR.md

@@ -3,16 +3,12 @@
 原文     | [HDR](http://learnopengl.com/#!Advanced-Lighting/HDR)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
+翻译     | Meow J
 校对     | 暂无
 
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
 一般来说，当存储在帧缓冲(Framebuffer)中时，亮度和颜色的值是默认被限制在0.0到1.0之间的。这个看起来无辜的语句使我们一直将亮度与颜色的值设置在这个范围内，尝试着与场景契合。这样是能够运行的，也能给出还不错的效果。但是如果我们遇上了一个特定的区域，其中有多个亮光源使这些数值总和超过了1.0，又会发生什么呢？答案是这些片段中超过1.0的亮度或者颜色值会被约束在1.0，从而导致场景混成一片，难以分辨：
 
-![](../img/05/06/hdr_clamped.png)
+![](http://learnopengl.com/img/advanced-lighting/hdr_clamped.png)
 
 这是由于大量片段的颜色值都非常接近1.0，在很大一个区域内每一个亮的片段都有相同的白色。这损失了很多的细节，使场景看起来非常假。
 
@@ -22,9 +18,9 @@
 
 HDR原本只是被运用在摄影上，摄影师对同一个场景采取不同曝光拍多张照片，捕捉大范围的色彩值。这些图片被合成为HDR图片，从而综合不同的曝光等级使得大范围的细节可见。看下面这个例子，左边这张图片在被光照亮的区域充满细节，但是在黑暗的区域就什么都看不见了；但是右边这张图的高曝光却可以让之前看不出来的黑暗区域显现出来。
 
-![](../img/05/06/hdr_image.png)
+![](http://learnopengl.com/img/advanced-lighting/hdr_image.png)
 
-这与我们眼睛工作的原理非常相似，也是HDR渲染的基础。当光线很弱的时候，人眼会自动调整从而使过暗和过亮的部分变得更清晰，就像人眼有一个能自动根据场景亮度调整的自动曝光滑块。
+这与我们眼睛工作的原理非常相似，也是HDR渲染的基础。当光线很弱的啥时候，人眼会自动调整从而使过暗和过亮的部分变得更清晰，就像人眼有一个能自动根据场景亮度调整的自动曝光滑块。
 
 HDR渲染和其很相似，我们允许用更大范围的颜色值渲染从而获取大范围的黑暗与明亮的场景细节，最后将所有HDR值转换成在[0.0, 1.0]范围的LDR(Low Dynamic Range,低动态范围)。转换HDR值到LDR值得过程叫做色调映射(Tone Mapping)，现在现存有很多的色调映射算法，这些算法致力于在转换过程中保留尽可能多的HDR细节。这些色调映射算法经常会包含一个选择性倾向黑暗或者明亮区域的参数。
 
@@ -90,7 +86,7 @@ void main()
 
 这里我们直接采样了浮点颜色缓冲并将其作为片段着色器的输出。然而，这个2D四边形的输出是被直接渲染到默认的帧缓冲中，导致所有片段着色器的输出值被约束在0.0到1.0间，尽管我们已经有了一些存在浮点颜色纹理的值超过了1.0。
 
-![](../img/05/06/hdr_direct.png)
+![](http://learnopengl.com/img/advanced-lighting/hdr_direct.png)
 
 很明显，在隧道尽头的强光的值被约束在1.0，因为一大块区域都是白色的，过程中超过1.0的地方损失了所有细节。因为我们直接转换HDR值到LDR值，这就像我们根本就没有应用HDR一样。为了修复这个问题我们需要做的是无损转化所有浮点颜色值回0.0-1.0范围中。我们需要应用到色调映射。
 
@@ -98,7 +94,7 @@ void main()
 
 色调映射(Tone Mapping)是一个损失很小的转换浮点颜色值至我们所需的LDR[0.0, 1.0]范围内的过程，通常会伴有特定的风格的色平衡(Stylistic Color Balance)。
 
-最简单的色调映射算法是Reinhard色调映射，它涉及到分散整个HDR颜色值到LDR颜色值上，所有的值都有对应。Reinhard色调映射算法平均地将所有亮度值分散到LDR上。我们将Reinhard色调映射应用到之前的片段着色器上，并且为了更好的测量加上一个Gamma校正过滤(包括SRGB纹理的使用)：
+最简单的色调映射算法是Reinhard色调映射，它涉及到分散整个HDR颜色值到LDR颜色值上，所有的值都有对应。Reinhard色调映射算法平均得将所有亮度值分散到LDR上。我们将Reinhard色调映射应用到之前的片段着色器上，并且为了更好的测量加上一个Gamma校正过滤(包括SRGB纹理的使用)：
 
 ```c++
 void main()
@@ -117,9 +113,9 @@ void main()
 
 有了Reinhard色调映射的应用，我们不再会在场景明亮的地方损失细节。当然，这个算法是倾向明亮的区域的，暗的区域会不那么精细也不那么有区分度。
 
-![](../img/05/06/hdr_reinhard.png)
+![](http://learnopengl.com/img/advanced-lighting/hdr_reinhard.png)
 
-现在你可以看到在隧道的尽头木头纹理变得可见了。用了这个非常简单地色调映射算法，我们可以合适的看到存在浮点帧缓冲中整个范围的HDR值，使我们能在不丢失细节的前提下，对场景光照有精确的控制。
+现在你可以看到在隧道的尽头木头纹理变得可见了。用了这个非常简单地色调映射算法，我们可以合适的看到存在浮点帧缓冲中整个范围的HDR值，给我们对于无损场景光照精确的控制。
 
 另一个有趣的色调映射应用是曝光(Exposure)参数的使用。你可能还记得之前我们在介绍里讲到的，HDR图片包含在不同曝光等级的细节。如果我们有一个场景要展现日夜交替，我们当然会在白天使用低曝光，在夜间使用高曝光，就像人眼调节方式一样。有了这个曝光参数，我们可以去设置可以同时在白天和夜晚不同光照条件工作的光照参数，我们只需要调整曝光参数就行了。
 
@@ -144,7 +140,7 @@ void main()
 
 在这里我们将`exposure`定义为默认为1.0的`uniform`，从而允许我们更加精确设定我们是要注重黑暗还是明亮的区域的HDR颜色值。举例来说，高曝光值会使隧道的黑暗部分显示更多的细节，然而低曝光值会显著减少黑暗区域的细节，但允许我们看到更多明亮区域的细节。下面这组图片展示了在不同曝光值下的通道：
 
-![](../img/05/06/hdr_exposure.png)
+![](http://learnopengl.com/img/advanced-lighting/hdr_exposure.png)
 
 这个图片清晰地展示了HDR渲染的优点。通过改变曝光等级，我们可以看见场景的很多细节，而这些细节可能在LDR渲染中都被丢失了。比如说隧道尽头，在正常曝光下木头结构隐约可见，但用低曝光木头的花纹就可以清晰看见了。对于近处的木头花纹来说，在高曝光下会能更好的看见。
 
@@ -152,11 +148,11 @@ void main()
 
 ### HDR拓展
 
-在这里展示的两个色调映射算法仅仅是大量(更先进)的色调映射算法中的一小部分，这些算法各有长短。一些色调映射算法倾向于特定的某种颜色/强度，也有一些算法同时显示低高曝光颜色从而能够显示更加多彩和精细的图像。也有一些技巧被称作自动曝光调整(Automatic Exposure Adjustment)或者叫人眼适应(Eye Adaptation)技术，它能够检测前一帧场景的亮度并且缓慢调整曝光参数模仿人眼使得场景在黑暗区域逐渐变亮或者在明亮区域逐渐变暗。
+在这里展示的两个色调映射算法仅仅是大量(更先进)的色调映射算法中的一小部分，这些算法各有长短.一些色调映射算法倾向于特定的某种颜色/强度，也有一些算法同时显示低于高曝光颜色从而能够显示更加多彩和精细的图像。也有一些技巧被称作自动曝光调整(Automatic Exposure Adjustment)或者叫人眼适应(Eye Adaptation)技术，它能够检测前一帧场景的亮度并且缓慢调整曝光参数模仿人眼使得场景在黑暗区域逐渐变亮或者在明亮区域逐渐变暗，
 
-HDR渲染的真正优点在庞大和复杂的场景中应用复杂光照算法会被显示出来，但是出于教学目的创建这样复杂的演示场景是很困难的，这个教程用的场景是很小的，而且缺乏细节。但是如此简单的演示也是能够显示出HDR渲染的一些优点：在明亮和黑暗区域无细节损失，因为它们可以通过色调映射重新获得；多个光照的叠加不会导致亮度被截断的区域的出现，光照可以被设定为它们原来的亮度值而不是被LDR值限制。而且，HDR渲染也使一些有趣的效果更加可行和真实; 其中一个效果叫做泛光(Bloom)，我们将在下一节讨论。
+HDR渲染的真正优点在庞大和复杂的场景中应用复杂光照算法会被显示出来，但是出于教学目的创建这样复杂的演示场景是很困难的，这个教程用的场景是很小的，而且缺乏细节。但是如此简单的演示也是能够显示出HDR渲染的一些优点：在明亮和黑暗区域无细节损失，因为它们可以由色调映射重新获取；多个光照的叠加不会导致亮度被约束的区域；光照可以被设定为他们原来的亮度而不是被LDR值限定。而且，HDR渲染也使一些有趣的效果更加可行和真实; 其中一个效果叫做泛光(Bloom)，我们将在下一节讨论他。
 
 ## 附加资源
 
 - [如果泛光效果不被应用HDR渲染还有好处吗？](http://gamedev.stackexchange.com/questions/62836/does-hdr-rendering-have-any-benefits-if-bloom-wont-be-applied): 一个StackExchange问题，其中有一个答案非常详细地解释HDR渲染的好处。
-- [什么是色调映射? 它与HDR有什么联系？](http://photo.stackexchange.com/questions/7630/what-is-tone-mapping-how-does-it-relate-to-hdr): 另一个非常有趣的答案，用了大量图片解释色调映射。
+- [什么是色调映射? 它与HDR有什么联系？](http://photo.stackexchange.com/questions/7630/what-is-tone-mapping-how-does-it-relate-to-hdr): 另一个非常有趣的答案，用了大量图片解释色调映射。

docs/05 Advanced Lighting/07 Bloom.md

@@ -4,58 +4,54 @@
       ---|---
 作者     | JoeyDeVries
 翻译     | [Django](http://bullteacher.com/)
-校对     | gjy_1992, [AoZhang](https://github.com/SuperAoao)
+校对     | gjy_1992
 
-!!! note
+明亮的光源和区域经常很难向观察者表达出来，因为监视器的亮度范围是有限的。一种区分明亮光源的方式是使它们在监视器上发出光芒，光源的的光芒向四周发散。这样观察者就会产生光源或亮区的确是强光区。（译注：这个问题的提出简单来说是为了解决这样的问题：例如有一张在阳光下的白纸，白纸在监视器上显示出是出白色，而前方的太阳也是纯白色的，所以基本上白纸和太阳就是一样的了，给太阳加一个光晕，这样太阳看起来似乎就比白纸更亮了）
 
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
+光晕效果可以使用一个后处理特效泛光来实现。泛光使所有明亮区域产生光晕效果。下面是一个使用了和没有使用光晕的对比（图片生成自虚幻引擎）：
 
-明亮的光源和区域经常很难向观察者表达出来，因为显示器的亮度范围是有限的。一种在显示器上区分明亮光源的方式是使它们发出光芒，光芒从光源向四周发散。这有效地给观众一种这些光源或明亮的区域非常亮的错觉。（译注：这个问题的提出简单来说是为了解决这样的问题：例如有一张在阳光下的白纸，白纸在显示器上显示出是出白色，而前方的太阳也是纯白色的，所以基本上白纸和太阳就是一样的了，给太阳加一个光晕，这样太阳看起来似乎就比白纸更亮了）
+![](http://learnopengl.com/img/advanced-lighting/bloom_example.png)
 
-这种光流，或发光效果，是通过一种叫做泛光(Bloom)的后期处理效果来实现的。泛光使场景中所有明亮的区域都具有类似发光的效果。下面是带有或不带有辉光的场景示例(图片由Epic Games提供)：
+Bloom是我们能够注意到一个明亮的物体真的有种明亮的感觉。泛光可以极大提升场景中的光照效果，并提供了极大的效果提升，尽管做到这一切只需一点改变。
 
-![](../img/05/07/bloom_example.png)
+Bloom和HDR结合使用效果很好。常见的一个误解是HDR和泛光是一样的，很多人认为两种技术是可以互换的。但是它们是两种不同的技术，用于各自不同的目的上。可以使用默认的8位精确度的帧缓冲，也可以在不使用泛光效果的时候，使用HDR。只不过在有了HDR之后再实现泛光就更简单了。
 
-泛光提供了一种针对物体明亮度的视觉效果。当用优雅微妙的方式实现泛光效果(有些游戏完全没能做到)，将会显著增强您的场景光照并能提供更加有张力的效果。
-
-泛光和HDR结合使用效果最好。很多人以为HDR和泛光是一样的，认为两种技术是可以互换的，这是一种常见误解。它们是两种完全不同的技术，用于各自不同的目的。可以使用默认的8位精确度的帧缓冲来实现泛光效果，也可以只使用HDR效果而不使用泛光效果。只不过在有了HDR之后再实现泛光就更简单了(正如我们稍后会看到的)。
-
-为实现泛光，我们像平时那样渲染一个有光场景，提取出场景的HDR颜色缓冲以及只有这个场景明亮区域可见的图片。然后对提取的亮度图像进行模糊处理，并将结果添加到原始HDR场景图像的上面。
+为实现泛光，我们像平时那样渲染一个有光场景，提取出场景的HDR颜色缓冲以及只有这个场景明亮区域可见的图片。被提取的带有亮度的图片接着被模糊，结果被添加到HDR场景上面。
 
 我们来一步一步解释这个处理过程。我们在场景中渲染一个带有4个立方体形式不同颜色的明亮的光源。带有颜色的发光立方体的亮度在1.5到15.0之间。如果我们将其渲染至HDR颜色缓冲，场景看起来会是这样的：
 
-![](../img/05/07/bloom_scene.png)
+![](http://learnopengl.com/img/advanced-lighting/bloom_scene.png)
 
 我们得到这个HDR颜色缓冲纹理，提取所有超出一定亮度的fragment。这样我们就会获得一个只有fragment超过了一定阈限的颜色区域：
 
-![](../img/05/07/bloom_extracted.png)
+![](http://learnopengl.com/img/advanced-lighting/bloom_extracted.png)
 
-我们将这个超过一定亮度阈限的纹理进行模糊处理。泛光效果的强度很大程度上是由模糊过滤器的范围和强度决定的。
+我们将这个超过一定亮度阈限的纹理进行模糊。泛光效果的强度很大程度上被模糊过滤器的范围和强度所决定。
 
-![](../img/05/07/bloom_blurred.png)
+![](http://learnopengl.com/img/advanced-lighting/bloom_blurred.png)
 
-最终的被模糊化的纹理就是我们用来获得发出光晕效果的东西。这个已模糊的纹理要添加到原来的HDR场景纹理之上。由于模糊滤镜的作用，明亮的区域在宽度和高度上都得到了扩展，因此场景中的明亮区域看起来会发光或流光。
+最终的被模糊化的纹理就是我们用来获得发出光晕效果的东西。这个已模糊的纹理要添加到原来的HDR场景纹理的上部。因为模糊过滤器的应用明亮区域发出光晕，所以明亮区域在长和宽上都有所扩展。
 
-![](../img/05/07/bloom_small.png)
+![](http://learnopengl.com/img/advanced-lighting/bloom_small.png)
 
-泛光本身并不是个复杂的技术，但很难获得正确的效果。它的品质很大程度上取决于所用的模糊过滤器的质量和类型。简单地改改模糊过滤器就会极大的改变泛光效果的品质。
+泛光本身并不是个复杂的技术，但很难获得正确的效果。它的品质很大程度上取决于所用的模糊过滤器的质量和类型。简单的改改模糊过滤器就会极大的改变泛光效果的品质。
 
 下面这几步就是泛光后处理特效的过程，它总结了实现泛光所需的步骤。
 
-![](../img/05/07/bloom_steps.png)
+![](http://learnopengl.com/img/advanced-lighting/bloom_steps.png)
 
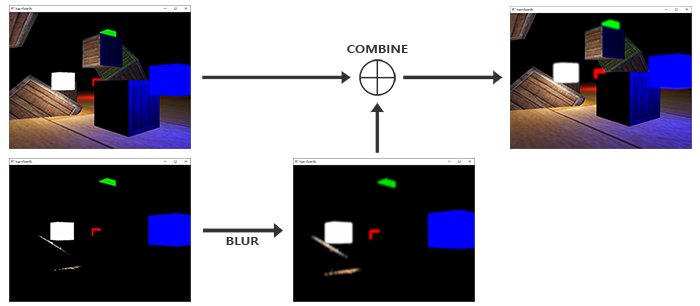
 首先我们需要根据一定的阈限提取所有明亮的颜色。我们先来做这件事。
 
 ## 提取亮色
 
-第一步我们要从渲染出来的场景中提取两张图片。我们可以渲染场景两次，每次使用一个不同的着色器渲染到不同的帧缓冲中，但我们可以使用一个叫做MRT（Multiple Render Targets，多渲染目标）的小技巧，这样我们就能指定多个像素着色器输出；有了它我们还能够在一个单独渲染处理中提取头两个图片。在像素着色器的输出前，我们指定一个布局location标识符，这样我们便可控制一个像素着色器写入到哪个颜色缓冲：
+第一步我们要从渲染出来的场景中提取两张图片。我们可以渲染场景两次，每次使用一个不同的不同的着色器渲染到不同的帧缓冲中，但我们可以使用一个叫做MRT（Multiple Render Targets多渲染目标）的小技巧，这样我们就能定义多个像素着色器了；有了它我们还能够在一个单独渲染处理中提取头两个图片。在像素着色器的输出前，我们指定一个布局location标识符，这样我们便可控制一个像素着色器写入到哪个颜色缓冲：
 
 ```c++
 layout (location = 0) out vec4 FragColor;
 layout (location = 1) out vec4 BrightColor;
 ```
 
-只有我们真的具有多个可供写入的缓冲区时这种方式才能工作。使用多个像素着色器输出的必要条件是，有多个颜色缓冲附加到了当前绑定的帧缓冲对象上。你可能从[帧缓冲](../04%20Advanced%20OpenGL/05%20Framebuffers.md)教程那里回忆起，当把一个纹理链接到帧缓冲的颜色缓冲上时，我们可以指定一个颜色附件。直到现在，我们一直使用着<var>GL_COLOR_ATTACHMENT0</var>，但通过使用<var>GL_COLOR_ATTACHMENT1</var>，我们可以得到一个附加了两个颜色缓冲的帧缓冲对象：
+只有我们真的具有多个地方可写的时候这才能工作。使用多个像素着色器输出的必要条件是，有多个颜色缓冲附加到了当前绑定的帧缓冲对象上。你可能从帧缓冲教程那里回忆起，当把一个纹理链接到帧缓冲的颜色缓冲上时，我们可以指定一个颜色附件。直到现在，我们一直使用着GL_COLOR_ATTACHMENT0，但通过使用GL_COLOR_ATTACHMENT1，我们可以得到一个附加了两个颜色缓冲的帧缓冲对象：
 
 ```c++
 // Set up floating point framebuffer to render scene to
@@ -88,7 +84,7 @@ GLuint attachments[2] = { GL_COLOR_ATTACHMENT0, GL_COLOR_ATTACHMENT1 };
 glDrawBuffers(2, attachments);
 ```
 
-当渲染到这个帧缓冲的时候，一个着色器使用一个布局location修饰符，fragment就会写入对应的颜色缓冲。这很棒，因为这样省去了我们为提取明亮区域的额外渲染步骤，因为我们现在可以直接从将被渲染的fragment提取出它们：
+当渲染到这个帧缓冲中的时候，一个着色器使用一个布局location修饰符，那么fragment就会用相应的颜色缓冲就会被用来渲染。这很棒，因为这样省去了我们为提取明亮区域的额外渲染步骤，因为我们现在可以直接从将被渲染的fragment提取出它们：
 
 ```c++
 #version 330 core
@@ -108,29 +104,29 @@ void main()
 }
 ```
 
-这里我们先正常计算光照，将其传递给第一个像素着色器的输出变量<var>FragColor</var>。然后我们使用当前储存在<var>FragColor</var>的东西来决定它的亮度是否超过了一定阈限。我们首先通过适当地将其转换为灰度来计算片段的亮度(通过取两个向量的点积，我们有效地将两个向量的每个单独分量相乘并将结果加在一起)。如果亮度超过某个阈值，我们将颜色输出到第二个颜色缓冲区。我们对光立方体做同样的处理。
+这里我们先正常计算光照，将其传递给第一个像素着色器的输出变量FragColor。然后我们使用当前储存在FragColor的东西来决定它的亮度是否超过了一定阈限。我们通过恰当地将其转为灰度的方式计算一个fragment的亮度，如果它超过了一定阈限，我们就把颜色输出到第二个颜色缓冲，那里保存着所有亮部；渲染发光的立方体也是一样的。
 
-这也说明了为什么泛光在HDR基础上能够工作得特别好。因为HDR中，我们可以将颜色值指定超过1.0这个默认的范围，我们能够得到对图像中的亮度更好的控制权。没有HDR我们必须将阈限设置为小于1.0的数，这种方式仍然可行，但是亮部很容易变得很多，这就导致光晕效果过重(比如白雪的光晕效果)。
+这也说明了为什么泛光在HDR基础上能够运行得很好。因为HDR中，我们可以将颜色值指定超过1.0这个默认的范围，我们能够得到对一个图像中的亮度的更好的控制权。没有HDR我们必须将阈限设置为小于1.0的数，虽然可行，但是亮部很容易变得很多，这就导致光晕效果过重。
 
-有了两个颜色缓冲，我们就有了一个正常场景的图像和一个提取出的亮区的图像。这些都在一个渲染步骤中完成。
+有了两个颜色缓冲，我们就有了一个正常场景的图像和一个提取出的亮区的图像；这些都在一个渲染步骤中完成。
 
-![](../img/05/07/bloom_attachments.png)
+![](http://learnopengl.com/img/advanced-lighting/bloom_attachments.png)
 
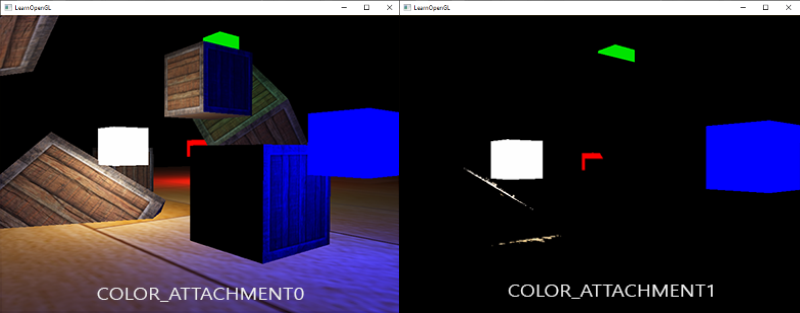
-有了一个提取出的亮区图像，我们现在需要对该图像进行模糊处理。我们可以使用帧缓冲章节中后处理部分那个简单的盒子过滤器，但我们最好还是使用一个更高级(也更漂亮)的模糊过滤器：**高斯模糊(Gaussian blur)**。
+有了一个提取出的亮区图像，我们现在就要把这个图像进行模糊处理。我们可以使用帧缓冲教程后处理部分的那个简单的盒子过滤器，但不过我们最好还是使用一个更高级的更漂亮的模糊过滤器：**高斯模糊(Gaussian blur)**。
 
 ## 高斯模糊
 
-在后处理教程那里，我们采用的模糊是一个图像中所有周围像素的均值，它的确为我们提供了一个简易实现的模糊，但效果并不是最好的。高斯模糊基于高斯曲线，高斯曲线通常被描述为一个钟形曲线，中间的值达到最大化，随着距离的增加，两边的值不断减少。高斯曲线在数学上有不同的形式，但是通常是这样的形状：
+在后处理教程那里，我们采用的模糊是一个图像中所有周围像素的均值，它的确为我们提供了一个简易实现的模糊，但是效果并不好。高斯模糊基于高斯曲线，高斯曲线通常被描述为一个钟形曲线，中间的值达到最大化，随着距离的增加，两边的值不断减少。高斯曲线在数学上有不同的形式，但是通常是这样的形状：
 
-![](../img/05/07/bloom_gaussian.png)
+![](http://learnopengl.com/img/advanced-lighting/bloom_gaussian.png)
 
 高斯曲线在它的中间处的面积最大，使用它的值作为权重使得近处的样本拥有最大的优先权。比如，如果我们从fragment的32×32的四方形区域采样，这个权重随着和fragment的距离变大逐渐减小；通常这会得到更好更真实的模糊效果，这种模糊叫做高斯模糊。
 
-为了实现高斯模糊过滤器，我们需要一个二维权重正方形，我们可以从二维高斯曲线方程中获得权重。然而这个过程有个问题，就是很快会消耗极大的性能。以一个32×32的模糊kernel为例，我们必须对每个fragment从一个纹理中采样1024次！
+要实现高斯模糊过滤我们需要一个二维四方形作为权重，从这个二维高斯曲线方程中去获取它。然而这个过程有个问题，就是很快会消耗极大的性能。以一个32×32的模糊kernel为例，我们必须对每个fragment从一个纹理中采样1024次！
 
 幸运的是，高斯方程有个非常巧妙的特性，它允许我们把二维方程分解为两个更小的方程：一个描述水平权重，另一个描述垂直权重。我们首先用水平权重在整个纹理上进行水平模糊，然后在经改变的纹理上进行垂直模糊。利用这个特性，结果是一样的，但是可以节省难以置信的性能，因为我们现在只需做32+32次采样，不再是1024了！这叫做两步高斯模糊。
 
-![](../img/05/07/bloom_gaussian_two_pass.png)
+![](http://learnopengl.com/img/advanced-lighting/bloom_gaussian_two_pass.png)
 
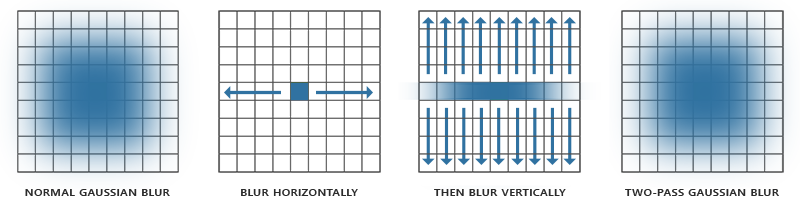
 这意味着我们如果对一个图像进行模糊处理，至少需要两步，最好使用帧缓冲对象做这件事。具体来说，我们将实现像乒乓球一样的帧缓冲来实现高斯模糊。它的意思是，有一对儿帧缓冲，我们把另一个帧缓冲的颜色缓冲放进当前的帧缓冲的颜色缓冲中，使用不同的着色效果渲染指定的次数。基本上就是不断地切换帧缓冲和纹理去绘制。这样我们先在场景纹理的第一个缓冲中进行模糊，然后在把第一个帧缓冲的颜色缓冲放进第二个帧缓冲进行模糊，接着，将第二个帧缓冲的颜色缓冲放进第一个，循环往复。
 
@@ -179,7 +175,7 @@ void main()
 GLuint pingpongFBO[2];
 GLuint pingpongBuffer[2];
 glGenFramebuffers(2, pingpongFBO);
-glGenTextures(2, pingpongBuffer);
+glGenTextures(2, pingpongColorbuffers);
 for (GLuint i = 0; i < 2; i++)
 {
     glBindFramebuffer(GL_FRAMEBUFFER, pingpongFBO[i]);
@@ -222,7 +218,7 @@ glBindFramebuffer(GL_FRAMEBUFFER, 0);
 
 通过对提取亮区纹理进行5次模糊，我们就得到了一个正确的模糊的场景亮区图像。
 
-![](../img/05/07/bloom_blurred_large.png)
+![](http://learnopengl.com/img/advanced-lighting/bloom_blurred_large.png)
 
 泛光的最后一步是把模糊处理的图像和场景原来的HDR纹理进行结合。
 
@@ -259,9 +255,9 @@ void main()
 
 把两个纹理结合以后，场景亮区便有了合适的光晕特效：
 
-![](../img/05/07/bloom.png)
+![](http://learnopengl.com/img/advanced-lighting/bloom.png)
 
-有颜色的立方体看起来仿佛更亮，它向外发射光芒，的确是一个更好的视觉效果。这个场景比较简单，所以泛光效果不算十分令人瞩目，但在更充足照明的场景中合理配置之后效果会有明显的不同。你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/5.advanced_lighting/7.bloom/bloom.cpp)找到这个简单示例的源代码。
+有颜色的立方体看起来仿佛更亮，它向外发射光芒，的确是一个更好的视觉效果。这个场景比较简单，所以泛光效果不算十分令人瞩目，但在更好的场景中合理配置之后效果会有巨大的不同。你可以在这里找到这个简单的例子的源码，以及模糊的顶点和像素着色器、立方体的像素着色器、后处理的顶点和像素着色器。
 
 这个教程我们只是用了一个相对简单的高斯模糊过滤器，它在每个方向上只有5个样本。通过沿着更大的半径或重复更多次数的模糊，进行采样我们就可以提升模糊的效果。因为模糊的质量与泛光效果的质量正相关，提升模糊效果就能够提升泛光效果。有些提升将模糊过滤器与不同大小的模糊kernel或采用多个高斯曲线来选择性地结合权重结合起来使用。来自Kalogirou和EpicGames的附加资源讨论了如何通过提升高斯模糊来显著提升泛光效果。
 
@@ -271,4 +267,4 @@ void main()
 
 - [Efficient Gaussian Blur with linear sampling](http://rastergrid.com/blog/2010/09/efficient-gaussian-blur-with-linear-sampling/)：非常详细地描述了高斯模糊，以及如何使用OpenGL的双线性纹理采样提升性能。
 - [Bloom Post Process Effect](https://udn.epicgames.com/Three/Bloom.html)：来自Epic Games关于通过对权重的多个高斯曲线结合来提升泛光效果的文章。
-- [How to do good bloom for HDR rendering](http://kalogirou.net/2006/05/20/how-to-do-good-bloom-for-hdr-rendering/)：Kalogirou的文章描述了如何使用更好的高斯模糊算法来提升泛光效果。
+- [How to do good bloom for HDR rendering](http://kalogirou.net/2006/05/20/how-to-do-good-bloom-for-hdr-rendering/)：Kalogirou的文章描述了如何使用更好的高斯模糊算法来提升泛光效果。

docs/05 Advanced Lighting/08 Deferred Shading.md

@@ -3,34 +3,28 @@
 原文     | [Deferred Shading](http://learnopengl.com/#!Advanced-Lighting/Deferred-Shading)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
-校对     | [KenLee](https://hellokenlee.github.io/)
-
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
+翻译     | Meow J
+校对     | 未校对
 
 我们现在一直使用的光照方式叫做**正向渲染(Forward Rendering)**或者**正向着色法(Forward Shading)**，它是我们渲染物体的一种非常直接的方式，在场景中我们根据所有光源照亮一个物体，之后再渲染下一个物体，以此类推。它非常容易理解，也很容易实现，但是同时它对程序性能的影响也很大，因为对于每一个需要渲染的物体，程序都要对每一个光源每一个需要渲染的片段进行迭代，这是**非常**多的！因为大部分片段着色器的输出都会被之后的输出覆盖，正向渲染还会在场景中因为高深的复杂度(多个物体重合在一个像素上)浪费大量的片段着色器运行时间。
 
 **延迟着色法(Deferred Shading)**，**或者说是延迟渲染(Deferred Rendering)**，为了解决上述问题而诞生了，它大幅度地改变了我们渲染物体的方式。这给我们优化拥有大量光源的场景提供了很多的选择，因为它能够在渲染上百甚至上千光源的同时还能够保持能让人接受的帧率。下面这张图片包含了一共1874个点光源，它是使用延迟着色法来完成的，而这对于正向渲染几乎是不可能的(图片来源：Hannes Nevalainen)。
 
-![](../img/05/08/deferred_example.png)
+![](http://learnopengl.com/img/advanced-lighting/deferred_example.png)
 
 延迟着色法基于我们**延迟(Defer)**或**推迟(Postpone)**大部分计算量非常大的渲染(像是光照)到后期进行处理的想法。它包含两个处理阶段(Pass)：在第一个几何处理阶段(Geometry Pass)中，我们先渲染场景一次，之后获取对象的各种几何信息，并储存在一系列叫做G缓冲(G-buffer)的纹理中；想想位置向量(Position Vector)、颜色向量(Color Vector)、法向量(Normal Vector)和/或镜面值(Specular Value)。场景中这些储存在G缓冲中的几何信息将会在之后用来做(更复杂的)光照计算。下面是一帧中G缓冲的内容：
 
-![](../img/05/08/deferred_g_buffer.png)
+![](http://learnopengl.com/img/advanced-lighting/deferred_g_buffer.png)
 
 我们会在第二个光照处理阶段(Lighting Pass)中使用G缓冲内的纹理数据。在光照处理阶段中，我们渲染一个屏幕大小的方形，并使用G缓冲中的几何数据对每一个片段计算场景的光照；在每个像素中我们都会对G缓冲进行迭代。我们对于渲染过程进行解耦，将它高级的片段处理挪到后期进行，而不是直接将每个对象从顶点着色器带到片段着色器。光照计算过程还是和我们以前一样，但是现在我们需要从对应的G缓冲而不是顶点着色器(和一些uniform变量)那里获取输入变量了。
 
 下面这幅图片很好地展示了延迟着色法的整个过程：
 
-![](../img/05/08/deferred_overview.png)
+![](http://learnopengl.com/img/advanced-lighting/deferred_overview.png)
 
 这种渲染方法一个很大的好处就是能保证在G缓冲中的片段和在屏幕上呈现的像素所包含的片段信息是一样的，因为深度测试已经最终将这里的片段信息作为最顶层的片段。这样保证了对于在光照处理阶段中处理的每一个像素都只处理一次，所以我们能够省下很多无用的渲染调用。除此之外，延迟渲染还允许我们做更多的优化，从而渲染更多的光源。
 
-当然这种方法也带来几个缺陷， 由于G缓冲要求我们在纹理颜色缓冲中存储相对比较大的场景数据，这会消耗比较多的显存，尤其是类似位置向量之类的需要高精度的场景数据。 另外一个缺点就是他不支持混色(因为我们只有最前面的片段信息)， 因此也不能使用MSAA了。针对这几个问题我们可以做一些变通来克服这些缺点，这些我们留会在教程的最后讨论。
-
-在几何处理阶段中填充G缓冲非常高效，因为我们直接储存像素位置，颜色或者是法线等对象信息到帧缓冲中，而这几乎不会消耗处理时间。在此基础上使用多渲染目标(Multiple Render Targets, MRT)技术，我们甚至可以在一个渲染处理之内完成这所有的工作。
+在几何处理阶段中填充G缓冲非常高效，因为我们直接储存像是位置，颜色或者是法线等对象信息到帧缓冲中，而这几乎不会消耗处理时间。在此基础上使用多渲染目标(Multiple Render Targets, MRT)技术，我们甚至可以在一个渲染处理之内完成这所有的工作。
 
 ## G缓冲
 
@@ -43,7 +37,7 @@ G缓冲(G-buffer)是对所有用来储存光照相关的数据，并在最后的
 - 所有光源的位置和颜色向量
 - 玩家或者观察者的位置向量
 
-有了这些(逐片段)变量的处置权，我们就能够计算我们很熟悉的(布林-)风氏光照(Blinn-Phong Lighting)了。光源的位置，颜色，和玩家的观察位置可以通过uniform变量来设置，但是其它变量对于每个对象的片段都是不同的。如果我们能以某种方式传输完全相同的数据到最终的延迟光照处理阶段中，我们就能计算与之前相同的光照效果了，尽管我们只是在渲染一个2D方形的片段。
+有了这些(逐片段)变量的处置权，我们就能够计算我们很熟悉的(布林-)冯氏光照(Blinn-Phong Lighting)了。光源的位置，颜色，和玩家的观察位置可以通过uniform变量来设置，但是其它变量对于每个对象的片段都是不同的。如果我们能以某种方式传输完全相同的数据到最终的延迟光照处理阶段中，我们就能计算与之前相同的光照效果了，尽管我们只是在渲染一个2D方形的片段。
 
 OpenGL并没有限制我们能在纹理中能存储的东西，所以现在你应该清楚在一个或多个屏幕大小的纹理中储存所有逐片段数据并在之后光照处理阶段中使用的可行性了。因为G缓冲纹理将会和光照处理阶段中的2D方形一样大，我们会获得和正向渲染设置完全一样的片段数据，但在光照处理阶段这里是一对一映射。
 
@@ -151,7 +145,7 @@ void main()
 
 如果我们现在想要渲染一大堆纳米装战士对象到`gBuffer`帧缓冲中，并通过一个一个分别投影它的颜色缓冲到铺屏四边形中尝试将他们显示出来，我们会看到向下面这样的东西：
 
-![](../img/05/08/deferred_g_buffer.png)
+![](http://learnopengl.com/img/advanced-lighting/deferred_g_buffer.png)
 
 尝试想象世界空间位置和法向量都是正确的。比如说，指向右侧的法向量将会被更多地对齐到红色上，从场景原点指向右侧的位置矢量也同样是这样。一旦你对G缓冲中的内容满意了，我们就该进入到下一步：光照处理阶段了。
 
@@ -222,13 +216,13 @@ void main()
 
 光照处理阶段着色器接受三个uniform纹理，代表G缓冲，它们包含了我们在几何处理阶段储存的所有数据。如果我们现在再使用当前片段的纹理坐标采样这些数据，我们将会获得和之前完全一样的片段值，这就像我们在直接渲染几何体。在片段着色器的一开始，我们通过一个简单的纹理查找从G缓冲纹理中获取了光照相关的变量。注意我们从`gAlbedoSpec`纹理中同时获取了`Albedo`颜色和`Spqcular`强度。
 
-因为我们现在已经有了必要的逐片段变量(和相关的uniform变量)来计算布林-风氏光照(Blinn-Phong Lighting)，我们不需要对光照代码做任何修改了。我们在延迟着色法中唯一需要改的就是获取光照输入变量的方法。
+因为我们现在已经有了必要的逐片段变量(和相关的uniform变量)来计算布林-冯氏光照(Blinn-Phong Lighting)，我们不需要对光照代码做任何修改了。我们在延迟着色法中唯一需要改的就是获取光照输入变量的方法。
 
 运行一个包含32个小光源的简单Demo会是像这样子的：
 
-![](../img/05/08/deferred_shading.png)
+![](http://learnopengl.com/img/advanced-lighting/deferred_shading.png)
 
-你可以在以下位置找到Demo的完整[源代码](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred)，和几何渲染阶段的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_geometry&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_geometry&type=fragment)着色器，还有光照渲染阶段的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred&type=fragment)着色器。
+你可以在以下位置找到Demo的完整[源代码](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred)，和几何渲染阶段的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_geometry&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_geometry&type=fragment)着色器，还有光照渲染阶段的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred&type=vertex)着色器。
 
 延迟着色法的其中一个缺点就是它不能进行[混合](../04 Advanced OpenGL/03 Blending.md)(Blending)，因为G缓冲中所有的数据都是从一个单独的片段中来的，而混合需要对多个片段的组合进行操作。延迟着色法另外一个缺点就是它迫使你对大部分场景的光照使用相同的光照算法，你可以通过包含更多关于材质的数据到G缓冲中来减轻这一缺点。
 
@@ -260,7 +254,7 @@ for (GLuint i = 0; i < lightPositions.size(); i++)
 
 然而，这些渲染出来的立方体并没有考虑到我们储存的延迟渲染器的几何深度(Depth)信息，并且结果是它被渲染在之前渲染过的物体之上，这并不是我们想要的结果。
 
-![](../img/05/08/deferred_lights_no_depth.png)
+![](http://learnopengl.com/img/advanced-lighting/deferred_lights_no_depth.png)
 
 我们需要做的就是首先复制出在几何渲染阶段中储存的深度信息，并输出到默认的帧缓冲的深度缓冲，然后我们才渲染光立方体。这样之后只有当它在之前渲染过的几何体上方的时候，光立方体的片段才会被渲染出来。我们可以使用`glBlitFramebuffer`复制一个帧缓冲的内容到另一个帧缓冲中，这个函数我们也在[抗锯齿](http://learnopengl-cn.readthedocs.org/zh/latest/04%20Advanced%20OpenGL/11%20Anti%20Aliasing/)的教程中使用过，用来还原多重采样的帧缓冲。`glBlitFramebuffer`这个函数允许我们复制一个用户定义的帧缓冲区域到另一个用户定义的帧缓冲区域。
 
@@ -279,7 +273,7 @@ glBindFramebuffer(GL_FRAMEBUFFER, 0);
 
 在这里我们复制整个读帧缓冲的深度缓冲信息到默认帧缓冲的深度缓冲，对于颜色缓冲和模板缓冲我们也可以这样处理。现在如果我们接下来再渲染光立方体，场景里的几何体将会看起来很真实了，而不只是简单地粘贴立方体到2D方形之上：
 
-![](../img/05/08/deferred_lights_depth.png)
+![](http://learnopengl.com/img/advanced-lighting/deferred_lights_depth.png)
 
 你可以在[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_light_cube)找到Demo的源代码，还有光立方体的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_light_cube&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_light_cube&type=fragment)着色器。
 
@@ -393,7 +387,7 @@ void main()
 
 使用光体积更好的方法是渲染一个实际的球体，并根据光体积的半径缩放。这些球的中心放置在光源的位置，由于它是根据光体积半径缩放的，这个球体正好覆盖了光的可视体积。这就是我们的技巧：我们使用大体相同的延迟片段着色器来渲染球体。因为球体产生了完全匹配于受影响像素的着色器调用，我们只渲染了受影响的像素而跳过其它的像素。下面这幅图展示了这一技巧：
 
-![](../img/05/08/deferred_light_volume_rendered.png)
+![](http://learnopengl.com/img/advanced-lighting/deferred_light_volume_rendered.png)
 
 它被应用在场景中每个光源上，并且所得的片段相加混合在一起。这个结果和之前场景是一样的，但这一次只渲染对于光源相关的片段。它有效地减少了从`nr_objects * nr_lights`到`nr_objects + nr_lights`的计算量，这使得多光源场景的渲染变得无比高效。这正是为什么延迟渲染非常适合渲染很大数量光源。
 
@@ -412,4 +406,4 @@ void main()
 ## 附加资源
 
 - [Tutorial 35: Deferred Shading - Part 1](http://ogldev.atspace.co.uk/www/tutorial35/tutorial35.html)：OGLDev的一个分成三部分的延迟着色法教程。在Part 2和3中介绍了渲染光体积
-- [Deferred Rendering for Current and Future Rendering Pipelines](https://software.intel.com/sites/default/files/m/d/4/1/d/8/lauritzen_deferred_shading_siggraph_2010.pdf)：Andrew Lauritzen的幻灯片，讨论了高级切片式延迟着色法和延迟光照
+- [Deferred Rendering for Current and Future Rendering Pipelines](https://software.intel.com/sites/default/files/m/d/4/1/d/8/lauritzen_deferred_shading_siggraph_2010.pdf)：Andrew Lauritzen的幻灯片，讨论了高级切片式延迟着色法和延迟光照

docs/05 Advanced Lighting/09 SSAO.md

@@ -3,18 +3,14 @@
 原文     | [SSAO](http://learnopengl.com/#!Advanced-Lighting/SSAO)
       ---|---
 作者     | JoeyDeVries
-翻译     | Krasjet
+翻译     | Meow J
 校对     | 未校对
 
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
 我们已经在前面的基础教程中简单介绍到了这部分内容：环境光照(Ambient Lighting)。环境光照是我们加入场景总体光照中的一个固定光照常量，它被用来模拟光的**散射(Scattering)**。在现实中，光线会以任意方向散射，它的强度是会一直改变的，所以间接被照到的那部分场景也应该有变化的强度，而不是一成不变的环境光。其中一种间接光照的模拟叫做**环境光遮蔽(Ambient Occlusion)**，它的原理是通过将褶皱、孔洞和非常靠近的墙面变暗的方法近似模拟出间接光照。这些区域很大程度上是被周围的几何体遮蔽的，光线会很难流失，所以这些地方看起来会更暗一些。站起来看一看你房间的拐角或者是褶皱，是不是这些地方会看起来有一点暗？
 
 下面这幅图展示了在使用和不使用SSAO时场景的不同。特别注意对比褶皱部分，你会发现(环境)光被遮蔽了许多：
 
-![](../img/05/09/ssao_example.png)
+![](http://learnopengl.com/img/advanced-lighting/ssao_example.png)
 
 尽管这不是一个非常明显的效果，启用SSAO的图像确实给我们更真实的感觉，这些小的遮蔽细节给整个场景带来了更强的深度感。
 
@@ -22,39 +18,38 @@
 
 SSAO背后的原理很简单：对于铺屏四边形(Screen-filled Quad)上的每一个片段，我们都会根据周边深度值计算一个**遮蔽因子(Occlusion Factor)**。这个遮蔽因子之后会被用来减少或者抵消片段的环境光照分量。遮蔽因子是通过采集片段周围球型核心(Kernel)的多个深度样本，并和当前片段深度值对比而得到的。高于片段深度值样本的个数就是我们想要的遮蔽因子。
 
-![](../img/05/09/ssao_crysis_circle.png)
+![](http://learnopengl.com/img/advanced-lighting/ssao_crysis_circle.png)
 
 上图中在几何体内灰色的深度样本都是高于片段深度值的，他们会增加遮蔽因子；几何体内样本个数越多，片段获得的环境光照也就越少。
 
 很明显，渲染效果的质量和精度与我们采样的样本数量有直接关系。如果样本数量太低，渲染的精度会急剧减少，我们会得到一种叫做**波纹(Banding)**的效果；如果它太高了，反而会影响性能。我们可以通过引入随机性到采样核心(Sample Kernel)的采样中从而减少样本的数目。通过随机旋转采样核心，我们能在有限样本数量中得到高质量的结果。然而这仍然会有一定的麻烦，因为随机性引入了一个很明显的噪声图案，我们将需要通过模糊结果来修复这一问题。下面这幅图片([John Chapman](http://john-chapman-graphics.blogspot.com/)的佛像)展示了波纹效果还有随机性造成的效果：
 
-![](../img/05/09/ssao_banding_noise.jpg)
+![](http://learnopengl.com/img/advanced-lighting/ssao_banding_noise.jpg)
 
 你可以看到，尽管我们在低样本数的情况下得到了很明显的波纹效果，引入随机性之后这些波纹效果就完全消失了。
 
 Crytek公司开发的SSAO技术会产生一种特殊的视觉风格。因为使用的采样核心是一个球体，它导致平整的墙面也会显得灰蒙蒙的，因为核心中一半的样本都会在墙这个几何体上。下面这幅图展示了孤岛危机的SSAO，它清晰地展示了这种灰蒙蒙的感觉：
 
-![](../img/05/09/ssao_crysis.jpg)
+![](http://learnopengl.com/img/advanced-lighting/ssao_crysis.jpg)
 
 由于这个原因，我们将不会使用球体的采样核心，而使用一个沿着表面法向量的半球体采样核心。
 
-![](../img/05/09/ssao_hemisphere.png)
+![](http://learnopengl.com/img/advanced-lighting/ssao_hemisphere.png)
 
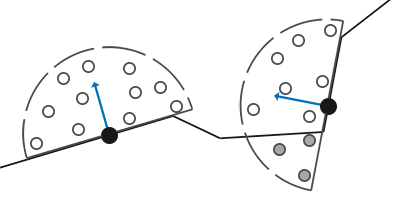
 通过在**法向半球体(Normal-oriented Hemisphere)**周围采样，我们将不会考虑到片段底部的几何体.它消除了环境光遮蔽灰蒙蒙的感觉，从而产生更真实的结果。这个SSAO教程将会基于法向半球法和John Chapman出色的[SSAO教程](http://john-chapman-graphics.blogspot.com/2013/01/ssao-tutorial.html)。
 
 ## 样本缓冲
 
 SSAO需要获取几何体的信息，因为我们需要一些方式来确定一个片段的遮蔽因子。对于每一个片段，我们将需要这些数据：
-
 - 逐片段**位置**向量
 - 逐片段的**法线**向量
-- 逐片段的**反射颜色**
+- **线性深度**纹理
 - **采样核心**
-- 用来旋转采样核心的随机旋转矢量
+- 用来旋转采样核心的逐片段随机旋转矢量
 
 通过使用一个逐片段观察空间位置，我们可以将一个采样半球核心对准片段的观察空间表面法线。对于每一个核心样本我们会采样线性深度纹理来比较结果。采样核心会根据旋转矢量稍微偏转一点；我们所获得的遮蔽因子将会之后用来限制最终的环境光照分量。
 
-![](../img/05/09/ssao_overview.png)
+![](http://learnopengl.com/img/advanced-lighting/ssao_overview.png)
 
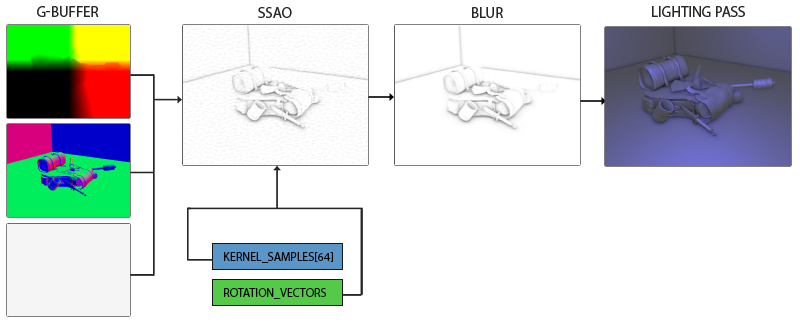
 由于SSAO是一种屏幕空间技巧，我们对铺屏2D四边形上每一个片段计算这一效果；也就是说我们没有场景中几何体的信息。我们能做的只是渲染几何体数据到屏幕空间纹理中，我们之后再会将此数据发送到SSAO着色器中，之后我们就能访问到这些几何体数据了。如果你看了前面一篇教程，你会发现这和延迟渲染很相似。这也就是说SSAO和延迟渲染能完美地兼容，因为我们已经存位置和法线向量到G缓冲中了。
 
@@ -121,7 +116,7 @@ glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
 
 我们需要沿着表面法线方向生成大量的样本。就像我们在这个教程的开始介绍的那样，我们想要生成形成半球形的样本。由于对每个表面法线方向生成采样核心非常困难，也不合实际，我们将在[切线空间](04 Normal Mapping.md)(Tangent Space)内生成采样核心，法向量将指向正z方向。
 
-![](../img/05/09/ssao_hemisphere.png)
+![](http://learnopengl.com/img/advanced-lighting/ssao_hemisphere.png)
 
 假设我们有一个单位半球，我们可以获得一个拥有最大64样本值的采样核心：
 
@@ -166,7 +161,7 @@ GLfloat lerp(GLfloat a, GLfloat b, GLfloat f)
 
 这就给了我们一个大部分样本靠近原点的核心分布。
 
-![](../img/05/09/ssao_kernel_weight.png)
+![](http://learnopengl.com/img/advanced-lighting/ssao_kernel_weight.png)
 
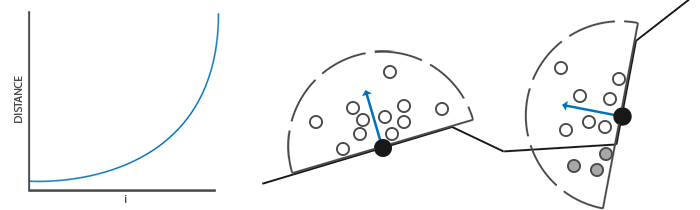
 每个核心样本将会被用来偏移观察空间片段位置从而采样周围的几何体。我们在教程开始的时候看到，如果没有变化采样核心，我们将需要大量的样本来获得真实的结果。通过引入一个随机的转动到采样核心中，我们可以很大程度上减少这一数量。
 
@@ -188,7 +183,7 @@ for (GLuint i = 0; i < 16; i++)
 }
 ```
 
-由于采样核心是沿着正z方向在切线空间内旋转，我们设定z分量为0.0，从而围绕z轴旋转。
+由于采样核心实验者正z方向在切线空间内旋转，我们设定z分量为0.0，从而围绕z轴旋转。
 
 我们接下来创建一个包含随机旋转向量的4x4纹理；记得设定它的封装方法为`GL_REPEAT`，从而保证它合适地平铺在屏幕上。
 
@@ -336,9 +331,9 @@ float sampleDepth = -texture(gPositionDepth, offset.xy).w;
 occlusion += (sampleDepth >= sample.z ? 1.0 : 0.0);
 ```
 
-这并没有完全结束，因为仍然还有一个小问题需要考虑。当检测一个靠近表面边缘的片段时，它将会考虑测试表面之下的表面的深度值；这些值将会(不正确地)影响遮蔽因子。我们可以通过引入一个范围检测从而解决这个问题，正如下图所示([John Chapman](http://john-chapman-graphics.blogspot.com/)的佛像)：
+这并没有完全结束，因为仍然还有一个小问题需要考虑。当检测一个靠近表面边缘的片段时，它将会考虑测试表面之下的表面的深度值；这些值将会(不正确地)音响遮蔽因子。我们可以通过引入一个范围检测从而解决这个问题，正如下图所示([John Chapman](http://john-chapman-graphics.blogspot.com/)的佛像)：
 
-![](../img/05/09/ssao_range_check.png)
+![](http://learnopengl.com/img/advanced-lighting/ssao_range_check.png)
 
 我们引入一个范围测试从而保证我们只当被测深度值在取样半径内时影响遮蔽因子。将代码最后一行换成：
 
@@ -349,7 +344,7 @@ occlusion += (sampleDepth >= sample.z ? 1.0 : 0.0) * rangeCheck;
 
 这里我们使用了GLSL的`smoothstep`函数，它非常光滑地在第一和第二个参数范围内插值了第三个参数。如果深度差因此最终取值在`radius`之间，它们的值将会光滑地根据下面这个曲线插值在0.0和1.0之间：
 
-![](../img/05/09/ssao_smoothstep.png)
+![](http://learnopengl.com/img/advanced-lighting/ssao_smoothstep.png)
 
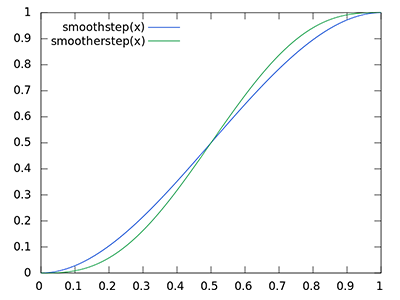
 如果我们使用一个在深度值在`radius`之外就突然移除遮蔽贡献的硬界限范围检测(Hard Cut-off Range Check)，我们将会在范围检测应用的地方看见一个明显的(很难看的)边缘。
 
@@ -363,7 +358,7 @@ FragColor = occlusion;
 
 下面这幅图展示了我们最喜欢的纳米装模型正在打盹的场景，环境遮蔽着色器产生了以下的纹理：
 
-![](../img/05/09/ssao_without_blur.png)
+![](http://learnopengl.com/img/advanced-lighting/ssao_without_blur.png)
 
 可见，环境遮蔽产生了非常强烈的深度感。仅仅通过环境遮蔽纹理我们就已经能清晰地看见模型一定躺在地板上而不是浮在空中。
 
@@ -411,7 +406,7 @@ void main() {
 
 这里我们遍历了周围在-2.0和2.0之间的SSAO纹理单元(Texel)，采样与噪声纹理维度相同数量的SSAO纹理。我们通过使用返回`vec2`纹理维度的`textureSize`，根据纹理单元的真实大小偏移了每一个纹理坐标。我们平均所得的结果，获得一个简单但是有效的模糊效果：
 
-![](../img/05/09/ssao.png)
+![](http://learnopengl.com/img/advanced-lighting/ssao.png)
 
 这就完成了，一个包含逐片段环境遮蔽数据的纹理；在光照处理阶段中可以直接使用。
 
@@ -471,7 +466,7 @@ void main()
 
 (除了将其改到观察空间)对比于之前的光照实现，唯一的真正改动就是场景环境分量与`AmbientOcclusion`值的乘法。通过在场景中加入一个淡蓝色的点光源，我们将会得到下面这个结果：
 
-![](../img/05/09/ssao_final.png)
+![](http://learnopengl.com/img/advanced-lighting/ssao_final.png)
 
 你可以在[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/ssao)找到完整的源代码，和以下着色器：
 

docs/06 In Practice/01 Debugging.md

@@ -3,16 +3,16 @@
 原文    | [Debugging](http://learnopengl.com/#!In-Practice/Debugging)
 -----   |  ----
 作者    | JoeydeVries
-翻译    | Krasjet
-校对    | [AoZhang](https://github.com/SuperAoao)
+翻译    | [Meow J](https://github.com/Meow-J)
+校对    | 暂无
 
-图形编程可以带来很多的乐趣，然而如果什么东西渲染错误，或者甚至根本就没有渲染，它同样可以给你带来大量的沮丧感！由于我们大部分时间都在与像素打交道，当出现错误的时候寻找错误的源头可能会非常困难。调试(Debug)这样的**视觉**错误与往常熟悉的CPU调试不同。我们没有一个可以用来输出文本的控制台，在GLSL代码中也不能设置断点，更没有方法方便地检测GPU的运行状态。
+图形编程可以带来很多的乐趣，然而如果什么东西渲染错误，或者甚至根本就没有渲染，它同样可以给你带来大量的沮丧感！由于我们大部分时间都在与像素打交道，当出现错误的时候寻找错误的源头可能会非常困难。调试(Debug)这样的**视觉**错误与往常熟悉的CPU调试不同。我们没有一个可以用来输出文本的控制台，在GLSL代码中也不能设置断点，更没有方法检测GPU的运行状态。
 
 在这篇教程中，我们将来见识几个调试OpenGL程序的技巧。OpenGL中的调试并不是很难，掌握住这些技巧对之后的学习会有非常大的帮助。
 
 ## glGetError()
 
-当你不正确使用OpenGL的时候（比如说在绑定之前配置一个缓冲），它会检测到，并在幕后生成一个或多个用户错误标记。我们可以使用一个叫做<fun>glGetError</fun>的函数查询这些错误标记，他会检测错误标记集，并且在OpenGL确实出错的时候返回一个错误值。
+当你不正确使用OpenGL的时候（比如说在绑定之前配置一个缓冲），它会检测到，并在幕后生成一个或多个用户错误标记。我们可以使用一个叫做<fun>glGetError</fun>的函数查询这些错误标记。，他会检测错误标记集，并且在OpenGL确实出错的时候返回一个错误值。
 
 ```c++
 GLenum glGetError();
@@ -37,7 +37,7 @@ GLenum glGetError();
 
 !!! important
 
-    注意当OpenGL是分布式(Distributely)运行的时候，如在X11系统上，其它的用户错误代码仍然可以被生成，只要它们有着不同的错误代码。调用<fun>glGetError</fun>只会重置一个错误代码标记，而不是所有。由于这一点，我们通常会建议在一个循环中调用<fun>glGetError</fun>。
+    注意如果OpenGL是分布式(Distributely)运行的时候，经常像是在X11系统上，其它的用户错误代码仍然可以被生成，只要它们有着不同的错误代码。调用<fun>glGetError</fun>只会重置一个错误代码标记，而不是所有。由于这一点，我们通常会建议在一个循环中调用<fun>glGetError</fun>。
 
 ```c++
 glBindTexture(GL_TEXTURE_2D, tex);
@@ -52,7 +52,7 @@ std::cout << glGetError() << std::endl; // 返回 1281 (非法值)
 std::cout << glGetError() << std::endl; // 返回 0 (无错误)
 ```
 
-<fun>glGetError</fun>非常棒的一点就是它能够非常简单地定位错误可能的来源，并且验证OpenGL使用的正确性。比如说你获得了一个黑屏的结果但是不知道什么造成了它：是不是帧缓冲设置错误？是不是我忘记绑定纹理了？通过在整个代码库中调用<fun>glGetError</fun>，您可以快速捕获OpenGL错误开始出现的第一个地方。
+<fun>glGetError</fun>非常棒的一点就是它能够非常简单地定位错误可能的来源，并且验证OpenGL使用的正确性。比如说你获得了一个黑屏的结果但是不知道什么造成了它：是不是帧缓冲设置错误？是不是我忘记绑定纹理了？通过在代码中各处调用<fun>glGetError</fun>，你可以非常快速地查明OpenGL错误开始出现的位置，这也就意味着这次调用之前的代码中哪里出错了。
 
 默认情况下<fun>glGetError</fun>只会打印错误数字，如果你不去记忆的话会非常难以理解。通常我们会写一个助手函数来简便地打印出错误字符串以及错误检测函数调用的位置。
 
@@ -91,11 +91,18 @@ glCheckError();
 
 ![](../img/06/01/debugging_glgeterror.png)
 
+还有一个**重要的**事情需要知道，GLEW有一个历史悠久的bug，调用<fun>glewInit()</fun>会设置一个<var>GL_INVALID_ENUM</var>的错误标记，所以第一次调用的<fun>glGetError</fun>永远会猝不及防地给你返回一个错误代码。如果要修复这个bug，我们建议您在调用<fun>glewInit</fun>之后立即调用<fun>glGetError</fun>消除这个标记：
+
+```c++
+glewInit();
+glGetError();
+```
+
 <fun>glGetError</fun>并不能帮助你很多，因为它返回的信息非常简单，但不可否认它经常能帮助你检查笔误或者快速定位错误来源。总而言之，是一个非常简单但有效的工具。
 
 ## 调试输出
 
-虽然没有<fun>glGetError</fun>普遍，但一个叫做<def>调试输出</def>(Debug Output)的OpenGL拓展是一个非常有用的工具，它在4.3版本之后变为了核心OpenGL的一部分。通过使用调试输出拓展，OpenGL自身会直接发送一个比起<fun>glGetError</fun>更为完善的错误或警告信息给用户。它不仅提供了更多的信息，也能够帮助你使用调试器(Debugger)捕捉错误源头。
+虽然没有<fun>glGetError</fun>普遍，但一个叫做<def>调试输出</def>(Debug Output)的OpenGL拓展十一个非常有用的工具，它在4.3版本之后变为了核心OpenGL的一部分。通过使用调试输出拓展，OpenGL自身会直接发送一个比起<fun>glGetError</fun>更为完善的错误或警告信息给用户。它不仅提供了更多的信息，也能够帮助你使用一个调试器(Debugger)捕捉错误源头。
 
 !!! important
 
@@ -108,7 +115,7 @@ glCheckError();
 在GLFW中请求一个调试输出非常简单，我们只需要传递一个提醒到GLFW中，告诉它我们需要一个调试输出上下文即可。我们需要在调用<fun>glfwCreateWindow</fun>之前完成这一请求。
 
 ```c++
-glfwWindowHint(GLFW_OPENGL_DEBUG_CONTEXT, true);
+glfwWindowHint(GLFW_OPENGL_DEBUG_CONTEXT, GL_TRUE);
 ```
 
 一旦GLFW初始化完成，如果我们使用的OpenGL 版本为4.3或以上的话我们就有一个调试上下文了，如果不是的话则祈祷系统仍然能够请求一个调试上下文吧。如果还是不行的话我们必须使用它的OpenGL拓展来请求调试输出。
@@ -130,19 +137,21 @@ if (flags & GL_CONTEXT_FLAG_DEBUG_BIT)
 调试输出工作的方式是这样的，我们首先将一个错误记录函数的回调（类似于GLFW输入的回调）传递给OpenGL，在这个回调函数中我们可以自由地处理OpenGL错误数据，在这里我们将输出一些有用的错误数据到控制台中。下面是这个就是OpenGL对调试输出所期待的回调函数的原型：
 
 ```c++
-void APIENTRY glDebugOutput(GLenum source, GLenum type, unsigned int id, GLenum severity, 
-                            GLsizei length, const char *message, const void *userParam);
+void APIENTRY glDebugOutput(GLenum source, GLenum type, GLuint id, GLenum severity, 
+                            GLsizei length, const GLchar *message, void *userParam);
 ```
 
+注意在OpenGL的某些实现中最后一个参数为`const void*`而不是`void*`。
+
 有了这一大堆的数据，我们可以创建一个非常有用的错误打印工具：
 
 ```c++
 void APIENTRY glDebugOutput(GLenum source, 
                             GLenum type, 
-                            unsigned int id, 
+                            GLuint id, 
                             GLenum severity, 
                             GLsizei length, 
-                            const char *message, 
+                            const GLchar *message, 
                             void *userParam)
 {
     // 忽略一些不重要的错误/警告代码
@@ -187,20 +196,6 @@ void APIENTRY glDebugOutput(GLenum source,
 
 当调试输出检测到了一个OpenGL错误，它会调用这个回调函数，我们将可以打印出非常多的OpenGL错误信息。注意我们忽略掉了一些错误代码，这些错误代码一般不能给我们任何有用的信息（比如NVidia驱动中的`131185`仅告诉我们缓冲成功创建了）。
 
-既然我们已经有了回调函数，那么是时候初始化调试输出了：
-
-```c++
-if (flags & GL_CONTEXT_FLAG_DEBUG_BIT)
-{
-    glEnable(GL_DEBUG_OUTPUT);
-    glEnable(GL_DEBUG_OUTPUT_SYNCHRONOUS); 
-    glDebugMessageCallback(glDebugOutput, nullptr);
-    glDebugMessageControl(GL_DONT_CARE, GL_DONT_CARE, GL_DONT_CARE, 0, nullptr, GL_TRUE);
-} 
-```
-
-在这里，我们告诉OpenGL启用调试输出，调用<fun>glEnable(GL_DEBUG_SYNCRHONOUS)</fun>告诉OpenGL在发生错误时直接调用回调函数。
-
 ### 过滤调试输出
 
 有了<fun>glDebugMessageControl</fun>，你可以潜在地过滤出你需要的错误类型。在这里我们不打算过滤任何来源，类型或者严重等级。如果我们仅希望显示OpenGL API的高严重等级错误消息，你可以设置为以下这样：
@@ -212,7 +207,7 @@ glDebugMessageControl(GL_DEBUG_SOURCE_API,
                       0, nullptr, GL_TRUE); 
 ```
 
-有了我们的配置，如果你的上下文支持调试输出的话，每个不正确的OpenGL指令都会打印出一大堆的有用数据。
+有了我们的配置，如果你的上下文支持调试出书的话，每个不正确的OpenGL指令都会打印出一大堆的有用数据。
 
 ![](../img/06/01/debugging_debug_output.png)
 
@@ -235,7 +230,7 @@ glDebugMessageInsert(GL_DEBUG_SOURCE_APPLICATION, GL_DEBUG_TYPE_ERROR, 0,
 
 如果你正在利用其它使用调试输出上下文的程序或OpenGL代码进行开发，这会非常有用。其它的开发者能快速了解你自定义OpenGL代码中任何**报告出来的**Bug。
 
-总而言之，调试输出（如果你能使用它）对与快速捕捉错误是非常有用的，完全值得你花一点时间来配置，它能够省下你非常多的开发时间。你可以在[这里](http://learnopengl.com/code_viewer_gh.php?code=src/7.in_practice/1.debugging/debugging.cpp)找到源码，里面<fun>glGetError</fun>和调试输出上下文都有配置；看看你是否能够修复所有的错误。
+总而言之，调试输出（如果你能使用它）对与快速捕捉错误是非常有用的，完全值得你花一点时间来配置，它能够省下你非常多的开发时间。你可以在[这里](http://learnopengl.com/code_viewer_gh.php?code=src/6.in_practice/1.debugging/debugging.cpp)找到源码，里面<fun>glGetError</fun>和调试输出上下文都有配置；看看你是否能够修复所有的错误。
 
 ## 调试着色器输出
 
@@ -261,7 +256,7 @@ void main()
 
 ![](../img/06/01/debugging_glsl_output.png)
 
-从视觉效果来看，我们可以看见世界空间的法向量应该是正确的，因为背包模型的右侧大部分都是红色的（这表明法线大概（正确地）指向正x轴），同样的，背包的前方大部分都为蓝色，即正z轴方向。
+从视觉效果来看，我们可以看见法向量应该是正确的，因为纳米装的右侧大部分都是红色的（这表明法线大概（正确地）指向正x轴），并且类似的纳米装的前方大部分都为蓝色，即正z轴方向。
 
 这一方法可以很容易拓展到你想要测试的任何变量。一旦你卡住了或者怀疑你的着色器有问题，尝试显示多个变量和/或中间结果，看看哪部分算法什么的没加上或者有错误。
 
@@ -271,13 +266,13 @@ void main()
 
 通过多年的经验你会最终能够知道不同GPU供应商之间的细微差别，但如果你想要保证你的着色器代码在所有的机器上都能运行，你可以直接对着官方的标准使用OpenGL的GLSL[参考编译器](https://www.khronos.org/opengles/sdk/tools/Reference-Compiler/)（Reference Compiler）来检查。你可以从[这里](https://www.khronos.org/opengles/sdk/tools/Reference-Compiler/)下载所谓的<def>GLSL语言校验器</def>(GLSL Lang Validator)的可执行版本，或者从[这里](https://github.com/KhronosGroup/glslang)找到完整的源码。
 
-有了这个GLSL语言校验器，你可以很方便的检查你的着色器代码，只需要把着色器文件作为程序的第一个参数即可。注意GLSL语言校验器是通过下列固定的后缀名来决定着色器的类型的：
+有了这个GLSL语言校验器，你可以很方便的检查你的着色器代码，只需要把着色器文件作为程序的第一格参数即可。注意GLSL语言校验器是通过下列固定的后缀名来决定着色器的类型的：
 
 - **.vert**：顶点着色器(Vertex Shader)
 - **.frag**：片段着色器(Fragment Shader)
 - **.geom**：几何着色器(Geometry Shader)
 - **.tesc**：细分控制着色器(Tessellation Control Shader)
-- **.tese**：细分计算着色器(Tessellation Evaluation Shader)
+- **.tese**：细分评估着色器(Tessellation Evaluation Shader)
 - **.comp**：计算着色器(Compute Shader)
 
 运行GLSL参考编译器非常简单：
@@ -294,7 +289,7 @@ glsllangvalidator shaderFile.vert
 
 ## 帧缓冲输出
 
-你的调试工具箱中另外一个技巧就是在OpenGL程序中一块特定区域显示帧缓冲的内容。你可能会比较频繁地使用[帧缓冲](../04 Advanced OpenGL/05 Framebuffers.md)，但由于帧缓冲的操作通常在后台进行，有时候想要知道出什么问题会非常困难。在你的程序中显示帧缓冲的内容是一个很有用的技巧，帮助你快速检查错误。
+你的调试工具箱中另外一个技巧就是在OpenGL程序中一块特定区域显示帧缓冲的内容。你可能会比较频繁地使用[帧缓冲](../04 Advanced OpenGL/05 Framebuffers.md)，但由于帧缓冲的魔法通常在幕后进行，有时候想要知道出什么问题会非常困难。在你的程序中显示帧缓冲的内容是一个很有用的技巧，帮助你快速检查错误。
 
 !!! important
 
@@ -368,27 +363,35 @@ int main()
 
 ## 外部调试软件
 
-当上面所有介绍到的技巧都不能使用的时候，我们仍可以使用一个第三方的工具来帮助我们调试。第三方应用通常将它们自己注入到OpenGL驱动中，并且能够拦截各种OpenGL调用，给你大量有用的数据。这些工具可以在很多方面帮助到你：对OpenGL函数使用进行性能测试，寻找瓶颈，检查缓冲内存，显示纹理和帧缓冲附件。如果你正在写（大规模）产品代码，这类的工具在开发过程中是非常有用的。
+当上面所有介绍到的技巧都不能使用的时候，我们仍可以使用一个第三方的工具来帮助我们调试。第三方应用通常将它们自己注入到OpenGL驱动中，并且能够拦截各种OpenGL调用，给你大量有用的数据。这些工具可以在很多方面帮助到你：对OpenGL函数使用进行性能测试，寻找瓶颈，检查缓冲内存，显示纹理和帧缓冲附件。如果你正在写（大规模）生产代码，这类的工具在开发过程中是非常有用的。
 
 我在下面列出了一些流行的调试工具，选几个尝试一下，看看哪个最适合你。
 
+### gDebugger
+
+gDebugger是一个非常易用的跨平台OpenGL程序调试工具。gDebugger会在你运行的OpenGL程序边上，提供OpenGL状态的详细概况。你可以随时暂停程序来检查当前状态，纹理内容以及缓冲使用。你可以在[这里](http://www.gremedy.com/)下载gDebugger。
+
+运行gDebugger只需要打开程序，创建一个工程，给它你OpenGL程序的位置于工作目录即可。
+
+![](../img/06/01/debugging_external_gdebugger.png)
+
 ### RenderDoc
 
-RenderDoc是一个很棒的（完全[开源](https://github.com/baldurk/renderdoc)的）独立调试工具。你只需要设置捕捉的程序以及工作目录就行了。你的程序会正常运行，当你想要检查一个特定的帧的时候，你只需要让RenderDoc在程序当前状态下捕捉一个或多个帧即可。在捕捉的帧当中，你可以观察管线状态，所有OpenGL指令，缓冲储存，以及使用的纹理。
+RenderDoc是另外一个很棒的（完全[开源](https://github.com/baldurk/renderdoc)的）独立调试工具。和gDebugger类似，你只需要设置捕捉的程序以及工作目录就行了。你的程序会正常运行，当你想要检查一个特定的帧的时候，你只需要让RenderDoc在程序当前状态下捕捉一个或多个帧即可。在捕捉的帧当中，你可以观察管线状态，所有OpenGL指令，缓冲储存，以及使用的纹理。
 
 ![](../img/06/01/debugging_external_renderdoc.png)
 
 ### CodeXL
 
-[CodeXL](https://gpuopen.com/compute-product/codexl/)是由AMD开发的一款GPU调试工具，它有独立版本也有Visual Studio插件版本。CodeXL可以给你非常多的信息，对于图形程序的性能测试也非常有用。CodeXL在NVidia与Intel的显卡上也能运行，不过会不支持OpenCL调试。
+[CodeXL](http://developer.amd.com/tools-and-sdks/opencl-zone/codexl/)是由AMD开发的一款GPU调试工具，它有独立版本也有Visual Studio插件版本。CodeXL可以给你非常多的信息，对于图形程序的性能测试也非常有用。CodeXL在NVidia与Intel的显卡上也能运行，不过会不支持OpenCL调试。
 
 ![](../img/06/01/debugging_external_codexl.png)
 
-我没有太多的CodeXL使用经验，我个人觉得RenderDoc会更容易使用一点，但我仍把它列在这里，因为它仍是一个非常可靠的工具，并且主要是由最大的GPU制造商之一开发的。
+我没有太多的CodeXL使用经验，我个人觉得gDebugger和RenderDoc会更容易使用一点，但我仍把它列在这里，因为它仍是一个非常可靠的工具，并且主要是由最大的GPU制造商之一AMD开发的。
 
 ### NVIDIA Nsight
 
-NVIDIA流行的[Nsight](https://developer.nvidia.com/nvidia-nsight-visual-studio-edition) GPU调试工具并不是一个独立程序，而是一个Visual Studio IDE或者Eclipse IDE的插件 (NVIDIA现在也提供[独立版本](https://developer.nvidia.com/nsight-graphics)了)。Nsight插件对图形开发者来说非常容易使用，因为它给出了GPU用量，逐帧GPU状态大量运行时的统计数据。
+NVIDIA流行的[Nsight](https://developer.nvidia.com/nvidia-nsight-visual-studio-edition) GPU调试工具并不是一个独立程序，而是一个Visual Studio IDE或者Eclipse IDE的插件。Nsight插件对图形开发者来说非常容易使用，因为它给出了GPU用量，逐帧GPU状态大量运行时的统计数据。
 
 当你在Visual Studio（或Eclipse）使用Nsight的调试或者性能测试指令启动程序的时候，Nsight将会在程序自身中运行。Nsight非常棒的一点就是它在你的程序中渲染了一套GUI系统，你可以使用它获取你程序各种各样有用的信息，可以是运行时也可以是逐帧分析。
 
@@ -396,9 +399,9 @@ NVIDIA流行的[Nsight](https://developer.nvidia.com/nvidia-nsight-visual-studio
 
 Nsight是一款非常有用的工具，在我看来比上述其它工具都有更好的表现，但它仍有一个非常重要的缺点，它只能在NVIDIA的显卡上工作。如果你正在使用一款NVIDIA的显卡（并且使用Visual Studio），Nsight是非常值得一试的。
 
-我知道我可能遗漏了一些其它的调试工具（比如我还能想到有Valve的[VOGL](https://github.com/ValveSoftware/vogl)和[APItrace](https://apitrace.github.io/)），但我觉得这个列表已经给你足够多的工具来实验了。
+我知道我可能遗漏了一些其它的调试工具（比如我还能想到有Valve的[VOGL](https://github.com/ValveSoftware/vogl)和[APItrace](https://apitrace.github.io/)），但我觉得这个列表已经给你足够多的工具来实验了。我并不是之前提到的任何一个工具的专家，所以如果我在哪里讲错了请在评论区留言，我会很乐意改正。
 
 ## 附加资源
 
 - [为什么你的代码会产生一个黑色窗口](http://retokoradi.com/2014/04/21/opengl-why-is-your-code-producing-a-black-window/)：Reto Koradi列举了你的屏幕没有产生任何输出的可能原因。
-- [调试输出](http://vallentinsource.com/opengl/debug-output)：Vallentin Source写的一份非常详细的调试输出教程，里面有在多个窗口系统中配置调试上下文的详细信息。
+- [调试输出](http://vallentinsource.com/opengl/debug-output)：Vallentin Source写的一份非常详细的调试输出教程，里面有在多个窗口系统中配置调试上下文的详细信息。

docs/06 In Practice/02 Text Rendering.md

@@ -1,4 +1,4 @@
-# 文本渲染
+# 文字渲染
 
 原文     | [Text Rendering](http://learnopengl.com/#!In-Practice/Text-Rendering)
       ---|---
@@ -6,31 +6,31 @@
 翻译     | [Geequlim](http://geequlim.com)
 校对     | gjy_1992, [BLumia](https://github.com/blumia/)
 
-当你在图形计算领域冒险到了一定阶段以后你可能会想使用OpenGL来绘制文本。然而，可能与你想象的并不一样，使用像OpenGL这样的底层库来把文本渲染到屏幕上并不是一件简单的事情。如果你只需要绘制128种不同的字符(Character)，那么事情可能会简单一些。但是如果你要绘制的字符有着不同的宽、高和边距，事情马上就复杂了。根据你使用语言的不同，你可能会需要多于128个字符。再者，如果你要绘制音乐符、数学符号这些特殊的符号；或者渲染竖排文本呢？一旦你把文本这些复杂的情况考虑进来，你就不会奇怪为什么OpenGL这样的底层API没有包含文本处理了。
+当你在图形计算领域冒险到了一定阶段以后你可能会想使用OpenGL来绘制文字。然而，可能与你想象的并不一样，使用像OpenGL这样的底层库来把文字渲染到屏幕上并不是一件简单的事情。如果你你只需要绘制128种字符，那么事情可能会简单一些。但是当我们要绘制的字符有着不同的宽、高和边距；如果你使用的语言中不止包含128个字符；当你要绘制音乐符、数学符号；以及考虑把如何处理文本自动转行等等情况考虑进来的时候...事情马上就会变得复杂得多，你甚至觉得这些工作并不属于像OpenGL这样的底层图形库该讨论的范畴。
 
-由于OpenGL本身并没有包含任何的文本处理能力，我们必须自己定义一套全新的系统让OpenGL绘制文本到屏幕上。由于文本字符没有图元，我们必须要有点创造力才行。需要使用的一些技术可以是：通过<var>GL_LINES</var>来绘制字形，创建文本的3D网格(Mesh)，或在3D环境中将字符纹理渲染到2D四边形上。
+由于OpenGL本身并没有定义如何渲染文字到屏幕，也没有用于表示文字的基本图形，我们必须自己定义一套全新的方式才能让OpenGL来绘制文字。目前一些技术包括：通过**`GL_LINES`**来绘制字形、创建文字的3D网格、将带有文字的纹理渲染到一个2D方块中。
 
-开发者最常用的一种方式是将字符纹理绘制到四边形上。绘制这些纹理四边形本身其实并不是很复杂，然而检索要绘制文本的纹理却变成了一项有挑战性的工作。本教程将探索多种文本渲染的实现方法，并且使用FreeType库实现一个更加高级但更灵活的渲染文本技术。
+开发者最常用的一种方式是将字符纹理绘制到矩形方块上。绘制这些纹理方块其实并不是很复杂，然而检索要绘制的文字的纹理却变成了一项挑战性的工作。本教程将探索多种文字渲染的实现方法，并且着重对更加现代而且灵活的渲染技术(使用FreeType库)进行讲解。
 
-## 经典文本渲染：位图字体
+## 经典文字渲染：位图字体
 
-早期的时候，渲染文本是通过选择一个需要的字体(Font)（或者自己创建一个），并提取这个字体中所有相关的字符，将它们放到一个单独的大纹理中来实现的。这样一张纹理叫做<def>位图字体</def>(Bitmap Font)，它在纹理的预定义区域中包含了我们想要使用的所有字符。字体的这些字符被称为<def>字形</def>(Glyph)。每个字形都关联着一个特定的纹理坐标区域。当你想要渲染一个字符的时候，你只需要通过渲染这一块特定的位图字体区域到2D四边形上即可。
+在早期渲染文字时，选择你应用程序的字体(或者创建你自己的字体)来绘制文字是通过将所有用到的文字加载在一张大纹理图中来实现的。这张纹理贴图我们把它叫做**位图字体(Bitmap Font)**，它包含了所有我们想要使用的字符。这些字符被称为**字形(Glyph)**。每个字形根据他们的编号被放到位图字体中的确切位置，在渲染这些字形的时候根据这些排列规则将他们取出并贴到指定的2D方块中。
 
-![](../img/06/02/bitmapfont.png)
+![](http://learnopengl.com/img/in-practice/bitmapfont.png)
 
-你可以看到，我们取一张位图字体，（通过仔细选择纹理坐标）从纹理中采样对应的字形，并渲染它们到多个2D四边形上，最终渲染出“OpenGL”文本。通过启用[混合](../04 Advanced OpenGL/03 Blending.md)，让背景保持透明，最终就能渲染一个字符串到屏幕上。这个位图字体是通过Codehead的位图[字体生成器](http://www.codehead.co.uk/cbfg/)生成的。
+上图展示了我们如何从一张位图字体的纹理中通过对字形的合理取样(通过小心地选择字形的纹理坐标)来实现绘制文字“OpenGL”到2D方块中的原理。通过对OpenGL启用混合并让位图字体的纹理背景保持透明，这样就能实现使用OpenGL绘制你想要文字到屏幕的功能。上图的这张位图字体是使用[Codehead的位图字体生成器](http://www.codehead.co.uk/cbfg/)生成的。
 
-使用这种方式绘制文本有许多优势也有很多缺点。首先，它相对来说很容易实现，并且因为位图字体已经预光栅化了，它的效率也很高。然而，这种方式不够灵活。当你想要使用不同的字体时，你需要重新编译一套全新的位图字体，而且你的程序会被限制在一个固定的分辨率。如果你对这些文本进行缩放的话你会看到文本的像素边缘。此外，这种方式通常会局限于非常小的字符集，如果你想让它来支持Extended或者Unicode字符的话就很不现实了。
+使用这种途径来绘制文字有许多优势也有很多缺点。首先，它相对来说很容易实现，并且因为位图字体被预渲染好，使得这种方法效率很高。然而，这种途径并不够灵活。当你想要使用不同的字体时，你不得不重新生成位图字体，以及你的程序会被限制在一个固定的分辨率：如果你对这些文字进行放大的话你会看到文字的像素边缘。此外，这种方式仅局限于用来绘制很少的字符，如果你想让它来扩展支持Unicode文字的话就很不现实了。
 
-这种绘制文本的方式曾经得益于它的高速和可移植性而非常流行，然而现在已经出现更加灵活的方式了。其中一个是我们即将讨论的使用FreeType库来加载TrueType字体的方式。
+这种绘制文字的方式曾经得益于它的高速和可移植性而非常流行，然而现在已经存在更加灵活的方式了。其中一个是我们即将展开讨论的使用FreeType库来加载TrueType字体的方式。
 
-## 现代文本渲染：FreeType
+## 现代文字渲染：FreeType
 
-FreeType是一个能够用于加载字体并将他们渲染到位图以及提供多种字体相关的操作的软件开发库。它是一个非常受欢迎的跨平台字体库，它被用于Mac OS X、Java、PlayStation主机、Linux、Android等平台。FreeType的真正吸引力在于它能够加载TrueType字体。
+FreeType是一个能够用于加载字体并将他们渲染到位图以及提供多种字体相关的操作的软件开发库。它是一个非常受欢迎的跨平台字体库，被用于 Mac OSX、Java、PlayStation主机、Linux、Android等。FreeType的真正吸引力在于它能够加载TrueType字体。
 
-TrueType字体不是用像素或其他不可缩放的方式来定义的，它是通过数学公式（曲线的组合）来定义的。类似于矢量图像，这些光栅化后的字体图像可以根据需要的字体高度来生成。通过使用TrueType字体，你可以轻易渲染不同大小的字形而不造成任何质量损失。
+TrueType字体不采用像素或其他不可缩放的方式来定义，而是一些通过数学公式(曲线的组合)。这些字形，类似于矢量图像，可以根据你需要的字体大小来生成像素图像。通过使用TrueType字体可以轻易呈现不同大小的字符符号并且没有任何质量损失。
 
-FreeType可以在他们的[官方网站](http://www.freetype.org/)中下载到。你可以选择自己用源码编译这个库，如果支持你的平台的话，你也可以使用他们预编译好的库。请确认你将**freetype.lib**添加到你项目的链接库中，并且确认编译器知道头文件的位置。
+FreeType可以在他们的[官方网站](http://www.freetype.org/)中下载到。你可以选择自己编译他们提供的源代码或者使用他们已编译好的针对你的平台的链接库。请确认你将freetype.lib添加到你项目的链接库中，同时你还要添加它的头文件目录到项目的搜索目录中。
 
 然后请确认包含合适的头文件：
 
@@ -39,13 +39,13 @@ FreeType可以在他们的[官方网站](http://www.freetype.org/)中下载到
 #include FT_FREETYPE_H  
 ```
 
-!!! attention
+!!! Attention
     
-    由于FreeType的开发方式（至少在我写这篇文章的时候），你不能将它们的头文件放到一个新的目录下。它们应该保存在你include目录的根目录下。通过使用像 `#include <FreeType/ft2build.h>` 这样的方式导入FreeType可能会出现一些头文件冲突的问题。
+    由于FreeType开发得比较早（至少在我写这篇文章以前就已经开发好了），你不能将它们的头文件放到一个新的目录下，它们应该保存在你包含目录的根目录下。通过使用像 `#include <FreeType/ft2build.h>` 这样的方式导入FreeType可能会出现各种头文件冲突的问题。
 
-FreeType所做的事就是加载TrueType字体并为每一个字形生成位图以及计算几个度量值(Metric)。我们可以提取出它生成的位图作为字形的纹理，并使用这些度量值定位字符的字形。
+FreeType要做的事就是加载TrueType字体并为每一个字形生成位图和几个度量值。我们可以取出它生成的位图作为字形的纹理，将这些度量值用作字形纹理的位置、偏移等描述。
 
-要加载一个字体，我们只需要初始化FreeType库，并且将这个字体加载为一个FreeType称之为<def>面</def>(Face)的东西。这里为我们加载一个从**Windows/Fonts**目录中拷贝来的TrueType字体文件**arial.ttf**。
+要加载一个字体，我们需要做的是初始化FreeType并且将这个字体加载为FreeType称之为面(Face)的东西。这里为我们加载一个从Windows/Fonts目录中拷贝来的TrueType字体文件arial.ttf。
 
 ```c++
 FT_Library ft;
@@ -54,58 +54,60 @@ if (FT_Init_FreeType(&ft))
 
 FT_Face face;
 if (FT_New_Face(ft, "fonts/arial.ttf", 0, &face))
-    std::cout << "ERROR::FREETYPE: Failed to load font" << std::endl;
+    std::cout << "ERROR::FREETYPE: Failed to load font" << std::endl;  
 ```
 
-这些FreeType函数在出现错误时将返回一个非零的整数值。
+这些FreeType函数在出现错误的情况下返回一个非零整数值。
 
-当面加载完成之后，我们需要定义字体大小，这表示着我们要从字体面中生成多大的字形：
+一旦我们加载字体面完成，我们还要定义文字大小，这表示着我们要从字体面中生成多大的字形：
 
 ```c++
 FT_Set_Pixel_Sizes(face, 0, 48);  
 ```
-此函数设置了字体面的宽度和高度，将宽度值设为0表示我们要从字体面通过给定的高度中动态计算出字形的宽度。
+此函数设置了字体面的宽度和高度，将宽度值设为0表示我们要从字体面通过给出的高度中动态计算出字形的宽度。
 
-一个FreeType面中包含了一个字形的集合。我们可以调用<fun>FT_Load_Char</fun>函数来将其中一个字形设置为激活字形。这里我们选择加载字符字形'X'：
+一个字体面中包含了所有字形的集合。我们可以通过调用`FT_Load_Char`函数来激活当前要表示的字形。这里我们选在加载字母字形'X'：
 
 ```c++
 if (FT_Load_Char(face, 'X', FT_LOAD_RENDER))
-    std::cout << "ERROR::FREETYTPE: Failed to load Glyph" << std::endl;
+    std::cout << "ERROR::FREETYTPE: Failed to load Glyph" << std::endl;  
 ```
 
-通过将<var>FT_LOAD_RENDER</var>设为加载标记之一，我们告诉FreeType去创建一个8位的灰度位图，我们可以通过`face->glyph->bitmap`来访问这个位图。
+通过将**`FT_LOAD_RENDER`**设为一个加载标识，我们告诉FreeType去创建一个8位的灰度位图，我们可以通过`face->glyph->bitmap`来取得这个位图。
 
-使用FreeType加载的每个字形没有相同的大小（不像位图字体那样）。使用FreeType生成的位图的大小恰好能包含这个字符可见区域。例如生成用于表示'.'的位图的大小要比表示'X'的小得多。因此，FreeType同样也加载了一些度量值来指定每个字符的大小和位置。下面这张图展示了FreeType对每一个字符字形计算的所有度量值。
+使用FreeType加载的字形位图并不像我们使用位图字体那样持有相同的尺寸大小。使用FreeType生产的字形位图的大小是恰好能包含这个字形的尺寸。例如生产用于表示'.'的位图的尺寸要比表示'X'的小得多。因此，FreeType在加载字形的时候还生产了几个度量值来描述生成的字形位图的大小和位置。下图展示了FreeType的所有度量值的涵义。
+
+![](http://learnopengl.com/img/in-practice/glyph.png)
+
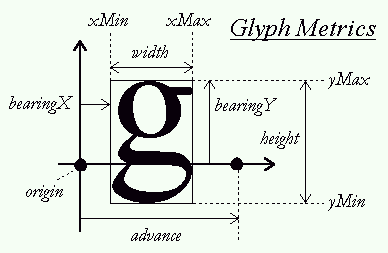
+每一个字形都放在一个水平的基线(Baseline)上，上图中被描黑的水平箭头表示该字形的基线。这条基线类似于拼音四格线中的第二根水平线，一些字形被放在基线以上(如'x'或'a')，而另一些则会超过基线以下(如'g'或'p')。FreeType的这些度量值中包含了字形在相对于基线上的偏移量用来描述字形相对于此基线的位置，字形的大小，以及与下一个字符之间的距离。下面列出了我们在渲染字形时所需要的度量值的属性：
 
-![](../img/06/02/glyph.png)
 
-每一个字形都放在一个水平的<def>基准线</def>(Baseline)上（即上图中水平箭头指示的那条线）。一些字形恰好位于基准线上（如'X'），而另一些则会稍微越过基准线以下（如'g'或'p'）（译注：即这些带有下伸部的字母，可以见[这里](https://www.supremo.tv/typeterms/)）。这些度量值精确定义了摆放字形所需的每个字形距离基准线的偏移量，每个字形的大小，以及需要预留多少空间来渲染下一个字形。下面这个表列出了我们需要的所有属性。
 
 属性|获取方式|生成位图描述
----|---|---
-**width**   | `face->glyph->bitmap.width` | 位图宽度（像素）
-**height**  | `face->glyph->bitmap.rows`  | 位图高度（像素）
-**bearingX** | `face->glyph->bitmap_left` | 水平距离，即位图相对于原点的水平位置（像素）
-**bearingY** | `face->glyph->bitmap_top` | 垂直距离，即位图相对于基准线的垂直位置（像素）
-**advance** | `face->glyph->advance.x`  | 水平预留值，即原点到下一个字形原点的水平距离（单位：1/64像素）
+---|---
+width   | face->glyph->bitmap.width | 宽度，单位:像素
+height  | face->glyph->bitmap.rows  | 高度，单位:像素
+bearingX| face->glyph->bitmap_left| 水平位置(相对于起点origin)，单位:像素
+bearingY| face->glyph->bitmap_top | 垂直位置(相对于基线Baseline)，单位:像素
+advance | face->glyph->advance.x  | 起点到下一个字形的起点间的距离(单位:1/64像素)
 
-在需要渲染字符时，我们可以加载一个字符字形，获取它的度量值，并生成一个纹理，但每一帧都这样做会非常没有效率。我们应将这些生成的数据储存在程序的某一个地方，在需要渲染字符的时候再去调用。我们会定义一个非常方便的结构体，并将这些结构体存储在一个<fun>map</fun>中。
+在我们想要渲染字符到屏幕的时候就能根据这些度量值来生成对应字形的纹理了，然而每次渲染都这样做显然不是高效的。我们应该将这些生成的数据储存在应用程序中，在渲染过程中再去取。方便起见，我们需要定义一个用来储存这些属性的结构体,并创建一个字符表来存储这些字形属性。
 
 ```c++
 struct Character {
-    GLuint     TextureID;  // 字形纹理的ID
-    glm::ivec2 Size;       // 字形大小
-    glm::ivec2 Bearing;    // 从基准线到字形左部/顶部的偏移值
-    GLuint     Advance;    // 原点距下一个字形原点的距离
+    GLuint     TextureID;  // 字形纹理ID
+    glm::ivec2 Size;       // 字形大大小
+    glm::ivec2 Bearing;    // 字形基于基线和起点的位置
+    GLuint     Advance;    // 起点到下一个字形起点的距离
 };
 
 std::map<GLchar, Character> Characters;
 ```
 
-对于这个教程来说，本着让一切简单的目的，我们只生成ASCII字符集的前128个字符。对每一个字符，我们生成一个纹理并保存相关数据至<fun>Character</fun>结构体中，之后再添加至<var>Characters</var>这个映射表中。这样子，渲染一个字符所需的所有数据就都被储存下来备用了。
+本教程本着让一切简单的目的，我们只生成表示128个ASCII字符的字符表。并为每一个字符储存纹理和一些度量值。这样，所有需要的字符就被存下来备用了。
 
 ```c++
-glPixelStorei(GL_UNPACK_ALIGNMENT, 1); //禁用字节对齐限制
+glPixelStorei(GL_UNPACK_ALIGNMENT, 1); //禁用byte-alignment限制
 for (GLubyte c = 0; c < 128; c++)
 {
     // 加载字符的字形 
@@ -114,7 +116,7 @@ for (GLubyte c = 0; c < 128; c++)
         std::cout << "ERROR::FREETYTPE: Failed to load Glyph" << std::endl;
         continue;
     }
-    // 生成纹理
+    // 生成字形纹理
     GLuint texture;
     glGenTextures(1, &texture);
     glBindTexture(GL_TEXTURE_2D, texture);
@@ -134,7 +136,7 @@ for (GLubyte c = 0; c < 128; c++)
     glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
     glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
     glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
-    // 储存字符供之后使用
+    // 将字符存储到字符表中备用
     Character character = {
         texture, 
         glm::ivec2(face->glyph->bitmap.width, face->glyph->bitmap.rows),
@@ -145,15 +147,15 @@ for (GLubyte c = 0; c < 128; c++)
 }
 ```
 
-在这个for循环中我们遍历了ASCII集中的全部128个字符，并获取它们对应的字符字形。对每一个字符，我们生成了一个纹理，设置了它的选项，并储存了它的度量值。有趣的是我们这里将纹理的`internalFormat`和`format`设置为<var>GL_RED</var>。通过字形生成的位图是一个8位灰度图，它的每一个颜色都由一个字节来表示。因此我们需要将位图缓冲的每一字节都作为纹理的颜色值。这是通过创建一个特殊的纹理实现的，这个纹理的每一字节都对应着纹理颜色的红色分量（颜色向量的第一个字节）。如果我们使用一个字节来表示纹理的颜色，我们需要注意OpenGL的一个限制：
+在这个for循环中我们将所有ASCII中的128个字符设置合适的字形。为每一个字符创建纹理并存储它们的部分度量值。有趣的是我们这里将纹理的格式设置为**GL_RED**。通过字形生成的位图是8位灰度图，他的每一个颜色表示为一个字节。因此我们需要将每一位都作为纹理的颜色值。我们通过创建每一个字节表示一个颜色的红色分量(颜色分量的第一个字节)来创建字形纹理。我们想用一个字节来表示纹理颜色，这需要提前通知OpenGL
 
 ```c++
 glPixelStorei(GL_UNPACK_ALIGNMENT, 1);   
 ```
 
-OpenGL要求所有的纹理都是4字节对齐的，即纹理的大小永远是4字节的倍数。通常这并不会出现什么问题，因为大部分纹理的宽度都为4的倍数并/或每像素使用4个字节，但是现在我们每个像素只用了一个字节，它可以是任意的宽度。通过将纹理解压对齐参数设为1，这样才能确保不会有对齐问题（它可能会造成段错误）。
+OpenGL要求所有的纹理颜都必须是4字节队列，这样纹理的内存大小就一定是4字节的整数倍。通常这并不会出现什么问题，因为通常的纹理都有4或者4的整数被的储存大小，但是现在我们只用一位来表示每一个像素颜色，此时的纹理可能有任意内存长度。通过将纹理解压参数设为1，这样才能确保不会有内存对齐的解析问题。
 
-当你处理完字形后不要忘记清理FreeType的资源。
+当你处理完字形后同样不要忘记清理FreeType的资源。
 
 ```c++
 FT_Done_Face(face);
@@ -162,7 +164,7 @@ FT_Done_FreeType(ft);
 
 ### 着色器
 
-我们将使用下面的顶点着色器来渲染字形：
+我们需要使用下面的顶点着色器来渲染字形：
 
 ```c++
 #version 330 core
@@ -175,10 +177,10 @@ void main()
 {
     gl_Position = projection * vec4(vertex.xy, 0.0, 1.0);
     TexCoords = vertex.zw;
-}
+}  
 ```
 
-我们将位置和纹理纹理坐标的数据合起来存在一个<fun>vec4</fun>中。这个顶点着色器将位置坐标与一个投影矩阵相乘，并将纹理坐标传递给片段着色器：
+我们将位置和纹理纹理坐标的数据合起来存在一个`vec4`中。顶点着色器将会将位置坐标与投影矩阵相乘，并将纹理坐标转发给片段着色器:
 
 ```c++
 #version 330 core
@@ -192,27 +194,26 @@ void main()
 {    
     vec4 sampled = vec4(1.0, 1.0, 1.0, texture(text, TexCoords).r);
     color = vec4(textColor, 1.0) * sampled;
-}
+}  
 ```
 
-片段着色器有两个uniform变量：一个是单颜色通道的字形位图纹理，另一个是颜色uniform，它可以用来调整文本的最终颜色。我们首先从位图纹理中采样颜色值，由于纹理数据中仅存储着红色分量，我们就采样纹理的**r**分量来作为取样的alpha值。通过变换颜色的alpha值，最终的颜色在字形背景颜色上会是透明的，而在真正的字符像素上是不透明的。我们也将RGB颜色与<var>textColor</var>这个uniform相乘，来变换文本颜色。
+片段着色器有两个uniform变量：一个是单颜色通道的字形位图纹理，另一个是文字的颜色，我们可以同调整它来改变最终输出的字体颜色。我们首先从位图纹理中采样，由于纹理数据中仅存储着红色分量，我们就通过**`r`**分量来作为取样颜色的aplpha值。结果值是一个字形背景为纯透明，而字符部分为不透明的白色的颜色。我们将此颜色与字体颜色uniform值相乘就得到了要输出的字符颜色了。
 
-当然我们需要启用[混合](../04 Advanced OpenGL/03 Blending.md)才能让这一切行之有效：
+当然我们必需开启混合才能让这一切行之有效：
 
 ```c++
 glEnable(GL_BLEND);
 glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);  
 ```
-
-对于投影矩阵，我们将使用一个正射投影矩阵(Orthographic Projection Matrix)。对于文本渲染我们（通常）都不需要透视，使用正射投影同样允许我们在屏幕坐标系中设定所有的顶点坐标，如果我们使用如下方式配置：
+至于投影矩阵我们将使用一个正交投影矩阵。对于文字渲染我们通常都不需要进行透视，使用正交投影也能保证我们所有的顶点坐标设置有效：
 
 ```c++
 glm::mat4 projection = glm::ortho(0.0f, 800.0f, 0.0f, 600.0f);
 ```
 
-我们设置投影矩阵的底部参数为`0.0f`，并将顶部参数设置为窗口的高度。这样做的结果是我们指定了y坐标的范围为屏幕底部(0.0f)至屏幕顶部(600.0f)。这意味着现在点(0.0, 0.0)对应左下角（译注：而不再是窗口正中间）。
+我们设置投影矩阵的底部参数为0.0f并将顶部参数设置为窗口的高度。这样做的结果是我们可以通过设置0.0f~600.0f的纵坐标来表示顶点在窗口中的垂直位置。这意味着现在点(0.0,0.0)表示左下角而不再是窗口正中间。
 
-最后要做的事是创建一个VBO和VAO用来渲染四边形。现在我们在初始化VBO时分配足够的内存，这样我们可以在渲染字符的时候再来更新VBO的内存。
+最后要做的事是创建一个VBO和VAO用来渲染方块。现在我们分配足够的内存来初始化VBO然后在我们渲染字符的时候再来更新VBO的内存。
 
 ```c++
 GLuint VAO, VBO;
@@ -227,24 +228,24 @@ glBindBuffer(GL_ARRAY_BUFFER, 0);
 glBindVertexArray(0);      
 ```
 
-每个2D四边形需要6个顶点，每个顶点又是由一个4float向量（译注：一个纹理坐标和一个顶点坐标）组成，因此我们将VBO的内存分配为6 * 4个float的大小。由于我们会在绘制字符时经常更新VBO的内存，所以我们将内存类型设置为<var>GL_DYNAMIC_DRAW</var>。
+每个2D方块需要6个顶点，每个顶点又是由一个4维向量（一个纹理坐标和一个顶点坐标）组成，因此我们将VBO的内存分配为6*4个float的大小。由于我们会在绘制字符时更新这断内存，所以我们将内存类型设置为`GL_DYNAMIC_DRAW`
 
-### 渲染一行文本
+### 渲染一行文字
 
-要渲染一个字符，我们从之前创建的<var>Characters</var>映射表中取出对应的<fun>Character</fun>结构体，并根据字符的度量值来计算四边形的维度。根据四边形的维度我们就能动态计算出6个描述四边形的顶点，并使用<fun>glBufferSubData</fun>函数更新VBO所管理内存的内容。
+要渲染一个字符，我们从之前创建的字符表中取出一个字符结构体，根据字符的度量值来计算方块的大小。根据方块的大小我们就能计算出6个描述方块的顶点，并使用`glBufferSubData`函数将其更新到VBO所在内内存中。
 
-我们创建一个叫做<fun>RenderText</fun>的函数渲染一个字符串：
+我们创建一个函数用来渲染一行文字:
 
 ```c++
 void RenderText(Shader &s, std::string text, GLfloat x, GLfloat y, GLfloat scale, glm::vec3 color)
 {
-    // 激活对应的渲染状态
+    // 激活合适的渲染状态
     s.Use();
     glUniform3f(glGetUniformLocation(s.Program, "textColor"), color.x, color.y, color.z);
     glActiveTexture(GL_TEXTURE0);
     glBindVertexArray(VAO);
 
-    // 遍历文本中所有的字符
+    // 对文本中的所有字符迭代
     std::string::const_iterator c;
     for (c = text.begin(); c != text.end(); c++)
     {
@@ -255,7 +256,7 @@ void RenderText(Shader &s, std::string text, GLfloat x, GLfloat y, GLfloat scale
 
         GLfloat w = ch.Size.x * scale;
         GLfloat h = ch.Size.y * scale;
-        // 对每个字符更新VBO
+        // 当前字符的VBO
         GLfloat vertices[6][4] = {
             { xpos,     ypos + h,   0.0, 0.0 },            
             { xpos,     ypos,       0.0, 1.0 },
@@ -265,23 +266,23 @@ void RenderText(Shader &s, std::string text, GLfloat x, GLfloat y, GLfloat scale
             { xpos + w, ypos,       1.0, 1.0 },
             { xpos + w, ypos + h,   1.0, 0.0 }           
         };
-        // 在四边形上绘制字形纹理
+        // 在方块上绘制字形纹理
         glBindTexture(GL_TEXTURE_2D, ch.textureID);
-        // 更新VBO内存的内容
+        // 更新当前字符的VBO
         glBindBuffer(GL_ARRAY_BUFFER, VBO);
         glBufferSubData(GL_ARRAY_BUFFER, 0, sizeof(vertices), vertices); 
         glBindBuffer(GL_ARRAY_BUFFER, 0);
-        // 绘制四边形
+        // 绘制方块
         glDrawArrays(GL_TRIANGLES, 0, 6);
         // 更新位置到下一个字形的原点，注意单位是1/64像素
-        x += (ch.Advance >> 6) * scale; // 位偏移6个单位来获取单位为像素的值 (2^6 = 64)
+        x += (ch.Advance >> 6) * scale; //(2^6 = 64)
     }
     glBindVertexArray(0);
     glBindTexture(GL_TEXTURE_2D, 0);
 }
 ```
 
-这个函数的内容应该非常明显了：我们首先计算出四边形的原点坐标（为<var>xpos</var>和<var>ypos</var>）和它的大小（为<var>w</var>和<var>h</var>），并生成6个顶点形成这个2D四边形；注意我们将每个度量值都使用<var>scale</var>进行缩放。接下来我们更新了VBO的内容、并渲染了这个四边形。
+这个函数的内容注释的比较详细了：我们首先计算出方块的起点坐标（即`xpos`和`ypos`）和它的大小（即`w`和`h`），并为该方块生成6个顶点；注意我们在缩放的同时会将部分度量值也进行缩放。接着我们更新方块的VBO、绑定字形纹理来渲染它。
 
 其中这行代码需要加倍留意：
 
@@ -289,13 +290,14 @@ void RenderText(Shader &s, std::string text, GLfloat x, GLfloat y, GLfloat scale
 GLfloat ypos = y - (ch.Size.y - ch.Bearing.y);   
 ```
 
-一些字符（如'p'或'q'）需要被渲染到基准线以下，因此字形四边形也应该被摆放在<fun>RenderText</fun>的<var>y</var>值以下。<var>ypos</var>的偏移量可以从字形的度量值中得出：
+一些字符(诸如'p'或'q')需要被渲染到基线以下，因此字形方块也应该讲y位置往下调整。调整的量就是便是字形度量值中字形的高度和BearingY的差：
 
-![](../img/06/02/glyph_offset.png)
+![](http://learnopengl.com/img/in-practice/glyph_offset.png)
 
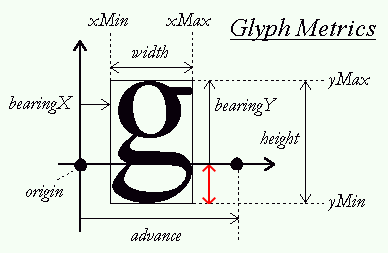
-要计算这段距离，即偏移量，我们需要找出字形在基准线之下延展出去的距离。在上图中这段距离用红色箭头标出。从度量值中可以看到，我们可以通过用字形的高度减去`bearingY`来计算这段向量的长度。对于那些正好位于基准线上的字符（如'X'），这个值正好是0.0。而对于那些超出基准线的字符（如'g'或'j'），这个值则是正的。
+要计算这段偏移量的距离，我们需要指出是字形在基线以下的部分最底断到基线的距离。在上图中这段距离用红色双向箭头标出。如你所见，在字形度量值中，我们可以通过用字形的高度减去bearingY来计算这段向量的长度。这段距离有可能是0.0f(如'x'字符)
+，或是超出基线底部的距离的长度(如'g'或'j')。
 
-如果你每件事都做对了，那么你现在已经可以使用下面的语句成功渲染字符串了：
+如果你每件事都做对了，那么你现在已经可以使用下面的句子成功地渲染字符串了：
 
 ```c++
 RenderText(shader, "This is sample text", 25.0f, 25.0f, 1.0f, glm::vec3(0.5, 0.8f, 0.2f));
@@ -304,20 +306,18 @@ RenderText(shader, "(C) LearnOpenGL.com", 540.0f, 570.0f, 0.5f, glm::vec3(0.3, 0
 
 渲染效果看上去像这样：
 
-![](../img/06/02/text_rendering.png)
+![](http://learnopengl.com/img/in-practice/text_rendering.png)
 
-你可以从[这里](http://learnopengl.com/code_viewer.php?code=in-practice/text_rendering)获取这个例子的源代码。
+你可以从这里获取这个例子的[源代码](http://learnopengl.com/code_viewer.php?code=in-practice/text_rendering)。
 
-为了让你更好理解我们是怎么计算四边形顶点的，我们可以关闭混合来看看真正渲染出来的四边形是什么样子的：
+通过关闭字形纹理的绑定，能够给你对文字方块的顶点计算更好的理解，它看上去像这样：
 
-![](../img/06/02/text_rendering_quads.png)
+![](http://learnopengl.com/img/in-practice/text_rendering_quads.png)
 
-可以看到，大部分的四边形都位于一条（想象中的）基准线上，而对应'p'或'('字形的四边形则稍微向下偏移了一些。
+可以看出，对应'p'和'('等字形的方块明显向下偏移了一些，通过这些你就能清楚地看到那条传说中的基线了。
 
-## 更进一步
+## 关于未来
 
-本教程演示了如何使用FreeType库绘制TrueType文本。这种方式灵活、可缩放并支持多种字符编码。然而，由于我们对每一个字形都生成并渲染了纹理，你的应用程序可能并不需要这么强大的功能。性能更好的位图字体也许是更可取的，因为对所有的字形我们只需要一个纹理。当然，最好的方式是结合这两种方式，动态生成包含所有字符字形的位图字体纹理，并用FreeType加载。这为渲染器节省了大量纹理切换的开销，并且根据字形的排列紧密程度也可以节省很多的性能开销。
+本教程演示了如何使用FreeType绘制TrueType文字。这种方式灵活、可缩放并支持多种字符编码。然而，你的应用程序可能并不需要这么强大的功能，性能更好的点阵字体也许是更可取的。当然你可以结合这两种方法通过动态生成位图字体中所有字符字形。这节省了从大量的纹理渲染器开关和基于每个字形紧密包装可以节省相当的一些性能。
 
-
-
-另一个使用FreeType字体的问题是字形纹理是储存为一个固定的字体大小的，因此直接对其放大就会出现锯齿边缘。此外，对字形进行旋转还会使它们看上去变得模糊。这个问题可以通过储存每个像素距最近的字形轮廓的距离，而不是光栅化的像素颜色，来缓解。这项技术被称为<def>有向距离场</def>(Signed Distance Fields)，Valve在几年前发表过一篇了[论文](https://steamcdn-a.akamaihd.net/apps/valve/2007/SIGGRAPH2007_AlphaTestedMagnification.pdf)，讨论了他们通过这项技术来获得非常棒的3D渲染效果。
+另一个使用FreeType字体的问题是字形纹理是对应着一个固定的字体大小的，因此直接对其放大就会出现锯齿边缘。此外，对字形进行旋转还会使它们看上去变得模糊。通过将每个像素设为最近的字形轮廓的像素，而不是直接设为实际栅格化的像素，可以减轻这些问题。这项技术被称为**有向距离场(Signed Distance Fields)**，Valve在几年前发表过一篇了[论文](http://www.valvesoftware.com/publications/2007/SIGGRAPH2007_AlphaTestedMagnification.pdf)，探讨了他们通过这项技术来获得好得惊人的3D渲染效果。

docs/06 In Practice/2D-Game/01 Breakout.md

@@ -4,7 +4,7 @@
       ---|---
 作者     | JoeyDeVries
 翻译     | HHz(qq:1158332489)
-校对     | Krasjet
+校对     |  Meow J
 
 看完前面的教程之后我们已经了解了非常多的OpenGL内部工作原理，并且我们已经能够用这些知识绘制一些复杂的图形。然而，除了之前的几个技术演示之外，我们还没有真正利用OpenGL开发一个实际应用。这篇教程为OpenGL 2D游戏制作系列教程的入门篇。这个系列教程将展示我们该如何将OpenGL应用到更大，更复杂的环境中。注意这个系列教程不一定会引入新的OpenGL概念，但会或多或少地向我们展示如何将所学的概念应用到更大的程序中去。
 

docs/06 In Practice/2D-Game/02 Setting up.md

@@ -4,106 +4,103 @@
       ---|---
 作者     | JoeyDeVries
 翻译     | [ZMANT](https://github.com/Itanq)
-校对     | Krasjet
+校对     | 暂无
 
-!!! note
+## 设置
 
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
+在我们开始实际构造这个游戏之前，我们首先需要设置一些简单的框架来处理这个游戏，这个游戏将会用到几个第三方库，它们大多数都已经在前面的教程中介绍过了。不管在那个地方需要用到新的库的时候，我们都会作出适当的介绍。
 
-在开始真正写游戏机制之前，我们首先需要配置一个简单的框架，用来存放这个游戏，这个游戏将会用到几个第三方库，它们的大多数都已经在前面的教程中介绍过了。在需要用到新的库的时候，我会作出适当的介绍。
+首先，我们定义一个叫做`Game`的类来包含所有有关的渲染和游戏设置代码。有了这个类，我们就可以用这个类把游戏代码(稍稍的)有组织的嵌入到游戏窗口代码中。用这种方式，你就可以把相同的代码迁移到完全不同的窗口库(比如 SDL或SFML)而不需要做太多的工作。
 
-首先，我们定义一个所谓的<def>超级</def>(Uber)游戏类，它会包含所有相关的渲染和游戏代码。这个游戏类的主要作用是（简单）管理你的游戏代码，并与此同时将所有的窗口代码从游戏中解耦。这样子的话，你就可以把相同的类迁移到完全不同的窗口库（比如SDL或SFML）而不需要做太多的工作。
+> 存在有成千上万的方式来抽象并概括游戏/图形代码然后封装到类和对象中。在这个教程中，你刚好会看到有一个方法来解决这个问题。如果你感到有一个更好的方法，尽量实现你的改进。
 
-!!! important
+这个`Game`类封装了一个初始化函数，一个更新函数，一个处理输入函数以及一个渲染函数：
 
-	抽象并归纳游戏或图形代码至类与对象中有成千上万种方式。在这个系列教程中你所看到的仅是其中的一种。如果你觉得能有更好的方式进行实现，你可以尝试改进我的这个实现。
-
-这个游戏类封装了一个初始化函数、一个更新函数、一个处理输入函数以及一个渲染函数：
-
-```c++
+```C++
 class Game
 {
     public:
-        // 游戏状态
+        // Game state
         GameState  State;	
         GLboolean  Keys[1024];
         GLuint	   Width, Height;
-        // 构造函数/析构函数
+        // Constructor/Destructor
         Game(GLuint width, GLuint height);
         ~Game();
-        // 初始化游戏状态（加载所有的着色器/纹理/关卡）
+        // Initialize game state (load all shaders/textures/levels)
         void Init();
-        // 游戏循环
+        // GameLoop
         void ProcessInput(GLfloat dt);
         void Update(GLfloat dt);
         void Render();
 };
 ```
 
-这个类应该包含了所有在一个游戏类中会出现的东西。我们通过给定一个宽度和高度（对应于你玩游戏时的分辨率）来初始化这个游戏，并且使用<fun>Init</fun>函数来加载着色器、纹理并且初始化所有的游戏状态。我们可以通过调用<fun>ProcessInput</fun>函数，并使用存储在<var>Keys</var>数组里的数据来处理输入。并且在<fun>Update</fun>函数里面我们可以更新游戏设置状态（比如玩家/球的移动）。最后，我们还可以调用<fun>Render</fun>函数来对游戏进行渲染。注意，我们将运动逻辑与渲染逻辑分开了。
+这个类可能就是你期望中的游戏类。我们通过一个`width`和`height`(对应于你玩游戏时的设备分辨率)来初始化一个游戏实例并且使用`Init`函数来加载着色器、纹理以及初始化游戏状态。我们可以通过调用`ProcessInput`函数来使用存储在`Keys`数组里的数据来处理输入并且在`Update`函数里面更新游戏设置状态(比如玩家/球的移动)。最后，我们还可以在`Render`函数里面渲染游戏。注意，我们在渲染逻辑里面分离出了运动逻辑。
 
-这个<fun>Game</fun>类同样了封装了一个叫做<var>State</var>的变量，它的类型是<def>GameState</def>，定义如下：
+这个`Game`类同样了封装了一个叫做`State`的变量，它的类型`GameState`如下定义：
 
-```c++
-// 代表了游戏的当前状态
+```C++
+// Represents the current state of the game
 enum GameState {
     GAME_ACTIVE,
     GAME_MENU,
     GAME_WIN
-}; 
+};
 ```
 
-这个类可以帮助我们跟踪游戏的当前状态。这样的话我们就可以根据当前游戏的状态来决定渲染和/或者处理不同的元素(Item)了（比如当我们在游戏菜单界面的时候就可能需要渲染和处理不同的元素了）。
+这可以使我们跟踪游戏当前的状态。这样我们就可以根据当前游戏的状态来决定渲染或者处理不同的元素(比如当我们在游戏菜单界面的时候就可能需要渲染和处理不同的元素)。
 
-目前为止，这个游戏类的函数还完全是空的，因为我们还没有写游戏的实际代码，但这里是`Game`类的[头文件](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_setting-up.h)和[代码文件](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_setting-up)。
+目前为止，这个`Game`类的函数还完全是空的，因为我们还没有写实际的实现代码，但这里就是`Game`类的[header](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_setting-up.h)和[code](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_setting-up)文件。
 
-## 工具类
+## 通用
 
-因为我们正在开发一个大型应用，所以我们将不得不频繁地重用一些OpenGL的概念，比如纹理和着色器等。因此，为这两个元素创建一个更加易用的接口也是情理之中的事了，就像在我们前面教程中创建的那个着色器类一样。
+因为我们正在开发一个大型应用，所以我们将不得不频繁的重用一些OpenGL的概念，比如纹理和着色器等。因此，为这两个元素(items)创建一个更加易用的接口就是情理之中的事了，就像在我们前面一个教程中创建的那个`shader`类一样。
 
-着色器类会接受两个或三个（如果有几何着色器）字符串，并生成一个编译好的着色器（如果失败的话则生成错误信息）。这个着色器类也包含很多工具(Utility)函数来帮助快速设置uniform值。纹理类会接受一个字节(Byte)数组以及宽度和高度，并（根据设定的属性）生成一个2D纹理图像。同样，这个纹理类也会封装一些工具函数。
+定义一个着色器类，它接收两个或三个字符串(如果有几何着色器)然后生成一个编译好的着色器(或者如果失败的话就生成一条错误信息)。这个着色器类同样也包含大量实用的函数来快速的设置`uniform`变量。同样也定义一个纹理类，它从给定的字节数组中生成一个2D纹理图像(基于它的内容)。并且这个纹理类同样也封装了许多实用的函数。
 
-我们并不会深入讨论这些类的实现细节，因为学到这里你应该可以很容易地理解它们是如何工作的了。出于这个原因，你可以在下面找到它们的头文件和代码文件，都有详细的注释：
+我们并不打算钻研这些类实现的细节，因为学到这里你应该可以很容易的理解它们是如何工作的了。出于这个原因你可以找到它们的头文件和实现的代码文件，有详细的注释，如下：
 
-- **着色器**：[头文件](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/shader.h)，[代码](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/shader)
-- **纹理**：[头文件](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/texture.h)，[代码](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/texture)
+>* Shader : [header](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/shader.h),[code](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/shader)
+>* Texture: [header](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/texture.h),[code](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/texture)
 
-注意当前的纹理类仅是为2D纹理设计的，但你很容易就可以将其扩张至更多的纹理类型。
+注意到当前的这个纹理类仅仅设置成单一的`2D`纹理，但你可以很容易的通过可选的纹理类型来扩展。
 
-## 资源管理
+## 资源管理器
 
-尽管着色器与纹理类的函数本身就很棒了，它们仍需要有一个字节数组或一些字符串来调用它们。我们可以很容易将文件加载代码嵌入到它们自己的类中，但这稍微有点违反了<def>单一功能原则</def>(Single Responsibility Principle)，即这两个类应当分别仅仅关注纹理或者着色器本身，而不是它们的文件加载机制。
+当着色器和纹理类的函数被他们自己使用的时候，他们确实需要一个字节数组或是几个字符串来初始化他们。我们可以很容易的在他们自己的类里面嵌入文件的加载代码，但这就稍微有点违反`单一职责原则`，(也就是说)在这个类里我们应该仅仅关注纹理或着色器本身而不需要关注他们的文件加载结构。
 
-出于这个原因，我们通常会用一个更加有组织的方法（译注：来实现文件的加载），就是创建一个所谓<def>资源管理器</def>的实体，专门加载游戏相关的资源。创建一个资源管理器有多种方法。在这个教程中我们选择使用一个单一实例(Singleton)的静态资源管理器，（由于它静态的本质）它在整个工程中都可以使用，它会封装所有的已加载资源以及一些相关的加载功能。
+出于这个原因，通常用一个更加有组织的方法(来实现文件的加载)，就是创建一个叫做`resource manager`的单独实体类来加载游戏相关的资源。这里有好几个方法来实现`resouce manager`；在这个教程里我们选择使用一个单独的静态`resouce manager`(就是给它静态属性)，也就是说可以在整个工程中使用它来加载资源以及使用和她相关加载功能。
 
-使用一个具有静态属性的单一实例类有很多优点也有很多缺点。它主要的缺点就是这样会损失OOP属性，并且丧失构造与析构的控制。不过，对于我们这种小项目来说是这些问题也是很容易处理的。
+使用具有静态属性的单独的类有很多好处，但它主要的坏处就是会失去`OOP`特性以及控制结构/破坏。不过，这些对于小项目来说是很容易处理的。
 
-和其它类的文件一样，这个资源管理器的代码如下：
+就像其他的类文件一样，这个资源管理器的列表如下：
 
-- **资源管理器**：[头文件](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/resource_manager.h)，[代码](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/resource_manager)
+>* Resource Manager: [header](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/resource_manager.h), [code](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/resource_manager)
 
-通过使用资源管理器，我们可以很容易地把着色器加载到程序里面：
+使用资源管理我们可以很容易的把着色器加载到程序里面，比如：
 
-```c++
+```C++
 Shader shader = ResourceManager::LoadShader("vertex.vs", "fragment.vs", nullptr, "test");
-// 接下来使用它
+// then use it
 shader.Use();
-// 或者
+// or
 ResourceManager::GetShader("test").Use();
 ```
 
-<fun>Game</fun>类、资源管理器类，以及很容易管理的<fun>Shader</fun>和<fun>Texture2D</fun>类一起组成了之后教程的基础，我们之后会广泛使用这些类来实现我们的Breakout游戏。
+通过定义的`Game`类和`resouce manager`类一起就可以很很容易管理`Shader`和`Texture2D`，基于这个基础，在以后的教程里我们将会广泛的使用这些类来实现这个`Breakout`游戏。
 
 ## 程序
 
-我们仍然需要为这个游戏创建一个窗口并且设置一些OpenGL的初始状态。我们确保使用OpenGL的[面剔除](../../04 Advanced OpenGL/04 Face culling.md)功能和[混合](../../04 Advanced OpenGL/03 Blending.md)功能。我们不需要使用深度测试，因为这个游戏完全是2D的，所有顶点都有相同的z值，所以开启深度测试并没有什么用，反而可能造成深度冲突(Z-fighting)。
+对这个游戏，我们仍然需要创建一个窗口并且设置OpenGL的初识状态。我们确保使用OpenGL的[面剔除](http://learnopengl.com/#!Advanced-OpenGL/Face-culling)功能和它的[混合](http://learnopengl.com/#!Advanced-OpenGL/Blending)功能。我们不需要使用深度测试；因为这个游戏完全是一个二维的，所有顶点的`z`坐标都具有相同的值。因此开启深度测试并没有什么用还有可能造成`z-fighting`现象。
 
-这个Breakout游戏的起始代码非常简单：我们用GLFW创建一个窗口，注册一些回调函数，创建一个Game对象，并将所有相关的信息都传到游戏类中。代码如下：
+这个`Breakout`游戏开始时候的代码相当的简单：我们用`GLFW`创建一个窗口，注册了一些回调函数，创建一个`Game`实例并且调用了`Game`类所有相关的函数。这个代码如下：
 
-- **程序**：[代码](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/program)
+>* Program: [code](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/program)
 
-运行这个代码，你应该能得到下面的输出：
+运行这个代码，你可能得到下面的输出：
 
-![](../../img/06/Breakout/02/setting-up.png)
+![ans](http://learnopengl.com/img/in-practice/breakout/setting-up.png)
+
+目前为止我们已经有了一个后面的教程需要的固定框架；我们将会持续的扩展这个`Game`类来封装一些新的功能。如果你准备好了就点击[下一个](http://learnopengl.com/#!In-Practice/2D-Game/Rendering-Sprites)教程。
 
-现在我们已经为之后的教程构建了一个坚实的框架，我们将不断地拓展这个游戏类，封装新的功能。如果你准备好了，就可以开始[下一节](03 Rendering Sprites.md)的学习了。

docs/06 In Practice/2D-Game/03 Rendering Sprites.md

@@ -4,43 +4,41 @@
    ---|---
 作者   | JoeyDeVires
 翻译   | [ZMANT](https://github.com/Itanq)
-校对   |  Krasjet
-
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
-为了给我们当前这个黑漆漆的游戏世界带来一点生机，我们将会渲染一些精灵(Sprite)来填补这些空虚。<def>精灵</def>有很多种定义，但这里主要是指一个2D图片，它通常是和一些摆放相关的属性数据一起使用，比如位置、旋转角度以及二维的大小。简单来说，精灵就是那些可以在2D游戏中渲染的图像/纹理对象。
-
-我们可以像前面大多数教程里做的那样，用顶点数据创建2D形状，将所有数据传进GPU并手动变换图形。然而，在我们这样的大型应用中，我们最好是对2D形状渲染做一些抽象化。如果我们要对每一个对象手动定义形状和变换的话，很快就会变得非常凌乱了。
-
-在这个教程中，我们将会定义一个渲染类，让我们用最少的代码渲染大量的精灵。这样，我们就可以从散沙一样的OpenGL渲染代码中抽象出游戏代码，这也是在一个大型工程中常用的做法。虽然我们首先还要去配置一个合适的投影矩阵。
-
-## 2D投影矩阵
-
-从这个[坐标系统](../../01 Getting started/08 Coordinate Systems.md)教程中，我们明白了投影矩阵的作用是把观察空间坐标转化为标准化设备坐标。通过生成合适的投影矩阵，我们就可以在不同的坐标系下计算，这可能比把所有的坐标都指定为标准化设备坐标（再计算）要更容易处理。
-
-我们不需要对坐标系应用透视，因为这个游戏完全是2D的，所以一个正射投影矩阵(Orthographic Projection Matrix)就可以了。由于正射投影矩阵几乎直接变换所有的坐标至裁剪空间，我们可以定义如下的投影矩阵指定世界坐标为屏幕坐标：
-
-```c++
-glm::mat4 projection = glm::ortho(0.0f, 800.0f, 600.0f, 0.0f, -1.0f, 1.0f);
-```
-
-前面的四个参数依次指定了投影平截头体的左、右、下、上边界。这个投影矩阵把所有在0到800之间的x坐标变换到-1到1之间，并把所有在0到600之间的y坐标变换到-1到1之间。这里我们指定了平截头体顶部的y坐标值为0，底部的y坐标值为600。所以，这个场景的左上角坐标为(0,0)，右下角坐标为(800,600)，就像屏幕坐标那样。观察空间坐标直接对应最终像素的坐标。
-
-![](../../img/06/Breakout/03/projection.png)
-
-这样我们就可以指定所有的顶点坐标为屏幕上的像素坐标了，这对2D游戏来说相当直观。
+校队   | 暂无
 
 ## 渲染精灵
 
-渲染一个实际的精灵应该不会太复杂。我们创建一个有纹理的四边形，它在之后可以使用一个模型矩阵来变换，然后我们会用之前定义的正射投影矩阵来投影它。
+为了给我们当前这个黑漆漆的游戏世界带来一点生机，我们将会渲染一些精灵(Sprite)来填补一些空虚。精灵有很多种定义，但主要是指一个2D图片，它通常是和一些属性数据一起使用，比如用一些数据来表示它在世界坐标下的位置，一个旋转的角度以及一个表示二维空间的大小的变量。在2D游戏中，我们主要使用精灵来渲染图片/纹理对象。
+
+就像前面那些教程里做的那样，我们可以把顶点数据传到GPU并且手动的通过一些操作来创建一些2D形状。然而，在一个大型应用中，就像我们正在做的这个，我们还是宁愿在渲染2D形状上做一些抽象。如果我们手动的去定义并转换每一个对象，那就相当的凌乱了。
+
+在这里，我们将会定义一个用最少的代码去渲染大量的精灵的渲染类。这样，我们就可以从像散沙一样的OpenGL渲染代码中摘要出游戏代码，这是在一个大型应用中常用的做法。尽管我们首先要做的是设置一个合适的投影矩阵。
+
+## 2D投影矩阵
+
+从这个[坐标系统](../../01 Getting started/08 Coordinate Systems.md)教程我们明白了投影矩阵的作用是把视图空间坐标转化为标准化设备坐标。通过生成合适的投影矩阵，我们就可以在不同的坐标系下计算，这可能比把所有的坐标指定为标准化设备坐标（再计算）要更容易处理。
+
+我们并不需要在坐标系执行任何的透视应用，因为这个游戏完全是在二维平面，所以一个正交投影矩阵就可以很好的工作了。因为正交投影矩阵几乎是直接把整个坐标变换到裁切空间，我们可以定义如下的矩阵来把世界坐标指定为屏幕坐标：
+
+```c++
+glm::mat4 projection = glm::ortho(0.0f,800.0f,600.0f,0.0f,-1.0f,1.0f);
+```
+
+前面的四个参数依次指定了投影椎体左、右、下、上边界。这个投影矩阵把所有在`0`到`800`之间的`x`坐标变换到`-1`到`1`之间以及把所有在`0`到`600`之间的`y`坐标变换到`-1`到`1`之间。这里我们指定了视椎体上部的`y`坐标值为`0`，同时其下部的`y`坐标值为`600`。结果就是这个场景的左上角坐标为`(0,0)`，右下角坐标为`(800,600)`，就像屏幕坐标那样。视图空间坐标直接对应像素坐标。
+
+![](../../img/06/Breakout/03/projection.png)
+
+这允许我们指定每个坐标都等于它们在屏幕上最终的像素坐标，这在2D游戏里相当直观。
+
+## 渲染精灵
+
+渲染一个实际的精灵不因太复杂化。我们创建一个纹理四边形，并且在使用了前面预先定义的正交投影矩阵（变换到标准化设备坐标）之后我们可以使用模型矩阵来变换它。
 
 !!! important
 
-	由于Breakout是一个静态的游戏，这里不需要观察/摄像机矩阵，我们可以直接使用投影矩阵把世界空间坐标变换到裁剪空间坐标。
+	由于`Breakout`游戏是一个静态游戏，这里不需要视图/摄像机矩阵，我们可以直接使用投影矩阵把世界空间坐标变换到裁切空间坐标
 
-为了变换精灵我们会使用下面这个顶点着色器：
+为了变换精灵我们使用了下面的顶点着色器：
 
 ```c++
 #version 330 core
@@ -58,9 +56,9 @@ void main()
 }
 ```
 
-注意，我们仅用了一个<fun>vec4</fun>变量来存储位置和纹理坐标数据。因为位置和纹理坐标数据都只包含了两个float，所以我们可以把他们组合在一起作为一个单一的顶点属性。
+注意，我们使用了一个单一的`vec4`变量来存储了位置和纹理坐标数据。因为位置和纹理坐标数据都只包含了两个浮点型数据，所以我们可以把他们组合在一起作为一个单一的顶点属性。
 
-片段着色器也比较直观。我们会在这里获取一个纹理和一个颜色向量，它们都会影响片段的最终颜色。有了这个uniform颜色向量，我们就可以很方便地在游戏代码中改变精灵的颜色了。
+像素着色器相对比较简单。我们设置了一个纹理和颜色向量，她们两个都会对像素最后的颜色产生影响。同样也设置了一个`uniform`颜色向量，我们就可以很容易的在游戏代码里面改变精灵的颜色。
 
 ```c++
 #version 330 core
@@ -71,12 +69,12 @@ uniform sampler2D image;
 uniform vec3 spriteColor;
 
 void main()
-{
+{    
     color = vec4(spriteColor, 1.0) * texture(image, TexCoords);
 }
 ```
 
-为了让精灵的渲染更加有条理，我们定义了一个<fun>SpriteRenderer</fun>类，有了它只需要一个函数就可以渲染精灵了。它的定义如下：
+为了让渲染精灵的代码更加有条理，我们定义了一个`SpriteRenderer`类，只需要一个单一的函数就可以渲染精灵，它的定义如下：
 
 ```c++
 class SpriteRenderer
@@ -96,19 +94,19 @@ class SpriteRenderer
 };
 ```
 
-<fun>SpriteRenderer</fun>类封装了一个着色器对象，一个顶点数组对象以及一个渲染和初始化函数。它的构造函数接受一个着色器对象用于之后的渲染。
+`SpriteRenderer`类封装了一个着色器对象，一个顶点数组对象以及一个渲染和初始化函数。它的构造函数接受一个着色器对象用于后面的渲染。
 
 ### 初始化
 
-首先，让我们深入研究一下负责配置<var>quadVAO</var>的<fun>initRenderData</fun>函数：
+首先，让我们探究一下负责配置`quadVAO`的`initRenderData`h函数：
 
 ```c++
 void SpriteRenderer::initRenderData()
 {
-    // 配置 VAO/VBO
+    // Configure VAO/VBO
     GLuint VBO;
     GLfloat vertices[] = { 
-        // 位置     // 纹理
+        // Pos      // Tex
         0.0f, 1.0f, 0.0f, 1.0f,
         1.0f, 0.0f, 1.0f, 0.0f,
         0.0f, 0.0f, 0.0f, 0.0f, 
@@ -132,20 +130,19 @@ void SpriteRenderer::initRenderData()
 }
 ```
 
-这里，我们首先定义了一组以四边形的左上角为(0,0)坐标的顶点。这意味着当我们在四边形上应用一个位移或缩放变换的时候，它们会从四边形的左上角开始进行变换。这在2D图形以及/或GUI系统中广为接受，元素的位置定义为元素左上角的位置。
+在这我们首先定义了一组以四边形的左上角为`(0,0)`的顶点坐标。这意味着当我们在四边形上申请一个移动或伸缩变换的时候，四边形的左上角会被变换。这在2D图形或GUI这类元素的位置是相对于元素左上角的系统而言很常见。
 
-接下来我们简单地向GPU传递顶点数据，并且配置顶点属性，当然在这里仅有一个顶点属性。因为所有的精灵共享着同样的顶点数据，我们只需要为这个精灵渲染器定义一个VAO就行了。
+下面我们简单的向`GPU`传递了顶点数据并且配置了顶点属性，这里的情况是只有一个单一的顶点属性。我们仅仅需要为每一个精灵渲染器定义一个单一的`VAO`，因为他们的顶点数据都是一样的。
 
 ### 渲染
 
-渲染精灵并不是太难；我们使用精灵渲染器的着色器，配置一个模型矩阵并且设置相关的uniform。这里最重要的就是变换的顺序：
+渲染精灵并不是太难；我们使用精灵渲染器的着色器对象，配置一个模型矩阵并且设置相关的`uniform`变量。这里最重要的就是变换的顺序：
 
 ```c++
-
 void SpriteRenderer::DrawSprite(Texture2D &texture, glm::vec2 position, 
   glm::vec2 size, GLfloat rotate, glm::vec3 color)
 {
-    // 准备变换
+    // Prepare transformations
     this->shader.Use();
     glm::mat4 model;
     model = glm::translate(model, glm::vec3(position, 0.0f));  
@@ -165,45 +162,45 @@ void SpriteRenderer::DrawSprite(Texture2D &texture, glm::vec2 position,
     glBindVertexArray(this->quadVAO);
     glDrawArrays(GL_TRIANGLES, 0, 6);
     glBindVertexArray(0);
-}  
+}
 ```
 
-当试图在一个场景中用旋转矩阵和缩放矩阵放置一个对象的时候，建议是首先做缩放变换，再旋转，最后才是位移变换。因为矩阵乘法是从右向左执行的，所以我们变换的矩阵顺序是相反的：移动，旋转，缩放。
+当试图在一个场景中用旋转矩阵和伸缩矩阵放置一个对象的时候，建议首先做伸缩变换，然后旋转最后是移动变换。因为矩阵乘法是从右向左执行的，所以我们变换的矩阵顺序是相反的：移动，旋转，缩放。
 
-旋转变换可能看起来稍微有点让人望而却步。我们从[变换](../../01 Getting started/07 Transformations.md)教程里面知道旋转总是围绕原点(0,0)转动的。因为我们指定了四边形的左上角为(0,0)，所有的旋转都会围绕这个(0,0)。简单来说，在四边形左上角的<def>旋转原点</def>(Origin of Rotation)会产生不想要的结果。我们想要做的是把旋转原点移到四边形的中心，这样旋转就会围绕四边形中心而不是左上角了。我们会在旋转之前把旋转原点移动到四边形中心来解决这个问题。
+旋转变换可能看起来稍微有点让人望而却步。我们从[变换](../../01 Getting started/07 Transformations/)教程里面知道旋转总是围绕原点`(0,0)`转动的。因为我们指定了四边形的左上角为`(0,0)`，所有的旋转都是围绕`(0,0)`的。主要是这个旋转的原点是四边形的左上角，这样就会造成不太友好的旋转效果。我们想要做的就是把旋转的点移到四边形的中心，这样旋转就是围绕四边形中心而不是左上角了。我们通过在旋转之前把旋转点移动到四边形中心解决了这个问题。
 
 ![](../../img/06/Breakout/03/rotation-origin.png)
 
-因为我们首先会缩放这个四边形，我们在位移精灵的中心时还需要把精灵的大小考虑进来（这也是为什么我们乘以了精灵的<var>size</var>向量）。在旋转变换应用之后，我们会反转之前的平移操作。
+因为我们首先缩放了这个四边形，我们不得不在把原点变换到精灵中心的时候输入一个`size`变量(这就是我们乘了精灵的`size`向量)。一旦应用了旋转变换之后，我们就需要做上一次变换的逆变换。
 
-把所有变换组合起来我们就能以任何想要的方式放置、缩放并平移每个精灵了。下面你可以找到精灵渲染器完整的源代码：
+把所有变换组合起来我们就可以以我们喜欢的方式移动、缩放并且旋转每一个精灵了。在下面你可以找到完整的精灵渲染器的源代码：
 
-- **精灵渲染器**：[头文件](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/sprite_renderer.h)，[代码](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/sprite_renderer)
+>* SpriteRenderer: [header](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/sprite_renderer.h),[code](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/sprite_renderer)
 
 ## 你好，精灵
 
-有了<fun>SpriteRenderer</fun>类，我们终于能够渲染实际的图像到屏幕上了！让我们来在游戏代码里面初始化一个精灵并且加载我们最喜爱的[纹理](../../img/06/Breakout/03/awesomeface.png)：
+使用`SpriteRenderer`类我们有了把实际图片渲染到屏幕的能力！让我们来在游戏代码里面初始化一个精灵并且加载一个我们最喜爱的[纹理](../../img/06/Breakout/03/awesomeface.png)：
 
 ```c++
 SpriteRenderer  *Renderer;
   
 void Game::Init()
 {
-    // 加载着色器
+    // Load shaders
     ResourceManager::LoadShader("shaders/sprite.vs", "shaders/sprite.frag", nullptr, "sprite");
-    // 配置着色器
+    // Configure shaders
     glm::mat4 projection = glm::ortho(0.0f, static_cast<GLfloat>(this->Width), 
         static_cast<GLfloat>(this->Height), 0.0f, -1.0f, 1.0f);
     ResourceManager::GetShader("sprite").Use().SetInteger("image", 0);
     ResourceManager::GetShader("sprite").SetMatrix4("projection", projection);
-    // 设置专用于渲染的控制
+    // Set render-specific controls
     Renderer = new SpriteRenderer(ResourceManager::GetShader("sprite"));
-    // 加载纹理
+    // Load textures
     ResourceManager::LoadTexture("textures/awesomeface.png", GL_TRUE, "face");
 }
 ```
 
-然后，在渲染函数里面我们就可以渲染一下我们心爱的吉祥物来检测是否一切都正常工作了：
+然后在渲染函数里面我们渲染一下我们的吉祥物来看看是否一切都按正确的方式工作了：
 
 ```c++
 void Game::Render()
@@ -213,12 +210,12 @@ void Game::Render()
 }
 ```
 
-这里我们把精灵放置在靠近屏幕中心的位置，它的高度会比宽度大一点。我们同样也把它旋转了45度并把它设置为绿色。注意，我们设定的精灵的位置是精灵四边形左上角的位置。
+这里我们把精灵放置在靠近屏幕中心的位置，它的高度稍微有点大于宽度。我们同样也把它旋转了`45.0f`度并且给了一个绿色。注意，我们设定的精灵的位置是精灵四边形左上角的位置。
 
-如果你一切都做对了你应该可以看到下面的结果：
+如果你一切都做对了你应该可以看到下面的输出：
 
 ![](../../img/06/Breakout/03/rendering-sprites.png)
 
-你可以在[这里](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_rendering-sprites)找到更新后的游戏类源代码。
+你可以在[这里](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_rendering-sprites)找到更新后的游戏源代码。
 
-现在我们已经让渲染系统正常工作了，我们可以在[下一节](04 Levels.md)教程中用它来构建游戏的关卡。
+目前我们的渲染系统正确工作了，我们在下一个教程里设置了游戏的等级，它在那里将会有更好的用处。

docs/06 In Practice/2D-Game/04 Levels.md

@@ -1,289 +0,0 @@
-# 关卡
-
-原文    | [Levels](https://learnopengl.com/#!In-Practice/2D-Game/Levels)
------   |  ----
-作者    | JoeydeVries
-翻译    | [包纸](https://github.com/ShirokoSama)
-校对    | 暂无
-
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
-Breakout不会只是一个单一的绿色笑脸，而是一些由许多彩色砖块组成的完整关卡。我们希望这些关卡有以下特性：他们足够灵活以便于支持任意数量的行或列、可以拥有不可摧毁的坚固砖块、支持多种类型的砖块且这些信息被存储在外部文件中。
-
-在本教程中，我们将简要介绍用于管理大量砖块的游戏关卡对象的代码，首先我们需要先定义什么是一个砖块。
-
-我们创建一个被称为游戏对象的组件作为一个游戏内物体的基本表示。这样的游戏对象持有一些状态数据，如其位置、大小与速率。它还持有颜色、旋转、是否坚硬(不可被摧毁)、是否被摧毁的属性，除此之外，它还存储了一个Texture2D变量作为其精灵(Sprite)。
-
-游戏中的每个物体都可以被表示为<fun>GameObject</fun>或这个类的派生类，你可以在下面找到<fun>GameObject</fun>的代码：
-
-- **GameObject**：[头文件](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_object.h)，[代码](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_object)
-
-Breakout中的关卡基本由砖块组成，因此我们可以用一个砖块的集合表示一个关卡。因为砖块需要和游戏对象几乎相同的状态，所以我们将关卡中的每个砖块表示为<fun>GameObject</fun>。<fun>GameLevel</fun>类的布局如下所示：
-
-```c++
-class GameLevel
-{
-public:
-    std::vector<GameObject> Bricks;
-
-    GameLevel() { }
-    // 从文件中加载关卡
-    void Load(const GLchar *file, GLuint levelWidth, GLuint levelHeight);
-    // 渲染关卡
-    void Draw(SpriteRenderer &renderer);
-    // 检查一个关卡是否已完成 (所有非坚硬的瓷砖均被摧毁)
-    GLboolean IsCompleted();
-private:
-    // 由砖块数据初始化关卡
-    void init(std::vector<std::vector<GLuint>> tileData, GLuint levelWidth, GLuint levelHeight);
-};
-```
-
-由于关卡数据从外部文本中加载，所以我们需要提出某种关卡的数据结构，以下是关卡数据在文本文件中可能的表示形式的一个例子：
-
-```c++
-1 1 1 1 1 1 
-2 2 0 0 2 2
-3 3 4 4 3 3
-```
-
-在这里一个关卡被存储在一个矩阵结构中，每个数字代表一种类型的砖块，并以空格分隔。在关卡代码中我们可以假定每个数字代表什么：
-
-- 数字0：无砖块，表示关卡中空的区域
-- 数字1：一个坚硬的砖块，不可被摧毁
-- 大于1的数字：一个可被摧毁的砖块，不同的数字区分砖块的颜色
-
-上面的示例关卡在被<fun>GameLevel</fun>处理后，看起来会像这样：
-
-![](../../img/06/Breakout/04/levels-example.png)
-
-<fun>GameLevel</fun>类使用两个函数从文件中生成一个关卡。它首先将所有数字在<fun>Load</fun>函数中加载到二维容器(vector)里，然后在<fun>init</fun>函数中处理这些数字，以创建所有的游戏对象。
-
-```c++
-void GameLevel::Load(const GLchar *file, GLuint levelWidth, GLuint levelHeight)
-{
-    // 清空过期数据
-    this->Bricks.clear();
-    // 从文件中加载
-    GLuint tileCode;
-    GameLevel level;
-    std::string line;
-    std::ifstream fstream(file);
-    std::vector<std::vector<GLuint>> tileData;
-    if (fstream)
-    {
-        while (std::getline(fstream, line)) // 读取关卡文件的每一行
-        {
-            std::istringstream sstream(line);
-            std::vector<GLuint> row;
-            while (sstream >> tileCode) // 读取被空格分隔的每个数字
-                row.push_back(tileCode);
-            tileData.push_back(row);
-        }
-        if (tileData.size() > 0)
-            this->init(tileData, levelWidth, levelHeight);
-    }
-} 
-```
-
-被加载后的<fun>tileData</fun>数据被传递到<fun>GameLevel</fun>的<fun>init</fun>函数：
-
-```c++
-void GameLevel::init(std::vector<std::vector<GLuint>> tileData, GLuint lvlWidth, GLuint lvlHeight)
-{
-    // 计算每个维度的大小
-    GLuint height = tileData.size();
-    GLuint width = tileData[0].size();
-    GLfloat unit_width = lvlWidth / static_cast<GLfloat>(width);
-    GLfloat unit_height = lvlHeight / height;
-    // 基于tileDataC初始化关卡     
-    for (GLuint y = 0; y < height; ++y)
-    {
-        for (GLuint x = 0; x < width; ++x)
-        {
-            // 检查砖块类型
-            if (tileData[y][x] == 1)
-            {
-                glm::vec2 pos(unit_width * x, unit_height * y);
-                glm::vec2 size(unit_width, unit_height);
-                GameObject obj(pos, size, 
-                    ResourceManager::GetTexture("block_solid"), 
-                    glm::vec3(0.8f, 0.8f, 0.7f)
-                );
-                obj.IsSolid = GL_TRUE;
-                this->Bricks.push_back(obj);
-            }
-            else if (tileData[y][x] > 1)    
-            {
-                glm::vec3 color = glm::vec3(1.0f); // 默认为白色
-                if (tileData[y][x] == 2)
-                    color = glm::vec3(0.2f, 0.6f, 1.0f);
-                else if (tileData[y][x] == 3)
-                    color = glm::vec3(0.0f, 0.7f, 0.0f);
-                else if (tileData[y][x] == 4)
-                    color = glm::vec3(0.8f, 0.8f, 0.4f);
-                else if (tileData[y][x] == 5)
-                    color = glm::vec3(1.0f, 0.5f, 0.0f);
-
-                glm::vec2 pos(unit_width * x, unit_height * y);
-                glm::vec2 size(unit_width, unit_height);
-                this->Bricks.push_back(
-                    GameObject(pos, size, ResourceManager::GetTexture("block"), color)
-                );
-            }
-        }
-    }  
-}
-```
-
-<fun>init</fun>函数遍历每个被加载的数字，处理后将一个相应的<fun>GameObject</fun>添加到关卡的容器中。每个砖块的尺寸(unit_width和unit_height)根据砖块的总数被自动计算以便于每块砖可以完美地适合屏幕边界。
-
-在这里我们用两个新的纹理加载游戏对象，分别为[block](https://learnopengl.com/img/in-practice/breakout/textures/block.png)纹理与[solid block](https://learnopengl.com/img/in-practice/breakout/textures/block_solid.png)纹理。
-
-![](../../img/06/Breakout/04/block-textures.png)
-
-这里有一个很好的小窍门，即这些纹理是完全灰度的。其效果是，我们可以在游戏代码中，通过将灰度值与定义好的颜色矢量相乘来巧妙地操纵它们的颜色，就如同我们在<fun>SpriteRenderer</fun>中所做的那样。这样一来，自定义的颜色/外观就不会显得怪异或不平衡。
-
-<fun>GameLevel</fun>类还包含一些其他的功能，比如渲染所有未被破坏的砖块，或验证是否所有的可破坏砖块均被摧毁。你可以在下面找到<fun>GameLevel</fun>类的源码：
-
-- **GameLevel**：[头文件](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_level.h)，[代码](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_level)
-
-因为支持任意数量的行和列，这个游戏关卡类给我们带来了很大的灵活性，用户可以通过修改关卡文件轻松创建自己的关卡。
-
-## 在游戏中
-
-我们希望在Breakout游戏中支持多个关卡，因此我们将在<fun>Game</fun>类中添加一个持有<fun>GameLevel</fun>变量的容器。同时我们还将存储当前的游戏关卡。
-
-```c++
-class Game
-{
-    [...]
-    std::vector<GameLevel> Levels;
-    GLuint                 Level;
-    [...]  
-};
-```
-
-这个教程的Breakout版本共有4个游戏关卡：
-
-- [Standard](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/levels/one)
-- [A few small gaps](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/levels/two)
-- [Space invader](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/levels/three)
-- [Bounce galore](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/levels/four)
-
-然后<fun>Game</fun>类的<fun>init</fun>函数初始化每个纹理和关卡：
-
-```c++
-void Game::Init()
-{
-    [...]
-    // 加载纹理
-    ResourceManager::LoadTexture("textures/background.jpg", GL_FALSE, "background");
-    ResourceManager::LoadTexture("textures/awesomeface.png", GL_TRUE, "face");
-    ResourceManager::LoadTexture("textures/block.png", GL_FALSE, "block");
-    ResourceManager::LoadTexture("textures/block_solid.png", GL_FALSE, "block_solid");
-    // 加载关卡
-    GameLevel one; one.Load("levels/one.lvl", this->Width, this->Height * 0.5);
-    GameLevel two; two.Load("levels/two.lvl", this->Width, this->Height * 0.5);
-    GameLevel three; three.Load("levels/three.lvl", this->Width, this->Height * 0.5);
-    GameLevel four; four.Load("levels/four.lvl", this->Width, this->Height * 0.5);
-    this->Levels.push_back(one);
-    this->Levels.push_back(two);
-    this->Levels.push_back(three);
-    this->Levels.push_back(four);
-    this->Level = 1;
-}  
-```
-
-现在剩下要做的就是通过调用当前关卡的<fun>Draw</fun>函数来渲染我们完成的关卡，然后使用给定的sprite渲染器调用每个<fun>GameObject</fun>的<fun>Draw</fun>函数。除了关卡之外，我们还会用一个很好的[背景图片](https://learnopengl.com/img/in-practice/breakout/textures/background.jpg)来渲染这个场景：
-
-```c++
-void Game::Render()
-{
-    if(this->State == GAME_ACTIVE)
-    {
-        // 绘制背景
-        Renderer->DrawSprite(ResourceManager::GetTexture("background"), 
-            glm::vec2(0, 0), glm::vec2(this->Width, this->Height), 0.0f
-        );
-        // 绘制关卡
-        this->Levels[this->Level].Draw(*Renderer);
-    }
-}
-```
-
-结果便是如下这个被呈现的关卡，它使我们的游戏变得开始生动起来：
-
-![](../../img/06/Breakout/04/levels.png)
-
-## 玩家挡板
-
-此时我们在场景底部引入一个由玩家控制的挡板，挡板只允许水平移动，并且在它接触任意场景边缘时停止。对于玩家挡板，我们将使用[以下](https://learnopengl.com/img/in-practice/breakout/textures/paddle.png)纹理：
-
-![](../../img/06/Breakout/04/paddle.png)
-
-一个挡板对象拥有位置、大小、渲染纹理等属性，所以我们理所当然地将其定义为一个<fun>GameObject</fun>。
-
-```c++
-// 初始化挡板的大小
-const glm::vec2 PLAYER_SIZE(100, 20);
-// 初始化当班的速率
-const GLfloat PLAYER_VELOCITY(500.0f);
-
-GameObject      *Player;
-  
-void Game::Init()
-{
-    [...]    
-    ResourceManager::LoadTexture("textures/paddle.png", true, "paddle");
-    [...]
-    glm::vec2 playerPos = glm::vec2(
-        this->Width / 2 - PLAYER_SIZE.x / 2, 
-        this->Height - PLAYER_SIZE.y
-    );
-    Player = new GameObject(playerPos, PLAYER_SIZE, ResourceManager::GetTexture("paddle"));
-}
-```
-
-这里我们定义了几个常量来初始化挡板的大小与速率。在<fun>Game</fun>的<fun>Init</fun>函数中我们计算挡板的初始位置，使其中心与场景的水平中心对齐。
-
-除此之外我们还需要在<fun>Game</fun>的<fun>Render</fun>函数中添加：
-
-```c++
-Player->Draw(*Renderer);
-```
-
-如果你现在启动游戏，你不仅会看到关卡画面，还会有一个在场景底部边缘的奇特的挡板。到目前为止，它除了静态地放置在那以外不会发生任何事情，因此我们需要进入游戏的<fun>ProcessInput</fun>函数，使得当玩家按下A和D时，挡板可以水平移动。
-
-```c++
-void Game::ProcessInput(GLfloat dt)
-{
-    if (this->State == GAME_ACTIVE)
-    {
-        GLfloat velocity = PLAYER_VELOCITY * dt;
-        // 移动挡板
-        if (this->Keys[GLFW_KEY_A])
-        {
-            if (Player->Position.x >= 0)
-                Player->Position.x -= velocity;
-        }
-        if (this->Keys[GLFW_KEY_D])
-        {
-            if (Player->Position.x <= this->Width - Player->Size.x)
-                Player->Position.x += velocity;
-        }
-    }
-} 
-```
-
-在这里，我们根据用户按下的键，向左或向右移动挡板(注意我们将速率与deltaTime相乘)。当挡板的x值小于0，它将移动出游戏场景的最左侧，所以我们只允许挡板的x值大于0时向左移动。对于右侧边缘我们做相同的处理，但我们必须比较场景的右侧边缘与挡板的右侧边缘，即场景宽度减去挡板宽度。
-
-现在启动游戏，将呈现一个玩家可控制在整个场景底部自由移动的挡板。
-
-![](../../img/06/Breakout/04/levels-player.png)
-
-你可以在下面找到更新后的<fun>Game</fun>类代码：
-
-- **Game**：[头文件](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_levels.h)，[代码](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_levels)

docs/06 In Practice/2D-Game/05 Collisions/01 Ball.md

@@ -1,162 +0,0 @@
-# 球
-
-原文     | [Ball](https://learnopengl.com/#!In-Practice/2D-Game/Collisions/Ball)
-      ---|---
-作者     | JoeyDeVries
-翻译     | [aillieo](https://github.com/aillieo)
-校对     | 暂未校对
-
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
-此时我们已经有了一个包含有很多砖块和玩家的一个挡板的关卡。与经典的Breakout内容相比还差一个球。游戏的目的是让球撞击所有的砖块，直到所有的可销毁砖块都被销毁，但同时也要满足条件：球不能碰触屏幕的下边缘。
-
-除了通用的游戏对象组件，球还需要有半径和一个布尔值，该布尔值用于指示球被固定(<def>stuck</def>)在玩家挡板上还是被允许自由运动的状态。当游戏开始时，球被初始固定在玩家挡板上，直到玩家按下任意键开始游戏。
-
-由于球只是一个附带了一些额外属性的<fun>GameObject</fun>，所以按照常规需要创建<fun>BallObject</fun>类作为<fun>GameObject</fun>的子类。
-
-```c++
-class BallObject : public GameObject
-{
-    public:
-        // 球的状态
-        GLfloat   Radius;
-        GLboolean Stuck;
-
-
-        BallObject();
-        BallObject(glm::vec2 pos, GLfloat radius, glm::vec2 velocity, Texture2D sprite);
-
-        glm::vec2 Move(GLfloat dt, GLuint window_width);
-        void      Reset(glm::vec2 position, glm::vec2 velocity);
-};
-```
-
-<fun>BallObject</fun>的构造函数不但初始化了其自身的值，而且实际上也潜在地初始化了<fun>GameObject</fun>。<fun>BallObject</fun>类拥有一个<fun>Move</fun>函数，该函数用于根据球的速度来移动球，并检查它是否碰到了场景的任何边界，如果碰到的话就会反转球的速度：
-
-
-```c++
-glm::vec2 BallObject::Move(GLfloat dt, GLuint window_width)
-{
-    // 如果没有被固定在挡板上
-    if (!this->Stuck)
-    {
-        // 移动球
-        this->Position += this->Velocity * dt;
-        // 检查是否在窗口边界以外，如果是的话反转速度并恢复到正确的位置
-        if (this->Position.x <= 0.0f)
-        {
-            this->Velocity.x = -this->Velocity.x;
-            this->Position.x = 0.0f;
-        }
-        else if (this->Position.x + this->Size.x >= window_width)
-        {
-            this->Velocity.x = -this->Velocity.x;
-            this->Position.x = window_width - this->Size.x;
-        }
-        if (this->Position.y <= 0.0f)
-        {
-            this->Velocity.y = -this->Velocity.y;
-            this->Position.y = 0.0f;
-        }
-
-    }
-    return this->Position;
-}
-```
-
-除了反转球的速度之外，我们还需要把球沿着边界重新放置回来。只有在没有被固定时球才能够移动。
-
-!!! Important
-
-	因为如果球碰触到底部边界时玩家会结束游戏（或失去一条命），所以在底部边界没有代码来控制球反弹。我们稍后需要在代码中某些地方实现这一逻辑。
-
-你可以在下边看到<fun>BallObject</fun>的代码：
-
-- BallObject: [header](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/ball_object_collisions.h), [code](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/ball_object_collisions)
-
-
-首先我们在游戏中添加球。与玩家挡板相似，我们创建一个球对象并且定义两个用来初始化球的常量。对于球的纹理，我们会使用在LearnOpenGL Breakout游戏中完美适用的一张图片：[球纹理](../../../img/06/Breakout/05/01/awesomeface.png)。
-
-```c++
-// 初始化球的速度
-const glm::vec2 INITIAL_BALL_VELOCITY(100.0f, -350.0f);
-// 球的半径
-const GLfloat BALL_RADIUS = 12.5f;
-
-BallObject     *Ball;
-
-void Game::Init()
-{
-    [...]
-    glm::vec2 ballPos = playerPos + glm::vec2(PLAYER_SIZE.x / 2 - BALL_RADIUS, -BALL_RADIUS * 2);
-    Ball = new BallObject(ballPos, BALL_RADIUS, INITIAL_BALL_VELOCITY,
-        ResourceManager::GetTexture("face"));
-}
-```
-然后我们在每帧中调用游戏代码中<fun>Update</fun>函数里的<fun>Move</fun>函数来更新球的位置：
-
-```c++
-void Game::Update(GLfloat dt)
-{
-    Ball->Move(dt, this->Width);
-}
-```
-
-除此之外，由于球初始是固定在挡板上的，我们必须让玩家能够从固定的位置重新移动它。我们选择使用空格键来从挡板释放球。这意味着我们必须稍微修改<fun>ProcessInput</fun>函数：
-
-```c++
-void Game::ProcessInput(GLfloat dt)
-{
-    if (this->State == GAME_ACTIVE)
-    {
-        GLfloat velocity = PLAYER_VELOCITY * dt;
-        // 移动玩家挡板
-        if (this->Keys[GLFW_KEY_A])
-        {
-            if (Player->Position.x >= 0)
-            {
-                Player->Position.x -= velocity;
-                if (Ball->Stuck)
-                    Ball->Position.x -= velocity;
-            }
-        }
-        if (this->Keys[GLFW_KEY_D])
-        {
-            if (Player->Position.x <= this->Width - Player->Size.x)
-            {
-                Player->Position.x += velocity;
-                if (Ball->Stuck)
-                    Ball->Position.x += velocity;
-            }
-        }
-        if (this->Keys[GLFW_KEY_SPACE])
-            Ball->Stuck = false;
-    }
-}
-```
-
-现在如果玩家按下了空格键，球的<var>Stuck</var>值会设置为<var>false</var>。我们还需要更新<fun>ProcessInput</fun>函数，当球被固定的时候，会跟随挡板的位置来移动球。
-
-最后我们需要渲染球，此时这应该很显而易见了：
-
-```c++
-void Game::Render()
-{
-    if (this->State == GAME_ACTIVE)
-    {
-        [...]
-        Ball->Draw(*Renderer);
-    }
-}
-```
-
-结果就是球会跟随着挡板，并且当我们按下空格键时球开始自由运动。球会在左侧、右侧和顶部边界合理地反弹，但看起来不会撞击任何的砖块，就像我们可以在下边的视频中看到的那样：
-
-<video src="../../../../img/06/Breakout/05/01/no_collisions.mp4" controls="controls"></video>
-
-
-
-我们要做的就是创建一个或多个函数用于检查球对象是否撞击关卡中的任何砖块，如果撞击的话就销毁砖块。这些所谓的碰撞检测(<def>collision detection</def>)功能将是我们[下一个](./02 Collision detection.md)教程的重点。
-

docs/06 In Practice/2D-Game/05 Collisions/02 Collision detection.md

@@ -1,164 +0,0 @@
-# 碰撞检测
-
-原文     | [Collision detection](https://learnopengl.com/#!In-Practice/2D-Game/Collisions/Collision-detection)
-      ---|---
-作者     | JoeyDeVries
-翻译     | [aillieo](https://github.com/aillieo)
-校对     | 暂未校对
-
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
-当试图判断两个物体之间是否有碰撞发生时，我们通常不使用物体本身的数据，因为这些物体常常会很复杂，这将导致碰撞检测变得很复杂。正因这一点，使用**重叠**在物体上的更简单的外形（通常有较简单明确的数学定义）来进行碰撞检测成为常用的方法。我们基于这些简单的外形来检测碰撞，这样代码会变得更简单且节省了很多性能。这些<def>碰撞外形</def>例如圆、球体、长方形和立方体等，与拥有上百个三角形的网格相比简单了很多。
-
-虽然它们确实提供了更简单更高效的碰撞检测算法，但这些简单的碰撞外形拥有一个共同的缺点，这些外形通常无法完全包裹物体。产生的影响就是当检测到碰撞时，实际的物体并没有真正的碰撞。必须记住的是这些外形仅仅是真实外形的近似。
-
-## AABB - AABB 碰撞
-
-AABB代表的是<def>轴对齐碰撞箱</def>(Axis-aligned Bounding Box)，碰撞箱是指与场景基础坐标轴（2D中的是x和y轴）对齐的长方形的碰撞外形。与坐标轴对齐意味着这个长方形没有经过旋转并且它的边线和场景中基础坐标轴平行（例如，左右边线和y轴平行）。这些碰撞箱总是和场景的坐标轴平行，这使得所有的计算都变得更简单。下边是我们用一个AABB包裹一个球对象（物体）：
-
-![](../../../img/06/Breakout/05/02/collisions_ball_aabb.png)
-
-Breakout中几乎所有的物体都是基于长方形的物体，因此很理所应当地使用轴对齐碰撞箱来进行碰撞检测。这就是我们接下来要做的。
-
-有多种方式来定义与坐标轴对齐的碰撞箱。其中一种定义AABB的方式是获取左上角点和右下角点的位置。我们定义的<fun>GameObject</fun>类已经包含了一个左上角点位置（它的Position vector）并且我们可以通过把左上角点的矢量加上它的尺寸（<fun>Position</fun> + <fun>Size</fun>）很容易地计算出右下角点。每个<fun>GameObject</fun>都包含一个AABB我们可以高效地使用它们碰撞。
-
-那么我们如何判断碰撞呢？当两个碰撞外形进入对方的区域时就会发生碰撞，例如定义了第一个物体的碰撞外形以某种形式进入了第二个物体的碰撞外形。对于AABB来说很容易判断，因为它们是与坐标轴对齐的：对于每个轴我们要检测两个物体的边界在此轴向是否有重叠。因此我们只是简单地检查两个物体的水平边界是否重合以及垂直边界是否重合。如果水平边界**和**垂直边界都有重叠那么我们就检测到一次碰撞。
-
-![](../../../img/06/Breakout/05/02/collisions_overlap.png)
-
-将这一概念转化为代码也是很直白的。我们对两个轴都检测是否重叠，如果都重叠就返回碰撞：
-
-```c++
-GLboolean CheckCollision(GameObject &one, GameObject &two) // AABB - AABB collision
-{
-    // x轴方向碰撞？
-    bool collisionX = one.Position.x + one.Size.x >= two.Position.x &&
-        two.Position.x + two.Size.x >= one.Position.x;
-    // y轴方向碰撞？
-    bool collisionY = one.Position.y + one.Size.y >= two.Position.y &&
-        two.Position.y + two.Size.y >= one.Position.y;
-    // 只有两个轴向都有碰撞时才碰撞
-    return collisionX && collisionY;
-}  
-```
-
-我们检查第一个物体的最右侧是否大于第二个物体的最左侧**并且**第二个物体的最右侧是否大于第一个物体的最左侧；垂直的轴向与此相似。如果您无法顺利地将这一过程可视化，可以尝试在纸上画边界线/长方形来自行判断。
-
-为更好地组织碰撞的代码，我们在<fun>Game</fun>类中加入一个额外的函数：
-
-```c++
-class Game
-{
-    public:
-        [...]
-        void DoCollisions();
-};
-```
-
-我们可以使用<fun>DoCollisions</fun>来检查球与关卡中的砖块是否发生碰撞。如果检测到碰撞，就将砖块的<fun>Destroyed</fun>属性设为<var>true</var>，此举会停止关卡中对此砖块的渲染。
-
-```c++
-void Game::DoCollisions()
-{
-    for (GameObject &box : this->Levels[this->Level].Bricks)
-    {
-        if (!box.Destroyed)
-        {
-            if (CheckCollision(*Ball, box))
-            {
-                if (!box.IsSolid)
-                    box.Destroyed = GL_TRUE;
-            }
-        }
-    }
-}  
-```
-
-接下来我们需要更新<fun>Game</fun>的<fun>Update</fun>函数：
-
-```c++
-void Game::Update(GLfloat dt)
-{
-    // 更新对象
-    Ball->Move(dt, this->Width);
-    // 检测碰撞
-    this->DoCollisions();
-}  
-```
-
-此时如果我们运行代码，球会与每个砖块进行碰撞检测，如果砖块不是实心的，则表示砖块被销毁。如果运行游戏以下是你会看到的：
-
-<video src="../../../../img/06/Breakout/05/02/collisions.mp4" controls="controls"></video>
-
-虽然碰撞检测确实生效，但并不是非常准确，因为球会在不直接接触到大多数砖块时与它们发生碰撞。我们来实现另一种碰撞检测技术。
-
-## AABB - 圆碰撞检测
-
-由于球是一个圆形的物体，AABB或许不是球的最佳碰撞外形。碰撞的代码中将球视为长方形框，因此常常会出现球碰撞了砖块但此时球精灵还没有接触到砖块。
-
-![](../../../img/06/Breakout/05/02/collisions_ball_aabb_touch.png)
-
-使用圆形碰撞外形而不是AABB来代表球会更合乎常理。因此我们在球对象中包含了<var>Radius</var>变量，为了定义圆形碰撞外形，我们需要的是一个位置矢量和一个半径。
-
-![](../../../img/06/Breakout/05/02/collisions_circle.png)
-
-这意味着我们不得不修改检测算法，因为当前的算法只适用于两个AABB的碰撞。检测圆和AABB碰撞的算法会稍稍复杂，关键点如下：我们会找到AABB上距离圆最近的一个点，如果圆到这一点的距离小于它的半径，那么就产生了碰撞。
-
-难点在于获取AABB上的最近点\(\bar{P}\)。下图展示了对于任意的AABB和圆我们如何计算该点：
-
-![](../../../img/06/Breakout/05/02/collisions_aabb_circle.png)
-
-首先我们要获取球心\(\bar{C}\)与AABB中心\(\bar{B}\)的矢量差\(\bar{D}\)。接下来用AABB的半边长(half-extents)\(w\)和\(\bar{h}\)来<def>限制(clamp)</def>矢量\(\bar{D}\)。长方形的半边长是指长方形的中心到它的边的距离；简单的说就是它的尺寸除以2。这一过程返回的是一个总是位于AABB的边上的位置矢量（除非圆心在AABB内部）。
-
-!!! Important
-
-	限制运算把一个值**限制**在给定范围内，并返回限制后的值。通常可以表示为：
-
-		float clamp(float value, float min, float max) {
-		    return std::max(min, std::min(max, value));
-		}  
-
-	例如，值<var>42.0f</var>被限制到<var>6.0f</var>和<var>3.0f</var>之间会得到<var>6.0f</var>；而<var>4.20f</var>会被限制为<var>4.20f</var>。  
-	限制一个2D的矢量表示将其<var>x</var>和<var>y</var>分量都限制在给定的范围内。
-
-这个限制后矢量\(\bar{P}\)就是AABB上距离圆最近的点。接下来我们需要做的就是计算一个新的差矢量\(\bar{D'}\)，它是圆心\(\bar{C}\)和\(\bar{P}\)的差矢量。
-
-![](../../../img/06/Breakout/05/02/collisions_aabb_circle_radius_compare.png)
-
-既然我们已经有了矢量\(\bar{D'}\)，我们就可以比较它的长度和圆的半径以判断是否发生了碰撞。
-
-这一过程通过下边的代码来表示：
-
-```c++
-GLboolean CheckCollision(BallObject &one, GameObject &two) // AABB - Circle collision
-{
-    // 获取圆的中心 
-    glm::vec2 center(one.Position + one.Radius);
-    // 计算AABB的信息（中心、半边长）
-    glm::vec2 aabb_half_extents(two.Size.x / 2, two.Size.y / 2);
-    glm::vec2 aabb_center(
-        two.Position.x + aabb_half_extents.x, 
-        two.Position.y + aabb_half_extents.y
-    );
-    // 获取两个中心的差矢量
-    glm::vec2 difference = center - aabb_center;
-    glm::vec2 clamped = glm::clamp(difference, -aabb_half_extents, aabb_half_extents);
-    // AABB_center加上clamped这样就得到了碰撞箱上距离圆最近的点closest
-    glm::vec2 closest = aabb_center + clamped;
-    // 获得圆心center和最近点closest的矢量并判断是否 length <= radius
-    difference = closest - center;
-    return glm::length(difference) < one.Radius;
-}      
-```
-
-我们创建了<fun>CheckCollision</fun>的一个重载函数用于专门处理一个<fun>BallObject</fun>和一个<fun>GameObject</fun>的情况。因为我们并没有在对象中保存碰撞外形的信息，因此我们必须为其计算：首先计算球心，然后是AABB的半边长及中心。
-
-使用这些碰撞外形的参数，我们计算出<var>difference</var>\(\bar{D}\)然后得到限制后的值<var>clamped</var>，并与AABB中心相加得到<var>closest</var>\(\bar{P}\)。然后计算出<var>center</var>和<var>closest</var>的矢量差\(\bar{D'}\)并返回两个外形是否碰撞。
-
-之前我们调用<fun>CheckCollision</fun>时将球对象作为其第一个参数，因此现在<fun>CheckCollision</fun>的重载变量会自动生效，我们无需修改任何代码。现在的结果会比之前的碰撞检测算法更准确。
-
-<video src="../../../../img/06/Breakout/05/02/collisions_circle.mp4" controls="controls"></video>
-
-看起来生效了，但仍缺少一些东西。我们准确地检测了所有碰撞，但碰撞并没有对球产生任何反作用。我们需要在碰撞时产生一些**反作用**，例如当碰撞发生时，更新球的位置和/或速度。这将是[下一个](./03 Collision resolution.md)教程的主题。

docs/06 In Practice/2D-Game/05 Collisions/03 Collision resolution.md

@@ -1,232 +0,0 @@
-# 碰撞处理
-
-原文     | [Collision resolution](https://learnopengl.com/#!In-Practice/2D-Game/Collisions/Collision-resolution)
-      ---|---
-作者     | JoeyDeVries
-翻译     | [aillieo](https://github.com/aillieo)
-校对     | 暂未校对
-
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
-上个教程的最后，我们得到了一种有效的碰撞检测方案。但是球对检测到的碰撞不会有反作用；它仅仅是径直穿过所有的砖块。我们希望球会从撞击到的砖块**反弹**。此教程将讨论如何使用AABB-圆碰撞方案实现这项称为<def>碰撞处理</def>(Collision Resolution)的功能。
-
-当碰撞发生时，我们希望出现两个现象：重新定位球，以免它进入另一个物体，其次是改变球的速度方向，使它看起来像是物体的反弹。
-
-### 碰撞重定位
-
-为了把球对象定位到碰撞的AABB的外部，我们必须明确球侵入碰撞框的距离。为此我们要回顾上一节教程中的示意图：
-
-![](../../../img/06/Breakout/05/03/collisions_aabb_circle_resolution.png)
-
-此时球少量进入了AABB，所以检测到了碰撞。我们现在希望将球从移出AABB的外形使其仅仅碰触到AABB，像是没有碰撞一样。为了确定需要将球从AABB中移出多少距离，我们需要找回矢量\(\bar{R}\)，它代表的是侵入AABB的程度。为得到\(\bar{R}\)我们用球的半径减去\(\bar{V}\)。矢量\(\bar{V}\)是最近点\(\bar{P}\)和球心\(\bar{C}\)的差矢量。
-
-有了\(\bar{R}\)之后我们将球的位置偏移\(\bar{R}\)就将球直接放置在与AABB紧邻的位置；此时球已经被重定位到合适的位置。
-
-### 碰撞方向
-
-下一步我们需要确定碰撞之后如何更新球的速度。对于Breakout我们使用以下规则来改变球的速度：
-
-1. 如果球撞击AABB的右侧或左侧，它的水平速度（<var>x</var>）将会反转。
-2. 如果球撞击AABB的上侧或下侧，它的垂直速度（<var>y</var>）将会反转。
-
-但是如何判断球撞击AABB的方向呢？解决这一问题有很多种方法，其中之一是对于每个砖块使用4个AABB而不是1个AABB，并把它们放置到砖块的每个边上。使用这种方法我们可以确定被碰撞的是哪个AABB和哪个边。但是有一种使用点乘(dot product)的更简单的方法。
-
-您或许还记得[变换](../../../01 Getting started/07 Transformations.md)教程中点乘可以得到两个正交化的矢量的夹角。如果我们定义指向北、南、西和东的四个矢量，然后计算它们和给定矢量的夹角会怎么样？由这四个方向矢量和给定的矢量点乘积的结果中的最高值（点乘积的最大值为`1.0f`，代表`0`度角）即是矢量的方向。
-
-这一过程如下代码所示：
-
-```c++
-Direction VectorDirection(glm::vec2 target)
-{
-    glm::vec2 compass[] = {
-        glm::vec2(0.0f, 1.0f),	// 上
-        glm::vec2(1.0f, 0.0f),	// 右
-        glm::vec2(0.0f, -1.0f),	// 下
-        glm::vec2(-1.0f, 0.0f)	// 左
-    };
-    GLfloat max = 0.0f;
-    GLuint best_match = -1;
-    for (GLuint i = 0; i < 4; i++)
-    {
-        GLfloat dot_product = glm::dot(glm::normalize(target), compass[i]);
-        if (dot_product > max)
-        {
-            max = dot_product;
-            best_match = i;
-        }
-    }
-    return (Direction)best_match;
-}    
-```
-
-此函数比较了<var>target</var>矢量和<var>compass</var>数组中各方向矢量。<var>compass</var>数组中与<var>target</var>角度最接近的矢量，即是返回给函数调用者的<var>Direction</var>。这里的<var>Direction</var>是一个<fun>Game</fun>类的头文件中定义的枚举类型：
-
-```c++
-enum Direction {
-	UP,
-	RIGHT,
-	DOWN,
-	LEFT
-};    
-```
-
-既然我们已经知道了如何获得\(\bar{R}\)以及如何判断球撞击AABB的方向，我们开始编写碰撞处理的代码。
-
-### AABB - 圆碰撞检测
-
-为了计算碰撞处理所需的数值我们要从碰撞的函数中获取更多的信息而不只只是一个<var>true</var>或<var>false</var>，因此我们要返回一个包含更多信息的<def>tuple</def>，这些信息即是碰撞发生时的方向及差矢量（\(\bar{R}\)）。你可以在头文件<var><tuple></var>中找到<var>tuple</var>。
-
-为了更好组织代码，我们把碰撞相关的数据使用typedef定义为<fun>Collision</fun>：
-
-```c++
-typedef std::tuple<GLboolean, Direction, glm::vec2> Collision;    
-```
-
-接下来我们还需要修改<fun>CheckCollision</fun>函数的代码，使其不仅仅返回<var>true</var>或<var>false</var>而是还包含方向和差矢量：
-
-```c++
-Collision CheckCollision(BallObject &one, GameObject &two) // AABB - AABB 碰撞
-{
-    [...]
-    if (glm::length(difference) <= one.Radius)
-        return std::make_tuple(GL_TRUE, VectorDirection(difference), difference);
-    else
-        return std::make_tuple(GL_FALSE, UP, glm::vec2(0, 0));
-}
-```
-
-<fun>Game</fun>类的<fun>DoCollision</fun>函数现在不仅仅只检测是否出现了碰撞，而且在碰撞发生时会有适当的动作。此函数现在会计算碰撞侵入的程度（如本教程一开始计时的示意图中所示）并且基于碰撞方向使球的位置矢量与其相加或相减。
-
-```c++
-void Game::DoCollisions()
-{
-    for (GameObject &box : this->Levels[this->Level].Bricks)
-    {
-        if (!box.Destroyed)
-        {
-            Collision collision = CheckCollision(*Ball, box);
-            if (std::get<0>(collision)) // 如果collision 是 true
-            {
-                // 如果砖块不是实心就销毁砖块
-                if (!box.IsSolid)
-                    box.Destroyed = GL_TRUE;
-                // 碰撞处理
-                Direction dir = std::get<1>(collision);
-                glm::vec2 diff_vector = std::get<2>(collision);
-                if (dir == LEFT || dir == RIGHT) // 水平方向碰撞
-                {
-                    Ball->Velocity.x = -Ball->Velocity.x; // 反转水平速度
-                    // 重定位
-                    GLfloat penetration = Ball->Radius - std::abs(diff_vector.x);
-                    if (dir == LEFT)
-                        Ball->Position.x += penetration; // 将球右移
-                    else
-                        Ball->Position.x -= penetration; // 将球左移
-                }
-                else // 垂直方向碰撞
-                {
-                    Ball->Velocity.y = -Ball->Velocity.y; // 反转垂直速度
-                    // 重定位
-                    GLfloat penetration = Ball->Radius - std::abs(diff_vector.y);
-                    if (dir == UP)
-                        Ball->Position.y -= penetration; // 将球上移
-                    else
-                        Ball->Position.y += penetration; // 将球下移
-                }
-            }
-        }
-    }
-}    
-```
-
-不要被函数的复杂度给吓到，因为它仅仅是我们目前为止的概念的直接转化。首先我们会检测碰撞如果发生了碰撞且砖块不是实心的那么就销毁砖块。然后我们从tuple中获取到了碰撞的方向<var>dir</var>以及表示\(\bar{V}\)的差矢量<var>diff_vector</var>，最终完成碰撞处理。
-
-我们首先检查碰撞方向是水平还是垂直，并据此反转速度。如果是水平方向，我们从<var>diff_vector</var>的x分量计算侵入量RR并根据碰撞方向用球的位置矢量加上或减去它。垂直方向的碰撞也是如此，但是我们要操作各矢量的y分量。
-
-现在运行你的应用程序，应该会向你展示一套奏效的碰撞方案，但可能会很难真正看到它的效果，因为一旦球碰撞到了一个砖块就会弹向底部并永远丢失。我们可以通过处理玩家挡板的碰撞来修复这一问题。
-
-## 玩家 - 球碰撞
-
-球和玩家之间的碰撞与我们之前讨论的碰撞稍有不同，因为这里应当基于撞击挡板的点与（挡板）中心的距离来改变球的水平速度。撞击点距离挡板的中心点越远，则水平方向的速度就会越大。
-
-```c++
-void Game::DoCollisions()
-{
-    [...]
-    Collision result = CheckCollision(*Ball, *Player);
-    if (!Ball->Stuck && std::get<0>(result))
-    {
-        // 检查碰到了挡板的哪个位置，并根据碰到哪个位置来改变速度
-        GLfloat centerBoard = Player->Position.x + Player->Size.x / 2;
-        GLfloat distance = (Ball->Position.x + Ball->Radius) - centerBoard;
-        GLfloat percentage = distance / (Player->Size.x / 2);
-        // 依据结果移动
-        GLfloat strength = 2.0f;
-        glm::vec2 oldVelocity = Ball->Velocity;
-        Ball->Velocity.x = INITIAL_BALL_VELOCITY.x * percentage * strength; 
-        Ball->Velocity.y = -Ball->Velocity.y;
-        Ball->Velocity = glm::normalize(Ball->Velocity) * glm::length(oldVelocity);
-    } 
-}
-```
-
-在我们完成了球和各砖块的碰撞检测之后，我们来检测球和玩家挡板是否发生碰撞。如果有碰撞（并且球不是被固定在挡板上）我们要计算球的中心与挡板中心的距离和挡板的半边长的百分比。之后球的水平速度会依据它撞击挡板的点到挡板中心的距离来更新。除了更新水平速度之外我们还需要反转它的y方向速度。
-
-注意旧的速度被存储为<var>oldVelocity</var>。之所以要存储旧的速度是因为我们只更新球的速度矢量中水平方向的速度并保持它的y速度不变。这将意味着矢量的长度会持续变化，其产生的影响是如果球撞击到挡板的边缘则会比撞击到挡板中心有更大(也因此更强)的速度矢量。为此新的速度矢量会正交化然后乘以旧速度矢量的长度。这样一来，球的力量和速度将总是一一致的，无论它撞击到挡板的哪个地方。
-
-### 粘板
-
-无论你有没有注意到，但当运行代码时，球和玩家挡板的碰撞处理仍旧有一个大问题。以下的视频清楚地展示了将会出现的现象：
-
-<video src="../../../../img/06/Breakout/05/03/collisions_sticky_paddle.mp4" controls="controls"></video>
-
-这种问题称为<def>粘板问题</def>(Sticky Paddle Issue)，出现的原因是玩家挡板以较高的速度移向球，导致球的中心进入玩家挡板。由于我们没有考虑球的中心在AABB内部的情况，游戏会持续试图对所有的碰撞做出响应，当球最终脱离时，已经对`y`向速度翻转了多次，以至于无法确定球在脱离后是向上还是向下运动。
-
-我们可以引入一个小的特殊处理来很容易地修复这种行为，这个处理之所以成为可能是基于我们可以假设碰撞总是发生在挡板顶部的事实。我们总是简单地返回正的<var>y</var>速度而不是反转<var>y</var>速度，这样当它被卡住时也可以立即脱离。
-
-```c++
- //Ball->Velocity.y = -Ball->Velocity.y;
-Ball->Velocity.y = -1 * abs(Ball->Velocity.y);  
-```
-
-如果你足够仔细就会觉得这一影响仍然是可以被注意到的，但是我个人将此方法当作一种可接受的折衷处理。
-
-### 底部边界
-
-与经典的Breakout内容相比唯一缺少的就是失败条件了，失败会重置关卡和玩家。在<fun>Game</fun>类的<fun>Update</fun>函数中，我们要检查球是否接触到了底部边界，如果接触到就重置游戏。
-
-```c++
-void Game::Update(GLfloat dt)
-{
-    [...]
-    if (Ball->Position.y >= this->Height) // 球是否接触底部边界？
-    {
-        this->ResetLevel();
-        this->ResetPlayer();
-    }
-}  
-```
-
-<fun>ResetLevel</fun>和<fun>ResetPlayer</fun>函数直接重新加载关卡并重置对象的各变量值为原始的值。现在游戏看起来应该是这样的：
-
-<video src="../../../../img/06/Breakout/05/03/collisions_complete.mp4" controls="controls"></video>
-
-就是这样了，我们创建完成了一个有相似机制的经典Breakout游戏的复制版。这里你可以找到Game类的源代码：[header](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_collisions.h)，[code](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_collisions)。
-
-## 一些注意事项
-
-在视频游戏的发展过程中，碰撞检测是一个困难的话题甚至可能是最大的挑战。大多数的碰撞检测和处理方案是和物理引擎合并在一起的，正如多数现代的游戏中看到的那样。我们在Breakout游戏中使用的碰撞方案是一个非常简单的方案并且是专门给这类游戏所专用的。
-
-需要强调的是这类碰撞检测和处理方式是不完美的。它只能计算每帧内可能发生的碰撞并且只能计算在该时间步时物体所在的各位置；这意味着如果一个物体拥有一个很大的速度以致于在一帧内穿过了另一个物体，它将看起来像是从来没有与另一个物体碰撞过。因此如果出现掉帧或出现了足够高的速度，这一碰撞检测方案将无法应对。
-
-（我们使用的碰撞方案）仍然会出现这几个问题：
-
-- 如果球运动得足够快，它可能在一帧内完整地穿过一个物体，而不会检测到碰撞。
-- 如果球在一帧内同时撞击了一个以上的物体，它将会检测到两次碰撞并两次反转速度；这样不改变它的原始速度。
-- 撞击到砖块的角时会在错误的方向反转速度，这是因为它在一帧内穿过的距离会引发<fun>VectorDirection</fun>返回水平方向还是垂直方向的差别。
-
-但是，本教程目的在于教会读者们图形学和游戏开发的基础知识。因此，这里的碰撞方案可以服务于此目的；它更容易理解且在正常的场景中可以较好地运作。需要记住的是存在有更好的（更复杂）碰撞方案，在几乎所有的场景中都可以很好地运作（包括可移动的物体）如<def>分离轴定理</def>(Separating Axis Theorem)。
-
-值得庆幸的是，有大量实用并且常常很高效的物理引擎（使用时间步无关的碰撞方案）可供您在游戏中使用。如果您希望在这一系统中有更深入的探索或需要更高级的物理系统又不理解其中的数学机理，[Box2D](http://box2d.org/about/)是一个实现了物理系统和碰撞检测的可以用在您的应用程序中的完美的2D物理库。

docs/06 In Practice/2D-Game/06 Particles.md

@@ -1,240 +1,236 @@
-# 粒子
-
-原文    | [Particles](http://learnopengl.com/#!In-Practice/2D-Game/Particles)
------   |  ----
-作者    | JoeydeVries
-翻译    | [ZMANT](https://github.com/Itanq)
-校对    | 暂无
-
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
-一个微粒,从OpenGL的角度看就是一个总是面向摄像机方向且(通常)包含一个大部分区域是透明的纹理的小四边形。一个微粒本身主要就是一个精灵(sprite),前面我们已经早就使用过了，但是当你把成千上万个这些微粒放在一起的时候,就可以创造出令人疯狂的效果.
-
-当处理这些微粒的时候，通常是由一个叫做粒子发射器或粒子生成器的东西完成的，从这个地方,持续不断的产生新的微粒并且旧的微粒随着时间逐渐消亡。如果这个粒子发射器产生一个带着类似烟雾纹理的微粒的时候，它的颜色亮度同时又随着与发射器距离的增加而变暗，那么就会产生出灼热的火焰的效果:
-
-![fire](../../img/06/Breakout/06/particles_example.jpg)
-
-一个单一的微粒通常有一个生命值变量，并且从它产生开始就一直在缓慢的减少。一旦它的生命值少于某个极限值（通常是0）我们就会杀掉这个粒子,这样下一个粒子产生时就可以让它来替换那个被杀掉的粒子。一个粒子发射器控制它产生的所有粒子并且根据它们的属性来改变它们的行为。一个粒子通常有下面的属性：
-
-```c++
-struct Particle {
-    glm::vec2 Position, Velocity;
-    glm::vec4 Color;
-    GLfloat Life;
-  
-    Particle() 
-      : Position(0.0f), Velocity(0.0f), Color(1.0f), Life(0.0f) { }
-};
-```
-
-看上面那个火焰的例子，那个粒子发射器可能在靠近发射器的地方产生每一个粒子，并且有一个向上的速度，这样每个粒子都是朝着正$y$轴方向移动。那似乎有3个不同区域，只是可能相比其他的区域，给了某个区域内的粒子更快的速度。我们也可以看到，$y$轴方向越高的粒子，它们的黄色或者说亮度就越低。一旦某个粒子到达某个高度的时候，它的生命值就会耗尽然后被杀掉；绝不可能直冲云霄。
-
-你可以想象到用这样一个系统，我们就可以创造一些有趣的效果比如火焰，青烟，烟雾，魔法效果，炮火残渣等等。在Breakout游戏里，我们将会使用下面那个小球来创建一个简单的粒子生成器来制作一些有趣的效果，结果看起来就像这样：
-
-<video src="../../../img/06/Breakout/06/particles.mp4" controls="controls"></video>
-
-上面那个粒子生成器在这个球的位置产生无数的粒子，根据球移动的速度给了粒子相应的速度，并且根据它们的生命值来改变他们的颜色亮度。
-
-为了渲染这些粒子，我们将会用到有不同实现的着色器：
-
-```c++
-#version 330 core
-layout (location = 0) in vec4 vertex; // <vec2 position, vec2 texCoords>
-
-out vec2 TexCoords;
-out vec4 ParticleColor;
-
-uniform mat4 projection;
-uniform vec2 offset;
-uniform vec4 color;
-
-void main()
-{
-    float scale = 10.0f;
-    TexCoords = vertex.zw;
-    ParticleColor = color;
-    gl_Position = projection * vec4((vertex.xy * scale) + offset, 0.0, 1.0);
-}
-```
-
-以及像素着色器:
-
-```c++
-#version 330 core
-in vec2 TexCoords;
-in vec4 ParticleColor;
-out vec4 color;
-
-uniform sampler2D sprite;
-
-void main()
-{
-    color = (texture(sprite, TexCoords) * ParticleColor);
-}
-```
-
-我们获取每个粒子的位置和纹理属性并且设置两个uniform变量：$offset$和$color$来改变每个粒子的输出状态。注意到，在顶点着色器里，我们把这个四边形的粒子缩小了10倍；你也可以把这个缩放变量设置成uniform类型的变量从而控制一些个别的粒子。
-
-首先,我们需要一个粒子数组，然后用Particle结构体的默认构造函数来实例化。
-
-```c++
-GLuint nr_particles = 500;
-std::vector<Particle> particles;
-  
-for (GLuint i = 0; i < nr_particles; ++i)
-    particles.push_back(Particle());
-```
-
-然后在每一帧里面，我们都会用一个起始变量来产生一些新的粒子并且对每个粒子（还活着的）更新它们的值。
-
-```c++
-GLuint nr_new_particles = 2;
-// Add new particles
-for (GLuint i = 0; i < nr_new_particles; ++i)
-{
-    int unusedParticle = FirstUnusedParticle();
-    RespawnParticle(particles[unusedParticle], object, offset);
-}
-// Update all particles
-for (GLuint i = 0; i < nr_particles; ++i)
-{
-    Particle &p = particles[i];
-    p.Life -= dt; // reduce life
-    if (p.Life > 0.0f)
-    {	// particle is alive, thus update
-        p.Position -= p.Velocity * dt;
-        p.Color.a -= dt * 2.5;
-    }
-}
-```
-
-第一个循环看起来可能有点吓人。因为这些粒子会随着时间消亡，我们就想在每一帧里面产生`nr_new_particles`个新粒子。但是一开始我们就知道了总的粒子数量是`nr_partiles`，所以我们不能简单的往粒子数组里面添加新的粒子。否则的话我们很快就会得到一个装满成千上万个粒子的数组，考虑到这个粒子数组里面其实只有一小部分粒子是存活的，这样就太浪费效率了。
-
-我们要做的就是找到第一个消亡的粒子然后用一个新产生的粒子来更新它。函数`FirstUnuseParticle`就是试图找到第一个消亡的粒子并且返回它的索引值给调用者。
-
-```c++
-GLuint lastUsedParticle = 0;
-GLuint FirstUnusedParticle()
-{
-    // Search from last used particle, this will usually return almost instantly
-    for (GLuint i = lastUsedParticle; i < nr_particles; ++i){
-        if (particles[i].Life <= 0.0f){
-            lastUsedParticle = i;
-            return i;
-        }
-    }
-    // Otherwise, do a linear search
-    for (GLuint i = 0; i < lastUsedParticle; ++i){
-        if (particles[i].Life <= 0.0f){
-            lastUsedParticle = i;
-            return i;
-        }
-    }
-    // Override first particle if all others are alive
-    lastUsedParticle = 0;
-    return 0;
-}
-```
-
-这个函数存储了它找到的上一个消亡的粒子的索引值，由于下一个消亡的粒子索引值总是在上一个消亡的粒子索引值的右边，所以我们首先从它存储的上一个消亡的粒子索引位置开始查找，如果我们没有任何消亡的粒子，我们就简单的做一个线性查找，如果没有粒子消亡就返回索引值`0`，结果就是第一个粒子被覆盖，需要注意的是，如果是最后一种情况，就意味着你粒子的生命值太长了，在每一帧里面需要产生更少的粒子，或者你只是没有保留足够的粒子，
-
-之后，一旦粒子数组中第一个消亡的粒子被发现的时候，我们就通过调用`RespawnParticle`函数更新它的值，函数接受一个`Particle`对象，一个`GameObject`对象和一个`offset`向量:
-
-```c++
-void RespawnParticle(Particle &particle, GameObject &object, glm::vec2 offset)
-{
-    GLfloat random = ((rand() % 100) - 50) / 10.0f;
-    GLfloat rColor = 0.5 + ((rand() % 100) / 100.0f);
-    particle.Position = object.Position + random + offset;
-    particle.Color = glm::vec4(rColor, rColor, rColor, 1.0f);
-    particle.Life = 1.0f;
-    particle.Velocity = object.Velocity * 0.1f;
-}
-```
-
-这个函数简单的重置这个粒子的生命值为1.0f，随机的给一个大于`0.5`的颜色值(经过颜色向量)并且(在物体周围)分配一个位置和速度基于游戏里的物体。
-
-对于更新函数里的第二个循环遍历了所有粒子，并且对于每个粒子的生命值都减去一个时间差；这样每个粒子的生命值就精确到了秒。然后再检查这个粒子是否是还活着的，若是,则更新它的位置和颜色属性。这里我们缓慢的减少粒子颜色值的`alpha`值，以至于它看起来就是随着时间而缓慢的消亡。
-
-最后保留下来就是实际需要渲染的粒子：
-
-```c++
-glBlendFunc(GL_SRC_ALPHA, GL_ONE);
-particleShader.Use();
-for (Particle particle : particles)
-{
-    if (particle.Life > 0.0f)
-    {
-        particleShader.SetVector2f("offset", particle.Position);
-        particleShader.SetVector4f("color", particle.Color);
-        particleTexture.Bind();
-        glBindVertexArray(particleVAO);
-        glDrawArrays(GL_TRIANGLES, 0, 6);
-        glBindVertexArray(0);
-    } 
-} 
-glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
-```
-
-在这，对于每个粒子，我们一一设置他们的`uniform`变量`offse`和`color`，绑定纹理，然后渲染`2D`四边形的粒子。有趣的是我们在这看到了两次调用函数`glBlendFunc`。当要渲染这些粒子的时候，我们使用`GL_ONE`替换默认的目的因子模式`GL_ONE_MINUS_SRC_ALPHA`，这样，这些粒子叠加在一起的时候就会产生一些平滑的发热效果，就像在这个教程前面那样使用混合模式来渲染出火焰的效果也是可以的，这样在有大多数粒子的中心就会产生更加灼热的效果。
-
-因为我们(就像这个系列教程的其他部分一样)喜欢让事情变得有条理，所以我们就创建了另一个类`ParticleGenerator`来封装我们刚刚谈到的所有功能。你可以在下面的链接里找到源码：
->* [header](http://www.learnopengl.com/code_viewer.php?code=in-practice/breakout/particle_generator.h)，[code](http://www.learnopengl.com/code_viewer.php?code=in-practice/breakout/particle_generator)
-
-然后在游戏代码里,我们创建这样一个粒子发射器并且用[这个](../../img/06/Breakout/06/particle.png)纹理初始化。
-
-```c++
-ParticleGenerator   *Particles; 
-
-void Game::Init()
-{
-    [...]
-    ResourceManager::LoadShader("shaders/particle.vs", "shaders/particle.frag", nullptr, "particle");
-    [...]
-    ResourceManager::LoadTexture("textures/particle.png", GL_TRUE, "particle"); 
-    [...]
-    Particles = new ParticleGenerator(
-        ResourceManager::GetShader("particle"), 
-        ResourceManager::GetTexture("particle"), 
-        500
-    );
-}
-```
-
-然后我们在`Game`类的`Updata`函数里为粒子生成器添加一条更新语句：
-
-```c++
-void Game::Update(GLfloat dt)
-{
-    [...]
-    // Update particles
-    Particles->Update(dt, *Ball, 2, glm::vec2(Ball->Radius / 2));
-    [...]
-}
-```
-
-每个粒子都将使用球的游戏对象属性对象，每帧产生两个粒子并且他们都是偏向球得中心，最后是渲染粒子：
-
-```c++
-void Game::Render()
-{
-    if (this->State == GAME_ACTIVE)
-    {
-        [...]
-        // Draw player
-        Player->Draw(*Renderer);
-        // Draw particles	
-        Particles->Draw();
-        // Draw ball
-        Ball->Draw(*Renderer);
-    }
-}
-```
-
-注意到，我们是在渲染球体之前且在渲染其他物体之后渲染粒子的，这样，粒子就会在所有其他物体面前，但在球体之后，你可以在[这里](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_particles)找到更新的`game`类的源码。
-
-如果你现在编译并运行你的程序，你可能会看到在球体之后有一条小尾巴。就像这个教程开始的那样，给了这个游戏更加现代化的面貌。这个系统还可以很容易的扩展到更高级效果的主体上，就用这个粒子生成器自由的去实验吧，看看你是否可以创建出你自己的特效。
-
-
+# 粒子
+
+原文    | [Particles](http://learnopengl.com/#!In-Practice/2D-Game/Particles)
+-----   |  ----
+作者    | JoeydeVries
+翻译    | [ZMANT](https://github.com/Itanq)
+校对    | 暂无
+
+一个微粒,从OpenGL的角度看就是一个总是面向摄像机方向且(通常)包含一个大部分区域是透明的纹理的小四边形.一个微粒本身主要就是一个精灵(sprite),前面我们已经早就使用过了,但是当你把成千上万个这些微粒放在一起的时候,就可以创造出令人疯狂的效果.
+
+当处理这些微粒的时候,通常是由一个叫做粒子发射器或粒子生成器的东西完成的,从这个地方,持续不断的产生新的微粒并且旧的微粒随着时间逐渐消亡.如果这个粒子发射器产生一个带着类似烟雾纹理的微粒的时候,它的颜色亮度同时又随着与发射器距离的增加而变暗,那么就会产生出灼热的火焰的效果:
+
+![fire](http://www.learnopengl.com/img/in-practice/breakout/particles_example.jpg)
+
+一个单一的微粒通常有一个生命值变量,并且从它产生开始就一直在缓慢的减少.一旦它的生命值少于某个极限值(通常是0)我们就会杀掉这个粒子,这样下一个粒子产生时就可以让它来替换那个被杀掉的粒子.一个粒子发射器控制它产生的所有粒子并且根据它们的属性来改变它们的行为.一个粒子通常有下面的属性:
+
+```c++
+struct Particle {
+    glm::vec2 Position, Velocity;
+    glm::vec4 Color;
+    GLfloat Life;
+  
+    Particle() 
+      : Position(0.0f), Velocity(0.0f), Color(1.0f), Life(0.0f) { }
+};
+```
+
+看上面那个火焰的例子,那个粒子发射器可能在靠近发射器的地方产生每一个粒子,并且有一个向上的速度,这样每个粒子都是朝着正$y$轴方向移动.那似乎有3个不同区域,只是可能相比其他的区域,给了某个区域内的粒子更快的速度.我们也可以看到,$y$轴方向越高的粒子,它们的黄色或者说亮度就越低.一旦某个粒子到达某个高度的时候,它的生命值就会耗尽然后被杀掉;绝不可能直冲云霄.
+
+你可以想象到用这样一个系统,我们就可以创造一些有趣的效果比如火焰,青烟,烟雾,魔法效果,炮火残渣等等.在Breakout游戏里,我们将会使用下面那个小球来创建一个简单的粒子生成器来制作一些有趣的效果,结果看起来就像这样:
+
+<video src="http://learnopengl.com/video/in-practice/breakout/particles.mp4" controls="controls"></video>
+
+上面那个粒子生成器在这个球的位置产生无数的粒子,根据球移动的速度给了粒子相应的速度,并且根据它们的生命值来改变他们的颜色亮度.
+
+为了渲染这些粒子,我们将会用到有不同实现的着色器:
+
+```c++
+#version 330 core
+layout (location = 0) in vec4 vertex; // <vec2 position, vec2 texCoords>
+
+out vec2 TexCoords;
+out vec4 ParticleColor;
+
+uniform mat4 projection;
+uniform vec2 offset;
+uniform vec4 color;
+
+void main()
+{
+    float scale = 10.0f;
+    TexCoords = vertex.zw;
+    ParticleColor = color;
+    gl_Position = projection * vec4((vertex.xy * scale) + offset, 0.0, 1.0);
+}
+```
+
+以及像素着色器:
+
+```c++
+#version 330 core
+in vec2 TexCoords;
+in vec4 ParticleColor;
+out vec4 color;
+
+uniform sampler2D sprite;
+
+void main()
+{
+    color = (texture(sprite, TexCoords) * ParticleColor);
+}
+```
+
+我们获取每个粒子的位置和纹理属性并且设置两个uniform变量:$offset$和$color$来改变每个粒子的输出状态.注意到,在顶点着色器里,我们把这个四边形的粒子缩小了10倍;你也可以把这个缩放变量设置成uniform类型的变量从而控制一些个别的粒子.
+
+首先,我们需要一个粒子数组,然后用Particle结构体的默认构造函数来实例化.
+
+```c++
+GLuint nr_particles = 500;
+std::vector<Particle> particles;
+  
+for (GLuint i = 0; i < nr_particles; ++i)
+    particles.push_back(Particle());
+```
+
+然后在每一帧里面,我们都会用一个起始变量来产生一些新的粒子并且对每个粒子(还活着的)更新它们的值.
+
+```c++
+GLuint nr_new_particles = 2;
+// Add new particles
+for (GLuint i = 0; i < nr_new_particles; ++i)
+{
+    int unusedParticle = FirstUnusedParticle();
+    RespawnParticle(particles[unusedParticle], object, offset);
+}
+// Uupdate all particles
+for (GLuint i = 0; i < nr_particles; ++i)
+{
+    Particle &p = particles[i];
+    p.Life -= dt; // reduce life
+    if (p.Life > 0.0f)
+    {	// particle is alive, thus update
+        p.Position -= p.Velocity * dt;
+        p.Color.a -= dt * 2.5;
+    }
+}
+```c++
+
+第一个循环看起来可能有点吓人.因为这些粒子会随着时间消亡,我们就想在每一帧里面产生`nr_new_particles`个新粒子.但是一开始我们就知道了总的粒子数量是`nr_partiles`,所以我们不能简单的往粒子数组里面添加新的粒子.否则的话我们很快就会得到一个装满成千上万个粒子的数组,考虑到这个粒子数组里面其实只有一小部分粒子是存活的,这样就太浪费效率了.
+
+我们要做的就是找到第一个消亡的粒子然后用一个新产生的粒子来更新它.函数`FirstUnuseParticle`就是试图找到第一个消亡的粒子并且返回它的索引值给调用者.
+
+```c++
+GLuint lastUsedParticle = 0;
+GLuint FirstUnusedParticle()
+{
+    // Search from last used particle, this will usually return almost instantly
+    for (GLuint i = lastUsedParticle; i < nr_particles; ++i){
+        if (particles[i].Life <= 0.0f){
+            lastUsedParticle = i;
+            return i;
+        }
+    }
+    // Otherwise, do a linear search
+    for (GLuint i = 0; i < lastUsedParticle; ++i){
+        if (particles[i].Life <= 0.0f){
+            lastUsedParticle = i;
+            return i;
+        }
+    }
+    // Override first particle if all others are alive
+    lastUsedParticle = 0;
+    return 0;
+}
+```
+
+这个函数存储了它找到的上一个消亡的粒子的索引值,由于下一个消亡的粒子索引值总是在上一个消亡的粒子索引值的右边,所以我们首先从它存储的上一个消亡的粒子索引位置开始查找,如果我们没有任何消亡的粒子,我们就简单的做一个线性查找.如果没有粒子消亡就返回索引值`0`,结果就是第一个粒子被覆盖.需要注意的是,如果是最后一种情况,就意味着你粒子的生命值太长了,在每一帧里面需要产生更少的粒子,或者你只是没有保留足够的粒子.
+
+之后,一旦粒子数组中第一个消亡的粒子被发现的时候,我们就通过调用`RespawnParticle`函数更新它的值,函数接受一个`Particle`对象,一个`GameObject`对象和一个`offset`向量:
+
+```c++
+void RespawnParticle(Particle &particle, GameObject &object, glm::vec2 offset)
+{
+    GLfloat random = ((rand() % 100) - 50) / 10.0f;
+    GLfloat rColor = 0.5 + ((rand() % 100) / 100.0f);
+    particle.Position = object.Position + random + offset;
+    particle.Color = glm::vec4(rColor, rColor, rColor, 1.0f);
+    particle.Life = 1.0f;
+    particle.Velocity = object.Velocity * 0.1f;
+}
+```
+
+这个函数简单的重置这个粒子的生命值为1.0f,随机的给一个大于`0.5`的颜色值(经过颜色向量)并且(在物体周围)分配一个位置和速度基于游戏里的物体.
+
+对于更新函数里的第二个循环遍历了所有粒子,并且对于每个粒子的生命值都减去一个时间差;这样每个粒子的生命值就精确到了秒.然后再检查这个粒子是否是还活着的,若是,则更新它的位置和颜色属性.这里我们缓慢的减少粒子颜色值的`alpha`值,以至于它看起来就是随着时间而缓慢的消亡.
+
+最后保留下来就是实际需要渲染的粒子:
+
+```c++
+glBlendFunc(GL_SRC_ALPHA, GL_ONE);
+particleShader.Use();
+for (Particle particle : particles)
+{
+    if (particle.Life > 0.0f)
+    {
+        particleShader.SetVector2f("offset", particle.Position);
+        particleShader.SetVector4f("color", particle.Color);
+        particleTexture.Bind();
+        glBindVertexArray(particleVAO);
+        glDrawArrays(GL_TRIANGLES, 0, 6);
+        glBindVertexArray(0);
+    } 
+} 
+glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
+```
+
+在这,对于每个粒子,我们一一设置他们的`uniform`变量`offse`和`color`,绑定纹理,然后渲染`2D`四边形的粒子.有趣的是我们在这看到了两次调用函数`glBlendFunc`.当要渲染这些粒子的时候,我们使用`GL_ONE`替换默认的目的因子模式`GL_ONE_MINUS_SRC_ALPHA`,这样,这些粒子叠加在一起的时候就会产生一些平滑的发热效果,就像在这个教程前面那样使用混合模式来渲染出火焰的效果也是可以的,这样在有大多数粒子的中心就会产生更加灼热的效果.
+
+因为我们(就像这个系列教程的其他部分一样)喜欢让事情变得有条理,所以我们就创建了另一个类`ParticleGenerator`来封装我们刚刚谈到的所有功能.你可以在下面的链接里找到源码:
+>* [header](http://www.learnopengl.com/code_viewer.php?code=in-practice/breakout/particle_generator.h),[code](http://www.learnopengl.com/code_viewer.php?code=in-practice/breakout/particle_generator)
+
+然后在游戏代码里,我们创建这样一个粒子发射器并且用[这个](http://www.learnopengl.com/img/in-practice/breakout/textures/particle.png)纹理初始化.
+
+```c++
+ParticleGenerator   *Particles; 
+
+void Game::Init()
+{
+    [...]
+    ResourceManager::LoadShader("shaders/particle.vs", "shaders/particle.frag", nullptr, "particle");
+    [...]
+    ResourceManager::LoadTexture("textures/particle.png", GL_TRUE, "particle"); 
+    [...]
+    Particles = new ParticleGenerator(
+        ResourceManager::GetShader("particle"), 
+        ResourceManager::GetTexture("particle"), 
+        500
+    );
+}
+```
+
+然后我们在`Game`类的`Updata`函数里为粒子生成器添加一条更新语句:
+
+```c++
+void Game::Update(GLfloat dt)
+{
+    [...]
+    // Update particles
+    Particles->Update(dt, *Ball, 2, glm::vec2(Ball->Radius / 2));
+    [...]
+}
+```
+
+每个粒子都将使用球的游戏对象属性对象,每帧产生两个粒子并且他们都是偏向球得中心,最后是渲染粒子:
+
+```c++
+void Game::Render()
+{
+    if (this->State == GAME_ACTIVE)
+    {
+        [...]
+        // Draw player
+        Player->Draw(*Renderer);
+        // Draw particles	
+        Particles->Draw();
+        // Draw ball
+        Ball->Draw(*Renderer);
+    }
+}
+```
+
+注意到,我们是在渲染球体之前且在渲染其他物体之后渲染粒子的,这样,粒子就会在所有其他物体面前,但报纸在球体之后,你可以在[这里](http://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_particles)找到更新的`game`类的源码.
+
+如果你现在编译并运行你的程序,你可能会看到在球体之后有一条小尾巴.就像这个教程开始的那样,给了这个游戏更加现代化的面貌.这个系统还可以很容易的扩展到更高级效果的主体上,就用这个粒子生成器自由的去实验吧,看看你是否可以创建出你自己的特效.
+
+

docs/06 In Practice/2D-Game/07 Postprocessing.md

@@ -1,231 +0,0 @@
-# 后期处理
-
-原文    | [Postprocessing](https://learnopengl.com/#!In-Practice/2D-Game/Postprocessing)
------   |  ----
-作者    | JoeydeVries
-翻译    | [包纸](https://github.com/ShirokoSama)
-校对    | 暂无
-
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
-如果我们可以通过几个后期处理(Postprocess)特效丰富Breakout游戏的视觉效果的话，会不会是一件很有趣的事情？利用OpenGL的帧缓冲，我们可以相对容易地创造出模糊的抖动效果、反转场景里的所有颜色、做一些“疯狂”的顶点运动、或是使用一些其他有趣的特效。
-
-!!! important
-
-    这章教程广泛运用了之前[帧缓冲](../../04 Advanced OpenGL/05 Framebuffers.md)与[抗锯齿](../../04 Advanced OpenGL/11 Anti Aliasing.md)章节的概念。
-
-在教程的帧缓冲章节里，我们演示了如何使用单个纹理，通过后期处理特效实现有趣的效果（反相、灰度、模糊、锐化、边缘检测）。在Breakout中我们将做一些类似的事情：我们会创建一个帧缓冲对象，并附带一个多重采样的渲染缓冲对象作为其颜色附件。游戏中所有的渲染相关代码都应该渲染至这个多重采样的帧缓冲，然后将其内容传输([Bit blit](https://en.wikipedia.org/wiki/Bit_blit))至一个不同的帧缓冲中，该帧缓冲用一个纹理作为其颜色附件。这个纹理会包含游戏的渲染后的抗锯齿图像，我们对它应用零或多个后期处理特效后渲染至一个大的2D四边形。（译注：这段表述的复杂流程与教程帧缓冲章节的内容相似，原文中包含大量易混淆的名词与代词，建议读者先仔细理解帧缓冲章节的内容与流程）。
-
-总结一下这些渲染步骤：
-
-1. 绑定至多重采样的帧缓冲
-2. 和往常一样渲染游戏
-3. 将多重采样的帧缓冲内容传输至一个普通的帧缓冲中（这个帧缓冲使用了一个纹理作为其颜色缓冲附件）
-4. 解除绑定（绑定回默认的帧缓冲）
-5. 在后期处理着色器中使用来自普通帧缓冲的颜色缓冲纹理
-6. 渲染屏幕大小的四边形作为后期处理着色器的输出
-
-我们的后期处理着色器允许使用三种特效：**shake**, **confuse**和**chaos**。
-
-- **shake**：轻微晃动场景并附加一个微小的模糊效果。
-- **shake**：反转场景中的颜色并颠倒x轴和y轴。
-- **chaos**: 利用边缘检测卷积核创造有趣的视觉效果，并以圆形旋转动画的形式移动纹理图片，实现“混沌”特效。
-
-以下是这些效果的示例：
-
-![](../../img/06/Breakout/07/postprocessing_effects.png)
-
-在2D四边形上操作的顶点着色器如下所示：
-
-```c++
-#version 330 core
-layout (location = 0) in vec4 vertex; // <vec2 position, vec2 texCoords>
-
-out vec2 TexCoords;
-
-uniform bool  chaos;
-uniform bool  confuse;
-uniform bool  shake;
-uniform float time;
-
-void main()
-{
-    gl_Position = vec4(vertex.xy, 0.0f, 1.0f); 
-    vec2 texture = vertex.zw;
-    if(chaos)
-    {
-        float strength = 0.3;
-        vec2 pos = vec2(texture.x + sin(time) * strength, texture.y + cos(time) * strength);        
-        TexCoords = pos;
-    }
-    else if(confuse)
-    {
-        TexCoords = vec2(1.0 - texture.x, 1.0 - texture.y);
-    }
-    else
-    {
-        TexCoords = texture;
-    }
-    if (shake)
-    {
-        float strength = 0.01;
-        gl_Position.x += cos(time * 10) * strength;        
-        gl_Position.y += cos(time * 15) * strength;        
-    }
-}  
-```
-
-基于uniform是否被设置为true，顶点着色器可以执行不同的分支。如果<var>chaos</var>或<var>confuse</var>被设置为true，顶点着色器将操纵纹理坐标来移动场景（以圆形动画变换纹理坐标或反转纹理坐标）。因为我们将纹理环绕方式设置为了<var>GL_REPEAT</var>，所以**chaos**特效会导致场景在四边形的各个部分重复。除此之外，如果**shake**被设置为true，它将微量移动顶点位置。需要注意的是，<var>chaos</var>与<var>confuse</var>不应同时为true，而<var>shake</var>则可以与其他特效一起生效。
-
-当任意特效被激活时，除了偏移顶点的位置和纹理坐标，我们也希望创造显著的视觉效果。我们可以在片段着色器中实现这一点：
-
-```c++
-#version 330 core
-in  vec2  TexCoords;
-out vec4  color;
-  
-uniform sampler2D scene;
-uniform vec2      offsets[9];
-uniform int       edge_kernel[9];
-uniform float     blur_kernel[9];
-
-uniform bool chaos;
-uniform bool confuse;
-uniform bool shake;
-
-void main()
-{
-    color = vec4(0.0f);
-    vec3 sample[9];
-    // 如果使用卷积矩阵，则对纹理的偏移像素进行采样
-    if(chaos || shake)
-        for(int i = 0; i < 9; i++)
-            sample[i] = vec3(texture(scene, TexCoords.st + offsets[i]));
-
-    // 处理特效
-    if(chaos)
-    {           
-        for(int i = 0; i < 9; i++)
-            color += vec4(sample[i] * edge_kernel[i], 0.0f);
-        color.a = 1.0f;
-    }
-    else if(confuse)
-    {
-        color = vec4(1.0 - texture(scene, TexCoords).rgb, 1.0);
-    }
-    else if(shake)
-    {
-        for(int i = 0; i < 9; i++)
-            color += vec4(sample[i] * blur_kernel[i], 0.0f);
-        color.a = 1.0f;
-    }
-    else
-    {
-        color =  texture(scene, TexCoords);
-    }
-}
-```
-
-这个着色器几乎直接构建自帧缓冲教程的片段着色器，并根据被激活的特效类型进行相应的后期处理。这一次，偏移矩阵(offset matrix)和卷积核作为uniform变量，由应用程序中的代码定义。好处是我们只需要设置这些内容一次，而不必在每个片段着色器执行时重新计算这些矩阵。例如，偏移矩阵的配置如下所示：
-
-```c++
-GLfloat offset = 1.0f / 300.0f;
-GLfloat offsets[9][2] = {
-    { -offset,  offset  },  // 左上
-    {  0.0f,    offset  },  // 中上
-    {  offset,  offset  },  // 右上
-    { -offset,  0.0f    },  // 左中
-    {  0.0f,    0.0f    },  // 正中
-    {  offset,  0.0f    },  // 右中
-    { -offset, -offset  },  // 左下
-    {  0.0f,   -offset  },  // 中下
-    {  offset, -offset  }   // 右下
-};
-glUniform2fv(glGetUniformLocation(shader.ID, "offsets"), 9, (GLfloat*)offsets);  
-```
-
-由于所有管理帧缓冲器的概念已经在之前的教程中有过广泛的讨论，所以这次我不会深入其细节。下面是<fun>PostProcessor</fun>类的代码，它管理初始化，读写帧缓冲并将一个四边形渲染至屏幕。如果你理解了帧缓冲与反锯齿章节的教程，你应该可以完全它的代码。
-
-- **PostProcessor**：[头文件](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/post_processor.h)，[代码](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/post_processor)
-
-有趣的是<fun>BeginRender</fun>和<fun>EndRender</fun>函数。由于我们必须将整个游戏场景渲染至帧缓冲中，因此我们可以在场景的渲染代码之前和之后分别调用<fun>BeginRender</fun>和<fun>EndRender</fun>。接着，这个类将处理幕后的帧缓冲操作。在游戏的渲染函数中使用<fun>PostProcessor</fun>类如下所示：
-
-```c++
-PostProcessor   *Effects;
-
-void Game::Render()
-{
-    if (this->State == GAME_ACTIVE)
-    {
-        Effects->BeginRender();
-            // 绘制背景
-            // 绘制关卡
-            // 绘制挡板
-            // 绘制粒子
-            // 绘制小球
-        Effects->EndRender();
-        Effects->Render(glfwGetTime());
-    }
-}
-```
-
-无论我们需要什么，我们只需要将需要的<fun>PostProcessor</fun>类中的特效属性设置为true，其效果就可以立即可见。
-
-## Shake it
-
-作为这些效果的演示，我们将模拟球击中坚固的混凝土块时的视觉冲击。无论在哪里发生碰撞，只要在短时间内实现晃动(shake)效果，便能增强撞击的冲击感。
-
-我们只想允许晃动效果持续一小段时间。我们可以通过声明一个持有晃动效果持续时间的变量<var>ShakeTime</var>来实现这个功能。无论碰撞何时发生，我们将这个变量重置为一个特定的持续时间:
-
-```c++
-GLfloat ShakeTime = 0.0f;  
-
-void Game::DoCollisions()
-{
-    for (GameObject &box : this->Levels[this->Level].Bricks)
-    {
-        if (!box.Destroyed)
-        {
-            Collision collision = CheckCollision(*Ball, box);
-            if (std::get<0>(collision)) // 如果发生了碰撞
-            {
-                // 如果不是实心的砖块则摧毁
-                if (!box.IsSolid)
-                    box.Destroyed = GL_TRUE;
-                else
-                {   // 如果是实心的砖块则激活shake特效
-                    ShakeTime = 0.05f;
-                    Effects->Shake = true;
-                }
-                [...]
-            }
-        }    
-    }
-    [...]
-}  
-```
-
-然后在游戏的<fun>Update</fun>函数中，我们减少<var>ShakeTime</var>变量的值直到其为0.0，并停用shake特效。
-
-```c++
-void Game::Update(GLfloat dt)
-{
-    [...]
-    if (ShakeTime > 0.0f)
-    {
-        ShakeTime -= dt;
-        if (ShakeTime <= 0.0f)
-            Effects->Shake = false;
-    }
-}  
-```
-
-这样，每当我们碰到一个实心砖块时，屏幕会短暂地抖动与模糊，给玩家一些小球与坚固物体碰撞的视觉反馈。
-
-<video src="https://learnopengl.com/video/in-practice/breakout/postprocessing_shake.mp4" controls="controls"></video>
-
-你可以在[这里](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_postprocessing)找到更新后的<fun>Game</fun>类。
-
-在[下一章](./08 Powerups.md)关于“道具”的教程中我们将带来另外两种的特效的使用。

docs/06 In Practice/2D-Game/08 Powerups.md

@@ -1,337 +0,0 @@
-# 道具
-
-原文    | [Powerups](https://learnopengl.com/#!In-Practice/2D-Game/Powerups)
------   |  ----
-作者    | JoeydeVries
-翻译    | [包纸](https://github.com/ShirokoSama)
-校对    | 暂无
-
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
-Breakout已经接近完成了，但我们可以至少再增加一种游戏机制让它变得更酷。“充电”（译注：Powerups，很多游戏中都会用这个单词指代可以提升能力的道具，本文之后也会用道具一词作为其翻译）怎么样？
-
-这个想法的含义是，无论一个砖块何时被摧毁，它都有一定几率产生一个道具块。这样的道具快会缓慢降落，而且当它与玩家挡板发生接触时，会发生基于道具类型的有趣效果。例如，某一种道具可以让玩家挡板变长，另一种道具则可以让小球穿过物体。我们还可以添加一些可以给玩家造成负面影响的负面道具。
-
-我们可以将道具建模为具有一些额外属性的<fun>GameObject</fun>，这也是为什么我们定义一个继承自<fun>GameObject</fun>的<fun>PowerUp</fun>类并在其中增添了一些额外的成员属性。
-
-```c++
-const glm::vec2 SIZE(60, 20);
-const glm::vec2 VELOCITY(0.0f, 150.0f);
-
-class PowerUp : public GameObject 
-{
-public:
-    // 道具类型
-    std::string Type;
-    GLfloat     Duration;   
-    GLboolean   Activated;
-    // 构造函数
-    PowerUp(std::string type, glm::vec3 color, GLfloat duration, 
-            glm::vec2 position, Texture2D texture) 
-        : GameObject(position, SIZE, texture, color, VELOCITY), 
-          Type(type), Duration(duration), Activated() 
-    { }
-}; 
-```
-
-<fun>PowerUp</fun>类仅仅是一个有一些额外状态的<fun>GameObject</fun>， 所以我们简单地将它定义为一个头文件，你可以在[这里](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/power_up.h)找到它。
-
-每个道具以字符串的形式定义它的类型，持有表示它有效时长的持续时间与表示当前是否被激活的属性。在Breakout中，我们将添加4种增益道具与2种负面道具：
-
-![](../../img/06/Breakout/08/powerups.png)
-
-- **Speed**: 增加小球20%的速度
-- **Sticky**: 当小球与玩家挡板接触时，小球会保持粘在挡板上的状态直到再次按下空格键，这可以让玩家在释放小球前找到更合适的位置
-- **Pass-Through**: 非实心砖块的碰撞处理被禁用，使小球可以穿过并摧毁多个砖块
-- **Pad-Size-Increase**: 增加玩家挡板50像素的宽度
-- **Confuse**: 短时间内激活confuse后期特效，迷惑玩家
-- **Chaos**: 短时间内激活chaos后期特效，使玩家迷失方向
-
-你可以在下面找到道具的高质量纹理：
-
-- **Texture**： [Speed](https://learnopengl.com/img/in-practice/breakout/textures/powerup_speed.png),[Sticky](https://learnopengl.com/img/in-practice/breakout/textures/powerup_sticky.png),[Pass-Through](https://learnopengl.com/img/in-practice/breakout/textures/powerup_passthrough.png),[Pad-Size-Increase](https://learnopengl.com/img/in-practice/breakout/textures/powerup_increase.png),[Confuse](https://learnopengl.com/img/in-practice/breakout/textures/powerup_confuse.png),[Chaos](https://learnopengl.com/img/in-practice/breakout/textures/powerup_chaos.png).
-
-与关卡中的砖块纹理类似，每个道具纹理都是完全灰度的，这使得我们在将其与颜色向量相乘时可以保持色彩的平衡。
-
-因为我们需要跟踪游戏中被激活的道具的类型、持续时间、相关效果等状态，所以我们将它们存储在一个容器内：
-
-```c++
-class Game {
-    public:
-        [...]
-        std::vector<PowerUp>  PowerUps;
-        [...]
-        void SpawnPowerUps(GameObject &block);
-        void UpdatePowerUps(GLfloat dt);
-};
-```
-
-我们还定义了两个管理道具的函数，<fun>SpawnPowerUps</fun>在给定的砖块位置生成一个道具，<fun>UpdatePowerUps</fun>管理所有当前被激活的道具。
-
-## SpawnPowerUps
-
-每次砖块被摧毁时我们希望以一定几率生成一个道具，这个功能可以在<fun>Game</fun>的<fun>SpawnPowerUps</fun>函数中找到：
-
-```c++
-GLboolean ShouldSpawn(GLuint chance)
-{
-    GLuint random = rand() % chance;
-    return random == 0;
-}
-void Game::SpawnPowerUps(GameObject &block)
-{
-    if (ShouldSpawn(75)) // 1/75的几率
-        this->PowerUps.push_back(
-             PowerUp("speed", glm::vec3(0.5f, 0.5f, 1.0f), 0.0f, block.Position, tex_speed
-         ));
-    if (ShouldSpawn(75))
-        this->PowerUps.push_back(
-            PowerUp("sticky", glm::vec3(1.0f, 0.5f, 1.0f), 20.0f, block.Position, tex_sticky 
-        );
-    if (ShouldSpawn(75))
-        this->PowerUps.push_back(
-            PowerUp("pass-through", glm::vec3(0.5f, 1.0f, 0.5f), 10.0f, block.Position, tex_pass
-        ));
-    if (ShouldSpawn(75))
-        this->PowerUps.push_back(
-            PowerUp("pad-size-increase", glm::vec3(1.0f, 0.6f, 0.4), 0.0f, block.Position, tex_size    
-        ));
-    if (ShouldSpawn(15)) // 负面道具被更频繁地生成
-        this->PowerUps.push_back(
-            PowerUp("confuse", glm::vec3(1.0f, 0.3f, 0.3f), 15.0f, block.Position, tex_confuse
-        ));
-    if (ShouldSpawn(15))
-        this->PowerUps.push_back(
-            PowerUp("chaos", glm::vec3(0.9f, 0.25f, 0.25f), 15.0f, block.Position, tex_chaos
-        ));
-}
-```
-
-这样的<fun>SpawnPowerUps</fun>函数以一定几率（1/75普通道具，1/15负面道具）生成一个新的<fun>PowerUp</fun>对象，并设置其属性。每种道具有特殊的颜色使它们更具有辨识度，同时根据类型决定其持续时间的秒数，若值为0.0f则表示它持续无限长的时间。除此之外，每个道具初始化时传入被摧毁砖块的位置与上一小节给出的对应纹理。
-
-## 激活道具
-
-接下来我们更新游戏的<fun>DoCollisions</fun>函数使它不只检查小球与砖块和挡板的碰撞，还检查挡板与所有未被销毁的道具的碰撞。注意我们在砖块被摧毁的同时调用<fun>SpawnPowerUps</fun>函数。
-
-```c++
-void Game::DoCollisions()
-{
-    for (GameObject &box : this->Levels[this->Level].Bricks)
-    {
-        if (!box.Destroyed)
-        {
-            Collision collision = CheckCollision(*Ball, box);
-            if (std::get<0>(collision))
-            {
-                if (!box.IsSolid)
-                {
-                    box.Destroyed = GL_TRUE;
-                    this->SpawnPowerUps(box);
-                }
-                [...]
-            }
-        }
-    }        
-    [...] 
-    for (PowerUp &powerUp : this->PowerUps)
-    {
-        if (!powerUp.Destroyed)
-        {
-            if (powerUp.Position.y >= this->Height)
-                powerUp.Destroyed = GL_TRUE;
-            if (CheckCollision(*Player, powerUp))
-            {   // 道具与挡板接触，激活它！
-                ActivatePowerUp(powerUp);
-                powerUp.Destroyed = GL_TRUE;
-                powerUp.Activated = GL_TRUE;
-            }
-        }
-    }  
-}
-```
-
-对所有未被销毁的道具，我们检查它是否接触到了屏幕底部或玩家挡板，无论哪种情况我们都销毁它，但当道具与玩家挡板接触时，激活这个道具。
-
-激活道具的操作可以通过将其<var>Activated</var>属性设为true来完成，实现其效果则需要将它传给<fun>ActivatePowerUp</fun>函数：
-
-```c++
-void ActivatePowerUp(PowerUp &powerUp)
-{
-    // 根据道具类型发动道具
-    if (powerUp.Type == "speed")
-    {
-        Ball->Velocity *= 1.2;
-    }
-    else if (powerUp.Type == "sticky")
-    {
-        Ball->Sticky = GL_TRUE;
-        Player->Color = glm::vec3(1.0f, 0.5f, 1.0f);
-    }
-    else if (powerUp.Type == "pass-through")
-    {
-        Ball->PassThrough = GL_TRUE;
-        Ball->Color = glm::vec3(1.0f, 0.5f, 0.5f);
-    }
-    else if (powerUp.Type == "pad-size-increase")
-    {
-        Player->Size.x += 50;
-    }
-    else if (powerUp.Type == "confuse")
-    {
-        if (!Effects->Chaos)
-            Effects->Confuse = GL_TRUE; // 只在chaos未激活时生效，chaos同理
-    }
-    else if (powerUp.Type == "chaos")
-    {
-        if (!Effects->Confuse)
-            Effects->Chaos = GL_TRUE;
-    }
-} 
-```
-
-<fun>ActivatePowerUp</fun>的目的正如其名称，它按本章教程之前所预设的那样激活了一个道具的效果。我们检查道具的类型并相应地改变游戏状态。对于**Sticky**和**Pass-through**效果，我们也相应地改变了挡板和小球的颜色来给玩家一些当前被激活了哪种效果的反馈。
-
-因为**Sticky**和**Pass-through**效果稍微改变了一些原有的游戏逻辑，所以我们将这些效果作为属性存储在小球对象中，这样我们可以根据小球当前激活了什么效果而改变游戏逻辑。我们只在<fun>BallObject</fun>的头文件中增加了两个属性，但为了完整性下面给出了更新后的代码：
-
-- **GameObject**: [头文件](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/ball_object.h)，[代码](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/ball_object)
-
-这样我们可以通过改动<fun>DoCollisions</fun>函数中小球与挡板碰撞的代码便捷地实现**Sticky**效果。
-
-```c++
-if (!Ball->Stuck && std::get<0>(result))
-{
-    [...]
-    Ball->Stuck = Ball->Sticky;
-}
-```
-
-在这里我们将小球的Stuck属性设置为它自己的Sticky属性，若**Stikcy**效果被激活，那么小球则会在与挡板接触时粘在上面，玩家不得不再次按下空格键才能释放它。
-
-在同样的<fun>DoCollisions</fun>函数中还有个为了实现**Pass-through**效果的类似小改动。当小球的<var>PassThrough</var>属性被设置为true时，我们不对非实心砖块做碰撞处理操作。
-
-```c++
-Direction dir = std::get<1>(collision);
-glm::vec2 diff_vector = std::get<2>(collision);
-if (!(Ball->PassThrough && !box.IsSolid)) 
-{
-    if (dir == LEFT || dir == RIGHT) // 水平碰撞
-    {
-        [...]
-    }
-    else 
-    {
-        [...]
-    }
-}  
-```
-
-其他效果可以通过简单的更改游戏的状态来实现，如小球的速度、挡板的尺寸、<fun>PostProcessor</fun>对象的效果。
-
-## 更新道具
-
-现在剩下要做的就是保证道具生成后可以移动，并且在它们的持续时间用尽后失效，否则道具将永远保持激活状态。
-
-在游戏的<fun>UpdatePowerUps</fun>函数中，我们根据道具的速度移动它，并减少已激活道具的持续时间，每当时间减少至小于0时，我们令其失效，并恢复相关变量的状态。
-
-```c++
-void Game::UpdatePowerUps(GLfloat dt)
-{
-    for (PowerUp &powerUp : this->PowerUps)
-    {
-        powerUp.Position += powerUp.Velocity * dt;
-        if (powerUp.Activated)
-        {
-            powerUp.Duration -= dt;
-
-            if (powerUp.Duration <= 0.0f)
-            {
-                // 之后会将这个道具移除
-                powerUp.Activated = GL_FALSE;
-                // 停用效果
-                if (powerUp.Type == "sticky")
-                {
-                    if (!isOtherPowerUpActive(this->PowerUps, "sticky"))
-                    {   // 仅当没有其他sticky效果处于激活状态时重置，以下同理
-                        Ball->Sticky = GL_FALSE;
-                        Player->Color = glm::vec3(1.0f);
-                    }
-                }
-                else if (powerUp.Type == "pass-through")
-                {
-                    if (!isOtherPowerUpActive(this->PowerUps, "pass-through"))
-                    {
-                        Ball->PassThrough = GL_FALSE;
-                        Ball->Color = glm::vec3(1.0f);
-                    }
-                }
-                else if (powerUp.Type == "confuse")
-                {
-                    if (!isOtherPowerUpActive(this->PowerUps, "confuse"))
-                    {
-                        Effects->Confuse = GL_FALSE;
-                    }
-                }
-                else if (powerUp.Type == "chaos")
-                {
-                    if (!isOtherPowerUpActive(this->PowerUps, "chaos"))
-                    {
-                        Effects->Chaos = GL_FALSE;
-                    }
-                }                
-            }
-        }
-    }
-    this->PowerUps.erase(std::remove_if(this->PowerUps.begin(), this->PowerUps.end(),
-        [](const PowerUp &powerUp) { return powerUp.Destroyed && !powerUp.Activated; }
-    ), this->PowerUps.end());
-}  
-```
-
-你可以看到对于每个效果，我们通过将相关元素重置来停用它。我们还将<fun>PowerUp</fun>的<var>Activated</var>属性设为false，在<fun>UpdatePowerUps</fun>结束时，我们通过循环PowerUps容器，若一个道具被销毁切被停用，则移除它。我们在算法开头使用<fun>remove_if</fun>函数，通过给定的lamda表达式消除这些对象。
-
-!!! important
-
-    <fun>remove_if</fun>函数将lamda表达式为true的元素移动至容器的末尾并返回一个迭代器指向应被移除的元素范围的开始部分。容器的<fun>erase</fun>函数接着擦除这个迭代器指向的元素与容器末尾元素之间的所有元素。
-
-可能会发生这样的情况：当一个道具在激活状态时，另一个道具与挡板发生了接触。在这种情况下我们有超过1个在当前<var>PowerUps</var>容器中处于激活状态的道具。然后，当这些道具中的一个被停用时，我们不应使其效果失效因为另一个相同类型的道具仍处于激活状态。出于这个原因，我们使用<fun>isOtherPowerUpActive</fun>检查是否有同类道具处于激活状态。只有当它返回false时，我们才停用这个道具的效果。这样，给定类型的道具的持续时间就可以延长至最近一次被激活后的持续时间。
-
-```c++
-GLboolean IsOtherPowerUpActive(std::vector<PowerUp> &powerUps, std::string type)
-{
-    for (const PowerUp &powerUp : powerUps)
-    {
-        if (powerUp.Activated)
-            if (powerUp.Type == type)
-                return GL_TRUE;
-    }
-    return GL_FALSE;
-}  
-```
-
-这个函数简单地检查是否有同类道具处于激活状态，如果有则返回<var>GL_TRUE</var>。
-
-最后剩下的一件事便是渲染道具：
-
-```c++
-void Game::Render()
-{
-    if (this->State == GAME_ACTIVE)
-    {
-        [...]
-        for (PowerUp &powerUp : this->PowerUps)
-            if (!powerUp.Destroyed)
-                powerUp.Draw(*Renderer);
-        [...]
-    }
-}    
-```
-
-结合所有的这些功能，我们有了一个可以运作的道具系统，它不仅使游戏更有趣，还使游戏更具有挑战性。它看上去会像这样：
-
-<video src="https://learnopengl.com/video/in-practice/breakout/powerups.mp4" controls="controls"></video>
-
-你可以在下面找到所有更新后的代码（当关卡重置时我们同时重置所有道具效果）：
-
-- **Game**: [头文件](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_powerups.h)，[代码](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_powerups)

docs/06 In Practice/2D-Game/09 Audio.md

@@ -1,87 +0,0 @@
-# 音效
-
-原文    | [Audio](https://learnopengl.com/#!In-Practice/2D-Game/Audio)
------   |  ----
-作者    | JoeydeVries
-翻译    | [包纸](https://github.com/ShirokoSama)
-校对    | 暂无
-
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
-无论我们将游戏音量调到多大，我们都不会听到来自游戏的任何音效。我们已经展示了这么多内容，但没有任何音频，游戏仍显得有些空洞。在本节教程中，我们将解决这个问题。
-
-OpenGL不提供关于音频的任何支持。我们不得不手动将音频加载为字节格式，处理并将其转化为音频流，并适当地管理多个音频流以供我们的游戏使用。然而这有一些复杂，并且需要一些底层的音频工程知识。
-
-如果你乐意，你可以手动加载来自多种扩展名的音频文件的音频流。然而，我们将使用被称为irrKlang的音频管理库。
-
-## irrKlang
-
-<img alt="GLM Logo" src="../../img/06/Breakout/09/irrklang.png" class="right" />
-
-IrrKlang是一个可以播放WAV，MP3，OGG和FLAC文件的高级二维和三维（Windows，Mac OS X，Linux）声音引擎和音频库。它还有一些可以自由调整的音频效果，如混响、延迟和失真。
-
-!!! important
-
-    3D音频意味着音频源可以有一个3D位置，然后根据相机到音频源的位置衰减音量，使其在一个3D世界里显得自然（想想3D世界中的枪声，通常你可以从音效中听出它来自什么方向/位置）。
-
-IrrKlang是一个易于使用的音频库，只需几行代码便可播放大多数音频文件，这使它成为我们Breakout游戏的完美选择。请注意，irrKlang有一个有一定限制的证书：允许你将irrKlang用于非商业目的，但是如果你想使用irrKlang商业版，就必须支付购买他们的专业版。由于Breakout和本教程系列是非商业性的，所以我们可以自由地使用他们的标准库。
-
-你可以从他们的[下载页面](http://www.ambiera.com/irrklang/downloads.html)下载irrKlang，我们将使用1.5版本。由于irrKlang是非开源的代码，因此我们不得不使用irrKlang为我们提供的任何东西。幸运的是，他们有大量的预编译库文件，所以你们大多数人应该可以很好地使用它。
-
-你需要引入了irrKlang的头文件，将他们的库文件（irrKlang.lib）添加到链接器设置中，并将他们的dll文件复制到适当的目录下（通常和.exe在同一目录下）。需要注意的是，如果你想要加载MP3文件，则还需要引入ikpMP3.dll文件。
-
-## 添加音乐
-
-为了这个游戏我特制了一个小小的音轨，让游戏更富有活力。在[这里](https://learnopengl.com/audio/in-practice/breakout/breakout.mp3)你可以找到我们将要用作游戏背景音乐的音轨。这个音轨会在游戏开始时播放并不断循环直到游戏结束。你可以随意用自己的音频替换它，或者用喜欢的方式使用它。
-
-<audio src="https://learnopengl.com/audio/in-practice/breakout/breakout.mp3" controls="controls"></audio>
-
-利用irrKlang库将其添加到Breakout游戏里非常简单。我们引入相应的头文件，创建<fun>irrKlang::ISoundEngine</fun>，用<fun>createIrrKlangDevice</fun>初始化它并使用这个引擎加载、播放音频：
-
-```c++
-#include <irrklang/irrKlang.h>
-using namespace irrklang;
-
-ISoundEngine *SoundEngine = createIrrKlangDevice();
-  
-void Game::Init()
-{
-    [...]
-    SoundEngine->play2D("audio/breakout.mp3", GL_TRUE);
-}
-```
-
-在这里，我们创建了一个<fun>SoundEngine</fun>，用于管理所有与音频相关的代码。一旦我们初始化了引擎，便可以调用<fun>play2D</fun>函数播放音频。第一个参数为文件名，第二个参数为是否循环播放。
-
-这就是全部了！现在运行游戏会使你的耳机或扬声器迸发出声波。
-
-## 添加音效
-
-我们还没有结束，因为音乐本身并不能使游戏完全充满活力。我们希望在游戏发生一些有趣事件时播放音效，作为给玩家的额外反馈，如我们撞击砖块、获得道具时。下面你可以找到我们需要的所有音效（来自freesound.org）：
-
-[bleep.mp3](https://learnopengl.com/audio/in-practice/breakout/bleep.mp3): 小球撞击非实心砖块时的音效
-
-<audio src="https://learnopengl.com/audio/in-practice/breakout/bleep.mp3" controls="controls"></audio>
-
-[solid.wav](https://learnopengl.com/audio/in-practice/breakout/solid.wav)：小球撞击实心砖块时的音效
-
-<audio src="https://learnopengl.com/audio/in-practice/breakout/solid.wav" controls="controls"></audio>
-
-[powerup.wav](https://learnopengl.com/audio/in-practice/breakout/powerup.wav): 获得道具时的音效
-
-<audio src="https://learnopengl.com/audio/in-practice/breakout/powerup.wav" controls="controls"></audio>
-
-[bleep.wav](https://learnopengl.com/audio/in-practice/breakout/bleep.wav): 小球在挡板上反弹时的音效
-
-<audio src="https://learnopengl.com/audio/in-practice/breakout/bleep.wav" controls="controls"></audio>
-
-无论在哪里发生碰撞，我们都会播放相应的音效。我不会详细阐述每一行的代码，并把更新后的代码放在了[这里](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/game_audio)，你应该可以轻松地找到相应的添加音效的地方。
-
-把这些集成在一起后我们的游戏显得更完整了，就像这样：
-
-<video src="https://learnopengl.com/video/in-practice/breakout/audio.mp4" controls="controls"></video>
-
-IrrKlang允许一些更精细的音频管理功能，如内存管理、声音特效和声音事件回调。看看他们的C++[教程](http://www.ambiera.com/irrklang/tutorials.html)并尝试一些功能吧。
-

docs/06 In Practice/2D-Game/10 Render Text.md

@@ -1,343 +0,0 @@
-# 渲染文本
-
-| 原文   | [Render text](https://learnopengl.com/#!In-Practice/2D-Game/Render-text) |
-| ---- | ---------------------------------------- |
-| 作者   | JoeydeVries                              |
-| 翻译   | [aillieo](https://github.com/aillieo)    |
-| 校对   | 暂无                                       |
-
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
-本教程中将通过增加生命值系统、获胜条件和渲染文本形式的反馈来对游戏做最后的完善。本教程很大程度上是建立在之前的教程[文本渲染](../02 Text Rendering.md)基础之上，因此如果没有看过的话，强烈建议您先一步一步学习之前的教程。
-
-在Breakout中，所有的文本渲染代码都封装在一个名为<fun>TextRenderer</fun>的类中，其中包含FreeType库的初始化、渲染配置和实际渲染代码等重要组成部分。以下是<fun>TextRenderer</fun>类的代码：
-
-- **TextRenderer**: [header](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/text_renderer.h), [code](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/text_renderer).
-- **Text shaders**: [vertex](https://learnopengl.com/code_viewer.php?code=in-practice/text_rendering&type=vertex), [fragment](https://learnopengl.com/code_viewer.php?code=in-practice/text_rendering&type=fragment).
-
-文本渲染器中函数的内容几乎与文本渲染教程中的代码完全一样。但用于向屏幕渲染字形的代码稍有不同：
-
-```C++
-void TextRenderer::RenderText(std::string text, GLfloat x, GLfloat y, GLfloat scale,glm::vec3 color)
-{
-    [...]
-    for (c = text.begin(); c != text.end(); c++)
-    {
-        GLfloat xpos = x + ch.Bearing.x * scale;
-        GLfloat ypos = y + (this->Characters['H'].Bearing.y - ch.Bearing.y) * scale;
-
-        GLfloat w = ch.Size.x * scale;
-        GLfloat h = ch.Size.y * scale;
-        // 为每个字符更新VBO
-        GLfloat vertices[6][4] = {
-            { xpos,     ypos + h,   0.0, 1.0 },
-            { xpos + w, ypos,       1.0, 0.0 },
-            { xpos,     ypos,       0.0, 0.0 },
-
-            { xpos,     ypos + h,   0.0, 1.0 },
-            { xpos + w, ypos + h,   1.0, 1.0 },
-            { xpos + w, ypos,       1.0, 0.0 }
-        };
-        [...]
-    }
-}
-```
-
-之所以会稍有不同，是因为相比于文本渲染教程我们此处使用了一个不同的正交投影矩阵。在文本渲染教程中，所有的<var>y</var>值取值从底部向顶部递增，但在游戏Breakout中，<var>y</var>值取值从顶部到底部递增，值为<var>0.0</var>的<var>y</var>值对应屏幕顶端。这意味着我们需要稍微改变计算垂直方向偏移的方法。
-
-由于现在我们将<fun>RenderText</fun>的<var>y</var>坐标参数从上向下渲染，我们将垂直偏移计算为一个字形从字形空间顶部向下推进的距离。回顾FreeType的字形矩阵图片，此垂直偏移用红色箭头标记。
-
-![](../../img/06/Breakout/10/glyph_offset.png)
-
-为计算垂直偏移，我们需要获取字形空间的顶部（基本上是原点发出的黑色垂直箭头的长度）。不幸的是，FreeType并不向我们提供这样的机制。我们已知的是有一些字形直接与顶部接触，如字符'H'、'T'或'X'。那么我们通过**接触顶部的**字形的<var>bearingY</var>减去顶部不确定字形的<var>bearingY</var>来计算红色矢量的长度。使用这种方法，我们依据字形顶部的点与顶部边差异的距离来向下推进字形。
-
-```C++
-GLfloat ypos = y + (this->Characters['H'].Bearing.y - ch.Bearing.y) * scale;
-
-```
-
-除了更新<var>ypos</var>的计算之外，我们还调换了一些顶点的顺序，用以确保所有的顶点在与现在的正交投影矩阵相乘后仍为正方向（详见教程[面剔除](../../04 Advanced OpenGL/04 Face culling.md)）。
-
-向游戏中加入<fun>TextRenderer</fun>并不难：
-
-```C++
-TextRenderer  *Text;
-
-void Game::Init()
-{
-    [...]
-    Text = new TextRenderer(this->Width, this->Height);
-    Text->Load("fonts/ocraext.TTF", 24);
-}
-
-```
-
-使用一个名为OCR A Extended的字体来初始化文本渲染器，该字体可以从[这里](http://fontzone.net/font-details/ocr-a-extended)下载。您可以使用任意不同的字体，如果不很喜欢这个字体。
-
-现在我们已经有了一个文本渲染器，接下来我们来完成游戏机制。
-
-## 玩家生命值
-
-当球碰到底部边界时，我们会给玩家额外的几次机会，而不是立即重置游戏。我们使用玩家生命值的形式来实现，玩家开始时会有初始数量的生命值（比如<var>3</var>），每当球碰到底部边界，玩家的生命值总数会减<var>1</var>。只有当玩家生命值变为<var>0</var>时才会重置游戏。这样对玩家来说完成关卡会稍容易一点，同时也会感受到难度。
-
-我们向game类中增加玩家的生命值以记录它（在构造函数中将其初始化为<var>3</var>）。
-
-```C++
-class Game
-{
-    [...]
-    public:
-        GLuint Lives;
-}
-```
-
-接下来我们修改game类的<fun>update</fun>函数，不再重置游戏，而是减少玩家生命值，只有当生命值为<var>0</var>时重置游戏。
-
-```C++
-void Game::Update(GLfloat dt)
-{
-    [...]
-    if (Ball->Position.y >= this->Height) // 球是否接触到底部边界?
-    {
-        --this->Lives;
-        // 玩家是否已失去所有生命值? : 游戏结束
-        if (this->Lives == 0)
-        {
-            this->ResetLevel();
-            this->State = GAME_MENU;
-        }
-        this->ResetPlayer();
-    }
-}
-```
-
-一旦玩家游戏结束（<var>lives</var>等于<var>0</var>），我们会重置关卡，并将游戏状态改变为<var>GAME_MENU</var>，稍后会详细讲。
-
-注意不要忘了在重置游戏/关卡时重置玩家生命值：
-
-```C++
-void Game::ResetLevel()
-{
-    [...]
-    this->Lives = 3;
-}
-```
-
-此时玩家生命值已可以运作，但玩家在游戏时却无法看到自己当前有多少生命值。这时就需要加入文本渲染器。
-
-```C++
-void Game::Render()
-{
-    if (this->State == GAME_ACTIVE)
-    {
-        [...]
-        std::stringstream ss; ss << this->Lives;
-        Text->RenderText("Lives:" + ss.str(), 5.0f, 5.0f, 1.0f);
-    }
-}
-
-```
-
-这里我们将生命值数量转化为一个字符串，并将其显示在屏幕左上角。看起来将会是像这样：
-
-![](../../img/06/Breakout/10/render_text_lives.png)
-
-一旦球接触到底部边界，玩家的生命值会减少，这会在屏幕左上角直接可见。
-
-## 关卡选择
-
-当玩家所处游戏状态为<var>GAME_MENU</var>时，我们希望玩家可以控制选择他想玩的关卡。玩家应该可以使用'w'或's'键在我们加载的所有关卡中滚动选择。当玩家感觉选中的是他想玩的关卡时，他可以按回车键将游戏状态从<var>GAME_MENU</var>切换到<var>GAME_ACTIVE</var>。
-
-允许玩家选择关卡并不难。我们要做的就是当玩家按下'w'或's'键时分别增加或减小game类中的变量<var>Level</var>的值：
-
-```C++
-if (this->State == GAME_MENU)
-{
-    if (this->Keys[GLFW_KEY_ENTER])
-        this->State = GAME_ACTIVE;
-    if (this->Keys[GLFW_KEY_W])
-        this->Level = (this->Level + 1) % 4;
-    if (this->Keys[GLFW_KEY_S])
-    {
-        if (this->Level > 0)
-            --this->Level;
-        else
-            this->Level = 3;
-    }
-}
-```
-
-我们使用取模运算(<fun>%</fun>)以保证变量<var>Level</var>在可接受的关卡值范围内（<var>0</var>和<var>3</var>之间）。除了变换关卡之外，在菜单状态时我们还需要将其渲染出来。我们要给玩家一些文本形式的指示，并在背景中展示出选中的关卡。
-
-```C++
-void Game::Render()
-{
-    if (this->State == GAME_ACTIVE || this->State == GAME_MENU)
-    {
-        [...] // 游戏状态渲染代码
-    }
-    if (this->State == GAME_MENU)
-    {
-        Text->RenderText("Press ENTER to start", 250.0f, Height / 2, 1.0f);
-        Text->RenderText("Press W or S to select level", 245.0f, Height / 2 + 20.0f, 0.75f);
-    }
-}
-```
-
-这里无论游戏处在<var>GAME_ACTIVE</var>状态还是<var>GAME_MENU</var>状态，都会渲染游戏，当游戏处在<var>GAME_MENU</var>状态需要渲染两行文本用于告知玩家选择一个关卡并且/或者确认选择。注意，为此必须在启动游戏时将游戏状态默认设置为<var>GAME_MENU</var>。
-
-![](../../img/06/Breakout/10/render_text_select.png)
-
-看起来很棒，但当你试图运行代码你很可能会注意到，当按下'w'或's'键时，游戏会在关卡之前快速滚动，很难选中你想玩的关卡。这是因为game会在多帧记录按键直到按键松开。这将导致<fun>ProcessInput</fun>函数处理按下的键不止一次。
-
-我们可以使用GUI系统中常见的一个小技巧来解决这一问题。这一小技巧就是：不仅记录当前按下的键，并且存储已经被按下的键，直到再次松开。然后我们会检查（在处理之前）是否还没有被处理，如果没有被处理的话，处理该按键并将其存储为正在被处理。一旦我们要在未松开时再次处理相同的按键，我们将不会处理该按键。这听起来让人稍微迷惑，但当你在实际应用中见到它，（很可能）就会明白它的意义。
-
-首先我们需要创建另一个布尔数组用来表示处理过的按键。我们在game类定义如下：
-
-```C++
-class Game
-{
-    [...]
-    public:
-        GLboolean KeysProcessed[1024];
-}
-```
-
-当相对应的按键被处理时，我们将其设置为<var>true</var>	，以确保按键只在之前没有被处理过（直到松开）时将其处理。
-
-```C++
-void Game::ProcessInput(GLfloat dt)
-{
-    if (this->State == GAME_MENU)
-    {
-        if (this->Keys[GLFW_KEY_ENTER] && !this->KeysProcessed[GLFW_KEY_ENTER])
-        {
-            this->State = GAME_ACTIVE;
-            this->KeysProcessed[GLFW_KEY_ENTER] = GL_TRUE;
-        }
-        if (this->Keys[GLFW_KEY_W] && !this->KeysProcessed[GLFW_KEY_W])
-        {
-            this->Level = (this->Level + 1) % 4;
-            this->KeysProcessed[GLFW_KEY_W] = GL_TRUE;
-        }
-        if (this->Keys[GLFW_KEY_S] && !this->KeysProcessed[GLFW_KEY_S])
-        {
-            if (this->Level > 0)
-                --this->Level;
-            else
-                this->Level = 3;
-            this->KeysProcessed[GLFW_KEY_S] = GL_TRUE;
-        }
-    }
-    [...]
-}
-
-```
-
-现在，当<var>KeysProcessed</var>数组中按键的值未被设置时，我们会处理按键并将其值设为<var>true</var>。下一次当到达同一按键的`if`条件时，它已经被处理过了所以我们会假装并没有按下此键，直到它被松开。
-
-之后，我们需要在松开按键时通过GLFW的按键回调函数，重置按键处理后的值，以便于下次再处理：
-
-```C++
-void key_callback(GLFWwindow* window, int key, int scancode, int action, int mode)
-{
-    [...]
-    if (key >= 0 && key < 1024)
-    {
-        if (action == GLFW_PRESS)
-            Breakout.Keys[key] = GL_TRUE;
-        else if (action == GLFW_RELEASE)
-        {
-            Breakout.Keys[key] = GL_FALSE;
-            Breakout.KeysProcessed[key] = GL_FALSE;
-        }
-    }
-}
-
-```
-
-启动游戏会展示一个整洁的关卡选择界面，现在可以每次按键清晰地选择一个关卡，无论按键被按下多久。
-
-## 获胜
-
-现在玩家可以选择关卡、玩游戏和游戏失败。有些不幸的是玩家在消除了所有的砖块之后会发现无法获得游戏胜利。现在来修复此问题。
-
-在所有实体砖块被消除之后玩家会取得胜利。我们已经在<fun>GameLevel</fun>类创建了一个函数用于检查这一条件：
-
-```C++
-GLboolean GameLevel::IsCompleted()
-{
-    for (GameObject &tile : this->Bricks)
-        if (!tile.IsSolid && !tile.Destroyed)
-            return GL_FALSE;
-    return GL_TRUE;
-}
-
-```
-
-我们会检查游戏关卡所有的砖块，如果有一个非实体砖块未被消除则返回<var>false</var>。我们所要做的就是在<fun>Update</fun>函数中检查此条件，一旦返回<var>true</var>，我们就将游戏状态改变为<var>GAME_WIN</var>：
-
-```C++
-void Game::Update(GLfloat dt)
-{
-    [...]
-    if (this->State == GAME_ACTIVE && this->Levels[this->Level].IsCompleted())
-    {
-        this->ResetLevel();
-        this->ResetPlayer();
-        Effects->Chaos = GL_TRUE;
-        this->State = GAME_WIN;
-    }
-}
-
-```
-
-在游戏激活状态，当关卡完成时，我们会重置游戏并且在<var>GAME_WIN</var>状态展示一条小的胜利的消息。为了增加趣味性我们会在<var>GAME_WIN</var>界面启用混沌效应。在函数<fun>Render</fun>中我们会祝贺玩家并询问其重新开始还是退出游戏。
-
-```C++
-void Game::Render()
-{
-    [...]
-    if (this->State == GAME_WIN)
-    {
-        Text->RenderText(
-            "You WON!!!", 320.0, Height / 2 - 20.0, 1.0, glm::vec3(0.0, 1.0, 0.0)
-        );
-        Text->RenderText(
-            "Press ENTER to retry or ESC to quit", 130.0, Height / 2, 1.0, glm::vec3(1.0, 1.0, 0.0)
-        );
-    }
-}
-
-```
-
-之后我们当然也要处理之前提到的按键：
-
-```C++
-void Game::ProcessInput(GLfloat dt)
-{
-    [...]
-    if (this->State == GAME_WIN)
-    {
-        if (this->Keys[GLFW_KEY_ENTER])
-        {
-            this->KeysProcessed[GLFW_KEY_ENTER] = GL_TRUE;
-            Effects->Chaos = GL_FALSE;
-            this->State = GAME_MENU;
-        }
-    }
-}
-```
-
-之后如果你真的可以赢得游戏，你将会看到以下图片：
-
-![](../../img/06/Breakout/10/render_text_win.png)
-
-就是这样！这是游戏Breakout我们要处理的最后一块拼图。尝试按照自己的意愿自定义并把它展示给你的家人和朋友！
-
-以下是最终版的游戏代码：
-
-- **Game**: [header](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/game.h), [code](https://learnopengl.com/code_viewer.php?code=in-practice/breakout/game).
-

docs/06 In Practice/2D-Game/11 Final thoughts.md

@@ -1,33 +0,0 @@
-# 结语
-
-原文    | [Final thoughts](https://learnopengl.com/#!In-Practice/2D-Game/Final-thoughts)
------   |  ----
-作者    | JoeydeVries
-翻译    | [包纸](https://github.com/ShirokoSama)
-校对    | 暂无
-
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
-与仅仅是用OpenGL创建一个技术演示相比，这一整章的教程给我们了一次体验在此之上的更多内容的机会。我们从零开始制作了一个2D游戏，并学习了如何对特定的底层图形学概念进行抽象、使用基础的碰撞检测技术、创建粒子、展示基于正射投影矩阵的场景。所有的这些都使用了之前教程中讨论过的概念。我们并没有真正地学习和使用OpenGL中新的、令人兴奋的图形技术，更多的是在将所有知识整合至一个更大的整体中。
-
-Breakout这样的一个简单游戏的制作可以被数千种方法完成，而我们的做法也只是其中之一。随着游戏越来越庞大，你开始应用的抽象思想与设计模式就会越多。如果希望进行更深入的学习与阅读，你可以在[game programming patterns](http://gameprogrammingpatterns.com/)找到大部分的抽象思想与设计模式。（译注：《游戏编程模式》一书国内已有中文翻译版，GPP翻译组译，人民邮电出版社）
-
-请记住，编写出一个有着非常干净、考虑周全的代码的游戏是一件很困难的任务（几乎不可能）。你只需要在编写游戏时使用在当时你认为正确的方法。随着你对视频游戏开发的实践越来越多，你学习的新的、更好地解决问题的方法就越多。不必因为编写“完美”代码的困难感到挫败，坚持编程吧！
-
-## 优化
-
-这些教程的内容和目前已完成的游戏代码的关注点都在于如何尽可能简单地阐述概念，而没有深入地优化细节。因此，很多性能相关的考虑都被忽略了。为了在游戏的帧率开始下降时可以提高性能，我们将列出一些现代的2D OpenGL游戏中常见的改进方案。
-
-- **渲染精灵表单/纹理图谱(Sprite sheet / Texture atlas)**：代替使用单个渲染精灵渲染单个纹理的渲染方式，我们将所有需要用到的纹理组合到单个大纹理中（如同位图字体），并用纹理坐标来选择合适的精灵与纹理。切换纹理状态是非常昂贵的操作，而使用这种方法让我们几乎可以不用在纹理间进行切换。除此之外，这样做还可以让GPU更有效率地缓存纹理，获得更快的查找速度。（译注：cache的局部性原理）
-- **实例化渲染**：代替一次只渲染一个四边形的渲染方式，我们可以将想要渲染的所有四边形批量化，并使用[实例化渲染](../../04 Advanced OpenGL/10 Instancing.md)在一次<><fun>draw call</fun>中成批地渲染四边形。这很容易实现，因为每个精灵都由相同的顶点组成，不同之处只有一个模型矩阵(Model Matrix)，我们可以很容易地将其包含在一个实例化数组中。这样可以使OpenGL每帧渲染更多的精灵。实例化渲染也可以用来渲染粒子和字符字形。
-- **三角形带(Triangle Strips)**：代替每次渲染两个三角形的渲染方式，我们可以用OpenGL的<var>TRIANGLE_STRIP</var>渲染图元渲染它们，只需4个顶点而非6个。这节约了三分之一需要传递给GPU的数据量。
-- **空间划分(Space partition)算法**：当检查可能发生的碰撞时，我们将小球与当前关卡中的每一个砖块进行比较，这么做有些浪费CPU资源，因为我们可以很容易得知在这一帧中，大多数砖块都不会与小球很接近。使用BSP，八叉树(Octress)或k-d(imension)树等空间划分算法，我们可以将可见的空间划分成许多较小的区域，并判断小球是否在这个区域中，从而为我们省去大量的碰撞检查。对于Breakout这样的简单游戏来说，这可能是过度的，但对于有着更复杂的碰撞检测算法的复杂游戏，这些算法可以显著地提高性能。
-- **最小化状态间的转换**：状态间的变化（如绑定纹理或切换着色器）在OpenGL中非常昂贵，因此你需要避免大量的状态变化。一种最小化状态间变化的方法是创建自己的状态管理器来存储OpenGL状态的当前值（比如绑定了哪个纹理），并且只在需要改变时进行切换，这可以避免不必要的状态变化。另外一种方式是基于状态切换对所有需要渲染的物体进行排序。首先渲染使用着色器A的所有对象，然后渲染使用着色器B的所有对象，以此类推。当然这可以扩展到着色器、纹理绑定、帧缓冲切换等。
-
-这些应该可以给你一些关于，我们可以用什么样的的高级技巧进一步提高2D游戏性能地提示。这也让你感受到了OpenGL的强大功能。通过亲手完成大部分的渲染，我们对整个渲染过程有了完整的掌握，从而可以实现对过程的优化。如果你对Breakout的性能并不满意，你可以把这些当做练习。
-
-## 开始创作！
-
-你已经看到了如何在OpenGL中创建一个简单的游戏，现在轮到你来创作属于自己的渲染/游戏程序了。到目前为止我们讨论的许多技术都可以应用于大部分2D游戏中，如渲染精灵、基础的碰撞检测、后期处理、文本渲染和粒子系统。现在你可以将这些技术以你认为合理的方式进行组合与修改，并开发你自己的手制游戏吧！

docs/07 PBR/01 Theory.md

@@ -1,412 +0,0 @@
-# 理论
-
-原文     | [Theory](https://learnopengl.com/#!PBR/Theory)
-      ---|---
-作者     | JoeyDeVries
-翻译     | [J.moons](https://github.com/JiangMuWen)
-校对     | Krasjet, JeremyYvv
-
-!!! note
-
-	本节暂未进行完全的重写，错误可能会很多。如果可能的话，请对照原文进行阅读。如果有报告本节的错误，将会延迟至重写之后进行处理。
-
-PBR，或者用更通俗一些的称呼是指<def>基于物理的渲染</def>(Physically Based Rendering)，它指的是一些在不同程度上都基于与现实世界的物理原理更相符的基本理论所构成的渲染技术的集合。正因为基于物理的渲染目的便是为了使用一种更符合物理学规律的方式来模拟光线，因此这种渲染方式与我们原来的Phong或者Blinn-Phong光照算法相比总体上看起来要更真实一些。除了看起来更好些以外，由于它与物理性质非常接近，因此我们（尤其是美术师们）可以直接以物理参数为依据来编写表面材质，而不必依靠粗劣的修改与调整来让光照效果看上去正常。使用基于物理参数的方法来编写材质还有一个更大的好处，就是不论光照条件如何，这些材质看上去都会是正确的，而在非PBR的渲染管线当中有些东西就不会那么真实了。
-
-虽然如此，基于物理的渲染仍然只是对基于物理原理的现实世界的一种近似，这也就是为什么它被称为**基于**物理的着色(Physically based Shading) 而非物理着色(Physical Shading)的原因。判断一种PBR光照模型是否是基于物理的，必须满足以下三个条件（不用担心，我们很快就会了解它们的）：
-
-1. 基于微平面(Microfacet)的表面模型。
-2. 能量守恒。
-3. 应用基于物理的BRDF。
-
-在这次的PBR系列教程之中，我们将会把重点放在最先由迪士尼(Disney)提出探讨并被Epic Games首先应用于实时渲染的PBR方案。他们基于<def>金属质地工作流</def>(Metallic Workflow)的方案有非常完备的文献记录，广泛应用于各种流行的引擎之中并且有着非常令人惊叹的视觉效果。完成这次的教程之后我们将会制作出类似于这样的一些东西：
-
-![](../img/07/01/ibl_specular_result_textured.png)
-
-请注意这个系列的教程所探讨的内容属于相当高端的领域，因此要求读者对OpenGL和着色器光照有较好的理解。读者将会需要这些相关的知识：[帧缓冲](../04 Advanced OpenGL/05 Framebuffers.md)，[立方体贴图](../04 Advanced OpenGL/06 Cubemaps.md)，[Gamma校正](../05 Advanced Lighting/02 Gamma Correction.md)，[HDR](../05 Advanced Lighting/06 HDR.md)和[法线贴图](../05 Advanced Lighting/04 Normal Mapping.md)。我们还会深入探讨一些高等数学的内容，我会尽我所能将相关的概念阐述清楚。
-
-## 微平面模型
-
-所有的PBR技术都基于微平面理论。这项理论认为，达到微观尺度之后任何平面都可以用被称为<def>微平面</def>(Microfacets)的细小镜面来进行描绘。根据平面粗糙程度的不同，这些细小镜面的取向排列可以相当不一致：
-
-![](../img/07/01/microfacets.png)
-
-产生的效果就是：一个平面越是粗糙，这个平面上的微平面的排列就越混乱。这些微小镜面这样无序取向排列的影响就是，当我们特指镜面光/镜面反射时，入射光线更趋向于向完全不同的方向<def>发散</def>(Scatter)开来，进而产生出分布范围更广泛的镜面反射。而与之相反的是，对于一个光滑的平面，光线大体上会更趋向于向同一个方向反射，造成更小更锐利的反射：
-
-![](../img/07/01/microfacets_light_rays.png)
-
-在微观尺度下，没有任何平面是完全光滑的。然而由于这些微平面已经微小到无法逐像素地继续对其进行区分，因此我们假设一个<def>粗糙度</def>(Roughness)参数，然后用统计学的方法来估计微平面的粗糙程度。我们可以基于一个平面的粗糙度来计算出众多微平面中，朝向方向沿着某个向量\(h\)方向的比例。这个向量\(h\)便是位于光线向量\(l\)和视线向量\(v\)之间的<def>半程向量</def>(Halfway Vector)。我们曾经在之前的[高级光照](../05 Advanced Lighting/01 Advanced Lighting.md)教程中谈到过中间向量，它的计算方法如下：
-
-$$
-h = \frac{l + v}{\|l + v\|}
-$$
-
-微平面的朝向方向与半程向量的方向越是一致，镜面反射的效果就越是强烈越是锐利。通过使用一个介于0到1之间的粗糙度参数，我们就能概略地估算微平面的取向情况了：
-
-![](../img/07/01/ndf.png)
-
-我们可以看到，较高的粗糙度显示出来的镜面反射的轮廓要更大一些。与之相反，较小的粗糙度显示出的镜面反射轮廓则更小更锐利。
-
-## 能量守恒
-
-微平面近似法使用了这样一种形式的<def>能量守恒</def>(Energy Conservation)：出射光线的能量永远不能超过入射光线的能量（发光面除外）。如上图我们可以看到，随着粗糙度的上升，镜面反射区域会增加，但是镜面反射的亮度却会下降。如果每个像素的镜面反射强度都一样（不管反射轮廓的大小），那么粗糙的平面就会放射出过多的能量，而这样就违背了能量守恒定律。这也就是为什么正如我们看到的一样，光滑平面的镜面反射更强烈而粗糙平面的反射更昏暗。
-
-为了遵守能量守恒定律，我们需要对漫反射光和镜面反射光做出明确的区分。当一束光线碰撞到一个表面的时候，它就会分离成一个<def>折射</def>部分和一个<def>反射</def>部分。反射部分就是会直接反射开而不进入平面的那部分光线，也就是我们所说的镜面光照。而折射部分就是余下的会进入表面并被吸收的那部分光线，也就是我们所说的漫反射光照。
-
-这里还有一些细节需要处理，因为当光线接触到一个表面的时候折射光是不会立即就被吸收的。通过物理学我们可以得知，光线实际上可以被认为是一束没有耗尽就不停向前运动的能量，而光束是通过碰撞的方式来消耗能量。每一种材料都是由无数微小的粒子所组成，这些粒子都能如下图所示一样与光线发生碰撞。这些粒子在每次的碰撞中都可以吸收光线所携带的一部分或者是全部的能量而后转变成为热量。
-
-![](../img/07/01/surface_reaction.png)
-
-一般来说，并非全部能量都会被吸收，而光线也会继续沿着（基本上）随机的方向<def>发散</def>，然后再和其他的粒子碰撞直至能量完全耗尽或者再次离开这个表面。而光线脱离物体表面后将会协同构成该表面的（漫反射）颜色。不过在基于物理的渲染之中我们进行了简化，假设对平面上的每一点所有的折射光都会被完全吸收而不会散开。而有一些被称为<def>次表面散射</def>(Subsurface Scattering)技术的着色器技术将这个问题考虑了进去，它们显著地提升了一些诸如皮肤，大理石或者蜡质这样材质的视觉效果，不过伴随而来的代价是性能的下降。
-
-对于<def>金属</def>(Metallic)表面，当讨论到反射与折射的时候还有一个细节需要注意。金属表面对光的反应与非金属（也被称为<def>介电质</def>(Dielectrics)）表面相比是不同的。它们遵从的反射与折射原理是相同的，但是**所有的**折射光都会被直接吸收而不会散开，只留下反射光或者说镜面反射光。亦即是说，金属表面只会显示镜面反射颜色，而不会显示出漫反射颜色。由于金属与电介质之间存在这样明显的区别，因此它们两者在PBR渲染管线中被区别处理，而我们将在文章的后面进一步详细探讨这个问题。
-
-反射光与折射光之间的这个区别使我们得到了另一条关于能量守恒的经验结论：反射光与折射光它们二者之间是**互斥**的关系。无论何种光线，其被材质表面所反射的能量将无法再被材质吸收。因此，诸如折射光这样的余下的进入表面之中的能量正好就是我们计算完反射之后余下的能量。
-
-我们按照能量守恒的关系，首先计算镜面反射部分，它的值等于入射光线被反射的能量所占的百分比。然后折射光部分就可以直接由镜面反射部分计算得出：
-
-```c++
-float kS = calculateSpecularComponent(...); // 反射/镜面 部分
-float kD = 1.0 - ks;                        // 折射/漫反射 部分
-```
-
-这样我们就能在遵守能量守恒定律的前提下知道入射光线的反射部分与折射部分所占的总量了。按照这种方法折射/漫反射与反射/镜面反射所占的份额都不会超过1.0，如此就能保证它们的能量总和永远不会超过入射光线的能量。而这些都是我们在前面的光照教程中没有考虑的问题。
-
-## 反射率方程
-
-在这里我们引入了一种被称为[渲染方程](https://learnopengl.com/wiki-rendereuqation)(Render Equation)的东西。它是某些聪明绝顶的人所构想出来的一个精妙的方程式，是如今我们所拥有的用来模拟光的视觉效果最好的模型。基于物理的渲染所坚定遵循的是一种被称为<def>反射率方程</def>(The Reflectance Equation)的渲染方程的特化版本。要正确地理解PBR，很重要的一点就是要首先透彻地理解反射率方程：
-
-$$
-L_o(p,\omega_o) = \int\limits_{\Omega} f_r(p,\omega_i,\omega_o) L_i(p,\omega_i) n \cdot \omega_i  d\omega_i
-$$
-
-反射率方程一开始可能会显得有些吓人，不过随着我们慢慢对其进行剖析，读者最终会逐渐理解它的。要正确地理解这个方程式，我们必须要稍微涉足一些<def>辐射度量学</def>(Radiometry)的内容。辐射度量学是一种用来度量电磁场辐射（包括可见光）的手段。有很多种辐射度量(radiometric quantities)可以用来测量曲面或者某个方向上的光，但是我们将只会讨论其中和反射率方程有关的一种。它被称为<def>辐射率</def>(Radiance)，在这里用\(L\)来表示。辐射率被用来量化来自单一方向上的光线的大小或者强度。由于辐射率是由许多物理变量集合而成的，一开始理解起来可能有些困难，因此我们首先关注一下这些物理量：
-
-**辐射通量**：辐射通量\(\Phi\)表示的是一个光源所输出的能量，以瓦特为单位。光是由多种不同波长的能量所集合而成的，而每种波长则与一种特定的（可见的）颜色相关。因此一个光源所放射出来的能量可以被视作这个光源包含的所有各种波长的一个函数。波长介于390nm到700nm（纳米）的光被认为是处于可见光光谱中，也就是说它们是人眼可见的波长。在下面你可以看到一幅图片，里面展示了日光中不同波长的光所具有的能量：
-
-![](../img/07/01/daylight_spectral_distribution.png)
-
-辐射通量将会计算这个由不同波长构成的函数的总面积。直接将这种对不同波长的计量作为参数输入计算机图形有一些不切实际，因此我们通常不直接使用波长的强度而是使用三原色编码，也就是**RGB**（或者按通常的称呼：光色）来作为辐射通量表示的简化。这套编码确实会带来一些信息上的损失，但是这对于视觉效果上的影响基本可以忽略。
-
-**立体角**：立体角用\(\omega\)表示，它可以为我们描述投射到单位球体上的一个截面的大小或者面积。投射到这个单位球体上的截面的面积就被称为<def>立体角</def>(Solid Angle)，你可以把立体角想象成为一个带有体积的方向：
-
-![](../img/07/01/solid_angle.png)
-
-可以把自己想象成为一个站在单位球面的中心的观察者，向着投影的方向看。这个投影轮廓的大小就是立体角。
-
-**辐射强度**：辐射强度(Radiant Intensity)表示的是在单位球面上，一个光源向每单位立体角所投送的辐射通量。举例来说，假设一个全向光源向所有方向均匀的辐射能量，辐射强度就能帮我们计算出它在一个单位面积（立体角）内的能量大小：
-
-![](../img/07/01/radiant_intensity.png)
-
-计算辐射强度的公式如下所示：
-
-$$
-I = \frac{d\Phi}{d\omega}
-$$
-
-其中\(I\)表示辐射通量\(\Phi\)除以立体角\(\omega\)。
-
-在理解了辐射通量，辐射强度与立体角的概念之后，我们终于可以开始讨论**辐射率**的方程式了。这个方程表示的是，一个拥有辐射强度\(\Phi\)的光源在单位面积\(A\)，单位立体角\(\omega\)上的辐射出的总能量：
-
-$$
-L=\frac{d^2\Phi}{ dA d\omega \cos\theta}
-$$
-
-![](../img/07/01/radiance.png)
-
-辐射率是辐射度量学上表示一个区域平面上光线总量的物理量，它受到<def>入射</def>(Incident)（或者来射）光线与平面法线间的夹角\(\theta\)的余弦值\(\cos \theta\)的影响：当直接辐射到平面上的程度越低时，光线就越弱，而当光线完全垂直于平面时强度最高。这和我们在前面的[基础光照](../02 Lighting/02 Basic Lighting.md)教程中对于漫反射光照的概念相似，其中\(\cos \theta\)就直接对应于光线的方向向量和平面法向量的点积：
-
-```c++
-float cosTheta = dot(lightDir, N);
-```
-
-辐射率方程很有用，因为它把大部分我们感兴趣的物理量都包含了进去。如果我们把立体角\(\omega\)和面积\(A\)看作是无穷小的，那么我们就能用辐射率来表示单束光线穿过空间中的一个点的通量。这就使我们可以计算得出作用于单个（片段）点上的单束光线的辐射率，我们实际上把立体角\(\omega\)转变为方向向量\(\omega\)然后把面\(A\)转换为点\(p\)。这样我们就能直接在我们的着色器中使用辐射率来计算单束光线对每个片段的作用了。
-
-事实上，当涉及到辐射率时，我们通常关心的是**所有**投射到点\(p\)上的光线的总和，而这个和就称为辐射照度或者<def>辐照度</def>(Irradiance)。在理解了辐射率和辐照度的概念之后，让我们再回过头来看看反射率方程：
-
-$$
-L_o(p,\omega_o) = \int\limits_{\Omega} f_r(p,\omega_i,\omega_o) L_i(p,\omega_i) n \cdot \omega_i  d\omega_i
-$$
-
-我们知道在渲染方程中\(L\)代表通过某个无限小的立体角\(\omega_i\)在某个点上的辐射率，而立体角可以视作是入射方向向量\(\omega_i\)。注意我们利用光线和平面间的入射角的余弦值\(\cos \theta\)来计算能量，亦即从辐射率公式\(L\)转化至反射率公式时的\(n \cdot \omega_i\)。用\(\omega_o\)表示观察方向，也就是出射方向，反射率公式计算了点\(p\)在\(\omega_o\)方向上被反射出来的辐射率\(L_o(p, \omega_o)\)的总和。或者换句话说：\(L_o\)表示了从\(\omega_o\)方向上观察，光线投射到点\(p\)上反射出来的辐照度。
-
-基于反射率公式是围绕所有入射辐射率的总和，也就是辐照度来计算的，所以我们需要计算的就不只是是单一的一个方向上的入射光，而是一个以点\(p\)为球心的半球领域\(\Omega\)内所有方向上的入射光。一个<def>半球领域</def>(Hemisphere)可以描述为以平面法线\(n\)为轴所环绕的半个球体：
-
-![](../img/07/01/hemisphere.png)
-
-为了计算某些面积的值，或者像是在半球领域的问题中计算某一个体积的时候我们会需要用到一种称为<def>积分</def>(Integral)的数学手段，也就是反射率公式中的符号\(\int\)，它的运算包含了半球领域\(\Omega\)内所有入射方向上的\(d\omega_i\) 。积分运算的值等于一个函数曲线的面积，它的计算结果要么是解析解要么就是数值解。由于渲染方程和反射率方程都没有解析解，我们将会用离散的方法来求得这个积分的数值解。这个问题就转化为，在半球领域\(\Omega\)中按一定的步长将反射率方程分散求解，然后再按照步长大小将所得到的结果平均化。这种方法被称为黎曼和(<def>Riemann sum</def>) ，我们可以用下面的代码粗略的演示一下：
-
-```c++
-int steps = 100;
-float sum = 0.0f;
-vec3 P    = ...;
-vec3 Wo   = ...;
-vec3 N    = ...;
-float dW  = 1.0f / steps;
-for(int i = 0; i < steps; ++i)
-{
-    vec3 Wi = getNextIncomingLightDir(i);
-    sum += Fr(p, Wi, Wo) * L(p, Wi) * dot(N, Wi) * dW;
-}
-```
-
-通过利用`dW`来对所有离散部分进行缩放，其和最后就等于积分函数的总面积或者总体积。这个用来对每个离散步长进行缩放的`dW`可以认为就是反射率方程中的\(d\omega_i\) 。在数学上，用来计算积分的\(d\omega_i\) 表示的是一个连续的符号，而我们使用的`dW`在代码中和它并没有直接的联系（因为它代表的是黎曼和中的离散步长），这样说是为了可以帮助你理解。请牢记，使用离散步长得到的是函数总面积的一个近似值。细心的读者可能已经注意到了，我们可以通过增加离散部分的数量来提高黎曼和的**准确度**(Accuracy)。
-
-反射率方程概括了在半球领域\(\Omega\)内，碰撞到了点\(p\)上的所有入射方向\(\omega_i\) 上的光线的辐射率，并受到\(f_r\)的约束，然后返回观察方向上反射光的\(L_o\)。正如我们所熟悉的那样，入射光辐射率可以由[光源](02 Lighting.md)处获得，此外还可以利用一个环境贴图来测算所有入射方向上的辐射率，我们将在未来的[IBL](03 IBL/01 Diffuse irradiance.md)教程中讨论这个方法。
-
-现在唯一剩下的未知符号就是\(f_r\)了，它被称为<def>BRDF</def>，或者<def>双向反射分布函数</def>(Bidirectional Reflective Distribution Function) ，它的作用是基于表面材质属性来对入射辐射率进行缩放或者加权。
-
-
-## BRDF
-
-<def>BRDF</def>，或者说<def>双向反射分布函数</def>，它接受入射（光）方向\(\omega_i\)，出射（观察）方向\(\omega_o\)，平面法线\(n\)以及一个用来表示微平面粗糙程度的参数\(a\)作为函数的输入参数。BRDF可以近似的求出每束光线对一个给定了材质属性的平面上最终反射出来的光线所作出的贡献程度。举例来说，如果一个平面拥有完全光滑的表面（比如镜面），那么对于所有的入射光线\(\omega_i\)（除了一束以外）而言BRDF函数都会返回0.0 ，只有一束与出射光线\(\omega_o\)拥有相同（被反射）角度的光线会得到1.0这个返回值。
-
-BRDF基于我们之前所探讨过的微平面理论来近似的求得材质的反射与折射属性。对于一个BRDF，为了实现物理学上的可信度，它必须遵守能量守恒定律，也就是说反射光线的总和永远不能超过入射光线的总量。严格上来说，同样采用\(\omega_i\)和\(\omega_o\)作为输入参数的 Blinn-Phong光照模型也被认为是一个BRDF。然而由于Blinn-Phong模型并没有遵循能量守恒定律，因此它不被认为是基于物理的渲染。现在已经有很好几种BRDF都能近似的得出物体表面对于光的反应，但是几乎所有实时渲染管线使用的都是一种被称为<def>Cook-Torrance BRDF</def>模型。
-
-Cook-Torrance BRDF兼有漫反射和镜面反射两个部分：
-
-$$
-f_r = k_d f_{lambert} +  k_s f_{cook-torrance}
-$$
-
-这里的\(k_d\)是早先提到过的入射光线中**被折射**部分的能量所占的比率，而\(k_s\)是**被反射**部分的比率。BRDF的左侧表示的是漫反射部分，这里用\(f_{lambert}\)来表示。它被称为<def>Lambertian漫反射</def>，这和我们之前在漫反射着色中使用的常数因子类似，用如下的公式来表示：
-
-$$
-f_{lambert} = \frac{c}{\pi}
-$$
-
-\(c\)表示表面颜色（回想一下漫反射表面纹理）。除以\(\pi\)是为了对漫反射光进行标准化，因为前面含有BRDF的积分方程是受\(\pi\)影响的（我们会在[IBL](03 IBL/01 Diffuse irradiance.md)的教程中探讨这个问题的）。
-
-!!! important
-
-	你也许会感到好奇，这个Lambertian漫反射和我们之前经常使用的漫反射到底有什么关系：之前我们是用表面法向量与光照方向向量进行点乘，然后再将结果与平面颜色相乘得到漫反射参数。点乘依然还在，但是却不在BRDF之内，而是转变成为了\(L_o\)积分末公式末尾处的\(n \cdot \omega_i\) 。
-
-目前存在着许多不同类型的模型来实现BRDF的漫反射部分，大多看上去都相当真实，但是相应的运算开销也非常的昂贵。不过按照Epic公司给出的结论，Lambertian漫反射模型已经足够应付大多数实时渲染的用途了。
-
-BRDF的镜面反射部分要稍微更高级一些，它的形式如下所示：
-
-$$
-f_{cook-torrance} = \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}
-$$
-
-Cook-Torrance BRDF的镜面反射部分包含三个函数，此外分母部分还有一个标准化因子 。字母D，F与G分别代表着一种类型的函数，各个函数分别用来近似的计算出表面反射特性的一个特定部分。三个函数分别为法线分布函数(Normal **D**istribution Function)，菲涅尔方程(**F**resnel Rquation)和几何函数(**G**eometry Function)：
-
-- **法线分布函数**：估算在受到表面粗糙度的影响下，朝向方向与半程向量一致的微平面的数量。这是用来估算微平面的主要函数。
-- **几何函数**：描述了微平面自成阴影的属性。当一个平面相对比较粗糙的时候，平面表面上的微平面有可能挡住其他的微平面从而减少表面所反射的光线。
-- **菲涅尔方程**：菲涅尔方程描述的是在不同的表面角下表面所反射的光线所占的比率。
-
-以上的每一种函数都是用来估算相应的物理参数的，而且你会发现用来实现相应物理机制的每种函数都有不止一种形式。它们有的非常真实，有的则性能高效。你可以按照自己的需求任意选择自己想要的函数的实现方法。英佩游戏公司的Brian Karis对于这些函数的多种近似实现方式进行了大量的[研究](http://graphicrants.blogspot.nl/2013/08/specular-brdf-reference.html)。我们将会采用Epic Games在Unreal Engine 4中所使用的函数，其中D使用Trowbridge-Reitz GGX，F使用Fresnel-Schlick近似(Fresnel-Schlick Approximation)，而G使用Smith's Schlick-GGX。
-
-
-### 法线分布函数
-
-<def>法线分布函数</def>\(D\)，从统计学上近似地表示了与某些（半程）向量\(h\)取向一致的微平面的比率。举例来说，假设给定向量\(h\)，如果我们的微平面中有35%与向量\(h\)取向一致，则法线分布函数或者说NDF将会返回0.35。目前有很多种NDF都可以从统计学上来估算微平面的总体取向度，只要给定一些粗糙度的参数。我们马上将要用到的是Trowbridge-Reitz GGX：
-
-$$
-NDF_{GGX TR}(n, h, \alpha) = \frac{\alpha^2}{\pi((n \cdot h)^2 (\alpha^2 - 1) + 1)^2}
-$$
-
-在这里\(h\)表示用来与平面上微平面做比较用的半程向量，而\(a\)表示表面粗糙度。
-
-如果我们把\(h\)当成是不同粗糙度参数下，平面法向量和光线方向向量之间的中间向量的话，我们可以得到如下图示的效果：
-
-![](../img/07/01/ndf.png)
-
-当粗糙度很低（也就是说表面很光滑）的时候，与半程向量取向一致的微平面会高度集中在一个很小的半径范围内。由于这种集中性，NDF最终会生成一个非常明亮的斑点。但是当表面比较粗糙的时候，微平面的取向方向会更加的随机。你将会发现与\(h\)向量取向一致的微平面分布在一个大得多的半径范围内，但是同时较低的集中性也会让我们的最终效果显得更加灰暗。
-
-使用GLSL代码编写的Trowbridge-Reitz GGX法线分布函数是下面这个样子的：
-
-```c++
-float D_GGX_TR(vec3 N, vec3 H, float a)
-{
-    float a2     = a*a;
-    float NdotH  = max(dot(N, H), 0.0);
-    float NdotH2 = NdotH*NdotH;
-
-    float nom    = a2;
-    float denom  = (NdotH2 * (a2 - 1.0) + 1.0);
-    denom        = PI * denom * denom;
-
-    return nom / denom;
-}
-```
-
-### 几何函数
-
-几何函数从统计学上近似的求得了微平面间相互遮蔽的比率，这种相互遮蔽会损耗光线的能量。
-
-![](../img/07/01/geometry_shadowing.png)
-
-与NDF类似，几何函数采用一个材料的粗糙度参数作为输入参数，粗糙度较高的表面其微平面间相互遮蔽的概率就越高。我们将要使用的几何函数是GGX与Schlick-Beckmann近似的结合体，因此又称为Schlick-GGX：
-
-$$
-G_{SchlickGGX}(n, v, k) = \frac{n \cdot v}{(n \cdot v)(1 - k) + k }
-$$
-
-这里的\(k\)是\(\alpha\)的重映射(Remapping)，取决于我们要用的是针对直接光照还是针对IBL光照的几何函数:
-
-$$
-k_{direct} = \frac{(\alpha + 1)^2}{8}
-$$
-
-$$
-k_{IBL} = \frac{\alpha^2}{2}
-$$
-
-注意，根据你的引擎把粗糙度转化为\(\alpha\)的方式不同，得到\(\alpha\)的值也有可能不同。在接下来的教程中，我们将会广泛的讨论这个重映射是如何起作用的。
-
-为了有效的估算几何部分，需要将观察方向（几何遮蔽(Geometry Obstruction)）和光线方向向量（几何阴影(Geometry Shadowing)）都考虑进去。我们可以使用<def>史密斯法</def>(Smith's method)来把两者都纳入其中：
-
-$$
-G(n, v, l, k) = G_{sub}(n, v, k) G_{sub}(n, l, k)
-$$
-
-使用史密斯法与Schlick-GGX作为\(G_{sub}\)可以得到如下所示不同粗糙度的视觉效果：
-
-![](../img/07/01/geometry.png)
-
-几何函数是一个值域为[0.0, 1.0]的乘数，其中白色或者说1.0表示没有微平面阴影，而黑色或者说0.0则表示微平面彻底被遮蔽。
-
-使用GLSL编写的几何函数代码如下：
-
-```c++
-float GeometrySchlickGGX(float NdotV, float k)
-{
-    float nom   = NdotV;
-    float denom = NdotV * (1.0 - k) + k;
-
-    return nom / denom;
-}
-
-float GeometrySmith(vec3 N, vec3 V, vec3 L, float k)
-{
-    float NdotV = max(dot(N, V), 0.0);
-    float NdotL = max(dot(N, L), 0.0);
-    float ggx1 = GeometrySchlickGGX(NdotV, k);
-    float ggx2 = GeometrySchlickGGX(NdotL, k);
-
-    return ggx1 * ggx2;
-}
-```
-
-### 菲涅尔方程
-
-菲涅尔（发音为Freh-nel）方程描述的是被反射的光线对比光线被折射的部分所占的比率，这个比率会随着我们观察的角度不同而不同。当光线碰撞到一个表面的时候，菲涅尔方程会根据观察角度告诉我们被反射的光线所占的百分比。利用这个反射比率和能量守恒原则，我们可以直接得出光线被折射的部分以及光线剩余的能量。
-
-当垂直观察的时候，任何物体或者材质表面都有一个<def>基础反射率</def>(Base Reflectivity)，但是如果以一定的角度往平面上看的时候[所有](http://filmicgames.com/archives/557)反光都会变得明显起来。你可以自己尝试一下，用垂直的视角观察你自己的木制/金属桌面，此时一定只有最基本的反射性。但是如果你从近乎90度（译注：应该是指和法线的夹角）的角度观察的话反光就会变得明显的多。如果从理想的90度视角观察，所有的平面理论上来说都能完全的反射光线。这种现象因<def>菲涅尔</def>而闻名，并体现在了菲涅尔方程之中。
-
-菲涅尔方程是一个相当复杂的方程式，不过幸运的是菲涅尔方程可以用<def>Fresnel-Schlick</def>近似法求得近似解：
-
-$$
-F_{Schlick}(h, v, F_0) = F_0 + (1 - F_0) ( 1 - (h \cdot v))^5
-$$
-
-\(F_0\)表示平面的基础反射率，它是利用所谓**折射指数**(Indices of Refraction)或者说IOR计算得出的。然后正如你可以从球体表面看到的那样，我们越是朝球面掠角的方向上看（此时视线和表面法线的夹角接近90度）菲涅尔现象就越明显，反光就越强：
-
-![](../img/07/01/fresnel.png)
-
-菲涅尔方程还存在一些细微的问题。其中一个问题是Fresnel-Schlick近似仅仅对<def>电介质</def>或者说非金属表面有定义。对于<def>导体</def>(Conductor)表面（金属），使用它们的折射指数计算基础折射率并不能得出正确的结果，这样我们就需要使用一种不同的菲涅尔方程来对导体表面进行计算。由于这样很不方便，所以我们预计算出平面对于<def>法向入射</def>的结果（\(F_0\)，处于0度角，好像直接看向表面一样），然后基于相应观察角的Fresnel-Schlick近似对这个值进行插值，用这种方法来进行进一步的估算。这样我们就能对金属和非金属材质使用同一个公式了。
-
-平面对于法向入射的响应或者说基础反射率可以在一些大型数据库中找到，比如[这个](http://refractiveindex.info/)。下面列举的这一些常见数值就是从Naty Hoffman的课程讲义中所得到的：
-
-<table align="center" border="1" rules=rows><tbody>
-    <tr>
-        <th style="text-align:center;">材料</th><th style="text-align:center;">\(F_0\) (线性)</th><th  style="text-align:center;">\(F_0\) (sRGB)</th><th style="text-align:center;" >颜色</th>
-    </tr>
-    <tr>
-        <td width="200" align="center" >水</td><td width="200" align="center">(0.02, 0.02, 0.02)</td><td width="200"  align="center">(0.15, 0.15, 0.15) </td><td width="60" style="background-color:#050505"></td>
-    </tr>
-    <tr>
-        <td align="center" >塑料/玻璃（低）</td><td align="center" >(0.03, 0.03, 0.03)</td><td align="center" >(0.21, 0.21, 0.21)</td><td style="background-color:#080808"></td>
-    </tr>
-	    <tr>
-        <td align="center" >塑料（高）</td><td align="center" >(0.05, 0.05, 0.05)</td><td align="center" >(0.24, 0.24, 0.24)</td><td style="background-color:#0D0D0D"></td>
-    </tr>
-	    <tr>
-        <td align="center" >玻璃（高）/红宝石</td><td align="center" >(0.08, 0.08, 0.08)</td><td align="center" >(0.31, 0.31, 0.31)</td><td style="background-color:#141414"></td>
-    </tr>
-	    <tr>
-        <td align="center" >钻石</td><td align="center" >(0.17, 0.17, 0.17)</td><td align="center" >(0.45, 0.45, 0.45)</td><td style="background-color:#2B2B2B"></td>
-    </tr>
-	    <tr>
-        <td align="center" >铁</td><td align="center" >(0.56, 0.57, 0.58)</td><td align="center" >(0.77, 0.78, 0.78)</td><td style="background-color:#8F9194"></td>
-    </tr>
-	    <tr>
-        <td align="center" >铜</td><td align="center" >(0.95, 0.64, 0.54)</td><td align="center" >(0.98, 0.82, 0.76)</td><td style="background-color:#F2A38A"></td>
-    </tr>
-	    <tr>
-        <td align="center" >金</td><td align="center" >(1.00, 0.71, 0.29)</td><td align="center" >(1.00, 0.86, 0.57)</td><td style="background-color:#FFB54A"></td>
-    </tr>
-	    <tr>
-        <td align="center" >铝</td><td align="center" >(0.91, 0.92, 0.92)</td><td align="center" >(0.96, 0.96, 0.97)</td><td style="background-color:#E8EBEB"></td>
-    </tr>
-	    <tr>
-        <td align="center" >银</td><td align="center" >(0.95, 0.93, 0.88)</td><td align="center" >(0.98, 0.97, 0.95)</td><td style="background-color:#F2EDE0"></td>
-    </tr>
-</table>
-
-这里可以观察到的一个有趣的现象，所有电介质材质表面的基础反射率都不会高于0.17，这其实是例外而非普遍情况。导体材质表面的基础反射率起点更高一些并且（大多）在0.5和1.0之间变化。此外，对于导体或者金属表面而言基础反射率一般是带有色彩的，这也是为什么\(F_0\)要用RGB三原色来表示的原因（法向入射的反射率可随波长不同而不同）。这种现象我们**只能**在金属表面观察的到。
-
-这些金属表面相比于电介质表面所独有的特性引出了所谓的<def>金属工作流</def>的概念。也就是我们需要额外使用一个被称为<def>金属度</def>(Metalness)的参数来参与编写表面材质。金属度用来描述一个材质表面是金属还是非金属的。
-
-!!! important
-
-	理论上来说，一个表面的金属度应该是二元的：要么是金属要么不是金属，不能两者皆是。但是，大多数的渲染管线都允许在0.0至1.0之间线性的调配金属度。这主要是由于材质纹理精度不足以描述一个拥有诸如细沙/沙状粒子/刮痕的金属表面。通过对这些小的类非金属粒子/刮痕调整金属度值，我们可以获得非常好看的视觉效果。
-
-通过预先计算电介质与导体的\(F_0\)值，我们可以对两种类型的表面使用相同的Fresnel-Schlick近似，但是如果是金属表面的话就需要对基础反射率添加色彩。我们一般是按下面这样来实现的：
-
-```c++
-vec3 F0 = vec3(0.04);
-F0      = mix(F0, surfaceColor.rgb, metalness);
-```
-
-我们为大多数电介质表面定义了一个近似的基础反射率。\(F_0\)取最常见的电解质表面的平均值，这又是一个近似值。不过对于大多数电介质表面而言使用0.04作为基础反射率已经足够好了，而且可以在不需要输入额外表面参数的情况下得到物理可信的结果。然后，基于金属表面特性，我们要么使用电介质的基础反射率要么就使用\(F_0\)来作为表面颜色。因为金属表面会吸收所有折射光线而没有漫反射，所以我们可以直接使用表面颜色纹理来作为它们的基础反射率。
-
-Fresnel Schlick近似可以用代码表示为：
-
-```c++
-vec3 fresnelSchlick(float cosTheta, vec3 F0)
-{
-    return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
-}
-```
-
-其中`cosTheta`是表面法向量\(n\)与观察方向\(v\)的点乘的结果。
-
-### Cook-Torrance反射率方程
-
-随着Cook-Torrance BRDF中所有元素都介绍完毕，我们现在可以将基于物理的BRDF纳入到最终的反射率方程当中去了：
-
-$$
-L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)})L_i(p,\omega_i) n \cdot \omega_i  d\omega_i
-$$
-
-这个方程现在完整的描述了一个基于物理的渲染模型，它现在可以认为就是我们一般意义上理解的基于物理的渲染也就是PBR。如果你还没有能完全理解我们将如何把所有这些数学运算结合到一起并融入到代码当中去的话也不必担心。在下一个教程当中，我们将探索如何实现反射率方程来在我们渲染的光照当中获得更加物理可信的结果，而所有这些零零星星的碎片将会慢慢组合到一起来。
-
-## 编写PBR材质
-
-在了解了PBR后面的数学模型之后，最后我们将通过说明美术师一般是如何编写一个我们可以直接输入PBR的平面物理属性的来结束这部分的讨论。PBR渲染管线所需要的每一个表面参数都可以用纹理来定义或者建模。使用纹理可以让我们逐个片段的来控制每个表面上特定的点对于光线是如何响应的：不论那个点是不是金属，粗糙或者平滑，也不论表面对于不同波长的光会有如何的反应。
-
-在下面你可以看到在一个PBR渲染管线当中经常会碰到的纹理列表，还有将它们输入PBR渲染器所能得到的相应的视觉输出：
-
-![](../img/07/01/textures.png)
-
-**反照率**：<def>反照率</def>(Albedo)纹理为每一个金属的纹素(Texel)（纹理像素）指定表面颜色或者基础反射率。这和我们之前使用过的漫反射纹理相当类似，不同的是所有光照信息都是由一个纹理中提取的。漫反射纹理的图像当中常常包含一些细小的阴影或者深色的裂纹，而反照率纹理中是不会有这些东西的。它应该只包含表面的颜色（或者折射吸收系数）。
-
-**法线**：法线贴图纹理和我们之前在[法线贴图](https://learnopengl-cn.github.io/05%20Advanced%20Lighting/04%20Normal%20Mapping/)教程中所使用的贴图是完全一样的。法线贴图使我们可以逐片段的指定独特的法线，来为表面制造出起伏不平的假象。
-
-**金属度**：金属(Metallic)贴图逐个纹素的指定该纹素是不是金属质地的。根据PBR引擎设置的不同，美术师们既可以将金属度编写为灰度值又可以编写为1或0这样的二元值。
-
-**粗糙度**：粗糙度(Roughness)贴图可以以纹素为单位指定某个表面有多粗糙。采样得来的粗糙度数值会影响一个表面的微平面统计学上的取向度。一个比较粗糙的表面会得到更宽阔更模糊的镜面反射（高光），而一个比较光滑的表面则会得到集中而清晰的镜面反射。某些PBR引擎预设采用的是对某些美术师来说更加直观的<def>光滑度</def>(Smoothness)贴图而非粗糙度贴图，不过这些数值在采样之时就马上用（1.0 – 光滑度）转换成了粗糙度。
-
-**AO**：<def>环境光遮蔽</def>(Ambient Occlusion)贴图或者说<def>AO</def>贴图为表面和周围潜在的几何图形指定了一个额外的阴影因子。比如如果我们有一个砖块表面，反照率纹理上的砖块裂缝部分应该没有任何阴影信息。然而AO贴图则会把那些光线较难逃逸出来的暗色边缘指定出来。在光照的结尾阶段引入环境遮蔽可以明显的提升你场景的视觉效果。网格/表面的环境遮蔽贴图要么通过手动生成，要么由3D建模软件自动生成。
-
-美术师们可以在纹素级别设置或调整这些基于物理的输入值，还可以以现实世界材料的表面物理性质来建立他们的材质数据。这是PBR渲染管线最大的优势之一，因为不论环境或者光照的设置如何改变这些表面的性质是不会改变的，这使得美术师们可以更便捷地获取物理可信的结果。在PBR渲染管线中编写的表面可以非常方便的在不同的PBR渲染引擎间共享使用，不论处于何种环境中它们看上去都会是正确的，因此看上去也会更自然。
-
-## 延伸阅读
-
-- [Background: Physics and Math of Shading by Naty Hoffmann](http://blog.selfshadow.com/publications/s2013-shading-course/hoffman/s2013_pbs_physics_math_notes.pdf)：由于在这一篇文章中要谈论的理论点太多，所以这里的理论知识都只是涉及到了皮毛。如果你希望了解更多关于光线背后的物理知识以及它们和PBR理论之间有什么关联的话，**这**才是你需要阅读的资源。
-- [Real shading in Unreal Engine 4](http://blog.selfshadow.com/publications/s2013-shading-course/karis/s2013_pbs_epic_notes_v2.pdf)：探讨了Epic Games在他们的Unreal 4引擎中所采用的PBR模型。我们这些教程中主要涉及的PBR系统就是基于他们的PBR模型。
-- [Marmoset: PBR Theory](https://www.marmoset.co/toolbag/learn/pbr-theory)：主要针对美术师的PBR介绍，不过仍然是很好的读物。
-- [Coding Labs: Physically based rendering](http://www.codinglabs.net/article_physically_based_rendering.aspx)：介绍渲染方程以及它和PBR直接的关系。
-- [Coding Labs: Physically Based Rendering - Cook–Torrance](http://www.codinglabs.net/article_physically_based_rendering_cook_torrance.aspx)：介绍了Cook-Torrance BRDF.
-- [Wolfire Games - Physically based rendering](http://blog.wolfire.com/2015/10/Physically-based-rendering)：介绍了PBR，由Lukas Orsvärn所著。

docs/07 PBR/02 Lighting.md

@@ -1,347 +0,0 @@
-# 光照
-
-原文     | [Lighting](https://learnopengl.com/#!PBR/Lighting)
-      ---|---
-作者     | JoeyDeVries
-翻译     | [KenLee](https://hellokenlee.github.io/)
-校对     | JeremyYvv
-
-	
-在[上一个教程](https://learnopengl-cn.github.io/07%20PBR/01%20Theory/)中，我们讨论了一些PBR的基础知识。在本章节中，我们把重点放在将之前讨论的理论转化为实际的渲染器，这个渲染器将使用直接的（或解析的）光源：比如点光源，定向灯或聚光灯。
-
-我们先来看看上一个章提到的反射方程的最终版：
-
-$$
-L_o(p,\omega_o) = \int\limits_{\Omega} 
-    	(k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)})
-    	L_i(p,\omega_i) n \cdot \omega_i  d\omega_i
-$$
-
-我们大致上清楚这个反射方程在干什么，但我们仍然留有一些迷雾尚未揭开。比如说我们究竟将怎样表示场景上的辐照度(Irradiance), 辐射率(Radiance) \(L\)？我们知道辐射率\(L\)（在计算机图形领域中）表示光源的辐射通量(Radiant flux)\(\phi\)，或光源在给定立体角\(\omega\)下发出的光能。在我们的情况下，不妨假设立体角\(\omega\)无限小，这样辐射度就表示光源在一条光线或单个方向向量上的辐射通量。
-
-基于以上的知识，我们如何将其转化为之前的教程中所积累的一些光照知识呢？ 那么想象一下，我们有一个点光源（一个在所有方向都具有相同亮度的光源），它的辐射通量为用RGB表示为**（23.47, 21.31, 20.79）**。该光源的辐射强度(Radiant Intensity)等于其在所有出射光线的辐射通量。 然而，当我们为一个表面上的特定的点\(p\)着色时，在其半球领域\(\Omega\)的所有可能的入射方向上，只有一个入射方向向量\(\omega_i\)直接来自于该点光源。 假设我们在场景中只有一个光源，位于空间中的某一个点，因而对于\(p\)点的其他可能的入射光线方向上的辐射率为0：
-
-![](../img/07/02/lighting_radiance_direct.png)
-
-如果从一开始，我们就假设点光源不受光线衰减（光照强度会随着距离变暗）的影响，那么无论我们把光源放在哪，入射光线的辐射率总是一样的（除去入射角\(cos\theta\)对辐射率的影响之外）。 这是因为无论我们从哪个角度观察它，点光源总具有相同的辐射强度，我们可以有效地将其辐射强度建模为其辐射通量: 一个常量向量**（23.47, 21.31, 20.79）**。
-
-然而，辐射率也需要将位置\(p\)作为输入，正如所有现实的点光源都会受光线衰减影响一样，点光源的辐射强度应该根据点\(p\)所在的位置和光源的位置以及他们之间的距离而做一些缩放。 因此，根据原始的辐射方程，我们会根据表面法向量\(n\)和入射角度\(w_i\)来缩放光源的辐射强度。
-
-在实现上来说：对于直接点光源的情况，辐射率函数\(L\)先获取光源的颜色值， 然后光源和某点\(p\)的距离衰减，接着按照\(n \cdot w_i\)缩放，但是仅仅有一条入射角为\(w_i\)的光线打在点\(p\)上， 这个\(w_i\)同时也等于在\(p\)点光源的方向向量。写成代码的话会是这样：
-```glsl
-vec3  lightColor  = vec3(23.47, 21.31, 20.79);
-vec3  wi          = normalize(lightPos - fragPos);
-float cosTheta    = max(dot(N, Wi), 0.0);
-float attenuation = calculateAttenuation(fragPos, lightPos);
-float radiance    = lightColor * attenuation * cosTheta;
-```
-
-除了一些术语上的差异外，这段代码对你们来说应该很熟悉：这正是我们一直以来怎么计算漫反射光照的！当涉及到直接光照(direct lighting)时，辐射率的计算方式和我们之前计算只有一个光源照射在物体表面的时候非常相似。
-
-!!! Important
-
-	请注意，这个假设成立的条件是点光源体积无限小，相当于在空间中的一个点。如果我们认为该光源是具有体积的，它的辐射率会在不只一个入射光方向上非零。
-
-对于其它类型的从单点发出来的光源我们类似地计算出辐射率。比如，定向光(directional light)拥有恒定的\(w_i\)而不会有衰减因子；而一个聚光灯光源则没有恒定的辐射强度，其辐射强度是根据聚光灯的方向向量来缩放的。
-
-这也让我们回到了对于表面的半球领域(hemisphere)\(\Omega\)的积分\(\int\)上。由于我们事先知道的所有贡献光源的位置，因此对物体表面上的一个点着色并不需要我们尝试去求解积分。我们可以直接拿光源的（已知的）数目，去计算它们的总辐照度，因为每个光源仅仅只有一个方向上的光线会影响物体表面的辐射率。这使得PBR对直接光源的计算相对简单，因为我们只需要有效地遍历所有有贡献的光源。而当我们之后把环境照明也考虑在内的[IBL](./03%20IBL/01%20Diffuse%20irradiance.md)教程中，我们就必须采取积分去计算了，这是因为光线可能会在任何一个方向入射。
-
-# 一个PBR表面模型
-
-现在让我们开始写片段着色器来实现上述的PBR模型吧~ 首先我们需要把PBR相关的输入放进片段着色器。
-
-```glsl
-#version 330 core
-out vec4 FragColor;
-in vec2 TexCoords;
-in vec3 WorldPos;
-in vec3 Normal;
-  
-uniform vec3 camPos;
-  
-uniform vec3  albedo;
-uniform float metallic;
-uniform float roughness;
-uniform float ao;
-```
-
-我们把通用的顶点着色器的输出作为输入的一部分。另一部分输入则是物体表面模型的一些材质参数。
-
-然后在片段着色器的开始部分我们做一下任何光照算法都需要做的计算:
-
-```glsl
-void main()
-{
-    vec3 N = normalize(Normal); 
-    vec3 V = normalize(camPos - WorldPos);
-    [...]
-}
-```
-
-## 直接光照
-
-在本教程的例子中我们会采用总共4个点光源来直接表示场景的辐照度。为了满足反射率方程，我们循环遍历每一个光源，计算他们各自的辐射率然后求和，接着根据BRDF和光源的入射角来缩放该辐射率。我们可以把循环当作在物体的半球领域内对所有直接光源求积分。首先我们来计算一些可以预计算的光照变量：
-
-```glsl
-vec3 Lo = vec3(0.0);
-for(int i = 0; i < 4; ++i) 
-{
-    vec3 L = normalize(lightPositions[i] - WorldPos);
-    vec3 H = normalize(V + L);
-  
-    float distance    = length(lightPositions[i] - WorldPos);
-    float attenuation = 1.0 / (distance * distance);
-    vec3 radiance     = lightColors[i] * attenuation; 
-    [...]  
-```
-
-由于我们在线性空间内计算光照（我们会在着色器的最后进行Gamma校正），我们使用在物理上更为准确的平方倒数作为衰减。
-
-!!! Important
-
-	相对于物理上正确来说，你可能仍然想使用常量，线性或者二次衰减方程（他们在物理上相对不准确），却可以为您提供在光的能量衰减更多的控制。
-
-然后，对于每一个光源我们都想计算完整的 Cook-Torrance specular BRDF项：
-
-$$
-\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}
-$$
-
-首先我们想计算的是镜面反射和漫反射之间的比值，或者说与表面折射的光线相比，它反射了多少光线。 我们从[上一个教程](./01%20Theory.md)知道可以使用菲涅尔方程计算（注意这里用的`clamp`是为了避免黑点）：
-
-```glsl
-vec3 fresnelSchlick(float cosTheta, vec3 F0)
-{
-    return F0 + (1.0 - F0) * pow(clamp(1.0 - cosTheta, 0.0, 1.0), 5.0);
-}  
-```
-
-Fresnel-Schlick近似法接收一个参数`F0`，被称为0°入射角的反射率，或者说是直接(垂直)观察表面时有多少光线会被反射。 这个参数`F0`会因为材料不同而不同，而且对于金属材质会带有颜色。在PBR金属流中我们简单地认为大多数的绝缘体在`F0`为0.04的时候看起来视觉上是正确的，对于金属表面我们根据反射率特别地指定`F0`。 因此代码上看起来会像是这样：
-
-```glsl
-vec3 F0 = vec3(0.04); 
-F0      = mix(F0, albedo, metallic);
-vec3 F  = fresnelSchlick(max(dot(H, V), 0.0), F0);
-```
-
-可以看到，对于非金属表面`F0`始终为0.04。对于金属表面，我们根据初始的`F0`和表现金属属性的反射率进行线性插值。
-
-我们已经算出\(F\)， 剩下的项就是计算法线分布函数\(D\)和几何遮蔽函数\(G\)了。
-
-在直接PBR光照着色器中\(D\)和\(G\)的计算代码类似于：
-
-```glsl
-float DistributionGGX(vec3 N, vec3 H, float roughness)
-{
-    float a      = roughness*roughness;
-    float a2     = a*a;
-    float NdotH  = max(dot(N, H), 0.0);
-    float NdotH2 = NdotH*NdotH;
-	
-    float num   = a2;
-    float denom = (NdotH2 * (a2 - 1.0) + 1.0);
-    denom = PI * denom * denom;
-	
-    return num / denom;
-}
-
-float GeometrySchlickGGX(float NdotV, float roughness)
-{
-    float r = (roughness + 1.0);
-    float k = (r*r) / 8.0;
-
-    float num   = NdotV;
-    float denom = NdotV * (1.0 - k) + k;
-	
-    return num / denom;
-}
-float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
-{
-    float NdotV = max(dot(N, V), 0.0);
-    float NdotL = max(dot(N, L), 0.0);
-    float ggx2  = GeometrySchlickGGX(NdotV, roughness);
-    float ggx1  = GeometrySchlickGGX(NdotL, roughness);
-	
-    return ggx1 * ggx2;
-}
-```
-
-这里比较重要的是和[理论章节](./01%20Theory.md)相比，我们直接把粗糙度(roughness)作为参数传给了上述函数；通过这种方式，我们可以针对每一个不同的项对粗糙度做一些修改。根据迪士尼公司给出的观察以及后来被Epic Games公司采用的光照模型，在几何遮蔽函数和法线分布函数中采用粗糙度的平方会让光照看起来更加自然。
-
-现在两个函数都给出了定义，在计算反射的循环中计算NDF和G项就变得很简单：
-
-```glsl
-float NDF = DistributionGGX(N, H, roughness);       
-float G   = GeometrySmith(N, V, L, roughness);       
-```
-
-这样我们就凑够了足够的项来计算Cook-Torrance BRDF:
-
-```glsl
-vec3 nominator    = NDF * G * F;
-float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0) + 0.001; 
-vec3 specular     = nominator / denominator;  
-```
-
-注意我们在分母项中加了一个0.001为了避免出现除零错误。
-
-现在我们终于可以计算每个光源在反射率方程中的贡献值了！因为菲涅尔方程直接给出了\(k_S\)， 我们可以使用`F`表示所有打在物体表面上的镜面反射光的贡献。 从\(k_S\)我们很容易计算折射的比值\(k_D\)：
-
-```glsl
-vec3 kS = F;
-vec3 kD = vec3(1.0) - kS;
-  
-kD *= 1.0 - metallic;	
-```
-
-我们可以看作\(k_S\)表示光能中被反射的能量的比例， 而剩下的光能会被折射， 比值即为\(k_D\)。更进一步来说，因为金属不会折射光线，因此不会有漫反射。所以如果表面是金属的，我们会把系数\(k_D\)变为0。 这样，我们终于集齐所有变量来计算我们出射光线的值：
-
-```glsl
-    const float PI = 3.14159265359;
-  
-    float NdotL = max(dot(N, L), 0.0);        
-    Lo += (kD * albedo / PI + specular) * radiance * NdotL;
-}
-```
-
-最终的结果`Lo`，或者说是出射光线的辐射率，实际上是反射率方程的在半球领域\(\Omega\)的积分的结果。但是我们实际上不需要去求积，因为对于所有可能的入射光线方向我们知道只有4个方向的入射光线会影响片段的着色。因为这样，我们可以直接循环N次计算这些入射光线的方向(N也就是场景中光源的数目)。
-
-剩下的工作就是加一个环境光照项给`Lo`，然后我们就拥有了片段的最后颜色：
-
-```glsl
-vec3 ambient = vec3(0.03) * albedo * ao;
-vec3 color   = ambient + Lo;  
-```
-
-## 线性空间和HDR渲染
-
-直到现在，我们假设的所有计算都在线性的颜色空间中进行的，因此我们需要在着色器最后做[伽马矫正]()。 在线性空间中计算光照是非常重要的，因为PBR要求所有输入都是线性的，如果不是这样，我们就会得到不正常的光照。另外，我们希望所有光照的输入都尽可能的接近他们在物理上的取值，这样他们的反射率或者说颜色值就会在色谱上有比较大的变化空间。`Lo`作为结果可能会变大得很快(超过1)，但是因为默认的低动态范围（LDR）而取值被截断。所以在伽马矫正之前我们采用色调映射使`Lo`从LDR的值映射为HDR的值。
-
-```glsl
-color = color / (color + vec3(1.0));
-color = pow(color, vec3(1.0/2.2)); 
-```
-
-这里我们采用的色调映射方法为Reinhard 操作，使得我们在伽马矫正后可以保留尽可能多的辐照度变化。 我们没有使用一个独立的帧缓冲或者采用后期处理，所以我们需要直接在每一步光照计算后采用色调映射和伽马矫正。
-
-![](../img/07/02/lighting_linear_vs_non_linear_and_hdr.png)
-
-采用线性颜色空间和HDR在PBR渲染管线中非常重要。如果没有这些操作，几乎是不可能正确地捕获到因光照强度变化的细节，这最终会导致你的计算变得不正确，在视觉上看上去非常不自然。
-
-## 完整的直接光照PBR着色器
-
-现在剩下的事情就是把做好色调映射和伽马矫正的颜色值传给片段着色器的输出，然后我们就拥有了自己的直接光照PBR着色器。 为了完整性，这里给出了完整的代码：
-
-```glsl
-#version 330 core
-out vec4 FragColor;
-in vec2 TexCoords;
-in vec3 WorldPos;
-in vec3 Normal;
-
-// material parameters
-uniform vec3  albedo;
-uniform float metallic;
-uniform float roughness;
-uniform float ao;
-
-// lights
-uniform vec3 lightPositions[4];
-uniform vec3 lightColors[4];
-
-uniform vec3 camPos;
-
-const float PI = 3.14159265359;
-  
-float DistributionGGX(vec3 N, vec3 H, float roughness);
-float GeometrySchlickGGX(float NdotV, float roughness);
-float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness);
-vec3 fresnelSchlickRoughness(float cosTheta, vec3 F0, float roughness);
-
-void main()
-{		
-    vec3 N = normalize(Normal);
-    vec3 V = normalize(camPos - WorldPos);
-
-    vec3 F0 = vec3(0.04); 
-    F0 = mix(F0, albedo, metallic);
-	           
-    // reflectance equation
-    vec3 Lo = vec3(0.0);
-    for(int i = 0; i < 4; ++i) 
-    {
-        // calculate per-light radiance
-        vec3 L = normalize(lightPositions[i] - WorldPos);
-        vec3 H = normalize(V + L);
-        float distance    = length(lightPositions[i] - WorldPos);
-        float attenuation = 1.0 / (distance * distance);
-        vec3 radiance     = lightColors[i] * attenuation;        
-        
-        // cook-torrance brdf
-        float NDF = DistributionGGX(N, H, roughness);        
-        float G   = GeometrySmith(N, V, L, roughness);      
-        vec3 F    = fresnelSchlick(max(dot(H, V), 0.0), F0);       
-        
-        vec3 kS = F;
-        vec3 kD = vec3(1.0) - kS;
-        kD *= 1.0 - metallic;	  
-        
-        vec3 nominator    = NDF * G * F;
-        float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0) + 0.001; 
-        vec3 specular     = nominator / denominator;
-            
-        // add to outgoing radiance Lo
-        float NdotL = max(dot(N, L), 0.0);                
-        Lo += (kD * albedo / PI + specular) * radiance * NdotL; 
-    }   
-  
-    vec3 ambient = vec3(0.03) * albedo * ao;
-    vec3 color = ambient + Lo;
-	
-    color = color / (color + vec3(1.0));
-    color = pow(color, vec3(1.0/2.2));  
-   
-    FragColor = vec4(color, 1.0);
-}  
-```
-
-希望经过上一个教程的[理论知识](./01%20Theory.md)以及学习过关于渲染方程的一些知识后，这个着色器看起来不会太可怕。如果我们采用这个着色器，加上4个点光源和一些球体，同时令这些球体的金属性(metallic)和粗糙度(roughness)沿垂直和水平方向分别变化，我们会得到这样的结果：
-
-![](../img/07/02/lighting_result.png)
-
-(上述图片)从下往上球体的金属性从0.0变到1.0， 从左到右球体的粗糙度从0.0变到1.0。你可以看到仅仅改变这两个值，显示的效果会发生巨大的改变！
-
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/6.pbr/1.1.lighting/lighting.cpp)找到整个demo的完整代码。
-
-# 带贴图的PBR
-
-把我们系统扩展成可以接受纹理作为参数可以让我们对物体的材质有更多的自定义空间：
-
-```glsl
-[...]
-uniform sampler2D albedoMap;
-uniform sampler2D normalMap;
-uniform sampler2D metallicMap;
-uniform sampler2D roughnessMap;
-uniform sampler2D aoMap;
-  
-void main()
-{
-    vec3 albedo     = pow(texture(albedoMap, TexCoords).rgb, 2.2);
-    vec3 normal     = getNormalFromNormalMap();
-    float metallic  = texture(metallicMap, TexCoords).r;
-    float roughness = texture(roughnessMap, TexCoords).r;
-    float ao        = texture(aoMap, TexCoords).r;
-    [...]
-}
-```
-
-不过需要注意的是一般来说反射率(albedo)纹理在美术人员创建的时候就已经在sRGB空间了，因此我们需要在光照计算之前先把他们转换到线性空间。一般来说，环境光遮蔽贴图(ambient occlusion maps)也需要我们转换到线性空间。不过金属性(Metallic)和粗糙度(Roughness)贴图大多数时间都会保证在线性空间中。
-
-只是把之前的球体的材质性质换成纹理属性，就在视觉上有巨大的提升：
-
-![](../img/07/02/lighting_textured.png)
-
-你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/6.pbr/1.2.lighting_textured/lighting_textured.cpp)找到纹理贴图示例的全部代码，以及我用的[纹理](http://freepbr.com/materials/rusted-iron-pbr-metal-material-alt/)(记得加上一张全白色的环境光遮蔽贴图)。注意金属表面会在场景中看起来有点黑，因为他们没有漫反射。它们会在考虑环境镜面光照的时候看起来更加自然，不过这是我们下一个教程的事情了。
-
-相比起在网上找到的其他PBR渲染结果来说，尽管在视觉上不算是非常震撼，因为我们还没考虑到[基于图片的光照(IBL)](./03%20IBL/01%20Diffuse%20irradiance.md)，但我们现在也算是有了一个基于物理的渲染器了，虽然还没考虑IBL，但你会发现你的光照看起来更加真实了。

docs/07 PBR/03 IBL/01 Diffuse irradiance.md

@@ -1,532 +0,0 @@
-# 漫反射辐照度
-
-原文     | [Diffuse irradiance](https://learnopengl.com/PBR/IBL/Diffuse-irradiance)
-      ---|---
-作者     | JoeyDeVries
-翻译     | [flyingSnow](https://github.com/flyingSnow-hu)
-校对     |  
-
-<def>基于图像的光照</def>(Image based lighting, IBL)是一类光照技术的集合。其光源不是如[前一节教程](https://learnopengl-cn.github.io/07%20PBR/02%20Lighting/)中描述的可分解的直接光源，而是将周围环境整体视为一个大光源。IBL 通常使用（取自现实世界或从3D场景生成的）环境立方体贴图 (Cubemap) ，我们可以将立方体贴图的每个像素视为光源，在渲染方程中直接使用它。这种方式可以有效地捕捉环境的全局光照和氛围，使物体**更好地融入**其环境。
-
-由于基于图像的光照算法会捕捉部分甚至全部的环境光照，通常认为它是一种更精确的环境光照输入格式，甚至也可以说是一种全局光照的粗略近似。基于此特性，IBL 对 PBR 很有意义，因为当我们将环境光纳入计算之后，物体在物理方面看起来会更加准确。
-
-要开始将 IBL 引入我们的 PBR 系统，让我们再次快速看一下反射方程：
-
-$$
-L_o(p,\omega_o) = \int\limits_{\Omega} 
-    	(k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)})
-    	L_i(p,\omega_i) n \cdot \omega_i  d\omega_i
-$$
-
-如前所述，我们的主要目标是计算半球 \(\Omega\) 上所有入射光方向 \(w_i\) 的积分。解决上一节教程中的积分非常简单，因为我们事先已经知道了对积分有贡献的、若干精确的光线方向 \(w_i\) 。然而这次，来自周围环境的**每个**方向 \(w_i\) 的入射光都可能具有一些辐射度，使得解决积分变得不那么简单。这为解决积分提出了两个要求：  
-
- * 给定任何方向向量 \(w_i\) ，我们需要一些方法来获取这个方向上场景的辐射度。  
- * 解决积分需要快速且实时。  
-
-现在看，第一个要求相对容易些。我们已经有了一些思路：表示环境或场景辐照度的一种方式是（预处理过的）环境立方体贴图，给定这样的立方体贴图，我们可以将立方体贴图的每个纹素视为一个光源。使用一个方向向量 \(w_i\) 对此立方体贴图进行采样，我们就可以获取该方向上的场景辐照度。
-
-如此，给定方向向量 \(w_i\) ，获取此方向上场景辐射度的方法就简化为：
-
-```c++
-vec3 radiance =  texture(_cubemapEnvironment, w_i).rgb;
-```
-
-为了以更有效的方式解决积分，我们需要对其大部分结果进行预处理——或称<def>预计算</def>。为此，我们必须深入研究反射方程：
-
-$$
-L_o(p,\omega_o) = \int\limits_{\Omega} 
-    	(k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)})
-    	L_i(p,\omega_i) n \cdot \omega_i  d\omega_i
-$$
-
-仔细研究反射方程，我们发现 BRDF 的漫反射 \(k_d\) 和镜面 \(k_s\) 项是相互独立的，我们可以将积分分成两部分：
-
-$$
-L_o(p,\omega_o) = 
-		\int\limits_{\Omega} (k_d\frac{c}{\pi}) L_i(p,\omega_i) n \cdot \omega_i  d\omega_i
-		+ 
-		\int\limits_{\Omega} (k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)})
-			L_i(p,\omega_i) n \cdot \omega_i  d\omega_i
-$$
-
-通过将积分分成两部分，我们可以分开研究漫反射和镜面反射部分，本教程的重点是漫反射积分部分。
-
-仔细观察漫反射积分，我们发现漫反射兰伯特项是一个常数项（颜色 \(c\) 、折射率 \(k_d\) 和 \(\pi\) 在整个积分是常数），不依赖于任何积分变量。基于此，我们可以将常数项移出漫反射积分：
-
-$$
-L_o(p,\omega_o) = 
-		k_d\frac{c}{\pi} \int\limits_{\Omega} L_i(p,\omega_i) n \cdot \omega_i  d\omega_i
-$$
-
-这给了我们一个只依赖于 \(w_i\) 的积分（假设 \(p\) 位于环境贴图的中心）。有了这些知识，我们就可以计算或预计算一个新的立方体贴图，它在每个采样方向——也就是纹素——中存储漫反射积分的结果，这些结果是通过<def>卷积</def>计算出来的。
-
-卷积的特性是，对数据集中的一个条目做一些计算时，要考虑到数据集中的所有其他条目。这里的数据集就是场景的辐射度或环境贴图。因此，要对立方体贴图中的每个采样方向做计算，我们都会考虑半球 \(\Omega\) 上的所有其他采样方向。
-
-为了对环境贴图进行卷积，我们通过对半球 \(\Omega\) 上的大量方向进行离散采样并对其辐射度取平均值，来计算每个输出采样方向 \(w_o\) 的积分。用来采样方向 \(w_i\) 的半球，要面向卷积的输出采样方向 \(w_o\) 。
-
-![](../../img/07/03/01/ibl_hemisphere_sample.png)
-
-这个预计算的立方体贴图，在每个采样方向 \(w_o\) 上存储其积分结果，可以理解为场景中所有能够击中面向 \(w_o\) 的表面的间接漫反射光的预计算总和。这样的立方体贴图被称为<def>辐照度图</def>，因为经过卷积计算的立方体贴图能让我们从任何方向有效地直接采样场景（预计算好的）辐照度。
-
-!!! important
-
-		辐射方程也依赖了位置 \(p\) ，不过这里我们假设它位于辐照度图的中心。这就意味着所有漫反射间接光只能来自同一个环境贴图，这样可能会破坏现实感（特别是在室内）。渲染引擎通过在场景中放置多个<def>反射探针</def>来解决此问题，每个反射探针单独预计算其周围环境的辐照度图。这样，位置 \(p\) 处的辐照度（以及辐射度）是取离其最近的反射探针之间的辐照度（辐射度）内插值。目前，我们假设总是从中心采样环境贴图，把反射探针的讨论留给后面的教程。
-
-下面是一个环境立方体贴图及其生成的辐照度图的示例（由 [Wave 引擎](http://www.indiedb.com/features/using-image-based-lighting-ibl)提供），每个方向 \(w_o\) 的场景辐射度取平均值。
-
-![](../../img/07/03/01/ibl_irradiance.png)
-
-由于立方体贴图每个纹素中存储了（ \(w_o\) 方向的）卷积结果，辐照度图看起来有点像环境的平均颜色或光照图。使用任何一个向量对立方体贴图进行采样，就可以获取该方向上的场景辐照度。
-
-## PBR 和 HDR
-
-我们在[光照教程](https://learnopengl-cn.github.io/07%20PBR/02%20Lighting/)中简单提到过：在 PBR 渲染管线中考虑高动态范围(High Dynamic Range, HDR)的场景光照非常重要。由于 PBR 的大部分输入基于实际物理属性和测量，因此为入射光值找到其[物理等效值](https://zh.wikipedia.org/wiki/%E6%B5%81%E6%98%8E)是很重要的。无论我们是对光线的辐射通量进行研究性猜测，还是使用它们的直接物理等效值，诸如一个简单灯泡和太阳之间的这种差异都是很重要的，如果不在 [HDR](https://learnopengl-cn.github.io/05%20Advanced%20Lighting/06%20HDR/) 渲染环境中工作，就无法正确指定每个光的相对强度。
-
-因此，PBR 和 HDR 需要密切合作，但这些与基于图像的光照有什么关系？我们在之前的教程中已经看到，让 PBR 在 HDR 下工作还比较容易。然而，回想一下基于图像的光照，我们将环境的间接光强度建立在环境立方体贴图的颜色值上，我们需要某种方式将光照的高动态范围存储到环境贴图中。
-
-我们一直使用的环境贴图是以立方体贴图形式储存——如同一个[天空盒](https://learnopengl-cn.github.io/04%20Advanced%20OpenGL/06%20Cubemaps/)——属于低动态范围(Low Dynamic Range, LDR)。我们直接使用各个面的图像的颜色值，其范围介于 0.0 和 1.0 之间，计算过程也是照值处理。这样虽然可能适合视觉输出，但作为物理输入参数，没有什么用处。
-
-### 辐射度的 HDR 文件格式
-
-谈及辐射度的文件格式，辐射度文件的格式（扩展名为 .hdr）存储了一张完整的立方体贴图，所有六个面数据都是浮点数，允许指定 0.0 到 1.0 范围之外的颜色值，以使光线具有正确的颜色强度。这个文件格式使用了一个聪明的技巧来存储每个浮点值：它并非直接存储每个通道的 32 位数据，而是每个通道存储 8 位，再以 alpha 通道存放指数——虽然确实会导致精度损失，但是非常有效率，不过需要解析程序将每种颜色重新转换为它们的浮点数等效值。
-
-[sIBL 档案](http://www.hdrlabs.com/sibl/archive.html) 中有很多可以免费获取的辐射度 HDR 环境贴图，下面是一个示例：
-
-![](../../img/07/03/01/ibl_hdr_radiance.png)
-
-可能与您期望的完全不同，因为图像非常扭曲，并且没有我们之前看到的环境贴图的六个立方体贴图面。这张环境贴图是从球体投影到平面上，以使我们可以轻松地将环境信息存储到一张<def>等距柱状投影图</def>(Equirectangular Map) 中。有一点确实需要说明：水平视角附近分辨率较高，而底部和顶部方向分辨率较低,在大多数情况下，这是一个不错的折衷方案，因为对于几乎所有渲染器来说，大部分有意义的光照和环境信息都在水平视角附近方向。
-
-### HDR 和 stb_image.h
-
-直接加载辐射度 HDR 图像需要一些[文件格式](http://radsite.lbl.gov/radiance/refer/Notes/picture_format.html)的知识，虽然不是很困难，但仍然很麻烦。幸运的是，一个常用的头文件库 [stb_image.h](https://github.com/nothings/stb/blob/master/stb_image.h) 支持将辐射度 HDR 图像直接加载为一个浮点数数组，完全符合我们的需要。将 stb_image 添加到项目中之后，加载HDR图像非常简单，如下：
-
-```c++
-#include "stb_image.h"
-[...]
-
-stbi_set_flip_vertically_on_load(true);
-int width, height, nrComponents;
-float *data = stbi_loadf("newport_loft.hdr", &width, &height, &nrComponents, 0);
-unsigned int hdrTexture;
-if (data)
-{
-    glGenTextures(1, &hdrTexture);
-    glBindTexture(GL_TEXTURE_2D, hdrTexture);
-    glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB16F, width, height, 0, GL_RGB, GL_FLOAT, data); 
-
-    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
-    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
-    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
-    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
-
-    stbi_image_free(data);
-}
-else
-{
-    std::cout << "Failed to load HDR image." << std::endl;
-}  
-```
-
-stb_image.h 自动将 HDR 值映射到一个浮点数列表：默认情况下，每个通道32位，每个颜色 3 个通道。我们要将等距柱状投影 HDR 环境贴图转存到 2D 浮点纹理中，这就是所要做的全部工作。
-
-### 从等距柱状投影到立方体贴图
-
-当然也可以直接使用等距柱状投影图获取环境信息，但是这些操作还是显得相对昂贵，在这种情况下，直接采样立方体贴图的性能更高。因此，在本教程中，我们首先将等距柱状投影图转换为立方体贴图以备进一步处理。请注意，在此过程中，我们还将展示如何对等距柱状格式的投影图采样，如同采样 3D 环境贴图一样，您可以自由选择您喜欢的任何解决方案。
-
-要将等距柱状投影图转换为立方体贴图，我们需要渲染一个（单位）立方体，并从内部将等距柱状图投影到立方体的每个面，并将立方体的六个面的图像构造成立方体贴图。此立方体的顶点着色器只是按原样渲染立方体，并将其局部坐标作为 3D 采样向量传递给片段着色器：
-
-```c++
-#version 330 core
-layout (location = 0) in vec3 aPos;
-
-out vec3 localPos;
-
-uniform mat4 projection;
-uniform mat4 view;
-
-void main()
-{
-    localPos = aPos;  
-    gl_Position =  projection * view * vec4(localPos, 1.0);
-}
-```
-
-而在片段着色器中，我们为立方体的每个部分着色，方法类似于将等距柱状投影图整齐地折叠到立方体的每个面一样。为了实现这一点，我们先获取片段的采样方向，这个方向是从立方体的局部坐标进行插值得到的，然后使用此方向向量和一些三角学魔法对等距柱状投影图进行采样，如同立方体图本身一样。我们直接将结果存储到立方体每个面的片段中，以下就是我们需要做的：
-
-```c++
-#version 330 core
-out vec4 FragColor;
-in vec3 localPos;
-
-uniform sampler2D equirectangularMap;
-
-const vec2 invAtan = vec2(0.1591, 0.3183);
-vec2 SampleSphericalMap(vec3 v)
-{
-    vec2 uv = vec2(atan(v.z, v.x), asin(v.y));
-    uv *= invAtan;
-    uv += 0.5;
-    return uv;
-}
-
-void main()
-{		
-    vec2 uv = SampleSphericalMap(normalize(localPos)); // make sure to normalize localPos
-    vec3 color = texture(equirectangularMap, uv).rgb;
-    
-    FragColor = vec4(color, 1.0);
-}
-
-```
-
-如果给定HDR等距柱状投影图，在场景的中心渲染一个立方体，将得到如下所示的内容：
-
-![](../../img/07/03/01/ibl_equirectangular_projection.png)
-
-这表明我们有效地将等距柱状投影图映射到了立方体，但我们还需要将源HDR图像转换为立方体贴图纹理。为了实现这一点，我们必须对同一个立方体渲染六次，每次面对立方体的一个面，并用[帧缓冲](https://learnopengl-cn.github.io/04%20Advanced%20OpenGL/05%20Framebuffers/)对象记录其结果：
-
-```c++
-unsigned int captureFBO, captureRBO;
-glGenFramebuffers(1, &captureFBO);
-glGenRenderbuffers(1, &captureRBO);
-
-glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
-glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
-glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 512, 512);
-glFramebufferRenderbuffer(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, GL_RENDERBUFFER, captureRBO);  
-```
-
-当然，我们此时就可以生成相应的立方体贴图了，首先为其六个面预先分配内存：
-
-```c++
-unsigned int envCubemap;
-glGenTextures(1, &envCubemap);
-glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
-for (unsigned int i = 0; i < 6; ++i)
-{
-    // note that we store each face with 16 bit floating point values
-    glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F, 
-                 512, 512, 0, GL_RGB, GL_FLOAT, nullptr);
-}
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
-```
-
-那剩下要做的就是将等距柱状 2D 纹理捕捉到立方体贴图的面上。
-
-之前在[帧缓冲](https://learnopengl-cn.github.io/04%20Advanced%20OpenGL/05%20Framebuffers/)和[点阴影](https://learnopengl-cn.github.io/05%20Advanced%20Lighting/03%20Shadows/02%20Point%20Shadows/)教程中讨论过的代码细节，我就不再次详细说明，实际过程可以概括为：面向立方体六个面设置六个不同的视图矩阵，给定投影矩阵的 fov 为 90 度以捕捉整个面，并渲染立方体六次，将结果存储在浮点帧缓冲中：
-
-```c++
-glm::mat4 captureProjection = glm::perspective(glm::radians(90.0f), 1.0f, 0.1f, 10.0f);
-glm::mat4 captureViews[] = 
-{
-   glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 1.0f,  0.0f,  0.0f), glm::vec3(0.0f, -1.0f,  0.0f)),
-   glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(-1.0f,  0.0f,  0.0f), glm::vec3(0.0f, -1.0f,  0.0f)),
-   glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f,  1.0f,  0.0f), glm::vec3(0.0f,  0.0f,  1.0f)),
-   glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f, -1.0f,  0.0f), glm::vec3(0.0f,  0.0f, -1.0f)),
-   glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f,  0.0f,  1.0f), glm::vec3(0.0f, -1.0f,  0.0f)),
-   glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f,  0.0f, -1.0f), glm::vec3(0.0f, -1.0f,  0.0f))
-};
-
-// convert HDR equirectangular environment map to cubemap equivalent
-equirectangularToCubemapShader.use();
-equirectangularToCubemapShader.setInt("equirectangularMap", 0);
-equirectangularToCubemapShader.setMat4("projection", captureProjection);
-glActiveTexture(GL_TEXTURE0);
-glBindTexture(GL_TEXTURE_2D, hdrTexture);
-
-glViewport(0, 0, 512, 512); // don't forget to configure the viewport to the capture dimensions.
-glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
-for (unsigned int i = 0; i < 6; ++i)
-{
-    equirectangularToCubemapShader.setMat4("view", captureViews[i]);
-    glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, 
-                           GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, envCubemap, 0);
-    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
-
-    renderCube(); // renders a 1x1 cube
-}
-glBindFramebuffer(GL_FRAMEBUFFER, 0);  
-```
-
-我们采用帧缓冲的颜色值并围绕立方体贴图的每个面切换纹理目标，直接将场景渲染到立方体贴图的一个面上。一旦这个流程完毕——我们只需做一次——立方体贴图 <var>envCubemap</var> 就应该是原 HDR 图的环境立方体贴图版。
-
-让我们编写一个非常简单的天空盒着色器来测试立方体贴图，用来显示周围的立方体贴图：
-
-```c++
-#version 330 core
-layout (location = 0) in vec3 aPos;
-
-uniform mat4 projection;
-uniform mat4 view;
-
-out vec3 localPos;
-
-void main()
-{
-    localPos = aPos;
-
-    mat4 rotView = mat4(mat3(view)); // remove translation from the view matrix
-    vec4 clipPos = projection * rotView * vec4(localPos, 1.0);
-
-    gl_Position = clipPos.xyww;
-}
-```
-
-注意这里的小技巧 xyww 可以确保渲染的立方体片段的深度值总是 1.0，即最大深度，如[立方体贴图](https://learnopengl-cn.github.io/04%20Advanced%20OpenGL/06%20Cubemaps/)教程中所述。注意我们需要将深度比较函数更改为 GL_LEQUAL：
-
-```c++
-glDepthFunc(GL_LEQUAL);  
-```
-
-这个片段着色器直接使用立方体的片段局部坐标，对环境立方体贴图采样：
-
-```c++
-#version 330 core
-out vec4 FragColor;
-
-in vec3 localPos;
-  
-uniform samplerCube environmentMap;
-  
-void main()
-{
-    vec3 envColor = texture(environmentMap, localPos).rgb;
-    
-    envColor = envColor / (envColor + vec3(1.0));
-    envColor = pow(envColor, vec3(1.0/2.2)); 
-  
-    FragColor = vec4(envColor, 1.0);
-}
-```
-
-我们使用插值的立方体顶点坐标对环境贴图进行采样，这些坐标直接对应于正确的采样方向向量。注意，相机的平移分量被忽略掉了，在立方体上渲染此着色器会得到非移动状态下的环境贴图。另外还请注意，当我们将环境贴图的 HDR 值直接输出到默认的 LDR 帧缓冲时，希望对颜色值进行正确的色调映射。此外，默认情况下，几乎所有 HDR 图都处于线性颜色空间中，因此我们需要在写入默认帧缓冲之前应用[伽马校正](https://learnopengl-cn.github.io/05%20Advanced%20Lighting/02%20Gamma%20Correction/)。
-
-现在，在之前渲染的球体上渲染环境贴图，效果应该如下图：
-
-![](../../img/07/03/01/ibl_hdr_environment_mapped.png)
-
-好的...我们用了相当多的设置终于来到了这里，我们设法成功地读取了 HDR 环境贴图，将它从等距柱状投影图转换为立方体贴图，并将 HDR 立方体贴图作为天空盒渲染到了场景中。此外，我们设置了一个小系统来渲染立方体贴图的所有六个面，我们在计算环境贴图卷积时还会需要它。您可以在[此处](https://learnopengl.com/code_viewer_gh.php?code=src/6.pbr/2.1.1.ibl_irradiance_conversion/ibl_irradiance_conversion.cpp)找到整个转化过程的源代码。
-
-## 立方体贴图的卷积
-
-如本节教程开头所述，我们的主要目标是计算所有间接漫反射光的积分，其中光照的辐照度以环境立方体贴图的形式给出。我们已经知道，在方向 \(w_i\) 上采样 HDR 环境贴图，可以获得场景在此方向上的辐射度 \(L(p, w_i)\) 。虽然如此，要解决积分，我们仍然不能仅从一个方向对环境贴图采样，而要从半球 \(\Omega\) 上所有可能的方向进行采样，这对于片段着色器而言还是过于昂贵。
-
-然而，计算上又不可能从 \(\Omega\) 的每个可能的方向采样环境光照，理论上可能的方向数量是无限的。不过我们可以对有限数量的方向采样以近似求解，在半球内均匀间隔或随机取方向可以获得一个相当精确的辐照度近似值，从而离散地计算积分 \(\int\) 。
-
-然而，对于每个片段实时执行此操作仍然太昂贵，因为仍然需要非常大的样本数量才能获得不错的结果，因此我们希望可以<def>预计算</def>。既然半球的朝向决定了我们捕捉辐照度的位置，我们可以预先计算每个可能的半球朝向的辐照度，这些半球朝向涵盖了所有可能的出射方向 \(w_o\) ：
-
-$$
-L_o(p,\omega_o) = 
-		k_d\frac{c}{\pi} \int\limits_{\Omega} L_i(p,\omega_i) n \cdot \omega_i  d\omega_i
-$$
-
-给定任何方向向量 \(w_i\) ，我们可以对预计算的辐照度图采样以获取方向 \(w_i\) 的总漫反射辐照度。为了确定片段上间接漫反射光的数量（辐照度），我们获取以表面法线为中心的半球的总辐照度。获取场景辐照度的方法就简化为：
-
-```c++
-vec3 irradiance = texture(irradianceMap, N);
-```
-
-现在，为了生成辐照度贴图，我们需要将环境光照求卷积，转换为立方体贴图。假设对于每个片段，表面的半球朝向法向量 \(N\) ，对立方体贴图进行卷积等于计算朝向 \(N\) 的半球 \(\Omega\) 中每个方向 \(w_i\) 的总平均辐射率。
-
-![](../../img/07/03/01/ibl_hemisphere_sample_normal.png)
-
-值得庆幸的是，本节教程中所有繁琐的设置并非毫无用处，因为我们现在可以直接获取转换后的立方体贴图，在片段着色器中对其进行卷积，渲染所有六个面，将其结果用帧缓冲捕捉到新的立方体贴图中。之前已经将等距柱状投影图转换为立方体贴图，这次我们可以采用完全相同的方法，但使用不同的片段着色器：
-
-```c++
-#version 330 core
-out vec4 FragColor;
-in vec3 localPos;
-
-uniform samplerCube environmentMap;
-
-const float PI = 3.14159265359;
-
-void main()
-{		
-    // the sample direction equals the hemisphere's orientation 
-    vec3 normal = normalize(localPos);
-  
-    vec3 irradiance = vec3(0.0);
-  
-    [...] // convolution code
-  
-    FragColor = vec4(irradiance, 1.0);
-}
-```
-
-<var>environmentMap</var> 是从等距柱状投影图转换而来的 HDR 立方体贴图。
-有很多方法可以对环境贴图进行卷积，但是对于本教程，我们的方法是：对于立方体贴图的每个纹素，在纹素所代表的方向的半球 \(\Omega\) 内生成固定数量的采样向量，并对采样结果取平均值。数量固定的采样向量将均匀地分布在半球内部。注意，积分是连续函数，在采样向量数量固定的情况下离散地采样只是一种近似计算方法，我们采样的向量越多，就越接近正确的结果。
-反射方程的积分 \(\int\) 是围绕立体角 \(dw\) 旋转，而这个立体角相当难以处理。为了避免对难处理的立体角求积分，我们使用球坐标 \(\theta\) 和 \(\phi\) 来代替立体角。
-
-![](../../img/07/03/01/ibl_spherical_integrate.png)
-
-对于围绕半球大圆的航向角 \(\phi\) ，我们在 \(0\) 到 \(2\pi\) 内采样，而从半球顶点出发的倾斜角 \(\theta\) ，采样范围是 \(0\) 到 \(\frac{1}{2}\pi\) 。于是我们更新一下反射积分方程：
-
-$$
-L_o(p,\phi_o, \theta_o) = 
-        k_d\frac{c}{\pi} \int_{\phi = 0}^{2\pi} \int_{\theta = 0}^{\frac{1}{2}\pi} L_i(p,\phi_i, \theta_i) \cos(\theta) \sin(\theta)  d\phi d\theta
-$$
-
-求解积分需要我们在半球 \(\Omega\) 内采集固定数量的离散样本并对其结果求平均值。分别给每个球坐标轴指定离散样本数量 \(n_1\) 和 \(n_2\) 以求其[黎曼和](https://en.wikipedia.org/wiki/Riemann_sum)，积分式会转换为以下离散版本：
-
-$$
-L_o(p,\phi_o, \theta_o) = 
-        k_d\frac{c}{\pi} \frac{1}{n1 n2} \sum_{\phi = 0}^{n1} \sum_{\theta = 0}^{n2} L_i(p,\phi_i, \theta_i) \cos(\theta) \sin(\theta)  d\phi d\theta
-$$
-
-当我们离散地对两个球坐标轴进行采样时，每个采样近似代表了半球上的一小块区域，如上图所示。注意，由于球的一般性质，当采样区域朝向中心顶部会聚时，天顶角 \(\theta\) 变高，半球的离散采样区域变小。为了平衡较小的区域贡献度，我们使用 \(sin\theta\) 来权衡区域贡献度，这就是多出来的 \(sin\) 的作用。
-
-给定每个片段的积分球坐标，对半球进行离散采样，过程代码如下：
-
-```c++
-vec3 irradiance = vec3(0.0);  
-
-vec3 up    = vec3(0.0, 1.0, 0.0);
-vec3 right = cross(up, normal);
-up         = cross(normal, right);
-
-float sampleDelta = 0.025;
-float nrSamples = 0.0; 
-for(float phi = 0.0; phi < 2.0 * PI; phi += sampleDelta)
-{
-    for(float theta = 0.0; theta < 0.5 * PI; theta += sampleDelta)
-    {
-        // spherical to cartesian (in tangent space)
-        vec3 tangentSample = vec3(sin(theta) * cos(phi),  sin(theta) * sin(phi), cos(theta));
-        // tangent space to world
-        vec3 sampleVec = tangentSample.x * right + tangentSample.y * up + tangentSample.z * N; 
-
-        irradiance += texture(environmentMap, sampleVec).rgb * cos(theta) * sin(theta);
-        nrSamples++;
-    }
-}
-irradiance = PI * irradiance * (1.0 / float(nrSamples));
-```
-
-我们以一个固定的 <var>sampleDelta</var> 增量值遍历半球，减小（或增加）这个增量将会增加（或减少）精确度。
-
-在两层循环内，我们获取一个球面坐标并将它们转换为 3D 直角坐标向量，将向量从切线空间转换为世界空间，并使用此向量直接采样 HDR 环境贴图。我们将每个采样结果加到 <var>irradiance</var>，最后除以采样的总数，得到平均采样辐照度。请注意，我们将采样的颜色值乘以系数 cos(θ) ，因为较大角度的光较弱，而系数 sin(θ) 则用于权衡较高半球区域的较小采样区域的贡献度。
-
-现在剩下要做的就是设置 OpenGL 渲染代码，以便我们可以对之前捕捉的 <var>envCubemap</var> 求卷积。首先我们创建一个辐照度立方体贴图（重复一遍，我们只需要在渲染循环之前执行一次）：
-
-```c++
-unsigned int irradianceMap;
-glGenTextures(1, &irradianceMap);
-glBindTexture(GL_TEXTURE_CUBE_MAP, irradianceMap);
-for (unsigned int i = 0; i < 6; ++i)
-{
-    glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F, 32, 32, 0, 
-                 GL_RGB, GL_FLOAT, nullptr);
-}
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
-```
-
-由于辐照度图对所有周围的辐射值取了平均值，因此它丢失了大部分高频细节，所以我们可以以较低的分辨率（32x32）存储，并让 OpenGL 的线性滤波完成大部分工作。接下来，我们将捕捉到的帧缓冲图像缩放到新的分辨率：
-
-```c++
-glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
-glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
-glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 32, 32);  
-```
-
-我们使用卷积着色器——和捕捉环境立方体贴图类似的方式——来对环境贴图求卷积：
-
-```c++
-irradianceShader.use();
-irradianceShader.setInt("environmentMap", 0);
-irradianceShader.setMat4("projection", captureProjection);
-glActiveTexture(GL_TEXTURE0);
-glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
-
-glViewport(0, 0, 32, 32); // don't forget to configure the viewport to the capture dimensions.
-glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
-for (unsigned int i = 0; i < 6; ++i)
-{
-    irradianceShader.setMat4("view", captureViews[i]);
-    glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, 
-                           GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, irradianceMap, 0);
-    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
-
-    renderCube();
-}
-glBindFramebuffer(GL_FRAMEBUFFER, 0);  
-```
-
-现在，完成这个流程之后，我们应该得到了一个预计算好的辐照度图，可以直接将其用于IBL 计算。为了查看我们是否成功地对环境贴图进行了卷积，让我们将天空盒的环境采样贴图替换为辐照度贴图：
-
-![](../../img/07/03/01/ibl_irradiance_map_background.png)
-
-如果它看起来像模糊的环境贴图，说明您已经成功地对环境贴图进行了卷积。
-
-## PBR 和间接辐照度光照
-
-辐照度图表示所有周围的间接光累积的反射率的漫反射部分的积分。注意光不是来自任何直接光源，而是来自周围环境，我们将间接漫反射和间接镜面反射视为环境光，取代了我们之前设定的常数项。
-
-首先，务必将预计算的辐照度图添加为一个立方体采样器：
-
-```c++
-uniform samplerCube irradianceMap;
-```
-
-给定一张辐照度图，它存储了场景中的所有间接漫反射光，获取片段的辐照度就简化为给定法线的一次纹理采样：
-
-```c++
-// vec3 ambient = vec3(0.03);
-vec3 ambient = texture(irradianceMap, N).rgb;
-```
-
-然而，由于间接光照包括漫反射和镜面反射两部分，正如我们从分割版的反射方程中看到的那样，我们需要对漫反射部分进行相应的加权。与我们在前一节教程中所做的类似，我们使用菲涅耳公式来计算表面的间接反射率，我们从中得出折射率或称漫反射率：
-
-```c++
-vec3 kS = fresnelSchlick(max(dot(N, V), 0.0), F0);
-vec3 kD = 1.0 - kS;
-vec3 irradiance = texture(irradianceMap, N).rgb;
-vec3 diffuse    = irradiance * albedo;
-vec3 ambient    = (kD * diffuse) * ao; 
-```
-
-由于环境光来自半球内围绕法线 N 的所有方向，因此没有一个确定的半向量来计算菲涅耳效应。为了模拟菲涅耳效应，我们用法线和视线之间的夹角计算菲涅耳系数。然而，之前我们是以受粗糙度影响的微表面半向量作为菲涅耳公式的输入，但我们目前没有考虑任何粗糙度，表面的反射率总是会相对较高。间接光和直射光遵循相同的属性，因此我们期望较粗糙的表面在边缘反射较弱。由于我们没有考虑表面的粗糙度，间接菲涅耳反射在粗糙非金属表面上看起来有点过强（为了演示目的略微夸大）：
-
-![](../../img/07/03/01/lighting_fresnel_no_roughness.png)
-
-我们可以通过在 [Sébastien Lagarde](https://seblagarde.wordpress.com/2011/08/17/hello-world/) 提出的 Fresnel-Schlick 方程中加入粗糙度项来缓解这个问题：
-
-```c++
-vec3 fresnelSchlickRoughness(float cosTheta, vec3 F0, float roughness)
-{
-    return F0 + (max(vec3(1.0 - roughness), F0) - F0) * pow(1.0 - cosTheta, 5.0);
-}   
-```
-
-在计算菲涅耳效应时纳入表面粗糙度，环境光代码最终确定为：
-
-```c++
-vec3 kS = fresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness); 
-vec3 kD = 1.0 - kS;
-vec3 irradiance = texture(irradianceMap, N).rgb;
-vec3 diffuse    = irradiance * albedo;
-vec3 ambient    = (kD * diffuse) * ao; 
-```
-
-如您所见，实践上基于图像的光照计算非常简单，只需要采样一次立方体贴图，大部分的工作量在于将环境贴图预计算或卷积成辐照度图。
-
-回到我们在[光照教程](https://learnopengl-cn.github.io/07%20PBR/02%20Lighting/)中建立的初始场景，场景中排列的球体金属度沿垂直方向递增，粗糙度沿水平方向递增。向场景中添加基于漫反射图像的光照之后，它看起来像这样：
-
-![](../../img/07/03/01/ibl_irradiance_result.png)
-
-现在看起来仍然有点奇怪，因为金属度较高的球体**需要**某种形式的反射以便看起来更像金属表面（因为金属表面没有漫反射），不过目前只有来自点光源的反射——而且可以说几乎没有。不过尽管如此，您也可以看出，球体在环境中的感觉更加和谐了（特别是在环境贴图之间切换的时候），因为表面会正确地响应环境光照。
-
-您可以在[此处](https://learnopengl.com/code_viewer_gh.php?code=src/6.pbr/2.1.2.ibl_irradiance/ibl_irradiance.cpp)找到以上讨论过的整套源代码。在[下一节教程](https://learnopengl-cn.github.io/07%20PBR/03%20IBL/02%20Specular%20IBL/)中，我们将添加反射积分的间接镜面反射部分，此时我们将真正看到 PBR 的力量。
-
-## 进阶阅读
-
- * [Coding Labs: Physically based rendering](http://www.codinglabs.net/article_physically_based_rendering.aspx)：介绍 PBR ，如何以及为何要生成辐照度图。
- * [The Mathematics of Shading](http://www.scratchapixel.com/lessons/mathematics-physics-for-computer-graphics/mathematics-of-shading)：借助 ScratchAPixel，对本教程中涉及的一些数学知识的简要介绍，特别是关于极坐标和积分。

docs/07 PBR/03 IBL/02 Specular IBL.md

@@ -1,676 +0,0 @@
-# 镜面反射 IBL
-
-原文     | [Specular IBL](https://learnopengl.com/PBR/IBL/Specular-IBL)
-      ---|---
-作者     | JoeyDeVries
-翻译     | [flyingSnow](https://github.com/flyingSnow-hu)
-校对     |  
-
-在[上一节教程](https://learnopengl-cn.github.io/07%20PBR/03%20IBL/01%20Diffuse%20irradiance/)中，我们预计算了辐照度图作为光照的间接漫反射部分，以将 PBR 与基于图像的照明相结合。在本教程中，我们将重点关注反射方程的镜面部分：
-
-$$
-L_o(p,\omega_o) = \int\limits_{\Omega} 
-    	(k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)})
-    	L_i(p,\omega_i) n \cdot \omega_i  d\omega_i
-$$
-
-你会注意到 Cook-Torrance 镜面部分（乘以\(k_s\)）在整个积分上不是常数，不仅受入射光方向影响，**还**受视角影响。如果试图解算所有入射光方向加所有可能的视角方向的积分，二者组合数会极其庞大，实时计算太昂贵。Epic Games 提出了一个解决方案，他们预计算镜面部分的卷积，为实时计算作了一些妥协，这种方案被称为<def>分割求和近似法</def>（split sum approximation）。
-分割求和近似将方程的镜面部分分割成两个独立的部分，我们可以单独求卷积，然后在 PBR 着色器中求和，以用于间接镜面反射部分 IBL。分割求和近似法类似于我们之前求辐照图预卷积的方法，需要 HDR 环境贴图作为其卷积输入。为了理解，我们回顾一下反射方程，但这次只关注镜面反射部分（在[上一节教程](](https://learnopengl-cn.github.io/07%20PBR/03%20IBL/01%20Diffuse%20irradiance/))中已经剥离了漫反射部分）：
-
-$$
-L_o(p,\omega_o) = 
-		\int\limits_{\Omega} (k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}
-			L_i(p,\omega_i) n \cdot \omega_i  d\omega_i
-			=
-		\int\limits_{\Omega} f_r(p, \omega_i, \omega_o) L_i(p,\omega_i) n \cdot \omega_i  d\omega_i
-$$
-
-由于与辐照度卷积相同的（性能）原因，我们无法以合理的性能实时求解积分的镜面反射部分。因此，我们最好预计算这个积分，以得到像镜面 IBL 贴图这样的东西，用片段的法线对这张图采样并计算。但是，有一个地方有点棘手：我们能够预计算辐照度图，是因为其积分仅依赖于\(\omega_i\)，并且可以将漫反射反射率常数项移出积分，但这一次，积分不仅仅取决于\(\omega_i\)，从 BRDF 可以看出：
-
-$$
-f_r(p, w_i, w_o) = \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}
-$$
-
-这次积分还依赖\(\omega_o\)，我们无法用两个方向向量采样预计算的立方体图。如前一个教程中所述，位置\(p\)与此处无关。在实时状态下，对每种可能的\(\omega_i\)和\(\omega_o\)的组合预计算该积分是不可行的。
-Epic Games 的分割求和近似法将预计算分成两个单独的部分求解，再将两部分组合起来得到后文给出的预计算结果。分割求和近似法将镜面反射积分拆成两个独立的积分：
-
-$$
-L_o(p,\omega_o) = 
-		\int\limits_{\Omega} L_i(p,\omega_i) d\omega_i
-		*
-		\int\limits_{\Omega} f_r(p, \omega_i, \omega_o) n \cdot \omega_i d\omega_i
-$$
-
-卷积的第一部分被称为<def>预滤波环境贴图</def>，它类似于辐照度图，是预先计算的环境卷积贴图，但这次考虑了粗糙度。因为随着粗糙度的增加，参与环境贴图卷积的采样向量会更分散，导致反射更模糊，所以对于卷积的每个粗糙度级别，我们将按顺序把模糊后的结果存储在预滤波贴图的 mipmap 中。例如，预过滤的环境贴图在其 5 个 mipmap 级别中存储 5 个不同粗糙度值的预卷积结果，如下图所示：
-
-![](../../img/07/03/02/ibl_prefilter_map.png)
-
-我们使用 Cook-Torrance BRDF 的法线分布函数(NDF)生成采样向量及其散射强度，该函数将法线和视角方向作为输入。由于我们在卷积环境贴图时事先不知道视角方向，因此 Epic Games 假设视角方向——也就是镜面反射方向——总是等于输出采样方向\(\omega_o\)，以作进一步近似。翻译成代码如下：
-
-```c++
-vec3 N = normalize(w_o);
-vec3 R = N;
-vec3 V = R;
-```
-
-这样，预过滤的环境卷积就不需要关心视角方向了。这意味着当从如下图的角度观察表面的镜面反射时，得到的掠角镜面反射效果不是很好（图片来自文章《Moving Frostbite to PBR》）。然而，通常可以认为这是一个体面的妥协：
-
-![](../../img/07/03/02/ibl_grazing_angles.png)
-
-等式的第二部分等于镜面反射积分的 BRDF 部分。如果我们假设每个方向的入射辐射度都是白色的（因此\(L(p, x) = 1.0\) ），就可以在给定粗糙度、光线 \(\omega_i\) 法线 \(n\) 夹角 \(n \cdot \omega_i\) 的情况下，预计算 BRDF 的响应结果。Epic Games 将预计算好的 BRDF 对每个粗糙度和入射角的组合的响应结果存储在一张 2D 查找纹理(LUT)上，称为<def>BRDF积分贴图</def>。2D 查找纹理存储是菲涅耳响应的系数（R 通道）和偏差值（G 通道），它为我们提供了分割版镜面反射积分的第二个部分：
-
-![](../../img/07/03/02/ibl_brdf_lut.png)
-
-生成查找纹理的时候，我们以 BRDF 的输入\(n⋅\omega_i\)（范围在 0.0 和 1.0 之间）作为横坐标，以粗糙度作为纵坐标。有了此 BRDF 积分贴图和预过滤的环境贴图，我们就可以将两者结合起来，以获得镜面反射积分的结果：
-
-```c++
-float lod             = getMipLevelFromRoughness(roughness);
-vec3 prefilteredColor = textureCubeLod(PrefilteredEnvMap, refVec, lod);
-vec2 envBRDF          = texture2D(BRDFIntegrationMap, vec2(NdotV, roughness)).xy;
-vec3 indirectSpecular = prefilteredColor * (F * envBRDF.x + envBRDF.y) 
-```
-
-至此，你应该对 Epic Games 的分割求和近似法的原理，以及它如何近似求解反射方程的间接镜面反射部分有了一些基本印象。让我们现在尝试一下自己构建预卷积部分。
-
-## 预滤波HDR环境贴图
-
-预滤波环境贴图的方法与我们对辐射度贴图求卷积的方法非常相似。对于卷积的每个粗糙度级别，我们将按顺序把模糊后的结果存储在预滤波贴图的 mipmap 中。
-首先，我们需要生成一个新的立方体贴图来保存预过滤的环境贴图数据。为了确保为其 mip 级别分配足够的内存，一个简单方法是调用 <fun>glGenerateMipmap</fun>。
-
-```c++
-unsigned int prefilterMap;
-glGenTextures(1, &prefilterMap);
-glBindTexture(GL_TEXTURE_CUBE_MAP, prefilterMap);
-for (unsigned int i = 0; i < 6; ++i)
-{
-    glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F, 128, 128, 0, GL_RGB, GL_FLOAT, nullptr);
-}
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR); 
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
-
-glGenerateMipmap(GL_TEXTURE_CUBE_MAP);
-```
-
-注意，因为我们计划采样 <var>prefilterMap</var> 的 mipmap，所以需要确保将其缩小过滤器设置为 <var>GL_LINEAR_MIPMAP_LINEAR</var> 以启用三线性过滤。它存储的是预滤波的镜面反射，基础 mip 级别的分辨率是每面 128×128，对于大多数反射来说可能已经足够了，但如果场景里有大量光滑材料（想想汽车上的反射），可能需要提高分辨率。
-
-在上一节教程中，我们使用球面坐标生成均匀分布在半球 \(\Omega\) 上的采样向量，以对环境贴图进行卷积。虽然这个方法非常适用于辐照度，但对于镜面反射效果较差。镜面反射依赖于表面的粗糙度，反射光线可能比较松散，也可能比较紧密，但是一定会围绕着反射向量\(r\)，除非表面极度粗糙：
-
-![](../../img/07/03/02/ibl_specular_lobe.png)
-
-所有可能出射的反射光构成的形状称为<def>镜面波瓣</def>。随着粗糙度的增加，镜面波瓣的大小增加；随着入射光方向不同，形状会发生变化。因此，镜面波瓣的形状高度依赖于材质。
-在微表面模型里给定入射光方向，则镜面波瓣指向微平面的半向量的反射方向。考虑到大多数光线最终会反射到一个基于半向量的镜面波瓣内，采样时以类似的方式选取采样向量是有意义的，因为大部分其余的向量都被浪费掉了，这个过程称为<def>重要性采样</def>。
-
-### 蒙特卡洛积分和重要性采样
-
-为了充分理解重要性采样，我们首先要了解一种数学结构，称为<def>蒙特卡洛积分</def>。蒙特卡洛积分主要是统计和概率理论的组合。蒙特卡洛可以帮助我们离散地解决人口统计问题，而不必考虑**所有**人。
-
-例如，假设您想要计算一个国家所有公民的平均身高。为了得到结果，你可以测量**每个**公民并对他们的身高求平均，这样会得到你需要的**确切**答案。但是，由于大多数国家人海茫茫，这个方法不现实：需要花费太多精力和时间。
-
-另一种方法是选择一个小得多的**完全随机**（无偏）的人口子集，测量他们的身高并对结果求平均。可能只测量 100 人，虽然答案并非绝对精确，但会得到一个相对接近真相的答案，这个理论被称作<def>大数定律</def>。我们的想法是，如果从总人口中测量一组较小的真正随机样本的\(N\)，结果将相对接近真实答案，并随着样本数 \(N\) 的增加而愈加接近。
-
-蒙特卡罗积分建立在大数定律的基础上，并采用相同的方法来求解积分。不为所有可能的（理论上是无限的）样本值 \(x\) 求解积分，而是简单地从总体中随机挑选样本 \(N\) 生成采样值并求平均。随着 \(N\) 的增加，我们的结果会越来越接近积分的精确结果：
-
-$$
-O =  \int\limits_{a}^{b} f(x) dx 
-      = 
-      \frac{1}{N} \sum_{i=0}^{N-1} \frac{f(x)}{pdf(x)}
-$$
-
-为了求解这个积分，我们在 \(a\) 到 \(b\) 上采样 \(N\) 个随机样本，将它们加在一起并除以样本总数来取平均。\(pdf\) 代表<def>概率密度函数</def> (probability density function)，它的含义是特定样本在整个样本集上发生的概率。例如，人口身高的 pdf 看起来应该像这样：
-
-![](../../img/07/03/02/ibl_pdf.png)
-
-从该图中我们可以看出，如果我们对人口任意随机采样，那么挑选身高为 1.70 的人口样本的可能性更高，而样本身高为 1.50 的概率较低。
-
-当涉及蒙特卡洛积分时，某些样本可能比其他样本具有更高的生成概率。这就是为什么对于任何一般的蒙特卡洛估计，我们都会根据 pdf 将采样值除以或乘以采样概率。到目前为止，我们每次需要估算积分的时候，生成的样本都是均匀分布的，概率完全相等。到目前为止，我们的估计是<def>无偏</def>的，这意味着随着样本数量的不断增加，我们最终将<def>收敛</def>到积分的**精确**解。
-
-但是，某些蒙特卡洛估算是<def>有偏</def>的，这意味着生成的样本并不是完全随机的，而是集中于特定的值或方向。这些有偏的蒙特卡洛估算具有<def>更快的收敛速度</def>，它们会以更快的速度收敛到精确解，但是由于其有偏性，可能永远不会收敛到精确解。通常来说，这是一个可以接受的折衷方案，尤其是在计算机图形学中。因为只要结果在视觉上可以接受，解决方案的精确性就不太重要。下文我们将会提到一种（有偏的）重要性采样，其生成的样本偏向特定的方向，在这种情况下，我们会将每个样本乘以或除以相应的 pdf 再求和。
-
-蒙特卡洛积分在计算机图形学中非常普遍，因为它是一种以高效的离散方式对连续的积分求近似而且非常直观的方法：对任何面积/体积进行采样——例如半球 \(\Omega\) ——在该面积/体积内生成数量 \(N\) 的随机采样，权衡每个样本对最终结果的贡献并求和。
-
-蒙特卡洛积分是一个庞大的数学主题，在此不再赘述，但有一点需要提到：生成随机样本的方法也多种多样。默认情况下，每次采样都是我们熟悉的完全（伪）随机，不过利用半随机序列的某些属性，我们可以生成虽然是随机样本但具有一些有趣性质的样本向量。例如，我们可以对一种名为<def>低差异序列</def>的东西进行蒙特卡洛积分，该序列生成的仍然是随机样本，但样本分布更均匀：
-
-![](../../img/07/03/02/ibl_low_discrepancy_sequence.png)
-
-当使用低差异序列生成蒙特卡洛样本向量时，该过程称为<def>拟蒙特卡洛积分</def>。拟蒙特卡洛方法具有更快的<def>收敛速度</def>，这使得它对于性能繁重的应用很有用。
-
-鉴于我们新获得的有关蒙特卡洛（Monte Carlo）和拟蒙特卡洛（Quasi-Monte Carlo）积分的知识，我们可以使用一个有趣的属性来获得更快的收敛速度，这就是<def>重要性采样</def>。我们在前文已经提到过它，但是在镜面反射的情况下，反射的光向量被限制在镜面波瓣中，波瓣的大小取决于表面的粗糙度。既然镜面波瓣外的任何（拟）随机生成的样本与镜面积分无关，因此将样本集中在镜面波瓣内生成是有意义的，但代价是蒙特卡洛估算会产生偏差。
-
-本质上来说，这就是重要性采样的核心：只在某些区域生成采样向量，该区域围绕微表面半向量，受粗糙度限制。通过将拟蒙特卡洛采样与低差异序列相结合，并使用重要性采样偏置样本向量的方法，我们可以获得很高的收敛速度。因为我们求解的速度更快，所以要达到足够的近似度，我们所需要的样本更少。因此，这套组合方法甚至可以允许图形应用程序实时求解镜面积分，虽然比预计算结果还是要慢得多。
-
-### 低差异序列
-
-在本教程中，我们将使用重要性采样来预计算间接反射方程的镜面反射部分，该采样基于拟蒙特卡洛方法给出了随机的低差异序列。我们将使用的序列被称为 <def>Hammersley 序列</def>，[Holger Dammertz](http://holger.dammertz.org/stuff/notes_HammersleyOnHemisphere.html) 曾仔细描述过它。Hammersley 序列是基于 <def>Van Der Corput 序列</def>，该序列是把十进制数字的二进制表示镜像翻转到小数点右边而得。（译注：原文为 Van Der Corpus 疑似笔误，下文各处同）
-
-给出一些巧妙的技巧，我们可以在着色器程序中非常有效地生成 Van Der Corput 序列，我们将用它来获得 Hammersley 序列，设总样本数为 <var>N</var>，样本索引为 <var>i</var>：
-
-```c++
-float RadicalInverse_VdC(uint bits) 
-{
-    bits = (bits << 16u) | (bits >> 16u);
-    bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
-    bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
-    bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
-    bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
-    return float(bits) * 2.3283064365386963e-10; // / 0x100000000
-}
-// ----------------------------------------------------------------------------
-vec2 Hammersley(uint i, uint N)
-{
-    return vec2(float(i)/float(N), RadicalInverse_VdC(i));
-}  
-```
-
-GLSL 的 <fun>Hammersley</fun> 函数可以获取大小为 <var>N</var> 的样本集中的低差异样本 <var>i</var>。
-
-!!! important
-
-	**无需位运算的 Hammersley 序列**
-
-	并非所有 OpenGL 相关驱动程序都支持位运算符（例如WebGL和OpenGL ES 2.0），在这种情况下，你可能需要不依赖位运算符的替代版本 Van Der Corput 序列：
-
-		float VanDerCorpus(uint n, uint base)
-		{
-		    float invBase = 1.0 / float(base);
-		    float denom   = 1.0;
-		    float result  = 0.0;
-
-		    for(uint i = 0u; i < 32u; ++i)
-		    {
-		        if(n > 0u)
-		        {
-		            denom   = mod(float(n), 2.0);
-		            result += denom * invBase;
-		            invBase = invBase / 2.0;
-		            n       = uint(float(n) / 2.0);
-		        }
-		    }
-
-		    return result;
-		}
-		// ----------------------------------------------------------------------------
-		vec2 HammersleyNoBitOps(uint i, uint N)
-		{
-		    return vec2(float(i)/float(N), VanDerCorpus(i, 2u));
-		}
-
-	请注意，由于旧硬件中的 GLSL 循环限制，该序列循环遍历了所有可能的 32 位，性能略差。但是如果你没有位运算符可用的话可以考虑它，它可以在所有硬件上运行。
-
-
-### GGX 重要性采样
-
-有别于均匀或纯随机地（比如蒙特卡洛）在积分半球 \(\Omega\) 产生采样向量，我们的采样会根据粗糙度，偏向微表面的半向量的宏观反射方向。采样过程将与我们之前看到的过程相似：开始一个大循环，生成一个随机（低差异）序列值，用该序列值在切线空间中生成样本向量，将样本向量变换到世界空间并对场景的辐射度采样。不同之处在于，我们现在使用低差异序列值作为输入来生成采样向量：
-
-```c++
-const uint SAMPLE_COUNT = 4096u;
-for(uint i = 0u; i < SAMPLE_COUNT; ++i)
-{
-    vec2 Xi = Hammersley(i, SAMPLE_COUNT);   
-}
-```
-
-此外，要构建采样向量，我们需要一些方法定向和偏移采样向量，以使其朝向特定粗糙度的镜面波瓣方向。我们可以如理论教程中所述使用 NDF，并将 GGX NDF 结合到 Epic Games 所述的球形采样向量的处理中：
-
-```c++
-vec3 ImportanceSampleGGX(vec2 Xi, vec3 N, float roughness)
-{
-    float a = roughness*roughness;
-	
-    float phi = 2.0 * PI * Xi.x;
-    float cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (a*a - 1.0) * Xi.y));
-    float sinTheta = sqrt(1.0 - cosTheta*cosTheta);
-	
-    // from spherical coordinates to cartesian coordinates
-    vec3 H;
-    H.x = cos(phi) * sinTheta;
-    H.y = sin(phi) * sinTheta;
-    H.z = cosTheta;
-	
-    // from tangent-space vector to world-space sample vector
-    vec3 up        = abs(N.z) < 0.999 ? vec3(0.0, 0.0, 1.0) : vec3(1.0, 0.0, 0.0);
-    vec3 tangent   = normalize(cross(up, N));
-    vec3 bitangent = cross(N, tangent);
-	
-    vec3 sampleVec = tangent * H.x + bitangent * H.y + N * H.z;
-    return normalize(sampleVec);
-}
-```
-
-基于特定的粗糙度输入和低差异序列值 <var>Xi</var>，我们获得了一个采样向量，该向量大体围绕着预估的微表面的半向量。注意，根据迪士尼对 PBR 的研究，Epic Games 使用了平方粗糙度以获得更好的视觉效果。
-
-使用低差异 Hammersley 序列和上述定义的样本生成方法，我们可以最终完成预滤波器卷积着色器：
-
-```c++
-#version 330 core
-out vec4 FragColor;
-in vec3 localPos;
-
-uniform samplerCube environmentMap;
-uniform float roughness;
-
-const float PI = 3.14159265359;
-
-float RadicalInverse_VdC(uint bits);
-vec2 Hammersley(uint i, uint N);
-vec3 ImportanceSampleGGX(vec2 Xi, vec3 N, float roughness);
-  
-void main()
-{		
-    vec3 N = normalize(localPos);    
-    vec3 R = N;
-    vec3 V = R;
-
-    const uint SAMPLE_COUNT = 1024u;
-    float totalWeight = 0.0;   
-    vec3 prefilteredColor = vec3(0.0);     
-    for(uint i = 0u; i < SAMPLE_COUNT; ++i)
-    {
-        vec2 Xi = Hammersley(i, SAMPLE_COUNT);
-        vec3 H  = ImportanceSampleGGX(Xi, N, roughness);
-        vec3 L  = normalize(2.0 * dot(V, H) * H - V);
-
-        float NdotL = max(dot(N, L), 0.0);
-        if(NdotL > 0.0)
-        {
-            prefilteredColor += texture(environmentMap, L).rgb * NdotL;
-            totalWeight      += NdotL;
-        }
-    }
-    prefilteredColor = prefilteredColor / totalWeight;
-
-    FragColor = vec4(prefilteredColor, 1.0);
-}  
-
-```
-
-输入的粗糙度随着预过滤的立方体贴图的 mipmap 级别变化（从0.0到1.0），我们根据据粗糙度预过滤环境贴图，把结果存在 <var>prefilteredColor</var> 里。再用 <var>prefilteredColor</var> 除以采样权重总和，其中对最终结果影响较小（<var>NdotL</var> 较小）的采样最终权重也较小。
-
-### 捕获预过滤 mipmap 级别
-
-剩下要做的就是让 OpenGL 在多个 mipmap 级别上以不同的粗糙度值预过滤环境贴图。有了最开始的辐照度教程作为基础，实际上很简单：
-
-```c++
-prefilterShader.use();
-prefilterShader.setInt("environmentMap", 0);
-prefilterShader.setMat4("projection", captureProjection);
-glActiveTexture(GL_TEXTURE0);
-glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
-
-glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
-unsigned int maxMipLevels = 5;
-for (unsigned int mip = 0; mip < maxMipLevels; ++mip)
-{
-    // reisze framebuffer according to mip-level size.
-    unsigned int mipWidth  = 128 * std::pow(0.5, mip);
-    unsigned int mipHeight = 128 * std::pow(0.5, mip);
-    glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
-    glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, mipWidth, mipHeight);
-    glViewport(0, 0, mipWidth, mipHeight);
-
-    float roughness = (float)mip / (float)(maxMipLevels - 1);
-    prefilterShader.setFloat("roughness", roughness);
-    for (unsigned int i = 0; i < 6; ++i)
-    {
-        prefilterShader.setMat4("view", captureViews[i]);
-        glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, 
-                               GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, prefilterMap, mip);
-
-        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
-        renderCube();
-    }
-}
-glBindFramebuffer(GL_FRAMEBUFFER, 0);   
-```
-
-这个过程类似于辐照度贴图卷积，但是这次我们将帧缓冲区缩放到适当的 mipmap 尺寸， mip 级别每增加一级，尺寸缩小为一半。此外，我们在 <fun>glFramebufferTexture2D</fun> 的最后一个参数中指定要渲染的目标 mip 级别，然后将要预过滤的粗糙度传给预过滤着色器。
-
-这样我们会得到一张经过适当预过滤的环境贴图，访问该贴图时指定的 mip 等级越高，获得的反射就越模糊。如果我们在天空盒着色器中显示这张预过滤的环境立方体贴图，并在其着色器中强制在其第一个 mip 级别以上采样，如下所示：
-
-```c++
-vec3 envColor = textureLod(environmentMap, WorldPos, 1.2).rgb;
-```
-
-我们得到的结果看起来确实像原始环境的模糊版本：
-
-![](../../img/07/03/02/ibl_prefilter_map_sample.png)
-
-如果 HDR 环境贴图的预过滤看起来差不多没问题，尝试一下不同的 mipmap 级别，观察预过滤贴图随着 mip 级别增加，反射逐渐从锐利变模糊的过程。
-
-## 预过滤卷积的伪像
-
-当前的预过滤贴图可以在大多数情况下正常工作，不过你迟早会遇到几个与预过滤卷积直接相关的渲染问题。我将在这里列出最常见的一些问题，以及如何修复它们。
-
-### 高粗糙度的立方体贴图接缝
-
-在具有粗糙表面的表面上对预过滤贴图采样，也就等同于在较低的 mip 级别上对预过滤贴图采样。在对立方体贴图进行采样时，默认情况下，OpenGL不会在立方体面**之间**进行线性插值。由于较低的 mip 级别具有更低的分辨率，并且预过滤贴图代表了与更大的采样波瓣卷积，因此缺乏**立方体的面和面之间的滤波**的问题就更明显：
-
-![](../../img/07/03/02/ibl_prefilter_seams.png)
-
-幸运的是，OpenGL 可以启用 <var>GL_TEXTURE_CUBE_MAP_SEAMLESS</var>，以为我们提供在立方体贴图的面之间进行正确过滤的选项：
-
-```c++
-glEnable(GL_TEXTURE_CUBE_MAP_SEAMLESS);  
-```
-
-### 预过滤卷积的亮点
-
-由于镜面反射中光强度的变化大，高频细节多，所以对镜面反射进行卷积需要大量采样，才能正确反映 HDR 环境反射的混乱变化。我们已经进行了大量的采样，但是在某些环境下，在某些较粗糙的 mip 级别上可能仍然不够，导致明亮区域周围出现点状图案：
-
-![](../../img/07/03/02/ibl_prefilter_dots.png)
-
-一种解决方案是进一步增加样本数量，但在某些情况下还是不够。另一种方案如 [Chetan Jags](https://chetanjags.wordpress.com/2015/08/26/image-based-lighting/) 所述，我们可以在预过滤卷积时，不直接采样环境贴图，而是基于积分的 PDF 和粗糙度采样环境贴图的 mipmap ，以减少伪像：
-
-```c++
-float D   = DistributionGGX(NdotH, roughness);
-float pdf = (D * NdotH / (4.0 * HdotV)) + 0.0001; 
-
-float resolution = 512.0; // resolution of source cubemap (per face)
-float saTexel  = 4.0 * PI / (6.0 * resolution * resolution);
-float saSample = 1.0 / (float(SAMPLE_COUNT) * pdf + 0.0001);
-
-float mipLevel = roughness == 0.0 ? 0.0 : 0.5 * log2(saSample / saTexel); 
-```
-
-既然要采样 mipmap ，不要忘记在环境贴图上开启三线性过滤：
-
-```c++
-glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
-glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR); 
-```
-
-设置立方体贴图的基本纹理后，让 OpenGL 生成 mipmap：
-
-```c++
-// convert HDR equirectangular environment map to cubemap equivalent
-[...]
-// then generate mipmaps
-glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
-glGenerateMipmap(GL_TEXTURE_CUBE_MAP);
-```
-
-这个方法效果非常好，可以去除预过滤贴图中较粗糙表面上的大多数甚至全部亮点。
-
-## 预计算 BRDF
-
-预过滤的环境贴图已经可以设置并运行，我们可以集中精力于求和近似的第二部分：BRDF。让我们再次简要回顾一下镜面部分的分割求和近似法：
-
-$$
-L_o(p,\omega_o) = 
-		\int\limits_{\Omega} L_i(p,\omega_i) d\omega_i
-		*
-		\int\limits_{\Omega} f_r(p, \omega_i, \omega_o) n \cdot \omega_i d\omega_i
-$$
-
-我们已经在预过滤贴图的各个粗糙度级别上预计算了分割求和近似的左半部分。右半部分要求我们在 \(n \cdot \omega_o\) 、表面粗糙度、菲涅尔系数 \(F_0\) 上计算 BRDF 方程的卷积。这等同于在纯白的环境光或者辐射度恒定为 \(L_i\)=1.0 的设置下，对镜面 BRDF 求积分。对3个变量做卷积有点复杂，不过我们可以把 \(F_0\) 移出镜面 BRDF 方程：
-
-$$
-\int\limits_{\Omega} f_r(p, \omega_i, \omega_o) n \cdot \omega_i d\omega_i = \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) \frac{F(\omega_o, h)}{F(\omega_o, h)} n \cdot \omega_i d\omega_i
-$$
-
-\(F\) 为菲涅耳方程。将菲涅耳分母移到 BRDF 下面可以得到如下等式：
-
-$$
-\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} F(\omega_o, h)  n \cdot \omega_i d\omega_i
-$$
-
-用 Fresnel-Schlick 近似公式替换右边的 \(F\) 可以得到：
-
-$$
-\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 + (1 - F_0){(1 - \omega_o \cdot h)}^5)  n \cdot \omega_i d\omega_i
-$$
-
-让我们用 \(\alpha\) 替换 \({(1 - \omega_o \cdot h)}^5\) 以便更轻松地求解 \(F_0\)：
-
-$$
-\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 + (1 - F_0)\alpha)  n \cdot \omega_i d\omega_i
-$$
-
-$$
-\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 + 1*\alpha - F_0*\alpha)  n \cdot \omega_i d\omega_i
-$$
-
-$$
-\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 * (1 - \alpha) + \alpha)  n \cdot \omega_i d\omega_i
-$$
-
-然后我们将菲涅耳函数 \(F\) 分拆到两个积分里：
-
-$$
-\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 * (1 - \alpha))  n \cdot \omega_i d\omega_i
-              +
-	\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (\alpha)  n \cdot \omega_i d\omega_i
-$$
-
-这样，\(F_0\)在整个积分上是恒定的，我们可以从积分中提取出\(F_0\)。接下来，我们将\(\alpha\)替换回其原始形式，从而得到最终分割求和的 BRDF 方程：
-
-$$
-F_0 \int\limits_{\Omega} f_r(p, \omega_i, \omega_o)(1 - {(1 - \omega_o \cdot h)}^5)  n \cdot \omega_i d\omega_i
-              +
-	\int\limits_{\Omega} f_r(p, \omega_i, \omega_o) {(1 - \omega_o \cdot h)}^5  n \cdot \omega_i d\omega_i
-$$
-
-公式中的两个积分分别表示 \(F_0\) 的比例和偏差。注意，由于 \(f(p, \omega_i, \omega_o)\) 已经包含 \(F\) 项，它们被约分了，这里的 \(f\) 中不计算 \(F\) 项。
-
-和之前卷积环境贴图类似，我们可以对 BRDF 方程求卷积，其输入是 \(n\) 和 \(\omega_o\) 的夹角，以及粗糙度，并将卷积的结果存储在纹理中。我们将卷积后的结果存储在 2D 查找纹理（Look Up Texture, LUT）中，这张纹理被称为 <def>BRDF 积分贴图</def>，稍后会将其用于 PBR 光照着色器中，以获得间接镜面反射的最终卷积结果。
-
-BRDF 卷积着色器在 2D 平面上执行计算，直接使用其 2D 纹理坐标作为卷积输入（<var>NdotV</var> 和 <var>roughness</var>）。代码与预滤波器的卷积代码大体相似，不同之处在于，它现在根据 BRDF 的几何函数和 Fresnel-Schlick 近似来处理采样向量：
-
-```c++
-vec2 IntegrateBRDF(float NdotV, float roughness)
-{
-    vec3 V;
-    V.x = sqrt(1.0 - NdotV*NdotV);
-    V.y = 0.0;
-    V.z = NdotV;
-
-    float A = 0.0;
-    float B = 0.0;
-
-    vec3 N = vec3(0.0, 0.0, 1.0);
-
-    const uint SAMPLE_COUNT = 1024u;
-    for(uint i = 0u; i < SAMPLE_COUNT; ++i)
-    {
-        vec2 Xi = Hammersley(i, SAMPLE_COUNT);
-        vec3 H  = ImportanceSampleGGX(Xi, N, roughness);
-        vec3 L  = normalize(2.0 * dot(V, H) * H - V);
-
-        float NdotL = max(L.z, 0.0);
-        float NdotH = max(H.z, 0.0);
-        float VdotH = max(dot(V, H), 0.0);
-
-        if(NdotL > 0.0)
-        {
-            float G = GeometrySmith(N, V, L, roughness);
-            float G_Vis = (G * VdotH) / (NdotH * NdotV);
-            float Fc = pow(1.0 - VdotH, 5.0);
-
-            A += (1.0 - Fc) * G_Vis;
-            B += Fc * G_Vis;
-        }
-    }
-    A /= float(SAMPLE_COUNT);
-    B /= float(SAMPLE_COUNT);
-    return vec2(A, B);
-}
-// ----------------------------------------------------------------------------
-void main() 
-{
-    vec2 integratedBRDF = IntegrateBRDF(TexCoords.x, TexCoords.y);
-    FragColor = integratedBRDF;
-}
-```
-
-如你所见，BRDF 卷积部分是从数学到代码的直接转换。我们将角度 \(\theta\) 和粗糙度作为输入，以重要性采样产生采样向量，在整个几何体上结合 BRDF 的菲涅耳项对向量进行处理，然后输出每个样本上 \(F_0\) 的系数和偏差，最后取平均值。
-
-你可能回想起[理论](https://learnopengl-cn.github.io/07%20PBR/01%20Theory/)教程中的一个细节：与 IBL 一起使用时，BRDF 的几何项略有不同，因为 \(k\) 变量的含义稍有不同：
-
-$$
-k_{direct} = \frac{(\alpha + 1)^2}{8}
-$$
-
-$$
-k_{IBL} = \frac{\alpha^2}{2}
-$$
-
-由于 BRDF 卷积是镜面 IBL 积分的一部分，因此我们要在 Schlick-GGX 几何函数中使用 \(k_{IBL}\)：
-
-```c++
-float GeometrySchlickGGX(float NdotV, float roughness)
-{
-    float a = roughness;
-    float k = (a * a) / 2.0;
-
-    float nom   = NdotV;
-    float denom = NdotV * (1.0 - k) + k;
-
-    return nom / denom;
-}
-// ----------------------------------------------------------------------------
-float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
-{
-    float NdotV = max(dot(N, V), 0.0);
-    float NdotL = max(dot(N, L), 0.0);
-    float ggx2 = GeometrySchlickGGX(NdotV, roughness);
-    float ggx1 = GeometrySchlickGGX(NdotL, roughness);
-
-    return ggx1 * ggx2;
-}  
-```
-
-请注意，虽然 \(k\) 还是从 a 计算出来的，但这里的 a 不是 <var>roughness</var> 的平方——如同最初对 a 的其他解释那样——在这里我们假装平方过了。我不确定这样处理是否与 Epic Games 或迪士尼原始论文不一致，但是直接将 <var>roughness</var> 赋给 a 得到的 BRDF 积分贴图与 Epic Games 的版本完全一致。
-
-最后，为了存储 BRDF 卷积结果，我们需要生成一张 512 × 512 分辨率的 2D 纹理。
-
-```c++
-unsigned int brdfLUTTexture;
-glGenTextures(1, &brdfLUTTexture);
-
-// pre-allocate enough memory for the LUT texture.
-glBindTexture(GL_TEXTURE_2D, brdfLUTTexture);
-glTexImage2D(GL_TEXTURE_2D, 0, GL_RG16F, 512, 512, 0, GL_RG, GL_FLOAT, 0);
-glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
-glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
-glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
-glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
-```
-
-请注意，我们使用的是 Epic Games 推荐的16位精度浮点格式。将环绕模式设置为 <var>GL_CLAMP_TO_EDGE</var> 以防止边缘采样的伪像。
-然后，我们复用同一个帧缓冲区对象，并在 NDC (译注：Normalized Device Coordinates) 屏幕空间四边形上运行此着色器：
-
-```c++
-glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
-glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
-glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 512, 512);
-glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, brdfLUTTexture, 0);
-
-glViewport(0, 0, 512, 512);
-brdfShader.use();
-glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
-RenderQuad();
-
-glBindFramebuffer(GL_FRAMEBUFFER, 0);  
-```
-
-分割积分和的 BRDF 卷积部分应该得到以下结果：
-
-![](../../img/07/03/02/ibl_brdf_lut.png)
-
-预过滤的环境贴图和 BRDF 的 2D LUT 都已经齐备，我们可以根据分割求和近似法重建间接镜面部分积分了。最后合并的结果将被用作间接镜面反射或环境镜面反射。
-
-## 完成 IBL 反射
-
-为了使反射方程的间接镜面反射部分正确运行，我们需要将分割求和近似法的两个部分缝合在一起。第一步是将预计算的光照数据声明到 PBR 着色器的最上面：
-
-```c++
-uniform samplerCube prefilterMap;
-uniform sampler2D   brdfLUT;  
-```
-
-首先，使用反射向量采样预过滤的环境贴图，获取表面的间接镜面反射。请注意，我们会根据表面粗糙度在合适的 mip 级别采样，以使更粗糙的表面产生更模糊的镜面反射。
-
-```c++
-void main()
-{
-    [...]
-    vec3 R = reflect(-V, N);   
-
-    const float MAX_REFLECTION_LOD = 4.0;
-    vec3 prefilteredColor = textureLod(prefilterMap, R,  roughness * MAX_REFLECTION_LOD).rgb;    
-    [...]
-}
-```
-
-在预过滤步骤中，我们仅将环境贴图卷积最多 5 个 mip 级别（0到4），此处记为 <var>MAX_REFLECTION_LOD</var>，以确保不会对一个没有数据的 mip 级别采样。
-然后我们用已知的材质粗糙度和视线-法线夹角作为输入，采样 BRDF LUT。
-
-```c++
-vec3 F        = FresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness);
-vec2 envBRDF  = texture(brdfLUT, vec2(max(dot(N, V), 0.0), roughness)).rg;
-vec3 specular = prefilteredColor * (F * envBRDF.x + envBRDF.y);
-```
-
-这样我们就从 BRDF LUT 中获得了 \(F_0\) 的系数和偏移，这里我们就直接用间接光菲涅尔项 <var>F</var> 代替\(F_0\)。把这个结果和 IBL 反射方程左边的预过滤部分结合起来，以重建整个近似积分，存入<var>specular</var>。
-
-于是我们得到了反射方程的间接镜面反射部分。现在，将其与[上一节教程](https://learnopengl-cn.github.io/07%20PBR/03%20IBL/01%20Diffuse%20irradiance/)中的反射方程的漫反射部分结合起来，我们可以获得完整的 PBR IBL 结果：
-
-```c++
-vec3 F = FresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness);
-
-vec3 kS = F;
-vec3 kD = 1.0 - kS;
-kD *= 1.0 - metallic;	  
-  
-vec3 irradiance = texture(irradianceMap, N).rgb;
-vec3 diffuse    = irradiance * albedo;
-  
-const float MAX_REFLECTION_LOD = 4.0;
-vec3 prefilteredColor = textureLod(prefilterMap, R,  roughness * MAX_REFLECTION_LOD).rgb;   
-vec2 envBRDF  = texture(brdfLUT, vec2(max(dot(N, V), 0.0), roughness)).rg;
-vec3 specular = prefilteredColor * (F * envBRDF.x + envBRDF.y);
-  
-vec3 ambient = (kD * diffuse + specular) * ao; 
-```
-
-请注意，<var>specular</var> 没有乘以 <var>kS</var>，因为已经乘过了菲涅耳系数。
-现在，在一系列粗糙度和金属度各异的球上运行此代码，我们终于可以在最终的 PBR 渲染器中看到其真实颜色：
-
-![](../../img/07/03/02/ibl_specular_result.png)
-
-我们甚至可以再疯狂一点，使用一些带酷炫纹理的 [PBR 材质](http://freepbr.com/)：
-
-![](../../img/07/03/02/ibl_specular_result_textured.png)
-
-或加载 Andrew Maximov 的[这款出色的免费 PBR 3D 模型](http://artisaverb.info/PBT.html)：
-
-![](../../img/07/03/02/ibl_specular_result_model.png)
-
-我敢肯定我们都同意现在的光照看起来更具说服力。更妙的是，无论我们使用哪种环境贴图，我们的光照看起来都是物理正确的。下面，您将看到几张不同的预计算 HDR 贴图，它们完全改变了光照动态，但是不需要调整任何光照变量，在外观上依然正确！
-
-![](../../img/07/03/02/ibl_specular_result_different_environments.png)
-
-好吧，这是一场长长的 PBR 冒险。有很多步骤可能会出错，所以如果遇到问题卡住，请仔细研究[球形场景](https://learnopengl.com/code_viewer_gh.php?code=src/6.pbr/2.2.1.ibl_specular/ibl_specular.cpp)或[带纹理的场景代码](https://learnopengl.com/code_viewer_gh.php?code=src/6.pbr/2.2.2.ibl_specular_textured/ibl_specular_textured.cpp)示例——也包括所有着色器，或者检查之后在评论中提问。
-
-### 下一步是？
-
-希望在本教程结束时，你会对 PBR 的相关内容有一个清晰的了解，甚至可以构造并运行一个实际的 PBR 渲染器。在这几节教程中，我们已经在应用程序开始阶段，渲染循环之前，预计算了所有 PBR 相关的基于图像的光照数据。出于教育目的，这很好，但对于任何 PBR 的实践应用来说，都不是很漂亮。首先，预计算实际上只需要执行一次，而不是每次启动时都要做。其次，当使用多个环境贴图时，你必须在每次程序启动时全部预计算一遍，这是个必须步骤。
-
-因此，通常只需要一次将环境贴图预计算为辐照度贴图和预过滤贴图，然后将其存储在磁盘上（注意，BRDF 积分贴图不依赖于环境贴图，因此只需要计算或加载一次）。这意味着您需要提出一种自定义图像格式来存储 HDR 立方体贴图，包括其 mip 级别。或者将图像存储为某种可用格式——例如支持存储 mip 级别的 .dds——并按其格式加载。
-
-此外，我们也在教程中描述了**整个**过程，包括生成预计算的 IBL 图像，以帮助我们进一步了解 PBR 管线。此外还可以通过 [cmftStudio](https://github.com/dariomanesku/cmftStudio) 或 [IBLBaker](https://github.com/derkreature/IBLBaker) 等一些出色的工具为您生成这些预计算贴图，也很好用。
-
-有一点内容我们跳过了，即如何将预计算的立方体贴图作为<def>反射探针</def>：立方体贴图插值和视差校正。这是一个在场景中放置多个反射探针的过程，这些探针在特定位置拍摄场景的立方体贴图快照，然后我们可以将其卷积，作为相应部分场景的 IBL 数据。基于相机的位置对附近的探针插值，我们可以实现局部的细节丰富的 IBL，受到的唯一限制就是探针放置的数量。这样一来，例如从一个明亮的室外部分移动到较暗的室内部分时，IBL 就能正确更新。我将来会在某个地方编写有关反射探针的教程，但现在，我建议阅读下面 Chetan Jags 的文章来作为入门。
-
-## 进阶阅读
-
- * [Real Shading in Unreal Engine 4](http://blog.selfshadow.com/publications/s2013-shading-course/karis/s2013_pbs_epic_notes_v2.pdf)：讲解了 Epic Games 的分割求和近似法。IBL PBR 部分的代码就脱胎于此文。
- * [Physically Based Shading and Image Based Lighting](http://www.trentreed.net/blog/physically-based-shading-and-image-based-lighting/)：Trent Reed 的精彩博客文章，介绍了如何将镜面反射 IBL 实时集成到 PBR 管道中。
- * [Image Based Lighting](https://chetanjags.wordpress.com/2015/08/26/image-based-lighting/)：Chetan Jags 对基于镜面反射的 IBL 及其一些注意事项（包括光照探针插值）进行了广泛的讲解。
- * [Moving Frostbite to PBR](https://seblagarde.files.wordpress.com/2015/07/course_notes_moving_frostbite_to_pbr_v32.pdf)：Sébastien Lagarde 和 Charles de Rousiers 撰写的，对于如何将 PBR 集成到 AAA 游戏引擎进行了详尽而深入的概述。
- * [Physically Based Rendering – Part Three](https://jmonkeyengine.github.io/wiki/jme3/advanced/pbr_part3.html)：JMonkeyEngine 团队对 IBL 和 PBR 进行了较高层次的概述。
- * [Implementation Notes: Runtime Environment Map Filtering for Image Based Lighting](https://placeholderart.wordpress.com/2015/07/28/implementation-notes-runtime-environment-map-filtering-for-image-based-lighting/)：Padraic Hennessy 撰写的大量有关预过滤 HDR 环境贴图并显著优化采样过程的文章。
-
-

docs/08 Guest Articles/2020/01 Skeletal Animation.md

@@ -1,780 +0,0 @@
-# 骨骼动画
-
-原文     | [Skeletal-Animation](https://learnopengl.com/Guest-Articles/2020/Skeletal-Animation)
-      ---|---
-作者     | Ankit Singh Kushwah
-翻译     | [orbitgw](https://github.com/orbitgw/)
-校对     | [orbitgw](https://github.com/orbitgw/)
-
-3D动画可以让我们的游戏栩栩如生。3D世界中的物体，比如人类和动物，当它们做某些事情移动四肢时，比如走路、跑步和攻击，会使我们感到更生动。本篇教程是关于你们一直在等待的骨骼动画。我们将首先彻底理解这个概念，然后了解使用Assimp制作3D模型动画所需的数据。我建议您完成本教程的[模型加载](../03/01%20Assimp.md)部分，因为本教程代码将从那里继续。你仍然可以理解这个概念，并以自己的方式实现它。所以让我们开始吧。
-
-## 插值
-要了解动画是如何工作的基础，我们需要了解插值(Interpolation)的概念。插值可以定义为随着时间的推移而发生的事情。就像敌人在时间T上从A点移动到B点一样，即随着时间的推移发生平移。炮塔平滑旋转以面对目标，即随着时间的推移发生旋转，树在时间T内从尺寸A放大到尺寸B，即随时间推移发生缩放。
-
-!!! note "译注"
-    (动画)插值就是**关键帧**的中间值。比如我们使用Blender制作动画，不需要设置每一帧的骨骼位置，只需要在几个关键帧中记录它们的位置，旋转，缩放等等信息。然后由程序自动计算出的中间的过渡帧就是我们的插值。通常插值可以使用曲线描述，比如我们的贝塞尔曲线。
-
-用于平移和缩放的简单插值方程如下所示：
-
-$$
-a = a \cdot (1 - t) + b \cdot t
-$$
-
-它被称为线性插值方程或Lerp。对于旋转，我们不能使用向量。原因是，如果我们继续尝试在X（俯仰）、Y（偏航）和Z（滚转）的向量上使用线性插值方程，插值就不会是线性的。你会遇到一些奇怪的问题，比如Gimbal Lock（请参阅下面的参考资料部分了解它）。为了避免这个问题，我们使用四元数进行旋转。四元数提供了一种叫做球面插值或Slerp方程的东西，它给出了与Lerp相同的结果，但对于两个旋转A和B。我无法解释这个方程是如何工作的，因为它目前不在范围内。您可以查看下面的参考资料部分来理解四元数。
-
-
-## 动画模型的组件：蒙皮、骨骼和关键帧
-
-动画的整个过程始于添加第一个组件，即blender或Maya等软件中的蒙皮(Skin)。蒙皮只不过是网格(Mesh)，它为模型添加了视觉方面，告诉观察者它的外观。但是，如果你想移动任何网格，那么就像现实世界一样，你需要添加骨骼。你可以看到下面的图片来了解它在blender等软件中的外观。
-
-![skin](../../../img/08/01/skin.png)
-![bones](../../../img/08/01/bones.png)
-![skin and bones](../../../img/08/01/merged.png)
-
-这些骨头通常是以分层的方式添加给人类和动物等角色的，原因很明显。我们想要四肢之间的父子关系(parent-child relationship)。例如，如果我们移动右肩，那么我们的右二头肌、前臂、手和手指也应该移动。这就是层次结构的样子：
-
-![parent_child](../../../img/08/01/parent_child.png)
-
-在上图中，如果你抓住髋骨(hip bone)并移动它，所有的肢体都会受到它的移动的影响。
-
-此时，我们已经准备好为动画创建关键帧了。关键帧是动画中不同时间点的姿势。我们将在这些关键帧之间进行插值，以便在代码中从一个姿势平滑地过渡到另一个姿势。下面您可以看到如何为简单的4帧跳跃动画创建姿势：
-
-![poses](../../../img/08/01/poses.gif)
-![interpolating](../../../img/08/01/interpolating.gif)
-
-
-## Assimp如何保存动画数据
-我们马上就会到代码部分，但首先我们需要了解assimp是如何保存导入的动画数据的。看下图：
-
-![assimp1](../../../img/08/01/assimp1.jpeg)
-
-
-就像[模型加载](../03/01%20Assimp.md)部分一样，我们将从`aiScene`指针开始，该指针包含指向根节点的指针，然后看看我们这里有什么，一个动画数组。这个`aiAnimation`数组包含一般信息，比如动画的持续时间，这里表示为`mDuration`，然后我们有一个`mTicksPerSecond`变量，它控制我们应该在帧之间插值的速度。如果您还记得上一节中的动画有关键帧。类似地，`aiAnimation`包含一个名为`Channels`的`aiNodeAnim`数组。此数组包含将要参与动画的所有骨骼及其关键帧。一个`aiNodeAnim`包含骨骼的名称，你会发现在这里插入三种类型的关键点，平移、旋转和缩放。
-
-好吧，还有最后一件事我们需要理解，并且很乐意去做的一件事就是写代码。
-
- 
-
-## 多个骨骼对顶点的影响
-
-当我们弯曲前臂时，我们会看到我们的二头肌弹出。我们也可以说前臂骨骼的变形正在影响我们肱二头肌上的顶点。类似地，可能有多个骨骼影响网格中的单个顶点。对于像固体金属机器人这样的角色，所有前臂顶点都只会受到前臂骨骼的影响，但对于像人类、动物等角色，可能有多达4块骨骼可以影响一个顶点。让我们看看assimp是如何存储这些信息的：
-
-![assimp2](../../../img/08/01/assimp2.jpeg)
- 
-我们再次从`aiScene`指针开始，该指针包含所有`aiMeshes`的数组。每个aiMesh对象都有一个`aiBone`数组，其中包含诸如此`aiBone`将对网格上的顶点集产生多大影响之类的信息。`aiBone`包含骨骼的名称，这是一个`aiVertexWeight`数组，基本上告诉此`aiBone`对网格上的顶点有多大影响。现在我们有了`aiBone`的另一个成员，它是`offsetMatrix`。这是一个4x4矩阵，用于将顶点从模型空间转换到骨骼空间。你可以在下面的图片中看到这一点：
-
-![mesh_space](../../../img/08/01/mesh_space.png)
-![bone_space](../../../img/08/01/bone_space.png)
-
-当顶点位于骨骼空间中时，它们将按照预期相对于骨骼进行变换。您很快就会在代码中看到这一点。
-
-## 最后让我们写代码
-谢谢你走到这一步。我们将从直接查看最终结果开始，这是我们的最终顶点着色器代码。这将给我们很好的感觉，我们最终需要什么。
-
-```c++
-#version 430 core
-
-layout(location = 0) in vec3 pos;
-layout(location = 1) in vec3 norm;
-layout(location = 2) in vec2 tex;
-layout(location = 5) in ivec4 boneIds; 
-layout(location = 6) in vec4 weights;
-	
-uniform mat4 projection;
-uniform mat4 view;
-uniform mat4 model;
-	
-const int MAX_BONES = 100;
-const int MAX_BONE_INFLUENCE = 4;
-uniform mat4 finalBonesMatrices[MAX_BONES];
-	
-out vec2 TexCoords;
-	
-void main()
-{
-    vec4 totalPosition = vec4(0.0f);
-    for(int i = 0 ; i < MAX_BONE_INFLUENCE ; i++)
-    {
-        if(boneIds[i] == -1) 
-            continue;
-        if(boneIds[i] >=MAX_BONES) 
-        {
-            totalPosition = vec4(pos,1.0f);
-            break;
-        }
-        vec4 localPosition = finalBonesMatrices[boneIds[i]] * vec4(pos,1.0f);
-        totalPosition += localPosition * weights[i];
-        vec3 localNormal = mat3(finalBonesMatrices[boneIds[i]]) * norm;
-    }
-		
-    mat4 viewModel = view * model;
-    gl_Position =  projection * viewModel * totalPosition;
-    TexCoords = tex;
-}
-```
-
-
-片段着色器与[这篇教程](../03/03%20Model.md)中的保持相同。从顶部开始，您可以看到两个新的属性布局声明。第一个骨骼ID，第二个是重量。我们还有一个统一的数组`finalBonesMatrix`，它存储所有骨骼的变换。`boneIds`包含用于读取最终`BonesMatrix`数组并将这些变换应用于pos顶点的索引，其各自的权重存储在权重数组中。这发生在上面循环的内部。现在，让我们先在Mesh类中添加对骨骼重量的支持：
-
-
-```c++
-#define MAX_BONE_INFLUENCE 4
-
-struct Vertex {
-    // position
-    glm::vec3 Position;
-    // normal
-    glm::vec3 Normal;
-    // texCoords
-    glm::vec2 TexCoords;
-	
-    // tangent
-    glm::vec3 Tangent;
-    // bitangent
-    glm::vec3 Bitangent;
-
-    //bone indexes which will influence this vertex
-    int m_BoneIDs[MAX_BONE_INFLUENCE];
-    //weights from each bone
-    float m_Weights[MAX_BONE_INFLUENCE];
-  
-};
-```
-我们为顶点添加了两个新属性，就像我们在顶点着色器中看到的那样。现在，让我们将它们加载到GPU缓冲区中，就像我们的`Mesh::setupMesh`函数中的其他属性一样：
-```c++
-class Mesh
-{
-    ...
-    
-    void setupMesh()
-    {
-        ....
-        
-        // ids
-        glEnableVertexAttribArray(3);
-        glVertexAttribIPointer(3, 4, GL_INT, sizeof(Vertex), (void*)offsetof(Vertex, m_BoneIDs));
-
-        // weights
-        glEnableVertexAttribArray(4);
-        glVertexAttribPointer(4, 4, GL_FLOAT, GL_FALSE, sizeof(Vertex), 
-            (void*)offsetof(Vertex, m_Weights));   
-  
-        ...
-    }    
-    ...
-}
-```
-就像以前一样，只是现在我们为`boneID`和`weights`添加了3个和4个布局位置ID。这里需要注意的一件重要的事情是我们如何传递`boneID`的数据。我们使用的是`glVertexAttribIPointer`，并将`GL_INT`作为第三个参数传递。
-
-现在我们可以从assimp数据结构中提取骨骼重量信息。让我们在Model类中进行一些更改：
-```c++
-struct BoneInfo
-{
-    /*id is index in finalBoneMatrices*/
-    int id;
-
-    /*offset matrix transforms vertex from model space to bone space*/
-    glm::mat4 offset;
-
-};
-```
-此`BoneInfo`将存储我们的偏移矩阵，以及一个唯一的id，该id将用作索引，将其存储在我们之前在着色器中看到的最终`BoneMatrices`数组中。现在我们将在Model中添加骨量提取支持：
-
-```c++
-class Model 
-{
-private:
-    ...
-    std::map<string, BoneInfo> m_BoneInfoMap; //
-    int m_BoneCounter = 0;
-
-    auto& GetBoneInfoMap() { return m_BoneInfoMap; }
-    int& GetBoneCount() { return m_BoneCounter; }    
-    ...
-    void SetVertexBoneDataToDefault(Vertex& vertex)
-    {
-        for (int i = 0; i < MAX_BONE_WEIGHTS; i++)
-        {
-            vertex.m_BoneIDs[i] = -1;
-            vertex.m_Weights[i] = 0.0f;
-        }
-    }
-
-    Mesh processMesh(aiMesh* mesh, const aiScene* scene)
-    {
-        vector vertices;
-        vector indices;
-        vector textures;
-
-        for (unsigned int i = 0; i < mesh->mNumVertices; i++)
-        {
-            Vertex vertex;
-
-            SetVertexBoneDataToDefault(vertex);
-
-            vertex.Position = AssimpGLMHelpers::GetGLMVec(mesh->mVertices[i]);
-            vertex.Normal = AssimpGLMHelpers::GetGLMVec(mesh->mNormals[i]);
-			
-            if (mesh->mTextureCoords[0])
-            {
-                glm::vec2 vec;
-                vec.x = mesh->mTextureCoords[0][i].x;
-                vec.y = mesh->mTextureCoords[0][i].y;
-                vertex.TexCoords = vec;
-            }
-            else
-                vertex.TexCoords = glm::vec2(0.0f, 0.0f);
-
-            vertices.push_back(vertex);
-        }
-        ...
-        ExtractBoneWeightForVertices(vertices,mesh,scene);
-
-        return Mesh(vertices, indices, textures);
-    }
-
-    void SetVertexBoneData(Vertex& vertex, int boneID, float weight)
-    {
-        for (int i = 0; i < MAX_BONE_WEIGHTS; ++i)
-        {
-            if (vertex.m_BoneIDs[i] < 0)
-            {
-                vertex.m_Weights[i] = weight;
-                vertex.m_BoneIDs[i] = boneID;
-                break;
-            }
-        }
-    }
-
-    void ExtractBoneWeightForVertices(std::vector& vertices, aiMesh* mesh, const aiScene* scene)
-    {
-        for (int boneIndex = 0; boneIndex < mesh->mNumBones; ++boneIndex)
-        {
-            int boneID = -1;
-            std::string boneName = mesh->mBones[boneIndex]->mName.C_Str();
-            if (m_BoneInfoMap.find(boneName) == m_BoneInfoMap.end())
-            {
-                BoneInfo newBoneInfo;
-                newBoneInfo.id = m_BoneCounter;
-                newBoneInfo.offset = AssimpGLMHelpers::ConvertMatrixToGLMFormat(
-                    mesh->mBones[boneIndex]->mOffsetMatrix);
-                m_BoneInfoMap[boneName] = newBoneInfo;
-                boneID = m_BoneCounter;
-                m_BoneCounter++;
-            }
-            else
-            {
-                boneID = m_BoneInfoMap[boneName].id;
-            }
-            assert(boneID != -1);
-            auto weights = mesh->mBones[boneIndex]->mWeights;
-            int numWeights = mesh->mBones[boneIndex]->mNumWeights;
-
-            for (int weightIndex = 0; weightIndex < numWeights; ++weightIndex)
-            {
-                int vertexId = weights[weightIndex].mVertexId;
-                float weight = weights[weightIndex].mWeight;
-                assert(vertexId <= vertices.size());
-                SetVertexBoneData(vertices[vertexId], boneID, weight);
-            }
-        }
-    }
-    ...
-};
-```
-我们首先声明一个映射`m_BoneInfoMap`和一个计数器`m_BoneCounter`，一旦我们读取到一个新的骨骼，它就会增加。我们在前面的图表中看到，每个`aiMesh`都包含与`aiMesh`关联的所有`aiBone`。骨量提取的整个过程都是从`processMesh`函数开始的。对于每个循环迭代，我们通过调用函数`SetVertexBoneDataToDefault`将`m_BoneID`和`m_Weights`设置为其默认值。就在`processMesh`函数结束之前，我们调用`ExtractBoneWeightData`。在`ExtractBoneWeightData`中，我们为每个aiBone运行for循环，并检查该骨骼是否已存在于`m_BoneInfoMap`中。如果我们找不到它，那么它被认为是一块新骨头，我们创建一个带有id的新`BoneInfo`，并将其关联的`mOffsetMatrix`存储到它。然后我们将这个新`BoneIInfo`存储在`m_BoneInfoMap`中，然后我们递增`m_BoneCounter`计数器，为下一块骨头创建一个id。如果我们在`m_BoneInfoMap`中找到骨骼名称，那么这意味着该骨骼会影响超出其范围的网格顶点。所以我们取它的Id，进一步了解它会影响哪些顶点。
-
-需要注意的一点是，我们正在调用`AssimpGLMHelpers::ConvertMatrixToGLMFormat`。Assimp以与GLM不同的格式存储其矩阵数据，因此此函数仅为我们提供GLM格式的矩阵。
-
-我们已经提取了骨骼的`offsetMatrix`，现在我们将简单地迭代其`aiVertexWeightarray`，提取将受此骨骼影响的所有顶点索引及其各自的权重，并调用`SetVertexBoneData`以使用提取的信息填充`Vertex.boneIds`和`Vertex.weights`。
-
-呜！到这里你应当休息一下。
-
-## 骨骼、动画和动画制作类
-这是类的视图：
-
-![bird_eye_view](../../../img/08/01/bird_eye_view.png)
-
-
-让我们提醒自己我们正在努力实现什么。对于每个渲染帧，我们希望平滑地插值继承中的所有骨骼，并获得它们的最终变换矩阵，这些矩阵将提供给着色器统一的finalBonesMatrix。以下是每个类的内容：
-
-**Bone** : 从aiNodeAnim读取所有关键帧数据的单个骨骼。它还将根据当前动画时间在关键帧之间进行插值，即平移、缩放和旋转。
-
-**AssimpNodeData** : 这个结构体将帮助我们将动画从Assimp提取出来。
-
-**Animation** : 从aiAnimation读取数据并创建Bones的继承记录的资源。
-
-**Animator** : 这将读取AssimpNodeData的继承方法，以递归方式插入所有骨骼，然后为我们准备所需的最终骨骼转换矩阵。
-
-这就是代码：
-```c++
-struct KeyPosition
-{
-    glm::vec3 position;
-    float timeStamp;
-};
-
-struct KeyRotation
-{
-    glm::quat orientation;
-    float timeStamp;
-};
-
-struct KeyScale
-{
-    glm::vec3 scale;
-    float timeStamp;
-};
-
-class Bone
-{
-private:
-    std::vector<KeyPosition> m_Positions;
-    std::vector<KeyRotation> m_Rotations;
-    std::vector<KeyScale> m_Scales;
-    int m_NumPositions;
-    int m_NumRotations;
-    int m_NumScalings;
-	
-    glm::mat4 m_LocalTransform;
-    std::string m_Name;
-    int m_ID;
-
-public:
-
-/*reads keyframes from aiNodeAnim*/
-    Bone(const std::string& name, int ID, const aiNodeAnim* channel)
-        :
-        m_Name(name),
-        m_ID(ID),
-        m_LocalTransform(1.0f)
-    {
-        m_NumPositions = channel->mNumPositionKeys;
-
-        for (int positionIndex = 0; positionIndex < m_NumPositions; ++positionIndex)
-        {
-            aiVector3D aiPosition = channel->mPositionKeys[positionIndex].mValue;
-            float timeStamp = channel->mPositionKeys[positionIndex].mTime;
-            KeyPosition data;
-            data.position = AssimpGLMHelpers::GetGLMVec(aiPosition);
-            data.timeStamp = timeStamp;
-            m_Positions.push_back(data);
-        }
-
-        m_NumRotations = channel->mNumRotationKeys;
-        for (int rotationIndex = 0; rotationIndex < m_NumRotations; ++rotationIndex)
-        {
-            aiQuaternion aiOrientation = channel->mRotationKeys[rotationIndex].mValue;
-            float timeStamp = channel->mRotationKeys[rotationIndex].mTime;
-            KeyRotation data;
-            data.orientation = AssimpGLMHelpers::GetGLMQuat(aiOrientation);
-            data.timeStamp = timeStamp;
-            m_Rotations.push_back(data);
-        }
-
-        m_NumScalings = channel->mNumScalingKeys;
-        for (int keyIndex = 0; keyIndex < m_NumScalings; ++keyIndex)
-        {
-            aiVector3D scale = channel->mScalingKeys[keyIndex].mValue;
-            float timeStamp = channel->mScalingKeys[keyIndex].mTime;
-            KeyScale data;
-            data.scale = AssimpGLMHelpers::GetGLMVec(scale);
-            data.timeStamp = timeStamp;
-            m_Scales.push_back(data);
-        }
-    }
-	
-    /*interpolates  b/w positions,rotations & scaling keys based on the curren time of 
-    the animation and prepares the local transformation matrix by combining all keys 
-    tranformations*/
-    void Update(float animationTime)
-    {
-        glm::mat4 translation = InterpolatePosition(animationTime);
-        glm::mat4 rotation = InterpolateRotation(animationTime);
-        glm::mat4 scale = InterpolateScaling(animationTime);
-        m_LocalTransform = translation * rotation * scale;
-    }
-
-    glm::mat4 GetLocalTransform() { return m_LocalTransform; }
-    std::string GetBoneName() const { return m_Name; }
-    int GetBoneID() { return m_ID; }
-	
-
-    /* Gets the current index on mKeyPositions to interpolate to based on 
-    the current animation time*/
-    int GetPositionIndex(float animationTime)
-    {
-        for (int index = 0; index < m_NumPositions - 1; ++index)
-        {
-            if (animationTime < m_Positions[index + 1].timeStamp)
-                return index;
-        }
-        assert(0);
-    }
-
-    /* Gets the current index on mKeyRotations to interpolate to based on the 
-    current animation time*/
-    int GetRotationIndex(float animationTime)
-    {
-        for (int index = 0; index < m_NumRotations - 1; ++index)
-        {
-            if (animationTime < m_Rotations[index + 1].timeStamp)
-                return index;
-        }
-        assert(0);
-    }
-
-    /* Gets the current index on mKeyScalings to interpolate to based on the 
-    current animation time */
-    int GetScaleIndex(float animationTime)
-    {
-        for (int index = 0; index < m_NumScalings - 1; ++index)
-        {
-            if (animationTime < m_Scales[index + 1].timeStamp)
-                return index;
-        }
-        assert(0);
-    }
-
-private:
-
-    /* Gets normalized value for Lerp & Slerp*/
-    float GetScaleFactor(float lastTimeStamp, float nextTimeStamp, float animationTime)
-    {
-        float scaleFactor = 0.0f;
-        float midWayLength = animationTime - lastTimeStamp;
-        float framesDiff = nextTimeStamp - lastTimeStamp;
-        scaleFactor = midWayLength / framesDiff;
-        return scaleFactor;
-    }
-
-    /*figures out which position keys to interpolate b/w and performs the interpolation 
-    and returns the translation matrix*/
-    glm::mat4 InterpolatePosition(float animationTime)
-    {
-        if (1 == m_NumPositions)
-            return glm::translate(glm::mat4(1.0f), m_Positions[0].position);
-
-        int p0Index = GetPositionIndex(animationTime);
-        int p1Index = p0Index + 1;
-        float scaleFactor = GetScaleFactor(m_Positions[p0Index].timeStamp,
-            m_Positions[p1Index].timeStamp, animationTime);
-        glm::vec3 finalPosition = glm::mix(m_Positions[p0Index].position,
-            m_Positions[p1Index].position, scaleFactor);
-        return glm::translate(glm::mat4(1.0f), finalPosition);
-    }
-
-    /*figures out which rotations keys to interpolate b/w and performs the interpolation 
-    and returns the rotation matrix*/
-    glm::mat4 InterpolateRotation(float animationTime)
-    {
-        if (1 == m_NumRotations)
-        {
-            auto rotation = glm::normalize(m_Rotations[0].orientation);
-            return glm::toMat4(rotation);
-        }
-
-        int p0Index = GetRotationIndex(animationTime);
-        int p1Index = p0Index + 1;
-        float scaleFactor = GetScaleFactor(m_Rotations[p0Index].timeStamp,
-            m_Rotations[p1Index].timeStamp, animationTime);
-        glm::quat finalRotation = glm::slerp(m_Rotations[p0Index].orientation,
-            m_Rotations[p1Index].orientation, scaleFactor);
-        finalRotation = glm::normalize(finalRotation);
-        return glm::toMat4(finalRotation);
-    }
-
-    /*figures out which scaling keys to interpolate b/w and performs the interpolation 
-    and returns the scale matrix*/
-    glm::mat4 Bone::InterpolateScaling(float animationTime)
-    {
-        if (1 == m_NumScalings)
-            return glm::scale(glm::mat4(1.0f), m_Scales[0].scale);
-
-        int p0Index = GetScaleIndex(animationTime);
-        int p1Index = p0Index + 1;
-        float scaleFactor = GetScaleFactor(m_Scales[p0Index].timeStamp,
-            m_Scales[p1Index].timeStamp, animationTime);
-        glm::vec3 finalScale = glm::mix(m_Scales[p0Index].scale, m_Scales[p1Index].scale
-            , scaleFactor);
-        return glm::scale(glm::mat4(1.0f), finalScale);
-    }
-	
-};
-```
-我们首先为我们的键类型创建3个结构。每个结构都有一个值和一个时间戳。时间戳告诉我们在动画的哪个点需要插值到它的值。Bone有一个构造函数，它从`aiNodeAnim`读取密钥并将密钥及其时间戳存储到`mPositionKeys`、`mRotationKeys`和`mScalingKeys`。主要插值过程从更新(float animationTime)开始，该过程在每帧调用一次。此函数调用所有键类型的相应插值函数，并组合所有最终插值结果，并将其存储到4x4矩阵`m_LocalTransform`中。平移和缩放关键点的插值函数相似，但对于旋转，我们使用Slerp在四元数之间进行插值。Lerp和Slerp都有3个论点。第一个参数取最后一个键，第二个参数取下一个键和第三个参数取范围为0-1的值，我们在这里称之为比例因子。让我们看看如何在函数`GetScaleFactor`中计算这个比例因子：
-
-![](../../../img/08/01/scale_factor.png)
-
-在代码中：
-
-**float midWayLength = animationTime - lastTimeStamp;**
-
-**float framesDiff = nextTimeStamp - lastTimeStamp;**
-
-**scaleFactor = midWayLength / framesDiff;**
-
-现在让我们继续转到**Animation**类：
-```c++
-struct AssimpNodeData
-{
-    glm::mat4 transformation;
-    std::string name;
-    int childrenCount;
-    std::vector<AssimpNodeData> children;
-};
-
-class Animation
-{
-public:
-    Animation() = default;
-
-    Animation(const std::string& animationPath, Model* model)
-    {
-        Assimp::Importer importer;
-        const aiScene* scene = importer.ReadFile(animationPath, aiProcess_Triangulate);
-        assert(scene && scene->mRootNode);
-        auto animation = scene->mAnimations[0];
-        m_Duration = animation->mDuration;
-        m_TicksPerSecond = animation->mTicksPerSecond;
-        ReadHeirarchyData(m_RootNode, scene->mRootNode);
-        ReadMissingBones(animation, *model);
-    }
-
-    ~Animation()
-    {
-    }
-
-    Bone* FindBone(const std::string& name)
-    {
-        auto iter = std::find_if(m_Bones.begin(), m_Bones.end(),
-            [&](const Bone& Bone)
-            {
-                return Bone.GetBoneName() == name;
-            }
-        );
-        if (iter == m_Bones.end()) return nullptr;
-        else return &(*iter);
-    }
-
-	
-    inline float GetTicksPerSecond() { return m_TicksPerSecond; }
-
-    inline float GetDuration() { return m_Duration;}
-
-    inline const AssimpNodeData& GetRootNode() { return m_RootNode; }
-
-    inline const std::map<std::string,BoneInfo>& GetBoneIDMap() 
-    { 
-        return m_BoneInfoMap;
-    }
-
-private:
-    void ReadMissingBones(const aiAnimation* animation, Model& model)
-    {
-        int size = animation->mNumChannels;
-
-        auto& boneInfoMap = model.GetBoneInfoMap();//getting m_BoneInfoMap from Model class
-        int& boneCount = model.GetBoneCount(); //getting the m_BoneCounter from Model class
-
-        //reading channels(bones engaged in an animation and their keyframes)
-        for (int i = 0; i < size; i++)
-        {
-            auto channel = animation->mChannels[i];
-            std::string boneName = channel->mNodeName.data;
-
-            if (boneInfoMap.find(boneName) == boneInfoMap.end())
-            {
-                boneInfoMap[boneName].id = boneCount;
-                boneCount++;
-            }
-            m_Bones.push_back(Bone(channel->mNodeName.data,
-                boneInfoMap[channel->mNodeName.data].id, channel));
-        }
-
-        m_BoneInfoMap = boneInfoMap;
-    }
-
-    void ReadHeirarchyData(AssimpNodeData& dest, const aiNode* src)
-    {
-        assert(src);
-
-        dest.name = src->mName.data;
-        dest.transformation = AssimpGLMHelpers::ConvertMatrixToGLMFormat(src->mTransformation);
-        dest.childrenCount = src->mNumChildren;
-
-        for (int i = 0; i < src->mNumChildren; i++)
-        {
-            AssimpNodeData newData;
-            ReadHeirarchyData(newData, src->mChildren[i]);
-            dest.children.push_back(newData);
-        }
-    }
-    float m_Duration;
-    int m_TicksPerSecond;
-    std::vector<Bone> m_Bones;
-    AssimpNodeData m_RootNode;
-    std::map<std::string, BoneInfo> m_BoneInfoMap;
-};
-```
-在这里，动画对象的创建从构造函数开始。这需要两个论点。首先，动画文件的路径&第二个参数是该动画的模型。稍后您将看到我们为什么需要此模型参考。然后，我们创建一个`Assimp::Importer`来读取动画文件，然后进行断言检查，如果找不到动画，该检查将引发错误。然后我们读取一般的动画数据，比如这个动画有多长，即`mDuration`和由`mTicksPerSecond`表示的动画速度。然后我们调用`ReadHeirarchyData`，它复制Assimp的`aiNode`继承权并创建`AssimpNodeData`的继承权。
-
-然后我们调用一个名为`ReadMissingBones`的函数。我不得不编写这个函数，因为有时当我单独加载FBX模型时，它缺少一些骨骼，而我在动画文件中找到了这些缺失的骨骼。此函数读取丢失的骨骼信息，并将其信息存储在模型的`m_BoneInfoMap`中，并在`m_BoneIInfoMap`中本地保存`m_BoneIinfoMap`的引用。
-
-我们已经准备好了动画。现在让我们看看我们的最后阶段，Animator类：
-
-```c++
-class Animator
-{	
-public:
-    Animator::Animator(Animation* Animation)
-    {
-        m_CurrentTime = 0.0;
-        m_CurrentAnimation = currentAnimation;
-
-        m_FinalBoneMatrices.reserve(100);
-
-        for (int i = 0; i < 100; i++)
-            m_FinalBoneMatrices.push_back(glm::mat4(1.0f));
-    }
-	
-    void Animator::UpdateAnimation(float dt)
-    {
-        m_DeltaTime = dt;
-        if (m_CurrentAnimation)
-        {
-            m_CurrentTime += m_CurrentAnimation->GetTicksPerSecond() * dt;
-            m_CurrentTime = fmod(m_CurrentTime, m_CurrentAnimation->GetDuration());
-            CalculateBoneTransform(&m_CurrentAnimation->GetRootNode(), glm::mat4(1.0f));
-        }
-    }
-	
-    void Animator::PlayAnimation(Animation* pAnimation)
-    {
-        m_CurrentAnimation = pAnimation;
-        m_CurrentTime = 0.0f;
-    }
-	
-    void Animator::CalculateBoneTransform(const AssimpNodeData* node, glm::mat4 parentTransform)
-    {
-        std::string nodeName = node->name;
-        glm::mat4 nodeTransform = node->transformation;
-	
-        Bone* Bone = m_CurrentAnimation->FindBone(nodeName);
-	
-        if (Bone)
-        {
-            Bone->Update(m_CurrentTime);
-            nodeTransform = Bone->GetLocalTransform();
-        }
-	
-        glm::mat4 globalTransformation = parentTransform * nodeTransform;
-	
-        auto boneInfoMap = m_CurrentAnimation->GetBoneIDMap();
-        if (boneInfoMap.find(nodeName) != boneInfoMap.end())
-        {
-            int index = boneInfoMap[nodeName].id;
-            glm::mat4 offset = boneInfoMap[nodeName].offset;
-            m_FinalBoneMatrices[index] = globalTransformation * offset;
-        }
-	
-        for (int i = 0; i < node->childrenCount; i++)
-            CalculateBoneTransform(&node->children[i], globalTransformation);
-    }
-	
-    std::vector<glm::mat4> GetFinalBoneMatrices() 
-    { 
-        return m_FinalBoneMatrices;  
-    }
-		
-private:
-    std::vector<glm::mat4> m_FinalBoneMatrices;
-    Animation* m_CurrentAnimation;
-    float m_CurrentTime;
-    float m_DeltaTime;	
-};
-```
-`Animator`构造函数将播放动画，然后继续将动画时间`m_CurrentTime`重置为0。它还初始化`m_FinalBoneMatrices`，这是一个`std::vector\<glm::mat4\>`。这里的主要注意点是`UpdateAnimation(float deltaTime)`函数。它以`m_TicksPerSecond`的速率推进`m_CurrentTime`，然后调用`CalculateBoneTransform`函数。我们将在开始时传递两个参数，第一个是`m_CurrentAnimation`的`m_RootNode`，第二个是作为`parentTransform`传递的身份矩阵。然后，通过在`animation`的`m_Bones`数组中查找`m_RootNodes`骨骼来检查该骨骼是否参与该动画。如果找到骨骼，则调用`bone.Update()`函数，该函数对所有骨骼进行插值，并将局部骨骼变换矩阵返回到`nodeTransform`。但这是局部空间矩阵，如果在着色器中传递，将围绕原点移动骨骼。因此，我们将这个`nodeTransform`与parentTransform相乘，并将结果存储在`globalTransformation`中。这就足够了，但顶点仍在默认模型空间中。我们在`m_BoneInfoMap`中找到偏移矩阵，然后将其与`globalTransfromMatrix`相乘。我们还将获得id索引，该索引将用于写入该骨骼到`m_FinalBoneMatrices`的最终转换。
-
-最后我们为该节点的每个子节点调用`CalculateBoneTransform`，并将`globalTransformation`作为`parentTransform`传递。当没有子节点需要进一步处理时，我们会跳出这个递归循环。
-
-## 让我们动起来
-我们辛勤工作的成果终于来了！以下是我们将如何在main.cpp中播放动画：
-```c++
-int main()
-{
-    ...
-	
-    Model ourModel(FileSystem::getPath("resources/objects/vampire/dancing_vampire.dae"));
-    Animation danceAnimation(FileSystem::getPath("resources/objects/vampire/dancing_vampire.dae"),
-        &ourModel);
-    Animator animator(&danceAnimation);
-
-    // draw in wireframe
-    //glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
-
-    // render loop
-    // -----------
-    while (!glfwWindowShouldClose(window))
-    {
-        // per-frame time logic
-        // --------------------
-        float currentFrame = glfwGetTime();
-        deltaTime = currentFrame - lastFrame;
-        lastFrame = currentFrame;
-
-        // input
-        // -----
-        processInput(window);
-        animator.UpdateAnimation(deltaTime);
-		
-        // render
-        // ------
-        glClearColor(0.05f, 0.05f, 0.05f, 1.0f);
-        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
-
-        // don't forget to enable shader before setting uniforms
-        ourShader.use();
-
-        // view/projection transformations
-        glm::mat4 projection = glm::perspective(glm::radians(camera.Zoom), 
-            (float)SCR_WIDTH / (float)SCR_HEIGHT, 0.1f, 100.0f);
-        glm::mat4 view = camera.GetViewMatrix();
-        ourShader.setMat4("projection", projection);
-        ourShader.setMat4("view", view);
-
-        auto transforms = animator.GetFinalBoneMatrices();
-        for (int i = 0; i < transforms.size(); ++i)
-            ourShader.setMat4("finalBonesMatrices[" + std::to_string(i) + "]", transforms[i]);
-
-        // render the loaded model
-        glm::mat4 model = glm::mat4(1.0f);
-        // translate it down so it's at the center of the scene
-        model = glm::translate(model, glm::vec3(0.0f, -0.4f, 0.0f)); 
-        // it's a bit too big for our scene, so scale it down
-        model = glm::scale(model, glm::vec3(.5f, .5f, .5f));	
-        ourShader.setMat4("model", model);
-        ourModel.Draw(ourShader);
-
-        // glfw: swap buffers and poll IO events (keys pressed/released, mouse moved etc.)
-        // -------------------------------------------------------------------------------
-        glfwSwapBuffers(window);
-        glfwPollEvents();
-    }
-
-    // glfw: terminate, clearing all previously allocated GLFW resources.
-    // ------------------------------------------------------------------
-    glfwTerminate();
-    return 0;
-```
-我们从加载模型开始，该模型将为着色器设置骨骼重量数据，然后通过为其提供路径来创建动画。然后，我们通过将创建的`Animation`传递给它来创建`Animator`对象。在渲染循环中，我们更新`Animator`，进行最终的骨骼变换并将其提供给着色器。这是我们一直在等待的输出:
-
-![output](../../../img/08/01/output.gif)
-
-从[此处](https://learnopengl.com/Model-Loading/Assimp)下载使用的模型。请注意，动画和网格是在单个DAE(collada)文件中烘焙的。你可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/8.guest/2020/skeletal_animation/skeletal_animation.cpp)找到这个演示的完整源代码。
-
-## 延伸阅读
-[Quaternions](http://www.songho.ca/math/quaternion/quaternion.html): An article by songho to understand quaternions in depth.
-[Skeletal Animation with Assimp](http://ogldev.atspace.co.uk/www/tutorial38/tutorial38.html): An article by OGL Dev.
-[Skeletal Animation with Java](https://youtu.be/f3Cr8Yx3GGA): A fantastic youtube playlist by Thin Matrix.
-[Why Quaternions should be used for Rotation](https://www.gamasutra.com/view/feature/131686/rotating_objects_using_quaternions.php): An awesome gamasutra article.

docs/08 Guest Articles/2022/03 Area Lights.md

@@ -1,475 +0,0 @@
-# 区域光
-
- 原文 | [Area Lights](https://learnopengl.com/Guest-Articles/2022/Area-Lights) 
- ---- | ------------------------------------------------------------ 
- 作者 | [Alexander Christensen](https://www.linkedin.com/in/alexanderchr/) 
- 翻译 | [XDzZyq](https://github.com/XDzzzzzZyq)                      
- 校对 | 暂无                                                         
-
-![article_image](../../../img/08/03/03/01article_image.png)
-
-<center>有纹理的矩形区域光[1]</center>
-
-# 前言
-
-光线无处不在。同样，合适的灯光在渲染中也十分重要。
-
-目前为止我们已经在第三章中[【投光物】](https://learnopengl-cn.github.io/02%20Lighting/05%20Light%20casters/)这一节学习了三种截然不同的灯光类型：<def>平行光、点光和聚光</def>。但是在现实生活中的光源通常具有一定范围和面积，而以上三种光源要么是来自一点，要么光线在空间中各个位置相同（平行光）。
-
-很显然我们无法通过以上三种光源去实现一种具有面积的光源。假设我们需要一个矩形光源，如果仅用点光或聚光实现，则需要成千上万的微小光源阵列在这个矩形区域中。又即使我们成功创建了这些光源，很明显，为了追求实时渲染的性能要求，渲染结果肯定不尽如人意（如果相机非常接近矩形光源，我们甚至可能还需要更密的灯光）。除此之外又可能出现的照明过度，所以为了能量守恒，每个光源的亮度又需要尽可能的小。很明显这种实现方式是不合理的。因此我们需要一种新的灯光类型：<def>区域光</def>。
-
-这种具有区域的光源在离线渲染中，通过蒙特卡洛采样，使用光线追踪可以相对简单粗暴地解决这个问题。但是本篇教程主要面向实时渲染领域，上述离线渲染的实现方式在本文中不会被提及。
-
-本篇教程描述了一种使用<def>线性变换余弦分布集</def>(Linearly Transformed Cosines)的方法从任意凸多面体中渲染区域光。该方法最初由Eric Heitz、Jonathan Dupuy、Stephen Hill和David Neubelt在SIGGRAPH2016年发表。后续人们又对该方法进行了拓展，除了矩形或多面体外又支持了圆形光源。
-
-在本文中，我们将主要研究矩形区域光的具体实现方法。
-
-## 前置知识
-
-区域光渲染是基于<def>物理渲染</def>(PBR)的，因此建议在开始学习前先熟悉其核心概念，以获得最佳学习体验。此外这个方法涉及到非常多的数学知识，建议先熟悉几个数学概念：积分、线性代数、三角函数、立体角角度测量和球面分布函数。不过如果你仅仅是想实现区域光，那么你完全可以直接复制文中【整体实现】所给出的代码。实现区域光所需要的理论知识比较深奥，刨根问底可能是值得的，但是不完全理解其原理不会影响应用。研究人员已经为帮我们完成了复杂的推导过程，感谢他们让我们的渲染看起来很酷！ :) 
-
-你可能还注意到封面图像有一个带纹理的光源。不过本文不会详细介绍如何实现这一点，尽管可能会在未来的章节中提及。所以让我们开始吧！
-
-!!! important
-	文末参考文献中有相关论文和实现原理
-
-假设我们有一个场景，并在场景中的某个位置放置一个矩形。我们希望这个矩形表示一个光源并发射光线。除此之外还有物理渲染中的BRDF函数，它描述了场景中表面如何散射光线（或者出射光和每条入射光间的比例）。 
-
-在渲染的时候，我们需要解决BRDF的积分，积分范围是自发光多面体（区域光源）在单位半球面围绕着着色点形成的立体角，以计算出射<def>辐照度</def>(Irradiance)。这个出射辐照度将反射回摄像机，从而完成渲染。
-
-在论文中描述了如何将线性变换作用于球面分布函数，从而构造一系列可以拟合不同材质和摄像机视角下BRDF特性的球面分布函数。这些特性在Eric Heitz的PPT[3]中有很好的表现。但由于本教程主要面向程序的实现，所以不会在这里画太多篇幅讲解理论推导。这些经过不同矩阵变换出的分布函数被统称为"线性变换余弦分布集"(Linearly Transformed Cosines)，之所以是“余弦”是因为所有的分布函数是来自一个变换后的受约余弦分布函数，同时具有近似的BRDF的重要特性。"受约"指的是余弦分布函数（或Lambertian分布）仅考虑正半球面。这很重要，因为单位球面固体角度测量值在区间[0, 4π]内，而光源可能永远不会照亮水平面以下的区域；因此我们将余弦分布函数约束到正半球面（上半球）（以入射着色点的表面法线为中心）。
-
-在物理渲染(PBR)中我们学到，GGX微表面模型中的BRDF分布函数具有复杂的形状。比如在接近入射角度处的各向异性拉伸、偏斜度和不同程度的材质粗糙度等特性。正是由于这些特性，BRDF能够产生写实的渲染效果。所以如果我们能够设计一个线性变换，通过矩阵乘法将这些特性添加到受约余弦分布中，那么我们就可以获得媲美BRDF的效果。论文[1]中描述了如何实现这一点。余弦分布是一个非常好的选择，因为我们对其积分有一个闭合形式（Closed-Form）的表示：
-$$
-D_o(ω_o)=\frac1π\cosθ_o
-$$
-总结一下，我们的目标是：构建一个三乘三线性变换矩阵并将其应用在受约余弦分布函数上，从而近似某一条件下BRDF分布函数。然后在区域光所在的立体角上进行计算并获得渲染结果。
-
-在线性代数中，我们可以在两个矩阵中应用乘法，同样也可以进行逆运算：
-$$
-A×B=C~~~~~~~~~~⇔~~~~~~~~~~C×B^{−1}=A
-$$
-如果我们为了得到了BRDF将矩阵M应用于余弦分布，那么我们可以逆运算，从而优雅地解决立体角的球面积分。下面的示意图展示了这个思想。正如论文作者建议的那样，我们可以将其视为变换回初始的余弦空间。
-
-![inverse_transformation](../../../img/08/03/03/02inverse_transformation.png)
-
-<center>反向变换回余弦空间，使用逆线性变换矩阵[2]</center>
-
-# 构建变换矩阵
-
-线性变换矩阵M需要能够表示BRDF的特性，比如在不同观察角度和材质粗糙度上矩阵M需要进行参数化。如下图：
-
-![matrix_construction](../../../img/08/03/03/03matrix_construction.png)
-
-<center>通过矩阵连乘构建线性变换，从而获得想要的BRDF特性[2]</center>
-
-<def>粗糙度</def>(roughness)直接从材质的粗糙度纹理中获取，<def>各向异性</def>(anisotropy)和<def>偏斜度</def>(skewness)来自于摄像机和表面法线的夹角，从而实现逼真的渲染效果。如上图所示，我们可以根据需求和要表示的特定BRDF模型选择任意程度的变换。在本教程中，我们将使用一个矩阵来近似GGX微表面模型。如前文所述，我们需要为每个粗糙度和观察角度的组合计算一个矩阵M。不仅如此，我们还需要对矩阵进行多次采样，从而最小化与目标BRDF的误差。显然，这对于实时渲染来说是不可行的，因此需要预先计算在不同粗糙度/观察角度下的矩阵M。由于矩阵M及其逆矩阵都是稀疏矩阵，只有5个非零值，我们可以通过归一化来将逆矩阵存储在一个4维向量中。这在实践中效果很好，并且可以将矩阵信息以2D纹理的形式传入到shader中去查表。本教程中我们选择一个64x64的纹理来节省显存。
-
-# 计算积分
-
-前文我们提到，计算区域光时我们需要在区域光所在立体角内积分<def>辐射度</def>(Radiance)，但是在实际操作中我们仅需要沿多面体光源的边缘进行积分。这个积分的等价转换过程十分神奇，不过由于教程篇幅的原因我仅引用一句ppt中的原话，希望读者进一步的了解：
-
-<center>“其中一种理解方法是斯托克斯定理(Stoke’s theorem)的应用，你可能在其他领域遇到过，比如流体模拟。”</center>
-
-<def>斯托克斯定理</def>讲的是：在向量场中，场中一个闭合曲线上的线积分等于其所围面积中<def>散度</def>(Curl)的<def>通量</def>(Flux)之和[11]。同理在对区域光光源的积分中，给定光源中任意两个顶点v1和v2，我们需要对下式进行积分求和：
-
-$$
-\arccos(v_1⋅v_2)\frac{v_1×v_2}{\|v_1×v_2\|}⋅n
-$$
-
-
-对于具有N个顶点的整个区域光光源来说，我们可以根据上式将全部边缘求和来准确地计算出该区域光所构成的立体角：
-
-
-$$
-∫_Ω≈\frac1{2π}∑_i\frac1N[\arccos(v_1⋅v_2)\frac{v_1×v_2}{\|v_1×v_2\|}⋅n]
-$$
-
-!!! note "译注"
-
-	具体公式推导可以参考文末延伸阅读中的中文笔记[14]
-
-下图中，向量v1和v2是从着色点到多面体光源的顶点的方向向量，“acos(v1·v2)”是投影到位于着色点附近的单位球体上的多面体弧长（以弧度为单位），向量u为归一化叉积所产生的垂直于v1和v2的单位向量。我们用着色点的法向量和向量u，将光源投影到与着色点相切的平面上，该平面的法向量为n。
-
-![edge_area_integral](../../../img/08/03/03/04edge_area_integral.png)
-
-<center>应用斯托克斯定理，通过边缘积分来计算转换后的光源积分[2]</center>
-
-除此之外，根据PPT[2]中所描述的，计算反余弦函数时造成的精度丢失会导致明显的瑕疵。论文中的解决方法是通过一个三次函数来近似反余弦函数。不过本教程中所采用的拟合函数跟ppt[2]所写的有所不同，这个版本的拟合效果更好。关于边缘积分的代码请参考如下：
-
-```glsl
-float IntegrateEdge(vec3 v1, vec3 v2, vec3 N) {
-    float x = dot(v1, v2);
-    float y = abs(x);
-    float a = 0.8543985 + (0.4965155 + 0.0145206*y)*y;
-    float b = 3.4175940 + (4.1616724 + y)*y;
-    float v = a / b;
-    float theta_sintheta = (x > 0.0) ? v : 0.5*inversesqrt(max(1.0 - x*x, 1e-7)) - v;
-    return dot(cross(v1, v2)*theta_sintheta, N);
-}
-```
-
-## 将多面体裁剪到正半球面
-
-上述的<fun>IntegrateEdge</fun>函数虽然是一个很好的解决方案，但有待提升。为了获得正确的辐照度，我们需要将变换后的余弦分布约束到上半球。这个过程也可以被称为“水平面裁剪”，涉及到很多分支。如下图：
-
-![horizon_clipping](../../../img/08/03/03/05horizon_clipping.png)
-
-如果光源多面体在水平面（相对于物体表面）以下，或者部分在水平面以下，这个多面体则需要被修正（裁剪）到上半球面。理论上来说，修正方法是将存在问题的每条边的较低的顶点上移，使其不再位于水平面以下。如果一条边完全位于水平面以下，则需要将其整体上移。最后以上判断条件下，计算所得到的边缘积分将小于修正前的值（甚至等于零），从而减少出射辐照度。但是，如果我们需要对所有边的每个顶点进行上述判断，shader中会增加许多分支语句（if-else）进而影响渲染性能。因此我们需要从公式入手，继续修改边缘积分的公式：删除与表面法向量的点积（从而不投影到平面上）。修正后的公式如下：
-
-
-$$
-\arccos(v_1⋅v_2)\frac{v_1×v_2}{\|v_1×v_2\|}
-$$
-
-
-需要注意的是，现在积分的结果是一个向量（与法向量点乘的前一步），我们可以将其视为向量形式因子或向量辐照度。我们将其称为向量F，向量F有一个比较明显的特性：向量F的模长为该光源在F方向上的辐照度的大小[2]。此外，我们假想释放辐照度大小为||F||的光源来自一个球体（Proxy Sphere），通过向量F我们可以得出该圆面相对余弦分布函数的张角和倾斜度。公式如下：
-
-
-$$
-\vec F=\arccos(v_1⋅v_2)\frac{v_1×v_2}{\|v_1×v_2\|}\\
-辐照度大小=\|\vec F\|\\
-张角=\arcsin\sqrt{\|\vec F\|}\\
-倾斜度=n\cdot \frac{\vec F}{\|\vec F\|}
-$$
-
-
-![edge_area_integral](../../../img/08/03/03/051edge_area_integral.png)
-
-通过构造<def>假想球体</def>(Proxy Sphere)我们可以完美解决上半球面修正的问题。不仅如此，通过预计算修正后的辐照度和修正前的比例与其张角和倾斜度的关系，我们可以得到第二张纹理LUT。在渲染过程中通过查表可以直接获得这一比例关系，从而高效地近似计算正半球修正。更多细节详见[1] [2]。
-
-!!! important
-	向量F的模长表示着色点接受的总辐照度，从面积A传输到面积B。这一点类似于我们将多面体光源的辐照度转换为多面体在经过半球面上立体角所的辐照度的过程。不过物体表面接收的辐照度受正半球修正和光源倾斜度的影响，这个比例关系被存储在了一个64×64的LUT中，横纵坐标分别为假想球体的张角和倾斜度。上文中之所以用“向量辐照度”作为向量F的名词，是因为作者想强调入射光的能量。对于向量F更完备的表述详见[13]
-
-# 整体实现
-
-恭喜大家已经完成了漫长的理论环节！如果没有完全理解也没关系，如下的代码直接复制粘贴也可以快速让你实现区域光。（如果你想继续挑战理论推导，可以看一看文末的参考资料）。接下来我们来整点有意思的。第一步是载入前文提到的那两个LUT，作为2D纹理存储在GPU里。在载入的过程中确保开启双线性插值以保证平滑采样，然后约束以保证读取的时候不会超过LUT的范围。
-
-```c++
-#include "ltc_matrix.hpp" // 包含了float数组 LTC1 和 LTC2
-
-unsigned int loadMTexture(float* matrixTable) {
-    unsigned int texture = 0;
-    glGenTextures(1, &texture);
-    glBindTexture(GL_TEXTURE_2D, texture);
-    glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, 64, 64, 0, GL_RGBA, GL_FLOAT, matrixTable);
-    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
-    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
-    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
-    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
-    glBindTexture(GL_TEXTURE_2D, 0);
-    return texture;
-}
-
-unsigned int m1 = loadMTexture(LTC1);
-unsigned int m2 = loadMTexture(LTC2);
-```
-
-上述函数所需要的逆变换矩阵作者已经很友好地为我们预先计算了它们，可以在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/8.guest/2022/7.area_lights/ltc_matrix.hpp)找到C++头文件，或者你也可以通过从[4]下载源代码来生成它们。我们还可以将它们作为DXT10压缩图像（.dds）加载。教程作者选择了C++头文件，因为大多数图像加载库不支持DXT10压缩（文件头没有标准化！）。虽然在学习时使用头文件存储数据很方便，但在发布游戏时最好使用.dds图像。
-
-第一个LUT纹理包含如前文所述的逆转换矩阵，而第二个LUT纹理包含Fresnel90、水平剪裁因子和几何衰减的Smith系数（总共3个值）。我们在渲染时将这两个纹理绑定到Shader中：
-
-```c++
-glActiveTexture(GL_TEXTURE0);
-glBindTexture(GL_TEXTURE_2D, m1);
-glActiveTexture(GL_TEXTURE1);
-glBindTexture(GL_TEXTURE_2D, m2);
-```
-
-除此之外我们还需要创建一个<def>顶点缓冲</def>(Vertex Buffer)来存储多面体光源的多面体。为了简化和技术演示，场景最好只有一个水平的地面组成，灯光的话最好是矩形。具体的C++实现代码详见[这里](https://learnopengl.com/code_viewer_gh.php?code=src/8.guest/2022/7.area_lights/1.area_light/area_lights.cpp)。
-
-## Shader
-
-<def>片元着色器</def>(Fragment Shader)是重中之重。在这里，我们采样LUT来构造逆矩阵，并检索几何衰减系数。我们还需要在物体表面的切空间中构造了正交变换矩阵，并计算边缘积分。所以我们需要一些参数输入和常规渲染的必要环节，比如材料和光源的信息。完整的代码如下所示：
-
-```glsl
-#version 330 core
-
-out vec4 fragColor;
-
-in vec3 worldPosition;
-in vec3 worldNormal;
-in vec2 texcoord;
-
-struct Light {
-    float intensity;
-    vec3 color;
-    vec3 points[4];
-    bool twoSided;
-};
-
-uniform Light areaLight;
-uniform vec3 areaLightTranslate;
-
-struct Material {
-    sampler2D diffuse; // 纹理映射
-    vec4 albedoRoughness; // (x,y,z) = 颜色, w = 粗糙度
-};
-uniform Material material;
-
-uniform vec3 viewPosition;
-uniform sampler2D LTC1; // 用于构建逆变换矩阵M
-uniform sampler2D LTC2; // GGX预积分, 菲涅尔, 0(unused), 几何衰减
-
-const float LUT_SIZE = 64.0; // LUT大小
-const float LUT_SCALE = (LUT_SIZE - 1.0)/LUT_SIZE;
-const float LUT_BIAS = 0.5/LUT_SIZE;
-```
-
-变量<fun>areaLightTranslate</fun>是作者用来移动光源的参数，作为演示并不一定需要。然后那些常量是采样LUT的时候需要的。其余的部分相比你已经很熟悉了。
-
-!!! important
-	LUT是图形学经常遇到的概念，它是Look-Up Table的简称，而且大多数情况以纹理贴图的形式在shader中发挥作用。结构体<var>Material</var>仅包含三通道的颜色信息和一通道的粗糙度信息。如果你采用延迟渲染，这种压缩方式非常有用。虽然颜色信息在本案例中未被使用，且物体的粗糙度是个定值，在大多数PBR渲染管线中粗糙度可以是表面纹理的形式。
-
-接下来是准备索引LUT所用的参数，进而构建uv坐标然后构建变换矩阵：
-
-```glsl
-vec3 N = normalize(worldNormal);
-vec3 V = normalize(viewPosition - worldPosition);
-vec3 P = worldPosition;
-float dotNV = clamp(dot(N, V), 0.0f, 1.0f);
-
-// 通过粗糙度和sqrt(1-cos_theta)采样M_texture
-vec2 uv = vec2(material.albedoRoughness.w, sqrt(1.0f - dotNV));
-uv = uv*LUT_SCALE + LUT_BIAS;
-
-// 获得inverse_M的四个参数
-vec4 t1 = texture(LTC1, uv);
-
-// 获得用于计算菲涅尔的两个参数
-vec4 t2 = texture(LTC2, uv);
-
-mat3 Minv = mat3(
-    vec3(t1.x, 0, t1.y),
-    vec3(   0, 1,    0),
-    vec3(t1.z, 0, t1.w)
-);
-```
-
-为了计算立体角，我们一共需要两个函数：一个用来计算单个边缘的积分，另一个是多次调用该函数并对结果求和，然后执行正半球修正。边缘积分函数是其中最短的，正如本教程前面所示，唯一的区别是我们现在不执行点积，而只返回叉积乘以弧长。另一个函数相当长，下面有完整的代码和一些描述计算的注释。
-
-```glsl
-vec3 IntegrateEdge(vec3 v1, vec3 v2, vec3 N) {
-    float x = dot(v1, v2);
-    float y = abs(x);
-    float a = 0.8543985 + (0.4965155 + 0.0145206*y)*y;
-    float b = 3.4175940 + (4.1616724 + y)*y;
-    float v = a / b;
-    float theta_sintheta = (x > 0.0) ? v : 0.5*inversesqrt(max(1.0 - x*x, 1e-7)) - v;
-    return cross(v1, v2)*theta_sintheta;
-}
-```
-
-```glsl
-vec3 LTC_Evaluate(vec3 N, vec3 V, vec3 P, mat3 Minv, vec3 points[4], bool twoSided) {
-    // 构建TBN矩阵的三个基向量
-    vec3 T1, T2;
-    T1 = normalize(V - N * dot(V, N));
-    T2 = cross(N, T1);
-
-    // 依据TBN矩阵旋转光源
-    Minv = Minv * transpose(mat3(T1, T2, N));
-
-    // 多边形四个顶点
-    vec3 L[4];
-
-    // 通过逆变换矩阵将顶点变换于 受约余弦分布 中
-    L[0] = Minv * (points[0] - P);
-    L[1] = Minv * (points[1] - P);
-    L[2] = Minv * (points[2] - P);
-    L[3] = Minv * (points[3] - P);
-
-    // use tabulated horizon-clipped sphere
-    // 判断着色点是否位于光源之后
-    vec3 dir = points[0] - P; // LTC 空间
-    vec3 lightNormal = cross(points[1] - points[0], points[3] - points[0]);
-    bool behind = (dot(dir, lightNormal) < 0.0);
-
-    // 投影至单位球面上
-    L[0] = normalize(L[0]);
-    L[1] = normalize(L[1]);
-    L[2] = normalize(L[2]);
-    L[3] = normalize(L[3]);
-
-    // 边缘积分
-    vec3 vsum = vec3(0.0);
-    vsum += IntegrateEdgeVec(L[0], L[1]);
-    vsum += IntegrateEdgeVec(L[1], L[2]);
-    vsum += IntegrateEdgeVec(L[2], L[3]);
-    vsum += IntegrateEdgeVec(L[3], L[0]);
-
-    // 计算正半球修正所需要的的参数
-    float len = length(vsum);
-
-    float z = vsum.z/len;
-    if (behind)
-        z = -z;
-
-    vec2 uv = vec2(z*0.5f + 0.5f, len); // range [0, 1]
-    uv = uv*LUT_SCALE + LUT_BIAS;
-
-    // 通过参数获得几何衰减系数
-    float scale = texture(LTC2, uv).w;
-
-    float sum = len*scale;
-    if (!behind && !twoSided)
-        sum = 0.0;
-
-    // 输出
-    vec3 Lo_i = vec3(sum, sum, sum);
-    return Lo_i;
-}
-```
-
-确实有些长，不过如果你理解了原理的话其实挺合理的。除此之外还有一点没提到的是变量<var>twoSided</var>，通过传入这个参数来控制开启/关闭区域光的双向照明。完整的代码在[这里](https://learnopengl.com/code_viewer_gh.php?code=src/8.guest/2022/7.area_lights/1.area_light/7.area_light.fs)
-
-## 结果
-
-[这里](https://learnopengl.com/code_viewer_gh.php?code=src/8.guest/2022/7.area_lights/1.area_light/area_lights.cpp)是C++代码，这份代码加上前文提供的shader和头文件即可运行。作者还额外增加了一些功能：
-
-- 按住R/Shift+R以减小/增加材料粗糙度。
-- 按住I/Shift+I以降低/增加光强度。
-- 使用箭头键移动光源。
-- 使用B启用/禁用双面照明。
-- 使用WASD键移动相机，通过鼠标旋转相机。还支持使用鼠标滚轮进行缩放。
-
-作者还增加了地面贴图让场景看起来更真实。如果编译成功你大概率可以看到如下结果：
-
-![program_example](../../../img/08/03/03/06program_example.png)
-
-# 评估性能
-
-结果看起来不错，不过也许你更想知道：
-
-- 如果添加更多灯光会如何
-- 渲染性能如何
-
-显然，根据图形硬件的不同，这两个问题可能会有不同的答案。但总的来说测试起来很简单：我们给shader传入一个数组来表示几个区域光，我们可以使用[OpenGL队列](https://www.khronos.org/opengl/wiki/Query_Object)来进行基准测试。这是一个有趣的案例因为区域光需要大量的计算——比其它类型的光源要多得多。比如对于点光源的测试，我们可以窗前100-200个并且采用向前渲染仍然具有可接受的帧率，但这对于区域光源来说是不可行的。因此如果你想发布一款游戏，通过性能评估来规划照明占用的性能十分重要。OpenGL队列的常规设置如下所示：
-
-```c++
-GLuint timeQuery;
-glGenQueries(1, &timeQuery);
-
-GLuint64 totalQueryTimeNs = 0;
-GLuint64 numQueries = 0;
-
-while (!glfwWindowShouldClose(window))
-{
-    [...]
-
-    glBeginQuery(GL_TIME_ELAPSED, timeQuery);
-    renderPlane();
-    glEndQuery(GL_TIME_ELAPSED);
-
-    GLuint64 elapsed = 0; // will be in nanoseconds
-    glGetQueryObjectui64v(timeQuery, GL_QUERY_RESULT, &elapsed);
-    numQueries++;
-    totalQueryTimeNs += elapsed;
-}
-
-double measuredAverageNs = (double)totalQueryTimeNs / (double)numQueries;
-double measuredAverageMs = measuredAverageNs * 1.0e-6;
-std::cout << "Total average time(ms) = " << measuredAverageMs << '\n';
-```
-
-上述测试方式比较初级，没有考虑异常值或方差。不过重要是统计结果从纳秒变成了毫秒。
-
-片元着色器将使用循环在遍历所有光源。但是我们可以重复利用其中的一些数据，比如我们不需要对每个光源执行LUT纹理查找。着色器的更改部分现在看起来如下：
-
-```glsl
-struct AreaLight
-{
-    float intensity;
-    vec3 color;
-    vec3 points[4];
-    bool twoSided;
-};
-uniform AreaLight areaLights[16];
-uniform int numAreaLights;
-
-// [...]
-
-void main() {
-    // [...]
-    for (int i = 0; i < numAreaLights; i++)
-    {
-        // Evaluate LTC shading
-        vec3 diffuse = LTC_Evaluate(N, V, P, mat3(1), areaLights[i].points, areaLights[i].twoSided);
-        vec3 specular = LTC_Evaluate(N, V, P, Minv, areaLights[i].points, areaLights[i].twoSided);
-
-        // GGX BRDF shadowing and Fresnel
-        specular *= mSpecular*t2.x + (1.0f - mSpecular) * t2.y;
-
-        // Add contribution
-        result += areaLights[i].color * areaLights[i].intensity * (specular + mDiffuse * diffuse);
-    }
-
-    fragColor = vec4(ToSRGB(result), 1.0f);
-}
-```
-
-!!! important
-	我们必须在OpenGL中指定一个固定长度的统一数组，即使实际情况中灯光数量不会那么多。因此，我们将<var>numAreaLights</var>设置为一个等于或小于最大允许光源数量的数字，在以上例子中为16。
-
-!!! note "译注"
-	如果有使用不定长数组的去修，可以使用Shader Storage Buffer SSBO 
-
-根据你的需求，可以使用多种不同的方式搭建测试程序。程序的核心是创建一个区域光位置阵列，并将它们输入到shader中。如何实现这一点在[【多光源】](https://learnopengl-cn.github.io/02%20Lighting/06%20Multiple%20lights/)一节中进行了讲解。一下为作者所展示的基础性能测试结果：
-
-| # area lights | Avg. rendering time (ms) |
-| :-----------: | :----------------------: |
-|       1       |         0.557326         |
-|       2       |         0.897486         |
-|       4       |         2.32212          |
-|       8       |          3.9175          |
-|      12       |         4.37243          |
-|      16       |         3.95511          |
-|      24       |         4.50246          |
-|      32       |         5.67573          |
-
-![multiple_benchmark](../../../img/08/03/03/07multiple_benchmark.png)
-
-![multiple_lights](../../../img/08/03/03/08multiple_lights.png)
-
-[这里](https://learnopengl.com/code_viewer_gh.php?code=src/8.guest/2022/7.area_lights/2.multiple_area_lights/multiple_area_lights.cpp)是测试用的源码，当然还有[修改后的shader](https://learnopengl.com/code_viewer_gh.php?code=src/8.guest/2022/7.area_lights/2.multiple_area_lights/7.multi_area_light.fs)
-
-### 小节
-
-虽然这个演示不是很精美，但不妨碍从中得出一些结论：
-
-- 灯光是伪随机放置在纹理平面周围的。
-- 这些测试是在2015年的“NVIDIA GeForce GTX 850M”笔记本电脑GPU上进行的。你可能会有更好的测试结果。
-- 这些灯光是使用向前渲染的。
-- 在执行这些基准测试时，我经历了很多变数。还有很多因素需要考虑，比如驱动的影响，程序在执行什么操作等等。上面的图表显示了总体趋势，渲染时间随灯光数量大致呈线性的增长。
-- 在渲染函数前后添加<fun>glBeginQuery(GL_TIME_ELAPSED)</fun>和<fun>glEndQuery(GL_TIME_ELAPSED)</fun>来记录测试数据。查询记录的结果可以用<fun>glGetQueryObjectui64v</fun>获得，并从纳秒转换为毫秒以计算平均值。
-
-这里特别有趣的关于正向渲染的要点：在这个演示场景中只有纹理平面（忽略显示光源的彩色平面）有<def>绘制调用</def>(Draw Call)。但如果有许多对象需要渲染，即计算每个光源、每个片片元、每个网格的亮度贡献，则这样的管线是非常低效的，因为深度测试会导致大量片元被覆盖。所以更好的实现方法是使用延迟渲染，这意味着无论绘制的对象数量如何，需要计算照明的片元紧跟屏幕大小有关。
-
-如果继续沿用向前渲染，则可以调用一个<def>计算着色器</def>(Compute Shader)，该着色器将屏幕空间划分为小区块，并为每个区块分配一个区域光列表（即向前渲染plus），以进行进一步优化。不过这个管线的基础是我们需要为每个区域光定义一个最大衰减半径时。这已经在虚幻引擎中完成（请参见[矩形区域光](https://docs.unrealengine.com/5.0/en-US/rectangular-area-lights-in-unreal-engine/)）。
-
-# 其他灯光类型
-
-除了矩形和多面体光源，还可以实现其他类型的区域光源例如条形灯或柱面灯。尽管超出了本文的范围，但数学基础可以在[12]中找到。作者本人并没有尝试实现，因此无法谈论其渲染性能或实施细节。不过为了完整起见此处稍微提一嘴巴。除此之外作者还发现了一些包括圆形区域灯的演示。
-
-# 总结
-
-感谢您的阅读。作者和译者都希望你喜欢并从这一节学到了一些东西。对我自己来说，学习这项令人敬畏的技术是一种巨大的乐趣，如果邀功请赏的话，所有的功劳理应都归功于发现它的研究人员们。正如本节开头所提到的，人们后来对这项技术进行了扩展，包括其他类型的多边形光源。出于简洁的原因，本教程省略了这些内容以及关于纹理映射的部分。说不定它们可能会在未来的章节中被提及。
-
-最后值得一提的是，在区域光中添加阴影是一个开放的研究领域。一些可能的想法涉及屏幕空间光线跟踪和算法降噪，例如[9]或[10]。虽然这些技术非常有趣，但有点超出了本系列教程的范围。如果你愿意，你当然可以进一步学习和了解。
-
-## 延伸阅读
-
-- [1]  *Real-Time Polygonal-Light Shading with Linearly Transformed Cosines*, ACM Siggraph '16, [LTC.pdf](https://drive.google.com/file/d/0BzvWIdpUpRx_d09ndGVjNVJzZjA/view?resourcekey=0-21tmiqk55JIZU8UoeJatXQ)
-- [2]  *Real-Time Area Lighting: a Journey from Research to Production*, presentation slides by Stephen Hill: [s2016_ltc_rnd.pdf](https://advances.realtimerendering.com/s2016/s2016_ltc_rnd.pdf)
-- [3]  *Real-Time Polygonal-Light Shading with Linearly Transformed Cosines*, presentationslides by Eric Heitz: [slides.pdf](https://drive.google.com/file/d/0BzvWIdpUpRx_Z2pZWWFtam5xTFE/view?resourcekey=0-K9rJBtyrgGtxfP3XHDUCyQ)
-- [4]  Main reference github repo: https://github.com/selfshadow/ltc_code. Contains precomputed matrices, source code for WebGL examples, and source code for recomputing the matrices with different BRDF-models.
-- [5]  *Lighting with Linearly Transformed Cosines*, blog post by Tom Grove further investigating the technique. [blog](https://tomgroveblog.wordpress.com/2016/04/30/ltcpost/)
-- [6]  *Real-Time Polygonal-Light Shading with Linearly Transformed Cosines*, Supplemental video showcasing the technique: [Youtube](https://www.youtube.com/watch?v=ZLRgEN7AQgM&ab_channel=JonathanDupuy)
-- [7]  *Adam - Unity*, award-winning real-time-rendered short film by the Unity Demo team using the technique: [Youtube](https://www.youtube.com/watch?v=GXI0l3yqBrA&ab_channel=Unity)
-- [8]  Interactive WebGL-demo: [blog.selfshadow.com](https://blog.selfshadow.com/ltc/webgl/ltc_quad.html)
-- [9]  *Combining Analytic Direct Illumination and Stochastic Shadows*, Eric Heitz et al.: [I3D2018 combining.pdf](https://research.nvidia.com/sites/default/files/pubs/2018-05_Combining-Analytic-Direct//I3D2018_combining.pdf)
-- [10] *Fast Analytic Soft Shadows from Area Lights*, Aakash KT et al.: [111-120.pdf](https://diglib.eg.org/bitstream/handle/10.2312/sr20211295/111-120.pdf)
-- [11] *Stoke's theorem*: [Wikipedia](https://en.wikipedia.org/wiki/Stokes'_theorem)
-- [12] *Linear-Light Shading with Linearly Transformed Cosines*: [HAL archives](https://hal.archives-ouvertes.fr/hal-02155101/document)
-- [13] Alan Watt and Mark Watt: *Advanced Animation and Rendering Techniques, Theory and Practice*, Addison Wesley, 1992
-- [14] 实时范围光Area Light渲染及其数学原理推导，XDzZyq：[笔记](https://www.bilibili.com/read/cv24390369)

docs/code_repo.md

@@ -1,9 +0,0 @@
-# 代码仓库
-
-你可以在每一篇教程中找到在线的代码范例，但如果你想自己运行教程的Demo或者将正常工作的范例代码与你的代码进行比较，你可以在[这里](https://github.com/JoeyDeVries/LearnOpenGL)找到在线的GitHub代码仓库。
-
-目前，`CMakeLists.txt`文件能够正常生成Visual Studio的工程文件和make文件，它能够在Windows和Linux上运行。但是它在Apple的macOS和其它的IDE上还没有进行非常完全的测试，所以如果出现问题你可以留言或者帮忙通过Pull Request来更新一下`CMakeLists.txt`文件让它支持不同的系统。
-
-我非常感谢Zwookie在制作Linux的CMake脚本时提供的巨大帮助。感谢Zwookie对CMakeLists的更新，现在它能够在Windows和Linux上生成工程文件了。
-
-你也可以查看Polytonic的[Glitter](https://github.com/Polytonic/Glitter)，它是一个非常简单的样板工程，它提供了已经预配置好的相关依赖项。

docs/css/admonition_fix.css

@@ -1,47 +0,0 @@
-.important .admonition-title, .attention .admonition-title {
-	display: none;
-}
-
-.note .admonition-title {
-	font-weight: bold;
-	font-size: 16px;
-	background: #6ab0de;
-	color: #FFF;
-	display: block;
-	margin: -12px;
-	margin-bottom: 10px !important;
-	padding: 6px 12px;
-	line-height: 1;
-}
-
-.admonition p{
-	margin: auto;
-}
-
-.important, .attention {
-	display: block;
-	margin: 20px;
-	padding: 15px;
-	color: #444;
-	border-radius: 5px;
-}
-
-.important {
-	background-color: #D8F5D8;
-	border: 2px solid #AFDFAF;
-}
-
-.attention {
-	background-color: #FFD2D2;
-	border: 2px solid #E0B3B3;
-}
-
-.note {
-	display: block;
-	padding: 12px;
-	margin: 20px;
-	color: #444;
-	border-radius: 5px;
-	background-color: #E7F2FA;
-	border: 2px solid #6AB0DE;
-}

docs/css/style.css

@@ -1,51 +1,49 @@
+.wy-nav-content {
+	max-width: 1300px;
+}
+
 body {
-	font-family: "Microsoft Yahei", "Lato", "proxima-nova", "Helvetica Neue", Arial, sans-serif;
+	font-family: "微软雅黑", "宋体", "Lato", "proxima-nova", "Helvetica Neue", Arial, sans-serif;
 }
 
 h1, h2, h3, h4, h5, h6 {
-	margin-bottom: 15px;
+	margin-bottom: 10px;
 	margin-top: 20px;
 }
 
 h1, h2 {
 	margin-top: 25px;
 	border-bottom: 1px solid #e1e4e5;
-	padding-bottom: 15px;
+	padding-bottom: 10px;
 }
 
-.col-md-9 p {
-	line-height: 180%;
-}
-
-.col-md-9 li {
-	margin-bottom: 3px;
-	line-height: 180%;
-}
-
-.col-md-9 pre {
-	  background-color: #f5f7ff;
+.wy-nav-content p, .wy-nav-content ol, .wy-nav-content ul, .wy-nav-content dl {
+	margin-bottom: 10px !important;
 }
 
 table td, table th {
 	font-size: 100% !important;
 }
 
-code {
-	font-size: 100%;
-	background: #F8F8F8;
-	font-family: Consolas, Menlo, Monaco, Lucida Console, Liberation Mono, DejaVu Sans Mono, Bitstream Vera Sans Mono, Courier New, monospace, serif;
+code,.rst-content tt {
+  font-size: 100%;
+  background: #F8F8F8;
 }
 
 p code {
-	font-size: 80%;
-	word-wrap: normal;
+  font-size: 80%;
+  word-wrap: normal;
+  font-family: Consolas, Menlo, Monaco, Lucida Console, Liberation Mono, DejaVu Sans Mono, Bitstream Vera Sans Mono, Courier New, monospace, serif;
 }
 
 div.admonition code {
-	display: inline-block;
-	overflow-x: visible;
-	line-height: 18px;
-	color: #404040;
+  display: inline-block;
+  overflow-x: visible;
+  line-height: 18px;
+  color: #404040;
+  border: 1px solid rgba(0, 0, 0, 0.2);
+  background: rgba(255, 255, 255, 0.7);
+  font-family: Consolas, Menlo, Monaco, Lucida Console, Liberation Mono, DejaVu Sans Mono, Bitstream Vera Sans Mono, Courier New, monospace, serif;
 }
 
 img {
@@ -53,7 +51,7 @@ img {
     margin-left: auto;
     margin-right: auto;
     border-radius: 7px;
-    border: 3px solid #dbdfe4;
+    border: 3px solid #bbb;
 }
 
 img.clean {
@@ -63,7 +61,7 @@ img.clean {
 img.left {
     float: left;
     margin: 10px;
-    border: 2px solid #dbdfe4;
+    border: 2px solid #bbb;
     border-radius: 3px;
     margin-right: 20px;
 }
@@ -89,10 +87,6 @@ img.large {
 	height: auto;
 }
 
-img.noborder {
-	border: none;
-}
-
 video {
 	display: block;
 	margin-left: auto;
@@ -107,11 +101,7 @@ video {
 
 .hljs-comment {
 	font-style: normal;
-	font-size: 90%;
-}
-
-a.nav-title {
-	cursor: pointer;
+	font-size: 85%;
 }
 
 def {
@@ -128,16 +118,3 @@ var {
     font-family: "Courier New", Courier, monospace;
     color: #227;
 }
-
-img.patreon {
-	border: none;
-	display: inline-block;
-	max-height: 13px;
-	margin-bottom: 2px;
-}
-
-img.paypal {
-	border: none;
-	display: inline-block;
-	max-height: 13px;
-}