mirror of
https://github.com/LearnOpenGL-CN/LearnOpenGL-CN.git
synced 2025-12-02 05:55:57 +08:00
Move all the images to this repo. Close #53
This commit is contained in:
@@ -73,11 +73,11 @@ glDepthFunc(GL_ALWAYS);
|
||||
|
||||
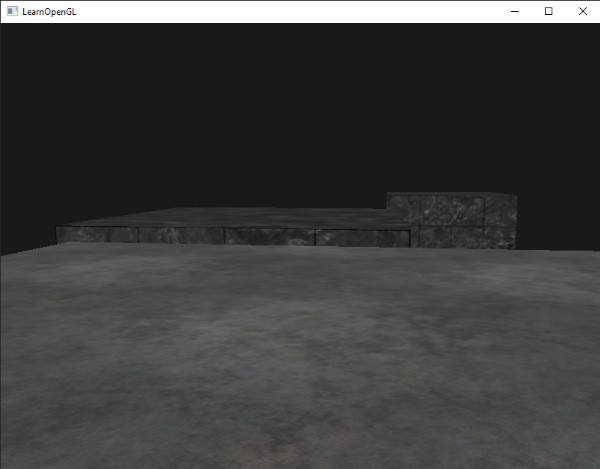
这和我们没有启用深度测试得到了相同的行为。深度测试只是简单地通过,所以这样最后绘制的片段就会呈现在之前绘制的片段前面,即使他们应该在前面。由于我们最后绘制地板平面,那么平面的片段会覆盖每个容器的片段:
|
||||
|
||||
|
||||

|
||||
|
||||
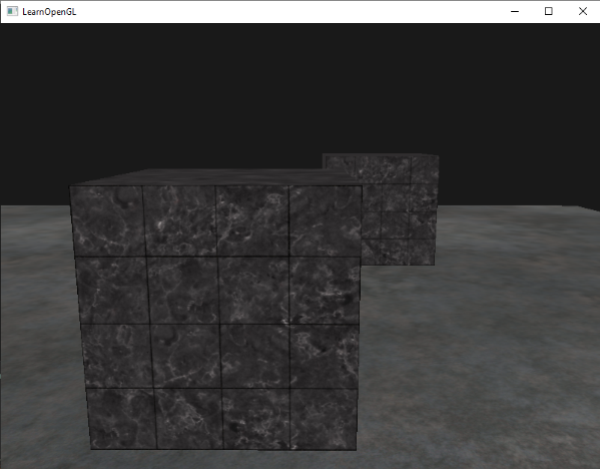
重新设置到`GL_LESS`给了我们曾经的场景:
|
||||
|
||||
|
||||

|
||||
|
||||
## 深度值精度
|
||||
|
||||
@@ -89,7 +89,7 @@ $$
|
||||
|
||||
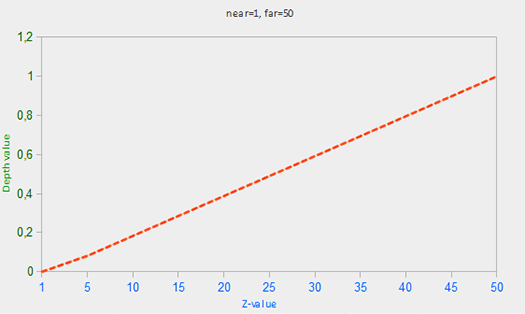
这里far和near是我们用来提供到投影矩阵设置可见视图截锥的远近值 (见[坐标系](../01 Getting started/08 Coordinate Systems.md))。方程带内锥截体的深度值 z,并将其转换到 [0,1] 范围。在下面的图给出 z 值和其相应的深度值的关系:
|
||||
|
||||
|
||||

|
||||
|
||||
!!! Important
|
||||
|
||||
@@ -105,7 +105,7 @@ $$
|
||||
|
||||
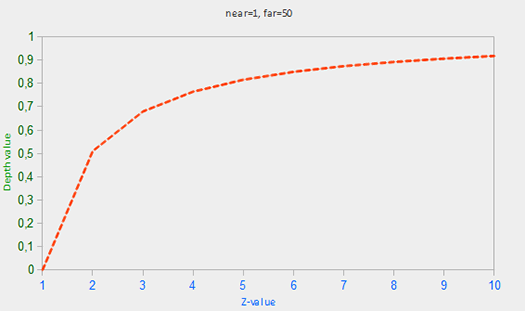
如果你不知道这个方程到底怎么回事也不必担心。要记住的重要一点是在深度缓冲区的值不是线性的屏幕空间 (它们在视图空间投影矩阵应用之前是线性)。值为 0.5 在深度缓冲区并不意味着该对象的 z 值是投影平头截体的中间;顶点的 z 值是实际上相当接近近平面!你可以看到 z 值和产生深度缓冲区的值在下列图中的非线性关系:
|
||||
|
||||
|
||||

|
||||
|
||||
正如你所看到,一个附近的物体的小的 z 值因此给了我们很高的深度精度。变换 (从观察者的角度) 的 z 值的方程式被嵌入在投影矩阵,所以当我们变换顶点坐标从视图到裁剪,然后到非线性方程应用了的屏幕空间中。如果你好奇的投影矩阵究竟做了什么我建议阅读[这个文章](http://www.songho.ca/opengl/gl_projectionmatrix.html)。
|
||||
|
||||
@@ -126,7 +126,7 @@ void main()
|
||||
|
||||
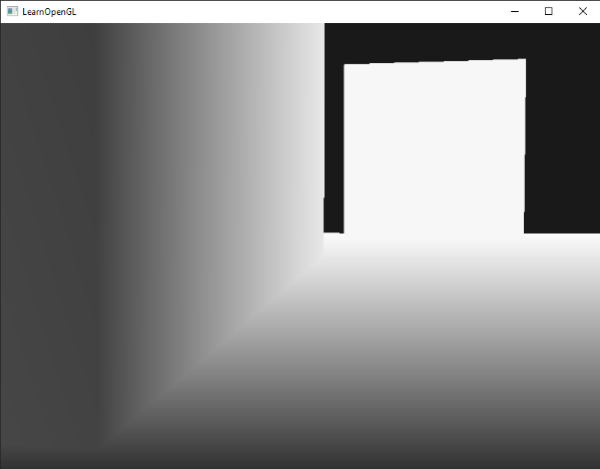
你可能还记得从上一节中的屏幕空间的深度值是非线性如他们在z很小的时候有很高的精度,,较大的 z 值有较低的精度。该片段的深度值会迅速增加,所以几乎所有顶点的深度值接近 1.0。如果我们小心的靠近物体,你最终可能会看到的色彩越来越暗,意味着它们的 z 值越来越小:
|
||||
|
||||
|
||||

|
||||
|
||||
这清楚地表明深度值的非线性特性。近的物体相对远的物体对的深度值比对象较大的影响。只移动几英寸就能让暗色完全变亮。
|
||||
|
||||
@@ -172,7 +172,7 @@ void main()
|
||||
|
||||
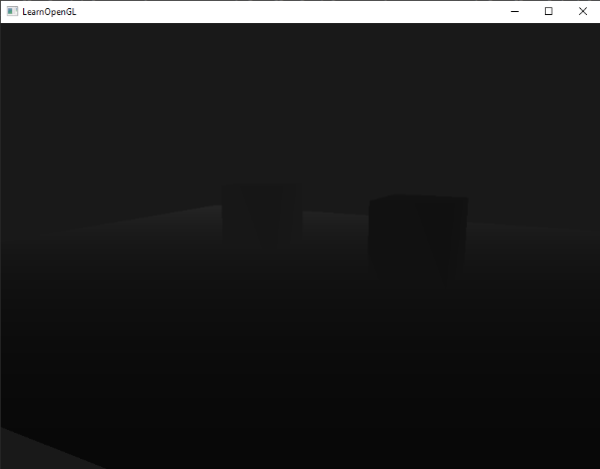
如果现在运行该应用程序,我们得到在距离实际上线性的深度值。尝试移动现场周围看到深度值线性变化
|
||||
|
||||
。
|
||||
。
|
||||
|
||||
颜色主要是黑色的因为深度值线性范围从 0.1 的近平面到 100 的远平面,那里离我们很远。其结果是,我们相对靠近近平面,从而得到较低 (较暗) 的深度值。
|
||||
|
||||
@@ -184,7 +184,7 @@ void main()
|
||||
|
||||
如果您移动摄像机到容器的里面,那么这个影响清晰可,容器的底部不断切换容器的平面和地板的平面:
|
||||
|
||||
|
||||

|
||||
|
||||
深度冲突是深度缓冲区的普遍问题,当对象的距离越远一般越强(因为深度缓冲区在z值非常大的时候没有很高的精度)。深度冲突还无法完全避免,但有一般的几个技巧,将有助于减轻或完全防止深度冲突在你的场景中的出现:
|
||||
|
||||
|
||||
@@ -16,7 +16,7 @@
|
||||
|
||||
下面是一个模板缓冲的简单例子:
|
||||
|
||||

|
||||

|
||||
|
||||
模板缓冲先清空模板缓冲设置所有片段的模板值为0,然后开启矩形片段用1填充。场景中的模板值为1的那些片段才会被渲染(其他的都被丢弃)。
|
||||
|
||||
@@ -102,7 +102,7 @@ GL_INVERT | Bitwise inverts the current stencil buffer value.
|
||||
|
||||
看了前面的部分你未必能理解模板测试是如何工作的,所以我们会展示一个用模板测试实现的一个特别的和有用的功能,叫做**物体轮廓(Object Outlining)**。
|
||||
|
||||

|
||||

|
||||
|
||||
物体轮廓就像它的名字所描述的那样,它能够给每个(或一个)物体创建一个有颜色的边。在策略游戏中当你打算选择一个单位的时候它特别有用。给物体加上轮廓的步骤如下:
|
||||
|
||||
@@ -190,7 +190,7 @@ glEnable(GL_DEPTH_TEST);
|
||||
|
||||
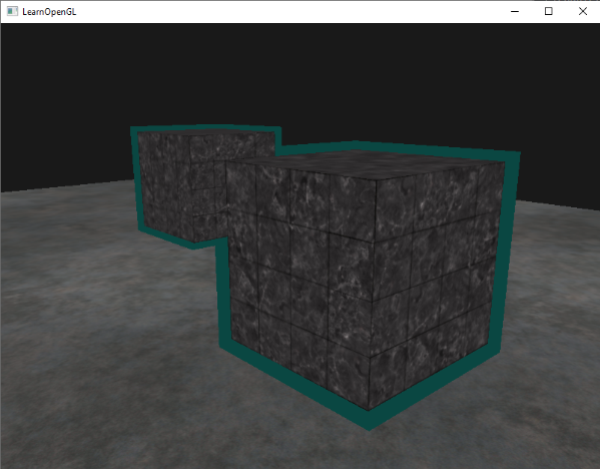
这个边框的算法的结果在深度测试教程的那个场景中,看起来像这样:
|
||||
|
||||
|
||||

|
||||
|
||||
在这里[查看源码](http://learnopengl.com/code_viewer.php?code=advanced/stencil_testing)和[着色器](http://learnopengl.com/code_viewer.php?code=advanced/depth_testing_func_shaders),看看完整的物体边框算法是怎样的。
|
||||
|
||||
|
||||
@@ -9,13 +9,13 @@
|
||||
|
||||
在OpenGL中,物体透明技术通常被叫做**混合(Blending)**。透明是物体(或物体的一部分)非纯色而是混合色,这种颜色来自于不同浓度的自身颜色和它后面的物体颜色。一个有色玻璃窗就是一种透明物体,玻璃有自身的颜色,但是最终的颜色包含了所有玻璃后面的颜色。这也正是混合这名称的出处,因为我们将多种(来自于不同物体)颜色混合为一个颜色,透明使得我们可以看穿物体。
|
||||
|
||||

|
||||

|
||||
|
||||
透明物体可以是完全透明(它使颜色完全穿透)或者半透明的(它使颜色穿透的同时也显示自身颜色)。一个物体的透明度,被定义为它的颜色的alpha值。alpha颜色值是一个颜色向量的第四个元素,你可能已经看到很多了。在这个教程前,我们一直把这个元素设置为1.0,这样物体的透明度就是0.0,同样的,当alpha值是0.0时就表示物体是完全透明的,alpha值为0.5时表示物体的颜色由50%的自身的颜色和50%的后面的颜色组成。
|
||||
|
||||
我们之前所使用的纹理都是由3个颜色元素组成的:红、绿、蓝,但是有些纹理同样有一个内嵌的aloha通道,它为每个纹理像素(Texel)包含着一个alpha值。这个alpha值告诉我们纹理的哪个部分有透明度,以及这个透明度有多少。例如,下面的窗子纹理的玻璃部分的alpha值为0.25(它的颜色是完全红色,但是由于它有75的透明度,它会很大程度上反映出网站的背景色,看起来就不那么红了),角落部分alpha是0.0。
|
||||
我们之前所使用的纹理都是由3个颜色元素组成的:红、绿、蓝,但是有些纹理同样有一个内嵌的aloha通道,它为每个纹理像素(Texel)包含着一个alpha值。这个alpha值告诉我们纹理的哪个部分有透明度,以及这个透明度有多少。例如,下面的[窗户纹理](../img/04/03/blending_transparent_window.png)的玻璃部分的alpha值为0.25(它的颜色是完全红色,但是由于它有75的透明度,它会很大程度上反映出网站的背景色,看起来就不那么红了),角落部分alpha是0.0。
|
||||
|
||||

|
||||

|
||||
|
||||
我们很快就会把这个窗子纹理加到场景中,但是首先,我们将讨论一点简单的技术来实现纹理的半透明,也就是完全透明和完全不透明。
|
||||
|
||||
@@ -25,7 +25,7 @@
|
||||
|
||||
下面的纹理正是这样的纹理,它既有完全不透明的部分(alpha值为1.0)也有完全透明的部分(alpha值为0.0),而没有半透明的部分。你可以看到没有草的部分,图片显示了网站的背景色,而不是它自身的那部分颜色。
|
||||
|
||||

|
||||

|
||||
|
||||
所以,当向场景中添加像这样的纹理时,我们不希望看到一个方块图像,而是只显示实际的纹理像素,剩下的部分可以被看穿。我们要忽略(丢弃)纹理透明部分的像素,不必将这些片段储存到颜色缓冲中。在此之前,我们还要学一下如何加载一个带有透明像素的纹理。
|
||||
|
||||
@@ -82,7 +82,7 @@ glBindVertexArray(0);
|
||||
```
|
||||
|
||||
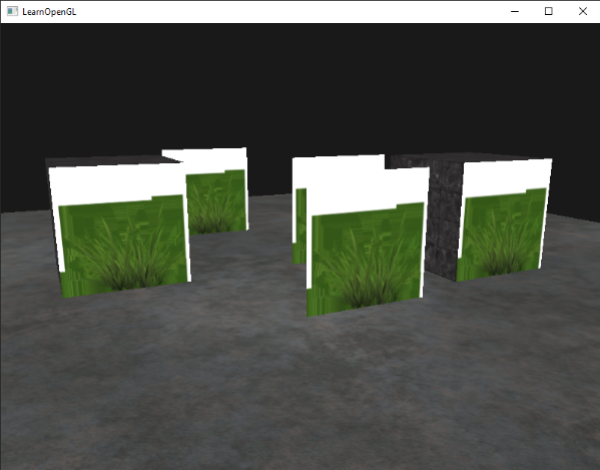
运行程序你将看到:
|
||||
|
||||

|
||||
|
||||
出现这种情况是因为OpenGL默认是不知道如何处理alpha值的,不知道何时忽略(丢弃)它们。我们不得不手动做这件事。幸运的是这很简单,感谢着色器,GLSL为我们提供了discard命令,它保证了片段不会被进一步处理,这样就不会进入颜色缓冲。有了这个命令我们就可以在片段着色器中检查一个片段是否有在一定的阈限下的alpha值,如果有,那么丢弃这个片段,就好像它不存在一样:
|
||||
|
||||
@@ -105,7 +105,7 @@ void main()
|
||||
|
||||
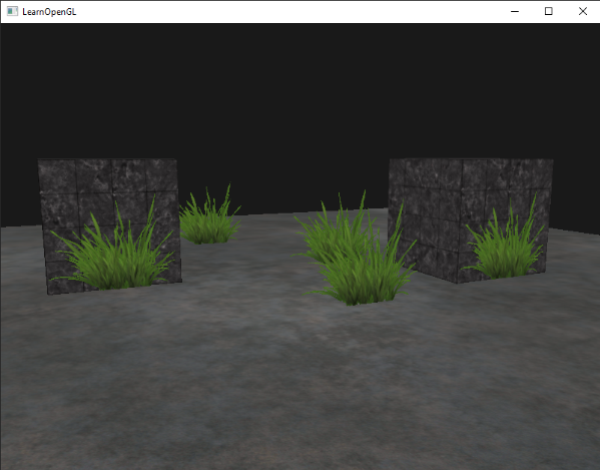
在这儿我们检查被采样纹理颜色包含着一个低于0.1这个阈限的alpha值,如果有,就丢弃这个片段。这个片段着色器能够保证我们只渲染哪些不是完全透明的片段。现在我们来看看效果:
|
||||
|
||||
|
||||

|
||||
|
||||
!!! Important
|
||||
|
||||
@@ -141,7 +141,7 @@ $$
|
||||
|
||||
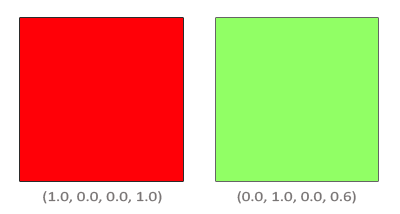
片段着色器运行完成并且所有的测试都通过以后,混合方程才能自由执行片段的颜色输出,当前它在颜色缓冲中(前面片段的颜色在当前片段之前储存)。源和目标颜色会自动被OpenGL设置,而源和目标因子可以让我们自由设置。我们来看一个简单的例子:
|
||||
|
||||
|
||||

|
||||
|
||||
我们有两个方块,我们希望在红色方块上绘制绿色方块。红色方块会成为目标颜色(它会先进入颜色缓冲),我们将在红色方块上绘制绿色方块。
|
||||
|
||||
@@ -153,7 +153,7 @@ $$
|
||||
|
||||
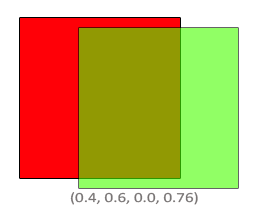
最终方块结合部分包含了60%的绿色和40%的红色,得到一种脏兮兮的颜色:
|
||||
|
||||
|
||||

|
||||
|
||||
最后的颜色被储存到颜色缓冲中,取代先前的颜色。
|
||||
|
||||
@@ -232,7 +232,7 @@ void main()
|
||||
|
||||
这一次(无论OpenGL什么时候去渲染一个片段),它都根据alpha值,把当前片段的颜色和颜色缓冲中的颜色进行混合。因为窗子的玻璃部分的纹理是半透明的,我们应该可以透过玻璃看到整个场景。
|
||||
|
||||
|
||||

|
||||
|
||||
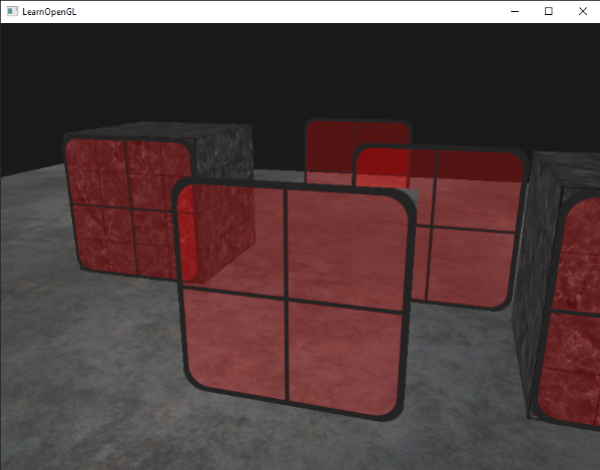
如果你仔细看看,就会注意到有些不对劲。前面的窗子透明部分阻塞了后面的。为什么会这样?
|
||||
|
||||
@@ -278,7 +278,7 @@ for(std::map<float,glm::vec3>::reverse_iterator it = sorted.rbegin(); it != sort
|
||||
|
||||
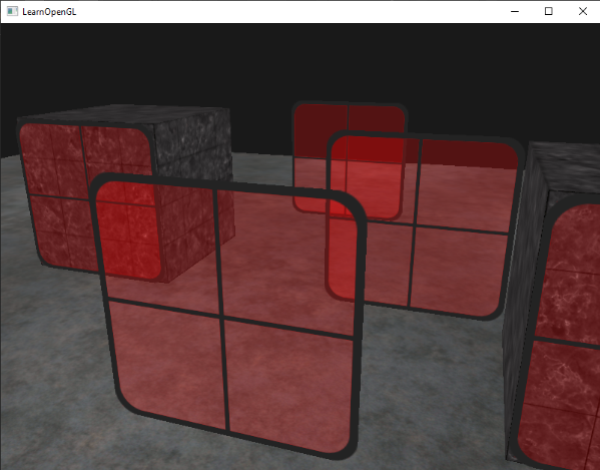
我们从map得来一个逆序的迭代器,迭代出每个逆序的条目,然后把每个窗子的四边形平移到相应的位置。这个相对简单的方法对透明物体进行了排序,修正了前面的问题,现在场景看起来像这样:
|
||||
|
||||
|
||||

|
||||
|
||||
你可以[从这里得到完整的带有排序的源码](http://learnopengl.com/code_viewer.php?code=advanced/blending_sorted)。
|
||||
|
||||
|
||||
@@ -22,7 +22,7 @@
|
||||
|
||||
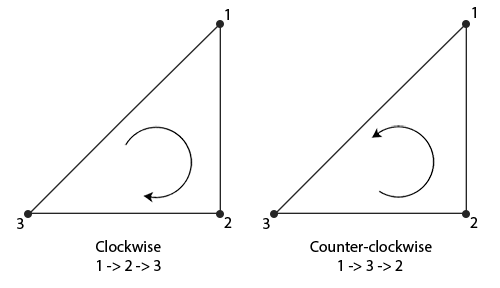
当我们定义一系列的三角顶点时,我们会把它们定义为一个特定的连接顺序(Winding Order),它们可能是**顺时针**的或**逆时针**的。每个三角形由3个顶点组成,我们从三角形的中间去看,从而把这三个顶点指定一个连接顺序。
|
||||
|
||||
|
||||

|
||||
|
||||
正如你所看到的那样,我们先定义了顶点1,接着我们定义顶点2或3,这个不同的选择决定了这个三角形的连接顺序。下面的代码展示出这点:
|
||||
|
||||
@@ -45,7 +45,7 @@ GLfloat vertices[] = {
|
||||
|
||||
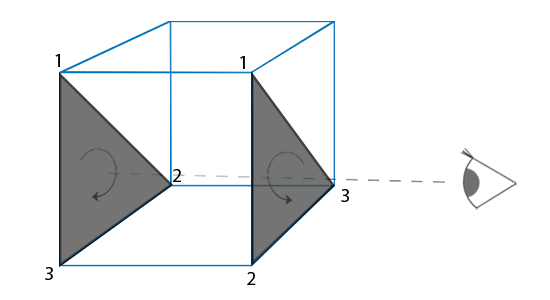
我们指定了它们以后,观察者面对的所有的三角形的顶点的连接顺序都是正确的,但是现在渲染的立方体另一面的三角形的顶点的连接顺序被反转。最终,我们所面对的三角形被视为正面朝向的三角形,后部的三角形被视为背面朝向的三角形。下图展示了这个效果:
|
||||
|
||||
|
||||

|
||||
|
||||
在顶点数据中,我们定义的是两个逆时针顺序的三角形。然而,从观察者的方面看,后面的三角形是顺时针的,如果我们仍以1、2、3的顺序以观察者当面的视野看的话。即使我们以逆时针顺序定义后面的三角形,它现在还是变为顺时针。它正是我们打算剔除(丢弃)的不可见的面!
|
||||
|
||||
@@ -95,7 +95,7 @@ glFrontFace(GL_CW);
|
||||
|
||||
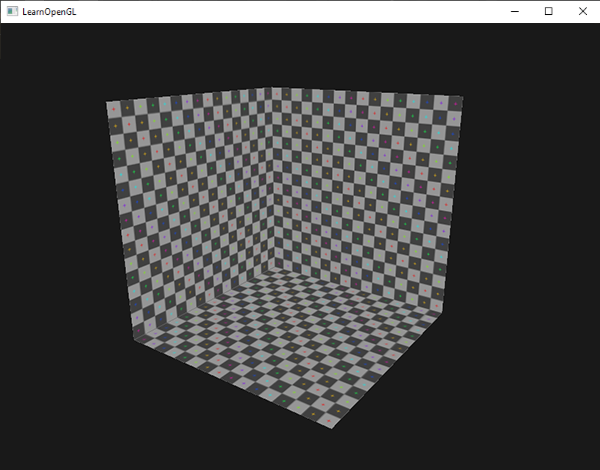
最后的结果只有背面被渲染了:
|
||||
|
||||
|
||||

|
||||
|
||||
要注意,你可以使用默认逆时针顺序剔除正面,来创建相同的效果:
|
||||
|
||||
|
||||
@@ -209,7 +209,7 @@ glBindFramebuffer(GL_FRAMEBUFFER, 0);
|
||||
2. 绑定到默认帧缓冲。
|
||||
3. 绘制一个四边形,让它平铺到整个屏幕上,用新的帧缓冲的颜色缓冲作为他的纹理。
|
||||
|
||||
我们使用在深度测试教程中同一个场景进行绘制,但是这次使用老气横秋的[箱子纹理](http://learnopengl.com/img/textures/container.jpg)。
|
||||
我们使用在深度测试教程中同一个场景进行绘制,但是这次使用老气横秋的[箱子纹理](../img/04/05/container.jpg)。
|
||||
|
||||
为了绘制四边形我们将会创建新的着色器。我们不打算引入任何花哨的变换矩阵,因为我们只提供已经是标准化设备坐标的[顶点坐标](http://learnopengl.com/code_viewer.php?code=advanced/framebuffers_quad_vertices),所以我们可以直接把它们作为顶点着色器的输出。顶点着色器看起来像这样:
|
||||
|
||||
@@ -269,7 +269,7 @@ glBindVertexArray(0);
|
||||
|
||||
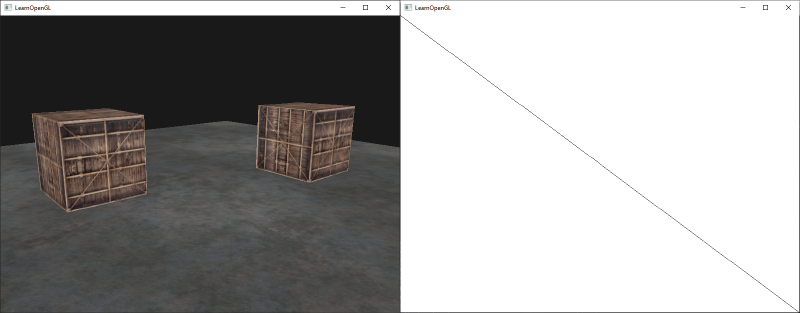
这里的确有很多地方会做错,所以如果你没有获得任何输出,尝试排查任何可能出现错误的地方,再次阅读教程中相关章节。如果每件事都做对了就一定能成功,你将会得到这样的输出:
|
||||
|
||||
|
||||

|
||||
|
||||
左侧展示了和深度测试教程中一样的输出结果,但是这次却是渲染到一个简单的四边形上的。如果我们以线框方式显示的话,那么显然,我们只是绘制了一个默认帧缓冲中单调的四边形。
|
||||
|
||||
@@ -295,7 +295,7 @@ void main()
|
||||
|
||||
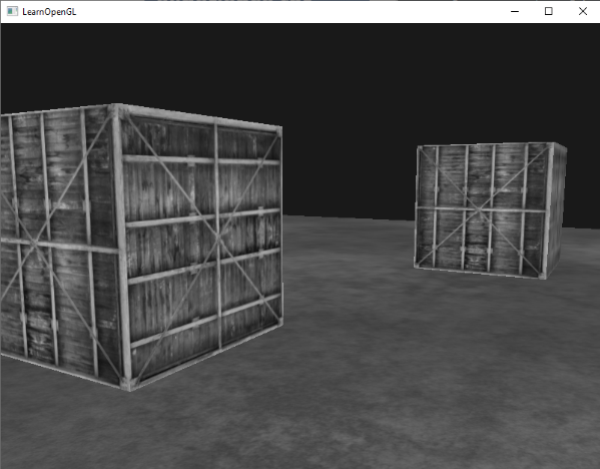
虽然反相是一种相对简单的后处理特效,但是已经很有趣了:
|
||||
|
||||
|
||||

|
||||
|
||||
整个场景现在的颜色都反转了,只需在着色器中写一行代码就能做到,酷吧?
|
||||
|
||||
@@ -322,7 +322,7 @@ void main()
|
||||
}
|
||||
```
|
||||
|
||||

|
||||

|
||||
|
||||
## Kernel effects
|
||||
|
||||
@@ -382,7 +382,7 @@ void main()
|
||||
|
||||
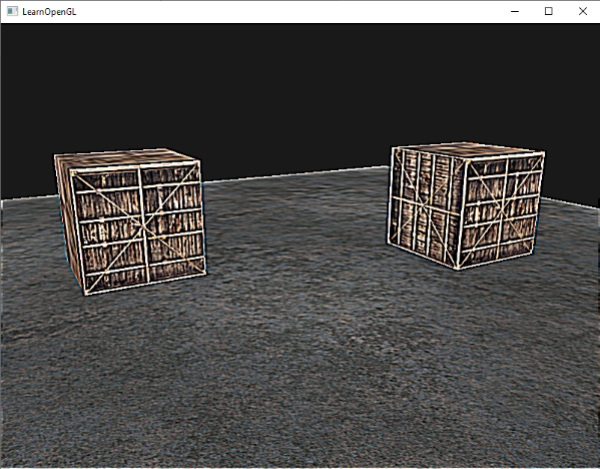
这个锐化的kernel看起来像这样:
|
||||
|
||||
|
||||

|
||||
|
||||
这里创建的有趣的效果就好像你的玩家吞了某种麻醉剂产生的幻觉一样。
|
||||
|
||||
@@ -406,7 +406,7 @@ float kernel[9] = float[](
|
||||
|
||||
通过在像素着色器中改变kernel的float数组,我们就完全改变了之后的后处理效果.现在看起来会像是这样:
|
||||
|
||||
|
||||

|
||||
|
||||
这样的模糊效果具有创建许多有趣效果的潜力.例如,我们可以随着时间的变化改变模糊量,创建出类似于某人喝醉酒的效果,或者,当我们的主角摘掉眼镜的时候增加模糊.模糊也能为我们在后面的教程中提供都颜色值进行平滑处理的能力.
|
||||
|
||||
@@ -422,11 +422,11 @@ $$
|
||||
|
||||
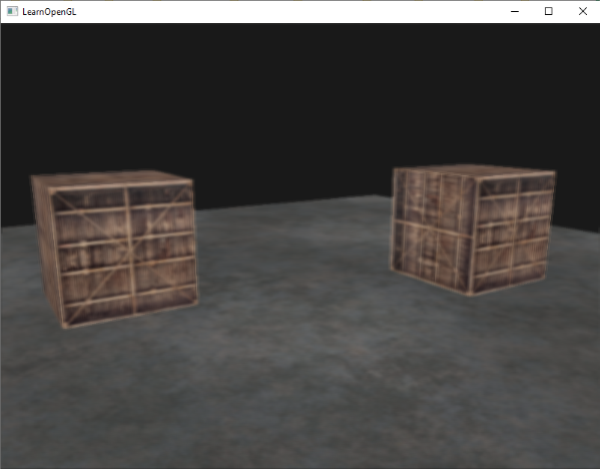
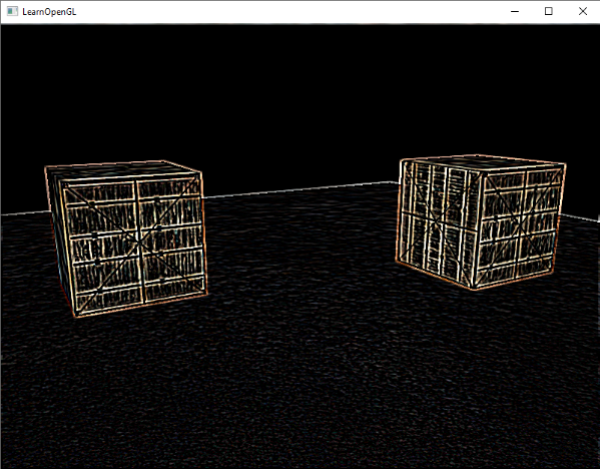
这个kernel将所有的边提高亮度,而对其他部分进行暗化处理,当我们值关心一副图像的边缘的时候,它非常有用.
|
||||
|
||||
|
||||

|
||||
|
||||
在一些像Photoshop这样的软件中使用这些kernel作为图像操作工具/过滤器一点都不奇怪.因为掀开可以具有很强的平行处理能力,我们以实时进行针对每个像素的图像操作便相对容易,图像编辑工具因而更经常使用显卡来进行图像处理。
|
||||
|
||||
## 练习
|
||||
|
||||
* 你可以使用帧缓冲来创建一个后视镜吗?做到它,你必须绘制场景两次:一次正常绘制,另一次摄像机旋转180度后绘制.尝试在你的显示器顶端创建一个小四边形,在上面应用后视镜的镜面纹理:[解决方案](http://learnopengl.com/code_viewer.php?code=advanced/framebuffers-exercise1),[视觉效果](http://learnopengl.com/img/advanced/framebuffers_mirror.png)
|
||||
* 你可以使用帧缓冲来创建一个后视镜吗?做到它,你必须绘制场景两次:一次正常绘制,另一次摄像机旋转180度后绘制.尝试在你的显示器顶端创建一个小四边形,在上面应用后视镜的镜面纹理:[解决方案](http://learnopengl.com/code_viewer.php?code=advanced/framebuffers-exercise1),[视觉效果](../img/04/05/framebuffers_mirror.png)
|
||||
* 自己随意调整一下kernel值,创建出你自己后处理特效.尝试在网上搜索其他有趣的kernel.
|
||||
|
||||
@@ -12,7 +12,7 @@
|
||||
|
||||
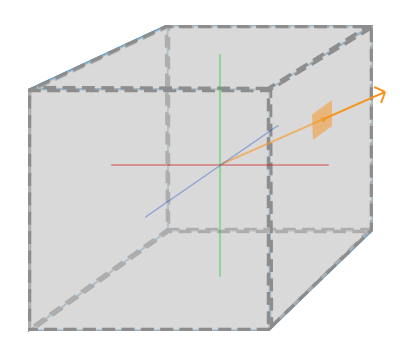
从立方体贴图上使用橘黄色向量采样一个纹理值看起来和下图有点像:
|
||||
|
||||
|
||||

|
||||
|
||||
!!! Important
|
||||
|
||||
@@ -96,17 +96,17 @@ void main()
|
||||
|
||||
天空盒(Skybox)是一个包裹整个场景的立方体,它由6个图像构成一个环绕的环境,给玩家一种他所在的场景比实际的要大得多的幻觉。比如有些在视频游戏中使用的天空盒的图像是群山、白云或者满天繁星。比如下面的夜空繁星的图像就来自《上古卷轴》:
|
||||
|
||||

|
||||

|
||||
|
||||
你现在可能已经猜到立方体贴图完全满足天空盒的要求:我们有一个立方体,它有6个面,每个面需要一个贴图。上图中使用了几个夜空的图片给予玩家一种置身广袤宇宙的感觉,可实际上,他还是在一个小盒子之中。
|
||||
|
||||
网上有很多这样的天空盒的资源。[这个网站](http://www.custommapmakers.org/skyboxes.php)就提供了很多。这些天空盒图像通常有下面的样式:
|
||||
|
||||

|
||||

|
||||
|
||||
如果你把这6个面折叠到一个立方体中,你机会获得模拟了一个巨大的风景的立方体。有些资源所提供的天空盒比如这个例子6个图是连在一起的,你必须手工它们切割出来,不过大多数情况它们都是6个单独的纹理图像。
|
||||
|
||||
这个细致(高精度)的天空盒就是我们将在场景中使用的那个,你可以[在这里下载](http://learnopengl.com/img/textures/skybox.rar)。
|
||||
这个细致(高精度)的天空盒就是我们将在场景中使用的那个,你可以[在这里下载](../img/04/06/skybox.rar)。
|
||||
|
||||
## 加载天空盒
|
||||
|
||||
@@ -220,7 +220,7 @@ glm::mat4 view = glm::mat4(glm::mat3(camera.GetViewMatrix()));
|
||||
|
||||
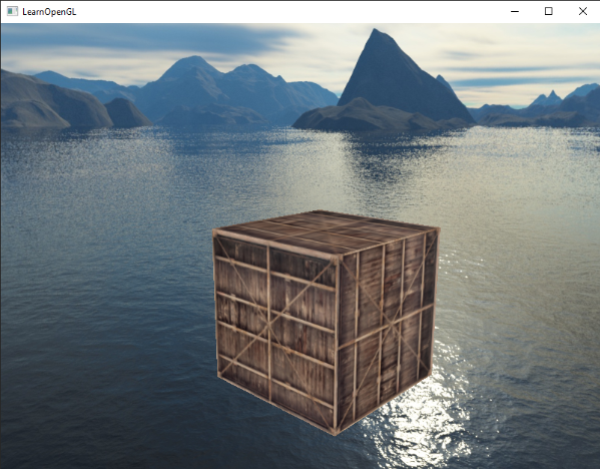
这会移除所有平移,但保留所有旋转,因此用户仍然能够向四面八方看。由于有了天空盒,场景即可变得巨大了。如果你添加些物体然后自由在其中游荡一会儿你会发现场景的真实度有了极大提升。最后的效果看起来像这样:
|
||||
|
||||
|
||||

|
||||
|
||||
[这里有全部源码](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps_skybox),你可以对比一下你写的。
|
||||
|
||||
@@ -259,7 +259,7 @@ void main()
|
||||
|
||||
反射的基本思路不难。下图展示了我们如何计算反射向量,然后使用这个向量去从一个立方体贴图中采样:
|
||||
|
||||

|
||||

|
||||
|
||||
我们基于观察方向向量I和物体的法线向量N计算出反射向量R。我们可以使用GLSL的内建函数reflect来计算这个反射向量。最后向量R作为一个方向向量对立方体贴图进行索引/采样,返回一个环境的颜色值。最后的效果看起来就像物体反射了天空盒。
|
||||
|
||||
@@ -319,13 +319,13 @@ glBindVertexArray(0);
|
||||
|
||||
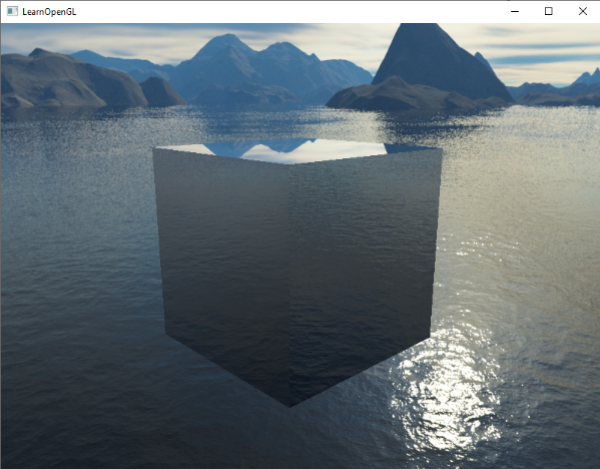
编译运行你的代码,你等得到一个镜子一样的箱子。箱子完美地反射了周围的天空盒:
|
||||
|
||||
|
||||

|
||||
|
||||
你可以[从这里找到全部源代码](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps_reflection)。
|
||||
|
||||
当反射应用于整个物体之上的时候,物体看上去就像有一个像钢和铬这种高反射材质。如果我们加载[模型教程](../03 Model Loading/03 Model.md)中的纳米铠甲模型,我们就会获得一个铬金属制铠甲:
|
||||
|
||||

|
||||

|
||||
|
||||
看起来挺惊艳,但是现实中大多数模型都不是完全反射的。我们可以引进反射贴图(reflection map)来使模型有另一层细节。和diffuse、specular贴图一样,我们可以从反射贴图上采样来决定fragment的反射率。使用反射贴图我们还可以决定模型的哪个部分有反射能力,以及强度是多少。本节的练习中,要由你来在我们早期创建的模型加载器引入反射贴图,这回极大的提升纳米服模型的细节。
|
||||
|
||||
@@ -335,7 +335,7 @@ glBindVertexArray(0);
|
||||
|
||||
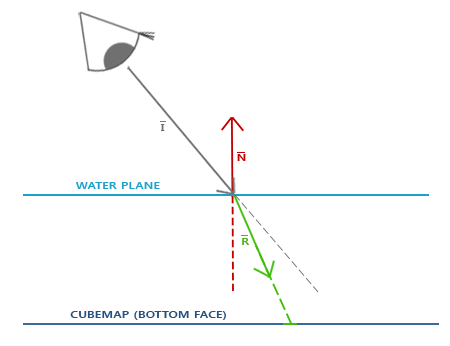
折射遵守[斯涅尔定律](http://en.wikipedia.org/wiki/Snell%27s_law),使用环境贴图看起来就像这样:
|
||||
|
||||
|
||||

|
||||
|
||||
我们有个观察向量I,一个法线向量N,这次折射向量是R。就像你所看到的那样,观察向量的方向有轻微弯曲。弯曲的向量R随后用来从立方体贴图上采样。
|
||||
|
||||
@@ -367,7 +367,7 @@ void main()
|
||||
|
||||
通过改变折射指数你可以创建出完全不同的视觉效果。编译运行应用,结果也不是太有趣,因为我们只是用了一个普通箱子,这不能显示出折射的效果,看起来像个放大镜。使用同一个着色器,纳米服模型却可以展示出我们期待的效果:玻璃制物体。
|
||||
|
||||

|
||||

|
||||
|
||||
你可以向想象一下,如果将光线、反射、折射和顶点的移动合理的结合起来就能创造出漂亮的水的图像。一定要注意,出于物理精确的考虑当光线离开物体的时候还要再次进行折射;现在我们简单的使用了单边(一次)折射,大多数目的都可以得到满足。
|
||||
|
||||
@@ -383,7 +383,7 @@ void main()
|
||||
|
||||
## 练习
|
||||
|
||||
- 尝试在模型加载中引进反射贴图,你将再次得到很大视觉效果的提升。这其中有几点需要注意:
|
||||
- 尝试在之前模型加载小节的模型加载器中引进反射贴图,你可以在[这里](../img/04/06/nanosuit_reflection.zip)找到升级过的纳米装模型,反射贴图也包含在里面。这其中有几点需要注意:
|
||||
- Assimp并不支持反射贴图,我们可以使用环境贴图的方式将反射贴图从`aiTextureType_AMBIENT`类型中来加载反射贴图的材质。
|
||||
- 我匆忙地使用反射贴图来作为镜面反射的贴图,而反射贴图并没有很好的映射在模型上:)。
|
||||
- 由于加载模型已经占用了3个纹理单元,因此你要绑定天空盒到第4个纹理单元上,这样才能在同一个着色器内从天空盒纹理中取样。
|
||||
@@ -391,4 +391,4 @@ void main()
|
||||
|
||||
如果你一切都做对了,那你应该看到和下图类似的效果:
|
||||
|
||||

|
||||

|
||||
|
||||
@@ -45,7 +45,7 @@ void main()
|
||||
|
||||
结果是我们绘制的点距离我们越远就越大:
|
||||
|
||||
|
||||

|
||||
|
||||
想象一下,每个顶点表示出来的点的大小的不同,如果用在像粒子生成之类的技术里会挺有意思的。
|
||||
|
||||
@@ -82,7 +82,7 @@ void main()
|
||||
|
||||
因为窗口的宽是800,当一个像素的x坐标小于400,那么它一定在窗口的左边,这样我们就让物体有个不同的颜色。
|
||||
|
||||
|
||||

|
||||
|
||||
我们现在可以计算出两个完全不同的片段着色器结果,每个显示在窗口的一端。这对于测试不同的光照技术很有好处。
|
||||
|
||||
@@ -111,7 +111,7 @@ void main()
|
||||
|
||||
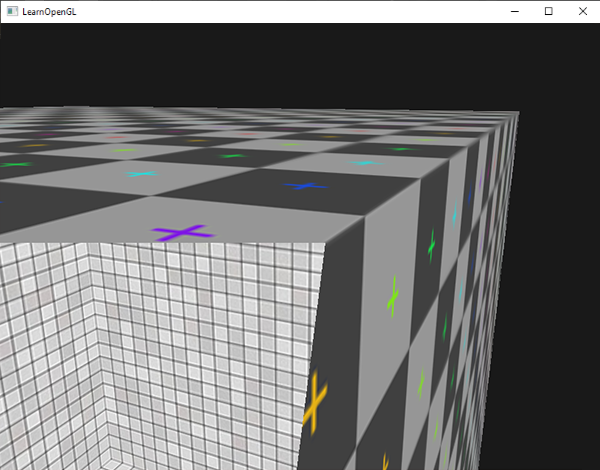
如果我们从箱子的一角往里看,就能看到里面用的是另一个纹理。
|
||||
|
||||

|
||||

|
||||
|
||||
注意,如果你开启了面剔除,你就看不到箱子里面有任何东西了,所以此时使用`gl_FrontFacing`毫无意义。
|
||||
|
||||
@@ -326,7 +326,7 @@ glBindBuffer(GL_UNIFORM_BUFFER, 0);
|
||||
|
||||
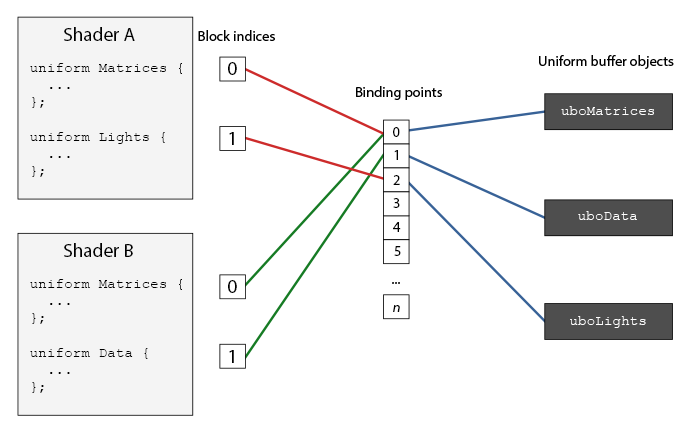
在OpenGL环境(context)中,定义了若干绑定点(binding points),在哪儿我们可以把一个uniform缓冲链接上去。当我们创建了一个uniform缓冲,我们把它链接到一个这个绑定点上,我们也把着色器中uniform块链接到同一个绑定点上,这样就把它们链接到一起了。下面的图标表示了这点:
|
||||
|
||||
|
||||

|
||||
|
||||
你可以看到,我们可以将多个uniform缓冲绑定到不同绑定点上。因为着色器A和着色器B都有一个链接到同一个绑定点0的uniform块,它们的uniform块分享同样的uniform数据—`uboMatrices`有一个前提条件是两个着色器必须都定义了Matrices这个uniform块。
|
||||
|
||||
@@ -457,7 +457,7 @@ glBindVertexArray(0);
|
||||
|
||||
我们只需要在去设置一个`model`的uniform即可。在一个像这样的场景中使用uniform缓冲对象在每个着色器中可以减少uniform的调用。最后效果看起来像这样:
|
||||
|
||||

|
||||

|
||||
|
||||
通过改变模型矩阵,每个立方体都移动到窗口的一边,由于片段着色器不同,物体的颜色也不同。这是一个相对简单的场景,我们可以使用uniform缓冲对象,但是任何大型渲染程序有成百上千的活动着色程序,彼时uniform缓冲对象就会闪闪发光了。
|
||||
|
||||
|
||||
@@ -51,7 +51,7 @@ triangles_adjacency |GL_TRIANGLES_ADJACENCY或GL_TRIANGLE_STRIP_ADJACENCY(6)
|
||||
|
||||
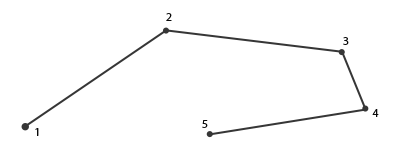
这种情况,你会奇怪什么是线条:一个线条是把多个点链接起来表示出一个连续的线,它最少有两个点来组成。每个后一个点在前一个新渲染的点后面渲染,你可以看看下面的图,其中包含5个顶点:
|
||||
|
||||
|
||||

|
||||
|
||||
上面的着色器,我们只能输出一个线段,因为顶点的最大值设置为2。
|
||||
|
||||
@@ -89,7 +89,7 @@ void main() {
|
||||
|
||||
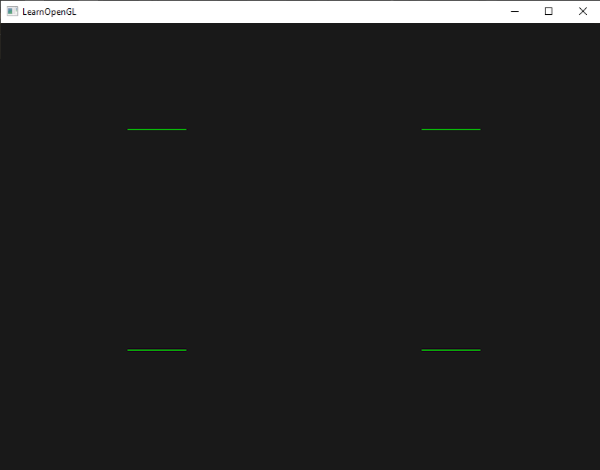
现在你了解了几何着色器的工作方式,你就可能猜出这个几何着色器做了什么。这个几何着色器接收一个基本图形——点,作为它的输入,使用输入点作为它的中心,创建了一个水平线基本图形。如果我们渲染它,结果就会像这样:
|
||||
|
||||
|
||||

|
||||
|
||||
并不是非常引人注目,但是考虑到它的输出是使用下面的渲染命令生成的就很有意思了:
|
||||
|
||||
@@ -147,7 +147,7 @@ glBindVertexArray(0);
|
||||
|
||||
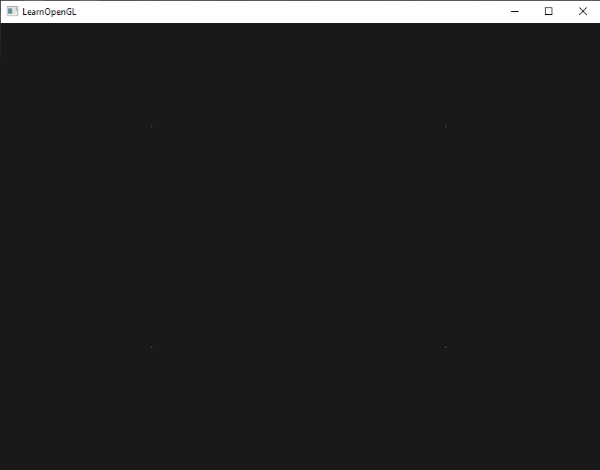
效果是黑色场景中有四个绿点(虽然很难看到):
|
||||
|
||||
|
||||

|
||||
|
||||
但我们不是已经学到了所有内容了吗?对,现在我们将通过为场景添加一个几何着色器来为这个小场景增加点活力。
|
||||
|
||||
@@ -182,7 +182,7 @@ glLinkProgram(program);
|
||||
|
||||
如果你现在编译和运行,就会看到和下面相似的结果:
|
||||
|
||||

|
||||

|
||||
|
||||
它和没用几何着色器一样!我承认有点无聊,但是事实上,我们仍能绘制证明几何着色器工作了的点,所以现在是时候来做点更有意思的事了!
|
||||
|
||||
@@ -193,11 +193,11 @@ glLinkProgram(program);
|
||||
|
||||
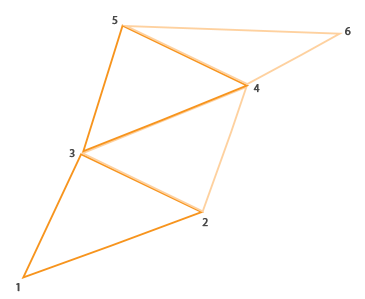
在OpenGL中三角形带(triangle strip)绘制起来更高效,因为它所使用的顶点更少。第一个三角形绘制完以后,每个后续的顶点会生成一个毗连前一个三角形的新三角形:每3个毗连的顶点都能构成一个三角形。如果我们有6个顶点,它们以三角形带的方式组合起来,那么我们会得到这些三角形:(1, 2, 3)、(2, 3, 4)、(3, 4, 5)、(4,5,6)因此总共可以表示出4个三角形。一个三角形带至少要用3个顶点才行,它能生曾N-2个三角形;6个顶点我们就能创建6-2=4个三角形。下面的图片表达了这点:
|
||||
|
||||
|
||||

|
||||
|
||||
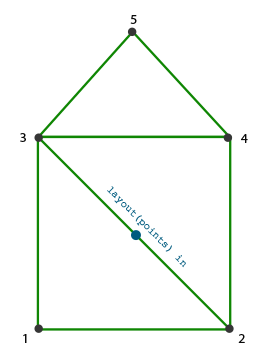
使用一个三角形带作为一个几何着色器的输出,我们可以轻松创建房子的形状,只要以正确的顺序来生成3个毗连的三角形。下面的图像显示,我们需要以何种顺序来绘制点,才能获得我们需要的三角形,图上的蓝点代表输入点:
|
||||
|
||||
|
||||

|
||||
|
||||
上图的内容转变为几何着色器:
|
||||
|
||||
@@ -229,7 +229,7 @@ void main()
|
||||
|
||||
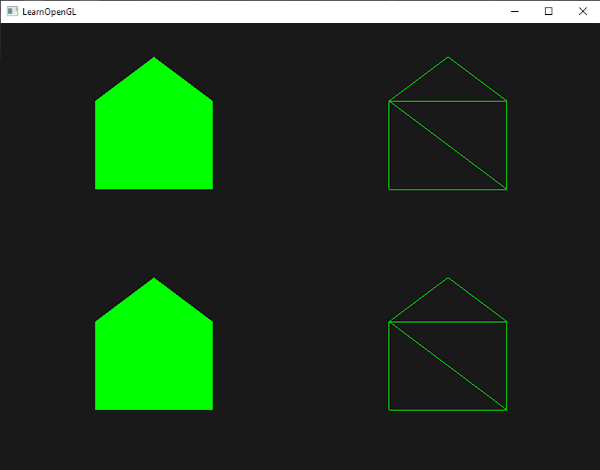
这个几何着色器生成5个顶点,每个顶点是点(point)的位置加上一个偏移量,来组成一个大三角形带。接着最后的基本图形被像素化,片段着色器处理整三角形带,结果是为我们绘制的每个点生成一个绿房子:
|
||||
|
||||
|
||||

|
||||
|
||||
可以看到,每个房子实则是由3个三角形组成,都是仅仅使用空间中一点来绘制的。绿房子看起来还是不够漂亮,所以我们再给每个房子加一个不同的颜色。我们将在顶点着色器中为每个顶点增加一个额外的代表颜色信息的顶点属性。
|
||||
|
||||
@@ -306,7 +306,7 @@ EndPrimitive();
|
||||
|
||||
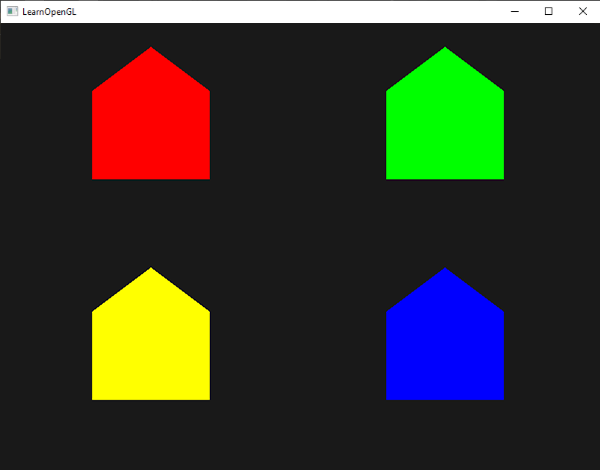
所有发射出去的顶点都把最后储存在fColor中的值嵌入到他们的数据中,和我们在他们的属性中定义的顶点颜色相同。所有的分房子便都有了自己的颜色:
|
||||
|
||||
|
||||

|
||||
|
||||
为了好玩儿,我们还可以假装这是在冬天,给最后一个顶点一个自己的白色,就像在屋顶上落了一些雪。
|
||||
|
||||
@@ -329,7 +329,7 @@ EndPrimitive();
|
||||
|
||||
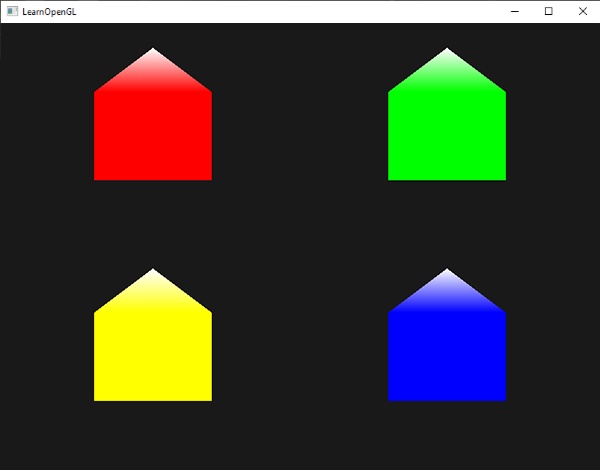
结果就像这样:
|
||||
|
||||
|
||||

|
||||
|
||||
你可以对比一下你的[源码](http://learnopengl.com/code_viewer.php?code=advanced/geometry_shader_houses)和[着色器](http://learnopengl.com/code_viewer.php?code=advanced/geometry_shader_houses_shaders)。
|
||||
|
||||
@@ -341,7 +341,7 @@ EndPrimitive();
|
||||
|
||||
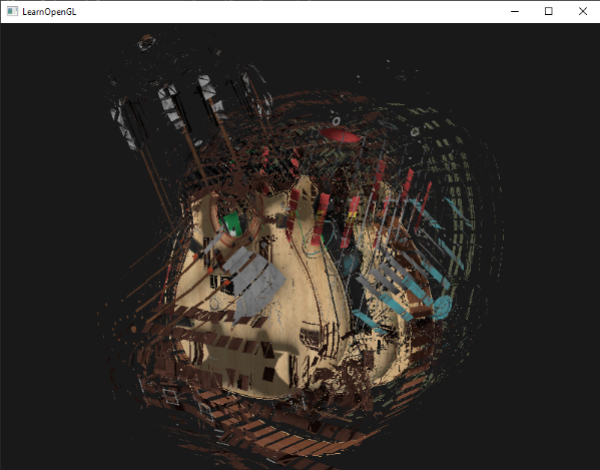
当我们说对一个物体进行爆破(Explode)的时候并不是说我们将要把之前的那堆顶点炸掉,但是我们打算把每个三角形沿着它们的法线向量移动一小段距离。效果是整个物体上的三角形看起来就像沿着它们的法线向量爆炸了一样。纳米服上的三角形的爆炸式效果看起来是这样的:
|
||||
|
||||
|
||||

|
||||
|
||||
这样一个几何着色器效果的一大好处是,它可以用到任何物体上,无论它们多复杂。
|
||||
|
||||
@@ -498,7 +498,7 @@ void main()
|
||||
|
||||
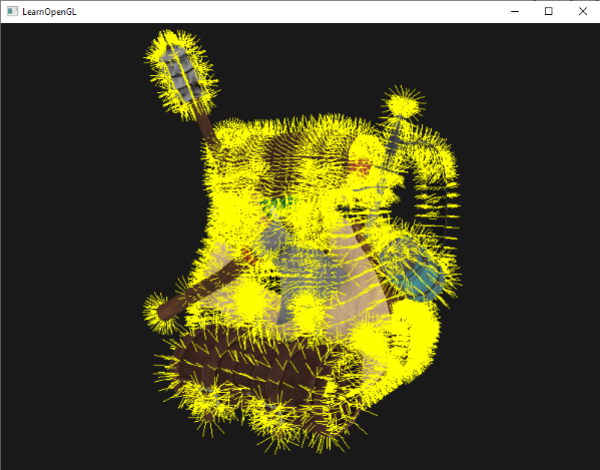
现在先使用普通着色器来渲染你的模型,然后使用特制的法线可视着色器,你会看到这样的效果:
|
||||
|
||||
|
||||

|
||||
|
||||
除了我们的纳米服现在看起来有点像一个带着隔热手套的全身多毛的家伙外,它给了我们一种非常有效的检查一个模型的法线向量是否有错误的方式。你可以想象下这样的几何着色器也经常能被用在给物体添加毛发上。
|
||||
|
||||
|
||||
@@ -31,7 +31,7 @@ for(GLuint i = 0; i < amount_of_models_to_draw; i++)
|
||||
|
||||
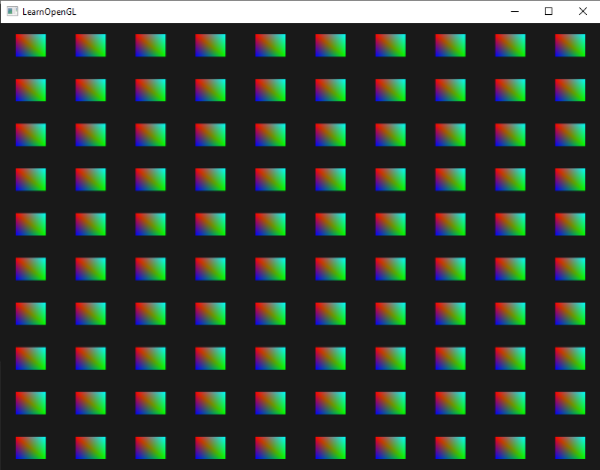
我们调用一个实例化渲染函数,在标准化设备坐标中绘制一百个2D四边形来看看实例化绘制的效果是怎样的。通过对一个储存着100个偏移量向量的索引,我们为每个实例四边形添加一个偏移量。最后,窗口被排列精美的四边形网格填满:
|
||||
|
||||
|
||||

|
||||
|
||||
每个四边形是2个三角形所组成的,因此总共有6个顶点。每个顶点包含一个2D标准设备坐标位置向量和一个颜色向量。下面是例子中所使用的顶点数据,每个三角形为了适应屏幕都很小:
|
||||
|
||||
@@ -176,7 +176,7 @@ glVertexAttribDivisor(2, 1);
|
||||
|
||||
如果我们现在再次使用`glDrawArraysInstanced`渲染四边形,我们会得到下面的输出:
|
||||
|
||||

|
||||

|
||||
|
||||
和前面的一样,但这次是使用实例数组实现的,它使我们为绘制实例向顶点着色器传递更多的数据(内存允许我们存多少就能存多少)。
|
||||
|
||||
@@ -193,7 +193,7 @@ void main()
|
||||
|
||||
结果是第一个实例的四边形被绘制的非常小,随着绘制实例的增加,`gl_InstanceID`越来越接近100,这样更多的四边形会更接近它们原来的大小。这是一种很好的将`gl_InstanceID`与实例数组结合使用的法则:
|
||||
|
||||
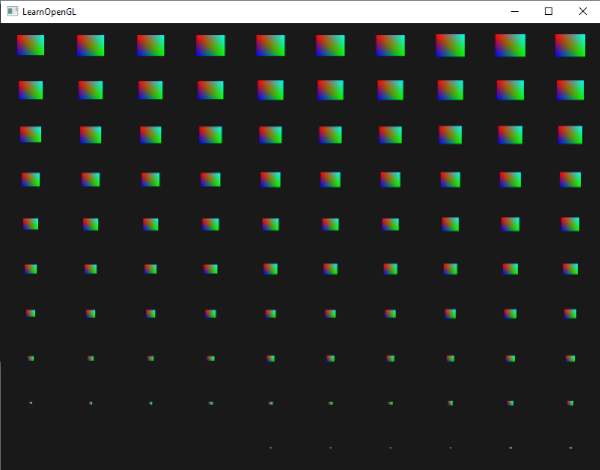
|
||||

|
||||
|
||||
如果你仍然不确定实例渲染如何工作,或者想看看上面的代码是如何组合起来的,你可以在[这里找到应用的源码](http://learnopengl.com/code_viewer.php?code=advanced/instancing_quads)。
|
||||
|
||||
@@ -262,7 +262,7 @@ for(GLuint i = 0; i < amount; i++)
|
||||
|
||||
结果是一个太空样子的场景,我们可以看到有一个自然的小行星带:
|
||||
|
||||
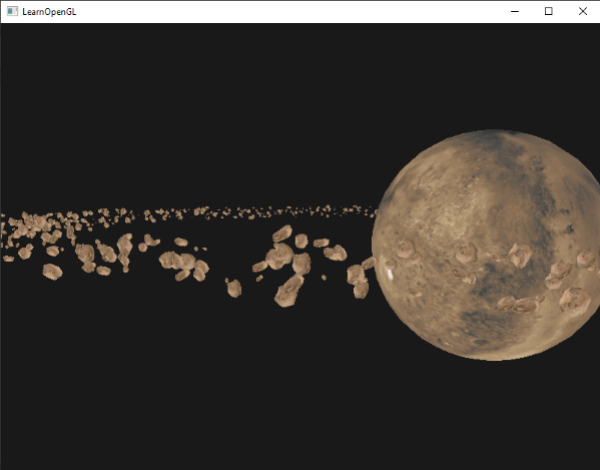
|
||||

|
||||
|
||||
这个场景包含1001次渲染函数调用,每帧渲染1000个小行星模型。你可以在这里找到[场景的源码](http://learnopengl.com/code_viewer.php?code=advanced/instancing_asteroids_normal),以及[顶点](http://learnopengl.com/code_viewer.php?code=advanced/instancing&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced/instancing&type=fragment)着色器。
|
||||
|
||||
@@ -341,7 +341,7 @@ for(GLuint i = 0; i < rock.meshes.size(); i++)
|
||||
|
||||
这里我们绘制和前面的例子里一样数量(amount)的小行星,只不过是使用的实例渲染。结果是相似的,但你会看在开始增加数量以后效果的不同。不实例渲染,我们可以流畅渲染1000到1500个小行星。而使用了实例渲染,我们可以设置为100000,每个模型由576个顶点,这几乎有5千7百万个顶点,而且帧率没有丝毫下降!
|
||||
|
||||
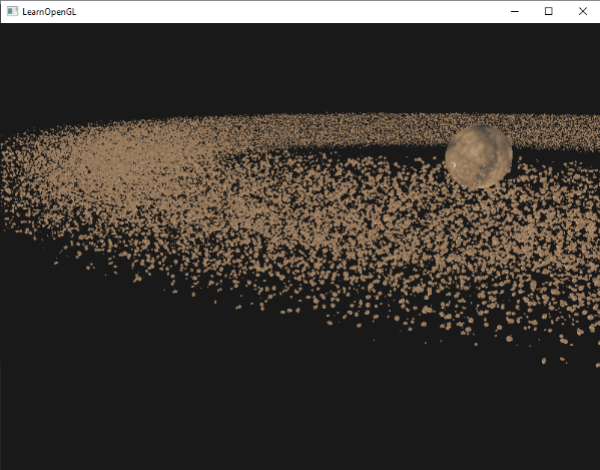
|
||||

|
||||
|
||||
上图渲染了十万小行星,半径为150.0f,偏移等于25.0f。你可以在这里找到这个演示实例渲染的[源码](http://learnopengl.com/code_viewer.php?code=advanced/instancing_asteroids_instanced)。
|
||||
|
||||
|
||||
@@ -8,11 +8,11 @@
|
||||
|
||||
在你的渲染大冒险中,你可能会遇到模型边缘有锯齿的问题。**锯齿边(Jagged Edge)**出现的原因是由顶点数据像素化之后成为片段的方式所引起的。下面是一个简单的立方体,它体现了锯齿边的效果:
|
||||
|
||||
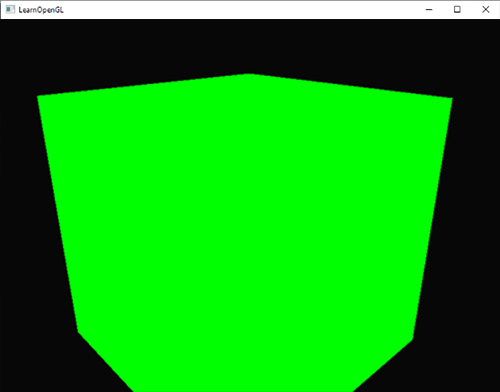
|
||||

|
||||
|
||||
也许不是立即可见的,如果你更近的看看立方体的边,你就会发现锯齿了。如果我们放大就会看到下面的情境:
|
||||
|
||||

|
||||

|
||||
|
||||
这当然不是我们在最终版本的应用里想要的效果。这个效果,很明显能看到边是由像素所构成的,这种现象叫做**走样(Aliasing)**。有很多技术能够减少走样,产生更平滑的边缘,这些技术叫做**抗锯齿技术**(Anti-aliasing,也被称为反走样技术)。
|
||||
|
||||
@@ -26,19 +26,19 @@
|
||||
|
||||
光栅化是你的最终的经处理的顶点和片段着色器之间的所有算法和处理的集合。光栅化将属于一个基本图形的所有顶点转化为一系列片段。顶点坐标理论上可以含有任何坐标,但片段却不是这样,这是因为它们与你的窗口的解析度有关。几乎永远都不会有顶点坐标和片段的一对一映射,所以光栅化必须以某种方式决定每个特定顶点最终结束于哪个片段/屏幕坐标上。
|
||||
|
||||
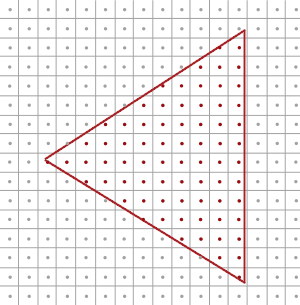
|
||||

|
||||
|
||||
这里我们看到一个屏幕像素网格,每个像素中心包含一个采样点(sample point),它被用来决定一个像素是否被三角形所覆盖。红色的采样点如果被三角形覆盖,那么就会为这个被覆盖像(屏幕)素生成一个片段。即使三角形覆盖了部分屏幕像素,但是采样点没被覆盖,这个像素仍然不会受到任何片段着色器影响到。
|
||||
|
||||
你可能已经明白走样的原因来自何处了。三角形渲染后的版本最后在你的屏幕上是这样的:
|
||||
|
||||

|
||||

|
||||
|
||||
由于屏幕像素总量的限制,有些边上的像素能被渲染出来,而有些则不会。结果就是我们渲染出的基本图形的非光滑边缘产生了上图的锯齿边。
|
||||
|
||||
多采样所做的正是不再使用单一采样点来决定三角形的覆盖范围,而是采用多个采样点。我们不再使用每个像素中心的采样点,取而代之的是4个子样本(subsample),用它们来决定像素的覆盖率。这意味着颜色缓冲的大小也由于每个像素的子样本的增加而增加了。
|
||||
|
||||
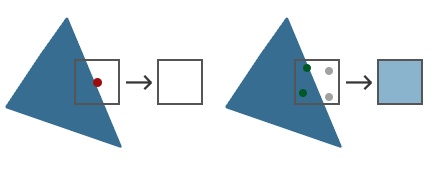
|
||||

|
||||
|
||||
左侧的图显示了我们普通决定一个三角形的覆盖范围的方式。这个像素并不会运行一个片段着色器(这就仍保持空白),因为它的采样点没有被三角形所覆盖。右边的图展示了多采样的版本,每个像素包含4个采样点。这里我们可以看到只有2个采样点被三角形覆盖。
|
||||
|
||||
@@ -52,13 +52,13 @@ MSAA的真正工作方式是,每个像素只运行一次片段着色器,无
|
||||
|
||||
结果是,颜色缓冲中所有基本图形的边都生成了更加平滑的样式。让我们看看当再次决定前面的三角形覆盖范围时多样本看起来是这样的:
|
||||
|
||||
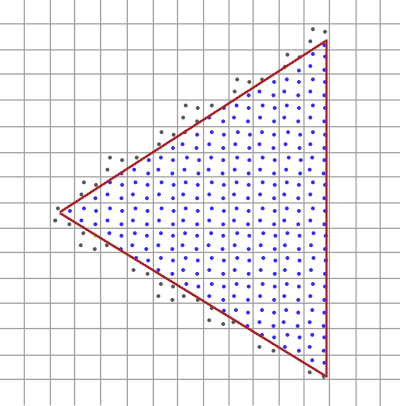
|
||||

|
||||
|
||||
这里每个像素包含着4个子样本(不相关的已被隐藏)蓝色的子样本是被三角形覆盖了的,灰色的没有被覆盖。三角形内部区域中的所有像素都会运行一次片段着色器,它输出的颜色被储存到所有4个子样本中。三角形的边缘并不是所有的子样本都会被覆盖,所以片段着色器的结果仅储存在部分子样本中。根据被覆盖子样本的数量,最终的像素颜色由三角形颜色和其他子样本所储存的颜色所决定。
|
||||
|
||||
大致上来说,如果更多的采样点被覆盖,那么像素的颜色就会更接近于三角形。如果我们用早期使用的三角形的颜色填充像素,我们会获得这样的结果:
|
||||
|
||||
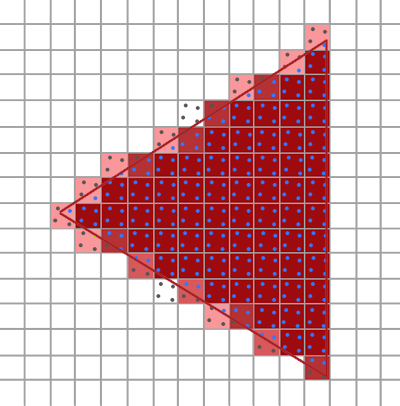
|
||||

|
||||
|
||||
对于每个像素来说,被三角形覆盖的子样本越少,像素受到三角形的颜色的影响也越少。现在三角形的硬边被比实际颜色浅一些的颜色所包围,因此观察者从远处看上去就比较平滑了。
|
||||
|
||||
@@ -86,7 +86,7 @@ glEnable(GL_MULTISAMPLE);
|
||||
|
||||
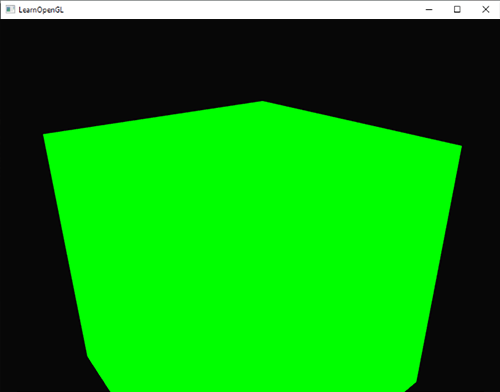
当默认帧缓冲有了多采样缓冲附件的时候,我们所要做的全部就是调用 `glEnable`开启多采样。因为实际的多采样算法在OpenGL驱动光栅化里已经实现了,所以我们无需再做什么了。如果我们现在来渲染教程开头的那个绿色立方体,我们会看到边缘变得平滑了:
|
||||
|
||||
|
||||

|
||||
|
||||
这个箱子看起来平滑多了,在场景中绘制任何物体都可以利用这个技术。可以[从这里找到](http://learnopengl.com/code_viewer.php?code=advanced/anti_aliasing_multisampling)这个简单的例子。
|
||||
|
||||
@@ -142,7 +142,7 @@ glBlitFramebuffer(0, 0, width, height, 0, 0, width, height, GL_COLOR_BUFFER_BIT,
|
||||
|
||||
如果我们渲染应用,我们将得到和没用帧缓冲一样的结果:一个绿色立方体,它使用MSAA显示出来,但边缘锯齿明显少了:
|
||||
|
||||

|
||||

|
||||
|
||||
你可以[在这里找到源代码](http://learnopengl.com/code_viewer.php?code=advanced/anti_aliasing_framebuffers)。
|
||||
|
||||
@@ -177,7 +177,7 @@ while(!glfwWindowShouldClose(window))
|
||||
|
||||
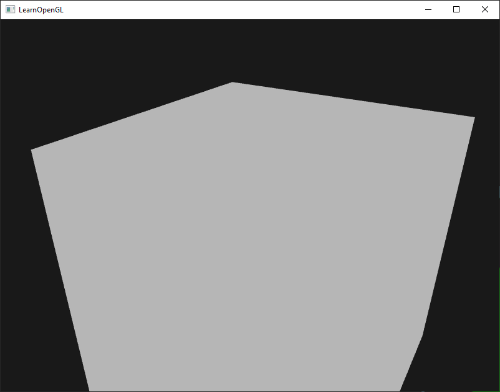
如果我们实现帧缓冲教程中讲的后处理代码,我们就能创造出没有锯齿边的所有效果很酷的后处理特效。使用模糊kernel过滤器,看起来会像这样:
|
||||
|
||||
|
||||

|
||||
|
||||
你可以[在这里找到所有MSAA版本的后处理源码](http://learnopengl.com/code_viewer.php?code=advanced/anti_aliasing_post_processing)。
|
||||
|
||||
|
||||
Reference in New Issue
Block a user