diff --git a/docs/01 Getting started/08 Coordinate Systems.md b/docs/01 Getting started/08 Coordinate Systems.md
index 26b85d1..dc5605c 100644
--- a/docs/01 Getting started/08 Coordinate Systems.md	
+++ b/docs/01 Getting started/08 Coordinate Systems.md	
@@ -24,7 +24,7 @@
 
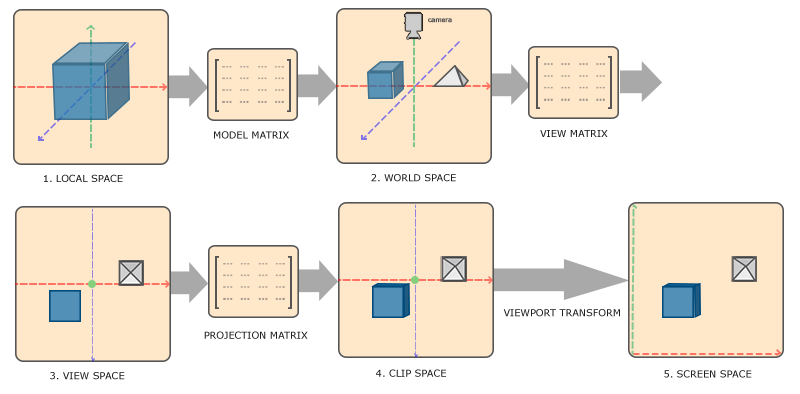
 为了将坐标从一个坐标系转换到另一个坐标系，我们需要用到几个转换矩阵，最重要的几个分别是**模型(Model)**、**视图(View)**、**投影(Projection)**三个矩阵。首先，顶点坐标开始于**局部空间(Local Space)**，称为**局部坐标(Local Coordinate)**，然后经过**世界坐标(World Coordinate)**，**观察坐标(View Coordinate)**，**裁剪坐标(Clip Coordinate)**，并最后以**屏幕坐标(Screen Coordinate)**结束。下面的图示显示了整个流程及各个转换过程做了什么：
 
-![coordinate_systems](http://learnopengl.com/img/getting-started/coordinate_systems.png)
+![coordinate_systems](../img/01/08/coordinate_systems.png)
 
 
  1. 局部坐标是对象相对于局部原点的坐标；也是对象开始的坐标。
@@ -77,7 +77,7 @@
 
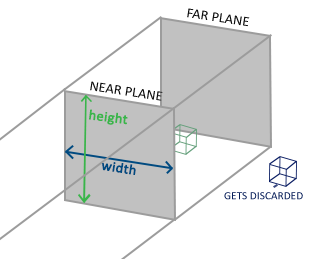
 正射投影(Orthographic Projection)矩阵定义了一个类似立方体的平截头体，指定了一个裁剪空间，每一个在这空间外面的顶点都会被裁剪。创建一个正射投影矩阵需要指定可见平截头体的宽、高和长度。所有在使用正射投影矩阵转换到裁剪空间后如果还处于这个平截头体里面的坐标就不会被裁剪。它的平截头体看起来像一个容器：
 
-![orthographic projection frustum](http://learnopengl.com/img/getting-started/orthographic_frustum.png)
+![orthographic projection frustum](../img/01/08/orthographic_frustum.png)
 
 上面的平截头体定义了由宽、高、**近**平面和**远**平面决定的可视的坐标系。任何出现在近平面前面或远平面后面的坐标都会被裁剪掉。正视平截头体直接将平截头体内部的顶点映射到标准化设备坐标系中，因为每个向量的w分量都是不变的；如果w分量等于1.0，则透视划分不会改变坐标的值。
 
@@ -95,7 +95,7 @@ glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f);
 
 如果你曾经体验过**实际生活**给你带来的景象，你就会注意到离你越远的东西看起来更小。这个神奇的效果我们称之为透视(Perspective)。透视的效果在我们看一条无限长的高速公路或铁路时尤其明显，正如下面图片显示的那样:
 
-![perspective](http://learnopengl.com/img/getting-started/perspective.png)
+![perspective](../img/01/08/perspective.png)
 
 正如你看到的那样，由于透视的原因，平行线似乎在很远的地方看起来会相交。这正是透视投影(Perspective Projection)想要模仿的效果，它是使用透视投影矩阵来完成的。这个投影矩阵不仅将给定的平截头体范围映射到裁剪空间，同样还修改了每个顶点坐标的w值，从而使得离观察者越远的顶点坐标w分量越大。被转换到裁剪空间的坐标都会在-w到w的范围之间(任何大于这个范围的对象都会被裁剪掉)。OpenGL要求所有可见的坐标都落在-1.0到1.0范围内从而作为最后的顶点着色器输出，因此一旦坐标在裁剪空间内，透视划分就会被应用到裁剪空间坐标：
 
@@ -113,7 +113,7 @@ glm::mat4 proj = glm::perspective(45.0f, (float)width/(float)height, 0.1f, 100.0
 
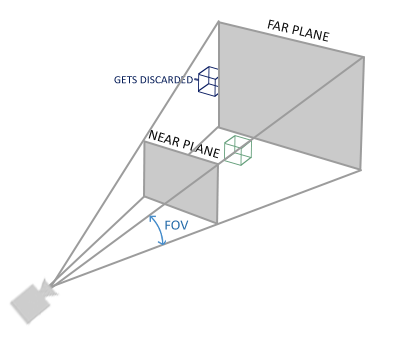
 `glm::perspective`所做的其实就是再次创建了一个定义了可视空间的大的**平截头体**，任何在这个平截头体以外的对象最后都不会出现在裁剪空间体积内，并且将会受到裁剪。一个透视平截头体可以被可视化为一个不均匀形状的盒子，在这个盒子内部的每个坐标都会被映射到裁剪空间的点。一张透视平截头体的照片如下所示：
 
-![ perspective_frustum](http://learnopengl.com/img/getting-started/perspective_frustum.png)
+![ perspective_frustum](../img/01/08/perspective_frustum.png)
 
 它的第一个参数定义了**fov**的值，它表示的是**视野(Field of View)**，并且设置了观察空间的大小。对于一个真实的观察效果，它的值经常设置为45.0，但想要看到更多结果你可以设置一个更大的值。第二个参数设置了宽高比，由视口的高除以宽。第三和第四个参数设置了平截头体的近和远平面。我们经常设置近距离为0.1而远距离设为100.0。所有在近平面和远平面的顶点且处于平截头体内的顶点都会被渲染。
 
@@ -123,7 +123,7 @@ glm::mat4 proj = glm::perspective(45.0f, (float)width/(float)height, 0.1f, 100.0
 
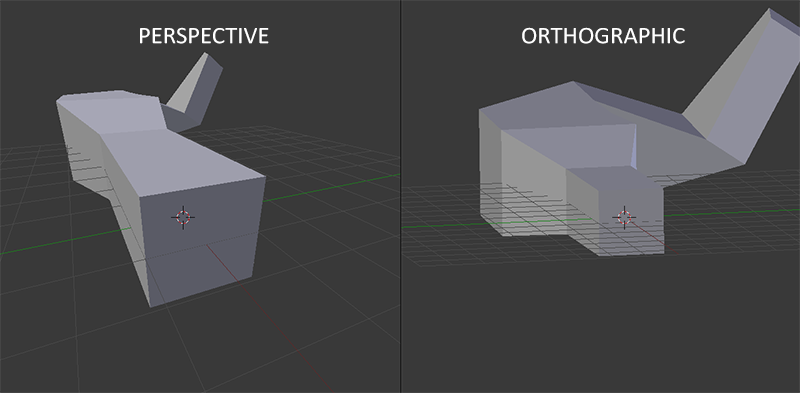
 当使用正射投影时，每一个顶点坐标都会直接映射到裁剪空间中而不经过任何精细的透视划分(它仍然会进行透视划分，只是w分量没有被操作(它保持为1)因此没有起作用)。因为正射投影没有使用透视，远处的对象不会显得小以产生神奇的视觉输出。由于这个原因，正射投影主要用于二维渲染以及一些建筑或工程的应用，或者是那些我们不需要使用投影来转换顶点的情况下。某些如Blender的进行三维建模的软件有时在建模时会使用正射投影，因为它在各个维度下都更准确地描绘了每个物体。下面你能够看到在Blender里面使用两种投影方式的对比：
 
-![perspective_orthographic](http://learnopengl.com/img/getting-started/perspective_orthographic.png)
+![perspective_orthographic](../img/01/08/perspective_orthographic.png)
 
 你可以看到使用透视投影的话，远处的顶点看起来比较小，而在正射投影中每个顶点距离观察者的距离都是一样的。
 
@@ -170,7 +170,7 @@ model = glm::rotate(model, -55.0f, glm::vec3(1.0f, 0.0f, 0.0f));
 
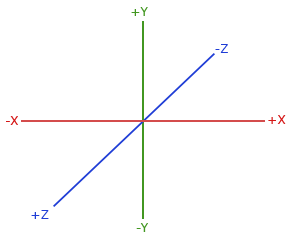
 	按照约定，OpenGL是一个右手坐标系。最基本的就是说正x轴在你的右手边，正y轴往上而正z轴是往后的。想象你的屏幕处于三个轴的中心且正z轴穿过你的屏幕朝向你。坐标系画起来如下：
 
-	![coordinate_systems_right_handed](http://learnopengl.com/img/getting-started/coordinate_systems_right_handed.png)
+	![coordinate_systems_right_handed](../img/01/08/coordinate_systems_right_handed.png)
 
 	为了理解为什么被称为右手坐标系，按如下的步骤做：
 
@@ -234,7 +234,7 @@ glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
 
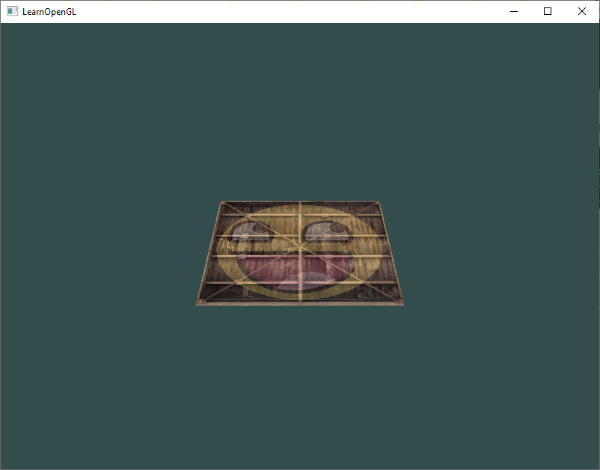
 让我们检查一下结果是否满足这些要求：
 
-![coordinate_systems_result](http://learnopengl.com/img/getting-started/coordinate_systems_result.png)
+![coordinate_systems_result](../img/01/08/coordinate_systems_result.png)
 
 它看起来就像是一个三维的平面，是静止在一些虚构的地板上的。如果你不是得到相同的结果，请检查下完整的[源代码](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems) 以及[顶点](http://learnopengl.com/code_viewer.php?code=getting-started/transform&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=getting-started/transform&type=fragment)着色器。
 
@@ -256,7 +256,7 @@ glDrawArrays(GL_TRIANGLES, 0, 36);
 
 如果一切顺利的话绘制效果将与下面的类似：
 
-<video src="http://learnopengl.com/video/getting-started/coordinate_system_no_depth.mp4" controls="controls"></video>
+<video src="../../img/01/08/coordinate_system_no_depth.mp4" controls="controls"></video>
 
 这有点像一个立方体，但又有种说不出的奇怪。立方体的某些本应被遮挡住的面被绘制在了这个立方体的其他面的上面。之所以这样是因为OpenGL是通过画一个一个三角形来画你的立方体的，所以它将会覆盖之前已经画在那里的像素。因为这个原因，有些三角形会画在其它三角形上面，虽然它们本不应该是被覆盖的。
 
@@ -280,7 +280,7 @@ glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
 
 我们来重新运行下程序看看OpenGL是否执行了深度测试：
 
-<video src="http://learnopengl.com/video/getting-started/coordinate_system_depth.mp4" controls="controls"></video>
+<video src="../../img/01/08/coordinate_system_depth.mp4" controls="controls"></video>
 
 就是这样！一个开启了深度测试，各个面都是纹理，并且还在旋转的立方体！如果你的程序有问题可以到[这里](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems_with_depth)下载源码进行比对。
 
@@ -324,7 +324,7 @@ glBindVertexArray(0);
 
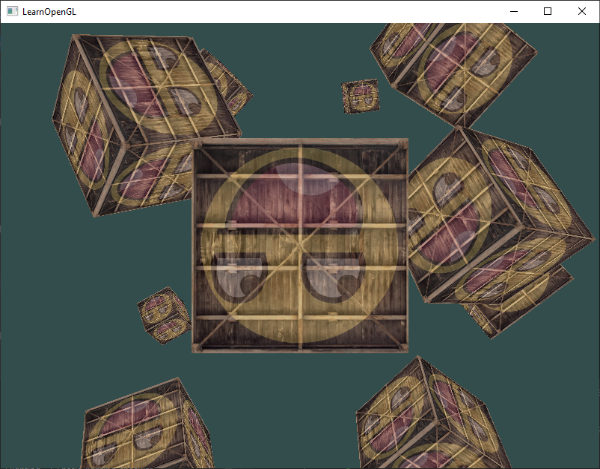
 这个代码将会每次都更新模型矩阵然后画出新的立方体，如此总共重复10次。然后我们应该就能看到一个拥有10个正在奇葩旋转着的立方体的世界。
 
-![coordinate_systems_multiple_objects](http://learnopengl.com/img/getting-started/coordinate_systems_multiple_objects.png)
+![coordinate_systems_multiple_objects](../img/01/08/coordinate_systems_multiple_objects.png)
 
 完美！这就像我们的箱子找到了志同道合的小伙伴一样。如果你在这里卡住了，你可以对照一下[代码](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems_multiple_objects) 以及[顶点着色器](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems&type=vertex)和[片段着色器](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems&type=fragment) 。
 
diff --git a/docs/01 Getting started/09 Camera.md b/docs/01 Getting started/09 Camera.md
index 05e0c10..4ec043b 100644
--- a/docs/01 Getting started/09 Camera.md	
+++ b/docs/01 Getting started/09 Camera.md	
@@ -14,7 +14,7 @@
 
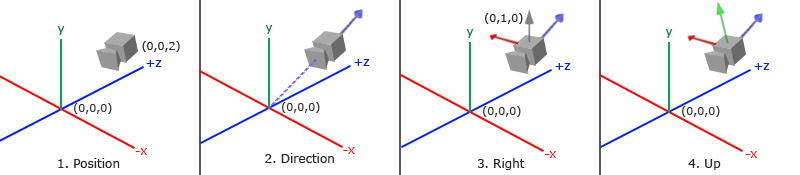
 当我们讨论摄像机/观察空间(Camera/View Space)的时候，是我们在讨论以摄像机的透视图作为场景原点时场景中所有可见顶点坐标。观察矩阵把所有的世界坐标变换到观察坐标，这些新坐标是相对于摄像机的位置和方向的。定义一个摄像机，我们需要一个摄像机在世界空间中的位置、观察的方向、一个指向它的右测的向量以及一个指向它上方的向量。细心的读者可能已经注意到我们实际上创建了一个三个单位轴相互垂直的、以摄像机的位置为原点的坐标系。
 
-![](http://learnopengl.com/img/getting-started/camera_axes.png)
+![](../img/01/09/camera_axes.png)
 
 ### 1. 摄像机位置
 
@@ -95,7 +95,7 @@ view = glm::lookAt(glm::vec3(camX, 0.0, camZ), glm::vec3(0.0, 0.0, 0.0), glm::ve
 
 如果你运行代码你会得到下面的东西：
 
-<video src="http://learnopengl.com/video/getting-started/camera_circle.mp4" controls="controls">
+<video src="../../img/01/09/camera_circle.mp4" controls="controls">
 </video>
 
 这一小段代码中，摄像机围绕场景转动。自己试试改变半径和位置/方向参数，看看LookAt矩阵是如何工作的。同时，这里有[源码](http://learnopengl.com/code_viewer.php?code=getting-started/camera_circle)、[顶点](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems&type=fragment)着色器。
@@ -144,7 +144,7 @@ void key_callback(GLFWwindow* window, int key, int scancode, int action, int mod
 
 如果你用这段代码更新`key_callback`函数，你就可以在场景中自由的前后左右移动了。
 
-<video src="http://learnopengl.com/video/getting-started/camera_inside.mp4" controls="controls">
+<video src="../../img/01/09/camera_inside.mp4" controls="controls">
 </video>
 
 你可能会注意到这个摄像机系统不能同时朝两个方向移动，当你按下一个按键时，它会先顿一下才开始移动。这是因为大多数事件输入系统一次只能处理一个键盘输入，它们的函数只有当我们激活了一个按键时才被调用。大多数GUI系统都是这样的，它对摄像机来说用并不合理。我们可以用一些小技巧解决这个问题。
@@ -234,7 +234,7 @@ void Do_Movement()
 与前面的部分结合在一起，我们有了一个更流畅点的摄像机系统：
 
 
-<video src="http://learnopengl.com/video/getting-started/camera_smooth.mp4" controls="controls">
+<video src="../../img/01/09/camera_smooth.mp4" controls="controls">
 </video>
 
 现在我们有了一个在任何系统上移动速度都一样的摄像机。这里是源码。我们可以看到任何移动都会影响返回的`deltaTime`值。
@@ -250,17 +250,17 @@ void Do_Movement()
 
 欧拉角(Euler Angle)是表示3D空间中可以表示任何旋转的三个值，由莱昂哈德·欧拉在18世纪提出。有三种欧拉角：俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll)，下面的图片展示了它们的含义：
 
-![](http://www.learnopengl.com/img/getting-started/camera_pitch_yaw_roll.png)
+![](../img/01/09/camera_pitch_yaw_roll.png)
 
 **俯仰角**是描述我们如何往上和往下看的角，它在第一张图中表示。第二张图显示了**偏航角**，偏航角表示我们往左和往右看的大小。**滚转角**代表我们如何翻滚摄像机。每个欧拉角都有一个值来表示，把三个角结合起来我们就能够计算3D空间中任何的旋转了。
 
 对于我们的摄像机系统来说，我们只关心俯仰角和偏航角，所以我们不会讨论滚转角。用一个给定的俯仰角和偏航角，我们可以把它们转换为一个代表新的方向向量的3D向量。俯仰角和偏航角转换为方向向量的处理需要一些三角学知识，我们以最基本的情况开始：
 
-![](http://www.learnopengl.com/img/getting-started/camera_triangle.png)
+![](../img/01/09/camera_triangle.png)
 
 如果我们把斜边边长定义为1，我们就能知道邻边的长度是\(\cos \ \color{red}x/\color{purple}h = \cos \ \color{red}x/\color{purple}1 = \cos\ \color{red}x\)，它的对边是\(\sin \ \color{green}y/\color{purple}h = \sin \ \color{green}y/\color{purple}1 = \sin\ \color{green}y\)。这样我们获得了能够得到x和y方向的长度的公式，它们取决于所给的角度。我们使用它来计算方向向量的元素：
 
-![](http://www.learnopengl.com/img/getting-started/camera_pitch.png)
+![](../img/01/09/camera_pitch.png)
 
 这个三角形看起来和前面的三角形很像，所以如果我们想象自己在xz平面上，正望向y轴，我们可以基于第一个三角形计算长度/y方向的强度(我们往上或往下看多少)。从图中我们可以看到一个给定俯仰角的y值等于sinθ:
 
@@ -277,7 +277,7 @@ direction.z = cos(glm::radians(pitch));
 
 看看我们是否能够为偏航角找到需要的元素：
 
-![](http://www.learnopengl.com/img/getting-started/camera_yaw.png)
+![](../img/01/09/camera_yaw.png)
 
 就像俯仰角一样我们可以看到x元素取决于cos(偏航角)的值，z值同样取决于偏航角的正弦值。把这个加到前面的值中，会得到基于俯仰角和偏航角的方向向量：
 
@@ -458,7 +458,7 @@ glfwSetScrollCallback(window, scroll_callback);
 
 现在我们实现了一个简单的摄像机系统，它能够让我们在3D环境中自由移动。
 
-<video src="http://learnopengl.com/video/getting-started/camera_mouse.mp4" controls="controls">
+<video src="../../img/01/09/camera_mouse.mp4" controls="controls">
 </video>
 
 自由的去实验，如果遇到困难对比[源代码](http://learnopengl.com/code_viewer.php?code=getting-started/camera_zoom)。
diff --git a/docs/02 Lighting/01 Colors.md b/docs/02 Lighting/01 Colors.md
index 031c25f..24b0404 100644
--- a/docs/02 Lighting/01 Colors.md	
+++ b/docs/02 Lighting/01 Colors.md	
@@ -17,7 +17,7 @@ glm::vec3 coral(1.0f, 0.5f, 0.31f);
 
 我们在现实生活中看到某一物体的颜色并不是这个物体的真实颜色，而是它所反射(Reflected)的颜色。换句话说，那些不能被物体吸收(Absorb)的颜色(被反射的颜色)就是我们能够感知到的物体的颜色。例如,太阳光被认为是由许多不同的颜色组合成的白色光(如下图所示)。如果我们将白光照在一个蓝色的玩具上，这个蓝色的玩具会吸收白光中除了蓝色以外的所有颜色，不被吸收的蓝色光被反射到我们的眼中，使我们看到了一个蓝色的玩具。下图显示的是一个珊瑚红的玩具，它以不同强度的方式反射了几种不同的颜色。
 
-![](http://learnopengl.com/img/lighting/light_reflection.png)
+![](../img/02/01/light_reflection.png)
 
 正如你所见，白色的阳光是一种所有可见颜色的集合，上面的物体吸收了其中的大部分颜色，它仅反射了那些代表这个物体颜色的部分，这些被反射颜色的组合就是我们感知到的颜色(此例中为珊瑚红)。
 
@@ -160,7 +160,7 @@ glBindVertexArray(0);
 
 请把上述的所有代码片段放在你程序中合适的位置，这样我们就能有一个干净的光照实验场地了。如果一切顺利，运行效果将会如下图所示：
 
-![](http://learnopengl.com/img/lighting/colors_scene.png)
+![](../img/02/01/colors_scene.png)
 
 没什么好看的是吗？但我保证在接下来的教程中它会给你有趣的视觉效果。
 
diff --git a/docs/02 Lighting/02 Basic Lighting.md b/docs/02 Lighting/02 Basic Lighting.md
index 33c9281..6dbde66 100644
--- a/docs/02 Lighting/02 Basic Lighting.md	
+++ b/docs/02 Lighting/02 Basic Lighting.md	
@@ -8,7 +8,7 @@
 
 现实世界的光照是极其复杂的，而且会受到诸多因素的影响，这是以目前我们所拥有的处理能力无法模拟的。因此OpenGL的光照仅仅使用了简化的模型并基于对现实的估计来进行模拟，这样处理起来会更容易一些，而且看起来也差不多一样。这些光照模型都是基于我们对光的物理特性的理解。其中一个模型被称为冯氏光照模型(Phong Lighting Model)。冯氏光照模型的主要结构由3个元素组成：环境(Ambient)、漫反射(Diffuse)和镜面(Specular)光照。这些光照元素看起来像下面这样：
 
-![](http://learnopengl.com/img/lighting/basic_lighting_phong.png)
+![](../img/02/02/basic_lighting_phong.png)
 
 - 环境光照(Ambient Lighting)：即使在黑暗的情况下，世界上也仍然有一些光亮(月亮、一个来自远处的光)，所以物体永远不会是完全黑暗的。我们使用环境光照来模拟这种情况，也就是无论如何永远都给物体一些颜色。
 - 漫反射光照(Diffuse Lighting)：模拟一个发光物对物体的方向性影响(Directional Impact)。它是冯氏光照模型最显著的组成部分。面向光源的一面比其他面会更亮。
@@ -36,13 +36,13 @@ void main()
 
 如果你现在运行你的程序，你会注意到冯氏光照的第一个阶段已经应用到你的物体上了。这个物体非常暗，但不是完全的黑暗，因为我们应用了环境光照(注意发光立方体没被环境光照影响是因为我们对它使用了另一个着色器)。它看起来应该像这样：
 
-![](http://learnopengl.com/img/lighting/ambient_lighting.png)
+![](../img/02/02/ambient_lighting.png)
 
 # 漫反射光照
 
 环境光本身不提供最明显的光照效果，但是漫反射光照(Diffuse Lighting)会对物体产生显著的视觉影响。漫反射光使物体上与光线排布越近的片段越能从光源处获得更多的亮度。为了更好的理解漫反射光照，请看下图：
 
-![](http://learnopengl.com/img/lighting/diffuse_light.png)
+![](../img/02/02/diffuse_light.png)
 
 图左上方有一个光源，它所发出的光线落在物体的一个片段上。我们需要测量这个光线与它所接触片段之间的角度。如果光线垂直于物体表面，这束光对物体的影响会最大化(译注：更亮)。为了测量光线和片段的角度，我们使用一个叫做法向量(Normal Vector)的东西，它是垂直于片段表面的一种向量(这里以黄色箭头表示)，我们在后面再讲这个东西。两个向量之间的角度就能够根据点乘计算出来。
 
@@ -168,7 +168,7 @@ color = vec4(result, 1.0f);
 
 如果你的应用(和着色器)编译成功了，你可能看到类似的输出：
 
-![](http://learnopengl.com/img/lighting/basic_lighting_diffuse.png)
+![](../img/02/02/basic_lighting_diffuse.png)
 
 你可以看到使用了散射光照，立方体看起来就真的像个立方体了。尝试在你的脑中想象，通过移动正方体，法向量和光的方向向量之间的夹角增大，片段变得更暗。
 
@@ -182,7 +182,7 @@ color = vec4(result, 1.0f);
 
 其次，如果模型矩阵执行了不等比缩放，法向量就不再垂直于表面了，顶点就会以这种方式被改变了。因此，我们不能用这样的模型矩阵去乘以法向量。下面的图展示了应用了不等比缩放的矩阵对法向量的影响：
 
-![](http://learnopengl.com/img/lighting/basic_lighting_normal_transformation.png)
+![](../img/02/02/basic_lighting_normal_transformation.png)
 
 无论何时当我们提交一个不等比缩放(注意：等比缩放不会破坏法线，因为法线的方向没被改变，而法线的长度很容易通过标准化进行修复)，法向量就不会再垂直于它们的表面了，这样光照会被扭曲。
 
@@ -208,7 +208,7 @@ Normal = mat3(transpose(inverse(model))) * normal;
 
 和环境光照一样，镜面光照(Specular Lighting)同样依据光的方向向量和物体的法向量，但是这次它也会依据观察方向，例如玩家是从什么方向看着这个片段的。镜面光照根据光的反射特性。如果我们想象物体表面像一面镜子一样，那么，无论我们从哪里去看那个表面所反射的光，镜面光照都会达到最大化。你可以从下面的图片看到效果：
 
-![](http://learnopengl.com/img/lighting/basic_lighting_specular_theory.png)
+![](../img/02/02/basic_lighting_specular_theory.png)
 
 我们通过反射法向量周围光的方向计算反射向量。然后我们计算反射向量和视线方向的角度，如果之间的角度越小，那么镜面光的作用就会越大。它的作用效果就是，当我们去看光被物体所反射的那个方向的时候，我们会看到一个高光。
 
@@ -251,7 +251,7 @@ vec3 specular = specularStrength * spec * lightColor;
 
 我们先计算视线方向与反射方向的点乘(确保它不是负值)，然后得到它的32次幂。这个32是高光的**发光值(Shininess)**。一个物体的发光值越高，反射光的能力越强，散射得越少，高光点越小。在下面的图片里，你会看到不同发光值对视觉(效果)的影响：
 
-![](http://learnopengl.com/img/lighting/basic_lighting_specular_shininess.png)
+![](../img/02/02/basic_lighting_specular_shininess.png)
 
 我们不希望镜面成分过于显眼，所以我们把指数设置为32。剩下的最后一件事情是把它添加到环境光颜色和散射光颜色里，然后再乘以物体颜色：
 
@@ -262,7 +262,7 @@ color = vec4(result, 1.0f);
 
 我们现在为冯氏光照计算了全部的光照元素。根据你的观察点，你可以看到类似下面的画面：
 
-![](http://learnopengl.com/img/lighting/basic_lighting_specular.png)
+![](../img/02/02/basic_lighting_specular.png)
 
 你可以[在这里找到完整源码](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting_specular)，在这里有[顶点](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting&type=fragment)着色器。
 
@@ -270,7 +270,7 @@ color = vec4(result, 1.0f);
 
     早期的光照着色器，开发者在顶点着色器中实现冯氏光照。在顶点着色器中做这件事的优势是，相比片段来说，顶点要少得多，因此会更高效，所以(开销大的)光照计算频率会更低。然而，顶点着色器中的颜色值是只是顶点的颜色值，片段的颜色值是它与周围的颜色值的插值。结果就是这种光照看起来不会非常真实，除非使用了大量顶点。
 
-    ![](http://learnopengl.com/img/lighting/basic_lighting_gouruad.png)
+    ![](../img/02/02/basic_lighting_gouruad.png)
 
     在顶点着色器中实现的冯氏光照模型叫做Gouraud着色，而不是冯氏着色。记住由于插值，这种光照连起来有点逊色。冯氏着色能产生更平滑的光照效果。
 
diff --git a/docs/02 Lighting/03 Materials.md b/docs/02 Lighting/03 Materials.md
index bb7147c..64eea8c 100644
--- a/docs/02 Lighting/03 Materials.md	
+++ b/docs/02 Lighting/03 Materials.md	
@@ -28,7 +28,7 @@ uniform Material material;
 
 这四个元素定义了一个物体的材质，通过它们我们能够模拟很多真实世界的材质。这里有一个列表[devernay.free.fr](http://devernay.free.fr/cours/opengl/materials.html)展示了几种材质属性，这些材质属性模拟外部世界的真实材质。下面的图片展示了几种真实世界材质对我们的立方体的影响：
 
-![](http://www.learnopengl.com/img/lighting/materials_real_world.png)
+![](../img/02/03/materials_real_world.png)
 
 如你所见，正确地指定一个物体的材质属性，似乎就是改变我们物体的相关属性的比例。效果显然很引人注目，但是对于大多数真实效果，我们最终需要更加复杂的形状，而不单单是一个立方体。在[后面的教程](../03 Model Loading/01 Assimp.md)中，我们会讨论更复杂的形状。
 
@@ -84,7 +84,7 @@ glUniform1f(matShineLoc, 32.0f);
 
 运行程序，会得到下面这样的结果：
 
-![](http://www.learnopengl.com/img/lighting/materials_with_material.png)
+![](../img/02/03/materials_with_material.png)
 
 看起来很奇怪不是吗？
 
@@ -142,7 +142,7 @@ glUniform3f(lightSpecularLoc, 1.0f, 1.0f, 1.0f);
 
 现在，我们调整了光是如何影响物体所有的材质的，我们得到一个更像前面教程的视觉输出。这次我们完全控制了物体光照和材质：
 
-![](http://www.learnopengl.com/img/lighting/materials_light.png)
+![](../img/02/03/materials_light.png)
 
 现在改变物体的外观相对简单了些。我们做点更有趣的事！
 
@@ -151,7 +151,7 @@ glUniform3f(lightSpecularLoc, 1.0f, 1.0f, 1.0f);
 
 目前为止，我们使用光源的颜色仅仅去改变物体各个元素的强度(通过选用从白到灰到黑范围内的颜色)，并没有影响物体的真实颜色(只是强度)。由于现在能够非常容易地访问光的属性了，我们可以随着时间改变它们的颜色来获得一些有很意思的效果。由于所有东西都已经在片段着色器做好了，改变光的颜色很简单，我们可以立即创建出一些有趣的效果：
 
-<video src="http://www.learnopengl.com/video/lighting/materials.mp4" controls="controls">
+<video src="../../img/02/03/materials.mp4" controls="controls">
 </video>
 
 如你所见，不同光的颜色极大地影响了物体的颜色输出。由于光的颜色直接影响物体反射的颜色(你可能想起在颜色教程中有讨论过)，它对视觉输出有显著的影响。
diff --git a/docs/02 Lighting/04 Lighting maps.md b/docs/02 Lighting/04 Lighting maps.md
index 25dbf15..b7fed2c 100644
--- a/docs/02 Lighting/04 Lighting maps.md	
+++ b/docs/02 Lighting/04 Lighting maps.md	
@@ -18,9 +18,9 @@
 
 这可能听起来极其相似，坦白来讲我们使用这样的系统已经有一段时间了。听起来很像在一个[之前的教程](../01 Getting started/06 Textures.md)中谈论的**纹理**，它基本就是一个纹理。我们其实是使用同一个潜在原则下的不同名称：使用一张图片覆盖住物体，以便我们为每个原始像素索引独立颜色值。在光照场景中，通过纹理来呈现一个物体的diffuse颜色，这个做法被称做**漫反射贴图(Diffuse texture)**(因为3D建模师就是这么称呼这个做法的)。
 
-为了演示漫反射贴图，我们将会使用[下面的图片](http://learnopengl.com/img/textures/container2.png)，它是一个有一圈钢边的木箱：
+为了演示漫反射贴图，我们将会使用[下面的图片](../img/02/04/container2.png)，它是一个有一圈钢边的木箱：
 
-![](http://www.learnopengl.com/img/textures/container2.png)
+![](../img/02/04/container2.png)
 
 在着色器中使用漫反射贴图和纹理教程介绍的一样。这次我们把纹理以sampler2D类型储存在Material结构体中。我们使用diffuse贴图替代早期定义的vec3类型的diffuse颜色。
 
@@ -85,7 +85,7 @@ glBindTexture(GL_TEXTURE_2D, diffuseMap);
 
 现在，使用一个diffuse贴图，我们在细节上再次获得惊人的提升，这次添加到箱子上的光照开始闪光了（名符其实）。你的箱子现在可能看起来像这样：
 
-![](http://www.learnopengl.com/img/lighting/materials_diffuse_map.png)
+![](../img/02/04/materials_diffuse_map.png)
 
 你可以在这里得到应用的[全部代码](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps_diffuse)。
 
@@ -94,9 +94,9 @@ glBindTexture(GL_TEXTURE_2D, diffuseMap);
 
 你可能注意到，specular高光看起来不怎么样，由于我们的物体是个箱子，大部分是木头，我们知道木头是不应该有镜面高光的。我们通过把物体设置specular材质设置为vec3(0.0f)来修正它。但是这样意味着铁边会不再显示镜面高光，我们知道钢铁是会显示一些镜面高光的。我们会想要控制物体部分地显示镜面高光，它带有修改了的亮度。这个问题看起来和diffuse贴图的讨论一样。这是巧合吗？我想不是。
 
-我们同样用一个纹理贴图，来获得镜面高光。这意味着我们需要生成一个黑白（或者你喜欢的颜色）纹理来定义specular亮度，把它应用到物体的每个部分。下面是一个[镜面贴图(Specular Map)](http://learnopengl.com/img/textures/container2_specular.png)的例子：
+我们同样用一个纹理贴图，来获得镜面高光。这意味着我们需要生成一个黑白（或者你喜欢的颜色）纹理来定义specular亮度，把它应用到物体的每个部分。下面是一个[镜面贴图(Specular Map)](../img/02/04/container2_specular.png)的例子：
 
-![](http://www.learnopengl.com/img/textures/container2_specular.png)
+![](../img/02/04/container2_specular.png)
 
 一个specular高光的亮度可以通过图片中每个纹理的亮度来获得。specular贴图的每个像素可以显示为一个颜色向量，比如：在那里黑色代表颜色向量vec3(0.0f)，灰色是vec3(0.5f)。在片段着色器中，我们采样相应的颜色值，把它乘以光的specular亮度。像素越“白”，乘积的结果越大，物体的specualr部分越亮。
 
@@ -144,7 +144,7 @@ color = vec4(ambient + diffuse + specular, 1.0f);
 
 如果你现在运行应用，你可以清晰地看到箱子的材质现在非常类似真实的铁边的木头箱子了：
 
-![](http://www.learnopengl.com/img/lighting/materials_specular_map.png)
+![](../img/02/04/materials_specular_map.png)
 
 你可以在这里找到[全部源码](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps_specular)。也对比一下你的[顶点着色器](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps&type=vertex)和[片段着色器](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps&type=fragment)。
 
@@ -154,5 +154,5 @@ color = vec4(ambient + diffuse + specular, 1.0f);
 
 - 调整光源的ambient，diffuse和specular向量值，看看它们如何影响实际输出的箱子外观。
 - 尝试在片段着色器中反转镜面贴图(Specular Map)的颜色值，然后木头就会变得反光而边框不会反光了（由于贴图中钢边依然有一些残余颜色，所以钢边依然会有一些高光，不过反光明显小了很多）。[参考解答](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps-exercise2)
-- 使用漫反射纹理(Diffuse Texture)原本的颜色而不是黑白色来创建镜面贴图，并观察，你会发现结果显得并不那么真实了。如果你不会处理图片，你可以使用这个[带颜色的镜面贴图](http://learnopengl.com/img/lighting/lighting_maps_specular_color.png)。[最终效果](learnopengl.com/img/lighting/lighting_maps_exercise3.png)
-- 添加一个叫做**放射光贴图(Emission Map)**的东西，即记录每个片段发光值(Emission Value)大小的贴图，发光值是(模拟)物体自身**发光(Emit)**时可能产生的颜色。这样的话物体就可以忽略环境光自身发光。通常在你看到游戏里某个东西(比如 [机器人的眼](http://www.witchbeam.com.au/unityboard/shaders_enemy.jpg),或是[箱子上的小灯](http://www.tomdalling.com/images/posts/modern-opengl-08/emissive.png))在发光时，使用的就是放射光贴图。使用[这个](http://learnopengl.com/img/textures/matrix.jpg)贴图(作者为 creativesam)作为放射光贴图并使用在箱子上，你就会看到箱子上有会发光的字了。[参考解答](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps-exercise4),[片段着色器](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps-exercise4_fragment), [最终效果](http://learnopengl.com/img/lighting/lighting_maps_exercise4.png)
+- 使用漫反射纹理(Diffuse Texture)原本的颜色而不是黑白色来创建镜面贴图，并观察，你会发现结果显得并不那么真实了。如果你不会处理图片，你可以使用这个[带颜色的镜面贴图](../img/02/04/lighting_maps_specular_color.png)。[最终效果](../img/02/04/lighting_maps_exercise3.png)
+- 添加一个叫做**放射光贴图(Emission Map)**的东西，即记录每个片段发光值(Emission Value)大小的贴图，发光值是(模拟)物体自身**发光(Emit)**时可能产生的颜色。这样的话物体就可以忽略环境光自身发光。通常在你看到游戏里某个东西(比如 [机器人的眼](http://www.witchbeam.com.au/unityboard/shaders_enemy.jpg),或是[箱子上的小灯](http://www.tomdalling.com/images/posts/modern-opengl-08/emissive.png))在发光时，使用的就是放射光贴图。使用[这个](../img/02/04/matrix.jpg)贴图(作者为 creativesam)作为放射光贴图并使用在箱子上，你就会看到箱子上有会发光的字了。[参考解答](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps-exercise4),[片段着色器](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps-exercise4_fragment), [最终效果](../img/02/04/lighting_maps_exercise4.png)
diff --git a/docs/02 Lighting/05 Light casters.md b/docs/02 Lighting/05 Light casters.md
index cc082ee..4c1a6e9 100644
--- a/docs/02 Lighting/05 Light casters.md	
+++ b/docs/02 Lighting/05 Light casters.md	
@@ -16,7 +16,7 @@
 
 我们知道的定向光源的一个好例子是，太阳。太阳和我们不是无限远，但它也足够远了，在计算光照的时候，我们感觉它就像无限远。在下面的图片里，来自于太阳的所有的光线都被定义为平行光：
 
-![](http://www.learnopengl.com/img/lighting/light_casters_directional.png)
+![](../img/02/05/light_casters_directional.png)
 
 因为所有的光线都是平行的，对于场景中的每个物体光的方向都保持一致，物体和光源的位置保持怎样的关系都无所谓。由于光的方向向量保持一致，光照计算会和场景中的其他物体相似。
 
@@ -82,7 +82,7 @@ glUniform3f(lightDirPos, -0.2f, -1.0f, -0.3f);
     
 如果你现在编译应用，飞跃场景，它看起来像有一个太阳一样的光源，把光抛到物体身上。你可以看到`diffuse`和`specular`元素都对该光源进行反射了，就像天空上有一个光源吗？看起来就像这样：
 
-![](http://www.learnopengl.com/img/lighting/light_casters_directional_light.png)
+![](../img/02/05/light_casters_directional_light.png)
 
 你可以在这里获得[应用的所有代码](http://learnopengl.com/code_viewer.php?code=lighting/light_casters_directional)，这里是[顶点](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=lighting/light_casters_directional&type=fragment)着色器代码。
 
@@ -90,7 +90,7 @@ glUniform3f(lightDirPos, -0.2f, -1.0f, -0.3f);
 
 定向光作为全局光可以照亮整个场景，这非常棒，但是另一方面除了定向光，我们通常也需要几个点光源(Point Light)，在场景里发亮。点光是一个在时间里有位置的光源，它向所有方向发光，光线随距离增加逐渐变暗。想象灯泡和火炬作为投光物，它们可以扮演点光的角色。
 
-![](http://www.learnopengl.com/img/lighting/light_casters_point.png)
+![](../img/02/05/light_casters_point.png)
 
 之前的教程我们已经使用了（最简单的）点光。我们指定了一个光源以及其所在的位置，它从这个位置向所有方向发散光线。然而，我们定义的光源所模拟光线的强度却不会因为距离变远而衰减，这使得看起来像是光源亮度极强。在大多数3D仿真场景中，我们更希望去模拟一个仅仅能照亮靠近光源点附近场景的光源，而不是照亮整个场景的光源。
 
@@ -114,7 +114,7 @@ $$
 
 由于二次项的光会以线性方式减少，指导距离足够大的时候，就会超过一次项，之后，光的亮度会减少的更快。最后的效果就是光在近距离时亮度很高，但是距离变远亮度迅速降低，最后亮度降低速度再次变慢。下面的图展示了在100以内的范围，这样的衰减效果。
 
-![](http://www.learnopengl.com/img/lighting/attenuation.png)
+![](../img/02/05/attenuation.png)
 
 你可以看到当距离很近的时候光有最强的亮度，但是随着距离增大，亮度明显减弱，大约接近100的时候，就会慢下来。这就是我们想要的。
 
@@ -187,7 +187,7 @@ specular *= attenuation;
 
 如果你运行应用后获得这样的效果：
 
-![](http://learnopengl.com/img/lighting/light_casters_point_light.png)
+![](../img/02/05/light_casters_point_light.png)
 
 你可以看到现在只有最近处的箱子的前面被照得最亮。后面的箱子一点都没被照亮，因为它们距离光源太远了。你可以在这里找到[应用源码](http://learnopengl.com/code_viewer.php?code=lighting/light_casters_point)和[片段着色器](http://learnopengl.com/code_viewer.php?code=lighting/light_casters_point&type=fragment)的代码。
 
@@ -200,7 +200,7 @@ specular *= attenuation;
 
 OpenGL中的聚光用世界空间位置，一个方向和一个指定了聚光半径的切光角来表示。我们计算的每个片段，如果片段在聚光的切光方向之间（就是在圆锥体内），我们就会把片段照亮。下面的图可以让你明白聚光是如何工作的：
 
-![](http://www.learnopengl.com/img/lighting/light_casters_spotlight_angles.png)
+![](../img/02/05/light_casters_spotlight_angles.png)
 
 * `LightDir`：从片段指向光源的向量。
 * `SpotDir`：聚光所指向的方向。
@@ -253,13 +253,13 @@ color = vec4(light.ambient*vec3(texture(material.diffuse,TexCoords)), 1.0f);
 
     你可能奇怪为什么if条件中使用>符号而不是<符号。为了在聚光以内，`theta`不是应该比光的切光值更小吗？这没错，但是不要忘了，角度值是以余弦值来表示的，一个0度的角表示为1.0的余弦值，当一个角是90度的时候被表示为0.0的余弦值，你可以在这里看到：
 
-    ![](http://www.learnopengl.com/img/lighting/light_casters_cos.png)
+    ![](../img/02/05/light_casters_cos.png)
 
     现在你可以看到，余弦越是接近1.0，角度就越小。这就解释了为什么θ需要比切光值更大了。切光值当前被设置为12.5的余弦，它等于0.9978，所以θ的余弦值在0.9979和1.0之间，片段会在聚光内，被照亮。
 
 运行应用，在聚光内的片段才会被照亮。这看起来像这样：
 
-![](http://www.learnopengl.com/img/lighting/light_casters_spotlight_hard.png)
+![](../img/02/05/light_casters_spotlight_hard.png)
 
 你可以在这里获得[全部源码](http://learnopengl.com/code_viewer.php?code=lighting/light_casters_spotlight_hard)和[片段着色器的源码](http://learnopengl.com/code_viewer.php?code=lighting/light_casters_spotlight_hard&type=fragment)。
 
@@ -310,7 +310,7 @@ specular* = intensity;
 
 确定你把`outerCutOff`值添加到了`Light`结构体，并在应用中设置了它的uniform值。对于下面的图片，内部切光角`12.5f`，外部切光角是`17.5f`：
 
-![](http://www.learnopengl.com/img/lighting/light_casters_spotlight.png)
+![](../img/02/05/light_casters_spotlight.png)
 
 看起来好多了。仔细看看内部和外部切光角，尝试创建一个符合你求的聚光。可以在这里找到应用源码，以及片段的源代码。
 
diff --git a/docs/02 Lighting/06 Multiple lights.md b/docs/02 Lighting/06 Multiple lights.md
index 4af7d83..e7a1eee 100644
--- a/docs/02 Lighting/06 Multiple lights.md	
+++ b/docs/02 Lighting/06 Multiple lights.md	
@@ -192,13 +192,13 @@ glm::vec3 pointLightPositions[] = {
 
 如果你在还是用了手电筒的话，将所有的光源结合起来看上去应该和下图差不多：
 
-![](http://learnopengl.com/img/lighting/multiple_lights_combined.png)
+![](../img/02/06/multiple_lights_combined.png)
 
 你可以在此处获取本教程的[源代码](http://learnopengl.com/code_viewer.php?code=lighting/multiple_lights)，同时可以查看[顶点着色器](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps&type=vertex)和[片段着色器](http://learnopengl.com/code_viewer.php?code=lighting/multiple_lights&type=fragment)的代码。
 
 上面的图片的光源都是使用默认的属性的效果，如果你尝试对光源属性做出各种修改尝试的话，会出现很多有意思的画面。很多艺术家和场景编辑器都提供大量的按钮或方式来修改光照以使用各种环境。使用最简单的光照属性的改变我们就足已创建有趣的视觉效果：
 
-![](http://learnopengl.com/img/lighting/multiple_lights_atmospheres.png)
+![](../img/02/06/multiple_lights_atmospheres.png)
 
 相信你现在已经对OpenGL的光照有很好的理解了。有了这些知识我们便可以创建丰富有趣的环境和氛围了。快试试改变所有的属性的值来创建你的光照环境吧！
 
diff --git a/docs/03 Model Loading/01 Assimp.md b/docs/03 Model Loading/01 Assimp.md
index 8cd8159..8493931 100644
--- a/docs/03 Model Loading/01 Assimp.md	
+++ b/docs/03 Model Loading/01 Assimp.md	
@@ -20,7 +20,7 @@
 当导入一个模型文件时，即Assimp加载一整个包含所有模型和场景数据的模型文件到一个scene对象时，Assimp会为这个模型文件中的所有场景节点、模型节点都生成一个具有对应关系的数据结构，且将这些场景中的各种元素与模型数据对应起来。下图展示了一个简化的Assimp生成的模型文件数据结构：
 
 
-![](http://learnopengl.com/img/model_loading/assimp_structure.png)
+![](../img/03/01/assimp_structure.png)
 
 
  - 所有的模型、场景数据都包含在scene对象中，如所有的材质和Mesh。同样，场景的根节点引用也包含在这个scene对象中
diff --git a/docs/03 Model Loading/03 Model.md b/docs/03 Model Loading/03 Model.md
index 4b11b31..e2309a4 100644
--- a/docs/03 Model Loading/03 Model.md	
+++ b/docs/03 Model Loading/03 Model.md	
@@ -353,13 +353,13 @@ vector<Texture> loadMaterialTextures(aiMaterial* mat, aiTextureType type, string
 
 现在在代码中，声明一个Model对象，把它模型的文件位置传递给它。模型应该自动加载（如果没有错误的话）在游戏循环中使用它的Draw函数绘制这个对象。没有更多的缓冲配置，属性指针和渲染命令，仅仅简单的一行。如果你创建几个简单的着色器，像素着色器只输出对象的漫反射贴图颜色，结果看上去会有点像这样：
 
-![](http://www.learnopengl.com/img/model_loading/model_diffuse.png)
+![](../img/03/03/model_diffuse.png)
 
 你可以从这里找到带有[顶点](http://learnopengl.com/code_viewer.php?code=model_loading/model&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=model_loading/model&type=fragment)着色器的[完整的源码](http://learnopengl.com/code_viewer.php?code=model_loading/model_diffuse)。
 
 因为我们之前学习过光照教程，可以更加富有创造性的引入两个点光源渲染方程，结合镜面贴图获得惊艳效果：
 
-![](http://www.learnopengl.com/img/model_loading/model_lighting.png)
+![](../img/03/03/model_lighting.png)
 
 甚至我不得不承认这个相比之前用过的容器酷炫多了。使用Assimp，你可以载入无数在互联网上找到的模型。有相当多可以以多种文件格式下载免费3D模型的资源网站。一定注意，有些模型仍然不能很好的载入，纹理路径无效或者这种格式Assimp不能读取。
 
diff --git a/docs/04 Advanced OpenGL/01 Depth testing.md b/docs/04 Advanced OpenGL/01 Depth testing.md
index 32e63c1..d869bb5 100644
--- a/docs/04 Advanced OpenGL/01 Depth testing.md	
+++ b/docs/04 Advanced OpenGL/01 Depth testing.md	
@@ -73,11 +73,11 @@ glDepthFunc(GL_ALWAYS);
 
 这和我们没有启用深度测试得到了相同的行为。深度测试只是简单地通过，所以这样最后绘制的片段就会呈现在之前绘制的片段前面，即使他们应该在前面。由于我们最后绘制地板平面，那么平面的片段会覆盖每个容器的片段:
 
-![](http://learnopengl.com/img/advanced/depth_testing_func_always.png)
+![](../img/04/01/depth_testing_func_always.png)
 
 重新设置到`GL_LESS`给了我们曾经的场景：
 
-![](http://learnopengl.com/img/advanced/depth_testing_func_less.png)
+![](../img/04/01/depth_testing_func_less.png)
 
 ## 深度值精度
 
@@ -89,7 +89,7 @@ $$
 
 这里far和near是我们用来提供到投影矩阵设置可见视图截锥的远近值 (见[坐标系](../01 Getting started/08 Coordinate Systems.md))。方程带内锥截体的深度值 z，并将其转换到 [0，1] 范围。在下面的图给出 z 值和其相应的深度值的关系:
 
-![](http://learnopengl.com/img/advanced/depth_linear_graph.png)
+![](../img/04/01/depth_linear_graph.png)
 
 !!! Important
 
@@ -105,7 +105,7 @@ $$
 
 如果你不知道这个方程到底怎么回事也不必担心。要记住的重要一点是在深度缓冲区的值不是线性的屏幕空间 (它们在视图空间投影矩阵应用之前是线性)。值为 0.5 在深度缓冲区并不意味着该对象的 z 值是投影平头截体的中间;顶点的 z 值是实际上相当接近近平面!你可以看到 z 值和产生深度缓冲区的值在下列图中的非线性关系:
 
-![](http://learnopengl.com/img/advanced/depth_non_linear_graph.png)
+![](../img/04/01/depth_non_linear_graph.png)
 
 正如你所看到，一个附近的物体的小的 z 值因此给了我们很高的深度精度。变换 (从观察者的角度) 的 z 值的方程式被嵌入在投影矩阵，所以当我们变换顶点坐标从视图到裁剪，然后到非线性方程应用了的屏幕空间中。如果你好奇的投影矩阵究竟做了什么我建议阅读[这个文章](http://www.songho.ca/opengl/gl_projectionmatrix.html)。
 
@@ -126,7 +126,7 @@ void main()
 
 你可能还记得从上一节中的屏幕空间的深度值是非线性如他们在z很小的时候有很高的精度，，较大的 z 值有较低的精度。该片段的深度值会迅速增加，所以几乎所有顶点的深度值接近 1.0。如果我们小心的靠近物体，你最终可能会看到的色彩越来越暗，意味着它们的 z 值越来越小:
 
-![](http://www.learnopengl.com/img/advanced/depth_testing_visible_depth.png)
+![](../img/04/01/depth_testing_visible_depth.png)
 
 这清楚地表明深度值的非线性特性。近的物体相对远的物体对的深度值比对象较大的影响。只移动几英寸就能让暗色完全变亮。
 
@@ -172,7 +172,7 @@ void main()
 
 如果现在运行该应用程序，我们得到在距离实际上线性的深度值。尝试移动现场周围看到深度值线性变化
 
-![](http://www.learnopengl.com/img/advanced/depth_testing_visible_linear.png)。
+![](../img/04/01/depth_testing_visible_linear.png)。
 
 颜色主要是黑色的因为深度值线性范围从 0.1 的近平面到 100 的远平面，那里离我们很远。其结果是，我们相对靠近近平面，从而得到较低 (较暗) 的深度值。
 
@@ -184,7 +184,7 @@ void main()
 
 如果您移动摄像机到容器的里面，那么这个影响清晰可，容器的底部不断切换容器的平面和地板的平面:
 
-![](http://www.learnopengl.com/img/advanced/depth_testing_z_fighting.png)
+![](../img/04/01/depth_testing_z_fighting.png)
 
 深度冲突是深度缓冲区的普遍问题，当对象的距离越远一般越强(因为深度缓冲区在z值非常大的时候没有很高的精度)。深度冲突还无法完全避免，但有一般的几个技巧，将有助于减轻或完全防止深度冲突在你的场景中的出现：
 
diff --git a/docs/04 Advanced OpenGL/02 Stencil testing.md b/docs/04 Advanced OpenGL/02 Stencil testing.md
index 62573a0..7cde8b6 100644
--- a/docs/04 Advanced OpenGL/02 Stencil testing.md	
+++ b/docs/04 Advanced OpenGL/02 Stencil testing.md	
@@ -16,7 +16,7 @@
 
 下面是一个模板缓冲的简单例子：
 
-![image description](http://learnopengl.com/img/advanced/stencil_buffer.png)
+![image description](../img/04/02/stencil_buffer.png)
 
 模板缓冲先清空模板缓冲设置所有片段的模板值为0，然后开启矩形片段用1填充。场景中的模板值为1的那些片段才会被渲染（其他的都被丢弃）。
 
@@ -102,7 +102,7 @@ GL_INVERT   | Bitwise inverts the current stencil buffer value.
 
 看了前面的部分你未必能理解模板测试是如何工作的，所以我们会展示一个用模板测试实现的一个特别的和有用的功能，叫做**物体轮廓(Object Outlining)**。
 
-![](http://learnopengl.com/img/advanced/stencil_object_outlining.png)
+![](../img/04/02/stencil_object_outlining.png)
 
 物体轮廓就像它的名字所描述的那样，它能够给每个（或一个）物体创建一个有颜色的边。在策略游戏中当你打算选择一个单位的时候它特别有用。给物体加上轮廓的步骤如下：
 
@@ -190,7 +190,7 @@ glEnable(GL_DEPTH_TEST);
 
 这个边框的算法的结果在深度测试教程的那个场景中，看起来像这样：
 
-![](http://learnopengl.com/img/advanced/stencil_scene_outlined.png)
+![](../img/04/02/stencil_scene_outlined.png)
 
 在这里[查看源码](http://learnopengl.com/code_viewer.php?code=advanced/stencil_testing)和[着色器](http://learnopengl.com/code_viewer.php?code=advanced/depth_testing_func_shaders)，看看完整的物体边框算法是怎样的。
 
diff --git a/docs/04 Advanced OpenGL/03 Blending.md b/docs/04 Advanced OpenGL/03 Blending.md
index 58102e5..9b0c63e 100644
--- a/docs/04 Advanced OpenGL/03 Blending.md	
+++ b/docs/04 Advanced OpenGL/03 Blending.md	
@@ -9,13 +9,13 @@
 
 在OpenGL中，物体透明技术通常被叫做**混合(Blending)**。透明是物体（或物体的一部分）非纯色而是混合色，这种颜色来自于不同浓度的自身颜色和它后面的物体颜色。一个有色玻璃窗就是一种透明物体，玻璃有自身的颜色，但是最终的颜色包含了所有玻璃后面的颜色。这也正是混合这名称的出处，因为我们将多种（来自于不同物体）颜色混合为一个颜色，透明使得我们可以看穿物体。
 
-![](http://learnopengl.com/img/advanced/blending_transparency.png)
+![](../img/04/03/blending_transparency.png)
 
 透明物体可以是完全透明（它使颜色完全穿透）或者半透明的（它使颜色穿透的同时也显示自身颜色）。一个物体的透明度，被定义为它的颜色的alpha值。alpha颜色值是一个颜色向量的第四个元素，你可能已经看到很多了。在这个教程前，我们一直把这个元素设置为1.0，这样物体的透明度就是0.0，同样的，当alpha值是0.0时就表示物体是完全透明的，alpha值为0.5时表示物体的颜色由50%的自身的颜色和50%的后面的颜色组成。
 
-我们之前所使用的纹理都是由3个颜色元素组成的：红、绿、蓝，但是有些纹理同样有一个内嵌的aloha通道，它为每个纹理像素(Texel)包含着一个alpha值。这个alpha值告诉我们纹理的哪个部分有透明度，以及这个透明度有多少。例如，下面的窗子纹理的玻璃部分的alpha值为0.25(它的颜色是完全红色，但是由于它有75的透明度，它会很大程度上反映出网站的背景色，看起来就不那么红了)，角落部分alpha是0.0。
+我们之前所使用的纹理都是由3个颜色元素组成的：红、绿、蓝，但是有些纹理同样有一个内嵌的aloha通道，它为每个纹理像素(Texel)包含着一个alpha值。这个alpha值告诉我们纹理的哪个部分有透明度，以及这个透明度有多少。例如，下面的[窗户纹理](../img/04/03/blending_transparent_window.png)的玻璃部分的alpha值为0.25(它的颜色是完全红色，但是由于它有75的透明度，它会很大程度上反映出网站的背景色，看起来就不那么红了)，角落部分alpha是0.0。
 
-![](http://learnopengl.com/img/advanced/blending_transparent_window.png)
+![](../img/04/03/blending_transparent_window.png)
 
 我们很快就会把这个窗子纹理加到场景中，但是首先，我们将讨论一点简单的技术来实现纹理的半透明，也就是完全透明和完全不透明。
 
@@ -25,7 +25,7 @@
 
 下面的纹理正是这样的纹理，它既有完全不透明的部分（alpha值为1.0）也有完全透明的部分（alpha值为0.0），而没有半透明的部分。你可以看到没有草的部分，图片显示了网站的背景色，而不是它自身的那部分颜色。
 
-![](http://learnopengl.com/img/textures/grass.png)
+![](../img/04/03/grass.png)
 
 所以，当向场景中添加像这样的纹理时，我们不希望看到一个方块图像，而是只显示实际的纹理像素，剩下的部分可以被看穿。我们要忽略(丢弃)纹理透明部分的像素，不必将这些片段储存到颜色缓冲中。在此之前，我们还要学一下如何加载一个带有透明像素的纹理。
 
@@ -82,7 +82,7 @@ glBindVertexArray(0);
 ```
 
 运行程序你将看到：
-![](http://learnopengl.com/img/advanced/blending_no_discard.png)
+![](../img/04/03/blending_no_discard.png)
 
 出现这种情况是因为OpenGL默认是不知道如何处理alpha值的，不知道何时忽略(丢弃)它们。我们不得不手动做这件事。幸运的是这很简单，感谢着色器，GLSL为我们提供了discard命令，它保证了片段不会被进一步处理，这样就不会进入颜色缓冲。有了这个命令我们就可以在片段着色器中检查一个片段是否有在一定的阈限下的alpha值，如果有，那么丢弃这个片段，就好像它不存在一样：
 
@@ -105,7 +105,7 @@ void main()
 
 在这儿我们检查被采样纹理颜色包含着一个低于0.1这个阈限的alpha值，如果有，就丢弃这个片段。这个片段着色器能够保证我们只渲染哪些不是完全透明的片段。现在我们来看看效果：
 
-![](http://learnopengl.com/img/advanced/blending_discard.png)
+![](../img/04/03/blending_discard.png)
 
 !!! Important
 
@@ -141,7 +141,7 @@ $$
 
 片段着色器运行完成并且所有的测试都通过以后，混合方程才能自由执行片段的颜色输出，当前它在颜色缓冲中（前面片段的颜色在当前片段之前储存）。源和目标颜色会自动被OpenGL设置，而源和目标因子可以让我们自由设置。我们来看一个简单的例子：
 
-![](http://learnopengl.com/img/advanced/blending_equation.png)
+![](../img/04/03/blending_equation.png)
 
 我们有两个方块，我们希望在红色方块上绘制绿色方块。红色方块会成为目标颜色（它会先进入颜色缓冲），我们将在红色方块上绘制绿色方块。
 
@@ -153,7 +153,7 @@ $$
 
 最终方块结合部分包含了60%的绿色和40%的红色，得到一种脏兮兮的颜色：
 
-![](http://learnopengl.com/img/advanced/blending_equation_mixed.png)
+![](../img/04/03/blending_equation_mixed.png)
 
 最后的颜色被储存到颜色缓冲中，取代先前的颜色。
 
@@ -232,7 +232,7 @@ void main()
 
 这一次（无论OpenGL什么时候去渲染一个片段），它都根据alpha值，把当前片段的颜色和颜色缓冲中的颜色进行混合。因为窗子的玻璃部分的纹理是半透明的，我们应该可以透过玻璃看到整个场景。
 
-![](http://learnopengl.com/img/advanced/blending_incorrect_order.png)
+![](../img/04/03/blending_incorrect_order.png)
 
 如果你仔细看看，就会注意到有些不对劲。前面的窗子透明部分阻塞了后面的。为什么会这样？
 
@@ -278,7 +278,7 @@ for(std::map<float,glm::vec3>::reverse_iterator it = sorted.rbegin(); it != sort
 
 我们从map得来一个逆序的迭代器，迭代出每个逆序的条目，然后把每个窗子的四边形平移到相应的位置。这个相对简单的方法对透明物体进行了排序，修正了前面的问题，现在场景看起来像这样：
 
-![](http://learnopengl.com/img/advanced/blending_sorted.png)
+![](../img/04/03/blending_sorted.png)
 
 你可以[从这里得到完整的带有排序的源码](http://learnopengl.com/code_viewer.php?code=advanced/blending_sorted)。
 
diff --git a/docs/04 Advanced OpenGL/04 Face culling.md b/docs/04 Advanced OpenGL/04 Face culling.md
index 961bc2f..b173f50 100644
--- a/docs/04 Advanced OpenGL/04 Face culling.md	
+++ b/docs/04 Advanced OpenGL/04 Face culling.md	
@@ -22,7 +22,7 @@
 
 当我们定义一系列的三角顶点时，我们会把它们定义为一个特定的连接顺序(Winding Order)，它们可能是**顺时针**的或**逆时针**的。每个三角形由3个顶点组成，我们从三角形的中间去看，从而把这三个顶点指定一个连接顺序。
 
-![](http://learnopengl.com/img/advanced/faceculling_windingorder.png)
+![](../img/04/04/faceculling_windingorder.png)
 
 正如你所看到的那样，我们先定义了顶点1，接着我们定义顶点2或3，这个不同的选择决定了这个三角形的连接顺序。下面的代码展示出这点：
 
@@ -45,7 +45,7 @@ GLfloat vertices[] = {
 
 我们指定了它们以后，观察者面对的所有的三角形的顶点的连接顺序都是正确的，但是现在渲染的立方体另一面的三角形的顶点的连接顺序被反转。最终，我们所面对的三角形被视为正面朝向的三角形，后部的三角形被视为背面朝向的三角形。下图展示了这个效果：
 
-![](http://learnopengl.com/img/advanced/faceculling_frontback.png)
+![](../img/04/04/faceculling_frontback.png)
 
 在顶点数据中，我们定义的是两个逆时针顺序的三角形。然而，从观察者的方面看，后面的三角形是顺时针的，如果我们仍以1、2、3的顺序以观察者当面的视野看的话。即使我们以逆时针顺序定义后面的三角形，它现在还是变为顺时针。它正是我们打算剔除（丢弃）的不可见的面！
 
@@ -95,7 +95,7 @@ glFrontFace(GL_CW);
 
 最后的结果只有背面被渲染了：
 
-![](http://learnopengl.com/img/advanced/faceculling_reverse.png)
+![](../img/04/04/faceculling_reverse.png)
 
 要注意，你可以使用默认逆时针顺序剔除正面，来创建相同的效果：
 
diff --git a/docs/04 Advanced OpenGL/05 Framebuffers.md b/docs/04 Advanced OpenGL/05 Framebuffers.md
index a712093..13ac4df 100644
--- a/docs/04 Advanced OpenGL/05 Framebuffers.md	
+++ b/docs/04 Advanced OpenGL/05 Framebuffers.md	
@@ -209,7 +209,7 @@ glBindFramebuffer(GL_FRAMEBUFFER, 0);
 2. 绑定到默认帧缓冲。
 3. 绘制一个四边形，让它平铺到整个屏幕上，用新的帧缓冲的颜色缓冲作为他的纹理。
 
-我们使用在深度测试教程中同一个场景进行绘制，但是这次使用老气横秋的[箱子纹理](http://learnopengl.com/img/textures/container.jpg)。
+我们使用在深度测试教程中同一个场景进行绘制，但是这次使用老气横秋的[箱子纹理](../img/04/05/container.jpg)。
 
 为了绘制四边形我们将会创建新的着色器。我们不打算引入任何花哨的变换矩阵，因为我们只提供已经是标准化设备坐标的[顶点坐标](http://learnopengl.com/code_viewer.php?code=advanced/framebuffers_quad_vertices)，所以我们可以直接把它们作为顶点着色器的输出。顶点着色器看起来像这样：
 
@@ -269,7 +269,7 @@ glBindVertexArray(0);
 
 这里的确有很多地方会做错，所以如果你没有获得任何输出，尝试排查任何可能出现错误的地方，再次阅读教程中相关章节。如果每件事都做对了就一定能成功，你将会得到这样的输出：
 
-![](http://learnopengl.com/img/advanced/framebuffers_screen_texture.png)
+![](../img/04/05/framebuffers_screen_texture.png)
 
 左侧展示了和深度测试教程中一样的输出结果，但是这次却是渲染到一个简单的四边形上的。如果我们以线框方式显示的话，那么显然，我们只是绘制了一个默认帧缓冲中单调的四边形。
 
@@ -295,7 +295,7 @@ void main()
 
 虽然反相是一种相对简单的后处理特效，但是已经很有趣了：
 
-![image description](http://learnopengl.com/img/advanced/framebuffers_grayscale.png)
+![image description](../img/04/05/framebuffers_grayscale.png)
 
 整个场景现在的颜色都反转了，只需在着色器中写一行代码就能做到，酷吧？
 
@@ -322,7 +322,7 @@ void main()
 }
 ```
 
-![](http://learnopengl.com/img/advanced/framebuffers_grayscale.png)
+![](../img/04/05/framebuffers_grayscale.png)
 
 ## Kernel effects
 
@@ -382,7 +382,7 @@ void main()
 
 这个锐化的kernel看起来像这样：
 
-![](http://learnopengl.com/img/advanced/framebuffers_sharpen.png)
+![](../img/04/05/framebuffers_sharpen.png)
 
 这里创建的有趣的效果就好像你的玩家吞了某种麻醉剂产生的幻觉一样。
 
@@ -406,7 +406,7 @@ float kernel[9] = float[](
 
 通过在像素着色器中改变kernel的float数组,我们就完全改变了之后的后处理效果.现在看起来会像是这样:
 
-![](http://learnopengl.com/img/advanced/framebuffers_blur.png)
+![](../img/04/05/framebuffers_blur.png)
 
 这样的模糊效果具有创建许多有趣效果的潜力.例如,我们可以随着时间的变化改变模糊量,创建出类似于某人喝醉酒的效果,或者,当我们的主角摘掉眼镜的时候增加模糊.模糊也能为我们在后面的教程中提供都颜色值进行平滑处理的能力.
 
@@ -422,11 +422,11 @@ $$
 
 这个kernel将所有的边提高亮度,而对其他部分进行暗化处理,当我们值关心一副图像的边缘的时候,它非常有用.
 
-![](http://learnopengl.com/img/advanced/framebuffers_edge_detection.png)
+![](../img/04/05/framebuffers_edge_detection.png)
 
 在一些像Photoshop这样的软件中使用这些kernel作为图像操作工具/过滤器一点都不奇怪.因为掀开可以具有很强的平行处理能力，我们以实时进行针对每个像素的图像操作便相对容易，图像编辑工具因而更经常使用显卡来进行图像处理。
 
 ## 练习
 
-* 你可以使用帧缓冲来创建一个后视镜吗?做到它,你必须绘制场景两次:一次正常绘制,另一次摄像机旋转180度后绘制.尝试在你的显示器顶端创建一个小四边形,在上面应用后视镜的镜面纹理:[解决方案](http://learnopengl.com/code_viewer.php?code=advanced/framebuffers-exercise1),[视觉效果](http://learnopengl.com/img/advanced/framebuffers_mirror.png)
+* 你可以使用帧缓冲来创建一个后视镜吗?做到它,你必须绘制场景两次:一次正常绘制,另一次摄像机旋转180度后绘制.尝试在你的显示器顶端创建一个小四边形,在上面应用后视镜的镜面纹理:[解决方案](http://learnopengl.com/code_viewer.php?code=advanced/framebuffers-exercise1),[视觉效果](../img/04/05/framebuffers_mirror.png)
 * 自己随意调整一下kernel值,创建出你自己后处理特效.尝试在网上搜索其他有趣的kernel.
diff --git a/docs/04 Advanced OpenGL/06 Cubemaps.md b/docs/04 Advanced OpenGL/06 Cubemaps.md
index 3b85b64..e5dc0c2 100644
--- a/docs/04 Advanced OpenGL/06 Cubemaps.md	
+++ b/docs/04 Advanced OpenGL/06 Cubemaps.md	
@@ -12,7 +12,7 @@
 
 从立方体贴图上使用橘黄色向量采样一个纹理值看起来和下图有点像：
 
-![](http://learnopengl.com/img/advanced/cubemaps_sampling.png)
+![](../img/04/06/cubemaps_sampling.png)
 
 !!! Important
 
@@ -96,17 +96,17 @@ void main()
 
 天空盒(Skybox)是一个包裹整个场景的立方体，它由6个图像构成一个环绕的环境，给玩家一种他所在的场景比实际的要大得多的幻觉。比如有些在视频游戏中使用的天空盒的图像是群山、白云或者满天繁星。比如下面的夜空繁星的图像就来自《上古卷轴》：
 
-![](http://learnopengl.com/img/advanced/cubemaps_morrowind.jpg)
+![](../img/04/06/cubemaps_morrowind.jpg)
 
 你现在可能已经猜到立方体贴图完全满足天空盒的要求：我们有一个立方体，它有6个面，每个面需要一个贴图。上图中使用了几个夜空的图片给予玩家一种置身广袤宇宙的感觉，可实际上，他还是在一个小盒子之中。
 
 网上有很多这样的天空盒的资源。[这个网站](http://www.custommapmakers.org/skyboxes.php)就提供了很多。这些天空盒图像通常有下面的样式：
 
-![](http://learnopengl.com/img/advanced/cubemaps_skybox.png)
+![](../img/04/06/cubemaps_skybox.png)
 
 如果你把这6个面折叠到一个立方体中，你机会获得模拟了一个巨大的风景的立方体。有些资源所提供的天空盒比如这个例子6个图是连在一起的，你必须手工它们切割出来，不过大多数情况它们都是6个单独的纹理图像。
 
-这个细致（高精度）的天空盒就是我们将在场景中使用的那个，你可以[在这里下载](http://learnopengl.com/img/textures/skybox.rar)。
+这个细致（高精度）的天空盒就是我们将在场景中使用的那个，你可以[在这里下载](../img/04/06/skybox.rar)。
 
 ## 加载天空盒
 
@@ -220,7 +220,7 @@ glm::mat4 view = glm::mat4(glm::mat3(camera.GetViewMatrix()));
 
 这会移除所有平移，但保留所有旋转，因此用户仍然能够向四面八方看。由于有了天空盒，场景即可变得巨大了。如果你添加些物体然后自由在其中游荡一会儿你会发现场景的真实度有了极大提升。最后的效果看起来像这样：
 
-![](http://learnopengl.com/img/advanced/cubemaps_skybox_result.png)
+![](../img/04/06/cubemaps_skybox_result.png)
 
 [这里有全部源码](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps_skybox)，你可以对比一下你写的。
 
@@ -259,7 +259,7 @@ void main()
 
 反射的基本思路不难。下图展示了我们如何计算反射向量，然后使用这个向量去从一个立方体贴图中采样：
 
-![](http://learnopengl.com/img/advanced/cubemaps_reflection_theory.png)
+![](../img/04/06/cubemaps_reflection_theory.png)
 
 我们基于观察方向向量I和物体的法线向量N计算出反射向量R。我们可以使用GLSL的内建函数reflect来计算这个反射向量。最后向量R作为一个方向向量对立方体贴图进行索引/采样，返回一个环境的颜色值。最后的效果看起来就像物体反射了天空盒。
 
@@ -319,13 +319,13 @@ glBindVertexArray(0);
 
 编译运行你的代码，你等得到一个镜子一样的箱子。箱子完美地反射了周围的天空盒：
 
-![](http://learnopengl.com/img/advanced/cubemaps_reflection.png)
+![](../img/04/06/cubemaps_reflection.png)
 
 你可以[从这里找到全部源代码](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps_reflection)。
 
 当反射应用于整个物体之上的时候，物体看上去就像有一个像钢和铬这种高反射材质。如果我们加载[模型教程](../03 Model Loading/03 Model.md)中的纳米铠甲模型，我们就会获得一个铬金属制铠甲：
 
-![](http://learnopengl.com/img/advanced/cubemaps_reflection_nanosuit.png)
+![](../img/04/06/cubemaps_reflection_nanosuit.png)
 
 看起来挺惊艳，但是现实中大多数模型都不是完全反射的。我们可以引进反射贴图（reflection map）来使模型有另一层细节。和diffuse、specular贴图一样，我们可以从反射贴图上采样来决定fragment的反射率。使用反射贴图我们还可以决定模型的哪个部分有反射能力，以及强度是多少。本节的练习中，要由你来在我们早期创建的模型加载器引入反射贴图，这回极大的提升纳米服模型的细节。
 
@@ -335,7 +335,7 @@ glBindVertexArray(0);
 
 折射遵守[斯涅尔定律](http://en.wikipedia.org/wiki/Snell%27s_law)，使用环境贴图看起来就像这样：
 
-![](http://learnopengl.com/img/advanced/cubemaps_refraction_theory.png)
+![](../img/04/06/cubemaps_refraction_theory.png)
 
 我们有个观察向量I，一个法线向量N，这次折射向量是R。就像你所看到的那样，观察向量的方向有轻微弯曲。弯曲的向量R随后用来从立方体贴图上采样。
 
@@ -367,7 +367,7 @@ void main()
 
 通过改变折射指数你可以创建出完全不同的视觉效果。编译运行应用，结果也不是太有趣，因为我们只是用了一个普通箱子，这不能显示出折射的效果，看起来像个放大镜。使用同一个着色器，纳米服模型却可以展示出我们期待的效果：玻璃制物体。
 
-![](http://learnopengl.com/img/advanced/cubemaps_refraction.png)
+![](../img/04/06/cubemaps_refraction.png)
 
 你可以向想象一下，如果将光线、反射、折射和顶点的移动合理的结合起来就能创造出漂亮的水的图像。一定要注意，出于物理精确的考虑当光线离开物体的时候还要再次进行折射；现在我们简单的使用了单边（一次）折射，大多数目的都可以得到满足。
 
@@ -383,7 +383,7 @@ void main()
 
 ## 练习
 
-- 尝试在模型加载中引进反射贴图，你将再次得到很大视觉效果的提升。这其中有几点需要注意：
+- 尝试在之前模型加载小节的模型加载器中引进反射贴图，你可以在[这里](../img/04/06/nanosuit_reflection.zip)找到升级过的纳米装模型，反射贴图也包含在里面。这其中有几点需要注意：
 	- Assimp并不支持反射贴图，我们可以使用环境贴图的方式将反射贴图从`aiTextureType_AMBIENT`类型中来加载反射贴图的材质。
 	- 我匆忙地使用反射贴图来作为镜面反射的贴图，而反射贴图并没有很好的映射在模型上:)。
 	- 由于加载模型已经占用了3个纹理单元，因此你要绑定天空盒到第4个纹理单元上，这样才能在同一个着色器内从天空盒纹理中取样。
@@ -391,4 +391,4 @@ void main()
 
 如果你一切都做对了，那你应该看到和下图类似的效果：
 
-![](http://learnopengl.com/img/advanced/cubemaps_reflection_map.png)
+![](../img/04/06/cubemaps_reflection_map.png)
diff --git a/docs/04 Advanced OpenGL/08 Advanced GLSL.md b/docs/04 Advanced OpenGL/08 Advanced GLSL.md
index bfd1efe..fc30f9c 100644
--- a/docs/04 Advanced OpenGL/08 Advanced GLSL.md	
+++ b/docs/04 Advanced OpenGL/08 Advanced GLSL.md	
@@ -45,7 +45,7 @@ void main()
 
 结果是我们绘制的点距离我们越远就越大：
 
-![](http://learnopengl.com/img/advanced/advanced_glsl_pointsize.png)
+![](../img/04/08/advanced_glsl_pointsize.png)
 
 想象一下，每个顶点表示出来的点的大小的不同，如果用在像粒子生成之类的技术里会挺有意思的。
 
@@ -82,7 +82,7 @@ void main()
 
 因为窗口的宽是800，当一个像素的x坐标小于400，那么它一定在窗口的左边，这样我们就让物体有个不同的颜色。
 
-![](http://learnopengl.com/img/advanced/advanced_glsl_frontfacing.png)
+![](../img/04/08/advanced_glsl_frontfacing.png)
 
 我们现在可以计算出两个完全不同的片段着色器结果，每个显示在窗口的一端。这对于测试不同的光照技术很有好处。
 
@@ -111,7 +111,7 @@ void main()
 
 如果我们从箱子的一角往里看，就能看到里面用的是另一个纹理。
 
-![](http://learnopengl.com/img/advanced/advanced_glsl_frontfacing.png)
+![](../img/04/08/advanced_glsl_frontfacing.png)
 
 注意，如果你开启了面剔除，你就看不到箱子里面有任何东西了，所以此时使用`gl_FrontFacing`毫无意义。
 
@@ -326,7 +326,7 @@ glBindBuffer(GL_UNIFORM_BUFFER, 0);
 
 在OpenGL环境（context）中，定义了若干绑定点（binding points），在哪儿我们可以把一个uniform缓冲链接上去。当我们创建了一个uniform缓冲，我们把它链接到一个这个绑定点上，我们也把着色器中uniform块链接到同一个绑定点上，这样就把它们链接到一起了。下面的图标表示了这点：
 
-![](http://learnopengl.com/img/advanced/advanced_glsl_binding_points.png)
+![](../img/04/08/advanced_glsl_binding_points.png)
 
 你可以看到，我们可以将多个uniform缓冲绑定到不同绑定点上。因为着色器A和着色器B都有一个链接到同一个绑定点0的uniform块，它们的uniform块分享同样的uniform数据—`uboMatrices`有一个前提条件是两个着色器必须都定义了Matrices这个uniform块。
 
@@ -457,7 +457,7 @@ glBindVertexArray(0);
 
 我们只需要在去设置一个`model`的uniform即可。在一个像这样的场景中使用uniform缓冲对象在每个着色器中可以减少uniform的调用。最后效果看起来像这样：
 
-![](http://learnopengl.com/img/advanced/advanced_glsl_uniform_buffer_objects.png)
+![](../img/04/08/advanced_glsl_uniform_buffer_objects.png)
 
 通过改变模型矩阵，每个立方体都移动到窗口的一边，由于片段着色器不同，物体的颜色也不同。这是一个相对简单的场景，我们可以使用uniform缓冲对象，但是任何大型渲染程序有成百上千的活动着色程序，彼时uniform缓冲对象就会闪闪发光了。
 
diff --git a/docs/04 Advanced OpenGL/09 Geometry Shader.md b/docs/04 Advanced OpenGL/09 Geometry Shader.md
index 4d16f83..bc8d104 100644
--- a/docs/04 Advanced OpenGL/09 Geometry Shader.md	
+++ b/docs/04 Advanced OpenGL/09 Geometry Shader.md	
@@ -51,7 +51,7 @@ triangles_adjacency |GL_TRIANGLES_ADJACENCY或GL_TRIANGLE_STRIP_ADJACENCY（6）
 
 这种情况，你会奇怪什么是线条：一个线条是把多个点链接起来表示出一个连续的线，它最少有两个点来组成。每个后一个点在前一个新渲染的点后面渲染，你可以看看下面的图，其中包含5个顶点：
 
-![](http://learnopengl.com/img/advanced/geometry_shader_line_strip.png)
+![](../img/04/09/geometry_shader_line_strip.png)
 
 上面的着色器，我们只能输出一个线段，因为顶点的最大值设置为2。
 
@@ -89,7 +89,7 @@ void main() {
 
 现在你了解了几何着色器的工作方式，你就可能猜出这个几何着色器做了什么。这个几何着色器接收一个基本图形——点，作为它的输入，使用输入点作为它的中心，创建了一个水平线基本图形。如果我们渲染它，结果就会像这样：
 
-![](http://learnopengl.com/img/advanced/geometry_shader_lines.png)
+![](../img/04/09/geometry_shader_lines.png)
 
 并不是非常引人注目，但是考虑到它的输出是使用下面的渲染命令生成的就很有意思了：
 
@@ -147,7 +147,7 @@ glBindVertexArray(0);
 
 效果是黑色场景中有四个绿点（虽然很难看到）：
 
-![](http://learnopengl.com/img/advanced/geometry_shader_points.png)
+![](../img/04/09/geometry_shader_points.png)
 
 但我们不是已经学到了所有内容了吗？对，现在我们将通过为场景添加一个几何着色器来为这个小场景增加点活力。
 
@@ -182,7 +182,7 @@ glLinkProgram(program);
 
 如果你现在编译和运行，就会看到和下面相似的结果：
 
-![](http://learnopengl.com/img/advanced/geometry_shader_points.png)
+![](../img/04/09/geometry_shader_points.png)
 
 它和没用几何着色器一样！我承认有点无聊，但是事实上，我们仍能绘制证明几何着色器工作了的点，所以现在是时候来做点更有意思的事了！
 
@@ -193,11 +193,11 @@ glLinkProgram(program);
 
 在OpenGL中三角形带(triangle strip)绘制起来更高效，因为它所使用的顶点更少。第一个三角形绘制完以后，每个后续的顶点会生成一个毗连前一个三角形的新三角形：每3个毗连的顶点都能构成一个三角形。如果我们有6个顶点，它们以三角形带的方式组合起来，那么我们会得到这些三角形：（1, 2, 3）、（2, 3, 4）、（3, 4, 5）、（4,5,6）因此总共可以表示出4个三角形。一个三角形带至少要用3个顶点才行，它能生曾N-2个三角形；6个顶点我们就能创建6-2=4个三角形。下面的图片表达了这点：
 
-![](http://learnopengl.com/img/advanced/geometry_shader_triangle_strip.png)
+![](../img/04/09/geometry_shader_triangle_strip.png)
 
 使用一个三角形带作为一个几何着色器的输出，我们可以轻松创建房子的形状，只要以正确的顺序来生成3个毗连的三角形。下面的图像显示，我们需要以何种顺序来绘制点，才能获得我们需要的三角形，图上的蓝点代表输入点：
 
-![](http://learnopengl.com/img/advanced/geometry_shader_house.png)
+![](../img/04/09/geometry_shader_house.png)
 
 上图的内容转变为几何着色器：
 
@@ -229,7 +229,7 @@ void main()
 
 这个几何着色器生成5个顶点，每个顶点是点（point）的位置加上一个偏移量，来组成一个大三角形带。接着最后的基本图形被像素化，片段着色器处理整三角形带，结果是为我们绘制的每个点生成一个绿房子：
 
-![](http://learnopengl.com/img/advanced/geometry_shader_houses.png)
+![](../img/04/09/geometry_shader_houses.png)
 
 可以看到，每个房子实则是由3个三角形组成，都是仅仅使用空间中一点来绘制的。绿房子看起来还是不够漂亮，所以我们再给每个房子加一个不同的颜色。我们将在顶点着色器中为每个顶点增加一个额外的代表颜色信息的顶点属性。
 
@@ -306,7 +306,7 @@ EndPrimitive();
 
 所有发射出去的顶点都把最后储存在fColor中的值嵌入到他们的数据中，和我们在他们的属性中定义的顶点颜色相同。所有的分房子便都有了自己的颜色：
 
-![](http://learnopengl.com/img/advanced/geometry_shader_houses_colored.png)
+![](../img/04/09/geometry_shader_houses_colored.png)
 
 为了好玩儿，我们还可以假装这是在冬天，给最后一个顶点一个自己的白色，就像在屋顶上落了一些雪。
 
@@ -329,7 +329,7 @@ EndPrimitive();
 
 结果就像这样：
 
-![](http://learnopengl.com/img/advanced/geometry_shader_houses_snow.png)
+![](../img/04/09/geometry_shader_houses_snow.png)
 
 你可以对比一下你的[源码](http://learnopengl.com/code_viewer.php?code=advanced/geometry_shader_houses)和[着色器](http://learnopengl.com/code_viewer.php?code=advanced/geometry_shader_houses_shaders)。
 
@@ -341,7 +341,7 @@ EndPrimitive();
 
 当我们说对一个物体进行爆破(Explode)的时候并不是说我们将要把之前的那堆顶点炸掉，但是我们打算把每个三角形沿着它们的法线向量移动一小段距离。效果是整个物体上的三角形看起来就像沿着它们的法线向量爆炸了一样。纳米服上的三角形的爆炸式效果看起来是这样的：
 
-![](http://learnopengl.com/img/advanced/geometry_shader_explosion.png)
+![](../img/04/09/geometry_shader_explosion.png)
 
 这样一个几何着色器效果的一大好处是，它可以用到任何物体上，无论它们多复杂。
 
@@ -498,7 +498,7 @@ void main()
 
 现在先使用普通着色器来渲染你的模型，然后使用特制的法线可视着色器，你会看到这样的效果：
 
-![](http://learnopengl.com/img/advanced/geometry_shader_normals.png)
+![](../img/04/09/geometry_shader_normals.png)
 
 除了我们的纳米服现在看起来有点像一个带着隔热手套的全身多毛的家伙外，它给了我们一种非常有效的检查一个模型的法线向量是否有错误的方式。你可以想象下这样的几何着色器也经常能被用在给物体添加毛发上。
 
diff --git a/docs/04 Advanced OpenGL/10 Instancing.md b/docs/04 Advanced OpenGL/10 Instancing.md
index 6843bb1..4b1da98 100644
--- a/docs/04 Advanced OpenGL/10 Instancing.md	
+++ b/docs/04 Advanced OpenGL/10 Instancing.md	
@@ -31,7 +31,7 @@ for(GLuint i = 0; i < amount_of_models_to_draw; i++)
 
 我们调用一个实例化渲染函数，在标准化设备坐标中绘制一百个2D四边形来看看实例化绘制的效果是怎样的。通过对一个储存着100个偏移量向量的索引，我们为每个实例四边形添加一个偏移量。最后，窗口被排列精美的四边形网格填满：
 
-![](http://learnopengl.com/img/advanced/instancing_quads.png)
+![](../img/04/10/instancing_quads.png)
 
 每个四边形是2个三角形所组成的，因此总共有6个顶点。每个顶点包含一个2D标准设备坐标位置向量和一个颜色向量。下面是例子中所使用的顶点数据，每个三角形为了适应屏幕都很小：
 
@@ -176,7 +176,7 @@ glVertexAttribDivisor(2, 1);
 
 如果我们现在再次使用`glDrawArraysInstanced`渲染四边形，我们会得到下面的输出：
 
-![](http://learnopengl.com/img/advanced/instancing_quads.png)
+![](../img/04/10/instancing_quads.png)
 
 和前面的一样，但这次是使用实例数组实现的，它使我们为绘制实例向顶点着色器传递更多的数据（内存允许我们存多少就能存多少）。
 
@@ -193,7 +193,7 @@ void main()
 
 结果是第一个实例的四边形被绘制的非常小，随着绘制实例的增加，`gl_InstanceID`越来越接近100，这样更多的四边形会更接近它们原来的大小。这是一种很好的将`gl_InstanceID`与实例数组结合使用的法则：
 
-![](http://learnopengl.com/img/advanced/instancing_quads_arrays.png)
+![](../img/04/10/instancing_quads_arrays.png)
 
 如果你仍然不确定实例渲染如何工作，或者想看看上面的代码是如何组合起来的，你可以在[这里找到应用的源码](http://learnopengl.com/code_viewer.php?code=advanced/instancing_quads)。
 
@@ -262,7 +262,7 @@ for(GLuint i = 0; i < amount; i++)
 
 结果是一个太空样子的场景，我们可以看到有一个自然的小行星带：
 
-![](http://learnopengl.com/img/advanced/instancing_asteroids.png)
+![](../img/04/10/instancing_asteroids.png)
 
 这个场景包含1001次渲染函数调用，每帧渲染1000个小行星模型。你可以在这里找到[场景的源码](http://learnopengl.com/code_viewer.php?code=advanced/instancing_asteroids_normal)，以及[顶点](http://learnopengl.com/code_viewer.php?code=advanced/instancing&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced/instancing&type=fragment)着色器。
 
@@ -341,7 +341,7 @@ for(GLuint i = 0; i < rock.meshes.size(); i++)
 
 这里我们绘制和前面的例子里一样数量（amount）的小行星，只不过是使用的实例渲染。结果是相似的，但你会看在开始增加数量以后效果的不同。不实例渲染，我们可以流畅渲染1000到1500个小行星。而使用了实例渲染，我们可以设置为100000，每个模型由576个顶点，这几乎有5千7百万个顶点，而且帧率没有丝毫下降！
 
-![](http://learnopengl.com/img/advanced/instancing_asteroids_quantity.png)
+![](../img/04/10/instancing_asteroids_quantity.png)
 
 上图渲染了十万小行星，半径为150.0f，偏移等于25.0f。你可以在这里找到这个演示实例渲染的[源码](http://learnopengl.com/code_viewer.php?code=advanced/instancing_asteroids_instanced)。
 
diff --git a/docs/04 Advanced OpenGL/11 Anti Aliasing.md b/docs/04 Advanced OpenGL/11 Anti Aliasing.md
index c08156f..77e835c 100644
--- a/docs/04 Advanced OpenGL/11 Anti Aliasing.md	
+++ b/docs/04 Advanced OpenGL/11 Anti Aliasing.md	
@@ -8,11 +8,11 @@
 
 在你的渲染大冒险中，你可能会遇到模型边缘有锯齿的问题。**锯齿边(Jagged Edge)**出现的原因是由顶点数据像素化之后成为片段的方式所引起的。下面是一个简单的立方体，它体现了锯齿边的效果：
 
-![](http://learnopengl.com/img/advanced/anti_aliasing_aliasing.png)
+![](../img/04/11/anti_aliasing_aliasing.png)
 
 也许不是立即可见的，如果你更近的看看立方体的边，你就会发现锯齿了。如果我们放大就会看到下面的情境：
 
-![](http://learnopengl.com/img/advanced/anti_aliasing_zoomed.png)
+![](../img/04/11/anti_aliasing_zoomed.png)
 
 这当然不是我们在最终版本的应用里想要的效果。这个效果，很明显能看到边是由像素所构成的，这种现象叫做**走样(Aliasing)**。有很多技术能够减少走样，产生更平滑的边缘，这些技术叫做**抗锯齿技术**(Anti-aliasing，也被称为反走样技术)。
 
@@ -26,19 +26,19 @@
 
 光栅化是你的最终的经处理的顶点和片段着色器之间的所有算法和处理的集合。光栅化将属于一个基本图形的所有顶点转化为一系列片段。顶点坐标理论上可以含有任何坐标，但片段却不是这样，这是因为它们与你的窗口的解析度有关。几乎永远都不会有顶点坐标和片段的一对一映射，所以光栅化必须以某种方式决定每个特定顶点最终结束于哪个片段/屏幕坐标上。
 
-![](http://learnopengl.com/img/advanced/anti_aliasing_rasterization.png)
+![](../img/04/11/anti_aliasing_rasterization.png)
 
 这里我们看到一个屏幕像素网格，每个像素中心包含一个采样点（sample point），它被用来决定一个像素是否被三角形所覆盖。红色的采样点如果被三角形覆盖，那么就会为这个被覆盖像（屏幕）素生成一个片段。即使三角形覆盖了部分屏幕像素，但是采样点没被覆盖，这个像素仍然不会受到任何片段着色器影响到。
 
 你可能已经明白走样的原因来自何处了。三角形渲染后的版本最后在你的屏幕上是这样的：
 
-![](http://learnopengl.com/img/advanced/anti_aliasing_rasterization_filled.png)
+![](../img/04/11/anti_aliasing_rasterization_filled.png)
 
 由于屏幕像素总量的限制，有些边上的像素能被渲染出来，而有些则不会。结果就是我们渲染出的基本图形的非光滑边缘产生了上图的锯齿边。
 
 多采样所做的正是不再使用单一采样点来决定三角形的覆盖范围，而是采用多个采样点。我们不再使用每个像素中心的采样点，取而代之的是4个子样本（subsample），用它们来决定像素的覆盖率。这意味着颜色缓冲的大小也由于每个像素的子样本的增加而增加了。
 
-![](http://learnopengl.com/img/advanced/anti_aliasing_sample_points.png)
+![](../img/04/11/anti_aliasing_sample_points.png)
 
 左侧的图显示了我们普通决定一个三角形的覆盖范围的方式。这个像素并不会运行一个片段着色器（这就仍保持空白），因为它的采样点没有被三角形所覆盖。右边的图展示了多采样的版本，每个像素包含4个采样点。这里我们可以看到只有2个采样点被三角形覆盖。
 
@@ -52,13 +52,13 @@ MSAA的真正工作方式是，每个像素只运行一次片段着色器，无
 
 结果是，颜色缓冲中所有基本图形的边都生成了更加平滑的样式。让我们看看当再次决定前面的三角形覆盖范围时多样本看起来是这样的：
 
-![](http://learnopengl.com/img/advanced/anti_aliasing_rasterization_samples.png)
+![](../img/04/11/anti_aliasing_rasterization_samples.png)
 
 这里每个像素包含着4个子样本（不相关的已被隐藏）蓝色的子样本是被三角形覆盖了的，灰色的没有被覆盖。三角形内部区域中的所有像素都会运行一次片段着色器，它输出的颜色被储存到所有4个子样本中。三角形的边缘并不是所有的子样本都会被覆盖，所以片段着色器的结果仅储存在部分子样本中。根据被覆盖子样本的数量，最终的像素颜色由三角形颜色和其他子样本所储存的颜色所决定。
 
 大致上来说，如果更多的采样点被覆盖，那么像素的颜色就会更接近于三角形。如果我们用早期使用的三角形的颜色填充像素，我们会获得这样的结果：
 
-![](http://learnopengl.com/img/advanced/anti_aliasing_rasterization_samples_filled.png)
+![](../img/04/11/anti_aliasing_rasterization_samples_filled.png)
 
 对于每个像素来说，被三角形覆盖的子样本越少，像素受到三角形的颜色的影响也越少。现在三角形的硬边被比实际颜色浅一些的颜色所包围，因此观察者从远处看上去就比较平滑了。
 
@@ -86,7 +86,7 @@ glEnable(GL_MULTISAMPLE);
 
 当默认帧缓冲有了多采样缓冲附件的时候，我们所要做的全部就是调用 `glEnable`开启多采样。因为实际的多采样算法在OpenGL驱动光栅化里已经实现了，所以我们无需再做什么了。如果我们现在来渲染教程开头的那个绿色立方体，我们会看到边缘变得平滑了：
 
-![](http://learnopengl.com/img/advanced/anti_aliasing_multisampled.png)
+![](../img/04/11/anti_aliasing_multisampled.png)
 
 这个箱子看起来平滑多了，在场景中绘制任何物体都可以利用这个技术。可以[从这里找到](http://learnopengl.com/code_viewer.php?code=advanced/anti_aliasing_multisampling)这个简单的例子。
 
@@ -142,7 +142,7 @@ glBlitFramebuffer(0, 0, width, height, 0, 0, width, height, GL_COLOR_BUFFER_BIT,
 
 如果我们渲染应用，我们将得到和没用帧缓冲一样的结果：一个绿色立方体，它使用MSAA显示出来，但边缘锯齿明显少了：
 
-![](http://learnopengl.com/img/advanced/anti_aliasing_multisampled.png)
+![](../img/04/11/anti_aliasing_multisampled.png)
 
 你可以[在这里找到源代码](http://learnopengl.com/code_viewer.php?code=advanced/anti_aliasing_framebuffers)。
 
@@ -177,7 +177,7 @@ while(!glfwWindowShouldClose(window))
 
 如果我们实现帧缓冲教程中讲的后处理代码，我们就能创造出没有锯齿边的所有效果很酷的后处理特效。使用模糊kernel过滤器，看起来会像这样：
 
-![](http://learnopengl.com/img/advanced/anti_aliasing_post_processing.png)
+![](../img/04/11/anti_aliasing_post_processing.png)
 
 你可以[在这里找到所有MSAA版本的后处理源码](http://learnopengl.com/code_viewer.php?code=advanced/anti_aliasing_post_processing)。
 
diff --git a/docs/05 Advanced Lighting/01 Advanced Lighting.md b/docs/05 Advanced Lighting/01 Advanced Lighting.md
index c921120..d9155f8 100644
--- a/docs/05 Advanced Lighting/01 Advanced Lighting.md	
+++ b/docs/05 Advanced Lighting/01 Advanced Lighting.md	
@@ -12,19 +12,19 @@
 
 Phong光照很棒，而且性能较高，但是它的镜面反射在某些条件下会失效，特别是当发光值属性低的时候，对应一个非常大的粗糙的镜面区域。下面的图片展示了，当我们使用镜面的发光值为1.0时，一个带纹理地板的效果：
 
-![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_phong_limit.png)
+![](../img/05/01/advanced_lighting_phong_limit.png)
 
 你可以看到，镜面区域边缘迅速减弱并截止。出现这个问题的原因是在视线向量和反射向量的角度不允许大于90度。如果大于90度的话，点乘的结果就会是负数，镜面的贡献成分就会变成0。你可能会想，这不是一个问题，因为大于90度时我们不应看到任何光，对吧？
 
 错了，这只适用于漫散射部分，当法线和光源之间的角度大于90度时意味着光源在被照亮表面的下方，这样光的散射成分就会是0.0。然而，对于镜面光照，我们不会测量光源和法线之间的角度，而是测量视线和反射方向向量之间的。看看下面的两幅图：
 
-![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_over_90.png)
+![](../img/05/01/advanced_lighting_over_90.png)
 
 现在看来问题就很明显了。左侧图片显示Phong反射的θ小于90度的情况。我们可以看到右侧图片视线和反射之间的角θ大于90度，这样镜面反射成分将会被消除。通常这也不是问题，因为视线方向距离反射方向很远，但如果我们使用一个数值较低的发光值参数的话，镜面半径就会足够大，以至于能够贡献一些镜面反射的成份了。在例子中，我们在角度大于90度时消除了这个贡献（如第一个图片所示）。
 
 1977年James F. Blinn引入了Blinn-Phong着色，它扩展了我们目前所使用的Phong着色。Blinn-Phong模型很大程度上和Phong是相似的，不过它稍微改进了Phong模型，使之能够克服我们所讨论到的问题。它放弃使用反射向量，而是基于我们现在所说的一个叫做半程向量（halfway vector）的向量，这是个单位向量，它在视线方向和光线方向的中间。半程向量和表面法线向量越接近，镜面反射成份就越大。
 
-![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_halfway_vector.png)
+![](../img/05/01/advanced_lighting_halfway_vector.png)
 
 当视线方向恰好与反射向量对称时，半程向量就与法线向量重合。这样观察者距离原来的反射方向越近，镜面反射的高光就会越强。
 
@@ -59,13 +59,13 @@ vec3 specular = lightColor * spec;
 
 引入了半程向量来计算镜面反射后，我们再也不会遇到Phong着色的骤然截止问题了。下图展示了两种不同方式下发光值指数为0.5时镜面区域的不同效果：
 
-![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_comparrison.png)
+![](../img/05/01/advanced_lighting_comparrison.png)
 
 Phong和Blinn-Phong着色之间另一个细微差别是，半程向量和表面法线之间的角度经常会比视线和反射向量之间的夹角更小。结果就是，为了获得和Phong着色相似的效果，必须把发光值参数设置的大一点。通常的经验是将其设置为Phong着色的发光值参数的2至4倍。
 
 下图是Phong指数为8.0和Blinn-Phong指数为32的时候，两种specular反射模型的对比：
 
-![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_comparrison2.png)
+![](../img/05/01/advanced_lighting_comparrison2.png)
 
 你可以看到Blinn-Phong的镜面反射成分要比Phong锐利一些。这通常需要使用一点小技巧才能获得之前你所看到的Phong着色的效果，但Blinn-Phong着色的效果比默认的Phong着色通常更加真实一些。
 
diff --git a/docs/05 Advanced Lighting/02 Gamma Correction.md b/docs/05 Advanced Lighting/02 Gamma Correction.md
index 67c4777..7d39fde 100644
--- a/docs/05 Advanced Lighting/02 Gamma Correction.md	
+++ b/docs/05 Advanced Lighting/02 Gamma Correction.md	
@@ -14,7 +14,7 @@
 
 人类所感知的亮度恰好和CRT所显示出来相似的指数关系非常匹配。为了更好的理解所有含义，请看下面的图片：
 
-![](http://learnopengl.com/img/advanced-lighting/gamma_correction_brightness.png)
+![](../img/05/02/gamma_correction_brightness.png)
 
 第一行是人眼所感知到的正常的灰阶，亮度要增加一倍（比如从0.1到0.2）你才会感觉比原来变亮了一倍（译注：这里的意思是说比如一个东西的亮度0.3，让人感觉它比原来变亮一倍，那么现在这个亮度应该成为0.6，而不是0.4，也就是说人眼感知到的亮度的变化并非线性均匀分布的。问题的关键在于这样的一倍相当于一个亮度级，例如假设0.1、0.2、0.4、0.8是我们定义的四个亮度级别，在0.1和0.2之间人眼只能识别出0.15这个中间级，而虽然0.4到0.8之间的差距更大，这个区间人眼也只能识别出一个颜色）。然而，当我们谈论光的物理亮度，比如光源发射光子的数量的时候，底部（第二行）的灰阶显示出的才是物理世界真实的亮度。如底部的灰阶显示，亮度加倍时返回的也是真实的物理亮度（译注：这里亮度是指光子数量和正相关的亮度，即物理亮度，前面讨论的是人的感知亮度；物理亮度和感知亮度的区别在于，物理亮度基于光子数量，感知亮度基于人的感觉，比如第二个灰阶里亮度0.1的光子数量是0.2的二分之一），但是由于这与我们的眼睛感知亮度不完全一致（对比较暗的颜色变化更敏感），所以它看起来有差异。
 
@@ -22,7 +22,7 @@
 
 监视器的这个非线性映射的确可以让亮度在我们眼中看起来更好，但当渲染图像时，会产生一个问题：我们在应用中配置的亮度和颜色是基于监视器所看到的，这样所有的配置实际上是非线性的亮度/颜色配置。请看下图：
 
-![](http://learnopengl.com/img/advanced-lighting/gamma_correction_gamma_curves.png)
+![](../img/05/02/gamma_correction_gamma_curves.png)
 
 点线代表线性颜色/亮度值（译注：这表示的是理想状态，Gamma为1），实线代表监视器显示的颜色。如果我们把一个点线线性的颜色翻一倍，结果就是这个值的两倍。比如，光的颜色向量\(\bar{L} = (0.5, 0.0, 0.0)\)代表的是暗红色。如果我们在线性空间中把它翻倍，就会变成\((1.0, 0.0, 0.0)\)，就像你在图中看到的那样。然而，由于我们定义的颜色仍然需要输出的监视器上，监视器上显示的实际颜色就会是\((0.218, 0.0, 0.0)\)。在这儿问题就出现了：当我们将理想中直线上的那个暗红色翻一倍时，在监视器上实际上亮度翻了4.5倍以上！
 
@@ -30,7 +30,7 @@
 
 因为所有中间亮度都是线性空间计算出来的（译注：计算的时候假设Gamma为1）监视器显以后，实际上都会不正确。当使用更高级的光照算法时，这个问题会变得越来越明显，你可以看看下图：
 
-![](http://learnopengl.com/img/advanced-lighting/gamma_correction_example.png)
+![](../img/05/02/gamma_correction_example.png)
 
 ## Gamma校正
 
@@ -81,7 +81,7 @@ void main()
 
 结果就是纹理编辑者，所创建的所有纹理都是在sRGB空间中的纹理，所以如果我们在渲染应用中使用这些纹理，我们必须考虑到这点。在我们应用gamma校正之前，这不是个问题，因为纹理在sRGB空间创建和展示，同样我们还是在sRGB空间中使用，从而不必gamma校正纹理显示也没问题。然而，现在我们是把所有东西都放在线性空间中展示的，纹理颜色就会变坏，如下图展示的那样：
 
-![](http://learnopengl.com/img/advanced-lighting/gamma_correction_srgbtextures.png)
+![](../img/05/02/gamma_correction_srgbtextures.png)
 
 纹理图像实在太亮了，发生这种情况是因为，它们实际上进行了两次gamma校正！想一想，当我们基于监视器上看到的情况创建一个图像，我们就已经对颜色值进行了gamma校正，所以再次显示在监视器上就没错。由于我们在渲染中又进行了一次gamma校正，图片就实在太亮了。
 
@@ -125,7 +125,7 @@ float attenuation = 1.0 / distance;
 
 双曲线比使用二次函数变体在不用gamma校正的时候看起来更真实，不过但我们开启gamma校正以后线性衰减看起来太弱了，符合物理的二次函数突然出现了更好的效果。下图显示了其中的不同：
 
-![](http://learnopengl.com/img/advanced-lighting/gamma_correction_attenuation.png)
+![](../img/05/02/gamma_correction_attenuation.png)
 
 这种差异产生的原因是，光的衰减方程改变了亮度值，而且屏幕上显示出来的也不是线性空间，在监视器上效果最好的衰减方程，并不是符合物理的。想想平方衰减方程，如果我们使用这个方程，而且不进行gamma校正，显示在监视器上的衰减方程实际上将变成\((1.0 / distance^2)^{2.2}\)。若不进行gamma校正，将产生更强烈的衰减。这也解释了为什么双曲线不用gamma校正时看起来更真实，因为它实际变成了\((1.0 / distance)^{2.2} = 1.0 / distance^{2.2}\)。这和物理公式是很相似的。
 
diff --git a/docs/05 Advanced Lighting/03 Shadows/01 Shadow Mapping.md b/docs/05 Advanced Lighting/03 Shadows/01 Shadow Mapping.md
index 4f973af..aa97dfd 100644
--- a/docs/05 Advanced Lighting/03 Shadows/01 Shadow Mapping.md	
+++ b/docs/05 Advanced Lighting/03 Shadows/01 Shadow Mapping.md	
@@ -10,7 +10,7 @@
 
 阴影是光线被阻挡的结果；当一个光源的光线由于其他物体的阻挡不能够达到一个物体的表面的时候，那么这个物体就在阴影中了。阴影能够使场景看起来真实得多，并且可以让观察者获得物体之间的空间位置关系。场景和物体的深度感因此能够得到极大提升，下图展示了有阴影和没有阴影的情况下的不同：
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_with_without.png)
+![](../../img/05/03/01/shadow_mapping_with_without.png)
 
 你可以看到，有阴影的时候你能更容易地区分出物体之间的位置关系，例如，当使用阴影的时候浮在地板上的立方体的事实更加清晰。
 
@@ -22,7 +22,7 @@
 
 阴影映射(Shadow Mapping)背后的思路非常简单：我们以光的位置为视角进行渲染，我们能看到的东西都将被点亮，看不见的一定是在阴影之中了。假设有一个地板，在光源和它之间有一个大盒子。由于光源处向光线方向看去，可以看到这个盒子，但看不到地板的一部分，这部分就应该在阴影中了。
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_theory.png)
+![](../../img/05/03/01/shadow_mapping_theory.png)
 
 这里的所有蓝线代表光源可以看到的fragment。黑线代表被遮挡的fragment：它们应该渲染为带阴影的。如果我们绘制一条从光源出发，到达最右边盒子上的一个片元上的线段或射线，那么射线将先击中悬浮的盒子，随后才会到达最右侧的盒子。结果就是悬浮的盒子被照亮，而最右侧的盒子将处于阴影之中。
 
@@ -30,7 +30,7 @@
 
 你可能记得在[深度测试](http://learnopengl.com/#!Advanced-OpenGL/Depth-testing)教程中，在深度缓冲里的一个值是摄像机视角下，对应于一个片元的一个0到1之间的深度值。如果我们从光源的透视图来渲染场景，并把深度值的结果储存到纹理中会怎样？通过这种方式，我们就能对光源的透视图所见的最近的深度值进行采样。最终，深度值就会显示从光源的透视图下见到的第一个片元了。我们管储存在纹理中的所有这些深度值，叫做深度贴图（depth map）或阴影贴图。
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_theory_spaces.png)
+![](../../img/05/03/01/shadow_mapping_theory_spaces.png)
 
 左侧的图片展示了一个定向光源（所有光线都是平行的）在立方体下的表面投射的阴影。通过储存到深度贴图中的深度值，我们就能找到最近点，用以决定片元是否在阴影中。我们使用一个来自光源的视图和投影矩阵来渲染场景就能创建一个深度贴图。这个投影和视图矩阵结合在一起成为一个\(T\)变换，它可以将任何三维位置转变到光源的可见坐标空间。
 
@@ -179,7 +179,7 @@ glBindFramebuffer(GL_FRAMEBUFFER, 0);
 
 最后，在光的透视图视角下，很完美地用每个可见片元的最近深度填充了深度缓冲。通过将这个纹理投射到一个2D四边形上（和我们在帧缓冲一节做的后处理过程类似），就能在屏幕上显示出来，我们会获得这样的东西：
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_depth_map.png)
+![](../../img/05/03/01/shadow_mapping_depth_map.png)
 
 将深度贴图渲染到四边形上的像素着色器：
 
@@ -353,7 +353,7 @@ float ShadowCalculation(vec4 fragPosLightSpace)
 
 激活这个着色器，绑定合适的纹理，激活第二个渲染阶段默认的投影以及视图矩阵，结果如下图所示：
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_shadows.png)
+![](../../img/05/03/01/shadow_mapping_shadows.png)
 
 如果你做对了，你会看到地板和上有立方体的阴影。你可以从这里找到demo程序的[源码](http://learnopengl.com/code_viewer.php?code=advanced-lighting/shadow_mapping_shadows)。
 
@@ -365,11 +365,11 @@ float ShadowCalculation(vec4 fragPosLightSpace)
 
 前面的图片中明显有不对的地方。放大看会发现明显的线条样式：
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_acne.png)
+![](../../img/05/03/01/shadow_mapping_acne.png)
 
 我们可以看到地板四边形渲染出很大一块交替黑线。这种阴影贴图的不真实感叫做**阴影失真(Shadow Acne)**，下图解释了成因：
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_acne_diagram.png)
+![](../../img/05/03/01/shadow_mapping_acne_diagram.png)
 
 因为阴影贴图受限于解析度，在距离光源比较远的情况下，多个片元可能从深度贴图的同一个值中去采样。图片每个斜坡代表深度贴图一个单独的纹理像素。你可以看到，多个片元从同一个深度值进行采样。
 
@@ -377,7 +377,7 @@ float ShadowCalculation(vec4 fragPosLightSpace)
 
 我们可以用一个叫做**阴影偏移**（shadow bias）的技巧来解决这个问题，我们简单的对表面的深度（或深度贴图）应用一个偏移量，这样片元就不会被错误地认为在表面之下了。
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_acne_bias.png)
+![](../../img/05/03/01/shadow_mapping_acne_bias.png)
 
 使用了偏移量后，所有采样点都获得了比表面深度更小的深度值，这样整个表面就正确地被照亮，没有任何阴影。我们可以这样实现这个偏移：
 
@@ -394,7 +394,7 @@ float bias = max(0.05 * (1.0 - dot(normal, lightDir)), 0.005);
 
 这里我们有一个偏移量的最大值0.05，和一个最小值0.005，它们是基于表面法线和光照方向的。这样像地板这样的表面几乎与光源垂直，得到的偏移就很小，而比如立方体的侧面这种表面得到的偏移就更大。下图展示了同一个场景，但使用了阴影偏移，效果的确更好：
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_with_bias.png)
+![](../../img/05/03/01/shadow_mapping_with_bias.png)
 
 选用正确的偏移数值，在不同的场景中需要一些像这样的轻微调校，但大多情况下，实际上就是增加偏移量直到所有失真都被移除的问题。
 
@@ -402,13 +402,13 @@ float bias = max(0.05 * (1.0 - dot(normal, lightDir)), 0.005);
 
 使用阴影偏移的一个缺点是你对物体的实际深度应用了平移。偏移有可能足够大，以至于可以看出阴影相对实际物体位置的偏移，你可以从下图看到这个现象（这是一个夸张的偏移值）：
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_peter_panning.png)
+![](../../img/05/03/01/shadow_mapping_peter_panning.png)
 
 这个阴影失真叫做悬浮(Peter Panning)，因为物体看起来轻轻悬浮在表面之上（译注Peter Pan就是童话彼得潘，而panning有平移、悬浮之意，而且彼得潘是个会飞的男孩…）。我们可以使用一个叫技巧解决大部分的Peter panning问题：当渲染深度贴图时候使用正面剔除（front face culling）你也许记得在面剔除教程中OpenGL默认是背面剔除。我们要告诉OpenGL我们要剔除正面。
 
 因为我们只需要深度贴图的深度值，对于实体物体无论我们用它们的正面还是背面都没问题。使用背面深度不会有错误，因为阴影在物体内部有错误我们也看不见。
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_culling.png)
+![](../../img/05/03/01/shadow_mapping_culling.png)
 
 为了修复peter游移，我们要进行正面剔除，先必须开启GL_CULL_FACE：
 
@@ -426,7 +426,7 @@ glCullFace(GL_BACK); // 不要忘记设回原先的culling face
 
 无论你喜不喜欢还有一个视觉差异，就是光的视锥不可见的区域一律被认为是处于阴影中，不管它真的处于阴影之中。出现这个状况是因为超出光的视锥的投影坐标比1.0大，这样采样的深度纹理就会超出他默认的0到1的范围。根据纹理环绕方式，我们将会得到不正确的深度结果，它不是基于真实的来自光源的深度值。
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_outside_frustum.png)
+![](../../img/05/03/01/shadow_mapping_outside_frustum.png)
 
 你可以在图中看到，光照有一个区域，超出该区域就成为了阴影；这个区域实际上代表着深度贴图的大小，这个贴图投影到了地板上。发生这种情况的原因是我们之前将深度贴图的环绕方式设置成了GL_REPEAT。
 
@@ -441,7 +441,7 @@ glTexParameterfv(GL_TEXTURE_2D, GL_TEXTURE_BORDER_COLOR, borderColor);
 
 现在如果我们采样深度贴图0到1坐标范围以外的区域，纹理函数总会返回一个1.0的深度值，阴影值为0.0。结果看起来会更真实：
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_clamp_edge.png)
+![](../../img/05/03/01/shadow_mapping_clamp_edge.png)
 
 仍有一部分是黑暗区域。那里的坐标超出了光的正交视锥的远平面。你可以看到这片黑色区域总是出现在光源视锥的极远处。
 
@@ -462,7 +462,7 @@ float ShadowCalculation(vec4 fragPosLightSpace)
 
 检查远平面，并将深度贴图限制为一个手工指定的边界颜色，就能解决深度贴图采样超出的问题，我们最终会得到下面我们所追求的效果：
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_over_sampling_fixed.png)
+![](../../img/05/03/01/shadow_mapping_over_sampling_fixed.png)
 
 这些结果意味着，只有在深度贴图范围以内的被投影的fragment坐标才有阴影，所以任何超出范围的都将会没有阴影。由于在游戏中通常这只发生在远处，就会比我们之前的那个明显的黑色区域效果更真实。
 
@@ -470,7 +470,7 @@ float ShadowCalculation(vec4 fragPosLightSpace)
 
 阴影现在已经附着到场景中了，不过这仍不是我们想要的。如果你放大看阴影，阴影映射对解析度的依赖很快变得很明显。
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_zoom.png)
+![](../../img/05/03/01/shadow_mapping_zoom.png)
 
 因为深度贴图有一个固定的解析度，多个片元对应于一个纹理像素。结果就是多个片元会从深度贴图的同一个深度值进行采样，这几个片元便得到的是同一个阴影，这就会产生锯齿边。
 
@@ -498,7 +498,7 @@ shadow /= 9.0;
 
 使用更多的样本，更改texelSize变量，你就可以增加阴影的柔和程度。下面你可以看到应用了PCF的阴影：
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_soft_shadows.png)
+![](../../img/05/03/01/shadow_mapping_soft_shadows.png)
 
 从稍微远一点的距离看去，阴影效果好多了，也不那么生硬了。如果你放大，仍会看到阴影贴图解析度的不真实感，但通常对于大多数应用来说效果已经很好了。
 
@@ -511,7 +511,7 @@ shadow /= 9.0;
 
 在渲染深度贴图的时候，正交(Orthographic)和投影(Projection)矩阵之间有所不同。正交投影矩阵并不会将场景用透视图进行变形，所有视线/光线都是平行的，这使它对于定向光来说是个很好的投影矩阵。然而透视投影矩阵，会将所有顶点根据透视关系进行变形，结果因此而不同。下图展示了两种投影方式所产生的不同阴影区域：
 
-![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_projection.png)
+![](../../img/05/03/01/shadow_mapping_projection.png)
 
 透视投影对于光源来说更合理，不像定向光，它是有自己的位置的。透视投影因此更经常用在点光源和聚光灯上，而正交投影经常用在定向光上。
 
diff --git a/docs/05 Advanced Lighting/03 Shadows/02 Point Shadows.md b/docs/05 Advanced Lighting/03 Shadows/02 Point Shadows.md
index 84e82d0..ec3aff4 100644
--- a/docs/05 Advanced Lighting/03 Shadows/02 Point Shadows.md	
+++ b/docs/05 Advanced Lighting/03 Shadows/02 Point Shadows.md	
@@ -19,7 +19,7 @@
 
 对于深度贴图，我们需要从一个点光源的所有渲染场景，普通2D深度贴图不能工作；如果我们使用立方体贴图会怎样？因为立方体贴图可以储存6个面的环境数据，它可以将整个场景渲染到立方体贴图的每个面上，把它们当作点光源四周的深度值来采样。
 
-![](http://learnopengl.com/img/advanced-lighting/point_shadows_diagram.png)
+![](../../img/05/03/02/point_shadows_diagram.png)
 
 生成后的深度立方体贴图被传递到光照像素着色器，它会用一个方向向量来采样立方体贴图，从而得到当前的fragment的深度（从光的透视图）。大部分复杂的事情已经在阴影映射教程中讨论过了。算法只是在深度立方体贴图生成上稍微复杂一点。
 
@@ -369,7 +369,7 @@ float ShadowCalculation(vec3 fragPos)
 
 有了这些着色器，我们已经能得到非常好的阴影效果了，这次从一个点光源所有周围方向上都有阴影。有一个位于场景中心的点光源，看起来会像这样：
 
-![](http://learnopengl.com/img/advanced-lighting/point_shadows.png)
+![](../../img/05/03/02/point_shadows.png)
 
 你可以从这里找到这个[demo的源码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/point_shadows)、[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/point_shadows&type=vertex)和[片段](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/point_shadows&type=fragment)着色器。
 
@@ -385,7 +385,7 @@ FragColor = vec4(vec3(closestDepth / far_plane), 1.0);
 
 结果是一个灰度场景，每个颜色代表着场景的线性深度值：
 
-![](http://learnopengl.com/img/advanced-lighting/point_shadows_depth_cubemap.png)
+![](../../img/05/03/02/point_shadows_depth_cubemap.png)
 
 你可能也注意到了带阴影部分在墙外。如果看起来和这个差不多，你就知道深度立方体贴图生成的没错。否则你可能做错了什么，也许是closestDepth仍然还在0到far_plane的范围。
 
@@ -420,7 +420,7 @@ shadow /= (samples * samples * samples);
 
 现在阴影看起来更加柔和平滑了，由此得到更加真实的效果：
 
-![](http://learnopengl.com/img/advanced-lighting/point_shadows_soft.png)
+![](../../img/05/03/02/point_shadows_soft.png)
 
 然而，samples设置为4.0，每个fragment我们会得到总共64个样本，这太多了！
 
@@ -465,7 +465,7 @@ float diskRadius = (1.0 + (viewDistance / far_plane)) / 25.0;
 
 PCF算法的结果如果没有变得更好，也是非常不错的，这是柔和的阴影效果：
 
-![](http://learnopengl.com/img/advanced-lighting/point_shadows_soft_better.png)
+![](../../img/05/03/02/point_shadows_soft_better.png)
 
 当然了，我们添加到每个样本的bias（偏移）高度依赖于上下文，总是要根据场景进行微调的。试试这些值，看看怎样影响了场景。
 这里是最终版本的顶点和像素着色器。
diff --git a/docs/05 Advanced Lighting/05 Parallax Mapping.md b/docs/05 Advanced Lighting/05 Parallax Mapping.md
index a04ad6b..e0a9dcc 100644
--- a/docs/05 Advanced Lighting/05 Parallax Mapping.md	
+++ b/docs/05 Advanced Lighting/05 Parallax Mapping.md	
@@ -10,29 +10,29 @@
 
 视差贴图属于位移贴图(Displacement Mapping)技术的一种，它对根据储存在纹理中的几何信息对顶点进行位移或偏移。一种实现的方式是比如有1000个顶点，更具纹理中的数据对平面特定区域的顶点的高度进行位移。这样的每个纹理像素包含了高度值纹理叫做高度贴图。一张简单的砖块表面的告诉贴图如下所示：
 
-![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_height_map.png)
+![](../img/05/05/parallax_mapping_height_map.png)
 
 整个平面上的每个顶点都根据从高度贴图采样出来的高度值进行位移，根据材质的几何属性平坦的平面变换成凹凸不平的表面。例如一个平坦的平面利用上面的高度贴图进行置换能得到以下结果：
 
-![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_plane_heightmap.png)
+![](../img/05/05/parallax_mapping_plane_heightmap.png)
 
 置换顶点有一个问题就是平面必须由很多顶点组成才能获得具有真实感的效果，否则看起来效果并不会很好。一个平坦的表面上有1000个顶点计算量太大了。我们能否不用这么多的顶点就能取得相似的效果呢？事实上，上面的表面就是用6个顶点渲染出来的（两个三角形）。上面的那个表面使用视差贴图技术渲染，位移贴图技术不需要额外的顶点数据来表达深度，它像法线贴图一样采用一种聪明的手段欺骗用户的眼睛。
 
 视差贴图背后的思想是修改纹理坐标使一个fragment的表面看起来比实际的更高或者更低，所有这些都根据观察方向和高度贴图。为了理解它如何工作，看看下面砖块表面的图片：
 
-[](http://learnopengl.com/img/advanced-lighting/parallax_mapping_plane_height.png)
+[](../img/05/05/parallax_mapping_plane_height.png)
 
 这里粗糙的红线代表高度贴图中的数值的立体表达，向量\(\color{orange}{\bar{V}}\)代表观察方向。如果平面进行实际位移，观察者会在点\(\color{blue}B\)看到表面。然而我们的平面没有实际上进行位移，观察方向将在点\(\color{green}A\)与平面接触。视差贴图的目的是，在\(\color{green}A\)位置上的fragment不再使用点\(\color{green}A\)的纹理坐标而是使用点\(\color{blue}B\)的。随后我们用点\(\color{blue}B\)的纹理坐标采样，观察者就像看到了点\(\color{blue}B\)一样。
 
 这个技巧就是描述如何从点\(\color{green}A\)得到点\(\color{blue}B\)的纹理坐标。视差贴图尝试通过对从fragment到观察者的方向向量\(\color{orange}{\bar{V}}\)进行缩放的方式解决这个问题，缩放的大小是\(\color{green}A\)处fragment的高度。所以我们将\(\color{orange}{\bar{V}}\)的长度缩放为高度贴图在点\(\color{green}A\)处\(\color{green}{H(A)}\)采样得来的值。下图展示了经缩放得到的向量\(\color{brown}{\bar{P}}\)：
 
-![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_scaled_height.png)
+![](../img/05/05/parallax_mapping_scaled_height.png)
 
 我们随后选出\(\color{brown}{\bar{P}}\)以及这个向量与平面对齐的坐标作为纹理坐标的偏移量。这能工作是因为向量\(\color{brown}{\bar{P}}\)是使用从高度贴图得到的高度值计算出来的，所以一个fragment的高度越高位移的量越大。
 
 这个技巧在大多数时候都没问题，但点\(\color{blue}B\)是粗略估算得到的。当表面的高度变化很快的时候，看起来就不会真实，因为向量\(\color{brown}{\bar{P}}\)最终不会和\(\color{blue}B\)接近，就像下图这样：
 
-![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_incorrect_p.png)
+![](../img/05/05/parallax_mapping_incorrect_p.png)
 
 视差贴图的另一个问题是，当表面被任意旋转以后很难指出从\(\color{brown}{\bar{P}}\)获取哪一个坐标。我们在视差贴图中使用了另一个坐标空间，这个空间\(\color{brown}{\bar{P}}\)向量的x和y元素总是与纹理表面对齐。如果你看了法线贴图教程，你也许猜到了，我们实现它的方法，是的，我们还是在切线空间中实现视差贴图。
 
@@ -46,7 +46,7 @@
 
 你可能已经注意到，上面链接上的那个位移贴图和教程一开始的那个高度贴图相比是颜色是相反的。这是因为使用反色高度贴图（也叫深度贴图）去模拟深度比模拟高度更容易。下图反映了这个轻微的改变：
 
-![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_depth.png)
+![](../img/05/05/parallax_mapping_depth.png)
 
 我们再次获得\(\color{green}A\)和\(\color{blue}B\)，但是这次我们用向量\(\color{orange}{\bar{V}}\)减去点\(\color{green}A\)的纹理坐标得到\(\color{brown}{\bar{P}}\)。我们通过在着色器中用1.0减去采样得到的高度贴图中的值来取得深度值，而不再是高度值，或者简单地在图片编辑软件中把这个纹理进行反色操作，就像我们对连接中的那个深度贴图所做的一样。
 
@@ -152,7 +152,7 @@ vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir)
 
 最后的纹理坐标随后被用来进行采样（diffuse和法线）贴图，下图所展示的位移效果中height_scale等于1：
 
-![](http://learnopengl.com/img/advanced-lighting/parallax_mapping.png)
+![](../img/05/05/parallax_mapping.png)
 
 这里你会看到只用法线贴图和与视差贴图相结合的法线贴图的不同之处。因为视差贴图尝试模拟深度，它实际上能够根据你观察它们的方向使砖块叠加到其他砖块上。
 
@@ -166,13 +166,13 @@ if(texCoords.x > 1.0 || texCoords.y > 1.0 || texCoords.x < 0.0 || texCoords.y <
 
 丢弃了超出默认范围的纹理坐标的所有fragment，视差贴图的表面边缘给出了正确的结果。注意，这个技巧不能在所有类型的表面上都能工作，但是应用于平面上它还是能够是平面看起来真的进行位移了：
 
-![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_edge_fix.png)
+![](../img/05/05/parallax_mapping_edge_fix.png)
 
 你可以在这里找到[源代码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping)，以及[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping&type=vertex)和[像素](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping&type=fragment)着色器。
 
 看起来不错，运行起来也很快，因为我们只要给视差贴图提供一个额外的纹理样本就能工作。当从一个角度看过去的时候，会有一些问题产生（和法线贴图相似），陡峭的地方会产生不正确的结果，从下图你可以看到：
 
-![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_issues.png)
+![](../img/05/05/parallax_mapping_issues.png)
 
 问题的原因是这只是一个大致近似的视差映射。还有一些技巧让我们在陡峭的高度上能够获得几乎完美的结果，即使当以一定角度观看的时候。例如，我们不再使用单一样本，取而代之使用多样本来找到最近点\(\color{blue}B\)会得到怎样的结果？
 
@@ -180,7 +180,7 @@ if(texCoords.x > 1.0 || texCoords.y > 1.0 || texCoords.x < 0.0 || texCoords.y <
 
 陡峭视差映射(Steep Parallax Mapping)是视差映射的扩展，原则是一样的，但不是使用一个样本而是多个样本来确定向量\(\color{brown}{\bar{P}}\)到\(\color{blue}B\)。它能得到更好的结果，它将总深度范围分布到同一个深度/高度的多个层中。从每个层中我们沿着\(\color{brown}{\bar{P}}\)方向移动采样纹理坐标，直到我们找到了一个采样得到的低于当前层的深度值的深度值。看看下面的图片：
 
-![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_steep_parallax_mapping_diagram.png)
+![](../img/05/05/parallax_mapping_steep_parallax_mapping_diagram.png)
 
 我们从上到下遍历深度层，我们把每个深度层和储存在深度贴图中的它的深度值进行对比。如果这个层的深度值小于深度贴图的值，就意味着这一层的\(\color{brown}{\bar{P}}\)向量部分在表面之下。我们继续这个处理过程直到有一层的深度高于储存在深度贴图中的值：这个点就在（经过位移的）表面下方。
 
@@ -232,7 +232,7 @@ return texCoords - currentTexCoords;
 
 有10个样本砖墙从一个角度看上去就已经很好了，但是当有一个强前面展示的木制表面一样陡峭的表面时，陡峭的视差映射的威力就显示出来了：
 
-![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_steep_parallax_mapping.png)
+![](../img/05/05/parallax_mapping_steep_parallax_mapping.png)
 
 我们可以通过对视差贴图的一个属性的利用，对算法进行一点提升。当垂直看一个表面的时候纹理时位移比以一定角度看时的小。我们可以在垂直看时使用更少的样本，以一定角度看时增加样本数量：
 
@@ -248,7 +248,7 @@ float numLayers = mix(maxLayers, minLayers, abs(dot(vec3(0.0, 0.0, 1.0), viewDir
 
 陡峭视差贴图同样有自己的问题。因为这个技术是基于有限的样本数量的，我们会遇到锯齿效果以及图层之间有明显的断层：
 
-![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_steep_artifact.png)
+![](../img/05/05/parallax_mapping_steep_artifact.png)
 
 我们可以通过增加样本的方式减少这个问题，但是很快就会花费很多性能。有些旨在修复这个问题的方法：不适用低于表面的第一个位置，而是在两个接近的深度层进行插值找出更匹配\(\color{blue}B\)的。
 
@@ -260,7 +260,7 @@ float numLayers = mix(maxLayers, minLayers, abs(dot(vec3(0.0, 0.0, 1.0), viewDir
 
 视差遮蔽映射(Parallax Occlusion Mapping)和陡峭视差映射的原则相同，但不是用触碰的第一个深度层的纹理坐标，而是在触碰之前和之后，在深度层之间进行线性插值。我们根据表面的高度距离啷个深度层的深度层值的距离来确定线性插值的大小。看看下面的图片就能了解它是如何工作的：
 
-[](http://learnopengl.com/img/advanced-lighting/parallax_mapping_parallax_occlusion_mapping_diagram.png)
+[](../img/05/05/parallax_mapping_parallax_occlusion_mapping_diagram.png)
 
 你可以看到大部分和陡峭视差映射一样，不一样的地方是有个额外的步骤，两个深度层的纹理坐标围绕着交叉点的线性插值。这也是近似的，但是比陡峭视差映射更精确。
 
@@ -287,7 +287,7 @@ return finalTexCoords;
 
 视差遮蔽映射的效果非常好，尽管有一些可以看到的轻微的不真实和锯齿的问题，这仍是一个好交易，因为除非是放得非常大或者观察角度特别陡，否则也看不到。
 
-![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_parallax_occlusion_mapping.png)
+![](../img/05/05/parallax_mapping_parallax_occlusion_mapping.png)
 
 你可以在这里找到[源代码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping)，及其[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping&type=vertex)和[像素](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping_occlusion&type=fragment)着色器。
 
diff --git a/docs/05 Advanced Lighting/06 HDR.md b/docs/05 Advanced Lighting/06 HDR.md
index f010518..1c97742 100644
--- a/docs/05 Advanced Lighting/06 HDR.md	
+++ b/docs/05 Advanced Lighting/06 HDR.md	
@@ -8,7 +8,7 @@
 
 一般来说，当存储在帧缓冲(Framebuffer)中时，亮度和颜色的值是默认被限制在0.0到1.0之间的。这个看起来无辜的语句使我们一直将亮度与颜色的值设置在这个范围内，尝试着与场景契合。这样是能够运行的，也能给出还不错的效果。但是如果我们遇上了一个特定的区域，其中有多个亮光源使这些数值总和超过了1.0，又会发生什么呢？答案是这些片段中超过1.0的亮度或者颜色值会被约束在1.0，从而导致场景混成一片，难以分辨：
 
-![](http://learnopengl.com/img/advanced-lighting/hdr_clamped.png)
+![](../img/05/06/hdr_clamped.png)
 
 这是由于大量片段的颜色值都非常接近1.0，在很大一个区域内每一个亮的片段都有相同的白色。这损失了很多的细节，使场景看起来非常假。
 
@@ -18,7 +18,7 @@
 
 HDR原本只是被运用在摄影上，摄影师对同一个场景采取不同曝光拍多张照片，捕捉大范围的色彩值。这些图片被合成为HDR图片，从而综合不同的曝光等级使得大范围的细节可见。看下面这个例子，左边这张图片在被光照亮的区域充满细节，但是在黑暗的区域就什么都看不见了；但是右边这张图的高曝光却可以让之前看不出来的黑暗区域显现出来。
 
-![](http://learnopengl.com/img/advanced-lighting/hdr_image.png)
+![](../img/05/06/hdr_image.png)
 
 这与我们眼睛工作的原理非常相似，也是HDR渲染的基础。当光线很弱的啥时候，人眼会自动调整从而使过暗和过亮的部分变得更清晰，就像人眼有一个能自动根据场景亮度调整的自动曝光滑块。
 
@@ -86,7 +86,7 @@ void main()
 
 这里我们直接采样了浮点颜色缓冲并将其作为片段着色器的输出。然而，这个2D四边形的输出是被直接渲染到默认的帧缓冲中，导致所有片段着色器的输出值被约束在0.0到1.0间，尽管我们已经有了一些存在浮点颜色纹理的值超过了1.0。
 
-![](http://learnopengl.com/img/advanced-lighting/hdr_direct.png)
+![](../img/05/06/hdr_direct.png)
 
 很明显，在隧道尽头的强光的值被约束在1.0，因为一大块区域都是白色的，过程中超过1.0的地方损失了所有细节。因为我们直接转换HDR值到LDR值，这就像我们根本就没有应用HDR一样。为了修复这个问题我们需要做的是无损转化所有浮点颜色值回0.0-1.0范围中。我们需要应用到色调映射。
 
@@ -113,7 +113,7 @@ void main()
 
 有了Reinhard色调映射的应用，我们不再会在场景明亮的地方损失细节。当然，这个算法是倾向明亮的区域的，暗的区域会不那么精细也不那么有区分度。
 
-![](http://learnopengl.com/img/advanced-lighting/hdr_reinhard.png)
+![](../img/05/06/hdr_reinhard.png)
 
 现在你可以看到在隧道的尽头木头纹理变得可见了。用了这个非常简单地色调映射算法，我们可以合适的看到存在浮点帧缓冲中整个范围的HDR值，给我们对于无损场景光照精确的控制。
 
@@ -140,7 +140,7 @@ void main()
 
 在这里我们将`exposure`定义为默认为1.0的`uniform`，从而允许我们更加精确设定我们是要注重黑暗还是明亮的区域的HDR颜色值。举例来说，高曝光值会使隧道的黑暗部分显示更多的细节，然而低曝光值会显著减少黑暗区域的细节，但允许我们看到更多明亮区域的细节。下面这组图片展示了在不同曝光值下的通道：
 
-![](http://learnopengl.com/img/advanced-lighting/hdr_exposure.png)
+![](../img/05/06/hdr_exposure.png)
 
 这个图片清晰地展示了HDR渲染的优点。通过改变曝光等级，我们可以看见场景的很多细节，而这些细节可能在LDR渲染中都被丢失了。比如说隧道尽头，在正常曝光下木头结构隐约可见，但用低曝光木头的花纹就可以清晰看见了。对于近处的木头花纹来说，在高曝光下会能更好的看见。
 
diff --git a/docs/05 Advanced Lighting/07 Bloom.md b/docs/05 Advanced Lighting/07 Bloom.md
index 58da16c..974be60 100644
--- a/docs/05 Advanced Lighting/07 Bloom.md	
+++ b/docs/05 Advanced Lighting/07 Bloom.md	
@@ -10,7 +10,7 @@
 
 光晕效果可以使用一个后处理特效泛光来实现。泛光使所有明亮区域产生光晕效果。下面是一个使用了和没有使用光晕的对比（图片生成自虚幻引擎）：
 
-![](http://learnopengl.com/img/advanced-lighting/bloom_example.png)
+![](../img/05/07/bloom_example.png)
 
 Bloom是我们能够注意到一个明亮的物体真的有种明亮的感觉。泛光可以极大提升场景中的光照效果，并提供了极大的效果提升，尽管做到这一切只需一点改变。
 
@@ -20,25 +20,25 @@ Bloom和HDR结合使用效果很好。常见的一个误解是HDR和泛光是一
 
 我们来一步一步解释这个处理过程。我们在场景中渲染一个带有4个立方体形式不同颜色的明亮的光源。带有颜色的发光立方体的亮度在1.5到15.0之间。如果我们将其渲染至HDR颜色缓冲，场景看起来会是这样的：
 
-![](http://learnopengl.com/img/advanced-lighting/bloom_scene.png)
+![](../img/05/07/bloom_scene.png)
 
 我们得到这个HDR颜色缓冲纹理，提取所有超出一定亮度的fragment。这样我们就会获得一个只有fragment超过了一定阈限的颜色区域：
 
-![](http://learnopengl.com/img/advanced-lighting/bloom_extracted.png)
+![](../img/05/07/bloom_extracted.png)
 
 我们将这个超过一定亮度阈限的纹理进行模糊。泛光效果的强度很大程度上被模糊过滤器的范围和强度所决定。
 
-![](http://learnopengl.com/img/advanced-lighting/bloom_blurred.png)
+![](../img/05/07/bloom_blurred.png)
 
 最终的被模糊化的纹理就是我们用来获得发出光晕效果的东西。这个已模糊的纹理要添加到原来的HDR场景纹理的上部。因为模糊过滤器的应用明亮区域发出光晕，所以明亮区域在长和宽上都有所扩展。
 
-![](http://learnopengl.com/img/advanced-lighting/bloom_small.png)
+![](../img/05/07/bloom_small.png)
 
 泛光本身并不是个复杂的技术，但很难获得正确的效果。它的品质很大程度上取决于所用的模糊过滤器的质量和类型。简单的改改模糊过滤器就会极大的改变泛光效果的品质。
 
 下面这几步就是泛光后处理特效的过程，它总结了实现泛光所需的步骤。
 
-![](http://learnopengl.com/img/advanced-lighting/bloom_steps.png)
+![](../img/05/07/bloom_steps.png)
 
 首先我们需要根据一定的阈限提取所有明亮的颜色。我们先来做这件事。
 
@@ -110,7 +110,7 @@ void main()
 
 有了两个颜色缓冲，我们就有了一个正常场景的图像和一个提取出的亮区的图像；这些都在一个渲染步骤中完成。
 
-![](http://learnopengl.com/img/advanced-lighting/bloom_attachments.png)
+![](../img/05/07/bloom_attachments.png)
 
 有了一个提取出的亮区图像，我们现在就要把这个图像进行模糊处理。我们可以使用帧缓冲教程后处理部分的那个简单的盒子过滤器，但不过我们最好还是使用一个更高级的更漂亮的模糊过滤器：**高斯模糊(Gaussian blur)**。
 
@@ -118,7 +118,7 @@ void main()
 
 在后处理教程那里，我们采用的模糊是一个图像中所有周围像素的均值，它的确为我们提供了一个简易实现的模糊，但是效果并不好。高斯模糊基于高斯曲线，高斯曲线通常被描述为一个钟形曲线，中间的值达到最大化，随着距离的增加，两边的值不断减少。高斯曲线在数学上有不同的形式，但是通常是这样的形状：
 
-![](http://learnopengl.com/img/advanced-lighting/bloom_gaussian.png)
+![](../img/05/07/bloom_gaussian.png)
 
 高斯曲线在它的中间处的面积最大，使用它的值作为权重使得近处的样本拥有最大的优先权。比如，如果我们从fragment的32×32的四方形区域采样，这个权重随着和fragment的距离变大逐渐减小；通常这会得到更好更真实的模糊效果，这种模糊叫做高斯模糊。
 
@@ -126,7 +126,7 @@ void main()
 
 幸运的是，高斯方程有个非常巧妙的特性，它允许我们把二维方程分解为两个更小的方程：一个描述水平权重，另一个描述垂直权重。我们首先用水平权重在整个纹理上进行水平模糊，然后在经改变的纹理上进行垂直模糊。利用这个特性，结果是一样的，但是可以节省难以置信的性能，因为我们现在只需做32+32次采样，不再是1024了！这叫做两步高斯模糊。
 
-![](http://learnopengl.com/img/advanced-lighting/bloom_gaussian_two_pass.png)
+![](../img/05/07/bloom_gaussian_two_pass.png)
 
 这意味着我们如果对一个图像进行模糊处理，至少需要两步，最好使用帧缓冲对象做这件事。具体来说，我们将实现像乒乓球一样的帧缓冲来实现高斯模糊。它的意思是，有一对儿帧缓冲，我们把另一个帧缓冲的颜色缓冲放进当前的帧缓冲的颜色缓冲中，使用不同的着色效果渲染指定的次数。基本上就是不断地切换帧缓冲和纹理去绘制。这样我们先在场景纹理的第一个缓冲中进行模糊，然后在把第一个帧缓冲的颜色缓冲放进第二个帧缓冲进行模糊，接着，将第二个帧缓冲的颜色缓冲放进第一个，循环往复。
 
@@ -218,7 +218,7 @@ glBindFramebuffer(GL_FRAMEBUFFER, 0);
 
 通过对提取亮区纹理进行5次模糊，我们就得到了一个正确的模糊的场景亮区图像。
 
-![](http://learnopengl.com/img/advanced-lighting/bloom_blurred_large.png)
+![](../img/05/07/bloom_blurred_large.png)
 
 泛光的最后一步是把模糊处理的图像和场景原来的HDR纹理进行结合。
 
@@ -255,7 +255,7 @@ void main()
 
 把两个纹理结合以后，场景亮区便有了合适的光晕特效：
 
-![](http://learnopengl.com/img/advanced-lighting/bloom.png)
+![](../img/05/07/bloom.png)
 
 有颜色的立方体看起来仿佛更亮，它向外发射光芒，的确是一个更好的视觉效果。这个场景比较简单，所以泛光效果不算十分令人瞩目，但在更好的场景中合理配置之后效果会有巨大的不同。你可以在这里找到这个简单的例子的源码，以及模糊的顶点和像素着色器、立方体的像素着色器、后处理的顶点和像素着色器。
 
diff --git a/docs/05 Advanced Lighting/08 Deferred Shading.md b/docs/05 Advanced Lighting/08 Deferred Shading.md
index 062351b..d5376b3 100644
--- a/docs/05 Advanced Lighting/08 Deferred Shading.md	
+++ b/docs/05 Advanced Lighting/08 Deferred Shading.md	
@@ -10,17 +10,17 @@
 
 **延迟着色法(Deferred Shading)**，**或者说是延迟渲染(Deferred Rendering)**，为了解决上述问题而诞生了，它大幅度地改变了我们渲染物体的方式。这给我们优化拥有大量光源的场景提供了很多的选择，因为它能够在渲染上百甚至上千光源的同时还能够保持能让人接受的帧率。下面这张图片包含了一共1874个点光源，它是使用延迟着色法来完成的，而这对于正向渲染几乎是不可能的(图片来源：Hannes Nevalainen)。
 
-![](http://learnopengl.com/img/advanced-lighting/deferred_example.png)
+![](../img/05/08/deferred_example.png)
 
 延迟着色法基于我们**延迟(Defer)**或**推迟(Postpone)**大部分计算量非常大的渲染(像是光照)到后期进行处理的想法。它包含两个处理阶段(Pass)：在第一个几何处理阶段(Geometry Pass)中，我们先渲染场景一次，之后获取对象的各种几何信息，并储存在一系列叫做G缓冲(G-buffer)的纹理中；想想位置向量(Position Vector)、颜色向量(Color Vector)、法向量(Normal Vector)和/或镜面值(Specular Value)。场景中这些储存在G缓冲中的几何信息将会在之后用来做(更复杂的)光照计算。下面是一帧中G缓冲的内容：
 
-![](http://learnopengl.com/img/advanced-lighting/deferred_g_buffer.png)
+![](../img/05/08/deferred_g_buffer.png)
 
 我们会在第二个光照处理阶段(Lighting Pass)中使用G缓冲内的纹理数据。在光照处理阶段中，我们渲染一个屏幕大小的方形，并使用G缓冲中的几何数据对每一个片段计算场景的光照；在每个像素中我们都会对G缓冲进行迭代。我们对于渲染过程进行解耦，将它高级的片段处理挪到后期进行，而不是直接将每个对象从顶点着色器带到片段着色器。光照计算过程还是和我们以前一样，但是现在我们需要从对应的G缓冲而不是顶点着色器(和一些uniform变量)那里获取输入变量了。
 
 下面这幅图片很好地展示了延迟着色法的整个过程：
 
-![](http://learnopengl.com/img/advanced-lighting/deferred_overview.png)
+![](../img/05/08/deferred_overview.png)
 
 这种渲染方法一个很大的好处就是能保证在G缓冲中的片段和在屏幕上呈现的像素所包含的片段信息是一样的，因为深度测试已经最终将这里的片段信息作为最顶层的片段。这样保证了对于在光照处理阶段中处理的每一个像素都只处理一次，所以我们能够省下很多无用的渲染调用。除此之外，延迟渲染还允许我们做更多的优化，从而渲染更多的光源。
 
@@ -145,7 +145,7 @@ void main()
 
 如果我们现在想要渲染一大堆纳米装战士对象到`gBuffer`帧缓冲中，并通过一个一个分别投影它的颜色缓冲到铺屏四边形中尝试将他们显示出来，我们会看到向下面这样的东西：
 
-![](http://learnopengl.com/img/advanced-lighting/deferred_g_buffer.png)
+![](../img/05/08/deferred_g_buffer.png)
 
 尝试想象世界空间位置和法向量都是正确的。比如说，指向右侧的法向量将会被更多地对齐到红色上，从场景原点指向右侧的位置矢量也同样是这样。一旦你对G缓冲中的内容满意了，我们就该进入到下一步：光照处理阶段了。
 
@@ -220,7 +220,7 @@ void main()
 
 运行一个包含32个小光源的简单Demo会是像这样子的：
 
-![](http://learnopengl.com/img/advanced-lighting/deferred_shading.png)
+![](../img/05/08/deferred_shading.png)
 
 你可以在以下位置找到Demo的完整[源代码](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred)，和几何渲染阶段的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_geometry&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_geometry&type=fragment)着色器，还有光照渲染阶段的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred&type=vertex)着色器。
 
@@ -254,7 +254,7 @@ for (GLuint i = 0; i < lightPositions.size(); i++)
 
 然而，这些渲染出来的立方体并没有考虑到我们储存的延迟渲染器的几何深度(Depth)信息，并且结果是它被渲染在之前渲染过的物体之上，这并不是我们想要的结果。
 
-![](http://learnopengl.com/img/advanced-lighting/deferred_lights_no_depth.png)
+![](../img/05/08/deferred_lights_no_depth.png)
 
 我们需要做的就是首先复制出在几何渲染阶段中储存的深度信息，并输出到默认的帧缓冲的深度缓冲，然后我们才渲染光立方体。这样之后只有当它在之前渲染过的几何体上方的时候，光立方体的片段才会被渲染出来。我们可以使用`glBlitFramebuffer`复制一个帧缓冲的内容到另一个帧缓冲中，这个函数我们也在[抗锯齿](http://learnopengl-cn.readthedocs.org/zh/latest/04%20Advanced%20OpenGL/11%20Anti%20Aliasing/)的教程中使用过，用来还原多重采样的帧缓冲。`glBlitFramebuffer`这个函数允许我们复制一个用户定义的帧缓冲区域到另一个用户定义的帧缓冲区域。
 
@@ -273,7 +273,7 @@ glBindFramebuffer(GL_FRAMEBUFFER, 0);
 
 在这里我们复制整个读帧缓冲的深度缓冲信息到默认帧缓冲的深度缓冲，对于颜色缓冲和模板缓冲我们也可以这样处理。现在如果我们接下来再渲染光立方体，场景里的几何体将会看起来很真实了，而不只是简单地粘贴立方体到2D方形之上：
 
-![](http://learnopengl.com/img/advanced-lighting/deferred_lights_depth.png)
+![](../img/05/08/deferred_lights_depth.png)
 
 你可以在[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_light_cube)找到Demo的源代码，还有光立方体的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_light_cube&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_light_cube&type=fragment)着色器。
 
@@ -387,7 +387,7 @@ void main()
 
 使用光体积更好的方法是渲染一个实际的球体，并根据光体积的半径缩放。这些球的中心放置在光源的位置，由于它是根据光体积半径缩放的，这个球体正好覆盖了光的可视体积。这就是我们的技巧：我们使用大体相同的延迟片段着色器来渲染球体。因为球体产生了完全匹配于受影响像素的着色器调用，我们只渲染了受影响的像素而跳过其它的像素。下面这幅图展示了这一技巧：
 
-![](http://learnopengl.com/img/advanced-lighting/deferred_light_volume_rendered.png)
+![](../img/05/08/deferred_light_volume_rendered.png)
 
 它被应用在场景中每个光源上，并且所得的片段相加混合在一起。这个结果和之前场景是一样的，但这一次只渲染对于光源相关的片段。它有效地减少了从`nr_objects * nr_lights`到`nr_objects + nr_lights`的计算量，这使得多光源场景的渲染变得无比高效。这正是为什么延迟渲染非常适合渲染很大数量光源。
 
diff --git a/docs/05 Advanced Lighting/09 SSAO.md b/docs/05 Advanced Lighting/09 SSAO.md
index dda524a..716f540 100644
--- a/docs/05 Advanced Lighting/09 SSAO.md	
+++ b/docs/05 Advanced Lighting/09 SSAO.md	
@@ -10,7 +10,7 @@
 
 下面这幅图展示了在使用和不使用SSAO时场景的不同。特别注意对比褶皱部分，你会发现(环境)光被遮蔽了许多：
 
-![](http://learnopengl.com/img/advanced-lighting/ssao_example.png)
+![](../img/05/09/ssao_example.png)
 
 尽管这不是一个非常明显的效果，启用SSAO的图像确实给我们更真实的感觉，这些小的遮蔽细节给整个场景带来了更强的深度感。
 
@@ -18,23 +18,23 @@
 
 SSAO背后的原理很简单：对于铺屏四边形(Screen-filled Quad)上的每一个片段，我们都会根据周边深度值计算一个**遮蔽因子(Occlusion Factor)**。这个遮蔽因子之后会被用来减少或者抵消片段的环境光照分量。遮蔽因子是通过采集片段周围球型核心(Kernel)的多个深度样本，并和当前片段深度值对比而得到的。高于片段深度值样本的个数就是我们想要的遮蔽因子。
 
-![](http://learnopengl.com/img/advanced-lighting/ssao_crysis_circle.png)
+![](../img/05/09/ssao_crysis_circle.png)
 
 上图中在几何体内灰色的深度样本都是高于片段深度值的，他们会增加遮蔽因子；几何体内样本个数越多，片段获得的环境光照也就越少。
 
 很明显，渲染效果的质量和精度与我们采样的样本数量有直接关系。如果样本数量太低，渲染的精度会急剧减少，我们会得到一种叫做**波纹(Banding)**的效果；如果它太高了，反而会影响性能。我们可以通过引入随机性到采样核心(Sample Kernel)的采样中从而减少样本的数目。通过随机旋转采样核心，我们能在有限样本数量中得到高质量的结果。然而这仍然会有一定的麻烦，因为随机性引入了一个很明显的噪声图案，我们将需要通过模糊结果来修复这一问题。下面这幅图片([John Chapman](http://john-chapman-graphics.blogspot.com/)的佛像)展示了波纹效果还有随机性造成的效果：
 
-![](http://learnopengl.com/img/advanced-lighting/ssao_banding_noise.jpg)
+![](../img/05/09/ssao_banding_noise.jpg)
 
 你可以看到，尽管我们在低样本数的情况下得到了很明显的波纹效果，引入随机性之后这些波纹效果就完全消失了。
 
 Crytek公司开发的SSAO技术会产生一种特殊的视觉风格。因为使用的采样核心是一个球体，它导致平整的墙面也会显得灰蒙蒙的，因为核心中一半的样本都会在墙这个几何体上。下面这幅图展示了孤岛危机的SSAO，它清晰地展示了这种灰蒙蒙的感觉：
 
-![](http://learnopengl.com/img/advanced-lighting/ssao_crysis.jpg)
+![](../img/05/09/ssao_crysis.jpg)
 
 由于这个原因，我们将不会使用球体的采样核心，而使用一个沿着表面法向量的半球体采样核心。
 
-![](http://learnopengl.com/img/advanced-lighting/ssao_hemisphere.png)
+![](../img/05/09/ssao_hemisphere.png)
 
 通过在**法向半球体(Normal-oriented Hemisphere)**周围采样，我们将不会考虑到片段底部的几何体.它消除了环境光遮蔽灰蒙蒙的感觉，从而产生更真实的结果。这个SSAO教程将会基于法向半球法和John Chapman出色的[SSAO教程](http://john-chapman-graphics.blogspot.com/2013/01/ssao-tutorial.html)。
 
@@ -49,7 +49,7 @@ SSAO需要获取几何体的信息，因为我们需要一些方式来确定一
 
 通过使用一个逐片段观察空间位置，我们可以将一个采样半球核心对准片段的观察空间表面法线。对于每一个核心样本我们会采样线性深度纹理来比较结果。采样核心会根据旋转矢量稍微偏转一点；我们所获得的遮蔽因子将会之后用来限制最终的环境光照分量。
 
-![](http://learnopengl.com/img/advanced-lighting/ssao_overview.png)
+![](../img/05/09/ssao_overview.png)
 
 由于SSAO是一种屏幕空间技巧，我们对铺屏2D四边形上每一个片段计算这一效果；也就是说我们没有场景中几何体的信息。我们能做的只是渲染几何体数据到屏幕空间纹理中，我们之后再会将此数据发送到SSAO着色器中，之后我们就能访问到这些几何体数据了。如果你看了前面一篇教程，你会发现这和延迟渲染很相似。这也就是说SSAO和延迟渲染能完美地兼容，因为我们已经存位置和法线向量到G缓冲中了。
 
@@ -116,7 +116,7 @@ glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
 
 我们需要沿着表面法线方向生成大量的样本。就像我们在这个教程的开始介绍的那样，我们想要生成形成半球形的样本。由于对每个表面法线方向生成采样核心非常困难，也不合实际，我们将在[切线空间](04 Normal Mapping.md)(Tangent Space)内生成采样核心，法向量将指向正z方向。
 
-![](http://learnopengl.com/img/advanced-lighting/ssao_hemisphere.png)
+![](../img/05/09/ssao_hemisphere.png)
 
 假设我们有一个单位半球，我们可以获得一个拥有最大64样本值的采样核心：
 
@@ -161,7 +161,7 @@ GLfloat lerp(GLfloat a, GLfloat b, GLfloat f)
 
 这就给了我们一个大部分样本靠近原点的核心分布。
 
-![](http://learnopengl.com/img/advanced-lighting/ssao_kernel_weight.png)
+![](../img/05/09/ssao_kernel_weight.png)
 
 每个核心样本将会被用来偏移观察空间片段位置从而采样周围的几何体。我们在教程开始的时候看到，如果没有变化采样核心，我们将需要大量的样本来获得真实的结果。通过引入一个随机的转动到采样核心中，我们可以很大程度上减少这一数量。
 
@@ -333,7 +333,7 @@ occlusion += (sampleDepth >= sample.z ? 1.0 : 0.0);
 
 这并没有完全结束，因为仍然还有一个小问题需要考虑。当检测一个靠近表面边缘的片段时，它将会考虑测试表面之下的表面的深度值；这些值将会(不正确地)音响遮蔽因子。我们可以通过引入一个范围检测从而解决这个问题，正如下图所示([John Chapman](http://john-chapman-graphics.blogspot.com/)的佛像)：
 
-![](http://learnopengl.com/img/advanced-lighting/ssao_range_check.png)
+![](../img/05/09/ssao_range_check.png)
 
 我们引入一个范围测试从而保证我们只当被测深度值在取样半径内时影响遮蔽因子。将代码最后一行换成：
 
@@ -344,7 +344,7 @@ occlusion += (sampleDepth >= sample.z ? 1.0 : 0.0) * rangeCheck;
 
 这里我们使用了GLSL的`smoothstep`函数，它非常光滑地在第一和第二个参数范围内插值了第三个参数。如果深度差因此最终取值在`radius`之间，它们的值将会光滑地根据下面这个曲线插值在0.0和1.0之间：
 
-![](http://learnopengl.com/img/advanced-lighting/ssao_smoothstep.png)
+![](../img/05/09/ssao_smoothstep.png)
 
 如果我们使用一个在深度值在`radius`之外就突然移除遮蔽贡献的硬界限范围检测(Hard Cut-off Range Check)，我们将会在范围检测应用的地方看见一个明显的(很难看的)边缘。
 
@@ -358,7 +358,7 @@ FragColor = occlusion;
 
 下面这幅图展示了我们最喜欢的纳米装模型正在打盹的场景，环境遮蔽着色器产生了以下的纹理：
 
-![](http://learnopengl.com/img/advanced-lighting/ssao_without_blur.png)
+![](../img/05/09/ssao_without_blur.png)
 
 可见，环境遮蔽产生了非常强烈的深度感。仅仅通过环境遮蔽纹理我们就已经能清晰地看见模型一定躺在地板上而不是浮在空中。
 
@@ -406,7 +406,7 @@ void main() {
 
 这里我们遍历了周围在-2.0和2.0之间的SSAO纹理单元(Texel)，采样与噪声纹理维度相同数量的SSAO纹理。我们通过使用返回`vec2`纹理维度的`textureSize`，根据纹理单元的真实大小偏移了每一个纹理坐标。我们平均所得的结果，获得一个简单但是有效的模糊效果：
 
-![](http://learnopengl.com/img/advanced-lighting/ssao.png)
+![](../img/05/09/ssao.png)
 
 这就完成了，一个包含逐片段环境遮蔽数据的纹理；在光照处理阶段中可以直接使用。
 
@@ -466,7 +466,7 @@ void main()
 
 (除了将其改到观察空间)对比于之前的光照实现，唯一的真正改动就是场景环境分量与`AmbientOcclusion`值的乘法。通过在场景中加入一个淡蓝色的点光源，我们将会得到下面这个结果：
 
-![](http://learnopengl.com/img/advanced-lighting/ssao_final.png)
+![](../img/05/09/ssao_final.png)
 
 你可以在[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/ssao)找到完整的源代码，和以下着色器：
 
diff --git a/docs/06 In Practice/02 Text Rendering.md b/docs/06 In Practice/02 Text Rendering.md
index 82ea624..3cb52fd 100644
--- a/docs/06 In Practice/02 Text Rendering.md	
+++ b/docs/06 In Practice/02 Text Rendering.md	
@@ -16,7 +16,7 @@
 
 在早期渲染文字时，选择你应用程序的字体(或者创建你自己的字体)来绘制文字是通过将所有用到的文字加载在一张大纹理图中来实现的。这张纹理贴图我们把它叫做**位图字体(Bitmap Font)**，它包含了所有我们想要使用的字符。这些字符被称为**字形(Glyph)**。每个字形根据他们的编号被放到位图字体中的确切位置，在渲染这些字形的时候根据这些排列规则将他们取出并贴到指定的2D方块中。
 
-![](http://learnopengl.com/img/in-practice/bitmapfont.png)
+![](../img/06/02/bitmapfont.png)
 
 上图展示了我们如何从一张位图字体的纹理中通过对字形的合理取样(通过小心地选择字形的纹理坐标)来实现绘制文字“OpenGL”到2D方块中的原理。通过对OpenGL启用混合并让位图字体的纹理背景保持透明，这样就能实现使用OpenGL绘制你想要文字到屏幕的功能。上图的这张位图字体是使用[Codehead的位图字体生成器](http://www.codehead.co.uk/cbfg/)生成的。
 
@@ -77,7 +77,7 @@ if (FT_Load_Char(face, 'X', FT_LOAD_RENDER))
 
 使用FreeType加载的字形位图并不像我们使用位图字体那样持有相同的尺寸大小。使用FreeType生产的字形位图的大小是恰好能包含这个字形的尺寸。例如生产用于表示'.'的位图的尺寸要比表示'X'的小得多。因此，FreeType在加载字形的时候还生产了几个度量值来描述生成的字形位图的大小和位置。下图展示了FreeType的所有度量值的涵义。
 
-![](http://learnopengl.com/img/in-practice/glyph.png)
+![](../img/06/02/glyph.png)
 
 每一个字形都放在一个水平的基线(Baseline)上，上图中被描黑的水平箭头表示该字形的基线。这条基线类似于拼音四格线中的第二根水平线，一些字形被放在基线以上(如'x'或'a')，而另一些则会超过基线以下(如'g'或'p')。FreeType的这些度量值中包含了字形在相对于基线上的偏移量用来描述字形相对于此基线的位置，字形的大小，以及与下一个字符之间的距离。下面列出了我们在渲染字形时所需要的度量值的属性：
 
@@ -292,7 +292,7 @@ GLfloat ypos = y - (ch.Size.y - ch.Bearing.y);
 
 一些字符(诸如'p'或'q')需要被渲染到基线以下，因此字形方块也应该讲y位置往下调整。调整的量就是便是字形度量值中字形的高度和BearingY的差：
 
-![](http://learnopengl.com/img/in-practice/glyph_offset.png)
+![](../img/06/02/glyph_offset.png)
 
 要计算这段偏移量的距离，我们需要指出是字形在基线以下的部分最底断到基线的距离。在上图中这段距离用红色双向箭头标出。如你所见，在字形度量值中，我们可以通过用字形的高度减去bearingY来计算这段向量的长度。这段距离有可能是0.0f(如'x'字符)
 ，或是超出基线底部的距离的长度(如'g'或'j')。
@@ -306,13 +306,13 @@ RenderText(shader, "(C) LearnOpenGL.com", 540.0f, 570.0f, 0.5f, glm::vec3(0.3, 0
 
 渲染效果看上去像这样：
 
-![](http://learnopengl.com/img/in-practice/text_rendering.png)
+![](../img/06/02/text_rendering.png)
 
 你可以从这里获取这个例子的[源代码](http://learnopengl.com/code_viewer.php?code=in-practice/text_rendering)。
 
 通过关闭字形纹理的绑定，能够给你对文字方块的顶点计算更好的理解，它看上去像这样：
 
-![](http://learnopengl.com/img/in-practice/text_rendering_quads.png)
+![](../img/06/02/text_rendering_quads.png)
 
 可以看出，对应'p'和'('等字形的方块明显向下偏移了一些，通过这些你就能清楚地看到那条传说中的基线了。
 
diff --git a/docs/06 In Practice/2D-Game/06 Particles.md b/docs/06 In Practice/2D-Game/06 Particles.md
index 410b2bd..9101a9b 100644
--- a/docs/06 In Practice/2D-Game/06 Particles.md	
+++ b/docs/06 In Practice/2D-Game/06 Particles.md	
@@ -10,7 +10,7 @@
 
 当处理这些微粒的时候,通常是由一个叫做粒子发射器或粒子生成器的东西完成的,从这个地方,持续不断的产生新的微粒并且旧的微粒随着时间逐渐消亡.如果这个粒子发射器产生一个带着类似烟雾纹理的微粒的时候,它的颜色亮度同时又随着与发射器距离的增加而变暗,那么就会产生出灼热的火焰的效果:
 
-![fire](http://www.learnopengl.com/img/in-practice/breakout/particles_example.jpg)
+![fire](../../img/06/Breakout/06/particles_example.jpg)
 
 一个单一的微粒通常有一个生命值变量,并且从它产生开始就一直在缓慢的减少.一旦它的生命值少于某个极限值(通常是0)我们就会杀掉这个粒子,这样下一个粒子产生时就可以让它来替换那个被杀掉的粒子.一个粒子发射器控制它产生的所有粒子并且根据它们的属性来改变它们的行为.一个粒子通常有下面的属性:
 
@@ -29,7 +29,7 @@ struct Particle {
 
 你可以想象到用这样一个系统,我们就可以创造一些有趣的效果比如火焰,青烟,烟雾,魔法效果,炮火残渣等等.在Breakout游戏里,我们将会使用下面那个小球来创建一个简单的粒子生成器来制作一些有趣的效果,结果看起来就像这样:
 
-<video src="http://learnopengl.com/video/in-practice/breakout/particles.mp4" controls="controls"></video>
+<video src="../../../img/06/Breakout/06/particles.mp4" controls="controls"></video>
 
 上面那个粒子生成器在这个球的位置产生无数的粒子,根据球移动的速度给了粒子相应的速度,并且根据它们的生命值来改变他们的颜色亮度.
 
@@ -179,7 +179,7 @@ glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
 因为我们(就像这个系列教程的其他部分一样)喜欢让事情变得有条理,所以我们就创建了另一个类`ParticleGenerator`来封装我们刚刚谈到的所有功能.你可以在下面的链接里找到源码:
 >* [header](http://www.learnopengl.com/code_viewer.php?code=in-practice/breakout/particle_generator.h),[code](http://www.learnopengl.com/code_viewer.php?code=in-practice/breakout/particle_generator)
 
-然后在游戏代码里,我们创建这样一个粒子发射器并且用[这个](http://www.learnopengl.com/img/in-practice/breakout/textures/particle.png)纹理初始化.
+然后在游戏代码里,我们创建这样一个粒子发射器并且用[这个](../../img/06/Breakout/06/particle.png)纹理初始化.
 
 ```c++
 ParticleGenerator   *Particles; 
diff --git a/docs/img/01/08/coordinate_system_depth.mp4 b/docs/img/01/08/coordinate_system_depth.mp4
new file mode 100644
index 0000000..e77a0ba
Binary files /dev/null and b/docs/img/01/08/coordinate_system_depth.mp4 differ
diff --git a/docs/img/01/08/coordinate_system_no_depth.mp4 b/docs/img/01/08/coordinate_system_no_depth.mp4
new file mode 100644
index 0000000..cf49354
Binary files /dev/null and b/docs/img/01/08/coordinate_system_no_depth.mp4 differ
diff --git a/docs/img/01/08/coordinate_systems.png b/docs/img/01/08/coordinate_systems.png
new file mode 100644
index 0000000..7a554a6
Binary files /dev/null and b/docs/img/01/08/coordinate_systems.png differ
diff --git a/docs/img/01/08/coordinate_systems_multiple_objects.png b/docs/img/01/08/coordinate_systems_multiple_objects.png
new file mode 100644
index 0000000..1511c4a
Binary files /dev/null and b/docs/img/01/08/coordinate_systems_multiple_objects.png differ
diff --git a/docs/img/01/08/coordinate_systems_result.png b/docs/img/01/08/coordinate_systems_result.png
new file mode 100644
index 0000000..490759a
Binary files /dev/null and b/docs/img/01/08/coordinate_systems_result.png differ
diff --git a/docs/img/01/08/coordinate_systems_right_handed.png b/docs/img/01/08/coordinate_systems_right_handed.png
new file mode 100644
index 0000000..7ca3587
Binary files /dev/null and b/docs/img/01/08/coordinate_systems_right_handed.png differ
diff --git a/docs/img/01/08/orthographic_frustum.png b/docs/img/01/08/orthographic_frustum.png
new file mode 100644
index 0000000..808247a
Binary files /dev/null and b/docs/img/01/08/orthographic_frustum.png differ
diff --git a/docs/img/01/08/perspective.png b/docs/img/01/08/perspective.png
new file mode 100644
index 0000000..b4d90da
Binary files /dev/null and b/docs/img/01/08/perspective.png differ
diff --git a/docs/img/01/08/perspective_frustum.png b/docs/img/01/08/perspective_frustum.png
new file mode 100644
index 0000000..b8c22d1
Binary files /dev/null and b/docs/img/01/08/perspective_frustum.png differ
diff --git a/docs/img/01/08/perspective_orthographic.png b/docs/img/01/08/perspective_orthographic.png
new file mode 100644
index 0000000..3395d8f
Binary files /dev/null and b/docs/img/01/08/perspective_orthographic.png differ
diff --git a/docs/img/01/09/camera_axes.png b/docs/img/01/09/camera_axes.png
new file mode 100644
index 0000000..88f0075
Binary files /dev/null and b/docs/img/01/09/camera_axes.png differ
diff --git a/docs/img/01/09/camera_circle.mp4 b/docs/img/01/09/camera_circle.mp4
new file mode 100644
index 0000000..e93ecd3
Binary files /dev/null and b/docs/img/01/09/camera_circle.mp4 differ
diff --git a/docs/img/01/09/camera_inside.mp4 b/docs/img/01/09/camera_inside.mp4
new file mode 100644
index 0000000..51d8610
Binary files /dev/null and b/docs/img/01/09/camera_inside.mp4 differ
diff --git a/docs/img/01/09/camera_mouse.mp4 b/docs/img/01/09/camera_mouse.mp4
new file mode 100644
index 0000000..68721cd
Binary files /dev/null and b/docs/img/01/09/camera_mouse.mp4 differ
diff --git a/docs/img/01/09/camera_pitch.png b/docs/img/01/09/camera_pitch.png
new file mode 100644
index 0000000..e9d9ff9
Binary files /dev/null and b/docs/img/01/09/camera_pitch.png differ
diff --git a/docs/img/01/09/camera_pitch_yaw_roll.png b/docs/img/01/09/camera_pitch_yaw_roll.png
new file mode 100644
index 0000000..f32c317
Binary files /dev/null and b/docs/img/01/09/camera_pitch_yaw_roll.png differ
diff --git a/docs/img/01/09/camera_smooth.mp4 b/docs/img/01/09/camera_smooth.mp4
new file mode 100644
index 0000000..7de90bd
Binary files /dev/null and b/docs/img/01/09/camera_smooth.mp4 differ
diff --git a/docs/img/01/09/camera_triangle.png b/docs/img/01/09/camera_triangle.png
new file mode 100644
index 0000000..24c5184
Binary files /dev/null and b/docs/img/01/09/camera_triangle.png differ
diff --git a/docs/img/01/09/camera_yaw.png b/docs/img/01/09/camera_yaw.png
new file mode 100644
index 0000000..c1d9aee
Binary files /dev/null and b/docs/img/01/09/camera_yaw.png differ
diff --git a/docs/img/02/01/colors_scene.png b/docs/img/02/01/colors_scene.png
new file mode 100644
index 0000000..c3d8070
Binary files /dev/null and b/docs/img/02/01/colors_scene.png differ
diff --git a/docs/img/02/01/light_reflection.png b/docs/img/02/01/light_reflection.png
new file mode 100644
index 0000000..e2e729e
Binary files /dev/null and b/docs/img/02/01/light_reflection.png differ
diff --git a/docs/img/02/02/ambient_lighting.png b/docs/img/02/02/ambient_lighting.png
new file mode 100644
index 0000000..2403367
Binary files /dev/null and b/docs/img/02/02/ambient_lighting.png differ
diff --git a/docs/img/02/02/basic_lighting_diffuse.png b/docs/img/02/02/basic_lighting_diffuse.png
new file mode 100644
index 0000000..68dabb8
Binary files /dev/null and b/docs/img/02/02/basic_lighting_diffuse.png differ
diff --git a/docs/img/02/02/basic_lighting_gouruad.png b/docs/img/02/02/basic_lighting_gouruad.png
new file mode 100644
index 0000000..f729b13
Binary files /dev/null and b/docs/img/02/02/basic_lighting_gouruad.png differ
diff --git a/docs/img/02/02/basic_lighting_normal_transformation.png b/docs/img/02/02/basic_lighting_normal_transformation.png
new file mode 100644
index 0000000..fa17d85
Binary files /dev/null and b/docs/img/02/02/basic_lighting_normal_transformation.png differ
diff --git a/docs/img/02/02/basic_lighting_phong.png b/docs/img/02/02/basic_lighting_phong.png
new file mode 100644
index 0000000..3e528fb
Binary files /dev/null and b/docs/img/02/02/basic_lighting_phong.png differ
diff --git a/docs/img/02/02/basic_lighting_specular.png b/docs/img/02/02/basic_lighting_specular.png
new file mode 100644
index 0000000..47770a5
Binary files /dev/null and b/docs/img/02/02/basic_lighting_specular.png differ
diff --git a/docs/img/02/02/basic_lighting_specular_shininess.png b/docs/img/02/02/basic_lighting_specular_shininess.png
new file mode 100644
index 0000000..644d86b
Binary files /dev/null and b/docs/img/02/02/basic_lighting_specular_shininess.png differ
diff --git a/docs/img/02/02/basic_lighting_specular_theory.png b/docs/img/02/02/basic_lighting_specular_theory.png
new file mode 100644
index 0000000..97af49d
Binary files /dev/null and b/docs/img/02/02/basic_lighting_specular_theory.png differ
diff --git a/docs/img/02/02/diffuse_light.png b/docs/img/02/02/diffuse_light.png
new file mode 100644
index 0000000..6b5bce4
Binary files /dev/null and b/docs/img/02/02/diffuse_light.png differ
diff --git a/docs/img/02/03/materials.mp4 b/docs/img/02/03/materials.mp4
new file mode 100644
index 0000000..1061a9d
Binary files /dev/null and b/docs/img/02/03/materials.mp4 differ
diff --git a/docs/img/02/03/materials_light.png b/docs/img/02/03/materials_light.png
new file mode 100644
index 0000000..a487232
Binary files /dev/null and b/docs/img/02/03/materials_light.png differ
diff --git a/docs/img/02/03/materials_real_world.png b/docs/img/02/03/materials_real_world.png
new file mode 100644
index 0000000..8558743
Binary files /dev/null and b/docs/img/02/03/materials_real_world.png differ
diff --git a/docs/img/02/03/materials_with_material.png b/docs/img/02/03/materials_with_material.png
new file mode 100644
index 0000000..538028c
Binary files /dev/null and b/docs/img/02/03/materials_with_material.png differ
diff --git a/docs/img/02/04/container2.png b/docs/img/02/04/container2.png
new file mode 100644
index 0000000..596e8da
Binary files /dev/null and b/docs/img/02/04/container2.png differ
diff --git a/docs/img/02/04/container2_specular.png b/docs/img/02/04/container2_specular.png
new file mode 100644
index 0000000..681bf6e
Binary files /dev/null and b/docs/img/02/04/container2_specular.png differ
diff --git a/docs/img/02/04/lighting_maps_exercise3.png b/docs/img/02/04/lighting_maps_exercise3.png
new file mode 100644
index 0000000..a414353
Binary files /dev/null and b/docs/img/02/04/lighting_maps_exercise3.png differ
diff --git a/docs/img/02/04/lighting_maps_specular_color.png b/docs/img/02/04/lighting_maps_specular_color.png
new file mode 100644
index 0000000..edd83e4
Binary files /dev/null and b/docs/img/02/04/lighting_maps_specular_color.png differ
diff --git a/docs/img/02/04/materials_diffuse_map.png b/docs/img/02/04/materials_diffuse_map.png
new file mode 100644
index 0000000..0d25de0
Binary files /dev/null and b/docs/img/02/04/materials_diffuse_map.png differ
diff --git a/docs/img/02/04/materials_specular_map (1).png b/docs/img/02/04/materials_specular_map (1).png
new file mode 100644
index 0000000..cd8ffb0
Binary files /dev/null and b/docs/img/02/04/materials_specular_map (1).png differ
diff --git a/docs/img/02/04/materials_specular_map.png b/docs/img/02/04/materials_specular_map.png
new file mode 100644
index 0000000..cd8ffb0
Binary files /dev/null and b/docs/img/02/04/materials_specular_map.png differ
diff --git a/docs/img/02/04/matrix.jpg b/docs/img/02/04/matrix.jpg
new file mode 100644
index 0000000..2361c1c
Binary files /dev/null and b/docs/img/02/04/matrix.jpg differ
diff --git a/docs/img/02/05/attenuation.png b/docs/img/02/05/attenuation.png
new file mode 100644
index 0000000..c09ec71
Binary files /dev/null and b/docs/img/02/05/attenuation.png differ
diff --git a/docs/img/02/05/light_casters_cos.png b/docs/img/02/05/light_casters_cos.png
new file mode 100644
index 0000000..6754ca1
Binary files /dev/null and b/docs/img/02/05/light_casters_cos.png differ
diff --git a/docs/img/02/05/light_casters_directional_light.png b/docs/img/02/05/light_casters_directional_light.png
new file mode 100644
index 0000000..3224891
Binary files /dev/null and b/docs/img/02/05/light_casters_directional_light.png differ
diff --git a/docs/img/02/05/light_casters_point.png b/docs/img/02/05/light_casters_point.png
new file mode 100644
index 0000000..e0ca399
Binary files /dev/null and b/docs/img/02/05/light_casters_point.png differ
diff --git a/docs/img/02/05/light_casters_point_light.png b/docs/img/02/05/light_casters_point_light.png
new file mode 100644
index 0000000..ac68dfe
Binary files /dev/null and b/docs/img/02/05/light_casters_point_light.png differ
diff --git a/docs/img/02/05/light_casters_spotlight.png b/docs/img/02/05/light_casters_spotlight.png
new file mode 100644
index 0000000..72c70ce
Binary files /dev/null and b/docs/img/02/05/light_casters_spotlight.png differ
diff --git a/docs/img/02/05/light_casters_spotlight_angles.png b/docs/img/02/05/light_casters_spotlight_angles.png
new file mode 100644
index 0000000..d5a54a8
Binary files /dev/null and b/docs/img/02/05/light_casters_spotlight_angles.png differ
diff --git a/docs/img/02/05/light_casters_spotlight_hard.png b/docs/img/02/05/light_casters_spotlight_hard.png
new file mode 100644
index 0000000..e00bd40
Binary files /dev/null and b/docs/img/02/05/light_casters_spotlight_hard.png differ
diff --git a/docs/img/02/05/materials_diffuse_map.png b/docs/img/02/05/materials_diffuse_map.png
new file mode 100644
index 0000000..6e658ab
Binary files /dev/null and b/docs/img/02/05/materials_diffuse_map.png differ
diff --git a/docs/img/02/06/multiple_lights_atmospheres.png b/docs/img/02/06/multiple_lights_atmospheres.png
new file mode 100644
index 0000000..5b4cce7
Binary files /dev/null and b/docs/img/02/06/multiple_lights_atmospheres.png differ
diff --git a/docs/img/02/06/multiple_lights_combined.png b/docs/img/02/06/multiple_lights_combined.png
new file mode 100644
index 0000000..0d28901
Binary files /dev/null and b/docs/img/02/06/multiple_lights_combined.png differ
diff --git a/docs/img/03/01/assimp_structure.png b/docs/img/03/01/assimp_structure.png
new file mode 100644
index 0000000..b93ef0d
Binary files /dev/null and b/docs/img/03/01/assimp_structure.png differ
diff --git a/docs/img/03/03/model_diffuse.png b/docs/img/03/03/model_diffuse.png
new file mode 100644
index 0000000..8a5d620
Binary files /dev/null and b/docs/img/03/03/model_diffuse.png differ
diff --git a/docs/img/03/03/model_lighting.png b/docs/img/03/03/model_lighting.png
new file mode 100644
index 0000000..8f109b5
Binary files /dev/null and b/docs/img/03/03/model_lighting.png differ
diff --git a/docs/img/04/01/depth_linear_graph.png b/docs/img/04/01/depth_linear_graph.png
new file mode 100644
index 0000000..c655e9e
Binary files /dev/null and b/docs/img/04/01/depth_linear_graph.png differ
diff --git a/docs/img/04/01/depth_non_linear_graph.png b/docs/img/04/01/depth_non_linear_graph.png
new file mode 100644
index 0000000..3f77efd
Binary files /dev/null and b/docs/img/04/01/depth_non_linear_graph.png differ
diff --git a/docs/img/04/01/depth_testing_func_always.png b/docs/img/04/01/depth_testing_func_always.png
new file mode 100644
index 0000000..d99c1af
Binary files /dev/null and b/docs/img/04/01/depth_testing_func_always.png differ
diff --git a/docs/img/04/01/depth_testing_func_less.png b/docs/img/04/01/depth_testing_func_less.png
new file mode 100644
index 0000000..5528eb3
Binary files /dev/null and b/docs/img/04/01/depth_testing_func_less.png differ
diff --git a/docs/img/04/01/depth_testing_visible_depth.png b/docs/img/04/01/depth_testing_visible_depth.png
new file mode 100644
index 0000000..fb9700d
Binary files /dev/null and b/docs/img/04/01/depth_testing_visible_depth.png differ
diff --git a/docs/img/04/01/depth_testing_visible_linear.png b/docs/img/04/01/depth_testing_visible_linear.png
new file mode 100644
index 0000000..c448465
Binary files /dev/null and b/docs/img/04/01/depth_testing_visible_linear.png differ
diff --git a/docs/img/04/01/depth_testing_z_fighting.png b/docs/img/04/01/depth_testing_z_fighting.png
new file mode 100644
index 0000000..01e4d24
Binary files /dev/null and b/docs/img/04/01/depth_testing_z_fighting.png differ
diff --git a/docs/img/04/02/stencil_buffer.png b/docs/img/04/02/stencil_buffer.png
new file mode 100644
index 0000000..787132e
Binary files /dev/null and b/docs/img/04/02/stencil_buffer.png differ
diff --git a/docs/img/04/02/stencil_object_outlining.png b/docs/img/04/02/stencil_object_outlining.png
new file mode 100644
index 0000000..0a1a9f0
Binary files /dev/null and b/docs/img/04/02/stencil_object_outlining.png differ
diff --git a/docs/img/04/02/stencil_scene_outlined.png b/docs/img/04/02/stencil_scene_outlined.png
new file mode 100644
index 0000000..d5426fc
Binary files /dev/null and b/docs/img/04/02/stencil_scene_outlined.png differ
diff --git a/docs/img/04/03/blending_discard.png b/docs/img/04/03/blending_discard.png
new file mode 100644
index 0000000..1069ff3
Binary files /dev/null and b/docs/img/04/03/blending_discard.png differ
diff --git a/docs/img/04/03/blending_equation.png b/docs/img/04/03/blending_equation.png
new file mode 100644
index 0000000..e5969de
Binary files /dev/null and b/docs/img/04/03/blending_equation.png differ
diff --git a/docs/img/04/03/blending_equation_mixed.png b/docs/img/04/03/blending_equation_mixed.png
new file mode 100644
index 0000000..c37c5c1
Binary files /dev/null and b/docs/img/04/03/blending_equation_mixed.png differ
diff --git a/docs/img/04/03/blending_incorrect_order.png b/docs/img/04/03/blending_incorrect_order.png
new file mode 100644
index 0000000..ea47641
Binary files /dev/null and b/docs/img/04/03/blending_incorrect_order.png differ
diff --git a/docs/img/04/03/blending_no_discard.png b/docs/img/04/03/blending_no_discard.png
new file mode 100644
index 0000000..45dc5fc
Binary files /dev/null and b/docs/img/04/03/blending_no_discard.png differ
diff --git a/docs/img/04/03/blending_sorted.png b/docs/img/04/03/blending_sorted.png
new file mode 100644
index 0000000..8c13905
Binary files /dev/null and b/docs/img/04/03/blending_sorted.png differ
diff --git a/docs/img/04/03/blending_transparency.png b/docs/img/04/03/blending_transparency.png
new file mode 100644
index 0000000..0ded390
Binary files /dev/null and b/docs/img/04/03/blending_transparency.png differ
diff --git a/docs/img/04/03/blending_transparent_window.png b/docs/img/04/03/blending_transparent_window.png
new file mode 100644
index 0000000..1188863
Binary files /dev/null and b/docs/img/04/03/blending_transparent_window.png differ
diff --git a/docs/img/04/03/grass.png b/docs/img/04/03/grass.png
new file mode 100644
index 0000000..0eafd97
Binary files /dev/null and b/docs/img/04/03/grass.png differ
diff --git a/docs/img/04/04/faceculling_frontback.png b/docs/img/04/04/faceculling_frontback.png
new file mode 100644
index 0000000..333a75f
Binary files /dev/null and b/docs/img/04/04/faceculling_frontback.png differ
diff --git a/docs/img/04/04/faceculling_reverse.png b/docs/img/04/04/faceculling_reverse.png
new file mode 100644
index 0000000..419633e
Binary files /dev/null and b/docs/img/04/04/faceculling_reverse.png differ
diff --git a/docs/img/04/04/faceculling_windingorder.png b/docs/img/04/04/faceculling_windingorder.png
new file mode 100644
index 0000000..15a33df
Binary files /dev/null and b/docs/img/04/04/faceculling_windingorder.png differ
diff --git a/docs/img/04/05/container.jpg b/docs/img/04/05/container.jpg
new file mode 100644
index 0000000..d07bee4
Binary files /dev/null and b/docs/img/04/05/container.jpg differ
diff --git a/docs/img/04/05/framebuffers_blur.png b/docs/img/04/05/framebuffers_blur.png
new file mode 100644
index 0000000..f738a31
Binary files /dev/null and b/docs/img/04/05/framebuffers_blur.png differ
diff --git a/docs/img/04/05/framebuffers_edge_detection.png b/docs/img/04/05/framebuffers_edge_detection.png
new file mode 100644
index 0000000..cfd6486
Binary files /dev/null and b/docs/img/04/05/framebuffers_edge_detection.png differ
diff --git a/docs/img/04/05/framebuffers_grayscale.png b/docs/img/04/05/framebuffers_grayscale.png
new file mode 100644
index 0000000..bdf0026
Binary files /dev/null and b/docs/img/04/05/framebuffers_grayscale.png differ
diff --git a/docs/img/04/05/framebuffers_inverse.png b/docs/img/04/05/framebuffers_inverse.png
new file mode 100644
index 0000000..95bb11b
Binary files /dev/null and b/docs/img/04/05/framebuffers_inverse.png differ
diff --git a/docs/img/04/05/framebuffers_screen_texture.png b/docs/img/04/05/framebuffers_screen_texture.png
new file mode 100644
index 0000000..82b2985
Binary files /dev/null and b/docs/img/04/05/framebuffers_screen_texture.png differ
diff --git a/docs/img/04/05/framebuffers_sharpen.png b/docs/img/04/05/framebuffers_sharpen.png
new file mode 100644
index 0000000..946a267
Binary files /dev/null and b/docs/img/04/05/framebuffers_sharpen.png differ
diff --git a/docs/img/04/06/cubemaps_morrowind.jpg b/docs/img/04/06/cubemaps_morrowind.jpg
new file mode 100644
index 0000000..b7f9c41
Binary files /dev/null and b/docs/img/04/06/cubemaps_morrowind.jpg differ
diff --git a/docs/img/04/06/cubemaps_reflection.png b/docs/img/04/06/cubemaps_reflection.png
new file mode 100644
index 0000000..36e9112
Binary files /dev/null and b/docs/img/04/06/cubemaps_reflection.png differ
diff --git a/docs/img/04/06/cubemaps_reflection_map.png b/docs/img/04/06/cubemaps_reflection_map.png
new file mode 100644
index 0000000..eb53854
Binary files /dev/null and b/docs/img/04/06/cubemaps_reflection_map.png differ
diff --git a/docs/img/04/06/cubemaps_reflection_nanosuit.png b/docs/img/04/06/cubemaps_reflection_nanosuit.png
new file mode 100644
index 0000000..4698451
Binary files /dev/null and b/docs/img/04/06/cubemaps_reflection_nanosuit.png differ
diff --git a/docs/img/04/06/cubemaps_reflection_theory.png b/docs/img/04/06/cubemaps_reflection_theory.png
new file mode 100644
index 0000000..2c67920
Binary files /dev/null and b/docs/img/04/06/cubemaps_reflection_theory.png differ
diff --git a/docs/img/04/06/cubemaps_refraction.png b/docs/img/04/06/cubemaps_refraction.png
new file mode 100644
index 0000000..cd2897f
Binary files /dev/null and b/docs/img/04/06/cubemaps_refraction.png differ
diff --git a/docs/img/04/06/cubemaps_refraction_theory.png b/docs/img/04/06/cubemaps_refraction_theory.png
new file mode 100644
index 0000000..eddbfef
Binary files /dev/null and b/docs/img/04/06/cubemaps_refraction_theory.png differ
diff --git a/docs/img/04/06/cubemaps_sampling.png b/docs/img/04/06/cubemaps_sampling.png
new file mode 100644
index 0000000..2e897a0
Binary files /dev/null and b/docs/img/04/06/cubemaps_sampling.png differ
diff --git a/docs/img/04/06/cubemaps_skybox.png b/docs/img/04/06/cubemaps_skybox.png
new file mode 100644
index 0000000..f15aef2
Binary files /dev/null and b/docs/img/04/06/cubemaps_skybox.png differ
diff --git a/docs/img/04/06/cubemaps_skybox_result.png b/docs/img/04/06/cubemaps_skybox_result.png
new file mode 100644
index 0000000..dea451b
Binary files /dev/null and b/docs/img/04/06/cubemaps_skybox_result.png differ
diff --git a/docs/img/04/06/nanosuit_reflection.zip b/docs/img/04/06/nanosuit_reflection.zip
new file mode 100644
index 0000000..23be089
Binary files /dev/null and b/docs/img/04/06/nanosuit_reflection.zip differ
diff --git a/docs/img/04/06/skybox.rar b/docs/img/04/06/skybox.rar
new file mode 100644
index 0000000..6cf3bb8
Binary files /dev/null and b/docs/img/04/06/skybox.rar differ
diff --git a/docs/img/04/08/advanced_glsl_binding_points.png b/docs/img/04/08/advanced_glsl_binding_points.png
new file mode 100644
index 0000000..e6f3bd5
Binary files /dev/null and b/docs/img/04/08/advanced_glsl_binding_points.png differ
diff --git a/docs/img/04/08/advanced_glsl_fragcoord.png b/docs/img/04/08/advanced_glsl_fragcoord.png
new file mode 100644
index 0000000..cb46573
Binary files /dev/null and b/docs/img/04/08/advanced_glsl_fragcoord.png differ
diff --git a/docs/img/04/08/advanced_glsl_frontfacing.png b/docs/img/04/08/advanced_glsl_frontfacing.png
new file mode 100644
index 0000000..18990a0
Binary files /dev/null and b/docs/img/04/08/advanced_glsl_frontfacing.png differ
diff --git a/docs/img/04/08/advanced_glsl_pointsize.png b/docs/img/04/08/advanced_glsl_pointsize.png
new file mode 100644
index 0000000..51ce262
Binary files /dev/null and b/docs/img/04/08/advanced_glsl_pointsize.png differ
diff --git a/docs/img/04/08/advanced_glsl_uniform_buffer_objects.png b/docs/img/04/08/advanced_glsl_uniform_buffer_objects.png
new file mode 100644
index 0000000..17bf78d
Binary files /dev/null and b/docs/img/04/08/advanced_glsl_uniform_buffer_objects.png differ
diff --git a/docs/img/04/09/geometry_shader_explosion.png b/docs/img/04/09/geometry_shader_explosion.png
new file mode 100644
index 0000000..196a12a
Binary files /dev/null and b/docs/img/04/09/geometry_shader_explosion.png differ
diff --git a/docs/img/04/09/geometry_shader_house.png b/docs/img/04/09/geometry_shader_house.png
new file mode 100644
index 0000000..9a010dc
Binary files /dev/null and b/docs/img/04/09/geometry_shader_house.png differ
diff --git a/docs/img/04/09/geometry_shader_houses.png b/docs/img/04/09/geometry_shader_houses.png
new file mode 100644
index 0000000..1b59b52
Binary files /dev/null and b/docs/img/04/09/geometry_shader_houses.png differ
diff --git a/docs/img/04/09/geometry_shader_houses_colored.png b/docs/img/04/09/geometry_shader_houses_colored.png
new file mode 100644
index 0000000..8a3d451
Binary files /dev/null and b/docs/img/04/09/geometry_shader_houses_colored.png differ
diff --git a/docs/img/04/09/geometry_shader_houses_snow.png b/docs/img/04/09/geometry_shader_houses_snow.png
new file mode 100644
index 0000000..d2baae0
Binary files /dev/null and b/docs/img/04/09/geometry_shader_houses_snow.png differ
diff --git a/docs/img/04/09/geometry_shader_line_strip.png b/docs/img/04/09/geometry_shader_line_strip.png
new file mode 100644
index 0000000..ac341f8
Binary files /dev/null and b/docs/img/04/09/geometry_shader_line_strip.png differ
diff --git a/docs/img/04/09/geometry_shader_lines.png b/docs/img/04/09/geometry_shader_lines.png
new file mode 100644
index 0000000..44e8cf7
Binary files /dev/null and b/docs/img/04/09/geometry_shader_lines.png differ
diff --git a/docs/img/04/09/geometry_shader_normals.png b/docs/img/04/09/geometry_shader_normals.png
new file mode 100644
index 0000000..04be50e
Binary files /dev/null and b/docs/img/04/09/geometry_shader_normals.png differ
diff --git a/docs/img/04/09/geometry_shader_points.png b/docs/img/04/09/geometry_shader_points.png
new file mode 100644
index 0000000..69cefc6
Binary files /dev/null and b/docs/img/04/09/geometry_shader_points.png differ
diff --git a/docs/img/04/09/geometry_shader_triangle_strip.png b/docs/img/04/09/geometry_shader_triangle_strip.png
new file mode 100644
index 0000000..b2d29c8
Binary files /dev/null and b/docs/img/04/09/geometry_shader_triangle_strip.png differ
diff --git a/docs/img/04/10/instancing_asteroids.png b/docs/img/04/10/instancing_asteroids.png
new file mode 100644
index 0000000..aeb135e
Binary files /dev/null and b/docs/img/04/10/instancing_asteroids.png differ
diff --git a/docs/img/04/10/instancing_asteroids_quantity.png b/docs/img/04/10/instancing_asteroids_quantity.png
new file mode 100644
index 0000000..e6844ae
Binary files /dev/null and b/docs/img/04/10/instancing_asteroids_quantity.png differ
diff --git a/docs/img/04/10/instancing_quads.png b/docs/img/04/10/instancing_quads.png
new file mode 100644
index 0000000..f05d4df
Binary files /dev/null and b/docs/img/04/10/instancing_quads.png differ
diff --git a/docs/img/04/10/instancing_quads_arrays.png b/docs/img/04/10/instancing_quads_arrays.png
new file mode 100644
index 0000000..5c9602c
Binary files /dev/null and b/docs/img/04/10/instancing_quads_arrays.png differ
diff --git a/docs/img/04/11/anti_aliasing_aliasing.png b/docs/img/04/11/anti_aliasing_aliasing.png
new file mode 100644
index 0000000..b8f4776
Binary files /dev/null and b/docs/img/04/11/anti_aliasing_aliasing.png differ
diff --git a/docs/img/04/11/anti_aliasing_multisampled.png b/docs/img/04/11/anti_aliasing_multisampled.png
new file mode 100644
index 0000000..d29e95d
Binary files /dev/null and b/docs/img/04/11/anti_aliasing_multisampled.png differ
diff --git a/docs/img/04/11/anti_aliasing_post_processing.png b/docs/img/04/11/anti_aliasing_post_processing.png
new file mode 100644
index 0000000..32c0251
Binary files /dev/null and b/docs/img/04/11/anti_aliasing_post_processing.png differ
diff --git a/docs/img/04/11/anti_aliasing_rasterization.png b/docs/img/04/11/anti_aliasing_rasterization.png
new file mode 100644
index 0000000..7ca46f0
Binary files /dev/null and b/docs/img/04/11/anti_aliasing_rasterization.png differ
diff --git a/docs/img/04/11/anti_aliasing_rasterization_filled.png b/docs/img/04/11/anti_aliasing_rasterization_filled.png
new file mode 100644
index 0000000..df83114
Binary files /dev/null and b/docs/img/04/11/anti_aliasing_rasterization_filled.png differ
diff --git a/docs/img/04/11/anti_aliasing_rasterization_samples.png b/docs/img/04/11/anti_aliasing_rasterization_samples.png
new file mode 100644
index 0000000..f40151f
Binary files /dev/null and b/docs/img/04/11/anti_aliasing_rasterization_samples.png differ
diff --git a/docs/img/04/11/anti_aliasing_rasterization_samples_filled.png b/docs/img/04/11/anti_aliasing_rasterization_samples_filled.png
new file mode 100644
index 0000000..cbface1
Binary files /dev/null and b/docs/img/04/11/anti_aliasing_rasterization_samples_filled.png differ
diff --git a/docs/img/04/11/anti_aliasing_sample_points.png b/docs/img/04/11/anti_aliasing_sample_points.png
new file mode 100644
index 0000000..7fb9a07
Binary files /dev/null and b/docs/img/04/11/anti_aliasing_sample_points.png differ
diff --git a/docs/img/04/11/anti_aliasing_zoomed.png b/docs/img/04/11/anti_aliasing_zoomed.png
new file mode 100644
index 0000000..3e402c8
Binary files /dev/null and b/docs/img/04/11/anti_aliasing_zoomed.png differ
diff --git a/docs/img/05/01/advanced_lighting_comparrison.png b/docs/img/05/01/advanced_lighting_comparrison.png
new file mode 100644
index 0000000..0bfcdb9
Binary files /dev/null and b/docs/img/05/01/advanced_lighting_comparrison.png differ
diff --git a/docs/img/05/01/advanced_lighting_comparrison2.png b/docs/img/05/01/advanced_lighting_comparrison2.png
new file mode 100644
index 0000000..c31d70d
Binary files /dev/null and b/docs/img/05/01/advanced_lighting_comparrison2.png differ
diff --git a/docs/img/05/01/advanced_lighting_halfway_vector.png b/docs/img/05/01/advanced_lighting_halfway_vector.png
new file mode 100644
index 0000000..a0336f7
Binary files /dev/null and b/docs/img/05/01/advanced_lighting_halfway_vector.png differ
diff --git a/docs/img/05/01/advanced_lighting_over_90.png b/docs/img/05/01/advanced_lighting_over_90.png
new file mode 100644
index 0000000..bd86be4
Binary files /dev/null and b/docs/img/05/01/advanced_lighting_over_90.png differ
diff --git a/docs/img/05/01/advanced_lighting_phong_limit.png b/docs/img/05/01/advanced_lighting_phong_limit.png
new file mode 100644
index 0000000..50c2749
Binary files /dev/null and b/docs/img/05/01/advanced_lighting_phong_limit.png differ
diff --git a/docs/img/05/02/gamma_correction_attenuation.png b/docs/img/05/02/gamma_correction_attenuation.png
new file mode 100644
index 0000000..53e2113
Binary files /dev/null and b/docs/img/05/02/gamma_correction_attenuation.png differ
diff --git a/docs/img/05/02/gamma_correction_brightness.png b/docs/img/05/02/gamma_correction_brightness.png
new file mode 100644
index 0000000..52e33b4
Binary files /dev/null and b/docs/img/05/02/gamma_correction_brightness.png differ
diff --git a/docs/img/05/02/gamma_correction_example.png b/docs/img/05/02/gamma_correction_example.png
new file mode 100644
index 0000000..ba6b632
Binary files /dev/null and b/docs/img/05/02/gamma_correction_example.png differ
diff --git a/docs/img/05/02/gamma_correction_gamma_curves.png b/docs/img/05/02/gamma_correction_gamma_curves.png
new file mode 100644
index 0000000..d047c98
Binary files /dev/null and b/docs/img/05/02/gamma_correction_gamma_curves.png differ
diff --git a/docs/img/05/02/gamma_correction_srgbtextures.png b/docs/img/05/02/gamma_correction_srgbtextures.png
new file mode 100644
index 0000000..a423864
Binary files /dev/null and b/docs/img/05/02/gamma_correction_srgbtextures.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_acne.png b/docs/img/05/03/01/shadow_mapping_acne.png
new file mode 100644
index 0000000..65be91e
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_acne.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_acne_bias.png b/docs/img/05/03/01/shadow_mapping_acne_bias.png
new file mode 100644
index 0000000..772afff
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_acne_bias.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_acne_diagram.png b/docs/img/05/03/01/shadow_mapping_acne_diagram.png
new file mode 100644
index 0000000..cd19b96
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_acne_diagram.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_clamp_edge.png b/docs/img/05/03/01/shadow_mapping_clamp_edge.png
new file mode 100644
index 0000000..15d7298
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_clamp_edge.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_culling.png b/docs/img/05/03/01/shadow_mapping_culling.png
new file mode 100644
index 0000000..9f5ded3
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_culling.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_depth_map.png b/docs/img/05/03/01/shadow_mapping_depth_map.png
new file mode 100644
index 0000000..27c39a1
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_depth_map.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_outside_frustum.png b/docs/img/05/03/01/shadow_mapping_outside_frustum.png
new file mode 100644
index 0000000..f328ed8
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_outside_frustum.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_over_sampling_fixed.png b/docs/img/05/03/01/shadow_mapping_over_sampling_fixed.png
new file mode 100644
index 0000000..7da2075
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_over_sampling_fixed.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_peter_panning.png b/docs/img/05/03/01/shadow_mapping_peter_panning.png
new file mode 100644
index 0000000..6dcd79d
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_peter_panning.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_projection.png b/docs/img/05/03/01/shadow_mapping_projection.png
new file mode 100644
index 0000000..b1843e7
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_projection.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_shadows.png b/docs/img/05/03/01/shadow_mapping_shadows.png
new file mode 100644
index 0000000..b21f826
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_shadows.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_soft_shadows.png b/docs/img/05/03/01/shadow_mapping_soft_shadows.png
new file mode 100644
index 0000000..a79bdf6
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_soft_shadows.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_theory.png b/docs/img/05/03/01/shadow_mapping_theory.png
new file mode 100644
index 0000000..e8e4ebd
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_theory.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_theory_spaces.png b/docs/img/05/03/01/shadow_mapping_theory_spaces.png
new file mode 100644
index 0000000..216573e
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_theory_spaces.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_with_bias.png b/docs/img/05/03/01/shadow_mapping_with_bias.png
new file mode 100644
index 0000000..e20e236
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_with_bias.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_with_without.png b/docs/img/05/03/01/shadow_mapping_with_without.png
new file mode 100644
index 0000000..ed5b0a9
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_with_without.png differ
diff --git a/docs/img/05/03/01/shadow_mapping_zoom.png b/docs/img/05/03/01/shadow_mapping_zoom.png
new file mode 100644
index 0000000..d30d639
Binary files /dev/null and b/docs/img/05/03/01/shadow_mapping_zoom.png differ
diff --git a/docs/img/05/03/02/point_shadows.png b/docs/img/05/03/02/point_shadows.png
new file mode 100644
index 0000000..846c2da
Binary files /dev/null and b/docs/img/05/03/02/point_shadows.png differ
diff --git a/docs/img/05/03/02/point_shadows_depth_cubemap.png b/docs/img/05/03/02/point_shadows_depth_cubemap.png
new file mode 100644
index 0000000..b6b9734
Binary files /dev/null and b/docs/img/05/03/02/point_shadows_depth_cubemap.png differ
diff --git a/docs/img/05/03/02/point_shadows_diagram.png b/docs/img/05/03/02/point_shadows_diagram.png
new file mode 100644
index 0000000..db272e4
Binary files /dev/null and b/docs/img/05/03/02/point_shadows_diagram.png differ
diff --git a/docs/img/05/03/02/point_shadows_soft.png b/docs/img/05/03/02/point_shadows_soft.png
new file mode 100644
index 0000000..eca4c35
Binary files /dev/null and b/docs/img/05/03/02/point_shadows_soft.png differ
diff --git a/docs/img/05/03/02/point_shadows_soft_better.png b/docs/img/05/03/02/point_shadows_soft_better.png
new file mode 100644
index 0000000..923c86b
Binary files /dev/null and b/docs/img/05/03/02/point_shadows_soft_better.png differ
diff --git a/docs/img/05/05/parallax_mapping.png b/docs/img/05/05/parallax_mapping.png
new file mode 100644
index 0000000..0e7995b
Binary files /dev/null and b/docs/img/05/05/parallax_mapping.png differ
diff --git a/docs/img/05/05/parallax_mapping_depth.png b/docs/img/05/05/parallax_mapping_depth.png
new file mode 100644
index 0000000..beefdde
Binary files /dev/null and b/docs/img/05/05/parallax_mapping_depth.png differ
diff --git a/docs/img/05/05/parallax_mapping_edge_fix.png b/docs/img/05/05/parallax_mapping_edge_fix.png
new file mode 100644
index 0000000..02b4afd
Binary files /dev/null and b/docs/img/05/05/parallax_mapping_edge_fix.png differ
diff --git a/docs/img/05/05/parallax_mapping_height_map.png b/docs/img/05/05/parallax_mapping_height_map.png
new file mode 100644
index 0000000..1988926
Binary files /dev/null and b/docs/img/05/05/parallax_mapping_height_map.png differ
diff --git a/docs/img/05/05/parallax_mapping_incorrect_p.png b/docs/img/05/05/parallax_mapping_incorrect_p.png
new file mode 100644
index 0000000..ce4e6d3
Binary files /dev/null and b/docs/img/05/05/parallax_mapping_incorrect_p.png differ
diff --git a/docs/img/05/05/parallax_mapping_issues.png b/docs/img/05/05/parallax_mapping_issues.png
new file mode 100644
index 0000000..7f64154
Binary files /dev/null and b/docs/img/05/05/parallax_mapping_issues.png differ
diff --git a/docs/img/05/05/parallax_mapping_parallax_occlusion_mapping.png b/docs/img/05/05/parallax_mapping_parallax_occlusion_mapping.png
new file mode 100644
index 0000000..914a6c8
Binary files /dev/null and b/docs/img/05/05/parallax_mapping_parallax_occlusion_mapping.png differ
diff --git a/docs/img/05/05/parallax_mapping_parallax_occlusion_mapping_diagram.png b/docs/img/05/05/parallax_mapping_parallax_occlusion_mapping_diagram.png
new file mode 100644
index 0000000..4533a7f
Binary files /dev/null and b/docs/img/05/05/parallax_mapping_parallax_occlusion_mapping_diagram.png differ
diff --git a/docs/img/05/05/parallax_mapping_plane_height.png b/docs/img/05/05/parallax_mapping_plane_height.png
new file mode 100644
index 0000000..57bc026
Binary files /dev/null and b/docs/img/05/05/parallax_mapping_plane_height.png differ
diff --git a/docs/img/05/05/parallax_mapping_plane_heightmap.png b/docs/img/05/05/parallax_mapping_plane_heightmap.png
new file mode 100644
index 0000000..b26ff93
Binary files /dev/null and b/docs/img/05/05/parallax_mapping_plane_heightmap.png differ
diff --git a/docs/img/05/05/parallax_mapping_scaled_height.png b/docs/img/05/05/parallax_mapping_scaled_height.png
new file mode 100644
index 0000000..feb6f70
Binary files /dev/null and b/docs/img/05/05/parallax_mapping_scaled_height.png differ
diff --git a/docs/img/05/05/parallax_mapping_steep_artifact.png b/docs/img/05/05/parallax_mapping_steep_artifact.png
new file mode 100644
index 0000000..c68ced0
Binary files /dev/null and b/docs/img/05/05/parallax_mapping_steep_artifact.png differ
diff --git a/docs/img/05/05/parallax_mapping_steep_parallax_mapping.png b/docs/img/05/05/parallax_mapping_steep_parallax_mapping.png
new file mode 100644
index 0000000..429f5c2
Binary files /dev/null and b/docs/img/05/05/parallax_mapping_steep_parallax_mapping.png differ
diff --git a/docs/img/05/05/parallax_mapping_steep_parallax_mapping_diagram.png b/docs/img/05/05/parallax_mapping_steep_parallax_mapping_diagram.png
new file mode 100644
index 0000000..c93b89b
Binary files /dev/null and b/docs/img/05/05/parallax_mapping_steep_parallax_mapping_diagram.png differ
diff --git a/docs/img/05/06/hdr_clamped.png b/docs/img/05/06/hdr_clamped.png
new file mode 100644
index 0000000..0f42479
Binary files /dev/null and b/docs/img/05/06/hdr_clamped.png differ
diff --git a/docs/img/05/06/hdr_direct.png b/docs/img/05/06/hdr_direct.png
new file mode 100644
index 0000000..0fd21a9
Binary files /dev/null and b/docs/img/05/06/hdr_direct.png differ
diff --git a/docs/img/05/06/hdr_exposure.png b/docs/img/05/06/hdr_exposure.png
new file mode 100644
index 0000000..e0ec2c3
Binary files /dev/null and b/docs/img/05/06/hdr_exposure.png differ
diff --git a/docs/img/05/06/hdr_image.png b/docs/img/05/06/hdr_image.png
new file mode 100644
index 0000000..a8b7c07
Binary files /dev/null and b/docs/img/05/06/hdr_image.png differ
diff --git a/docs/img/05/06/hdr_reinhard.png b/docs/img/05/06/hdr_reinhard.png
new file mode 100644
index 0000000..d765ace
Binary files /dev/null and b/docs/img/05/06/hdr_reinhard.png differ
diff --git a/docs/img/05/07/bloom.png b/docs/img/05/07/bloom.png
new file mode 100644
index 0000000..b28998c
Binary files /dev/null and b/docs/img/05/07/bloom.png differ
diff --git a/docs/img/05/07/bloom_attachments.png b/docs/img/05/07/bloom_attachments.png
new file mode 100644
index 0000000..0c6fc1e
Binary files /dev/null and b/docs/img/05/07/bloom_attachments.png differ
diff --git a/docs/img/05/07/bloom_blurred.png b/docs/img/05/07/bloom_blurred.png
new file mode 100644
index 0000000..9d9158d
Binary files /dev/null and b/docs/img/05/07/bloom_blurred.png differ
diff --git a/docs/img/05/07/bloom_blurred_large.png b/docs/img/05/07/bloom_blurred_large.png
new file mode 100644
index 0000000..2219eb1
Binary files /dev/null and b/docs/img/05/07/bloom_blurred_large.png differ
diff --git a/docs/img/05/07/bloom_example.png b/docs/img/05/07/bloom_example.png
new file mode 100644
index 0000000..4c314ce
Binary files /dev/null and b/docs/img/05/07/bloom_example.png differ
diff --git a/docs/img/05/07/bloom_extracted.png b/docs/img/05/07/bloom_extracted.png
new file mode 100644
index 0000000..19d8ebf
Binary files /dev/null and b/docs/img/05/07/bloom_extracted.png differ
diff --git a/docs/img/05/07/bloom_gaussian.png b/docs/img/05/07/bloom_gaussian.png
new file mode 100644
index 0000000..e7b14c3
Binary files /dev/null and b/docs/img/05/07/bloom_gaussian.png differ
diff --git a/docs/img/05/07/bloom_gaussian_two_pass.png b/docs/img/05/07/bloom_gaussian_two_pass.png
new file mode 100644
index 0000000..569eaba
Binary files /dev/null and b/docs/img/05/07/bloom_gaussian_two_pass.png differ
diff --git a/docs/img/05/07/bloom_scene.png b/docs/img/05/07/bloom_scene.png
new file mode 100644
index 0000000..6c4c2f8
Binary files /dev/null and b/docs/img/05/07/bloom_scene.png differ
diff --git a/docs/img/05/07/bloom_small.png b/docs/img/05/07/bloom_small.png
new file mode 100644
index 0000000..b589f6e
Binary files /dev/null and b/docs/img/05/07/bloom_small.png differ
diff --git a/docs/img/05/07/bloom_steps.png b/docs/img/05/07/bloom_steps.png
new file mode 100644
index 0000000..338ca6d
Binary files /dev/null and b/docs/img/05/07/bloom_steps.png differ
diff --git a/docs/img/05/08/deferred_example.png b/docs/img/05/08/deferred_example.png
new file mode 100644
index 0000000..2e0c3ce
Binary files /dev/null and b/docs/img/05/08/deferred_example.png differ
diff --git a/docs/img/05/08/deferred_g_buffer.png b/docs/img/05/08/deferred_g_buffer.png
new file mode 100644
index 0000000..642e67f
Binary files /dev/null and b/docs/img/05/08/deferred_g_buffer.png differ
diff --git a/docs/img/05/08/deferred_light_volume_rendered.png b/docs/img/05/08/deferred_light_volume_rendered.png
new file mode 100644
index 0000000..0826660
Binary files /dev/null and b/docs/img/05/08/deferred_light_volume_rendered.png differ
diff --git a/docs/img/05/08/deferred_lights_depth.png b/docs/img/05/08/deferred_lights_depth.png
new file mode 100644
index 0000000..81a2ead
Binary files /dev/null and b/docs/img/05/08/deferred_lights_depth.png differ
diff --git a/docs/img/05/08/deferred_lights_no_depth.png b/docs/img/05/08/deferred_lights_no_depth.png
new file mode 100644
index 0000000..6ba4d46
Binary files /dev/null and b/docs/img/05/08/deferred_lights_no_depth.png differ
diff --git a/docs/img/05/08/deferred_overview.png b/docs/img/05/08/deferred_overview.png
new file mode 100644
index 0000000..f8bc33a
Binary files /dev/null and b/docs/img/05/08/deferred_overview.png differ
diff --git a/docs/img/05/08/deferred_shading.png b/docs/img/05/08/deferred_shading.png
new file mode 100644
index 0000000..9192481
Binary files /dev/null and b/docs/img/05/08/deferred_shading.png differ
diff --git a/docs/img/05/09/ssao.png b/docs/img/05/09/ssao.png
new file mode 100644
index 0000000..5709c1f
Binary files /dev/null and b/docs/img/05/09/ssao.png differ
diff --git a/docs/img/05/09/ssao_banding_noise.jpg b/docs/img/05/09/ssao_banding_noise.jpg
new file mode 100644
index 0000000..8630a3f
Binary files /dev/null and b/docs/img/05/09/ssao_banding_noise.jpg differ
diff --git a/docs/img/05/09/ssao_crysis.jpg b/docs/img/05/09/ssao_crysis.jpg
new file mode 100644
index 0000000..6200ec8
Binary files /dev/null and b/docs/img/05/09/ssao_crysis.jpg differ
diff --git a/docs/img/05/09/ssao_crysis_circle.png b/docs/img/05/09/ssao_crysis_circle.png
new file mode 100644
index 0000000..9a4e707
Binary files /dev/null and b/docs/img/05/09/ssao_crysis_circle.png differ
diff --git a/docs/img/05/09/ssao_example.png b/docs/img/05/09/ssao_example.png
new file mode 100644
index 0000000..965463c
Binary files /dev/null and b/docs/img/05/09/ssao_example.png differ
diff --git a/docs/img/05/09/ssao_final.png b/docs/img/05/09/ssao_final.png
new file mode 100644
index 0000000..0762d09
Binary files /dev/null and b/docs/img/05/09/ssao_final.png differ
diff --git a/docs/img/05/09/ssao_hemisphere (1).png b/docs/img/05/09/ssao_hemisphere (1).png
new file mode 100644
index 0000000..a3b29d6
Binary files /dev/null and b/docs/img/05/09/ssao_hemisphere (1).png differ
diff --git a/docs/img/05/09/ssao_hemisphere.png b/docs/img/05/09/ssao_hemisphere.png
new file mode 100644
index 0000000..a3b29d6
Binary files /dev/null and b/docs/img/05/09/ssao_hemisphere.png differ
diff --git a/docs/img/05/09/ssao_kernel_weight.png b/docs/img/05/09/ssao_kernel_weight.png
new file mode 100644
index 0000000..4fb116c
Binary files /dev/null and b/docs/img/05/09/ssao_kernel_weight.png differ
diff --git a/docs/img/05/09/ssao_overview.png b/docs/img/05/09/ssao_overview.png
new file mode 100644
index 0000000..8c71208
Binary files /dev/null and b/docs/img/05/09/ssao_overview.png differ
diff --git a/docs/img/05/09/ssao_range_check.png b/docs/img/05/09/ssao_range_check.png
new file mode 100644
index 0000000..49399e8
Binary files /dev/null and b/docs/img/05/09/ssao_range_check.png differ
diff --git a/docs/img/05/09/ssao_smoothstep.png b/docs/img/05/09/ssao_smoothstep.png
new file mode 100644
index 0000000..62382de
Binary files /dev/null and b/docs/img/05/09/ssao_smoothstep.png differ
diff --git a/docs/img/05/09/ssao_without_blur.png b/docs/img/05/09/ssao_without_blur.png
new file mode 100644
index 0000000..48faa84
Binary files /dev/null and b/docs/img/05/09/ssao_without_blur.png differ
diff --git a/docs/img/06/02/bitmapfont.png b/docs/img/06/02/bitmapfont.png
new file mode 100644
index 0000000..e029219
Binary files /dev/null and b/docs/img/06/02/bitmapfont.png differ
diff --git a/docs/img/06/02/glyph.png b/docs/img/06/02/glyph.png
new file mode 100644
index 0000000..a482089
Binary files /dev/null and b/docs/img/06/02/glyph.png differ
diff --git a/docs/img/06/02/glyph_offset.png b/docs/img/06/02/glyph_offset.png
new file mode 100644
index 0000000..9927d23
Binary files /dev/null and b/docs/img/06/02/glyph_offset.png differ
diff --git a/docs/img/06/02/text_rendering.png b/docs/img/06/02/text_rendering.png
new file mode 100644
index 0000000..a808cff
Binary files /dev/null and b/docs/img/06/02/text_rendering.png differ
diff --git a/docs/img/06/02/text_rendering_quads.png b/docs/img/06/02/text_rendering_quads.png
new file mode 100644
index 0000000..a02d81e
Binary files /dev/null and b/docs/img/06/02/text_rendering_quads.png differ
diff --git a/docs/img/06/Breakout/06/particle.png b/docs/img/06/Breakout/06/particle.png
new file mode 100644
index 0000000..bc0f6ba
Binary files /dev/null and b/docs/img/06/Breakout/06/particle.png differ
diff --git a/docs/img/06/Breakout/06/particles.mp4 b/docs/img/06/Breakout/06/particles.mp4
new file mode 100644
index 0000000..c0d13fc
Binary files /dev/null and b/docs/img/06/Breakout/06/particles.mp4 differ
diff --git a/docs/img/06/Breakout/06/particles_example.jpg b/docs/img/06/Breakout/06/particles_example.jpg
new file mode 100644
index 0000000..0e43488
Binary files /dev/null and b/docs/img/06/Breakout/06/particles_example.jpg differ