mirrors/LearnOpenGL-CN
1
0
Fork 0
mirror of https://github.com/LearnOpenGL-CN/LearnOpenGL-CN.git synced 2025-08-23 12:45:29 +08:00
Code Activity

Move all the images to this repo. Close #53

Browse Source
This commit is contained in:
Meow J
2016-09-17 02:11:48 +08:00
parent b384a9f176
commit f0dd66f4b9
246 changed files with 221 additions and 221 deletions
Download Patch File Download Diff File Expand all files Collapse all files

18
docs/01 Getting started/09 Camera.md
View File

@@ -14,7 +14,7 @@
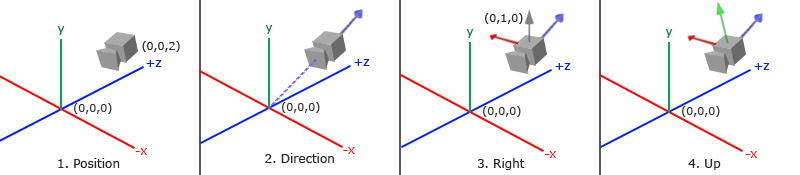
当我们讨论摄像机/观察空间(Camera/View Space)的时候，是我们在讨论以摄像机的透视图作为场景原点时场景中所有可见顶点坐标。观察矩阵把所有的世界坐标变换到观察坐标，这些新坐标是相对于摄像机的位置和方向的。定义一个摄像机，我们需要一个摄像机在世界空间中的位置、观察的方向、一个指向它的右测的向量以及一个指向它上方的向量。细心的读者可能已经注意到我们实际上创建了一个三个单位轴相互垂直的、以摄像机的位置为原点的坐标系。
![](http://learnopengl.com/img/getting-started/camera_axes.png)
![](../img/01/09/camera_axes.png)
### 1. 摄像机位置
@@ -95,7 +95,7 @@ view = glm::lookAt(glm::vec3(camX, 0.0, camZ), glm::vec3(0.0, 0.0, 0.0), glm::ve
如果你运行代码你会得到下面的东西：
<video src="http://learnopengl.com/video/getting-started/camera_circle.mp4" controls="controls">
<video src="../../img/01/09/camera_circle.mp4" controls="controls">
</video>
这一小段代码中，摄像机围绕场景转动。自己试试改变半径和位置/方向参数，看看LookAt矩阵是如何工作的。同时，这里有[源码](http://learnopengl.com/code_viewer.php?code=getting-started/camera_circle)、[顶点](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems&type=fragment)着色器。
@@ -144,7 +144,7 @@ void key_callback(GLFWwindow* window, int key, int scancode, int action, int mod
如果你用这段代码更新`key_callback`函数，你就可以在场景中自由的前后左右移动了。
<video src="http://learnopengl.com/video/getting-started/camera_inside.mp4" controls="controls">
<video src="../../img/01/09/camera_inside.mp4" controls="controls">
</video>
你可能会注意到这个摄像机系统不能同时朝两个方向移动，当你按下一个按键时，它会先顿一下才开始移动。这是因为大多数事件输入系统一次只能处理一个键盘输入，它们的函数只有当我们激活了一个按键时才被调用。大多数GUI系统都是这样的，它对摄像机来说用并不合理。我们可以用一些小技巧解决这个问题。
@@ -234,7 +234,7 @@ void Do_Movement()
与前面的部分结合在一起，我们有了一个更流畅点的摄像机系统：
<video src="http://learnopengl.com/video/getting-started/camera_smooth.mp4" controls="controls">
<video src="../../img/01/09/camera_smooth.mp4" controls="controls">
</video>
现在我们有了一个在任何系统上移动速度都一样的摄像机。这里是源码。我们可以看到任何移动都会影响返回的`deltaTime`值。
@@ -250,17 +250,17 @@ void Do_Movement()
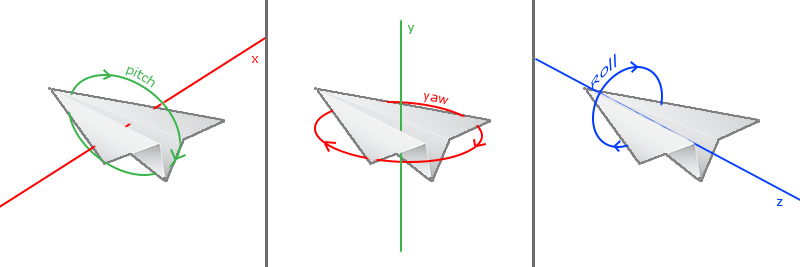
欧拉角(Euler Angle)是表示3D空间中可以表示任何旋转的三个值，由莱昂哈德·欧拉在18世纪提出。有三种欧拉角：俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll)，下面的图片展示了它们的含义：
![](http://www.learnopengl.com/img/getting-started/camera_pitch_yaw_roll.png)
![](../img/01/09/camera_pitch_yaw_roll.png)
**俯仰角**是描述我们如何往上和往下看的角，它在第一张图中表示。第二张图显示了**偏航角**，偏航角表示我们往左和往右看的大小。**滚转角**代表我们如何翻滚摄像机。每个欧拉角都有一个值来表示，把三个角结合起来我们就能够计算3D空间中任何的旋转了。
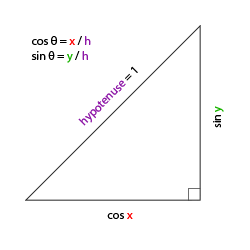
对于我们的摄像机系统来说，我们只关心俯仰角和偏航角，所以我们不会讨论滚转角。用一个给定的俯仰角和偏航角，我们可以把它们转换为一个代表新的方向向量的3D向量。俯仰角和偏航角转换为方向向量的处理需要一些三角学知识，我们以最基本的情况开始：
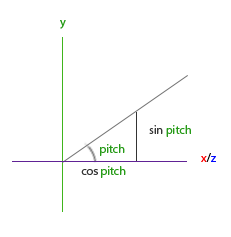
![](http://www.learnopengl.com/img/getting-started/camera_triangle.png)
![](../img/01/09/camera_triangle.png)
如果我们把斜边边长定义为1，我们就能知道邻边的长度是\(\cos \ \color{red}x/\color{purple}h = \cos \ \color{red}x/\color{purple}1 = \cos\ \color{red}x\)，它的对边是\(\sin \ \color{green}y/\color{purple}h = \sin \ \color{green}y/\color{purple}1 = \sin\ \color{green}y\)。这样我们获得了能够得到x和y方向的长度的公式，它们取决于所给的角度。我们使用它来计算方向向量的元素：
![](http://www.learnopengl.com/img/getting-started/camera_pitch.png)
![](../img/01/09/camera_pitch.png)
这个三角形看起来和前面的三角形很像，所以如果我们想象自己在xz平面上，正望向y轴，我们可以基于第一个三角形计算长度/y方向的强度(我们往上或往下看多少)。从图中我们可以看到一个给定俯仰角的y值等于sinθ:
@@ -277,7 +277,7 @@ direction.z = cos(glm::radians(pitch));
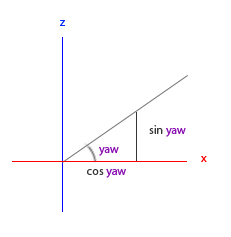
看看我们是否能够为偏航角找到需要的元素：
![](http://www.learnopengl.com/img/getting-started/camera_yaw.png)
![](../img/01/09/camera_yaw.png)
就像俯仰角一样我们可以看到x元素取决于cos(偏航角)的值，z值同样取决于偏航角的正弦值。把这个加到前面的值中，会得到基于俯仰角和偏航角的方向向量：
@@ -458,7 +458,7 @@ glfwSetScrollCallback(window, scroll_callback);
现在我们实现了一个简单的摄像机系统，它能够让我们在3D环境中自由移动。
<video src="http://learnopengl.com/video/getting-started/camera_mouse.mp4" controls="controls">
<video src="../../img/01/09/camera_mouse.mp4" controls="controls">
</video>
自由的去实验，如果遇到困难对比[源代码](http://learnopengl.com/code_viewer.php?code=getting-started/camera_zoom)。