mirrors/LearnOpenGL-CN
1
0
Fork 0
mirror of https://github.com/LearnOpenGL-CN/LearnOpenGL-CN.git synced 2025-08-23 04:35:28 +08:00
Code Activity

Replace all the math equations with latex

Browse Source
This commit is contained in:
Meow J
2016-07-05 18:47:06 +08:00
parent ca728d41d6
commit e6c891f7cc
14 changed files with 171 additions and 657 deletions
Download Patch File Download Diff File Expand all files Collapse all files

575
docs/05 Advanced Lighting/04 Normal Mapping.md
View File

@@ -29,8 +29,10 @@
由于法线向量是个几何工具，而纹理通常只用于储存颜色信息，用纹理储存法线向量不是非常直接。如果你想一想，就会知道纹理中的颜色向量用r、g、b元素代表一个3D向量。类似的我们也可以将法线向量的x、y、z元素储存到纹理中，代替颜色的r、g、b元素。法线向量的范围在-1到1之间，所以我们先要将其映射到0到1的范围：
1
vec3 rgb_normal = normal * 0.5 - 0.5; // transforms from [-1,1] to [0,1]
```c++
vec3 rgb_normal = normal * 0.5 - 0.5; // transforms from [-1,1] to [0,1]
```
将法线向量变换为像这样的RGB颜色元素，我们就能把根据表面的形状的fragment的法线保存在2D纹理中。教程开头展示的那个砖块的例子的法线贴图如下所示：
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_normal_map.png)
@@ -92,555 +94,46 @@ void main()
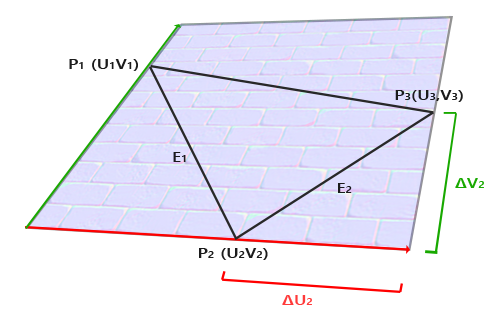
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_surface_edges.png)
上图中我们可以看到边<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>E</mi>
<mn>2</mn>
</msub>
</math>纹理坐标的不同，<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>E</mi>
<mn>2</mn>
</msub>
</math>是一个三角形的边，这个三角形的另外两条边是<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
</math>和<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
</math>，它们与切线向量*T*和副切线向量*B*方向相同。这样我们可以把边</math>和<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>E</mi>
<mn>1</mn>
</msub>
</math>和<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>E</mi>
<mn>2</mn>
</msub>
</math>用切线向量 *T* 和副切线向量 *B* 的线性组合表示出来（译注：注意*T*和*B*都是单位长度，在*TB*平面中所有点的*T*、*B*坐标都在0到1之间，因此可以进行这样的组合）：
上图中我们可以看到边\(E_2\)纹理坐标的不同，\(E_2\)是一个三角形的边，这个三角形的另外两条边是\(\Delta U_2\)和\(\Delta V_2\)，它们与切线向量\(T\)和副切线向量\(B\)方向相同。这样我们可以把边\(E_1\)和\(E_2\)用切线向量\(T\)和副切线向量\(B\)的线性组合表示出来（译注：注意\(T\)和\(B\)都是单位长度，在\(TB\)平面中所有点的\(T\)、\(B\)坐标都在0到1之间，因此可以进行这样的组合）：
```math
$$
E_1 = \Delta U_1T + \Delta V_1B
$$
$$
E_2 = \Delta U_2T + \Delta V_2B
```
$$
我们也可以写成这样：
```math
$$
(E_{1x}, E_{1y}, E_{1z}) = \Delta U_1(T_x, T_y, T_z) + \Delta V_1(B_x, B_y, B_z)
```
$$
*E*是两个向量位置的差，*U*和*V*是纹理坐标的差。然后我们得到两个未知数（切线*T*和副切线*B*）和两个等式。你可能想起你的代数课了，这是让我们去接*T*和*B*。
$$
(E_{2x}, E_{2y}, E_{2z}) = \Delta U_2(T_x, T_y, T_z) + \Delta V_2(B_x, B_y, B_z)
$$
\(E\)是两个向量位置的差，\(\Delta U\)和\(\Delta V\)是纹理坐标的差。然后我们得到两个未知数（切线*T*和副切线*B*）和两个等式。你可能想起你的代数课了，这是让我们去接\(T\)和\(B\)。
上面的方程允许我们把它们写成另一种格式：矩阵乘法
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mo>=</mo>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>1</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>1</mn>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>T</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>B</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
</math>
$$
\begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix} = \begin{bmatrix} \Delta U_1 & \Delta V_1 \\ \Delta U_2 & \Delta V_2 \end{bmatrix} \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix}
$$
尝试会以一下矩阵乘法，它们确实是同一种等式。把等式写成矩阵形式的好处是，解*T*和*B*会因此变得很容易。两边都乘以<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<mi>U</mi>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<mi>V</mi>
</math>的反数等于：
尝试会意一下矩阵乘法，它们确实是同一种等式。把等式写成矩阵形式的好处是，解\(T\)和\(B\)会因此变得很容易。两边都乘以\(\Delta U \Delta V\)的逆矩阵等于：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<msup>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>1</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>1</mn>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mrow class="MJX-TeXAtom-ORD">
<mo>&#x2212;<!-- − --></mo>
<mn>1</mn>
</mrow>
</msup>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mo>=</mo>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>T</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>B</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
</math>
$$
\begin{bmatrix} \Delta U_1 & \Delta V_1 \\ \Delta U_2 & \Delta V_2 \end{bmatrix}^{-1} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix} = \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix}
$$
这样我们就可以解出*T*和*B*了。这需要我们计算出delta纹理坐标矩阵的拟阵。我不打算讲解计算逆矩阵的细节，但大致是把它变化为，1除以矩阵的行列式，再乘以它的共轭矩阵。
这样我们就可以解出\(T\)和\(B\)了。这需要我们计算出delta纹理坐标矩阵的拟阵。我不打算讲解计算逆矩阵的细节，但大致是把它变化为，1除以矩阵的行列式，再乘以它的共轭矩阵。
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>T</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>B</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mo>=</mo>
<mfrac>
<mn>1</mn>
<mrow>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>1</mn>
</msub>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
<mo>&#x2013;</mo>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>1</mn>
</msub>
</mrow>
</mfrac>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
</mtd>
<mtd>
<mo>&#x2212;<!-- − --></mo>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>1</mn>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<mo>&#x2212;<!-- − --></mo>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>1</mn>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
</math>
$$
\begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix} = \frac{1}{\Delta U_1 \Delta V_2 - \Delta U_2 \Delta V_1} \begin{bmatrix} \Delta V_2 & -\Delta V_1 \\ -\Delta U_2 & \Delta U_1 \end{bmatrix} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix}
$$
有了最后这个等式，我们就可以用公式、三角形的两条边以及纹理坐标计算出切线向量*T*和副切线*B*。
有了最后这个等式，我们就可以用公式、三角形的两条边以及纹理坐标计算出切线向量\(T\)和副切线\(B\)。
如果你对这些数学内容不理解也不用担心。当你知道我们可以用一个三角形的顶点和纹理坐标（因为纹理坐标和切线向量在同一空间中）计算出切线和副切线你就已经部分地达到目的了（译注：上面的推导已经很清楚了，如果你不明白可以参考任意线性代数教材，就像作者所说的记住求得切线空间的公式也行，不过不管怎样都得理解切线空间的含义）。
@@ -649,6 +142,8 @@ E_2 = \Delta U_2T + \Delta V_2B
这个教程的demo场景中有一个简单的2D平面，它朝向正z方向。这次我们会使用切线空间来实现法线贴图，所以我们可以使平面朝向任意方向，法线贴图仍然能够工作。使用前面讨论的数学方法，我们来手工计算出表面的切线和副切线向量。
假设平面使用下面的向量建立起来（1、2、3和1、3、4，它们是两个三角形）：
```c++
// positions
glm::vec3 pos1(-1.0, 1.0, 0.0);
glm::vec3 pos2(-1.0, -1.0, 0.0);
@@ -661,20 +156,18 @@ glm::vec2 uv3(1.0, 0.0);
glm::vec2 uv4(1.0, 1.0);
// normal vector
glm::vec3 nm(0.0, 0.0, 1.0);
```
我们先计算第一个三角形的边和deltaUV坐标：
1
2
3
4
```c++
glm::vec3 edge1 = pos2 - pos1;
glm::vec3 edge2 = pos3 - pos1;
glm::vec2 deltaUV1 = uv2 - uv1;
glm::vec2 deltaUV2 = uv3 - uv1;
```
有了计算切线和副切线的必备数据，我们就可以开始写出来自于前面部分中的下列等式：