mirrors/LearnOpenGL-CN
1
0
Fork 0
mirror of https://github.com/LearnOpenGL-CN/LearnOpenGL-CN.git synced 2025-08-23 04:35:28 +08:00
Code Activity

Replace all the math equations with latex

Browse Source
This commit is contained in:
Meow J
2016-07-05 18:47:06 +08:00
parent ca728d41d6
commit e6c891f7cc
14 changed files with 171 additions and 657 deletions
Download Patch File Download Diff File Expand all files Collapse all files

31
docs/05 Advanced Lighting/02 Gamma Correction.md
View File

@@ -1,6 +1,6 @@
本文作者JoeyDeVries，由Django翻译自[http://learnopengl.com](http://learnopengl.com)
## Gamma校正(Gamma Correction)
# Gamma校正(Gamma Correction)
当我们计算出场景中所有像素的最终颜色以后，我们就必须把它们显示在监视器上。过去，大多数监视器是阴极射线管显示器（CRT）。这些监视器有一个物理特性就是两倍的输入电压产生的不是两倍的亮度。输入电压产生约为输入电压的2.2次幂的亮度，这叫做监视器Gamma（译注：Gamma也叫灰度系数，每种显示设备都有自己的Gamma值，都不相同，有一个公式：设备输出亮度 = 电压的Gamma次幂，任何设备Gamma基本上都不会等于1，等于1是一种理想的线性状态，这种理想状态是：如果电压和亮度都是在0到1的区间，那么多少电压就等于多少亮度。对于CRT，Gamma通常为2.2，因而，输出亮度 = 输入电压的2.2次幂，你可以从本节第二张图中看到Gamma2.2实际显示出来的总会比预期暗，相反Gamma0.45就会比理想预期亮，如果你讲Gamma0.45叠加到Gamma2.2的显示设备上，便会对偏暗的显示效果做到校正，这个简单的思路就是本节的核心）。
@@ -16,7 +16,7 @@
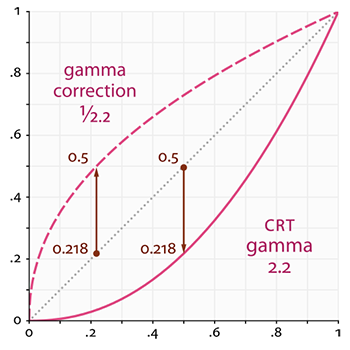
![](http://learnopengl.com/img/advanced-lighting/gamma_correction_gamma_curves.png)
点线代表线性颜色/亮度值（译注：这表示的是理想状态，Gamma为1），实线代表监视器显示的颜色。如果我们把一个点线线性的颜色翻一倍，结果就是这个值的两倍。比如，光的颜色向量L=(0.5, 0.0, 0.0)代表的是暗红色。如果我们在线性空间中把它翻倍，就会变成(1.0, 0.0, 0.0)，就像你在图中看到的那样。然而，由于我们定义的颜色仍然需要输出的监视器上，监视器上显示的实际颜色就会是(0.218, 0.0, 0.0)。在这儿问题就出现了：当我们将理想中直线上的那个暗红色翻一倍时，在监视器上实际上亮度翻了4.5倍以上！
点线代表线性颜色/亮度值（译注：这表示的是理想状态，Gamma为1），实线代表监视器显示的颜色。如果我们把一个点线线性的颜色翻一倍，结果就是这个值的两倍。比如，光的颜色向量\(\bar{L} = (0.5, 0.0, 0.0)\)代表的是暗红色。如果我们在线性空间中把它翻倍，就会变成\((1.0, 0.0, 0.0)\)，就像你在图中看到的那样。然而，由于我们定义的颜色仍然需要输出的监视器上，监视器上显示的实际颜色就会是\((0.218, 0.0, 0.0)\)。在这儿问题就出现了：当我们将理想中直线上的那个暗红色翻一倍时，在监视器上实际上亮度翻了4.5倍以上！
直到现在，我们还一直假设我们所有的工作都是在线性空间中进行的（译注：Gamma为1），但最终还是要把所哟的颜色输出到监视器上，所以我们配置的所有颜色和光照变量从物理角度来看都是不正确的，在我们的监视器上很少能够正确地显示。出于这个原因，我们（以及艺术家）通常将光照值设置得比本来更亮一些（由于监视器会将其亮度显示的更暗一些），如果不是这样，在线性空间里计算出来的光照就会不正确。同时，还要记住，监视器所显示出来的图像和线性图像的最小亮度是相同的，它们最大的亮度也是相同的；只是中间亮度部分会被压暗。
@@ -24,22 +24,11 @@
![](http://learnopengl.com/img/advanced-lighting/gamma_correction_example.png)
Gamma校正
## Gamma校正
Gamma校正的思路是在最终的颜色输出上应用监视器Gamma的倒数。回头看前面的Gamma曲线图，你会有一个短划线，它是监视器Gamma曲线的翻转曲线。我们在颜色显示到监视器的时候把每个颜色输出都加上这个翻转的Gamma曲线，这样应用了监视器Gamma以后最终的颜色将会变为线性的。我们所得到的中间色调就会更亮，所以虽然监视器使它们变暗，但是我们又将其平衡回来了。
我们来看另一个例子。还是那个暗红色（0.5, 0.0, 0.0）。在将颜色显示到监视器之前，我们先对颜色应用Gamma校正曲线。线性的颜色显示在监视器上相当于降低了2.2次幂的亮度，所以倒数就是1/2.2次幂。Gamma校正后的暗红色就会成为
```math
{(0.5, 0.0, 0.0)}^{1/2.2} = {(0.5, 0.0, 0.0)}^{0.45}={(0.73, 0.0, 0.0)}
```
校正后的颜色接着被发送给监视器，最终显示出来的颜色是
```math
(0.73, 0.0, 0.0)^{2.2} = (0.5, 0.0, 0.0)
```
你会发现使用了Gamma校正，监视器最终会显示出我们在应用中设置的那种线性的颜色。
我们来看另一个例子。还是那个暗红色\((0.5, 0.0, 0.0)\)。在将颜色显示到监视器之前，我们先对颜色应用Gamma校正曲线。线性的颜色显示在监视器上相当于降低了\(2.2\)次幂的亮度，所以倒数就是\(1/2.2\)次幂。Gamma校正后的暗红色就会成为\((0.5, 0.0, 0.0)^{1/2.2} = (0.5, 0.0, 0.0)^{0.45} = (0.73, 0.0, 0.0)\)。校正后的颜色接着被发送给监视器，最终显示出来的颜色是\((0.73, 0.0, 0.0)^{2.2} = (0.5, 0.0, 0.0)\)。你会发现使用了Gamma校正，监视器最终会显示出我们在应用中设置的那种线性的颜色。
!!! Important
@@ -130,17 +119,7 @@ float attenuation = 1.0 / distance;
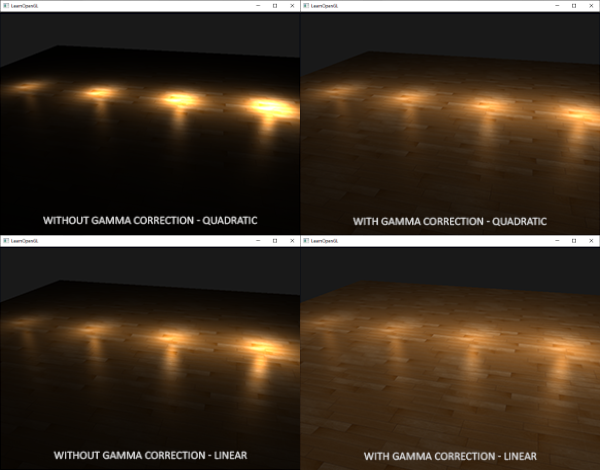
![](http://learnopengl.com/img/advanced-lighting/gamma_correction_attenuation.png)
这种差异产生的原因是，光的衰减方程改变了亮度值，而且屏幕上显示出来的也不是线性空间，在监视器上效果最好的衰减方程，并不是符合物理的。想想平方衰减方程，如果我们使用这个方程，而且不进行gamma校正，显示在监视器上的衰减方程实际上将变成：
```math
{(1.0 / distance2)}^{2.2}
```
若不进行gamma校正，将产生更强烈的衰减。这也解释了为什么双曲线不用gamma校正时看起来更真实，因为它实际变成了
```math
{(1.0 / distance)}^{2.2} = 1.0 / distance^{2.2}
```
这和物理公式是很相似的。
这种差异产生的原因是，光的衰减方程改变了亮度值，而且屏幕上显示出来的也不是线性空间，在监视器上效果最好的衰减方程，并不是符合物理的。想想平方衰减方程，如果我们使用这个方程，而且不进行gamma校正，显示在监视器上的衰减方程实际上将变成\((1.0 / distance^2)^{2.2}\)。若不进行gamma校正，将产生更强烈的衰减。这也解释了为什么双曲线不用gamma校正时看起来更真实，因为它实际变成了\((1.0 / distance)^{2.2} = 1.0 / distance^{2.2}\)。这和物理公式是很相似的。
!!! Important