mirror of
https://github.com/LearnOpenGL-CN/LearnOpenGL-CN.git
synced 2025-12-02 05:55:57 +08:00
Update all the equations in chapter 1
This commit is contained in:
@@ -20,7 +20,7 @@
|
||||
|
||||
|
||||
|
||||
数学家喜欢在字母上面加一横表示向量,比如说。当用在公式中时它们通常是这样的:
|
||||
数学家喜欢在字母上面加一横表示向量,比如说\(\bar{v}\)。当用在公式中时它们通常是这样的:
|
||||
|
||||
$$
|
||||
\bar{v} = \begin{pmatrix} \color{red}x \\ \color{green}y \\ \color{blue}z \end{pmatrix}
|
||||
@@ -34,7 +34,9 @@ $$
|
||||
|
||||
**标量(Scalar)**只是一个数字(或者说是仅有一个分量的矢量)。当把一个向量加/减/乘/除一个标量,我们可以简单的把向量的每个分量分别进行该运算。对于加法来说会像这样:
|
||||
|
||||

|
||||
$$
|
||||
\begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix} + x = \begin{pmatrix} \color{red}1 + x \\ \color{green}2 + x \\ \color{blue}3 + x \end{pmatrix}
|
||||
$$
|
||||
|
||||
其中的+可以是+,-,·或÷,其中·是乘号。注意-和÷运算时不能颠倒,因为颠倒的运算是没有定义的(标量-/÷矢量)
|
||||
|
||||
@@ -42,13 +44,17 @@ $$
|
||||
|
||||
对一个向量取反会将其方向逆转。一个指向东北的向量取反后就指向西南方向了。我们在一个向量的每个分量前加负号就可以实现取反了(或者说用-1数乘该向量):
|
||||
|
||||

|
||||
$$
|
||||
-\bar{v} = -\begin{pmatrix} \color{red}{v_x} \\ \color{blue}{v_y} \\ \color{green}{v_z} \end{pmatrix} = \begin{pmatrix} -\color{red}{v_x} \\ -\color{blue}{v_y} \\ -\color{green}{v_z} \end{pmatrix}
|
||||
$$
|
||||
|
||||
### 向量加减
|
||||
|
||||
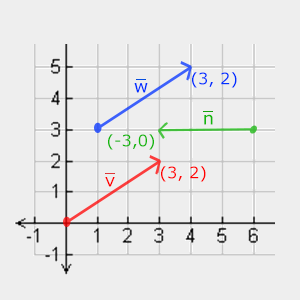
向量的加法可以被定义为是**分量的(Component-wise)**相加,即将一个向量中的每一个分量加上另一个向量的对应分量:
|
||||
|
||||

|
||||
$$
|
||||
\bar{v} = \begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix}, \bar{k} = \begin{pmatrix} \color{red}4 \\ \color{green}5 \\ \color{blue}6 \end{pmatrix} \rightarrow \bar{v} + \bar{k} = \begin{pmatrix} \color{red}1 + \color{red}4 \\ \color{green}2 + \color{green}5 \\ \color{blue}3 + \color{blue}6 \end{pmatrix} = \begin{pmatrix} \color{red}5 \\ \color{green}7 \\ \color{blue}9 \end{pmatrix}
|
||||
$$
|
||||
|
||||
向量v = (4, 2)和k = (1, 2)直观地表示为:
|
||||
|
||||
@@ -56,7 +62,9 @@ $$
|
||||
|
||||
就像普通数字的加减一样,向量的减法等于加上第二个向量的相反数:
|
||||
|
||||

|
||||
$$
|
||||
\bar{v} = \begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix}, \bar{k} = \begin{pmatrix} \color{red}4 \\ \color{green}5 \\ \color{blue}6 \end{pmatrix} \rightarrow \bar{v} + -\bar{k} = \begin{pmatrix} \color{red}1 + (-\color{red}{4}) \\ \color{green}2 + (-\color{green}{5}) \\ \color{blue}3 + (-\color{blue}{6}) \end{pmatrix} = \begin{pmatrix} -\color{red}{3} \\ -\color{green}{3} \\ -\color{blue}{3} \end{pmatrix}
|
||||
$$
|
||||
|
||||
两个向量的相减会得到这两个向量指向位置的差. 这在我们想要获取两点的差会非常有用.
|
||||
|
||||
@@ -68,53 +76,67 @@ $$
|
||||
|
||||
|
||||
|
||||
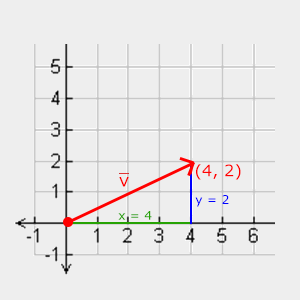
因为两条边(x和y)是已知的,而且我们希望知道斜边的长度,所以我们可以通过勾股定理来计算出它:
|
||||
因为两条边(x和y)是已知的,而且我们希望知道斜边\(\color{red}{\bar{v}}\)的长度,所以我们可以通过勾股定理来计算出它:
|
||||
|
||||

|
||||
$$
|
||||
||\color{red}{\bar{v}}|| = \sqrt{\color{green}x^2 + \color{blue}y^2}
|
||||
$$
|
||||
|
||||
表示向量的大小,我们也可以很容易加上把这个公式拓展到三维空间
|
||||
\(||\color{red}{\bar{v}}||\)表示向量\(\color{red}{\bar{v}}\)的大小,我们也可以很容易加上\(z^2\)把这个公式拓展到三维空间
|
||||
|
||||
例子中向量(4, 2)的长度等于:
|
||||
|
||||

|
||||
$$
|
||||
||\color{red}{\bar{v}}|| = \sqrt{\color{green}4^2 + \color{blue}2^2} = \sqrt{\color{green}16 + \color{blue}4} = \sqrt{20} = 4.47
|
||||
$$
|
||||
|
||||
结果是4.47。
|
||||
|
||||
有一个特殊类型向量叫做**单位向量(Unit Vector)**。单位向量有一个特别的性质——它的长度是1。我们可以用任意向量的每个分量除以向量的长度得到它的单位向量:
|
||||
有一个特殊类型向量叫做**单位向量(Unit Vector)**。单位向量有一个特别的性质——它的长度是1。我们可以用任意向量的每个分量除以向量的长度得到它的单位向量\(\hat{n}\):
|
||||
|
||||

|
||||
$$
|
||||
\hat{n} = \frac{\bar{v}}{||\bar{v}||}
|
||||
$$
|
||||
|
||||
我们把这种方法叫做一个向量的**标准化(Normalizing)**。单位向量头上有一个^样子的记号,并且它会变得很有用,特别是在我们只关心方向不关系长度的时候(如果我们改变向量的长度,它的方向并不会改变)。
|
||||
|
||||
### 向量相乘(Vector-vector Multiplication)
|
||||
|
||||
两个向量相乘是一种很奇怪的情况。普通的乘法在向量上是没有定义的,因为它在视觉上是没有意义的,但是有两种特定情境,当需要乘法时我们可以从中选择:一个是**点乘(Dot Product)**,记作,另一个是**叉乘(Cross Product)**,记作。
|
||||
两个向量相乘是一种很奇怪的情况。普通的乘法在向量上是没有定义的,因为它在视觉上是没有意义的,但是有两种特定情境,当需要乘法时我们可以从中选择:一个是**点乘(Dot Product)**,记作\(\bar{v} \cdot \bar{k}\),另一个是**叉乘(Cross Product)**,记作\(\bar{v} \times \bar{k}\)。
|
||||
|
||||
#### 点乘(Dot Product)
|
||||
|
||||
两个向量的点乘等于它们的数乘结果乘以两个向量之间夹角的余弦值。听起来有点费解,先看一下公式:
|
||||
|
||||

|
||||
$$
|
||||
\bar{v} \cdot \bar{k} = ||\bar{v}|| \cdot ||\bar{k}|| \cdot \cos \theta
|
||||
$$
|
||||
|
||||
它们之间的夹角我们记作。为什么这很有用?想象如果和都是单位向量,它们的长度等于1。公式会有效简化成:
|
||||
它们之间的夹角我们记作\(\theta\)。为什么这很有用?想象如果\(\bar{v}\)和\(\bar{k}\)都是单位向量,它们的长度等于1。公式会有效简化成:
|
||||
|
||||

|
||||
$$
|
||||
\bar{v} \cdot \bar{k} = 1 \cdot 1 \cdot \cos \theta = \cos \theta
|
||||
$$
|
||||
|
||||
现在点乘**只**和两个向量的角度有关。你也许记得当90度的余弦是0,0度的余弦是1。使用点乘可以很容易测试两个向量是否正交(Orthogonal)或平行(正交意味着两个向量互为**直角**)。你可能想要了解更多的关于正弦或余弦的知识,我推荐你看[可汗学院](https://www.khanacademy.org/math/trigonometry/basic-trigonometry/basic_trig_ratios/v/basic-trigonometry)的基础三角学视频。
|
||||
|
||||
!!! Important
|
||||
|
||||
你可以通过点乘的结果计算两个非单位向量的夹角,点乘的结果除以两个向量的大小之积,得到的结果就是夹角的余弦值,即。
|
||||
你可以通过点乘的结果计算两个非单位向量的夹角,点乘的结果除以两个向量的大小之积,得到的结果就是夹角的余弦值,即\(cos \theta\)。
|
||||
|
||||
译注:通过上面点乘定义式可推出:
|
||||
|
||||

|
||||
$$
|
||||
\cos \theta = \frac{||\bar{v}|| \cdot ||\bar{k}||}{\bar{v} \cdot \bar{k}}
|
||||
$$
|
||||
|
||||
所以,我们如何计算点乘?点乘是按分量逐个相乘,然后再把结果相加。两个单位向量点乘就像这样(你可以用两个长度为1的验证):
|
||||
|
||||

|
||||
$$
|
||||
\begin{pmatrix} \color{red}{0.6} \\ -\color{green}{0.8} \\ \color{blue}0 \end{pmatrix} \cdot \begin{pmatrix} \color{red}0 \\ \color{green}1 \\ \color{blue}0 \end{pmatrix} = (\color{red}{0.6} * \color{red}0) + (-\color{green}{0.8} * \color{green}1) + (\color{blue}0 * \color{blue}0) = -0.8
|
||||
$$
|
||||
|
||||
计算两个单位余弦的角度,我们使用反余弦 ,结果是143.1度。现在我们很快就计算出了两个向量的角度。点乘在计算光照的时候会很有用。
|
||||
计算两个单位余弦的角度,我们使用反余弦\(cos^{-1}\) ,结果是143.1度。现在我们很快就计算出了两个向量的角度。点乘在计算光照的时候会很有用。
|
||||
|
||||
#### 叉乘(Cross Product)
|
||||
|
||||
@@ -124,7 +146,9 @@ $$
|
||||
|
||||
不同于其他运算,如果你没有钻研过线性代数,会觉得叉乘很反直觉,所以最好记住公式,就没问题(记不住也没问题)。下面你会看到两个正交向量A和B叉乘结果:
|
||||
|
||||

|
||||
$$
|
||||
\begin{pmatrix} \color{red}{A_{x}} \\ \color{green}{A_{y}} \\ \color{blue}{A_{z}} \end{pmatrix} \times \begin{pmatrix} \color{red}{B_{x}} \\ \color{green}{B_{y}} \\ \color{blue}{B_{z}} \end{pmatrix} = \begin{pmatrix} \color{green}{A_{y}} \cdot \color{blue}{B_{z}} - \color{blue}{A_{z}} \cdot \color{green}{B_{y}} \\ \color{blue}{A_{z}} \cdot \color{red}{B_{x}} - \color{red}{A_{x}} \cdot \color{blue}{B_{z}} \\ \color{red}{A_{x}} \cdot \color{green}{B_{y}} - \color{green}{A_{y}} \cdot \color{red}{B_{x}} \end{pmatrix}
|
||||
$$
|
||||
|
||||
就像你所看到的,看起来毫无头绪。可如果你这么做了,你会得到第三个向量,它正交于你的输入向量。
|
||||
|
||||
@@ -132,7 +156,9 @@ $$
|
||||
|
||||
现在我们已经讨论了向量的全部内容,是时候看看矩阵了!矩阵简单说是一个矩形的数字、符号或表达式数组。矩阵中每一项叫做矩阵的**元素(Element)**。下面是一个2×3矩阵的例子:
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}
|
||||
$$
|
||||
|
||||
矩阵可以通过(i, j)进行索引,i是行,j是列,这就是上面的矩阵叫做2×3矩阵的原因(3列2行,也叫做矩阵的**维度(Dimension)**)。这与你在索引2D图像时的(x, y)相反,获取4的索引是(2, 1)(第二行,第一列)(译注:如果是图像索引应该是(1, 2),先算列,再算行)。
|
||||
|
||||
@@ -142,25 +168,35 @@ $$
|
||||
|
||||
矩阵与标量的加减如下所示:
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} + \color{green}3 = \begin{bmatrix} 1 + \color{green}3 & 2 + \color{green}3 \\ 3 + \color{green}3 & 4 + \color{green}3 \end{bmatrix} = \begin{bmatrix} 4 & 5 \\ 6 & 7 \end{bmatrix}
|
||||
$$
|
||||
|
||||
标量值要加到矩阵的每一个元素上。矩阵与标量的减法也是同样的:
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} - \color{green}3 = \begin{bmatrix} 1 - \color{green}3 & 2 - \color{green}3 \\ 3 - \color{green}3 & 4 - \color{green}3 \end{bmatrix} = \begin{bmatrix} -2 & -1 \\ 0 & 1 \end{bmatrix}
|
||||
$$
|
||||
|
||||
矩阵与矩阵之间的加减就是两个矩阵对应元素的加减运算,所以总体的规则和与标量运算是差不多的,只不过在相同索引下的元素才能进行运算。这也就是说加法和减法只在同维度的矩阵中是有定义的。一个3×2矩阵和一个2×3矩阵(或一个3×3矩阵与4×4矩阵)是不能进行加减的。我们看看两个2×2矩阵是怎样加减的:
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} \color{red}1 & \color{red}2 \\ \color{green}3 & \color{green}4 \end{bmatrix} + \begin{bmatrix} \color{red}5 & \color{red}6 \\ \color{green}7 & \color{green}8 \end{bmatrix} = \begin{bmatrix} \color{red}1 + \color{red}5 & \color{red}2 + \color{red}6 \\ \color{green}3 + \color{green}7 & \color{green}4 + \color{green}8 \end{bmatrix} = \begin{bmatrix} \color{red}6 & \color{red}8 \\ \color{green}{10} & \color{green}{12} \end{bmatrix}
|
||||
$$
|
||||
|
||||
同样的法则也适用于减法:
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} \color{red}4 & \color{red}2 \\ \color{green}1 & \color{green}6 \end{bmatrix} - \begin{bmatrix} \color{red}2 & \color{red}4 \\ \color{green}0 & \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}4 - \color{red}2 & \color{red}2 - \color{red}4 \\ \color{green}1 - \color{green}0 & \color{green}6 - \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}2 & -\color{red}2 \\ \color{green}1 & \color{green}5 \end{bmatrix}
|
||||
$$
|
||||
|
||||
### 矩阵的数乘(Matrix-scalar Products)
|
||||
|
||||
和矩阵与标量的加减一样,矩阵与标量之间的乘法也是矩阵的每一个元素分别乘以该标量。下面的例子展示了乘法的过程:
|
||||
|
||||

|
||||
$$
|
||||
\color{green}2 \cdot \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} \color{green}2 \cdot 1 & \color{green}2 \cdot 2 \\ \color{green}2 \cdot 3 & \color{green}2 \cdot 4 \end{bmatrix} = \begin{bmatrix} 2 & 4 \\ 6 & 8 \end{bmatrix}
|
||||
$$
|
||||
|
||||
现在我们也就能明白为什么一个单独的数字要叫做标量(Scalar)了。简单来说,标量就是用它的值缩放(Scale)矩阵的所有元素(译注:注意Scalar是由Scale + -ar演变过来的)。前面的例子里,所有的元素都被放大了2倍。
|
||||
|
||||
@@ -171,15 +207,17 @@ $$
|
||||
矩阵之间的乘法不见得有多复杂,但的确很难让人适应。矩阵乘法基本上意味着遵照规定好的法则进行相乘。当然,相乘还有一些限制:
|
||||
|
||||
1. 只有当左侧矩阵的列数与右侧矩阵的行数相等,两个矩阵才能相乘。
|
||||
2. 矩阵相乘不遵守**交换律(Commutative)**,。
|
||||
2. 矩阵相乘不遵守**交换律(Commutative)**,\(A \cdot B \neq B \cdot A\)。
|
||||
|
||||
我们先看一个两个2×2矩阵相乘的例子:
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} \color{red}1 & \color{red}2 \\ \color{green}3 & \color{green}4 \end{bmatrix} \cdot \begin{bmatrix} \color{blue}5 & \color{purple}6 \\ \color{blue}7 & \color{purple}8 \end{bmatrix} = \begin{bmatrix} \color{red}1 \cdot \color{blue}5 + \color{red}2 \cdot \color{blue}7 & \color{red}1 \cdot \color{purple}6 + \color{red}2 \cdot \color{purple}8 \\ \color{green}3 \cdot \color{blue}5 + \color{green}4 \cdot \color{blue}7 & \color{green}3 \cdot \color{purple}6 + \color{green}4 \cdot \color{purple}8 \end{bmatrix} = \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix}
|
||||
$$
|
||||
|
||||
现在你可能会在想了:我勒个去,刚刚到底发生了什么? 矩阵的乘法是一系列乘法和加法组合的结果,它使用到了左侧矩阵的行和右侧矩阵的列。我们可以看下面的图片:
|
||||
|
||||

|
||||

|
||||
|
||||
我们先把左侧矩阵的行和右侧矩阵的列拿出来。这些我们挑出来行和列决定着作为结果的2×2矩阵的输出值。如果我们拿出来的是左矩阵的第一行,最终的值就会出现在作为结果的矩阵的第一行,如果我们拿出来的是右矩阵的第一列,最终值会出现在作为结果的矩阵的第一列。这正是红框里的情况。如果想计算结果矩阵右下角的值,我们要用第一个矩阵的第二行和第二个矩阵的第二列(译注:简单来说就是结果矩阵的元素的行取决于第一个矩阵,列取决于第二个矩阵)。
|
||||
|
||||
@@ -191,7 +229,10 @@ $$
|
||||
|
||||
我们用一个更大的例子来结束矩阵与矩阵乘法的讨论。尝试使用颜色来让这个公式更容易理解。作为一个有用的练习,你可以自己回答这个乘法问题然后对比你的结果和图中的这个(如果你用笔计算,你很快就能掌握它们)。
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} \color{red}4 & \color{red}2 & \color{red}0 \\ \color{green}0 & \color{green}8 & \color{green}1 \\ \color{blue}0 & \color{blue}1 & \color{blue}0 \end{bmatrix} \cdot \begin{bmatrix} \color{red}4 & \color{green}2 & \color{blue}1 \\ \color{red}2 & \color{green}0 & \color{blue}4 \\ \color{red}9 & \color{green}4 & \color{blue}2 \end{bmatrix} = \begin{bmatrix} \color{red}4 \cdot \color{red}4 + \color{red}2 \cdot \color{red}2 + \color{red}0 \cdot \color{red}9 & \color{red}4 \cdot \color{green}2 + \color{red}2 \cdot \color{green}0 + \color{red}0 \cdot \color{green}4 & \color{red}4 \cdot \color{blue}1 + \color{red}2 \cdot \color{blue}4 + \color{red}0 \cdot \color{blue}2 \\ \color{green}0 \cdot \color{red}4 + \color{green}8 \cdot \color{red}2 + \color{green}1 \cdot \color{red}9 & \color{green}0 \cdot \color{green}2 + \color{green}8 \cdot \color{green}0 + \color{green}1 \cdot \color{green}4 & \color{green}0 \cdot \color{blue}1 + \color{green}8 \cdot \color{blue}4 + \color{green}1 \cdot \color{blue}2 \\ \color{blue}0 \cdot \color{red}4 + \color{blue}1 \cdot \color{red}2 + \color{blue}0 \cdot \color{red}9 & \color{blue}0 \cdot \color{green}2 + \color{blue}1 \cdot \color{green}0 + \color{blue}0 \cdot \color{green}4 & \color{blue}0 \cdot \color{blue}1 + \color{blue}1 \cdot \color{blue}4 + \color{blue}0 \cdot \color{blue}2 \end{bmatrix}
|
||||
\\ = \begin{bmatrix} 20 & 8 & 12 \\ 25 & 4 & 34 \\ 2 & 0 & 4 \end{bmatrix}
|
||||
$$
|
||||
|
||||
就像你所看到的那样,矩阵与矩阵相乘复杂而容易犯错(这就是我们通常让计算机做这件事的原因),而且当矩阵变大以后很快就会出现问题。如果你仍然希望了解更多,对矩阵的数学属性感到好奇,我强烈推荐你看看[可汗学院](https://www.khanacademy.org/math/algebra2/algebra-matrices)的矩阵内容视频。
|
||||
|
||||
@@ -207,9 +248,11 @@ $$
|
||||
|
||||
在OpenGL中,因为有一些原因我们通常使用4×4的变换矩阵,而其中最重要的原因就是因为每一个向量都有4个分量的。我们能想到的最简单的变换矩阵就是**单位矩阵(Identity Matrix)**。单位矩阵是一个除了对角线以外都是0的N × N矩阵。就像你看到的,这个变换矩阵使一个向量完全不变:
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix} = \begin{bmatrix} \color{red}1 \cdot 1 \\ \color{green}1 \cdot 2 \\ \color{blue}1 \cdot 3 \\ \color{purple}1 \cdot 4 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix}
|
||||
$$
|
||||
|
||||
向量看起来完全没动。从乘法法则来看很明显:第一个结果分量是矩阵的第一行的每个对应分量乘以向量的每一个分量。因为每行的分量除了第一个都是0,可得: ,这对向量的其他3个分量同样适用。
|
||||
向量看起来完全没动。从乘法法则来看很明显:第一个结果分量是矩阵的第一行的每个对应分量乘以向量的每一个分量。因为每行的分量除了第一个都是0,可得: \(\color{red}1\cdot1 + \color{red}0\cdot2 + \color{red}0\cdot3 + \color{red}0\cdot4 = 1\),这对向量的其他3个分量同样适用。
|
||||
|
||||
!!! Important
|
||||
|
||||
@@ -219,15 +262,17 @@ $$
|
||||
|
||||
当我们对一个向量进行缩放的时候就是对向量的长度进行缩放,而它的方向保持不变。如果我们进行2或3维操作,那么我们可以分别定义一个有2或3个缩放变量的向量,每个变量缩放一个轴(x、y或z)。
|
||||
|
||||
我们可以尝试去缩放向量。我们可以把向量沿着x轴缩放0.5,使它的宽度缩小为原来的二分之一;我们可以沿着y轴把向量的高度缩放为原来的两倍。我们看看把向量缩放(0.5, 2)所获得的是什么样的:
|
||||
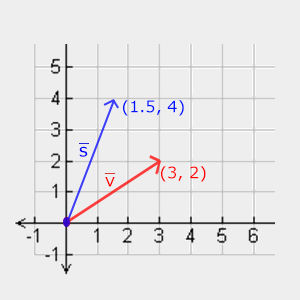
我们可以尝试去缩放向量\(\color{red}{\bar{v}} = (3,2)\)。我们可以把向量沿着x轴缩放0.5,使它的宽度缩小为原来的二分之一;我们可以沿着y轴把向量的高度缩放为原来的两倍。我们看看把向量缩放(0.5, 2)所获得的\(\color{blue}{\bar{s}}\)是什么样的:
|
||||
|
||||
|
||||
|
||||
记住,OpenGL通常是在3D空间操作的,对于2D的情况我们可以把z轴缩放1这样z轴的值就不变了。我们刚刚的缩放操作是**不均匀(Non-uniform)**缩放,因为每个轴的缩放因子(Scaling Factor)都不一样。如果每个轴的缩放都一样那么就叫**均匀缩放(Uniform Scale)**。
|
||||
|
||||
我们下面设置一个变换矩阵来为我们提供缩放功能。我们从单位矩阵了解到,每个对角线元素乘以对应的向量分量。如果我们把1变为3会怎样?这种情况,我们就把向量的每个分量乘以3了,这事实上就把向量缩放3。如果我们把缩放变量表示为我们可以为任意向量(x, y, z)定义一个缩放矩阵:
|
||||
我们下面设置一个变换矩阵来为我们提供缩放功能。我们从单位矩阵了解到,每个对角线元素乘以对应的向量分量。如果我们把1变为3会怎样?这种情况,我们就把向量的每个分量乘以3了,这事实上就把向量缩放3。如果我们把缩放变量表示为\((\color{red}{S_1}, \color{green}{S_2}, \color{blue}{S_3})\)我们可以为任意向量\((x,y,z)\)定义一个缩放矩阵:
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} \color{red}{S_1} & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}{S_2} & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}{S_3} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{S_1} \cdot x \\ \color{green}{S_2} \cdot y \\ \color{blue}{S_3} \cdot z \\ 1 \end{pmatrix}
|
||||
$$
|
||||
|
||||
注意,第四个缩放的向量仍然是1,因为不会缩放3D空间中的w分量。w分量另有其他用途,在后面我们会看到。
|
||||
|
||||
@@ -235,9 +280,11 @@ $$
|
||||
|
||||
**平移(Translation)**是在原来向量的基础上加上另一个的向量从而获得一个在不同位置的新向量的过程,这样就基于平移向量**移动(Move)**了向量。我们已经讨论了向量加法,所以你应该不会陌生。
|
||||
|
||||
和缩放矩阵一样,在4×4矩阵上有几个特别的位置用来执行特定的操作,对于平移来说它们是第四列最上面的3个值。如果我们把缩放向量表示为我们就能把平移矩阵定义为:
|
||||
和缩放矩阵一样,在4×4矩阵上有几个特别的位置用来执行特定的操作,对于平移来说它们是第四列最上面的3个值。如果我们把缩放向量表示为\((\color{red}{T_x},\color{green}{T_y},\color{blue}{T_z})\)我们就能把平移矩阵定义为:
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}{T_x} \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}{T_y} \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}{T_z} \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x + \color{red}{T_x} \\ y + \color{green}{T_y} \\ z + \color{blue}{T_z} \\ 1 \end{pmatrix}
|
||||
$$
|
||||
|
||||
这样是能工作的,因为所有的平移值都要乘以向量的w列,所以平移值会加到向量的原始坐标上(想想矩阵乘法法则)。而如果你用3x3矩阵我们的平移值就没地方放也没地方乘了,所以是不行的。
|
||||
|
||||
@@ -266,7 +313,7 @@ $$
|
||||
|
||||
PI约等于3.14159265359。
|
||||
|
||||
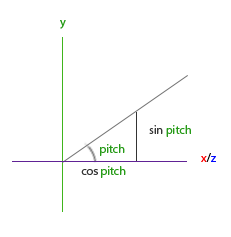
转半圈会向右旋转360/2 = 180度,向右旋转1/5圈表示向右旋转360/5 = 72度。这表明2D空间的向量是由向右旋转72度得到的:
|
||||
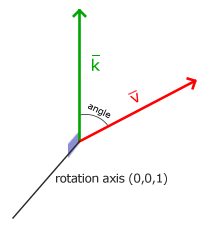
转半圈会向右旋转360/2 = 180度,向右旋转1/5圈表示向右旋转360/5 = 72度。这表明2D空间的向量\(\color{red}{\bar{v}}\)是由\(\color{green}{\bar{k}}\)向右旋转72度得到的:
|
||||
|
||||
|
||||
|
||||
@@ -274,23 +321,31 @@ $$
|
||||
|
||||
使用三角学就能把一个向量变换为一个经过旋转特定角度的新向量。这通常是使用一系列正弦和余弦各种巧妙的组合得到的(一般简称sin和cos)。当然,讨论如何生成变换矩阵超出了这个教程的范围。
|
||||
|
||||
旋转矩阵在3D空间中每个单位轴都有不同定义,这个角度表示为:
|
||||
旋转矩阵在3D空间中每个单位轴都有不同定义,这个角度表示为\(\theta\):
|
||||
|
||||
沿x轴旋转:
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}{\cos \theta} & - \color{green}{\sin \theta} & \color{green}0 \\ \color{blue}0 & \color{blue}{\sin \theta} & \color{blue}{\cos \theta} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ \color{green}{\cos \theta} \cdot y - \color{green}{\sin \theta} \cdot z \\ \color{blue}{\sin \theta} \cdot y + \color{blue}{\cos \theta} \cdot z \\ 1 \end{pmatrix}
|
||||
$$
|
||||
|
||||
沿y轴旋转:
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} \color{red}{\cos \theta} & \color{red}0 & \color{red}{\sin \theta} & \color{red}0 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}0 \\ - \color{blue}{\sin \theta} & \color{blue}0 & \color{blue}{\cos \theta} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{\cos \theta} \cdot x + \color{red}{\sin \theta} \cdot z \\ y \\ - \color{blue}{\sin \theta} \cdot x + \color{blue}{\cos \theta} \cdot z \\ 1 \end{pmatrix}
|
||||
$$
|
||||
|
||||
沿z轴旋转:
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} \color{red}{\cos \theta} & - \color{red}{\sin \theta} & \color{red}0 & \color{red}0 \\ \color{green}{\sin \theta} & \color{green}{\cos \theta} & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{\cos \theta} \cdot x - \color{red}{\sin \theta} \cdot y \\ \color{green}{\sin \theta} \cdot x + \color{green}{\cos \theta} \cdot y \\ z \\ 1 \end{pmatrix}
|
||||
$$
|
||||
|
||||
利用旋转矩阵我们可以把我们的位置向量(Position Vectors)沿一个或多个轴进行旋转。也可以把多个矩阵结合起来,比如先沿着X轴旋转再沿着Y轴旋转。但是这会很快导致一个问题——**万向节死锁(Gimbal Lock,可以看看[这个视频](https://www.youtube.com/watch?v=zc8b2Jo7mno)[(优酷)](http://v.youku.com/v_show/id_XNzkyOTIyMTI=.html)来了解)**。我们不会讨论它的细节,但是一个更好的解决方案是沿着任意轴比如(0.662, 0.2, 0.7222)(注意,这是个单位向量)旋转,而不是使用一系列旋转矩阵的组合。这样一个(超级麻烦)的矩阵是存在的,下面代表任意旋转轴:
|
||||
利用旋转矩阵我们可以把我们的位置向量(Position Vectors)沿一个或多个轴进行旋转。也可以把多个矩阵结合起来,比如先沿着X轴旋转再沿着Y轴旋转。但是这会很快导致一个问题——**万向节死锁(Gimbal Lock,可以看看[这个视频](https://www.youtube.com/watch?v=zc8b2Jo7mno)[(优酷)](http://v.youku.com/v_show/id_XNzkyOTIyMTI=.html)来了解)**。我们不会讨论它的细节,但是一个更好的解决方案是沿着任意轴比如(0.662, 0.2, 0.7222)(注意,这是个单位向量)旋转,而不是使用一系列旋转矩阵的组合。这样一个(超级麻烦)的矩阵是存在的,下面\((\color{red}{R_x}, \color{green}{R_y}, \color{blue}{R_z})\)代表任意旋转轴:
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} \cos \theta + \color{red}{R_x}^2(1 - \cos \theta) & \color{red}{R_x}\color{green}{R_y}(1 - \cos \theta) - \color{blue}{R_z} \sin \theta & \color{red}{R_x}\color{blue}{R_z}(1 - \cos \theta) + \color{green}{R_y} \sin \theta & 0 \\ \color{green}{R_y}\color{red}{R_x} (1 - \cos \theta) + \color{blue}{R_z} \sin \theta & \cos \theta + \color{green}{R_y}^2(1 - \cos \theta) & \color{green}{R_y}\color{blue}{R_z}(1 - \cos \theta) - \color{red}{R_x} \sin \theta & 0 \\ \color{blue}{R_z}\color{red}{R_x}(1 - \cos \theta) - \color{green}{R_y} \sin \theta & \color{blue}{R_z}\color{green}{R_y}(1 - \cos \theta) + \color{red}{R_x} \sin \theta & \cos \theta + \color{blue}{R_z}^2(1 - \cos \theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
|
||||
$$
|
||||
|
||||
在数学上讨论如何生成这样的矩阵仍然超出了本节内容。但是记住,即使这样一个矩阵也不能完全解决万向节死锁问题(尽管会极大地避免)。避免万向节死锁的真正解决方案是使用**四元数(Quaternion)**,它不仅安全,而且计算更加友好。有关四元数会在后面的教程中讨论。
|
||||
|
||||
@@ -298,13 +353,17 @@ $$
|
||||
|
||||
使用矩阵变换的真正力量在于,根据矩阵之前的乘法,我们可以把多个变换组合到一个矩阵中。让我们看看我们是否能生成一个多个变换相结合而成的变换矩阵。我们有一个顶点(x, y, z),我们希望将其缩放2倍,然后用位移(1, 2, 3)来平移它。我们需要一个平移和缩放矩阵来完成这些变换。结果的变换矩阵看起来像这样:
|
||||
|
||||

|
||||
$$
|
||||
Trans . Scale = \begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} . \begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} = \begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix}
|
||||
$$
|
||||
|
||||
注意,当矩阵相乘时我们先写平移再写缩放变换的。矩阵乘法是不可交换的,这意味着它们的顺序很重要。当矩阵相乘时,在最右边的矩阵是第一个乘以向量的,所以你应该从右向左读这个乘法。我们建议您在组合矩阵时,先进行缩放操作,然后是旋转,最后才是平移,否则它们会(消极地)互相影响。比如,如果你先平移然后缩放,平移的向量也会同样被缩放(译注:比如向某方向移动2米,2米也许会被缩放成1米)!
|
||||
|
||||
将我们的矢量左乘最终的变换矩阵会得到以下结果:
|
||||
|
||||

|
||||
$$
|
||||
\begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} . \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \color{red}2x + \color{red}1 \\ \color{green}2y + \color{green}2 \\ \color{blue}2z + \color{blue}3 \\ 1 \end{bmatrix}
|
||||
$$
|
||||
|
||||
不错!向量先缩放2倍,然后平移了(1, 2, 3)个单位。
|
||||
|
||||
|
||||
@@ -99,7 +99,9 @@ glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f);
|
||||
|
||||
正如你看到的那样,由于透视的原因,平行线似乎在很远的地方看起来会相交。这正是透视投影想要模仿的效果,它是使用透视投影矩阵来完成的。这个投影矩阵不仅将给定的平截头体范围映射到裁剪空间,同样还修改了每个顶点坐标的w值,从而使得离观察者越远的顶点坐标w分量越大。被转换到裁剪空间的坐标都会在-w到w的范围之间(任何大于这个范围的对象都会被裁剪掉)。OpenGL要求所有可见的坐标都落在-1.0到1.0范围内从而作为最后的顶点着色器输出,因此一旦坐标在裁剪空间内,透视划分就会被应用到裁剪空间坐标:
|
||||
|
||||

|
||||
$$
|
||||
out = \begin{pmatrix} x /w \\ y / w \\ z / w \end{pmatrix}
|
||||
$$
|
||||
|
||||
每个顶点坐标的分量都会除以它的w分量,得到一个距离观察者的较小的顶点坐标。这是也是另一个w分量很重要的原因,因为它能够帮助我们进行透射投影。最后的结果坐标就是处于标准化设备空间内的。如果你对研究正射投影矩阵和透视投影矩阵是如何计算的很感兴趣(且不会对数学感到恐惧的话)我推荐[这篇由Songho写的文章](http://www.songho.ca/opengl/gl_projectionmatrix.html)。
|
||||
|
||||
@@ -129,7 +131,9 @@ glm::mat4 proj = glm::perspective(45.0f, (float)width/(float)height, 0.1f, 100.0
|
||||
|
||||
我们为上述的每一个步骤都创建了一个转换矩阵:模型矩阵、观察矩阵和投影矩阵。一个顶点的坐标将会根据以下过程被转换到裁剪坐标:
|
||||
|
||||

|
||||
$$
|
||||
V_{clip} = M_{projection} \cdot M_{view} \cdot M_{model} \cdot V_{local}
|
||||
$$
|
||||
|
||||
注意每个矩阵被运算的顺序是相反的(记住我们需要从右往左乘上每个矩阵)。最后的顶点应该被赋予顶点着色器中的`gl_Position`且OpenGL将会自动进行透视划分和裁剪。
|
||||
|
||||
|
||||
@@ -64,9 +64,11 @@ glm::vec3 cameraUp = glm::cross(cameraDirection, cameraRight);
|
||||
|
||||
使用矩阵的好处之一是如果你定义了一个坐标空间,里面有3个相互垂直的轴,你可以用这三个轴外加一个平移向量来创建一个矩阵,你可以用这个矩阵乘以任何向量来变换到那个坐标空间。这正是LookAt矩阵所做的,现在我们有了3个相互垂直的轴和一个定义摄像机空间的位置坐标,我们可以创建我们自己的LookAt矩阵了:
|
||||
|
||||

|
||||
$$
|
||||
LookAt = \begin{bmatrix} \color{red}{R_x} & \color{red}{R_y} & \color{red}{R_z} & 0 \\ \color{green}{U_x} & \color{green}{U_y} & \color{green}{U_z} & 0 \\ \color{blue}{D_x} & \color{blue}{D_y} & \color{blue}{D_z} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} 1 & 0 & 0 & -\color{purple}{P_x} \\ 0 & 1 & 0 & -\color{purple}{P_y} \\ 0 & 0 & 1 & -\color{purple}{P_z} \\ 0 & 0 & 0 & 1 \end{bmatrix}
|
||||
$$
|
||||
|
||||
是右向量,是上向量,是方向向量是摄像机位置向量。注意,位置向量是相反的,因为我们最终希望把世界平移到与我们自身移动的相反方向。使用这个LookAt矩阵坐标观察矩阵可以很高效地把所有世界坐标变换为观察坐标LookAt矩阵就像它的名字表达的那样:它会创建一个观察矩阵looks at(看着)一个给定目标。
|
||||
\(\color{red}R\)是右向量,\(\color{green}U\)是上向量,\(\color{blue}D\)是方向向量\(\color{purple}P\)是摄像机位置向量。注意,位置向量是相反的,因为我们最终希望把世界平移到与我们自身移动的相反方向。使用这个LookAt矩阵坐标观察矩阵可以很高效地把所有世界坐标变换为观察坐标LookAt矩阵就像它的名字表达的那样:它会创建一个观察矩阵looks at(看着)一个给定目标。
|
||||
|
||||
幸运的是,GLM已经提供了这些支持。我们要做的只是定义一个摄像机位置,一个目标位置和一个表示上向量的世界空间中的向量(我们使用上向量计算右向量)。接着GLM就会创建一个LookAt矩阵,我们可以把它当作我们的观察矩阵:
|
||||
|
||||
@@ -256,7 +258,7 @@ void Do_Movement()
|
||||
|
||||
|
||||
|
||||
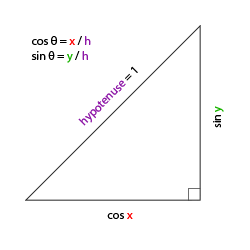
如果我们把斜边边长定义为1,我们就能知道邻边的长度是,它的对边是。这样我们获得了能够得到x和y方向的长度的公式,它们取决于所给的角度。我们使用它来计算方向向量的元素:
|
||||
如果我们把斜边边长定义为1,我们就能知道邻边的长度是\(\cos \ \color{red}x/\color{purple}h = \cos \ \color{red}x/\color{purple}1 = \cos\ \color{red}x\),它的对边是\(\sin \ \color{green}y/\color{purple}h = \sin \ \color{green}y/\color{purple}1 = \sin\ \color{green}y\)。这样我们获得了能够得到x和y方向的长度的公式,它们取决于所给的角度。我们使用它来计算方向向量的元素:
|
||||
|
||||
|
||||
|
||||
|
||||
Reference in New Issue
Block a user