Fix all the titles

2025-08-22 20:25:28 +08:00 · 2016-07-06 01:42:55 +08:00
parent 5dad4f21d8
commit 3ef7a53627
44 changed files with 512 additions and 527 deletions
--- a/started/02
+++ b/started/02
@@ -58,7 +58,7 @@ CMake是一个工程文件生成工具，可以使用预定义好的CMake脚本

 现在，让我们打开Visual Studio，创建一个新的工程。如果提供了多个选项，选择Visual C++，然后选择**空工程(Empty Project)**，别忘了给你的工程起一个合适的名字。现在我们有了一个空的工程去创建我们的OpenGL程序。

-## 链接(Linking)
+## 链接

 为了使我们的程序使用GLFW，我们需要把GLFW库**链接(Link)**进工程。于是我们需要在链接器的设置里写上**glfw3.lib**。但是我们的工程还不知道在哪寻找这个文件，于是我们首先需要将我们放第三方库的目录添加进设置。

@@ -138,7 +138,7 @@ GLEW是OpenGL Extension Wrangler Library的缩写，它管理我们上面提到

 我们现在成功编译了GLFW和GLEW库，我们将进入[下一节](http://learnopengl-cn.readthedocs.org/zh/latest/01%20Getting%20started/03%20Hello%20Window/)去使用GLFW和GLEW来设置OpenGL上下文并创建窗口。记住确保你的头文件和库文件的目录设置正确，以及链接器里引用的库文件名正确。如果仍然遇到错误，请参考额外资源中的例子。

-##额外的资源
+## 额外的资源

 - [Building applications](http://www.opengl-tutorial.org/miscellaneous/building-your-own-c-application/): 提供了很多编译链接相关的信息以及一大批错误的解决方法。
 - [GLFW with Code::Blocks](http://wiki.codeblocks.org/index.php?title=Using_GLFW_with_Code::Blocks):使用Code::Blocks IDE编译GLFW。
--- a/started/03
+++ b/started/03
@@ -63,7 +63,7 @@ glfwMakeContextCurrent(window);

 `glfwCreateWindow`函数需要窗口的宽和高作为它的前两个参数；第三个参数表示只这个窗口的名称(标题)，这里我们使用**"LearnOpenGL"**，当然你也可以使用你喜欢的名称；最后两个参数我们暂时忽略，先置为空指针就行。它的返回值`GLFWwindow`对象的指针会在其他的GLFW操作中使用到。创建完窗口我们就可以通知GLFW给我们的窗口在当前的线程中创建我们等待已久的OpenGL上下文了。

-### GLEW
+## GLEW

 在之前的教程中已经提到过，GLEW是用来管理OpenGL的函数指针的，所以在调用任何OpenGL的函数之前我们需要初始化GLEW。

@@ -78,7 +78,7 @@ if (glewInit() != GLEW_OK)

 请注意，我们在初始化GLEW之前设置`glewExperimental`变量的值为`GL_TRUE`，这样做能让GLEW在管理OpenGL的函数指针时更多地使用现代化的技术，如果把它设置为`GL_FALSE`的话可能会在使用OpenGL的核心模式(Core-profile)时出现一些问题。

-### 视口(Viewport)
+## 视口(Viewport)

 在我们绘制之前还有一件重要的事情要做，我们必须告诉OpenGL渲染窗口的尺寸大小，这样OpenGL才只能知道要显示数据的窗口坐标。我们可以通过调用`glViewport`函数来设置这些维度：

@@ -88,11 +88,11 @@ glViewport(0, 0, 800, 600);

 前两个参数设置窗口左下角的位置。第三个和第四个参数设置渲染窗口的宽度和高度,我们设置成与GLFW的窗口的宽高大小，我们也可以将这个值设置成比窗口小的数值，然后所有的OpenGL渲染将会显示在一个较小的区域。

-!!!Important
+!!! Important

 	OpenGL使用`glViewport`定义的位置和宽高进行位置坐标的转换，将OpenGL中的位置坐标转换为你的屏幕坐标。例如，OpenGL中的坐标(0.5,0.5)有可能被转换为屏幕中的坐标(200,450)。注意，OpenGL只会把-1到1之间的坐标转换为屏幕坐标，因此在此例中(-1，1)转换为屏幕坐标是(0,600)。

-## 准备好你的引擎
+# 准备好你的引擎

 我们可不希望只绘制一个图像之后我们的应用程序就关闭窗口并立即退出。我们希望程序在我们明确地关闭它之前一直保持运行状态并能够接受用户输入。因此，我们需要在程序中添加一个while循环，我们可以把它称之为游戏循环(Game Loop)，这样我们的程序就能在我们让GLFW退出前保持运行了。下面几行的代码就实现了一个简单的游戏循环：

@@ -115,7 +115,7 @@ while(!glfwWindowShouldClose(window))

 	应用程序使用单缓冲区绘图可能会存在图像闪烁的问题。 这是因为生成的图像不是一下子被绘制出来的，而是按照从左到右，由上而下逐像素地绘制而成的。最终图像不是在瞬间显示给用户,而是通过一步一步地计算结果绘制的，这可能会花费一些时间。为了规避这些问题，我们应用双缓冲区渲染窗口应用程序。前面的缓冲区保存着计算后可显示给用户的图像，被显示到屏幕上；所有的的渲染命令被传递到后台的缓冲区进行计算。当所有的渲染命令执行结束后，我们交换前台缓冲和后台缓冲，这样图像就立即呈显出来，之后清空缓冲区。

-### 最后一件事
+## 最后一件事

 当游戏循环结束后我们需要释放之前的操作分配的资源，我们可以在main函数的最后调用`glfwTerminate`函数来释放GLFW分配的内存。

@@ -131,7 +131,7 @@ return 0;
 如果你没有编译通过或者有什么问题的话，首先请检查你程序的的链接选项是否正确
 。然后对比本教程的代码，检查你的代码是不是哪里写错了，你也可以[点击这里](http://learnopengl.com/code_viewer.php?code=getting-started/hellowindow)获取我的完整代码。

-### 输入
+## 输入

 我们同样也希望能够在GLFW中实现一些键盘控制，这是通过设置GLFW的**回调函数(Callback Function)**来实现的。回调函数事实上是一个函数指针，当我们为GLFW设置回调函数后，GLWF会在恰当的时候调用它。**按键回调(KeyCallback)**是众多回调函数中的一种，当我们为GLFW设置按键回调之后，GLFW会在用户有键盘交互时调用它。该回调函数的原型如下所示：

@@ -163,9 +163,9 @@ glfwSetKeyCallback(window, key_callback);
 除了按键回调函数之外，我们还能为GLFW注册其他的回调函数。例如，我们可以注册一个函数来处理窗口尺寸变化、处理一些错误信息等。我们可以在创建窗口之后到开始游戏循环之前注册各种回调函数。


-### 渲染(Rendering)
+## 渲染

-我们要把所有的渲染操作放到游戏循环中，因为我们想让这些渲染操作在每次游戏循环迭代的时候都能被执行。我们将做如下的操作：
+我们要把所有的渲染(Rendering)操作放到游戏循环中，因为我们想让这些渲染操作在每次游戏循环迭代的时候都能被执行。我们将做如下的操作：

 ```c++
 // 程序循环
--- a/Triangle.md
+++ b/Triangle.md
@@ -6,9 +6,8 @@
 翻译     | [Django](http://bullteacher.com/)
 校对     | Geequlim

-## 图形渲染管线(Pipeline)

-在OpenGL中任何事物都在3D空间中，但是屏幕和窗口是一个2D像素阵列，所以OpenGL的大部分工作都是关于如何把3D坐标转变为适应你屏幕的2D像素。3D坐标转为2D坐标的处理过程是由OpenGL的**图形渲染管线**(Pipeline，大多译为管线，实际上指的是一堆原始图形数据途经一个输送管道，期间经过各种变化处理最终出现在屏幕的过程)管理的。图形渲染管线可以被划分为两个主要部分：第一个部分把你的3D坐标转换为2D坐标，第二部分是把2D坐标转变为实际的有颜色的像素。这个教程里，我们会简单地讨论一下图形渲染管线，以及如何使用它创建一些像素，这对我们来说是有好处的。
+在OpenGL中，任何事物都在3D空间中，但是屏幕和窗口是一个2D像素阵列，所以OpenGL的大部分工作都是关于如何把3D坐标转变为适应你屏幕的2D像素。3D坐标转为2D坐标的处理过程是由OpenGL的**图形渲染管线**(graphics Pipeline，大多译为管线，实际上指的是一堆原始图形数据途经一个输送管道，期间经过各种变化处理最终出现在屏幕的过程)管理的。图形渲染管线可以被划分为两个主要部分：第一个部分把你的3D坐标转换为2D坐标，第二部分是把2D坐标转变为实际的有颜色的像素。这个教程里，我们会简单地讨论一下图形渲染管线，以及如何使用它创建一些像素，这对我们来说是有好处的。

 !!! Important

@@ -57,9 +56,9 @@

 在现代OpenGL中，我们**必须**定义至少一个顶点着色器和一个片段着色器(因为GPU中没有默认的顶点/片段着色器)。出于这个原因，开始学习现代OpenGL的时候非常困难，因为在你能够渲染自己的第一个三角形之前需要一大堆知识。本节结束就是你可以最终渲染出你的三角形的时候，你也会了解到很多图形编程知识。

-## 顶点输入(Vertex Input)
+## 顶点输入

-开始绘制一些东西之前，我们必须给OpenGL输入一些顶点数据。OpenGL是一个3D图形库，所以我们在OpenGL中指定的所有坐标都是在3D坐标里(x、y和z)。OpenGL不是简单的把你所有的3D坐标变换为你屏幕上的2D像素；OpenGL只是在当它们的3个轴(x、y和z)在特定的-1.0到1.0的范围内时才处理3D坐标。所有在这个范围内的坐标叫做**标准化设备坐标**(Normalized Device Coordinates，NDC)会最终显示在你的屏幕上(所有出了这个范围的都不会显示)。
+开始绘制一些东西之前，我们必须给OpenGL输入一些顶点(Vertex)数据。OpenGL是一个3D图形库，所以我们在OpenGL中指定的所有坐标都是在3D坐标里(x、y和z)。OpenGL不是简单的把你所有的3D坐标变换为你屏幕上的2D像素；OpenGL只是在当它们的3个轴(x、y和z)在特定的-1.0到1.0的范围内时才处理3D坐标。所有在这个范围内的坐标叫做**标准化设备坐标**(Normalized Device Coordinates，NDC)会最终显示在你的屏幕上(所有出了这个范围的都不会显示)。

 由于我们希望渲染一个三角形，我们指定所有的这三个顶点都有一个3D位置。我们把它们以`GLfloat`数组的方式定义为标准化设备坐标(也就是在OpenGL的可见区域)中。

@@ -124,9 +123,9 @@ glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);

 现在我们把顶点数据储存在显卡的内存中，用VBO顶点缓冲对象管理。下面我们会创建一个顶点和片段着色器，来处理这些数据。现在我们开始着手创建它们吧。

-## 顶点着色器(Vertex Shader)
+## 顶点着色器

-顶点着色器是几个着色器中的一个，它是可编程的。现代OpenGL需要我们至少设置一个顶点和一个片段着色器，如果我们打算做渲染的话。我们会简要介绍一下着色器以及配置两个非常简单的着色器来绘制我们第一个三角形。下个教程里我们会更详细的讨论着色器。
+顶点着色器(Vertex Shader)是几个着色器中的一个，它是可编程的。现代OpenGL需要我们至少设置一个顶点和一个片段着色器，如果我们打算做渲染的话。我们会简要介绍一下着色器以及配置两个非常简单的着色器来绘制我们第一个三角形。下个教程里我们会更详细的讨论着色器。

 我们需要做的第一件事是用着色器语言GLSL写顶点着色器，然后编译这个着色器，这样我们就可以在应用中使用它了。下面你会看到一个非常基础的顶点着色器的源代码，它就是使用GLSL写的：

@@ -155,7 +154,7 @@ void main()

 这个顶点着色器可能是能想到的最简单的了，因为我们什么都没有处理就把输入数据输出了。在真实的应用里输入数据通常都没有在标准化设备坐标中，所以我们首先就必须把它们放进OpenGL的可视区域内。

-## 编译一个着色器
+## 编译着色器

 我们已经写了一个顶点着色器源码，但是为了OpenGL能够使用它，我们必须在运行时动态编译它的源码。

@@ -195,9 +194,9 @@ glCompileShader(vertexShader);

 如果编译的时候没有任何错误，顶点着色器就被编译成功了。

-## 片段着色器(Fragment Shader)
+## 片段着色器

-片段着色器是第二个也是最终我们打算创建的用于渲染三角形的着色器。片段着色器的全部，都是用来计算你的像素的最后颜色输出。为了让事情比较简单，我们的片段着色器只输出橘黄色。
+片段着色器(Fragment Shader)是第二个也是最终我们打算创建的用于渲染三角形的着色器。片段着色器的全部，都是用来计算你的像素的最后颜色输出。为了让事情比较简单，我们的片段着色器只输出橘黄色。

 !!! Important

@@ -327,7 +326,7 @@ someOpenGLFunctionThatDrawsOurTriangle();

 我们绘制一个物体的时候必须重复这件事。这看起来也不多，但是如果有超过5个顶点属性，100多个不同物体呢(这其实并不罕见)。绑定合适的缓冲对象，为每个物体配置所有顶点属性很快就变成一件麻烦事。有没有一些方法可以使我们把所有的配置储存在一个对象中，并且可以通过绑定这个对象来恢复状态？

-### 顶点数组对象(Vertex Array Object, VAO)
+### 顶点数组对象

 **顶点数组对象(Vertex Array Object, VAO)**可以像顶点缓冲对象一样绑定，任何随后的顶点属性调用都会储存在这个VAO中。这有一个好处，当配置顶点属性指针时，你只用做一次，每次绘制一个物体的时候，我们绑定相应VAO就行了。切换不同顶点数据和属性配置就像绑定一个不同的VAO一样简单。所有状态我们都放到了VAO里。

@@ -407,9 +406,9 @@ glBindVertexArray(0);

 如果你的输出和这个不一样，你可能做错了什么，去看源码，看看是否遗漏了什么东西或者在评论部分提问。

-## 索引缓冲对象(Element Buffer Objects，EBO)
+## 索引缓冲对象

-这是我们最后一件在渲染顶点这个问题上要讨论的事——索引缓冲对象简称EBO(或IBO)。解释索引缓冲对象的工作方式最好是举例子：假设我们不再绘制一个三角形而是矩形。我们就可以绘制两个三角形来组成一个矩形(OpenGL主要就是绘制三角形)。这会生成下面的顶点的集合：
+这是我们最后一件在渲染顶点这个问题上要讨论的事——索引缓冲对象(Element Buffer Objects，EBO)。解释索引缓冲对象的工作方式最好是举例子：假设我们不再绘制一个三角形而是矩形。我们就可以绘制两个三角形来组成一个矩形(OpenGL主要就是绘制三角形)。这会生成下面的顶点的集合：

 ```c++
 GLfloat vertices[] = {
--- a/Shaders.md
+++ b/Shaders.md
@@ -1,4 +1,4 @@
-# 着色器(Shader)
+# 着色器

 原文     | [Shaders](http://learnopengl.com/#!Getting-started/Shaders)
      ---|---
@@ -6,11 +6,11 @@
 翻译     | [Django](http://bullteacher.com/)
 校对     | Geequlim

-在[Hello Triangle](http://learnopengl-cn.readthedocs.org/zh/latest/01%20Getting%20started/04%20Hello%20Triangle/)教程中提到，着色器是运行在GPU上的小程序。这些小程序为图形渲染管线的一个特定部分而运行。从基本意义上来说，着色器不是别的，只是一种把输入转化为输出的程序。着色器也是一种相当独立的程序，它们不能相互通信；只能通过输入和输出的方式来进行沟通。
+在[Hello Triangle](http://learnopengl-cn.readthedocs.org/zh/latest/01%20Getting%20started/04%20Hello%20Triangle/)教程中提到，着色器(Shader)是运行在GPU上的小程序。这些小程序为图形渲染管线的一个特定部分而运行。从基本意义上来说，着色器不是别的，只是一种把输入转化为输出的程序。着色器也是一种相当独立的程序，它们不能相互通信；只能通过输入和输出的方式来进行沟通。

 前面的教程里我们简要地触及了一点着色器的皮毛。了解了如何恰当地使用它们。现在我们会用一种更加通用的方式详细解释着色器，特别是OpenGL着色器语言。

-## GLSL
+# GLSL

 着色器是使用一种叫GLSL的类C语言写成的。GLSL是为图形计算量身定制的，它包含针对向量和矩阵操作的有用特性。

@@ -51,9 +51,9 @@ std::cout << "Maximum nr of vertex attributes supported: " << nrAttributes << st

 GLSL有像其他编程语言相似的数据类型。GLSL有C风格的默认基础数据类型：`int`、`float`、`double`、`uint`和`bool`。GLSL也有两种容器类型，教程中我们会使用很多，它们是向量(Vector)和矩阵(Matrix)，其中矩阵我们会在之后的教程里再讨论。

-## 向量(Vector)
+### 向量

-GLSL中的向量可以包含有1、2、3或者4个分量，分量类型可以是前面默认基础类型的任意一个。它们可以是下面的形式(n代表元素数量)：
+GLSL中的向量(Vector)可以包含有1、2、3或者4个分量，分量类型可以是前面默认基础类型的任意一个。它们可以是下面的形式(n代表元素数量)：

  类型|含义
   ---|---
@@ -86,7 +86,7 @@ vec4 otherResult = vec4(result.xyz, 1.0f);

 向量是一种灵活的数据类型，我们可以把用在所有输入和输出上。学完教程你会看到很多如何创造性地管理向量的例子。

-## 输入与输出(in vs out)
+## 输入与输出

 着色器是各自独立的小程序，但是它们都是一个整体的局部，出于这样的原因，我们希望每个着色器都有输入和输出，这样才能进行数据交流和传递。GLSL定义了`in`和`out`关键字来实现这个目的。每个着色器使用这些关键字定义输入和输出，无论在哪儿，一个输出变量就能与一个下一个阶段的输入变量相匹配。他们在顶点和片段着色器之间有点不同。

@@ -100,7 +100,7 @@ vec4 otherResult = vec4(result.xyz, 1.0f);

 所以，如果我们打算从一个着色器向另一个着色器发送数据，我们必须**在发送方着色器中声明一个输出，在接收方着色器中声明一个同名输入**。当名字和类型都一样的时候，OpenGL就会把两个变量链接到一起，它们之间就能发送数据了(这是在链接程序(Program)对象时完成的)。为了展示这是这么工作的，我们会改变前面教程里的那个着色器，让顶点着色器为片段着色器决定颜色。

-#### 顶点着色器
+**顶点着色器**

 ```c++
 #version 330 core
@@ -114,7 +114,7 @@ void main()
    vertexColor = vec4(0.5f, 0.0f, 0.0f, 1.0f); // 把输出颜色设置为暗红色
 }
 ```
-#### 片段着色器
+**片段着色器**

 ```c++
 #version 330 core
@@ -296,7 +296,7 @@ glEnableVertexAttribArray(1);

 这正是这个三角形里发生的事。我们有3个顶点，和相应的3个颜色，从这个三角形的像素来看它可能包含50,000左右的像素，片段着色器为这些像素进行插值。如果你仔细看这些颜色，你会发现其中的奥秘：红到紫再到蓝。像素插值会应用到所有片段着色器的输入属性上。

-## 我们自己的着色器类
+# 我们自己的着色器类

 编写、编译、管理着色器是件麻烦事。在着色器的最后主题里，我们会写一个类来让我们的生活轻松一点，这个类从硬盘读着色器，然后编译和链接它们，对它们进行错误检测，这就变得很好用了。这也会给你一些关于如何把我们目前所学的知识封装到一个抽象的对象里的灵感。

@@ -335,9 +335,13 @@ public:

 shader类保留了着色器程序的ID。它的构造器需要顶点和片段着色器源代码的文件路径，我们可以把各自的文本文件储存在硬盘上。`Use`函数看似平常，但是能够显示这个自造类如何让我们的生活变轻松(虽然只有一点)。

-### 从文件读取
+## 从文件读取

-我们使用C++文件流读取着色器内容，储存到几个string对象里([译注1])
+我们使用C++文件流读取着色器内容，储存到几个string对象里：(译注1)
+
+!!! note "译注1"
+
+	实际上把着色器代码保存在文件中适合学习OpenGL的时候，实际开发中最好把一个着色器直接储存为多个字符串，这样具有更高的灵活度。

 ```c++
 Shader(const GLchar * vertexPath, const GLchar * fragmentPath)
@@ -439,10 +443,8 @@ while(...)

 使用新着色器类的[程序](http://learnopengl.com/code_viewer.php?code=getting-started/shaders-using-object)，[着色器类](http://learnopengl.com/code_viewer.php?type=header&code=shader)，[顶点着色器](http://learnopengl.com/code_viewer.php?type=vertex&code=getting-started/basic)，[片段着色器](http://learnopengl.com/code_viewer.php?type=fragment&code=getting-started/basic)。

-## 练习
+# 练习

 1. 修改顶点着色器让三角形上下颠倒：[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/shaders-exercise1)
 2. 通过使用uniform定义一个水平偏移，在顶点着色器中使用这个偏移量把三角形移动到屏幕右侧：[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/shaders-exercise2)
 3. 使用`out`关键字把顶点位置输出到片段着色器，把像素的颜色设置为与顶点位置相等(看看顶点位置值是如何在三角形中进行插值的)。做完这些后，尝试回答下面的问题：为什么在三角形的左下角是黑的?：[参考解答](http://learnopengl.com/code_viewer.php?code=getting-started/shaders-exercise3)
-
-[译注1]: http://learnopengl-cn.readthedocs.org/zh/latest/01%20Getting%20started/05%20Shaders/#_5 "译者注：实际上把着色器代码保存在文件中适合学习OpenGL的时候，实际开发中最好把一个着色器直接储存为多个字符串，这样具有更高的灵活度。"
--- a/Textures.md
+++ b/Textures.md
@@ -1,4 +1,4 @@
-# 纹理(Textures)
+# 纹理

 原文     | [Textures](http://learnopengl.com/#!Getting-started/Textures)
      ---|---
@@ -38,11 +38,11 @@ GLfloat texCoords[] = {

 纹理采样有几种不同的插值方式。我们需要自己告诉OpenGL在纹理中采用哪种采样方式。

-### 纹理环绕方式(Texture Wrapping)
+## 纹理环绕方式

 纹理坐标通常的范围是从(0, 0)到(1, 1)，如果我们把纹理坐标设置为范围以外会发生什么？OpenGL默认的行为是重复这个纹理图像(我们简单地忽略浮点纹理坐标的整数部分)，但OpenGL提供了更多的选择：

-环绕方式            | 描述
+环绕方式(Wrapping)            | 描述
                 ---|---
 GL_REPEAT           | 纹理的默认行为，重复纹理图像
 GL_MIRRORED_REPEAT  | 和`GL_REPEAT`一样，除了重复的图片是镜像放置的
@@ -71,11 +71,13 @@ float borderColor[] = { 1.0f, 1.0f, 0.0f, 1.0f };
 glTexParameterfv(GL_TEXTURE_2D, GL_TEXTURE_BORDER_COLOR, borderColor);
 ```

-### 纹理过滤(Texture Filtering)
+## 纹理过滤

-纹理坐标不依赖于解析度，它可以是任何浮点数值，这样OpenGL需要描述出哪个纹理像素对应哪个纹理坐标(Texture Pixel，也叫Texel，[译注1])。当你有一个很大的物体但是纹理解析度很低的时候这就变得很重要了。你可能已经猜到了，OpenGL也有一个叫做纹理过滤的选项。有多种不同的选项可用，但是现在我们只讨论最重要的两种：`GL_NEAREST`和`GL_LINEAR`。
+纹理坐标不依赖于解析度，它可以是任何浮点数值，这样OpenGL需要描述出哪个纹理像素对应哪个纹理坐标(Texture Pixel，也叫Texel，译注1)。当你有一个很大的物体但是纹理解析度很低的时候这就变得很重要了。你可能已经猜到了，OpenGL也有一个叫做纹理过滤(Texture Filtering)的选项。有多种不同的选项可用，但是现在我们只讨论最重要的两种：`GL_NEAREST`和`GL_LINEAR`。

-[译注1]: http://learnopengl-cn.readthedocs.org/zh/latest/01%20Getting%20started/06%20Textures/ "Texture Pixel也叫Texel，你可以想象你打开一张.jpg格式图片不断放大你会发现它是由无数像素点组成的，这个点就是纹理像素；注意不要和纹理坐标搞混，纹理坐标是你给模型顶点设置的那个数组，OpenGL以这个顶点的纹理坐标数据去查找纹理图像上的像素，然后进行采样提取纹理像素的颜色"
+!!! note "译注1"
+
+	Texture Pixel也叫Texel，你可以想象你打开一张.jpg格式图片不断放大你会发现它是由无数像素点组成的，这个点就是纹理像素；注意不要和纹理坐标搞混，纹理坐标是你给模型顶点设置的那个数组，OpenGL以这个顶点的纹理坐标数据去查找纹理图像上的像素，然后进行采样提取纹理像素的颜色

 **GL_NEAREST(Nearest Neighbor Filtering，邻近过滤)** 是一种OpenGL默认的纹理过滤方式。当设置为`GL_NEAREST`的时候，OpenGL选择最接近纹理坐标中心点的那个像素。下图你会看到四个像素，加号代表纹理坐标。左上角的纹理像素是距离纹理坐标最近的那个，这样它就会选择这个作为采样颜色：

@@ -98,7 +100,7 @@ glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
 ```

-#### 多级渐远纹理(Mipmaps)
+### 多级渐远纹理

 想象一下，如果我们在一个有着上千物体的大房间，每个物体上都有纹理。距离观察者远的与距离近的物体的纹理的解析度是相同的。由于远处的物体可能只产生很少的片段，OpenGL从高解析度纹理中为这些片段获取正确的颜色值就很困难。这是因为它不得不拾为一个纹理跨度很大的片段取纹理颜色。在小物体上这会产生人工感，更不用说在小物体上使用高解析度纹理浪费内存的问题了。

@@ -127,13 +129,13 @@ glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

 常见的错误是，为多级渐远纹理过滤选项设置放大过滤。这样没有任何效果，因为多级渐远纹理主要使用在纹理被缩小的情况下的：纹理放大不会使用多级渐远纹理，为多级渐远纹理设置放大过滤选项会产生一个`GL_INVALID_ENUM`错误。

-## 加载和创建纹理
+# 加载和创建纹理

 使用纹理之前要做的第一件事是把它们加载到应用中。纹理图像可能储存为各种各样的格式，每种都有自己的数据结构和排列，所以我们如何才能把这些图像加载到应用中呢？一个解决方案是写一个我们自己的某种图像格式加载器比如.PNG，用它来把图像转化为byte序列。写自己的图像加载器虽然不难，但是仍然挺烦人的，而且如果要支持更多文件格式呢？你就不得不为每种你希望支持的格式写加载器了。

 另一个解决方案是，也许是更好的一种选择，就是使用一个支持多种流行格式的图像加载库，来为我们解决这个问题。就像SOIL这种库①。

-### SOIL
+## SOIL

 SOIL是Simple OpenGL Image Library(简易OpenGL图像库)的缩写，它支持大多数流行的图像格式，使用起来也很简单，你可以从他们的主页下载。像大多数其他库一样，你必须自己生成**.lib**。你可以使用**/projects**文件夹里的解决方案(Solution)文件之一(不用担心他们的Visual Studio版本太老，你可以把它们转变为新的版本；这总是可行的。译注：用VS2010的时候，你要用VC8而不是VC9的解决方案，想必更高版本的情况亦是如此)，你也可以使用CMake自己生成。你还要添加**src**文件夹里面的文件到你的**includes**文件夹；对了，不要忘记添加**SOIL.lib**到你的连接器选项，并在你代码文件的开头加上`#include <SOIL.h>`。

@@ -146,7 +148,7 @@ unsigned char* image = SOIL_load_image("container.jpg", &width, &height, 0, SOIL

 函数首先需要输入图片文件的路径。然后需要两个int指针作为第二个和第三个参数，SOIL会返回图片的宽度和高度到其中。之后，我们需要图片的宽度和高度来生成纹理。第四个参数指定图片的通道(Channel)数量，但是这里我们只需留`0`。最后一个参数告诉SOIL如何来加载图片：我们只对图片的RGB感兴趣。结果储存为一个大的char/byte数组。

-### 生成纹理
+## 生成纹理

 和之前生成的OpenGL对象一样，纹理也是使用ID引用的。

@@ -204,7 +206,7 @@ SOIL_free_image_data(image);
 glBindTexture(GL_TEXTURE_2D, 0);
 ```

-### 应用纹理
+## 应用纹理

 后面的部分我们会使用`glDrawElements`绘制[Hello Triangle](http://learnopengl-cn.readthedocs.org/zh/latest/01%20Getting%20started/04%20Hello%20Triangle/)教程的最后一部分的矩形。我们需要告知OpenGL如何采样纹理，这样我们必须更新顶点纹理坐标数据：

@@ -290,9 +292,9 @@ color = texture(ourTexture, TexCoord) * vec4(ourColor, 1.0f);

 这个箱子看起来有点70年代迪斯科风格。

-### 纹理单元(Texture Units)
+## 纹理单元

-你可能感到奇怪为什么`sampler2D`是个uniform变量，你却不用`glUniform`给它赋值，使用`glUniform1i`我们就可以给纹理采样器确定一个位置，这样的话我们能够一次在一个片段着色器中设置多纹理。一个纹理的位置通常称为一个纹理单元。一个纹理的默认纹理单元是0，它是默认激活的纹理单元，所以教程前面部分我们不用给它确定一个位置。
+你可能感到奇怪为什么`sampler2D`是个uniform变量，你却不用`glUniform`给它赋值，使用`glUniform1i`我们就可以给纹理采样器确定一个位置，这样的话我们能够一次在一个片段着色器中设置多纹理。一个纹理的位置通常称为一个纹理单元(Texture Units)。一个纹理的默认纹理单元是0，它是默认激活的纹理单元，所以教程前面部分我们不用给它确定一个位置。

 纹理单元的主要目的是让我们在着色器中可以使用多于一个的纹理。通过把纹理单元赋值给采样器，我们可以一次绑定多纹理，只要我们首先激活相应的纹理单元。就像`glBindTexture`一样，我们可以使用`glActiveTexture`激活纹理单元，传入我们需要使用的纹理单元：

@@ -360,7 +362,7 @@ glBindVertexArray(0);

 如果你看到了图片上的笑脸容器，你就做对了。你可以对比[程序源代码](http://learnopengl.com/code_viewer.php?code=getting-started/textures_combined)，以及[顶点着色器](http://learnopengl.com/code_viewer.php?type=vertex&code=getting-started/texture)和[片段着色器](http://learnopengl.com/code_viewer.php?type=fragment&code=getting-started/texture)。

-### 练习
+## 练习

 为了更熟练地使用纹理，建议在继续之后的学习之前做完这些练习：

--- a/Transformations.md
+++ b/Transformations.md
@@ -1,4 +1,4 @@
-# 变换(Transformations)
+# 变换

 原文     | [Transformations](http://learnopengl.com/#!Getting-started/Transformations)
      ---|---
@@ -12,9 +12,9 @@

 为了深入了解变换，我们首先要在讨论矩阵之前了解一点向量(Vector)。这一节的目标是让你拥有将来需要的最基础的数学背景知识. 如果你发现这节十分困难，尽量尝试去理解它们，当你以后需要它们的时候回过头来复习这些概念。

-## 向量(Vector)
+# 向量

-向量最最基本的定义就是一个方向。或者更正式的说，向量有一个**方向(Direction)**和**大小(Magnitude，也叫做强度或长度)**。你可以把向量想成一个藏宝图上的指示：“向左走10步，向北走3步，然后向右走5步”；“左”就是方向，“10步”就是向量的长度。你可以发现，这个藏宝图的指示一共有3个向量。向量可以在任意**维度**(Dimension)上，但是我们通常只使用2至4维。如果一个向量有2个维度，它表示一个平面的方向(想象一下2D的图像)，当它有3个维度的时候它可以表达一个3D世界的方向。
+向量(Vector)最最基本的定义就是一个方向。或者更正式的说，向量有一个**方向(Direction)**和**大小(Magnitude，也叫做强度或长度)**。你可以把向量想成一个藏宝图上的指示：“向左走10步，向北走3步，然后向右走5步”；“左”就是方向，“10步”就是向量的长度。你可以发现，这个藏宝图的指示一共有3个向量。向量可以在任意**维度**(Dimension)上，但是我们通常只使用2至4维。如果一个向量有2个维度，它表示一个平面的方向(想象一下2D的图像)，当它有3个维度的时候它可以表达一个3D世界的方向。

 下面你会看到3个向量，每个向量在图像中都用一个箭头(x, y)表示。我们在2D图片中展示这些向量，因为这样子会更直观. 你仍然可以把这些2D向量当做z坐标为0的3D向量。由于向量表示的是方向，起始于何处**并不会**改变它的值。下图我们可以看到向量\(\color{red}{\bar{v}}\)和\(\color{blue}{\bar{w}}\)是相等的，尽管他们的起始点不同：

@@ -30,7 +30,7 @@ $$

 和普通数字一样，我们也可以用向量进行多种运算(其中一些你可能已经知道了)。

-### 向量与标量运算(Scalar Vector Operations)
+## 向量与标量运算

 **标量(Scalar)**只是一个数字(或者说是仅有一个分量的矢量)。当把一个向量加/减/乘/除一个标量，我们可以简单的把向量的每个分量分别进行该运算。对于加法来说会像这样:

@@ -40,15 +40,15 @@ $$

 其中的+可以是+，-，·或÷，其中·是乘号。注意－和÷运算时不能颠倒，因为颠倒的运算是没有定义的(标量-/÷矢量)

-### 向量取反(Vector Negation)
+## 向量取反

-对一个向量取反会将其方向逆转。一个指向东北的向量取反后就指向西南方向了。我们在一个向量的每个分量前加负号就可以实现取反了(或者说用-1数乘该向量):
+对一个向量取反(Negation)会将其方向逆转。一个指向东北的向量取反后就指向西南方向了。我们在一个向量的每个分量前加负号就可以实现取反了(或者说用-1数乘该向量):

 $$
 -\bar{v} = -\begin{pmatrix} \color{red}{v_x} \\ \color{blue}{v_y} \\ \color{green}{v_z} \end{pmatrix} = \begin{pmatrix} -\color{red}{v_x} \\ -\color{blue}{v_y} \\ -\color{green}{v_z} \end{pmatrix}
 $$

-### 向量加减
+## 向量加减

 向量的加法可以被定义为是**分量的(Component-wise)**相加，即将一个向量中的每一个分量加上另一个向量的对应分量：

@@ -70,9 +70,9 @@ $$

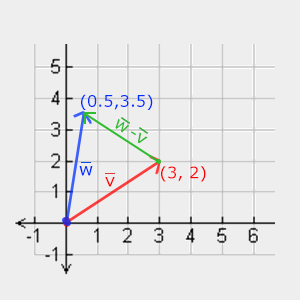
 ![](http://learnopengl.com/img/getting-started/vectors_subtraction.png)

-### 长度(Length)
+## 长度

-我们使用**勾股定理(Pythagoras Theorem)**来获取向量的长度/大小. 如果你把向量的x与y分量画出来，该向量会形成一个以x与y分量为边的三角形:
+我们使用**勾股定理(Pythagoras Theorem)**来获取向量的长度(Length)/大小(Magnitude). 如果你把向量的x与y分量画出来，该向量会形成一个以x与y分量为边的三角形:

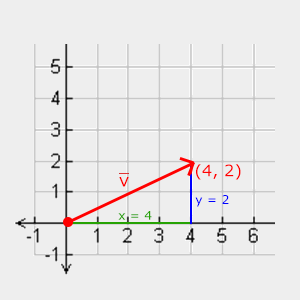
 ![](http://learnopengl.com/img/getting-started/vectors_triangle.png)

@@ -100,13 +100,13 @@ $$

 我们把这种方法叫做一个向量的**标准化(Normalizing)**。单位向量头上有一个^样子的记号，并且它会变得很有用，特别是在我们只关心方向不关系长度的时候(如果我们改变向量的长度，它的方向并不会改变)。

-### 向量相乘(Vector-vector Multiplication)
+## 向量相乘

 两个向量相乘是一种很奇怪的情况。普通的乘法在向量上是没有定义的，因为它在视觉上是没有意义的，但是有两种特定情境，当需要乘法时我们可以从中选择：一个是**点乘(Dot Product)**，记作\(\bar{v} \cdot \bar{k}\)，另一个是**叉乘(Cross Product)**，记作\(\bar{v} \times \bar{k}\)。

-#### 点乘(Dot Product)
+### 点乘

-两个向量的点乘等于它们的数乘结果乘以两个向量之间夹角的余弦值。听起来有点费解，先看一下公式：
+两个向量的点乘(Dot Product)等于它们的数乘结果乘以两个向量之间夹角的余弦值。听起来有点费解，先看一下公式：

 $$
 \bar{v} \cdot \bar{k} = ||\bar{v}|| \cdot ||\bar{k}|| \cdot \cos \theta
@@ -138,9 +138,9 @@ $$

 计算两个单位余弦的角度，我们使用反余弦\(cos^{-1}\) ，结果是143.1度。现在我们很快就计算出了两个向量的角度。点乘在计算光照的时候会很有用。

-#### 叉乘(Cross Product)
+### 叉乘

-叉乘只在3D空间有定义，它需要两个不平行向量作为输入，生成正交于两个输入向量的第三个向量。如果输入的两个向量也是正交的，那么叉乘的结果将会返回3个互相正交的向量。接下来的教程中，这很有用。下面的图片展示了3D空间中叉乘的样子：
+叉乘(Cross Product)只在3D空间有定义，它需要两个不平行向量作为输入，生成正交于两个输入向量的第三个向量。如果输入的两个向量也是正交的，那么叉乘的结果将会返回3个互相正交的向量。接下来的教程中，这很有用。下面的图片展示了3D空间中叉乘的样子：

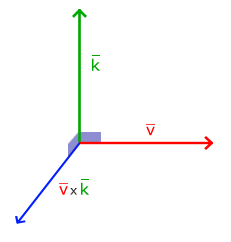
 ![](http://learnopengl.com/img/getting-started/vectors_crossproduct.png)

@@ -152,9 +152,9 @@ $$

 就像你所看到的，看起来毫无头绪。可如果你这么做了，你会得到第三个向量，它正交于你的输入向量。

-## 矩阵(Matrix)
+# 矩阵

-现在我们已经讨论了向量的全部内容，是时候看看矩阵了！矩阵简单说是一个矩形的数字、符号或表达式数组。矩阵中每一项叫做矩阵的**元素(Element)**。下面是一个2×3矩阵的例子：
+现在我们已经讨论了向量的全部内容，是时候看看矩阵(Matrix)了！矩阵简单说是一个矩形的数字、符号或表达式数组。矩阵中每一项叫做矩阵的**元素(Element)**。下面是一个2×3矩阵的例子：

 $$
 \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}
@@ -164,7 +164,7 @@ $$

 关于矩阵基本也就是这些了，它就是矩形数学表达式阵列。矩阵也有非常漂亮的数学属性，就跟向量一样。矩阵有几个运算，叫做：矩阵加法、减法和乘法。

-### 矩阵的加减
+## 矩阵的加减

 矩阵与标量的加减如下所示：

@@ -190,7 +190,7 @@ $$
 \begin{bmatrix} \color{red}4 & \color{red}2 \\ \color{green}1 & \color{green}6 \end{bmatrix} - \begin{bmatrix} \color{red}2 & \color{red}4 \\ \color{green}0 & \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}4 - \color{red}2 & \color{red}2  - \color{red}4 \\ \color{green}1 - \color{green}0 & \color{green}6 - \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}2 & -\color{red}2 \\ \color{green}1 & \color{green}5 \end{bmatrix}
 $$

-### 矩阵的数乘(Matrix-scalar Products)
+## 矩阵的数乘

 和矩阵与标量的加减一样，矩阵与标量之间的乘法也是矩阵的每一个元素分别乘以该标量。下面的例子展示了乘法的过程：

@@ -202,7 +202,7 @@ $$

 到目前为止都还好，我们的例子都不复杂。不过矩阵与矩阵的乘法就不一样了。

-### 矩阵相乘(Matrix-matrix Multiplication)
+### 矩阵相乘

 矩阵之间的乘法不见得有多复杂，但的确很难让人适应。矩阵乘法基本上意味着遵照规定好的法则进行相乘。当然，相乘还有一些限制：

@@ -238,13 +238,13 @@ $$

 不管怎样，反正现在我们知道如何进行矩阵相乘了，我们可以开始了解好东西了。

-## 矩阵与向量相乘
+# 矩阵与向量相乘

 到目前，通过这些教程我们已经相当了解向量了。我们用向量来表示位置、颜色和纹理坐标。让我们进到兔子洞更深处：向量基本上就是一个**N×1**矩阵，N是向量分量的个数(也叫**N维(N-dimensional)**向量)。如果你仔细思考这个问题，会很有意思。向量和矩阵一样都是一个数字序列，但是它只有1列。所以，这个新信息能如何帮助我们？如果我们有一个M×N矩阵，我们可以用这个矩阵乘以我们的N×1向量，因为我们的矩阵的列数等于向量的行数，所以它们就能相乘。

 但是为什么我们关心矩阵是否能够乘以一个向量？有很多有意思的2D/3D变换本质上都是矩阵，而矩阵与我们的向量相乘会变换我们的向量。假如你仍然有些困惑，我们看一些例子，你很快就能明白了。

-### 单位矩阵(Identity Matrix)
+## 单位矩阵

 在OpenGL中，因为有一些原因我们通常使用4×4的变换矩阵，而其中最重要的原因就是因为每一个向量都有4个分量的。我们能想到的最简单的变换矩阵就是**单位矩阵(Identity Matrix)**。单位矩阵是一个除了对角线以外都是0的N × N矩阵。就像你看到的，这个变换矩阵使一个向量完全不变：

@@ -258,9 +258,9 @@ $$

 	你可能会奇怪一个没变换的变换矩阵有什么用？单位矩阵通常是生成其他变换矩阵的起点，如果我们深挖线性代数，这就是一个对证明定理、解线性方程非常有用的矩阵。

-### 缩放(Scaling)
+## 缩放

-当我们对一个向量进行缩放的时候就是对向量的长度进行缩放，而它的方向保持不变。如果我们进行2或3维操作，那么我们可以分别定义一个有2或3个缩放变量的向量，每个变量缩放一个轴(x、y或z)。
+当我们对一个向量进行缩放(Scaling)的时候就是对向量的长度进行缩放，而它的方向保持不变。如果我们进行2或3维操作，那么我们可以分别定义一个有2或3个缩放变量的向量，每个变量缩放一个轴(x、y或z)。

 我们可以尝试去缩放向量\(\color{red}{\bar{v}} = (3,2)\)。我们可以把向量沿着x轴缩放0.5，使它的宽度缩小为原来的二分之一；我们可以沿着y轴把向量的高度缩放为原来的两倍。我们看看把向量缩放(0.5, 2)所获得的\(\color{blue}{\bar{s}}\)是什么样的：

@@ -276,7 +276,7 @@ $$

 注意，第四个缩放的向量仍然是1，因为不会缩放3D空间中的w分量。w分量另有其他用途，在后面我们会看到。

-### 平移(Translation)
+## 平移

 **平移(Translation)**是在原来向量的基础上加上另一个的向量从而获得一个在不同位置的新向量的过程，这样就基于平移向量**移动(Move)**了向量。我们已经讨论了向量加法，所以你应该不会陌生。

@@ -298,9 +298,9 @@ $$

 有了平移矩阵我们就可以在3个方向(x、y、z)上移动物体，它是我们的变换工具箱中非常有用的一个变换矩阵。

-### 旋转(Rotation)
+### 旋转

-上面几个的变换内容相对容易理解，在2D或3D空间中也容易表示出来，但旋转稍复杂些。如果你想知道旋转矩阵是如何构造出来的，我推荐你去看可汗学院[线性代数](https://www.khanacademy.org/math/linear-algebra/matrix_transformations)视频。
+上面几个的变换内容相对容易理解，在2D或3D空间中也容易表示出来，但旋转(Rotation)稍复杂些。如果你想知道旋转矩阵是如何构造出来的，我推荐你去看可汗学院[线性代数](https://www.khanacademy.org/math/linear-algebra/matrix_transformations)视频。

 首先我们来定义一个向量的旋转到底是什么。2D或3D空间中点的旋转用**角(Angle)**来表示。角可以是角度制或弧度制的，周角是360度或2 [PI](https://en.wikipedia.org/wiki/Pi)弧度。我个人更喜欢用角度，因为它们看起来更直观。

@@ -367,15 +367,15 @@ $$

 不错！向量先缩放2倍，然后平移了(1, 2, 3)个单位。

-## 实践
+# 实践

 现在我们已经解释了所有变换背后的理论，是时候将这些知识利用起来了。OpenGL没有任何自带的矩阵和向量形式，所以我们必须自己定义数学类和方法。在这个教程中我们更愿意抽象所有的数学细节，使用已经做好了的数学库。幸运的是有个使用简单的专门为OpenGL量身定做的数学库，那就是GLM。

-### GLM
+## GLM

 GLM是Open**GL** **M**athematics的缩写，它是一个只有头文件的库，也就是说我们只需包含合适的头文件就行了；不用链接和编译。GLM可以从他们的[网站](http://glm.g-truc.net/0.9.5/index.html)上下载。把头文件的根目录复制到你的`includes`文件夹，然后你就可以使用这个库了。

-![](http://learnopengl.com/img/getting-started/glm.png)
+<img alt="OpenGL Logo" src="../../img/01/07/glm.png" class="right" />

 我们需要的GLM的大多数功能都可以从下面这3个头文件中找到：

--- a/Systems.md
+++ b/Systems.md
@@ -1,4 +1,4 @@
-# 坐标系统(Coordinate System)
+# 坐标系统

 原文     | [Coordinate Systems](http://learnopengl.com/#!Getting-started/Coordinate-Systems)
      ---|---
@@ -8,7 +8,7 @@

 在上一个教程中，我们学习了如何有效地利用矩阵变换来对所有顶点进行转换。OpenGL希望在所有顶点着色器运行后，所有我们可见的顶点都变为标准化设备坐标(Normalized Device Coordinate, NDC)。也就是说，每个顶点的x，y，z坐标都应该在-1.0到1.0之间，超出这个坐标范围的顶点都将不可见。我们通常会自己设定一个坐标的范围，之后再在顶点着色器中将这些坐标转换为标准化设备坐标。然后将这些标准化设备坐标传入光栅器(Rasterizer)，再将他们转换为屏幕上的二维坐标或像素。

-将坐标转换为标准化设备坐标，接着再转化为屏幕坐标的过程通常是分步，也就是类似于流水线那样子，实现的，在流水线里面我们在将对象转换到屏幕空间之前会先将其转换到多个坐标系统。将对象的坐标转换到几个过渡坐标系(Intermediate Coordinate System)的优点在于，在这些特定的坐标系统中进行一些操作或运算更加方便和容易，这一点很快将会变得很明显。对我们来说比较重要的总共有5个不同的坐标系统：
+将坐标转换为标准化设备坐标，接着再转化为屏幕坐标的过程通常是分步，也就是类似于流水线那样子，实现的，在流水线里面我们在将对象转换到屏幕空间之前会先将其转换到多个坐标系统(Coordinate System)。将对象的坐标转换到几个过渡坐标系(Intermediate Coordinate System)的优点在于，在这些特定的坐标系统中进行一些操作或运算更加方便和容易，这一点很快将会变得很明显。对我们来说比较重要的总共有5个不同的坐标系统：

 - 局部空间(Local Space，或者称为物体空间(Object Space))
 - 世界空间(World Space)
@@ -20,7 +20,7 @@

 你现在可能对什么是空间或坐标系到底是什么感到困惑，所以接下来我们将会通过展示完整的图片来解释每一个坐标系实际做了什么。

-### 整体概述
+## 概述

 为了将坐标从一个坐标系转换到另一个坐标系，我们需要用到几个转换矩阵，最重要的几个分别是**模型(Model)**、**视图(View)**、**投影(Projection)**三个矩阵。首先，顶点坐标开始于**局部空间(Local Space)**，称为**局部坐标(Local Coordinate)**，然后经过**世界坐标(World Coordinate)**，**观察坐标(View Coordinate)**，**裁剪坐标(Clip Coordinate)**，并最后以**屏幕坐标(Screen Coordinate)**结束。下面的图示显示了整个流程及各个转换过程做了什么：

@@ -36,26 +36,26 @@

 你可能了解了每个单独的坐标空间的作用。我们之所以将顶点转换到各个不同的空间的原因是有些操作在特定的坐标系统中才有意义且更方便。例如，当修改对象时，如果在局部空间中则是有意义的；当对对象做相对于其它对象的位置的操作时，在世界坐标系中则是有意义的；等等这些。如果我们愿意，本可以定义一个直接从局部空间到裁剪空间的转换矩阵，但那样会失去灵活性。接下来我们将要更仔细地讨论各个坐标系。

-### 局部空间(Local Space)
+## 局部空间

-局部空间是指对象所在的坐标空间，例如，对象最开始所在的地方。想象你在一个模型建造软件(比如说Blender)中创建了一个立方体。你创建的立方体的原点有可能位于(0，0，0)，即使有可能在最后的应用中位于完全不同的另外一个位置。甚至有可能你创建的所有模型都以(0，0，0)为初始位置，然而他们会在世界的不同位置。则你的模型的所有顶点都是在**局部**空间：他们相对于你的对象来说都是局部的。
+局部空间(Local Space)是指对象所在的坐标空间，例如，对象最开始所在的地方。想象你在一个模型建造软件(比如说Blender)中创建了一个立方体。你创建的立方体的原点有可能位于(0，0，0)，即使有可能在最后的应用中位于完全不同的另外一个位置。甚至有可能你创建的所有模型都以(0，0，0)为初始位置，然而他们会在世界的不同位置。则你的模型的所有顶点都是在**局部**空间：他们相对于你的对象来说都是局部的。

 我们一直使用的那个箱子的坐标范围为-0.5到0.5，设定(0, 0)为它的原点。这些都是局部坐标。


-### 世界空间(World Space)
+## 世界空间

-如果我们想将我们所有的对象导入到程序当中，它们有可能会全挤在世界的原点上(0，0，0)，然而这并不是我们想要的结果。我们想为每一个对象定义一个位置，从而使对象位于更大的世界当中。世界空间中的坐标就如它们听起来那样：是指顶点相对于(游戏)世界的坐标。物体变换到的最终空间就是世界坐标系，并且你会想让这些物体分散开来摆放(从而显得更真实)。对象的坐标将会从局部坐标转换到世界坐标；该转换是由**模型矩阵(Model Matrix)**实现的。
+如果我们想将我们所有的对象导入到程序当中，它们有可能会全挤在世界的原点上(0，0，0)，然而这并不是我们想要的结果。我们想为每一个对象定义一个位置，从而使对象位于更大的世界当中。世界空间(World Space)中的坐标就如它们听起来那样：是指顶点相对于(游戏)世界的坐标。物体变换到的最终空间就是世界坐标系，并且你会想让这些物体分散开来摆放(从而显得更真实)。对象的坐标将会从局部坐标转换到世界坐标；该转换是由**模型矩阵(Model Matrix)**实现的。

 模型矩阵是一种转换矩阵，它能通过对对象进行平移、缩放、旋转来将它置于它本应该在的位置或方向。你可以想象一下，我们需要转换一栋房子，通过将它缩小(因为它在局部坐标系中显得太大了)，将它往郊区的方向平移，然后沿着y轴往坐标旋转。经过这样的变换之后，它将恰好能够与邻居的房子重合。你能够想到上一节讲到的利用模型矩阵将各个箱子放置到这个屏幕上；我们能够将箱子中的局部坐标转换为观察坐标或世界坐标。

-### 观察空间(View Space)
+## 观察空间

-观察空间经常被人们称之OpenGL的**摄像机(Camera)**(所以有时也称为摄像机空间(Camera Space)或视觉空间(Eye Space))。观察空间就是将对象的世界空间的坐标转换为观察者视野前面的坐标。因此观察空间就是从摄像机的角度观察到的空间。而这通常是由一系列的平移和旋转的组合来平移和旋转场景从而使得特定的对象被转换到摄像机前面。这些组合在一起的转换通常存储在一个**观察矩阵(View Matrix)**里，用来将世界坐标转换到观察空间。在下一个教程我们将广泛讨论如何创建一个这样的观察矩阵来模拟一个摄像机。
+观察空间(View Space)经常被人们称之OpenGL的**摄像机(Camera)**(所以有时也称为摄像机空间(Camera Space)或视觉空间(Eye Space))。观察空间就是将对象的世界空间的坐标转换为观察者视野前面的坐标。因此观察空间就是从摄像机的角度观察到的空间。而这通常是由一系列的平移和旋转的组合来平移和旋转场景从而使得特定的对象被转换到摄像机前面。这些组合在一起的转换通常存储在一个**观察矩阵(View Matrix)**里，用来将世界坐标转换到观察空间。在下一个教程我们将广泛讨论如何创建一个这样的观察矩阵来模拟一个摄像机。

-### 裁剪空间(Clip Space)
+## 裁剪空间

-在一个顶点着色器运行的最后，OpenGL期望所有的坐标都能落在一个给定的范围内，且任何在这个范围之外的点都应该被裁剪掉(Clipped)。被裁剪掉的坐标就被忽略了，所以剩下的坐标就将变为屏幕上可见的片段。这也就是**裁剪空间**名字的由来。
+在一个顶点着色器运行的最后，OpenGL期望所有的坐标都能落在一个给定的范围内，且任何在这个范围之外的点都应该被裁剪掉(Clipped)。被裁剪掉的坐标就被忽略了，所以剩下的坐标就将变为屏幕上可见的片段。这也就是**裁剪空间(Clip Space)**名字的由来。

 因为将所有可见的坐标都放置在-1.0到1.0的范围内不是很直观，所以我们会指定自己的坐标集(Coordinate Set)并将它转换回标准化设备坐标系，就像OpenGL期望它做的那样。

@@ -73,9 +73,9 @@

 投影矩阵将观察坐标转换为裁剪坐标的过程采用两种不同的方式，每种方式分别定义自己的平截头体。我们可以创建一个正射投影矩阵(Orthographic Projection Matrix)或一个透视投影矩阵(Perspective Projection Matrix)。

-#### 正射投影(Orthographic Projection)
+### 正射投影

-正射投影矩阵定义了一个类似立方体的平截头体，指定了一个裁剪空间，每一个在这空间外面的顶点都会被裁剪。创建一个正射投影矩阵需要指定可见平截头体的宽、高和长度。所有在使用正射投影矩阵转换到裁剪空间后如果还处于这个平截头体里面的坐标就不会被裁剪。它的平截头体看起来像一个容器：
+正射投影(Orthographic Projection)矩阵定义了一个类似立方体的平截头体，指定了一个裁剪空间，每一个在这空间外面的顶点都会被裁剪。创建一个正射投影矩阵需要指定可见平截头体的宽、高和长度。所有在使用正射投影矩阵转换到裁剪空间后如果还处于这个平截头体里面的坐标就不会被裁剪。它的平截头体看起来像一个容器：

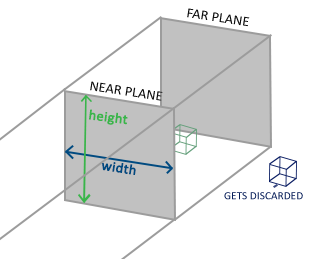
 ![orthographic projection frustum](http://learnopengl.com/img/getting-started/orthographic_frustum.png)

@@ -91,13 +91,13 @@ glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f);

 正射投影矩阵直接将坐标映射到屏幕的二维平面内，但实际上一个直接的投影矩阵将会产生不真实的结果，因为这个投影没有将**透视(Perspective)**考虑进去。所以我们需要**透视投影**矩阵来解决这个问题。

-#### 透视投影(Perspective Projection)
+#### 透视投影

-如果你曾经体验过**实际生活**给你带来的景象，你就会注意到离你越远的东西看起来更小。这个神奇的效果我们称之为透视。透视的效果在我们看一条无限长的高速公路或铁路时尤其明显，正如下面图片显示的那样:
+如果你曾经体验过**实际生活**给你带来的景象，你就会注意到离你越远的东西看起来更小。这个神奇的效果我们称之为透视(Perspective)。透视的效果在我们看一条无限长的高速公路或铁路时尤其明显，正如下面图片显示的那样:

 ![perspective](http://learnopengl.com/img/getting-started/perspective.png)

-正如你看到的那样，由于透视的原因，平行线似乎在很远的地方看起来会相交。这正是透视投影想要模仿的效果，它是使用透视投影矩阵来完成的。这个投影矩阵不仅将给定的平截头体范围映射到裁剪空间，同样还修改了每个顶点坐标的w值，从而使得离观察者越远的顶点坐标w分量越大。被转换到裁剪空间的坐标都会在-w到w的范围之间(任何大于这个范围的对象都会被裁剪掉)。OpenGL要求所有可见的坐标都落在-1.0到1.0范围内从而作为最后的顶点着色器输出，因此一旦坐标在裁剪空间内，透视划分就会被应用到裁剪空间坐标：
+正如你看到的那样，由于透视的原因，平行线似乎在很远的地方看起来会相交。这正是透视投影(Perspective Projection)想要模仿的效果，它是使用透视投影矩阵来完成的。这个投影矩阵不仅将给定的平截头体范围映射到裁剪空间，同样还修改了每个顶点坐标的w值，从而使得离观察者越远的顶点坐标w分量越大。被转换到裁剪空间的坐标都会在-w到w的范围之间(任何大于这个范围的对象都会被裁剪掉)。OpenGL要求所有可见的坐标都落在-1.0到1.0范围内从而作为最后的顶点着色器输出，因此一旦坐标在裁剪空间内，透视划分就会被应用到裁剪空间坐标：

 $$
 out = \begin{pmatrix} x /w \\ y / w \\ z / w \end{pmatrix}
@@ -145,7 +145,7 @@ $$

 这一章的主题可能会比较难理解，如果你仍然不确定每个空间的作用的话，你也不必太担心。接下来你会看到我们是怎样好好运用这些坐标空间的并且会有足够的展示例子在接下来的教程中。

-## 进入三维
+# 进入3D

 既然我们知道了如何将三维坐标转换为二维坐标，我们可以开始将我们的对象展示为三维对象而不是目前我们所展示的缺胳膊少腿的二维平面。

@@ -179,7 +179,7 @@ model = glm::rotate(model, -55.0f, glm::vec3(1.0f, 0.0f, 0.0f));
 	- 使你的食指往上。
 	- 向下90度弯曲你的中指。 

-如果你都正确地做了，那么你的大拇指朝着正x轴方向，食指朝着正y轴方向，中指朝着正z轴方向。如果你用左手来做这些动作，你会发现z轴的方向是相反的。这就是有名的左手坐标系，它被DirectX广泛地使用。注意在标准化设备坐标系中OpenGL使用的是左手坐标系(投影矩阵改变了惯用手的习惯)。
+	如果你都正确地做了，那么你的大拇指朝着正x轴方向，食指朝着正y轴方向，中指朝着正z轴方向。如果你用左手来做这些动作，你会发现z轴的方向是相反的。这就是有名的左手坐标系，它被DirectX广泛地使用。注意在标准化设备坐标系中OpenGL使用的是左手坐标系(投影矩阵改变了惯用手的习惯)。

 在下一个教程中我们将会详细讨论如何在场景中移动。目前的观察矩阵是这样的：

@@ -262,9 +262,9 @@ glDrawArrays(GL_TRIANGLES, 0, 36);

 幸运的是，OpenGL存储深度信息在z缓冲区(Z-buffer)里面，它允许OpenGL决定何时覆盖一个像素何时不覆盖。通过使用z缓冲区我们可以设置OpenGL来进行深度测试。

-### z缓冲区
+### Z缓冲区

-OpenGL存储它的所有深度信息于z缓冲区中，也被称为深度缓冲区(Depth Buffer)。GLFW会自动为你生成这样一个缓冲区 (就如它有一个颜色缓冲区来存储输出图像的颜色)。深度存储在每个片段里面(作为片段的z值)当片段像输出它的颜色时，OpenGL会将它的深度值和z缓冲进行比较然后如果当前的片段在其它片段之后它将会被丢弃，然后重写。这个过程称为**深度测试(Depth Testing)**并且它是由OpenGL自动完成的。
+OpenGL存储它的所有深度信息于Z缓冲区(Z-buffer)中，也被称为深度缓冲区(Depth Buffer)。GLFW会自动为你生成这样一个缓冲区 (就如它有一个颜色缓冲区来存储输出图像的颜色)。深度存储在每个片段里面(作为片段的z值)当片段像输出它的颜色时，OpenGL会将它的深度值和z缓冲进行比较然后如果当前的片段在其它片段之后它将会被丢弃，然后重写。这个过程称为**深度测试(Depth Testing)**并且它是由OpenGL自动完成的。

 然而，如果我们想要确定OpenGL是否真的执行深度测试，首先我们要告诉OpenGL我们想要开启深度测试；而这通常是默认关闭的。我们通过`glEnable`函数来开启深度测试。`glEnable`和`glDisable`函数允许我们开启或关闭某一个OpenGL的功能。该功能会一直是开启或关闭的状态直到另一个调用来关闭或开启它。现在我们想开启深度测试就需要开启`GL_DEPTH_TEST`：

--- a/started/09
+++ b/started/09
@@ -10,13 +10,13 @@

 本节我们将会讨论如何在OpenGL中模拟一个摄像机，将会讨论FPS风格的可自由在3D场景中移动的摄像机。我们也会讨论键盘和鼠标输入，最终完成一个自定义的摄像机类。

-### 摄像机/观察空间(Camera/View Space)
+## 摄像机/观察空间

-当我们讨论摄像机/观察空间的时候，是我们在讨论以摄像机的透视图作为场景原点时场景中所有可见顶点坐标。观察矩阵把所有的世界坐标变换到观察坐标，这些新坐标是相对于摄像机的位置和方向的。定义一个摄像机，我们需要一个摄像机在世界空间中的位置、观察的方向、一个指向它的右测的向量以及一个指向它上方的向量。细心的读者可能已经注意到我们实际上创建了一个三个单位轴相互垂直的、以摄像机的位置为原点的坐标系。
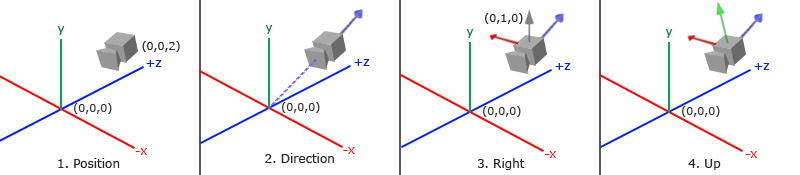
+当我们讨论摄像机/观察空间(Camera/View Space)的时候，是我们在讨论以摄像机的透视图作为场景原点时场景中所有可见顶点坐标。观察矩阵把所有的世界坐标变换到观察坐标，这些新坐标是相对于摄像机的位置和方向的。定义一个摄像机，我们需要一个摄像机在世界空间中的位置、观察的方向、一个指向它的右测的向量以及一个指向它上方的向量。细心的读者可能已经注意到我们实际上创建了一个三个单位轴相互垂直的、以摄像机的位置为原点的坐标系。

 ![](http://learnopengl.com/img/getting-started/camera_axes.png)

-#### 1. 摄像机位置
+### 1. 摄像机位置

 获取摄像机位置很简单。摄像机位置简单来说就是世界空间中代表摄像机位置的向量。我们把摄像机位置设置为前面教程中的那个相同的位置：

@@ -28,7 +28,7 @@ glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f);

 	不要忘记正z轴是从屏幕指向你的，如果我们希望摄像机向后移动，我们就往z轴正方向移动。

-#### 2. 摄像机方向
+### 2. 摄像机方向

 下一个需要的向量是摄像机的方向，比如它指向哪个方向。现在我们让摄像机指向场景原点：(0, 0, 0)。用摄像机位置向量减去场景原点向量的结果就是摄像机指向向量。由于我们知道摄像机指向z轴负方向，我们希望方向向量指向摄像机的z轴正方向。如果我们改变相减的顺序，我们就会获得一个指向摄像机正z轴方向的向量(译注：注意看前面的那个图，所说的「方向向量/Direction Vector」是指向z的正方向的，而不是摄像机所注视的那个方向)：

@@ -41,7 +41,7 @@ glm::vec3 cameraDirection = glm::normalize(cameraPos - cameraTarget);

 	方向向量(Direction Vector)并不是最好的名字，因为它正好指向从它到目标向量的相反方向。

-#### 3. 右轴(Right axis)
+### 3. 右轴

 我们需要的另一个向量是一个**右向量(Right Vector)**，它代表摄像机空间的x轴的正方向。为获取右向量我们需要先使用一个小技巧：定义一个**上向量(Up Vector)**。我们把上向量和第二步得到的摄像机方向向量进行叉乘。两个向量叉乘的结果就是同时垂直于两向量的向量，因此我们会得到指向x轴正方向的那个向量(如果我们交换两个向量的顺序就会得到相反的指向x轴负方向的向量)：

@@ -50,7 +50,7 @@ glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f);
 glm::vec3 cameraRight = glm::normalize(glm::cross(up, cameraDirection));
 ```

-#### 4. 上轴(Up axis)
+#### 4. 上轴

 现在我们已经有了x轴向量和z轴向量，获取摄像机的正y轴相对简单；我们把右向量和方向向量(Direction Vector)进行叉乘：

@@ -60,7 +60,7 @@ glm::vec3 cameraUp = glm::cross(cameraDirection, cameraRight);

 在叉乘和一些小技巧的帮助下，我们创建了所有观察/摄像机空间的向量。对于想学到更多数学原理的读者，提示一下，在线性代数中这个处理叫做[Gram-Schmidt(葛兰—施密特)正交](http://en.wikipedia.org/wiki/Gram%E2%80%93Schmidt_process)。使用这些摄像机向量我们就可以创建一个**LookAt**矩阵了，它在创建摄像机的时候非常有用。

-### Look At
+## Look At

 使用矩阵的好处之一是如果你定义了一个坐标空间，里面有3个相互垂直的轴，你可以用这三个轴外加一个平移向量来创建一个矩阵，你可以用这个矩阵乘以任何向量来变换到那个坐标空间。这正是LookAt矩阵所做的，现在我们有了3个相互垂直的轴和一个定义摄像机空间的位置坐标，我们可以创建我们自己的LookAt矩阵了：

@@ -100,7 +100,7 @@ view = glm::lookAt(glm::vec3(camX, 0.0, camZ), glm::vec3(0.0, 0.0, 0.0), glm::ve

 这一小段代码中，摄像机围绕场景转动。自己试试改变半径和位置/方向参数，看看LookAt矩阵是如何工作的。同时，这里有[源码](http://learnopengl.com/code_viewer.php?code=getting-started/camera_circle)、[顶点](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=getting-started/coordinate_systems&type=fragment)着色器。

-## 自由移动
+# 自由移动

 让摄像机绕着场景转很有趣，但是让我们自己移动摄像机更有趣！首先我们必须设置一个摄像机系统，在我们的程序前面定义一些摄像机变量很有用：

@@ -200,7 +200,7 @@ while(!glfwWindowShouldClose(window))

 至此，你可以同时向多个方向移动了，并且当你按下按钮也会立刻运动了。如遇困难查看[源码](http://learnopengl.com/code_viewer.php?code=getting-started/camera_keyboard)。

-### 移动速度
+## 移动速度

 目前我们的移动速度是个常量。看起来不错，但是实际情况下根据处理器的能力不同，有的人在同一段时间内会比其他人绘制更多帧。也就是调用了更多次`do_movement`函数。每个人的运动速度就都不同了。当你要发布的你应用的时候，你必须确保在所有硬件上移动速度都一样。

@@ -240,15 +240,15 @@ void Do_Movement()
 现在我们有了一个在任何系统上移动速度都一样的摄像机。这里是源码。我们可以看到任何移动都会影响返回的`deltaTime`值。


-## 自由观看
+# 视角移动

 只用键盘移动没什么意思。特别是我们还不能转向。是时候使用鼠标了！

 为了能够改变方向，我们必须根据鼠标的输入改变`cameraFront`向量。然而，根据鼠标旋转改变方向向量有点复杂，需要更多的三角学知识。如果你对三角学知之甚少，别担心，你可以跳过这一部分，直接复制粘贴我们的代码；当你想了解更多的时候再回来看。

-### 欧拉角
+## 欧拉角

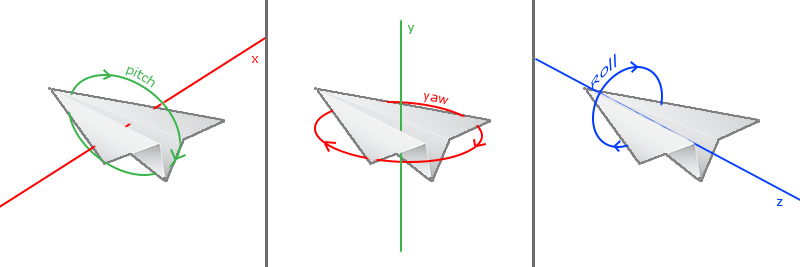
-欧拉角是表示3D空间中可以表示任何旋转的三个值，由莱昂哈德·欧拉在18世纪提出。有三种欧拉角：俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll)，下面的图片展示了它们的含义：
+欧拉角(Euler Angle)是表示3D空间中可以表示任何旋转的三个值，由莱昂哈德·欧拉在18世纪提出。有三种欧拉角：俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll)，下面的图片展示了它们的含义：

 ![](http://www.learnopengl.com/img/getting-started/camera_pitch_yaw_roll.png)

@@ -293,7 +293,7 @@ direction.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));

 这样我们就有了一个可以把俯仰角和偏航角转化为用来自由旋转的摄像机的3个维度的方向向量了。你可能会奇怪：我们怎么得到俯仰角和偏航角？

-### 鼠标输入
+## 鼠标输入

 偏航角和俯仰角是从鼠标移动获得的，鼠标水平移动影响偏航角，鼠标垂直移动影响俯仰角。它的思想是储存上一帧鼠标的位置，在当前帧中我们当前计算鼠标位置和上一帧的位置相差多少。如果差别越大那么俯仰角或偏航角就改变越大。

@@ -426,7 +426,7 @@ void mouse_callback(GLFWwindow* window, double xpos, double ypos)

 现在我们可以自由的在3D场景中移动了！如果你遇到困难，[这是](http://www.learnopengl.com/code_viewer.php?code=getting-started/camera_mouse)源码。

-### 缩放
+## 缩放

 我们还要往摄像机系统里加点东西，实现一个缩放接口。前面教程中我们说视野(Field of View或fov)定义了我们可以看到场景中多大的范围。当视野变小时可视区域就会减小，产生放大了的感觉。我们用鼠标滚轮来放大。和鼠标移动、键盘输入一样我们需要一个鼠标滚轮的回调函数：

@@ -467,7 +467,7 @@ glfwSetScrollCallback(window, scroll_callback);

 	注意，使用欧拉角作为摄像机系统并不完美。你仍然可能遇到[万向节死锁](http://en.wikipedia.org/wiki/Gimbal_lock)。最好的摄像机系统是使用四元数的，后面会有讨论。

-## 摄像机类
+# 摄像机类

 接下来的教程我们会使用一个摄像机来浏览场景，从各个角度观察结果。然而由于一个摄像机会占教程的很大的篇幅，我们会从细节抽象出创建一个自己的摄像机对象。与着色器教程不同我们不会带你一步一步创建摄像机类，如果你想知道怎么工作的的话，只会给你提供一个(有完整注释的)源码。

--- a/started/10
+++ b/started/10
@@ -10,8 +10,7 @@

 这些就是我们在前几章学习的内容，尝试在教程的基础上进行改动程序，或者实验你自己的想法并解决问题. 一旦你认为你真正熟悉了我们讨论的所有的东西，你就可以进行[下一节](http://learnopengl-cn.readthedocs.org/zh/latest/02%20Lighting/01%20Colors/)的学习.

-词汇表
--------
+## 词汇表

 - **OpenGL**: 一个定义了函数布局和输出的图形API的正式规范.
 - **GLEW**: 一个拓展加载库用来为我们加载并设定所有OpenGL函数指针从而让我们能够使用所有(现代)OpenGL函数.
--- a/Lighting/01
+++ b/Lighting/01
@@ -49,7 +49,7 @@ glm::vec3 result = lightColor * toyColor; // = (0.33f, 0.21f, 0.06f);

 目前有了这些颜色相关的理论已经足够了，接下来我们将创建一个场景用来做更多的实验。

-## 创建一个光照场景
+# 创建一个光照场景

 在接下来的教程中，我们将通过模拟真实世界中广泛存在的光照和颜色现象来创建有趣的视觉效果。现在我们将在场景中创建一个看得到的物体来代表光源，并且在场景中至少添加一个物体来模拟光照。

@@ -166,4 +166,4 @@ glBindVertexArray(0);

 如果你在把上述代码片段放到一起编译遇到困难，可以去认真地看看我的[源代码](http://learnopengl.com/code_viewer.php?code=lighting/colors_scene)。你好最自己实现一遍这些操作。

-现在我们有了一些关于颜色的知识，并且创建了一个基本的场景能够绘制一些漂亮的光线。你现在可以阅读[下一个教程](http://learnopengl-cn.readthedocs.org/zh/latest/02%20Lighting/02%20Basic%20Lighting/)，真正的魔法即将开始！
+现在我们有了一些关于颜色的知识，并且创建了一个基本的场景能够绘制一些漂亮的光线。你现在可以阅读[下一节](http://learnopengl-cn.readthedocs.org/zh/latest/02%20Lighting/02%20Basic%20Lighting/)，真正的魔法即将开始！
--- a/Lighting.md
+++ b/Lighting.md
@@ -16,13 +16,13 @@

 为了创建有趣的视觉场景，我们希望模拟至少这三种光照元素。我们将以最简单的一个开始：**环境光照**。

-## 环境光照(Ambient Lighting)
+# 环境光照

 光通常都不是来自于同一光源，而是来自散落于我们周围的很多光源，即使它们可能并不是那么显而易见。光的一个属性是，它可以向很多方向发散和反弹，所以光最后到达的地点可能并不是它所临近的直射方向；光能够像这样**反射(Reflect)**到其他表面，一个物体的光照可能受到来自一个非直射的光源影响。考虑到这种情况的算法叫做**全局照明(Global Illumination)**算法，但是这种算法既开销高昂又极其复杂。

-因为我们不是复杂和昂贵算法的死忠粉丝，所以我们将会使用一种简化的全局照明模型，叫做环境光照。如你在前面章节所见，我们使用一个(数值)很小的常量(光)颜色添加进物体**片段**(Fragment，指当前讨论的光线在物体上的照射点)的最终颜色里，这看起来就像即使没有直射光源也始终存在着一些发散的光。
+因为我们不是复杂和昂贵算法的死忠粉丝，所以我们将会使用一种简化的全局照明模型，叫做环境光照(Ambient Lighting)。如你在前面章节所见，我们使用一个(数值)很小的常量(光)颜色添加进物体**片段**(Fragment，指当前讨论的光线在物体上的照射点)的最终颜色里，这看起来就像即使没有直射光源也始终存在着一些发散的光。

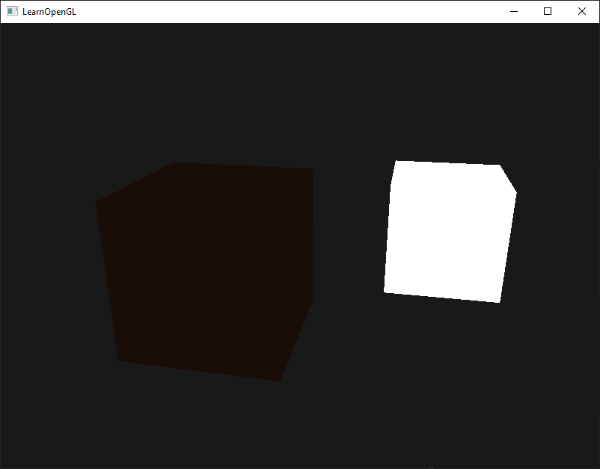
-把环境光添加到场景里非常简单。我们用光的颜色乘以一个(数值)很小常量环境因子，再乘以物体的颜色，然后使用它作为片段的颜色：
+把环境光照添加到场景里非常简单。我们用光的颜色乘以一个(数值)很小常量环境因子，再乘以物体的颜色，然后使用它作为片段的颜色：

 ```c++
 void main()
@@ -38,9 +38,9 @@ void main()

 ![](http://learnopengl.com/img/lighting/ambient_lighting.png)

-## 漫反射光照(Diffuse Lighting)
+# 漫反射光照

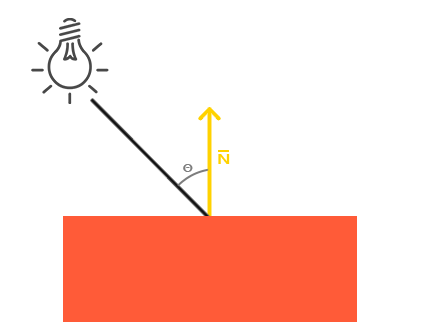
-环境光本身不提供最明显的光照效果，但是漫反射光照会对物体产生显著的视觉影响。漫反射光使物体上与光线排布越近的片段越能从光源处获得更多的亮度。为了更好的理解漫反射光照，请看下图：
+环境光本身不提供最明显的光照效果，但是漫反射光照(Diffuse Lighting)会对物体产生显著的视觉影响。漫反射光使物体上与光线排布越近的片段越能从光源处获得更多的亮度。为了更好的理解漫反射光照，请看下图：

 ![](http://learnopengl.com/img/lighting/diffuse_light.png)

@@ -59,9 +59,9 @@ void main()
 - 法向量：一个垂直于顶点表面的向量。
 - 定向的光线：作为光的位置和片段的位置之间的向量差的方向向量。为了计算这个光线，我们需要光的位置向量和片段的位置向量。

-### 法向量(Normal Vector)
+## 法向量

-法向量是垂直于顶点表面的(单位)向量。由于顶点自身并没有表面(它只是空间中一个独立的点)，我们利用顶点周围的顶点计算出这个顶点的表面。我们能够使用叉乘这个技巧为立方体所有的顶点计算出法线，但是由于3D立方体不是一个复杂的形状，所以我们可以简单的把法线数据手工添加到顶点数据中。更新的顶点数据数组可以在[这里](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting_vertex_data)找到。试着去想象一下，这些法向量真的是垂直于立方体的各个面的表面的(一个立方体由6个面组成)。
+法向量(Normal Vector)是垂直于顶点表面的(单位)向量。由于顶点自身并没有表面(它只是空间中一个独立的点)，我们利用顶点周围的顶点计算出这个顶点的表面。我们能够使用叉乘这个技巧为立方体所有的顶点计算出法线，但是由于3D立方体不是一个复杂的形状，所以我们可以简单的把法线数据手工添加到顶点数据中。更新的顶点数据数组可以在[这里](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting_vertex_data)找到。试着去想象一下，这些法向量真的是垂直于立方体的各个面的表面的(一个立方体由6个面组成)。

 因为我们向顶点数组添加了额外的数据，所以我们应该更新光照的顶点着色器：

@@ -102,7 +102,7 @@ void main()
 in vec3 Normal;
 ```

-### 计算漫反射光照
+## 计算漫反射光照

 每个顶点现在都有了法向量，但是我们仍然需要光的位置向量和片段的位置向量。由于光的位置是一个静态变量，我们可以简单的在片段着色器中把它声明为uniform：

@@ -174,7 +174,7 @@ color = vec4(result, 1.0f);

 如果你遇到很多困难，可以对比[完整的源代码](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting_diffuse)以及[片段着色器](http://learnopengl.com/code_viewer.php?code=lighting/basic_lighting_diffuse&type=fragment)代码。

-### 最后一件事
+## 最后一件事

 现在我们已经把法向量从顶点着色器传到了片段着色器。可是，目前片段着色器里，我们都是在世界空间坐标中进行计算的，所以，我们不是应该把法向量转换为世界空间坐标吗？基本正确，但是这不是简单地把它乘以一个模型矩阵就能搞定的。

@@ -202,11 +202,11 @@ Normal = mat3(transpose(inverse(model))) * normal;

    对于着色器来说，逆矩阵也是一种开销比较大的操作，因此，无论何时，在着色器中只要可能就应该尽量避免逆操作，因为它们必须为你场景中的每个顶点进行这样的处理。以学习的目的这样做很好，但是对于一个对于效率有要求的应用来说，在绘制之前，你最好用CPU计算出正规矩阵，然后通过uniform把值传递给着色器(和模型矩阵一样)。

-## 镜面光照(Specular Lighting)
+# 镜面光照

 如果你还没被这些光照计算搞得精疲力尽，我们就再把镜面高光(Specular Highlight)加进来，这样冯氏光照才算完整。

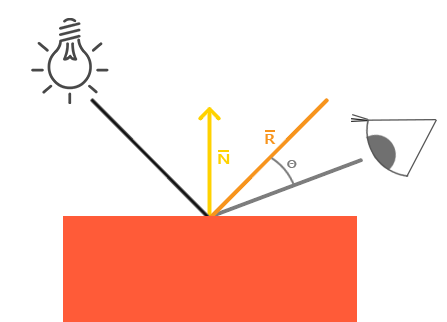
-和环境光照一样，镜面光照同样依据光的方向向量和物体的法向量，但是这次它也会依据观察方向，例如玩家是从什么方向看着这个片段的。镜面光照根据光的反射特性。如果我们想象物体表面像一面镜子一样，那么，无论我们从哪里去看那个表面所反射的光，镜面光照都会达到最大化。你可以从下面的图片看到效果：
+和环境光照一样，镜面光照(Specular Lighting)同样依据光的方向向量和物体的法向量，但是这次它也会依据观察方向，例如玩家是从什么方向看着这个片段的。镜面光照根据光的反射特性。如果我们想象物体表面像一面镜子一样，那么，无论我们从哪里去看那个表面所反射的光，镜面光照都会达到最大化。你可以从下面的图片看到效果：

 ![](http://learnopengl.com/img/lighting/basic_lighting_specular_theory.png)

--- a/Materials.md
+++ b/Materials.md
@@ -1,4 +1,4 @@
-# 材质(Material)
+# 材质

 原文     | [Materials](http://learnopengl.com/#!Lighting/Materials)
      ---|---
@@ -37,7 +37,7 @@ uniform Material material;
 让我们试试在着色器中实现这样的一个材质系统。


-## 设置材质
+# 设置材质

 我们在片段着色器中创建了一个uniform材质结构体，所以下面我们希望改变光照计算来顺应新的材质属性。由于所有材质元素都储存在结构体中，我们可以从uniform变量`material`取得它们：

@@ -89,7 +89,7 @@ glUniform1f(matShineLoc, 32.0f);
 看起来很奇怪不是吗？


-### 光的属性
+## 光的属性

 这个物体太亮了。物体过亮的原因是环境、漫反射和镜面三个颜色任何一个光源都会去全力反射。光源对环境、漫反射和镜面元素同时具有不同的强度。前面的教程，我们通过使用一个强度值改变环境和镜面强度的方式解决了这个问题。我们想做一个相同的系统，但是这次为每个光照元素指定了强度向量。如果我们想象`lightColor`是`vec3(1.0)`，代码看起来像是这样：

@@ -147,7 +147,7 @@ glUniform3f(lightSpecularLoc, 1.0f, 1.0f, 1.0f);
 现在改变物体的外观相对简单了些。我们做点更有趣的事！


-### 不同的光源颜色
+## 不同的光源颜色

 目前为止，我们使用光源的颜色仅仅去改变物体各个元素的强度(通过选用从白到灰到黑范围内的颜色)，并没有影响物体的真实颜色(只是强度)。由于现在能够非常容易地访问光的属性了，我们可以随着时间改变它们的颜色来获得一些有很意思的效果。由于所有东西都已经在片段着色器做好了，改变光的颜色很简单，我们可以立即创建出一些有趣的效果：

--- a/Lighting/04
+++ b/Lighting/04
@@ -12,7 +12,7 @@

 所以，前面的材质系统对于除了最简单的模型以外都是不够的，所以我们需要扩展前面的系统，我们要介绍diffuse和specular贴图。它们允许你对一个物体的diffuse（而对于简洁的ambient成分来说，它们几乎总是是一样的）和specular成分能够有更精确的影响。

-## 漫反射贴图
+# 漫反射贴图

 我们希望通过某种方式对每个原始像素独立设置diffuse颜色。有可以让我们基于物体原始像素的位置来获取颜色值的系统吗？

@@ -90,11 +90,11 @@ glBindTexture(GL_TEXTURE_2D, diffuseMap);
 你可以在这里得到应用的[全部代码](http://learnopengl.com/code_viewer.php?code=lighting/lighting_maps_diffuse)。


-## 镜面贴图
+# 镜面贴图

 你可能注意到，specular高光看起来不怎么样，由于我们的物体是个箱子，大部分是木头，我们知道木头是不应该有镜面高光的。我们通过把物体设置specular材质设置为vec3(0.0f)来修正它。但是这样意味着铁边会不再显示镜面高光，我们知道钢铁是会显示一些镜面高光的。我们会想要控制物体部分地显示镜面高光，它带有修改了的亮度。这个问题看起来和diffuse贴图的讨论一样。这是巧合吗？我想不是。

-我们同样用一个纹理贴图，来获得镜面高光。这意味着我们需要生成一个黑白（或者你喜欢的颜色）纹理来定义specular亮度，把它应用到物体的每个部分。下面是一个[specular贴图](http://learnopengl.com/img/textures/container2_specular.png)的例子：
+我们同样用一个纹理贴图，来获得镜面高光。这意味着我们需要生成一个黑白（或者你喜欢的颜色）纹理来定义specular亮度，把它应用到物体的每个部分。下面是一个[镜面贴图(Specular Map)](http://learnopengl.com/img/textures/container2_specular.png)的例子：

 ![](http://www.learnopengl.com/img/textures/container2_specular.png)

@@ -107,7 +107,7 @@ glBindTexture(GL_TEXTURE_2D, diffuseMap);
 使用Photoshop或Gimp之类的工具，通过将图片进行裁剪，将某部分调整成黑白图样，并调整亮度/对比度的做法，可以非常容易将一个diffuse纹理贴图处理为specular贴图。


-### 镜面贴图采样
+## 镜面贴图采样

 一个specular贴图和其他纹理一样，所以代码和diffuse贴图的代码也相似。确保合理的加载了图片，生成一个纹理对象。由于我们在同样的片段着色器中使用另一个纹理采样器，我们必须为specular贴图使用一个不同的纹理单元(参见[纹理](http://learnopengl-cn.readthedocs.org/zh/latest/01%20Getting%20started/06%20Textures/))，所以在渲染前让我们把它绑定到合适的纹理单元

--- a/Lighting/05
+++ b/Lighting/05
@@ -8,11 +8,11 @@

 我们目前使用的所有光照都来自于一个单独的光源，这是空间中的一个点。它的效果不错，但是在真实世界，我们有多种类型的光，它们每个表现都不同。一个光源把光投射到物体上，叫做投光。这个教程里我们讨论几种不同的投光类型。学习模拟不同的光源是你未来丰富你的场景的另一个工具。

-我们首先讨论定向光(directional light)，接着是作为之前学到知识的扩展的点光(point light)，最后我们讨论聚光灯(Spotlight)。下面的教程我们会把这几种不同的光类型整合到一个场景中。
+我们首先讨论定向光(directional light)，接着是作为之前学到知识的扩展的点光(point light)，最后我们讨论聚光(Spotlight)。下面的教程我们会把这几种不同的光类型整合到一个场景中。

-## 定向光(Directional Light)
+# 定向光

-当一个光源很远的时候，来自光源的每条光线接近于平行。这看起来就像所有的光线来自于同一个方向，无论物体和观察者在哪儿。当一个光源被设置为无限远时，它被称为定向光(也被成为平行光)，因为所有的光线都有着同一个方向；它会独立于光源的位置。
+当一个光源很远的时候，来自光源的每条光线接近于平行。这看起来就像所有的光线来自于同一个方向，无论物体和观察者在哪儿。当一个光源被设置为无限远时，它被称为定向光(Directional Light)，因为所有的光线都有着同一个方向；它会独立于光源的位置。

 我们知道的定向光源的一个好例子是，太阳。太阳和我们不是无限远，但它也足够远了，在计算光照的时候，我们感觉它就像无限远。在下面的图片里，来自于太阳的所有的光线都被定义为平行光：

@@ -88,9 +88,9 @@ glUniform3f(lightDirPos, -0.2f, -1.0f, -0.3f);



-## 定点光(Point Light)
+# 点光源

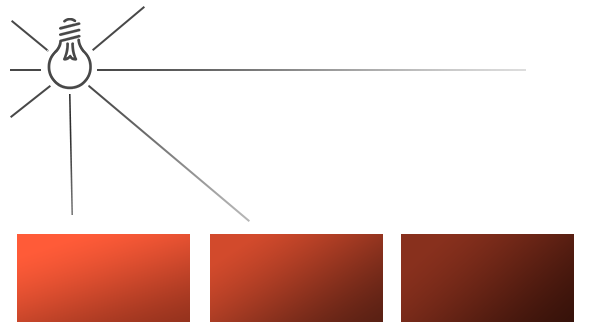
-定向光作为全局光可以照亮整个场景，这非常棒，但是另一方面除了定向光，我们通常也需要几个定点光，在场景里发亮。点光是一个在时间里有位置的光源，它向所有方向发光，光线随距离增加逐渐变暗。想象灯泡和火炬作为投光物，它们可以扮演点光的角色。
+定向光作为全局光可以照亮整个场景，这非常棒，但是另一方面除了定向光，我们通常也需要几个点光源(Point Light)，在场景里发亮。点光是一个在时间里有位置的光源，它向所有方向发光，光线随距离增加逐渐变暗。想象灯泡和火炬作为投光物，它们可以扮演点光的角色。

 ![](http://www.learnopengl.com/img/lighting/light_casters_point.png)

@@ -98,7 +98,7 @@ glUniform3f(lightDirPos, -0.2f, -1.0f, -0.3f);

 如果你把10个箱子添加到之前教程的光照场景中，你会注意到黑暗中的每个箱子都会有同样的亮度，就像箱子在光照的前面；没有公式定义光的距离衰减。我们想让黑暗中与光源比较近的箱子被轻微地照亮。

-### 衰减(Attenuation)
+## 衰减

 随着光线穿越距离的变远使得亮度也相应地减少的现象，通常称之为**衰减(Attenuation)**。一种随着距离减少亮度的方式是使用线性等式。这样的一个随着距离减少亮度的线性方程，可以使远处的物体更暗。然而，这样的线性方程效果会有点假。在真实世界，通常光在近处时非常亮，但是一个光源的亮度，开始的时候减少的非常快，之后随着距离的增加，减少的速度会慢下来。我们需要一种不同的方程来减少光的亮度。

@@ -120,9 +120,7 @@ $$

 你可以看到当距离很近的时候光有最强的亮度，但是随着距离增大，亮度明显减弱，大约接近100的时候，就会慢下来。这就是我们想要的。

-
-
-#### 选择正确的值
+### 选择正确的值

 但是，我们把这三个项设置为什么值呢？正确的值的设置由很多因素决定：环境、你希望光所覆盖的距离范围、光的类型等。大多数场合，这是经验的问题，也要适度调整。下面的表格展示一些各项的值，它们模拟现实（某种类型的）光源，覆盖特定的半径（距离）。第一栏定义一个光的距离，它覆盖所给定的项。这些值是大多数光的良好开始，它是来自Ogre3D的维基的礼物：

@@ -143,7 +141,7 @@ $$

 就像你所看到的，常数项\(K_c\)一直都是1.0。一次项\(K_l\)为了覆盖更远的距离通常很小，二次项\(K_q\)就更小了。尝试用这些值进行实验，看看它们在你的实现中各自的效果。我们的环境中，32到100的距离对大多数光通常就足够了。

-#### 实现衰减
+### 实现衰减

 为了实现衰减，在着色器中我们会需要三个额外数值：也就是公式的常量、一次项和二次项。最好把它们储存在之前定义的Light结构体中。要注意的是我们计算`lightDir`，就是在前面的教程中我们所做的，不是像之前的定向光的那部分。

@@ -198,28 +196,26 @@ specular *= attenuation;
 定点光就是一个可配的置位置和衰减值应用到光照计算中。还有另一种类型光可用于我们照明库当中。


-## 聚光灯(Spotlight)
+## 聚光

-我们要讨论的最后一种类型光是聚光灯(Spotlight)。聚光灯是一种位于环境中某处的光源，它不是向所有方向照射，而是只朝某个方向照射。结果是只有一个聚光灯照射方向的确定半径内的物体才会被照亮，其他的都保持黑暗。聚光灯的好例子是路灯或手电筒。
+我们要讨论的最后一种类型光是聚光(Spotlight)。聚光是一种位于环境中某处的光源，它不是向所有方向照射，而是只朝某个方向照射。结果是只有一个聚光照射方向的确定半径内的物体才会被照亮，其他的都保持黑暗。聚光的好例子是路灯或手电筒。

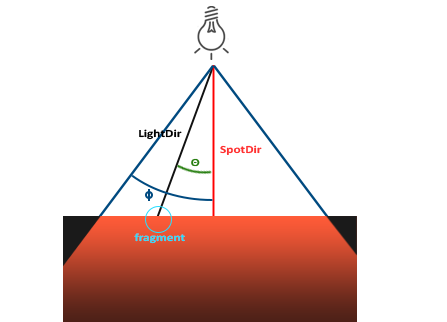
-OpenGL中的聚光灯用世界空间位置，一个方向和一个指定了聚光灯半径的切光角来表示。我们计算的每个片段，如果片段在聚光灯的切光方向之间（就是在圆锥体内），我们就会把片段照亮。下面的图可以让你明白聚光灯是如何工作的：
+OpenGL中的聚光用世界空间位置，一个方向和一个指定了聚光半径的切光角来表示。我们计算的每个片段，如果片段在聚光的切光方向之间（就是在圆锥体内），我们就会把片段照亮。下面的图可以让你明白聚光是如何工作的：

 ![](http://www.learnopengl.com/img/lighting/light_casters_spotlight_angles.png)

 * `LightDir`：从片段指向光源的向量。
-* `SpotDir`：聚光灯所指向的方向。
-* `Phi`\(\phi\)：定义聚光灯半径的切光角。每个落在这个角度之外的，聚光灯都不会照亮。
-* `Theta`\(\theta\)：`LightDir`向量和`SpotDir`向量之间的角度。\(\theta\)值应该比\(\Phi\)值小，这样才会在聚光灯内。
+* `SpotDir`：聚光所指向的方向。
+* `Phi`\(\phi\)：定义聚光半径的切光角。每个落在这个角度之外的，聚光都不会照亮。
+* `Theta`\(\theta\)：`LightDir`向量和`SpotDir`向量之间的角度。\(\theta\)值应该比\(\Phi\)值小，这样才会在聚光内。

-所以我们大致要做的是，计算`LightDir`向量和`SpotDir`向量的点乘（返回两个单位向量的点乘，还记得吗？），然后在和切光角\(\phi\)对比。现在你应该明白聚光灯是我们下面将创建的手电筒的范例。
+所以我们大致要做的是，计算`LightDir`向量和`SpotDir`向量的点乘（返回两个单位向量的点乘，还记得吗？），然后在和切光角\(\phi\)对比。现在你应该明白聚光是我们下面将创建的手电筒的范例。

+## 手电筒

+手电筒(Flashlight)是一个坐落在观察者位置的聚光，通常瞄准玩家透视图的前面。基本上说，一个手电筒是一个普通的聚光，但是根据玩家的位置和方向持续的更新它的位置和方向。

-### 手电筒
-
-手电筒是一个坐落在观察者位置的聚光灯，通常瞄准玩家透视图的前面。基本上说，一个手电筒是一个普通的聚光灯，但是根据玩家的位置和方向持续的更新它的位置和方向。
-
-所以我们需要为片段着色器提供的值，是聚光灯的位置向量（来计算光的方向坐标），聚光灯的方向向量和切光角。我们可以把这些值储存在`Light`结构体中：
+所以我们需要为片段着色器提供的值，是聚光的位置向量（来计算光的方向坐标），聚光的方向向量和切光角。我们可以把这些值储存在`Light`结构体中：

 ```c++
 struct Light
@@ -241,7 +237,7 @@ glUniform1f(lightSpotCutOffLoc, glm::cos(glm::radians(12.5f)));

 你可以看到，我们为切光角设置一个角度，但是我们根据一个角度计算了余弦值，把这个余弦结果传给了片段着色器。这么做的原因是在片段着色器中，我们计算`LightDir`和`SpotDir`向量的点乘，而点乘返回一个余弦值，不是一个角度，所以我们不能直接把一个角度和余弦值对比。为了获得这个角度，我们必须计算点乘结果的反余弦，这个操作开销是很大的。所以为了节约一些性能，我们先计算给定切光角的余弦值，然后把结果传递给片段着色器。由于每个角度都被表示为余弦了，我们可以直接对比它们，而不用进行任何开销高昂的操作。

-现在剩下要做的是计算\(\theta\)值，用它和\(\phi\)值对比，以决定我们是否在或不在聚光灯的内部：
+现在剩下要做的是计算\(\theta\)值，用它和\(\phi\)值对比，以决定我们是否在或不在聚光的内部：

 ```c++
 float theta = dot(lightDir, normalize(-light.direction));
@@ -257,25 +253,25 @@ color = vec4(light.ambient*vec3(texture(material.diffuse,TexCoords)), 1.0f);

 !!! Important

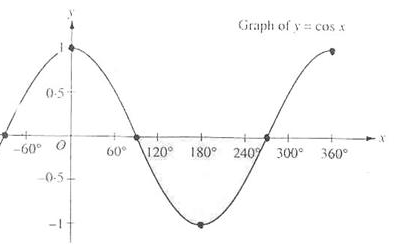
-    你可能奇怪为什么if条件中使用>符号而不是<符号。为了在聚光灯以内，`theta`不是应该比光的切光值更小吗？这没错，但是不要忘了，角度值是以余弦值来表示的，一个0度的角表示为1.0的余弦值，当一个角是90度的时候被表示为0.0的余弦值，你可以在这里看到：
+    你可能奇怪为什么if条件中使用>符号而不是<符号。为了在聚光以内，`theta`不是应该比光的切光值更小吗？这没错，但是不要忘了，角度值是以余弦值来表示的，一个0度的角表示为1.0的余弦值，当一个角是90度的时候被表示为0.0的余弦值，你可以在这里看到：

    ![](http://www.learnopengl.com/img/lighting/light_casters_cos.png)

-    现在你可以看到，余弦越是接近1.0，角度就越小。这就解释了为什么θ需要比切光值更大了。切光值当前被设置为12.5的余弦，它等于0.9978，所以θ的余弦值在0.9979和1.0之间，片段会在聚光灯内，被照亮。
+    现在你可以看到，余弦越是接近1.0，角度就越小。这就解释了为什么θ需要比切光值更大了。切光值当前被设置为12.5的余弦，它等于0.9978，所以θ的余弦值在0.9979和1.0之间，片段会在聚光内，被照亮。

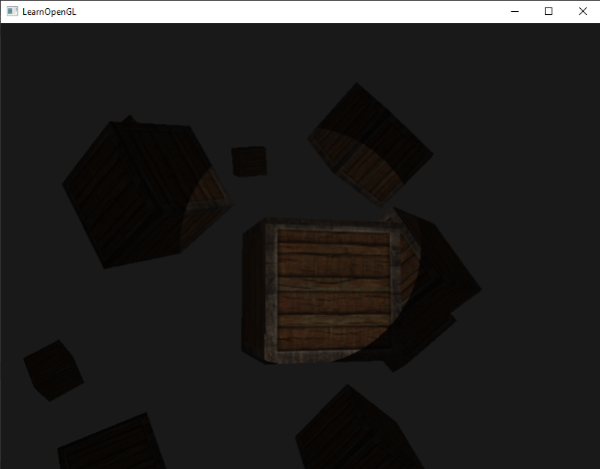
-运行应用，在聚光灯内的片段才会被照亮。这看起来像这样：
+运行应用，在聚光内的片段才会被照亮。这看起来像这样：

 ![](http://www.learnopengl.com/img/lighting/light_casters_spotlight_hard.png)

 你可以在这里获得[全部源码](http://learnopengl.com/code_viewer.php?code=lighting/light_casters_spotlight_hard)和[片段着色器的源码](http://learnopengl.com/code_viewer.php?code=lighting/light_casters_spotlight_hard&type=fragment)。

-它看起来仍然有点假，原因是聚光灯有了一个硬边。片段着色器一旦到达了聚光灯的圆锥边缘，它就立刻黑了下来，却没有任何平滑减弱的过度。一个真实的聚光灯的光会在它的边界处平滑减弱的。
+它看起来仍然有点假，原因是聚光有了一个硬边。片段着色器一旦到达了聚光的圆锥边缘，它就立刻黑了下来，却没有任何平滑减弱的过度。一个真实的聚光的光会在它的边界处平滑减弱的。

 ## 平滑/软化边缘

-为创建聚光灯的平滑边，我们希望去模拟的聚光灯有一个内圆锥和外圆锥。我们可以把内圆锥设置为前面部分定义的圆锥，我们希望外圆锥从内边到外边逐步的变暗。
+为创建聚光的平滑边，我们希望去模拟的聚光有一个内圆锥和外圆锥。我们可以把内圆锥设置为前面部分定义的圆锥，我们希望外圆锥从内边到外边逐步的变暗。

-为创建外圆锥，我们简单定义另一个余弦值，它代表聚光灯的方向向量和外圆锥的向量（等于它的半径）的角度。然后，如果片段在内圆锥和外圆锥之间，就会给它计算出一个0.0到1.0之间的亮度。如果片段在内圆锥以内这个亮度就等于1.0，如果在外面就是0.0。
+为创建外圆锥，我们简单定义另一个余弦值，它代表聚光的方向向量和外圆锥的向量（等于它的半径）的角度。然后，如果片段在内圆锥和外圆锥之间，就会给它计算出一个0.0到1.0之间的亮度。如果片段在内圆锥以内这个亮度就等于1.0，如果在外面就是0.0。

 我们可以使用下面的公式计算这样的值：

@@ -283,7 +279,7 @@ $$
 \begin{equation} I = \frac{\theta - \gamma}{\epsilon} \end{equation}
 $$

-这里\(\epsilon\)是内部（\(\phi\)）和外部圆锥（\(\gamma\)）（\epsilon =  \phi - \gamma）的差。结果\(I\)的值是聚光灯在当前片段的亮度。
+这里\(\epsilon\)是内部（\(\phi\)）和外部圆锥（\(\gamma\)）（\epsilon =  \phi - \gamma）的差。结果\(I\)的值是聚光在当前片段的亮度。

 很难用图画描述出这个公式是怎样工作的，所以我们尝试使用一个例子：

@@ -300,7 +296,7 @@ $$

 就像你看到的那样我们基本是根据θ在外余弦和内余弦之间插值。如果你仍然不明白怎么继续，不要担心。你可以简单的使用这个公式计算，当你更加老道和明白的时候再来看。

-由于我们现在有了一个亮度值，当在聚光灯外的时候是个负的，当在内部圆锥以内大于1。如果我们适当地把这个值固定，我们在片段着色器中就再不需要if-else了，我们可以简单地用计算出的亮度值乘以光的元素：
+由于我们现在有了一个亮度值，当在聚光外的时候是个负的，当在内部圆锥以内大于1。如果我们适当地把这个值固定，我们在片段着色器中就再不需要if-else了，我们可以简单地用计算出的亮度值乘以光的元素：

 ```c++
 float theta = dot(lightDir, normalize(-light.direction));
@@ -319,9 +315,9 @@ specular* = intensity;

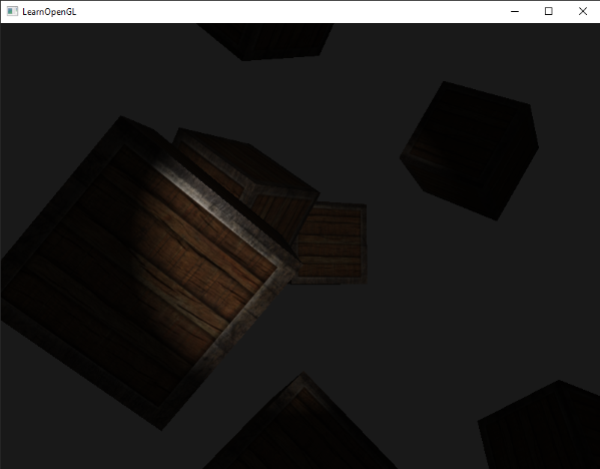
 ![](http://www.learnopengl.com/img/lighting/light_casters_spotlight.png)

-看起来好多了。仔细看看内部和外部切光角，尝试创建一个符合你求的聚光灯。可以在这里找到应用源码，以及片段的源代码。
+看起来好多了。仔细看看内部和外部切光角，尝试创建一个符合你求的聚光。可以在这里找到应用源码，以及片段的源代码。

-这样的一个手电筒/聚光灯类型的灯光非常适合恐怖游戏，结合定向和点光，环境会真的开始被照亮了。[下一个教程](http://learnopengl-cn.readthedocs.org/zh/latest/02%20Lighting/06%20Multiple%20lights/)，我们会结合所有我们目前讨论了的光和技巧。
+这样的一个手电筒/聚光类型的灯光非常适合恐怖游戏，结合定向和点光，环境会真的开始被照亮了。[下一个教程](http://learnopengl-cn.readthedocs.org/zh/latest/02%20Lighting/06%20Multiple%20lights/)，我们会结合所有我们目前讨论了的光和技巧。

 ## 练习

--- a/Lighting/06
+++ b/Lighting/06
@@ -1,4 +1,4 @@
-# 多光源(Multiple lights)
+# 多光源

 原文     | [Multiple lights](http://learnopengl.com/#!Lighting/Multiple-lights)
      ---|---
@@ -35,9 +35,9 @@ void main()

 即使对每一种光源的运算实现不同，但此算法的结构一般是与上述出入不大的。我们将定义几个用于计算各个光源的函数，并将这些函数的结算结果（返回颜色）添加到输出颜色向量中。例如，靠近被照射物体的光源计算结果将返回比远离背照射物体的光源更明亮的颜色。

-## 平行光（Directional light）
+## 平行光

-我们要在片段着色器中定义一个函数用来计算平行光在对应的照射点上的光照颜色，这个函数需要几个参数并返回一个计算平行光照结果的颜色。
+我们要在片段着色器中定义一个函数用来计算平行光(Directional light)在对应的照射点上的光照颜色，这个函数需要几个参数并返回一个计算平行光照结果的颜色。

 首先我们需要设置一系列用于表示平行光的变量，正如上一节中所讲过的，我们可以将这些变量定义在一个叫做**DirLight**的结构体中，并定义一个这个结构体类型的uniform变量。

@@ -83,9 +83,9 @@ vec3 CalcDirLight(DirLight light, vec3 normal, vec3 viewDir)

 我们从之前的教程中复制了代码，并用两个向量来作为函数参数来计算出平行光的光照颜色向量，该结果是一个由该平行光的环境反射、漫反射和镜面反射的各个分量组成的一个向量。

-## 定点光（Point light）
+## 点光源

-和计算平行光一样，我们同样需要定义一个函数用于计算定点光照。同样的，我们定义一个包含定点光源所需属性的结构体：
+和计算平行光一样，我们同样需要定义一个函数用于计算点光源(Point Light)。同样的，我们定义一个包含点光源所需属性的结构体：

 ```c++
 struct PointLight {
@@ -103,7 +103,7 @@ struct PointLight {
 uniform PointLight pointLights[NR_POINT_LIGHTS];
 ```

-如你所见，我们在GLSL中使用预处理器指令来定义定点光源的数目。之后我们使用这个`NR_POINT_LIGHTS`常量来创建一个`PointLight`结构体的数组。和C语言一样，GLSL也是用一对中括号来创建数组的。现在我们有了4个`PointLight`结构体对象了。
+如你所见，我们在GLSL中使用预处理器指令来定义点光源的数目。之后我们使用这个`NR_POINT_LIGHTS`常量来创建一个`PointLight`结构体的数组。和C语言一样，GLSL也是用一对中括号来创建数组的。现在我们有了4个`PointLight`结构体对象了。

 !!! Important

@@ -144,7 +144,7 @@ vec3 CalcPointLight(PointLight light, vec3 normal, vec3 fragPos, vec3 viewDir)

 ## 把它们放到一起

-我们现在定义了用于计算平行光和定点光的函数，现在我们把这些代码放到一起，写入文开始的一般结构中：
+我们现在定义了用于计算平行光和点光源的函数，现在我们把这些代码放到一起，写入文开始的一般结构中：

 ```c++
 void main()
--- a/Lighting/07
+++ b/Lighting/07
@@ -18,8 +18,8 @@

 在[下一个教程](http://learnopengl-cn.readthedocs.org/zh/latest/03%20Model%20Loading/01%20Assimp/)当中，我们将加入更高级的形状到我们的场景中，这些形状将会在我们之前讨论过的光照模型中非常好看。

-词汇表
--------
+## 词汇表
+

 - **颜色向量(Color Vector)**：一个通过红绿蓝(RGB)分量的组合描绘大部分真实颜色的向量. 一个对象的颜色实际上是该对象不能吸收的反射颜色分量。
 - **冯氏光照模型(Phong Lighting Model)**：一个通过计算环境，漫反射，和镜面反射分量的值来估计真实光照的模型。
--- a/Loading/01
+++ b/Loading/01
@@ -1,4 +1,4 @@
-# Assimp开源模型导入库
+# Assimp

 原文     | [Assimp](http://learnopengl.com/#!Model-Loading/Assimp)
      ---|---
@@ -33,9 +33,9 @@

 !!! Important

-    **Mesh(网格,或被译为“模型点云”)**
+    **网格(Mesh)**
    
-    用建模工具构建物体时，美工通常不会直接使用单个形状来构建一个完整的模型。一般来说，一个模型会由几个子模型/形状组合拼接而成。而模型中的那些子模型/形状就是我们所说的一个Mesh。例如一个人形模型，美工通常会把头、四肢、衣服、武器这些组件都分别构建出来，然后在把所有的组件拼合在一起，形成最终的完整模型。一个Mesh（包含顶点、索引和材质属性）是我们在OpenGL中绘制物体的最小单位。一个模型通常有多个Mesh组成。
+    用建模工具构建物体时，美工通常不会直接使用单个形状来构建一个完整的模型。一般来说，一个模型会由几个子模型/形状组合拼接而成。而模型中的那些子模型/形状就是我们所说的一个网格。例如一个人形模型，美工通常会把头、四肢、衣服、武器这些组件都分别构建出来，然后在把所有的组件拼合在一起，形成最终的完整模型。一个网格（包含顶点、索引和材质属性）是我们在OpenGL中绘制物体的最小单位。一个模型通常有多个网格组成。

 下一节教程中，我们将用上述描述的数据结构来创建我们自己的Model类和Mesh类，用于加载和保存那些导入的模型。如果我们想要绘制一个模型，我们不会去渲染整个模型，而是去渲染这个模型所包含的所有独立的Mesh。不管怎样，我们开始导入模型之前，我们需要先把Assimp导入到我们的工程中。

@@ -67,4 +67,4 @@ Required library DirectX not found! Install the library (including dev packages)

    如果你想要让Assimp使用多线程支持来提高性能，你可以使用<b>Boost</b>库来编译 Assimp。在[Boost安装页面](http://assimp.sourceforge.net/lib_html/install.html)，你能找到关于Boost的完整安装介绍。

-现在，你应该已经能够编译Assimp库，并链接Assimp到你的工程里去了。下一节内容：[导入完美的3D物件！](http://learnopengl-cn.readthedocs.org/zh/latest/03%20Model%20Loading/02%20Mesh/)
+现在，你应该已经能够编译Assimp库，并链接Assimp到你的工程里去了。下一步：[导入完美的3D物件！](http://learnopengl-cn.readthedocs.org/zh/latest/03%20Model%20Loading/02%20Mesh/)
--- a/Loading/02
+++ b/Loading/02
@@ -1,4 +1,4 @@
-# 网格(Mesh)
+# 网格

 原文     | [Mesh](http://learnopengl.com/#!Model-Loading/Mesh)
      ---|---
--- a/Loading/03
+++ b/Loading/03
@@ -1,4 +1,4 @@
-# 模型(Model)
+# 模型

 原文     | [Model](http://learnopengl.com/#!Model-Loading/Model)
      ---|---
@@ -6,7 +6,7 @@
 翻译     | [Django](http://bullteacher.com/)
 校对     | [Geequlim](http://geequlim.com)

-现在是时候着手启用Assimp，并开始创建实际的加载和转换代码了。本教程的目标是创建另一个类，这个类可以表达模型的全部。更确切的说，一个模型包含多个网格(Mesh)，一个网格可能带有多个对象。一个别墅，包含一个木制阳台，一个尖顶或许也有一个游泳池，它仍然被加载为一个单一模型。我们通过Assimp加载模型，把它们转变为多个网格（Mesh）对象，这些对象是是先前教程里创建的。
+现在是时候着手启用Assimp，并开始创建实际的加载和转换代码了。本教程的目标是创建另一个类，这个类可以表达模型(Model)的全部。更确切的说，一个模型包含多个网格(Mesh)，一个网格可能带有多个对象。一个别墅，包含一个木制阳台，一个尖顶或许也有一个游泳池，它仍然被加载为一个单一模型。我们通过Assimp加载模型，把它们转变为多个`Mesh`对象，这些对象是是上一节教程里创建的。

 闲话少说，我把Model类的结构呈现给你：

@@ -46,7 +46,7 @@ void Draw(Shader shader)
 }
 ```

-## 把一个3D模型导入到OpenGL
+## 导入3D模型到OpenGL

 为了导入一个模型，并把它转换为我们自己的数据结构，第一件需要做的事是包含合适的Assimp头文件，这样编译器就不会对我们抱怨了。

@@ -133,7 +133,7 @@ void processNode(aiNode* node, const aiScene* scene)

 下一步是用上个教程创建的`Mesh`类开始真正处理Assimp的数据。

-## 从Assimp到网格
+### 从Assimp到网格

 把一个`aiMesh`对象转换为一个我们自己定义的网格对象并不难。我们所要做的全部是获取每个网格相关的属性并把这些属性储存到我们自己的对象。通常`processMesh`函数的结构会是这样：

@@ -210,7 +210,7 @@ else

 `Vertex`结构体现在完全被所需的顶点属性填充了，我们能把它添加到`vertices`向量的尾部。要对每个网格的顶点做相同的处理。

-## 顶点
+### 顶点

 Assimp的接口定义每个网格有一个以面（faces）为单位的数组，每个面代表一个单独的图元，在我们的例子中（由于`aiProcess_Triangulate`选项）总是三角形，一个面包含索引，这些索引定义我们需要绘制的顶点以在那样的顺序提供给每个图元，所以如果我们遍历所有面，把所有面的索引储存到`indices`向量，我们需要这么做：

@@ -228,7 +228,7 @@ for(GLuint i = 0; i < mesh->mNumFaces; i++)

 

-## 材质
+### 材质

 如同节点，一个网格只有一个指向材质对象的索引，获取网格实际的材质，我们需要索引场景的`mMaterials`数组。网格的材质索引被设置在`mMaterialIndex`属性中，通过这个属性我们同样能够检验一个网格是否包含一个材质：

@@ -278,7 +278,7 @@ vector<Texture> loadMaterialTextures(aiMaterial* mat, aiTextureType type, string

 这就是使用Assimp来导入一个模型的全部了。你可以在这里找到[Model类的代码](http://learnopengl.com/code_viewer.php?code=model_loading/model_unoptimized)。

-## 重大优化
+# 重大优化

 我们现在还没做完。因为我们还想做一个重大的优化（但是不是必须的）。大多数场景重用若干纹理，把它们应用到网格；还是思考那个别墅，它有个花岗岩的纹理作为墙面。这个纹理也可能应用到地板、天花板，楼梯，或者一张桌子、一个附近的小物件。加载纹理需要不少操作，当前的实现中一个新的纹理被加载和生成，来为每个网格使用，即使同样的纹理之前已经被加载了好几次。这会很快转变为你的模型加载实现的瓶颈。

@@ -343,7 +343,7 @@ vector<Texture> loadMaterialTextures(aiMaterial* mat, aiTextureType type, string

 你可以从这里获得优化的[Model类的完整源代码](http://learnopengl.com/code_viewer.php?code=model&type=header)。

-## 和箱子模型告别!
+# 和箱子模型告别

 现在给我们导入一个天才艺术家创建的模型看看效果，不是我这个天才做的（你不得不承认，这个箱子也许是你见过的最漂亮的立体图形）。因为我不想过于自夸，所以我会时不时的给其他艺术家进入这个行列的机会，这次我们会加载Crytek原版的孤岛危机游戏中的纳米铠甲。这个模型被输出为obj和mtl文件，mtl包含模型的diffuse和specular以及法线贴图（后面会讲）。你可以下载这个模型，注意，所有的纹理和模型文件都应该放在同一个目录，以便载入纹理。

--- a/testing.md
+++ b/testing.md
@@ -1,4 +1,4 @@
-# 深度测试(Depth testing)
+# 深度测试

 原文     | [Depth testing](http://learnopengl.com/#!Advanced-OpenGL/Depth-testing)
      ---|---
@@ -6,9 +6,9 @@
 翻译     | [Django](http://bullteacher.com/)
 校对     | [Geequlim](http://geequlim.com)

-在[坐标系的教程](http://learnopengl-cn.readthedocs.org/zh/latest/01%20Getting%20started/08%20Coordinate%20Systems/)中我们呈现了一个3D容器,使用**深度缓冲**,以防止被其他面遮挡的面渲染到前面。在本教程中我们将细致地讨论被深度缓冲区(depth-buffer或z-buffer)所存储的**深度值**以及它是如何确定一个片段是否被其他片段遮挡。
+在[坐标系的教程](http://learnopengl-cn.readthedocs.org/zh/latest/01%20Getting%20started/08%20Coordinate%20Systems/)中我们呈现了一个3D容器,使用**深度缓冲(Depth Buffer)**,以防止被其他面遮挡的面渲染到前面。在本教程中我们将细致地讨论被深度缓冲(或z-buffer)所存储的**深度值**以及它是如何确定一个片段是否被其他片段遮挡。

-**深度缓冲**就像**颜色缓冲**(存储所有的片段颜色:视觉输出)那样存储每个片段的信息，(通常) 和颜色缓冲区有相同的宽度和高度。深度缓冲由窗口系统自动创建并将其深度值存储为 16、 24 或 32 位浮点数。在大多数系统中深度缓冲区为24位。
+**深度缓冲**就像**颜色缓冲(Color Buffer)**(存储所有的片段颜色:视觉输出)那样存储每个片段的信息，(通常) 和颜色缓冲区有相同的宽度和高度。深度缓冲由窗口系统自动创建并将其深度值存储为 16、 24 或 32 位浮点数。在大多数系统中深度缓冲区为24位。

 当深度测试启用的时候， OpenGL 测试深度缓冲区内的深度值。OpenGL 执行深度测试的时候，如果此测试通过，深度缓冲内的值将被设为新的深度值。如果深度测试失败，则丢弃该片段。

@@ -111,7 +111,7 @@ $$

 接下来我们看看这个非线性的深度值。

-### 深度缓冲区的可视化
+## 深度缓冲区的可视化

 我们知道在片段渲染器的内置`gl_FragCoord`向量的 z 值包含那个片段的深度值。如果我们要吧深度值作为颜色输出，那么我们可以在场景中显示的所有片段的深度值。我们可以返回基于片段的深度值的颜色向量:

@@ -178,7 +178,7 @@ void main()

 ## 深度冲突

-两个平面或三角形如此紧密相互平行深度缓冲区不具有足够的精度以至于无法得到哪一个靠前。结果是，这两个形状不断似乎切换顺序导致怪异出问题。这被称为深度冲突，因为它看上去像形状争夺顶靠前的位置。
+两个平面或三角形如此紧密相互平行深度缓冲区不具有足够的精度以至于无法得到哪一个靠前。结果是，这两个形状不断似乎切换顺序导致怪异出问题。这被称为**深度冲突(Z-fighting)**，因为它看上去像形状争夺顶靠前的位置。

 我们到目前为止一直在使用的场景中有几个地方深度冲突很显眼。容器被置于确切高度地板被安置这意味着容器的底平面与地板平面共面。两个平面的深度值是相同的，因此深度测试也没有办法找出哪个是正确。

--- a/testing.md
+++ b/testing.md
@@ -6,9 +6,9 @@
 翻译     | [Django](http://bullteacher.com/)
 校对     | [Geequlim](http://geequlim.com)

-当片段着色器处理完片段之后，**模板测试(stencil test)** 就开始执行了，和深度测试一样，它能丢弃一些片段。仍然保留下来的片段进入深度测试阶段，深度测试可能丢弃更多。模板测试基于另一个缓冲，这个缓冲叫做**模板缓冲(stencil buffer)**，我们被允许在渲染时更新它来获取有意思的效果。
+当片段着色器处理完片段之后，**模板测试(Stencil Test)** 就开始执行了，和深度测试一样，它能丢弃一些片段。仍然保留下来的片段进入深度测试阶段，深度测试可能丢弃更多。模板测试基于另一个缓冲，这个缓冲叫做**模板缓冲(Stencil Buffer)**，我们被允许在渲染时更新它来获取有意思的效果。

-模板缓冲中的模板值（stencil value）通常是8位的，因此每个片段（像素）共有256种不同的模板值（译注：8位就是1字节大小，因此和char的容量一样是256个不同值）。这样我们就能将这些模板值设置为我们链接的，然后在模板测试时根据这个模板值，我们就可以决定丢弃或保留它了。
+模板缓冲中的**模板值(Stencil Value)**通常是8位的，因此每个片段/像素共有256种不同的模板值（译注：8位就是1字节大小，因此和char的容量一样是256个不同值）。这样我们就能将这些模板值设置为我们链接的，然后在模板测试时根据这个模板值，我们就可以决定丢弃或保留它了。

 !!! Important

@@ -31,16 +31,16 @@

 你可以开启`GL_STENCIL_TEST`来开启模板测试。接着所有渲染函数调用都会以这样或那样的方式影响到模板缓冲。

-```c
+```c++
 glEnable(GL_STENCIL_TEST);
 ```
 要注意的是，像颜色和深度缓冲一样，在每次循环，你也得清空模板缓冲。

-```c
+```c++
 glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT | GL_STENCIL_BUFFER_BIT);
 ```

-同时，和深度测试的`glDepthMask`函数一样，模板缓冲也有一个相似函数。`glStencilMask`允许我们给模板值设置一个**位遮罩（bitmask）**，它与模板值进行按位与（and）运算决定缓冲是否可写。默认设置的位遮罩都是1，这样就不会影响输出，但是如果我们设置为0x00，所有写入深度缓冲最后都是0。这和深度缓冲的`glDepthMask(GL_FALSE)`很类似：
+同时，和深度测试的`glDepthMask`函数一样，模板缓冲也有一个相似函数。`glStencilMask`允许我们给模板值设置一个**位遮罩(Bitmask)**，它与模板值进行按位与(AND)运算决定缓冲是否可写。默认设置的位遮罩都是1，这样就不会影响输出，但是如果我们设置为0x00，所有写入深度缓冲最后都是0。这和深度缓冲的`glDepthMask(GL_FALSE)`很类似：

 ```c++

@@ -55,7 +55,7 @@ glStencilMask(0x00);

 大多数情况你的模板遮罩（stencil mask）写为0x00或0xFF就行，但是最好知道有一个选项可以自定义位遮罩。

-## 模板函数（stencil functions）
+## 模板函数

 和深度测试一样，我们也有几个不同控制权，决定何时模板测试通过或失败以及它怎样影响模板缓冲。一共有两种函数可供我们使用去配置模板测试：`glStencilFunc`和`glStencilOp`。

@@ -98,9 +98,9 @@ GL_INVERT   | Bitwise inverts the current stencil buffer value.

 使用`glStencilFunc`和`glStencilOp`，我们就可以指定在什么时候以及我们打算怎么样去更新模板缓冲了，我们也可以指定何时让测试通过或不通过。什么时候片段会被抛弃。

-## 物体轮廓
+# 物体轮廓

-看了前面的部分你未必能理解模板测试是如何工作的，所以我们会展示一个用模板测试实现的一个特别的和有用的功能，叫做物体轮廓（object outlining）。
+看了前面的部分你未必能理解模板测试是如何工作的，所以我们会展示一个用模板测试实现的一个特别的和有用的功能，叫做**物体轮廓(Object Outlining)**。

 ![](http://learnopengl.com/img/advanced/stencil_object_outlining.png)

--- a/Blending.md
+++ b/Blending.md
@@ -1,4 +1,4 @@
-# 混合（Blending）
+# 混合

 原文     | [Blending](http://learnopengl.com/#!Advanced-OpenGL/Blending)
      ---|---
@@ -7,7 +7,7 @@
 校对     | [Geequlim](http://geequlim.com)


-在OpenGL中，物体透明技术通常被叫做混合(Blending)。透明是物体（或物体的一部分）非纯色而是混合色，这种颜色来自于不同浓度的自身颜色和它后面的物体颜色。一个有色玻璃窗就是一种透明物体，玻璃有自身的颜色，但是最终的颜色包含了所有玻璃后面的颜色。这也正是混合这名称的出处，因为我们将多种（来自于不同物体）颜色混合为一个颜色，透明使得我们可以看穿物体。
+在OpenGL中，物体透明技术通常被叫做**混合(Blending)**。透明是物体（或物体的一部分）非纯色而是混合色，这种颜色来自于不同浓度的自身颜色和它后面的物体颜色。一个有色玻璃窗就是一种透明物体，玻璃有自身的颜色，但是最终的颜色包含了所有玻璃后面的颜色。这也正是混合这名称的出处，因为我们将多种（来自于不同物体）颜色混合为一个颜色，透明使得我们可以看穿物体。

 ![](http://learnopengl.com/img/advanced/blending_transparency.png)

@@ -120,7 +120,7 @@ void main()

 ## 混合

-上述丢弃片段的方式，不能使我们获得渲染半透明图像，我们要么渲染出像素，要么完全地丢弃它。为了渲染出不同的透明度级别，我们需要开启**混合**(Blending)。像大多数OpenGL的功能一样，我们可以开启`GL_BLEND`来启用混合功能：
+上述丢弃片段的方式，不能使我们获得渲染半透明图像，我们要么渲染出像素，要么完全地丢弃它。为了渲染出不同的透明度级别，我们需要开启**混合**(Blending)。像大多数OpenGL的功能一样，我们可以开启`GL_BLEND`来启用**混合(Blending)**功能：

 ```c++
 glEnable(GL_BLEND);
@@ -203,7 +203,7 @@ OpenGL给了我们更多的自由，我们可以改变方程源和目标部分

 通常我们可以简单地省略`glBlendEquation`因为GL_FUNC_ADD在大多数时候就是我们想要的，但是如果你如果你真想尝试努力打破主流常规，其他的方程或许符合你的要求。

-### 渲染半透明纹理
+## 渲染半透明纹理

 现在我们知道OpenGL如何处理混合，是时候把我们的知识运用起来了，我们来添加几个半透明窗子。我们会使用本教程开始时用的那个场景，但是不再渲染草纹理，取而代之的是来自教程开始处半透明窗子纹理。

@@ -244,7 +244,7 @@ void main()

    对于全透明物体，比如草叶，我们选择简单的丢弃透明像素而不是混合，这样就减少了令我们头疼的问题（没有深度测试问题）。

-### 别打乱顺序
+## 别打乱顺序

 要让混合在多物体上有效，我们必须先绘制最远的物体，最后绘制最近的物体。普通的无混合物体仍然可以使用深度缓冲正常绘制，所以不必给它们排序。我们一定要保证它们在透明物体前绘制好。当无透明度物体和透明物体一起绘制的时候，通常要遵循以下原则：

--- a/culling.md
+++ b/culling.md
@@ -1,4 +1,4 @@
-# 面剔除（Face culling）
+# 面剔除

 原文     | [Face culling](http://learnopengl.com/#!Advanced-OpenGL/Face-culling)
      ---|---
@@ -18,9 +18,9 @@
 这正是**面剔除**(Face culling)所要做的。OpenGL允许检查所有正面朝向（Front facing）观察者的面，并渲染它们，而丢弃所有背面朝向（Back facing）的面，这样就节约了我们很多片段着色器的命令（它们很昂贵！）。我们必须告诉OpenGL我们使用的哪个面是正面，哪个面是反面。OpenGL使用一种聪明的手段解决这个问题——分析顶点数据的连接顺序（Winding order）。


-## 顶点连接顺序（Winding order）
+## 顶点连接顺序

-当我们定义一系列的三角顶点时，我们会把它们定义为一个特定的连接顺序，它们可能是顺时针的或逆时针的。每个三角形由3个顶点组成，我们从三角形的中间去看，从而把这三个顶点指定一个连接顺序。
+当我们定义一系列的三角顶点时，我们会把它们定义为一个特定的连接顺序(Winding Order)，它们可能是**顺时针**的或**逆时针**的。每个三角形由3个顶点组成，我们从三角形的中间去看，从而把这三个顶点指定一个连接顺序。

 ![](http://learnopengl.com/img/advanced/faceculling_windingorder.png)

--- a/Framebuffers.md
+++ b/Framebuffers.md
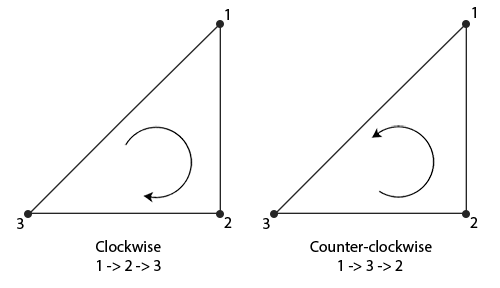
@@ -8,8 +8,6 @@

 到目前为止，我们使用了几种不同类型的屏幕缓冲：用于写入颜色值的颜色缓冲，用于写入深度信息的深度缓冲，以及允许我们基于一些条件丢弃指定片段的模板缓冲。把这几种缓冲结合起来叫做帧缓冲(Framebuffer)，它被储存于内存中。OpenGL给了我们自己定义帧缓冲的自由，我们可以选择性的定义自己的颜色缓冲、深度和模板缓冲。

-[译注1]: http://learnopengl-cn.readthedocs.org "framebuffer，在维基百科有framebuffer的详细介绍能够帮助你更好的理解"
-
 我们目前所做的渲染操作都是是在默认的帧缓冲之上进行的。当你创建了你的窗口的时候默认帧缓冲就被创建和配置好了（GLFW为我们做了这件事）。通过创建我们自己的帧缓冲我们能够获得一种额外的渲染方式。

 你也许不能立刻理解应用程序的帧缓冲的含义，通过帧缓冲可以将你的场景渲染到一个不同的帧缓冲中，可以使我们能够在场景中创建镜子这样的效果，或者做出一些炫酷的特效。首先我们会讨论它们是如何工作的，然后我们将利用帧缓冲来实现一些炫酷的效果。
@@ -40,7 +38,7 @@ glBindFramebuffer(GL_FRAMEBUFFER, fbo);

 如果你不知道什么是样本也不用担心，我们会在后面的教程中讲到。

-从上面的需求中你可以看到，我们需要为帧缓冲创建一些附件，还需要把这些附件附加到帧缓冲上。当我们做完所有上面提到的条件的时候我们就可以用  `glCheckFramebufferStatus` 带上 `GL_FRAMEBUFFER` 这个参数来检查是否真的成功做到了。然后检查当前绑定的帧缓冲，返回了这些规范中的哪个值。如果返回的是 `GL_FRAMEBUFFER_COMPLETE`就对了：
+从上面的需求中你可以看到，我们需要为帧缓冲创建一些附件(Attachment)，还需要把这些附件附加到帧缓冲上。当我们做完所有上面提到的条件的时候我们就可以用  `glCheckFramebufferStatus` 带上 `GL_FRAMEBUFFER` 这个参数来检查是否真的成功做到了。然后检查当前绑定的帧缓冲，返回了这些规范中的哪个值。如果返回的是 `GL_FRAMEBUFFER_COMPLETE`就对了：

 ```c++
 if(glCheckFramebufferStatus(GL_FRAMEBUFFER) == GL_FRAMEBUFFER_COMPLETE)
@@ -61,7 +59,7 @@ glDeleteFramebuffers(1, &fbo);

 现在在执行完成检测前，我们需要把一个或更多的附件附加到帧缓冲上。一个附件就是一个内存地址，这个内存地址里面包含一个为帧缓冲准备的缓冲，它可以是个图像。当创建一个附件的时候我们有两种方式可以采用：纹理或渲染缓冲（renderbuffer）对象。

-## 纹理附件
+### 纹理附件

 当把一个纹理附加到帧缓冲上的时候，所有渲染命令会写入到纹理上，就像它是一个普通的颜色/深度或者模板缓冲一样。使用纹理的好处是，所有渲染操作的结果都会被储存为一个纹理图像，这样我们就可以简单的在着色器中使用了。

@@ -106,9 +104,9 @@ glTexImage2D( GL_TEXTURE_2D, 0, GL_DEPTH24_STENCIL8, 800, 600, 0, GL_DEPTH_STENC
 glFramebufferTexture2D(GL_FRAMEBUFFER, GL_DEPTH_STENCIL_ATTACHMENT, GL_TEXTURE_2D, texture, 0);
 ```

-### 渲染缓冲对象附件（Renderbuffer object attachments）
+### 缓冲对象附件

-在介绍了帧缓冲的可行附件类型——纹理后，OpenGL引进了渲染缓冲对象（Renderbuffer objects），所以在过去那些美好时光里纹理是附件的唯一可用的类型。和纹理图像一样，渲染缓冲对象也是一个缓冲，它可以是一堆字节、整数、像素或者其他东西。渲染缓冲对象的一大优点是，它以OpenGL原生渲染格式储存它的数据，因此在离屏渲染到帧缓冲的时候，这些数据就相当于被优化过的了。
+在介绍了帧缓冲的可行附件类型——纹理后，OpenGL引进了渲染缓冲对象(Renderbuffer objects)，所以在过去那些美好时光里纹理是附件的唯一可用的类型。和纹理图像一样，渲染缓冲对象也是一个缓冲，它可以是一堆字节、整数、像素或者其他东西。渲染缓冲对象的一大优点是，它以OpenGL原生渲染格式储存它的数据，因此在离屏渲染到帧缓冲的时候，这些数据就相当于被优化过的了。

 渲染缓冲对象将所有渲染数据直接储存到它们的缓冲里，而不会进行针对特定纹理格式的任何转换，这样它们就成了一种快速可写的存储介质了。然而，渲染缓冲对象通常是只写的，不能修改它们（就像获取纹理，不能写入纹理一样）。可以用`glReadPixels`函数去读取，函数返回一个当前绑定的帧缓冲的特定像素区域，而不是直接返回附件本身。

@@ -280,13 +278,13 @@ glBindVertexArray(0);
 然而这有什么好处呢？好处就是我们现在可以自由的获取已经渲染场景中的任何像素，然后把它当作一个纹理图像了，我们可以在片段着色器中创建一些有意思的效果。所有这些有意思的效果统称为后处理特效。


-### 后处理
+# 后期处理

-现在，整个场景渲染到了一个单独的纹理上，我们可以创建一些有趣的效果，只要简单操纵纹理数据就能做到。这部分，我们会向你展示一些流行的后处理特效，以及怎样添加一些创造性去创建出你自己的特效。
+现在，整个场景渲染到了一个单独的纹理上，我们可以创建一些有趣的效果，只要简单操纵纹理数据就能做到。这部分，我们会向你展示一些流行的后期处理(Post-processing)特效，以及怎样添加一些创造性去创建出你自己的特效。

 ### 反相

-我们已经取得了渲染输出的每个颜色，所以在片段着色器里返回这些颜色的反色并不难。我们得到屏幕纹理的颜色，然后用1.0减去它：
+我们已经取得了渲染输出的每个颜色，所以在片段着色器里返回这些颜色的反色(Inversion)并不难。我们得到屏幕纹理的颜色，然后用1.0减去它：

 ```c++
 void main()
@@ -326,7 +324,7 @@ void main()

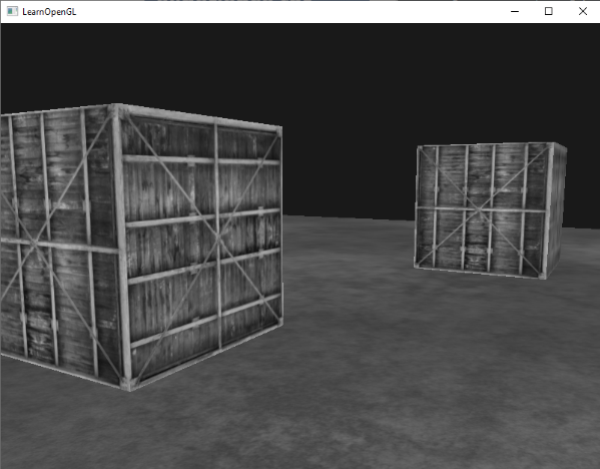
 ![](http://learnopengl.com/img/advanced/framebuffers_grayscale.png)

-### Kernel effects
+## Kernel effects

 在单独纹理图像上进行后处理的另一个好处是我们可以从纹理的其他部分进行采样。比如我们可以从当前纹理值的周围采样多个纹理值。创造性地把它们结合起来就能创造出有趣的效果了。

@@ -388,9 +386,9 @@ void main()

 这里创建的有趣的效果就好像你的玩家吞了某种麻醉剂产生的幻觉一样。

-### Blur
+### 模糊

-创建模糊效果的kernel定义如下：
+创建模糊(Blur)效果的kernel定义如下：

 $$
 \(\begin{bmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{bmatrix} / 16\)
@@ -416,7 +414,7 @@ float kernel[9] = float[](

 ### 边检测

-下面的边检测kernel与锐化kernel类似:
+下面的边检测(Edge-detection)kernel与锐化kernel类似:

 $$
 \begin{bmatrix} 1 & 1 & 1 \\ 1 & -8 & 1 \\ 1 & 1 & 1 \end{bmatrix}
--- a/Cubemaps.md
+++ b/Cubemaps.md
@@ -1,4 +1,4 @@
-# 立方体贴图(Cubemap)
+# 立方体贴图

 原文     | [Cubemaps](http://learnopengl.com/#!Advanced-OpenGL/Cubemaps)
      ---|---
@@ -6,11 +6,11 @@
 翻译     | [Django](http://bullteacher.com/)
 校对     | [Geequlim](http://geequlim.com)

-我们之前一直使用的是2D纹理，还有更多的纹理类型我们没有探索过，本教程中我们讨论的纹理类型是将多个纹理组合起来映射到一个单一纹理，它就是cubemap。
+我们之前一直使用的是2D纹理，还有更多的纹理类型我们没有探索过，本教程中我们讨论的纹理类型是将多个纹理组合起来映射到一个单一纹理，它就是**立方体贴图(Cube Map)**。

-基本上说cubemap它包含6个2D纹理，这每个2D纹理是一个立方体（cube）的一个面，也就是说它是一个有贴图的立方体。你可能会奇怪这样的立方体有什么用？为什么费事地把6个独立纹理结合为一个单独的纹理，只使用6个各自独立的不行吗？这是因为cubemap有自己特有的属性，可以使用方向向量对它们索引和采样。想象一下，我们有一个1×1×1的单位立方体，有个以原点为起点的方向向量在它的中心。
+基本上说立方体贴图它包含6个2D纹理，这每个2D纹理是一个立方体（cube）的一个面，也就是说它是一个有贴图的立方体。你可能会奇怪这样的立方体有什么用？为什么费事地把6个独立纹理结合为一个单独的纹理，只使用6个各自独立的不行吗？这是因为立方体贴图有自己特有的属性，可以使用方向向量对它们索引和采样。想象一下，我们有一个1×1×1的单位立方体，有个以原点为起点的方向向量在它的中心。

-从cubemap上使用橘黄色向量采样一个纹理值看起来和下图有点像：
+从立方体贴图上使用橘黄色向量采样一个纹理值看起来和下图有点像：

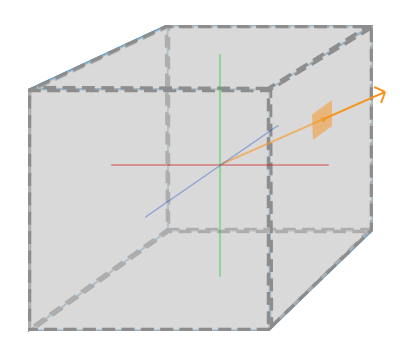
 ![](http://learnopengl.com/img/advanced/cubemaps_sampling.png)

@@ -19,11 +19,11 @@
        方向向量的大小无关紧要。一旦提供了方向，OpenGL就会获取方向向量触碰到立方体表面上的相应的纹理像素（texel），这样就返回了正确的纹理采样值。


-方向向量触碰到立方体表面的一点也就是cubemap的纹理位置，这意味着只要立方体的中心位于原点上，我们就可以使用立方体的位置向量来对cubemap进行采样。然后我们就可以获取所有顶点的纹理坐标，就和立方体上的顶点位置一样。所获得的结果是一个纹理坐标，通过这个纹理坐标就能获取到cubemap上正确的纹理。
+方向向量触碰到立方体表面的一点也就是立方体贴图的纹理位置，这意味着只要立方体的中心位于原点上，我们就可以使用立方体的位置向量来对立方体贴图进行采样。然后我们就可以获取所有顶点的纹理坐标，就和立方体上的顶点位置一样。所获得的结果是一个纹理坐标，通过这个纹理坐标就能获取到立方体贴图上正确的纹理。

-### 创建一个Cubemap
+## 创建一个立方体贴图

-Cubemap和其他纹理一样，所以要创建一个cubemap，在进行任何纹理操作之前，需要生成一个纹理，激活相应纹理单元然后绑定到合适的纹理目标上。这次要绑定到 `GL_TEXTURE_CUBE_MAP`纹理类型：
+立方体贴图和其他纹理一样，所以要创建一个立方体贴图，在进行任何纹理操作之前，需要生成一个纹理，激活相应纹理单元然后绑定到合适的纹理目标上。这次要绑定到 `GL_TEXTURE_CUBE_MAP`纹理类型：

 ```c++
 GLuint textureID;
@@ -31,9 +31,9 @@ glGenTextures(1, &textureID);
 glBindTexture(GL_TEXTURE_CUBE_MAP, textureID);
 ```

-由于cubemap包含6个纹理，立方体的每个面一个纹理，我们必须调用`glTexImage2D`函数6次，函数的参数和前面教程讲的相似。然而这次我们必须把纹理目标（target）参数设置为cubemap特定的面，这是告诉OpenGL我们创建的纹理是对应立方体哪个面的。因此我们便需要为cubemap的每个面调用一次 `glTexImage2D`。
+由于立方体贴图包含6个纹理，立方体的每个面一个纹理，我们必须调用`glTexImage2D`函数6次，函数的参数和前面教程讲的相似。然而这次我们必须把纹理目标（target）参数设置为立方体贴图特定的面，这是告诉OpenGL我们创建的纹理是对应立方体哪个面的。因此我们便需要为立方体贴图的每个面调用一次 `glTexImage2D`。

-由于cubemap有6个面，OpenGL就提供了6个不同的纹理目标，来应对cubemap的各个面。
+由于立方体贴图有6个面，OpenGL就提供了6个不同的纹理目标，来应对立方体贴图的各个面。

 纹理目标（Texture target）	   | 方位
                            ---|---
@@ -59,9 +59,9 @@ for(GLuint i = 0; i < textures_faces.size(); i++)
 }
 ```

-这儿我们有个vector叫`textures_faces`，它包含cubemap所各个纹理的文件路径，并且以上表所列的顺序排列。它将为每个当前绑定的cubemp的每个面生成一个纹理。
+这儿我们有个vector叫`textures_faces`，它包含立方体贴图所各个纹理的文件路径，并且以上表所列的顺序排列。它将为每个当前绑定的cubemp的每个面生成一个纹理。

-由于cubemap和其他纹理没什么不同，我们也要定义它的环绕方式和过滤方式：
+由于立方体贴图和其他纹理没什么不同，我们也要定义它的环绕方式和过滤方式：

 ```c++
 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
@@ -73,14 +73,14 @@ glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);

 别被 `GL_TEXTURE_WRAP_R`吓到，它只是简单的设置了纹理的R坐标，R坐标对应于纹理的第三个维度（就像位置的z一样）。我们把放置方式设置为 `GL_CLAMP_TO_EDGE` ，由于纹理坐标在两个面之间，所以可能并不能触及哪个面（由于硬件限制），因此使用 `GL_CLAMP_TO_EDGE` 后OpenGL会返回它们的边界的值，尽管我们可能在两个两个面中间进行的采样。

-在绘制物体之前，将使用cubemap，而在渲染前我们要激活相应的纹理单元并绑定到cubemap上，这和普通的2D纹理没什么区别。
+在绘制物体之前，将使用立方体贴图，而在渲染前我们要激活相应的纹理单元并绑定到立方体贴图上，这和普通的2D纹理没什么区别。

-在片段着色器中，我们也必须使用一个不同的采样器——**samplerCube**，用它来从`texture`函数中采样，但是这次使用的是一个`vec3`方向向量，取代`vec2`。下面是一个片段着色器使用了cubemap的例子：
+在片段着色器中，我们也必须使用一个不同的采样器——**samplerCube**，用它来从`texture`函数中采样，但是这次使用的是一个`vec3`方向向量，取代`vec2`。下面是一个片段着色器使用了立方体贴图的例子：

 ```c++
-in vec3 textureDir; // 用一个三维方向向量来表示Cubemap纹理的坐标
+in vec3 textureDir; // 用一个三维方向向量来表示立方体贴图纹理的坐标

-uniform samplerCube cubemap;  // Cubemap纹理采样器
+uniform samplerCube cubemap;  // 立方体贴图纹理采样器

 void main()
 {
@@ -88,17 +88,17 @@ void main()
 }
 ```

-看起来不错，但是何必这么做呢？因为恰巧使用cubemap可以简单的实现很多有意思的技术。其中之一便是著名的**天空盒(Skybox)**。
+看起来不错，但是何必这么做呢？因为恰巧使用立方体贴图可以简单的实现很多有意思的技术。其中之一便是著名的**天空盒(Skybox)**。



-## 天空盒(Skybox)
+# 天空盒

-天空盒是一个包裹整个场景的立方体，它由6个图像构成一个环绕的环境，给玩家一种他所在的场景比实际的要大得多的幻觉。比如有些在视频游戏中使用的天空盒的图像是群山、白云或者满天繁星。比如下面的夜空繁星的图像就来自《上古卷轴》：
+天空盒(Skybox)是一个包裹整个场景的立方体，它由6个图像构成一个环绕的环境，给玩家一种他所在的场景比实际的要大得多的幻觉。比如有些在视频游戏中使用的天空盒的图像是群山、白云或者满天繁星。比如下面的夜空繁星的图像就来自《上古卷轴》：

 ![](http://learnopengl.com/img/advanced/cubemaps_morrowind.jpg)

-你现在可能已经猜到cubemap完全满足天空盒的要求：我们有一个立方体，它有6个面，每个面需要一个贴图。上图中使用了几个夜空的图片给予玩家一种置身广袤宇宙的感觉，可实际上，他还是在一个小盒子之中。
+你现在可能已经猜到立方体贴图完全满足天空盒的要求：我们有一个立方体，它有6个面，每个面需要一个贴图。上图中使用了几个夜空的图片给予玩家一种置身广袤宇宙的感觉，可实际上，他还是在一个小盒子之中。

 网上有很多这样的天空盒的资源。[这个网站](http://www.custommapmakers.org/skyboxes.php)就提供了很多。这些天空盒图像通常有下面的样式：

@@ -108,9 +108,9 @@ void main()

 这个细致（高精度）的天空盒就是我们将在场景中使用的那个，你可以[在这里下载](http://learnopengl.com/img/textures/skybox.rar)。

-### 加载一个天空盒
+## 加载天空盒

-由于天空盒实际上就是一个cubemap，加载天空盒和之前我们加载cubemap的没什么大的不同。为了加载天空盒我们将使用下面的函数，它接收一个包含6个纹理文件路径的vector：
+由于天空盒实际上就是一个立方体贴图，加载天空盒和之前我们加载立方体贴图的没什么大的不同。为了加载天空盒我们将使用下面的函数，它接收一个包含6个纹理文件路径的vector：

 ```c++
 GLuint loadCubemap(vector<const GLchar*> faces)
@@ -142,9 +142,9 @@ GLuint loadCubemap(vector<const GLchar*> faces)
 }
 ```

-这个函数没什么特别之处。这就是我们前面已经见过的cubemap代码，只不过放进了一个可管理的函数中。
+这个函数没什么特别之处。这就是我们前面已经见过的立方体贴图代码，只不过放进了一个可管理的函数中。

-然后，在我们调用这个函数之前，我们将把合适的纹理路径加载到一个vector之中，顺序还是按照cubemap枚举的特定顺序：
+然后，在我们调用这个函数之前，我们将把合适的纹理路径加载到一个vector之中，顺序还是按照立方体贴图枚举的特定顺序：

 ```c++
 vector<const GLchar*> faces;
@@ -157,15 +157,15 @@ faces.push_back("front.jpg");
 GLuint cubemapTexture = loadCubemap(faces);
 ```

-现在我们已经用`cubemapTexture`作为id把天空盒加载为cubemap。我们现在可以把它绑定到一个立方体来替换不完美的`clear color`，在前面的所有教程中这个东西做背景已经很久了。
+现在我们已经用`cubemapTexture`作为id把天空盒加载为立方体贴图。我们现在可以把它绑定到一个立方体来替换不完美的`clear color`，在前面的所有教程中这个东西做背景已经很久了。



-### 天空盒的显示
+## 显示天空盒

 因为天空盒绘制在了一个立方体上，我们还需要另一个VAO、VBO以及一组全新的顶点，和任何其他物体一样。你可以[从这里获得顶点数据](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps_skybox_data)。

-cubemap用于给3D立方体帖上纹理，可以用立方体的位置作为纹理坐标进行采样。当一个立方体的中心位于原点(0，0，0)的时候，它的每一个位置向量也就是以原点为起点的方向向量。这个方向向量就是我们要得到的立方体某个位置的相应纹理值。出于这个理由，我们只需要提供位置向量，而无需纹理坐标。为了渲染天空盒，我们需要一组新着色器，它们不会太复杂。因为我们只有一个顶点属性，顶点着色器非常简单：
+立方体贴图用于给3D立方体帖上纹理，可以用立方体的位置作为纹理坐标进行采样。当一个立方体的中心位于原点(0，0，0)的时候，它的每一个位置向量也就是以原点为起点的方向向量。这个方向向量就是我们要得到的立方体某个位置的相应纹理值。出于这个理由，我们只需要提供位置向量，而无需纹理坐标。为了渲染天空盒，我们需要一组新着色器，它们不会太复杂。因为我们只有一个顶点属性，顶点着色器非常简单：

 ```c++
 #version 330 core
@@ -197,7 +197,7 @@ void main()
 }
 ```

-片段着色器比较明了，我们把顶点属性中的位置向量作为纹理的方向向量，使用它们从cubemap采样纹理值。渲染天空盒现在很简单，我们有了一个cubemap纹理，我们简单绑定cubemap纹理，天空盒就自动地用天空盒的cubemap填充了。为了绘制天空盒，我们将把它作为场景中第一个绘制的物体并且关闭深度写入。这样天空盒才能成为所有其他物体的背景来绘制出来。
+片段着色器比较明了，我们把顶点属性中的位置向量作为纹理的方向向量，使用它们从立方体贴图采样纹理值。渲染天空盒现在很简单，我们有了一个立方体贴图纹理，我们简单绑定立方体贴图纹理，天空盒就自动地用天空盒的立方体贴图填充了。为了绘制天空盒，我们将把它作为场景中第一个绘制的物体并且关闭深度写入。这样天空盒才能成为所有其他物体的背景来绘制出来。

 ```c++

@@ -212,7 +212,7 @@ glDepthMask(GL_TRUE);
 // ... Draw rest of the scene
 ```

-如果你运行程序就会陷入困境，我们希望天空盒以玩家为中心，这样无论玩家移动了多远，天空盒都不会变近，这样就产生一种四周的环境真的非常大的印象。当前的视图矩阵对所有天空盒的位置进行了转转缩放和平移变换，所以玩家移动，cubemap也会跟着移动！我们打算移除视图矩阵的平移部分，这样移动就影响不到天空盒的位置向量了。在基础光照教程里我们提到过我们可以只用4X4矩阵的3×3部分去除平移。我们可以简单地将矩阵转为33矩阵再转回来，就能达到目标
+如果你运行程序就会陷入困境，我们希望天空盒以玩家为中心，这样无论玩家移动了多远，天空盒都不会变近，这样就产生一种四周的环境真的非常大的印象。当前的视图矩阵对所有天空盒的位置进行了转转缩放和平移变换，所以玩家移动，立方体贴图也会跟着移动！我们打算移除视图矩阵的平移部分，这样移动就影响不到天空盒的位置向量了。在基础光照教程里我们提到过我们可以只用4X4矩阵的3×3部分去除平移。我们可以简单地将矩阵转为33矩阵再转回来，就能达到目标

 ```c++
 glm::mat4 view = glm::mat4(glm::mat3(camera.GetViewMatrix()));
@@ -226,7 +226,7 @@ glm::mat4 view = glm::mat4(glm::mat3(camera.GetViewMatrix()));

 尝试用不同的天空盒实验，看看它们对场景有多大影响。

-### 优化
+## 优化

 现在我们在渲染场景中的其他物体之前渲染了天空盒。这么做没错，但是不怎么高效。如果我们先渲染了天空盒，那么我们就是在为每一个屏幕上的像素运行片段着色器，即使天空盒只有部分在显示着；fragment可以使用前置深度测试（early depth testing）简单地被丢弃，这样就节省了我们宝贵的带宽。

@@ -249,19 +249,19 @@ void main()

 你可以在这里找到优化过的版本的[源码](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps_skybox_optimized)。

-### 环境映射
+# 环境映射

-我们现在有了一个把整个环境映射到为一个单独纹理的对象，我们利用这个信息能做的不仅是天空盒。使用带有场景环境的cubemap，我们还可以让物体有一个反射或折射属性。像这样使用了环境cubemap的技术叫做**环境贴图技术**，其中最重要的两个是**反射(reflection)**和**折射(refraction)**。
+我们现在有了一个把整个环境映射到为一个单独纹理的对象，我们利用这个信息能做的不仅是天空盒。使用带有场景环境的立方体贴图，我们还可以让物体有一个反射或折射属性。像这样使用了环境立方体贴图的技术叫做**环境贴图技术**，其中最重要的两个是**反射(reflection)**和**折射(refraction)**。

-#### 反射(reflection)
+## 反射

-凡是是一个物体（或物体的某部分）反射他周围的环境的属性，比如物体的颜色多少有些等于它周围的环境，这要基于观察者的角度。例如一个镜子是一个反射物体：它会基于观察者的角度泛着它周围的环境。
+凡是是一个物体（或物体的某部分）反射(Reflect)他周围的环境的属性，比如物体的颜色多少有些等于它周围的环境，这要基于观察者的角度。例如一个镜子是一个反射物体：它会基于观察者的角度泛着它周围的环境。

-反射的基本思路不难。下图展示了我们如何计算反射向量，然后使用这个向量去从一个cubemap中采样：
+反射的基本思路不难。下图展示了我们如何计算反射向量，然后使用这个向量去从一个立方体贴图中采样：

 ![](http://learnopengl.com/img/advanced/cubemaps_reflection_theory.png)

-我们基于观察方向向量I和物体的法线向量N计算出反射向量R。我们可以使用GLSL的内建函数reflect来计算这个反射向量。最后向量R作为一个方向向量对cubemap进行索引/采样，返回一个环境的颜色值。最后的效果看起来就像物体反射了天空盒。
+我们基于观察方向向量I和物体的法线向量N计算出反射向量R。我们可以使用GLSL的内建函数reflect来计算这个反射向量。最后向量R作为一个方向向量对立方体贴图进行索引/采样，返回一个环境的颜色值。最后的效果看起来就像物体反射了天空盒。

 因为我们在场景中已经设置了一个天空盒，创建反射就不难了。我们改变一下箱子使用的那个片段着色器，给箱子一个反射属性：

@@ -282,7 +282,7 @@ void main()
 }
 ```

-我们先来计算观察/摄像机方向向量I，然后使用它来计算反射向量R，接着我们用R从天空盒cubemap采样。要注意的是，我们有了片段的插值Normal和Position变量，所以我们需要修正顶点着色器适应它。
+我们先来计算观察/摄像机方向向量I，然后使用它来计算反射向量R，接着我们用R从天空盒立方体贴图采样。要注意的是，我们有了片段的插值Normal和Position变量，所以我们需要修正顶点着色器适应它。

 ```c++
 #version 330 core
@@ -308,7 +308,7 @@ void main()

 因为我们使用法线，你还得更新顶点数据，更新属性指针。还要确保设置`cameraPos`的uniform。

-然后在渲染箱子前我们还得绑定cubemap纹理：
+然后在渲染箱子前我们还得绑定立方体贴图纹理：

 ```c++
 glBindVertexArray(cubeVAO);
@@ -329,15 +329,15 @@ glBindVertexArray(0);

 看起来挺惊艳，但是现实中大多数模型都不是完全反射的。我们可以引进反射贴图（reflection map）来使模型有另一层细节。和diffuse、specular贴图一样，我们可以从反射贴图上采样来决定fragment的反射率。使用反射贴图我们还可以决定模型的哪个部分有反射能力，以及强度是多少。本节的练习中，要由你来在我们早期创建的模型加载器引入反射贴图，这回极大的提升纳米服模型的细节。

-#### 折射(refraction)
+## 折射

-环境映射的另一个形式叫做折射，它和反射差不多。折射是光线通过特定材质对光线方向的改变。我们通常看到像水一样的表面，光线并不是直接通过的，而是让光线弯曲了一点。它看起来像你把半只手伸进水里的效果。
+环境映射的另一个形式叫做折射(Refraction)，它和反射差不多。折射是光线通过特定材质对光线方向的改变。我们通常看到像水一样的表面，光线并不是直接通过的，而是让光线弯曲了一点。它看起来像你把半只手伸进水里的效果。

 折射遵守[斯涅尔定律](http://en.wikipedia.org/wiki/Snell%27s_law)，使用环境贴图看起来就像这样：

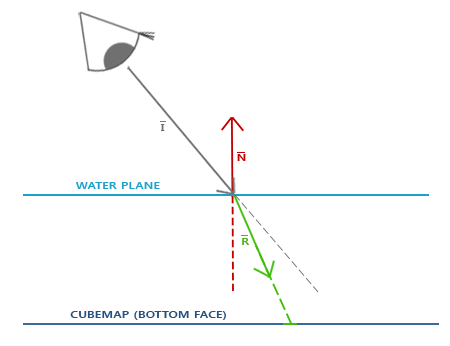
 ![](http://learnopengl.com/img/advanced/cubemaps_refraction_theory.png)

-我们有个观察向量I，一个法线向量N，这次折射向量是R。就像你所看到的那样，观察向量的方向有轻微弯曲。弯曲的向量R随后用来从cubemap上采样。
+我们有个观察向量I，一个法线向量N，这次折射向量是R。就像你所看到的那样，观察向量的方向有轻微弯曲。弯曲的向量R随后用来从立方体贴图上采样。

 折射可以通过GLSL的内建函数refract来实现，除此之外还需要一个法线向量，一个观察方向和一个两种材质之间的折射指数。

@@ -353,7 +353,7 @@ glBindVertexArray(0);

 我们使用这些折射指数来计算光线通过两个材质的比率。在我们的例子中，光线/视线从空气进入玻璃（如果我们假设箱子是玻璃做的）所以比率是1.001.52 = 0.658。

-我们已经绑定了cubemap，提供了定点数据，设置了摄像机位置的uniform。现在只需要改变片段着色器：
+我们已经绑定了立方体贴图，提供了定点数据，设置了摄像机位置的uniform。现在只需要改变片段着色器：

 ```c++
 void main()
@@ -371,27 +371,23 @@ void main()

 你可以向想象一下，如果将光线、反射、折射和顶点的移动合理的结合起来就能创造出漂亮的水的图像。一定要注意，出于物理精确的考虑当光线离开物体的时候还要再次进行折射；现在我们简单的使用了单边（一次）折射，大多数目的都可以得到满足。

-#### 动态环境贴图（Dynamic environment maps）
+## 动态环境贴图

 现在，我们已经使用了静态图像组合的天空盒，看起来不错，但是没有考虑到物体可能移动的实际场景。我们到现在还没注意到这点，是因为我们目前还只使用了一个物体。如果我们有个镜子一样的物体，它周围有多个物体，只有天空盒在镜子中可见，和场景中只有这一个物体一样。

-使用帧缓冲可以为提到的物体的所有6个不同角度创建一个场景的纹理，把它们每次渲染迭代储存为一个cubemap。之后我们可以使用这个（动态生成的）cubemap来创建真实的反射和折射表面，这样就能包含所有其他物体了。这种方法叫做动态环境映射（dynamic environment mapping）,因为我们动态地创建了一个物体的以其四周为参考的cubemap，并把它用作环境贴图。
+使用帧缓冲可以为提到的物体的所有6个不同角度创建一个场景的纹理，把它们每次渲染迭代储存为一个立方体贴图。之后我们可以使用这个（动态生成的）立方体贴图来创建真实的反射和折射表面，这样就能包含所有其他物体了。这种方法叫做动态环境映射(Dynamic Environment Mapping),因为我们动态地创建了一个物体的以其四周为参考的立方体贴图，并把它用作环境贴图。

-它看起效果很好，但是有一个劣势：使用环境贴图我们必须为每个物体渲染场景6次，这需要非常大的开销。现代应用尝试尽量使用天空盒子，凡可能预编译cubemap就创建少量动态环境贴图。动态环境映射是个非常棒的技术，要想在不降低执行效率的情况下实现它就需要很多巧妙的技巧。
+它看起效果很好，但是有一个劣势：使用环境贴图我们必须为每个物体渲染场景6次，这需要非常大的开销。现代应用尝试尽量使用天空盒子，凡可能预编译立方体贴图就创建少量动态环境贴图。动态环境映射是个非常棒的技术，要想在不降低执行效率的情况下实现它就需要很多巧妙的技巧。



 ## 练习

-尝试在模型加载中引进反射贴图，你将再次得到很大视觉效果的提升。这其中有几点需要注意：
-
- Assimp并不支持反射贴图，我们可以使用环境贴图的方式将反射贴图从`aiTextureType_AMBIENT`类型中来加载反射贴图的材质。
- 我匆忙地使用反射贴图来作为镜面反射的贴图，而反射贴图并没有很好的映射在模型上:)。
- 由于加载模型已经占用了3个纹理单元，因此你要绑定天空盒到第4个纹理单元上，这样才能在同一个着色器内从天空盒纹理中取样。
-
-You can find the solution source code here together with the updated model and mesh class. The shaders used for rendering the reflection maps can be found here: vertex shader and fragment shader. 
-
-你可以在此获取解决方案的[源代码](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1)，这其中还包括升级过的[Model](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1-model)和[Mesh](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1-mesh)类，还有用来绘制反射贴图的[顶点着色器](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1-vertex)和[片段着色器](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1-fragment)。
+- 尝试在模型加载中引进反射贴图，你将再次得到很大视觉效果的提升。这其中有几点需要注意：
+	- Assimp并不支持反射贴图，我们可以使用环境贴图的方式将反射贴图从`aiTextureType_AMBIENT`类型中来加载反射贴图的材质。
+	- 我匆忙地使用反射贴图来作为镜面反射的贴图，而反射贴图并没有很好的映射在模型上:)。
+	- 由于加载模型已经占用了3个纹理单元，因此你要绑定天空盒到第4个纹理单元上，这样才能在同一个着色器内从天空盒纹理中取样。
+- 你可以在此获取解决方案的[源代码](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1)，这其中还包括升级过的[Model](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1-model)和[Mesh](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1-mesh)类，还有用来绘制反射贴图的[顶点着色器](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1-vertex)和[片段着色器](http://learnopengl.com/code_viewer.php?code=advanced/cubemaps-exercise1-fragment)。

 如果你一切都做对了，那你应该看到和下图类似的效果：

--- a/OpenGL/07
+++ b/OpenGL/07
@@ -6,7 +6,6 @@
 翻译     | [Django](http://bullteacher.com/)
 校对     | [Geequlim](http://geequlim.com)

-## 缓冲数据写入

 我们在OpenGL中大量使用缓冲来储存数据已经有一会儿了。有一些有趣的方式来操纵缓冲，也有一些有趣的方式通过纹理来向着色器传递大量数据。本教程中，我们会讨论一些更加有意思的缓冲函数，以及如何使用纹理对象来储存大量数据（教程中纹理部分还没写）。

@@ -43,7 +42,7 @@ glUnmapBuffer(GL_ARRAY_BUFFER);

 ## 分批处理顶点属性

-使用`glVertexAttribPointer`函数可以指定缓冲内容的顶点数组的属性的布局(layout)。我们已经知道，通过使用顶点属性指针我们可以交叉属性，也就是说我们可以把每个顶点的位置、法线、纹理坐标放在彼此挨着的地方。现在我们了解了更多的缓冲的内容，可以采取另一种方式了。
+使用`glVertexAttribPointer`函数可以指定缓冲内容的顶点数组的属性的布局(Layout)。我们已经知道，通过使用顶点属性指针我们可以交叉(Interleave)属性，也就是说我们可以把每个顶点的位置、法线、纹理坐标放在彼此挨着的地方。现在我们了解了更多的缓冲的内容，可以采取另一种方式了。

 我们可以做的是把每种类型的属性的所有向量数据批量保存在一个布局，而不是交叉布局。与交叉布局123123123123不同，我们采取批量方式111122223333。

@@ -74,7 +73,7 @@ glVertexAttribPointer(

 这是我们有了另一种设置和指定顶点属性的方式。使用哪个方式对OpenGL来说也不会有立竿见影的效果，这只是一种采用更加组织化的方式去设置顶点属性。选用哪种方式取决于你的偏好和应用类型。

- ## 复制缓冲
+## 复制缓冲

 当你的缓冲被数据填充以后，你可能打算让其他缓冲能分享这些数据或者打算把缓冲的内容复制到另一个缓冲里。`glCopyBufferSubData`函数让我们能够相对容易地把一个缓冲的数据复制到另一个缓冲里。函数的原型是：

--- a/OpenGL/08
+++ b/OpenGL/08
@@ -9,21 +9,19 @@

 这章不会向你展示什么新的功能，也不会对你的场景的视觉效果有较大提升。本文多多少少地深入探讨了一些GLSL有趣的知识，它们可能在将来能帮助你。基本来说有些不可不知的内容和功能在你去使用GLSL创建OpenGL应用的时候能让你的生活更轻松。

-我们会讨论一些内建变量、组织着色器输入和输出的新方式以及一个叫做uniform缓冲对象的非常有用的工具。
+我们会讨论一些内建变量(Built-in Variable)、组织着色器输入和输出的新方式以及一个叫做uniform缓冲对象(Uniform Buffer Object)的非常有用的工具。

-## GLSL的内建变量
+# GLSL的内建变量

 着色器是很小的，如果我们需要从当前着色器以外的别的资源里的数据，那么我们就不得不传给它。我们学过了使用顶点属性、uniform和采样器可以实现这个目标。GLSL有几个以**gl\_**为前缀的变量，使我们有一个额外的手段来获取和写入数据。其中两个我们已经打过交道了：`gl_Position`和`gl_FragCoord`，前一个是顶点着色器的输出向量，后一个是片段着色器的变量。

 我们会讨论几个有趣的GLSL内建变量，并向你解释为什么它们对我们来说很有好处。注意，我们不会讨论到GLSL中所有的内建变量，因此如果你想看到所有的内建变量还是最好去查看[OpenGL的wiki](http://www.opengl.org/wiki/Built-in_Variable_(GLSL)。

-### 顶点着色器变量
-
-#### gl_Position
+## 顶点着色器变量

 我们已经了解`gl_Position`是顶点着色器裁切空间输出的位置向量。如果你想让屏幕上渲染出东西`gl_Position`必须使用。否则我们什么都看不到。

-#### gl_PointSize
+### gl_PointSize

 我们可以使用的另一个可用于渲染的基本图形(primitive)是**GL\_POINTS**，使用它每个顶点作为一个基本图形，被渲染为一个点(point)。可以使用`glPointSize`函数来设置这个点的大小，但我们还可以在顶点着色器里修改点的大小。

@@ -51,7 +49,7 @@ void main()

 想象一下，每个顶点表示出来的点的大小的不同，如果用在像粒子生成之类的技术里会挺有意思的。

- #### gl_VertexID
+### gl_VertexID

 `gl_Position`和`gl_PointSize`都是输出变量，因为它们的值是作为顶点着色器的输出被读取的；我们可以向它们写入数据来影响结果。顶点着色器为我们提供了一个有趣的输入变量，我们只能从它那里读取，这个变量叫做`gl_VertexID`。

@@ -59,11 +57,11 @@ void main()

 尽管目前看似没用，但是我们最好知道我们能获取这样的信息。

-### 片段着色器的变量
+## 片段着色器的变量

 在片段着色器中也有一些有趣的变量。GLSL给我们提供了两个有意思的输入变量，它们是`gl_FragCoord`和`gl_FrontFacing`。

-#### gl_FragCoord
+### gl_FragCoord

 在讨论深度测试的时候，我们已经看过`gl_FragCoord`好几次了，因为`gl_FragCoord`向量的z元素和特定的fragment的深度值相等。然而，我们也可以使用这个向量的x和y元素来实现一些有趣的效果。

@@ -88,9 +86,7 @@ void main()

 我们现在可以计算出两个完全不同的片段着色器结果，每个显示在窗口的一端。这对于测试不同的光照技术很有好处。

-
-
-#### gl_FrontFacing
+### gl_FrontFacing

 片段着色器另一个有意思的输入变量是`gl_FrontFacing`变量。在面剔除教程中，我们提到过OpenGL可以根据顶点绘制顺序弄清楚一个面是正面还是背面。如果我们不适用面剔除，那么`gl_FrontFacing`变量能告诉我们当前片段是某个正面的一部分还是背面的一部分。然后我们可以决定做一些事情，比如为正面计算出不同的颜色。

@@ -119,7 +115,7 @@ void main()

 注意，如果你开启了面剔除，你就看不到箱子里面有任何东西了，所以此时使用`gl_FrontFacing`毫无意义。

-#### gl_FragDepth
+### gl_FragDepth

 输入变量`gl_FragCoord`让我们可以读得当前片段的窗口空间坐标和深度值，但是它是只读的。我们不能影响到这个片段的窗口屏幕坐标，但是可以设置这个像素的深度值。GLSL给我们提供了一个叫做`gl_FragDepth`的变量，我们可以用它在着色器中遂舍之像素的深度值。

@@ -168,11 +164,11 @@ void main()



-## 接口块(Interface blocks)
+# 接口块

 到目前位置，每次我们打算从顶点向片段着色器发送数据，我们都会声明一个相互匹配的输出/输入变量。从一个着色器向另一个着色器发送数据，一次将它们声明好是最简单的方式，但是随着应用变得越来越大，你也许会打算发送的不仅仅是变量，最好还可以包括数组和结构体。

-为了帮助我们组织这些变量，GLSL为我们提供了一些叫做接口块(Interface blocks)的东西，好让我们能够组织这些变量。声明接口块和声明struct有点像，不同之处是它现在基于块（block），使用in和out关键字来声明，最后它将成为一个输入或输出块（block）。
+为了帮助我们组织这些变量，GLSL为我们提供了一些叫做接口块(Interface Blocks)的东西，好让我们能够组织这些变量。声明接口块和声明struct有点像，不同之处是它现在基于块（block），使用in和out关键字来声明，最后它将成为一个输入或输出块（block）。

 ```c++
 #version 330 core
@@ -218,11 +214,11 @@ void main()

 如果两个interface block名一致，它们对应的输入和输出就会匹配起来。这是另一个可以帮助我们组织代码的有用功能，特别是在跨着色阶段的情况，比如几何着色器。

-## uniform缓冲对象 (Uniform buffer objects)
+# Uniform缓冲对象

 我们使用OpenGL很长时间了，也学到了一些很酷的技巧，但是产生了一些烦恼。比如说，当时用一个以上的着色器的时候，我们必须一次次设置uniform变量，尽管对于每个着色器来说它们都是一样的，所以为什么还麻烦地多次设置它们呢？

-OpenGL为我们提供了一个叫做uniform缓冲对象的工具，使我们能够声明一系列的全局uniform变量， 它们会在几个着色器程序中保持一致。当时用uniform缓冲的对象时相关的uniform只能设置一次。我们仍需为每个着色器手工设置唯一的uniform。创建和配置一个uniform缓冲对象需要费点功夫。
+OpenGL为我们提供了一个叫做uniform缓冲对象(Uniform Buffer Object)的工具，使我们能够声明一系列的全局uniform变量， 它们会在几个着色器程序中保持一致。当时用uniform缓冲的对象时相关的uniform只能设置一次。我们仍需为每个着色器手工设置唯一的uniform。创建和配置一个uniform缓冲对象需要费点功夫。

 因为uniform缓冲对象是一个缓冲，因此我们可以使用`glGenBuffers`创建一个，然后绑定到`GL_UNIFORM_BUFFER`缓冲目标上，然后把所有相关uniform数据存入缓冲。有一些原则，像uniform缓冲对象如何储存数据，我们会在稍后讨论。首先我们我们在一个简单的顶点着色器中，用uniform块(uniform block)储存投影和视图矩阵：

@@ -252,7 +248,7 @@ void main()



-### uniform块布局(uniform block layout)
+## Uniform块布局

 一个uniform块的内容被储存到一个缓冲对象中，实际上就是在一块内存中。因为这块内存也不清楚它保存着什么类型的数据，我们就必须告诉OpenGL哪一块内存对应着色器中哪一个uniform变量。

@@ -312,7 +308,7 @@ layout (std140) uniform ExampleBlock

 在定义uniform块前面添加layout (std140)声明，我们就能告诉OpenGL这个uniform块使用了std140布局。另外还有两种其他的布局可以选择，它们需要我们在填充缓冲之前查询每个偏移量。我们已经了解了分享布局（shared layout）和其他的布局都将被封装（packed）。当使用封装（packed）布局的时候，不能保证布局在别的程序中能够保持一致，因为它允许编译器从uniform块中优化出去uniform变量，这在每个着色器中都可能不同。

-### 使用uniform缓冲
+## 使用uniform缓冲

 我们讨论了uniform块在着色器中的定义和如何定义它们的内存布局，但是我们还没有讨论如何使用它们。

@@ -371,7 +367,7 @@ glBindBuffer(GL_UNIFORM_BUFFER, 0);

 同样的处理也能够应用到uniform块中其他uniform变量上。

-### 一个简单的例子
+## 一个简单的例子

 我们来师范一个真实的使用uniform缓冲对象的例子。如果我们回头看看前面所有演示的代码，我们一直使用了3个矩阵：投影、视图和模型矩阵。所有这些矩阵中，只有模型矩阵是频繁变化的。如果我们有多个着色器使用了这些矩阵，我们可能最好还是使用uniform缓冲对象。

--- a/Shader.md
+++ b/Shader.md
@@ -6,9 +6,7 @@
 翻译     | [Django](http://bullteacher.com/)
 校对     | [Geequlim](http://geequlim.com)

-## 几何着色器(Geometry Shader)
-
-在顶点和片段着色器之间有一个可选的着色器，叫做几何着色器（geometry shader）。几何着色器以一个或多个表示为一个单独基本图形（primitive）的顶点作为输入，比如可以是一个点或者三角形。几何着色器在将这些顶点发送到下一个着色阶段之前，可以将这些顶点转变为它认为合适的内容。几何着色器有意思的地方在于它可以把（一个或多个）顶点转变为完全不同的基本图形（primitive），从而生成比原来多得多的顶点。
+在顶点和片段着色器之间有一个可选的着色器，叫做几何着色器(Geometry Shader)。几何着色器以一个或多个表示为一个单独基本图形（primitive）的顶点作为输入，比如可以是一个点或者三角形。几何着色器在将这些顶点发送到下一个着色阶段之前，可以将这些顶点转变为它认为合适的内容。几何着色器有意思的地方在于它可以把（一个或多个）顶点转变为完全不同的基本图形（primitive），从而生成比原来多得多的顶点。

 我们直接用一个例子深入了解一下：

@@ -57,7 +55,7 @@ triangles_adjacency |GL_TRIANGLES_ADJACENCY或GL_TRIANGLE_STRIP_ADJACENCY（6）

 上面的着色器，我们只能输出一个线段，因为顶点的最大值设置为2。

-为生成更有意义的结果，我们需要某种方式从前一个着色阶段获得输出。GLSL为我们提供了一个内建变量，它叫做**gl_in**，它的内部看起来可能像这样：
+为生成更有意义的结果，我们需要某种方式从前一个着色阶段获得输出。GLSL为我们提供了一个内建变量，它叫做`gl_in`，它的内部看起来可能像这样：

 ```c++
 in gl_Vertex
@@ -189,7 +187,7 @@ glLinkProgram(program);
 它和没用几何着色器一样！我承认有点无聊，但是事实上，我们仍能绘制证明几何着色器工作了的点，所以现在是时候来做点更有意思的事了！


-### 创建几个房子
+## 造几个房子

 绘制点和线没什么意思，所以我们将在每个点上使用几何着色器绘制一个房子。我们可以通过把几何着色器的输出设置为`triangle_strip`来达到这个目的，总共要绘制3个三角形：两个用来组成方形和另表示一个屋顶。

@@ -337,11 +335,11 @@ EndPrimitive();

 你可以看到，使用几何着色器，你可以使用最简单的基本图形就能获得漂亮的新玩意。因为这些形状是在你的GPU超快硬件上动态生成的，这要比使用顶点缓冲自己定义这些形状更为高效。几何缓冲在简单的经常被重复的形状比如体素（voxel）的世界和室外的草地上，是一种非常强大的优化工具。

-### 爆炸式物体
+# 爆破物体

 绘制房子的确很有趣，但我们不会经常这么用。这就是为什么现在我们将撬起物体缺口，形成爆炸式物体的原因！虽然这个我们也不会经常用到，但是它能向你展示一些几何着色器的强大之处。

-当我们说对一个物体进行爆破的时候并不是说我们将要把之前的那堆顶点炸掉，但是我们打算把每个三角形沿着它们的法线向量移动一小段距离。效果是整个物体上的三角形看起来就像沿着它们的法线向量爆炸了一样。纳米服上的三角形的爆炸式效果看起来是这样的：
+当我们说对一个物体进行爆破(Explode)的时候并不是说我们将要把之前的那堆顶点炸掉，但是我们打算把每个三角形沿着它们的法线向量移动一小段距离。效果是整个物体上的三角形看起来就像沿着它们的法线向量爆炸了一样。纳米服上的三角形的爆炸式效果看起来是这样的：

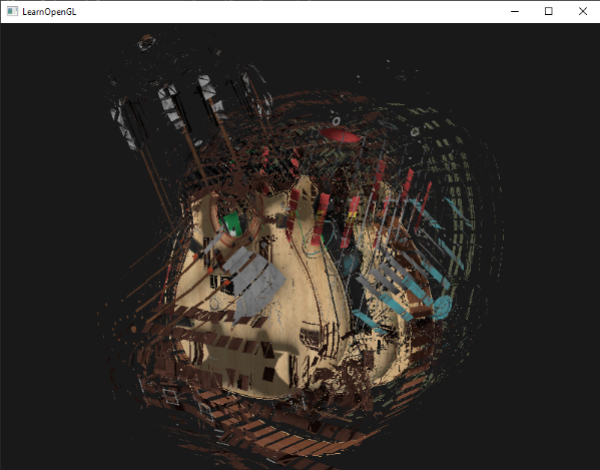
 ![](http://learnopengl.com/img/advanced/geometry_shader_explosion.png)

@@ -418,7 +416,7 @@ glUniform1f(glGetUniformLocation(shader.Program, "time"), glfwGetTime());

 最后的结果是一个随着时间持续不断地爆炸的3D模型（不断爆炸不断回到正常状态）。尽管没什么大用处，它却向你展示出很多几何着色器的高级用法。你可以用[完整的源码](http://learnopengl.com/code_viewer.php?code=advanced/geometry_shader_explode)和[着色器](http://learnopengl.com/code_viewer.php?code=advanced/geometry_shader_explode_shaders)对比一下你自己的。

-### 把法线向量显示出来
+# 显示法向量

 在这部分我们将使用几何着色器写一个例子，非常有用：显示一个法线向量。当编写光照着色器的时候，你最终会遇到奇怪的视频输出问题，你很难决定是什么导致了这个问题。通常导致光照错误的是，不正确的加载顶点数据，以及给它们指定了不合理的顶点属性，又或是在着色器中不合理的管理，导致产生了不正确的法线向量。我们所希望的是有某种方式可以检测出法线向量是否正确。把法线向量显示出来正是这样一种方法，恰好几何着色器能够完美地达成这个目的。

--- a/Instancing.md
+++ b/Instancing.md
@@ -1,4 +1,4 @@
-# 实例化(Instancing)
+# 实例化

 原文     | [Instancing](http://learnopengl.com/#!Advanced-OpenGL/Instancing)
      ---|---
@@ -21,9 +21,9 @@ for(GLuint i = 0; i < amount_of_models_to_draw; i++)

 像这样绘制出你模型的其他实例，多次绘制之后，很快将达到一个瓶颈，这是因为你`glDrawArrays`或`glDrawElements`这样的函数(Draw call)过多。这样渲染顶点数据，会明显降低执行效率，这是因为OpenGL在它可以绘制你的顶点数据之前必须做一些准备工作(比如告诉GPU从哪个缓冲读取数据，以及在哪里找到顶点属性，所有这些都会使CPU到GPU的总线变慢)。所以即使渲染顶点超快，而多次给你的GPU下达这样的渲染命令却未必。

-如果我们能够将数据一次发送给GPU，就会更方便，然后告诉OpenGL使用一个绘制函数，将这些数据绘制为多个物体。这就是我们将要展开讨论的**实例化(instancing)**。
+如果我们能够将数据一次发送给GPU，就会更方便，然后告诉OpenGL使用一个绘制函数，将这些数据绘制为多个物体。这就是我们将要展开讨论的**实例化(Instancing)**。

-**实例化(instancing)**是一种只调用一次渲染函数却能绘制出很多物体的技术，它节省渲染物体时从CPU到GPU的通信时间，而且只需做一次即可。要使用实例化渲染，我们必须将`glDrawArrays`和`glDrawElements`各自改为`glDrawArraysInstanced`和`glDrawElementsInstanced`。这些用于实例化的函数版本需要设置一个额外的参数，叫做**实例数量(instance count)**，它设置我们打算渲染实例的数量。这样我们就只需要把所有需要的数据发送给GPU一次就行了，然后告诉GPU它该如何使用一个函数来绘制所有这些实例。
+实例化是一种只调用一次渲染函数却能绘制出很多物体的技术，它节省渲染物体时从CPU到GPU的通信时间，而且只需做一次即可。要使用实例化渲染，我们必须将`glDrawArrays`和`glDrawElements`各自改为`glDrawArraysInstanced`和`glDrawElementsInstanced`。这些用于实例化的函数版本需要设置一个额外的参数，叫做**实例数量(Instance Count)**，它设置我们打算渲染实例的数量。这样我们就只需要把所有需要的数据发送给GPU一次就行了，然后告诉GPU它该如何使用一个函数来绘制所有这些实例。

 就其本身而言，这个函数用处不大。渲染同一个物体一千次对我们来说没用，因为每个渲染出的物体不仅相同而且还在同一个位置；我们只能看到一个物体！出于这个原因GLSL在着色器中嵌入了另一个内建变量，叫做**`gl_InstanceID`**。

@@ -127,9 +127,9 @@ glBindVertexArray(0);

 `glDrawArraysInstanced`的参数和`glDrawArrays`一样，除了最后一个参数设置了我们打算绘制实例的数量。我们想展示100个四边形，它们以10×10网格形式展现，所以这儿就是100.运行代码，你会得到100个相似的有色四边形。

-## 实例化数组(instanced arrays)
+## 实例化数组

-在这种特定条件下，前面的实现很好，但是当我们有100个实例的时候（这很正常），最终我们将碰到uniform数据数量的上线。为避免这个问题另一个可替代方案是实例化数组，它使用顶点属性来定义，这样就允许我们使用更多的数据了，当顶点着色器渲染一个新实例时它才会被更新。
+在这种特定条件下，前面的实现很好，但是当我们有100个实例的时候（这很正常），最终我们将碰到uniform数据数量的上线。为避免这个问题另一个可替代方案是实例化数组(Instanced Array)，它使用顶点属性来定义，这样就允许我们使用更多的数据了，当顶点着色器渲染一个新实例时它才会被更新。

 使用顶点属性，每次运行顶点着色器都将让GLSL获取到下个顶点属性集合，它们属于当前顶点。当把顶点属性定义为实例数组时，顶点着色器只更新每个实例的顶点属性的内容而不是顶点的内容。这使我们在每个顶点数据上使用标准顶点属性，用实例数组来储存唯一的实例数据。

@@ -199,7 +199,7 @@ void main()

 这些例子不是实例的好例子，不过挺有意思的。它们可以让你对实例的工作方式有一个概括的理解，但是当绘制拥有极大数量的相同物体的时候，它极其有用，现在我们还没有展示呢。出于这个原因，我们将在接下来的部分进入太空来看看实例渲染的威力。

-### 小行星带
+# 小行星带

 想象一下，在一个场景中有一个很大的行星，行星周围有一圈小行星带。这样一个小行星大可能包含成千上万的石块，对于大多数显卡来说几乎是难以完成的渲染任务。这个场景对于实例渲染来说却不再话下，由于所有小行星可以使用一个模型来表示。每个小行星使用一个变换矩阵就是一个经过少量变化的独一无二的小行星了。

--- a/Aliasing.md
+++ b/Aliasing.md
@@ -6,7 +6,7 @@
 翻译     | [Django](http://bullteacher.com/)
 校对     | [Geequlim](http://geequlim.com)

-在你的渲染大冒险中，你可能会遇到模型边缘有锯齿的问题。锯齿边出现的原因是由顶点数据像素化之后成为片段的方式所引起的。下面是一个简单的立方体，它体现了锯齿边的效果：
+在你的渲染大冒险中，你可能会遇到模型边缘有锯齿的问题。**锯齿边(Jagged Edge)**出现的原因是由顶点数据像素化之后成为片段的方式所引起的。下面是一个简单的立方体，它体现了锯齿边的效果：

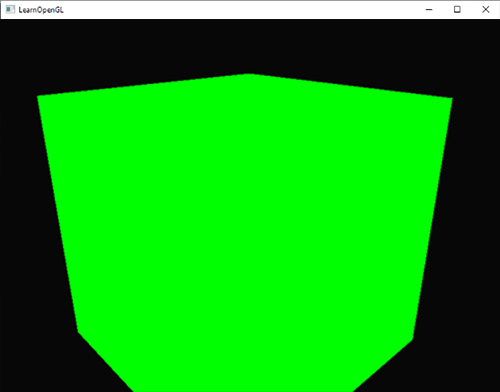
 ![](http://learnopengl.com/img/advanced/anti_aliasing_aliasing.png)

@@ -14,15 +14,15 @@

 ![](http://learnopengl.com/img/advanced/anti_aliasing_zoomed.png)

-这当然不是我们在最终版本的应用里想要的效果。这个效果，很明显能看到边是由像素所构成的，这种现象叫做走样（aliasing）。有很多技术能够减少走样，产生更平滑的边缘，这些技术叫做反走样技术(anti-aliasing,也被称为抗锯齿技术)。
+这当然不是我们在最终版本的应用里想要的效果。这个效果，很明显能看到边是由像素所构成的，这种现象叫做**走样(Aliasing)**。有很多技术能够减少走样，产生更平滑的边缘，这些技术叫做**抗锯齿技术**(Anti-aliasing，也被称为反走样技术)。

-首先，我们有一个叫做超级采样抗锯齿技术（super sample anti-aliasing SSAA），它暂时使用一个更高的解析度（以超级采样方式）来渲染场景，当视频输出在帧缓冲中被更新时，解析度便降回原来的普通解析度。这个额外的解析度被用来防止锯齿边。虽然它确实为我们提供了一种解决走样问题的方案，但却由于必须绘制比平时更多的片段而降低了性能。所以这个技术只流行了一段时间。
+首先，我们有一个叫做**超级采样抗锯齿技术(Super Sample Anti-aliasing, SSAA)**，它暂时使用一个更高的解析度（以超级采样方式）来渲染场景，当视频输出在帧缓冲中被更新时，解析度便降回原来的普通解析度。这个额外的解析度被用来防止锯齿边。虽然它确实为我们提供了一种解决走样问题的方案，但却由于必须绘制比平时更多的片段而降低了性能。所以这个技术只流行了一段时间。

-这个技术的基础上诞生了更为现代的技术，叫做多采样抗锯齿（multisample anti-aliasing）或叫MSAA，虽然它借用了SSAA的理念，但却以更加高效的方式实现了它。这节教程我们会展开讨论这个MSAA技术，它是OpenGL内建的。
+这个技术的基础上诞生了更为现代的技术，叫做**多采样抗锯齿(Multisample Anti-aliasing)**或叫MSAA，虽然它借用了SSAA的理念，但却以更加高效的方式实现了它。这节教程我们会展开讨论这个MSAA技术，它是OpenGL内建的。

-## 多重采样(Multisampling)
+## 多重采样

-为了理解什么是多重采样，以及它是如何解决锯齿问题的，我们先要更深入了解一个OpenGL光栅化的工作方式。
+为了理解什么是多重采样(Multisampling)，以及它是如何解决锯齿问题的，我们先要更深入了解一个OpenGL光栅化的工作方式。

 光栅化是你的最终的经处理的顶点和片段着色器之间的所有算法和处理的集合。光栅化将属于一个基本图形的所有顶点转化为一系列片段。顶点坐标理论上可以含有任何坐标，但片段却不是这样，这是因为它们与你的窗口的解析度有关。几乎永远都不会有顶点坐标和片段的一对一映射，所以光栅化必须以某种方式决定每个特定顶点最终结束于哪个片段/屏幕坐标上。

@@ -68,7 +68,7 @@ MSAA的真正工作方式是，每个像素只运行一次片段着色器，无

 ## OpenGL中的MSAA

-如果我们打算在OpenGL中使用MSAA，那么我们必须使用一个可以为每个像素储存一个以上的颜色值的颜色缓冲(因为多采样需要我们为每个采样点储存一个颜色)。我们这就需要一个新的缓冲类型，它可以储存要求数量的多重采样样本，它叫做**多样本缓冲(multisample buffer)**。
+如果我们打算在OpenGL中使用MSAA，那么我们必须使用一个可以为每个像素储存一个以上的颜色值的颜色缓冲(因为多采样需要我们为每个采样点储存一个颜色)。我们这就需要一个新的缓冲类型，它可以储存要求数量的多重采样样本，它叫做**多样本缓冲(Multisample Buffer)**。

 多数窗口系统可以为我们提供一个多样本缓冲，以代替默认的颜色缓冲。GLFW同样给了我们这个功能，我们所要作的就是提示GLFW，我们希望使用一个带有N个样本的多样本缓冲，而不是普通的颜色缓冲，这要在创建窗口前调用`glfwWindowHint`来完成：

--- a/Lighting.md
+++ b/Lighting.md
@@ -8,8 +8,6 @@

 在光照教程中，我们简单的介绍了Phong光照模型，它给我们的场景带来的基本的现实感。Phong模型看起来还不错，但本章我们把重点放在一些细微差别上。

-
-
 ## Blinn-Phong

 Phong光照很棒，而且性能较高，但是它的镜面反射在某些条件下会失效，特别是当发光值属性低的时候，对应一个非常大的粗糙的镜面区域。下面的图片展示了，当我们使用镜面的发光值为1.0时，一个带纹理地板的效果：
--- a/Correction.md
+++ b/Correction.md
@@ -1,8 +1,16 @@
-本文作者JoeyDeVries，由Django翻译自[http://learnopengl.com](http://learnopengl.com)
+# Gamma校正

-# Gamma校正(Gamma Correction)
+原文     | [Gamma Correction](http://learnopengl.com/#!Advanced-Lighting/Gamma-Correction)
+      ---|---
+作者     | JoeyDeVries
+翻译     | [Django](http://bullteacher.com/)
+校对     | 暂无

-当我们计算出场景中所有像素的最终颜色以后，我们就必须把它们显示在监视器上。过去，大多数监视器是阴极射线管显示器（CRT）。这些监视器有一个物理特性就是两倍的输入电压产生的不是两倍的亮度。输入电压产生约为输入电压的2.2次幂的亮度，这叫做监视器Gamma（译注：Gamma也叫灰度系数，每种显示设备都有自己的Gamma值，都不相同，有一个公式：设备输出亮度 = 电压的Gamma次幂，任何设备Gamma基本上都不会等于1，等于1是一种理想的线性状态，这种理想状态是：如果电压和亮度都是在0到1的区间，那么多少电压就等于多少亮度。对于CRT，Gamma通常为2.2，因而，输出亮度 = 输入电压的2.2次幂，你可以从本节第二张图中看到Gamma2.2实际显示出来的总会比预期暗，相反Gamma0.45就会比理想预期亮，如果你讲Gamma0.45叠加到Gamma2.2的显示设备上，便会对偏暗的显示效果做到校正，这个简单的思路就是本节的核心）。
+当我们计算出场景中所有像素的最终颜色以后，我们就必须把它们显示在监视器上。过去，大多数监视器是阴极射线管显示器（CRT）。这些监视器有一个物理特性就是两倍的输入电压产生的不是两倍的亮度。输入电压产生约为输入电压的2.2次幂的亮度，这叫做监视器Gamma。
+
+!!! note "译注"
+
+	Gamma也叫灰度系数，每种显示设备都有自己的Gamma值，都不相同，有一个公式：设备输出亮度 = 电压的Gamma次幂，任何设备Gamma基本上都不会等于1，等于1是一种理想的线性状态，这种理想状态是：如果电压和亮度都是在0到1的区间，那么多少电压就等于多少亮度。对于CRT，Gamma通常为2.2，因而，输出亮度 = 输入电压的2.2次幂，你可以从本节第二张图中看到Gamma2.2实际显示出来的总会比预期暗，相反Gamma0.45就会比理想预期亮，如果你讲Gamma0.45叠加到Gamma2.2的显示设备上，便会对偏暗的显示效果做到校正，这个简单的思路就是本节的核心

 人类所感知的亮度恰好和CRT所显示出来相似的指数关系非常匹配。为了更好的理解所有含义，请看下面的图片：

@@ -26,7 +34,7 @@

 ## Gamma校正

-Gamma校正的思路是在最终的颜色输出上应用监视器Gamma的倒数。回头看前面的Gamma曲线图，你会有一个短划线，它是监视器Gamma曲线的翻转曲线。我们在颜色显示到监视器的时候把每个颜色输出都加上这个翻转的Gamma曲线，这样应用了监视器Gamma以后最终的颜色将会变为线性的。我们所得到的中间色调就会更亮，所以虽然监视器使它们变暗，但是我们又将其平衡回来了。
+Gamma校正(Gamma Correction)的思路是在最终的颜色输出上应用监视器Gamma的倒数。回头看前面的Gamma曲线图，你会有一个短划线，它是监视器Gamma曲线的翻转曲线。我们在颜色显示到监视器的时候把每个颜色输出都加上这个翻转的Gamma曲线，这样应用了监视器Gamma以后最终的颜色将会变为线性的。我们所得到的中间色调就会更亮，所以虽然监视器使它们变暗，但是我们又将其平衡回来了。

 我们来看另一个例子。还是那个暗红色\((0.5, 0.0, 0.0)\)。在将颜色显示到监视器之前，我们先对颜色应用Gamma校正曲线。线性的颜色显示在监视器上相当于降低了\(2.2\)次幂的亮度，所以倒数就是\(1/2.2\)次幂。Gamma校正后的暗红色就会成为\((0.5, 0.0, 0.0)^{1/2.2} = (0.5, 0.0, 0.0)^{0.45} = (0.73, 0.0, 0.0)\)。校正后的颜色接着被发送给监视器，最终显示出来的颜色是\((0.73, 0.0, 0.0)^{2.2} = (0.5, 0.0, 0.0)\)。你会发现使用了Gamma校正，监视器最终会显示出我们在应用中设置的那种线性的颜色。

@@ -103,7 +111,7 @@ glTexImage2D(GL_TEXTURE_2D, 0, GL_SRGB, width, height, 0, GL_RGB, GL_UNSIGNED_BY

 ## 衰减

-在使用了gamma校正之后，另一个不同之处是光照衰减。真实的物理世界中，光照的衰减和光源的距离的平方成反比。
+在使用了gamma校正之后，另一个不同之处是光照衰减(Attenuation)。真实的物理世界中，光照的衰减和光源的距离的平方成反比。

 ```c++
 float attenuation = 1.0 / (distance * distance);
@@ -129,12 +137,8 @@ float attenuation = 1.0 / distance;

 总而言之，gamma校正使你可以在线性空间中进行操作。因为线性空间更符合物理世界，大多数物理公式现在都可以获得较好效果，比如真实的光的衰减。你的光照越真实，使用gamma校正获得漂亮的效果就越容易。这也正是为什么当引进gamma校正时，建议只去调整光照参数的原因。

- 
-
 ## 附加资源

-[cambridgeincolour.com](http://www.cambridgeincolour.com/tutorials/gamma-correction.htm):更多关于gamma和gamma校正的内容。
-
-[wolfire.com](http://blog.wolfire.com/2010/02/Gamma-correct-lighting): David Rosen关于在渲染领域使用gamma校正的好处。
-
-[renderwonk.com](http://renderwonk.com/blog/index.php/archive/adventures-with-gamma-correct-rendering/): 一些额外的实践上的思考。
+- [cambridgeincolour.com](http://www.cambridgeincolour.com/tutorials/gamma-correction.htm):更多关于gamma和gamma校正的内容。
+- [wolfire.com](http://blog.wolfire.com/2010/02/Gamma-correct-lighting): David Rosen关于在渲染领域使用gamma校正的好处。
+- [renderwonk.com](http://renderwonk.com/blog/index.php/archive/adventures-with-gamma-correct-rendering/): 一些额外的实践上的思考。
--- a/Lighting/03
+++ b/Lighting/03
@@ -1,6 +1,4 @@
-## 阴影映射(Shadow Mapping)
-
-本文作者JoeyDeVries，由Django翻译自[http://learnopengl.com](http://learnopengl.com)
+# 阴影映射

 原文     | [Shadow Mapping](http://learnopengl.com/#!Advanced-Lighting/Shadows/Shadow-Mapping)
      ---|---
@@ -20,9 +18,9 @@

 视频游戏中较多使用的一种技术是阴影贴图（shadow mapping），效果不错，而且相对容易实现。阴影贴图并不难以理解，性能也不会太低，而且非常容易扩展成更高级的算法（比如 [Omnidirectional Shadow Maps](http://learnopengl.com/#!Advanced-Lighting/Shadows/Point-Shadows)和 [Cascaded Shadow Maps](http://learnopengl.com/#!Advanced-Lighting/Shadows/CSM)）。

-### 阴影映射
+## 阴影映射

-阴影映射背后的思路非常简单：我们以光的位置为视角进行渲染，我们能看到的东西都将被点亮，看不见的一定是在阴影之中了。假设有一个地板，在光源和它之间有一个大盒子。由于光源处向光线方向看去，可以看到这个盒子，但看不到地板的一部分，这部分就应该在阴影中了。
+阴影映射(Shadow Mapping)背后的思路非常简单：我们以光的位置为视角进行渲染，我们能看到的东西都将被点亮，看不见的一定是在阴影之中了。假设有一个地板，在光源和它之间有一个大盒子。由于光源处向光线方向看去，可以看到这个盒子，但看不到地板的一部分，这部分就应该在阴影中了。

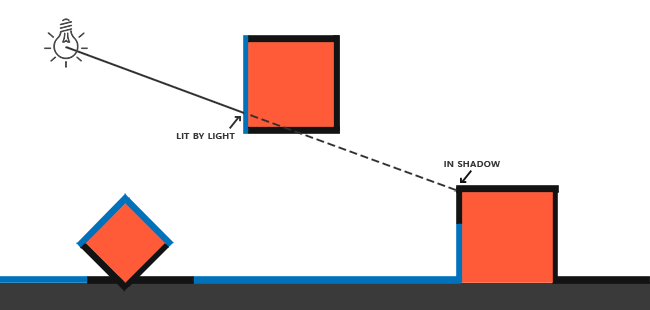
 ![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_theory.png)

@@ -44,9 +42,9 @@

 深度映射由两个步骤组成：首先，我们渲染深度贴图，然后我们像往常一样渲染场景，使用生成的深度贴图来计算片元是否在阴影之中。听起来有点复杂，但随着我们一步一步地讲解这个技术，就能理解了。

-### 深度贴图（depth map）
+## 深度贴图

-第一步我们需要生成一张深度贴图。深度贴图是从光的透视图里渲染的深度纹理，用它计算阴影。因为我们需要将场景的渲染结果储存到一个纹理中，我们将再次需要帧缓冲。
+第一步我们需要生成一张深度贴图(Depth Map)。深度贴图是从光的透视图里渲染的深度纹理，用它计算阴影。因为我们需要将场景的渲染结果储存到一个纹理中，我们将再次需要帧缓冲。

 首先，我们要为渲染的深度贴图创建一个帧缓冲对象：

@@ -105,9 +103,9 @@ RenderScene();

 这段代码隐去了一些细节，但它表达了阴影映射的基本思路。这里一定要记得调用glViewport。因为阴影贴图经常和我们原来渲染的场景（通常是窗口解析度）有着不同的解析度，我们需要改变视口（viewport）的参数以适应阴影贴图的尺寸。如果我们忘了更新视口参数，最后的深度贴图要么太小要么就不完整。

-### 光源空间的变换（light spacce transform）
+### 光源空间的变换

-前面那段代码中一个不清楚的函数是COnfigureShaderAndMatrices。它是用来在第二个步骤确保为每个物体设置了合适的投影和视图矩阵，以及相关的模型矩阵。然而，第一个步骤中，我们从光的位置的视野下使用了不同的投影和视图矩阵来渲染的场景。
+前面那段代码中一个不清楚的函数是`ConfigureShaderAndMatrices`。它是用来在第二个步骤确保为每个物体设置了合适的投影和视图矩阵，以及相关的模型矩阵。然而，第一个步骤中，我们从光的位置的视野下使用了不同的投影和视图矩阵来渲染的场景。

 因为我们使用的是一个所有光线都平行的定向光。出于这个原因，我们将为光源使用正交投影矩阵，透视图将没有任何变形：

@@ -132,9 +130,9 @@ glm::mat4 lightSpaceMatrix = lightProjection * lightView;

 这个lightSpaceMatrix正是前面我们称为\(T\)的那个变换矩阵。有了lightSpaceMatrix只要给shader提供光空间的投影和视图矩阵，我们就能像往常那样渲染场景了。然而，我们只关心深度值，并非所有片元计算都在我们的着色器中进行。为了提升性能，我们将使用一个与之不同但更为简单的着色器来渲染出深度贴图。

-### 渲染出深度贴图
+### 渲染至深度贴图

-当我们以光的透视图进行场景渲染的时候，我们会用一个比较简单的着色器，这个着色器除了把顶点变换到光空间以外，不会做得更多了。这个简单的着色器叫做simpleDepthShader，就是使用下面的这个着色器：
+当我们以光的透视图进行场景渲染的时候，我们会用一个比较简单的着色器，这个着色器除了把顶点变换到光空间以外，不会做得更多了。这个简单的着色器叫做`simpleDepthShader`，就是使用下面的这个着色器：

 ```c++
 #version 330 core
@@ -203,7 +201,7 @@ void main()

 你可以在[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/shadow_mapping_depth_map)获得把场景渲染成深度贴图的源码。

-### 渲染阴影
+## 渲染阴影

 正确地生成深度贴图以后我们就可以开始生成阴影了。这段代码在像素着色器中执行，用来检验一个片元是否在阴影之中，不过我们在顶点着色器中进行光空间的变换：

@@ -359,17 +357,17 @@ float ShadowCalculation(vec4 fragPosLightSpace)

 如果你做对了，你会看到地板和上有立方体的阴影。你可以从这里找到demo程序的[源码](http://learnopengl.com/code_viewer.php?code=advanced-lighting/shadow_mapping_shadows)。

-### 改进阴影贴图
+## 改进阴影贴图

 我们试图让阴影映射工作，但是你也看到了，阴影映射还是有点不真实，我们修复它才能获得更好的效果，这是下面的部分所关注的焦点。

-#### 阴影失真（shadow acne）
+### 阴影失真

 前面的图片中明显有不对的地方。放大看会发现明显的线条样式：

 ![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_acne.png)

-我们可以看到地板四边形渲染出很大一块交替黑线。这种阴影贴图的不真实感叫做阴影失真，下图解释了成因：
+我们可以看到地板四边形渲染出很大一块交替黑线。这种阴影贴图的不真实感叫做**阴影失真(Shadow Acne)**，下图解释了成因：

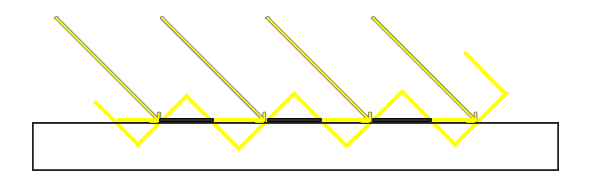
 ![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_acne_diagram.png)

@@ -400,13 +398,13 @@ float bias = max(0.05 * (1.0 - dot(normal, lightDir)), 0.005);

 选用正确的偏移数值，在不同的场景中需要一些像这样的轻微调校，但大多情况下，实际上就是增加偏移量直到所有失真都被移除的问题。

-#### 悬浮
+### 悬浮

 使用阴影偏移的一个缺点是你对物体的实际深度应用了平移。偏移有可能足够大，以至于可以看出阴影相对实际物体位置的偏移，你可以从下图看到这个现象（这是一个夸张的偏移值）：

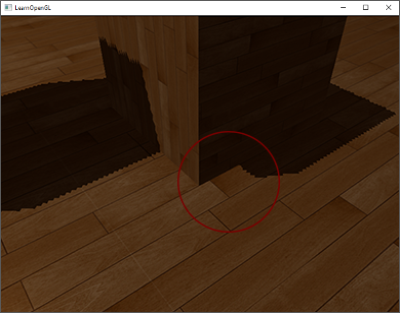
 ![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_peter_panning.png)

-这个阴影失真叫做Peter panning，因为物体看起来轻轻悬浮在表面之上（译注Peter Pan就是童话彼得潘，而panning有平移、悬浮之意，而且彼得潘是个会飞的男孩…）。我们可以使用一个叫技巧解决大部分的Peter panning问题：当渲染深度贴图时候使用正面剔除（front face culling）你也许记得在面剔除教程中OpenGL默认是背面剔除。我们要告诉OpenGL我们要剔除正面。
+这个阴影失真叫做悬浮(Peter Panning)，因为物体看起来轻轻悬浮在表面之上（译注Peter Pan就是童话彼得潘，而panning有平移、悬浮之意，而且彼得潘是个会飞的男孩…）。我们可以使用一个叫技巧解决大部分的Peter panning问题：当渲染深度贴图时候使用正面剔除（front face culling）你也许记得在面剔除教程中OpenGL默认是背面剔除。我们要告诉OpenGL我们要剔除正面。

 因为我们只需要深度贴图的深度值，对于实体物体无论我们用它们的正面还是背面都没问题。使用背面深度不会有错误，因为阴影在物体内部有错误我们也看不见。

@@ -424,7 +422,7 @@ glCullFace(GL_BACK); // 不要忘记设回原先的culling face

 另一个要考虑到的地方是接近阴影的物体仍然会出现不正确的效果。必须考虑到何时使用正面剔除对物体才有意义。不过使用普通的偏移值通常就能避免peter panning。

-#### 采样超出
+### 采样过多

 无论你喜不喜欢还有一个视觉差异，就是光的视锥不可见的区域一律被认为是处于阴影中，不管它真的处于阴影之中。出现这个状况是因为超出光的视锥的投影坐标比1.0大，这样采样的深度纹理就会超出他默认的0到1的范围。根据纹理环绕方式，我们将会得到不正确的深度结果，它不是基于真实的来自光源的深度值。

@@ -468,7 +466,7 @@ float ShadowCalculation(vec4 fragPosLightSpace)

 这些结果意味着，只有在深度贴图范围以内的被投影的fragment坐标才有阴影，所以任何超出范围的都将会没有阴影。由于在游戏中通常这只发生在远处，就会比我们之前的那个明显的黑色区域效果更真实。

-#### PCF
+## PCF

 阴影现在已经附着到场景中了，不过这仍不是我们想要的。如果你放大看阴影，阴影映射对解析度的依赖很快变得很明显。

@@ -509,10 +507,9 @@ shadow /= 9.0;
 实际上PCF还有更多的内容，以及很多技术要点需要考虑以提升柔和阴影的效果，但处于本章内容长度考虑，我们将留在以后讨论。

 
-
 ### 正交 vs 投影

-在渲染深度贴图的时候，正交和投影矩阵之间有所不同。正交投影矩阵并不会将场景用透视图进行变形，所有视线/光线都是平行的，这使它对于定向光来说是个很好的投影矩阵。然而透视投影矩阵，会将所有顶点根据透视关系进行变形，结果因此而不同。下图展示了两种投影方式所产生的不同阴影区域：
+在渲染深度贴图的时候，正交(Orthographic)和投影(Projection)矩阵之间有所不同。正交投影矩阵并不会将场景用透视图进行变形，所有视线/光线都是平行的，这使它对于定向光来说是个很好的投影矩阵。然而透视投影矩阵，会将所有顶点根据透视关系进行变形，结果因此而不同。下图展示了两种投影方式所产生的不同阴影区域：

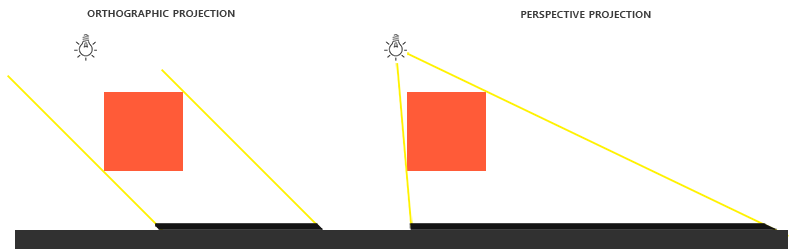
 ![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_projection.png)

@@ -545,14 +542,9 @@ void main()

 这个深度值与我们见到的用正交投影的很相似。需要注意的是，这个只适用于调试；正交或投影矩阵的深度检查仍然保持原样，因为相关的深度并没有改变。

-### 附加资源
+## 附加资源

-[Tutorial 16 : Shadow](http://www.opengl-tutorial.org/intermediate-tutorials/tutorial-16-shadow-mapping/)
-
-[mapping：opengl-tutorial.org](http://ogldev.atspace.co.uk/www/tutorial23/tutorial23.html) 提供的类似的阴影映射教程，里面有一些额外的解释。
-
-[Shadow Mapping – Part 1：ogldev](http://ogldev.atspace.co.uk/www/tutorial23/tutorial23.html)提供的另一个阴影映射教程。
-
-[How Shadow Mapping Works](https://www.youtube.com/watch?v=EsccgeUpdsM)：的一个第三方YouTube视频教程，里面解释了阴影映射及其实现。
-
-[Common Techniques to Improve Shadow Depth Maps](https://msdn.microsoft.com/en-us/library/windows/desktop/ee416324%28v=vs.85%29.aspx)：微软的一篇好文章，其中理出了很多提升阴影贴图质量的技术。
+- [Tutorial 16 : Shadow mapping](http://www.opengl-tutorial.org/intermediate-tutorials/tutorial-16-shadow-mapping/)：提供的类似的阴影映射教程，里面有一些额外的解释。
+- [Shadow Mapping – Part 1：ogldev](http://ogldev.atspace.co.uk/www/tutorial23/tutorial23.html)：提供的另一个阴影映射教程。
+- [How Shadow Mapping Works](https://www.youtube.com/watch?v=EsccgeUpdsM)：的一个第三方YouTube视频教程，里面解释了阴影映射及其实现。
+- [Common Techniques to Improve Shadow Depth Maps](https://msdn.microsoft.com/en-us/library/windows/desktop/ee416324%28v=vs.85%29.aspx)：微软的一篇好文章，其中理出了很多提升阴影贴图质量的技术。
--- a/Lighting/03
+++ b/Lighting/03
@@ -1,6 +1,10 @@
-本文作者JoeyDeVries，由Django翻译自[http://learnopengl.com](http://learnopengl.com)
+# 点光源阴影

-## 点光源阴影(Shadow Mapping)
+原文     | [Point Shadows](http://learnopengl.com/#!Advanced-Lighting/Shadows/Point-Shadows)
+      ---|---
+作者     | JoeyDeVries
+翻译     | [Django](http://bullteacher.com/)
+校对     | 暂无

 上个教程我们学到了如何使用阴影映射技术创建动态阴影。效果不错，但它只适合定向光，因为阴影只是在单一定向光源下生成的。所以它也叫定向阴影映射，深度（阴影）贴图生成自定向光的视角。

@@ -13,15 +17,15 @@
 本节代码基于前面的阴影映射教程，所以如果你对传统阴影映射不熟悉，还是建议先读一读阴影映射教程。
 算法和定向阴影映射差不多：我们从光的透视图生成一个深度贴图，基于当前fragment位置来对深度贴图采样，然后用储存的深度值和每个fragment进行对比，看看它是否在阴影中。定向阴影映射和万向阴影映射的主要不同在于深度贴图的使用上。

-对于深度贴图，我们需要从一个点光源的所有渲染场景，普通2D深度贴图不能工作；如果我们使用cubemap会怎样？因为cubemap可以储存6个面的环境数据，它可以将整个场景渲染到cubemap的每个面上，把它们当作点光源四周的深度值来采样。
+对于深度贴图，我们需要从一个点光源的所有渲染场景，普通2D深度贴图不能工作；如果我们使用立方体贴图会怎样？因为立方体贴图可以储存6个面的环境数据，它可以将整个场景渲染到立方体贴图的每个面上，把它们当作点光源四周的深度值来采样。

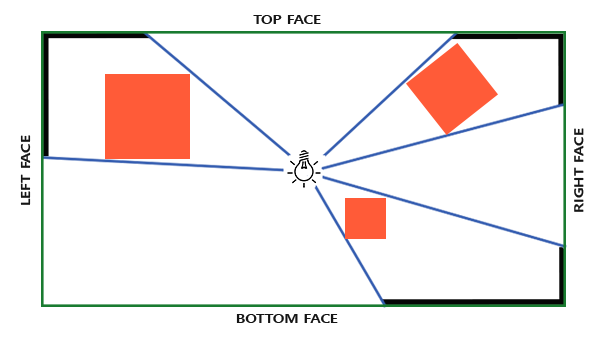
 ![](http://learnopengl.com/img/advanced-lighting/point_shadows_diagram.png)

-生成后的深度cubemap被传递到光照像素着色器，它会用一个方向向量来采样cubemap，从而得到当前的fragment的深度（从光的透视图）。大部分复杂的事情已经在阴影映射教程中讨论过了。算法只是在深度cubemap生成上稍微复杂一点。
+生成后的深度立方体贴图被传递到光照像素着色器，它会用一个方向向量来采样立方体贴图，从而得到当前的fragment的深度（从光的透视图）。大部分复杂的事情已经在阴影映射教程中讨论过了。算法只是在深度立方体贴图生成上稍微复杂一点。

-#### 生成深度cubemap
+## 生成深度立方体贴图

-为创建一个光周围的深度值的cubemap，我们必须渲染场景6次：每次一个面。显然渲染场景6次需要6个不同的视图矩阵，每次把一个不同的cubemap面附加到帧缓冲对象上。这看起来是这样的：
+为创建一个光周围的深度值的立方体贴图，我们必须渲染场景6次：每次一个面。显然渲染场景6次需要6个不同的视图矩阵，每次把一个不同的立方体贴图面附加到帧缓冲对象上。这看起来是这样的：

 ```c++
 for(int i = 0; i < 6; i++)
@@ -33,16 +37,16 @@ for(int i = 0; i < 6; i++)
 }
 ```

-这会很耗费性能因为一个深度贴图下需要进行很多渲染调用。这个教程中我们将转而使用另外的一个小技巧来做这件事，几何着色器允许我们使用一次渲染过程来建立深度cubemap。
+这会很耗费性能因为一个深度贴图下需要进行很多渲染调用。这个教程中我们将转而使用另外的一个小技巧来做这件事，几何着色器允许我们使用一次渲染过程来建立深度立方体贴图。

-首先，我们需要创建一个cubemap：
+首先，我们需要创建一个立方体贴图：

 ```c++
 GLuint depthCubemap;
 glGenTextures(1, &depthCubemap);
 ```

-然后生成cubemap的每个面，将它们作为2D深度值纹理图像：
+然后生成立方体贴图的每个面，将它们作为2D深度值纹理图像：

 ```c++
 const GLuint SHADOW_WIDTH = 1024, SHADOW_HEIGHT = 1024;
@@ -62,7 +66,7 @@ glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
 ```

-正常情况下，我们把cubemap纹理的一个面附加到帧缓冲对象上，渲染场景6次，每次将帧缓冲的深度缓冲目标改成不同cubemap面。由于我们将使用一个几何着色器，它允许我们把所有面在一个过程渲染，我们可以使用glFramebufferTexture直接把cubemap附加成帧缓冲的深度附件：
+正常情况下，我们把立方体贴图纹理的一个面附加到帧缓冲对象上，渲染场景6次，每次将帧缓冲的深度缓冲目标改成不同立方体贴图面。由于我们将使用一个几何着色器，它允许我们把所有面在一个过程渲染，我们可以使用glFramebufferTexture直接把立方体贴图附加成帧缓冲的深度附件：

 ```c++
 glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
@@ -72,9 +76,9 @@ glReadBuffer(GL_NONE);
 glBindFramebuffer(GL_FRAMEBUFFER, 0);
 ```

-还要记得调用glDrawBuffer和glReadBuffer：当生成一个深度cubemap时我们只关心深度值，所以我们必须显式告诉OpenGL这个帧缓冲对象不会渲染到一个颜色缓冲里。
+还要记得调用glDrawBuffer和glReadBuffer：当生成一个深度立方体贴图时我们只关心深度值，所以我们必须显式告诉OpenGL这个帧缓冲对象不会渲染到一个颜色缓冲里。

-万向阴影贴图有两个渲染阶段：首先我们生成深度贴图，然后我们正常使用深度贴图渲染，在场景中创建阴影。帧缓冲对象和cubemap的处理看起是这样的：
+万向阴影贴图有两个渲染阶段：首先我们生成深度贴图，然后我们正常使用深度贴图渲染，在场景中创建阴影。帧缓冲对象和立方体贴图的处理看起是这样的：

 ```c++
 // 1. first render to depth cubemap
@@ -92,11 +96,11 @@ glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
 RenderScene();
 ```

-这个过程和默认的阴影映射一样，尽管这次我们渲染和使用的是一个cubemap深度纹理，而不是2D深度纹理。在我们实际开始从光的视角的所有方向渲染场景之前，我们先得计算出合适的变换矩阵。
+这个过程和默认的阴影映射一样，尽管这次我们渲染和使用的是一个立方体贴图深度纹理，而不是2D深度纹理。在我们实际开始从光的视角的所有方向渲染场景之前，我们先得计算出合适的变换矩阵。

 ### 光空间的变换

-设置了帧缓冲和cubemap，我们需要一些方法来讲场景的所有几何体变换到6个光的方向中相应的光空间。与阴影映射教程类似，我们将需要一个光空间的变换矩阵T，但是这次是每个面都有一个。
+设置了帧缓冲和立方体贴图，我们需要一些方法来讲场景的所有几何体变换到6个光的方向中相应的光空间。与阴影映射教程类似，我们将需要一个光空间的变换矩阵T，但是这次是每个面都有一个。

 每个光空间的变换矩阵包含了投影和视图矩阵。对于投影矩阵来说，我们将使用一个透视投影矩阵；光源代表一个空间中的点，所以透视投影矩阵更有意义。每个光空间变换矩阵使用同样的投影矩阵：

@@ -107,9 +111,9 @@ GLfloat far = 25.0f;
 glm::mat4 shadowProj = glm::perspective(90.0f, aspect, near, far);
 ```

-非常重要的一点是，这里glm::perspective的视野参数，设置为90度。90度我们才能保证视野足够大到可以合适地填满cubemap的一个面，cubemap的所有面都能与其他面在边缘对齐。
+非常重要的一点是，这里glm::perspective的视野参数，设置为90度。90度我们才能保证视野足够大到可以合适地填满立方体贴图的一个面，立方体贴图的所有面都能与其他面在边缘对齐。

-因为投影矩阵在每个方向上并不会改变，我们可以在6个变换矩阵中重复使用。我们要为每个方向提供一个不同的视图矩阵。用glm::lookAt创建6个观察方向，每个都按顺序注视着cubemap的的一个方向：右、左、上、下、近、远：
+因为投影矩阵在每个方向上并不会改变，我们可以在6个变换矩阵中重复使用。我们要为每个方向提供一个不同的视图矩阵。用glm::lookAt创建6个观察方向，每个都按顺序注视着立方体贴图的的一个方向：右、左、上、下、近、远：

 ```c++
 std::vector<glm::mat4> shadowTransforms;
@@ -127,15 +131,13 @@ shadowTransforms.push_back(shadowProj *
                 glm::lookAt(lightPos, lightPos + glm::vec3(0.0,0.0,-1.0), glm::vec3(0.0,-1.0,0.0));
 ```

-这里我们创建了6个视图矩阵，把它们乘以投影矩阵，来得到6个不同的光空间变换矩阵。glm::lookAt的target参数是它注视的cubemap的面的一个方向。
-
-这些变换矩阵发送到着色器渲染到cubemap里。
-
+这里我们创建了6个视图矩阵，把它们乘以投影矩阵，来得到6个不同的光空间变换矩阵。glm::lookAt的target参数是它注视的立方体贴图的面的一个方向。

+这些变换矩阵发送到着色器渲染到立方体贴图里。

 ### 深度着色器

-为了把值渲染到深度cubemap，我们将需要3个着色器：顶点和像素着色器，以及一个它们之间的几何着色器。
+为了把值渲染到深度立方体贴图，我们将需要3个着色器：顶点和像素着色器，以及一个它们之间的几何着色器。

 几何着色器是负责将所有世界空间的顶点变换到6个不同的光空间的着色器。因此顶点着色器简单地将顶点变换到世界空间，然后直接发送到几何着色器：

@@ -153,7 +155,7 @@ void main()

 紧接着几何着色器以3个三角形的顶点作为输入，它还有一个光空间变换矩阵的uniform数组。几何着色器接下来会负责将顶点变换到光空间；这里它开始变得有趣了。

-几何着色器有一个内建变量叫做gl_Layer，它指定发散出基本图形送到cubemap的哪个面。当不管它时，几何着色器就会像往常一样把它的基本图形发送到输送管道的下一阶段，但当我们更新这个变量就能控制每个基本图形将渲染到cubemap的哪一个面。当然这只有当我们有了一个附加到激活的帧缓冲的cubemap纹理才有效：
+几何着色器有一个内建变量叫做gl_Layer，它指定发散出基本图形送到立方体贴图的哪个面。当不管它时，几何着色器就会像往常一样把它的基本图形发送到输送管道的下一阶段，但当我们更新这个变量就能控制每个基本图形将渲染到立方体贴图的哪一个面。当然这只有当我们有了一个附加到激活的帧缓冲的立方体贴图纹理才有效：

 ```c++
 #version 330 core
@@ -180,7 +182,7 @@ void main()
 }
 ```

-几何着色器相对简单。我们输入一个三角形，输出总共6个三角形（6*3顶点，所以总共18个顶点）。在main函数中，我们遍历cubemap的6个面，我们每个面指定为一个输出面，把这个面的interger（整数）存到gl_Layer。然后，我们通过把面的光空间变换矩阵乘以FragPos，将每个世界空间顶点变换到相关的光空间，生成每个三角形。注意，我们还要将最后的FragPos变量发送给像素着色器，我们需要计算一个深度值。
+几何着色器相对简单。我们输入一个三角形，输出总共6个三角形（6*3顶点，所以总共18个顶点）。在main函数中，我们遍历立方体贴图的6个面，我们每个面指定为一个输出面，把这个面的interger（整数）存到gl_Layer。然后，我们通过把面的光空间变换矩阵乘以FragPos，将每个世界空间顶点变换到相关的光空间，生成每个三角形。注意，我们还要将最后的FragPos变量发送给像素着色器，我们需要计算一个深度值。

 上个教程，我们使用的是一个空的像素着色器，让OpenGL配置深度贴图的深度值。这次我们将计算自己的深度，这个深度就是每个fragment位置和光源位置之间的线性距离。计算自己的深度值使得之后的阴影计算更加直观。

@@ -206,11 +208,11 @@ void main()

 像素着色器将来自几何着色器的FragPos、光的位置向量和视锥的远平面值作为输入。这里我们把fragment和光源之间的距离，映射到0到1的范围，把它写入为fragment的深度值。

-使用这些着色器渲染场景，cubemap附加的帧缓冲对象激活以后，你会得到一个完全填充的深度cubemap，以便于进行第二阶段的阴影计算。
+使用这些着色器渲染场景，立方体贴图附加的帧缓冲对象激活以后，你会得到一个完全填充的深度立方体贴图，以便于进行第二阶段的阴影计算。

-### 万向阴影贴图
+## 万向阴影贴图

-所有事情都做好了，是时候来渲染万向阴影了。这个过程和定向阴影映射教程相似，尽管这次我们绑定的深度贴图是一个cubemap，而不是2D纹理，并且将光的投影的远平面发送给了着色器。
+所有事情都做好了，是时候来渲染万向阴影(Omnidirectional Shadow)了。这个过程和定向阴影映射教程相似，尽管这次我们绑定的深度贴图是一个立方体贴图，而不是2D纹理，并且将光的投影的远平面发送给了着色器。

 ```c++
 glViewport(0, 0, SCR_WIDTH, SCR_HEIGHT);
@@ -309,9 +311,9 @@ void main()

 有一些细微的不同：光照代码一样，但我们现在有了一个uniform变量samplerCube，shadowCalculation函数用fragment的位置作为它的参数，取代了光空间的fragment位置。我们现在还要引入光的视锥的远平面值，后面我们会需要它。像素着色器的最后，我们计算出阴影元素，当fragment在阴影中时它是1.0，不在阴影中时是0.0。我们使用计算出来的阴影元素去影响光照的diffuse和specular元素。

-在ShadowCalculation函数中有很多不同之处，现在是从cubemap中进行采样，不再使用2D纹理了。我们来一步一步的讨论一下的它的内容。
+在ShadowCalculation函数中有很多不同之处，现在是从立方体贴图中进行采样，不再使用2D纹理了。我们来一步一步的讨论一下的它的内容。

-我们需要做的第一件事是获取cubemap的森都。你可能已经从教程的cubemap部分想到，我们已经将深度储存为fragment和光位置之间的距离了；我们这里采用相似的处理方式：
+我们需要做的第一件事是获取立方体贴图的森都。你可能已经从教程的立方体贴图部分想到，我们已经将深度储存为fragment和光位置之间的距离了；我们这里采用相似的处理方式：

 ```c++
 float ShadowCalculation(vec3 fragPos)
@@ -321,7 +323,7 @@ float ShadowCalculation(vec3 fragPos)
 }
 ```

-在这里，我们得到了fragment的位置与光的位置之间的不同的向量，使用这个向量作为一个方向向量去对cubemap进行采样。方向向量不需要是单位向量，所以无需对它进行标准化。最后的closestDepth是光源和它最接近的可见fragment之间的标准化的深度值。
+在这里，我们得到了fragment的位置与光的位置之间的不同的向量，使用这个向量作为一个方向向量去对立方体贴图进行采样。方向向量不需要是单位向量，所以无需对它进行标准化。最后的closestDepth是光源和它最接近的可见fragment之间的标准化的深度值。

 closestDepth值现在在0到1的范围内了，所以我们先将其转换会0到far_plane的范围，这需要把他乘以far_plane：

@@ -329,7 +331,7 @@ closestDepth值现在在0到1的范围内了，所以我们先将其转换会0
 closestDepth *= far_plane;
 ```

-下一步我们获取当前fragment和光源之间的深度值，我们可以简单的使用fragToLight的长度来获取它，这取决于我们如何计算cubemap中的深度值：
+下一步我们获取当前fragment和光源之间的深度值，我们可以简单的使用fragToLight的长度来获取它，这取决于我们如何计算立方体贴图中的深度值：

 ```c++
 float currentDepth = length(fragToLight);
@@ -371,7 +373,7 @@ float ShadowCalculation(vec3 fragPos)

 你可以从这里找到这个[demo的源码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/point_shadows)、[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/point_shadows&type=vertex)和[片段](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/point_shadows&type=fragment)着色器。

-#### 把cubemap深度缓冲显示出来
+### 显示立方体贴图深度缓冲

 如果你想我一样第一次并没有做对，那么就要进行调试排错，将深度贴图显示出来以检查其是否正确。因为我们不再用2D深度贴图纹理，深度贴图的显示不会那么显而易见。

@@ -385,9 +387,9 @@ FragColor = vec4(vec3(closestDepth / far_plane), 1.0);

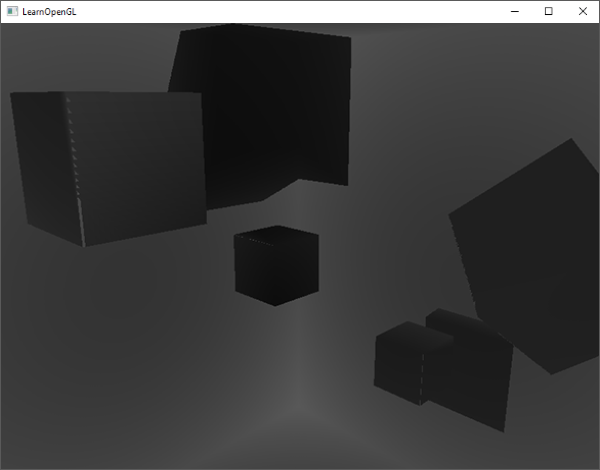
 ![](http://learnopengl.com/img/advanced-lighting/point_shadows_depth_cubemap.png)

-你可能也注意到了带阴影部分在墙外。如果看起来和这个差不多，你就知道深度cubemap生成的没错。否则你可能做错了什么，也许是closestDepth仍然还在0到far_plane的范围。
+你可能也注意到了带阴影部分在墙外。如果看起来和这个差不多，你就知道深度立方体贴图生成的没错。否则你可能做错了什么，也许是closestDepth仍然还在0到far_plane的范围。

-#### PCF
+## PCF

 由于万向阴影贴图基于传统阴影映射的原则，它便也继承了由解析度产生的非真实感。如果你放大就会看到锯齿边了。PCF或称Percentage-closer filtering允许我们通过对fragment位置周围过滤多个样本，并对结果平均化。

@@ -435,7 +437,7 @@ vec3 sampleOffsetDirections[20] = vec3[]
 );
 ```

-然后我们把PCF算法与从sampleOffsetDirections得到的样本数量进行适配，使用它们从cubemap里采样。这么做的好处是与之前的PCF算法相比，我们需要的样本数量变少了。
+然后我们把PCF算法与从sampleOffsetDirections得到的样本数量进行适配，使用它们从立方体贴图里采样。这么做的好处是与之前的PCF算法相比，我们需要的样本数量变少了。

 ```c++
 float shadow = 0.0;
@@ -453,7 +455,7 @@ for(int i = 0; i < samples; ++i)
 shadow /= float(samples);
 ```

-这里我们把一个偏移量添加到指定的diskRadius中，它在fragToLight方向向量周围从cubemap里采样。
+这里我们把一个偏移量添加到指定的diskRadius中，它在fragToLight方向向量周围从立方体贴图里采样。

 另一个在这里可以应用的有意思的技巧是，我们可以基于观察者里一个fragment的距离来改变diskRadius；这样我们就能根据观察者的距离来增加偏移半径了，当距离更远的时候阴影更柔和，更近了就更锐利。

@@ -470,12 +472,8 @@ PCF算法的结果如果没有变得更好，也是非常不错的，这是柔

 我还要提醒一下使用几何着色器来生成深度贴图不会一定比每个面渲染场景6次更快。使用几何着色器有它自己的性能局限，在第一个阶段使用它可能获得更好的性能表现。这取决于环境的类型，以及特定的显卡驱动等等，所以如果你很关心性能，就要确保对两种方法有大致了解，然后选择对你场景来说更高效的那个。我个人还是喜欢使用几何着色器来进行阴影映射，原因很简单，因为它们使用起来更简单。

+## 附加资源

-
-### 附加资源
-
-[Shadow Mapping for point light sources in OpenGL](http://www.sunandblackcat.com/tipFullView.php?l=eng&topicid=36)：sunandblackcat的万向阴影映射教程。
-
-[Multipass Shadow Mapping With Point Lights](http://ogldev.atspace.co.uk/www/tutorial43/tutorial43.html)：ogldev的万向阴影映射教程。
-
-[Omni-directional Shadows](http://www.cg.tuwien.ac.at/~husky/RTR/OmnidirShadows-whyCaps.pdf)：Peter Houska的关于万向阴影映射的一组很好的ppt。
+- [Shadow Mapping for point light sources in OpenGL](http://www.sunandblackcat.com/tipFullView.php?l=eng&topicid=36)：sunandblackcat的万向阴影映射教程。
+- [Multipass Shadow Mapping With Point Lights](http://ogldev.atspace.co.uk/www/tutorial43/tutorial43.html)：ogldev的万向阴影映射教程。
+- [Omni-directional Shadows](http://www.cg.tuwien.ac.at/~husky/RTR/OmnidirShadows-whyCaps.pdf)：Peter Houska的关于万向阴影映射的一组很好的ppt。
--- a/Lighting/03
+++ b/Lighting/03
@@ -1,6 +1,6 @@
 # CSM

-# 未完成
+**未完成**

 这篇教程暂时还没有完成，您可以经常来刷新看看是否有更新的进展。

--- a/Lighting/04
+++ b/Lighting/04
@@ -1,6 +1,10 @@
-本文作者JoeyDeVries，由Django翻译自[http://learnopengl.com](http://learnopengl.com)
+# 法线贴图

-## 法线贴图 （Normal Mapping）
+原文     | [Normal Mapping](http://learnopengl.com/#!Advanced-Lighting/Normal-Mapping)
+      ---|---
+作者     | JoeyDeVries
+翻译     | [Django](http://bullteacher.com/)
+校对     | 暂无

 我们的场景中已经充满了多边形物体，其中每个都可能由成百上千平坦的三角形组成。我们以向三角形上附加纹理的方式来增加额外细节，提升真实感，隐藏多边形几何体是由无数三角形组成的事实。纹理确有助益，然而当你近看它们时，这个事实便隐藏不住了。现实中的物体表面并非是平坦的，而是表现出无数（凹凸不平的）细节。

@@ -20,9 +24,7 @@

 你可以看到细节获得了极大提升，开销却不大。因为我们只需要改变每个fragment的法线向量，并不需要改变所有光照公式。现在我们是为每个fragment传递一个法线，不再使用插值表面法线。这样光照使表面拥有了自己的细节。

- 
-
-### 法线贴图
+## 法线贴图

 为使法线贴图工作，我们需要为每个fragment提供一个法线。像diffuse贴图和specular贴图一样，我们可以使用一个2D纹理来储存法线数据。2D纹理不仅可以储存颜色和光照数据，还可以储存法线向量。这样我们可以从2D纹理中采样得到特定纹理的法线向量。

@@ -76,9 +78,7 @@ void main()

 另一个稍微有点难的解决方案是，在一个不同的坐标空间中进行光照，这个坐标空间里，法线贴图向量总是指向这个坐标空间的正z方向；所有的光照向量都相对与这个正z方向进行变换。这样我们就能始终使用同样的法线贴图，不管朝向问题。这个坐标空间叫做切线空间（tangent space）。

- 
-
-### 切线空间
+## 切线空间

 法线贴图中的法线向量在切线空间中，法线永远指着正z方向。切线空间是位于三角形表面之上的空间：法线相对于单个三角形的本地参考框架。它就像法线贴图向量的本地空间；它们都被定义为指向正z方向，无论最终变换到什么方向。使用一个特定的矩阵我们就能将本地/切线空寂中的法线向量转成世界或视图坐标，使它们转向到最终的贴图表面的方向。

@@ -86,7 +86,7 @@ void main()

 这种矩阵叫做TBN矩阵这三个字母分别代表tangent、bitangent和normal向量。这是建构这个矩阵所需的向量。要建构这样一个把切线空间转变为不同空间的变异矩阵，我们需要三个相互垂直的向量，它们沿一个表面的法线贴图对齐于：上、右、前；这和我们在[摄像机教程](http://learnopengl-cn.readthedocs.org/zh/latest/01%20Getting%20started/09%20Camera/)中做的类似。

-已知上向量是表面的法线向量。右和前向量是切线和副切线向量。下面的图片展示了一个表面的三个向量：
+已知上向量是表面的法线向量。右和前向量是切线(Tagent)和副切线(Bitangent)向量。下面的图片展示了一个表面的三个向量：

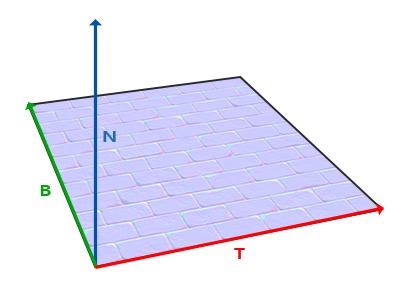
 ![](http://learnopengl.com/img/advanced-lighting/normal_mapping_tbn_vectors.png)

@@ -160,7 +160,6 @@ glm::vec3 nm(0.0, 0.0, 1.0);

 我们先计算第一个三角形的边和deltaUV坐标：

-
 ```c++
 glm::vec3 edge1 = pos2 - pos1;
 glm::vec3 edge2 = pos3 - pos1;
@@ -168,7 +167,6 @@ glm::vec2 deltaUV1 = uv2 - uv1;
 glm::vec2 deltaUV2 = uv3 - uv1;
 ```

-
 有了计算切线和副切线的必备数据，我们就可以开始写出来自于前面部分中的下列等式：

 ```c++
@@ -340,7 +338,7 @@ RenderQuad();

 你可以在这里找到[源代码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/normal_mapping)、[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/normal_mapping&type=vertex)和[像素](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/normal_mapping&type=fragment)着色器。

-### 复杂的物体
+### 复杂物体

 我们已经说明了如何通过手工计算切线和副切线向量，来使用切线空间和法线贴图。幸运的是，计算这些切线和副切线向量对于你来说不是经常能遇到的事；大多数时候，在模型加载器中实现了一次就行了，我们是在使用了Assimp的那个加载器中实现的。

@@ -385,9 +383,7 @@ vector<Texture> specularMaps = this->loadMaterialTextures(

 高精度网格和使用法线贴图的低精度网格几乎区分不出来。所以法线贴图不仅看起来漂亮，它也是一个将高精度多边形转换为低精度多边形而不失细节的重要工具。

- 
-
-### 最后一件事
+## 最后一件事

 关于法线贴图还有最后一个技巧要讨论，它可以在不必花费太多性能开销的情况下稍稍提升画质表现。

@@ -408,9 +404,9 @@ mat3 TBN = mat3(T, B, N)

 这样稍微花费一些性能开销就能对法线贴图进行一点提升。看看最后的那个附加资源： Normal Mapping Mathematics视频，里面有对这个过程的解释。

-### 附加资源
+## 附加资源

-* [Tutorial 26: Normal Mapping](http://ogldev.atspace.co.uk/www/tutorial26/tutorial26.html)：ogldev的法线贴图教程。
-* [How Normal Mapping Works](https://www.youtube.com/watch?v=LIOPYmknj5Q)：TheBennyBox的讲述法线贴图如何工作的视频。
-* [Normal Mapping Mathematics](https://www.youtube.com/watch?v=4FaWLgsctqY)：TheBennyBox关于法线贴图的数学原理的教程。
-* [Tutorial 13: Normal Mapping](http://www.opengl-tutorial.org/intermediate-tutorials/tutorial-13-normal-mapping/)：opengl-tutorial.org提供的法线贴图教程。
+- [Tutorial 26: Normal Mapping](http://ogldev.atspace.co.uk/www/tutorial26/tutorial26.html)：ogldev的法线贴图教程。
+- [How Normal Mapping Works](https://www.youtube.com/watch?v=LIOPYmknj5Q)：TheBennyBox的讲述法线贴图如何工作的视频。
+- [Normal Mapping Mathematics](https://www.youtube.com/watch?v=4FaWLgsctqY)：TheBennyBox关于法线贴图的数学原理的教程。
+- [Tutorial 13: Normal Mapping](http://www.opengl-tutorial.org/intermediate-tutorials/tutorial-13-normal-mapping/)：opengl-tutorial.org提供的法线贴图教程。
--- a/Lighting/05
+++ b/Lighting/05
@@ -1,10 +1,14 @@
-本文作者JoeyDeVries，由Django翻译自[http://learnopengl.com](http://learnopengl.com)
+# 视差贴图

-## 视差贴图(Parallax Mapping)
+原文     | [Parallax Mapping](http://learnopengl.com/#!Advanced-Lighting/Parallax-Mapping)
+      ---|---
+作者     | JoeyDeVries
+翻译     | [Django](http://bullteacher.com/)
+校对     | 暂无

-视差贴图技术和法线贴图差不多，但它有着不同的原则。和法线贴图一样视差贴图能够极大提升表面细节，使之具有深度感。它也是利用了视错觉，然而对深度有着更好的表达，与法线贴图一起用能够产生难以置信的效果。视差贴图和光照无关，我在这里是作为法线贴图的技术延续来讨论它的。需要注意的是在开始学习视差贴图之前强烈建议先对法线贴图，特别是切线空间有较好的理解。
+视差贴图(Parallax Mapping)技术和法线贴图差不多，但它有着不同的原则。和法线贴图一样视差贴图能够极大提升表面细节，使之具有深度感。它也是利用了视错觉，然而对深度有着更好的表达，与法线贴图一起用能够产生难以置信的效果。视差贴图和光照无关，我在这里是作为法线贴图的技术延续来讨论它的。需要注意的是在开始学习视差贴图之前强烈建议先对法线贴图，特别是切线空间有较好的理解。

-视差贴图属于位移贴图（译注：displacement mapping也叫置换贴图）技术的一种，它对根据储存在纹理中的几何信息对顶点进行位移或偏移。一种实现的方式是比如有1000个顶点，更具纹理中的数据对平面特定区域的顶点的高度进行位移。这样的每个纹理像素包含了高度值纹理叫做高度贴图。一张简单的砖块表面的告诉贴图如下所示：
+视差贴图属于位移贴图(Displacement Mapping)技术的一种，它对根据储存在纹理中的几何信息对顶点进行位移或偏移。一种实现的方式是比如有1000个顶点，更具纹理中的数据对平面特定区域的顶点的高度进行位移。这样的每个纹理像素包含了高度值纹理叫做高度贴图。一张简单的砖块表面的告诉贴图如下所示：

 ![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_height_map.png)

@@ -36,9 +40,7 @@

 理论都有了，下面我们来动手实现视差贴图。

- 
-
-### 视差贴图
+## 视差贴图

 我们将使用一个简单的2D平面，在把它发送给GPU之前我们先计算它的切线和副切线向量；和法线贴图教程做的差不多。我们将向平面贴diffuse纹理、法线贴图以及一个位移贴图，你可以点击链接下载。这个例子中我们将视差贴图和法线贴图连用。因为视差贴图生成表面位移了的幻觉，当光照不匹配时这种幻觉就被破坏了。法线贴图通常根据高度贴图生成，法线贴图和高度贴图一起用能保证光照能和位移想匹配。

@@ -174,11 +176,9 @@ if(texCoords.x > 1.0 || texCoords.y > 1.0 || texCoords.x < 0.0 || texCoords.y <

 问题的原因是这只是一个大致近似的视差映射。还有一些技巧让我们在陡峭的高度上能够获得几乎完美的结果，即使当以一定角度观看的时候。例如，我们不再使用单一样本，取而代之使用多样本来找到最近点\(\color{blue}B\)会得到怎样的结果？

+## 陡峭视差映射

-
-### 陡峭视差映射（Steep Parallax Mapping）
-
-陡峭视差映射是视差映射的扩展，原则是一样的，但不是使用一个样本而是多个样本来确定向量\(\color{brown}{\bar{P}}\)到\(\color{blue}B\)。它能得到更好的结果，它将总深度范围分布到同一个深度/高度的多个层中。从每个层中我们沿着\(\color{brown}{\bar{P}}\)方向移动采样纹理坐标，直到我们找到了一个采样得到的低于当前层的深度值的深度值。看看下面的图片：
+陡峭视差映射(Steep Parallax Mapping)是视差映射的扩展，原则是一样的，但不是使用一个样本而是多个样本来确定向量\(\color{brown}{\bar{P}}\)到\(\color{blue}B\)。它能得到更好的结果，它将总深度范围分布到同一个深度/高度的多个层中。从每个层中我们沿着\(\color{brown}{\bar{P}}\)方向移动采样纹理坐标，直到我们找到了一个采样得到的低于当前层的深度值的深度值。看看下面的图片：

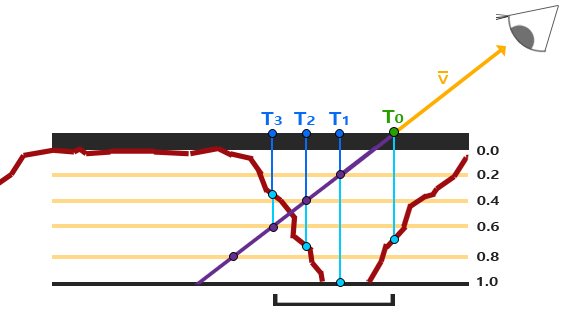
 ![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_steep_parallax_mapping_diagram.png)

@@ -256,15 +256,15 @@ float numLayers = mix(maxLayers, minLayers, abs(dot(vec3(0.0, 0.0, 1.0), viewDir

 

-### Parallax Occlusion Mapping
+## 视差遮蔽映射

-Parallax Occlusion Mapping和陡峭视差映射的原则相同，但不是用触碰的第一个深度层的纹理坐标，而是在触碰之前和之后，在深度层之间进行线性插值。我们根据表面的高度距离啷个深度层的深度层值的距离来确定线性插值的大小。看看下面的图pain就能了解它是如何工作的：
+视差遮蔽映射(Parallax Occlusion Mapping)和陡峭视差映射的原则相同，但不是用触碰的第一个深度层的纹理坐标，而是在触碰之前和之后，在深度层之间进行线性插值。我们根据表面的高度距离啷个深度层的深度层值的距离来确定线性插值的大小。看看下面的图片就能了解它是如何工作的：

 [](http://learnopengl.com/img/advanced-lighting/parallax_mapping_parallax_occlusion_mapping_diagram.png)

 你可以看到大部分和陡峭视差映射一样，不一样的地方是有个额外的步骤，两个深度层的纹理坐标围绕着交叉点的线性插值。这也是近似的，但是比陡峭视差映射更精确。

-Parallax Occlusion Mapping的代码基于陡峭视差映射，所以并不难：
+视差遮蔽映射的代码基于陡峭视差映射，所以并不难：

 ```c++
 [...] // steep parallax mapping code here
@@ -285,7 +285,7 @@ return finalTexCoords;

 在对（位移的）表面几何进行交叉，找到深度层之后，我们获取交叉前的纹理坐标。然后我们计算来自相应深度层的几何之间的深度之间的距离，并在两个值之间进行插值。线性插值的方式是在两个层的纹理坐标之间进行的基础插值。函数最后返回最终的经过插值的纹理坐标。

-Parallax Occlusion Mapping的效果非常好，尽管有一些可以看到的轻微的不真实和锯齿的问题，这仍是一个好交易，因为除非是放得非常大或者观察角度特别陡，否则也看不到。
+视差遮蔽映射的效果非常好，尽管有一些可以看到的轻微的不真实和锯齿的问题，这仍是一个好交易，因为除非是放得非常大或者观察角度特别陡，否则也看不到。

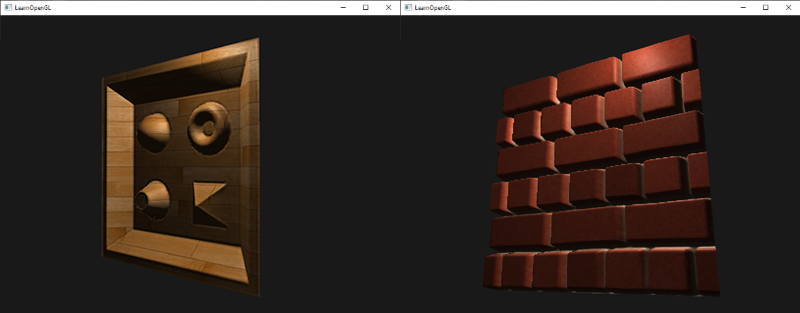
 ![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_parallax_occlusion_mapping.png)

@@ -295,8 +295,7 @@ Parallax Occlusion Mapping的效果非常好，尽管有一些可以看到的轻

 

-### 附加资源
+## 附加资源

-[Parallax Occlusion Mapping in GLSL](http://sunandblackcat.com/tipFullView.php?topicid=28)：sunandblackcat.com上的视差贴图教程。
-
-[How Parallax Displacement Mapping Works](https://www.youtube.com/watch?v=xvOT62L-fQI)：TheBennyBox的关于视差贴图原理的视频教程。
+- [Parallax Occlusion Mapping in GLSL](http://sunandblackcat.com/tipFullView.php?topicid=28)：sunandblackcat.com上的视差贴图教程。
+- [How Parallax Displacement Mapping Works](https://www.youtube.com/watch?v=xvOT62L-fQI)：TheBennyBox的关于视差贴图原理的视频教程。
--- a/Lighting/06
+++ b/Lighting/06
@@ -1,45 +1,49 @@
-本文作者JoeyDeVries，由Meow J翻译自[http://learnopengl.com](http://learnopengl.com/#!Advanced-Lighting/HDR)
+# HDR

-## HDR
+原文     | [HDR](http://learnopengl.com/#!Advanced-Lighting/HDR)
+      ---|---
+作者     | JoeyDeVries
+翻译     | Meow J
+校对     | 暂无

-一般来说，当存储在帧缓冲(Framebuffer)中时，亮度和颜色的值是默认被限制在0.0到1.0之间的. 这个看起来无辜的语句使我们一直将亮度与颜色的值设置在这个范围内，尝试着与场景契合. 这样是能够运行的，也能给出还不错的效果. 但是如果我们遇上了一个特定的区域，其中有多个亮光源使这些数值总和超过了1.0，又会发生什么呢? 答案是这些片段中超过1.0的亮度或者颜色值会被约束在1.0, 从而导致场景混成一片，难以分辨:
+一般来说，当存储在帧缓冲(Framebuffer)中时，亮度和颜色的值是默认被限制在0.0到1.0之间的。这个看起来无辜的语句使我们一直将亮度与颜色的值设置在这个范围内，尝试着与场景契合。这样是能够运行的，也能给出还不错的效果。但是如果我们遇上了一个特定的区域，其中有多个亮光源使这些数值总和超过了1.0，又会发生什么呢？答案是这些片段中超过1.0的亮度或者颜色值会被约束在1.0，从而导致场景混成一片，难以分辨：

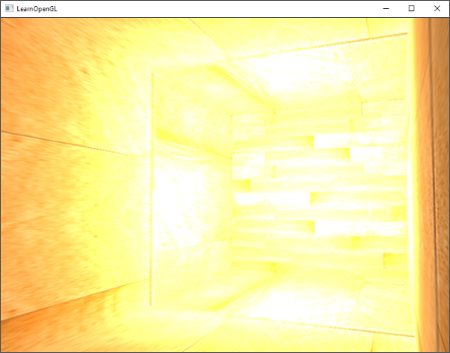
 ![](http://learnopengl.com/img/advanced-lighting/hdr_clamped.png)

-这是由于大量片段的颜色值都非常接近1.0，在很大一个区域内每一个亮的片段都有相同的白色. 这损失了很多的细节，使场景看起来非常假.
+这是由于大量片段的颜色值都非常接近1.0，在很大一个区域内每一个亮的片段都有相同的白色。这损失了很多的细节，使场景看起来非常假。

-解决这个问题的一个方案是减小光源的强度从而保证场景内没有一个片段亮于1.0. 然而这并不是一个好的方案，因为你需要使用不切实际的光照参数. 一个更好的方案是让颜色暂时超过1.0，然后将其转换至0.0到1.0的区间内，从而防止损失细节.
+解决这个问题的一个方案是减小光源的强度从而保证场景内没有一个片段亮于1.0。然而这并不是一个好的方案，因为你需要使用不切实际的光照参数。一个更好的方案是让颜色暂时超过1.0，然后将其转换至0.0到1.0的区间内，从而防止损失细节。

-显示器被限制为只能显示值为0.0到1.0间的颜色，但是在光照方程中却没有这个限制. 通过使片段的颜色超过1.0，我们有了一个更大的颜色范围，这也被称作HDR(High Dynamic Range, 高动态范围). 有了HDR，亮的东西可以变得非常亮，暗的东西可以变得非常暗，而且充满细节.
+显示器被限制为只能显示值为0.0到1.0间的颜色，但是在光照方程中却没有这个限制。通过使片段的颜色超过1.0，我们有了一个更大的颜色范围，这也被称作**HDR(High Dynamic Range, 高动态范围)**。有了HDR，亮的东西可以变得非常亮，暗的东西可以变得非常暗，而且充满细节。

-HDR原本只是被运用在摄影上，摄影师对同一个场景采取不同曝光拍多张照片，捕捉大范围的色彩值. 这些图片被合成为HDR图片，从而综合不同的曝光等级使得大范围的细节可见. 看下面这个例子，左边这张图片在被光照亮的区域充满细节，但是在黑暗的区域就什么都看不见了；但是右边这张图的高曝光却可以让之前看不出来的黑暗区域显现出来.
+HDR原本只是被运用在摄影上，摄影师对同一个场景采取不同曝光拍多张照片，捕捉大范围的色彩值。这些图片被合成为HDR图片，从而综合不同的曝光等级使得大范围的细节可见。看下面这个例子，左边这张图片在被光照亮的区域充满细节，但是在黑暗的区域就什么都看不见了；但是右边这张图的高曝光却可以让之前看不出来的黑暗区域显现出来。

 ![](http://learnopengl.com/img/advanced-lighting/hdr_image.png)

-这与我们眼睛工作的原理非常相似，也是HDR渲染的基础. 当光线很弱的啥时候，人眼会自动调整从而使过暗和过亮的部分变得更清晰，就像人眼有一个能自动根据场景亮度调整的自动曝光滑块.
+这与我们眼睛工作的原理非常相似，也是HDR渲染的基础。当光线很弱的啥时候，人眼会自动调整从而使过暗和过亮的部分变得更清晰，就像人眼有一个能自动根据场景亮度调整的自动曝光滑块。

-HDR渲染和其很相似，我们允许用更大范围的颜色值渲染从而获取大范围的黑暗与明亮的场景细节，最后将所有HDR值转换成在[0.0, 1.0]范围的LDR(Low Dynamic Range,低动态范围). 转换HDR值到LDR值得过程叫做色调映射(Tone Mapping)，现在现存有很多的色调映射算法，这些算法致力于在转换过程中保留尽可能多的HDR细节. 这些色调映射算法经常会包含一个选择性倾向黑暗或者明亮区域的参数.
+HDR渲染和其很相似，我们允许用更大范围的颜色值渲染从而获取大范围的黑暗与明亮的场景细节，最后将所有HDR值转换成在[0.0, 1.0]范围的LDR(Low Dynamic Range,低动态范围)。转换HDR值到LDR值得过程叫做色调映射(Tone Mapping)，现在现存有很多的色调映射算法，这些算法致力于在转换过程中保留尽可能多的HDR细节。这些色调映射算法经常会包含一个选择性倾向黑暗或者明亮区域的参数。

-在实时渲染中，HDR不仅允许我们超过LDR的范围[0.0, 1.0]与保留更多的细节，同时还让我们能够根据光源的**真实**强度指定它的强度. 比如太阳有比闪光灯之类的东西更高的强度，那么我们为什么不这样子设置呢?(比如说设置一个10.0的漫亮度) 这允许我们用更现实的光照参数恰当地配置一个场景的光照，而这在LDR渲染中是不能实现的，因为他们会被上限约束在1.0.
+在实时渲染中，HDR不仅允许我们超过LDR的范围[0.0, 1.0]与保留更多的细节，同时还让我们能够根据光源的**真实**强度指定它的强度。比如太阳有比闪光灯之类的东西更高的强度，那么我们为什么不这样子设置呢?(比如说设置一个10.0的漫亮度) 这允许我们用更现实的光照参数恰当地配置一个场景的光照，而这在LDR渲染中是不能实现的，因为他们会被上限约束在1.0。

-因为显示器只能显示在0.0到1.0范围之内的颜色，我们肯定要做一些转换从而使得当前的HDR颜色值符合显示器的范围. 简单地取平均值重新转换这些颜色值并不能很好的解决这个问题，因为明亮的地方会显得更加显著. 我们能做的是用一个不同的方程与/或曲线来转换这些HDR值到LDR值，从而给我们对于场景的亮度完全掌控，这就是之前说的色调变换，也是HDR渲染的最终步骤.
+因为显示器只能显示在0.0到1.0范围之内的颜色，我们肯定要做一些转换从而使得当前的HDR颜色值符合显示器的范围。简单地取平均值重新转换这些颜色值并不能很好的解决这个问题，因为明亮的地方会显得更加显著。我们能做的是用一个不同的方程与/或曲线来转换这些HDR值到LDR值，从而给我们对于场景的亮度完全掌控，这就是之前说的色调变换，也是HDR渲染的最终步骤。

-### 浮点帧缓冲(Floating Point Framebuffers)
+## 浮点帧缓冲

-在实现HDR渲染之前，我们首先需要一些防止颜色值在每一个片段着色器运行后被限制约束的方法. 当帧缓冲使用了一个标准化的定点格式(像`GL_RGB`)为其颜色缓冲的内部格式，OpenGL会在将这些值存入帧缓冲前自动将其约束到0.0到1.0之间. 这一操作对大部分帧缓冲格式都是成立的，除了专门用来存放被拓展范围值的浮点格式.
+在实现HDR渲染之前，我们首先需要一些防止颜色值在每一个片段着色器运行后被限制约束的方法。当帧缓冲使用了一个标准化的定点格式(像`GL_RGB`)为其颜色缓冲的内部格式，OpenGL会在将这些值存入帧缓冲前自动将其约束到0.0到1.0之间。这一操作对大部分帧缓冲格式都是成立的，除了专门用来存放被拓展范围值的浮点格式。

-当一个帧缓冲的颜色缓冲的内部格式被设定成了`GL_RGB16F`, `GL_RGBA16F`, `GL_RGB32F` 或者`GL_RGBA32F`时，这些帧缓冲被叫做浮点帧缓冲(Floating Point Framebuffer)，浮点帧缓冲可以存储超过0.0到1.0范围的浮点值，所以非常适合HDR渲染.
+当一个帧缓冲的颜色缓冲的内部格式被设定成了`GL_RGB16F`, `GL_RGBA16F`, `GL_RGB32F` 或者`GL_RGBA32F`时，这些帧缓冲被叫做浮点帧缓冲(Floating Point Framebuffer)，浮点帧缓冲可以存储超过0.0到1.0范围的浮点值，所以非常适合HDR渲染。

-想要创建一个浮点帧缓冲，我们只需要改变颜色缓冲的内部格式参数就行了（注意`GL_FLOAT`参数):
+想要创建一个浮点帧缓冲，我们只需要改变颜色缓冲的内部格式参数就行了（注意`GL_FLOAT`参数)：

 ```c++
 glBindTexture(GL_TEXTURE_2D, colorBuffer);
 glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB16F, SCR_WIDTH, SCR_HEIGHT, 0, GL_RGB, GL_FLOAT, NULL);  
 ```

-默认的帧缓冲默认一个颜色分量只占用8位(bits). 当使用一个使用32位每颜色分量的浮点帧缓冲时(使用`GL_RGB32F` 或者`GL_RGBA32F`)，我们需要四倍的内存来存储这些颜色. 所以除非你需要一个非常高的精确度，32位不是必须的，使用`GLRGB16F`就足够了.
+默认的帧缓冲默认一个颜色分量只占用8位(bits)。当使用一个使用32位每颜色分量的浮点帧缓冲时(使用`GL_RGB32F` 或者`GL_RGBA32F`)，我们需要四倍的内存来存储这些颜色。所以除非你需要一个非常高的精确度，32位不是必须的，使用`GLRGB16F`就足够了。

-有了一个带有浮点颜色缓冲的帧缓冲，我们可以放心渲染场景到这个帧缓冲中. 在这个教程的例子当中，我们先渲染一个光照的场景到浮点帧缓冲中，之后再在一个铺屏四边形(Screen-filling Quad)上应用这个帧缓冲的颜色缓冲，代码会是这样子:
+有了一个带有浮点颜色缓冲的帧缓冲，我们可以放心渲染场景到这个帧缓冲中。在这个教程的例子当中，我们先渲染一个光照的场景到浮点帧缓冲中，之后再在一个铺屏四边形(Screen-filling Quad)上应用这个帧缓冲的颜色缓冲，代码会是这样子：

 ```c++
 glBindFramebuffer(GL_FRAMEBUFFER, hdrFBO);
@@ -54,7 +58,7 @@ glBindTexture(GL_TEXTURE_2D, hdrColorBufferTexture);
 RenderQuad();
 ```

-这里场景的颜色值存在一个可以包含任意颜色值的浮点颜色缓冲中，值可能是超过1.0的. 这个简单的演示中，场景被创建为一个被拉伸的立方体通道和四个点光源，其中一个非常亮的在隧道的尽头:
+这里场景的颜色值存在一个可以包含任意颜色值的浮点颜色缓冲中，值可能是超过1.0的。这个简单的演示中，场景被创建为一个被拉伸的立方体通道和四个点光源，其中一个非常亮的在隧道的尽头：

 ```c++
 std::vector<glm::vec3> lightColors;
@@ -64,7 +68,7 @@ lightColors.push_back(glm::vec3(0.0f, 0.0f, 0.2f));
 lightColors.push_back(glm::vec3(0.0f, 0.1f, 0.0f));  
 ```

-渲染至浮点帧缓冲和渲染至一个普通的帧缓冲是一样的. 新的东西就是这个的`hdrShader`的片段着色器，用来渲染最终拥有浮点颜色缓冲纹理的2D四边形. 我们来定义一个简单的直通片段着色器(Pass-through Fragment Shader):
+渲染至浮点帧缓冲和渲染至一个普通的帧缓冲是一样的。新的东西就是这个的`hdrShader`的片段着色器，用来渲染最终拥有浮点颜色缓冲纹理的2D四边形。我们来定义一个简单的直通片段着色器(Pass-through Fragment Shader)：

 ```c++
 #version 330 core
@@ -80,17 +84,17 @@ void main()
 }  
 ```

-这里我们直接采样了浮点颜色缓冲并将其作为片段着色器的输出. 然而，这个2D四边形的输出是被直接渲染到默认的帧缓冲中，导致所有片段着色器的输出值被约束在0.0到1.0间，尽管我们已经有了一些存在浮点颜色纹理的值超过了1.0.
+这里我们直接采样了浮点颜色缓冲并将其作为片段着色器的输出。然而，这个2D四边形的输出是被直接渲染到默认的帧缓冲中，导致所有片段着色器的输出值被约束在0.0到1.0间，尽管我们已经有了一些存在浮点颜色纹理的值超过了1.0。

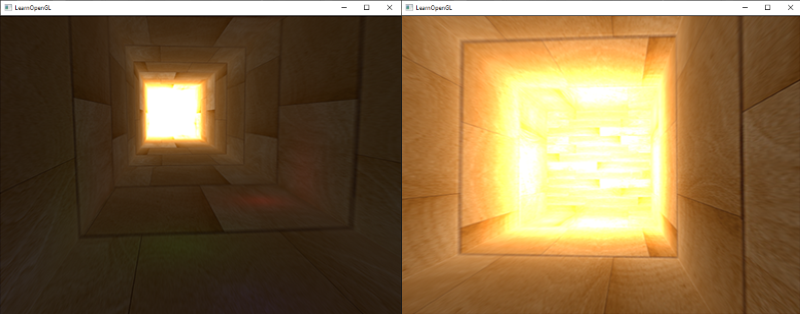
 ![](http://learnopengl.com/img/advanced-lighting/hdr_direct.png)

-很明显，在隧道尽头的强光的值被约束在1.0，因为一大块区域都是白色的，过程中超过1.0的地方损失了所有细节. 因为我们直接转换HDR值到LDR值，这就像我们根本就没有应用HDR一样. 为了修复这个问题我们需要做的是无损转化所有浮点颜色值回0.0-1.0范围中. 我们需要应用到色调映射.
+很明显，在隧道尽头的强光的值被约束在1.0，因为一大块区域都是白色的，过程中超过1.0的地方损失了所有细节。因为我们直接转换HDR值到LDR值，这就像我们根本就没有应用HDR一样。为了修复这个问题我们需要做的是无损转化所有浮点颜色值回0.0-1.0范围中。我们需要应用到色调映射。

-### 色调映射(Tone Mapping)
+## 色调映射

-色调映射是一个损失很小的转换浮点颜色值至我们所需的LDR[0.0, 1.0]范围内的过程，通常会伴有特定的风格的色平衡(Stylistic Color Balance).
+色调映射(Tone Mapping)是一个损失很小的转换浮点颜色值至我们所需的LDR[0.0, 1.0]范围内的过程，通常会伴有特定的风格的色平衡(Stylistic Color Balance)。

-最简单的色调映射算法是Reinhard色调映射，它涉及到分散整个HDR颜色值到LDR颜色值上，所有的值都有对应. Reinhard色调映射算法平均得将所有亮度值分散到LDR上. 我们将Reinhard色调映射应用到之前的片段着色器上，并且为了更好的测量加上一个Gamma校正过滤(包括SRGB纹理的使用):
+最简单的色调映射算法是Reinhard色调映射，它涉及到分散整个HDR颜色值到LDR颜色值上，所有的值都有对应。Reinhard色调映射算法平均得将所有亮度值分散到LDR上。我们将Reinhard色调映射应用到之前的片段着色器上，并且为了更好的测量加上一个Gamma校正过滤(包括SRGB纹理的使用)：

 ```c++
 void main()
@@ -107,15 +111,15 @@ void main()
 }   
 ```

-有了Reinhard色调映射的应用，我们不再会在场景明亮的地方损失细节. 当然，这个算法是倾向明亮的区域的，暗的区域会不那么精细也不那么有区分度.
+有了Reinhard色调映射的应用，我们不再会在场景明亮的地方损失细节。当然，这个算法是倾向明亮的区域的，暗的区域会不那么精细也不那么有区分度。

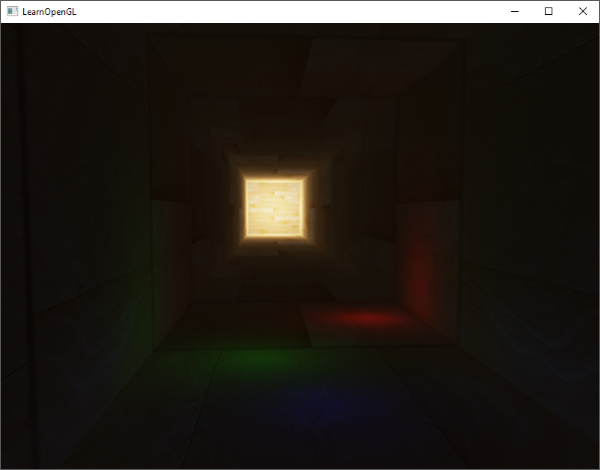
 ![](http://learnopengl.com/img/advanced-lighting/hdr_reinhard.png)

-现在你可以看到在隧道的尽头木头纹理变得可见了. 用了这个非常简单地色调映射算法，我们可以合适的看到存在浮点帧缓冲中整个范围的HDR值，给我们对于无损场景光照精确的控制.
+现在你可以看到在隧道的尽头木头纹理变得可见了。用了这个非常简单地色调映射算法，我们可以合适的看到存在浮点帧缓冲中整个范围的HDR值，给我们对于无损场景光照精确的控制。

-另一个有趣的色调映射应用是曝光(Exposure)参数的使用. 你可能还记得之前我们在介绍里讲到的，HDR图片包含在不同曝光等级的细节. 如果我们有一个场景要展现日夜交替，我们当然会在白天使用低曝光，在夜间使用高曝光，就像人眼调节方式一样. 有了这个曝光参数，我们可以去设置可以同时在白天和夜晚不同光照条件工作的光照参数，我们只需要调整曝光参数就行了.
+另一个有趣的色调映射应用是曝光(Exposure)参数的使用。你可能还记得之前我们在介绍里讲到的，HDR图片包含在不同曝光等级的细节。如果我们有一个场景要展现日夜交替，我们当然会在白天使用低曝光，在夜间使用高曝光，就像人眼调节方式一样。有了这个曝光参数，我们可以去设置可以同时在白天和夜晚不同光照条件工作的光照参数，我们只需要调整曝光参数就行了。

-一个简单的曝光色调映射算法会像这样:
+一个简单的曝光色调映射算法会像这样：

 ```c++
 uniform float exposure;
@@ -134,21 +138,21 @@ void main()
 }  
 ```

-在这里我们将`exposure`定义为默认为1.0的`uniform`，从而允许我们更加精确设定我们是要注重黑暗还是明亮的区域的HDR颜色值. 举例来说，高曝光值会使隧道的黑暗部分显示更多的细节，然而低曝光值会显著减少黑暗区域的细节，但允许我们看到更多明亮区域的细节. 下面这组图片展示了在不同曝光值下的通道:
+在这里我们将`exposure`定义为默认为1.0的`uniform`，从而允许我们更加精确设定我们是要注重黑暗还是明亮的区域的HDR颜色值。举例来说，高曝光值会使隧道的黑暗部分显示更多的细节，然而低曝光值会显著减少黑暗区域的细节，但允许我们看到更多明亮区域的细节。下面这组图片展示了在不同曝光值下的通道：

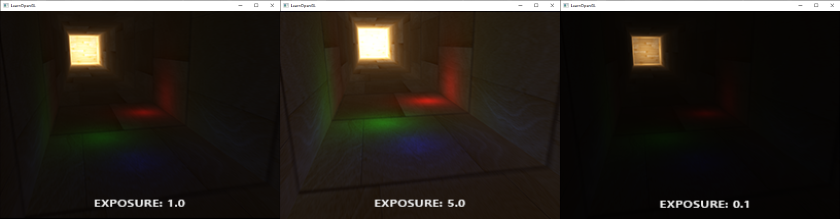
 ![](http://learnopengl.com/img/advanced-lighting/hdr_exposure.png)

-这个图片清晰地展示了HDR渲染的优点. 通过改变曝光等级，我们可以看见场景的很多细节，而这些细节可能在LDR渲染中都被丢失了. 比如说隧道尽头，在正常曝光下木头结构隐约可见，但用低曝光木头的花纹就可以清晰看见了. 对于近处的木头花纹来说，在高曝光下会能更好的看见.
+这个图片清晰地展示了HDR渲染的优点。通过改变曝光等级，我们可以看见场景的很多细节，而这些细节可能在LDR渲染中都被丢失了。比如说隧道尽头，在正常曝光下木头结构隐约可见，但用低曝光木头的花纹就可以清晰看见了。对于近处的木头花纹来说，在高曝光下会能更好的看见。

-你可以在[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/hdr "这里")找到这个演示的源码和HDR的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/hdr&type=vertex "顶点")和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/hdr&type=fragment "片段")着色器.
+你可以在[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/hdr "这里")找到这个演示的源码和HDR的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/hdr&type=vertex "顶点")和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/hdr&type=fragment "片段")着色器。

 ### HDR拓展

-在这里展示的两个色调映射算法仅仅是大量(更先进)的色调映射算法中的一小部分，这些算法各有长短.一些色调映射算法倾向于特定的某种颜色/强度，也有一些算法同时显示低于高曝光颜色从而能够显示更加多彩和精细的图像. 也有一些技巧被称作自动曝光调整(Automatic Exposure Adjustment)或者叫人眼适应(Eye Adaptation)技术，它能够检测前一帧场景的亮度并且缓慢调整曝光参数模仿人眼使得场景在黑暗区域逐渐变亮或者在明亮区域逐渐变暗.
+在这里展示的两个色调映射算法仅仅是大量(更先进)的色调映射算法中的一小部分，这些算法各有长短.一些色调映射算法倾向于特定的某种颜色/强度，也有一些算法同时显示低于高曝光颜色从而能够显示更加多彩和精细的图像。也有一些技巧被称作自动曝光调整(Automatic Exposure Adjustment)或者叫人眼适应(Eye Adaptation)技术，它能够检测前一帧场景的亮度并且缓慢调整曝光参数模仿人眼使得场景在黑暗区域逐渐变亮或者在明亮区域逐渐变暗，

-HDR渲染的真正优点在庞大和复杂的场景中应用复杂光照算法会被显示出来，但是出于教学目的创建这样复杂的演示场景是很困难的，这个教程用的场景是很小的，而且缺乏细节. 但是如此简单的演示也是能够显示出HDR渲染的一些优点: 在明亮和黑暗区域无细节损失，因为它们可以由色调映射重新获取；多个光照的叠加不会导致亮度被约束的区域；光照可以被设定为他们原来的亮度而不是被LDR值限定. 而且，HDR渲染也使一些有趣的效果更加可行和真实; 其中一个效果叫做泛光(Bloom)，我们将在下一节讨论他.
+HDR渲染的真正优点在庞大和复杂的场景中应用复杂光照算法会被显示出来，但是出于教学目的创建这样复杂的演示场景是很困难的，这个教程用的场景是很小的，而且缺乏细节。但是如此简单的演示也是能够显示出HDR渲染的一些优点：在明亮和黑暗区域无细节损失，因为它们可以由色调映射重新获取；多个光照的叠加不会导致亮度被约束的区域；光照可以被设定为他们原来的亮度而不是被LDR值限定。而且，HDR渲染也使一些有趣的效果更加可行和真实; 其中一个效果叫做泛光(Bloom)，我们将在下一节讨论他。

-### 附加资源
+## 附加资源

- [如果泛光效果不被应用HDR渲染还有好处吗?](http://gamedev.stackexchange.com/questions/62836/does-hdr-rendering-have-any-benefits-if-bloom-wont-be-applied): 一个StackExchange问题，其中有一个答案非常详细地解释HDR渲染的好处.
- [什么是色调映射? 它与HDR有什么联系?](http://photo.stackexchange.com/questions/7630/what-is-tone-mapping-how-does-it-relate-to-hdr): 另一个非常有趣的答案，用了大量图片解释色调映射.
+- [如果泛光效果不被应用HDR渲染还有好处吗？](http://gamedev.stackexchange.com/questions/62836/does-hdr-rendering-have-any-benefits-if-bloom-wont-be-applied): 一个StackExchange问题，其中有一个答案非常详细地解释HDR渲染的好处。
+- [什么是色调映射? 它与HDR有什么联系？](http://photo.stackexchange.com/questions/7630/what-is-tone-mapping-how-does-it-relate-to-hdr): 另一个非常有趣的答案，用了大量图片解释色调映射。
--- a/Lighting/07
+++ b/Lighting/07
@@ -1,18 +1,22 @@
-本文作者JoeyDeVries，由Django翻译自[http://learnopengl.com](http://learnopengl.com)
+# 泛光

-## 泛光(Bloom)
+原文     | [Bloom](http://learnopengl.com/#!Advanced-Lighting/Bloom)
+      ---|---
+作者     | JoeyDeVries
+翻译     | [Django](http://bullteacher.com/)
+校对     | gjy_1992

 明亮的光源和区域经常很难向观察者表达出来，因为监视器的亮度范围是有限的。一种区分明亮光源的方式是使它们在监视器上发出光芒，光源的的光芒向四周发散。这样观察者就会产生光源或亮区的确是强光区。（译注：这个问题的提出简单来说是为了解决这样的问题：例如有一张在阳光下的白纸，白纸在监视器上显示出是出白色，而前方的太阳也是纯白色的，所以基本上白纸和太阳就是一样的了，给太阳加一个光晕，这样太阳看起来似乎就比白纸更亮了）

-光晕效果可以使用一个后处理特效bloom来实现。bloom使所有明亮区域产生光晕效果。下面是一个使用了和没有使用光晕的对比（图片生成自虚幻引擎）：
+光晕效果可以使用一个后处理特效泛光来实现。泛光使所有明亮区域产生光晕效果。下面是一个使用了和没有使用光晕的对比（图片生成自虚幻引擎）：

 ![](http://learnopengl.com/img/advanced-lighting/bloom_example.png)

-Bloom是我们能够注意到一个明亮的物体真的有种明亮的感觉。bloom可以极大提升场景中的光照效果，并提供了极大的效果提升，尽管做到这一切只需一点改变。
+Bloom是我们能够注意到一个明亮的物体真的有种明亮的感觉。泛光可以极大提升场景中的光照效果，并提供了极大的效果提升，尽管做到这一切只需一点改变。

-Bloom和HDR结合使用效果很好。常见的一个误解是HDR和bloom是一样的，很多人认为两种技术是可以互换的。但是它们是两种不同的技术，用于各自不同的目的上。可以使用默认的8位精确度的帧缓冲，也可以在不使用bloom效果的时候，使用HDR。只不过在有了HDR之后再实现bloom就更简单了。
+Bloom和HDR结合使用效果很好。常见的一个误解是HDR和泛光是一样的，很多人认为两种技术是可以互换的。但是它们是两种不同的技术，用于各自不同的目的上。可以使用默认的8位精确度的帧缓冲，也可以在不使用泛光效果的时候，使用HDR。只不过在有了HDR之后再实现泛光就更简单了。

-为实现bloom，我们像平时那样渲染一个有光场景，提取出场景的HDR颜色缓冲以及只有这个场景明亮区域可见的图片。被提取的带有亮度的图片接着被模糊，结果被添加到HDR场景上面。
+为实现泛光，我们像平时那样渲染一个有光场景，提取出场景的HDR颜色缓冲以及只有这个场景明亮区域可见的图片。被提取的带有亮度的图片接着被模糊，结果被添加到HDR场景上面。

 我们来一步一步解释这个处理过程。我们在场景中渲染一个带有4个立方体形式不同颜色的明亮的光源。带有颜色的发光立方体的亮度在1.5到15.0之间。如果我们将其渲染至HDR颜色缓冲，场景看起来会是这样的：

@@ -22,7 +26,7 @@ Bloom和HDR结合使用效果很好。常见的一个误解是HDR和bloom是一

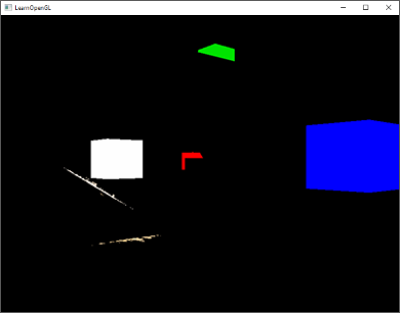
 ![](http://learnopengl.com/img/advanced-lighting/bloom_extracted.png)

-我们将这个超过一定亮度阈限的纹理进行模糊。bloom效果的强度很大程度上被模糊过滤器的范围和强度所决定。
+我们将这个超过一定亮度阈限的纹理进行模糊。泛光效果的强度很大程度上被模糊过滤器的范围和强度所决定。

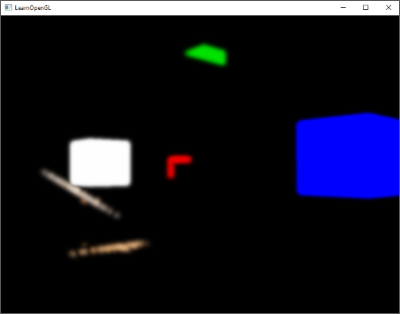
 ![](http://learnopengl.com/img/advanced-lighting/bloom_blurred.png)

@@ -30,17 +34,15 @@ Bloom和HDR结合使用效果很好。常见的一个误解是HDR和bloom是一

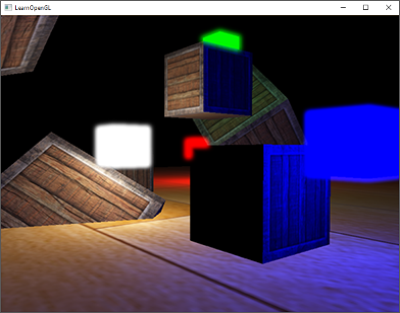
 ![](http://learnopengl.com/img/advanced-lighting/bloom_small.png)

-bloom本身并不是个复杂的技术，但很难获得正确的效果。它的品质很大程度上取决于所用的模糊过滤器的质量和类型。简单的改改模糊过滤器就会极大的改变bloom效果的品质。
+泛光本身并不是个复杂的技术，但很难获得正确的效果。它的品质很大程度上取决于所用的模糊过滤器的质量和类型。简单的改改模糊过滤器就会极大的改变泛光效果的品质。

-下面这几步就是bloom后处理特效的过程，它总结了实现bloom所需的步骤。
+下面这几步就是泛光后处理特效的过程，它总结了实现泛光所需的步骤。

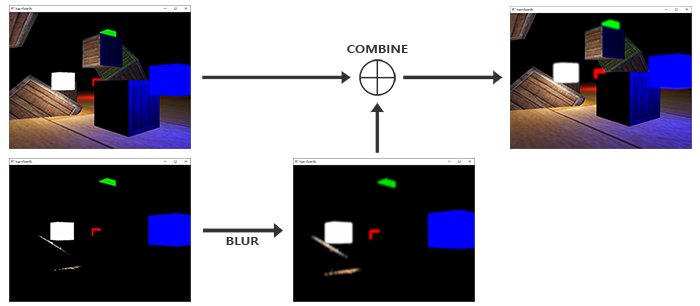
 ![](http://learnopengl.com/img/advanced-lighting/bloom_steps.png)

 首先我们需要根据一定的阈限提取所有明亮的颜色。我们先来做这件事。

- 
-
-### 提取亮色
+## 提取亮色

 第一步我们要从渲染出来的场景中提取两张图片。我们可以渲染场景两次，每次使用一个不同的不同的着色器渲染到不同的帧缓冲中，但我们可以使用一个叫做MRT（Multiple Render Targets多渲染目标）的小技巧，这样我们就能定义多个像素着色器了；有了它我们还能够在一个单独渲染处理中提取头两个图片。在像素着色器的输出前，我们指定一个布局location标识符，这样我们便可控制一个像素着色器写入到哪个颜色缓冲：

@@ -104,15 +106,15 @@ void main()

 这里我们先正常计算光照，将其传递给第一个像素着色器的输出变量FragColor。然后我们使用当前储存在FragColor的东西来决定它的亮度是否超过了一定阈限。我们通过恰当地将其转为灰度的方式计算一个fragment的亮度，如果它超过了一定阈限，我们就把颜色输出到第二个颜色缓冲，那里保存着所有亮部；渲染发光的立方体也是一样的。

-这也说明了为什么bloom在HDR基础上能够运行得很好。因为HDR中，我们可以将颜色值指定超过1.0这个默认的范围，我们能够得到对一个图像中的亮度的更好的控制权。没有HDR我们必须将阈限设置为小于1.0的数，虽然可行，但是亮部很容易变得很多，这就导致光晕效果过重。
+这也说明了为什么泛光在HDR基础上能够运行得很好。因为HDR中，我们可以将颜色值指定超过1.0这个默认的范围，我们能够得到对一个图像中的亮度的更好的控制权。没有HDR我们必须将阈限设置为小于1.0的数，虽然可行，但是亮部很容易变得很多，这就导致光晕效果过重。

 有了两个颜色缓冲，我们就有了一个正常场景的图像和一个提取出的亮区的图像；这些都在一个渲染步骤中完成。

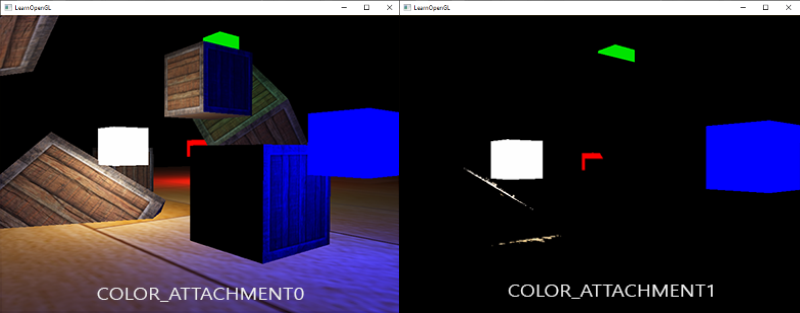
 ![](http://learnopengl.com/img/advanced-lighting/bloom_attachments.png)

-有了一个提取出的亮区图像，我们现在就要把这个图像进行模糊处理。我们可以使用帧缓冲教程后处理部分的那个简单的盒子过滤器，但不过我们最好还是使用一个更高级的更漂亮的模糊过滤器：高斯模糊。
+有了一个提取出的亮区图像，我们现在就要把这个图像进行模糊处理。我们可以使用帧缓冲教程后处理部分的那个简单的盒子过滤器，但不过我们最好还是使用一个更高级的更漂亮的模糊过滤器：**高斯模糊(Gaussian blur)**。

-### 高斯模糊
+## 高斯模糊

 在后处理教程那里，我们采用的模糊是一个图像中所有周围像素的均值，它的确为我们提供了一个简易实现的模糊，但是效果并不好。高斯模糊基于高斯曲线，高斯曲线通常被描述为一个钟形曲线，中间的值达到最大化，随着距离的增加，两边的值不断减少。高斯曲线在数学上有不同的形式，但是通常是这样的形状：

@@ -218,13 +220,13 @@ glBindFramebuffer(GL_FRAMEBUFFER, 0);

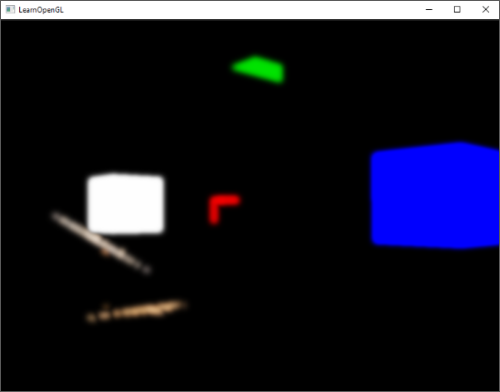
 ![](http://learnopengl.com/img/advanced-lighting/bloom_blurred_large.png)

-bloom的最后一步是把模糊处理的图像和场景原来的HDR纹理进行结合。
+泛光的最后一步是把模糊处理的图像和场景原来的HDR纹理进行结合。

 

-### 把两个纹理混合
+## 把两个纹理混合

-有了场景的HDR纹理和模糊处理的亮区纹理，我们只需把它们结合起来就能实现bloom或称光晕效果了。最终的像素着色器（大部分和HDR教程用的差不多）要把两个纹理混合：
+有了场景的HDR纹理和模糊处理的亮区纹理，我们只需把它们结合起来就能实现泛光或称光晕效果了。最终的像素着色器（大部分和HDR教程用的差不多）要把两个纹理混合：

 ```c++
 #version 330 core
@@ -249,20 +251,20 @@ void main()
 }
 ```

-要注意的是我们要在应用色调映射之前添加bloom效果。这样添加的亮区的bloom，也会柔和转换为LDR，光照效果相对会更好。
+要注意的是我们要在应用色调映射之前添加泛光效果。这样添加的亮区的泛光，也会柔和转换为LDR，光照效果相对会更好。

 把两个纹理结合以后，场景亮区便有了合适的光晕特效：

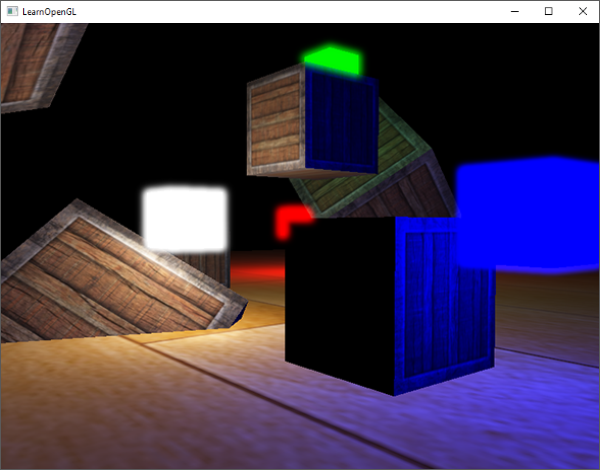
 ![](http://learnopengl.com/img/advanced-lighting/bloom.png)

-有颜色的立方体看起来仿佛更亮，它向外发射光芒，的确是一个更好的视觉效果。这个场景比较简单，所以bloom效果不算十分令人瞩目，但在更好的场景中合理配置之后效果会有巨大的不同。你可以在这里找到这个简单的例子的源码，以及模糊的顶点和像素着色器、立方体的像素着色器、后处理的顶点和像素着色器。
+有颜色的立方体看起来仿佛更亮，它向外发射光芒，的确是一个更好的视觉效果。这个场景比较简单，所以泛光效果不算十分令人瞩目，但在更好的场景中合理配置之后效果会有巨大的不同。你可以在这里找到这个简单的例子的源码，以及模糊的顶点和像素着色器、立方体的像素着色器、后处理的顶点和像素着色器。

-这个教程我们只是用了一个相对简单的高斯模糊过滤器，它在每个方向上只有5个样本。通过沿着更大的半径或重复更多次数的模糊，进行采样我们就可以提升模糊的效果。因为模糊的质量与bloom效果的质量正相关，提升模糊效果就能够提升bloom效果。有些提升将模糊过滤器与不同大小的模糊kernel或采用多个高斯曲线来选择性地结合权重结合起来使用。来自Kalogirou和EpicGames的附加资源讨论了如何通过提升高斯模糊来显著提升bloom效果。
+这个教程我们只是用了一个相对简单的高斯模糊过滤器，它在每个方向上只有5个样本。通过沿着更大的半径或重复更多次数的模糊，进行采样我们就可以提升模糊的效果。因为模糊的质量与泛光效果的质量正相关，提升模糊效果就能够提升泛光效果。有些提升将模糊过滤器与不同大小的模糊kernel或采用多个高斯曲线来选择性地结合权重结合起来使用。来自Kalogirou和EpicGames的附加资源讨论了如何通过提升高斯模糊来显著提升泛光效果。

 

-### 附加资源
+## 附加资源

-* [Efficient Gaussian Blur with linear sampling](http://rastergrid.com/blog/2010/09/efficient-gaussian-blur-with-linear-sampling/)：非常详细地描述了高斯模糊，以及如何使用OpenGL的双线性纹理采样提升性能。
-* [Bloom Post Process Effect](https://udn.epicgames.com/Three/Bloom.html)：来自Epic Games关于通过对权重的多个高斯曲线结合来提升bloom效果的文章。
-* [How to do good bloom for HDR rendering](http://kalogirou.net/2006/05/20/how-to-do-good-bloom-for-hdr-rendering/)：Kalogirou的文章描述了如何使用更好的高斯模糊算法来提升bloom效果。
+- [Efficient Gaussian Blur with linear sampling](http://rastergrid.com/blog/2010/09/efficient-gaussian-blur-with-linear-sampling/)：非常详细地描述了高斯模糊，以及如何使用OpenGL的双线性纹理采样提升性能。
+- [Bloom Post Process Effect](https://udn.epicgames.com/Three/Bloom.html)：来自Epic Games关于通过对权重的多个高斯曲线结合来提升泛光效果的文章。
+- [How to do good bloom for HDR rendering](http://kalogirou.net/2006/05/20/how-to-do-good-bloom-for-hdr-rendering/)：Kalogirou的文章描述了如何使用更好的高斯模糊算法来提升泛光效果。
--- a/Lighting/09
+++ b/Lighting/09
@@ -38,7 +38,7 @@ Crytek公司开发的SSAO技术会产生一种特殊的视觉风格。因为使

 通过在**法向半球体(Normal-oriented Hemisphere)**周围采样，我们将不会考虑到片段底部的几何体.它消除了环境光遮蔽灰蒙蒙的感觉，从而产生更真实的结果。这个SSAO教程将会基于法向半球法和John Chapman出色的[SSAO教程](http://john-chapman-graphics.blogspot.com/2013/01/ssao-tutorial.html)。

-## 样本缓冲(Sample buffers)
+## 样本缓冲

 SSAO需要获取几何体的信息，因为我们需要一些方式来确定一个片段的遮蔽因子。对于每一个片段，我们将需要这些数据：
 - 逐片段**位置**向量
@@ -112,7 +112,7 @@ glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);

 接下来我们需要真正的半球采样核心和一些方法来随机旋转它。

-## 法向半球(Normal-oriented Hemisphere)
+## 法向半球

 我们需要沿着表面法线方向生成大量的样本。就像我们在这个教程的开始介绍的那样，我们想要生成形成半球形的样本。由于对每个表面法线方向生成采样核心非常困难，也不合实际，我们将在[切线空间](http://learnopengl-cn.readthedocs.org/zh/latest/05%20Advanced%20Lighting/04%20Normal%20Mapping/)(Tangent Space)内生成采样核心，法向量将指向正z方向。

--- a/Rendering.md
+++ b/Rendering.md
@@ -12,9 +12,9 @@

 开发者最常用的一种方式是将字符纹理绘制到矩形方块上。绘制这些纹理方块其实并不是很复杂，然而检索要绘制的文字的纹理却变成了一项挑战性的工作。本教程将探索多种文字渲染的实现方法，并且着重对更加现代而且灵活的渲染技术(使用FreeType库)进行讲解。

-## 经典文字渲染：使用位图字体
+## 经典文字渲染：位图字体

-在早期渲染文字时，选择你应用程序的字体(或者创建你自己的字体)来绘制文字是通过将所有用到的文字加载在一张大纹理图中来实现的。这张纹理贴图我们把它叫做位图字体(Bitmap Font)，它包含了所有我们想要使用的字符。这些字符被称为**字形(glyph)**。每个字形根据他们的编号被放到位图字体中的确切位置，在渲染这些字形的时候根据这些排列规则将他们取出并贴到指定的2D方块中。
+在早期渲染文字时，选择你应用程序的字体(或者创建你自己的字体)来绘制文字是通过将所有用到的文字加载在一张大纹理图中来实现的。这张纹理贴图我们把它叫做**位图字体(Bitmap Font)**，它包含了所有我们想要使用的字符。这些字符被称为**字形(Glyph)**。每个字形根据他们的编号被放到位图字体中的确切位置，在渲染这些字形的时候根据这些排列规则将他们取出并贴到指定的2D方块中。

 ![](http://learnopengl.com/img/in-practice/bitmapfont.png)

@@ -24,7 +24,7 @@

 这种绘制文字的方式曾经得益于它的高速和可移植性而非常流行，然而现在已经存在更加灵活的方式了。其中一个是我们即将展开讨论的使用FreeType库来加载TrueType字体的方式。

-## 现代文字渲染：使用FreeType
+## 现代文字渲染：FreeType

 FreeType是一个能够用于加载字体并将他们渲染到位图以及提供多种字体相关的操作的软件开发库。它是一个非常受欢迎的跨平台字体库，被用于 Mac OSX、Java、PlayStation主机、Linux、Android等。FreeType的真正吸引力在于它能够加载TrueType字体。

@@ -320,4 +320,4 @@ RenderText(shader, "(C) LearnOpenGL.com", 540.0f, 570.0f, 0.5f, glm::vec3(0.3, 0

 本教程演示了如何使用FreeType绘制TrueType文字。这种方式灵活、可缩放并支持多种字符编码。然而，你的应用程序可能并不需要这么强大的功能，性能更好的点阵字体也许是更可取的。当然你可以结合这两种方法通过动态生成位图字体中所有字符字形。这节省了从大量的纹理渲染器开关和基于每个字形紧密包装可以节省相当的一些性能。

-另一个使用FreeType字体的问题是字形纹理是对应着一个固定的字体大小的，因此直接对其放大就会出现锯齿边缘。此外，对字形进行旋转还会使它们看上去变得模糊。通过将每个像素设为最近的字形轮廓的像素，而不是直接设为实际栅格化的像素，可以减轻这些问题。这项技术被称为**signed distance fields**，Valve在几年前发表过一篇了[论文](http://www.valvesoftware.com/publications/2007/SIGGRAPH2007_AlphaTestedMagnification.pdf)，探讨了他们通过这项技术来获得好得惊人的3D渲染效果。
+另一个使用FreeType字体的问题是字形纹理是对应着一个固定的字体大小的，因此直接对其放大就会出现锯齿边缘。此外，对字形进行旋转还会使它们看上去变得模糊。通过将每个像素设为最近的字形轮廓的像素，而不是直接设为实际栅格化的像素，可以减轻这些问题。这项技术被称为**有向距离场(Signed Distance Fields)**，Valve在几年前发表过一篇了[论文](http://www.valvesoftware.com/publications/2007/SIGGRAPH2007_AlphaTestedMagnification.pdf)，探讨了他们通过这项技术来获得好得惊人的3D渲染效果。
--- a/Practice/2D-Game/01
+++ b/Practice/2D-Game/01
@@ -1,7 +1,10 @@
+# Breakout
+
 原文     | [Breakout](http://www.learnopengl.com/#!In-Practice/2D-Game/Breakout)
+      ---|---
 作者     | JoeyDeVries
 翻译     | HHz(qq:1158332489)
-校对     | 等待校对....
+校对     | 暂无

 看完前面的教程之后我们已适当地了解了OpenGL的内部运作原理，并且我们已经能够用这些知识绘制一些复杂的图像。然而，我们还只能做出一些小Demo，并未达到用OpenGL开发实际应用的水平。这一部分主要介绍了一个用OpenGL制作的很简单的2D小游戏。本部分教程将展现OpenGL在较大较复杂程序中的强大之处。

@@ -25,7 +28,7 @@
 因为小球不时可能会遇上砖块之间的缝隙，所以它会继续弹开周围砖层进而离开缝隙。它后来若又进入了某个缺口依然遵循这个原则，这就是为什么本节要叫这个名字（Breakout）的原因 ，小球必须 “Breakout”(弹出来).
 *PS：这段话不好翻译，大概就是介绍打砖块的游戏规则

-## OpenGL Breakout
+# OpenGL Breakout

    我们将完全利用opengl实现这个经典的电脑游戏（几乎是2d游戏的基础），这个版本的Breakout将能够运行在一些可出特效的显卡上。

@@ -43,6 +46,6 @@

 这些教程将结合前面大量的概念,讲述了在之前所学的功能如何放在一起形成一个游戏。因此,最重要的是你完成了前面部分的教程。

-同样，有些东西也会提及其他教程的一些概念（比如说帧缓冲Framebuffers），So，有必要时 被提及的教程会列出
+同样，有些东西也会提及其他教程的一些概念（比如说帧缓冲Framebuffers），所以，有必要时被提及的教程会列出。

 如果你已准备好开发本游戏，可以开始下一节了。
--- a/docs/intro.md
+++ b/docs/intro.md
@@ -24,12 +24,16 @@ LearnOpenGL被分解成了许多大的主题。每个主题包括一些小节，

 	**红色**方框是一些警告或者一些你需要特别注意的特性。

+!!! note "译注"
+
+	**蓝色**方框是翻译时为了帮助读者理解附加的一些信息。
+
 ### 代码

 你在网站中将会看到很多小片的代码，它们将会在下面这样的代码框中：

 ```c++
-//这个方框是代码
+// 这个方框是代码
 ```

 由于这样至提供了代码的片段，当需要的时候我会提供个链接到当前工程的源代码的。
--- a/Practice/03
+++ b/Practice/03