# 变换(Transformations)
## 投影
让我们回看在前一章中创建的色彩鲜艳的正方形。如果仔细看,它更像一个矩形,你甚至可以将窗口的宽度从600像素改为900像素,失真就会更加明显。这发生了什么呢?
如果你查看顶点着色器的代码,我们只是直接地传递坐标。换句话说,当一个顶点的X坐标为0.5时,我们让OpenGL在屏幕的X坐标为0.5的位置绘制它。下图展示了OpenGL坐标系(仅含X和Y轴)。
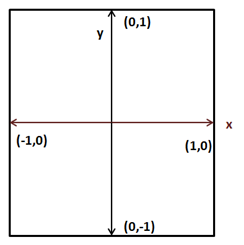
将这些坐标投影到窗口坐标系(其原点位于上图的左上角),需要考虑到窗口的大小。因此,如果我们的窗口大小为900x480,OpenGL坐标(1, 0)将被投影到窗口坐标(900, 0),最终创建一个矩形而不是一个正方形。
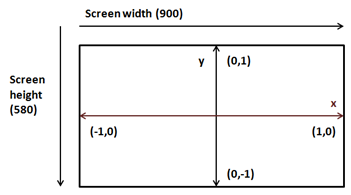
但是,问题远比这更严重。将四边形的Z坐标从0.0修改为1.0和-1.0,你发现了什么?四边形完全是绘制在同一个地方,不管它是否沿着Z轴位移。为什么会发生这种情况?远处的物体应该比近处的物体绘制得更小,但是我们使用相同的X和Y坐标绘制它们。
但稍等一下,这不应该由Z坐标来处理吗?这半对半错。Z坐标告诉OpenGL一个物体的远近,但是OpenGL对你的物体的大小一无所知。你可以有两个不同大小的物体,一个更近更小,一个更远更大,而且可以以相同的大小正确地投影到屏幕上(有相同的屏幕X和Y坐标,但Z坐标不同)。OpenGL只使用正在传递的坐标,所以我们必须处理这个问题,我们需要正确地投影坐标。
既然已经确诊了这个问题,该怎么解决呢?答案是使用投影矩阵(Projection Matrix)或截锥体(Frustum)。投影矩阵将处理绘制区域的宽高比(大小与高度之间的关系),这样物体就不会变形。它还可以处理距离,所以较远的物体将会被绘制得更小。投影矩阵还将考虑我们的视野和应该显示的距离有多远。
对于不熟悉矩阵的人,矩阵(Matrix)是以行和列排列的二维数组。矩阵中的每个数字被称为元素。矩阵阶次是行和列的数量。例如,此处是一个2x2矩阵(有2行2列)。
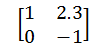
矩阵有许多可以应用于它们的基本运算(如加法、乘法等),你可以在数学书中查阅,其中与三维图形相关的矩阵对空间中点的变换非常有用。
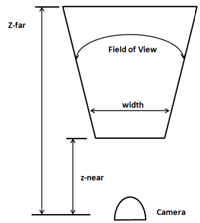
你可以把投影矩阵想象成一个摄像机,它有一个视野和最小和最大距离。该摄像机的可视区域是一个截断的金字塔,下图为该区域的俯视图。
投影矩阵将正确地投影三维坐标,以便它们能够在二维屏幕上正确地显示。该矩阵的数学表示如下(不要害怕):

其中屏幕宽高比(Aspect Ratio)指的是屏幕宽度与屏幕高度的关系($屏幕宽高比=宽度/高度$)。为了获得给定点的投影坐标,只需要将投影矩阵乘以原始坐标,结果是投影后的另一个向量。
因此,我们需要处理一组数学实体,如向量、矩阵,并包括可以对它们进行的运算。我们可以选择从头开始编写所有的代码,或者使用已实现的库。当然我们会选择容易的方法,使用JOML(Java OpenGL Math Library,Java OpenGL 数学库)处理LWJGL内的数学运算。为了使用该库,我们只需要在`pom.xml`文件添加另一个依赖项。
```xml
org.joml
joml
${joml.version}
```
然后设置要使用的库版本。
```xml
[...]
1.9.6
[...]
```
现在一切都准备好了,来定义我们的投影矩阵。在`Renderer`类中创建`Matrix4f`类(由JOML库提供)的实例。`Matrix4f`类提供了一个`perspective`方法来创建投影矩阵,该方法需要以下参数:
* 视野:可视区域角的弧度大小,我们将定义一个储存该值的常数。
* 屏幕宽高比。
* 最近视距(z-near)。
* 最远视距(z-far)。
我们将在`init`方法中实例化该矩阵,因此需要传递对`Window`实例的阴影以获取窗口大小(你可以查看源代码)。代码如下:
```java
/**
* 视野弧度
*/
private static final float FOV = (float) Math.toRadians(60.0f);
private static final float Z_NEAR = 0.01f;
private static final float Z_FAR = 1000.f;
private Matrix4f projectionMatrix;
```
投影矩阵的创建如下所示:
```java
float aspectRatio = (float) window.getWidth() / window.getHeight();
projectionMatrix = new Matrix4f().perspective(FOV, aspectRatio,
Z_NEAR, Z_FAR);
```
现在我们省略宽高比可变的情况(通过调整窗口大小),这可以在`render`方法中检查并相应地改变投影矩阵。
现在有了矩阵,该如何使用它呢?我们需要在着色器中使用它,并且它应该被应用到所有顶点上。首先,你可能会想到把它捆绑在顶点输入中(就像坐标和颜色那样)。但这样,我们会浪费很多空间,因为投影矩阵在几次渲染期间都不会发生改变。你可能还想在Java代码中用矩阵处理所有顶点,但这样我们输入的VBO就是没用的了,这样就不能使用显卡中的处理器资源了。
答案是使用“`uniform`”。Uniform是着色器可以使用的全局的GLSL变量,我们将使用它与着色器交流。
所以我们需要修改顶点着色器的代码,并声明一个新的名为`projectionMatrix`的Uniform,并用它来计算投影后的位置。
```glsl
#version 330
layout (location=0) in vec3 position;
layout (location=1) in vec3 inColour;
out vec3 exColour;
uniform mat4 projectionMatrix;
void main()
{
gl_Position = projectionMatrix * vec4(position, 1.0);
exColour = inColour;
}
```
如上所述,我们把`projectionMatrix`定义为一个4x4的矩阵,新的坐标是通过把它与原始坐标相乘得到的。现在我们需要把投影矩阵的值传递给着色器,首先需要确定Uniform的位置。
这是通过调用方法`glGetUniformLocation`实现的,它有两个参数:
* 着色器程序的ID
* Uniform名(它应该与着色器里定义的名称相同)
此方法返回储存Uniform位置的ID。由于可能有一个以上的Uniform,我们将把这些ID储存在由变量名作为索引的Map中(此后我们需要那个ID)。因此,在`ShaderProgram`需要创建一个新的字段来保存这些ID:
```java
private final Map uniforms;
```
然后由构造方法初始化它:
```java
uniforms = new HashMap<>();
```
最后,我们创建了一个方法来创建新的Uniform和储存获得的位置。
```java
public void createUniform(String uniformName) throws Exception {
int uniformLocation = glGetUniformLocation(programId,
uniformName);
if (uniformLocation < 0) {
throw new Exception("Could not find uniform:" +
uniformName);
}
uniforms.put(uniformName, uniformLocation);
}
```
现在,在着色器程序编译后,我们就可以在`Renderer`类中调用`createUniform`方法(本例中,我们将在投影矩阵实例化后调用它)。
```java
shaderProgram.createUniform("projectionMatrix");
```
此时,我们已经准备好一个可以储存投影矩阵数据的储存器。由于投影矩阵在渲染期间不会变化,所以可以在创建Uniform后直接设置值,但我们将在`render`方法中做此事。稍后你可以看到,我们可以重用该Uniform来执行每次渲染调用中需要执行的其他操作。
我们将在`ShaderProgram`类中创建另一个名为`setUniform`的方法来设置数据,通过使用JOML库提供的实用方法将矩阵转换为4x4的`FloatBuffer`对象,并将它们发送到Uniform中。
```java
public void setUniform(String uniformName, Matrix4f value) {
// 转储矩阵到FloatBuffer
try (MemoryStack stack = MemoryStack.stackPush()) {
FloatBuffer fb = stack.mallocFloat(16);
value.get(fb);
glUniformMatrix4fv(uniforms.get(uniformName), false, fb);
}
}
```
如你所见,我们用与此前不同的方式创建缓冲区。我们使用的是自动管理的缓冲区,并将它们分配到堆栈上。这是因为这个缓冲区的大小很小,并且在该方法之外不会使用它。因此我们使用`MemoryStack`类。
现在,在着色器绑定之后,可以在`Renderer`类的`render`方法中调用该方法:
```java
shaderProgram.setUniform("projectionMatrix", projectionMatrix);
```
我们就要完成了,现在可以正确地渲染四边形,所以现在可以启动程序,然后得到一个...黑色背景,没有任何彩色四边形。发生了什么?我们把什么弄坏了吗?实际上没有任何问题。记住我们正在模拟摄像机观察场景的效果。我们提供了两个距离,一个是最远视距(1000f)和一个最近视距(0.01f)。而我们的坐标是:
```java
float[] positions = new float[]{
-0.5f, 0.5f, 0.0f,
-0.5f, -0.5f, 0.0f,
0.5f, -0.5f, 0.0f,
0.5f, 0.5f, 0.0f,
};
```
也就是说,我们坐标中的Z坐标位于可视区域之外。将它们赋值为-0.05f,现在你会看到像这样的一个巨大的绿色正方形:
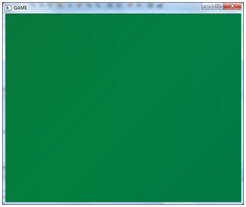
这是因为,我们正绘制出离摄像机太近的正方形,实际上是在放大它。如果现在把一个`-1.05f`的值赋值给Z坐标,就可以看到彩色正方形了。
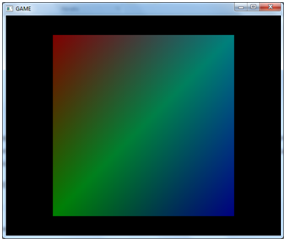
如果继续向后移动四边形,我们会看到它变小了。还要注意到四边形不再像矩形了。
## 使用变换
回想一下到目前为止我们都做了什么。我们已经学会了如何将数据以有效的格式传递给显卡,以及如何使用顶点和片元着色器来投影这些顶点并设置它们的颜色。现在应该开始在三维空间中绘制更复杂的模型了,但为了做到它,我们必须能够加载模型,并在指定的位置以适当的大小和所需的旋转将它渲染在三维空间中。
现在为了实现这样的渲染,我们需要提供一些基本操作来操作模型:
* 位移(Translation): 在三个轴中的任意一个轴上移动一个物体。
* 旋转(Rotation): 按任意一个轴旋转物体任意角度。
* 缩放(Scale): 调整物体的大小。
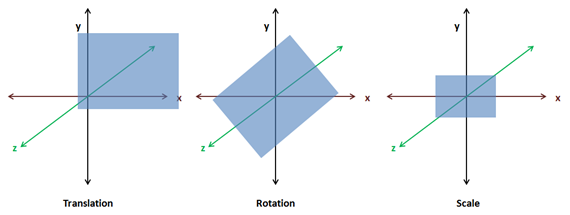
上面的操作统称为变换(Transformation)。你可能猜到要实现这一点的方法是把坐标乘以一组矩阵(一个用于移动,一个用于旋转,一个用于缩放)。这三个矩阵将被组合成一个称为“世界矩阵”的矩阵,并作为一个Uniform传递给顶点着色器。
之所以被称为世界矩阵,是因为我们正在将模型坐标转换为世界坐标。当学习加载3D模型时,你会发现这些模型是在它们自己的坐标系中定义的,它们不知道你的三维空间的大小,但它们需要在里面渲染。因此,当我们用矩阵乘以坐标时,实际上做的是从一个坐标系(模型坐标系)转换到另一个坐标系(三维世界坐标系)。
世界矩阵应该这样计算(顺序很重要,因为乘法交换律不适用于矩阵):
$$世界矩阵=\left[位移矩阵\right]\left[旋转矩阵\right]\left[缩放矩阵\right]$$
如果把投影矩阵包含在变换矩阵中,它会是这样的:
$$
\begin{array}{lcl}
Transf & = & \left[投影矩阵\right]\left[位移矩阵\right]\left[旋转矩阵\right]\left[缩放矩阵\right] \\
& = & \left[投影矩阵\right]\left[世界矩阵\right]
\end{array}
$$
位移矩阵是这样定义的:
$$
\begin{bmatrix}
1 & 0 & 0 & dx \\
0 & 1 & 0 & dy \\
0 & 0 & 1 & dz \\
0 & 0 & 0 & 1
\end{bmatrix}
$$
位移矩阵的参数如下:
* dx: 沿X轴位移。
* dy: 沿Y轴位移。
* dz: 沿Z轴位移。
缩放矩阵是这样定义的;
$$
\begin{bmatrix}
sx & 0 & 0 & 0 \\
0 & sy & 0 & 0 \\
0 & 0 & sz & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
$$
缩放矩阵的参数如下:
* sx: 沿着X轴缩放。
* sy: 沿着Y轴缩放。
* sz: 沿着Z轴缩放。
旋转矩阵要复杂得多,但请记住,它可以由每个绕单独的轴旋转的旋转矩阵相乘得到。
现在,为了实践这些理论,我们需要重构代码一点点。在游戏中,我们将加载一组模型,用来根据游戏逻辑在不同的位置渲染许多物体(想象一个FPS游戏,它载入了三个不同敌人的模型。确实只有三个模型,但使用这些模型,我们可以渲染想要的任意数量的敌人)。我们需要为每个对象创建一个VAO和一组VBO吗?答案是不需要,只需要每个模型加载一次就行。我们需要做的是根据它的位置,大小和旋转来独立地绘制它。当渲染这些模型时,我们需要对它们进行变换。
因此,我们将创建一个名为`GameItem`的新类,该类将模型加载到`Mesh`实例中。一个`GameItem`实例将由变量储存它的位置、旋转状态和缩放。如下是该类的定义。
```java
package org.lwjglb.engine;
import org.joml.Vector3f;
import org.lwjglb.engine.graph.Mesh;
public class GameItem {
private final Mesh mesh;
private final Vector3f position;
private float scale;
private final Vector3f rotation;
public GameItem(Mesh mesh) {
this.mesh = mesh;
position = new Vector3f(0, 0, 0);
scale = 1;
rotation = new Vector3f(0, 0, 0);
}
public Vector3f getPosition() {
return position;
}
public void setPosition(float x, float y, float z) {
this.position.x = x;
this.position.y = y;
this.position.z = z;
}
public float getScale() {
return scale;
}
public void setScale(float scale) {
this.scale = scale;
}
public Vector3f getRotation() {
return rotation;
}
public void setRotation(float x, float y, float z) {
this.rotation.x = x;
this.rotation.y = y;
this.rotation.z = z;
}
public Mesh getMesh() {
return mesh;
}
}
```
我们将创建一个名为`Transformation`的类,让它来处理变换。
```java
package org.lwjglb.engine.graph;
import org.joml.Matrix4f;
import org.joml.Vector3f;
public class Transformation {
private final Matrix4f projectionMatrix;
private final Matrix4f worldMatrix;
public Transformation() {
worldMatrix = new Matrix4f();
projectionMatrix = new Matrix4f();
}
public final Matrix4f getProjectionMatrix(float fov, float width, float height, float zNear, float zFar) {
float aspectRatio = width / height;
projectionMatrix.identity();
projectionMatrix.perspective(fov, aspectRatio, zNear, zFar);
return projectionMatrix;
}
public Matrix4f getWorldMatrix(Vector3f offset, Vector3f rotation, float scale) {
worldMatrix.identity().translate(offset).
rotateX((float)Math.toRadians(rotation.x)).
rotateY((float)Math.toRadians(rotation.y)).
rotateZ((float)Math.toRadians(rotation.z)).
scale(scale);
return worldMatrix;
}
}
```
如你所见,这个类把投影矩阵和世界矩阵组合起来。给定一组参数来进行位移、旋转和缩放,然后返回世界矩阵。`getWorldMatrix`返回的结果将为每个`GameItem`实例变换坐标。该类还提供了获得投影矩阵的方法。
需要注意的一件事是,`Matrix4f`类的`mul`方法修改了该实例的内容。因此,如果直接将投影矩阵与变换矩阵相乘,我们会修改投影矩阵本身,这就是为什么总是在每次调用时将每个矩阵初始化为单位矩阵。
在`Renderer`类的构造方法中,我们仅实例化了没有任何参数的`Transformation`类,而在`init`方法中,我们只创建了Uniform。
```java
public Renderer() {
transformation = new Transformation();
}
public void init(Window window) throws Exception {
// ... 此前的一些代码 ...
// 为世界矩阵和投影矩阵创建Uniform
shaderProgram.createUniform("projectionMatrix");
shaderProgram.createUniform("worldMatrix");
window.setClearColor(0.0f, 0.0f, 0.0f, 0.0f);
}
```
在`Renderer`类的渲染方法中,现在可以接收到一个`GameItem`的数组:
```java
public void render(Window window, GameItem[] gameItems) {
clear();
if ( window.isResized() ) {
glViewport(0, 0, window.getWidth(), window.getHeight());
window.setResized(false);
}
shaderProgram.bind();
// 更新投影矩阵
Matrix4f projectionMatrix = transformation.getProjectionMatrix(FOV, window.getWidth(), window.getHeight(), Z_NEAR, Z_FAR);
shaderProgram.setUniform("projectionMatrix", projectionMatrix);
// 渲染每一个游戏项
for(GameItem gameItem : gameItems) {
// 为该项设置世界矩阵
Matrix4f worldMatrix =
transformation.getWorldMatrix(
gameItem.getPosition(),
gameItem.getRotation(),
gameItem.getScale());
shaderProgram.setUniform("worldMatrix", worldMatrix);
// 为该游戏项渲染网格
gameItem.getMesh().render();
}
shaderProgram.unbind();
}
```
每次调用`render`时就更新投影矩阵一次,这样我们可以处理窗口大小的调整操作。然后我们遍历`GameItem`数组,并根据它们各自的位置、旋转和缩放创建变换矩阵,该矩阵将被传递到着色器并绘制`Mesh`。投影矩阵对于所有要渲染的项目都是相同的,这就是为什么它在`Transformation`类中是单独一个变量的原因。
我们将渲染代码移动到`Mesh`类中:
```java
public void render() {
// 绘制Mesh
glBindVertexArray(getVaoId());
glDrawElements(GL_TRIANGLES, getVertexCount(), GL_UNSIGNED_INT, 0);
// 重置状态
glBindVertexArray(0);
}
```
顶点着色器只需简单地添加一个新的`worldMatrix`矩阵,然后用它与`projectionMatrix`一同计算坐标:
```glsl
#version 330
layout (location=0) in vec3 position;
layout (location=1) in vec3 inColour;
out vec3 exColour;
uniform mat4 worldMatrix;
uniform mat4 projectionMatrix;
void main()
{
gl_Position = projectionMatrix * worldMatrix * vec4(position, 1.0);
exColour = inColour;
}
```
如你所见,代码完全一致。我们使用Uniform来正确地投影坐标,并且考虑截锥、位置、缩放和旋转等。
另外一个重要的问题是,为什么不直接使用位移、旋转和缩放矩阵,而是把它们组合成一个世界矩阵呢?原因是我们应该尽量减少在着色器中使用的矩阵。还要记住,在着色器中所做的矩阵乘法是每个顶点一次,投影矩阵在渲染调用期间不会改变,而每一个`GameItem`实例的世界矩阵也不会改变。如果独立位移、旋转和缩放矩阵,我们要做更多的矩阵乘法运算。在一个有超多顶点的模型中,这是很多余的操作。
但你现在可能会想,如果每个`GameItem`中的世界矩阵都不会发生变化,为什么不在Java类中做矩阵乘法?我们将投影矩阵和世界矩阵与每个`GameItem`相乘,把它们作为一个Uniform,在此情况下,我们确实能省下更多的操作。但当我们向游戏引擎中添加更多的特性时,我们需要在着色器中使用世界坐标,所以最好独立地处理这两个矩阵。
最后只需要修改`DummyGame`类,创建一个`GameItem`实例,让其与`Mesh`关联,并添加一些逻辑来位移、旋转和缩放四边形。因为这只是个测试示例,没有添加太多内容,所以你可以在本书的源代码中找到相关代码。