Temporarily fix #52

docs/05 Advanced Lighting/04 Normal Mapping.md

@@ -10,17 +10,17 @@
 
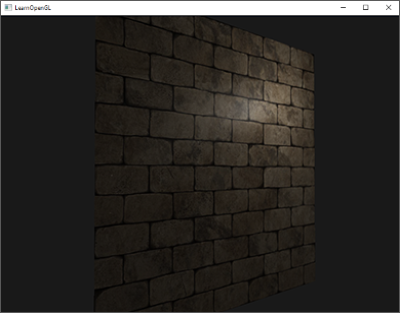
 例如，砖块的表面。砖块的表面非常粗糙，显然不是完全平坦的：它包含着接缝处水泥凹痕，以及非常多的细小的空洞。如果我们在一个有光的场景中看这样一个砖块的表面，问题就出来了。下图中我们可以看到砖块纹理应用到了平坦的表面，并被一个点光源照亮。
 
-![](http://learnopengl.com/img/advanced-lighting/normal_mapping_flat.png)
+![](../img/05/04/normal_mapping_flat.png)
 
 光照并没有呈现出任何裂痕和孔洞，完全忽略了砖块之间凹进去的线条；表面看起来完全就是平的。我们可以使用specular贴图根据深度或其他细节阻止部分表面被照的更亮，以此部分地解决问题，但这并不是一个好方案。我们需要的是某种可以告知光照系统给所有有关物体表面类似深度这样的细节的方式。
 
 如果我们以光的视角来看这个问题：是什么使表面被视为完全平坦的表面来照亮？答案会是表面的法线向量。以光照算法的视角考虑的话，只有一件事决定物体的形状，这就是垂直于它的法线向量。砖块表面只有一个法线向量，表面完全根据这个法线向量被以一致的方式照亮。如果每个fragment都是用自己的不同的法线会怎样？这样我们就可以根据表面细微的细节对法线向量进行改变；这样就会获得一种表面看起来要复杂得多的幻觉：
 
-![](http://learnopengl.com/img/advanced-lighting/normal_mapping_surfaces.png)
+![](../img/05/04/normal_mapping_surfaces.png)
 
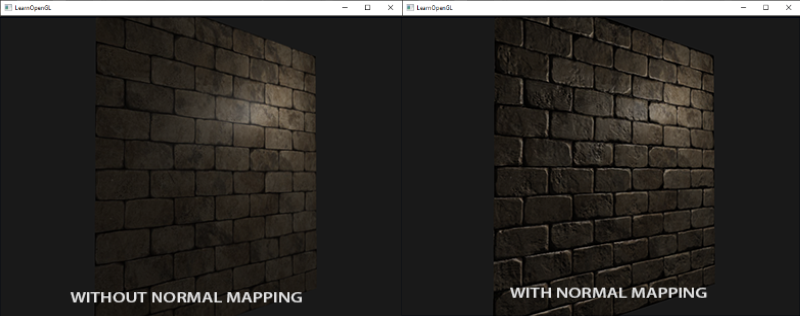
 每个fragment使用了自己的法线，我们就可以让光照相信一个表面由很多微小的（垂直于法线向量的）平面所组成，物体表面的细节将会得到极大提升。这种每个fragment使用各自的法线，替代一个面上所有fragment使用同一个法线的技术叫做法线贴图（normal mapping）或凹凸贴图（bump mapping）。应用到砖墙上，效果像这样：
 
-![](http://learnopengl.com/img/advanced-lighting/normal_mapping_compare.png)
+![](../img/05/04/normal_mapping_compare.png)
 
 你可以看到细节获得了极大提升，开销却不大。因为我们只需要改变每个fragment的法线向量，并不需要改变所有光照公式。现在我们是为每个fragment传递一个法线，不再使用插值表面法线。这样光照使表面拥有了自己的细节。
 
@@ -37,7 +37,7 @@ vec3 rgb_normal = normal * 0.5 - 0.5; // transforms from [-1,1] to [0,1]
 
 将法线向量变换为像这样的RGB颜色元素，我们就能把根据表面的形状的fragment的法线保存在2D纹理中。教程开头展示的那个砖块的例子的法线贴图如下所示：
 
-![](http://learnopengl.com/img/advanced-lighting/normal_mapping_normal_map.png)
+![](../img/05/04/normal_mapping_normal_map.png)
 
 这会是一种偏蓝色调的纹理（你在网上找到的几乎所有法线贴图都是这样的）。这是因为所有法线的指向都偏向z轴（0, 0, 1）这是一种偏蓝的颜色。法线向量从z轴方向也向其他方向轻微偏移，颜色也就发生了轻微变化，这样看起来便有了一种深度。例如，你可以看到在每个砖块的顶部，颜色倾向于偏绿，这是因为砖块的顶部的法线偏向于指向正y轴方向（0, 1, 0），这样它就是绿色的了。
 
@@ -62,17 +62,17 @@ void main()
 
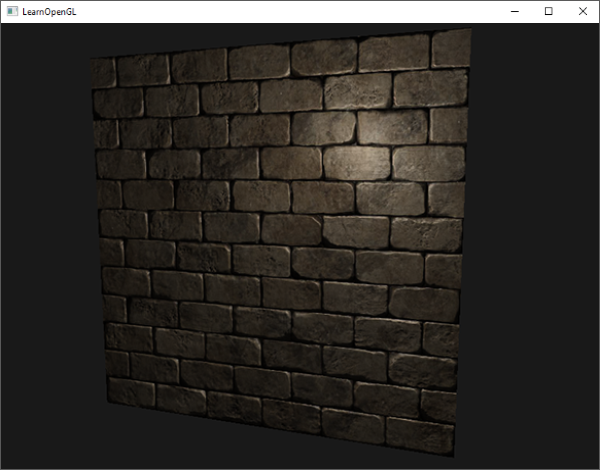
 通过慢慢随着时间慢慢移动光源，你就能明白法线贴图是什么意思了。运行这个例子你就能得到本教程开始的那个效果：
 
-![](http://learnopengl.com/img/advanced-lighting/normal_mapping_correct.png)
+![](../img/05/04/normal_mapping_correct.png)
 
 你可以在这里找到这个简单demo的源代码及其顶点和像素着色器。
 
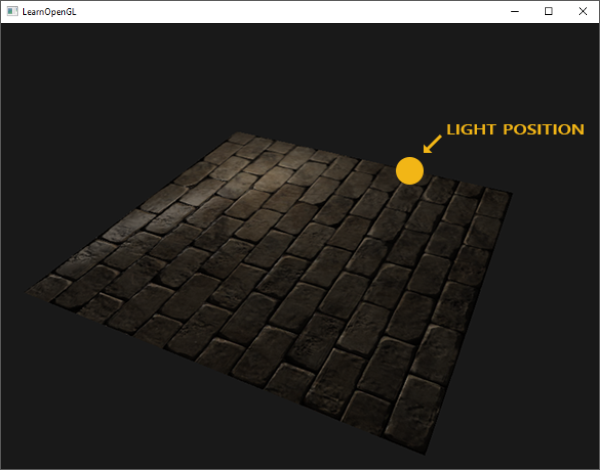
 然而有个问题限制了刚才讲的那种法线贴图的使用。我们使用的那个法线贴图里面的所有法线向量都是指向正z方向的。上面的例子能用，是因为那个平面的表面法线也是指向正z方向的。可是，如果我们在表面法线指向正y方向的平面上使用同一个法线贴图会发生什么？
 
-![](http://learnopengl.com/img/advanced-lighting/normal_mapping_ground.png)
+![](../img/05/04/normal_mapping_ground.png)
 
 光照看起来完全不对！发生这种情况是平面的表面法线现在指向了y，而采样得到的法线仍然指向的是z。结果就是光照仍然认为表面法线和之前朝向正z方向时一样；这样光照就不对了。下面的图片展示了这个表面上采样的法线的近似情况：
 
-![](http://learnopengl.com/img/advanced-lighting/normal_mapping_ground_normals.png)
+![](../img/05/04/normal_mapping_ground_normals.png)
 
 你可以看到所有法线都指向z方向，它们本该朝着表面法线指向y方向的。一个可行方案是为每个表面制作一个单独的法线贴图。如果是一个立方体的话我们就需要6个法线贴图，但是如果模型上有无数的朝向不同方向的表面，这就不可行了（译注：实际上对于复杂模型可以把朝向各个方向的法线储存在同一张贴图上，你可能看到过不只是蓝色的法线贴图，不过用那样的法线贴图有个问题是你必须记住模型的起始朝向，如果模型运动了还要记录模型的变换，这是非常不方便的；此外就像作者所说的，如果把一个diffuse纹理应用在同一个物体的不同表面上，就像立方体那样的，就需要做6个法线贴图，这也不可取）。
 
@@ -88,11 +88,11 @@ void main()
 
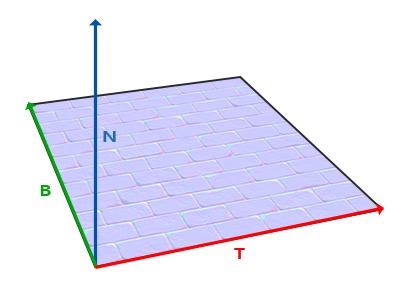
 已知上向量是表面的法线向量。右和前向量是切线(Tagent)和副切线(Bitangent)向量。下面的图片展示了一个表面的三个向量：
 
-![](http://learnopengl.com/img/advanced-lighting/normal_mapping_tbn_vectors.png)
+![](../img/05/04/normal_mapping_tbn_vectors.png)
 
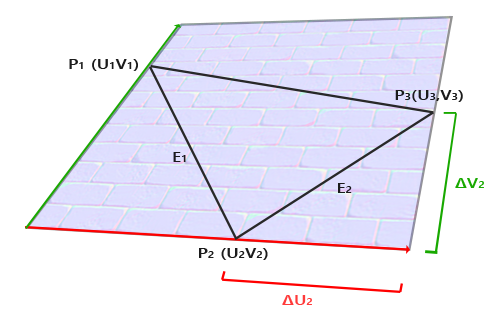
 计算出切线和副切线并不像法线向量那么容易。从图中可以看到法线贴图的切线和副切线与纹理坐标的两个方向对齐。我们就是用到这个特性计算每个表面的切线和副切线的。需要用到一些数学才能得到它们；请看下图：
 
-![](http://learnopengl.com/img/advanced-lighting/normal_mapping_surface_edges.png)
+![](../img/05/04/normal_mapping_surface_edges.png)
 
 上图中我们可以看到边\(E_2\)纹理坐标的不同，\(E_2\)是一个三角形的边，这个三角形的另外两条边是\(\Delta U_2\)和\(\Delta V_2\)，它们与切线向量\(T\)和副切线向量\(B\)方向相同。这样我们可以把边\(E_1\)和\(E_2\)用切线向量\(T\)和副切线向量\(B\)的线性组合表示出来（译注：注意\(T\)和\(B\)都是单位长度，在\(TB\)平面中所有点的\(T\)、\(B\)坐标都在0到1之间，因此可以进行这样的组合）：
 
@@ -191,7 +191,7 @@ bitangent1 = glm::normalize(bitangent1);
 
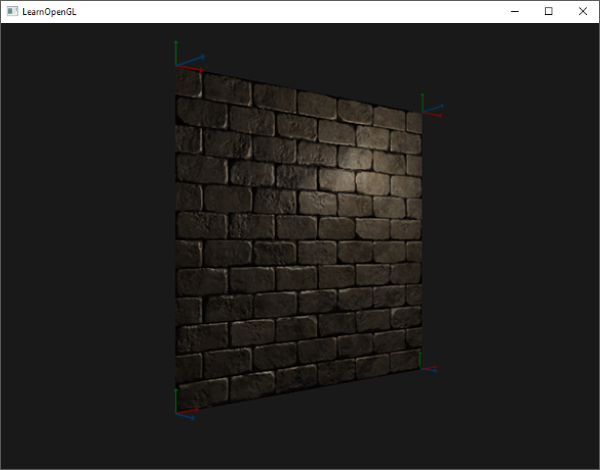
 最后的切线和副切线向量的值应该是(1, 0, 0)和(0, 1, 0)，它们和法线(0, 0, 1)组成相互垂直的TBN矩阵。在平面上显示出来TBN应该是这样的：
 
-![](http://learnopengl.com/img/advanced-lighting/normal_mapping_tbn_shown.png)
+![](../img/05/04/normal_mapping_tbn_shown.png)
 
 每个顶点定义了切线和副切线向量，我们就可以开始实现正确的法线贴图了。
 
@@ -334,7 +334,7 @@ RenderQuad();
 
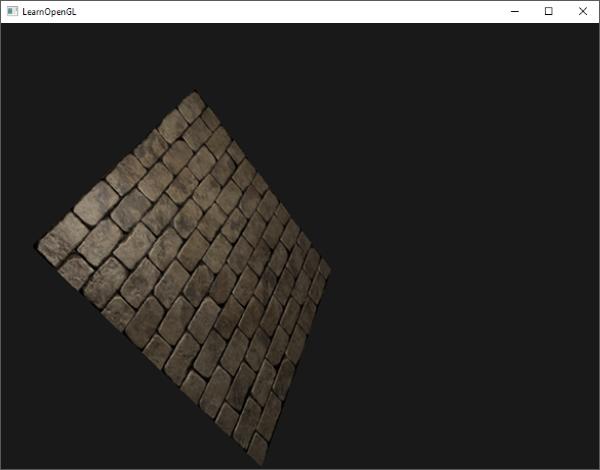
 看起来是正确的法线贴图：
 
-![](http://learnopengl.com/img/advanced-lighting/normal_mapping_correct_tangent.png)
+![](../img/05/04/normal_mapping_correct_tangent.png)
 
 你可以在这里找到[源代码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/normal_mapping)、[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/normal_mapping&type=vertex)和[像素](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/normal_mapping&type=fragment)着色器。
 
@@ -373,13 +373,13 @@ vector<Texture> specularMaps = this->loadMaterialTextures(
 
 运行程序，用新的模型加载器，加载一个有specular和法线贴图的模型，看起来会像这样：
 
-![](http://learnopengl.com/img/advanced-lighting/normal_mapping_complex_compare.png)
+![](../img/05/04/normal_mapping_complex_compare.png)
 
 你可以看到在没有太多点的额外开销的情况下法线贴图难以置信地提升了物体的细节。
 
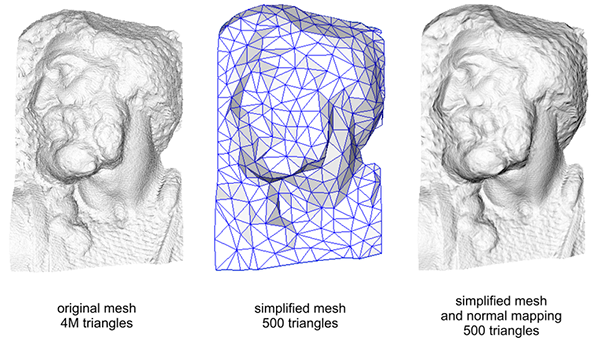
 使用法线贴图也是一种提升你的场景的表现的重要方式。在使用法线贴图之前你不得不使用相当多的顶点才能表现出一个更精细的网格，但使用了法线贴图我们可以使用更少的顶点表现出同样丰富的细节。下图来自Paolo Cignoni，图中对比了两种方式：
 
-![](http://learnopengl.com/img/advanced-lighting/normal_mapping_comparison.png)
+![](../img/05/04/normal_mapping_comparison.png)
 
 高精度网格和使用法线贴图的低精度网格几乎区分不出来。所以法线贴图不仅看起来漂亮，它也是一个将高精度多边形转换为低精度多边形而不失细节的重要工具。