mirror of
https://github.com/LearnOpenGL-CN/LearnOpenGL-CN.git
synced 2025-08-23 12:45:29 +08:00
convert 04/09 04/10 04/11
This commit is contained in:
503
04 Advanced OpenGL/09 Geometry Shader.md
Normal file
503
04 Advanced OpenGL/09 Geometry Shader.md
Normal file
@@ -0,0 +1,503 @@
|
||||
## 几何着色器(Geometry Shader)
|
||||
|
||||
本文作者JoeyDeVries,由Django翻译自http://learnopengl.com
|
||||
|
||||
在顶点和像素着色器张志坚有一个可选的着色器阶段,叫做几何着色器(geometry shader)。几何着色器以一个或多个表示为一个单独基本图形(primitive)的顶点作为输入,比如可以是一个点或者三角形。几何着色器在将这些顶点发送到下一个着色阶段之前,可以将这些顶点转变为它认为合适的内容。几何着色器有意思的地方在于它可以把(一个或多个)顶点转变为完全不同的基本图形(primitive),从而生成比原来多得多的顶点。
|
||||
|
||||
我们直接用一个例子深入了解一下:
|
||||
|
||||
```c++
|
||||
#version 330 core
|
||||
layout (points) in;
|
||||
layout (line_strip, max_vertices = 2) out;
|
||||
|
||||
void main() {
|
||||
gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
|
||||
EmitVertex();
|
||||
|
||||
gl_Position = gl_in[0].gl_Position + vec4(0.1, 0.0, 0.0, 0.0);
|
||||
EmitVertex();
|
||||
|
||||
EndPrimitive();
|
||||
}
|
||||
```
|
||||
|
||||
每个几何着色器开始位置我们需要声明输入的基本图形(primitive)类型,这个输入是我们从顶点着色器中接收到的。我们在in关键字前面声明一个layout标识符。这个输入layout修饰符可以从一个顶点着色器接收以下基本图形值:
|
||||
|
||||
|
||||
基本图形|描述
|
||||
---|---
|
||||
points |绘制GL_POINTS基本图形的时候(1)
|
||||
lines |当绘制GL_LINES或GL_LINE_STRIP(2)时
|
||||
lines_adjacency | GL_LINES_ADJACENCY或GL_LINE_STRIP_ADJACENCY(4)
|
||||
triangles |GL_TRIANGLES, GL_TRIANGLE_STRIP或GL_TRIANGLE_FAN(3)
|
||||
triangles_adjacency |GL_TRIANGLES_ADJACENCYGL_TRIANGLE_STRIP_ADJACENCY(6)
|
||||
|
||||
这是我们能够给渲染函数的几乎所有的基本图形。如果我们选择以GL_TRIANGLES绘制顶点,我们要把输入修饰符设置为triangles。括号里的数字代表一个基本图形所能包含的最少的顶点数。
|
||||
|
||||
当我们需要指定一个几何着色器所输出的基本图形类型时,我们就在out关键字前面加一个layout修饰符。和输入layout标识符一样,output的layout标识符也可以接受以下基本图形值:
|
||||
|
||||
* points
|
||||
* line_strip
|
||||
* triangle_strip
|
||||
|
||||
使用这3个输出修饰符我们可以从输入的基本图形创建任何我们想要的形状。为了生成一个三角形,我们定义一个triangle_strip作为输出,然后输出3个顶点。
|
||||
|
||||
几何着色器同时希望我们设置一个它能输出的顶点数量的最大值(如果你超出了这个数值,OpenGL就会忽略剩下的顶点),我们可以在out关键字的layout标识符上做这件事。在这个特殊的情况中,我们将使用最大值为2个顶点,来输出一个line_strip。
|
||||
|
||||
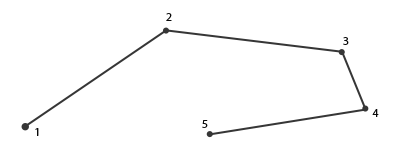
这种情况,你会奇怪什么是线条:一个线条是把多个点链接起来表示出一个连续的线,它最少有两个点来组成。每个后一个点在前一个新渲染的点后面渲染,你可以看看下面的图,其中包含5个顶点:
|
||||
|
||||
|
||||
|
||||
上面的着色器,我们只能输出一个线段,因为顶点的最大值设置的是2。
|
||||
|
||||
为生成更有意义的结果,我们需要某种方式从前一个着色阶段获得输出。GLSL为我们提供了一个内建变量,它叫做gl_in,它的内部看起来可能像这样:
|
||||
|
||||
```c++
|
||||
in gl_Vertex
|
||||
{
|
||||
vec4 gl_Position;
|
||||
float gl_PointSize;
|
||||
float gl_ClipDistance[];
|
||||
} gl_in[];
|
||||
|
||||
```
|
||||
|
||||
这里它被声明为一个interface block(前面的教程已经讨论过),它包含几个有意思的变量,其中最有意思的是gl_Position,它包含着和我们设置的顶点着色器的输出相似的向量。
|
||||
|
||||
要注意的是,它被声明为一个数组,因为大多数渲染基本图形(primitive)由一个以上顶点组成,几何着色器接收一个基本图形的所有顶点作为它的输入。
|
||||
|
||||
使用从前一个顶点着色阶段的顶点数据,我们就可以开始生成新的数据了,这是通过2个几何着色器函数EmitVertex和EndPrimitive来完成的。几何着色器需要你去生成/输出至少一个你定义为输出的基本图形。在我们的例子里我们打算至少生成一个线条(line strip)基本图形。
|
||||
|
||||
```c++
|
||||
void main() {
|
||||
gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
|
||||
EmitVertex();
|
||||
|
||||
gl_Position = gl_in[0].gl_Position + vec4(0.1, 0.0, 0.0, 0.0);
|
||||
EmitVertex();
|
||||
|
||||
EndPrimitive();
|
||||
}
|
||||
```
|
||||
|
||||
每次我们调用EmitVertex,当前设置到gl_Position的向量就会被添加到基本图形上。无论何时调用EndPrimitive,所有为这个基本图形发射出去的顶点都将结合为一个特定的输出渲染基本图形。一个或多个EmitVertex函数调用后,重复调用EndPrimitive就能生成多个基本图形。这个特殊的例子里,发射了两个顶点,它们被从顶点原来的位置平移了一段距离,然后调用EndPrimitive将这两个顶点结合为一个单独的有两个顶点的线条。
|
||||
|
||||
现在你了解了几何着色器的工作方式,你就可能猜出这个几何着色器做了什么。这个几何着色器接收一个point基本图形作为它的输入,使用输入点作为它的中心,创建了一个水平线基本图形。如果我们渲染它,结果就会像这样:
|
||||
|
||||

|
||||
|
||||
并不是非常引人注目,但是考虑到它的输出是使用下面的渲染命令生成的就很有意思了:
|
||||
|
||||
```c++
|
||||
glDrawArrays(GL_POINTS, 0, 4);
|
||||
```
|
||||
|
||||
这是个相对简单的例子,它向你展示了我们如何使用几何着色器来动态地在运行时生成新的形状。本章的后面,我们会讨论一些可以使用几何着色器获得有趣的效果,但是现在我们将以创建一个简单的几何着色器开始。
|
||||
|
||||
### 使用几何着色器
|
||||
|
||||
为了展示几何着色器的使用,我们将渲染一个简单的场景,在场景中我们只绘制4个点,这4个点在标准化设备坐标的z平面上。这些点的坐标是:
|
||||
|
||||
```c++
|
||||
GLfloat points[] = {
|
||||
-0.5f, 0.5f, // Top-left
|
||||
0.5f, 0.5f, // Top-right
|
||||
0.5f, -0.5f, // Bottom-right
|
||||
-0.5f, -0.5f // Bottom-left
|
||||
};
|
||||
```
|
||||
|
||||
顶点着色器只在z平面绘制点,所以我们只需要一个基本顶点着色器:
|
||||
|
||||
```c++
|
||||
#version 330 core
|
||||
layout (location = 0) in vec2 position;
|
||||
|
||||
void main()
|
||||
{
|
||||
gl_Position = vec4(position.x, position.y, 0.0f, 1.0f);
|
||||
}
|
||||
```
|
||||
|
||||
我们会简单地为所有点输出绿色,我们直接在像素着色器里进行硬编码:
|
||||
|
||||
```c++
|
||||
#version 330 core
|
||||
out vec4 color;
|
||||
|
||||
void main()
|
||||
{
|
||||
color = vec4(0.0f, 1.0f, 0.0f, 1.0f);
|
||||
}
|
||||
```
|
||||
|
||||
为点(point)的顶点(vertex)生成一个VAO和VBO,然后使用glDrawArrays进行绘制:
|
||||
|
||||
```c++
|
||||
shader.Use();
|
||||
glBindVertexArray(VAO);
|
||||
glDrawArrays(GL_POINTS, 0, 4);
|
||||
glBindVertexArray(0);
|
||||
```
|
||||
|
||||
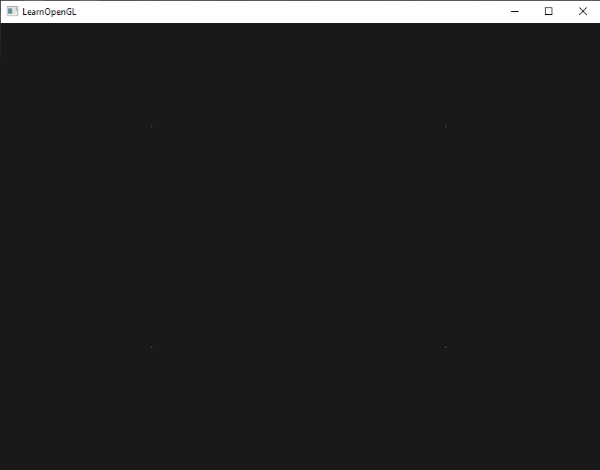
效果是黑色场景中有四个绿点(虽然很难看到):
|
||||
|
||||
|
||||
|
||||
但我们不是已经学到了所有内容了吗?对,现在我们将通过为场景添加一个几何着色器来为这个小场景增加点活力。
|
||||
|
||||
出于学习的目的我们将创建一个叫pass-through的几何着色器,它用一个point基本图形作为它的输入,并把它无修改地传(pass)到下一个着色器。
|
||||
|
||||
```c++
|
||||
#version 330 core
|
||||
layout (points) in;
|
||||
layout (points, max_vertices = 1) out;
|
||||
|
||||
void main() {
|
||||
gl_Position = gl_in[0].gl_Position;
|
||||
EmitVertex();
|
||||
EndPrimitive();
|
||||
}
|
||||
```
|
||||
|
||||
现在这个几何着色器应该很容易理解了。它简单地将它接收到的输入的无修改的顶点位置发射出去,然后生成一个point基本图形。
|
||||
|
||||
一个几何着色器需要像顶点和像素着色器一样被编译和链接,但是这次我们将使用GL_GEOMETRY_SHADER作为着色器的类型来创建这个着色器:
|
||||
|
||||
```c++
|
||||
geometryShader = glCreateShader(GL_GEOMETRY_SHADER);
|
||||
glShaderSource(geometryShader, 1, &gShaderCode, NULL);
|
||||
glCompileShader(geometryShader);
|
||||
...
|
||||
glAttachShader(program, geometryShader);
|
||||
glLinkProgram(program);
|
||||
```
|
||||
|
||||
编译着色器的代码和顶点、像素着色器的基本一样。要记得检查编译和链接错误!
|
||||
|
||||
如果你现在编译和运行,就会看到和下面相似的结果:
|
||||
|
||||

|
||||
|
||||
它和没用几何着色器一样!我承认有点无聊,但是事实上,我们仍能绘制证明几何着色器工作了的点,所以现在是时候来做点更有意思的事了!
|
||||
|
||||
|
||||
|
||||
### 创建几个房子
|
||||
|
||||
绘制点和线没什么意思,所以我们将在每个点上使用几何着色器绘制一个房子。我们可以通过把几何着色器的输出设置为triangle_strip来达到这个目的,总共要绘制3个三角形:两个方形和一个屋顶。
|
||||
|
||||
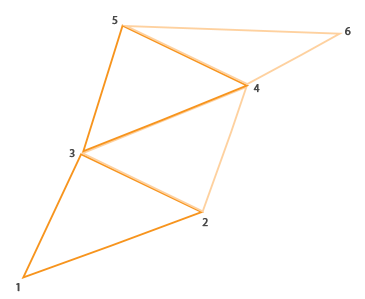
在OpenGL中triangle strip(三角形带)绘制起来更高效,因为它所使用的顶点更少。第一个三角形绘制完以后,每个后续的顶点会生成一个毗连前一个三角形的新三角形:每3个毗连的顶点都能构成一个三角形。如果我们有6个顶点,它们以triangle strip的方式组合起来,那么我们会得到这些三角形:(1, 2, 3)、(2, 3, 4)、(3, 4, 5)、(4,5,6)因此总共可以表示出4个三角形。一个triangle strip至少要用3个顶点才行,它能生曾N-2个三角形;6个顶点我们就能创建6-2=4个三角形。下面的图片表达了这点:
|
||||
|
||||
|
||||
|
||||
使用一个triangle strip作为一个几何着色器的输出,我们可以轻松创建房子的形状,只要以正确的顺序来生成3个毗连的三角形。下面的图像显示,我们需要以何种顺序来绘制点,才能获得我们需要的三角形,图上的蓝点代表输入点:
|
||||
|
||||

|
||||
|
||||
上图的内容转变为几何着色器:
|
||||
|
||||
```c++
|
||||
#version 330 core
|
||||
layout (points) in;
|
||||
layout (triangle_strip, max_vertices = 5) out;
|
||||
|
||||
void build_house(vec4 position)
|
||||
{
|
||||
gl_Position = position + vec4(-0.2f, -0.2f, 0.0f, 0.0f); // 1:bottom-left
|
||||
EmitVertex();
|
||||
gl_Position = position + vec4( 0.2f, -0.2f, 0.0f, 0.0f); // 2:bottom-right
|
||||
EmitVertex();
|
||||
gl_Position = position + vec4(-0.2f, 0.2f, 0.0f, 0.0f); // 3:top-left
|
||||
EmitVertex();
|
||||
gl_Position = position + vec4( 0.2f, 0.2f, 0.0f, 0.0f); // 4:top-right
|
||||
EmitVertex();
|
||||
gl_Position = position + vec4( 0.0f, 0.4f, 0.0f, 0.0f); // 5:top
|
||||
EmitVertex();
|
||||
EndPrimitive();
|
||||
}
|
||||
|
||||
void main()
|
||||
{
|
||||
build_house(gl_in[0].gl_Position);
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
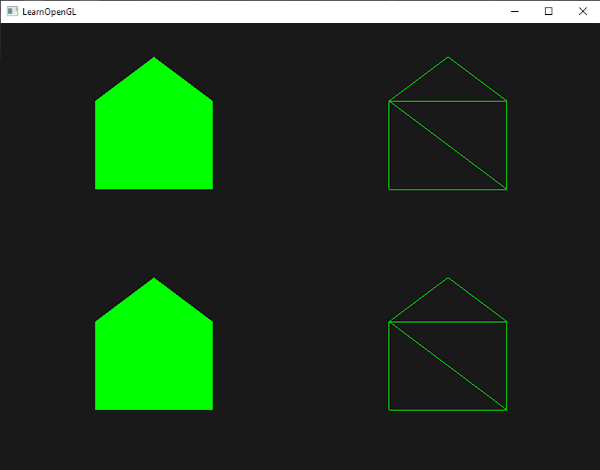
这个几何着色器生成5个顶点,每个顶点是点(point)的位置加上一个偏移量,来组成一个大triangle strip。接着最后的基本图形被像素化,像素着色器处理整个triangle strip,结果是为我们绘制的每个点生成一个绿房子:
|
||||
|
||||
|
||||
|
||||
可以看到,每个房子实则是由3个三角形组成,都是仅仅使用空间中一点来绘制的。绿房子绿房子看起来还是不够漂亮,所以我们再给每个房子加一个不同的颜色。我们将在顶点着色器中为每个顶点增加一个额外的代表颜色信息的顶点属性。
|
||||
|
||||
下面是更新了的顶点数据:
|
||||
|
||||
```c++
|
||||
GLfloat points[] = {
|
||||
-0.5f, 0.5f, 1.0f, 0.0f, 0.0f, // Top-left
|
||||
0.5f, 0.5f, 0.0f, 1.0f, 0.0f, // Top-right
|
||||
0.5f, -0.5f, 0.0f, 0.0f, 1.0f, // Bottom-right
|
||||
-0.5f, -0.5f, 1.0f, 1.0f, 0.0f // Bottom-left
|
||||
};
|
||||
```
|
||||
|
||||
然后我们更新顶点着色器,使用一个interface block来像几何着色器发送颜色属性:
|
||||
|
||||
```c++
|
||||
#version 330 core
|
||||
layout (location = 0) in vec2 position;
|
||||
layout (location = 1) in vec3 color;
|
||||
|
||||
out VS_OUT {
|
||||
vec3 color;
|
||||
} vs_out;
|
||||
|
||||
void main()
|
||||
{
|
||||
gl_Position = vec4(position.x, position.y, 0.0f, 1.0f);
|
||||
vs_out.color = color;
|
||||
}
|
||||
```
|
||||
|
||||
接着我们还需要在几何着色器中声明同样的interface block(使用一个不同的接口名):
|
||||
|
||||
```c++
|
||||
in VS_OUT {
|
||||
vec3 color;
|
||||
} gs_in[];
|
||||
```
|
||||
|
||||
因为几何着色器把多个顶点作为它的输入,从顶点着色器来的输入数据总是被以数组的形式表示出来,即使现在我们只有一个顶点。
|
||||
|
||||
!!! Important
|
||||
|
||||
我们不是必须使用interface block来把数据发送到几何着色器中。我们还可以这么写:
|
||||
|
||||
in vec3 vColor[];
|
||||
|
||||
如果顶点着色器发送的颜色向量是out vec3 vColor那么interface block就会在比如几何着色器这样的着色器中更轻松地完成工作。事实上,几何着色器的输入可以非常大,把它们组成一个大的interface block数组会更有意义。
|
||||
|
||||
|
||||
然后我们还要为下一个像素着色阶段僧名一个输出颜色向量:
|
||||
|
||||
```c++
|
||||
out vec3 fColor;
|
||||
```
|
||||
|
||||
因为像素着色器只需要一个(已进行了插值的)颜色,传送多个颜色没有意义。fColor向量这样就不是一个数组,而是一个单一的向量。当发射一个顶点时,为了它的像素着色器运行,每个顶点都会储存最后在fColor中储存的值。对于这些房子来说,我们可以在第一个顶点被发射,对整个房子上色前,只使用来自顶点着色器的颜色填充fColor一次:
|
||||
|
||||
```c++
|
||||
fColor = gs_in[0].color; // gs_in[0] since there's only one input vertex
|
||||
gl_Position = position + vec4(-0.2f, -0.2f, 0.0f, 0.0f); // 1:bottom-left
|
||||
EmitVertex();
|
||||
gl_Position = position + vec4( 0.2f, -0.2f, 0.0f, 0.0f); // 2:bottom-right
|
||||
EmitVertex();
|
||||
gl_Position = position + vec4(-0.2f, 0.2f, 0.0f, 0.0f); // 3:top-left
|
||||
EmitVertex();
|
||||
gl_Position = position + vec4( 0.2f, 0.2f, 0.0f, 0.0f); // 4:top-right
|
||||
EmitVertex();
|
||||
gl_Position = position + vec4( 0.0f, 0.4f, 0.0f, 0.0f); // 5:top
|
||||
EmitVertex();
|
||||
EndPrimitive();
|
||||
```
|
||||
|
||||
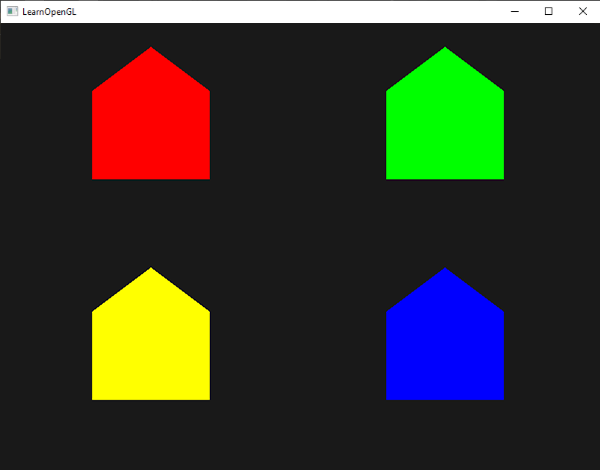
所有发射出去的顶点都把最后储存在fColor中的值嵌入到他们的数据中,和我们在他们的属性中定义的顶点颜色相同。所有的分房子便都有了自己的颜色:
|
||||
|
||||
|
||||
|
||||
为了好玩儿,我们还可以假装这是在冬天,给最后一个顶点一个自己的白色,就像在屋顶上落了一些雪。
|
||||
|
||||
```c++
|
||||
fColor = gs_in[0].color;
|
||||
gl_Position = position + vec4(-0.2f, -0.2f, 0.0f, 0.0f); // 1:bottom-left
|
||||
EmitVertex();
|
||||
gl_Position = position + vec4( 0.2f, -0.2f, 0.0f, 0.0f); // 2:bottom-right
|
||||
EmitVertex();
|
||||
gl_Position = position + vec4(-0.2f, 0.2f, 0.0f, 0.0f); // 3:top-left
|
||||
EmitVertex();
|
||||
gl_Position = position + vec4( 0.2f, 0.2f, 0.0f, 0.0f); // 4:top-right
|
||||
EmitVertex();
|
||||
gl_Position = position + vec4( 0.0f, 0.4f, 0.0f, 0.0f); // 5:top
|
||||
fColor = vec3(1.0f, 1.0f, 1.0f);
|
||||
EmitVertex();
|
||||
EndPrimitive();
|
||||
|
||||
```
|
||||
|
||||
结果就像这样:
|
||||
|
||||
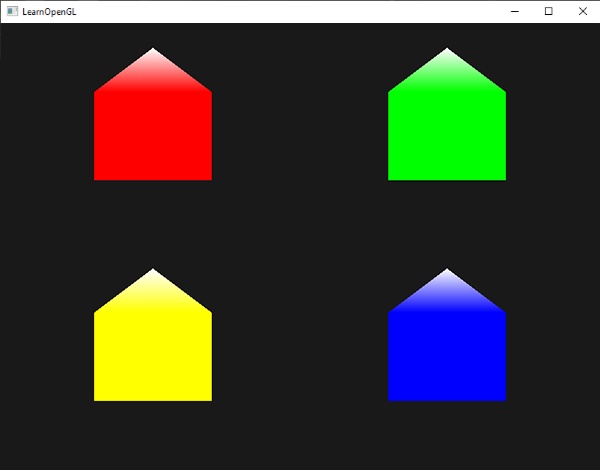
|
||||
|
||||
你可以对比一下你的源码和着色器。
|
||||
|
||||
你可以看到,使用几何着色器,你可以使用最简单的基本图形就能获得漂亮的新玩意。因为这些形状是在你的GPU超快硬件上动态生成额,这要比使用顶点缓冲自己定义这些形状更为高效。几何缓冲在简单的经常被重复的形状比如体素(voxel)的世界和室外的草地上,是一种非常强大的优化工具。
|
||||
|
||||
#### 爆炸式物体
|
||||
|
||||
绘制房子的确很有趣,但我们不会经常这么用。这就是为什么现在我们将撬起物体缺口,形成爆炸式物体的原因!虽然这个我们也不会经常用到,但是它能向你展示一些几何着色器的强大之处。
|
||||
|
||||
当我们说对一个物体进行爆破的时候并不是说我们将要把之前的那堆顶点炸掉,但是我们打算把每个三角形沿着它们的法线向量移动一小段距离。效果是整个物体上的三角形看起来就像沿着它们的法线向量爆炸了一样。纳米服上的三角形的爆炸式效果看起来是这样的:
|
||||
|
||||
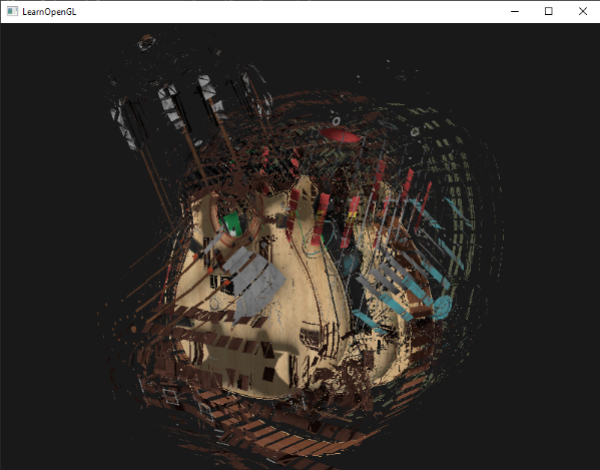
|
||||
|
||||
这样一个几何着色器效果的一大好处是,它可以用到任何物体上,无论它们多复杂。
|
||||
|
||||
因为我们打算沿着三角形的法线向量移动三角形的每个顶点,我们需要先计算它的法线向量。我们要做的是计算出一个向量,它垂直于三角形的表面,使用这三个我们已经的到的顶点就能做到。你可能记得变换教程中,我们可以使用叉乘获取一个垂直于两个其他向量的向量。如果我们有两个向量a和b,它们平行于三角形的表面,我们就可以对这两个向量进行叉乘得到法线向量了。下面的几何着色器函数做的正是这件事,它使用3个输入顶点坐标获取法线向量:
|
||||
|
||||
```c++
|
||||
vec3 GetNormal()
|
||||
{
|
||||
vec3 a = vec3(gl_in[0].gl_Position) - vec3(gl_in[1].gl_Position);
|
||||
vec3 b = vec3(gl_in[2].gl_Position) - vec3(gl_in[1].gl_Position);
|
||||
return normalize(cross(a, b));
|
||||
}
|
||||
```
|
||||
|
||||
这里我们使用减法获取了两个向量a和b,它们平行于三角形的表面。两个向量相减得到一个两个向量的差值,由于所有3个点都在三角形平面上,任何向量相减都会得到一个平行于平面的向量。一定要注意,如果我们调换了a和b的叉乘顺序,我们得到的法线向量就会使反的,顺序很重要!
|
||||
|
||||
知道了如何计算法线向量,我们就能创建一个explode函数,函数返回的是一个新向量,它把位置向量沿着法线向量方向平移:
|
||||
|
||||
```c++
|
||||
vec4 explode(vec4 position, vec3 normal)
|
||||
{
|
||||
float magnitude = 2.0f;
|
||||
vec3 direction = normal * ((sin(time) + 1.0f) / 2.0f) * magnitude;
|
||||
return position + vec4(direction, 0.0f);
|
||||
}
|
||||
```
|
||||
|
||||
函数本身并不复杂,sin(正弦)函数把一个time变量作为它的参数,它根据时间来返回一个-1.0到1.0之间的值。因为我们不想让物体坍缩,所以我们把sin返回的值做成0到1的范围。最后的值去乘以法线向量,direction向量被添加到位置向量上。
|
||||
|
||||
爆炸效果的完整的几何着色器是这样的,它使用我们的模型加载器,绘制出一个模型:
|
||||
|
||||
```c++
|
||||
#version 330 core
|
||||
layout (triangles) in;
|
||||
layout (triangle_strip, max_vertices = 3) out;
|
||||
|
||||
in VS_OUT {
|
||||
vec2 texCoords;
|
||||
} gs_in[];
|
||||
|
||||
out vec2 TexCoords;
|
||||
|
||||
uniform float time;
|
||||
|
||||
vec4 explode(vec4 position, vec3 normal) { ... }
|
||||
|
||||
vec3 GetNormal() { ... }
|
||||
|
||||
void main() {
|
||||
vec3 normal = GetNormal();
|
||||
|
||||
gl_Position = explode(gl_in[0].gl_Position, normal);
|
||||
TexCoords = gs_in[0].texCoords;
|
||||
EmitVertex();
|
||||
gl_Position = explode(gl_in[1].gl_Position, normal);
|
||||
TexCoords = gs_in[1].texCoords;
|
||||
EmitVertex();
|
||||
gl_Position = explode(gl_in[2].gl_Position, normal);
|
||||
TexCoords = gs_in[2].texCoords;
|
||||
EmitVertex();
|
||||
EndPrimitive();
|
||||
}
|
||||
```
|
||||
|
||||
注意我们同样在发射一个顶点前输出了合适的纹理坐标。
|
||||
|
||||
也不要忘记在OpenGL代码中设置time变量:
|
||||
|
||||
```c++
|
||||
glUniform1f(glGetUniformLocation(shader.Program, "time"), glfwGetTime());
|
||||
```
|
||||
|
||||
最后的结果是一个随着时间持续不断地爆炸的3D模型(不断爆炸不断回到正常状态)。尽管没什么大用处,它却向你展示出很多几何着色器的高级用法。你可以用完整的源码和着色器对比一下你自己的。
|
||||
|
||||
#### 把法线向量显示出来
|
||||
|
||||
在这部分我们将使用几何着色器写一个例子,非常有用:显示一个法线向量。当编写光照着色器的时候,你最终会遇到奇怪的视频输出问题,你很难决定是什么导致了这个问题。通常导致光照错误的是,不正确的加载顶点数据,以及给它们指定了不合理的顶点属性,又或是在着色器中不合法的管理,导致产生了不正确的法线向量。我们所希望的是有某种方式可以检测出法线向量是否正确。把法线向量显示出来正是这样一种方法,恰好几何着色器能够完美地达成这个目的。
|
||||
|
||||
思路是这样的:我们先不用几何着色器,正常绘制场景,然后我们再次绘制一遍场景,但这次只显示我们通过几何着色器生成的法线向量。几何着色器把一个triangle基本图形作为输入类型,用它们生成3条和法线向量同向的线段,每个顶点一条。伪代码应该是这样的:
|
||||
|
||||
```c++
|
||||
shader.Use();
|
||||
DrawScene();
|
||||
normalDisplayShader.Use();
|
||||
DrawScene();
|
||||
```
|
||||
|
||||
这次我们会创建一个使用模型提供的顶点法线,而不是自己去生成。为了适应缩放和旋转我们会在把它变换到裁切空间坐标前,使用法线矩阵来法线(几何着色器用他的位置向量做为裁切空间坐标,所以我们还要把法线向量变换到同一个空间)。这些都能在顶点着色器中完成:
|
||||
|
||||
```c++
|
||||
#version 330 core
|
||||
layout (location = 0) in vec3 position;
|
||||
layout (location = 1) in vec3 normal;
|
||||
|
||||
out VS_OUT {
|
||||
vec3 normal;
|
||||
} vs_out;
|
||||
|
||||
uniform mat4 projection;
|
||||
uniform mat4 view;
|
||||
uniform mat4 model;
|
||||
|
||||
void main()
|
||||
{
|
||||
gl_Position = projection * view * model * vec4(position, 1.0f);
|
||||
mat3 normalMatrix = mat3(transpose(inverse(view * model)));
|
||||
vs_out.normal = normalize(vec3(projection * vec4(normalMatrix * normal, 1.0)));
|
||||
}
|
||||
```
|
||||
|
||||
经过变换的裁切空间法线向量接着通过一个interface block被传递到下个着色阶段。几何着色器接收每个顶点(带有位置和法线向量),从每个位置向量绘制出一个法线向量:
|
||||
|
||||
```c++
|
||||
#version 330 core
|
||||
layout (triangles) in;
|
||||
layout (line_strip, max_vertices = 6) out;
|
||||
|
||||
in VS_OUT {
|
||||
vec3 normal;
|
||||
} gs_in[];
|
||||
|
||||
const float MAGNITUDE = 0.4f;
|
||||
|
||||
void GenerateLine(int index)
|
||||
{
|
||||
gl_Position = gl_in[index].gl_Position;
|
||||
EmitVertex();
|
||||
gl_Position = gl_in[index].gl_Position + vec4(gs_in[index].normal, 0.0f) * MAGNITUDE;
|
||||
EmitVertex();
|
||||
EndPrimitive();
|
||||
}
|
||||
|
||||
void main()
|
||||
{
|
||||
GenerateLine(0); // First vertex normal
|
||||
GenerateLine(1); // Second vertex normal
|
||||
GenerateLine(2); // Third vertex normal
|
||||
}
|
||||
```
|
||||
|
||||
到现在为止,像这样的几何着色器的内容就不言自明了。需要注意的是我们我们把法线向量乘以一个MAGNITUDE向量来限制显示出的法线向量的大小(否则它们就太大了)。
|
||||
|
||||
由于把法线显示出来通常用于调试的目的,我们可以在像素着色器的帮助下把它们显示为单色的线(如果你愿意也可以更炫一点)。
|
||||
|
||||
```c++
|
||||
#version 330 core
|
||||
out vec4 color;
|
||||
|
||||
void main()
|
||||
{
|
||||
color = vec4(1.0f, 1.0f, 0.0f, 1.0f);
|
||||
}
|
||||
```
|
||||
|
||||
现在先使用普通着色器来渲染你的模型,然后使用特制的法线可视着色器,你会看到这样的效果:
|
||||
|
||||
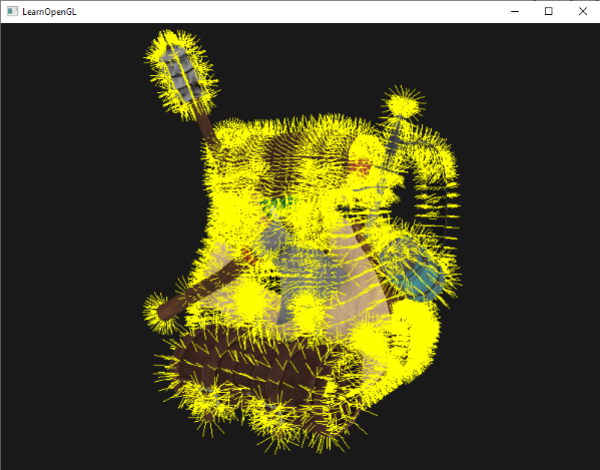
|
||||
|
||||
除了我们的纳米服现在看起来有点像一个带着隔热手套的全身多毛的家伙外,它给了我们一种非常有效的检查一个模型的法线向量是否有错误的方式。你可以想象下这样的几何着色器也经常能被用在给物体添加毛发上。
|
||||
|
||||
你可以从这里找到[源码](http://learnopengl.com/code_viewer.php?code=advanced/geometry_shader_normals)和可显示法线的[着色器](http://learnopengl.com/code_viewer.php?code=advanced/geometry_shader_normals_shaders)。
|
||||
Reference in New Issue
Block a user