Replace html with tags

01 Getting started/08 Coordinate Systems.md

@@ -52,6 +52,8 @@
 因为将所有可见的坐标都放置在-1.0到1.0的范围内不是很直观，我们会指定自己的坐标集的方式并将它转换回规则化设备坐标系就像OpenGL期望它做的那样。
 为了将顶点坐标从观察空间转换到裁剪空间，我们定义一个投影矩阵，它指定了坐标的范围，例如，每个维度都是从-1000到1000。投影矩阵接着会将在它指定的范围内的坐标转换到规则化设备坐标系中（-1.0，1.0）。所有在范围外的坐标在-1.0到1.0之间都不会被绘制出来且会被裁剪。在投影矩阵所指定的范围内，坐标（1250，500，750）将是不可见的，这是由于它的x坐标超出了范围，随后被转化为在规则化设备坐标中坐标值大于1.0的值并且被裁剪掉。
 
+!!! Important
+
     注意那些如果只是图元的一部分例如三角形，超出了裁剪区域，则OpenGL会重新构建三角形以使一个或多个三角形能适应在裁剪范围内。
 
 由投影矩阵创建的观察区域被称为平截头体，且每个出现在平截头体范围内的坐标都会最终出现在用户的屏幕上。将坐标转化到指定的规则化设备坐标系，它可以很容易被映射到2维观察空间的坐标系的整个过程称为投影，因为它投影矩阵能将3维坐标投影到容易映射的规则化设备坐标系中。
@@ -78,9 +80,8 @@
 ![perspective](http://learnopengl.com/img/getting-started/perspective.png)
 正如你看到的那样，由于透视的原因，线在很远的地方看起来会相交。这个投影矩阵将给定的平截头体范围映射到裁剪空间，但每个顶点坐标仍然产生了w值，顶点如果离观察者越远，则w分量越大。被转换到裁剪控件的坐标都会在-w到w的范围之间（任何处于这个范围的对象都会被裁剪）。OpenGL需要可见的坐标都落在-1.0到1.0范围内作为最后的顶点着色器输出，因此一旦坐标在裁剪空间内，透视划分就会被应用到裁剪空间坐标内：
 
-<p>
-out = \begin{pmatrix} x /w \\ y / w \\ z / w \end{pmatrix}
-</p>
+![](../img/coordinate_system_1.png)
+
 每个顶点坐标的分量都会除以它的w分量，得到一个距离观察者的较小的顶点坐标。这是另一个w分量很重要的原因，因为它帮助我们进行透射投影。最后的结果坐标就是处于规则化设备空间内的。如果你对研究正视投影矩阵和透视投影矩阵是如何计算的很感兴趣（且不会对数学感到恐惧）我推荐这篇由Songho写的[文章](http://www.songho.ca/opengl/gl_projectionmatrix.html)。
 一个透视投影矩阵可以在GLM中被创建，如下：
 
@@ -91,25 +92,29 @@ glm::perspective所做的其实就是再次创建了一个定义了可视空间
 
 它的第一个参数定义了fov的值，代表了视界范围，且设置了视图空间有多大。对于一个真实的视图，它的值经常设置为45.0，但想要看到更多结果你可以设置一个更大的值。第二个参数设置了宽高比，由视图的高除以宽。第三和第四个参数设置了平截头体的近和远平面。我们经常设置近距离为0.1而远距离设为100.0。所有在近平面和远平面的顶点且处于平截头体内的顶点都会被渲染。
 
-> 当你把透视矩阵的near值设置太大时（如10.0），OpenGL会将靠近摄像机的坐标都裁剪掉（在0.0和10.0之间），这提供了一个相似的视觉效果就如视频游戏中如果你移动得太靠近某个对象时你会把它看穿那样。
+!!! Important
+
+	当你把透视矩阵的near值设置太大时（如10.0），OpenGL会将靠近摄像机的坐标都裁剪掉（在0.0和10.0之间），这提供了一个相似的视觉效果就如视频游戏中如果你移动得太靠近某个对象时你会把它看穿那样。
 
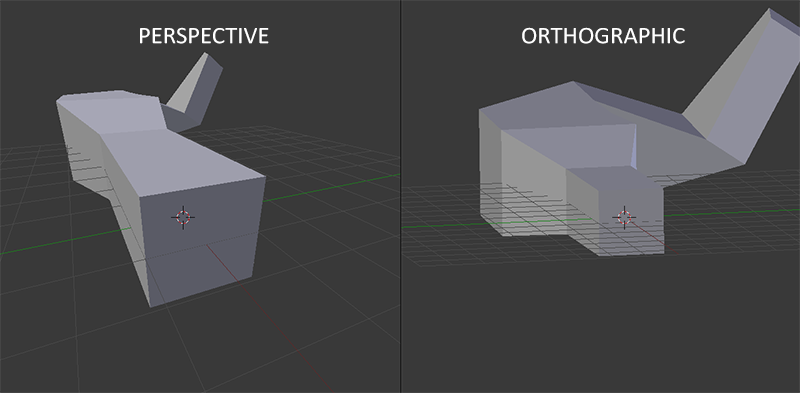
 当使用正视投影时，每一个顶点坐标都会直接映射到裁剪空间中而不经过任何透视划分（它仍然有进行透视划分，只是w分量没有被操作（它保持为1）因此没有起作用）。因为正视投影没有使用透视投影，远处的对象不会显得小以产生神奇的视觉输出。由于这个原因，正视投影主要用于二维渲染以及一些建筑或工程的应用这些我们不需要使用投影来变形顶点。某些应用如Blender是用来进行三维建模的，有时在建模时会使用正视投影，因为它更准确地藐视了每个对象的各个方面。下面你能够看到在Blender里面使用两种投影方式的对比：
+
 ![perspective_orthographic](http://learnopengl.com/img/getting-started/perspective_orthographic.png)
+
 你可以看到使用透视投影的话，远处的顶点看起来比较小，而在正视投影中每个顶点距离观察者的距离都是一样的。
 
 组合
 --
 我们为上述的每一个步骤都创建了一个转换矩阵：模型矩阵、视图矩阵和投影矩阵。一个顶点的坐标将会被转换到裁剪坐标，如下：
 
-<p>
-V_{clip} =M_{projection} \cdot M_{view} \cdot M_{model} \cdot V_{local}
-</p>
+![](../img/coordinate_system_2.png)
 
 注意每个矩阵被运算的顺序是相反的（记住我们需要从右往左乘上每个矩阵）。最后的顶点应该被赋予顶点着色器中的gl_Position 且OpenGL 将会自动进行透视划分和裁剪。
 
-> 然后呢？
-> 顶点着色器的输出需要所有的顶点都在裁剪空间内，而这是我们的转换矩阵所做的。OpenGL然后在裁剪空间中执行透视划分从而将它们转换到规则化设备坐标。OpenGL
-> 然后会使用 glViewPort内部的参数来将规则化设备坐标映射到屏幕坐标，每个坐标都关联了一个屏幕上的点（在我们的例子中屏幕是800 *600）。这个过程成为视口转换。
+!!! Important
+
+	**然后呢？**
+
+	顶点着色器的输出需要所有的顶点都在裁剪空间内，而这是我们的转换矩阵所做的。OpenGL然后在裁剪空间中执行透视划分从而将它们转换到规则化设备坐标。OpenGL然后会使用 glViewPort内部的参数来将规则化设备坐标映射到屏幕坐标，每个坐标都关联了一个屏幕上的点（在我们的例子中屏幕是800 *600）。这个过程成为视口转换。
 
 这一章的主题比较难理解所以如果你仍然不确定每个空间的作用的话，你也不必太担心。接下来你会看到我们是怎样好好运用这些坐标空间的并且会有足够的展示例子在接下来的教程中。
 
@@ -129,18 +134,20 @@ V_{clip} =M_{projection} \cdot M_{view} \cdot M_{model} \cdot V_{local}
 
 这就是视图空间所做的，我们移动整个场景正如我们相反地想让摄像机所做的那样。因为我们想要往后移动且OpenGL是一个右手坐标系所以我们沿着z轴的负方向移动。我们实现这个，通过将场景沿着z轴正方向平移。这个我们的感觉就是我们在往后移动。
 
+!!! Important
+
+	**右手坐标系**
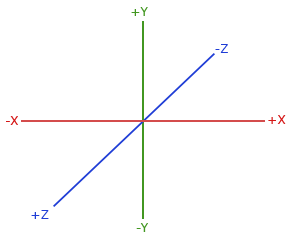
+	按照约定，OpenGL是一个右手坐标系。最基本的就是说正x轴在你的右手边，正y轴往上而正z轴是往后的。想象你的屏幕处于三个轴的中心且正z轴穿过你的屏幕朝向你。坐标系画起来如下：
+
+	![coordinate_systems_right_handed](http://learnopengl.com/img/getting-started/coordinate_systems_right_handed.png)
+
+	为了理解为什么成为右手坐标系，按如下的步骤做：
+
+		- 张开你的右手使正y轴沿着你的手往上。
+		- 使你的大拇指往右。
+		- 使你的食指往上。
+		- 向下90度弯曲你的中指。 
 
-> **右手坐标系**
-> ----- 按照约定，OpenGL是一个右手坐标系。最基本的就是说正x轴在你的右手边，正y轴往上而正z轴是往后的。想象你的屏幕处于三个轴的中心且正z轴穿过你的屏幕朝向你。坐标系画起来如下：
-> ![coordinate_systems_right_handed](http://learnopengl.com/img/getting-started/coordinate_systems_right_handed.png)
-> 
-> 为了理解为什么成为右手坐标系，按如下的步骤做：
-> 
->  - 张开你的右手使正y轴沿着你的手往上。
->  - 使你的大拇指往右。
->  - 使你的食指往上。
->  - 向下90度弯曲你的中指。 
->  
 如果你都正确地做了，那么你的大拇指朝着正x轴方向，食指朝着正y轴方向，中指朝着正z轴方向。如果你用左手来做这些动作，你会发现z轴的方向是相反的。这就是有名的左手坐标系，被DirectX广泛地使用。注意在规则化设备坐标系中OpenGL使用的是左手坐标系（投影矩阵转换了使用右手或左手的习惯）。
 
 接下来我们将会讨论如何利用更多细节来在场景中移动。现在视图矩阵看起来像这样的：
@@ -154,7 +161,9 @@ V_{clip} =M_{projection} \cdot M_{view} \cdot M_{model} \cdot V_{local}
     glm::mat4 projection;
     projection = glm::perspective(45.0f, screenWidth / screenHeight, 0.1f, 100.0f);
 
-> 再重复一次，在glm指定角度的时候要注意。这里我们将参数fov设置为45度，但有些GLM的实现是将fov当成弧度，在这种情况你需要使用glm::radians(45.0)来设置。
+!!! Attention
+
+	再重复一次，在glm指定角度的时候要注意。这里我们将参数fov设置为45度，但有些GLM的实现是将fov当成弧度，在这种情况你需要使用glm::radians(45.0)来设置。
 
 既然我们创建了转换矩阵，我们应该将它们传入着色器。首先，让我们在顶点着色器中声明一个单位转换矩阵然后将它乘以顶点坐标：