mirrors/LearnOpenGL-CN
1
0
Fork 0
mirror of https://github.com/LearnOpenGL-CN/LearnOpenGL-CN.git synced 2025-08-23 12:45:29 +08:00
Code Activity

Replace all the math equations with latex

Browse Source
This commit is contained in:
Meow J
2016-07-05 18:45:44 +08:00
parent 39b512cfbd
commit 449223fd84
14 changed files with 171 additions and 657 deletions
Download Patch File Download Diff File Expand all files Collapse all files

2
docs/05 Advanced Lighting/01 Advanced Lighting.md
View File

@@ -34,7 +34,7 @@ Phong光照很棒，而且性能较高，但是它的镜面反射在某些条件
得到半程向量很容易，我们将光的方向向量和视线向量相加，然后将结果归一化（normalize）；
![](http://learnopengl-cn.readthedocs.org/zh/latest/img/05_01_01.png)
\(\bar{H} = \frac{\bar{L} + \bar{V}}{||\bar{L} + \bar{V}||}\)
翻译成GLSL代码如下：

31
docs/05 Advanced Lighting/02 Gamma Correction.md
View File

@@ -1,6 +1,6 @@
本文作者JoeyDeVries，由Django翻译自[http://learnopengl.com](http://learnopengl.com)
## Gamma校正(Gamma Correction)
# Gamma校正(Gamma Correction)
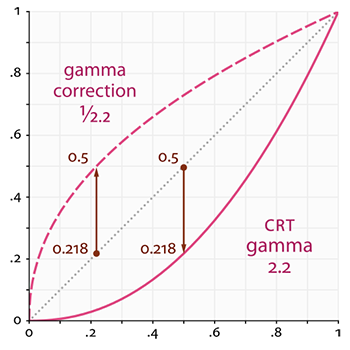
当我们计算出场景中所有像素的最终颜色以后，我们就必须把它们显示在监视器上。过去，大多数监视器是阴极射线管显示器（CRT）。这些监视器有一个物理特性就是两倍的输入电压产生的不是两倍的亮度。输入电压产生约为输入电压的2.2次幂的亮度，这叫做监视器Gamma（译注：Gamma也叫灰度系数，每种显示设备都有自己的Gamma值，都不相同，有一个公式：设备输出亮度 = 电压的Gamma次幂，任何设备Gamma基本上都不会等于1，等于1是一种理想的线性状态，这种理想状态是：如果电压和亮度都是在0到1的区间，那么多少电压就等于多少亮度。对于CRT，Gamma通常为2.2，因而，输出亮度 = 输入电压的2.2次幂，你可以从本节第二张图中看到Gamma2.2实际显示出来的总会比预期暗，相反Gamma0.45就会比理想预期亮，如果你讲Gamma0.45叠加到Gamma2.2的显示设备上，便会对偏暗的显示效果做到校正，这个简单的思路就是本节的核心）。
@@ -16,7 +16,7 @@
![](http://learnopengl.com/img/advanced-lighting/gamma_correction_gamma_curves.png)
点线代表线性颜色/亮度值（译注：这表示的是理想状态，Gamma为1），实线代表监视器显示的颜色。如果我们把一个点线线性的颜色翻一倍，结果就是这个值的两倍。比如，光的颜色向量L=(0.5, 0.0, 0.0)代表的是暗红色。如果我们在线性空间中把它翻倍，就会变成(1.0, 0.0, 0.0)，就像你在图中看到的那样。然而，由于我们定义的颜色仍然需要输出的监视器上，监视器上显示的实际颜色就会是(0.218, 0.0, 0.0)。在这儿问题就出现了：当我们将理想中直线上的那个暗红色翻一倍时，在监视器上实际上亮度翻了4.5倍以上！
点线代表线性颜色/亮度值（译注：这表示的是理想状态，Gamma为1），实线代表监视器显示的颜色。如果我们把一个点线线性的颜色翻一倍，结果就是这个值的两倍。比如，光的颜色向量\(\bar{L} = (0.5, 0.0, 0.0)\)代表的是暗红色。如果我们在线性空间中把它翻倍，就会变成\((1.0, 0.0, 0.0)\)，就像你在图中看到的那样。然而，由于我们定义的颜色仍然需要输出的监视器上，监视器上显示的实际颜色就会是\((0.218, 0.0, 0.0)\)。在这儿问题就出现了：当我们将理想中直线上的那个暗红色翻一倍时，在监视器上实际上亮度翻了4.5倍以上！
直到现在，我们还一直假设我们所有的工作都是在线性空间中进行的（译注：Gamma为1），但最终还是要把所哟的颜色输出到监视器上，所以我们配置的所有颜色和光照变量从物理角度来看都是不正确的，在我们的监视器上很少能够正确地显示。出于这个原因，我们（以及艺术家）通常将光照值设置得比本来更亮一些（由于监视器会将其亮度显示的更暗一些），如果不是这样，在线性空间里计算出来的光照就会不正确。同时，还要记住，监视器所显示出来的图像和线性图像的最小亮度是相同的，它们最大的亮度也是相同的；只是中间亮度部分会被压暗。
@@ -24,22 +24,11 @@
![](http://learnopengl.com/img/advanced-lighting/gamma_correction_example.png)
Gamma校正
## Gamma校正
Gamma校正的思路是在最终的颜色输出上应用监视器Gamma的倒数。回头看前面的Gamma曲线图，你会有一个短划线，它是监视器Gamma曲线的翻转曲线。我们在颜色显示到监视器的时候把每个颜色输出都加上这个翻转的Gamma曲线，这样应用了监视器Gamma以后最终的颜色将会变为线性的。我们所得到的中间色调就会更亮，所以虽然监视器使它们变暗，但是我们又将其平衡回来了。
我们来看另一个例子。还是那个暗红色（0.5, 0.0, 0.0）。在将颜色显示到监视器之前，我们先对颜色应用Gamma校正曲线。线性的颜色显示在监视器上相当于降低了2.2次幂的亮度，所以倒数就是1/2.2次幂。Gamma校正后的暗红色就会成为
```math
{(0.5, 0.0, 0.0)}^{1/2.2} = {(0.5, 0.0, 0.0)}^{0.45}={(0.73, 0.0, 0.0)}
```
校正后的颜色接着被发送给监视器，最终显示出来的颜色是
```math
(0.73, 0.0, 0.0)^{2.2} = (0.5, 0.0, 0.0)
```
你会发现使用了Gamma校正，监视器最终会显示出我们在应用中设置的那种线性的颜色。
我们来看另一个例子。还是那个暗红色\((0.5, 0.0, 0.0)\)。在将颜色显示到监视器之前，我们先对颜色应用Gamma校正曲线。线性的颜色显示在监视器上相当于降低了\(2.2\)次幂的亮度，所以倒数就是\(1/2.2\)次幂。Gamma校正后的暗红色就会成为\((0.5, 0.0, 0.0)^{1/2.2} = (0.5, 0.0, 0.0)^{0.45} = (0.73, 0.0, 0.0)\)。校正后的颜色接着被发送给监视器，最终显示出来的颜色是\((0.73, 0.0, 0.0)^{2.2} = (0.5, 0.0, 0.0)\)。你会发现使用了Gamma校正，监视器最终会显示出我们在应用中设置的那种线性的颜色。
!!! Important
@@ -130,17 +119,7 @@ float attenuation = 1.0 / distance;
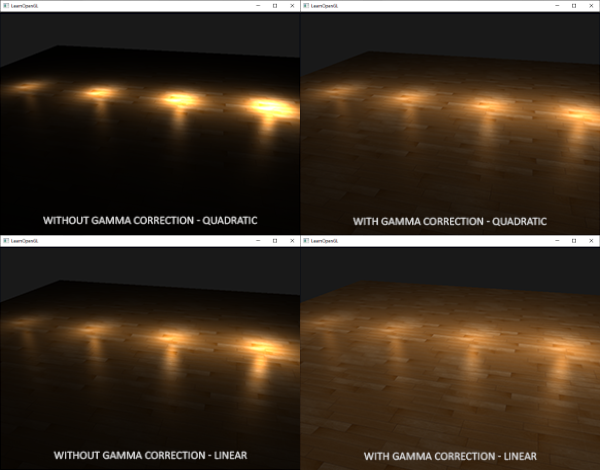
![](http://learnopengl.com/img/advanced-lighting/gamma_correction_attenuation.png)
这种差异产生的原因是，光的衰减方程改变了亮度值，而且屏幕上显示出来的也不是线性空间，在监视器上效果最好的衰减方程，并不是符合物理的。想想平方衰减方程，如果我们使用这个方程，而且不进行gamma校正，显示在监视器上的衰减方程实际上将变成：
```math
{(1.0 / distance2)}^{2.2}
```
若不进行gamma校正，将产生更强烈的衰减。这也解释了为什么双曲线不用gamma校正时看起来更真实，因为它实际变成了
```math
{(1.0 / distance)}^{2.2} = 1.0 / distance^{2.2}
```
这和物理公式是很相似的。
这种差异产生的原因是，光的衰减方程改变了亮度值，而且屏幕上显示出来的也不是线性空间，在监视器上效果最好的衰减方程，并不是符合物理的。想想平方衰减方程，如果我们使用这个方程，而且不进行gamma校正，显示在监视器上的衰减方程实际上将变成\((1.0 / distance^2)^{2.2}\)。若不进行gamma校正，将产生更强烈的衰减。这也解释了为什么双曲线不用gamma校正时看起来更真实，因为它实际变成了\((1.0 / distance)^{2.2} = 1.0 / distance^{2.2}\)。这和物理公式是很相似的。
!!! Important

6
docs/05 Advanced Lighting/03 Shadows/01 Shadow Mapping.md
View File

@@ -34,13 +34,13 @@
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_theory_spaces.png)
左侧的图片展示了一个定向光源（所有光线都是平行的）在立方体下的表面投射的阴影。通过储存到深度贴图中的深度值，我们就能找到最近点，用以决定片元是否在阴影中。我们使用一个来自光源的视图和投影矩阵来渲染场景就能创建一个深度贴图。这个投影和视图矩阵结合在一起成为一个T变换，它可以将任何三维位置转变到光源的可见坐标空间。
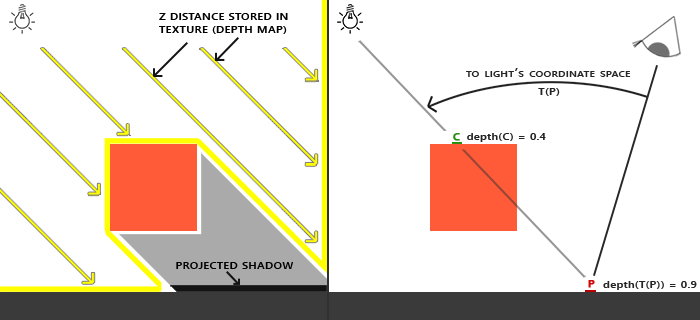
左侧的图片展示了一个定向光源（所有光线都是平行的）在立方体下的表面投射的阴影。通过储存到深度贴图中的深度值，我们就能找到最近点，用以决定片元是否在阴影中。我们使用一个来自光源的视图和投影矩阵来渲染场景就能创建一个深度贴图。这个投影和视图矩阵结合在一起成为一个\(T\)变换，它可以将任何三维位置转变到光源的可见坐标空间。
!!! Important
定向光并没有位置，因为它被规定为无穷远。然而，为了实现阴影贴图，我们得从一个光的透视图渲染场景，这样就得在光的方向的某一点上渲染场景。
在右边的图中我们显示出同样的平行光和观察者。我们渲染一个点P处的片元，需要决定它是否在阴影中。我们先得使用T把P变换到光源的坐标空间里。既然点P是从光的透视图中看到的，它的z坐标就对应于它的深度，例子中这个值是0.9。使用点P在光源的坐标空间的坐标，我们可以索引深度贴图，来获得从光的视角中最近的可见深度，结果是点C，最近的深度是0.4。因为索引深度贴图的结果是一个小于点P的深度，我们可以断定P被挡住了，它在阴影中了。
在右边的图中我们显示出同样的平行光和观察者。我们渲染一个点\(\bar{\color{red}{P}}\)处的片元，需要决定它是否在阴影中。我们先得使用\(T\)把\(\bar{\color{red}{P}}\)变换到光源的坐标空间里。既然点\(\bar{\color{red}{P}}\)是从光的透视图中看到的，它的z坐标就对应于它的深度，例子中这个值是0.9。使用点\(\bar{\color{red}{P}}\)在光源的坐标空间的坐标，我们可以索引深度贴图，来获得从光的视角中最近的可见深度，结果是点\(\bar{\color{green}{C}}\)，最近的深度是0.4。因为索引深度贴图的结果是一个小于点\(\bar{\color{red}{P}}\)的深度，我们可以断定\(\bar{\color{red}{P}}\)被挡住了，它在阴影中了。
深度映射由两个步骤组成：首先，我们渲染深度贴图，然后我们像往常一样渲染场景，使用生成的深度贴图来计算片元是否在阴影之中。听起来有点复杂，但随着我们一步一步地讲解这个技术，就能理解了。
@@ -130,7 +130,7 @@ glm::mat4 lightView = glm::lookAt(glm::vec(-2.0f, 4.0f, -1.0f), glm::vec3(0.0f),
glm::mat4 lightSpaceMatrix = lightProjection * lightView;
```
这个lightSpaceMatrix正是前面我们称为T的那个变换矩阵。有了lightSpaceMatrix只要给shader提供光空间的投影和视图矩阵，我们就能像往常那样渲染场景了。然而，我们只关心深度值，并非所有片元计算都在我们的着色器中进行。为了提升性能，我们将使用一个与之不同但更为简单的着色器来渲染出深度贴图。
这个lightSpaceMatrix正是前面我们称为\(T\)的那个变换矩阵。有了lightSpaceMatrix只要给shader提供光空间的投影和视图矩阵，我们就能像往常那样渲染场景了。然而，我们只关心深度值，并非所有片元计算都在我们的着色器中进行。为了提升性能，我们将使用一个与之不同但更为简单的着色器来渲染出深度贴图。
### 渲染出深度贴图

7
docs/05 Advanced Lighting/03 Shadows/03 CSM.md
View File

@@ -0,0 +1,7 @@
# CSM
# 未完成
这篇教程暂时还没有完成，您可以经常来刷新看看是否有更新的进展。
<img src="../../../img/development.png" class="clean">

575
docs/05 Advanced Lighting/04 Normal Mapping.md
View File

@@ -29,8 +29,10 @@
由于法线向量是个几何工具，而纹理通常只用于储存颜色信息，用纹理储存法线向量不是非常直接。如果你想一想，就会知道纹理中的颜色向量用r、g、b元素代表一个3D向量。类似的我们也可以将法线向量的x、y、z元素储存到纹理中，代替颜色的r、g、b元素。法线向量的范围在-1到1之间，所以我们先要将其映射到0到1的范围：
1
vec3 rgb_normal = normal * 0.5 - 0.5; // transforms from [-1,1] to [0,1]
```c++
vec3 rgb_normal = normal * 0.5 - 0.5; // transforms from [-1,1] to [0,1]
```
将法线向量变换为像这样的RGB颜色元素，我们就能把根据表面的形状的fragment的法线保存在2D纹理中。教程开头展示的那个砖块的例子的法线贴图如下所示：
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_normal_map.png)
@@ -92,555 +94,46 @@ void main()
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_surface_edges.png)
上图中我们可以看到边<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>E</mi>
<mn>2</mn>
</msub>
</math>纹理坐标的不同，<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>E</mi>
<mn>2</mn>
</msub>
</math>是一个三角形的边，这个三角形的另外两条边是<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
</math>和<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
</math>，它们与切线向量*T*和副切线向量*B*方向相同。这样我们可以把边</math>和<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>E</mi>
<mn>1</mn>
</msub>
</math>和<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>E</mi>
<mn>2</mn>
</msub>
</math>用切线向量 *T* 和副切线向量 *B* 的线性组合表示出来（译注：注意*T*和*B*都是单位长度，在*TB*平面中所有点的*T*、*B*坐标都在0到1之间，因此可以进行这样的组合）：
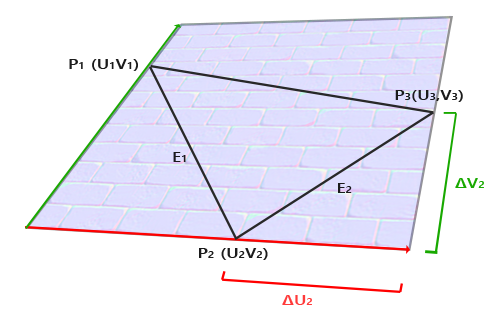
上图中我们可以看到边\(E_2\)纹理坐标的不同，\(E_2\)是一个三角形的边，这个三角形的另外两条边是\(\Delta U_2\)和\(\Delta V_2\)，它们与切线向量\(T\)和副切线向量\(B\)方向相同。这样我们可以把边\(E_1\)和\(E_2\)用切线向量\(T\)和副切线向量\(B\)的线性组合表示出来（译注：注意\(T\)和\(B\)都是单位长度，在\(TB\)平面中所有点的\(T\)、\(B\)坐标都在0到1之间，因此可以进行这样的组合）：
```math
$$
E_1 = \Delta U_1T + \Delta V_1B
$$
$$
E_2 = \Delta U_2T + \Delta V_2B
```
$$
我们也可以写成这样：
```math
$$
(E_{1x}, E_{1y}, E_{1z}) = \Delta U_1(T_x, T_y, T_z) + \Delta V_1(B_x, B_y, B_z)
```
$$
*E*是两个向量位置的差，*U*和*V*是纹理坐标的差。然后我们得到两个未知数（切线*T*和副切线*B*）和两个等式。你可能想起你的代数课了，这是让我们去接*T*和*B*。
$$
(E_{2x}, E_{2y}, E_{2z}) = \Delta U_2(T_x, T_y, T_z) + \Delta V_2(B_x, B_y, B_z)
$$
\(E\)是两个向量位置的差，\(\Delta U\)和\(\Delta V\)是纹理坐标的差。然后我们得到两个未知数（切线*T*和副切线*B*）和两个等式。你可能想起你的代数课了，这是让我们去接\(T\)和\(B\)。
上面的方程允许我们把它们写成另一种格式：矩阵乘法
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mo>=</mo>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>1</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>1</mn>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>T</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>B</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
</math>
$$
\begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix} = \begin{bmatrix} \Delta U_1 & \Delta V_1 \\ \Delta U_2 & \Delta V_2 \end{bmatrix} \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix}
$$
尝试会以一下矩阵乘法，它们确实是同一种等式。把等式写成矩阵形式的好处是，解*T*和*B*会因此变得很容易。两边都乘以<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<mi>U</mi>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<mi>V</mi>
</math>的反数等于：
尝试会意一下矩阵乘法，它们确实是同一种等式。把等式写成矩阵形式的好处是，解\(T\)和\(B\)会因此变得很容易。两边都乘以\(\Delta U \Delta V\)的逆矩阵等于：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<msup>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>1</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>1</mn>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mrow class="MJX-TeXAtom-ORD">
<mo>&#x2212;<!-- − --></mo>
<mn>1</mn>
</mrow>
</msup>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mo>=</mo>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>T</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>B</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
</math>
$$
\begin{bmatrix} \Delta U_1 & \Delta V_1 \\ \Delta U_2 & \Delta V_2 \end{bmatrix}^{-1} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix} = \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix}
$$
这样我们就可以解出*T*和*B*了。这需要我们计算出delta纹理坐标矩阵的拟阵。我不打算讲解计算逆矩阵的细节，但大致是把它变化为，1除以矩阵的行列式，再乘以它的共轭矩阵。
这样我们就可以解出\(T\)和\(B\)了。这需要我们计算出delta纹理坐标矩阵的拟阵。我不打算讲解计算逆矩阵的细节，但大致是把它变化为，1除以矩阵的行列式，再乘以它的共轭矩阵。
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>T</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>B</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mo>=</mo>
<mfrac>
<mn>1</mn>
<mrow>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>1</mn>
</msub>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
<mo>&#x2013;</mo>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>1</mn>
</msub>
</mrow>
</mfrac>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
</mtd>
<mtd>
<mo>&#x2212;<!-- − --></mo>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>1</mn>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<mo>&#x2212;<!-- − --></mo>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>1</mn>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
</math>
$$
\begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix} = \frac{1}{\Delta U_1 \Delta V_2 - \Delta U_2 \Delta V_1} \begin{bmatrix} \Delta V_2 & -\Delta V_1 \\ -\Delta U_2 & \Delta U_1 \end{bmatrix} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix}
$$
有了最后这个等式，我们就可以用公式、三角形的两条边以及纹理坐标计算出切线向量*T*和副切线*B*。
有了最后这个等式，我们就可以用公式、三角形的两条边以及纹理坐标计算出切线向量\(T\)和副切线\(B\)。
如果你对这些数学内容不理解也不用担心。当你知道我们可以用一个三角形的顶点和纹理坐标（因为纹理坐标和切线向量在同一空间中）计算出切线和副切线你就已经部分地达到目的了（译注：上面的推导已经很清楚了，如果你不明白可以参考任意线性代数教材，就像作者所说的记住求得切线空间的公式也行，不过不管怎样都得理解切线空间的含义）。
@@ -649,6 +142,8 @@ E_2 = \Delta U_2T + \Delta V_2B
这个教程的demo场景中有一个简单的2D平面，它朝向正z方向。这次我们会使用切线空间来实现法线贴图，所以我们可以使平面朝向任意方向，法线贴图仍然能够工作。使用前面讨论的数学方法，我们来手工计算出表面的切线和副切线向量。
假设平面使用下面的向量建立起来（1、2、3和1、3、4，它们是两个三角形）：
```c++
// positions
glm::vec3 pos1(-1.0, 1.0, 0.0);
glm::vec3 pos2(-1.0, -1.0, 0.0);
@@ -661,20 +156,18 @@ glm::vec2 uv3(1.0, 0.0);
glm::vec2 uv4(1.0, 1.0);
// normal vector
glm::vec3 nm(0.0, 0.0, 1.0);
```
我们先计算第一个三角形的边和deltaUV坐标：
1
2
3
4
```c++
glm::vec3 edge1 = pos2 - pos1;
glm::vec3 edge2 = pos3 - pos1;
glm::vec2 deltaUV1 = uv2 - uv1;
glm::vec2 deltaUV2 = uv3 - uv1;
```
有了计算切线和副切线的必备数据，我们就可以开始写出来自于前面部分中的下列等式：

34
docs/05 Advanced Lighting/05 Parallax Mapping.md
View File

@@ -18,21 +18,21 @@
[](http://learnopengl.com/img/advanced-lighting/parallax_mapping_plane_height.png)
这里粗糙的红线代表高度贴图中的数值的立体表达，向量V代表观察方向。如果平面进行实际位移，观察者会在点B看到表面。然而我们的平面没有实际上进行位移，观察方向将在点A与平面接触。视差贴图的目的是，在A位置上的fragment不再使用点A的纹理坐标而是使用点B的。随后我们用点B的纹理坐标采样，观察者就像看到了点B一样。
这里粗糙的红线代表高度贴图中的数值的立体表达，向量\(\color{orange}{\bar{V}}\)代表观察方向。如果平面进行实际位移，观察者会在点\(\color{blue}B\)看到表面。然而我们的平面没有实际上进行位移，观察方向将在点\(\color{green}A\)与平面接触。视差贴图的目的是，在\(\color{green}A\)位置上的fragment不再使用点\(\color{green}A\)的纹理坐标而是使用点\(\color{blue}B\)的。随后我们用点\(\color{blue}B\)的纹理坐标采样，观察者就像看到了点\(\color{blue}B\)一样。
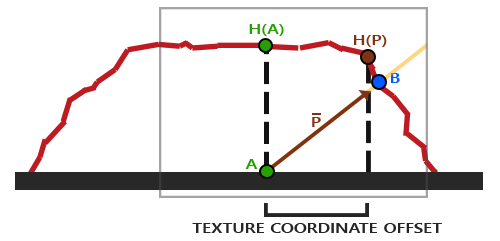
这个技巧就是描述如何从点A得到点B的纹理坐标。视差贴图尝试通过对从fragment到观察者的方向向量V进行缩放的方式解决这个问题，缩放的大小是A处fragment的高度。所以我们将V的长度缩放为高度贴图在点A处H（A）采样得来的值。下图展示了经缩放得到的向量P：
这个技巧就是描述如何从点\(\color{green}A\)得到点\(\color{blue}B\)的纹理坐标。视差贴图尝试通过对从fragment到观察者的方向向量\(\color{orange}{\bar{V}}\)进行缩放的方式解决这个问题，缩放的大小是\(\color{green}A\)处fragment的高度。所以我们将\(\color{orange}{\bar{V}}\)的长度缩放为高度贴图在点\(\color{green}A\)处\(\color{green}{H(A)}\)采样得来的值。下图展示了经缩放得到的向量\(\color{brown}{\bar{P}}\)：
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_scaled_height.png)
我们随后选出P以及这个向量与平面对齐的坐标作为纹理坐标的偏移量。这能工作是因为向量P是使用从高度贴图得到的高度值计算出来的，所以一个fragment的高度越高位移的量越大。
我们随后选出\(\color{brown}{\bar{P}}\)以及这个向量与平面对齐的坐标作为纹理坐标的偏移量。这能工作是因为向量\(\color{brown}{\bar{P}}\)是使用从高度贴图得到的高度值计算出来的，所以一个fragment的高度越高位移的量越大。
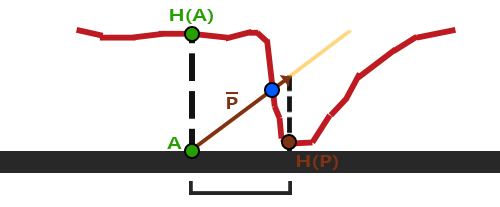
这个技巧在大多数时候都没问题，但点B是粗略估算得到的。当表面的高度变化很快的时候，看起来就不会真实，因为向量P最终不会和B接近，就像下图这样：
这个技巧在大多数时候都没问题，但点\(\color{blue}B\)是粗略估算得到的。当表面的高度变化很快的时候，看起来就不会真实，因为向量\(\color{brown}{\bar{P}}\)最终不会和\(\color{blue}B\)接近，就像下图这样：
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_incorrect_p.png)
视差贴图的另一个问题是，当表面被任意旋转以后很难指出从P获取哪一个坐标。我们在视差贴图中使用了另一个坐标空间，这个空间P向量的x和y元素总是与纹理表面对齐。如果你看了法线贴图教程，你也许猜到了，我们实现它的方法，是的，我们还是在切线空间中实现视差贴图。
视差贴图的另一个问题是，当表面被任意旋转以后很难指出从\(\color{brown}{\bar{P}}\)获取哪一个坐标。我们在视差贴图中使用了另一个坐标空间，这个空间\(\color{brown}{\bar{P}}\)向量的x和y元素总是与纹理表面对齐。如果你看了法线贴图教程，你也许猜到了，我们实现它的方法，是的，我们还是在切线空间中实现视差贴图。
将fragment到观察者的向量V转换到切线空间中，经变换的P向量的x和y元素将于表面的切线和副切线向量对齐。由于切线和副切线向量与表面纹理坐标的方向相同，我们可以用P的x和y元素作为纹理坐标的偏移量，这样就不用考虑表面的方向了。
将fragment到观察者的向量\(\color{orange}{\bar{V}}\)转换到切线空间中，经变换的\(\color{brown}{\bar{P}}\)向量的x和y元素将于表面的切线和副切线向量对齐。由于切线和副切线向量与表面纹理坐标的方向相同，我们可以用\(\color{brown}{\bar{P}}\)的x和y元素作为纹理坐标的偏移量，这样就不用考虑表面的方向了。
理论都有了，下面我们来动手实现视差贴图。
@@ -46,9 +46,9 @@
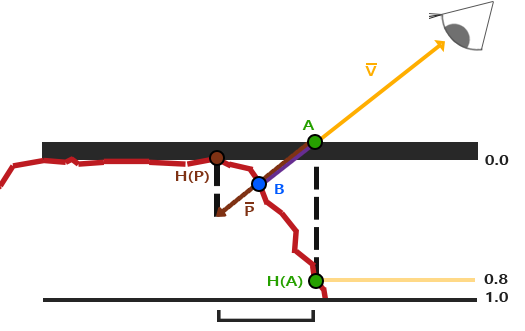
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_depth.png)
我们再次获得A和B，但是这次我们用向量V减去点A的纹理坐标得到P。我们通过在着色器中用1.0减去采样得到的高度贴图中的值来取得深度值，而不再是高度值，或者简单地在图片编辑软件中把这个纹理进行反色操作，就像我们对连接中的那个深度贴图所做的一样。
我们再次获得\(\color{green}A\)和\(\color{blue}B\)，但是这次我们用向量\(\color{orange}{\bar{V}}\)减去点\(\color{green}A\)的纹理坐标得到\(\color{brown}{\bar{P}}\)。我们通过在着色器中用1.0减去采样得到的高度贴图中的值来取得深度值，而不再是高度值，或者简单地在图片编辑软件中把这个纹理进行反色操作，就像我们对连接中的那个深度贴图所做的一样。
位移贴图是在像素着色器中实现的，因为三角形表面的所有位移效果都不同。在像素着色器中我们将需要计算fragment到观察者到方向向量V所以我们需要观察者位置和在切线空间中的fragment位置。法线贴图教程中我们已经有了一个顶点着色器，它把这些向量发送到切线空间，所以我们可以复制那个顶点着色器：
位移贴图是在像素着色器中实现的，因为三角形表面的所有位移效果都不同。在像素着色器中我们将需要计算fragment到观察者到方向向量\(\color{orange}{\bar{V}}\)所以我们需要观察者位置和在切线空间中的fragment位置。法线贴图教程中我们已经有了一个顶点着色器，它把这些向量发送到切线空间，所以我们可以复制那个顶点着色器：
```c++
#version 330 core
@@ -142,9 +142,9 @@ vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir)
}
```
这个相对简单的函数是我们所讨论过的内容的直接表述。我们用本来的纹理坐标texCoords从高度贴图中来采样出当前fragment高度H(A)。然后计算出P，x和y元素在切线空间中，viewDir向量除以它的z元素，用fragment的高度对它进行缩放。我们同时引入额一个height_scale的uniform，来进行一些额外的控制，因为视差效果如果没有一个缩放参数通常会过于强烈。然后我们用P减去纹理坐标来获得最终的经过位移纹理坐标。
这个相对简单的函数是我们所讨论过的内容的直接表述。我们用本来的纹理坐标texCoords从高度贴图中来采样出当前fragment高度\(\color{green}{H(A)}\)。然后计算出\(\color{brown}{\bar{P}}\)，x和y元素在切线空间中，viewDir向量除以它的z元素，用fragment的高度对它进行缩放。我们同时引入额一个height_scale的uniform，来进行一些额外的控制，因为视差效果如果没有一个缩放参数通常会过于强烈。然后我们用\(\color{brown}{\bar{P}}\)减去纹理坐标来获得最终的经过位移纹理坐标。
有一个地方需要注意，就是viewDir.xy除以viewDir.z那里。因为viewDir向量是经过了标准化的，viewDir.z会在0.0到1.0之间的某处。当viewDir大致平行于表面时，它的z元素接近于0.0，除法会返回比viewDir垂直于表面的时候更大的P向量。所以基本上我们增加了P的大小，当以一个角度朝向一个表面相比朝向顶部时它对纹理坐标会进行更大程度的缩放；这回在角上获得更大的真实度。
有一个地方需要注意，就是viewDir.xy除以viewDir.z那里。因为viewDir向量是经过了标准化的，viewDir.z会在0.0到1.0之间的某处。当viewDir大致平行于表面时，它的z元素接近于0.0，除法会返回比viewDir垂直于表面的时候更大的\(\color{brown}{\bar{P}}\)向量。所以基本上我们增加了\(\color{brown}{\bar{P}}\)的大小，当以一个角度朝向一个表面相比朝向顶部时它对纹理坐标会进行更大程度的缩放；这回在角上获得更大的真实度。
有些人更喜欢在等式中不使用viewDir.z，因为普通的视差贴图会在角上产生不想要的结果；这个技术叫做有偏移量限制的视差贴图（Parallax Mapping with Offset Limiting）。选择哪一个技术是个人偏好问题，但我倾向于普通的视差贴图。
@@ -172,19 +172,19 @@ if(texCoords.x > 1.0 || texCoords.y > 1.0 || texCoords.x < 0.0 || texCoords.y <
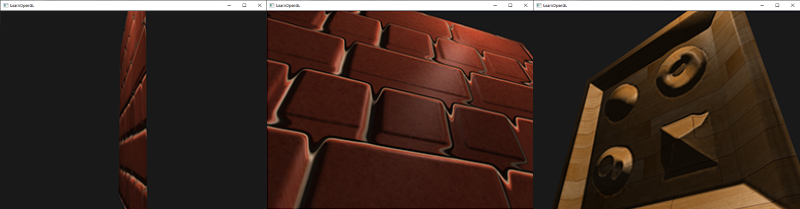
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_issues.png)
问题的原因是这只是一个大致近似的视差映射。还有一些技巧让我们在陡峭的高度上能够获得几乎完美的结果，即使当以一定角度观看的时候。例如，我们不再使用单一样本，取而代之使用多样本来找到最近点B会得到怎样的结果？
问题的原因是这只是一个大致近似的视差映射。还有一些技巧让我们在陡峭的高度上能够获得几乎完美的结果，即使当以一定角度观看的时候。例如，我们不再使用单一样本，取而代之使用多样本来找到最近点\(\color{blue}B\)会得到怎样的结果？
### 陡峭视差映射（Steep Parallax Mapping）
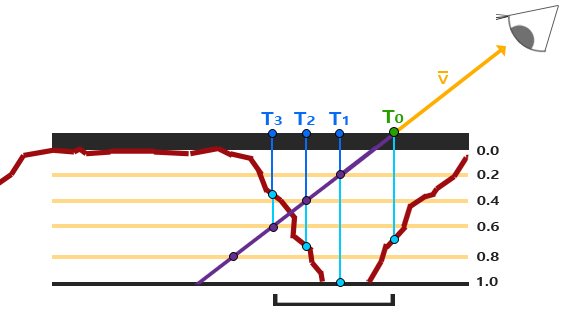
陡峭视差映射是视差映射的扩展，原则是一样的，但不是使用一个样本而是多个样本来确定向量P到B。它能得到更好的结果，它将总深度范围分布到同一个深度/高度的多个层中。从每个层中我们沿着P方向移动采样纹理坐标，直到我们找到了一个采样得到的低于当前层的深度值的深度值。看看下面的图片：
陡峭视差映射是视差映射的扩展，原则是一样的，但不是使用一个样本而是多个样本来确定向量\(\color{brown}{\bar{P}}\)到\(\color{blue}B\)。它能得到更好的结果，它将总深度范围分布到同一个深度/高度的多个层中。从每个层中我们沿着\(\color{brown}{\bar{P}}\)方向移动采样纹理坐标，直到我们找到了一个采样得到的低于当前层的深度值的深度值。看看下面的图片：
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_steep_parallax_mapping_diagram.png)
我们从上到下遍历深度层，我们把每个深度层和储存在深度贴图中的它的深度值进行对比。如果这个层的深度值小于深度贴图的值，就意味着这一层的P向量部分在表面之下。我们继续这个处理过程直到有一层的深度高于储存在深度贴图中的值：这个点就在（经过位移的）表面下方。
我们从上到下遍历深度层，我们把每个深度层和储存在深度贴图中的它的深度值进行对比。如果这个层的深度值小于深度贴图的值，就意味着这一层的\(\color{brown}{\bar{P}}\)向量部分在表面之下。我们继续这个处理过程直到有一层的深度高于储存在深度贴图中的值：这个点就在（经过位移的）表面下方。
这个例子中我们可以看到第二层(D(2) = 0.73)的深度贴图的值仍低于第二层的深度值0.4，所以我们继续。下一次迭代，这一层的深度值0.6大于深度贴图中采样的深度值(D(3) = 0.37)。我们便可以假设第三层向量P是可用的位移几何位置。我们可以用从向量P3的纹理坐标偏移T3来对fragment的纹理坐标进行位移。你可以看到随着深度曾的增加精确度也在提高。
这个例子中我们可以看到第二层(D(2) = 0.73)的深度贴图的值仍低于第二层的深度值0.4，所以我们继续。下一次迭代，这一层的深度值0.6大于深度贴图中采样的深度值(D(3) = 0.37)。我们便可以假设第三层向量\(\color{brown}{\bar{P}}\)是可用的位移几何位置。我们可以用从向量\(\color{brown}{\bar{P_3}}\)的纹理坐标偏移\(T_3\)来对fragment的纹理坐标进行位移。你可以看到随着深度曾的增加精确度也在提高。
为实现这个技术，我们只需要改变ParallaxMapping函数，因为所有需要的变量都有了：
@@ -205,7 +205,7 @@ vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir)
}
```
我们先定义层的数量，计算每一层的深度，最后计算纹理坐标偏移，每一层我们必须沿着P的方向进行移动。
我们先定义层的数量，计算每一层的深度，最后计算纹理坐标偏移，每一层我们必须沿着\(\color{brown}{\bar{P}}\)的方向进行移动。
然后我们遍历所有层，从上开始，知道找到小于这一层的深度值的深度贴图值：
@@ -228,7 +228,7 @@ return texCoords - currentTexCoords;
```
这里我们循环每一层深度，直到沿着P向量找到第一个返回低于（位移）表面的深度的纹理坐标偏移量。从fragment的纹理坐标减去最后的偏移量，来得到最终的经过位移的纹理坐标向量，这次就比传统的视差映射更精确了。
这里我们循环每一层深度，直到沿着\(\color{brown}{\bar{P}}\)向量找到第一个返回低于（位移）表面的深度的纹理坐标偏移量。从fragment的纹理坐标减去最后的偏移量，来得到最终的经过位移的纹理坐标向量，这次就比传统的视差映射更精确了。
有10个样本砖墙从一个角度看上去就已经很好了，但是当有一个强前面展示的木制表面一样陡峭的表面时，陡峭的视差映射的威力就显示出来了：
@@ -250,7 +250,7 @@ float numLayers = mix(maxLayers, minLayers, abs(dot(vec3(0.0, 0.0, 1.0), viewDir
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_steep_artifact.png)
我们可以通过增加样本的方式减少这个问题，但是很快就会花费很多性能。有些旨在修复这个问题的方法：不适用低于表面的第一个位置，而是在两个接近的深度层进行插值找出更匹配B的。
我们可以通过增加样本的方式减少这个问题，但是很快就会花费很多性能。有些旨在修复这个问题的方法：不适用低于表面的第一个位置，而是在两个接近的深度层进行插值找出更匹配\(\color{blue}B\)的。
两种最流行的解决方法叫做Relief Parallax Mapping和Parallax Occlusion Mapping，Relief Parallax Mapping更精确一些，但是比Parallax Occlusion Mapping性能开销更多。因为Parallax Occlusion Mapping的效果和前者差不多但是效率更高，因此这种方式更经常使用，所以我们将在下面讨论一下。

42
docs/05 Advanced Lighting/08 Deferred Shading.md
View File

@@ -293,37 +293,53 @@ glBindFramebuffer(GL_FRAMEBUFFER, 0);
为了获取一个光源的体积半径，我们需要解一个对于一个我们认为是**黑暗(Dark)**的亮度(Brightness)的衰减方程，它可以是0.0，或者是更亮一点的但仍被认为黑暗的值，像是0.03。为了展示我们如何计算光源的体积半径，我们将会使用一个在[投光物](http://learnopengl-cn.readthedocs.org/zh/latest/02%20Lighting/05%20Light%20casters/)这节中引入的一个更加复杂，但非常灵活的衰减方程：
![](../img/deferred_shading_1.png)
$$
F_{light} = \frac{I}{K_c + K_l * d + K_q * d^2}
$$
我们现在想要在![](../img/F_light.png)等于0的前提下解这个方程，也就是说光在该距离完全是黑暗的。然而这个方程永远不会真正等于0.0，所以它没有解。所以，我们不会求表达式等于0.0时候的解，相反我们会求当亮度值靠近于0.0的解，这时候它还是能被看做是黑暗的。在这个教程的演示场景中，我们选择![](../img/5256.png)作为一个合适的光照值；除以256是因为默认的8-bit帧缓冲可以每个分量显示这么多强度值(Intensity)。
我们现在想要在\(F_{light}\)等于0的前提下解这个方程，也就是说光在该距离完全是黑暗的。然而这个方程永远不会真正等于0.0，所以它没有解。所以，我们不会求表达式等于0.0时候的解，相反我们会求当亮度值靠近于0.0的解，这时候它还是能被看做是黑暗的。在这个教程的演示场景中，我们选择\(5/256\)作为一个合适的光照值；除以256是因为默认的8-bit帧缓冲可以每个分量显示这么多强度值(Intensity)。
!!! Important
我们使用的衰减方程在它的可视范围内基本都是黑暗的，所以如果我们想要限制它为一个比![](../img/5256.png)更加黑暗的亮度，光体积就会变得太大从而变得低效。只要是用户不能在光体积边缘看到一个突兀的截断，这个参数就没事了。当然它还是依赖于场景的类型，一个高的亮度阀值会产生更小的光体积，从而获得更高的效率，然而它同样会产生一个很容易发现的副作用，那就是光会在光体积边界看起来突然断掉。
我们使用的衰减方程在它的可视范围内基本都是黑暗的，所以如果我们想要限制它为一个比\(5/256\)更加黑暗的亮度，光体积就会变得太大从而变得低效。只要是用户不能在光体积边缘看到一个突兀的截断，这个参数就没事了。当然它还是依赖于场景的类型，一个高的亮度阀值会产生更小的光体积，从而获得更高的效率，然而它同样会产生一个很容易发现的副作用，那就是光会在光体积边界看起来突然断掉。
我们要求的衰减方程会是这样：
![](../img/deferred_shading_2.png)
$$
\frac{5}{256} = \frac{I_{max}}{Attenuation}
$$
在这里，![](../img/I_max.png)是光源最亮的颜色分量。我们之所以使用光源最亮的颜色分量是因为解光源最亮的强度值方程最好地反映了理想光体积半径。
在这里，\(I_{max}\)是光源最亮的颜色分量。我们之所以使用光源最亮的颜色分量是因为解光源最亮的强度值方程最好地反映了理想光体积半径。
从这里我们继续解方程：
![](../img/deferred_shading_3.png)
$$
\frac{5}{256} * Attenuation = I_{max}
$$
![](../img/deferred_shading_4.png)
$$
5 * Attenuation = I_{max} * 256
$$
![](../img/deferred_shading_5.png)
$$
Attenuation = I_{max} * \frac{256}{5}
$$
![](../img/deferred_shading_6.png)
$$
K_c + K_l * d + K_q * d^2 = I_{max} * \frac{256}{5}
$$
![](../img/deferred_shading_7.png)
$$
K_q * d^2 + K_l * d + K_c - I_{max} * \frac{256}{5} = 0
$$
最后的方程形成了![](../img/quad_formula.png)的形式，我们可以用求根公式来解这个二次方程：
最后的方程形成了\(ax^2 + bx + c = 0\)的形式，我们可以用求根公式来解这个二次方程：
![](../img/deferred_shading_8.png)
$$
x = \frac{-K_l + \sqrt{K_l^2 - 4 * K_q * (K_c - I_{max} * \frac{256}{5})}}{2 * K_q}
$$
它给我们了一个通用公式从而允许我们计算x的值，即光源的光体积半径，只要我们提供了一个常量，线性和二次项参数：
它给我们了一个通用公式从而允许我们计算\(x\)的值，即光源的光体积半径，只要我们提供了一个常量，线性和二次项参数：
```c++
GLfloat constant = 1.0;