Fix all the titles

docs/01 Getting started/08 Coordinate Systems.md

@@ -1,4 +1,4 @@
-# 坐标系统(Coordinate System)
+# 坐标系统
 
 原文     | [Coordinate Systems](http://learnopengl.com/#!Getting-started/Coordinate-Systems)
       ---|---
@@ -8,7 +8,7 @@
 
 在上一个教程中，我们学习了如何有效地利用矩阵变换来对所有顶点进行转换。OpenGL希望在所有顶点着色器运行后，所有我们可见的顶点都变为标准化设备坐标(Normalized Device Coordinate, NDC)。也就是说，每个顶点的x，y，z坐标都应该在-1.0到1.0之间，超出这个坐标范围的顶点都将不可见。我们通常会自己设定一个坐标的范围，之后再在顶点着色器中将这些坐标转换为标准化设备坐标。然后将这些标准化设备坐标传入光栅器(Rasterizer)，再将他们转换为屏幕上的二维坐标或像素。
 
-将坐标转换为标准化设备坐标，接着再转化为屏幕坐标的过程通常是分步，也就是类似于流水线那样子，实现的，在流水线里面我们在将对象转换到屏幕空间之前会先将其转换到多个坐标系统。将对象的坐标转换到几个过渡坐标系(Intermediate Coordinate System)的优点在于，在这些特定的坐标系统中进行一些操作或运算更加方便和容易，这一点很快将会变得很明显。对我们来说比较重要的总共有5个不同的坐标系统：
+将坐标转换为标准化设备坐标，接着再转化为屏幕坐标的过程通常是分步，也就是类似于流水线那样子，实现的，在流水线里面我们在将对象转换到屏幕空间之前会先将其转换到多个坐标系统(Coordinate System)。将对象的坐标转换到几个过渡坐标系(Intermediate Coordinate System)的优点在于，在这些特定的坐标系统中进行一些操作或运算更加方便和容易，这一点很快将会变得很明显。对我们来说比较重要的总共有5个不同的坐标系统：
 
  - 局部空间(Local Space，或者称为物体空间(Object Space))
  - 世界空间(World Space)
@@ -20,7 +20,7 @@
 
 你现在可能对什么是空间或坐标系到底是什么感到困惑，所以接下来我们将会通过展示完整的图片来解释每一个坐标系实际做了什么。
 
-### 整体概述
+## 概述
 
 为了将坐标从一个坐标系转换到另一个坐标系，我们需要用到几个转换矩阵，最重要的几个分别是**模型(Model)**、**视图(View)**、**投影(Projection)**三个矩阵。首先，顶点坐标开始于**局部空间(Local Space)**，称为**局部坐标(Local Coordinate)**，然后经过**世界坐标(World Coordinate)**，**观察坐标(View Coordinate)**，**裁剪坐标(Clip Coordinate)**，并最后以**屏幕坐标(Screen Coordinate)**结束。下面的图示显示了整个流程及各个转换过程做了什么：
 
@@ -36,26 +36,26 @@
 
 你可能了解了每个单独的坐标空间的作用。我们之所以将顶点转换到各个不同的空间的原因是有些操作在特定的坐标系统中才有意义且更方便。例如，当修改对象时，如果在局部空间中则是有意义的；当对对象做相对于其它对象的位置的操作时，在世界坐标系中则是有意义的；等等这些。如果我们愿意，本可以定义一个直接从局部空间到裁剪空间的转换矩阵，但那样会失去灵活性。接下来我们将要更仔细地讨论各个坐标系。
 
-### 局部空间(Local Space)
+## 局部空间
 
-局部空间是指对象所在的坐标空间，例如，对象最开始所在的地方。想象你在一个模型建造软件(比如说Blender)中创建了一个立方体。你创建的立方体的原点有可能位于(0，0，0)，即使有可能在最后的应用中位于完全不同的另外一个位置。甚至有可能你创建的所有模型都以(0，0，0)为初始位置，然而他们会在世界的不同位置。则你的模型的所有顶点都是在**局部**空间：他们相对于你的对象来说都是局部的。
+局部空间(Local Space)是指对象所在的坐标空间，例如，对象最开始所在的地方。想象你在一个模型建造软件(比如说Blender)中创建了一个立方体。你创建的立方体的原点有可能位于(0，0，0)，即使有可能在最后的应用中位于完全不同的另外一个位置。甚至有可能你创建的所有模型都以(0，0，0)为初始位置，然而他们会在世界的不同位置。则你的模型的所有顶点都是在**局部**空间：他们相对于你的对象来说都是局部的。
 
 我们一直使用的那个箱子的坐标范围为-0.5到0.5，设定(0, 0)为它的原点。这些都是局部坐标。
 
 
-### 世界空间(World Space)
+## 世界空间
 
-如果我们想将我们所有的对象导入到程序当中，它们有可能会全挤在世界的原点上(0，0，0)，然而这并不是我们想要的结果。我们想为每一个对象定义一个位置，从而使对象位于更大的世界当中。世界空间中的坐标就如它们听起来那样：是指顶点相对于(游戏)世界的坐标。物体变换到的最终空间就是世界坐标系，并且你会想让这些物体分散开来摆放(从而显得更真实)。对象的坐标将会从局部坐标转换到世界坐标；该转换是由**模型矩阵(Model Matrix)**实现的。
+如果我们想将我们所有的对象导入到程序当中，它们有可能会全挤在世界的原点上(0，0，0)，然而这并不是我们想要的结果。我们想为每一个对象定义一个位置，从而使对象位于更大的世界当中。世界空间(World Space)中的坐标就如它们听起来那样：是指顶点相对于(游戏)世界的坐标。物体变换到的最终空间就是世界坐标系，并且你会想让这些物体分散开来摆放(从而显得更真实)。对象的坐标将会从局部坐标转换到世界坐标；该转换是由**模型矩阵(Model Matrix)**实现的。
 
 模型矩阵是一种转换矩阵，它能通过对对象进行平移、缩放、旋转来将它置于它本应该在的位置或方向。你可以想象一下，我们需要转换一栋房子，通过将它缩小(因为它在局部坐标系中显得太大了)，将它往郊区的方向平移，然后沿着y轴往坐标旋转。经过这样的变换之后，它将恰好能够与邻居的房子重合。你能够想到上一节讲到的利用模型矩阵将各个箱子放置到这个屏幕上；我们能够将箱子中的局部坐标转换为观察坐标或世界坐标。
 
-### 观察空间(View Space)
+## 观察空间
 
-观察空间经常被人们称之OpenGL的**摄像机(Camera)**(所以有时也称为摄像机空间(Camera Space)或视觉空间(Eye Space))。观察空间就是将对象的世界空间的坐标转换为观察者视野前面的坐标。因此观察空间就是从摄像机的角度观察到的空间。而这通常是由一系列的平移和旋转的组合来平移和旋转场景从而使得特定的对象被转换到摄像机前面。这些组合在一起的转换通常存储在一个**观察矩阵(View Matrix)**里，用来将世界坐标转换到观察空间。在下一个教程我们将广泛讨论如何创建一个这样的观察矩阵来模拟一个摄像机。
+观察空间(View Space)经常被人们称之OpenGL的**摄像机(Camera)**(所以有时也称为摄像机空间(Camera Space)或视觉空间(Eye Space))。观察空间就是将对象的世界空间的坐标转换为观察者视野前面的坐标。因此观察空间就是从摄像机的角度观察到的空间。而这通常是由一系列的平移和旋转的组合来平移和旋转场景从而使得特定的对象被转换到摄像机前面。这些组合在一起的转换通常存储在一个**观察矩阵(View Matrix)**里，用来将世界坐标转换到观察空间。在下一个教程我们将广泛讨论如何创建一个这样的观察矩阵来模拟一个摄像机。
 
-### 裁剪空间(Clip Space)
+## 裁剪空间
 
-在一个顶点着色器运行的最后，OpenGL期望所有的坐标都能落在一个给定的范围内，且任何在这个范围之外的点都应该被裁剪掉(Clipped)。被裁剪掉的坐标就被忽略了，所以剩下的坐标就将变为屏幕上可见的片段。这也就是**裁剪空间**名字的由来。
+在一个顶点着色器运行的最后，OpenGL期望所有的坐标都能落在一个给定的范围内，且任何在这个范围之外的点都应该被裁剪掉(Clipped)。被裁剪掉的坐标就被忽略了，所以剩下的坐标就将变为屏幕上可见的片段。这也就是**裁剪空间(Clip Space)**名字的由来。
 
 因为将所有可见的坐标都放置在-1.0到1.0的范围内不是很直观，所以我们会指定自己的坐标集(Coordinate Set)并将它转换回标准化设备坐标系，就像OpenGL期望它做的那样。
 
@@ -73,9 +73,9 @@
 
 投影矩阵将观察坐标转换为裁剪坐标的过程采用两种不同的方式，每种方式分别定义自己的平截头体。我们可以创建一个正射投影矩阵(Orthographic Projection Matrix)或一个透视投影矩阵(Perspective Projection Matrix)。
 
-#### 正射投影(Orthographic Projection)
+### 正射投影
 
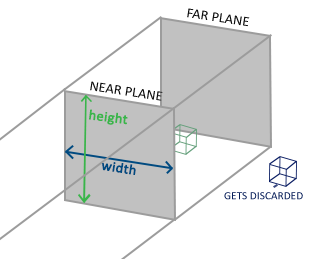
-正射投影矩阵定义了一个类似立方体的平截头体，指定了一个裁剪空间，每一个在这空间外面的顶点都会被裁剪。创建一个正射投影矩阵需要指定可见平截头体的宽、高和长度。所有在使用正射投影矩阵转换到裁剪空间后如果还处于这个平截头体里面的坐标就不会被裁剪。它的平截头体看起来像一个容器：
+正射投影(Orthographic Projection)矩阵定义了一个类似立方体的平截头体，指定了一个裁剪空间，每一个在这空间外面的顶点都会被裁剪。创建一个正射投影矩阵需要指定可见平截头体的宽、高和长度。所有在使用正射投影矩阵转换到裁剪空间后如果还处于这个平截头体里面的坐标就不会被裁剪。它的平截头体看起来像一个容器：
 
 ![orthographic projection frustum](http://learnopengl.com/img/getting-started/orthographic_frustum.png)
 
@@ -91,13 +91,13 @@ glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f);
 
 正射投影矩阵直接将坐标映射到屏幕的二维平面内，但实际上一个直接的投影矩阵将会产生不真实的结果，因为这个投影没有将**透视(Perspective)**考虑进去。所以我们需要**透视投影**矩阵来解决这个问题。
 
-#### 透视投影(Perspective Projection)
+#### 透视投影
 
-如果你曾经体验过**实际生活**给你带来的景象，你就会注意到离你越远的东西看起来更小。这个神奇的效果我们称之为透视。透视的效果在我们看一条无限长的高速公路或铁路时尤其明显，正如下面图片显示的那样:
+如果你曾经体验过**实际生活**给你带来的景象，你就会注意到离你越远的东西看起来更小。这个神奇的效果我们称之为透视(Perspective)。透视的效果在我们看一条无限长的高速公路或铁路时尤其明显，正如下面图片显示的那样:
 
 ![perspective](http://learnopengl.com/img/getting-started/perspective.png)
 
-正如你看到的那样，由于透视的原因，平行线似乎在很远的地方看起来会相交。这正是透视投影想要模仿的效果，它是使用透视投影矩阵来完成的。这个投影矩阵不仅将给定的平截头体范围映射到裁剪空间，同样还修改了每个顶点坐标的w值，从而使得离观察者越远的顶点坐标w分量越大。被转换到裁剪空间的坐标都会在-w到w的范围之间(任何大于这个范围的对象都会被裁剪掉)。OpenGL要求所有可见的坐标都落在-1.0到1.0范围内从而作为最后的顶点着色器输出，因此一旦坐标在裁剪空间内，透视划分就会被应用到裁剪空间坐标：
+正如你看到的那样，由于透视的原因，平行线似乎在很远的地方看起来会相交。这正是透视投影(Perspective Projection)想要模仿的效果，它是使用透视投影矩阵来完成的。这个投影矩阵不仅将给定的平截头体范围映射到裁剪空间，同样还修改了每个顶点坐标的w值，从而使得离观察者越远的顶点坐标w分量越大。被转换到裁剪空间的坐标都会在-w到w的范围之间(任何大于这个范围的对象都会被裁剪掉)。OpenGL要求所有可见的坐标都落在-1.0到1.0范围内从而作为最后的顶点着色器输出，因此一旦坐标在裁剪空间内，透视划分就会被应用到裁剪空间坐标：
 
 $$
 out = \begin{pmatrix} x /w \\ y / w \\ z / w \end{pmatrix}
@@ -145,7 +145,7 @@ $$
 
 这一章的主题可能会比较难理解，如果你仍然不确定每个空间的作用的话，你也不必太担心。接下来你会看到我们是怎样好好运用这些坐标空间的并且会有足够的展示例子在接下来的教程中。
 
-## 进入三维
+# 进入3D
 
 既然我们知道了如何将三维坐标转换为二维坐标，我们可以开始将我们的对象展示为三维对象而不是目前我们所展示的缺胳膊少腿的二维平面。
 
@@ -179,7 +179,7 @@ model = glm::rotate(model, -55.0f, glm::vec3(1.0f, 0.0f, 0.0f));
 	- 使你的食指往上。
 	- 向下90度弯曲你的中指。 
 
-如果你都正确地做了，那么你的大拇指朝着正x轴方向，食指朝着正y轴方向，中指朝着正z轴方向。如果你用左手来做这些动作，你会发现z轴的方向是相反的。这就是有名的左手坐标系，它被DirectX广泛地使用。注意在标准化设备坐标系中OpenGL使用的是左手坐标系(投影矩阵改变了惯用手的习惯)。
+	如果你都正确地做了，那么你的大拇指朝着正x轴方向，食指朝着正y轴方向，中指朝着正z轴方向。如果你用左手来做这些动作，你会发现z轴的方向是相反的。这就是有名的左手坐标系，它被DirectX广泛地使用。注意在标准化设备坐标系中OpenGL使用的是左手坐标系(投影矩阵改变了惯用手的习惯)。
 
 在下一个教程中我们将会详细讨论如何在场景中移动。目前的观察矩阵是这样的：
 
@@ -262,9 +262,9 @@ glDrawArrays(GL_TRIANGLES, 0, 36);
 
 幸运的是，OpenGL存储深度信息在z缓冲区(Z-buffer)里面，它允许OpenGL决定何时覆盖一个像素何时不覆盖。通过使用z缓冲区我们可以设置OpenGL来进行深度测试。
 
-### z缓冲区
+### Z缓冲区
 
-OpenGL存储它的所有深度信息于z缓冲区中，也被称为深度缓冲区(Depth Buffer)。GLFW会自动为你生成这样一个缓冲区 (就如它有一个颜色缓冲区来存储输出图像的颜色)。深度存储在每个片段里面(作为片段的z值)当片段像输出它的颜色时，OpenGL会将它的深度值和z缓冲进行比较然后如果当前的片段在其它片段之后它将会被丢弃，然后重写。这个过程称为**深度测试(Depth Testing)**并且它是由OpenGL自动完成的。
+OpenGL存储它的所有深度信息于Z缓冲区(Z-buffer)中，也被称为深度缓冲区(Depth Buffer)。GLFW会自动为你生成这样一个缓冲区 (就如它有一个颜色缓冲区来存储输出图像的颜色)。深度存储在每个片段里面(作为片段的z值)当片段像输出它的颜色时，OpenGL会将它的深度值和z缓冲进行比较然后如果当前的片段在其它片段之后它将会被丢弃，然后重写。这个过程称为**深度测试(Depth Testing)**并且它是由OpenGL自动完成的。
 
 然而，如果我们想要确定OpenGL是否真的执行深度测试，首先我们要告诉OpenGL我们想要开启深度测试；而这通常是默认关闭的。我们通过`glEnable`函数来开启深度测试。`glEnable`和`glDisable`函数允许我们开启或关闭某一个OpenGL的功能。该功能会一直是开启或关闭的状态直到另一个调用来关闭或开启它。现在我们想开启深度测试就需要开启`GL_DEPTH_TEST`：