Fix all the titles

docs/01 Getting started/07 Transformations.md

@@ -1,4 +1,4 @@
-# 变换(Transformations)
+# 变换
 
 原文     | [Transformations](http://learnopengl.com/#!Getting-started/Transformations)
       ---|---
@@ -12,9 +12,9 @@
 
 为了深入了解变换，我们首先要在讨论矩阵之前了解一点向量(Vector)。这一节的目标是让你拥有将来需要的最基础的数学背景知识. 如果你发现这节十分困难，尽量尝试去理解它们，当你以后需要它们的时候回过头来复习这些概念。
 
-## 向量(Vector)
+# 向量
 
-向量最最基本的定义就是一个方向。或者更正式的说，向量有一个**方向(Direction)**和**大小(Magnitude，也叫做强度或长度)**。你可以把向量想成一个藏宝图上的指示：“向左走10步，向北走3步，然后向右走5步”；“左”就是方向，“10步”就是向量的长度。你可以发现，这个藏宝图的指示一共有3个向量。向量可以在任意**维度**(Dimension)上，但是我们通常只使用2至4维。如果一个向量有2个维度，它表示一个平面的方向(想象一下2D的图像)，当它有3个维度的时候它可以表达一个3D世界的方向。
+向量(Vector)最最基本的定义就是一个方向。或者更正式的说，向量有一个**方向(Direction)**和**大小(Magnitude，也叫做强度或长度)**。你可以把向量想成一个藏宝图上的指示：“向左走10步，向北走3步，然后向右走5步”；“左”就是方向，“10步”就是向量的长度。你可以发现，这个藏宝图的指示一共有3个向量。向量可以在任意**维度**(Dimension)上，但是我们通常只使用2至4维。如果一个向量有2个维度，它表示一个平面的方向(想象一下2D的图像)，当它有3个维度的时候它可以表达一个3D世界的方向。
 
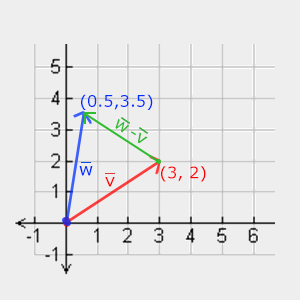
 下面你会看到3个向量，每个向量在图像中都用一个箭头(x, y)表示。我们在2D图片中展示这些向量，因为这样子会更直观. 你仍然可以把这些2D向量当做z坐标为0的3D向量。由于向量表示的是方向，起始于何处**并不会**改变它的值。下图我们可以看到向量\(\color{red}{\bar{v}}\)和\(\color{blue}{\bar{w}}\)是相等的，尽管他们的起始点不同：
 
@@ -30,7 +30,7 @@ $$
 
 和普通数字一样，我们也可以用向量进行多种运算(其中一些你可能已经知道了)。
 
-### 向量与标量运算(Scalar Vector Operations)
+## 向量与标量运算
 
 **标量(Scalar)**只是一个数字(或者说是仅有一个分量的矢量)。当把一个向量加/减/乘/除一个标量，我们可以简单的把向量的每个分量分别进行该运算。对于加法来说会像这样:
 
@@ -40,15 +40,15 @@ $$
 
 其中的+可以是+，-，·或÷，其中·是乘号。注意－和÷运算时不能颠倒，因为颠倒的运算是没有定义的(标量-/÷矢量)
 
-### 向量取反(Vector Negation)
+## 向量取反
 
-对一个向量取反会将其方向逆转。一个指向东北的向量取反后就指向西南方向了。我们在一个向量的每个分量前加负号就可以实现取反了(或者说用-1数乘该向量):
+对一个向量取反(Negation)会将其方向逆转。一个指向东北的向量取反后就指向西南方向了。我们在一个向量的每个分量前加负号就可以实现取反了(或者说用-1数乘该向量):
 
 $$
 -\bar{v} = -\begin{pmatrix} \color{red}{v_x} \\ \color{blue}{v_y} \\ \color{green}{v_z} \end{pmatrix} = \begin{pmatrix} -\color{red}{v_x} \\ -\color{blue}{v_y} \\ -\color{green}{v_z} \end{pmatrix}
 $$
 
-### 向量加减
+## 向量加减
 
 向量的加法可以被定义为是**分量的(Component-wise)**相加，即将一个向量中的每一个分量加上另一个向量的对应分量：
 
@@ -70,9 +70,9 @@ $$
 
 ![](http://learnopengl.com/img/getting-started/vectors_subtraction.png)
 
-### 长度(Length)
+## 长度
 
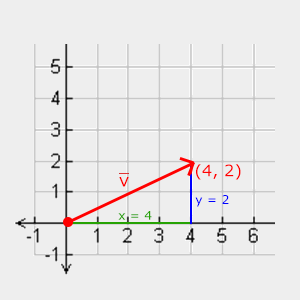
-我们使用**勾股定理(Pythagoras Theorem)**来获取向量的长度/大小. 如果你把向量的x与y分量画出来，该向量会形成一个以x与y分量为边的三角形:
+我们使用**勾股定理(Pythagoras Theorem)**来获取向量的长度(Length)/大小(Magnitude). 如果你把向量的x与y分量画出来，该向量会形成一个以x与y分量为边的三角形:
 
 ![](http://learnopengl.com/img/getting-started/vectors_triangle.png)
 
@@ -100,13 +100,13 @@ $$
 
 我们把这种方法叫做一个向量的**标准化(Normalizing)**。单位向量头上有一个^样子的记号，并且它会变得很有用，特别是在我们只关心方向不关系长度的时候(如果我们改变向量的长度，它的方向并不会改变)。
 
-### 向量相乘(Vector-vector Multiplication)
+## 向量相乘
 
 两个向量相乘是一种很奇怪的情况。普通的乘法在向量上是没有定义的，因为它在视觉上是没有意义的，但是有两种特定情境，当需要乘法时我们可以从中选择：一个是**点乘(Dot Product)**，记作\(\bar{v} \cdot \bar{k}\)，另一个是**叉乘(Cross Product)**，记作\(\bar{v} \times \bar{k}\)。
 
-#### 点乘(Dot Product)
+### 点乘
 
-两个向量的点乘等于它们的数乘结果乘以两个向量之间夹角的余弦值。听起来有点费解，先看一下公式：
+两个向量的点乘(Dot Product)等于它们的数乘结果乘以两个向量之间夹角的余弦值。听起来有点费解，先看一下公式：
 
 $$
 \bar{v} \cdot \bar{k} = ||\bar{v}|| \cdot ||\bar{k}|| \cdot \cos \theta
@@ -138,9 +138,9 @@ $$
 
 计算两个单位余弦的角度，我们使用反余弦\(cos^{-1}\) ，结果是143.1度。现在我们很快就计算出了两个向量的角度。点乘在计算光照的时候会很有用。
 
-#### 叉乘(Cross Product)
+### 叉乘
 
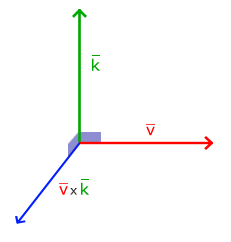
-叉乘只在3D空间有定义，它需要两个不平行向量作为输入，生成正交于两个输入向量的第三个向量。如果输入的两个向量也是正交的，那么叉乘的结果将会返回3个互相正交的向量。接下来的教程中，这很有用。下面的图片展示了3D空间中叉乘的样子：
+叉乘(Cross Product)只在3D空间有定义，它需要两个不平行向量作为输入，生成正交于两个输入向量的第三个向量。如果输入的两个向量也是正交的，那么叉乘的结果将会返回3个互相正交的向量。接下来的教程中，这很有用。下面的图片展示了3D空间中叉乘的样子：
 
 ![](http://learnopengl.com/img/getting-started/vectors_crossproduct.png)
 
@@ -152,9 +152,9 @@ $$
 
 就像你所看到的，看起来毫无头绪。可如果你这么做了，你会得到第三个向量，它正交于你的输入向量。
 
-## 矩阵(Matrix)
+# 矩阵
 
-现在我们已经讨论了向量的全部内容，是时候看看矩阵了！矩阵简单说是一个矩形的数字、符号或表达式数组。矩阵中每一项叫做矩阵的**元素(Element)**。下面是一个2×3矩阵的例子：
+现在我们已经讨论了向量的全部内容，是时候看看矩阵(Matrix)了！矩阵简单说是一个矩形的数字、符号或表达式数组。矩阵中每一项叫做矩阵的**元素(Element)**。下面是一个2×3矩阵的例子：
 
 $$
 \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}
@@ -164,7 +164,7 @@ $$
 
 关于矩阵基本也就是这些了，它就是矩形数学表达式阵列。矩阵也有非常漂亮的数学属性，就跟向量一样。矩阵有几个运算，叫做：矩阵加法、减法和乘法。
 
-### 矩阵的加减
+## 矩阵的加减
 
 矩阵与标量的加减如下所示：
 
@@ -190,7 +190,7 @@ $$
 \begin{bmatrix} \color{red}4 & \color{red}2 \\ \color{green}1 & \color{green}6 \end{bmatrix} - \begin{bmatrix} \color{red}2 & \color{red}4 \\ \color{green}0 & \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}4 - \color{red}2 & \color{red}2  - \color{red}4 \\ \color{green}1 - \color{green}0 & \color{green}6 - \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}2 & -\color{red}2 \\ \color{green}1 & \color{green}5 \end{bmatrix}
 $$
 
-### 矩阵的数乘(Matrix-scalar Products)
+## 矩阵的数乘
 
 和矩阵与标量的加减一样，矩阵与标量之间的乘法也是矩阵的每一个元素分别乘以该标量。下面的例子展示了乘法的过程：
 
@@ -202,7 +202,7 @@ $$
 
 到目前为止都还好，我们的例子都不复杂。不过矩阵与矩阵的乘法就不一样了。
 
-### 矩阵相乘(Matrix-matrix Multiplication)
+### 矩阵相乘
 
 矩阵之间的乘法不见得有多复杂，但的确很难让人适应。矩阵乘法基本上意味着遵照规定好的法则进行相乘。当然，相乘还有一些限制：
 
@@ -238,13 +238,13 @@ $$
 
 不管怎样，反正现在我们知道如何进行矩阵相乘了，我们可以开始了解好东西了。
 
-## 矩阵与向量相乘
+# 矩阵与向量相乘
 
 到目前，通过这些教程我们已经相当了解向量了。我们用向量来表示位置、颜色和纹理坐标。让我们进到兔子洞更深处：向量基本上就是一个**N×1**矩阵，N是向量分量的个数(也叫**N维(N-dimensional)**向量)。如果你仔细思考这个问题，会很有意思。向量和矩阵一样都是一个数字序列，但是它只有1列。所以，这个新信息能如何帮助我们？如果我们有一个M×N矩阵，我们可以用这个矩阵乘以我们的N×1向量，因为我们的矩阵的列数等于向量的行数，所以它们就能相乘。
 
 但是为什么我们关心矩阵是否能够乘以一个向量？有很多有意思的2D/3D变换本质上都是矩阵，而矩阵与我们的向量相乘会变换我们的向量。假如你仍然有些困惑，我们看一些例子，你很快就能明白了。
 
-### 单位矩阵(Identity Matrix)
+## 单位矩阵
 
 在OpenGL中，因为有一些原因我们通常使用4×4的变换矩阵，而其中最重要的原因就是因为每一个向量都有4个分量的。我们能想到的最简单的变换矩阵就是**单位矩阵(Identity Matrix)**。单位矩阵是一个除了对角线以外都是0的N × N矩阵。就像你看到的，这个变换矩阵使一个向量完全不变：
 
@@ -258,9 +258,9 @@ $$
 
 	你可能会奇怪一个没变换的变换矩阵有什么用？单位矩阵通常是生成其他变换矩阵的起点，如果我们深挖线性代数，这就是一个对证明定理、解线性方程非常有用的矩阵。
 
-### 缩放(Scaling)
+## 缩放
 
-当我们对一个向量进行缩放的时候就是对向量的长度进行缩放，而它的方向保持不变。如果我们进行2或3维操作，那么我们可以分别定义一个有2或3个缩放变量的向量，每个变量缩放一个轴(x、y或z)。
+当我们对一个向量进行缩放(Scaling)的时候就是对向量的长度进行缩放，而它的方向保持不变。如果我们进行2或3维操作，那么我们可以分别定义一个有2或3个缩放变量的向量，每个变量缩放一个轴(x、y或z)。
 
 我们可以尝试去缩放向量\(\color{red}{\bar{v}} = (3,2)\)。我们可以把向量沿着x轴缩放0.5，使它的宽度缩小为原来的二分之一；我们可以沿着y轴把向量的高度缩放为原来的两倍。我们看看把向量缩放(0.5, 2)所获得的\(\color{blue}{\bar{s}}\)是什么样的：
 
@@ -276,7 +276,7 @@ $$
 
 注意，第四个缩放的向量仍然是1，因为不会缩放3D空间中的w分量。w分量另有其他用途，在后面我们会看到。
 
-### 平移(Translation)
+## 平移
 
 **平移(Translation)**是在原来向量的基础上加上另一个的向量从而获得一个在不同位置的新向量的过程，这样就基于平移向量**移动(Move)**了向量。我们已经讨论了向量加法，所以你应该不会陌生。
 
@@ -298,9 +298,9 @@ $$
 
 有了平移矩阵我们就可以在3个方向(x、y、z)上移动物体，它是我们的变换工具箱中非常有用的一个变换矩阵。
 
-### 旋转(Rotation)
+### 旋转
 
-上面几个的变换内容相对容易理解，在2D或3D空间中也容易表示出来，但旋转稍复杂些。如果你想知道旋转矩阵是如何构造出来的，我推荐你去看可汗学院[线性代数](https://www.khanacademy.org/math/linear-algebra/matrix_transformations)视频。
+上面几个的变换内容相对容易理解，在2D或3D空间中也容易表示出来，但旋转(Rotation)稍复杂些。如果你想知道旋转矩阵是如何构造出来的，我推荐你去看可汗学院[线性代数](https://www.khanacademy.org/math/linear-algebra/matrix_transformations)视频。
 
 首先我们来定义一个向量的旋转到底是什么。2D或3D空间中点的旋转用**角(Angle)**来表示。角可以是角度制或弧度制的，周角是360度或2 [PI](https://en.wikipedia.org/wiki/Pi)弧度。我个人更喜欢用角度，因为它们看起来更直观。
 
@@ -367,15 +367,15 @@ $$
 
 不错！向量先缩放2倍，然后平移了(1, 2, 3)个单位。
 
-## 实践
+# 实践
 
 现在我们已经解释了所有变换背后的理论，是时候将这些知识利用起来了。OpenGL没有任何自带的矩阵和向量形式，所以我们必须自己定义数学类和方法。在这个教程中我们更愿意抽象所有的数学细节，使用已经做好了的数学库。幸运的是有个使用简单的专门为OpenGL量身定做的数学库，那就是GLM。
 
-### GLM
+## GLM
 
 GLM是Open**GL** **M**athematics的缩写，它是一个只有头文件的库，也就是说我们只需包含合适的头文件就行了；不用链接和编译。GLM可以从他们的[网站](http://glm.g-truc.net/0.9.5/index.html)上下载。把头文件的根目录复制到你的`includes`文件夹，然后你就可以使用这个库了。
 
-![](http://learnopengl.com/img/getting-started/glm.png)
+<img alt="OpenGL Logo" src="../../img/01/07/glm.png" class="right" />
 
 我们需要的GLM的大多数功能都可以从下面这3个头文件中找到：