mirrors/LearnOpenGL-CN
1
0
Fork 0
mirror of https://github.com/LearnOpenGL-CN/LearnOpenGL-CN.git synced 2025-08-23 12:45:29 +08:00
Code Activity

Revert all the changes since 851f9ec

Browse Source
This commit is contained in:
Meow J
2016-07-04 19:21:32 +08:00
parent d8ebc4ee4f
commit 12a8b3eb38
144 changed files with 134 additions and 166 deletions
Download Patch File Download Diff File Expand all files Collapse all files

92
docs/05 Advanced Lighting/01 Advanced Lighting.md
View File

@@ -1,92 +0,0 @@
# 高级光照
原文 | [Advanced Lighting](http://learnopengl.com/#!Advanced-Lighting/Advanced-Lighting)
---|---
作者 | JoeyDeVries
翻译 | [Django](http://bullteacher.com/)
校对 | gjy_1992
在光照教程中，我们简单的介绍了Phong光照模型，它给我们的场景带来的基本的现实感。Phong模型看起来还不错，但本章我们把重点放在一些细微差别上。
## Blinn-Phong
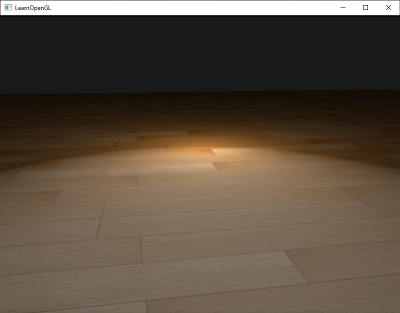
Phong光照很棒，而且性能较高，但是它的镜面反射在某些条件下会失效，特别是当发光值属性低的时候，对应一个非常大的粗糙的镜面区域。下面的图片展示了，当我们使用镜面的发光值为1.0时，一个带纹理地板的效果：
![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_phong_limit.png)
你可以看到，镜面区域边缘迅速减弱并截止。出现这个问题的原因是在视线向量和反射向量的角度不允许大于90度。如果大于90度的话，点乘的结果就会是负数，镜面的贡献成分就会变成0。你可能会想，这不是一个问题，因为大于90度时我们不应看到任何光，对吧？
错了，这只适用于漫散射部分，当法线和光源之间的角度大于90度时意味着光源在被照亮表面的下方，这样光的散射成分就会是0.0。然而，对于镜面光照，我们不会测量光源和法线之间的角度，而是测量视线和反射方向向量之间的。看看下面的两幅图：
![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_over_90.png)
现在看来问题就很明显了。左侧图片显示Phong反射的θ小于90度的情况。我们可以看到右侧图片视线和反射之间的角θ大于90度，这样镜面反射成分将会被消除。通常这也不是问题，因为视线方向距离反射方向很远，但如果我们使用一个数值较低的发光值参数的话，镜面半径就会足够大，以至于能够贡献一些镜面反射的成份了。在例子中，我们在角度大于90度时消除了这个贡献（如第一个图片所示）。
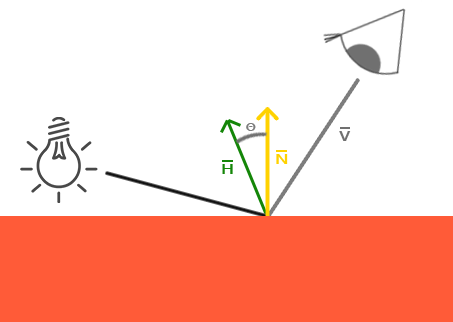
1977年James F. Blinn引入了Blinn-Phong着色，它扩展了我们目前所使用的Phong着色。Blinn-Phong模型很大程度上和Phong是相似的，不过它稍微改进了Phong模型，使之能够克服我们所讨论到的问题。它放弃使用反射向量，而是基于我们现在所说的一个叫做半程向量（halfway vector）的向量，这是个单位向量，它在视线方向和光线方向的中间。半程向量和表面法线向量越接近，镜面反射成份就越大。
![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_halfway_vector.png)
当视线方向恰好与反射向量对称时，半程向量就与法线向量重合。这样观察者距离原来的反射方向越近，镜面反射的高光就会越强。
这里，你可以看到无论观察者往哪里看，半程向量和表面法线之间的夹角永远都不会超过90度（当然除了光源远远低于表面的情况）。这样会产生和Phong反射稍稍不同的结果，但这时看起来会更加可信，特别是发光值参数比较低的时候。Blinn-Phong着色模型也正是早期OpenGL固定函数输送管道（fixed function pipeline）所使用的着色模型。
得到半程向量很容易，我们将光的方向向量和视线向量相加，然后将结果归一化（normalize）；
![](http://learnopengl-cn.readthedocs.org/zh/latest/img/05_01_01.png)
翻译成GLSL代码如下：
```c++
vec3 lightDir = normalize(lightPos - FragPos);
vec3 viewDir = normalize(viewPos - FragPos);
vec3 halfwayDir = normalize(lightDir + viewDir);
```
实际的镜面反射的计算，就成为计算表面法线和半程向量的点乘，并对其结果进行约束（大于或等于0），然后获取它们之间角度的余弦，再添加上发光值参数：
```c++
float spec = pow(max(dot(normal, halfwayDir), 0.0), shininess);
vec3 specular = lightColor * spec;
```
除了我们刚刚讨论的，Blinn-Phong没有更多的内容了。Blinn-Phong和Phong的镜面反射唯一不同之处在于，现在我们要测量法线和半程向量之间的角度，而半程向量是视线方向和反射向量之间的夹角。
!!! Important
Blinn-Phong着色的一个附加好处是，它比Phong着色性能更高，因为我们不必计算更加复杂的反射向量了。
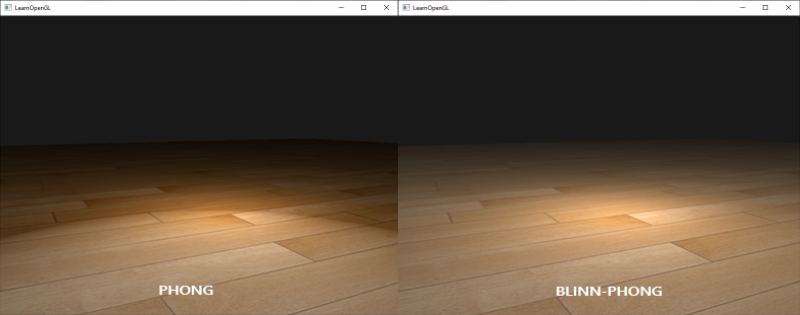
引入了半程向量来计算镜面反射后，我们再也不会遇到Phong着色的骤然截止问题了。下图展示了两种不同方式下发光值指数为0.5时镜面区域的不同效果：
![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_comparrison.png)
Phong和Blinn-Phong着色之间另一个细微差别是，半程向量和表面法线之间的角度经常会比视线和反射向量之间的夹角更小。结果就是，为了获得和Phong着色相似的效果，必须把发光值参数设置的大一点。通常的经验是将其设置为Phong着色的发光值参数的2至4倍。
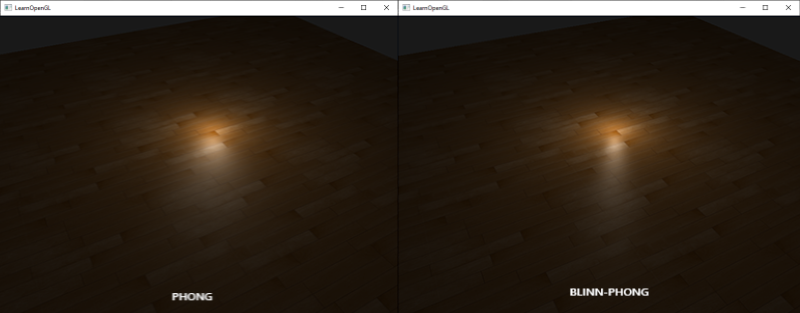
下图是Phong指数为8.0和Blinn-Phong指数为32的时候，两种specular反射模型的对比：
![](http://learnopengl.com/img/advanced-lighting/advanced_lighting_comparrison2.png)
你可以看到Blinn-Phong的镜面反射成分要比Phong锐利一些。这通常需要使用一点小技巧才能获得之前你所看到的Phong着色的效果，但Blinn-Phong着色的效果比默认的Phong着色通常更加真实一些。
这里我们用到了一个简单像素着色器，它可以在普通Phong反射和Blinn-Phong反射之间进行切换：
```c++
void main()
{
[...]
float spec = 0.0;
if(blinn)
{
vec3 halfwayDir = normalize(lightDir + viewDir);
spec = pow(max(dot(normal, halfwayDir), 0.0), 16.0);
}
else
{
vec3 reflectDir = reflect(-lightDir, normal);
spec = pow(max(dot(viewDir, reflectDir), 0.0), 8.0);
}
```
你可以在这里找到这个简单的[demo的源码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/blinn_phong)以及[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/blinn_phong&type=vertex)和[片段](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/blinn_phong&type=fragment)着色器。按下b键，这个demo就会从Phong切换到Blinn-Phong光照，反之亦然。

161
docs/05 Advanced Lighting/02 Gamma Correction.md
View File

@@ -1,161 +0,0 @@
本文作者JoeyDeVries，由Django翻译自[http://learnopengl.com](http://learnopengl.com)
## Gamma校正(Gamma Correction)
当我们计算出场景中所有像素的最终颜色以后，我们就必须把它们显示在监视器上。过去，大多数监视器是阴极射线管显示器（CRT）。这些监视器有一个物理特性就是两倍的输入电压产生的不是两倍的亮度。输入电压产生约为输入电压的2.2次幂的亮度，这叫做监视器Gamma（译注：Gamma也叫灰度系数，每种显示设备都有自己的Gamma值，都不相同，有一个公式：设备输出亮度 = 电压的Gamma次幂，任何设备Gamma基本上都不会等于1，等于1是一种理想的线性状态，这种理想状态是：如果电压和亮度都是在0到1的区间，那么多少电压就等于多少亮度。对于CRT，Gamma通常为2.2，因而，输出亮度 = 输入电压的2.2次幂，你可以从本节第二张图中看到Gamma2.2实际显示出来的总会比预期暗，相反Gamma0.45就会比理想预期亮，如果你讲Gamma0.45叠加到Gamma2.2的显示设备上，便会对偏暗的显示效果做到校正，这个简单的思路就是本节的核心）。
人类所感知的亮度恰好和CRT所显示出来相似的指数关系非常匹配。为了更好的理解所有含义，请看下面的图片：
![](http://learnopengl.com/img/advanced-lighting/gamma_correction_brightness.png)
第一行是人眼所感知到的正常的灰阶，亮度要增加一倍（比如从0.1到0.2）你才会感觉比原来变亮了一倍（译注：这里的意思是说比如一个东西的亮度0.3，让人感觉它比原来变亮一倍，那么现在这个亮度应该成为0.6，而不是0.4，也就是说人眼感知到的亮度的变化并非线性均匀分布的。问题的关键在于这样的一倍相当于一个亮度级，例如假设0.1、0.2、0.4、0.8是我们定义的四个亮度级别，在0.1和0.2之间人眼只能识别出0.15这个中间级，而虽然0.4到0.8之间的差距更大，这个区间人眼也只能识别出一个颜色）。然而，当我们谈论光的物理亮度，也就是光子的数量的多少的时候，底部的灰阶显示出的才是这时讨论的亮度。底部的灰阶显示出的是双倍的亮度所返回的物理亮度（译注：这里亮度是指光子数量和正相关的亮度，即物理亮度，前面讨论的是人的感知亮度；物理亮度和感知亮度的区别在于，物理亮度基于光子数量，感知亮度基于人的感觉，比如第二个灰阶里亮度0.1的光子数量是0.2的二分之一），但是由于这与我们的眼睛感知亮度不完全一致（对比较暗的颜色变化更敏感），所以它看起来很奇怪。
因为人眼看到颜色的亮度更倾向于顶部的灰阶，监视器使用的也是一种指数关系（电压的2.2次幂），所以物理亮度通过监视器能够被映射到顶部的非线性亮度；因此看起来效果不错（译注：CRT亮度是是电压的2.2次幂而人眼相当于2次幂，因此CRT这个缺陷正好能满足人的需要）。
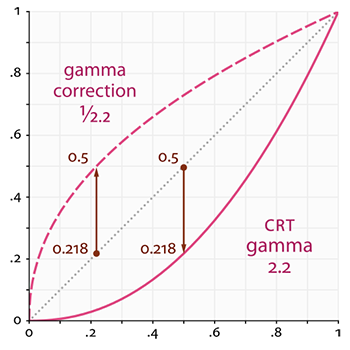
监视器的这个非线性映射的确可以让亮度在我们眼中看起来更好，但当渲染图像时，会产生一个问题：我们在应用中配置的亮度和颜色是基于监视器所看到的，这样所有的配置实际上是非线性的亮度/颜色配置。请看下图：
![](http://learnopengl.com/img/advanced-lighting/gamma_correction_gamma_curves.png)
点线代表线性颜色/亮度值（译注：这表示的是理想状态，Gamma为1），实线代表监视器显示的颜色。如果我们把一个点线线性的颜色翻一倍，结果就是这个值的两倍。比如，光的颜色向量L=(0.5, 0.0, 0.0)代表的是暗红色。如果我们在线性空间中把它翻倍，就会变成(1.0, 0.0, 0.0)，就像你在图中看到的那样。然而，由于我们定义的颜色仍然需要输出的监视器上，监视器上显示的实际颜色就会是(0.218, 0.0, 0.0)。在这儿问题就出现了：当我们将理想中直线上的那个暗红色翻一倍时，在监视器上实际上亮度翻了4.5倍以上！
直到现在，我们还一直假设我们所有的工作都是在线性空间中进行的（译注：Gamma为1），但最终还是要把所哟的颜色输出到监视器上，所以我们配置的所有颜色和光照变量从物理角度来看都是不正确的，在我们的监视器上很少能够正确地显示。出于这个原因，我们（以及艺术家）通常将光照值设置得比本来更亮一些（由于监视器会将其亮度显示的更暗一些），如果不是这样，在线性空间里计算出来的光照就会不正确。同时，还要记住，监视器所显示出来的图像和线性图像的最小亮度是相同的，它们最大的亮度也是相同的；只是中间亮度部分会被压暗。
因为所有中间亮度都是线性空间计算出来的（译注：计算的时候假设Gamma为1）监视器显以后，实际上都会不正确。当使用更高级的光照算法时，这个问题会变得越来越明显，你可以看看下图：
![](http://learnopengl.com/img/advanced-lighting/gamma_correction_example.png)
Gamma校正
Gamma校正的思路是在最终的颜色输出上应用监视器Gamma的倒数。回头看前面的Gamma曲线图，你会有一个短划线，它是监视器Gamma曲线的翻转曲线。我们在颜色显示到监视器的时候把每个颜色输出都加上这个翻转的Gamma曲线，这样应用了监视器Gamma以后最终的颜色将会变为线性的。我们所得到的中间色调就会更亮，所以虽然监视器使它们变暗，但是我们又将其平衡回来了。
我们来看另一个例子。还是那个暗红色（0.5, 0.0, 0.0）。在将颜色显示到监视器之前，我们先对颜色应用Gamma校正曲线。线性的颜色显示在监视器上相当于降低了2.2次幂的亮度，所以倒数就是1/2.2次幂。Gamma校正后的暗红色就会成为
```math
{(0.5, 0.0, 0.0)}^{1/2.2} = {(0.5, 0.0, 0.0)}^{0.45}={(0.73, 0.0, 0.0)}
```
校正后的颜色接着被发送给监视器，最终显示出来的颜色是
```math
(0.73, 0.0, 0.0)^{2.2} = (0.5, 0.0, 0.0)
```
你会发现使用了Gamma校正，监视器最终会显示出我们在应用中设置的那种线性的颜色。
!!! Important
2.2通常是是大多数显示设备的大概平均gamma值。基于gamma2.2的颜色空间叫做sRGB颜色空间。每个监视器的gamma曲线都有所不同，但是gamma2.2在大多数监视器上表现都不错。出于这个原因，游戏经常都会为玩家提供改变游戏gamma设置的选项，以适应每个监视器（译注：现在Gamma2.2相当于一个标准，后文中你会看到。但现在你可能会问，前面不是说Gamma2.2看起来不是正好适合人眼么，为何还需要校正。这是因为你在程序中设置的颜色，比如光照都是基于线性Gamma，即Gamma1，所以你理想中的亮度和实际表达出的不一样，如果要表达出你理想中的亮度就要对这个光照进行校正）。
有两种在你的场景中应用gamma校正的方式：
使用OpenGL内建的sRGB帧缓冲。
自己在像素着色器中进行gamma校正。
第一个选项也许是最简单的方式，但是我们也会丧失一些控制权。开启GL_FRAMEBUFFER_SRGB，可以告诉OpenGL每个后续的绘制命令里，在颜色储存到颜色缓冲之前先校正sRGB颜色。sRGB这个颜色空间大致对应于gamma2.2，它也是家用设备的一个标准。开启GL_FRAMEBUFFER_SRGB以后，每次像素着色器运行后续帧缓冲，OpenGL将自动执行gamma校正，包括默认帧缓冲。
开启GL_FRAMEBUFFER_SRGB简单的调用glEnable就行：
```c++
glEnable(GL_FRAMEBUFFER_SRGB);
```
自此，你渲染的图像就被进行gamma校正处理，你不需要做任何事情硬件就帮你处理了。有时候，你应该记得这个建议：gamma校正将把线性颜色空间转变为非线性空间，所以在最后一步进行gamma校正是极其重要的。如果你在最后输出之前就进行gamma校正，所有的后续操作都是在操作不正确的颜色值。例如，如果你使用多个怎还冲，你可能打算让两个帧缓冲之间传递的中间结果仍然保持线性空间颜色，只是给发送给监视器的最后的那个帧缓冲应用gamma校正。
第二个方法稍微复杂点，但同时也是我们对gamma操作有完全的控制权。我们在每个相关像素着色器运行的最后应用gamma校正，所以在发送到帧缓冲前，颜色就被校正了。
```c++
void main()
{
// do super fancy lighting
[...]
// apply gamma correction
float gamma = 2.2;
fragColor.rgb = pow(fragColor.rgb, vec3(1.0/gamma));
}
```
最后一行代码，将fragColor的每个颜色元素应用有一个1.0/gamma的幂运算，校正像素着色器的颜色输出。
这个方法有个问题就是为了保持一致，你必须在像素着色器里加上这个gamma校正，所以如果你有很多像素着色器，它们可能分别用于不同物体，那么你就必须在每个着色器里都加上gamma校正了。一个更简单的方案是在你的渲染循环中引入后处理阶段，在后处理四边形上应用gamma校正，这样你只要做一次就好了。
这些单行代码代表了gamma校正的实现。不太令人印象深刻，但当你进行gamma校正的时候有一些额外的事情别忘了考虑。
#### sRGB纹理
因为监视器总是在sRGB空间中显示应用了gamma的颜色，无论什么时候当你在计算机上绘制、编辑或者画出一个图片的时候，你所选的颜色都是根据你在监视器上看到的那种。这实际意味着所有你创建或编辑的图片并不是在线性空间，而是在sRGB空间中（译注：sRGB空间定义的gamma接近于2.2），假如在你的屏幕上对暗红色翻一倍，便是根据你所感知到的亮度进行的，并不等于将红色元素加倍。
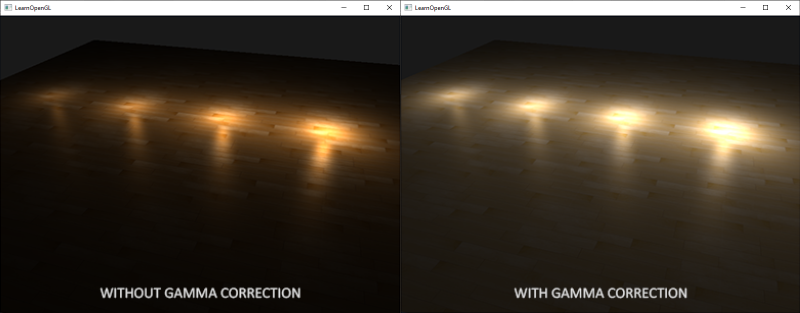
结果就是纹理编辑者，所创建的所有纹理都是在sRGB空间中的纹理，所以如果我们在渲染应用中使用这些纹理，我们必须考虑到这点。在我们应用gamma校正之前，这不是个问题，因为纹理在sRGB空间创建和展示，同样我们还是在sRGB空间中使用，从而不必gamma校正纹理显示也没问题。然而，现在我们是把所有东西都放在线性空间中展示的，纹理颜色就会变坏，如下图展示的那样：
![](http://learnopengl.com/img/advanced-lighting/gamma_correction_srgbtextures.png)
纹理图像实在太亮了，发生这种情况是因为，它们实际上进行了两次gamma校正！想一想，当我们基于监视器上看到的情况创建一个图像，我们就已经对颜色值进行了gamma校正，所以再次显示在监视器上就没错。由于我们在渲染中又进行了一次gamma校正，图片就实在太亮了。
为了修复这个问题，我们得确保纹理制作者是在线性空间中进行创作的。但是，由于大多数纹理制作者并不知道什么是gamma校正，并且在sRGB空间中进行创作更简单，这也许不是一个好办法。
另一个解决方案是重校，或把这些sRGB纹理在进行任何颜色值的计算前变回线性空间。我们可以这样做：
```c++
float gamma = 2.2;
vec3 diffuseColor = pow(texture(diffuse, texCoords).rgb, vec3(gamma));
```
为每个sRGB空间的纹理做这件事非常烦人。幸好，OpenGL给我们提供了另一个方案来解决我们的麻烦，这就是GL_SRGB和GL_SRGB_ALPHA内部纹理格式。
如果我们在OpenGL中创建了一个纹理，把它指定为以上两种sRGB纹理格式其中之一，OpenGL将自动把颜色校正到线性空间中，这样我们所使用的所有颜色值都是在线性空间中的了。我们可以这样把一个纹理指定为一个sRGB纹理：
```c++
glTexImage2D(GL_TEXTURE_2D, 0, GL_SRGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, image);
```
如果你还打算在你的纹理中引入alpha元素，必究必须将纹理的内部格式指定为GL_SRGB_ALPHA。
因为不是所有纹理都是在sRGB空间中的所以当你把纹理指定为sRGB纹理时要格外小心。比如diffuse纹理，这种为物体上色的纹理几乎都是在sRGB空间中的。而为了获取光照参数的纹理，像specular贴图和法线贴图几乎都在线性空间中，所以如果你把它们也配置为sRGB纹理的话，光照就坏掉了。指定sRGB纹理时要当心。
将diffuse纹理定义为sRGB纹理之后，你将获得你所期望的视觉输出，但这次每个物体都会只进行一次gamma校正。
## 衰减
在使用了gamma校正之后，另一个不同之处是光照衰减。真实的物理世界中，光照的衰减和光源的距离的平方成反比。
```c++
float attenuation = 1.0 / (distance * distance);
```
然而，当我们使用这个衰减公式的时候，衰减效果总是过于强烈，光只能照亮一小圈，看起来并不真实。出于这个原因，我们使用在基本光照教程中所讨论的那种衰减方程，它给了我们更大的控制权，此外我们还可以使用双曲线函数：
```c++
float attenuation = 1.0 / distance;
```
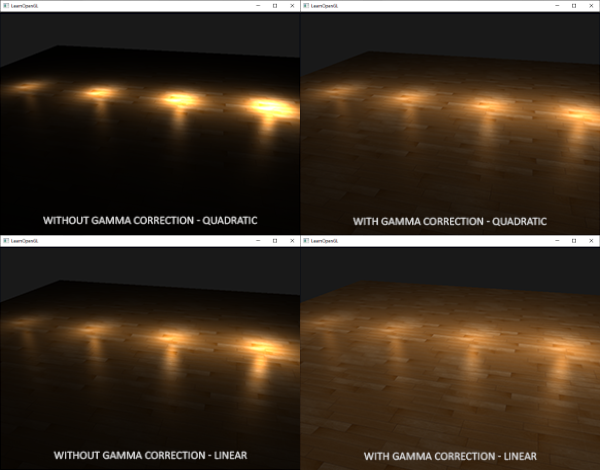
双曲线比使用二次函数变体在不用gamma校正的时候看起来更真实，不过但我们开启gamma校正以后线性衰减看起来太弱了，符合物理的二次函数突然出现了更好的效果。下图显示了其中的不同：
![](http://learnopengl.com/img/advanced-lighting/gamma_correction_attenuation.png)
这种差异产生的原因是，光的衰减方程改变了亮度值，而且屏幕上显示出来的也不是线性空间，在监视器上效果最好的衰减方程，并不是符合物理的。想想平方衰减方程，如果我们使用这个方程，而且不进行gamma校正，显示在监视器上的衰减方程实际上将变成：
```math
{(1.0 / distance2)}^{2.2}
```
若不进行gamma校正，将产生更强烈的衰减。这也解释了为什么双曲线不用gamma校正时看起来更真实，因为它实际变成了
```math
{(1.0 / distance)}^{2.2} = 1.0 / distance^{2.2}
```
这和物理公式是很相似的。
!!! Important
我们在基础光照教程中讨论的更高级的那个衰减方程在有gamma校正的场景中也仍然有用，因为它可以让我们对衰减拥有更多准确的控制权（不过，在进行gamma校正的场景中当然需要不同的参数）。
我创建的这个简单的demo场景，你可以在这里找到源码以及顶点和像素着色器。按下空格就能在有gamma校正和无gamma校正的场景进行切换，两个场景使用的是相同的纹理和衰减。这不是效果最好的demo，不过它能展示出如何应用所有这些技术。
总而言之，gamma校正使你可以在线性空间中进行操作。因为线性空间更符合物理世界，大多数物理公式现在都可以获得较好效果，比如真实的光的衰减。你的光照越真实，使用gamma校正获得漂亮的效果就越容易。这也正是为什么当引进gamma校正时，建议只去调整光照参数的原因。
### 附加资源
[cambridgeincolour.com](http://www.cambridgeincolour.com/tutorials/gamma-correction.htm):更多关于gamma和gamma校正的内容。
[wolfire.com](http://blog.wolfire.com/2010/02/Gamma-correct-lighting): David Rosen关于在渲染领域使用gamma校正的好处。
[renderwonk.com](http://renderwonk.com/blog/index.php/archive/adventures-with-gamma-correct-rendering/): 一些额外的实践上的思考。

558
docs/05 Advanced Lighting/03 Shadows/01 Shadow Mapping.md
View File

@@ -1,558 +0,0 @@
## 阴影映射(Shadow Mapping)
本文作者JoeyDeVries，由Django翻译自[http://learnopengl.com](http://learnopengl.com)
原文 | [Shadow Mapping](http://learnopengl.com/#!Advanced-Lighting/Shadows/Shadow-Mapping)
---|---
作者 | JoeyDeVries
翻译 | [Django](http://bullteacher.com/)
校对 | gjy_1992
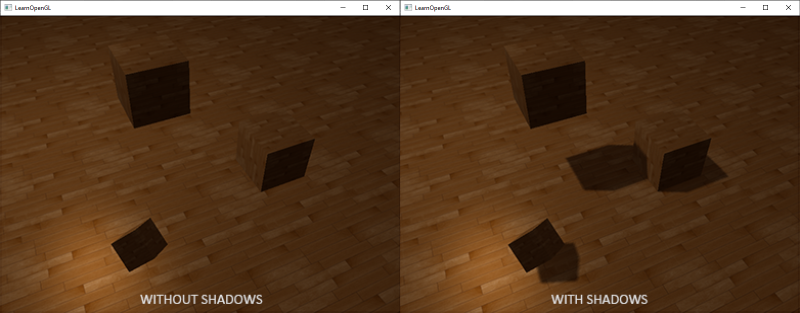
阴影是光线被阻挡的结果；当一个光源的光线由于其他物体的阻挡不能够达到一个物体的表面的时候，那么这个物体就在阴影中了。阴影能够使场景看起来真实得多，并且可以让观察者获得物体之间的空间位置关系。场景和物体的深度感因此能够得到极大提升，下图展示了有阴影和没有阴影的情况下的不同：
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_with_without.png)
你可以看到，有阴影的时候你能更容易地区分出物体之间的位置关系，例如，当使用阴影的时候浮在地板上的立方体的事实更加清晰。
阴影还是比较不好实现的，因为当前实时渲染领域还没找到一种完美的阴影算法。目前有几种近似阴影技术，但它们都有自己的弱点和不足，这点我们必须要考虑到。
视频游戏中较多使用的一种技术是阴影贴图（shadow mapping），效果不错，而且相对容易实现。阴影贴图并不难以理解，性能也不会太低，而且非常容易扩展成更高级的算法（比如 [Omnidirectional Shadow Maps](http://learnopengl.com/#!Advanced-Lighting/Shadows/Point-Shadows)和 [Cascaded Shadow Maps](http://learnopengl.com/#!Advanced-Lighting/Shadows/CSM)）。
### 阴影映射
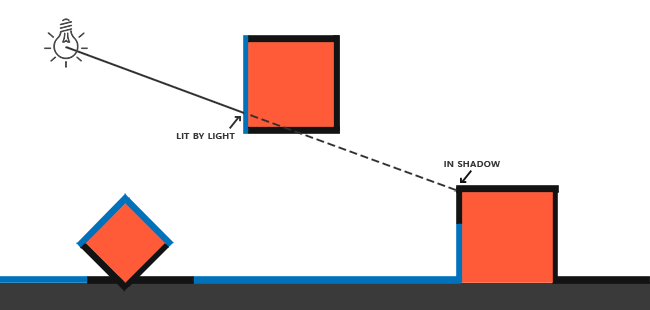
阴影映射背后的思路非常简单：我们以光的位置为视角进行渲染，我们能看到的东西都将被点亮，看不见的一定是在阴影之中了。假设有一个地板，在光源和它之间有一个大盒子。由于光源处向光线方向看去，可以看到这个盒子，但看不到地板的一部分，这部分就应该在阴影中了。
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_theory.png)
这里的所有蓝线代表光源可以看到的fragment。黑线代表被遮挡的fragment：它们应该渲染为带阴影的。如果我们绘制一条从光源出发，到达最右边盒子上的一个片元上的线段或射线，那么射线将先击中悬浮的盒子，随后才会到达最右侧的盒子。结果就是悬浮的盒子被照亮，而最右侧的盒子将处于阴影之中。
我们希望得到射线第一次击中的那个物体，然后用这个最近点和射线上其他点进行对比。然后我们将测试一下看看射线上的其他点是否比最近点更远，如果是的话，这个点就在阴影中。对从光源发出的射线上的成千上万个点进行遍历是个极端消耗性能的举措，实时渲染上基本不可取。我们可以采取相似举措，不用投射出光的射线。我们所使用的是非常熟悉的东西：深度缓冲。
你可能记得在[深度测试](http://learnopengl.com/#!Advanced-OpenGL/Depth-testing)教程中，在深度缓冲里的一个值是摄像机视角下，对应于一个片元的一个0到1之间的深度值。如果我们从光源的透视图来渲染场景，并把深度值的结果储存到纹理中会怎样？通过这种方式，我们就能对光源的透视图所见的最近的深度值进行采样。最终，深度值就会显示从光源的透视图下见到的第一个片元了。我们管储存在纹理中的所有这些深度值，叫做深度贴图（depth map）或阴影贴图。
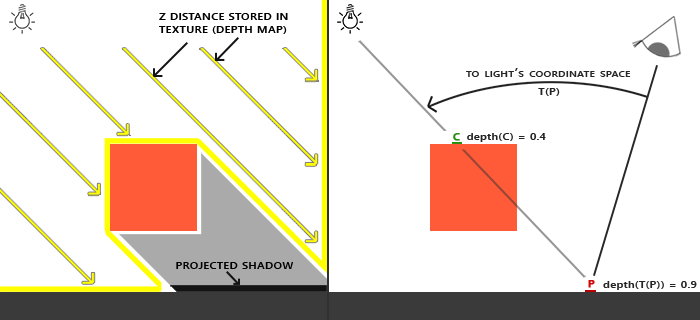
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_theory_spaces.png)
左侧的图片展示了一个定向光源（所有光线都是平行的）在立方体下的表面投射的阴影。通过储存到深度贴图中的深度值，我们就能找到最近点，用以决定片元是否在阴影中。我们使用一个来自光源的视图和投影矩阵来渲染场景就能创建一个深度贴图。这个投影和视图矩阵结合在一起成为一个T变换，它可以将任何三维位置转变到光源的可见坐标空间。
!!! Important
定向光并没有位置，因为它被规定为无穷远。然而，为了实现阴影贴图，我们得从一个光的透视图渲染场景，这样就得在光的方向的某一点上渲染场景。
在右边的图中我们显示出同样的平行光和观察者。我们渲染一个点P处的片元，需要决定它是否在阴影中。我们先得使用T把P变换到光源的坐标空间里。既然点P是从光的透视图中看到的，它的z坐标就对应于它的深度，例子中这个值是0.9。使用点P在光源的坐标空间的坐标，我们可以索引深度贴图，来获得从光的视角中最近的可见深度，结果是点C，最近的深度是0.4。因为索引深度贴图的结果是一个小于点P的深度，我们可以断定P被挡住了，它在阴影中了。
深度映射由两个步骤组成：首先，我们渲染深度贴图，然后我们像往常一样渲染场景，使用生成的深度贴图来计算片元是否在阴影之中。听起来有点复杂，但随着我们一步一步地讲解这个技术，就能理解了。
### 深度贴图（depth map）
第一步我们需要生成一张深度贴图。深度贴图是从光的透视图里渲染的深度纹理，用它计算阴影。因为我们需要将场景的渲染结果储存到一个纹理中，我们将再次需要帧缓冲。
首先，我们要为渲染的深度贴图创建一个帧缓冲对象：
```c++
GLuint depthMapFBO;
glGenFramebuffers(1, &depthMapFBO);
```
然后，创建一个2D纹理，提供给帧缓冲的深度缓冲使用：
```c++
const GLuint SHADOW_WIDTH = 1024, SHADOW_HEIGHT = 1024;
GLuint depthMap;
glGenTextures(1, &depthMap);
glBindTexture(GL_TEXTURE_2D, depthMap);
glTexImage2D(GL_TEXTURE_2D, 0, GL_DEPTH_COMPONENT,
SHADOW_WIDTH, SHADOW_HEIGHT, 0, GL_DEPTH_COMPONENT, GL_FLOAT, NULL);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
```
生成深度贴图不太复杂。因为我们只关心深度值，我们要把纹理格式指定为GL_DEPTH_COMPONENT。我们还要把纹理的高宽设置为1024：这是深度贴图的解析度。
把我们把生成的深度纹理作为帧缓冲的深度缓冲：
```c++
glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, GL_TEXTURE_2D, depthMap, 0);
glDrawBuffer(GL_NONE);
glReadBuffer(GL_NONE);
glBindFramebuffer(GL_FRAMEBUFFER, 0);
```
我们需要的只是在从光的透视图下渲染场景的时候深度信息，所以颜色缓冲没有用。然而帧缓冲对象不是完全不包含颜色缓冲的，所以我们需要显式告诉OpenGL我们不适用任何颜色数据进行渲染。我们通过将调用glDrawBuffer和glReadBuffer把读和绘制缓冲设置为GL_NONE来做这件事。
合理配置将深度值渲染到纹理的帧缓冲后，我们就可以开始第一步了：生成深度贴图。两个步骤的完整的渲染阶段，看起来有点像这样：
```c++
// 1. 首选渲染深度贴图
glViewport(0, 0, SHADOW_WIDTH, SHADOW_HEIGHT);
glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
glClear(GL_DEPTH_BUFFER_BIT);
ConfigureShaderAndMatrices();
RenderScene();
glBindFramebuffer(GL_FRAMEBUFFER, 0);
// 2. 像往常一样渲染场景，但这次使用深度贴图
glViewport(0, 0, SCR_WIDTH, SCR_HEIGHT);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
ConfigureShaderAndMatrices();
glBindTexture(GL_TEXTURE_2D, depthMap);
RenderScene();
```
这段代码隐去了一些细节，但它表达了阴影映射的基本思路。这里一定要记得调用glViewport。因为阴影贴图经常和我们原来渲染的场景（通常是窗口解析度）有着不同的解析度，我们需要改变视口（viewport）的参数以适应阴影贴图的尺寸。如果我们忘了更新视口参数，最后的深度贴图要么太小要么就不完整。
### 光源空间的变换（light spacce transform）
前面那段代码中一个不清楚的函数是COnfigureShaderAndMatrices。它是用来在第二个步骤确保为每个物体设置了合适的投影和视图矩阵，以及相关的模型矩阵。然而，第一个步骤中，我们从光的位置的视野下使用了不同的投影和视图矩阵来渲染的场景。
因为我们使用的是一个所有光线都平行的定向光。出于这个原因，我们将为光源使用正交投影矩阵，透视图将没有任何变形：
```c++
GLfloat near_plane = 1.0f, far_plane = 7.5f;
glm::mat4 lightProjection = glm::ortho(-10.0f, 10.0f, -10.0f, 10.0f, near_plane, far_plane);
```
这里有个本节教程的demo场景中使用的正交投影矩阵的例子。因为投影矩阵间接决定可视区域的范围，以及哪些东西不会被裁切，你需要保证投影视锥（frustum）的大小，以包含打算在深度贴图中包含的物体。当物体和片元不在深度贴图中时，它们就不会产生阴影。
为了创建一个视图矩阵来变换每个物体，把它们变换到从光源视角可见的空间中，我们将使用glm::lookAt函数；这次从光源的位置看向场景中央。
```c++
glm::mat4 lightView = glm::lookAt(glm::vec(-2.0f, 4.0f, -1.0f), glm::vec3(0.0f), glm::vec3(1.0));
```
二者相结合为我们提供了一个光空间的变换矩阵，它将每个世界空间坐标变换到光源处所见到的那个空间；这正是我们渲染深度贴图所需要的。
```c++
glm::mat4 lightSpaceMatrix = lightProjection * lightView;
```
这个lightSpaceMatrix正是前面我们称为T的那个变换矩阵。有了lightSpaceMatrix只要给shader提供光空间的投影和视图矩阵，我们就能像往常那样渲染场景了。然而，我们只关心深度值，并非所有片元计算都在我们的着色器中进行。为了提升性能，我们将使用一个与之不同但更为简单的着色器来渲染出深度贴图。
### 渲染出深度贴图
当我们以光的透视图进行场景渲染的时候，我们会用一个比较简单的着色器，这个着色器除了把顶点变换到光空间以外，不会做得更多了。这个简单的着色器叫做simpleDepthShader，就是使用下面的这个着色器：
```c++
#version 330 core
layout (location = 0) in vec3 position;
uniform mat4 lightSpaceMatrix;
uniform mat4 model;
void main()
{
gl_Position = lightSpaceMatrix * model * vec4(position, 1.0f);
}
```
这个顶点着色器将一个单独模型的一个顶点，使用lightSpaceMatrix变换到光空间中。
由于我们没有颜色缓冲，最后的片元不需要任何处理，所以我们可以简单地使用一个空像素着色器：
```c++
#version 330 core
void main()
{
// gl_FragDepth = gl_FragCoord.z;
}
```
这个空像素着色器什么也不干，运行完后，深度缓冲会被更新。我们可以取消那行的注释，来显式设置深度，但是这个（指注释掉那行之后）是更有效率的，因为底层无论如何都会默认去设置深度缓冲。
渲染深度缓冲现在成了：
```c++
simpleDepthShader.Use();
glUniformMatrix4fv(lightSpaceMatrixLocation, 1, GL_FALSE, glm::value_ptr(lightSpaceMatrix));
glViewport(0, 0, SHADOW_WIDTH, SHADOW_HEIGHT);
glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
glClear(GL_DEPTH_BUFFER_BIT);
RenderScene(simpleDepthShader);
glBindFramebuffer(GL_FRAMEBUFFER, 0);
```
这里的RenderScene函数的参数是一个着色器程序（shader program），它调用所有相关的绘制函数，并在需要的地方设置相应的模型矩阵。
最后，在光的透视图视角下，很完美地用每个可见片元的最近深度填充了深度缓冲。通过将这个纹理投射到一个2D四边形上（和我们在帧缓冲一节做的后处理过程类似），就能在屏幕上显示出来，我们会获得这样的东西：
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_depth_map.png)
将深度贴图渲染到四边形上的像素着色器：
```c++
#version 330 core
out vec4 color;
in vec2 TexCoords;
uniform sampler2D depthMap;
void main()
{
float depthValue = texture(depthMap, TexCoords).r;
color = vec4(vec3(depthValue), 1.0);
}
```
要注意的是当用透视投影矩阵取代正交投影矩阵来显示深度时，有一些轻微的改动，因为使用透视投影时，深度是非线性的。本节教程的最后，我们会讨论这些不同之处。
你可以在[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/shadow_mapping_depth_map)获得把场景渲染成深度贴图的源码。
### 渲染阴影
正确地生成深度贴图以后我们就可以开始生成阴影了。这段代码在像素着色器中执行，用来检验一个片元是否在阴影之中，不过我们在顶点着色器中进行光空间的变换：
```c++
#version 330 core
layout (location = 0) in vec3 position;
layout (location = 1) in vec3 normal;
layout (location = 2) in vec2 texCoords;
out vec2 TexCoords;
out VS_OUT {
vec3 FragPos;
vec3 Normal;
vec2 TexCoords;
vec4 FragPosLightSpace;
} vs_out;
uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;
uniform mat4 lightSpaceMatrix;
void main()
{
gl_Position = projection * view * model * vec4(position, 1.0f);
vs_out.FragPos = vec3(model * vec4(position, 1.0));
vs_out.Normal = transpose(inverse(mat3(model))) * normal;
vs_out.TexCoords = texCoords;
vs_out.FragPosLightSpace = lightSpaceMatrix * vec4(vs_out.FragPos, 1.0);
}
```
这儿的新的地方是FragPosLightSpace这个输出向量。我们用同一个lightSpaceMatrix，把世界空间顶点位置转换为光空间。顶点着色器传递一个普通的经变换的世界空间顶点位置vs_out.FragPos和一个光空间的vs_out.FragPosLightSpace给像素着色器。
像素着色器使用Blinn-Phong光照模型渲染场景。我们接着计算出一个shadow值，当fragment在阴影中时是1.0，在阴影外是0.0。然后，diffuse和specular颜色会乘以这个阴影元素。由于阴影不会是全黑的（由于散射），我们把ambient分量从乘法中剔除。
```c++
#version 330 core
out vec4 FragColor;
in VS_OUT {
vec3 FragPos;
vec3 Normal;
vec2 TexCoords;
vec4 FragPosLightSpace;
} fs_in;
uniform sampler2D diffuseTexture;
uniform sampler2D shadowMap;
uniform vec3 lightPos;
uniform vec3 viewPos;
float ShadowCalculation(vec4 fragPosLightSpace)
{
[...]
}
void main()
{
vec3 color = texture(diffuseTexture, fs_in.TexCoords).rgb;
vec3 normal = normalize(fs_in.Normal);
vec3 lightColor = vec3(1.0);
// Ambient
vec3 ambient = 0.15 * color;
// Diffuse
vec3 lightDir = normalize(lightPos - fs_in.FragPos);
float diff = max(dot(lightDir, normal), 0.0);
vec3 diffuse = diff * lightColor;
// Specular
vec3 viewDir = normalize(viewPos - fs_in.FragPos);
vec3 reflectDir = reflect(-lightDir, normal);
float spec = 0.0;
vec3 halfwayDir = normalize(lightDir + viewDir);
spec = pow(max(dot(normal, halfwayDir), 0.0), 64.0);
vec3 specular = spec * lightColor;
// 计算阴影
float shadow = ShadowCalculation(fs_in.FragPosLightSpace);
vec3 lighting = (ambient + (1.0 - shadow) * (diffuse + specular)) * color;
FragColor = vec4(lighting, 1.0f);
}
```
像素着色器大部分是从高级光照教程中复制过来，只不过加上了个阴影计算。我们声明一个shadowCalculation函数，用它计算阴影。像素着色器的最后，我们我们把diffuse和specular乘以(1-阴影元素)，这表示这个片元有多大成分不在阴影中。这个像素着色器还需要两个额外输入，一个是光空间的片元位置和第一个渲染阶段得到的深度贴图。
首先要检查一个片元是否在阴影中，把光空间片元位置转换为裁切空间的标准化设备坐标。当我们在顶点着色器输出一个裁切空间顶点位置到gl_Position时，OpenGL自动进行一个透视除法，将裁切空间坐标的范围-w到w转为-1到1，这要将x、y、z元素除以向量的w元素来实现。由于裁切空间的FragPosLightSpace并不会通过gl_Position传到像素着色器里，我们必须自己做透视除法：
```c++
float ShadowCalculation(vec4 fragPosLightSpace)
{
// 执行透视除法
vec3 projCoords = fragPosLightSpace.xyz / fragPosLightSpace.w;
[...]
}
```
返回了片元在光空间的-1到1的范围。
!!! Important
当使用正交投影矩阵，顶点w元素仍保持不变，所以这一步实际上毫无意义。可是，当使用透视投影的时候就是必须的了，所以为了保证在两种投影矩阵下都有效就得留着这行。
因为来自深度贴图的深度在0到1的范围，我们也打算使用projCoords从深度贴图中去采样，所以我们将NDC坐标变换为0到1的范围：
（译者注：这里的意思是，上面的projCoords的xyz分量都是[-1,1]（下面会指出这对于远平面之类的点才成立），而为了和深度贴图的深度相比较，z分量需要变换到[0,1]；为了作为从深度贴图中采样的坐标，xy分量也需要变换到[0,1]。所以整个projCoords向量都需要变换到[0,1]范围。）
```c++
projCoords = projCoords * 0.5 + 0.5;
```
有了这些投影坐标，我们就能从深度贴图中采样得到0到1的结果，从第一个渲染阶段的projCoords坐标直接对应于变换过的NDC坐标。我们将得到光的位置视野下最近的深度：
```c++
float closestDepth = texture(shadowMap, projCoords.xy).r;
```
为了得到片元的当前深度，我们简单获取投影向量的z坐标，它等于来自光的透视视角的片元的深度。
```c++
float currentDepth = projCoords.z;
```
实际的对比就是简单检查currentDepth是否高于closetDepth，如果是，那么片元就在阴影中。
```c++
float shadow = currentDepth > closestDepth ? 1.0 : 0.0;
```
完整的shadowCalculation函数是这样的：
```c++
float ShadowCalculation(vec4 fragPosLightSpace)
{
// 执行透视除法
vec3 projCoords = fragPosLightSpace.xyz / fragPosLightSpace.w;
// 变换到[0,1]的范围
projCoords = projCoords * 0.5 + 0.5;
// 取得最近点的深度(使用[0,1]范围下的fragPosLight当坐标)
float closestDepth = texture(shadowMap, projCoords.xy).r;
// 取得当前片元在光源视角下的深度
float currentDepth = projCoords.z;
// 检查当前片元是否在阴影中
float shadow = currentDepth > closestDepth ? 1.0 : 0.0;
return shadow;
}
```
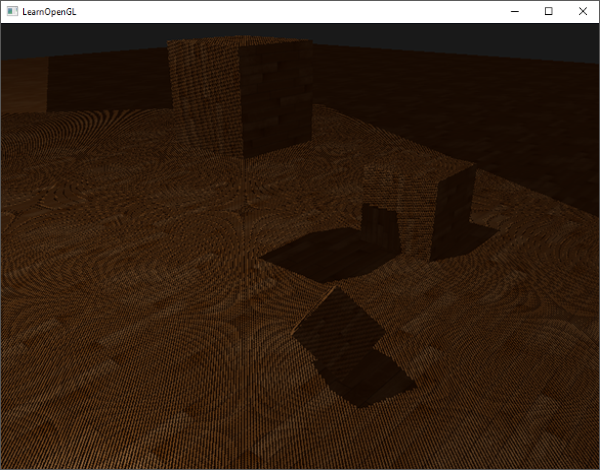
激活这个着色器，绑定合适的纹理，激活第二个渲染阶段默认的投影以及视图矩阵，结果如下图所示：
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_shadows.png)
如果你做对了，你会看到地板和上有立方体的阴影。你可以从这里找到demo程序的[源码](http://learnopengl.com/code_viewer.php?code=advanced-lighting/shadow_mapping_shadows)。
### 改进阴影贴图
我们试图让阴影映射工作，但是你也看到了，阴影映射还是有点不真实，我们修复它才能获得更好的效果，这是下面的部分所关注的焦点。
#### 阴影失真（shadow acne）
前面的图片中明显有不对的地方。放大看会发现明显的线条样式：
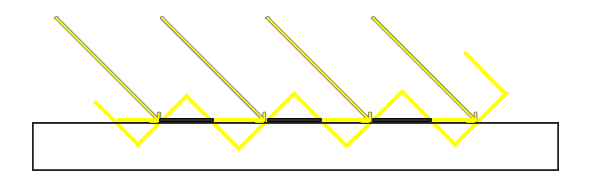
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_acne.png)
我们可以看到地板四边形渲染出很大一块交替黑线。这种阴影贴图的不真实感叫做阴影失真，下图解释了成因：
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_acne_diagram.png)
因为阴影贴图受限于解析度，在距离光源比较远的情况下，多个片元可能从深度贴图的同一个值中去采样。图片每个斜坡代表深度贴图一个单独的纹理像素。你可以看到，多个片元从同一个深度值进行采样。
虽然很多时候没问题，但是当光源以一个角度朝向表面的时候就会出问题，这种情况下深度贴图也是从一个角度下进行渲染的。多个片元就会从同一个斜坡的深度纹理像素中采样，有些在地板上面，有些在地板下面；这样我们所得到的阴影就有了差异。因为这个，有些片元被认为是在阴影之中，有些不在，由此产生了图片中的条纹样式。
我们可以用一个叫做**阴影偏移**（shadow bias）的技巧来解决这个问题，我们简单的对表面的深度（或深度贴图）应用一个偏移量，这样片元就不会被错误地认为在表面之下了。
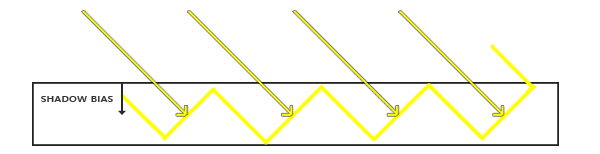
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_acne_bias.png)
使用了偏移量后，所有采样点都获得了比表面深度更小的深度值，这样整个表面就正确地被照亮，没有任何阴影。我们可以这样实现这个偏移：
```c++
float bias = 0.005;
float shadow = currentDepth - bias > closestDepth ? 1.0 : 0.0;
```
一个0.005的偏移就能帮到很大的忙，但是有些表面坡度很大，仍然会产生阴影失真。有一个更加可靠的办法能够根据表面朝向光线的角度更改偏移量：使用点乘：
```c++
float bias = max(0.05 * (1.0 - dot(normal, lightDir)), 0.005);
```
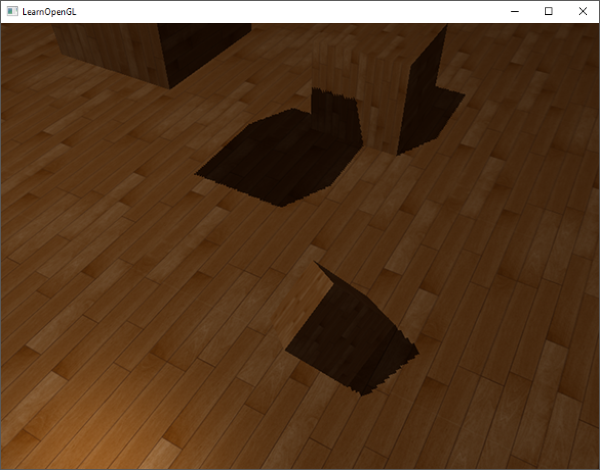
这里我们有一个偏移量的最大值0.05，和一个最小值0.005，它们是基于表面法线和光照方向的。这样像地板这样的表面几乎与光源垂直，得到的偏移就很小，而比如立方体的侧面这种表面得到的偏移就更大。下图展示了同一个场景，但使用了阴影偏移，效果的确更好：
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_with_bias.png)
选用正确的偏移数值，在不同的场景中需要一些像这样的轻微调校，但大多情况下，实际上就是增加偏移量直到所有失真都被移除的问题。
#### 悬浮
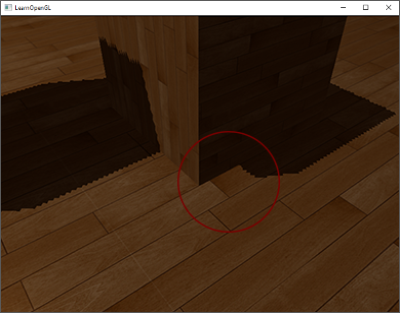
使用阴影偏移的一个缺点是你对物体的实际深度应用了平移。偏移有可能足够大，以至于可以看出阴影相对实际物体位置的偏移，你可以从下图看到这个现象（这是一个夸张的偏移值）：
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_peter_panning.png)
这个阴影失真叫做Peter panning，因为物体看起来轻轻悬浮在表面之上（译注Peter Pan就是童话彼得潘，而panning有平移、悬浮之意，而且彼得潘是个会飞的男孩…）。我们可以使用一个叫技巧解决大部分的Peter panning问题：当渲染深度贴图时候使用正面剔除（front face culling）你也许记得在面剔除教程中OpenGL默认是背面剔除。我们要告诉OpenGL我们要剔除正面。
因为我们只需要深度贴图的深度值，对于实体物体无论我们用它们的正面还是背面都没问题。使用背面深度不会有错误，因为阴影在物体内部有错误我们也看不见。
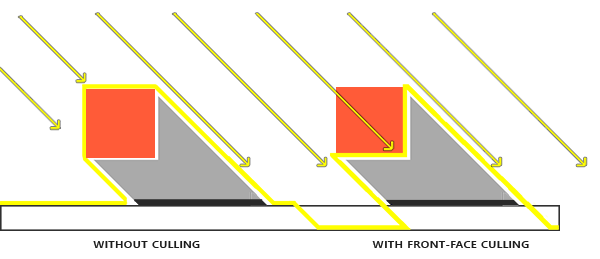
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_culling.png)
为了修复peter游移，我们要进行正面剔除，先必须开启GL_CULL_FACE：
```c++
glCullFace(GL_FRONT);
RenderSceneToDepthMap();
glCullFace(GL_BACK); // 不要忘记设回原先的culling face
```
这十分有效地解决了peter panning的问题，但只针对实体物体，内部不会对外开口。我们的场景中，在立方体上工作的很好，但在地板上无效，因为正面剔除完全移除了地板。地面是一个单独的平面，不会被完全剔除。如果有人打算使用这个技巧解决peter panning必须考虑到只有剔除物体的正面才有意义。
另一个要考虑到的地方是接近阴影的物体仍然会出现不正确的效果。必须考虑到何时使用正面剔除对物体才有意义。不过使用普通的偏移值通常就能避免peter panning。
#### 采样超出
无论你喜不喜欢还有一个视觉差异，就是光的视锥不可见的区域一律被认为是处于阴影中，不管它真的处于阴影之中。出现这个状况是因为超出光的视锥的投影坐标比1.0大，这样采样的深度纹理就会超出他默认的0到1的范围。根据纹理环绕方式，我们将会得到不正确的深度结果，它不是基于真实的来自光源的深度值。
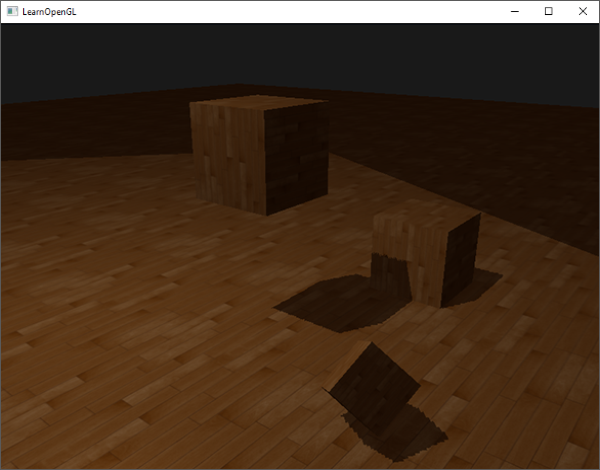
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_outside_frustum.png)
你可以在图中看到，光照有一个区域，超出该区域就成为了阴影；这个区域实际上代表着深度贴图的大小，这个贴图投影到了地板上。发生这种情况的原因是我们之前将深度贴图的环绕方式设置成了GL_REPEAT。
我们宁可让所有超出深度贴图的坐标的深度范围是1.0，这样超出的坐标将永远不在阴影之中。我们可以储存一个边框颜色，然后把深度贴图的纹理环绕选项设置为GL_CLAMP_TO_BORDER：
```c++
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_BORDER);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_BORDER);
GLfloat borderColor[] = { 1.0, 1.0, 1.0, 1.0 };
glTexParameterfv(GL_TEXTURE_2D, GL_TEXTURE_BORDER_COLOR, borderColor);
```
现在如果我们采样深度贴图0到1坐标范围以外的区域，纹理函数总会返回一个1.0的深度值，阴影值为0.0。结果看起来会更真实：
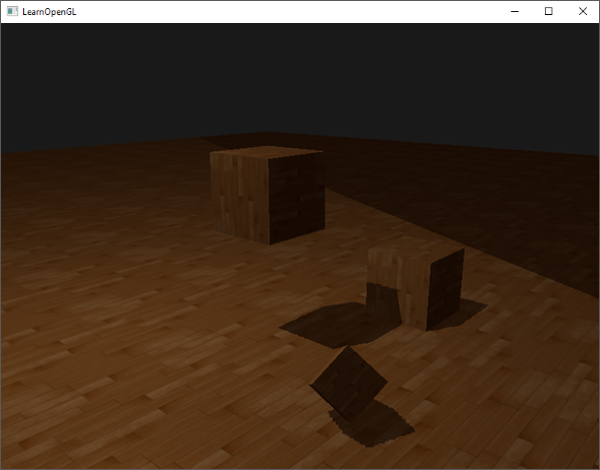
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_clamp_edge.png)
仍有一部分是黑暗区域。那里的坐标超出了光的正交视锥的远平面。你可以看到这片黑色区域总是出现在光源视锥的极远处。
当一个点比光的远平面还要远时，它的投影坐标的z坐标大于1.0。这种情况下，GL_CLAMP_TO_BORDER环绕方式不起作用，因为我们把坐标的z元素和深度贴图的值进行了对比；它总是为大于1.0的z返回true。
解决这个问题也很简单，我们简单的强制把shadow的值设为0.0，不管投影向量的z坐标是否大于1.0：
```c++
float ShadowCalculation(vec4 fragPosLightSpace)
{
[...]
if(projCoords.z > 1.0)
shadow = 0.0;
return shadow;
}
```
检查远平面，并将深度贴图限制为一个手工指定的边界颜色，就能解决深度贴图采样超出的问题，我们最终会得到下面我们所追求的效果：
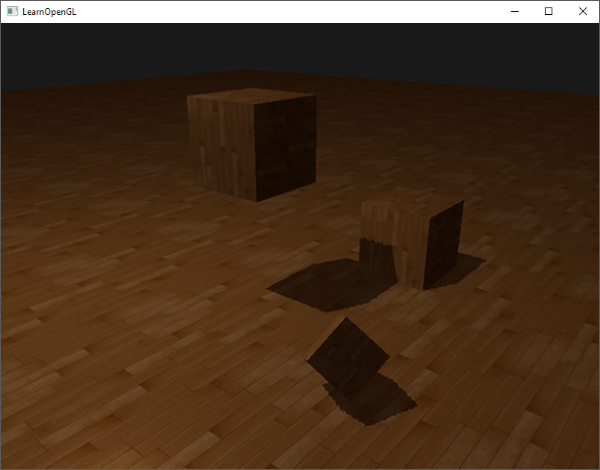
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_over_sampling_fixed.png)
这些结果意味着，只有在深度贴图范围以内的被投影的fragment坐标才有阴影，所以任何超出范围的都将会没有阴影。由于在游戏中通常这只发生在远处，就会比我们之前的那个明显的黑色区域效果更真实。
#### PCF
阴影现在已经附着到场景中了，不过这仍不是我们想要的。如果你放大看阴影，阴影映射对解析度的依赖很快变得很明显。
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_zoom.png)
因为深度贴图有一个固定的解析度，多个片元对应于一个纹理像素。结果就是多个片元会从深度贴图的同一个深度值进行采样，这几个片元便得到的是同一个阴影，这就会产生锯齿边。
你可以通过增加深度贴图解析度的方式来降低锯齿块，也可以尝试尽可能的让光的视锥接近场景。
另一个（并不完整的）解决方案叫做PCF（percentage-closer filtering），这是一种多个不同过滤方式的组合，它产生柔和阴影，使它们出现更少的锯齿块和硬边。核心思想是从深度贴图中多次采样，每一次采样的纹理坐标都稍有不同。每个独立的样本可能在也可能不再阴影中。所有的次生结果接着结合在一起，进行平均化，我们就得到了柔和阴影。
一个简单的PCF的实现是简单的从纹理像素四周对深度贴图采样，然后把结果平均起来：
```c++
float shadow = 0.0;
vec2 texelSize = 1.0 / textureSize(shadowMap, 0);
for(int x = -1; x <= 1; ++x)
{
for(int y = -1; y <= 1; ++y)
{
float pcfDepth = texture(shadowMap, projCoords.xy + vec2(x, y) * texelSize).r;
shadow += currentDepth - bias > pcfDepth ? 1.0 : 0.0;
}
}
shadow /= 9.0;
```
这个textureSize返回一个给定采样器纹理的0级mipmap的vec2类型的宽和高。用1除以它返回一个单独纹理像素的大小，我们用以对纹理坐标进行偏移，确保每个新样本，来自不同的深度值。这里我们采样得到9个值，它们在投影坐标的x和y值的周围，为阴影阻挡进行测试，并最终通过样本的总数目将结果平均化。
使用更多的样本，更改texelSize变量，你就可以增加阴影的柔和程度。下面你可以看到应用了PCF的阴影：
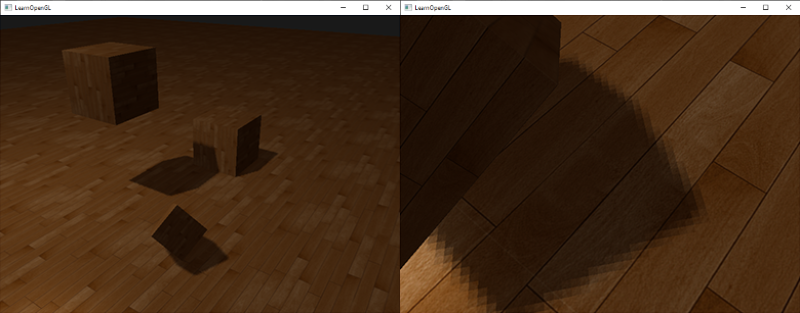
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_soft_shadows.png)
从稍微远一点的距离看去，阴影效果好多了，也不那么生硬了。如果你放大，仍会看到阴影贴图解析度的不真实感，但通常对于大多数应用来说效果已经很好了。
你可以从[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/shadow_mapping)找到这个例子的全部源码和第二个阶段的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/shadow_mapping&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/shadow_mapping&type=fragment)着色器。
实际上PCF还有更多的内容，以及很多技术要点需要考虑以提升柔和阴影的效果，但处于本章内容长度考虑，我们将留在以后讨论。
### 正交 vs 投影
在渲染深度贴图的时候，正交和投影矩阵之间有所不同。正交投影矩阵并不会将场景用透视图进行变形，所有视线/光线都是平行的，这使它对于定向光来说是个很好的投影矩阵。然而透视投影矩阵，会将所有顶点根据透视关系进行变形，结果因此而不同。下图展示了两种投影方式所产生的不同阴影区域：
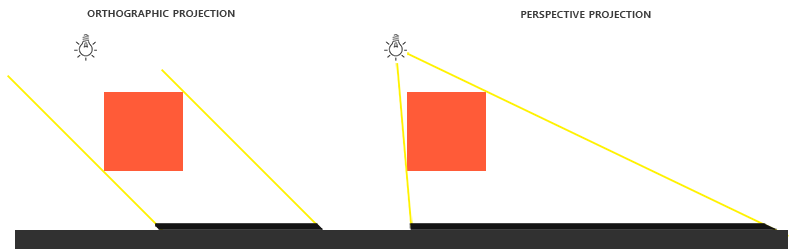
![](http://learnopengl.com/img/advanced-lighting/shadow_mapping_projection.png)
透视投影对于光源来说更合理，不像定向光，它是有自己的位置的。透视投影因此更经常用在点光源和聚光灯上，而正交投影经常用在定向光上。
另一个细微差别是，透视投影矩阵，将深度缓冲视觉化经常会得到一个几乎全白的结果。发生这个是因为透视投影下，深度变成了非线性的深度值，它的大多数可辨范围接近于近平面。为了可以像使用正交投影一样合适的观察到深度值，你必须先讲过非线性深度值转变为线性的，我们在深度测试教程中已经讨论过。
```c++
#version 330 core
out vec4 color;
in vec2 TexCoords;
uniform sampler2D depthMap;
uniform float near_plane;
uniform float far_plane;
float LinearizeDepth(float depth)
{
float z = depth * 2.0 - 1.0; // Back to NDC
return (2.0 * near_plane * far_plane) / (far_plane + near_plane - z * (far_plane - near_plane));
}
void main()
{
float depthValue = texture(depthMap, TexCoords).r;
color = vec4(vec3(LinearizeDepth(depthValue) / far_plane), 1.0); // perspective
// color = vec4(vec3(depthValue), 1.0); // orthographic
}
```
这个深度值与我们见到的用正交投影的很相似。需要注意的是，这个只适用于调试；正交或投影矩阵的深度检查仍然保持原样，因为相关的深度并没有改变。
### 附加资源
[Tutorial 16 : Shadow](http://www.opengl-tutorial.org/intermediate-tutorials/tutorial-16-shadow-mapping/)
[mapping：opengl-tutorial.org](http://ogldev.atspace.co.uk/www/tutorial23/tutorial23.html) 提供的类似的阴影映射教程，里面有一些额外的解释。
[Shadow Mapping – Part 1：ogldev](http://ogldev.atspace.co.uk/www/tutorial23/tutorial23.html)提供的另一个阴影映射教程。
[How Shadow Mapping Works](https://www.youtube.com/watch?v=EsccgeUpdsM)：的一个第三方YouTube视频教程，里面解释了阴影映射及其实现。
[Common Techniques to Improve Shadow Depth Maps](https://msdn.microsoft.com/en-us/library/windows/desktop/ee416324%28v=vs.85%29.aspx)：微软的一篇好文章，其中理出了很多提升阴影贴图质量的技术。

481
docs/05 Advanced Lighting/03 Shadows/02 Point Shadows.md
View File

@@ -1,481 +0,0 @@
本文作者JoeyDeVries，由Django翻译自[http://learnopengl.com](http://learnopengl.com)
## 点光源阴影(Shadow Mapping)
上个教程我们学到了如何使用阴影映射技术创建动态阴影。效果不错，但它只适合定向光，因为阴影只是在单一定向光源下生成的。所以它也叫定向阴影映射，深度（阴影）贴图生成自定向光的视角。
!!! Important
本节我们的焦点是在各种方向生成动态阴影。这个技术可以适用于点光源，生成所有方向上的阴影。
这个技术叫做点光阴影，过去的名字是万向阴影贴图（omnidirectional shadow maps）技术。
本节代码基于前面的阴影映射教程，所以如果你对传统阴影映射不熟悉，还是建议先读一读阴影映射教程。
算法和定向阴影映射差不多：我们从光的透视图生成一个深度贴图，基于当前fragment位置来对深度贴图采样，然后用储存的深度值和每个fragment进行对比，看看它是否在阴影中。定向阴影映射和万向阴影映射的主要不同在于深度贴图的使用上。
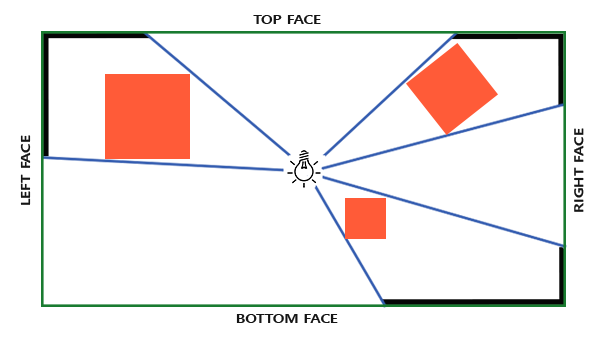
对于深度贴图，我们需要从一个点光源的所有渲染场景，普通2D深度贴图不能工作；如果我们使用cubemap会怎样？因为cubemap可以储存6个面的环境数据，它可以将整个场景渲染到cubemap的每个面上，把它们当作点光源四周的深度值来采样。
![](http://learnopengl.com/img/advanced-lighting/point_shadows_diagram.png)
生成后的深度cubemap被传递到光照像素着色器，它会用一个方向向量来采样cubemap，从而得到当前的fragment的深度（从光的透视图）。大部分复杂的事情已经在阴影映射教程中讨论过了。算法只是在深度cubemap生成上稍微复杂一点。
#### 生成深度cubemap
为创建一个光周围的深度值的cubemap，我们必须渲染场景6次：每次一个面。显然渲染场景6次需要6个不同的视图矩阵，每次把一个不同的cubemap面附加到帧缓冲对象上。这看起来是这样的：
```c++
for(int i = 0; i < 6; i++)
{
GLuint face = GL_TEXTURE_CUBE_MAP_POSITIVE_X + i;
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, face, depthCubemap, 0);
BindViewMatrix(lightViewMatrices[i]);
RenderScene();
}
```
这会很耗费性能因为一个深度贴图下需要进行很多渲染调用。这个教程中我们将转而使用另外的一个小技巧来做这件事，几何着色器允许我们使用一次渲染过程来建立深度cubemap。
首先，我们需要创建一个cubemap：
```c++
GLuint depthCubemap;
glGenTextures(1, &depthCubemap);
```
然后生成cubemap的每个面，将它们作为2D深度值纹理图像：
```c++
const GLuint SHADOW_WIDTH = 1024, SHADOW_HEIGHT = 1024;
glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
for (GLuint i = 0; i < 6; ++i)
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_DEPTH_COMPONENT,
SHADOW_WIDTH, SHADOW_HEIGHT, 0, GL_DEPTH_COMPONENT, GL_FLOAT, NULL);
```
不要忘记设置合适的纹理参数：
```c++
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
```
正常情况下，我们把cubemap纹理的一个面附加到帧缓冲对象上，渲染场景6次，每次将帧缓冲的深度缓冲目标改成不同cubemap面。由于我们将使用一个几何着色器，它允许我们把所有面在一个过程渲染，我们可以使用glFramebufferTexture直接把cubemap附加成帧缓冲的深度附件：
```c++
glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
glFramebufferTexture(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, depthCubemap, 0);
glDrawBuffer(GL_NONE);
glReadBuffer(GL_NONE);
glBindFramebuffer(GL_FRAMEBUFFER, 0);
```
还要记得调用glDrawBuffer和glReadBuffer：当生成一个深度cubemap时我们只关心深度值，所以我们必须显式告诉OpenGL这个帧缓冲对象不会渲染到一个颜色缓冲里。
万向阴影贴图有两个渲染阶段：首先我们生成深度贴图，然后我们正常使用深度贴图渲染，在场景中创建阴影。帧缓冲对象和cubemap的处理看起是这样的：
```c++
// 1. first render to depth cubemap
glViewport(0, 0, SHADOW_WIDTH, SHADOW_HEIGHT);
glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
glClear(GL_DEPTH_BUFFER_BIT);
ConfigureShaderAndMatrices();
RenderScene();
glBindFramebuffer(GL_FRAMEBUFFER, 0);
// 2. then render scene as normal with shadow mapping (using depth cubemap)
glViewport(0, 0, SCR_WIDTH, SCR_HEIGHT);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
ConfigureShaderAndMatrices();
glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
RenderScene();
```
这个过程和默认的阴影映射一样，尽管这次我们渲染和使用的是一个cubemap深度纹理，而不是2D深度纹理。在我们实际开始从光的视角的所有方向渲染场景之前，我们先得计算出合适的变换矩阵。
### 光空间的变换
设置了帧缓冲和cubemap，我们需要一些方法来讲场景的所有几何体变换到6个光的方向中相应的光空间。与阴影映射教程类似，我们将需要一个光空间的变换矩阵T，但是这次是每个面都有一个。
每个光空间的变换矩阵包含了投影和视图矩阵。对于投影矩阵来说，我们将使用一个透视投影矩阵；光源代表一个空间中的点，所以透视投影矩阵更有意义。每个光空间变换矩阵使用同样的投影矩阵：
```c++
GLfloat aspect = (GLfloat)SHADOW_WIDTH/(GLfloat)SHADOW_HEIGHT;
GLfloat near = 1.0f;
GLfloat far = 25.0f;
glm::mat4 shadowProj = glm::perspective(90.0f, aspect, near, far);
```
非常重要的一点是，这里glm::perspective的视野参数，设置为90度。90度我们才能保证视野足够大到可以合适地填满cubemap的一个面，cubemap的所有面都能与其他面在边缘对齐。
因为投影矩阵在每个方向上并不会改变，我们可以在6个变换矩阵中重复使用。我们要为每个方向提供一个不同的视图矩阵。用glm::lookAt创建6个观察方向，每个都按顺序注视着cubemap的的一个方向：右、左、上、下、近、远：
```c++
std::vector<glm::mat4> shadowTransforms;
shadowTransforms.push_back(shadowProj *
glm::lookAt(lightPos, lightPos + glm::vec3(1.0,0.0,0.0), glm::vec3(0.0,-1.0,0.0));
shadowTransforms.push_back(shadowProj *
glm::lookAt(lightPos, lightPos + glm::vec3(-1.0,0.0,0.0), glm::vec3(0.0,-1.0,0.0));
shadowTransforms.push_back(shadowProj *
glm::lookAt(lightPos, lightPos + glm::vec3(0.0,1.0,0.0), glm::vec3(0.0,0.0,1.0));
shadowTransforms.push_back(shadowProj *
glm::lookAt(lightPos, lightPos + glm::vec3(0.0,-1.0,0.0), glm::vec3(0.0,0.0,-1.0));
shadowTransforms.push_back(shadowProj *
glm::lookAt(lightPos, lightPos + glm::vec3(0.0,0.0,1.0), glm::vec3(0.0,-1.0,0.0));
shadowTransforms.push_back(shadowProj *
glm::lookAt(lightPos, lightPos + glm::vec3(0.0,0.0,-1.0), glm::vec3(0.0,-1.0,0.0));
```
这里我们创建了6个视图矩阵，把它们乘以投影矩阵，来得到6个不同的光空间变换矩阵。glm::lookAt的target参数是它注视的cubemap的面的一个方向。
这些变换矩阵发送到着色器渲染到cubemap里。
### 深度着色器
为了把值渲染到深度cubemap，我们将需要3个着色器：顶点和像素着色器，以及一个它们之间的几何着色器。
几何着色器是负责将所有世界空间的顶点变换到6个不同的光空间的着色器。因此顶点着色器简单地将顶点变换到世界空间，然后直接发送到几何着色器：
```c++
#version 330 core
layout (location = 0) in vec3 position;
uniform mat4 model;
void main()
{
gl_Position = model * vec4(position, 1.0);
}
```
紧接着几何着色器以3个三角形的顶点作为输入，它还有一个光空间变换矩阵的uniform数组。几何着色器接下来会负责将顶点变换到光空间；这里它开始变得有趣了。
几何着色器有一个内建变量叫做gl_Layer，它指定发散出基本图形送到cubemap的哪个面。当不管它时，几何着色器就会像往常一样把它的基本图形发送到输送管道的下一阶段，但当我们更新这个变量就能控制每个基本图形将渲染到cubemap的哪一个面。当然这只有当我们有了一个附加到激活的帧缓冲的cubemap纹理才有效：
```c++
#version 330 core
layout (triangles) in;
layout (triangle_strip, max_vertices=18) out;
uniform mat4 shadowMatrices[6];
out vec4 FragPos; // FragPos from GS (output per emitvertex)
void main()
{
for(int face = 0; face < 6; ++face)
{
gl_Layer = face; // built-in variable that specifies to which face we render.
for(int i = 0; i < 3; ++i) // for each triangle's vertices
{
FragPos = gl_in[i].gl_Position;
gl_Position = shadowMatrices[face] * FragPos;
EmitVertex();
}
EndPrimitive();
}
}
```
几何着色器相对简单。我们输入一个三角形，输出总共6个三角形（6*3顶点，所以总共18个顶点）。在main函数中，我们遍历cubemap的6个面，我们每个面指定为一个输出面，把这个面的interger（整数）存到gl_Layer。然后，我们通过把面的光空间变换矩阵乘以FragPos，将每个世界空间顶点变换到相关的光空间，生成每个三角形。注意，我们还要将最后的FragPos变量发送给像素着色器，我们需要计算一个深度值。
上个教程，我们使用的是一个空的像素着色器，让OpenGL配置深度贴图的深度值。这次我们将计算自己的深度，这个深度就是每个fragment位置和光源位置之间的线性距离。计算自己的深度值使得之后的阴影计算更加直观。
```c++
#version 330 core
in vec4 FragPos;
uniform vec3 lightPos;
uniform float far_plane;
void main()
{
// get distance between fragment and light source
float lightDistance = length(FragPos.xyz - lightPos);
// map to [0;1] range by dividing by far_plane
lightDistance = lightDistance / far_plane;
// Write this as modified depth
gl_FragDepth = gl_FragCoord.z;
}
```
像素着色器将来自几何着色器的FragPos、光的位置向量和视锥的远平面值作为输入。这里我们把fragment和光源之间的距离，映射到0到1的范围，把它写入为fragment的深度值。
使用这些着色器渲染场景，cubemap附加的帧缓冲对象激活以后，你会得到一个完全填充的深度cubemap，以便于进行第二阶段的阴影计算。
### 万向阴影贴图
所有事情都做好了，是时候来渲染万向阴影了。这个过程和定向阴影映射教程相似，尽管这次我们绑定的深度贴图是一个cubemap，而不是2D纹理，并且将光的投影的远平面发送给了着色器。
```c++
glViewport(0, 0, SCR_WIDTH, SCR_HEIGHT);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
shader.Use();
// ... send uniforms to shader (including light's far_plane value)
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
// ... bind other textures
RenderScene();
```
这里的renderScene函数在一个大立方体房间中渲染一些立方体，它们散落在大立方体各处，光源在场景中央。
顶点着色器和像素着色器和原来的阴影映射着色器大部分都一样：不同之处是在光空间中像素着色器不再需要一个fragment位置，现在我们可以使用一个方向向量采样深度值。
因为这个顶点着色器不再需要将他的位置向量变换到光空间，所以我们可以去掉FragPosLightSpace变量：
```c++
#version 330 core
layout (location = 0) in vec3 position;
layout (location = 1) in vec3 normal;
layout (location = 2) in vec2 texCoords;
out vec2 TexCoords;
out VS_OUT {
vec3 FragPos;
vec3 Normal;
vec2 TexCoords;
} vs_out;
uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;
void main()
{
gl_Position = projection * view * model * vec4(position, 1.0f);
vs_out.FragPos = vec3(model * vec4(position, 1.0));
vs_out.Normal = transpose(inverse(mat3(model))) * normal;
vs_out.TexCoords = texCoords;
}
```
片段着色器的Blinn-Phong光照代码和我们之前阴影相乘的结尾部分一样：
```c++
#version 330 core
out vec4 FragColor;
in VS_OUT {
vec3 FragPos;
vec3 Normal;
vec2 TexCoords;
} fs_in;
uniform sampler2D diffuseTexture;
uniform samplerCube depthMap;
uniform vec3 lightPos;
uniform vec3 viewPos;
uniform float far_plane;
float ShadowCalculation(vec3 fragPos)
{
[...]
}
void main()
{
vec3 color = texture(diffuseTexture, fs_in.TexCoords).rgb;
vec3 normal = normalize(fs_in.Normal);
vec3 lightColor = vec3(0.3);
// Ambient
vec3 ambient = 0.3 * color;
// Diffuse
vec3 lightDir = normalize(lightPos - fs_in.FragPos);
float diff = max(dot(lightDir, normal), 0.0);
vec3 diffuse = diff * lightColor;
// Specular
vec3 viewDir = normalize(viewPos - fs_in.FragPos);
vec3 reflectDir = reflect(-lightDir, normal);
float spec = 0.0;
vec3 halfwayDir = normalize(lightDir + viewDir);
spec = pow(max(dot(normal, halfwayDir), 0.0), 64.0);
vec3 specular = spec * lightColor;
// Calculate shadow
float shadow = ShadowCalculation(fs_in.FragPos);
vec3 lighting = (ambient + (1.0 - shadow) * (diffuse + specular)) * color;
FragColor = vec4(lighting, 1.0f);
}
```
有一些细微的不同：光照代码一样，但我们现在有了一个uniform变量samplerCube，shadowCalculation函数用fragment的位置作为它的参数，取代了光空间的fragment位置。我们现在还要引入光的视锥的远平面值，后面我们会需要它。像素着色器的最后，我们计算出阴影元素，当fragment在阴影中时它是1.0，不在阴影中时是0.0。我们使用计算出来的阴影元素去影响光照的diffuse和specular元素。
在ShadowCalculation函数中有很多不同之处，现在是从cubemap中进行采样，不再使用2D纹理了。我们来一步一步的讨论一下的它的内容。
我们需要做的第一件事是获取cubemap的森都。你可能已经从教程的cubemap部分想到，我们已经将深度储存为fragment和光位置之间的距离了；我们这里采用相似的处理方式：
```c++
float ShadowCalculation(vec3 fragPos)
{
vec3 fragToLight = fragPos - lightPos;
float closestDepth = texture(depthMap, fragToLight).r;
}
```
在这里，我们得到了fragment的位置与光的位置之间的不同的向量，使用这个向量作为一个方向向量去对cubemap进行采样。方向向量不需要是单位向量，所以无需对它进行标准化。最后的closestDepth是光源和它最接近的可见fragment之间的标准化的深度值。
closestDepth值现在在0到1的范围内了，所以我们先将其转换会0到far_plane的范围，这需要把他乘以far_plane：
```c++
closestDepth *= far_plane;
```
下一步我们获取当前fragment和光源之间的深度值，我们可以简单的使用fragToLight的长度来获取它，这取决于我们如何计算cubemap中的深度值：
```c++
float currentDepth = length(fragToLight);
```
返回的是和closestDepth范围相同的深度值。
现在我们可以将两个深度值对比一下，看看哪一个更接近，以此决定当前的fragment是否在阴影当中。我们还要包含一个阴影偏移，所以才能避免阴影失真，这在前面教程中已经讨论过了。
```c++
float bias = 0.05;
float shadow = currentDepth - bias > closestDepth ? 1.0 : 0.0;
```
完整的ShadowCalculation现在变成了这样：
```c++
float ShadowCalculation(vec3 fragPos)
{
// Get vector between fragment position and light position
vec3 fragToLight = fragPos - lightPos;
// Use the light to fragment vector to sample from the depth map
float closestDepth = texture(depthMap, fragToLight).r;
// It is currently in linear range between [0,1]. Re-transform back to original value
closestDepth *= far_plane;
// Now get current linear depth as the length between the fragment and light position
float currentDepth = length(fragToLight);
// Now test for shadows
float bias = 0.05;
float shadow = currentDepth - bias > closestDepth ? 1.0 : 0.0;
return shadow;
}
```
有了这些着色器，我们已经能得到非常好的阴影效果了，这次从一个点光源所有周围方向上都有阴影。有一个位于场景中心的点光源，看起来会像这样：
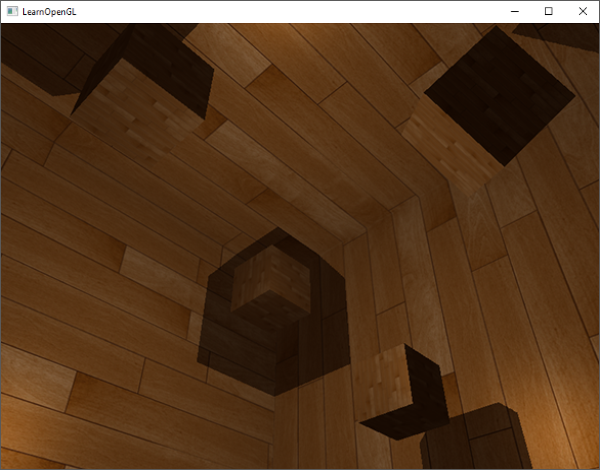
![](http://learnopengl.com/img/advanced-lighting/point_shadows.png)
你可以从这里找到这个[demo的源码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/point_shadows)、[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/point_shadows&type=vertex)和[片段](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/point_shadows&type=fragment)着色器。
#### 把cubemap深度缓冲显示出来
如果你想我一样第一次并没有做对，那么就要进行调试排错，将深度贴图显示出来以检查其是否正确。因为我们不再用2D深度贴图纹理，深度贴图的显示不会那么显而易见。
一个简单的把深度缓冲显示出来的技巧是，在ShadowCalculation函数中计算标准化的closestDepth变量，把变量显示为：
```c++
FragColor = vec4(vec3(closestDepth / far_plane), 1.0);
```
结果是一个灰度场景，每个颜色代表着场景的线性深度值：
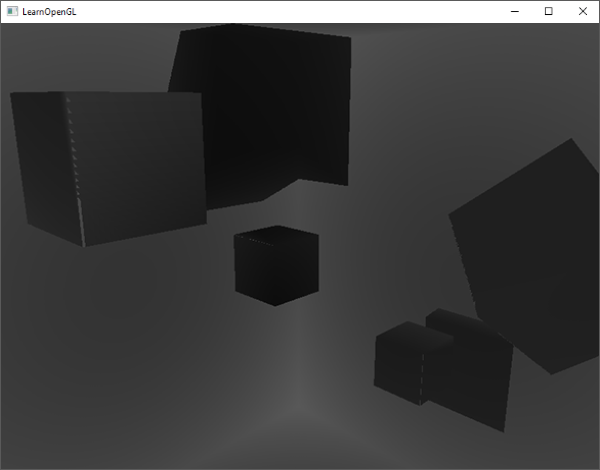
![](http://learnopengl.com/img/advanced-lighting/point_shadows_depth_cubemap.png)
你可能也注意到了带阴影部分在墙外。如果看起来和这个差不多，你就知道深度cubemap生成的没错。否则你可能做错了什么，也许是closestDepth仍然还在0到far_plane的范围。
#### PCF
由于万向阴影贴图基于传统阴影映射的原则，它便也继承了由解析度产生的非真实感。如果你放大就会看到锯齿边了。PCF或称Percentage-closer filtering允许我们通过对fragment位置周围过滤多个样本，并对结果平均化。
如果我们用和前面教程同样的那个简单的PCF过滤器，并加入第三个维度，就是这样的：
```c+++
float shadow = 0.0;
float bias = 0.05;
float samples = 4.0;
float offset = 0.1;
for(float x = -offset; x < offset; x += offset / (samples * 0.5))
{
for(float y = -offset; y < offset; y += offset / (samples * 0.5))
{
for(float z = -offset; z < offset; z += offset / (samples * 0.5))
{
float closestDepth = texture(depthMap, fragToLight + vec3(x, y, z)).r;
closestDepth *= far_plane; // Undo mapping [0;1]
if(currentDepth - bias > closestDepth)
shadow += 1.0;
}
}
}
shadow /= (samples * samples * samples);
```
这段代码和我们传统的阴影映射没有多少不同。这里我们根据样本的数量动态计算了纹理偏移量，我们在三个轴向采样三次，最后对子样本进行平均化。
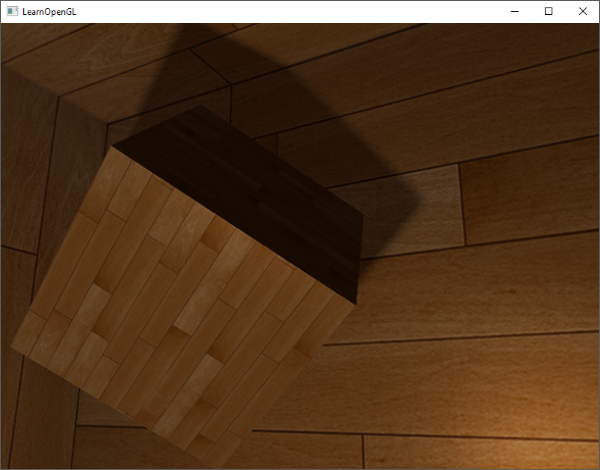
现在阴影看起来更加柔和平滑了，由此得到更加真实的效果：
![](http://learnopengl.com/img/advanced-lighting/point_shadows_soft.png)
然而，samples设置为4.0，每个fragment我们会得到总共64个样本，这太多了！
大多数这些样本都是多余的，它们在原始方向向量近处采样，不如在采样方向向量的垂直方向进行采样更有意义。可是，没有（简单的）方式能够指出哪一个子方向是多余的，这就难了。有个技巧可以使用，用一个偏移量方向数组，它们差不多都是分开的，每一个指向完全不同的方向，剔除彼此接近的那些子方向。下面就是一个有着20个偏移方向的数组：
```c++
vec3 sampleOffsetDirections[20] = vec3[]
(
vec3( 1, 1, 1), vec3( 1, -1, 1), vec3(-1, -1, 1), vec3(-1, 1, 1),
vec3( 1, 1, -1), vec3( 1, -1, -1), vec3(-1, -1, -1), vec3(-1, 1, -1),
vec3( 1, 1, 0), vec3( 1, -1, 0), vec3(-1, -1, 0), vec3(-1, 1, 0),
vec3( 1, 0, 1), vec3(-1, 0, 1), vec3( 1, 0, -1), vec3(-1, 0, -1),
vec3( 0, 1, 1), vec3( 0, -1, 1), vec3( 0, -1, -1), vec3( 0, 1, -1)
);
```
然后我们把PCF算法与从sampleOffsetDirections得到的样本数量进行适配，使用它们从cubemap里采样。这么做的好处是与之前的PCF算法相比，我们需要的样本数量变少了。
```c++
float shadow = 0.0;
float bias = 0.15;
int samples = 20;
float viewDistance = length(viewPos - fragPos);
float diskRadius = 0.05;
for(int i = 0; i < samples; ++i)
{
float closestDepth = texture(depthMap, fragToLight + sampleOffsetDirections[i] * diskRadius).r;
closestDepth *= far_plane; // Undo mapping [0;1]
if(currentDepth - bias > closestDepth)
shadow += 1.0;
}
shadow /= float(samples);
```
这里我们把一个偏移量添加到指定的diskRadius中，它在fragToLight方向向量周围从cubemap里采样。
另一个在这里可以应用的有意思的技巧是，我们可以基于观察者里一个fragment的距离来改变diskRadius；这样我们就能根据观察者的距离来增加偏移半径了，当距离更远的时候阴影更柔和，更近了就更锐利。
```c++
float diskRadius = (1.0 + (viewDistance / far_plane)) / 25.0;
```
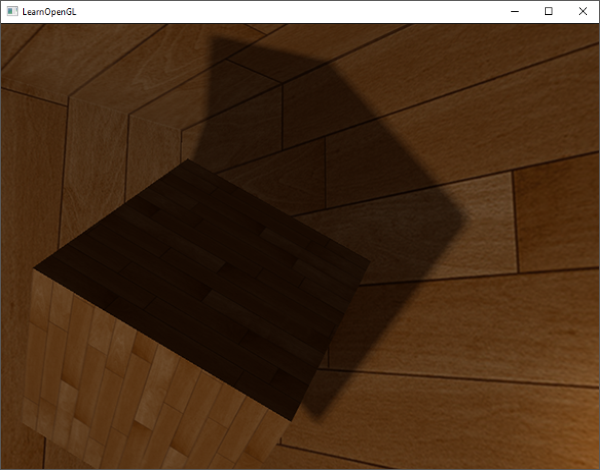
PCF算法的结果如果没有变得更好，也是非常不错的，这是柔和的阴影效果：
![](http://learnopengl.com/img/advanced-lighting/point_shadows_soft_better.png)
当然了，我们添加到每个样本的bias（偏移）高度依赖于上下文，总是要根据场景进行微调的。试试这些值，看看怎样影响了场景。
这里是最终版本的顶点和像素着色器。
我还要提醒一下使用几何着色器来生成深度贴图不会一定比每个面渲染场景6次更快。使用几何着色器有它自己的性能局限，在第一个阶段使用它可能获得更好的性能表现。这取决于环境的类型，以及特定的显卡驱动等等，所以如果你很关心性能，就要确保对两种方法有大致了解，然后选择对你场景来说更高效的那个。我个人还是喜欢使用几何着色器来进行阴影映射，原因很简单，因为它们使用起来更简单。
### 附加资源
[Shadow Mapping for point light sources in OpenGL](http://www.sunandblackcat.com/tipFullView.php?l=eng&topicid=36)：sunandblackcat的万向阴影映射教程。
[Multipass Shadow Mapping With Point Lights](http://ogldev.atspace.co.uk/www/tutorial43/tutorial43.html)：ogldev的万向阴影映射教程。
[Omni-directional Shadows](http://www.cg.tuwien.ac.at/~husky/RTR/OmnidirShadows-whyCaps.pdf)：Peter Houska的关于万向阴影映射的一组很好的ppt。

0
docs/05 Advanced Lighting/03 Shadows/03 CSM.md
View File

923
docs/05 Advanced Lighting/04 Normal Mapping.md
View File

@@ -1,923 +0,0 @@
本文作者JoeyDeVries，由Django翻译自[http://learnopengl.com](http://learnopengl.com)
## 法线贴图 （Normal Mapping）
我们的场景中已经充满了多边形物体，其中每个都可能由成百上千平坦的三角形组成。我们以向三角形上附加纹理的方式来增加额外细节，提升真实感，隐藏多边形几何体是由无数三角形组成的事实。纹理确有助益，然而当你近看它们时，这个事实便隐藏不住了。现实中的物体表面并非是平坦的，而是表现出无数（凹凸不平的）细节。
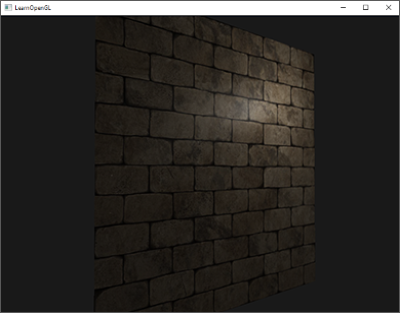
例如，砖块的表面。砖块的表面非常粗糙，显然不是完全平坦的：它包含着接缝处水泥凹痕，以及非常多的细小的空洞。如果我们在一个有光的场景中看这样一个砖块的表面，问题就出来了。下图中我们可以看到砖块纹理应用到了平坦的表面，并被一个点光源照亮。
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_flat.png)
光照并没有呈现出任何裂痕和孔洞，完全忽略了砖块之间凹进去的线条；表面看起来完全就是平的。我们可以使用specular贴图根据深度或其他细节阻止部分表面被照的更亮，以此部分地解决问题，但这并不是一个好方案。我们需要的是某种可以告知光照系统给所有有关物体表面类似深度这样的细节的方式。
如果我们一光的视角来看这个问题：是什么使表面被视为完全平坦的表面来照亮？答案会是表面的法线向量。以光照算法的视角考虑的话，只有一件事决定物体的形状，这就是垂直于它的法线向量。砖块表面只有一个法线向量，表面完全根据这个法线向量被以一致的方式照亮。如果每个fragment都是用自己的不同的法线会怎样？这样我们就可以根据表面细微的细节对法线向量进行改变；这样就会获得一种表面看起来要复杂得多的幻觉：
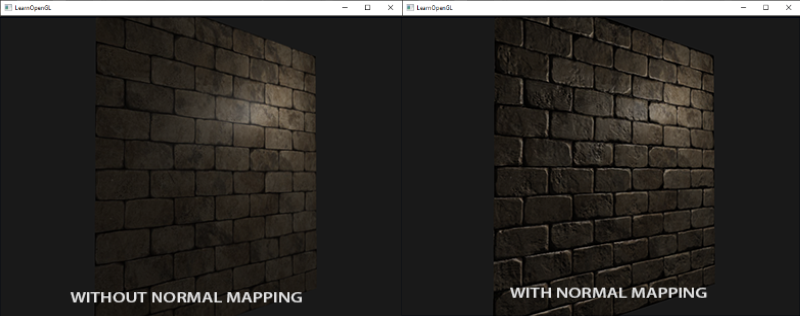
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_surfaces.png)
每个fragment使用了自己的法线，我们就可以让光照相信一个表面由很多微小的（垂直于法线向量的）平面所组成，物体表面的细节将会得到极大提升。这种每个fragment使用各自的法线，替代一个面上所有fragment使用同一个法线的技术叫做法线贴图（normal mapping）或凹凸贴图（bump mapping）。应用到砖墙上，效果像这样：
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_compare.png)
你可以看到细节获得了极大提升，开销却不大。因为我们只需要改变每个fragment的法线向量，并不需要改变所有光照公式。现在我们是为每个fragment传递一个法线，不再使用插值表面法线。这样光照使表面拥有了自己的细节。
### 法线贴图
为使法线贴图工作，我们需要为每个fragment提供一个法线。像diffuse贴图和specular贴图一样，我们可以使用一个2D纹理来储存法线数据。2D纹理不仅可以储存颜色和光照数据，还可以储存法线向量。这样我们可以从2D纹理中采样得到特定纹理的法线向量。
由于法线向量是个几何工具，而纹理通常只用于储存颜色信息，用纹理储存法线向量不是非常直接。如果你想一想，就会知道纹理中的颜色向量用r、g、b元素代表一个3D向量。类似的我们也可以将法线向量的x、y、z元素储存到纹理中，代替颜色的r、g、b元素。法线向量的范围在-1到1之间，所以我们先要将其映射到0到1的范围：
1
vec3 rgb_normal = normal * 0.5 - 0.5; // transforms from [-1,1] to [0,1]
将法线向量变换为像这样的RGB颜色元素，我们就能把根据表面的形状的fragment的法线保存在2D纹理中。教程开头展示的那个砖块的例子的法线贴图如下所示：
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_normal_map.png)
这会是一种偏蓝色调的纹理（你在网上找到的几乎所有法线贴图都是这样的）。这是因为所有法线的指向都偏向z轴（0, 0, 1）这是一种偏蓝的颜色。法线向量从z轴方向也向其他方向轻微偏移，颜色也就发生了轻微变化，这样看起来便有了一种深度。例如，你可以看到在每个砖块的顶部，颜色倾向于偏绿，这是因为砖块的顶部的法线偏向于指向正y轴方向（0, 1, 0），这样它就是绿色的了。
在一个简单的朝向正z轴的平面上，我们可以用这个diffuse纹理和这个法线贴图来渲染前面部分的图片。要注意的是这个链接里的法线贴图和上面展示的那个不一样。原因是OpenGL读取的纹理的y（或V）坐标和纹理通常被创建的方式相反。链接里的法线贴图的y（或绿色）元素是相反的（你可以看到绿色现在在下边）；如果你没考虑这个，光照就不正确了（译注：如果你现在不再使用SOIL了，那就不要用链接里的那个法线贴图，这个问题是SOIL载入纹理上下颠倒所致，它也会把法线在y方向上颠倒）。加载纹理，把它们绑定到合适的纹理单元，然后使用下面的改变了的像素着色器来渲染一个平面：
```c++
uniform sampler2D normalMap;
void main()
{
// 从法线贴图范围[0,1]获取法线
normal = texture(normalMap, fs_in.TexCoords).rgb;
// 将法线向量转换为范围[-1,1]
normal = normalize(normal * 2.0 - 1.0);
[...]
// 像往常那样处理光照
}
```
这里我们将被采样的法线颜色从0到1重新映射回-1到1，便能将RGB颜色重新处理成法线，然后使用采样出的法线向量应用于光照的计算。在例子中我们使用的是Blinn-Phong着色器。
通过慢慢随着时间慢慢移动光源，你就能明白法线贴图是什么意思了。运行这个例子你就能得到本教程开始的那个效果：
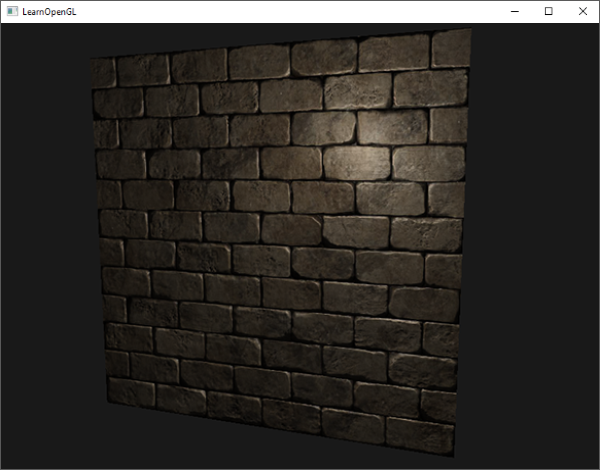
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_correct.png)
你可以在这里找到这个简单demo的源代码及其顶点和像素着色器。
然而有个问题限制了刚才讲的那种法线贴图的使用。我们使用的那个法线贴图里面的所有法线向量都是指向正z方向的。上面的例子能用，是因为那个平面的表面法线也是指向正z方向的。可是，如果我们在表面法线指向正y方向的平面上使用同一个法线贴图会发生什么？
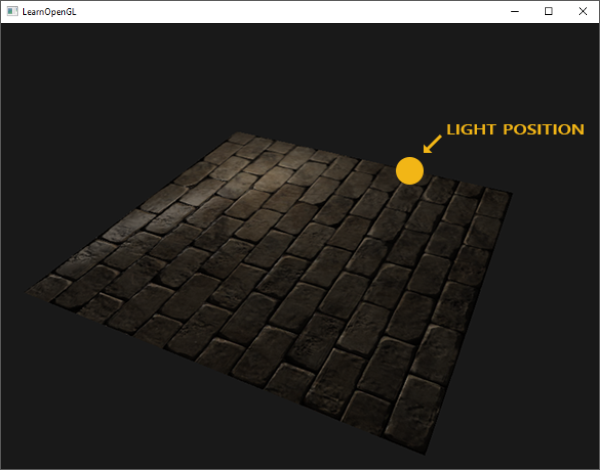
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_ground.png)
光照看起来完全不对！发生这种情况是平面的表面法线现在指向了y，而采样得到的法线仍然指向的是z。结果就是光照仍然认为表面法线和之前朝向正z方向时一样；这样光照就不对了。下面的图片展示了这个表面上采样的法线的近似情况：
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_ground_normals.png)
你可以看到所有法线都指向z方向，它们本该朝着表面法线指向y方向的。一个可行方案是为每个表面制作一个单独的法线贴图。如果是一个立方体的话我们就需要6个法线贴图，但是如果模型上有无数的朝向不同方向的表面，这就不可行了（译注：实际上对于复杂模型可以把朝向各个方向的法线储存在同一张贴图上，你可能看到过不只是蓝色的法线贴图，不过用那样的法线贴图有个问题是你必须记住模型的起始朝向，如果模型运动了还要记录模型的变换，这是非常不方便的；此外就像作者所说的，如果把一个diffuse纹理应用在同一个物体的不同表面上，就像立方体那样的，就需要做6个法线贴图，这也不可取）。
另一个稍微有点难的解决方案是，在一个不同的坐标空间中进行光照，这个坐标空间里，法线贴图向量总是指向这个坐标空间的正z方向；所有的光照向量都相对与这个正z方向进行变换。这样我们就能始终使用同样的法线贴图，不管朝向问题。这个坐标空间叫做切线空间（tangent space）。
### 切线空间
法线贴图中的法线向量在切线空间中，法线永远指着正z方向。切线空间是位于三角形表面之上的空间：法线相对于单个三角形的本地参考框架。它就像法线贴图向量的本地空间；它们都被定义为指向正z方向，无论最终变换到什么方向。使用一个特定的矩阵我们就能将本地/切线空寂中的法线向量转成世界或视图坐标，使它们转向到最终的贴图表面的方向。
我们可以说，上个部分那个朝向正y的法线贴图错误的贴到了表面上。法线贴图被定义在切线空间中，所以一种解决问题的方式是计算出一种矩阵，把法线从切线空间变换到一个不同的空间，这样它们就能和表面法线方向对齐了：法线向量都会指向正y方向。切线空间的一大好处是我们可以为任何类型的表面计算出一个这样的矩阵，由此我们可以把切线空间的z方向和表面的法线方向对齐。
这种矩阵叫做TBN矩阵这三个字母分别代表tangent、bitangent和normal向量。这是建构这个矩阵所需的向量。要建构这样一个把切线空间转变为不同空间的变异矩阵，我们需要三个相互垂直的向量，它们沿一个表面的法线贴图对齐于：上、右、前；这和我们在[摄像机教程](http://learnopengl-cn.readthedocs.org/zh/latest/01%20Getting%20started/09%20Camera/)中做的类似。
已知上向量是表面的法线向量。右和前向量是切线和副切线向量。下面的图片展示了一个表面的三个向量：
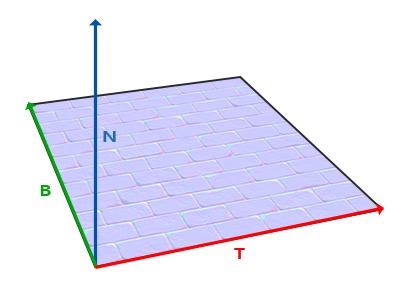
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_tbn_vectors.png)
计算出切线和副切线并不像法线向量那么容易。从图中可以看到法线贴图的切线和副切线与纹理坐标的两个方向对齐。我们就是用到这个特性计算每个表面的切线和副切线的。需要用到一些数学才能得到它们；请看下图：
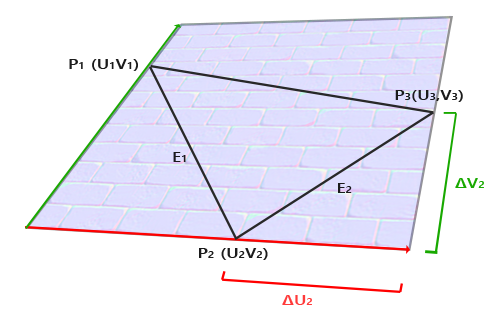
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_surface_edges.png)
上图中我们可以看到边<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>E</mi>
<mn>2</mn>
</msub>
</math>纹理坐标的不同，<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>E</mi>
<mn>2</mn>
</msub>
</math>是一个三角形的边，这个三角形的另外两条边是<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
</math>和<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
</math>，它们与切线向量*T*和副切线向量*B*方向相同。这样我们可以把边</math>和<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>E</mi>
<mn>1</mn>
</msub>
</math>和<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>E</mi>
<mn>2</mn>
</msub>
</math>用切线向量 *T* 和副切线向量 *B* 的线性组合表示出来（译注：注意*T*和*B*都是单位长度，在*TB*平面中所有点的*T*、*B*坐标都在0到1之间，因此可以进行这样的组合）：
```math
E_1 = \Delta U_1T + \Delta V_1B
E_2 = \Delta U_2T + \Delta V_2B
```
我们也可以写成这样：
```math
(E_{1x}, E_{1y}, E_{1z}) = \Delta U_1(T_x, T_y, T_z) + \Delta V_1(B_x, B_y, B_z)
```
*E*是两个向量位置的差，*U*和*V*是纹理坐标的差。然后我们得到两个未知数（切线*T*和副切线*B*）和两个等式。你可能想起你的代数课了，这是让我们去接*T*和*B*。
上面的方程允许我们把它们写成另一种格式：矩阵乘法
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mo>=</mo>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>1</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>1</mn>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>T</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>B</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
</math>
尝试会以一下矩阵乘法，它们确实是同一种等式。把等式写成矩阵形式的好处是，解*T*和*B*会因此变得很容易。两边都乘以<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<mi>U</mi>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<mi>V</mi>
</math>的反数等于：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<msup>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>1</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>1</mn>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mrow class="MJX-TeXAtom-ORD">
<mo>&#x2212;<!-- − --></mo>
<mn>1</mn>
</mrow>
</msup>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mo>=</mo>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>T</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>B</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
</math>
这样我们就可以解出*T*和*B*了。这需要我们计算出delta纹理坐标矩阵的拟阵。我不打算讲解计算逆矩阵的细节，但大致是把它变化为，1除以矩阵的行列式，再乘以它的共轭矩阵。
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>T</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>T</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>B</mi>
<mi>x</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>y</mi>
</msub>
</mtd>
<mtd>
<msub>
<mi>B</mi>
<mi>z</mi>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mo>=</mo>
<mfrac>
<mn>1</mn>
<mrow>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>1</mn>
</msub>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
<mo>&#x2013;</mo>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>1</mn>
</msub>
</mrow>
</mfrac>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>2</mn>
</msub>
</mtd>
<mtd>
<mo>&#x2212;<!-- − --></mo>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>V</mi>
<mn>1</mn>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<mo>&#x2212;<!-- − --></mo>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>2</mn>
</msub>
</mtd>
<mtd>
<mi mathvariant="normal">&#x0394;<!-- Δ --></mi>
<msub>
<mi>U</mi>
<mn>1</mn>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
<mrow>
<mo>[</mo>
<mtable rowspacing="4pt" columnspacing="1em">
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
<mtr>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>x</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>y</mi>
</mrow>
</msub>
</mtd>
<mtd>
<msub>
<mi>E</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>z</mi>
</mrow>
</msub>
</mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
</math>
有了最后这个等式，我们就可以用公式、三角形的两条边以及纹理坐标计算出切线向量*T*和副切线*B*。
如果你对这些数学内容不理解也不用担心。当你知道我们可以用一个三角形的顶点和纹理坐标（因为纹理坐标和切线向量在同一空间中）计算出切线和副切线你就已经部分地达到目的了（译注：上面的推导已经很清楚了，如果你不明白可以参考任意线性代数教材，就像作者所说的记住求得切线空间的公式也行，不过不管怎样都得理解切线空间的含义）。
### 手工计算切线和副切线
这个教程的demo场景中有一个简单的2D平面，它朝向正z方向。这次我们会使用切线空间来实现法线贴图，所以我们可以使平面朝向任意方向，法线贴图仍然能够工作。使用前面讨论的数学方法，我们来手工计算出表面的切线和副切线向量。
假设平面使用下面的向量建立起来（1、2、3和1、3、4，它们是两个三角形）：
// positions
glm::vec3 pos1(-1.0, 1.0, 0.0);
glm::vec3 pos2(-1.0, -1.0, 0.0);
glm::vec3 pos3(1.0, -1.0, 0.0);
glm::vec3 pos4(1.0, 1.0, 0.0);
// texture coordinates
glm::vec2 uv1(0.0, 1.0);
glm::vec2 uv2(0.0, 0.0);
glm::vec2 uv3(1.0, 0.0);
glm::vec2 uv4(1.0, 1.0);
// normal vector
glm::vec3 nm(0.0, 0.0, 1.0);
我们先计算第一个三角形的边和deltaUV坐标：
1
2
3
4
glm::vec3 edge1 = pos2 - pos1;
glm::vec3 edge2 = pos3 - pos1;
glm::vec2 deltaUV1 = uv2 - uv1;
glm::vec2 deltaUV2 = uv3 - uv1;
有了计算切线和副切线的必备数据，我们就可以开始写出来自于前面部分中的下列等式：
```c++
GLfloat f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y);
tangent1.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x);
tangent1.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y);
tangent1.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z);
tangent1 = glm::normalize(tangent1);
bitangent1.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x);
bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y);
bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z);
bitangent1 = glm::normalize(bitangent1);
[...] // similar procedure for calculating tangent/bitangent for plane's second triangle
```
我们预先计算出等式的分数部分f，然后把它和每个向量的元素进行相应矩阵乘法。如果你把代码和最终的等式对比你会发现，这就是直接套用。最后我们还要进行标准化，来确保切线/副切线向量最后是单位向量。
因为一个三角形永远是平坦的形状，我们只需为每个三角形计算一个切线/副切线，它们对于每个三角形上的顶点都是一样的。要注意的是大多数实现通常三角形和三角形之间都会共享顶点。这种情况下开发者通常将每个顶点的法线和切线/副切线等顶点属性平均化，以获得更加柔和的效果。我们的平面的三角形之间分享了一些顶点，但是因为两个三角形相互并行，因此并不需要将结果平均化，但无论何时只要你遇到这种情况记住它就是件好事。
最后的切线和副切线向量的值应该是(1, 0, 0)和(0, 1, 0)，它们和法线(0, 0, 1)组成相互垂直的TBN矩阵。在平面上显示出来TBN应该是这样的：
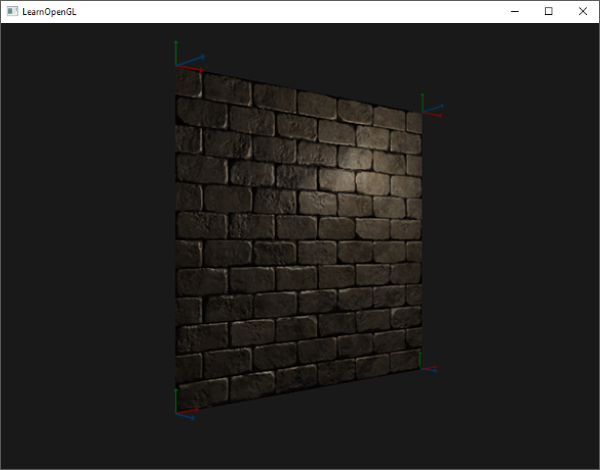
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_tbn_shown.png)
每个顶点定义了切线和副切线向量，我们就可以开始实现正确的法线贴图了。
### 切线空间法线贴图
为让法线贴图工作，我们先得在着色器中创建一个TBN矩阵。我们先将前面计算出来的切线和副切线向量传给顶点着色器，作为它的属性：
```c++
#version 330 core
layout (location = 0) in vec3 position;
layout (location = 1) in vec3 normal;
layout (location = 2) in vec2 texCoords;
layout (location = 3) in vec3 tangent;
layout (location = 4) in vec3 bitangent;
```
在顶点着色器的main函数中我们创建TBN矩阵：
```c++
void main()
{
[...]
vec3 T = normalize(vec3(model * vec4(tangent, 0.0)));
vec3 B = normalize(vec3(model * vec4(bitangent, 0.0)));
vec3 N = normalize(vec3(model * vec4(normal, 0.0)));
mat3 TBN = mat3(T, B, N)
}
```
我们先将所有TBN向量变换到我们所操作的坐标系中，现在是世界空间，我们可以乘以model矩阵。然后我们创建实际的TBN矩阵，直接把相应的向量应用到mat3构造器就行。注意，如果我们希望更精确的话就不要讲TBN向量乘以model矩阵，而是使用法线矩阵，但我们只关心向量的方向，不会平移也和缩放这个变换。
从技术上讲，顶点着色器中无需副切线。所有的这三个TBN向量都是相互垂直的所以我们可以在顶点着色器中庸T和N向量的叉乘，自己计算出副切线：vec3 B = cross(T, N);
现在我们有了TBN矩阵，如果来使用它呢？基本有两种方式可以使用，我们会把这两种方式都说明一下：
我们可以用TBN矩阵把所有向量从切线空间转到世界空间，传给像素着色器，然后把采样得到的法线用TBN矩阵从切线空间变换到世界空间；法线就处于和其他光照变量一样的空间中了。
我们用TBN的逆矩阵把所有世界空间的向量转换到切线空间，使用这个矩阵将除法线以外的所有相关光照变量转换到切线空间中；这样法线也能和其他光照变量处于同一空间之中。
我们来看看第一种情况。我们从法线贴图重采样得来的法线向量，是以切线空间表达的，尽管其他光照向量是以世界空间表达的。把TBN传给像素着色器，我们就能将采样得来的切线空间的法线乘以这个TBN矩阵，将法线向量变换到和其他光照向量一样的参考空间中。这种方式随后所有光照计算都可以简单的理解。
把TBN矩阵发给像素着色器很简单：
```c++
out VS_OUT {
vec3 FragPos;
vec2 TexCoords;
mat3 TBN;
} vs_out;
void main()
{
[...]
vs_out.TBN = mat3(T, B, N);
}
```
在像素着色器中我们用mat3作为输入变量：
```c++
in VS_OUT {
vec3 FragPos;
vec2 TexCoords;
mat3 TBN;
} fs_in;
```
有了TBN矩阵我们现在就可以更新法线贴图代码，引入切线到世界空间变换：
```c++
normal = texture(normalMap, fs_in.TexCoords).rgb;
normal = normalize(normal * 2.0 - 1.0);
normal = normalize(fs_in.TBN * normal);
```
因为最后的normal现在在世界空间中了，就不用改变其他像素着色器的代码了，因为光照代码就是假设法线向量在世界空间中。
我们同样看看第二种情况，我们用TBN矩阵的逆矩阵将所有相关的世界空间向量转变到采样所得法线向量的空间：切线空间。TBN的建构还是一样，但我们在将其发送给像素着色器之前先要求逆矩阵：
```c++
vs_out.TBN = transpose(mat3(T, B, N));
```
注意，这里我们使用transpose函数，而不是inverse函数。正交矩阵（每个轴既是单位向量同时相互垂直）的一大属性是一个正交矩阵的置换矩阵与它的逆矩阵相等。这个属性和重要因为逆矩阵的求得比求置换开销大；结果却是一样的。
在像素着色器中我们不用对法线向量变换，但我们要把其他相关向量转换到切线空间，它们是lightDir和viewDir。这样每个向量还是在同一个空间（切线空间）中了。
```c++
void main()
{
vec3 normal = texture(normalMap, fs_in.TexCoords).rgb;
normal = normalize(normal * 2.0 - 1.0);
vec3 lightDir = fs_in.TBN * normalize(lightPos - fs_in.FragPos);
vec3 viewDir = fs_in.TBN * normalize(viewPos - fs_in.FragPos);
[...]
}
```
第二种方法看似要做的更多，它还需要在像素着色器中进行更多的乘法操作，所以为何还用第二种方法呢？
将向量从世界空间转换到切线空间有个额外好处，我们可以把所有相关向量在顶点着色器中转换到切线空间，不用在像素着色器中做这件事。这是可行的，因为lightPos和viewPos不是每个fragment运行都要改变，对于fs_in.FragPos，我们也可以在顶点着色器计算它的切线空间位置。基本上，不需要把任何向量在像素着色器中进行变换，而第一种方法中就是必须的，因为采样出来的法线向量对于每个像素着色器都不一样。
所以现在不是把TBN矩阵的逆矩阵发送给像素着色器，而是将切线空间的光源位置，观察位置以及顶点位置发送给像素着色器。这样我们就不用在像素着色器里进行矩阵乘法了。这是一个极佳的优化，因为顶点着色器通常比像素着色器运行的少。这也是为什么这种方法是一种更好的实现方式的原因。
```c++
out VS_OUT {
vec3 FragPos;
vec2 TexCoords;
vec3 TangentLightPos;
vec3 TangentViewPos;
vec3 TangentFragPos;
} vs_out;
uniform vec3 lightPos;
uniform vec3 viewPos;
[...]
void main()
{
[...]
mat3 TBN = transpose(mat3(T, B, N));
vs_out.TangentLightPos = TBN * lightPos;
vs_out.TangentViewPos = TBN * viewPos;
vs_out.TangentFragPos = TBN * vec3(model * vec4(position, 0.0));
}
```
在像素着色器中我们使用这些新的输入变量来计算切线空间的光照。因为法线向量已经在切线空间中了，光照就有意义了。
将法线贴图应用到切线空间上，我们会得到混合教程一开始那个例子相似的结果，但这次我们可以将平面朝向各个方向，光照一直都会是正确的：
```c++
glm::mat4 model;
model = glm::rotate(model, (GLfloat)glfwGetTime() * -10, glm::normalize(glm::vec3(1.0, 0.0, 1.0)));
glUniformMatrix4fv(modelLoc 1, GL_FALSE, glm::value_ptr(model));
RenderQuad();
```
看起来是正确的法线贴图：
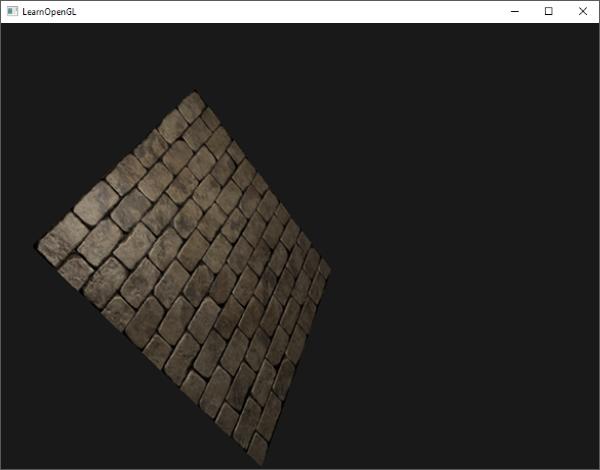
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_correct_tangent.png)
你可以在这里找到[源代码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/normal_mapping)、[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/normal_mapping&type=vertex)和[像素](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/normal_mapping&type=fragment)着色器。
### 复杂的物体
我们已经说明了如何通过手工计算切线和副切线向量，来使用切线空间和法线贴图。幸运的是，计算这些切线和副切线向量对于你来说不是经常能遇到的事；大多数时候，在模型加载器中实现了一次就行了，我们是在使用了Assimp的那个加载器中实现的。
Assimp有个很有用的配置，在我们加载模型的时候调用aiProcess_CalcTangentSpace。当aiProcess_CalcTangentSpace应用到Assimp的ReadFile函数时，Assimp会为每个加载的顶点计算出柔和的切线和副切线向量，它所使用的方法和我们本教程使用的类似。
```c++
const aiScene* scene = importer.ReadFile(
path, aiProcess_Triangulate | aiProcess_FlipUVs | aiProcess_CalcTangentSpace
);
```
我们可以通过下面的代码用Assimp获取计算出来的切线空间：
```c++
vector.x = mesh->mTangents[i].x;
vector.y = mesh->mTangents[i].y;
vector.z = mesh->mTangents[i].z;
vertex.Tangent = vector;
```
然后，你还必须更新模型加载器，用以从带纹理模型中加载法线贴图。wavefront的模型格式（.obj）导出的法线贴图有点不一样，Assimp的aiTextureType_NORMAL并不会加载它的法线贴图，而aiTextureType_HEIGHT却能，所以我们经常这样加载它们：
```c++
vector<Texture> specularMaps = this->loadMaterialTextures(
material, aiTextureType_HEIGHT, "texture_normal"
);
```
当然，对于每个模型的类型和文件格式来说都是不同的。同样了解aiProcess_CalcTangentSpace并不能总是很好的工作也很重要。计算切线是需要根据纹理坐标的，有些模型制作者使用一些纹理小技巧比如镜像一个模型上的纹理表面时也镜像了另一半的纹理坐标；这样当不考虑这个镜像的特别操作的时候（Assimp就不考虑）结果就不对了。
运行程序，用新的模型加载器，加载一个有specular和法线贴图的模型，看起来会像这样：
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_complex_compare.png)
你可以看到在没有太多点的额外开销的情况下法线贴图难以置信地提升了物体的细节。
使用法线贴图也是一种提升你的场景的表现的重要方式。在使用法线贴图之前你不得不使用相当多的顶点才能表现出一个更精细的网格，但使用了法线贴图我们可以使用更少的顶点表现出同样丰富的细节。下图来自Paolo Cignoni，图中对比了两种方式：
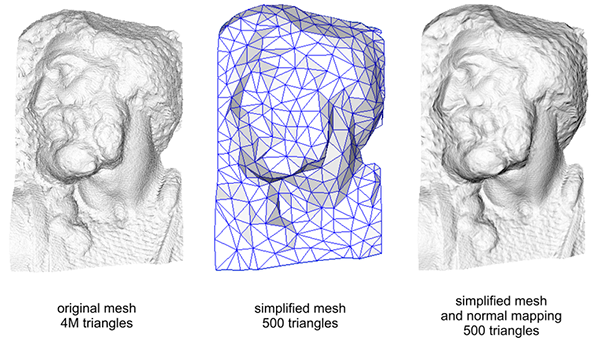
![](http://learnopengl.com/img/advanced-lighting/normal_mapping_comparison.png)
高精度网格和使用法线贴图的低精度网格几乎区分不出来。所以法线贴图不仅看起来漂亮，它也是一个将高精度多边形转换为低精度多边形而不失细节的重要工具。
### 最后一件事
关于法线贴图还有最后一个技巧要讨论，它可以在不必花费太多性能开销的情况下稍稍提升画质表现。
当在更大的网格上计算切线向量的时候，它们往往有很大数量的共享顶点，当发下贴图应用到这些表面时将切线向量平均化通常能获得更好更平滑的结果。这样做有个问题，就是TBN向量可能会不能互相垂直，这意味着TBN矩阵不再是正交矩阵了。法线贴图可能会稍稍偏移，但这仍然可以改进。
使用叫做*格拉姆-施密特*正交化过程（Gram-Schmidt process）的数学技巧，我们可以对TBN向量进行重正交化，这样每个向量就又会重新垂直了。在顶点着色器中我们这样做：
```c++
vec3 T = normalize(vec3(model * vec4(tangent, 0.0)));
vec3 N = normalize(vec3(model * vec4(tangent, 0.0)));
// re-orthogonalize T with respect to N
T = normalize(T - dot(T, N) * N);
// then retrieve perpendicular vector B with the cross product of T and N
vec3 B = cross(T, N);
mat3 TBN = mat3(T, B, N)
```
这样稍微花费一些性能开销就能对法线贴图进行一点提升。看看最后的那个附加资源： Normal Mapping Mathematics视频，里面有对这个过程的解释。
### 附加资源
* [Tutorial 26: Normal Mapping](http://ogldev.atspace.co.uk/www/tutorial26/tutorial26.html)：ogldev的法线贴图教程。
* [How Normal Mapping Works](https://www.youtube.com/watch?v=LIOPYmknj5Q)：TheBennyBox的讲述法线贴图如何工作的视频。
* [Normal Mapping Mathematics](https://www.youtube.com/watch?v=4FaWLgsctqY)：TheBennyBox关于法线贴图的数学原理的教程。
* [Tutorial 13: Normal Mapping](http://www.opengl-tutorial.org/intermediate-tutorials/tutorial-13-normal-mapping/)：opengl-tutorial.org提供的法线贴图教程。

302
docs/05 Advanced Lighting/05 Parallax Mapping.md
View File

@@ -1,302 +0,0 @@
本文作者JoeyDeVries，由Django翻译自[http://learnopengl.com](http://learnopengl.com)
## 视差贴图(Parallax Mapping)
视差贴图技术和法线贴图差不多，但它有着不同的原则。和法线贴图一样视差贴图能够极大提升表面细节，使之具有深度感。它也是利用了视错觉，然而对深度有着更好的表达，与法线贴图一起用能够产生难以置信的效果。视差贴图和光照无关，我在这里是作为法线贴图的技术延续来讨论它的。需要注意的是在开始学习视差贴图之前强烈建议先对法线贴图，特别是切线空间有较好的理解。
视差贴图属于位移贴图（译注：displacement mapping也叫置换贴图）技术的一种，它对根据储存在纹理中的几何信息对顶点进行位移或偏移。一种实现的方式是比如有1000个顶点，更具纹理中的数据对平面特定区域的顶点的高度进行位移。这样的每个纹理像素包含了高度值纹理叫做高度贴图。一张简单的砖块表面的告诉贴图如下所示：
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_height_map.png)
整个平面上的每个顶点都根据从高度贴图采样出来的高度值进行位移，根据材质的几何属性平坦的平面变换成凹凸不平的表面。例如一个平坦的平面利用上面的高度贴图进行置换能得到以下结果：
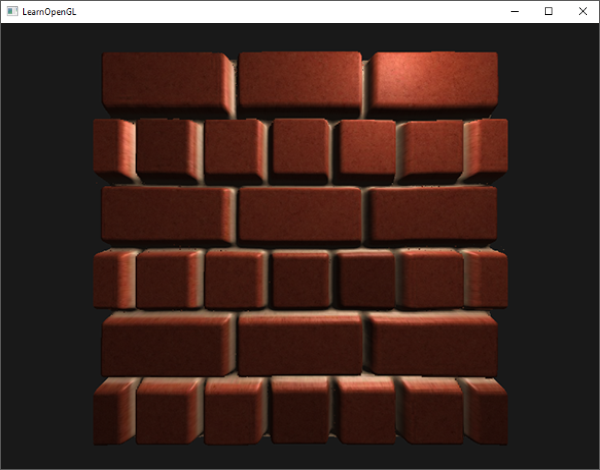
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_plane_heightmap.png)
置换顶点有一个问题就是平面必须由很多顶点组成才能获得具有真实感的效果，否则看起来效果并不会很好。一个平坦的表面上有1000个顶点计算量太大了。我们能否不用这么多的顶点就能取得相似的效果呢？事实上，上面的表面就是用6个顶点渲染出来的（两个三角形）。上面的那个表面使用视差贴图技术渲染，位移贴图技术不需要额外的顶点数据来表达深度，它像法线贴图一样采用一种聪明的手段欺骗用户的眼睛。
视差贴图背后的思想是修改纹理坐标使一个fragment的表面看起来比实际的更高或者更低，所有这些都根据观察方向和高度贴图。为了理解它如何工作，看看下面砖块表面的图片：
[](http://learnopengl.com/img/advanced-lighting/parallax_mapping_plane_height.png)
这里粗糙的红线代表高度贴图中的数值的立体表达，向量V代表观察方向。如果平面进行实际位移，观察者会在点B看到表面。然而我们的平面没有实际上进行位移，观察方向将在点A与平面接触。视差贴图的目的是，在A位置上的fragment不再使用点A的纹理坐标而是使用点B的。随后我们用点B的纹理坐标采样，观察者就像看到了点B一样。
这个技巧就是描述如何从点A得到点B的纹理坐标。视差贴图尝试通过对从fragment到观察者的方向向量V进行缩放的方式解决这个问题，缩放的大小是A处fragment的高度。所以我们将V的长度缩放为高度贴图在点A处H（A）采样得来的值。下图展示了经缩放得到的向量P：
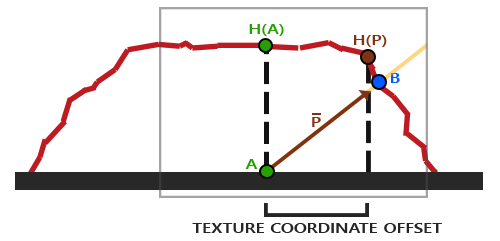
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_scaled_height.png)
我们随后选出P以及这个向量与平面对齐的坐标作为纹理坐标的偏移量。这能工作是因为向量P是使用从高度贴图得到的高度值计算出来的，所以一个fragment的高度越高位移的量越大。
这个技巧在大多数时候都没问题，但点B是粗略估算得到的。当表面的高度变化很快的时候，看起来就不会真实，因为向量P最终不会和B接近，就像下图这样：
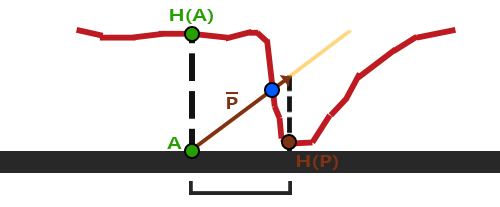
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_incorrect_p.png)
视差贴图的另一个问题是，当表面被任意旋转以后很难指出从P获取哪一个坐标。我们在视差贴图中使用了另一个坐标空间，这个空间P向量的x和y元素总是与纹理表面对齐。如果你看了法线贴图教程，你也许猜到了，我们实现它的方法，是的，我们还是在切线空间中实现视差贴图。
将fragment到观察者的向量V转换到切线空间中，经变换的P向量的x和y元素将于表面的切线和副切线向量对齐。由于切线和副切线向量与表面纹理坐标的方向相同，我们可以用P的x和y元素作为纹理坐标的偏移量，这样就不用考虑表面的方向了。
理论都有了，下面我们来动手实现视差贴图。
### 视差贴图
我们将使用一个简单的2D平面，在把它发送给GPU之前我们先计算它的切线和副切线向量；和法线贴图教程做的差不多。我们将向平面贴diffuse纹理、法线贴图以及一个位移贴图，你可以点击链接下载。这个例子中我们将视差贴图和法线贴图连用。因为视差贴图生成表面位移了的幻觉，当光照不匹配时这种幻觉就被破坏了。法线贴图通常根据高度贴图生成，法线贴图和高度贴图一起用能保证光照能和位移想匹配。
你可能已经注意到，上面链接上的那个位移贴图和教程一开始的那个高度贴图相比是颜色是相反的。这是因为使用反色高度贴图（也叫深度贴图）去模拟深度比模拟高度更容易。下图反映了这个轻微的改变：
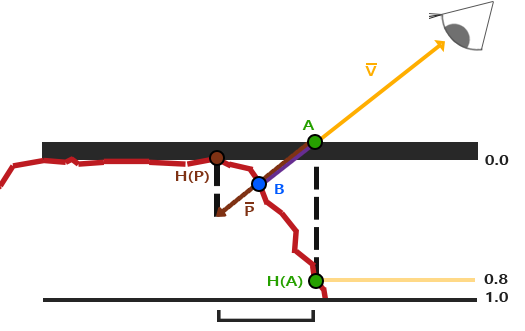
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_depth.png)
我们再次获得A和B，但是这次我们用向量V减去点A的纹理坐标得到P。我们通过在着色器中用1.0减去采样得到的高度贴图中的值来取得深度值，而不再是高度值，或者简单地在图片编辑软件中把这个纹理进行反色操作，就像我们对连接中的那个深度贴图所做的一样。
位移贴图是在像素着色器中实现的，因为三角形表面的所有位移效果都不同。在像素着色器中我们将需要计算fragment到观察者到方向向量V所以我们需要观察者位置和在切线空间中的fragment位置。法线贴图教程中我们已经有了一个顶点着色器，它把这些向量发送到切线空间，所以我们可以复制那个顶点着色器：
```c++
#version 330 core
layout (location = 0) in vec3 position;
layout (location = 1) in vec3 normal;
layout (location = 2) in vec2 texCoords;
layout (location = 3) in vec3 tangent;
layout (location = 4) in vec3 bitangent;
out VS_OUT {
vec3 FragPos;
vec2 TexCoords;
vec3 TangentLightPos;
vec3 TangentViewPos;
vec3 TangentFragPos;
} vs_out;
uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;
uniform vec3 lightPos;
uniform vec3 viewPos;
void main()
{
gl_Position = projection * view * model * vec4(position, 1.0f);
vs_out.FragPos = vec3(model * vec4(position, 1.0));
vs_out.TexCoords = texCoords;
vec3 T = normalize(mat3(model) * tangent);
vec3 B = normalize(mat3(model) * bitangent);
vec3 N = normalize(mat3(model) * normal);
mat3 TBN = transpose(mat3(T, B, N));
vs_out.TangentLightPos = TBN * lightPos;
vs_out.TangentViewPos = TBN * viewPos;
vs_out.TangentFragPos = TBN * vs_out.FragPos;
}
```
在这里有件事很重要，我们需要把position和在切线空间中的观察者的位置viewPos发送给像素着色器。
在像素着色器中，我们实现视差贴图的逻辑。像素着色器看起来会是这样的：
```c++
#version 330 core
out vec4 FragColor;
in VS_OUT {
vec3 FragPos;
vec2 TexCoords;
vec3 TangentLightPos;
vec3 TangentViewPos;
vec3 TangentFragPos;
} fs_in;
uniform sampler2D diffuseMap;
uniform sampler2D normalMap;
uniform sampler2D depthMap;
uniform float height_scale;
vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir);
void main()
{
// Offset texture coordinates with Parallax Mapping
vec3 viewDir = normalize(fs_in.TangentViewPos - fs_in.TangentFragPos);
vec2 texCoords = ParallaxMapping(fs_in.TexCoords, viewDir);
// then sample textures with new texture coords
vec3 diffuse = texture(diffuseMap, texCoords);
vec3 normal = texture(normalMap, texCoords);
normal = normalize(normal * 2.0 - 1.0);
// proceed with lighting code
[...]
}
```
我们定义了一个叫做ParallaxMapping的函数，它把fragment的纹理坐标作和切线空间中的fragment到观察者的方向向量为输入。这个函数返回经位移的纹理坐标。然后我们使用这些经位移的纹理坐标进行diffuse和法线贴图的采样。最后fragment的diffuse颜色和法线向量就正确的对应于表面的经位移的位置上了。
我们来看看ParallaxMapping函数的内部：
```c++
vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir)
{
float height = texture(depthMap, texCoords).r;
vec3 p = viewDir.xy / viewDir.z * (height * height_scale);
return texCoords - p;
}
```
这个相对简单的函数是我们所讨论过的内容的直接表述。我们用本来的纹理坐标texCoords从高度贴图中来采样出当前fragment高度H(A)。然后计算出P，x和y元素在切线空间中，viewDir向量除以它的z元素，用fragment的高度对它进行缩放。我们同时引入额一个height_scale的uniform，来进行一些额外的控制，因为视差效果如果没有一个缩放参数通常会过于强烈。然后我们用P减去纹理坐标来获得最终的经过位移纹理坐标。
有一个地方需要注意，就是viewDir.xy除以viewDir.z那里。因为viewDir向量是经过了标准化的，viewDir.z会在0.0到1.0之间的某处。当viewDir大致平行于表面时，它的z元素接近于0.0，除法会返回比viewDir垂直于表面的时候更大的P向量。所以基本上我们增加了P的大小，当以一个角度朝向一个表面相比朝向顶部时它对纹理坐标会进行更大程度的缩放；这回在角上获得更大的真实度。
有些人更喜欢在等式中不使用viewDir.z，因为普通的视差贴图会在角上产生不想要的结果；这个技术叫做有偏移量限制的视差贴图（Parallax Mapping with Offset Limiting）。选择哪一个技术是个人偏好问题，但我倾向于普通的视差贴图。
最后的纹理坐标随后被用来进行采样（diffuse和法线）贴图，下图所展示的位移效果中height_scale等于1：
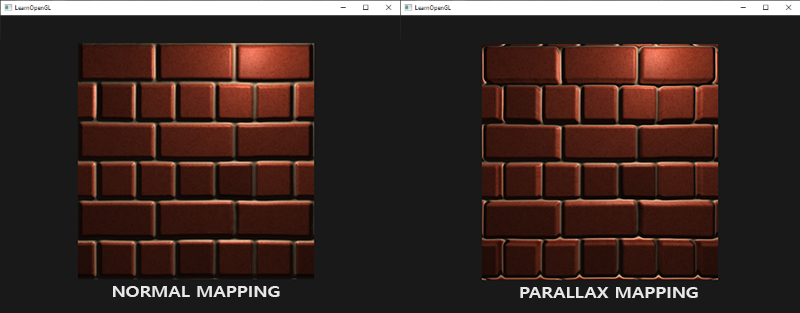
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping.png)
这里你会看到只用法线贴图和与视差贴图相结合的法线贴图的不同之处。因为视差贴图尝试模拟深度，它实际上能够根据你观察它们的方向使砖块叠加到其他砖块上。
在视差贴图的那个平面里你仍然能看到在边上有古怪的失真。原因是在平面的边缘上，纹理坐标超出了0到1的范围进行采样，根据纹理的环绕方式导致了不真实的结果。解决的方法是当它超出默认纹理坐标范围进行采样的时候就丢弃这个fragment：
```c++
texCoords = ParallaxMapping(fs_in.TexCoords, viewDir);
if(texCoords.x > 1.0 || texCoords.y > 1.0 || texCoords.x < 0.0 || texCoords.y < 0.0)
discard;
```
丢弃了超出默认范围的纹理坐标的所有fragment，视差贴图的表面边缘给出了正确的结果。注意，这个技巧不能在所有类型的表面上都能工作，但是应用于平面上它还是能够是平面看起来真的进行位移了：
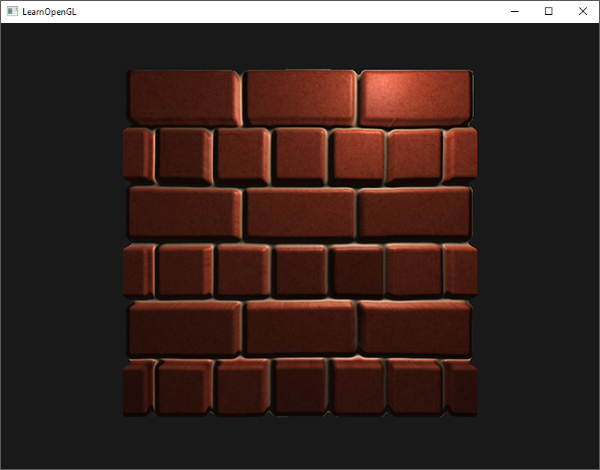
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_edge_fix.png)
你可以在这里找到[源代码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping)，以及[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping&type=vertex)和[像素](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping&type=fragment)着色器。
看起来不错，运行起来也很快，因为我们只要给视差贴图提供一个额外的纹理样本就能工作。当从一个角度看过去的时候，会有一些问题产生（和法线贴图相似），陡峭的地方会产生不正确的结果，从下图你可以看到：
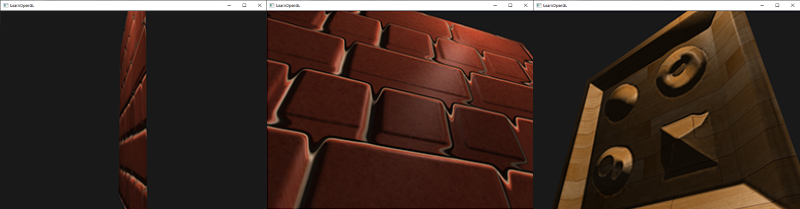
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_issues.png)
问题的原因是这只是一个大致近似的视差映射。还有一些技巧让我们在陡峭的高度上能够获得几乎完美的结果，即使当以一定角度观看的时候。例如，我们不再使用单一样本，取而代之使用多样本来找到最近点B会得到怎样的结果？
### 陡峭视差映射（Steep Parallax Mapping）
陡峭视差映射是视差映射的扩展，原则是一样的，但不是使用一个样本而是多个样本来确定向量P到B。它能得到更好的结果，它将总深度范围分布到同一个深度/高度的多个层中。从每个层中我们沿着P方向移动采样纹理坐标，直到我们找到了一个采样得到的低于当前层的深度值的深度值。看看下面的图片：
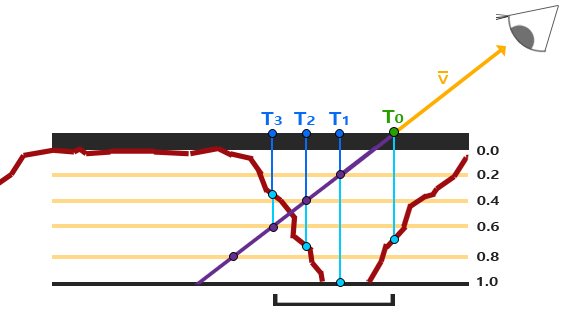
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_steep_parallax_mapping_diagram.png)
我们从上到下遍历深度层，我们把每个深度层和储存在深度贴图中的它的深度值进行对比。如果这个层的深度值小于深度贴图的值，就意味着这一层的P向量部分在表面之下。我们继续这个处理过程直到有一层的深度高于储存在深度贴图中的值：这个点就在（经过位移的）表面下方。
这个例子中我们可以看到第二层(D(2) = 0.73)的深度贴图的值仍低于第二层的深度值0.4，所以我们继续。下一次迭代，这一层的深度值0.6大于深度贴图中采样的深度值(D(3) = 0.37)。我们便可以假设第三层向量P是可用的位移几何位置。我们可以用从向量P3的纹理坐标偏移T3来对fragment的纹理坐标进行位移。你可以看到随着深度曾的增加精确度也在提高。
为实现这个技术，我们只需要改变ParallaxMapping函数，因为所有需要的变量都有了：
```c++
vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir)
{
// number of depth layers
const float numLayers = 10;
// calculate the size of each layer
float layerDepth = 1.0 / numLayers;
// depth of current layer
float currentLayerDepth = 0.0;
// the amount to shift the texture coordinates per layer (from vector P)
vec2 P = viewDir.xy * height_scale;
float deltaTexCoords = P / numLayers;
[...]
}
```
我们先定义层的数量，计算每一层的深度，最后计算纹理坐标偏移，每一层我们必须沿着P的方向进行移动。
然后我们遍历所有层，从上开始，知道找到小于这一层的深度值的深度贴图值：
```c++
// get initial values
vec2 currentTexCoords = texCoords;
float currentDepthMapValue = texture(depthMap, currentTexCoords).r;
while(currentLayerDepth < currentDepthMapValue)
{
// shift texture coordinates along direction of P
currentTexCoords -= deltaTexCoords;
// get depthmap value at current texture coordinates
currentDepthMapValue = texture(depthMap, currentTexCoords).r;
// get depth of next layer
currentLayerDepth += layerDepth;
}
return texCoords - currentTexCoords;
```
这里我们循环每一层深度，直到沿着P向量找到第一个返回低于（位移）表面的深度的纹理坐标偏移量。从fragment的纹理坐标减去最后的偏移量，来得到最终的经过位移的纹理坐标向量，这次就比传统的视差映射更精确了。
有10个样本砖墙从一个角度看上去就已经很好了，但是当有一个强前面展示的木制表面一样陡峭的表面时，陡峭的视差映射的威力就显示出来了：
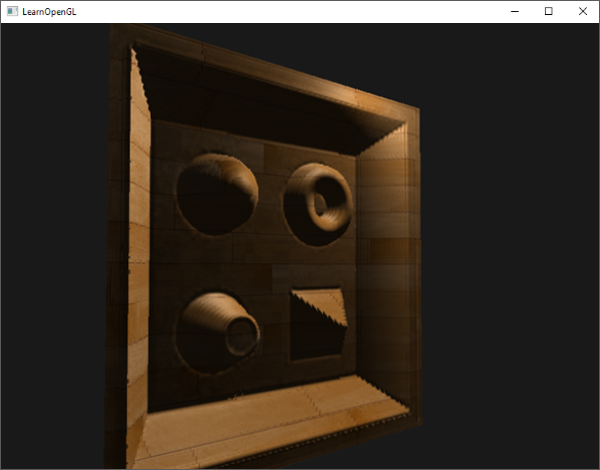
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_steep_parallax_mapping.png)
我们可以通过对视差贴图的一个属性的利用，对算法进行一点提升。当垂直看一个表面的时候纹理时位移比以一定角度看时的小。我们可以在垂直看时使用更少的样本，以一定角度看时增加样本数量：
```c++
const float minLayers = 8;
const float maxLayers = 32;
float numLayers = mix(maxLayers, minLayers, abs(dot(vec3(0.0, 0.0, 1.0), viewDir)));
```
这里我们得到viewDir和正z方向的点乘，使用它的结果根据我们看向表面的角度调整样本数量（注意正z方向等于切线空间中的表面的法线）。如果我们所看的方向平行于表面，我们就是用32层。
你可以在这里找到最新的像素着色器代码。这里也提供木制玩具箱的表面贴图：diffuse、法线、深度。
陡峭视差贴图同样有自己的问题。因为这个技术是基于有限的样本数量的，我们会遇到锯齿效果以及图层之间有明显的断层：
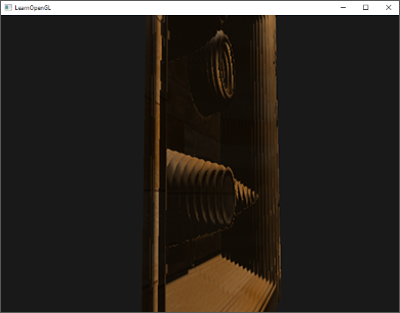
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_steep_artifact.png)
我们可以通过增加样本的方式减少这个问题，但是很快就会花费很多性能。有些旨在修复这个问题的方法：不适用低于表面的第一个位置，而是在两个接近的深度层进行插值找出更匹配B的。
两种最流行的解决方法叫做Relief Parallax Mapping和Parallax Occlusion Mapping，Relief Parallax Mapping更精确一些，但是比Parallax Occlusion Mapping性能开销更多。因为Parallax Occlusion Mapping的效果和前者差不多但是效率更高，因此这种方式更经常使用，所以我们将在下面讨论一下。
### Parallax Occlusion Mapping
Parallax Occlusion Mapping和陡峭视差映射的原则相同，但不是用触碰的第一个深度层的纹理坐标，而是在触碰之前和之后，在深度层之间进行线性插值。我们根据表面的高度距离啷个深度层的深度层值的距离来确定线性插值的大小。看看下面的图pain就能了解它是如何工作的：
[](http://learnopengl.com/img/advanced-lighting/parallax_mapping_parallax_occlusion_mapping_diagram.png)
你可以看到大部分和陡峭视差映射一样，不一样的地方是有个额外的步骤，两个深度层的纹理坐标围绕着交叉点的线性插值。这也是近似的，但是比陡峭视差映射更精确。
Parallax Occlusion Mapping的代码基于陡峭视差映射，所以并不难：
```c++
[...] // steep parallax mapping code here
// get texture coordinates before collision (reverse operations)
vec2 prevTexCoords = currentTexCoords + deltaTexCoords;
// get depth after and before collision for linear interpolation
float afterDepth = currentDepthMapValue - currentLayerDepth;
float beforeDepth = texture(depthMap, prevTexCoords).r - currentLayerDepth + layerDepth;
// interpolation of texture coordinates
float weight = afterDepth / (afterDepth - beforeDepth);
vec2 finalTexCoords = prevTexCoords * weight + currentTexCoords * (1.0 - weight);
return finalTexCoords;
```
在对（位移的）表面几何进行交叉，找到深度层之后，我们获取交叉前的纹理坐标。然后我们计算来自相应深度层的几何之间的深度之间的距离，并在两个值之间进行插值。线性插值的方式是在两个层的纹理坐标之间进行的基础插值。函数最后返回最终的经过插值的纹理坐标。
Parallax Occlusion Mapping的效果非常好，尽管有一些可以看到的轻微的不真实和锯齿的问题，这仍是一个好交易，因为除非是放得非常大或者观察角度特别陡，否则也看不到。
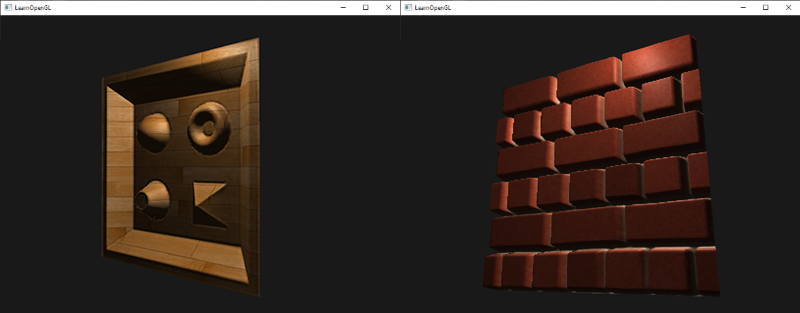
![](http://learnopengl.com/img/advanced-lighting/parallax_mapping_parallax_occlusion_mapping.png)
你可以在这里找到[源代码](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping)，及其[顶点](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping&type=vertex)和[像素](http://www.learnopengl.com/code_viewer.php?code=advanced-lighting/parallax_mapping_occlusion&type=fragment)着色器。
视差贴图是提升场景细节非常好的技术，但是使用的时候还是要考虑到它会带来一点不自然。大多数时候视差贴图用在地面和墙壁表面，这种情况下查明表面的轮廓并不容易，同时观察角度往往趋向于垂直于表面。这样视差贴图的不自然也就很难能被注意到了，对于提升物体的细节可以祈祷难以置信的效果。
### 附加资源
[Parallax Occlusion Mapping in GLSL](http://sunandblackcat.com/tipFullView.php?topicid=28)：sunandblackcat.com上的视差贴图教程。
[How Parallax Displacement Mapping Works](https://www.youtube.com/watch?v=xvOT62L-fQI)：TheBennyBox的关于视差贴图原理的视频教程。

154
docs/05 Advanced Lighting/06 HDR.md
View File

@@ -1,154 +0,0 @@
本文作者JoeyDeVries，由Meow J翻译自[http://learnopengl.com](http://learnopengl.com/#!Advanced-Lighting/HDR)
## HDR
一般来说，当存储在帧缓冲(Framebuffer)中时，亮度和颜色的值是默认被限制在0.0到1.0之间的. 这个看起来无辜的语句使我们一直将亮度与颜色的值设置在这个范围内，尝试着与场景契合. 这样是能够运行的，也能给出还不错的效果. 但是如果我们遇上了一个特定的区域，其中有多个亮光源使这些数值总和超过了1.0，又会发生什么呢? 答案是这些片段中超过1.0的亮度或者颜色值会被约束在1.0, 从而导致场景混成一片，难以分辨:
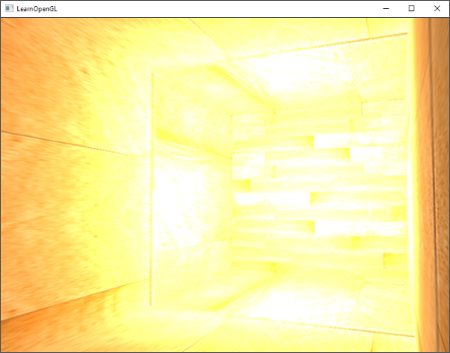
![](http://learnopengl.com/img/advanced-lighting/hdr_clamped.png)
这是由于大量片段的颜色值都非常接近1.0，在很大一个区域内每一个亮的片段都有相同的白色. 这损失了很多的细节，使场景看起来非常假.
解决这个问题的一个方案是减小光源的强度从而保证场景内没有一个片段亮于1.0. 然而这并不是一个好的方案，因为你需要使用不切实际的光照参数. 一个更好的方案是让颜色暂时超过1.0，然后将其转换至0.0到1.0的区间内，从而防止损失细节.
显示器被限制为只能显示值为0.0到1.0间的颜色，但是在光照方程中却没有这个限制. 通过使片段的颜色超过1.0，我们有了一个更大的颜色范围，这也被称作HDR(High Dynamic Range, 高动态范围). 有了HDR，亮的东西可以变得非常亮，暗的东西可以变得非常暗，而且充满细节.
HDR原本只是被运用在摄影上，摄影师对同一个场景采取不同曝光拍多张照片，捕捉大范围的色彩值. 这些图片被合成为HDR图片，从而综合不同的曝光等级使得大范围的细节可见. 看下面这个例子，左边这张图片在被光照亮的区域充满细节，但是在黑暗的区域就什么都看不见了；但是右边这张图的高曝光却可以让之前看不出来的黑暗区域显现出来.
![](http://learnopengl.com/img/advanced-lighting/hdr_image.png)
这与我们眼睛工作的原理非常相似，也是HDR渲染的基础. 当光线很弱的啥时候，人眼会自动调整从而使过暗和过亮的部分变得更清晰，就像人眼有一个能自动根据场景亮度调整的自动曝光滑块.
HDR渲染和其很相似，我们允许用更大范围的颜色值渲染从而获取大范围的黑暗与明亮的场景细节，最后将所有HDR值转换成在[0.0, 1.0]范围的LDR(Low Dynamic Range,低动态范围). 转换HDR值到LDR值得过程叫做色调映射(Tone Mapping)，现在现存有很多的色调映射算法，这些算法致力于在转换过程中保留尽可能多的HDR细节. 这些色调映射算法经常会包含一个选择性倾向黑暗或者明亮区域的参数.
在实时渲染中，HDR不仅允许我们超过LDR的范围[0.0, 1.0]与保留更多的细节，同时还让我们能够根据光源的**真实**强度指定它的强度. 比如太阳有比闪光灯之类的东西更高的强度，那么我们为什么不这样子设置呢?(比如说设置一个10.0的漫亮度) 这允许我们用更现实的光照参数恰当地配置一个场景的光照，而这在LDR渲染中是不能实现的，因为他们会被上限约束在1.0.
因为显示器只能显示在0.0到1.0范围之内的颜色，我们肯定要做一些转换从而使得当前的HDR颜色值符合显示器的范围. 简单地取平均值重新转换这些颜色值并不能很好的解决这个问题，因为明亮的地方会显得更加显著. 我们能做的是用一个不同的方程与/或曲线来转换这些HDR值到LDR值，从而给我们对于场景的亮度完全掌控，这就是之前说的色调变换，也是HDR渲染的最终步骤.
### 浮点帧缓冲(Floating Point Framebuffers)
在实现HDR渲染之前，我们首先需要一些防止颜色值在每一个片段着色器运行后被限制约束的方法. 当帧缓冲使用了一个标准化的定点格式(像`GL_RGB`)为其颜色缓冲的内部格式，OpenGL会在将这些值存入帧缓冲前自动将其约束到0.0到1.0之间. 这一操作对大部分帧缓冲格式都是成立的，除了专门用来存放被拓展范围值的浮点格式.
当一个帧缓冲的颜色缓冲的内部格式被设定成了`GL_RGB16F`, `GL_RGBA16F`, `GL_RGB32F` 或者`GL_RGBA32F`时，这些帧缓冲被叫做浮点帧缓冲(Floating Point Framebuffer)，浮点帧缓冲可以存储超过0.0到1.0范围的浮点值，所以非常适合HDR渲染.
想要创建一个浮点帧缓冲，我们只需要改变颜色缓冲的内部格式参数就行了（注意`GL_FLOAT`参数):
```c++
glBindTexture(GL_TEXTURE_2D, colorBuffer);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB16F, SCR_WIDTH, SCR_HEIGHT, 0, GL_RGB, GL_FLOAT, NULL);
```
默认的帧缓冲默认一个颜色分量只占用8位(bits). 当使用一个使用32位每颜色分量的浮点帧缓冲时(使用`GL_RGB32F` 或者`GL_RGBA32F`)，我们需要四倍的内存来存储这些颜色. 所以除非你需要一个非常高的精确度，32位不是必须的，使用`GLRGB16F`就足够了.
有了一个带有浮点颜色缓冲的帧缓冲，我们可以放心渲染场景到这个帧缓冲中. 在这个教程的例子当中，我们先渲染一个光照的场景到浮点帧缓冲中，之后再在一个铺屏四边形(Screen-filling Quad)上应用这个帧缓冲的颜色缓冲，代码会是这样子:
```c++
glBindFramebuffer(GL_FRAMEBUFFER, hdrFBO);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
// [...] 渲染(光照的)场景
glBindFramebuffer(GL_FRAMEBUFFER, 0);
// 现在使用一个不同的着色器将HDR颜色缓冲渲染至2D铺屏四边形上
hdrShader.Use();
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_2D, hdrColorBufferTexture);
RenderQuad();
```
这里场景的颜色值存在一个可以包含任意颜色值的浮点颜色缓冲中，值可能是超过1.0的. 这个简单的演示中，场景被创建为一个被拉伸的立方体通道和四个点光源，其中一个非常亮的在隧道的尽头:
```c++
std::vector<glm::vec3> lightColors;
lightColors.push_back(glm::vec3(200.0f, 200.0f, 200.0f));
lightColors.push_back(glm::vec3(0.1f, 0.0f, 0.0f));
lightColors.push_back(glm::vec3(0.0f, 0.0f, 0.2f));
lightColors.push_back(glm::vec3(0.0f, 0.1f, 0.0f));
```
渲染至浮点帧缓冲和渲染至一个普通的帧缓冲是一样的. 新的东西就是这个的`hdrShader`的片段着色器，用来渲染最终拥有浮点颜色缓冲纹理的2D四边形. 我们来定义一个简单的直通片段着色器(Pass-through Fragment Shader):
```c++
#version 330 core
out vec4 color;
in vec2 TexCoords;
uniform sampler2D hdrBuffer;
void main()
{
vec3 hdrColor = texture(hdrBuffer, TexCoords).rgb;
color = vec4(hdrColor, 1.0);
}
```
这里我们直接采样了浮点颜色缓冲并将其作为片段着色器的输出. 然而，这个2D四边形的输出是被直接渲染到默认的帧缓冲中，导致所有片段着色器的输出值被约束在0.0到1.0间，尽管我们已经有了一些存在浮点颜色纹理的值超过了1.0.
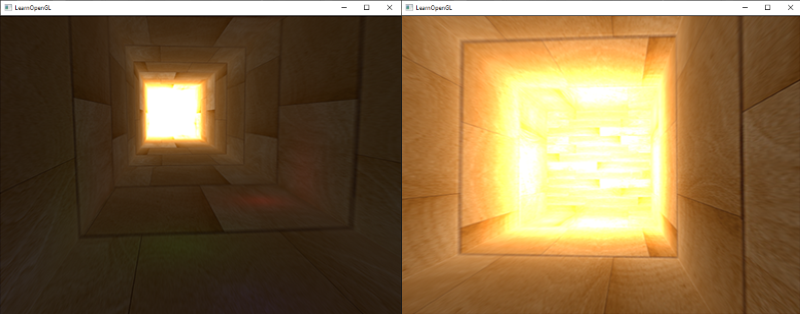
![](http://learnopengl.com/img/advanced-lighting/hdr_direct.png)
很明显，在隧道尽头的强光的值被约束在1.0，因为一大块区域都是白色的，过程中超过1.0的地方损失了所有细节. 因为我们直接转换HDR值到LDR值，这就像我们根本就没有应用HDR一样. 为了修复这个问题我们需要做的是无损转化所有浮点颜色值回0.0-1.0范围中. 我们需要应用到色调映射.
### 色调映射(Tone Mapping)
色调映射是一个损失很小的转换浮点颜色值至我们所需的LDR[0.0, 1.0]范围内的过程，通常会伴有特定的风格的色平衡(Stylistic Color Balance).
最简单的色调映射算法是Reinhard色调映射，它涉及到分散整个HDR颜色值到LDR颜色值上，所有的值都有对应. Reinhard色调映射算法平均得将所有亮度值分散到LDR上. 我们将Reinhard色调映射应用到之前的片段着色器上，并且为了更好的测量加上一个Gamma校正过滤(包括SRGB纹理的使用):
```c++
void main()
{
const float gamma = 2.2;
vec3 hdrColor = texture(hdrBuffer, TexCoords).rgb;
// Reinhard色调映射
vec3 mapped = hdrColor / (hdrColor + vec3(1.0));
// Gamma校正
mapped = pow(mapped, vec3(1.0 / gamma));
color = vec4(mapped, 1.0);
}
```
有了Reinhard色调映射的应用，我们不再会在场景明亮的地方损失细节. 当然，这个算法是倾向明亮的区域的，暗的区域会不那么精细也不那么有区分度.
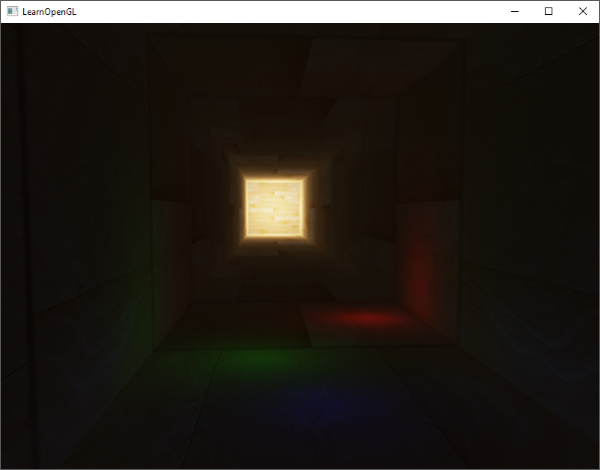
![](http://learnopengl.com/img/advanced-lighting/hdr_reinhard.png)
现在你可以看到在隧道的尽头木头纹理变得可见了. 用了这个非常简单地色调映射算法，我们可以合适的看到存在浮点帧缓冲中整个范围的HDR值，给我们对于无损场景光照精确的控制.
另一个有趣的色调映射应用是曝光(Exposure)参数的使用. 你可能还记得之前我们在介绍里讲到的，HDR图片包含在不同曝光等级的细节. 如果我们有一个场景要展现日夜交替，我们当然会在白天使用低曝光，在夜间使用高曝光，就像人眼调节方式一样. 有了这个曝光参数，我们可以去设置可以同时在白天和夜晚不同光照条件工作的光照参数，我们只需要调整曝光参数就行了.
一个简单的曝光色调映射算法会像这样:
```c++
uniform float exposure;
void main()
{
const float gamma = 2.2;
vec3 hdrColor = texture(hdrBuffer, TexCoords).rgb;
// 曝光色调映射
vec3 mapped = vec3(1.0) - exp(-hdrColor * exposure);
// Gamma校正
mapped = pow(mapped, vec3(1.0 / gamma));
color = vec4(mapped, 1.0);
}
```
在这里我们将`exposure`定义为默认为1.0的`uniform`，从而允许我们更加精确设定我们是要注重黑暗还是明亮的区域的HDR颜色值. 举例来说，高曝光值会使隧道的黑暗部分显示更多的细节，然而低曝光值会显著减少黑暗区域的细节，但允许我们看到更多明亮区域的细节. 下面这组图片展示了在不同曝光值下的通道:
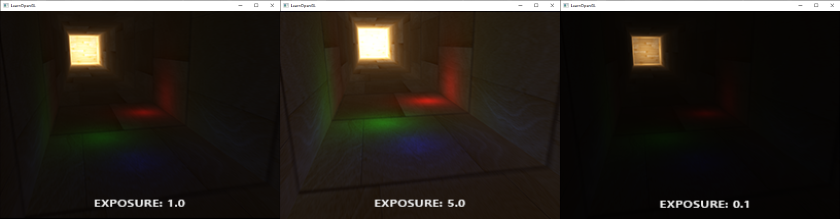
![](http://learnopengl.com/img/advanced-lighting/hdr_exposure.png)
这个图片清晰地展示了HDR渲染的优点. 通过改变曝光等级，我们可以看见场景的很多细节，而这些细节可能在LDR渲染中都被丢失了. 比如说隧道尽头，在正常曝光下木头结构隐约可见，但用低曝光木头的花纹就可以清晰看见了. 对于近处的木头花纹来说，在高曝光下会能更好的看见.
你可以在[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/hdr "这里")找到这个演示的源码和HDR的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/hdr&type=vertex "顶点")和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/hdr&type=fragment "片段")着色器.
### HDR拓展
在这里展示的两个色调映射算法仅仅是大量(更先进)的色调映射算法中的一小部分，这些算法各有长短.一些色调映射算法倾向于特定的某种颜色/强度，也有一些算法同时显示低于高曝光颜色从而能够显示更加多彩和精细的图像. 也有一些技巧被称作自动曝光调整(Automatic Exposure Adjustment)或者叫人眼适应(Eye Adaptation)技术，它能够检测前一帧场景的亮度并且缓慢调整曝光参数模仿人眼使得场景在黑暗区域逐渐变亮或者在明亮区域逐渐变暗.
HDR渲染的真正优点在庞大和复杂的场景中应用复杂光照算法会被显示出来，但是出于教学目的创建这样复杂的演示场景是很困难的，这个教程用的场景是很小的，而且缺乏细节. 但是如此简单的演示也是能够显示出HDR渲染的一些优点: 在明亮和黑暗区域无细节损失，因为它们可以由色调映射重新获取；多个光照的叠加不会导致亮度被约束的区域；光照可以被设定为他们原来的亮度而不是被LDR值限定. 而且，HDR渲染也使一些有趣的效果更加可行和真实; 其中一个效果叫做泛光(Bloom)，我们将在下一节讨论他.
### 附加资源
- [如果泛光效果不被应用HDR渲染还有好处吗?](http://gamedev.stackexchange.com/questions/62836/does-hdr-rendering-have-any-benefits-if-bloom-wont-be-applied): 一个StackExchange问题，其中有一个答案非常详细地解释HDR渲染的好处.
- [什么是色调映射? 它与HDR有什么联系?](http://photo.stackexchange.com/questions/7630/what-is-tone-mapping-how-does-it-relate-to-hdr): 另一个非常有趣的答案，用了大量图片解释色调映射.

268
docs/05 Advanced Lighting/07 Bloom.md
View File

@@ -1,268 +0,0 @@
本文作者JoeyDeVries，由Django翻译自[http://learnopengl.com](http://learnopengl.com)
## 泛光(Bloom)
明亮的光源和区域经常很难向观察者表达出来，因为监视器的亮度范围是有限的。一种区分明亮光源的方式是使它们在监视器上发出光芒，光源的的光芒向四周发散。这样观察者就会产生光源或亮区的确是强光区。（译注：这个问题的提出简单来说是为了解决这样的问题：例如有一张在阳光下的白纸，白纸在监视器上显示出是出白色，而前方的太阳也是纯白色的，所以基本上白纸和太阳就是一样的了，给太阳加一个光晕，这样太阳看起来似乎就比白纸更亮了）
光晕效果可以使用一个后处理特效bloom来实现。bloom使所有明亮区域产生光晕效果。下面是一个使用了和没有使用光晕的对比（图片生成自虚幻引擎）：
![](http://learnopengl.com/img/advanced-lighting/bloom_example.png)
Bloom是我们能够注意到一个明亮的物体真的有种明亮的感觉。bloom可以极大提升场景中的光照效果，并提供了极大的效果提升，尽管做到这一切只需一点改变。
Bloom和HDR结合使用效果很好。常见的一个误解是HDR和bloom是一样的，很多人认为两种技术是可以互换的。但是它们是两种不同的技术，用于各自不同的目的上。可以使用默认的8位精确度的帧缓冲，也可以在不使用bloom效果的时候，使用HDR。只不过在有了HDR之后再实现bloom就更简单了。
为实现bloom，我们像平时那样渲染一个有光场景，提取出场景的HDR颜色缓冲以及只有这个场景明亮区域可见的图片。被提取的带有亮度的图片接着被模糊，结果被添加到HDR场景上面。
我们来一步一步解释这个处理过程。我们在场景中渲染一个带有4个立方体形式不同颜色的明亮的光源。带有颜色的发光立方体的亮度在1.5到15.0之间。如果我们将其渲染至HDR颜色缓冲，场景看起来会是这样的：
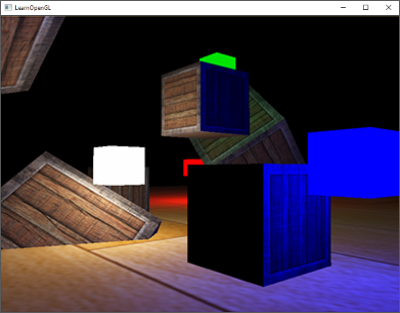
![](http://learnopengl.com/img/advanced-lighting/bloom_scene.png)
我们得到这个HDR颜色缓冲纹理，提取所有超出一定亮度的fragment。这样我们就会获得一个只有fragment超过了一定阈限的颜色区域：
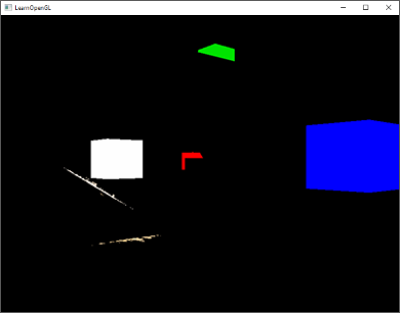
![](http://learnopengl.com/img/advanced-lighting/bloom_extracted.png)
我们将这个超过一定亮度阈限的纹理进行模糊。bloom效果的强度很大程度上被模糊过滤器的范围和强度所决定。
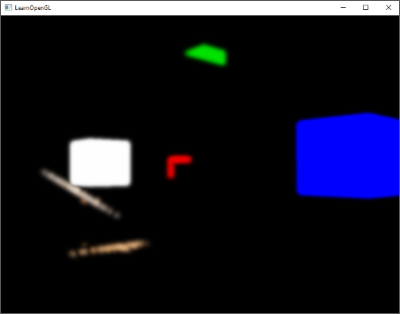
![](http://learnopengl.com/img/advanced-lighting/bloom_blurred.png)
最终的被模糊化的纹理就是我们用来获得发出光晕效果的东西。这个已模糊的纹理要添加到原来的HDR场景纹理的上部。因为模糊过滤器的应用明亮区域发出光晕，所以明亮区域在长和宽上都有所扩展。
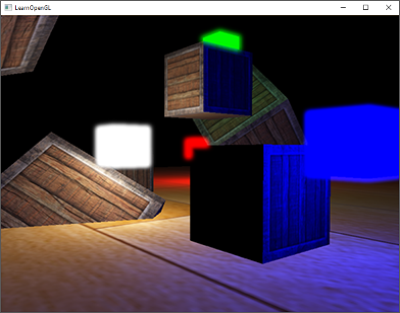
![](http://learnopengl.com/img/advanced-lighting/bloom_small.png)
bloom本身并不是个复杂的技术，但很难获得正确的效果。它的品质很大程度上取决于所用的模糊过滤器的质量和类型。简单的改改模糊过滤器就会极大的改变bloom效果的品质。
下面这几步就是bloom后处理特效的过程，它总结了实现bloom所需的步骤。
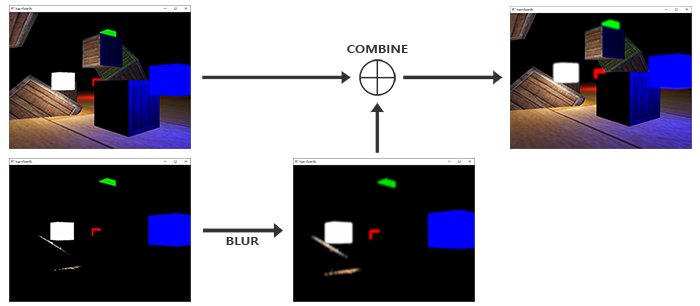
![](http://learnopengl.com/img/advanced-lighting/bloom_steps.png)
首先我们需要根据一定的阈限提取所有明亮的颜色。我们先来做这件事。
### 提取亮色
第一步我们要从渲染出来的场景中提取两张图片。我们可以渲染场景两次，每次使用一个不同的不同的着色器渲染到不同的帧缓冲中，但我们可以使用一个叫做MRT（Multiple Render Targets多渲染目标）的小技巧，这样我们就能定义多个像素着色器了；有了它我们还能够在一个单独渲染处理中提取头两个图片。在像素着色器的输出前，我们指定一个布局location标识符，这样我们便可控制一个像素着色器写入到哪个颜色缓冲：
```c++
layout (location = 0) out vec4 FragColor;
layout (location = 1) out vec4 BrightColor;
```
只有我们真的具有多个地方可写的时候这才能工作。使用多个像素着色器输出的必要条件是，有多个颜色缓冲附加到了当前绑定的帧缓冲对象上。你可能从帧缓冲教程那里回忆起，当把一个纹理链接到帧缓冲的颜色缓冲上时，我们可以指定一个颜色附件。直到现在，我们一直使用着GL_COLOR_ATTACHMENT0，但通过使用GL_COLOR_ATTACHMENT1，我们可以得到一个附加了两个颜色缓冲的帧缓冲对象：
```c++
// Set up floating point framebuffer to render scene to
GLuint hdrFBO;
glGenFramebuffers(1, &hdrFBO);
glBindFramebuffer(GL_FRAMEBUFFER, hdrFBO);
GLuint colorBuffers[2];
glGenTextures(2, colorBuffers);
for (GLuint i = 0; i < 2; i++)
{
glBindTexture(GL_TEXTURE_2D, colorBuffers[i]);
glTexImage2D(
GL_TEXTURE_2D, 0, GL_RGB16F, SCR_WIDTH, SCR_HEIGHT, 0, GL_RGB, GL_FLOAT, NULL
);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
// attach texture to framebuffer
glFramebufferTexture2D(
GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0 + i, GL_TEXTURE_2D, colorBuffers[i], 0
);
}
```
我们需要显式告知OpenGL我们正在通过glDrawBuffers渲染到多个颜色缓冲，否则OpenGL只会渲染到帧缓冲的第一个颜色附件，而忽略所有其他的。我们可以通过传递多个颜色附件的枚举来做这件事，我们以下面的操作进行渲染：
```c++
GLuint attachments[2] = { GL_COLOR_ATTACHMENT0, GL_COLOR_ATTACHMENT1 };
glDrawBuffers(2, attachments);
```
当渲染到这个帧缓冲中的时候，一个着色器使用一个布局location修饰符，那么fragment就会用相应的颜色缓冲就会被用来渲染。这很棒，因为这样省去了我们为提取明亮区域的额外渲染步骤，因为我们现在可以直接从将被渲染的fragment提取出它们：
```c++
#version 330 core
layout (location = 0) out vec4 FragColor;
layout (location = 1) out vec4 BrightColor;
[...]
void main()
{
[...] // first do normal lighting calculations and output results
FragColor = vec4(lighting, 1.0f);
// Check whether fragment output is higher than threshold, if so output as brightness color
float brightness = dot(FragColor.rgb, vec3(0.2126, 0.7152, 0.0722));
if(brightness > 1.0)
BrightColor = vec4(FragColor.rgb, 1.0);
}
```
这里我们先正常计算光照，将其传递给第一个像素着色器的输出变量FragColor。然后我们使用当前储存在FragColor的东西来决定它的亮度是否超过了一定阈限。我们通过恰当地将其转为灰度的方式计算一个fragment的亮度，如果它超过了一定阈限，我们就把颜色输出到第二个颜色缓冲，那里保存着所有亮部；渲染发光的立方体也是一样的。
这也说明了为什么bloom在HDR基础上能够运行得很好。因为HDR中，我们可以将颜色值指定超过1.0这个默认的范围，我们能够得到对一个图像中的亮度的更好的控制权。没有HDR我们必须将阈限设置为小于1.0的数，虽然可行，但是亮部很容易变得很多，这就导致光晕效果过重。
有了两个颜色缓冲，我们就有了一个正常场景的图像和一个提取出的亮区的图像；这些都在一个渲染步骤中完成。
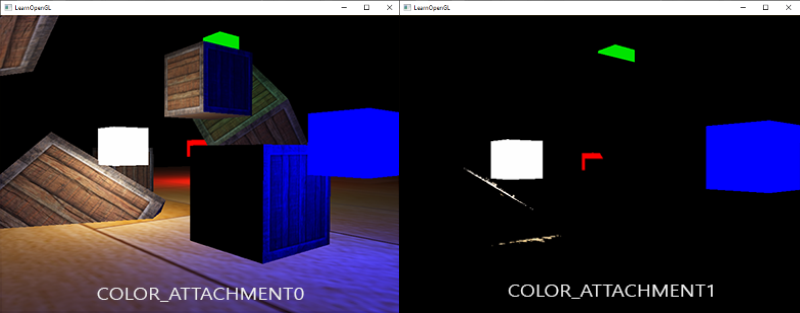
![](http://learnopengl.com/img/advanced-lighting/bloom_attachments.png)
有了一个提取出的亮区图像，我们现在就要把这个图像进行模糊处理。我们可以使用帧缓冲教程后处理部分的那个简单的盒子过滤器，但不过我们最好还是使用一个更高级的更漂亮的模糊过滤器：高斯模糊。
### 高斯模糊
在后处理教程那里，我们采用的模糊是一个图像中所有周围像素的均值，它的确为我们提供了一个简易实现的模糊，但是效果并不好。高斯模糊基于高斯曲线，高斯曲线通常被描述为一个钟形曲线，中间的值达到最大化，随着距离的增加，两边的值不断减少。高斯曲线在数学上有不同的形式，但是通常是这样的形状：
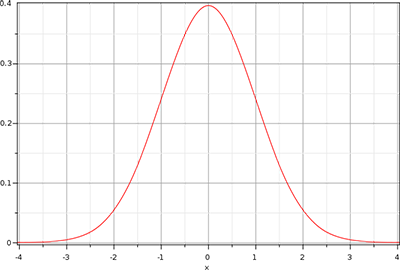
![](http://learnopengl.com/img/advanced-lighting/bloom_gaussian.png)
高斯曲线在它的中间处的面积最大，使用它的值作为权重使得近处的样本拥有最大的优先权。比如，如果我们从fragment的32×32的四方形区域采样，这个权重随着和fragment的距离变大逐渐减小；通常这会得到更好更真实的模糊效果，这种模糊叫做高斯模糊。
要实现高斯模糊过滤我们需要一个二维四方形作为权重，从这个二维高斯曲线方程中去获取它。然而这个过程有个问题，就是很快会消耗极大的性能。以一个32×32的模糊kernel为例，我们必须对每个fragment从一个纹理中采样1024次！
幸运的是，高斯方程有个非常巧妙的特性，它允许我们把二维方程分解为两个更小的方程：一个描述水平权重，另一个描述垂直权重。我们首先用水平权重在整个纹理上进行水平模糊，然后在经改变的纹理上进行垂直模糊。利用这个特性，结果是一样的，但是可以节省难以置信的性能，因为我们现在只需做32+32次采样，不再是1024了！这叫做两步高斯模糊。
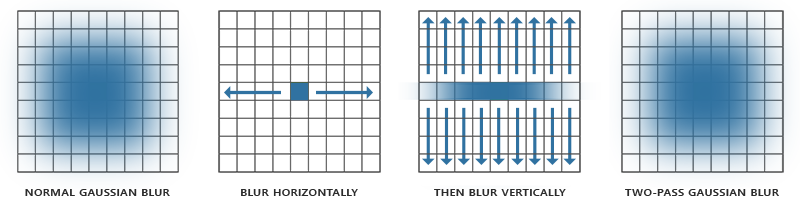
![](http://learnopengl.com/img/advanced-lighting/bloom_gaussian_two_pass.png)
这意味着我们如果对一个图像进行模糊处理，至少需要两步，最好使用帧缓冲对象做这件事。具体来说，我们将实现像乒乓球一样的帧缓冲来实现高斯模糊。它的意思是，有一对儿帧缓冲，我们把另一个帧缓冲的颜色缓冲放进当前的帧缓冲的颜色缓冲中，使用不同的着色效果渲染指定的次数。基本上就是不断地切换帧缓冲和纹理去绘制。这样我们先在场景纹理的第一个缓冲中进行模糊，然后在把第一个帧缓冲的颜色缓冲放进第二个帧缓冲进行模糊，接着，将第二个帧缓冲的颜色缓冲放进第一个，循环往复。
在我们研究帧缓冲之前，先讨论高斯模糊的像素着色器：
```c++
#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
uniform sampler2D image;
uniform bool horizontal;
uniform float weight[5] = float[] (0.227027, 0.1945946, 0.1216216, 0.054054, 0.016216);
void main()
{
vec2 tex_offset = 1.0 / textureSize(image, 0); // gets size of single texel
vec3 result = texture(image, TexCoords).rgb * weight[0]; // current fragment's contribution
if(horizontal)
{
for(int i = 1; i < 5; ++i)
{
result += texture(image, TexCoords + vec2(tex_offset.x * i, 0.0)).rgb * weight[i];
result += texture(image, TexCoords - vec2(tex_offset.x * i, 0.0)).rgb * weight[i];
}
}
else
{
for(int i = 1; i < 5; ++i)
{
result += texture(image, TexCoords + vec2(0.0, tex_offset.y * i)).rgb * weight[i];
result += texture(image, TexCoords - vec2(0.0, tex_offset.y * i)).rgb * weight[i];
}
}
FragColor = vec4(result, 1.0);
}
```
这里我们使用一个比较小的高斯权重做例子，每次我们用它来指定当前fragment的水平或垂直样本的特定权重。你会发现我们基本上是将模糊过滤器根据我们在uniform变量horizontal设置的值分割为一个水平和一个垂直部分。通过用1.0除以纹理的大小（从textureSize得到一个vec2）得到一个纹理像素的实际大小，以此作为偏移距离的根据。
我们为图像的模糊处理创建两个基本的帧缓冲，每个只有一个颜色缓冲纹理：
```c++
GLuint pingpongFBO[2];
GLuint pingpongBuffer[2];
glGenFramebuffers(2, pingpongFBO);
glGenTextures(2, pingpongColorbuffers);
for (GLuint i = 0; i < 2; i++)
{
glBindFramebuffer(GL_FRAMEBUFFER, pingpongFBO[i]);
glBindTexture(GL_TEXTURE_2D, pingpongBuffer[i]);
glTexImage2D(
GL_TEXTURE_2D, 0, GL_RGB16F, SCR_WIDTH, SCR_HEIGHT, 0, GL_RGB, GL_FLOAT, NULL
);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glFramebufferTexture2D(
GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, pingpongBuffer[i], 0
);
}
```
得到一个HDR纹理后，我们用提取出来的亮区纹理填充一个帧缓冲，然后对其模糊处理10次（5次垂直5次水平）：
```c++
GLboolean horizontal = true, first_iteration = true;
GLuint amount = 10;
shaderBlur.Use();
for (GLuint i = 0; i < amount; i++)
{
glBindFramebuffer(GL_FRAMEBUFFER, pingpongFBO[horizontal]);
glUniform1i(glGetUniformLocation(shaderBlur.Program, "horizontal"), horizontal);
glBindTexture(
GL_TEXTURE_2D, first_iteration ? colorBuffers[1] : pingpongBuffers[!horizontal]
);
RenderQuad();
horizontal = !horizontal;
if (first_iteration)
first_iteration = false;
}
glBindFramebuffer(GL_FRAMEBUFFER, 0);
```
每次循环我们根据我们打算渲染的是水平还是垂直来绑定两个缓冲其中之一，而将另一个绑定为纹理进行模糊。第一次迭代，因为两个颜色缓冲都是空的所以我们随意绑定一个去进行模糊处理。重复这个步骤10次，亮区图像就进行一个重复5次的高斯模糊了。这样我们可以对任意图像进行任意次模糊处理；高斯模糊循环次数越多，模糊的强度越大。
通过对提取亮区纹理进行5次模糊，我们就得到了一个正确的模糊的场景亮区图像。
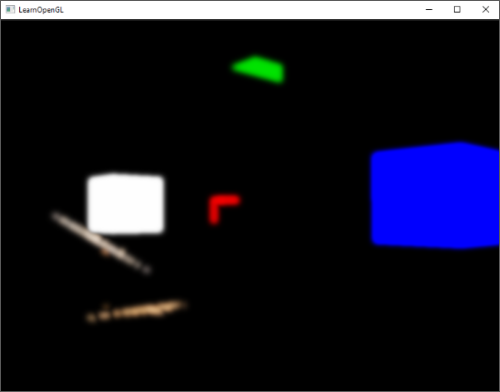
![](http://learnopengl.com/img/advanced-lighting/bloom_blurred_large.png)
bloom的最后一步是把模糊处理的图像和场景原来的HDR纹理进行结合。
### 把两个纹理混合
有了场景的HDR纹理和模糊处理的亮区纹理，我们只需把它们结合起来就能实现bloom或称光晕效果了。最终的像素着色器（大部分和HDR教程用的差不多）要把两个纹理混合：
```c++
#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
uniform sampler2D scene;
uniform sampler2D bloomBlur;
uniform float exposure;
void main()
{
const float gamma = 2.2;
vec3 hdrColor = texture(scene, TexCoords).rgb;
vec3 bloomColor = texture(bloomBlur, TexCoords).rgb;
hdrColor += bloomColor; // additive blending
// tone mapping
vec3 result = vec3(1.0) - exp(-hdrColor * exposure);
// also gamma correct while we're at it
result = pow(result, vec3(1.0 / gamma));
FragColor = vec4(result, 1.0f);
}
```
要注意的是我们要在应用色调映射之前添加bloom效果。这样添加的亮区的bloom，也会柔和转换为LDR，光照效果相对会更好。
把两个纹理结合以后，场景亮区便有了合适的光晕特效：
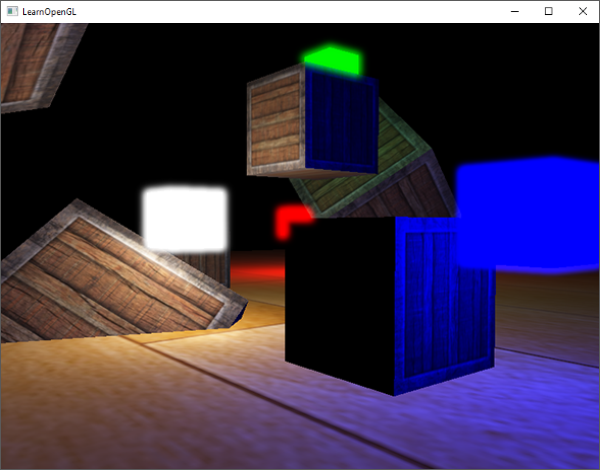
![](http://learnopengl.com/img/advanced-lighting/bloom.png)
有颜色的立方体看起来仿佛更亮，它向外发射光芒，的确是一个更好的视觉效果。这个场景比较简单，所以bloom效果不算十分令人瞩目，但在更好的场景中合理配置之后效果会有巨大的不同。你可以在这里找到这个简单的例子的源码，以及模糊的顶点和像素着色器、立方体的像素着色器、后处理的顶点和像素着色器。
这个教程我们只是用了一个相对简单的高斯模糊过滤器，它在每个方向上只有5个样本。通过沿着更大的半径或重复更多次数的模糊，进行采样我们就可以提升模糊的效果。因为模糊的质量与bloom效果的质量正相关，提升模糊效果就能够提升bloom效果。有些提升将模糊过滤器与不同大小的模糊kernel或采用多个高斯曲线来选择性地结合权重结合起来使用。来自Kalogirou和EpicGames的附加资源讨论了如何通过提升高斯模糊来显著提升bloom效果。
### 附加资源
* [Efficient Gaussian Blur with linear sampling](http://rastergrid.com/blog/2010/09/efficient-gaussian-blur-with-linear-sampling/)：非常详细地描述了高斯模糊，以及如何使用OpenGL的双线性纹理采样提升性能。
* [Bloom Post Process Effect](https://udn.epicgames.com/Three/Bloom.html)：来自Epic Games关于通过对权重的多个高斯曲线结合来提升bloom效果的文章。
* [How to do good bloom for HDR rendering](http://kalogirou.net/2006/05/20/how-to-do-good-bloom-for-hdr-rendering/)：Kalogirou的文章描述了如何使用更好的高斯模糊算法来提升bloom效果。

393
docs/05 Advanced Lighting/08 Deferred Shading.md
View File

@@ -1,393 +0,0 @@
# 延迟着色法(Deferred Shading)
原文 | [Deferred Shading](http://learnopengl.com/#!Advanced-Lighting/Deferred-Shading)
---|---
作者 | JoeyDeVries
翻译 | Meow J
校对 | 未校对
我们现在一直使用的光照方式叫做**正向渲染(Forward Rendering)**或者**正向着色法(Forward Shading)**，它是我们渲染物体的一种非常直接的方式，在场景中我们根据所有光源照亮一个物体，之后再渲染下一个物体，以此类推。它非常容易理解，也很容易实现，但是同时它对程序性能的影响也很大，因为对于每一个需要渲染的物体，程序都要对每一个光源每一个需要渲染的片段进行迭代，这是**非常**多的！因为大部分片段着色器的输出都会被之后的输出覆盖，正向渲染还会在场景中因为高深的复杂度(多个物体重合在一个像素上)浪费大量的片段着色器运行时间。
**延迟着色法(Deferred Shading)**，**或者说是延迟渲染(Deferred Rendering)**，为了解决上述问题而诞生了，它大幅度地改变了我们渲染物体的方式。这给我们优化拥有大量光源的场景提供了很多的选择，因为它能够在渲染上百甚至上千光源的同时还能够保持能让人接受的帧率。下面这张图片包含了一共1874个点光源，它是使用延迟着色法来完成的，而这对于正向渲染几乎是不可能的(图片来源：Hannes Nevalainen)。
![](http://learnopengl.com/img/advanced-lighting/deferred_example.png)
延迟着色法基于我们**延迟(Defer)**或**推迟(Postpone)**大部分计算量非常大的渲染(像是光照)到后期进行处理的想法。它包含两个处理阶段(Pass)：在第一个几何处理阶段(Geometry Pass)中，我们先渲染场景一次，之后获取对象的各种几何信息，并储存在一系列叫做G缓冲(G-buffer)的纹理中；想想位置向量(Position Vector)、颜色向量(Color Vector)、法向量(Normal Vector)和/或镜面值(Specular Value)。场景中这些储存在G缓冲中的几何信息将会在之后用来做(更复杂的)光照计算。下面是一帧中G缓冲的内容：
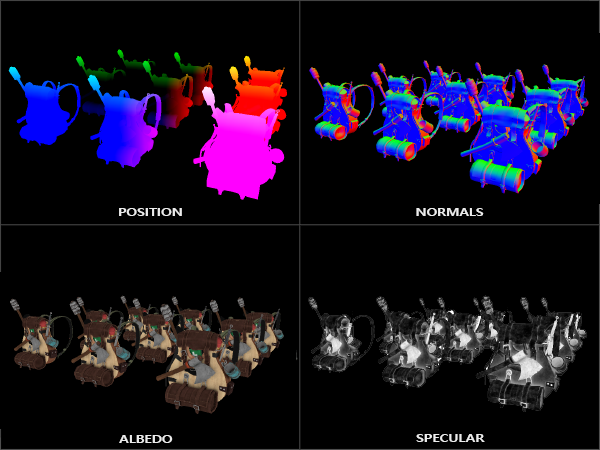
![](http://learnopengl.com/img/advanced-lighting/deferred_g_buffer.png)
我们会在第二个光照处理阶段(Lighting Pass)中使用G缓冲内的纹理数据。在光照处理阶段中，我们渲染一个屏幕大小的方形，并使用G缓冲中的几何数据对每一个片段计算场景的光照；在每个像素中我们都会对G缓冲进行迭代。我们对于渲染过程进行解耦，将它高级的片段处理挪到后期进行，而不是直接将每个对象从顶点着色器带到片段着色器。光照计算过程还是和我们以前一样，但是现在我们需要从对应的G缓冲而不是顶点着色器(和一些uniform变量)那里获取输入变量了。
下面这幅图片很好地展示了延迟着色法的整个过程：
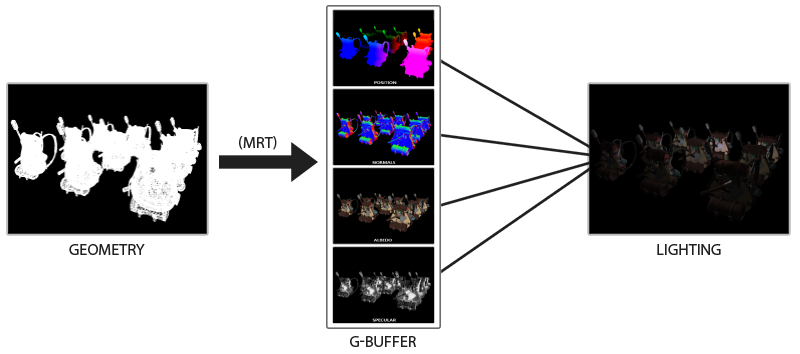
![](http://learnopengl.com/img/advanced-lighting/deferred_overview.png)
这种渲染方法一个很大的好处就是能保证在G缓冲中的片段和在屏幕上呈现的像素所包含的片段信息是一样的，因为深度测试已经最终将这里的片段信息作为最顶层的片段。这样保证了对于在光照处理阶段中处理的每一个像素都只处理一次，所以我们能够省下很多无用的渲染调用。除此之外，延迟渲染还允许我们做更多的优化，从而渲染更多的光源。
在几何处理阶段中填充G缓冲非常高效，因为我们直接储存像是位置，颜色或者是法线等对象信息到帧缓冲中，而这几乎不会消耗处理时间。在此基础上使用多渲染目标(Multiple Render Targets, MRT)技术，我们甚至可以在一个渲染处理之内完成这所有的工作。
## G缓冲
G缓冲(G-buffer)是对所有用来储存光照相关的数据，并在最后的光照处理阶段中使用的所有纹理的总称。趁此机会，让我们顺便复习一下在正向渲染中照亮一个片段所需要的所有数据：
- 一个3D**位置**向量来计算(插值)片段位置变量供`lightDir`和`viewDir`使用
- 一个RGB漫反射**颜色**向量，也就是反照率(Albedo)
- 一个3D**法**向量来判断平面的斜率
- 一个镜面强度(Specular Intensity)浮点值
- 所有光源的位置和颜色向量
- 玩家或者观察者的位置向量
有了这些(逐片段)变量的处置权，我们就能够计算我们很熟悉的(布林-)冯氏光照(Blinn-Phong Lighting)了。光源的位置，颜色，和玩家的观察位置可以通过uniform变量来设置，但是其它变量对于每个对象的片段都是不同的。如果我们能以某种方式传输完全相同的数据到最终的延迟光照处理阶段中，我们就能计算与之前相同的光照效果了，尽管我们只是在渲染一个2D方形的片段。
OpenGL并没有限制我们能在纹理中能存储的东西，所以现在你应该清楚在一个或多个屏幕大小的纹理中储存所有逐片段数据并在之后光照处理阶段中使用的可行性了。因为G缓冲纹理将会和光照处理阶段中的2D方形一样大，我们会获得和正向渲染设置完全一样的片段数据，但在光照处理阶段这里是一对一映射。
整个过程在伪代码中会是这样的：
```c++
while(...) // 游戏循环
{
// 1. 几何处理阶段：渲染所有的几何/颜色数据到G缓冲
glBindFramebuffer(GL_FRAMEBUFFER, gBuffer);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
gBufferShader.Use();
for(Object obj : Objects)
{
ConfigureShaderTransformsAndUniforms();
obj.Draw();
}
// 2. 光照处理阶段：使用G缓冲计算场景的光照
glBindFramebuffer(GL_FRAMEBUFFER, 0);
glClear(GL_COLOR_BUFFER_BIT);
lightingPassShader.Use();
BindAllGBufferTextures();
SetLightingUniforms();
RenderQuad();
}
```
对于每一个片段我们需要储存的数据有：一个**位置**向量、一个**法**向量，一个**颜色**向量，一个镜面强度值。所以我们在几何处理阶段中需要渲染场景中所有的对象并储存这些数据分量到G缓冲中。我们可以再次使用**多渲染目标(Multiple Render Targets)**来在一个渲染处理之内渲染多个颜色缓冲，在之前的[泛光教程](http://learnopengl-cn.readthedocs.org/zh/latest/05%20Advanced%20Lighting/07%20Bloom/)中我们也简单地提及了它。
对于几何渲染处理阶段，我们首先需要初始化一个帧缓冲对象，我们很直观的称它为`gBuffer`，它包含了多个颜色缓冲和一个单独的深度渲染缓冲对象(Depth Renderbuffer Object)。对于位置和法向量的纹理，我们希望使用高精度的纹理(每分量16或32位的浮点数)，而对于反照率和镜面值，使用默认的纹理(每分量8位浮点数)就够了。
```c++
GLuint gBuffer;
glGenFramebuffers(1, &gBuffer);
glBindFramebuffer(GL_FRAMEBUFFER, gBuffer);
GLuint gPosition, gNormal, gColorSpec;
// - 位置颜色缓冲
glGenTextures(1, &gPosition);
glBindTexture(GL_TEXTURE_2D, gPosition);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB16F, SCR_WIDTH, SCR_HEIGHT, 0, GL_RGB, GL_FLOAT, NULL);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, gPosition, 0
// - 法线颜色缓冲
glGenTextures(1, &gNormal);
glBindTexture(GL_TEXTURE_2D, gNormal);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB16F, SCR_WIDTH, SCR_HEIGHT, 0, GL_RGB, GL_FLOAT, NULL);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT1, GL_TEXTURE_2D, gNormal, 0);
// - 颜色 + 镜面颜色缓冲
glGenTextures(1, &gAlbedoSpec);
glBindTexture(GL_TEXTURE_2D, gAlbedoSpec);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, SCR_WIDTH, SCR_HEIGHT, 0, GL_RGBA, GL_FLOAT, NULL);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT2, GL_TEXTURE_2D, gAlbedoSpec, 0);
// - 告诉OpenGL我们将要使用(帧缓冲的)哪种颜色附件来进行渲染
GLuint attachments[3] = { GL_COLOR_ATTACHMENT0, GL_COLOR_ATTACHMENT1, GL_COLOR_ATTACHMENT2 };
glDrawBuffers(3, attachments);
// 之后同样添加渲染缓冲对象(Render Buffer Object)为深度缓冲(Depth Buffer)，并检查完整性
[...]
```
由于我们使用了多渲染目标，我们需要显式告诉OpenGL我们需要使用`glDrawBuffers`渲染的是和`GBuffer`关联的哪个颜色缓冲。同样需要注意的是，我们使用RGB纹理来储存位置和法线的数据，因为每个对象只有三个分量；但是我们将颜色和镜面强度数据合并到一起，存储到一个单独的RGBA纹理里面，这样我们就不需要声明一个额外的颜色缓冲纹理了。随着你的延迟渲染管线变得越来越复杂，需要更多的数据的时候，你就会很快发现新的方式来组合数据到一个单独的纹理当中。
接下来我们需要渲染它们到G缓冲中。假设每个对象都有漫反射，一个法线和一个镜面强度纹理，我们会想使用一些像下面这个片段着色器的东西来渲染它们到G缓冲中去。
```c++
#version 330 core
layout (location = 0) out vec3 gPosition;
layout (location = 1) out vec3 gNormal;
layout (location = 2) out vec4 gAlbedoSpec;
in vec2 TexCoords;
in vec3 FragPos;
in vec3 Normal;
uniform sampler2D texture_diffuse1;
uniform sampler2D texture_specular1;
void main()
{
// 存储第一个G缓冲纹理中的片段位置向量
gPosition = FragPos;
// 同样存储对每个逐片段法线到G缓冲中
gNormal = normalize(Normal);
// 和漫反射对每个逐片段颜色
gAlbedoSpec.rgb = texture(texture_diffuse1, TexCoords).rgb;
// 存储镜面强度到gAlbedoSpec的alpha分量
gAlbedoSpec.a = texture(texture_specular1, TexCoords).r;
}
```
因为我们使用了多渲染目标，这个布局指示符(Layout Specifier)告诉了OpenGL我们需要渲染到当前的活跃帧缓冲中的哪一个颜色缓冲。注意我们并没有储存镜面强度到一个单独的颜色缓冲纹理中，因为我们可以储存它单独的浮点值到其它颜色缓冲纹理的alpha分量中。
!!! Attention
请记住，因为有光照计算，所以保证所有变量在一个坐标空间当中至关重要。在这里我们在世界空间中存储(并计算)所有的变量。
如果我们现在想要渲染一大堆纳米装战士对象到`gBuffer`帧缓冲中，并通过一个一个分别投影它的颜色缓冲到铺屏四边形中尝试将他们显示出来，我们会看到向下面这样的东西：
![](http://learnopengl.com/img/advanced-lighting/deferred_g_buffer.png)
尝试想象世界空间位置和法向量都是正确的。比如说，指向右侧的法向量将会被更多地对齐到红色上，从场景原点指向右侧的位置矢量也同样是这样。一旦你对G缓冲中的内容满意了，我们就该进入到下一步：光照处理阶段了。
## 延迟光照处理阶段
现在我们已经有了一大堆的片段数据储存在G缓冲中供我们处置，我们可以选择通过一个像素一个像素地遍历各个G缓冲纹理，并将储存在它们里面的内容作为光照算法的输入，来完全计算场景最终的光照颜色。由于所有的G缓冲纹理都代表的是最终变换的片段值，我们只需要对每一个像素执行一次昂贵的光照运算就行了。这使得延迟光照非常高效，特别是在需要调用大量重型片段着色器的复杂场景中。
对于这个光照处理阶段，我们将会渲染一个2D全屏的方形(有一点像后期处理效果)并且在每个像素上运行一个昂贵的光照片段着色器。
```c++
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
shaderLightingPass.Use();
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_2D, gPosition);
glActiveTexture(GL_TEXTURE1);
glBindTexture(GL_TEXTURE_2D, gNormal);
glActiveTexture(GL_TEXTURE2);
glBindTexture(GL_TEXTURE_2D, gAlbedoSpec);
// 同样发送光照相关的uniform
SendAllLightUniformsToShader(shaderLightingPass);
glUniform3fv(glGetUniformLocation(shaderLightingPass.Program, "viewPos"), 1, &camera.Position[0]);
RenderQuad();
```
我们在渲染之前绑定了G缓冲中所有相关的纹理，并且发送光照相关的uniform变量到着色器中。
光照处理阶段的片段着色器和我们之前一直在用的光照教程着色器是非常相似的，除了我们添加了一个新的方法，从而使我们能够获取光照的输入变量，当然这些变量我们会从G缓冲中直接采样。
```c++
#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
uniform sampler2D gPosition;
uniform sampler2D gNormal;
uniform sampler2D gAlbedoSpec;
struct Light {
vec3 Position;
vec3 Color;
};
const int NR_LIGHTS = 32;
uniform Light lights[NR_LIGHTS];
uniform vec3 viewPos;
void main()
{
// 从G缓冲中获取数据
vec3 FragPos = texture(gPosition, TexCoords).rgb;
vec3 Normal = texture(gNormal, TexCoords).rgb;
vec3 Albedo = texture(gAlbedoSpec, TexCoords).rgb;
float Specular = texture(gAlbedoSpec, TexCoords).a;
// 然后和往常一样地计算光照
vec3 lighting = Albedo * 0.1; // 硬编码环境光照分量
vec3 viewDir = normalize(viewPos - FragPos);
for(int i = 0; i < NR_LIGHTS; ++i)
{
// 漫反射
vec3 lightDir = normalize(lights[i].Position - FragPos);
vec3 diffuse = max(dot(Normal, lightDir), 0.0) * Albedo * lights[i].Color;
lighting += diffuse;
}
FragColor = vec4(lighting, 1.0);
}
```
光照处理阶段着色器接受三个uniform纹理，代表G缓冲，它们包含了我们在几何处理阶段储存的所有数据。如果我们现在再使用当前片段的纹理坐标采样这些数据，我们将会获得和之前完全一样的片段值，这就像我们在直接渲染几何体。在片段着色器的一开始，我们通过一个简单的纹理查找从G缓冲纹理中获取了光照相关的变量。注意我们从`gAlbedoSpec`纹理中同时获取了`Albedo`颜色和`Spqcular`强度。
因为我们现在已经有了必要的逐片段变量(和相关的uniform变量)来计算布林-冯氏光照(Blinn-Phong Lighting)，我们不需要对光照代码做任何修改了。我们在延迟着色法中唯一需要改的就是获取光照输入变量的方法。
运行一个包含32个小光源的简单Demo会是像这样子的：
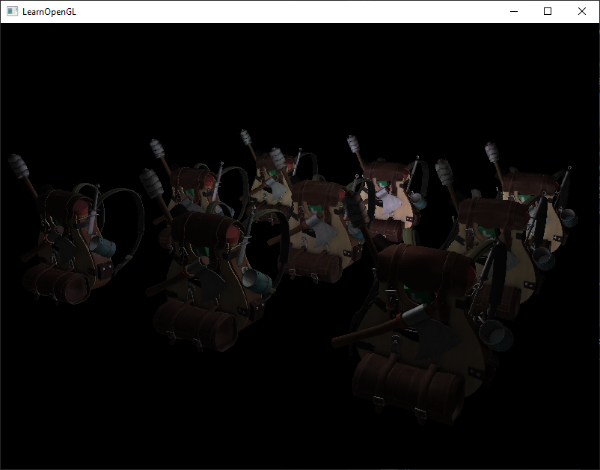
![](http://learnopengl.com/img/advanced-lighting/deferred_shading.png)
你可以在以下位置找到Demo的完整[源代码](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred)，和几何渲染阶段的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_geometry&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_geometry&type=fragment)着色器，还有光照渲染阶段的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred&type=vertex)着色器。
延迟着色法的其中一个缺点就是它不能进行[混合](http://learnopengl-cn.readthedocs.org/zh/latest/04%20Advanced%20OpenGL/03%20Blending/)(Blending)，因为G缓冲中所有的数据都是从一个单独的片段中来的，而混合需要对多个片段的组合进行操作。延迟着色法另外一个缺点就是它迫使你对大部分场景的光照使用相同的光照算法，你可以通过包含更多关于材质的数据到G缓冲中来减轻这一缺点。
为了克服这些缺点(特别是混合)，我们通常分割我们的渲染器为两个部分：一个是延迟渲染的部分，另一个是专门为了混合或者其他不适合延迟渲染管线的着色器效果而设计的的正向渲染的部分。为了展示这是如何工作的，我们将会使用正向渲染器渲染光源为一个小立方体，因为光照立方体会需要一个特殊的着色器(会输出一个光照颜色)。
## 结合延迟渲染与正向渲染
现在我们想要渲染每一个光源为一个3D立方体，并放置在光源的位置上随着延迟渲染器一起发出光源的颜色。很明显，我们需要做的第一件事就是在延迟渲染方形之上正向渲染所有的光源，它会在延迟渲染管线的最后进行。所以我们只需要像正常情况下渲染立方体，只是会在我们完成延迟渲染操作之后进行。代码会像这样：
```c++
// 延迟渲染光照渲染阶段
[...]
RenderQuad();
// 现在像正常情况一样正向渲染所有光立方体
shaderLightBox.Use();
glUniformMatrix4fv(locProjection, 1, GL_FALSE, glm::value_ptr(projection));
glUniformMatrix4fv(locView, 1, GL_FALSE, glm::value_ptr(view));
for (GLuint i = 0; i < lightPositions.size(); i++)
{
model = glm::mat4();
model = glm::translate(model, lightPositions[i]);
model = glm::scale(model, glm::vec3(0.25f));
glUniformMatrix4fv(locModel, 1, GL_FALSE, glm::value_ptr(model));
glUniform3fv(locLightcolor, 1, &lightColors[i][0]);
RenderCube();
}
```
然而，这些渲染出来的立方体并没有考虑到我们储存的延迟渲染器的几何深度(Depth)信息，并且结果是它被渲染在之前渲染过的物体之上，这并不是我们想要的结果。
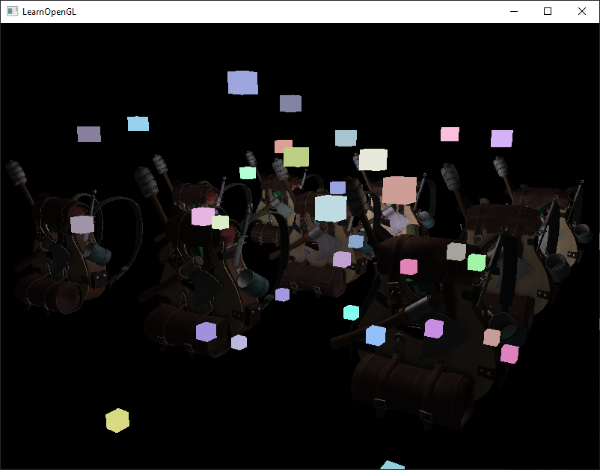
![](http://learnopengl.com/img/advanced-lighting/deferred_lights_no_depth.png)
我们需要做的就是首先复制出在几何渲染阶段中储存的深度信息，并输出到默认的帧缓冲的深度缓冲，然后我们才渲染光立方体。这样之后只有当它在之前渲染过的几何体上方的时候，光立方体的片段才会被渲染出来。我们可以使用`glBlitFramebuffer`复制一个帧缓冲的内容到另一个帧缓冲中，这个函数我们也在[抗锯齿](http://learnopengl-cn.readthedocs.org/zh/latest/04%20Advanced%20OpenGL/11%20Anti%20Aliasing/)的教程中使用过，用来还原多重采样的帧缓冲。`glBlitFramebuffer`这个函数允许我们复制一个用户定义的帧缓冲区域到另一个用户定义的帧缓冲区域。
我们储存所有延迟渲染阶段中所有物体的深度信息在`gBuffer`这个FBO中。如果我们仅仅是简单复制它的深度缓冲内容到默认帧缓冲的深度缓冲中，那么光立方体就会像是场景中所有的几何体都是正向渲染出来的一样渲染出来。就像在抗锯齿教程中介绍的那样，我们需要指定一个帧缓冲为读帧缓冲(Read Framebuffer)，并且类似地指定一个帧缓冲为写帧缓冲(Write Framebuffer)：
```c++
glBindFramebuffer(GL_READ_FRAMEBUFFER, gBuffer);
glBindFramebuffer(GL_DRAW_FRAMEBUFFER, 0); // 写入到默认帧缓冲
glBlitFramebuffer(
0, 0, SCR_WIDTH, SCR_HEIGHT, 0, 0, SCR_WIDTH, SCR_HEIGHT, GL_DEPTH_BUFFER_BIT, GL_NEAREST
);
glBindFramebuffer(GL_FRAMEBUFFER, 0);
// 现在像之前一样渲染光立方体
[...]
```
在这里我们复制整个读帧缓冲的深度缓冲信息到默认帧缓冲的深度缓冲，对于颜色缓冲和模板缓冲我们也可以这样处理。现在如果我们接下来再渲染光立方体，场景里的几何体将会看起来很真实了，而不只是简单地粘贴立方体到2D方形之上：
![](http://learnopengl.com/img/advanced-lighting/deferred_lights_depth.png)
你可以在[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_light_cube)找到Demo的源代码，还有光立方体的[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_light_cube&type=vertex)和[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_light_cube&type=fragment)着色器。
有了这种方法，我们就能够轻易地结合延迟着色法和正向着色法了。这真是太棒了，我们现在可以应用混合或者渲染需要特殊着色器效果的物体了，这在延迟渲染中是不可能做到的。
## 更多的光源
延迟渲染一直被称赞的原因就是它能够渲染大量的光源而不消耗大量的性能。然而，延迟渲染它本身并不能支持非常大量的光源，因为我们仍然必须要对场景中每一个光源计算每一个片段的光照分量。真正让大量光源成为可能的是我们能够对延迟渲染管线引用的一个非常棒的优化：**光体积(Light Volumes)**
通常情况下，当我们渲染一个复杂光照场景下的片段着色器时，我们会计算场景中**每一个**光源的贡献，不管它们离这个片段有多远。很大一部分的光源根本就不会到达这个片段，所以为什么我们还要浪费这么多光照运算呢？
隐藏在光体积背后的想法就是计算光源的半径，或是体积，也就是光能够到达片段的范围。由于大部分光源都使用了某种形式的衰减(Attenuation)，我们可以用它来计算光源能够到达的最大路程，或者说是半径。我们接下来只需要对那些在一个或多个光体积内的片段进行繁重的光照运算就行了。这可以给我们省下来很可观的计算量，因为我们现在只在需要的情况下计算光照。
这个方法的难点基本就是找出一个光源光体积的大小，或者是半径。
### 计算一个光源的体积或半径
为了获取一个光源的体积半径，我们需要解一个对于一个我们认为是**黑暗(Dark)**的亮度(Brightness)的衰减方程，它可以是0.0，或者是更亮一点的但仍被认为黑暗的值，像是0.03。为了展示我们如何计算光源的体积半径，我们将会使用一个在[投光物](http://learnopengl-cn.readthedocs.org/zh/latest/02%20Lighting/05%20Light%20casters/)这节中引入的一个更加复杂，但非常灵活的衰减方程：
![](../img/deferred_shading_1.png)
我们现在想要在![](../img/F_light.png)等于0的前提下解这个方程，也就是说光在该距离完全是黑暗的。然而这个方程永远不会真正等于0.0，所以它没有解。所以，我们不会求表达式等于0.0时候的解，相反我们会求当亮度值靠近于0.0的解，这时候它还是能被看做是黑暗的。在这个教程的演示场景中，我们选择![](../img/5256.png)作为一个合适的光照值；除以256是因为默认的8-bit帧缓冲可以每个分量显示这么多强度值(Intensity)。
!!! Important
我们使用的衰减方程在它的可视范围内基本都是黑暗的，所以如果我们想要限制它为一个比![](../img/5256.png)更加黑暗的亮度，光体积就会变得太大从而变得低效。只要是用户不能在光体积边缘看到一个突兀的截断，这个参数就没事了。当然它还是依赖于场景的类型，一个高的亮度阀值会产生更小的光体积，从而获得更高的效率，然而它同样会产生一个很容易发现的副作用，那就是光会在光体积边界看起来突然断掉。
我们要求的衰减方程会是这样：
![](../img/deferred_shading_2.png)
在这里，![](../img/I_max.png)是光源最亮的颜色分量。我们之所以使用光源最亮的颜色分量是因为解光源最亮的强度值方程最好地反映了理想光体积半径。
从这里我们继续解方程：
![](../img/deferred_shading_3.png)
![](../img/deferred_shading_4.png)
![](../img/deferred_shading_5.png)
![](../img/deferred_shading_6.png)
![](../img/deferred_shading_7.png)
最后的方程形成了![](../img/quad_formula.png)的形式，我们可以用求根公式来解这个二次方程：
![](../img/deferred_shading_8.png)
它给我们了一个通用公式从而允许我们计算x的值，即光源的光体积半径，只要我们提供了一个常量，线性和二次项参数：
```c++
GLfloat constant = 1.0;
GLfloat linear = 0.7;
GLfloat quadratic = 1.8;
GLfloat lightMax = std::fmaxf(std::fmaxf(lightColor.r, lightColor.g), lightColor.b);
GLfloat radius =
(-linear + std::sqrtf(linear * linear - 4 * quadratic * (constant - (256.0 / 5.0) * lightMax)))
/ (2 * quadratic);
```
它会返回一个大概在1.0到5.0范围内的半径值，它取决于光的最大强度。
对于场景中每一个光源，我们都计算它的半径，并仅在片段在光源的体积内部时才计算该光源的光照。下面是更新过的光照处理阶段片段着色器，它考虑到了计算出来的光体积。注意这种方法仅仅用作教学目的，在实际场景中是不可行的，我们会在后面讨论它：
```c++
struct Light {
[...]
float Radius;
};
void main()
{
[...]
for(int i = 0; i < NR_LIGHTS; ++i)
{
// 计算光源和该片段间距离
float distance = length(lights[i].Position - FragPos);
if(distance < lights[i].Radius)
{
// 执行大开销光照
[...]
}
}
}
```
这次的结果和之前一模一样，但是这次物体只对所在光体积的光源计算光照。
你可以在[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_final)找到Demo最终的源码，并且还有更新的光照渲染阶段的[片段着色器](http://learnopengl.com/code_viewer.php?code=advanced-lighting/deferred_final&type=fragment)
### 真正使用光体积
上面那个片段着色器在实际情况下不能真正地工作，并且它只演示了我们可以**不知怎样**能使用光体积减少光照运算。然而事实上，你的GPU和GLSL并不擅长优化循环和分支。这一缺陷的原因是GPU中着色器的运行是高度并行的，大部分的架构要求对于一个大的线程集合，GPU需要对它运行完全一样的着色器代码从而获得高效率。这通常意味着一个着色器运行时总是执行一个if语句**所有的**分支从而保证着色器运行都是一样的，这使得我们之前的**半径检测**优化完全变得无用，我们仍然在对所有光源计算光照！
使用光体积更好的方法是渲染一个实际的球体，并根据光体积的半径缩放。这些球的中心放置在光源的位置，由于它是根据光体积半径缩放的，这个球体正好覆盖了光的可视体积。这就是我们的技巧：我们使用大体相同的延迟片段着色器来渲染球体。因为球体产生了完全匹配于受影响像素的着色器调用，我们只渲染了受影响的像素而跳过其它的像素。下面这幅图展示了这一技巧：
![](http://learnopengl.com/img/advanced-lighting/deferred_light_volume_rendered.png)
它被应用在场景中每个光源上，并且所得的片段相加混合在一起。这个结果和之前场景是一样的，但这一次只渲染对于光源相关的片段。它有效地减少了从`nr_objects * nr_lights`到`nr_objects + nr_lights`的计算量，这使得多光源场景的渲染变得无比高效。这正是为什么延迟渲染非常适合渲染很大数量光源。
然而这个方法仍然有一个问题：面剔除(Face Culling)需要被启用(否则我们会渲染一个光效果两次)，并且在它启用的时候用户可能进入一个光源的光体积，然而这样之后这个体积就不再被渲染了(由于背面剔除)，这会使得光源的影响消失。这个问题可以通过一个模板缓冲技巧来解决。
渲染光体积确实会带来沉重的性能负担，虽然它通常比普通的延迟渲染更快，这仍然不是最好的优化。另外两个基于延迟渲染的更流行(并且更高效)的拓展叫做**延迟光照(Deferred Lighting)**和**切片式延迟着色法(Tile-based Deferred Shading)**。这些方法会很大程度上提高大量光源渲染的效率，并且也能允许一个相对高效的多重采样抗锯齿(MSAA)。然而受制于这篇教程的长度，我将会在之后的教程中介绍这些优化。
## 延迟渲染 vs 正向渲染
仅仅是延迟着色法它本身(没有光体积)已经是一个很大的优化了，每个像素仅仅运行一个单独的片段着色器，然而对于正向渲染，我们通常会对一个像素运行多次片段着色器。当然，延迟渲染确实带来一些缺点：大内存开销，没有MSAA和混合(仍需要正向渲染的配合)。
当你有一个很小的场景并且没有很多的光源时候，延迟渲染并不一定会更快一点，甚至有些时候由于开销超过了它的优点还会更慢。然而在一个更复杂的场景中，延迟渲染会快速变成一个重要的优化，特别是有了更先进的优化拓展的时候。
最后我仍然想指出，基本上所有能通过正向渲染完成的效果能够同样在延迟渲染场景中实现，这通常需要一些小的翻译步骤。举个例子，如果我们想要在延迟渲染器中使用法线贴图(Normal Mapping)，我们需要改变几何渲染阶段着色器来输出一个世界空间法线(World-space Normal)，它从法线贴图中提取出来(使用一个TBN矩阵)而不是表面法线，光照渲染阶段中的光照运算一点都不需要变。如果你想要让视差贴图工作，首先你需要在采样一个物体的漫反射，镜面，和法线纹理之前首先置换几何渲染阶段中的纹理坐标。一旦你了解了延迟渲染背后的理念，变得有创造力并不是什么难事。
## 附加资源
- [Tutorial 35: Deferred Shading - Part 1](http://ogldev.atspace.co.uk/www/tutorial35/tutorial35.html)：OGLDev的一个分成三部分的延迟着色法教程。在Part 2和3中介绍了渲染光体积
- [Deferred Rendering for Current and Future Rendering Pipelines](https://software.intel.com/sites/default/files/m/d/4/1/d/8/lauritzen_deferred_shading_siggraph_2010.pdf)：Andrew Lauritzen的幻灯片，讨论了高级切片式延迟着色法和延迟光照

495
docs/05 Advanced Lighting/09 SSAO.md
View File

@@ -1,495 +0,0 @@
# SSAO
原文 | [SSAO](http://learnopengl.com/#!Advanced-Lighting/SSAO)
---|---
作者 | JoeyDeVries
翻译 | Meow J
校对 | 未校对
我们已经在前面的基础教程中简单介绍到了这部分内容：环境光照(Ambient Lighting)。环境光照是我们加入场景总体光照中的一个固定光照常量，它被用来模拟光的**散射(Scattering)**。在现实中，光线会以任意方向散射，它的强度是会一直改变的，所以间接被照到的那部分场景也应该有变化的强度，而不是一成不变的环境光。其中一种间接光照的模拟叫做**环境光遮蔽(Ambient Occlusion)**，它的原理是通过将褶皱、孔洞和非常靠近的墙面变暗的方法近似模拟出间接光照。这些区域很大程度上是被周围的几何体遮蔽的，光线会很难流失，所以这些地方看起来会更暗一些。站起来看一看你房间的拐角或者是褶皱，是不是这些地方会看起来有一点暗？
下面这幅图展示了在使用和不使用SSAO时场景的不同。特别注意对比褶皱部分，你会发现(环境)光被遮蔽了许多：
![](http://learnopengl.com/img/advanced-lighting/ssao_example.png)
尽管这不是一个非常明显的效果，启用SSAO的图像确实给我们更真实的感觉，这些小的遮蔽细节给整个场景带来了更强的深度感。
环境光遮蔽这一技术会带来很大的性能开销，因为它还需要考虑周围的几何体。我们可以对空间中每一点发射大量光线来确定其遮蔽量，但是这在实时运算中会很快变成大问题。在2007年，Crytek公司发布了一款叫做**屏幕空间环境光遮蔽(Screen-Space Ambient Occlusion, SSAO)**的技术，并用在了他们的看家作孤岛危机上。这一技术使用了屏幕空间场景的深度而不是真实的几何体数据来确定遮蔽量。这一做法相对于真正的环境光遮蔽不但速度快，而且还能获得很好的效果，使得它成为近似实时环境光遮蔽的标准。
SSAO背后的原理很简单：对于铺屏四边形(Screen-filled Quad)上的每一个片段，我们都会根据周边深度值计算一个**遮蔽因子(Occlusion Factor)**。这个遮蔽因子之后会被用来减少或者抵消片段的环境光照分量。遮蔽因子是通过采集片段周围球型核心(Kernel)的多个深度样本，并和当前片段深度值对比而得到的。高于片段深度值样本的个数就是我们想要的遮蔽因子。
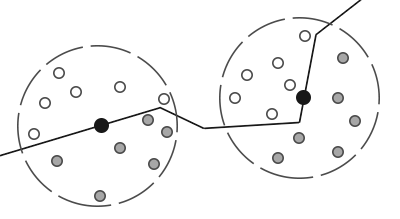
![](http://learnopengl.com/img/advanced-lighting/ssao_crysis_circle.png)
上图中在几何体内灰色的深度样本都是高于片段深度值的，他们会增加遮蔽因子；几何体内样本个数越多，片段获得的环境光照也就越少。
很明显，渲染效果的质量和精度与我们采样的样本数量有直接关系。如果样本数量太低，渲染的精度会急剧减少，我们会得到一种叫做**波纹(Banding)**的效果；如果它太高了，反而会影响性能。我们可以通过引入随机性到采样核心(Sample Kernel)的采样中从而减少样本的数目。通过随机旋转采样核心，我们能在有限样本数量中得到高质量的结果。然而这仍然会有一定的麻烦，因为随机性引入了一个很明显的噪声图案，我们将需要通过模糊结果来修复这一问题。下面这幅图片([John Chapman](http://john-chapman-graphics.blogspot.com/)的佛像)展示了波纹效果还有随机性造成的效果：
![](http://learnopengl.com/img/advanced-lighting/ssao_banding_noise.jpg)
你可以看到，尽管我们在低样本数的情况下得到了很明显的波纹效果，引入随机性之后这些波纹效果就完全消失了。
Crytek公司开发的SSAO技术会产生一种特殊的视觉风格。因为使用的采样核心是一个球体，它导致平整的墙面也会显得灰蒙蒙的，因为核心中一半的样本都会在墙这个几何体上。下面这幅图展示了孤岛危机的SSAO，它清晰地展示了这种灰蒙蒙的感觉：
![](http://learnopengl.com/img/advanced-lighting/ssao_crysis.jpg)
由于这个原因，我们将不会使用球体的采样核心，而使用一个沿着表面法向量的半球体采样核心。
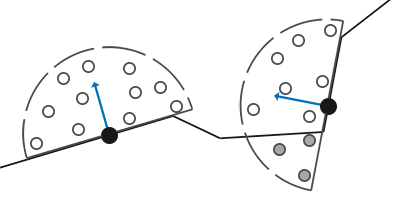
![](http://learnopengl.com/img/advanced-lighting/ssao_hemisphere.png)
通过在**法向半球体(Normal-oriented Hemisphere)**周围采样，我们将不会考虑到片段底部的几何体.它消除了环境光遮蔽灰蒙蒙的感觉，从而产生更真实的结果。这个SSAO教程将会基于法向半球法和John Chapman出色的[SSAO教程](http://john-chapman-graphics.blogspot.com/2013/01/ssao-tutorial.html)。
## 样本缓冲(Sample buffers)
SSAO需要获取几何体的信息，因为我们需要一些方式来确定一个片段的遮蔽因子。对于每一个片段，我们将需要这些数据：
- 逐片段**位置**向量
- 逐片段的**法线**向量
- **线性深度**纹理
- **采样核心**
- 用来旋转采样核心的逐片段随机旋转矢量
通过使用一个逐片段观察空间位置，我们可以将一个采样半球核心对准片段的观察空间表面法线。对于每一个核心样本我们会采样线性深度纹理来比较结果。采样核心会根据旋转矢量稍微偏转一点；我们所获得的遮蔽因子将会之后用来限制最终的环境光照分量。
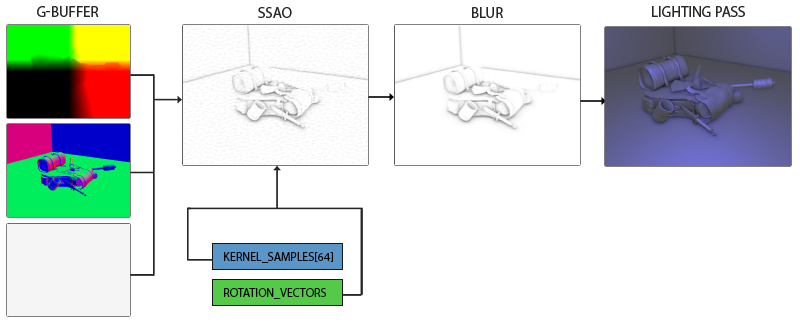
![](http://learnopengl.com/img/advanced-lighting/ssao_overview.png)
由于SSAO是一种屏幕空间技巧，我们对铺屏2D四边形上每一个片段计算这一效果；也就是说我们没有场景中几何体的信息。我们能做的只是渲染几何体数据到屏幕空间纹理中，我们之后再会将此数据发送到SSAO着色器中，之后我们就能访问到这些几何体数据了。如果你看了前面一篇教程，你会发现这和延迟渲染很相似。这也就是说SSAO和延迟渲染能完美地兼容，因为我们已经存位置和法线向量到G缓冲中了。
!!! Important
在这个教程中，我们将会在一个简化版本的延迟渲染器([延迟着色法](http://learnopengl-cn.readthedocs.org/zh/latest/05%20Advanced%20Lighting/08%20Deferred%20Shading/)教程中)的基础上实现SSAO，所以如果你不知道什么是延迟着色法，请先读完那篇教程。
由于我们已经有了逐片段位置和法线数据(G缓冲中)，我们只需要更新一下几何着色器，让它包含片段的线性深度就行了。回忆我们在深度测试那一节学过的知识，我们可以从`gl_FragCoord.z`中提取线性深度：
```c++
#version 330 core
layout (location = 0) out vec4 gPositionDepth;
layout (location = 1) out vec3 gNormal;
layout (location = 2) out vec4 gAlbedoSpec;
in vec2 TexCoords;
in vec3 FragPos;
in vec3 Normal;
const float NEAR = 0.1; // 投影矩阵的近平面
const float FAR = 50.0f; // 投影矩阵的远平面
float LinearizeDepth(float depth)
{
float z = depth * 2.0 - 1.0; // 回到NDC
return (2.0 * NEAR * FAR) / (FAR + NEAR - z * (FAR - NEAR));
}
void main()
{
// 储存片段的位置矢量到第一个G缓冲纹理
gPositionDepth.xyz = FragPos;
// 储存线性深度到gPositionDepth的alpha分量
gPositionDepth.a = LinearizeDepth(gl_FragCoord.z);
// 储存法线信息到G缓冲
gNormal = normalize(Normal);
// 和漫反射颜色
gAlbedoSpec.rgb = vec3(0.95);
}
```
提取出来的线性深度是在观察空间中的，所以之后的运算也是在观察空间中。确保G缓冲中的位置和法线都在观察空间中(乘上观察矩阵也一样)。观察空间线性深度值之后会被保存在`gPositionDepth`颜色缓冲的alpha分量中，省得我们再声明一个新的颜色缓冲纹理。
!!! Important
通过一些小技巧来通过深度值重构实际位置值是可能的，Matt Pettineo在他的[博客](https://mynameismjp.wordpress.com/2010/09/05/position-from-depth-3/)里提到了这一技巧。这一技巧需要在着色器里进行一些计算，但是省了我们在G缓冲中存储位置数据，从而省了很多内存。为了示例的简单，我们将不会使用这些优化技巧，你可以自行探究。
`gPositionDepth`颜色缓冲纹理被设置成了下面这样：
```c++
glGenTextures(1, &gPositionDepth);
glBindTexture(GL_TEXTURE_2D, gPositionDepth);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA16F, SCR_WIDTH, SCR_HEIGHT, 0, GL_RGBA, GL_FLOAT, NULL);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
```
这给我们了一个线性深度纹理，我们可以用它来对每一个核心样本获取深度值。注意我们把线性深度值存储为了浮点数据；这样从0.1到50.0范围深度值都不会被限制在[0.0, 1.0]之间了。如果你不用浮点值存储这些深度数据，确保你首先将值除以`FAR`来标准化它们，再存储到`gPositionDepth`纹理中，并在以后的着色器中用相似的方法重建它们。同样需要注意的是`GL_CLAMP_TO_EDGE`的纹理封装方法。这保证了我们不会不小心采样到在屏幕空间中纹理默认坐标区域之外的深度值。
接下来我们需要真正的半球采样核心和一些方法来随机旋转它。
## 法向半球(Normal-oriented Hemisphere)
我们需要沿着表面法线方向生成大量的样本。就像我们在这个教程的开始介绍的那样，我们想要生成形成半球形的样本。由于对每个表面法线方向生成采样核心非常困难，也不合实际，我们将在[切线空间](http://learnopengl-cn.readthedocs.org/zh/latest/05%20Advanced%20Lighting/04%20Normal%20Mapping/)(Tangent Space)内生成采样核心，法向量将指向正z方向。
![](http://learnopengl.com/img/advanced-lighting/ssao_hemisphere.png)
假设我们有一个单位半球，我们可以获得一个拥有最大64样本值的采样核心：
```c++
std::uniform_real_distribution<GLfloat> randomFloats(0.0, 1.0); // 随机浮点数，范围0.0 - 1.0
std::default_random_engine generator;
std::vector<glm::vec3> ssaoKernel;
for (GLuint i = 0; i < 64; ++i)
{
glm::vec3 sample(
randomFloats(generator) * 2.0 - 1.0,
randomFloats(generator) * 2.0 - 1.0,
randomFloats(generator)
);
sample = glm::normalize(sample);
sample *= randomFloats(generator);
GLfloat scale = GLfloat(i) / 64.0;
ssaoKernel.push_back(sample);
}
```
我们在切线空间中以-1.0到1.0为范围变换x和y方向，并以0.0和1.0为范围变换样本的z方向(如果以-1.0到1.0为范围，取样核心就变成球型了)。由于采样核心将会沿着表面法线对齐，所得的样本矢量将会在半球里。
目前，所有的样本都是平均分布在采样核心里的，但是我们更愿意将更多的注意放在靠近真正片段的遮蔽上，也就是将核心样本靠近原点分布。我们可以用一个加速插值函数实现它：
```c++
...[接上函数]
scale = lerp(0.1f, 1.0f, scale * scale);
sample *= scale;
ssaoKernel.push_back(sample);
}
```
`lerp`被定义为：
```c++
GLfloat lerp(GLfloat a, GLfloat b, GLfloat f)
{
return a + f * (b - a);
}
```
这就给了我们一个大部分样本靠近原点的核心分布。
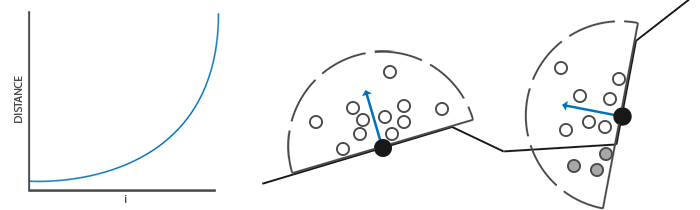
![](http://learnopengl.com/img/advanced-lighting/ssao_kernel_weight.png)
每个核心样本将会被用来偏移观察空间片段位置从而采样周围的几何体。我们在教程开始的时候看到，如果没有变化采样核心，我们将需要大量的样本来获得真实的结果。通过引入一个随机的转动到采样核心中，我们可以很大程度上减少这一数量。
## 随机核心转动
通过引入一些随机性到采样核心上，我们可以大大减少获得不错结果所需的样本数量。我们可以对场景中每一个片段创建一个随机旋转向量，但这会很快将内存耗尽。所以，更好的方法是创建一个小的随机旋转向量纹理平铺在屏幕上。
我们创建一个4x4朝向切线空间平面法线的随机旋转向量数组：
```c++
std::vector<glm::vec3> ssaoNoise;
for (GLuint i = 0; i < 16; i++)
{
glm::vec3 noise(
randomFloats(generator) * 2.0 - 1.0,
randomFloats(generator) * 2.0 - 1.0,
0.0f);
ssaoNoise.push_back(noise);
}
```
由于采样核心实验者正z方向在切线空间内旋转，我们设定z分量为0.0，从而围绕z轴旋转。
我们接下来创建一个包含随机旋转向量的4x4纹理；记得设定它的封装方法为`GL_REPEAT`，从而保证它合适地平铺在屏幕上。
```c++
GLuint noiseTexture;
glGenTextures(1, &noiseTexture);
glBindTexture(GL_TEXTURE_2D, noiseTexture);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB16F, 4, 4, 0, GL_RGB, GL_FLOAT, &ssaoNoise[0]);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
```
现在我们有了所有的相关输入数据，接下来我们需要实现SSAO。
## SSAO着色器
SSAO着色器在2D的铺屏四边形上运行，它对于每一个生成的片段计算遮蔽值(为了在最终的光照着色器中使用)。由于我们需要存储SSAO阶段的结果，我们还需要在创建一个帧缓冲对象：
```c++
GLuint ssaoFBO;
glGenFramebuffers(1, &ssaoFBO);
glBindFramebuffer(GL_FRAMEBUFFER, ssaoFBO);
GLuint ssaoColorBuffer;
glGenTextures(1, &ssaoColorBuffer);
glBindTexture(GL_TEXTURE_2D, ssaoColorBuffer);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RED, SCR_WIDTH, SCR_HEIGHT, 0, GL_RGB, GL_FLOAT, NULL);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, ssaoColorBuffer, 0);
```
由于环境遮蔽的结果是一个灰度值，我们将只需要纹理的红色分量，所以我们将颜色缓冲的内部格式设置为`GL_RED`。
渲染SSAO完整的过程会像这样：
```c++
// 几何处理阶段: 渲染到G缓冲中
glBindFramebuffer(GL_FRAMEBUFFER, gBuffer);
[...]
glBindFramebuffer(GL_FRAMEBUFFER, 0);
// 使用G缓冲渲染SSAO纹理
glBindFramebuffer(GL_FRAMEBUFFER, ssaoFBO);
glClear(GL_COLOR_BUFFER_BIT);
shaderSSAO.Use();
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_2D, gPositionDepth);
glActiveTexture(GL_TEXTURE1);
glBindTexture(GL_TEXTURE_2D, gNormal);
glActiveTexture(GL_TEXTURE2);
glBindTexture(GL_TEXTURE_2D, noiseTexture);
SendKernelSamplesToShader();
glUniformMatrix4fv(projLocation, 1, GL_FALSE, glm::value_ptr(projection));
RenderQuad();
glBindFramebuffer(GL_FRAMEBUFFER, 0);
// 光照处理阶段: 渲染场景光照
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
shaderLightingPass.Use();
[...]
glActiveTexture(GL_TEXTURE3);
glBindTexture(GL_TEXTURE_2D, ssaoColorBuffer);
[...]
RenderQuad();
```
`shaderSSAO`这个着色器将对应G缓冲纹理(包括线性深度)，噪声纹理和法向半球核心样本作为输入参数：
```c++
#version 330 core
out float FragColor;
in vec2 TexCoords;
uniform sampler2D gPositionDepth;
uniform sampler2D gNormal;
uniform sampler2D texNoise;
uniform vec3 samples[64];
uniform mat4 projection;
// 屏幕的平铺噪声纹理会根据屏幕分辨率除以噪声大小的值来决定
const vec2 noiseScale = vec2(800.0/4.0, 600.0/4.0); // 屏幕 = 800x600
void main()
{
[...]
}
```
注意我们这里有一个`noiseScale`的变量。我们想要将噪声纹理平铺(Tile)在屏幕上，但是由于`TexCoords`的取值在0.0和1.0之间，`texNoise`纹理将不会平铺。所以我们将通过屏幕分辨率除以噪声纹理大小的方式计算`TexCoords`的缩放大小，并在之后提取相关输入向量的时候使用。
```c++
vec3 fragPos = texture(gPositionDepth, TexCoords).xyz;
vec3 normal = texture(gNormal, TexCoords).rgb;
vec3 randomVec = texture(texNoise, TexCoords * noiseScale).xyz;
```
由于我们将`texNoise`的平铺参数设置为`GL_REPEAT`，随机的值将会在全屏不断重复。加上`fragPog`和`normal`向量，我们就有足够的数据来创建一个TBN矩阵，将向量从切线空间变换到观察空间。
```c++
vec3 tangent = normalize(randomVec - normal * dot(randomVec, normal));
vec3 bitangent = cross(normal, tangent);
mat3 TBN = mat3(tangent, bitangent, normal);
```
通过使用一个叫做Gramm-Schmidt处理(Gramm-Schmidt Process)的过程，我们创建了一个正交基(Orthogonal Basis)，每一次它都会根据`randomVec`的值稍微倾斜。注意因为我们使用了一个随机向量来构造切线向量，我们没必要有一个恰好沿着几何体表面的TBN矩阵，也就是不需要逐顶点切线(和双切)向量。
接下来我们对每个核心样本进行迭代，将样本从切线空间变换到观察空间，将它们加到当前像素位置上，并将片段位置深度与储存在原始深度缓冲中的样本深度进行比较。我们来一步步讨论它：
```c++
float occlusion = 0.0;
for(int i = 0; i < kernelSize; ++i)
{
// 获取样本位置
vec3 sample = TBN * samples[i]; // 切线->观察空间
sample = fragPos + sample * radius;
[...]
}
```
这里的`kernelSize`和`radius`变量都可以用来调整效果；在这里我们分别保持他们的默认值为`64`和`1.0`。对于每一次迭代我们首先变换各自样本到观察空间。之后我们会加观察空间核心偏移样本到观察空间片段位置上；最后再用`radius`乘上偏移样本来增加(或减少)SSAO的有效取样半径。
接下来我们变换`sample`到屏幕空间，从而我们可以就像正在直接渲染它的位置到屏幕上一样取样`sample`的(线性)深度值。由于这个向量目前在观察空间，我们将首先使用`projection`矩阵uniform变换它到裁剪空间。
```c++
vec4 offset = vec4(sample, 1.0);
offset = projection * offset; // 观察->裁剪空间
offset.xyz /= offset.w; // 透视划分
offset.xyz = offset.xyz * 0.5 + 0.5; // 变换到0.0 - 1.0的值域
```
在变量被变换到裁剪空间之后，我们用`xyz`分量除以`w`分量进行透视划分。结果所得的标准化设备坐标之后变换到**[0.0, 1.0]**范围以便我们使用它们去取样深度纹理：
```c++
float sampleDepth = -texture(gPositionDepth, offset.xy).w;
```
我们使用`offset`向量的`x`和`y`分量采样线性深度纹理从而获取样本位置从观察者视角的深度值(第一个不被遮蔽的可见片段)。我们接下来检查样本的当前深度值是否大于存储的深度值，如果是的，添加到最终的贡献因子上。
```c++
occlusion += (sampleDepth >= sample.z ? 1.0 : 0.0);
```
这并没有完全结束，因为仍然还有一个小问题需要考虑。当检测一个靠近表面边缘的片段时，它将会考虑测试表面之下的表面的深度值；这些值将会(不正确地)音响遮蔽因子。我们可以通过引入一个范围检测从而解决这个问题，正如下图所示([John Chapman](http://john-chapman-graphics.blogspot.com/)的佛像)：
![](http://learnopengl.com/img/advanced-lighting/ssao_range_check.png)
我们引入一个范围测试从而保证我们只当被测深度值在取样半径内时影响遮蔽因子。将代码最后一行换成：
```c++
float rangeCheck = smoothstep(0.0, 1.0, radius / abs(fragPos.z - sampleDepth));
occlusion += (sampleDepth >= sample.z ? 1.0 : 0.0) * rangeCheck;
```
这里我们使用了GLSL的`smoothstep`函数，它非常光滑地在第一和第二个参数范围内插值了第三个参数。如果深度差因此最终取值在`radius`之间，它们的值将会光滑地根据下面这个曲线插值在0.0和1.0之间：
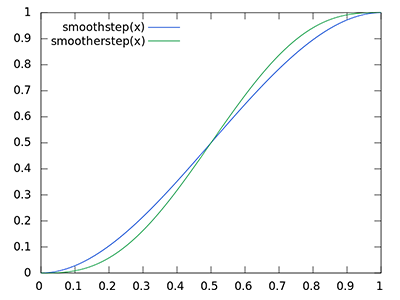
![](http://learnopengl.com/img/advanced-lighting/ssao_smoothstep.png)
如果我们使用一个在深度值在`radius`之外就突然移除遮蔽贡献的硬界限范围检测(Hard Cut-off Range Check)，我们将会在范围检测应用的地方看见一个明显的(很难看的)边缘。
最后一步，我们需要将遮蔽贡献根据核心的大小标准化，并输出结果。注意我们用1.0减去了遮蔽因子，以便直接使用遮蔽因子去缩放环境光照分量。
```c++
}
occlusion = 1.0 - (occlusion / kernelSize);
FragColor = occlusion;
```
下面这幅图展示了我们最喜欢的纳米装模型正在打盹的场景，环境遮蔽着色器产生了以下的纹理：
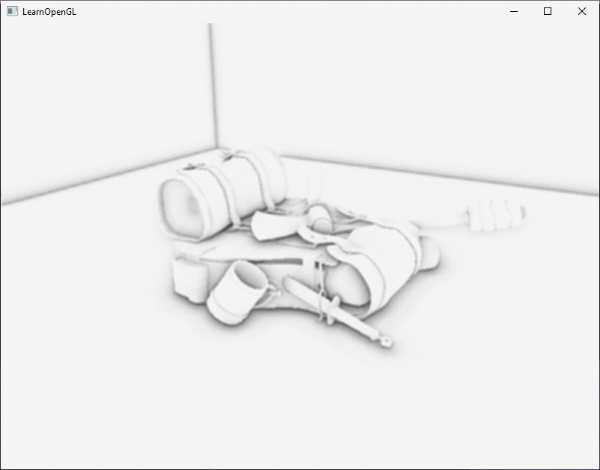
![](http://learnopengl.com/img/advanced-lighting/ssao_without_blur.png)
可见，环境遮蔽产生了非常强烈的深度感。仅仅通过环境遮蔽纹理我们就已经能清晰地看见模型一定躺在地板上而不是浮在空中。
现在的效果仍然看起来不是很完美，由于重复的噪声纹理再图中清晰可见。为了创建一个光滑的环境遮蔽结果，我们需要模糊环境遮蔽纹理。
## 环境遮蔽模糊
在SSAO阶段和光照阶段之间，我们想要进行模糊SSAO纹理的处理，所以我们又创建了一个帧缓冲对象来储存模糊结果。
```c++
GLuint ssaoBlurFBO, ssaoColorBufferBlur;
glGenFramebuffers(1, &ssaoBlurFBO);
glBindFramebuffer(GL_FRAMEBUFFER, ssaoBlurFBO);
glGenTextures(1, &ssaoColorBufferBlur);
glBindTexture(GL_TEXTURE_2D, ssaoColorBufferBlur);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RED, SCR_WIDTH, SCR_HEIGHT, 0, GL_RGB, GL_FLOAT, NULL);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, ssaoColorBufferBlur, 0);
```
由于平铺的随机向量纹理保持了一致的随机性，我们可以使用这一性质来创建一个简单的模糊着色器：
```c++
#version 330 core
in vec2 TexCoords;
out float fragColor;
uniform sampler2D ssaoInput;
void main() {
vec2 texelSize = 1.0 / vec2(textureSize(ssaoInput, 0));
float result = 0.0;
for (int x = -2; x < 2; ++x)
{
for (int y = -2; y < 2; ++y)
{
vec2 offset = vec2(float(x), float(y)) * texelSize;
result += texture(ssaoInput, TexCoords + offset).r;
}
}
fragColor = result / (4.0 * 4.0);
}
```
这里我们遍历了周围在-2.0和2.0之间的SSAO纹理单元(Texel)，采样与噪声纹理维度相同数量的SSAO纹理。我们通过使用返回`vec2`纹理维度的`textureSize`，根据纹理单元的真实大小偏移了每一个纹理坐标。我们平均所得的结果，获得一个简单但是有效的模糊效果：
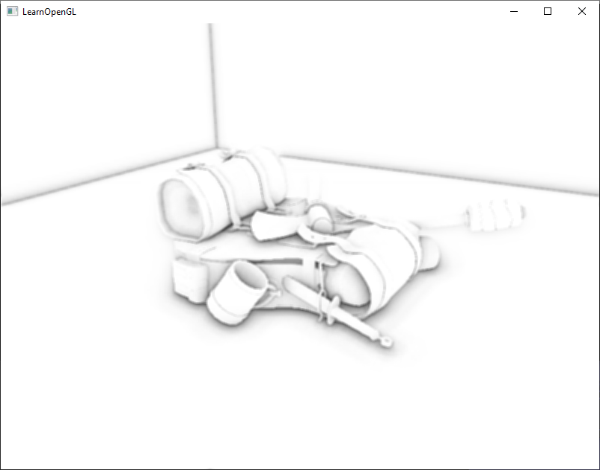
![](http://learnopengl.com/img/advanced-lighting/ssao.png)
这就完成了，一个包含逐片段环境遮蔽数据的纹理；在光照处理阶段中可以直接使用。
## 应用环境遮蔽
应用遮蔽因子到光照方程中极其简单：我们要做的只是将逐片段环境遮蔽因子乘到光照环境分量上。如果我们使用上个教程中的Blinn-Phong延迟光照着色器并做出一点修改，我们将会得到下面这个片段着色器：
```c++
#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
uniform sampler2D gPositionDepth;
uniform sampler2D gNormal;
uniform sampler2D gAlbedo;
uniform sampler2D ssao;
struct Light {
vec3 Position;
vec3 Color;
float Linear;
float Quadratic;
float Radius;
};
uniform Light light;
void main()
{
// 从G缓冲中提取数据
vec3 FragPos = texture(gPositionDepth, TexCoords).rgb;
vec3 Normal = texture(gNormal, TexCoords).rgb;
vec3 Diffuse = texture(gAlbedo, TexCoords).rgb;
float AmbientOcclusion = texture(ssao, TexCoords).r;
// Blinn-Phong (观察空间中)
vec3 ambient = vec3(0.3 * AmbientOcclusion); // 这里我们加上遮蔽因子
vec3 lighting = ambient;
vec3 viewDir = normalize(-FragPos); // Viewpos 为 (0.0.0)，在观察空间中
// 漫反射
vec3 lightDir = normalize(light.Position - FragPos);
vec3 diffuse = max(dot(Normal, lightDir), 0.0) * Diffuse * light.Color;
// 镜面
vec3 halfwayDir = normalize(lightDir + viewDir);
float spec = pow(max(dot(Normal, halfwayDir), 0.0), 8.0);
vec3 specular = light.Color * spec;
// 衰减
float dist = length(light.Position - FragPos);
float attenuation = 1.0 / (1.0 + light.Linear * dist + light.Quadratic * dist * dist);
diffuse *= attenuation;
specular *= attenuation;
lighting += diffuse + specular;
FragColor = vec4(lighting, 1.0);
}
```
(除了将其改到观察空间)对比于之前的光照实现，唯一的真正改动就是场景环境分量与`AmbientOcclusion`值的乘法。通过在场景中加入一个淡蓝色的点光源，我们将会得到下面这个结果：
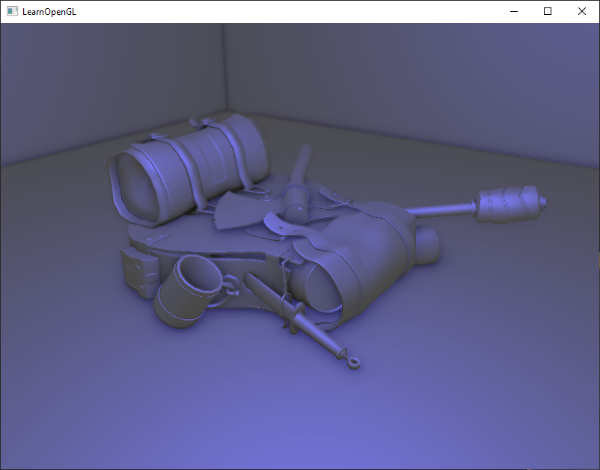
![](http://learnopengl.com/img/advanced-lighting/ssao_final.png)
你可以在[这里](http://learnopengl.com/code_viewer.php?code=advanced-lighting/ssao)找到完整的源代码，和以下着色器：
- 几何：[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/ssao_geometry&type=vertex)，[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/ssao_geometry&type=fragment)
- SSAO：[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/ssao&type=vertex)，[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/ssao&type=fragment)
- 模糊：[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/ssao&type=vertex)，[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/ssao_blur&type=fragment)
- 光照：[顶点](http://learnopengl.com/code_viewer.php?code=advanced-lighting/ssao&type=vertex)，[片段](http://learnopengl.com/code_viewer.php?code=advanced-lighting/ssao_lighting&type=fragment)
屏幕空间环境遮蔽是一个可高度自定义的效果，它的效果很大程度上依赖于我们根据场景类型调整它的参数。对所有类型的场景并不存在什么完美的参数组合方式。一些场景只在小半径情况下工作，又有些场景会需要更大的半径和更大的样本数量才能看起来更真实。当前这个演示用了64个样本，属于比较多的了，你可以调调更小的核心大小从而获得更好的结果。
一些你可以调整(比如说通过uniform)的参数：核心大小，半径和/或噪声核心的大小。你也可以提升最终的遮蔽值到一个用户定义的幂从而增加它的强度：
```c++
occlusion = 1.0 - (occlusion / kernelSize);
FragColor = pow(occlusion, power);
```
多试试不同的场景和不同的参数，来欣赏SSAO的可定制性。
尽管SSAO是一个很微小的效果，可能甚至不是很容易注意到，它在很大程度上增加了合适光照场景的真实性，它也绝对是一个在你工具箱中必备的技术。
## 附加资源
- [SSAO教程](http://john-chapman-graphics.blogspot.nl/2013/01/ssao-tutorial.html)：John Chapman优秀的SSAO教程；本教程很大一部分代码和技巧都是基于他的文章
- [了解你的SSAO效果](https://mtnphil.wordpress.com/2013/06/26/know-your-ssao-artifacts/)：关于提高SSAO特定效果的一篇很棒的文章
- [深度值重构SSAO](http://ogldev.atspace.co.uk/www/tutorial46/tutorial46.html)：OGLDev的一篇在SSAO之上的拓展教程，它讨论了通过仅仅深度值重构位置矢量，节省了存储开销巨大的位置矢量到G缓冲的过程